Study of Orifice Design on Oleo-Pneumatic Shock Absorber

Abstract

Aircraft oil-strut shock absorbers rely on orifice designs to control fluid flow and optimize damping performance. However, the complex nature of cavitating flows poses significant challenges in predicting the influence of orifice geometry on energy dissipation and system reliability. This study presents a comprehensive computational fluid dynamics (CFD) analysis of the effects of circular, rectangular, semicircular, and cutback orifice profiles on the internal flow characteristics and damping behavior of oleo-pneumatic shock absorbers. High-fidelity simulations reveal that the rectangular orifice generates higher damping pressures and velocity magnitude than those generated by others designs, while the semicircular shape reduces cavitation inception and exhibits a more gradual pressure recovery. Furthermore, the study highlights the importance of considering both geometric and thermodynamic factors in the design and analysis of cavitating flow systems, as liquid properties and vapor pressure significantly impact bubble growth and collapse behavior. Increasing the orifice length had a negligible impact on damping but moderately raised orifice velocities. This research provides valuable insights for optimizing shock absorber performance across a range of operating conditions, ultimately enhancing vehicle safety and passenger comfort.

1. Introduction

Shock absorbers are critical components in aircraft and automotive suspension systems. They are responsible for effectively attenuating vibrations and dissipating kinetic energy during landing or over rough terrain. The damping performance and dynamic stability is dictated by complex fluid flows within hydraulic control elements. Orifices play a pivotal role, creating pressure drops to develop controllable damping forces. However, excessive pressure reduction increases the risk of cavitation—the formation of vapor bubbles that can induce noise, component erosion, and performance loss if left uncontrolled. Hence, the characterization and optimization of the orifice shape to minimize cavitation risk is an enduring focus across industries.

Previous studies have examined simplified orifices and established correlations between geometric factors, like the length–diameter ratio, corner radii, and profile curvature, and incipient cavitation. Pearce and Lichtarowicz [1] presented experimental studies of the influence of geometry on the discharge coefficient for a range of submerged long orifice designs under both cavitating and non-cavitating conditions. Without cavitation, at high Reynolds numbers (10k), the discharge coefficient was found to remain constant for any given orifice. Under cavitating conditions, an alternative equation was presented that gives the discharge coefficient as a function of a cavitation parameter. Nurick et al. [2] presented a comprehensive study of a range of orifice designs with varying length and diameter (L/D) ratios, and different orifice inlet conditions. They observed that the orifice inlet has a significant effect on cavitation inception and the discharge coefficient. The onset of cavitation strongly depends on the sharpness of the orifice entrance, and even slight changes in the sharpness can have a significant impact on cavitation characteristics. At sufficient velocities, cavitation forms inside the orifice, which alters the pressure drops and flow resistance [3]. The unstable collapse of vapor cavities can also induce material pitting and erosion, decreasing the service life [4]. Hence, the orifice shape plays a critical role in controlling cavitation mechanisms, damping levels, and durability. Ref. [5] presented computational fluid dynamics (CFD) models to simulate cavitating flow through orifices and analyze the impact of key design parameters. The models were validated against published experimental data on discharge coefficients and cavitation inception. Ge et al. [6] investigated the influence of liquid properties on cavitation in a converging–diverging nozzle using a numerical approach. They found that the liquid viscosity and surface tension significantly impact the cavitation inception and the bubble growth rate. Higher viscosity and surface tension tend to suppress cavitation, while lower values promote more extensive cavitation regions. Ge et al. [7] extended the investigation of the effect of temperature on cavitation intensity and dynamics through experiments conducted at various cavitation numbers and temperatures. The results reveal that thermodynamic effects significantly influence cavitation extent at elevated temperatures (above 58 °C) in water, and three distinct regimes of instability, namely, sheet cavitation, periodic single-cloud cavitation, and aperiodic multi-cloud cavitation, were identified based on their temporal-spatial evolutions. Ge et al. [8] also investigated the optimum reacting conditions for enhancing cavitating treatment intensity. The results show that the cavitation length, thickness, and the transition between sheet and cloud cavitation regimes are influenced by a combination of the pressure drop, the inertial/viscous effects (controlled by the Reynolds number, Re), and the thermal effect, with the cavitation intensity peaking at a transition temperature of 58 °C. Apte et al. [9] evaluated turbulence models in simulating cavitating flow within a venturi nozzle. They compared the models’ ability to capture key features, like cavity shedding and the interaction between cavitation and turbulence, with experimental data. Their results showed that most turbulence models do not adequately simulate turbulence-related aspects such as Reynolds stress and turbulent kinetic energy. Li et al. [10] studied the flow field of an organ pipe cavitation nozzle using RNG $k-ϵ$, DES, and LES turbulence models, finding that the LES model most accurately predicts the periodic shedding of cavitating clouds, closely matching high-speed photographic observations. The LES model excels in simulating the dynamic behaviors and vortex structures within the nozzle, providing a superior depiction of cavitation phenomena compared to the RNG $k-ϵ$ and DES models, and offering valuable insights for the further simulation and analysis of cavitating jets. Although these works represent important developments in the study of cavitating flows and discharge coefficient, they were developed in the context of flow through pipes, not shock absorbers.

Early research by Milwitzky and Cook [11] presented a basic model with a single degree of freedom for shock absorber dynamics during landing impact. Currey [12] studied the correlation between energy dissipation and the physical attributes of the gas chamber in oleo-pneumatic landing gears. Thermodynamic models were developed to characterize the compression and expansion processes experienced by nitrogen gas during piston stroke motion. Daniels [13] presented a nonlinear model of an A-6 Intruder aircraft’s main landing gear, including effects like polytropic gas forces, velocity-squared damping, and stick-slip friction. The model was validated through simulations of both quasi-static and dynamic drop tests performed at NASA Langley Research Center, providing a verified methodology for comprehensive landing gear system modeling. More recently, Pecora [14] presented a numerical formulation to simulate oleo-pneumatic landing gear drop dynamics using a simplified four-state variable model that balances simplicity and accuracy. The proposed method captures relevant impact physics and compares well to experimental drop-test data for a reference landing gear. Alonso et al. [15] proposed a new method for analyzing the damping force of a twin-tube shock absorber that takes into account the compressibility of both the fluid and the chambers, and the effects of cavitation. The calculated damping force is compared to the ideal damping force, which assumes that no cavitation occurs. With growing computing capacity, transient multiphase flows in such complex geometries can be resolved using CFD techniques. Ding et al. [16] conducted computational fluid dynamics (CFD) simulations to calculate the discharge coefficient of square-edged orifices on shock absorbers and obtained a high level of consistency with experimental measurements. Their investigation revealed that the prevailing discharge coefficient estimation methods found in aircraft design manuals are inadequate, generating substantial discrepancies (17%) between estimated values and simulated results. They emphasized that the landing gear’s dynamic response is also highly influenced by the discharge coefficient. While CFD predictions closely match experimental data, the estimation method’s errors reached 30%. Bharath et al. [17] used CFD modeling to identify the parameters that influence the performance of shock absorbers. The results showed that the orifice area, the mass flow rate, the orifice thickness, and the pressure in the upper chamber have a significant impact on the discharge coefficient and consequently on the shock absorber’s behavior. Du et al. [18] performed oleo-pneumatic shock absorber simulations to analyze internal two-phase flow as compared with engineering estimations, giving a difference of 7% in damping force. The study analyzed the effect of varying orifice lengths and diameters on the pressure, temperature, velocity, and damping force inside the shock absorber. The key findings showed that the increased length reduces the maximum internal pressure, speed, and damping force. Increasing the orifice diameter significantly impacted the shock absorber’s performance, leading to a considerable reduction in the maximum pressure, flow rate, and oil damping force. Al-Shabab et al. [19] used Large Edge Simulations (LES) to investigate the internal flow in simplified shock absorbers with an open top surface. The turbulent behavior of the mixing layer was studied in detail. They found significant flow disturbances upstream of and through the orifice, leading to notable turbulence levels in those regions. They also highlighted concerns related to the low pressure near the orifice surface that could lead for cavitation bubbles.

Even though previous studies have investigated the internal flow in shock absorbers, there is a lack of comprehensive research exploring the impact of the orifice shape and dimensions on the multiphase flow dynamics and damping performance of shock absorbers. The present work aims to elucidate the complex interactions between the orifice geometry, cavitating flow dynamics, and damping performance of aircraft shock absorbers during drop-test conditions [11]. The specific objectives were as follows:

• To quantify the influence of the orifice shape and length-to-diameter ratio on the pressure drop, velocity distribution, and vapor formation using high-fidelity CFD analysis;
• To compare the discharge coefficients and damping loads of circular, rectangular, semicircular, and cutback orifice profiles during critical conditions, such as a drop test;
• To provide design guidelines for optimizing the orifice geometry based on target shock absorber performance metrics.

By achieving these objectives, this study provides novel insights into the complex flow physics and performance trade-offs associated with different orifice designs in shock absorbers. These findings have practical implications on the development of high-efficiency, reliable damping systems for aerospace and automotive applications, ultimately enhancing vehicle safety and passenger comfort.

2. Numerical Methodology

The present study used the open-source CFD software OpenFOAM V2212 to investigate the cavitating flow in shock absorber orifices. The compressible Unsteady Reynolds Averaged Navier–Stokes (URANS) equations were coupled with the volume of fluid (VOF) method for multiphase flow modeling. The k-omega Shear Stress Transport (SST) turbulence model was used. The set of governing equations for the conservation of the mixture mass, momentum, and energy are:

$$\frac{\partial {\rho }_m}{\partial t}+\nabla ·\left({\rho }_m{\mathbf{U}}_{\mathbf{m}}\right)=0,$$

(1)

$$\frac{\partial \left({\rho }_m{\mathbf{U}}_{\mathbf{m}}\right)}{\partial t}+\nabla ·\left(\rho {\mathbf{U}}_{\mathbf{m}}{\mathbf{U}}_{\mathbf{m}}\right)=-\nabla p_m+\nabla ·\left[{\mu }_m(\nabla {\mathbf{U}}_{\mathbf{m}}+\nabla {\mathbf{U}}_{\mathbf{m}}^T)\right]+{\rho }_m\mathbf{g}+\mathbf{F},$$

(2)

$$\frac{\partial \left(\rho E\right)}{\partial t}+\nabla ·\left[{\mathbf{U}}_{\mathbf{m}}(\rho E+p)\right]=\nabla ·[k\nabla T],$$

(3)

where the quantities denoted by the subscript m refer to the mixture, $\rho$ is the mixture density, ${\mathbf{U}}_{\mathbf{m}}$ is the velocity vector field of the mixture, p is the pressure, $\mu$ is the mixture dynamic viscosity, $\mathbf{g}$ is the gravitational acceleration, $\mathbf{F}$ represents the surface tension force, E is the total energy, k is the thermal conductivity, T is the temperature, $\alpha$ is the vapor volume fraction, $\dot{m}$ is the mass transfer rate due to cavitation, and ${\rho }_v$ is the vapor density. The mixture properties are defined by means of phase averaging applied to the mixture density ${\rho }_m={\rho }_l\alpha +{\rho }_v(1-\alpha )$ and viscosity ${\mu }_m={\mu }_l\alpha +{\mu }_v(1-\alpha )$, where the subscripts l and v are the liquid and gas, respectively. The liquid volume fraction is defined by $\alpha =V_l/(V_l+V_v)$, and the transport of the volume fraction is given by

$$\frac{\partial \alpha }{\partial t}+{\mathbf{U}}_m·\nabla \alpha =R(\frac{{\rho }_m}{{\rho }_l{\rho }_v}),$$

(4)

where R is the total mass transfer due to the condensation, computed by the cavitation model.

Based on the Rayleight–Plesset equation for spherical bubble dynamics, the Schnerr–Sauer cavitation model [20] defines the mass transfer by

$$R=\frac{{\rho }_v{\rho }_l}{{\rho }_m}\alpha (1-\alpha )\frac{3}{R_B}\sqrt{\frac{2|p-p_{sat}|}{3{\rho }_l}},$$

(5)

where $p_{sat}$ is the saturation pressure and the $R_B$ is the radius of the vapor bubble used to compute the ${\alpha }_v$ as

$${\alpha }_v=(1+{\alpha }_{nuc}-\alpha )=\frac{\frac{4}{3}\pi R_b^3{n}_b}{1+\frac{4}{3}\pi R_b^3{n}_b},$$

(6)

where $n_b$ is the nuclei concentration ($n_b=8.6\times {10}^7$ m⁻³) and the nucleation volume fraction, ${\alpha }_{nuc}$, is defined as:

$${\alpha }_{nuc}=\frac{\frac{\pi d_{nuc}^3{n}_b}{6}}{1+\frac{\pi d_{nuc}^3{n}_b}{6}},$$

(7)

where $d_{nuc}$ is the diameter of the nuclei ($d_{nuc}=2\times {10}^{-6}$ m).

To simulate the piston motion and compression of the gas chamber, dynamic mesh capabilities were utilized at the the bottom surface. The piston motion was specified based on experimental stroke profiles for the drop test [11]. As the piston moves over the stroke, the mesh becomes compressed, requiring dynamic mesh adaptation. This motion was handled using the velocity Laplacian solver. This enables transient modeling of the shock absorber behavior as the piston oscillates over multiple strokes under impact loading, capturing multiphase interactions and evolving flow fields.

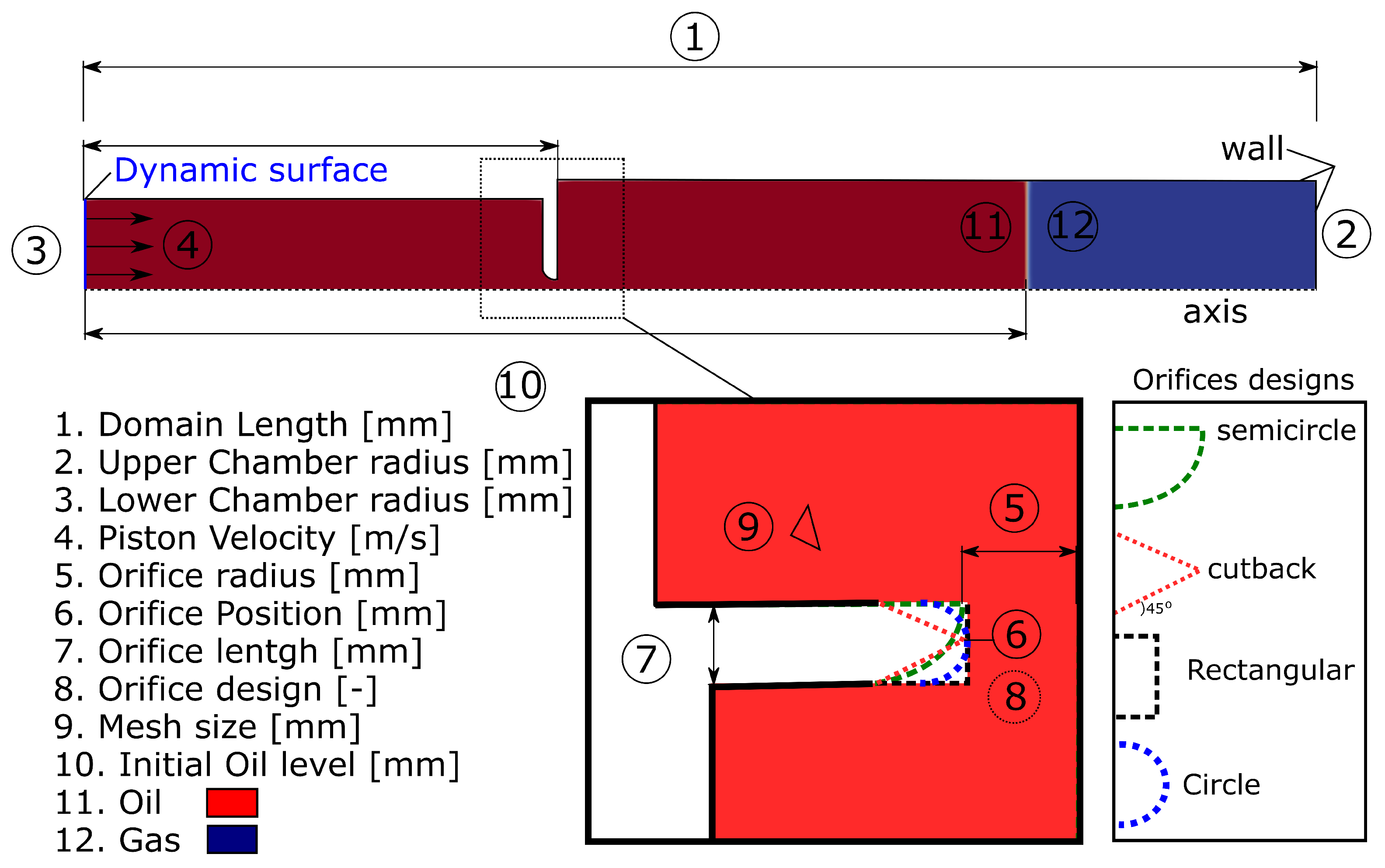
The axisymmetric shock absorber geometry is illustrated in Figure 1 and the baseline parameters are summarized in

Table 1. Parameters for the shock absorber simulation.

Parameter	Value
Parameter	value
Domain length [mm]	505
Upper Chamber radius [mm]	45.27
Lower Chamber radius [mm]	37.31
Piston velocity [m/s]	$179299.37t^5-82455.08t^4+14299.84t^3-1281.65t^2+62.22t-0.042$
Orifice radius [mm]	4.05
Orifice position [mm]	193.97
Orifice length [mm]	4.05–12.00
Oil level [mm]	386
Total time [s]	0.15
Saturation pressure [Pa]	2300
Initial pressure [Pa]	299,921.941
Initial fluid temperature [K]	300
Oil Density [kg/m3]	867
Gas Density [kg/m3]	1.205
Oil Kinematic Viscosity [m2/s]	1.35 × ${10}^{-2}$

. The geometry consisted of upper and lower cylinders connected by a central orifice plate. The orifice had a radius of 4.05 mm with the short length ranging from 4.05 to 12 mm. Four orifices designs were tested: semicircular, cutback, rectangular, and circular. The total chamber height was 505 mm with the oil filling up to a level of 386 mm initially. A piston velocity profile varying in time was specified to simulate the drop-test experiment [11]. The liquid density and saturation pressure were 867 kg/m³ and 2300 Pa, respectively. A total simulation time of 0.15 s was sufficient to capture the full piston stroke and damping behavior. The model incorporates real-gas behavior for the compressible gas chamber along with cavitation effects once the liquid pressure drops below saturation levels. This combination of geometry, operating conditions, and physics modeling enables the high-fidelity prediction of the interactive multiphase flows that dictate shock absorber performance.

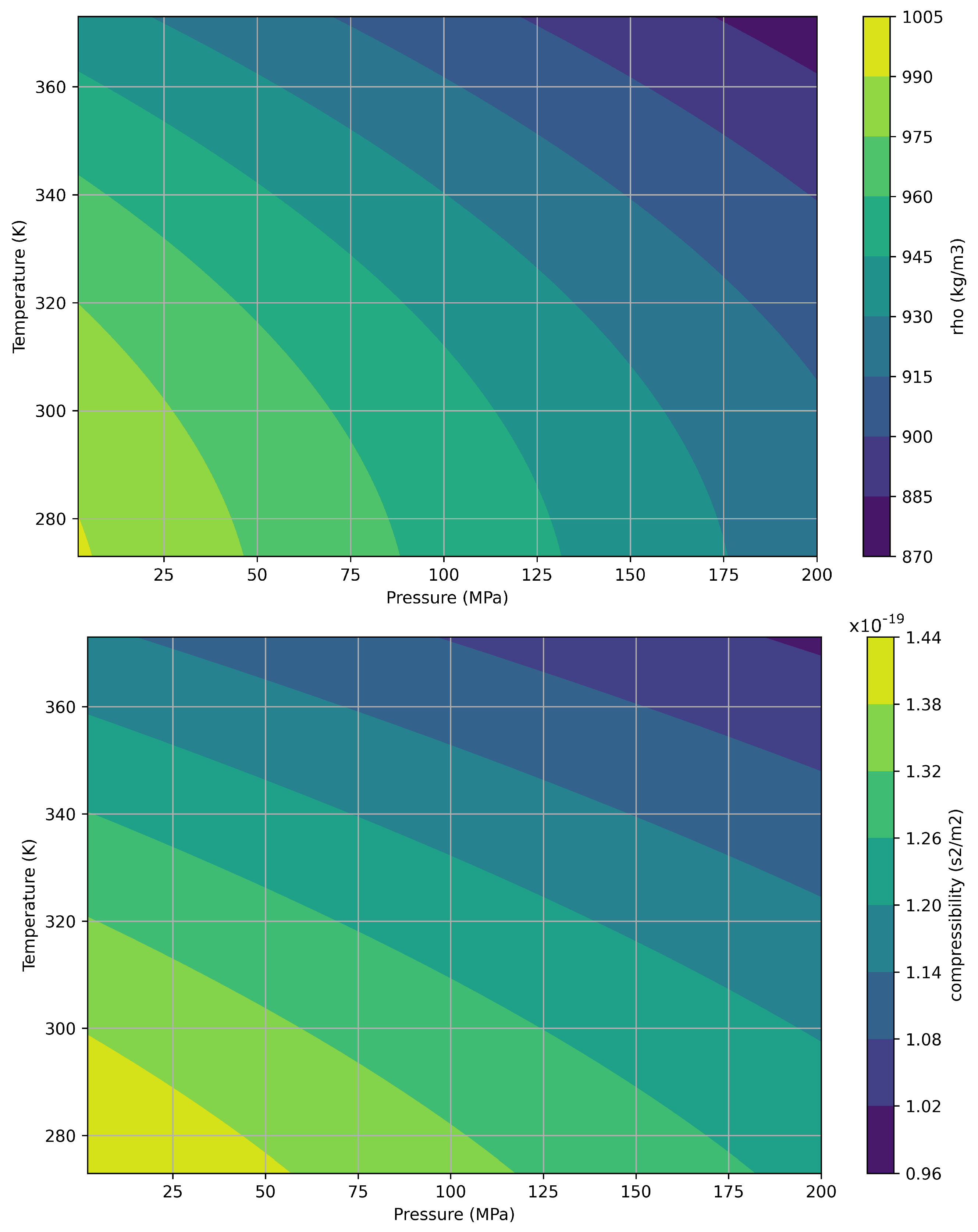
Modeling multiphase flows requires an appropriate equation of state to deal with thermodynamic equilibrium between phases, describing the state of matter as a function of the pressure, temperature, and molar volume. In this study, nitrogen was assumed to be a perfect gas governed by $\rho =p{\left(RT\right)}^{-1}$, in which $\rho$ is the density, p is the pressure, R is the universal gas constant, and T is the temperature. This simplification provided computational efficiency. For the oil, a polynomial function was used:

$$1/\rho =C_0+C_{1}T+C_2{T}^2-C_{3}p-C_{4}pT,$$

(8)

where $C_0$ is $1.278\times {10}^{-3}$, $C_1$ is $-2.105\times {10}^{-6}$, $C_2$ is $3.968\times {10}^{-9}$, $C_3$ is $4.377\times {10}^{-13}$, and $C_4$ is $-2.022\times {10}^{-16}$. This formulation aims to capture the phase transition complexities despite higher evaluation demands. The compressibility of the fluid is defined as:

$$\psi ={\left(\rho (C_3+C_{4}T)\right)}^2,$$

(9)

Figure 2 shows the result of the equation of state for density as a function of the pressure and temperature.

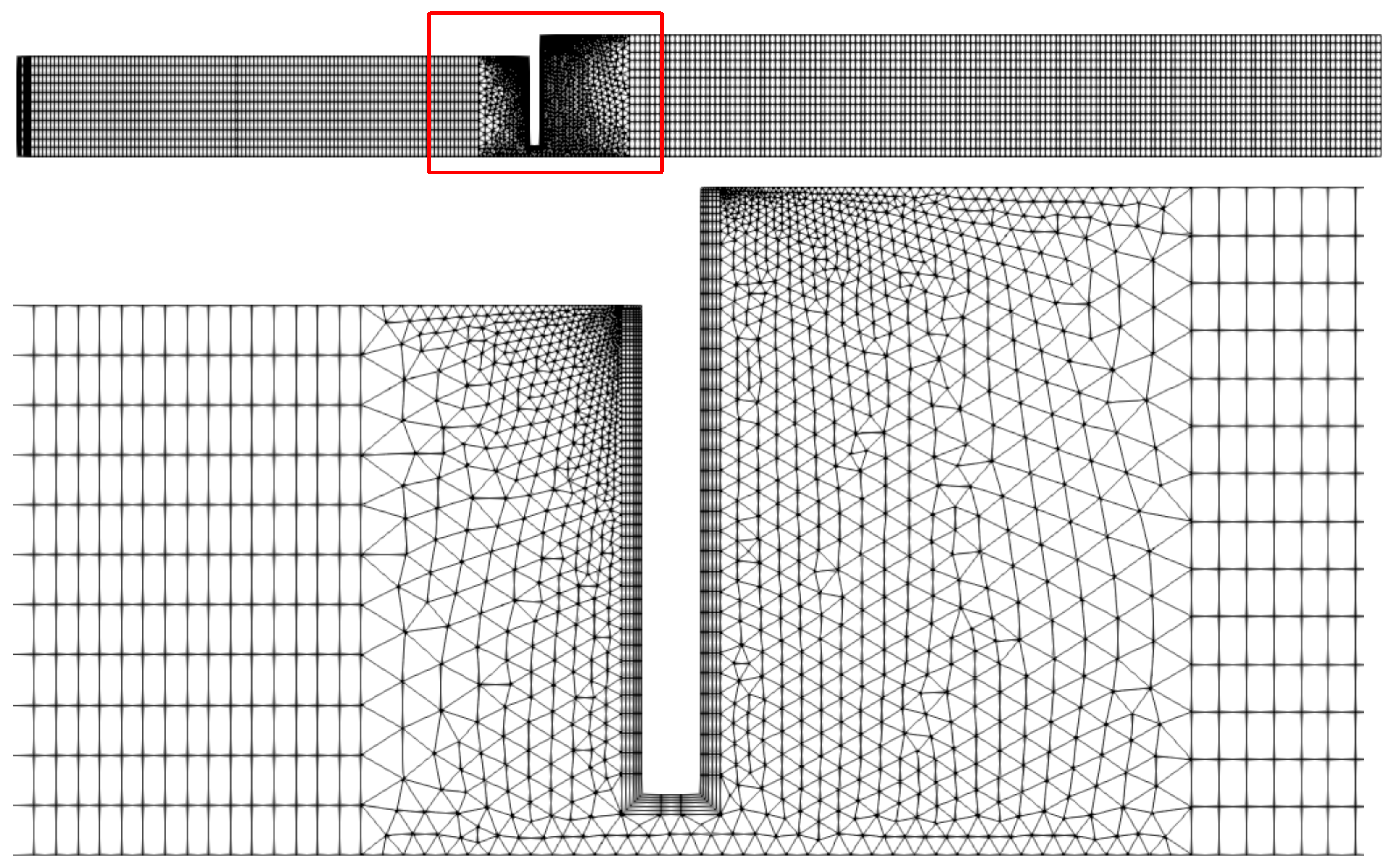
The mesh was generated using the Gmesh 4.13 software with refined cells near the orifice walls and interfaces to accurately capture the gradients. An unstructured hybrid mesh was used with prism layers near the walls. The shock absorber geometry was created using the axisymmetric domain of a cylinder with the orifice plate separating the lower and upper chambers. Four different orifice shapes were modeled: circular, semicircular, rectangular, and cutback.

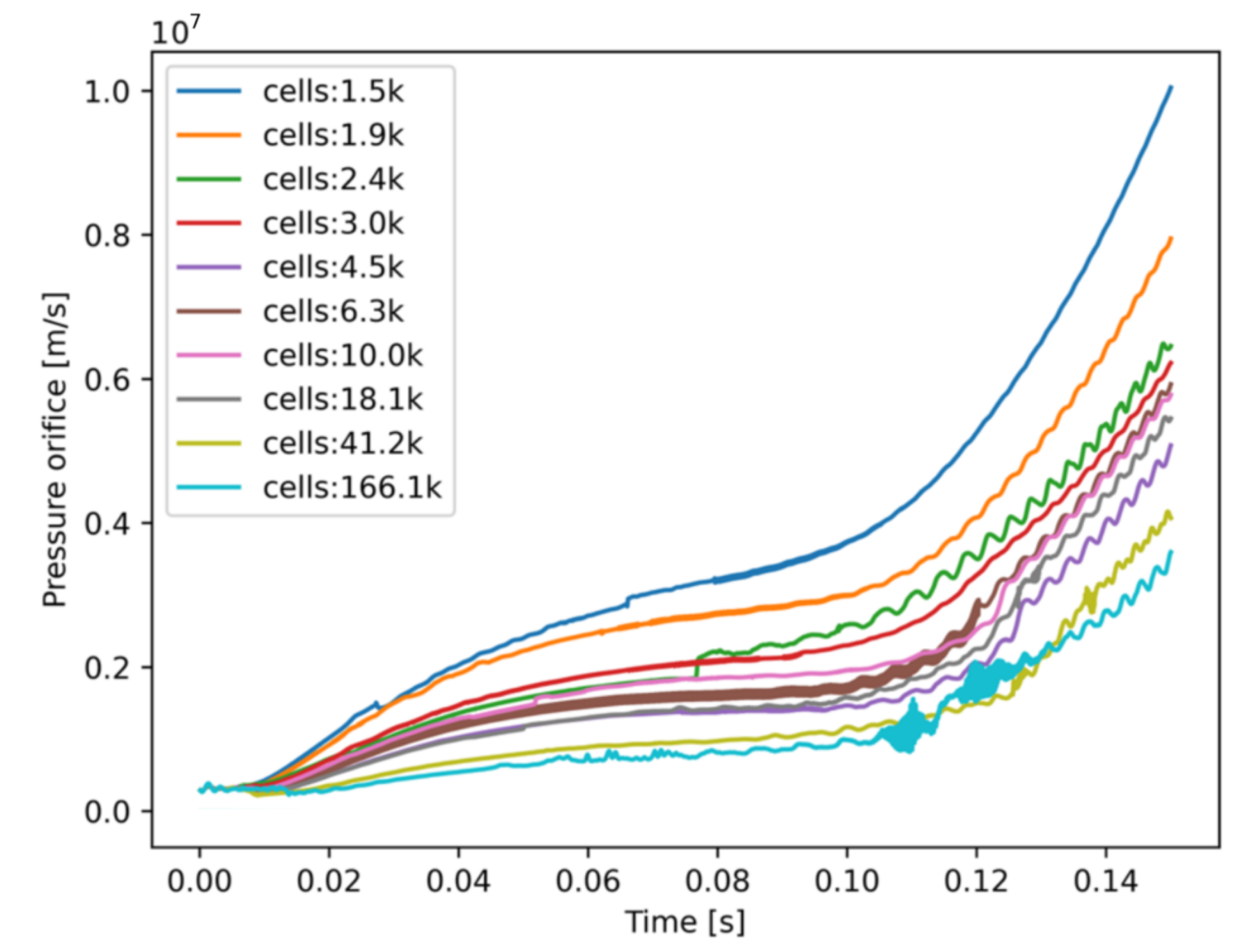
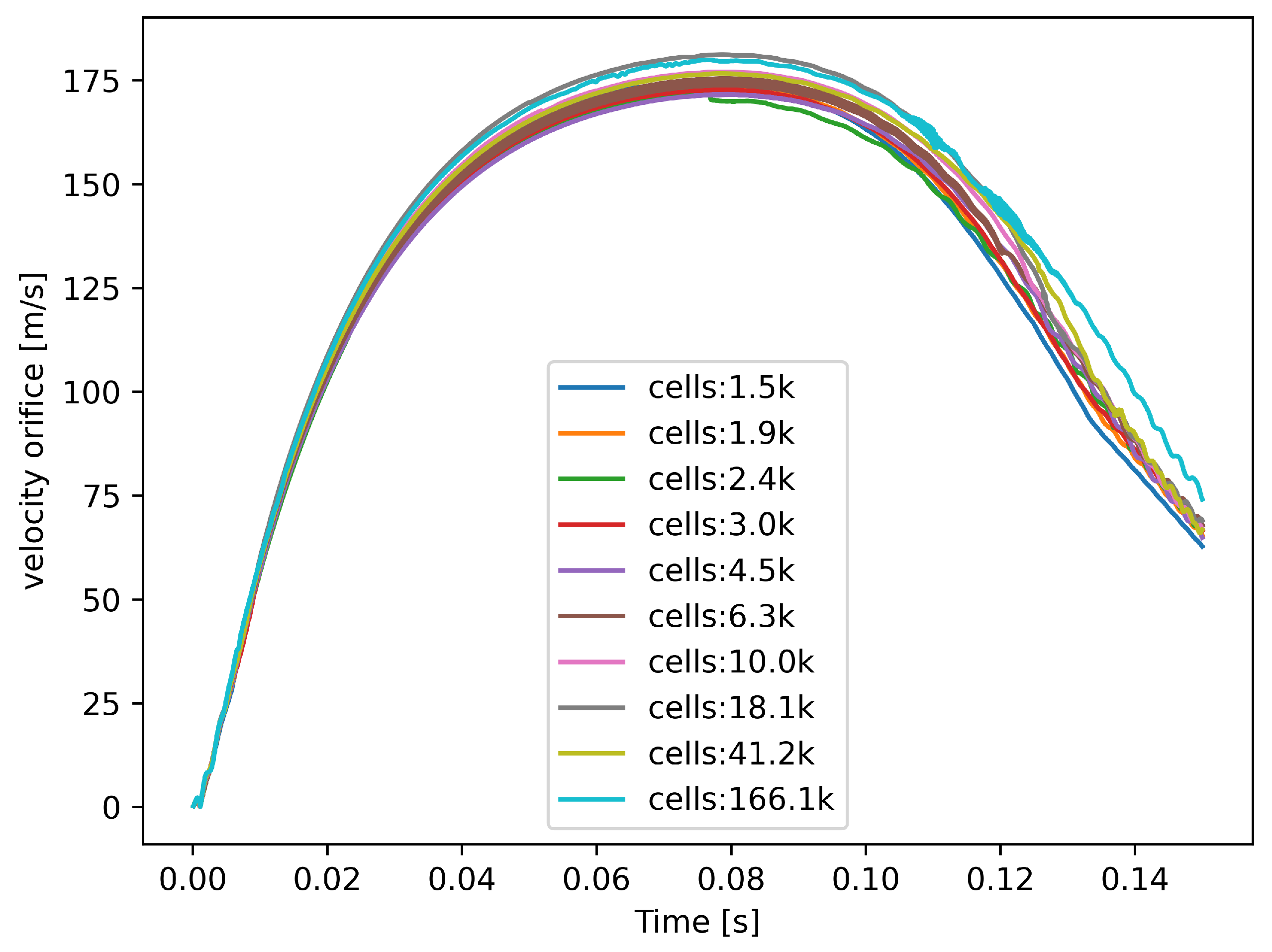
Due to the complex nature of the cavitating flow in shock absorber orifices and the challenges associated with obtaining accurate experimental measurements in such high-speed, multiphase conditions, the current study relied on a comprehensive computational approach to investigate the flow dynamics and performance characteristics. To ensure the accuracy and grid independence of the CFD results, a thorough grid refinement study was conducted. Ten progressively refined grids were generated, with cell counts ranging from 1.5 k to 166 k, to capture the flow dynamics throughout the domain and near the wall boundaries. Figure 3 presents the pressure and velocity magnitude profiles for a probe located at the orifice throughout the piston stroke for each mesh level. The velocity profile at the orifice exhibited minimal variation, particularly for grids with more than 41.2 k cells, indicating that the velocity field was well resolved even with relatively coarse meshes. However, the pressure profiles showed more pronounced differences between the grid levels. As the probe was located in the region with the highest pressure gradient, coarse meshes tended to overestimate the pressure and damp the natural fluctuations occurring at this location. Conversely, fine meshes captured the transient pressure instabilities when the velocity magnitude at the orifice reached its peak. Overall, the pressure trend and magnitude converged for meshes with more than 41.2 k cells, suggesting that further refinement would not have significantly improved the results, and the numerical error in the damping force predictions used for the shock absorber performance evaluation was minimized. Consequently, the grid with 41.2 k cells, shown in Figure 4, was selected for all subsequent simulations as it provided a good balance between accuracy and computational expense.

3. Results

3.1. Pressure Drop

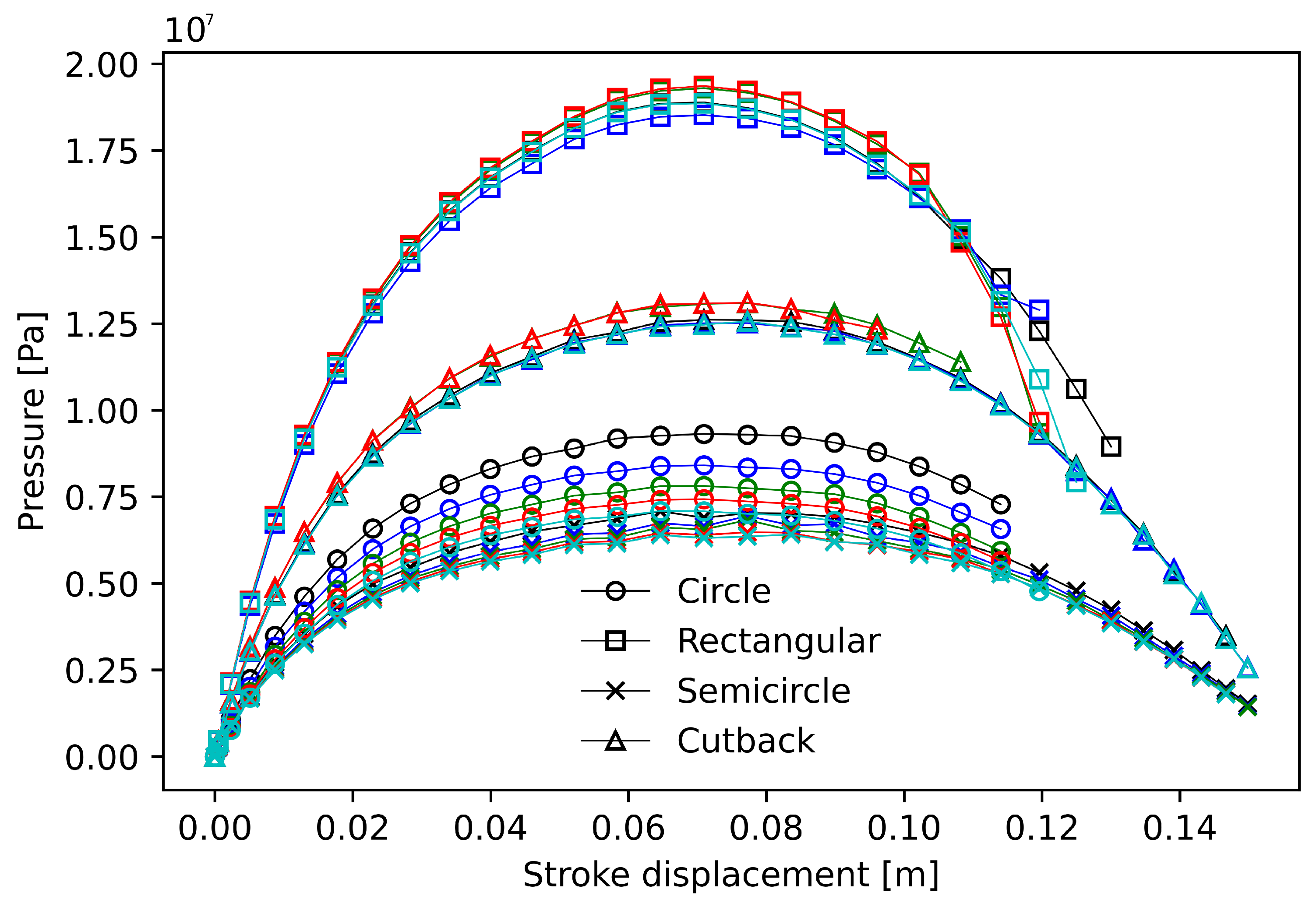
Figure 5 shows the pressure drop alongside the stroke displacement generated by the various length and diameter ($L/D$) designs and orifice shapes: circular, semicircular, rectangular, and cutback. The orifice shape is represented by different markers: circular ∘, semicircular x, rectangular □, and cutback △. The $L/D$ ratio is shown with different color schemes: black $L/D=0.5$, blue $L/D=0.69$, green $L/D=0.89$, red $L/D=1.08$, and cyan $L/D=1.28$. While the rectangular orifice produced the highest damping pressures overall, the semicircular shape experienced the lowest. The cutback orifice exhibited lower damping than the rectangular orifice, but higher dampening than the circular orifice. The higher pressure generation capacity of the rectangular profile can be beneficial for energy dissipation. However, this also translates into larger damping forces that may adversely affect component loading. The semicircular shape, while protecting from extreme loads, compromises the absorption capacity due to its lower flow resistance. The circular configuration seems to balance these competing factors more optimally. The orifice length produced an interesting behavior according to shape. On sharp edges (rectangular and cutback), the increase in the orifice length showed a marginal increase in pressure drop. Moreover, for the circular shapes, the pressure difference decreased, with the largest difference being with the circle orifice shape. The uncertainty analysis for the pressure drop predictions revealed varying levels of uncertainty across the different orifice designs and length-to-diameter ($L/D$) ratios. The rectangular shape exhibited the lowest deviation among all shapes, with an average deviation of 1.67% across all L/D ratios throughout the stroke. The cutback design followed with an average deviation of 2.17%, while the semicircle and circle designs showed higher uncertainties, with average deviations of 2.90% and 8.50%, respectively.

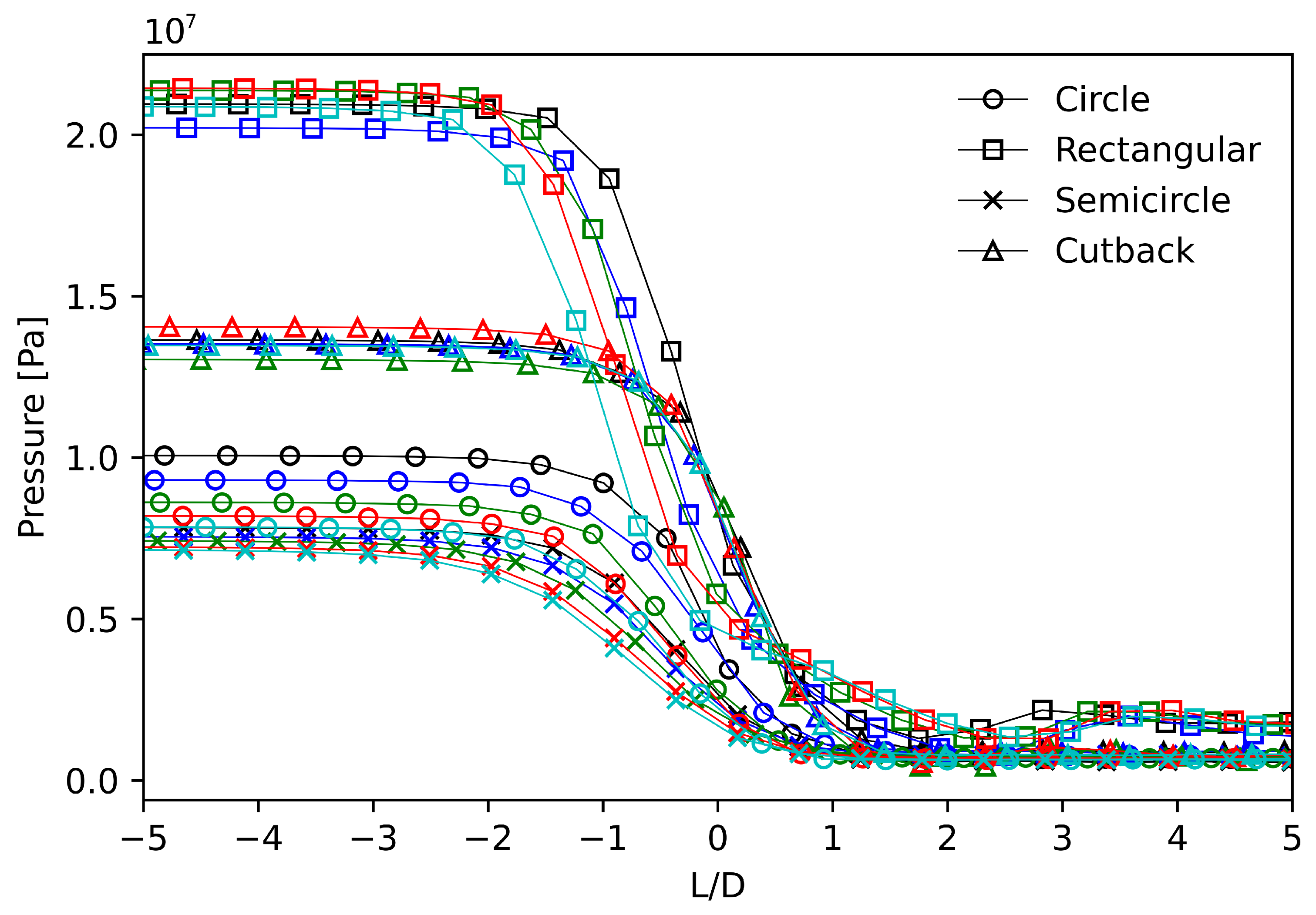
Figure 6 shows the pressure probes distributed axially at non-dimensional lengths from −5 to +5 $L/D$ alongside the pressure drops created across the various orifice designs and their downstream influence. The CFD results show the rectangular shape producing the highest overall pressure downstream of the orifice, followed by the cutback, circular, and semicircular shapes. The constrained flow and sharp corners of the rectangle also promoted the strongest pressure gradient across the orifice. Upstream, most designs sustained the same pressure level. When considering the variability of the pressure drop predictions with respect to the $L/D$ ratio, the rectangular orifice design exhibited the lowest average deviation of 6.1% across all L/D sizes. The semicircle design followed with an average deviation of 8.5%, while the circle and cutback designs showed a slightly higher variability, with average deviations of 9.09% and 10.99%, respectively.

3.2. Orifice Velocity

The orifice geometry significantly impacts velocities within shock absorbers by altering the flow accelerations and shear patterns. Sharper inlets and corners cause rapid velocity changes and flow separation that leads to recirculation and turbulence. Rounded profiles promote smoother accelerations but can still produce downstream separation and unstable shear layers. The turbulence enhances mixing but results in pressure fluctuations that can trigger cavitation. CFD studies reveal that circular orifices experience flow separation along the walls, while rectangular shapes maintain the attached flow. However, post-orifice velocities are higher for rectangles as the separated flows for circles reduce the effective area. The shear layer growth also differs with rectangular shapes displaying wider mixing zones. The optimized contouring of orifice walls can balance smooth acceleration with directed shear patterns to stabilize flows. Velocity field predictions provide insights into how the profile affects the flow stability, pressure drops, cavitation risk, and energy dissipation, which influence overall shock absorber performance.

The CFD study revealed substantial differences in the velocity magnitudes produced within the orifices depending on the shape profile, as shown in Figure 7. The rectangular geometry generated the highest velocities, frequently surpassing 125 m/s. Interestingly, for the rectangular design, an increase in the orifice length seemed to promote higher velocities at the orifice, while for the other designs, this parameter had a marginal effect on the velocity magnitude. The cutback shape experienced the lowest peak velocities due to the greater flow separation that occurred along its sharp walls. The circular designs exhibited similar trends. Although high velocities aid energy dissipation, which is desired in shock absorbers, excessively accelerated flows increase the risks of erosion and cavitation. Remarkably, the results showed low deviation in the orifice velocity with respect to the $L/D$ ratios. The rectangular orifice demonstrated an average variability of 2.14%, followed by the cutback with 1.46%. The round orifices presented exceptionally low uncertainty regarding the $L/D$ ratio, with 0.41% for the circle and 0.18% for the semicircle, indicating their robustness in maintaining consistent velocity profiles across different orifice lengths.

3.3. Cavitation Effect

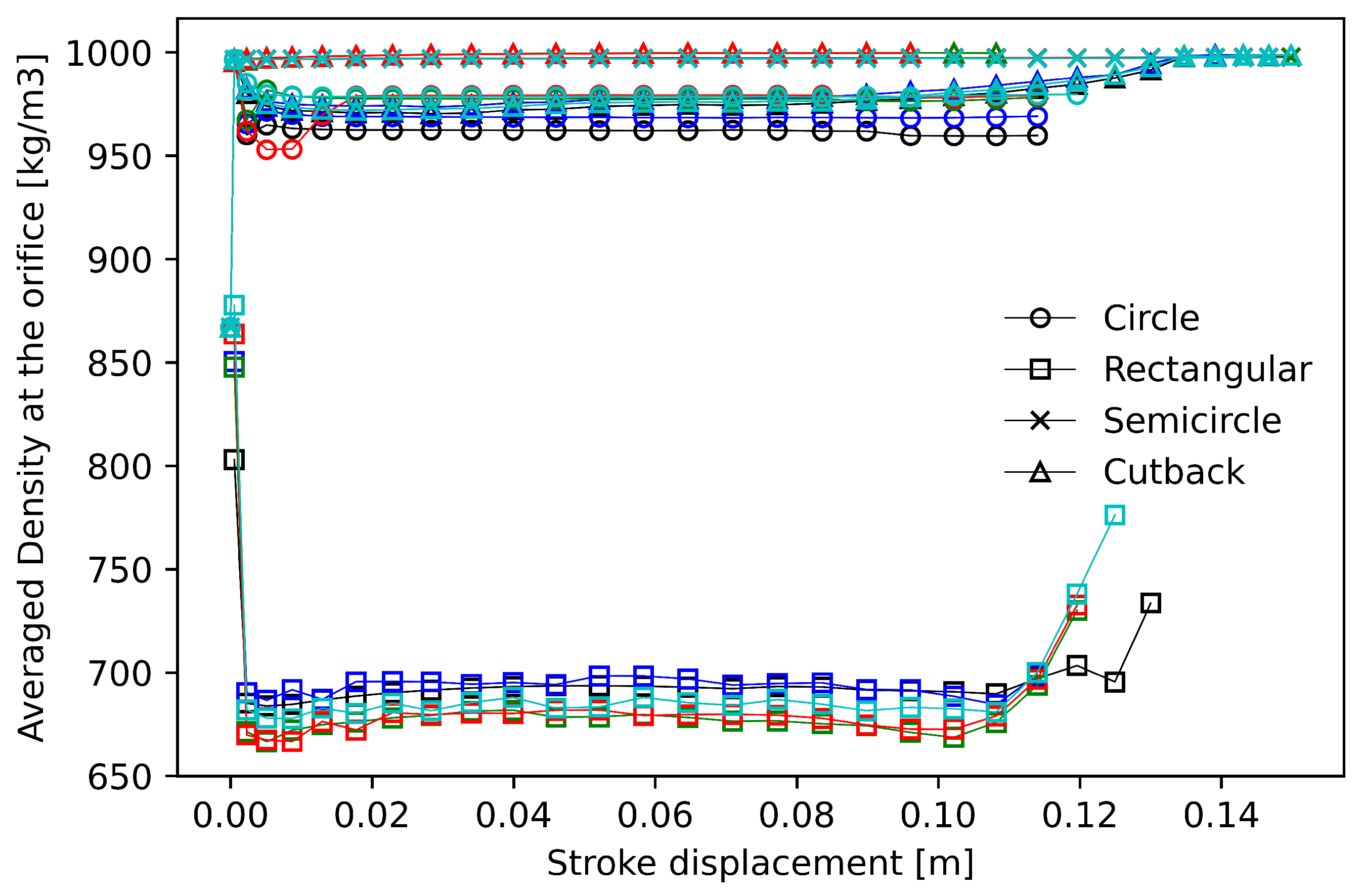
To investigate cavitation inception, a series of probes was strategically positioned between the orifice edge and the axis line. The change in the averaged density at this probe line as a function of the stroke position is depicted in Figure 8, highlighting the distinct cavitation behavior within the orifice contraction. The observed density drop for the rectangular, circular, and cutback shapes clearly indicates the onset of vapor formation at the orifice. However, the semicircular shape exhibited a constant density throughout the stroke, suggesting that cavitation did not initiate at the orifice but rather developed further downstream, as will be shown later. The sharp density drop associated with the rectangular orifice is particularly striking, considering that the probe line for this design was located in the middle of the orifice thickness, confirming that cavitation occurred at the orifice opening. The minimal differences observed between the circle and cutback designs suggest that the smooth contraction rate does not play a crucial role in this context. Moreover, increasing the orifice length appeared to have a limited influence on the cavitation behavior at the orifice.

Figure 9 shows a comparative study of the oil–gas interaction for the various orifice shapes at two significant time instances during the piston stroke. At t = 0.025 s, when the accelerated jet impinged on the top wall, the rectangular profile revealed strong disturbances caused by vapor structures shearing off and interacting with the separating boundary layer, indicating intense cavitation activity. Conversely, the jet emerging from the rounded circular shape exhibited minimal influence of cavitation occurring upstream, suggesting a well-regulated vapor growth and collapse process due to the smooth contours of the circular orifice. The cutback geometry displayed a moderate interaction between the persistent cavitating cloud and the mixing layer turbulence. The smoother semicircular passage, on the other hand, optimized the jet characteristics by effectively balancing localized cavitation and dissipation. At t = 0.05 s, the recirculation resulting from the interaction of the strong liquid jet emanating from the orifice with the induced flow from the top and side walls becomes apparent. This phenomenon not only caused the gas region to move from the top to the lower part of the upper chamber, but also re-energized the strong shear layer, underlining the complex and dynamic nature of the flow in the presence of cavitation.

3.4. Discharge Coefficient

The discharge coefficient ($Cd$) is a key parameter governing flow through shock absorber orifices. While classical $Cd$ equations developed for pipes can provide initial estimates, the complex geometries and unsteady multiphase flows in shock absorbers necessitate dedicated analyses. The contraction shape, abrupt flow accelerations, and transient vapor formations make shock absorbers $Cd$ difficult to theorize; although $Cd$ can be calculated from $Cd=Q/\left(A\sqrt{(2\Delta P/\rho )}\right)$, where $\Delta P$ is the pressure drop across the orifice, Q is the volumetric flow rate, A is the effective area, and $\rho$ is density at the orifice. Open channel theories often assume a steady, incompressible flow with slow area changes, whereas shock absorbers experience rapidly changing passages, densities, and back pressures. Hence, CFD modeling is better suited to capture the unsteadiness and compressibility effects that influence $Cd$.

Table 2. Time-averaged discharge coefficients for various orifice shapes across length–diameter ($L/D$) ratios compared to theoretical values from Dixon [21].

$\mathit{L}/\mathit{D}$	Rectangular	Circle	Semi Circle	Cutback	Theory [21]
0.5	0.66	0.94	0.95	0.85	0.65
0.69	0.64	0.95	0.94	0.94	0.68
0.89	0.62	0.95	0.95	0.98	0.71
1.08	0.62	0.95	0.96	0.93	0.77
1.28	0.62	0.95	0.96	0.94	0.78

shows a comparison of the averaged discharge coefficient across various orifice shapes and $L/D$ ratios. As the piston velocity of the drop test is time dependent, $Cd$ was averaged in time. The present work is compared to the engineering formulation of Dixon et al. [21]: for $L/D$ < 1: $C_d=0.61+0.16{(L/D)}^2$ and for 1 < $L/D$ < 2: $C_d=0.73+0.040(L/D)$. Dixon et al. [21] highlighted that, over the range of $L/D$ values from 0 to 2, the discharge coefficient was observed to markedly increase from 0.61 up to 0.81. This was, according to them, due to mitigated resistance resulting from a diffuser-induced improvement in flow reattachment and pressure buildup. The circular and semicircular orifice designs exhibited the highest $Cd$ values, consistently ranging from 0.94 to 0.96 across all $L/D$ ratios. These values are significantly higher than the theoretical predictions, suggesting that the smooth entry geometry and the diffuser effect at higher $L/D$ ratios contribute to enhanced flow efficiency. The cutback design also showed relatively high $Cd$ values, ranging from 0.85 to 0.98, with a peak at $L/D$ = 0.89. In contrast, the rectangular orifice design exhibited the lowest $Cd$ values, ranging from 0.62 to 0.66, which are closer to the theoretical predictions. The lower $Cd$ values for the rectangular design could be attributed to flow instabilities at lower $L/D$ ratios and the sensitivity to entry geometry. Interestingly, the rectangular design showed a slight decrease in $Cd$ with an increasing $L/D$ ratio, whereas the other designs maintained relatively consistent values. This suggests that the rectangular geometry may be more susceptible to flow separation and more influenced by the pressure and density drop at the orifice, as seen previously in Figure 6 and Figure 8, respectively. Overall, the results highlight the significant influence of the orifice shape and $L/D$ ratio on the discharge coefficient, with the circular and semicircular designs demonstrating superior performance compared to the rectangular design. Dixon et al. [21] also suggested that small changes in the geometry at the entry, i.e., rounding or chamfering, can mitigate the flow separation, generating a higher $Cd$ and potentially eliminating the increase in $Cd$ with length, as observed in engineering formulations.

3.5. Conclusions

This study presents a comprehensive CFD analysis of the influence of orifice design on the internal cavitating flow and energy dissipation in oleo-pneumatic shock absorbers. The investigation focused on the effects of orifice shape (circular, rectangular, semicircle, and cutback) and the length-to-diameter ($L/D$) ratio on the pressure drop, velocity distribution, cavitation inception, and discharge coefficients. The key findings are as follows:

• The rectangular orifice design exhibited the highest damping pressure drop and the steepest pressure gradient along the orifice length, making it favorable for energy dissipation;
• The cutback and rectangular geometries demonstrated early cavitation inception, while the circular shapes resisted initial vapor formation, highlighting the strong influence of the orifice entrance sharpness on the cavitation characteristics;
• The semicircular profile achieved a balance between smooth flow and controlled cavitation, optimizing the operating range;
• When examining the impact of $L/D$ variation on the results, we observed a moderate level of difference across all the designs investigated. Notably, the pressure drop across the rectangular orifice exhibited the most significant variation, reaching up to 10%;
• The discharge coefficient was significantly affected by the orifice shape and $L/D$ ratio, with the circular and semicircular designs showing superior performance compared to the rectangular design.

This study highlights the importance of orifice shape and $L/D$ ratios in the design and optimization of shock absorbers, emphasizing the use of rounded or chamfered orifices to minimize cavitation and optimize $L/D$ ratios for balanced damping and cavitation control. The findings suggest that circular or semicircular designs are optimal for enhancing energy dissipation and flow efficiency. Validating these results through experimental research will refine design guidelines, enhancing the performance, safety, and durability of aerospace and automotive shock absorbers. Future research should broaden the scope to include diverse operating conditions and innovative orifice designs, and integrate CFD with structural simulations to deepen the understanding of shock absorber dynamics.