Sill Role Effect on the Flow Characteristics (Experimental and Regression Model Analytical)
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Equipment
2.2. Dimensional Analysis
2.3. Statistical Indicators
3. Results and Discussion
3.1. Energy Dissipation of Gate without Sill
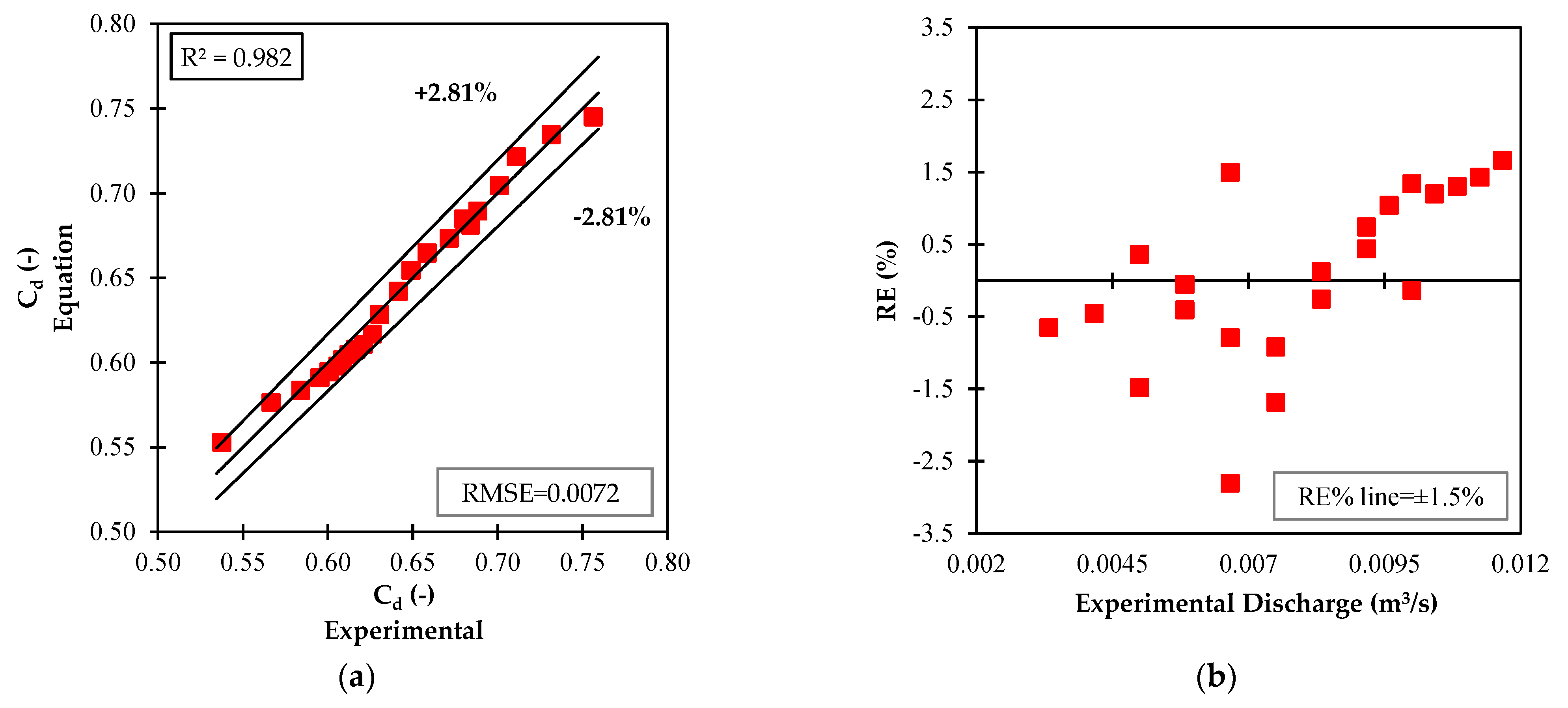
3.2. Cd without Sill
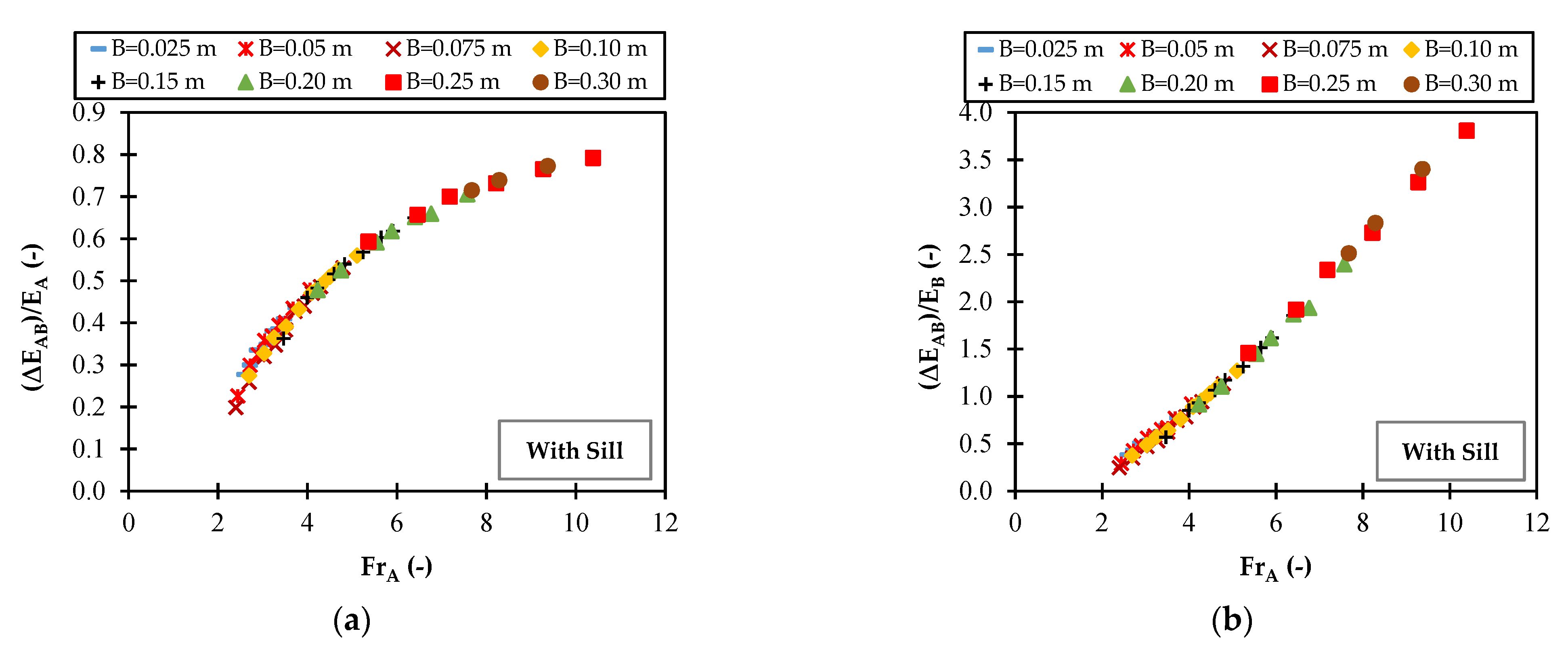
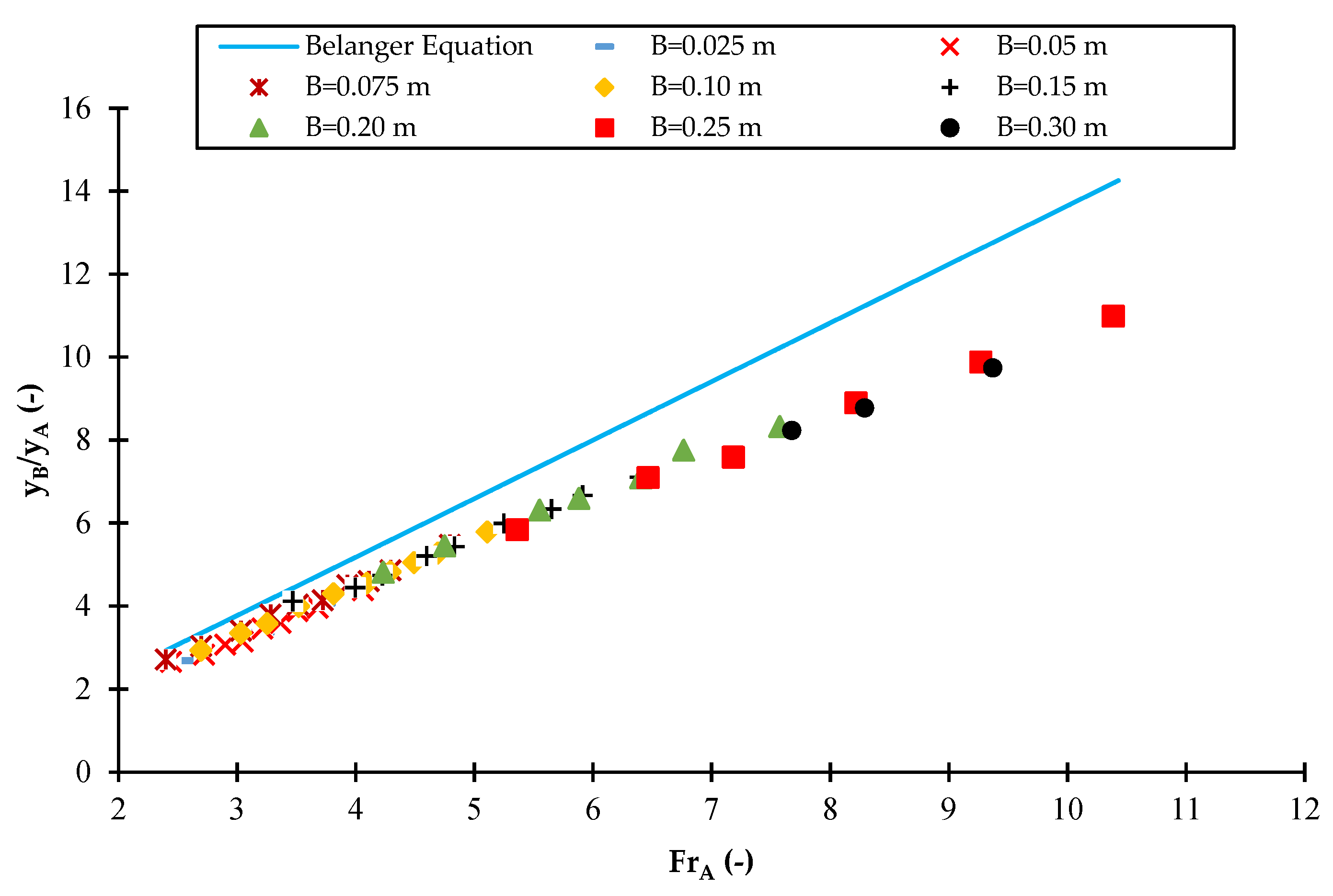
3.3. Energy Dissipation of the Gate with Sill
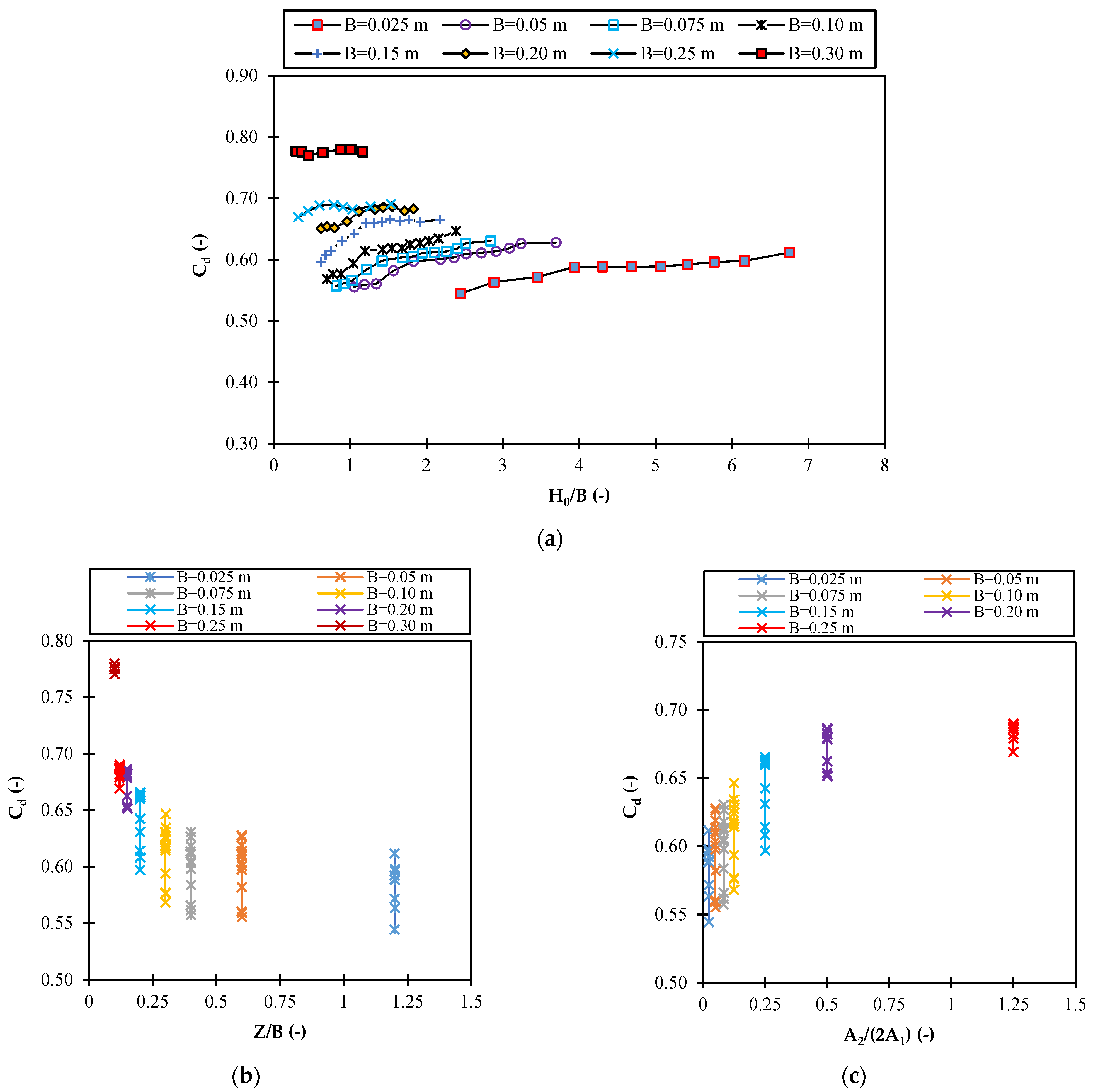
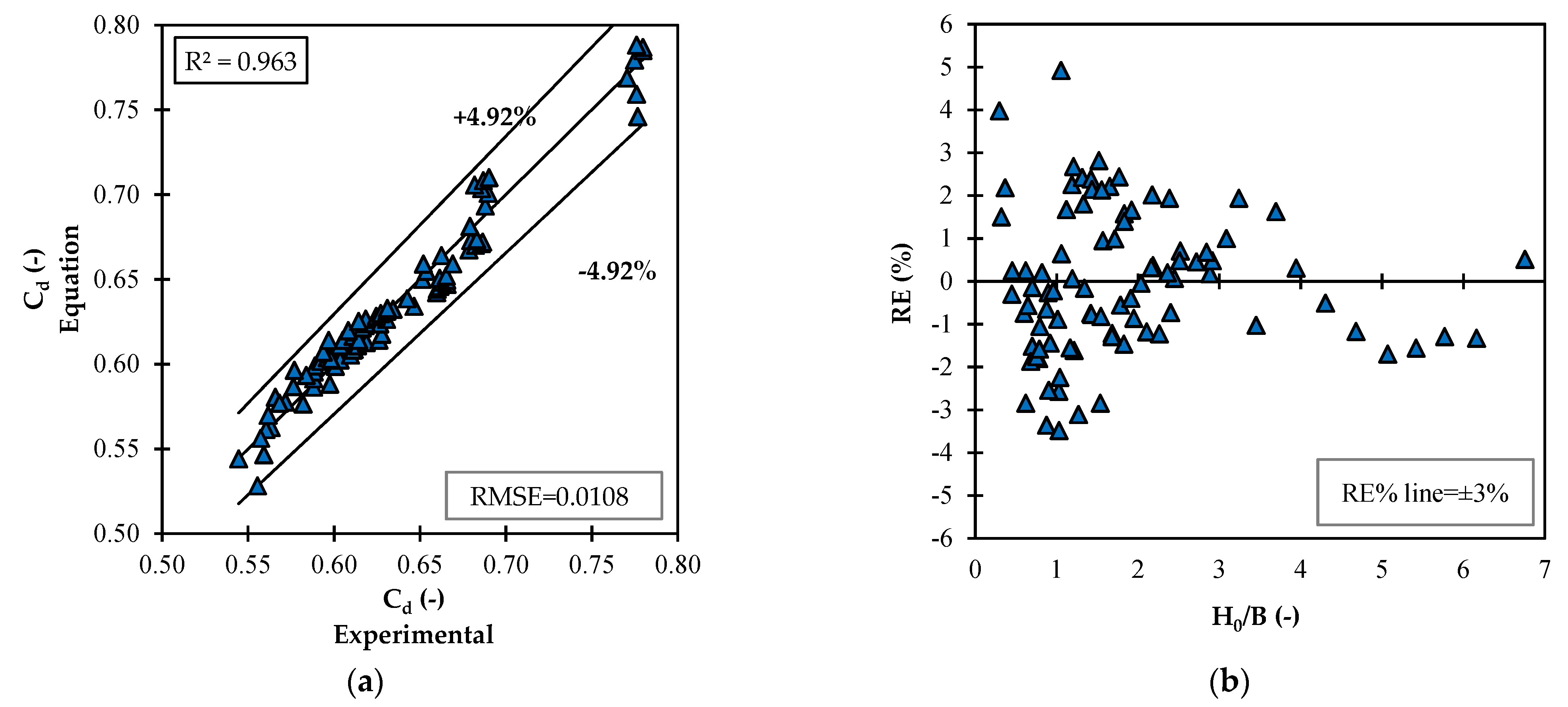
3.4. Cd with Sill
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Negm, A.M.; Alhamid, A.A.; El-Saiad, A.A. Submerged flow below sluice gate with sill. In Proceedings of the International Conference on Hydro-Science and Engineering Hydro-Science and Engineering ICHE98, Berlin, Germany, 31 August–3 September 1998; University of Mississippi: Oxford, MS, USA, 1998. Advances in Hydro-Science and Engineering. Volume 3. [Google Scholar]
- Henry, H.R. Discussion on Diffusion of submerged jets, by Albertson, M.L. et al. Trans. Am. Soc. Civ. Eng. 1950, 115, 687. [Google Scholar]
- Rajaratnam, N.; Subramanya, K. Flow Equation for the Sluice Gate. J. Irrig. Drain. Div. 1967, 93, 167–186. [Google Scholar] [CrossRef]
- Rajaratnam, N. Free Flow Immediately Below Sluice Gates. J. Hydraul. Div. 1977, 103, 345–351. [Google Scholar] [CrossRef]
- Swamee, P.K. Sluice Gate Discharge Equations. J. Irrig. Drain. Eng. 1992, 118, 56–60. [Google Scholar] [CrossRef]
- Shivapur, A.V.; Shesha Prakash, M.N. Inclined Sluice Gate for Flow Measurement. ISH J. Hydraul. Eng. 2005, 11, 46–56. [Google Scholar] [CrossRef]
- Nasehi Oskuyi, N.; Salmasi, F. Vertical Sluice Gate Discharge Coefficient. J. Civ. Eng. Urban. 2012, 2, 108–114. [Google Scholar]
- Daneshfaraz, R.; Ghahramanzadeh, A.; Ghaderi, A.; Joudi, A.R.; Abraham, J. Investigation of the Effect of Edge Shape on Characteristics of Flow Under Vertical Gates. J. Am. Water Work. Assoc. 2016, 108, E425–E432. [Google Scholar] [CrossRef]
- Salmasi, F.; Nouri, M.; Sihag, P.; Abraham, J. Application of SVM, ANN, GRNN, RF, GP and RT Models for Predicting Discharge Coefficients of Oblique Sluice Gates Using Experimental Data. Water Supply 2021, 21, 232–248. [Google Scholar] [CrossRef]
- Salmasi, F.; Abraham, J. Expert System for Determining Discharge Coefficients for Inclined Slide Gates Using Genetic Programming. J. Irrig. Drain. Eng. 2020, 146, 06020013. [Google Scholar] [CrossRef]
- Alhamid, A.A. Coefficient of Discharge for Free Flow Sluice Gates. J. King Saud Univ.-Eng. Sci. 1999, 11, 33–47. [Google Scholar] [CrossRef]
- Salmasi, F.; Norouzi Sarkarabad, R. Investigation of different geometric shapes of sills on discharge coefficient of vertical sluice gate. Amirkabir J. Civ. Eng. 2018, 52, 2. [Google Scholar]
- Karami, S.; Heidari, M.M.; Adib Rad, M.H. Investigation of Free Flow Under the Sluice Gate with the Sill Using Flow-3D Model. Iran. J. Sci. Technol. Trans. Civ. Eng. 2020, 44, 317–324. [Google Scholar] [CrossRef]
- Salmasi, F.; Abraham, J. Prediction of discharge coefficients for sluice gates equipped with different geometric sills under the gate using multiple non-linear regression (MNLR). J. Hydrol. 2020, 597, 125728. [Google Scholar] [CrossRef]
- Ghorbani, M.A.; Salmasi, F.; Saggi, M.K.; Bhatia, A.S.; Kahya, E.; Norouzi, R. Deep learning under H2O framework. A novel approach for quantitative analysis of discharge coefficient in sluice gates. J. Hydroinformatics 2020, 22, 1603–1619. [Google Scholar] [CrossRef]
- Lauria, A.; Calomino, F.; Alfonsi, G.; D’Ippolito, A. Discharge Coefficients for Sluice Gates Set in Weirs at Different Upstream Wall Inclinations. Water 2020, 12, 245. [Google Scholar] [CrossRef]
- Abbaspour, A.; Hosseinzadeh Dalir, A.; Farsadizadeh, D.; Sadraddini, A.A. Effect of Sinusoidal Corrugated Bed on Hydraulic Jump Characteristics. J. Hydro-Environ. Res. 2009, 3, 109–117. [Google Scholar] [CrossRef]
- Murzyn, F.; Chanson, H. Experimental assessment of scale effects affecting two-phase flow properties in hydraulic jumps. Exp. Fluids 2008, 45, 513–521. [Google Scholar] [CrossRef]
- Nasrabadi, M.; Mehri, Y.; Ghassemi, A.; Omid, M.H. Predicting Submerged Hydraulic Jump Characteristics Using Machine Learning Methods. Water Supply 2021, 21, 4180–4194. [Google Scholar] [CrossRef]
- Chow, V.T. Open-Channel Hydraulics; McGraw-Hill Book Co.: New York, NY, USA, 1959. [Google Scholar]
- Watts, F.J.; Simons, D.B.; Richardson, E.V. Variation of α and β values in Lined Open Channels. J. Hydraul. Div. Am. Soc. Civ. Eng. 1967, 93, 217–234, (see also Discussions: Vol. 94, 1968, HY3, pp. 834–837; HY6, pp. 1560–1564; and vol. 95, 1969, HY3, p. 1059). [Google Scholar] [CrossRef]
- Temple, D.M. Velocity Distribution Coefficients for Grass-lined Channels. J. Hydraul. Eng. Am. Soc. Civ. Eng. 1986, 12, 193–205. [Google Scholar] [CrossRef]
- Henderson, F.M. Open Channel Flow; MacMillan Publishing Co.: New York, NY, USA, 1966. [Google Scholar]
- Chaudhry, M.H. Open Channel Flow, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Belanger, J.B.C.J. Essai sur la solution numerique de quelques problemes relatifs au movement permanent des eaux courantes. In Test on the Numerical Solution of Some Problems Relating to the Permanent Movement of Running Waters; Kessinger Publishing: Whitefish, MT, USA, 1828. (In French) [Google Scholar]
- Hager, W.H. Underflow of Standard Sluice Gate. Exp. Fluids 1999, 27, 339–350. [Google Scholar] [CrossRef]
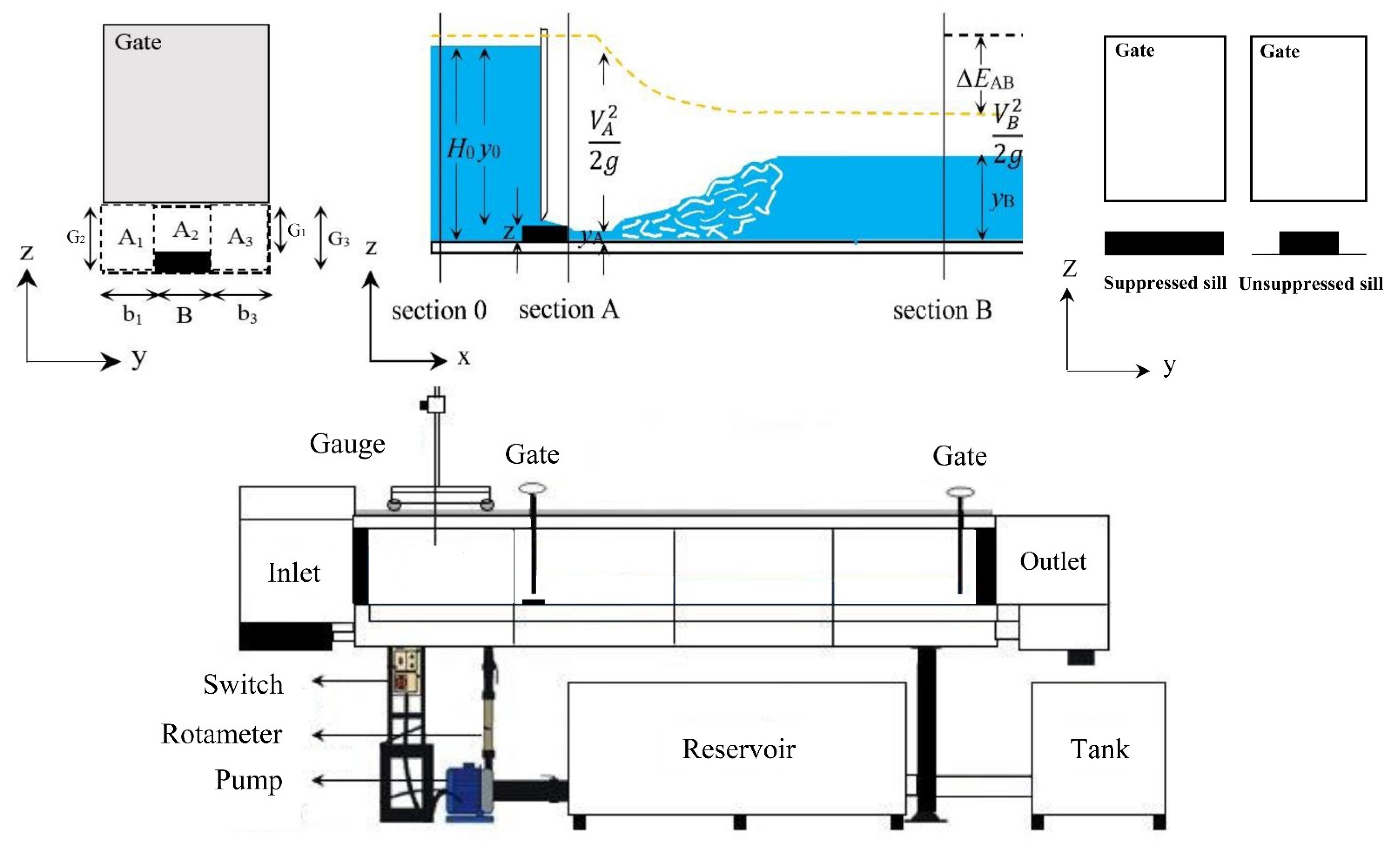






| Gate Openings (m) | |||||
|---|---|---|---|---|---|
| 0.01 | 0.02 | 0.04 | |||
| q (m3/s·m) | R (kg/m) | q (m3/s·m) | R (kg/m) | q (m3/s·m) | R (kg/m) |
| 0.0111 | 7.77 | 0.0167 | 1.96 | 0.0278 | 0.21 |
| 0.0139 | 17.53 | 0.0194 | 4.02 | 0.0306 | 0.49 |
| 0.0167 | 35.52 | 0.0222 | 7.36 | 0.0319 | 0.69 |
| 0.0194 | 59.62 | 0.025 | 11.90 | 0.0333 | 0.93 |
| 0.0222 | 89.92 | 0.0278 | 17.58 | 0.0347 | 1.27 |
| - | - | 0.0306 | 24.78 | 0.0361 | 1.61 |
| - | - | 0.0333 | 35.61 | 0.0375 | 1.96 |
| - | - | - | - | 0.0389 | 2.36 |
| - | - | - | - | 0.0417 | 3.58 |
| Q (L/min) | Sill widths (m) | |||||||
| 0.025 | 0.05 | 0.075 | 0.10 | |||||
| αA | αB | αA | αB | αA | αB | αA | αB | |
| 450 | - | - | - | - | 1.024 | 1.002 | 1.045 | 1.003 |
| 500 | - | - | 1.021 | 1.001 | 1.018 | 1.005 | 1.040 | 1.006 |
| 550 | 1.022 | 1.001 | 1.013 | 1.002 | 1.015 | 1.008 | 1.030 | 1.009 |
| 575 | 1.019 | 1.002 | 1.009 | 1.009 | 1.007 | 1.025 | 1.015 | 1.018 |
| 600 | 1.010 | 1.008 | 1.003 | 1.030 | 1.005 | 1.038 | 1.005 | 1.038 |
| 625 | 1.008 | 1.020 | 1.002 | 1.065 | 1.002 | 1.065 | 1.001 | 1.062 |
| 650 | 1.006 | 1.050 | 1.001 | 1.075 | 1.001 | 1.080 | 1.001 | 1.095 |
| 675 | 1.001 | 1.075 | 1.000 | 1.095 | 1.001 | 1.098 | 1.001 | 1.100 |
| 700 | 1.001 | 1.090 | 1.000 | 1.100 | 1.000 | 1.105 | 1.001 | 1.108 |
| 750 | 1.001 | 1.100 | 1.000 | 1.105 | 1.000 | 1.130 | 1.000 | 1.119 |
| Q (L/min) | Sill widths (m) | |||||||
| 0.15 | 0.20 | 0.25 | 0.30 | |||||
| αA | αB | αA | αB | αA | αB | αA | αB | |
| 300 | - | - | - | - | 1.009 | 1.004 | - | - |
| 325 | - | - | - | - | - | - | 1.001 | 1.050 |
| 350 | - | - | - | - | 1.007 | 1.009 | 1.001 | 1.084 |
| 375 | - | - | - | 1.005 | 1.030 | 1.000 | 1.100 | |
| 400 | - | - | - | - | 1.001 | 1.075 | - | - |
| 450 | - | - | 1.020 | 1.002 | 1.000 | 1.098 | - | - |
| 500 | 1.030 | 1.002 | 1.015 | 1.005 | 1.000 | 1.107 | - | - |
| 550 | 1.028 | 1.004 | 1.012 | 1.009 | - | - | - | - |
| 575 | 1.028 | 1.006 | 1.007 | 1.020 | - | - | - | - |
| 600 | 1.015 | 1.008 | 1.003 | 1.055 | - | - | - | - |
| 625 | 1.010 | 1.010 | 1.001 | 1.085 | - | - | - | - |
| 650 | 1.008 | 1.020 | 1.000 | 1.140 | - | - | - | - |
| 675 | 1.001 | 1.055 | - | - | - | - | - | - |
| 700 | 1.001 | 1.085 | - | - | - | - | - | - |
| 750 | 1.000 | 1.130 | - | - | - | - | - | - |
| Q (L/min) | Sill Widths (m) | |||||||||||
| 0.025 | 0.05 | |||||||||||
| with α EA (m) | without α EA (m) | RE (%) | with α EB (m) | without α EB (m) | RE (%) | with α EA (m) | without α EA (m) | RE (%) | with α EB (m) | without α EB (m) | RE (%) | |
| 500 | - | - | - | - | - | - | 0.096 | 0.094 | 1.56 | 0.073 | 0.073 | 0.01 |
| 550 | 0.107 | 0.105 | 1.63 | 0.086 | 0.086 | 0.01 | 0.111 | 0.110 | 1.04 | 0.077 | 0.077 | 0.03 |
| 575 | 0.115 | 0.113 | 1.43 | 0.079 | 0.079 | 0.03 | 0.121 | 0.120 | 0.71 | 0.081 | 0.081 | 0.11 |
| 600 | 0.124 | 0.123 | 0.80 | 0.082 | 0.082 | 0.11 | 0.130 | 0.130 | 0.21 | 0.084 | 0.083 | 0.39 |
| 625 | 0.136 | 0.135 | 0.66 | 0.088 | 0.088 | 0.23 | 0.141 | 0.141 | 0.13 | 0.089 | 0.089 | 0.72 |
| 650 | 0.146 | 0.145 | 0.50 | 0.090 | 0.090 | 0.59 | 0.151 | 0.151 | 0.07 | 0.092 | 0.092 | 0.81 |
| 675 | 0.155 | 0.155 | 0.08 | 0.096 | 0.095 | 0.78 | 0.162 | 0.162 | 0.01 | 0.098 | 0.097 | 0.90 |
| 700 | 0.165 | 0.165 | 0.07 | 0.098 | 0.097 | 0.93 | 0.175 | 0.175 | 0.01 | 0.100 | 0.099 | 0.97 |
| 750 | 0.186 | 0.186 | 0.04 | 0.106 | 0.105 | 0.93 | 0.204 | 0.204 | 0.01 | 0.107 | 0.106 | 0.93 |
| Q (L/min) | Sill widths (m) | |||||||||||
| 0.075 | 0.10 | |||||||||||
| with α EA (m) | without α EA (m) | RE (%) | with α EB (m) | without α EB (m) | RE (%) | with α EA (m) | without α EA (m) | RE (%) | with α EB (m) | without α EB (m) | RE (%) | |
| 450 | 0.088 | 0.086 | 1.75 | 0.069 | 0.069 | 0.07 | 0.099 | 0.095 | 3.41 | 0.069 | 0.069 | 0.04 |
| 500 | 0.104 | 0.102 | 1.39 | 0.076 | 0.076 | 0.08 | 0.118 | 0.114 | 3.18 | 0.077 | 0.077 | 0.07 |
| 550 | 0.123 | 0.122 | 1.22 | 0.083 | 0.083 | 0.08 | 0.134 | 0.131 | 2.46 | 0.083 | 0.083 | 0.09 |
| 575 | 0.137 | 0.136 | 0.59 | 0.089 | 0.089 | 0.09 | 0.148 | 0.146 | 1.27 | 0.089 | 0.089 | 0.16 |
| 600 | 0.151 | 0.150 | 0.39 | 0.093 | 0.092 | 0.09 | 0.165 | 0.164 | 0.44 | 0.093 | 0.093 | 0.32 |
| 625 | 0.164 | 0.164 | 0.13 | 0.095 | 0.094 | 0.09 | 0.182 | 0.182 | 0.09 | 0.097 | 0.096 | 0.50 |
| 650 | 0.179 | 0.179 | 0.09 | 0.101 | 0.100 | 0.10 | 0.197 | 0.197 | 0.07 | 0.102 | 0.101 | 0.72 |
| 675 | 0.193 | 0.193 | 0.07 | 0.103 | 0.102 | 0.10 | 0.213 | 0.213 | 0.07 | 0.105 | 0.105 | 0.72 |
| 700 | 0.207 | 0.207 | 0.01 | 0.107 | 0.107 | 0.11 | 0.230 | 0.230 | 0.05 | 0.109 | 0.109 | 0.75 |
| 750 | 0.247 | 0.247 | 0.01 | 0.117 | 0.116 | 0.12 | 0.266 | 0.266 | 0.01 | 0.118 | 0.117 | 0.74 |
| Q (L/min) | Sill widths (m) | |||||||||||
| 0.15 | 0.20 | |||||||||||
| with α EA (m) | without α EA (m) | RE (%) | with α EB (m) | without α EB (m) | RE (%) | with α EA (m) | without α EA (m) | RE (%) | with α EB (m) | without α EB (m) | RE (%) | |
| 450 | - | - | - | - | - | - | 0.155 | 0.152 | 1.77 | 0.079 | 0.079 | 0.01 |
| 500 | 0.135 | 0.131 | 2.51 | 0.084 | 0.084 | 0.02 | 0.189 | 0.186 | 1.36 | 0.088 | 0.088 | 0.03 |
| 550 | 0.167 | 0.163 | 2.43 | 0.088 | 0.088 | 0.03 | 0.242 | 0.239 | 1.11 | 0.098 | 0.098 | 0.05 |
| 575 | 0.183 | 0.179 | 2.46 | 0.092 | 0.092 | 0.05 | 0.266 | 0.264 | 0.66 | 0.101 | 0.101 | 0.11 |
| 600 | 0.205 | 0.202 | 1.35 | 0.098 | 0.098 | 0.07 | 0.302 | 0.302 | 0.29 | 0.105 | 0.105 | 0.30 |
| 625 | 0.222 | 0.220 | 0.91 | 0.101 | 0.101 | 0.07 | 0.332 | 0.332 | 0.05 | 0.114 | 0.113 | 0.40 |
| 650 | 0.251 | 0.250 | 0.74 | 0.108 | 0.108 | 0.12 | 0.393 | 0.393 | 0.01 | 0.116 | 0.116 | 0.66 |
| 675 | 0.280 | 0.280 | 0.09 | 0.111 | 0.111 | 0.32 | - | - | - | - | - | - |
| 700 | 0.303 | 0.303 | 0.08 | 0.116 | 0.116 | 0.47 | - | - | - | - | - | - |
| 750 | 0.349 | 0.349 | 0.03 | 0.123 | 0.122 | 0.70 | - | - | - | - | - | - |
| Q (L/min) | Sill widths (m) | |||||||||||
| 0.25 | 0.30 | |||||||||||
| with α EA (m) | without α EA (m) | RE (%) | with α EB (m) | without α EB (m) | RE (%) | with α EA (m) | without α EA (m) | RE (%) | with α EB (m) | without α EB (m) | RE (%) | |
| 300 | 0154 | 0.153 | 0.83 | 0.062 | 0.062 | 0.03 | 0.375 | 0.375 | 0.08 | 0.068 | 0.068 | 0.25 |
| 325 | - | - | - | - | - | - | 0.425 | 0.425 | 0.06 | 0.073 | 0.072 | 0.40 |
| 350 | 0.214 | 0.213 | 0.62 | 0.073 | 0.073 | 0.05 | 0.492 | 0.492 | 0.04 | 0.078 | 0.078 | 0.45 |
| 375 | 0.256 | 0.255 | 0.48 | 0.076 | 0.076 | 0.17 | - | - | - | - | - | - |
| 400 | 0.315 | 0.315 | 0.08 | 0.085 | 0.084 | 0.34 | - | - | - | - | - | - |
| 450 | 0.398 | 0.398 | 0.01 | 0.094 | 0.094 | 0.42 | - | - | - | - | - | - |
| 500 | 0.495 | 0.495 | 0.01 | 0.103 | 0.103 | 0.42 | - | - | - | - | - | - |
| Types of Channel | α Values | ||
|---|---|---|---|
| Min | Mean | Max | |
| Regular channels, flumes, Spillways | 1.10 | 1.15 | 1.20 |
| Natural channels | 1.15 | 1.30 | 1.50 |
| Rivers with ice cover | 1.20 | 1.50 | 2.00 |
| River valleys, over flooded | 1.50 | 1.75 | 2.00 |
| B (m) | Without Sill G = 0.04 | 0.025 | 0.05 | 0.075 | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Q (L/min) | 300 | ∆EAB/EA (%) | - | - | - | - | - | - | - | 59.3 | 71.5 |
| 350 | - | - | - | - | - | - | - | 65.7 | 77.3 | ||
| 400 | - | - | - | - | - | - | - | 73.2 | - | ||
| 450 | - | - | - | 19.9 | 27.4 | - | 47.8 | 76.5 | - | ||
| 500 | 21.5 | - | 22.6 | 25.9 | 32.8 | 36.3 | 52.5 | 79.2 | - | ||
| 550 | 25.8 | 27.7 | 29.9 | 32 | 36.5 | 46 | 59.2 | - | - | ||
| 600 | 29.7 | 33.5 | 35.8 | 38.3 | 43.2 | 51.6 | 65.1 | - | - | ||
| 650 | 34.3 | 38.1 | 39.4 | 44 | 48.9 | 56.9 | 70.6 | - | - | ||
| 300 | ∆EAB/EB (%) | - | - | - | - | - | - | - | 145.9 | 251.3 | |
| 350 | - | - | - | - | - | - | - | 191.8 | 340.2 | ||
| 400 | - | - | - | - | - | - | - | 273.1 | - | ||
| 450 | - | - | - | 24.8 | 38.8 | - | 91.6 | 326.4 | - | ||
| 500 | 27.3 | - | 29.2 | 34.9 | 48.8 | 57 | 110.4 | 380.7 | - | ||
| 550 | 34.7 | 38.3 | 42.7 | 47 | 57.5 | 85.3 | 144.9 | - | - | ||
| 600 | 42.3 | 50.4 | 55.8 | 62.2 | 76.2 | 106.8 | 186.8 | - | - | ||
| 650 | 52.2 | 61.5 | 65 | 78.5 | 95.5 | 131.8 | 239.7 | - | - | ||
| B (m) | Without Sill | 0.025 | 0.025 | 0.075 | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Q (L/min) | 350 | Cd (-) | - | - | 0.5554 | 0.5573 | 0.5683 | 0.5969 | 0.6515 | 0.6897 | 0.7797 |
| 375 | - | - | 0.5592 | 0.5617 | 0.5763 | 0.6083 | 0.6538 | 0.6860 | 0.7760 | ||
| 400 | 0.5377 | 0.5445 | 0.5604 | 0.5658 | 0.5769 | 0.6143 | 0.6520 | 0.6818 | - | ||
| 450 | 0.5667 | 0.5675 | 0.5820 | 0.5838 | 0.5938 | 0.6310 | 0.6625 | 0.6868 | - | ||
| Mode | Mean AE (-) | Mean RE (%) | Max Relative Error (%) | Min Relative Error (%) | RMSE (-) | R2 |
|---|---|---|---|---|---|---|
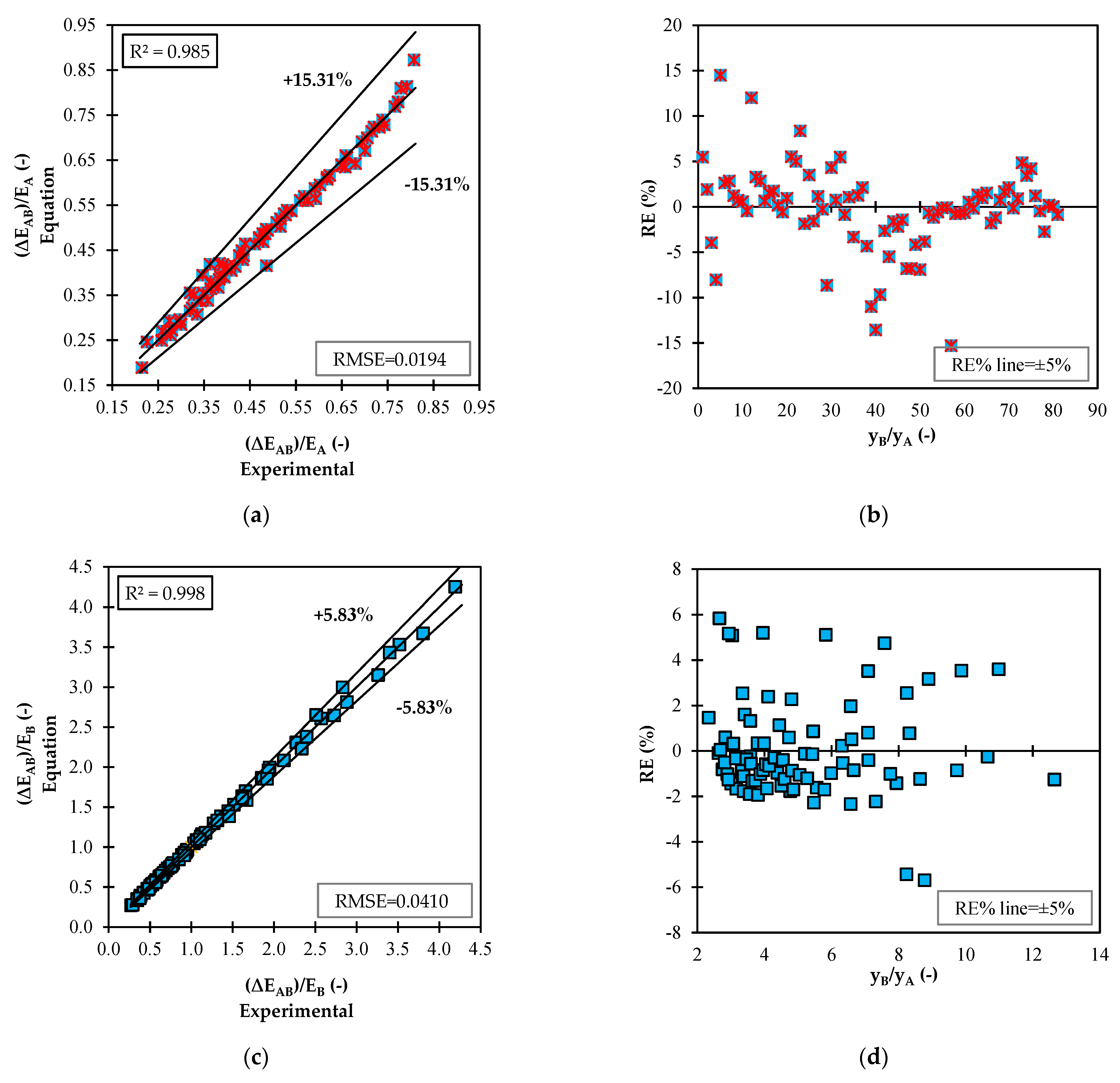
| 0.0134 | 3.12 | 14.49 | −15.31 | 0.0194 | 0.985 | |
| 0.0233 | 1.62 | 5.83 | −5.7 | 0.0410 | 0.998 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbaszadeh, H.; Norouzi, R.; Sume, V.; Kuriqi, A.; Daneshfaraz, R.; Abraham, J. Sill Role Effect on the Flow Characteristics (Experimental and Regression Model Analytical). Fluids 2023, 8, 235. https://doi.org/10.3390/fluids8080235
Abbaszadeh H, Norouzi R, Sume V, Kuriqi A, Daneshfaraz R, Abraham J. Sill Role Effect on the Flow Characteristics (Experimental and Regression Model Analytical). Fluids. 2023; 8(8):235. https://doi.org/10.3390/fluids8080235
Chicago/Turabian StyleAbbaszadeh, Hamidreza, Reza Norouzi, Veli Sume, Alban Kuriqi, Rasoul Daneshfaraz, and John Abraham. 2023. "Sill Role Effect on the Flow Characteristics (Experimental and Regression Model Analytical)" Fluids 8, no. 8: 235. https://doi.org/10.3390/fluids8080235
APA StyleAbbaszadeh, H., Norouzi, R., Sume, V., Kuriqi, A., Daneshfaraz, R., & Abraham, J. (2023). Sill Role Effect on the Flow Characteristics (Experimental and Regression Model Analytical). Fluids, 8(8), 235. https://doi.org/10.3390/fluids8080235










