Improving Pump Characteristics through Double Curvature Impellers: Experimental Measurements and 3D CFD Analysis
Abstract
:1. Introduction
2. Materials and Methods
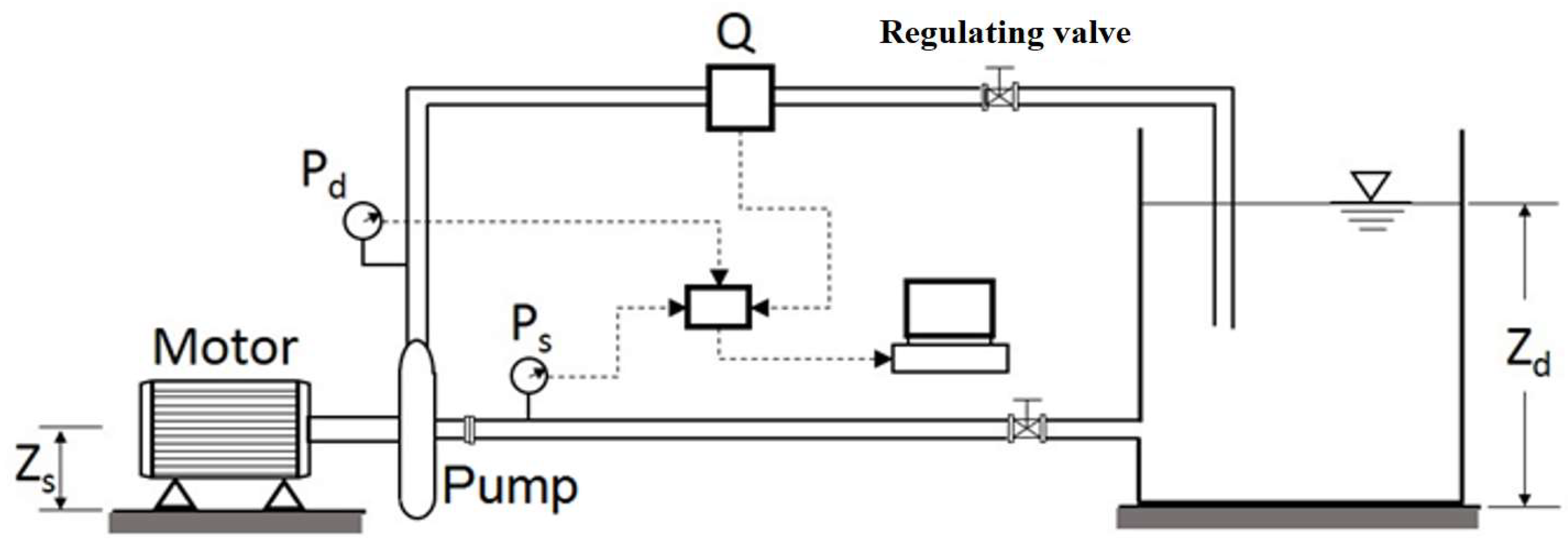
2.1. Experimental Facility, Used Impellers, and Measurements
2.2. Numerical Simulation
2.2.1. Governing Equations
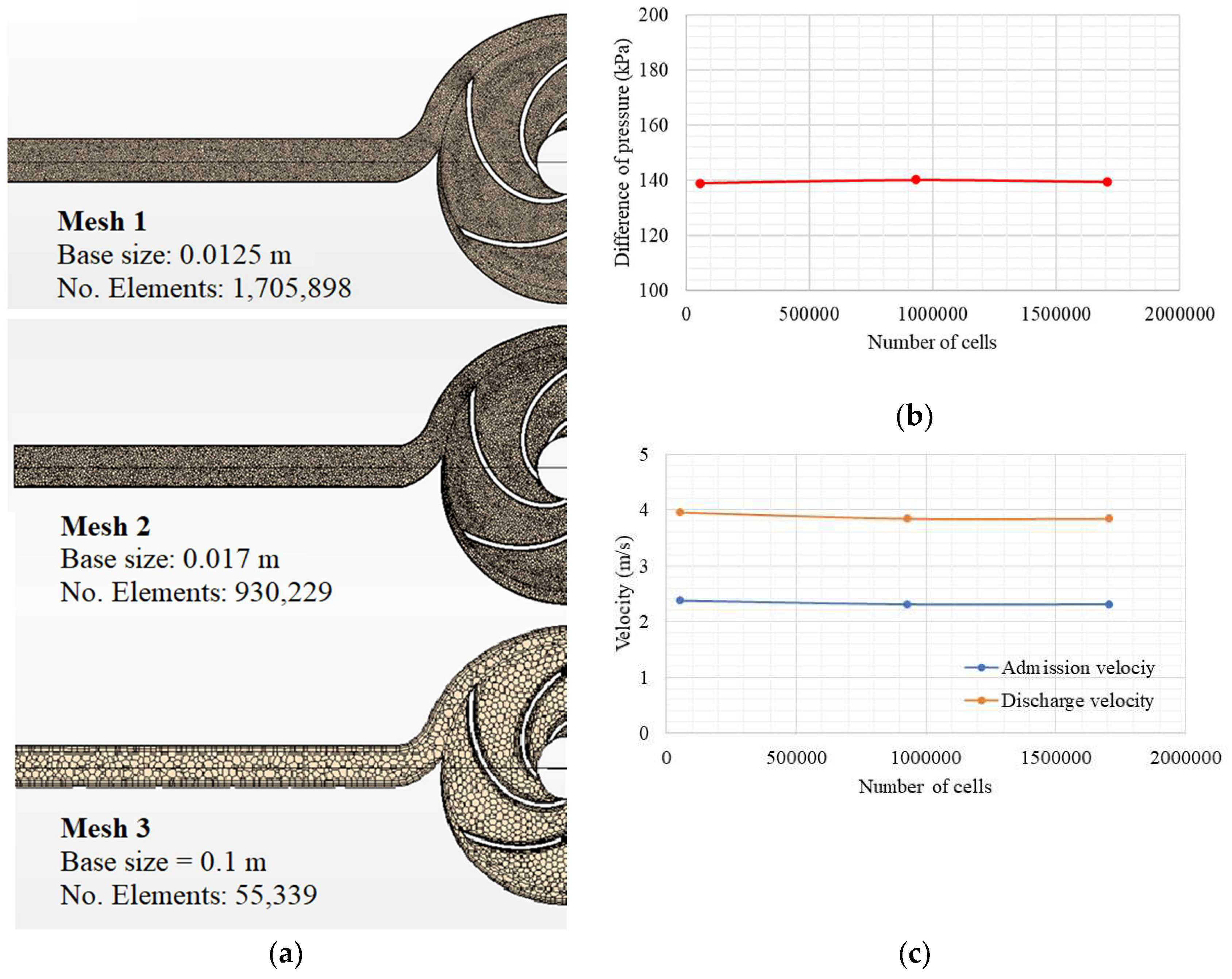
2.2.2. Geometric, Mesh, and Boundary Conditions
3. Analysis of Results
3.1. Experimental Curves
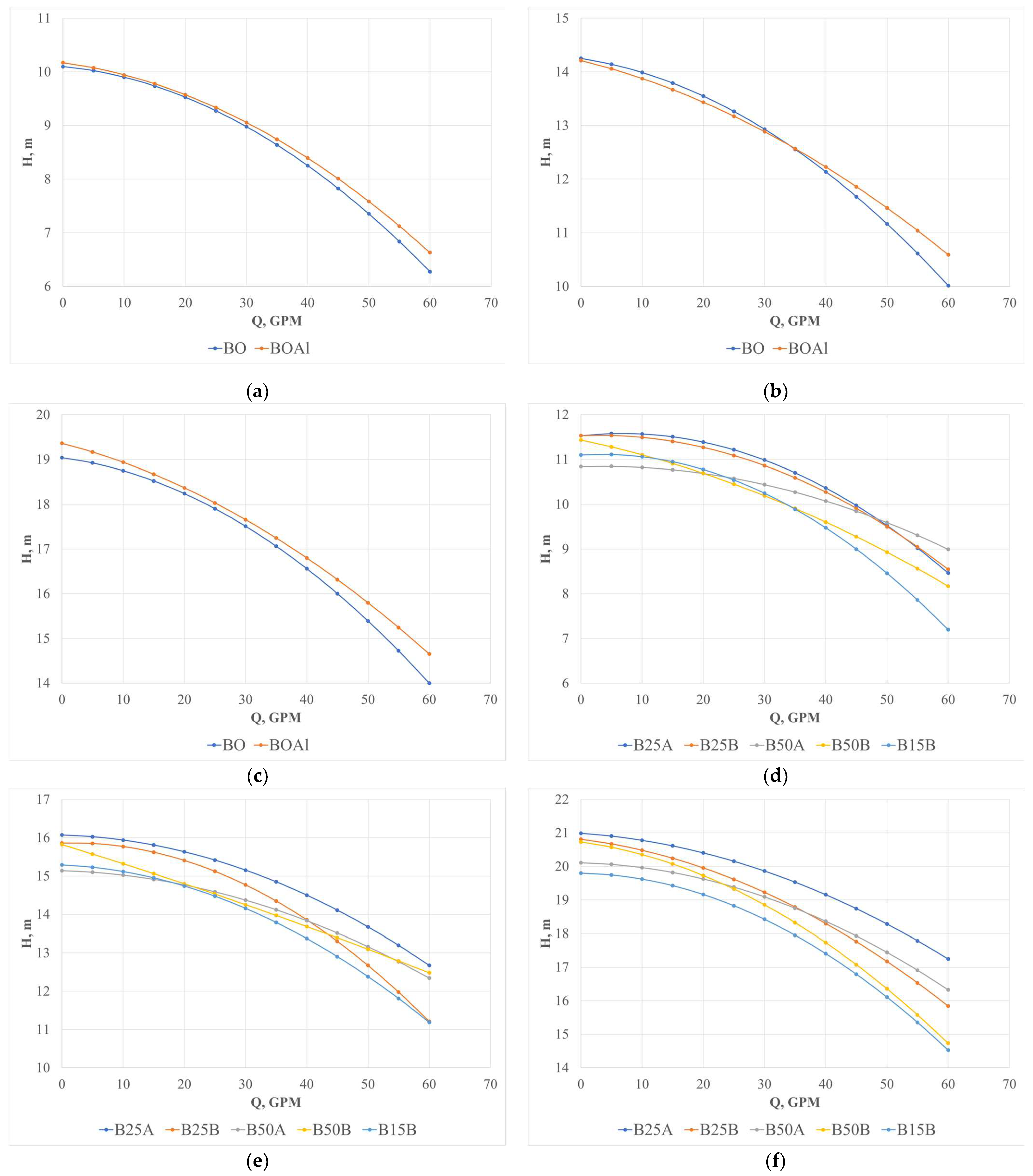
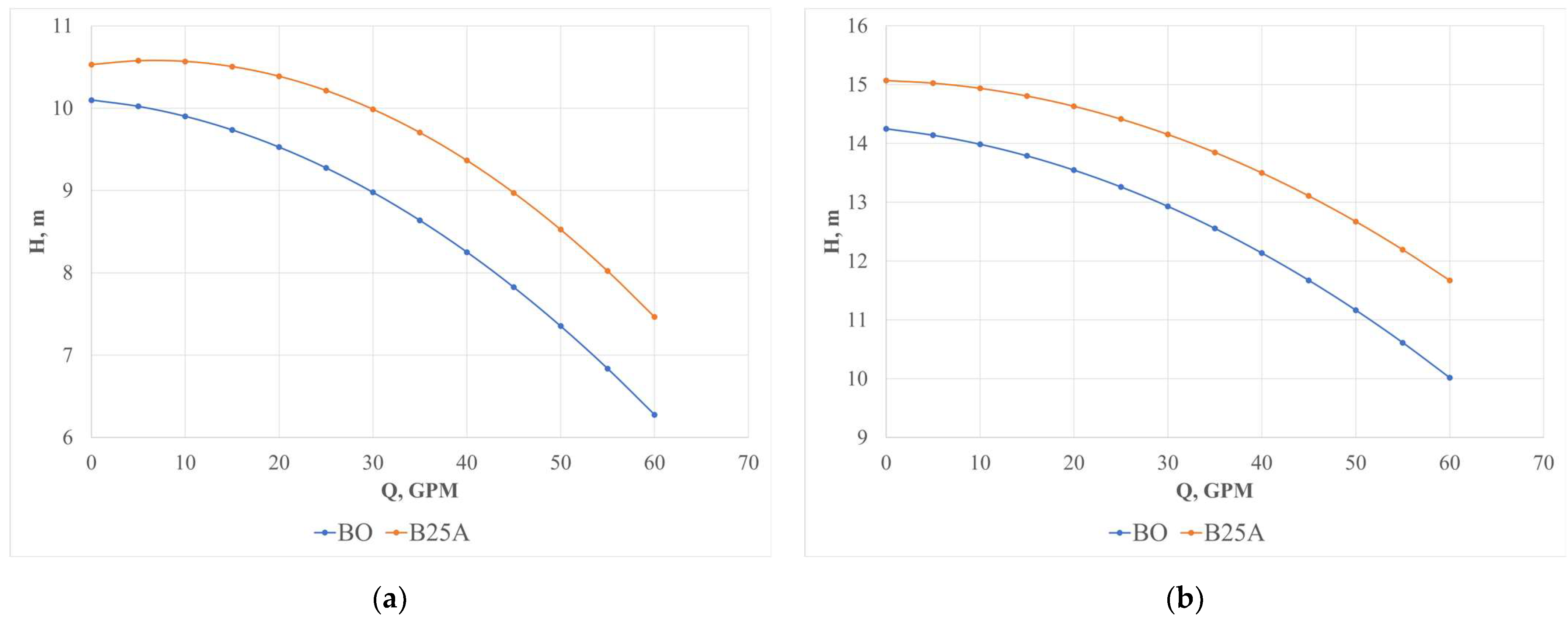
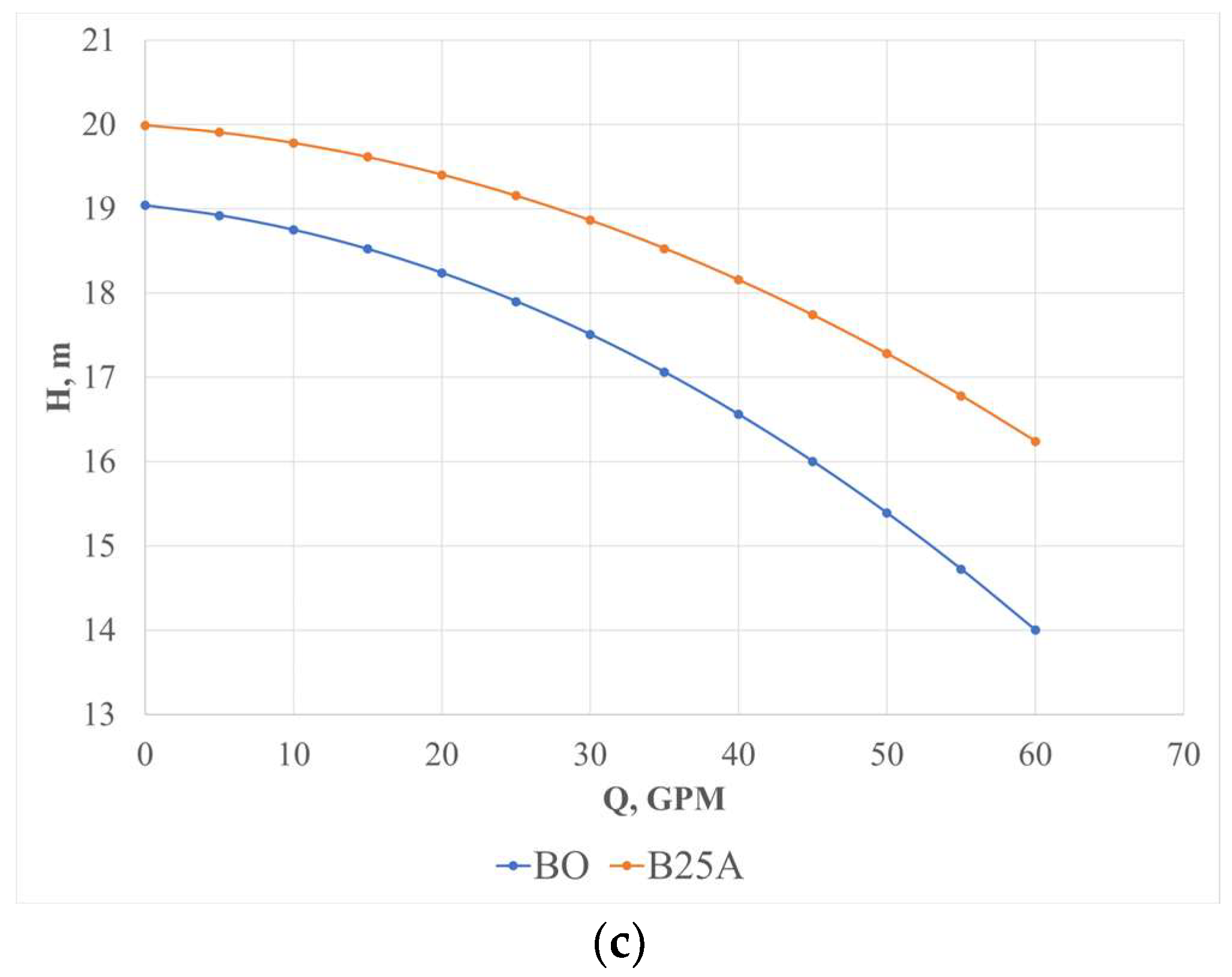
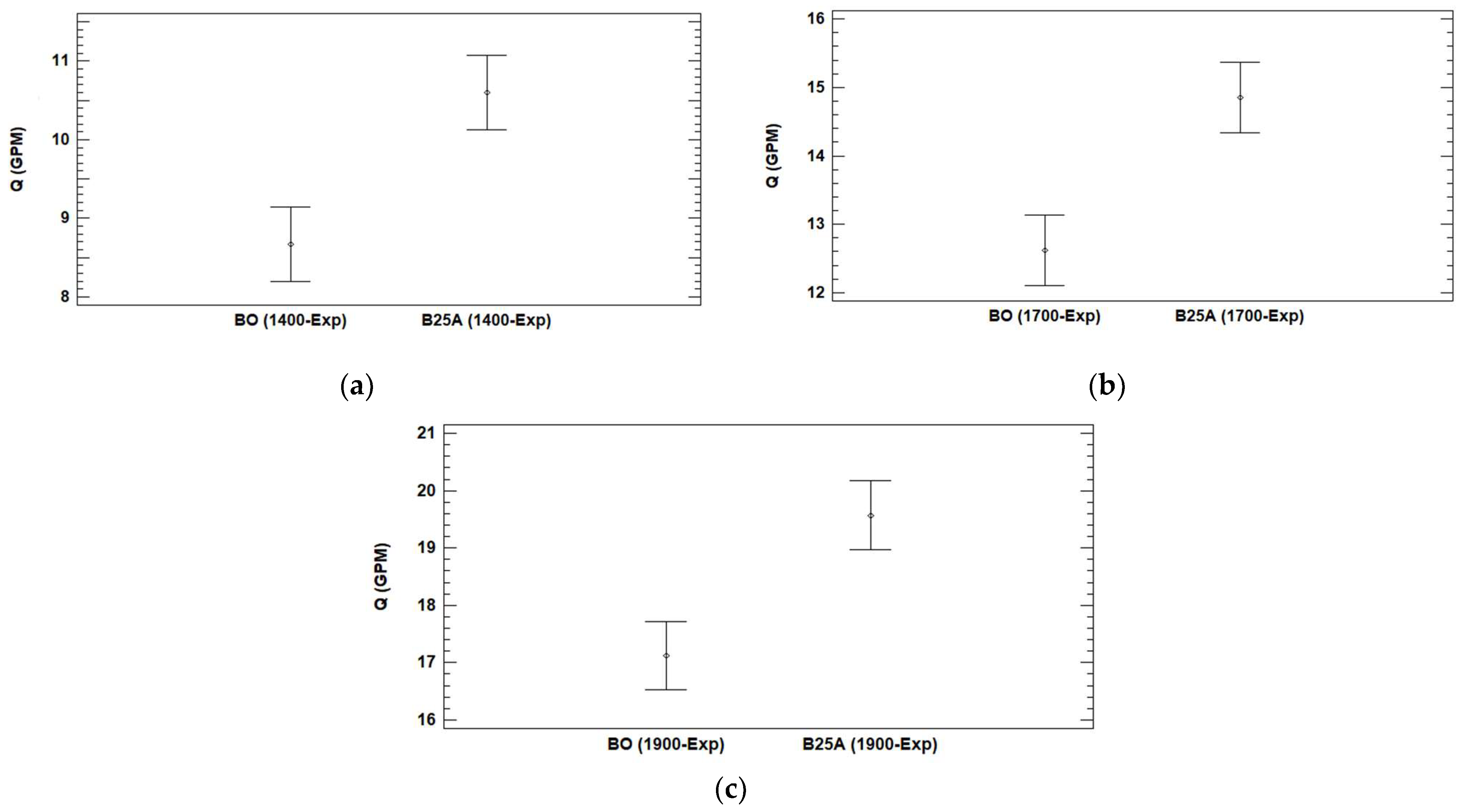
3.1.1. Head–Flow Rate Curve
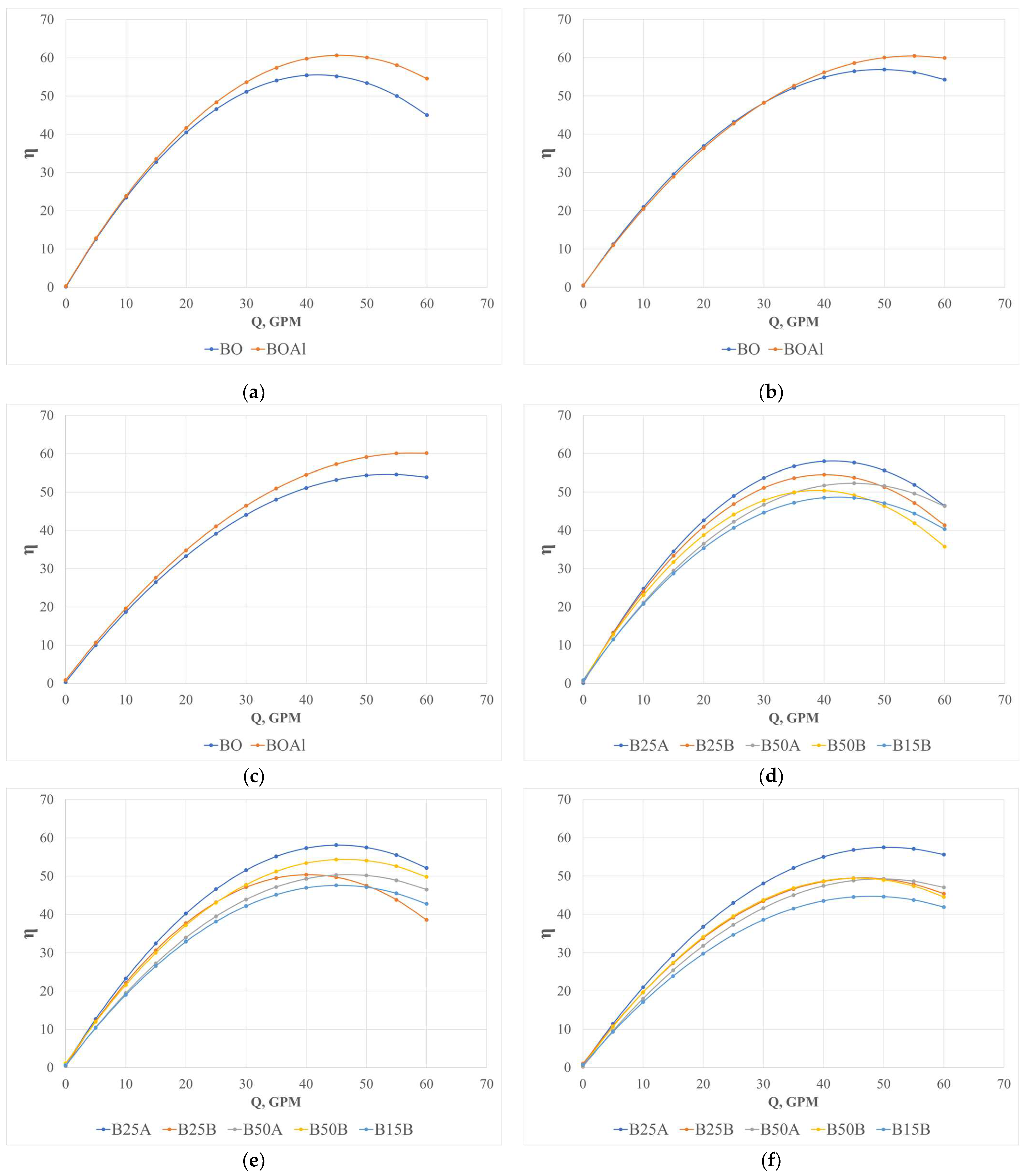
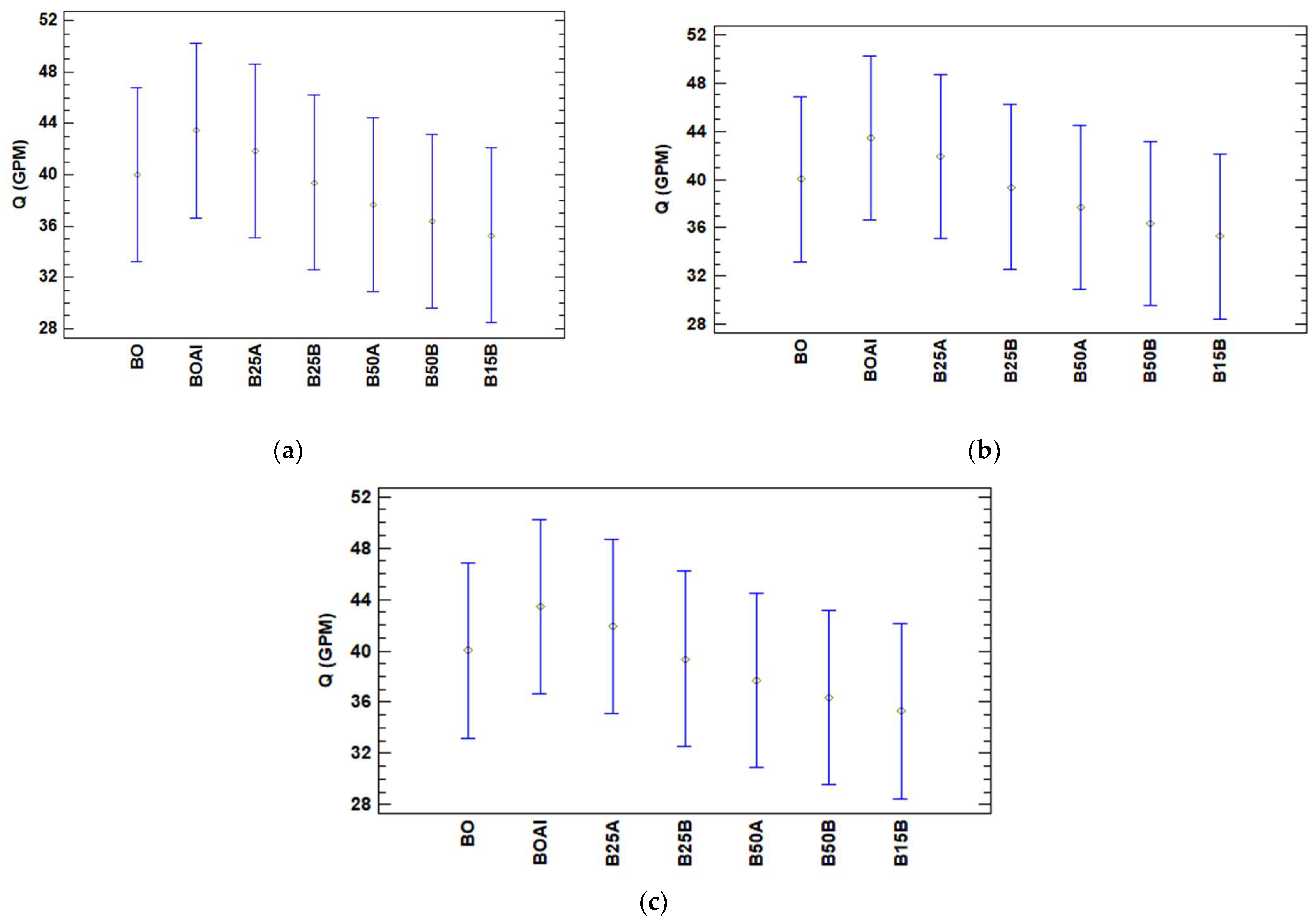
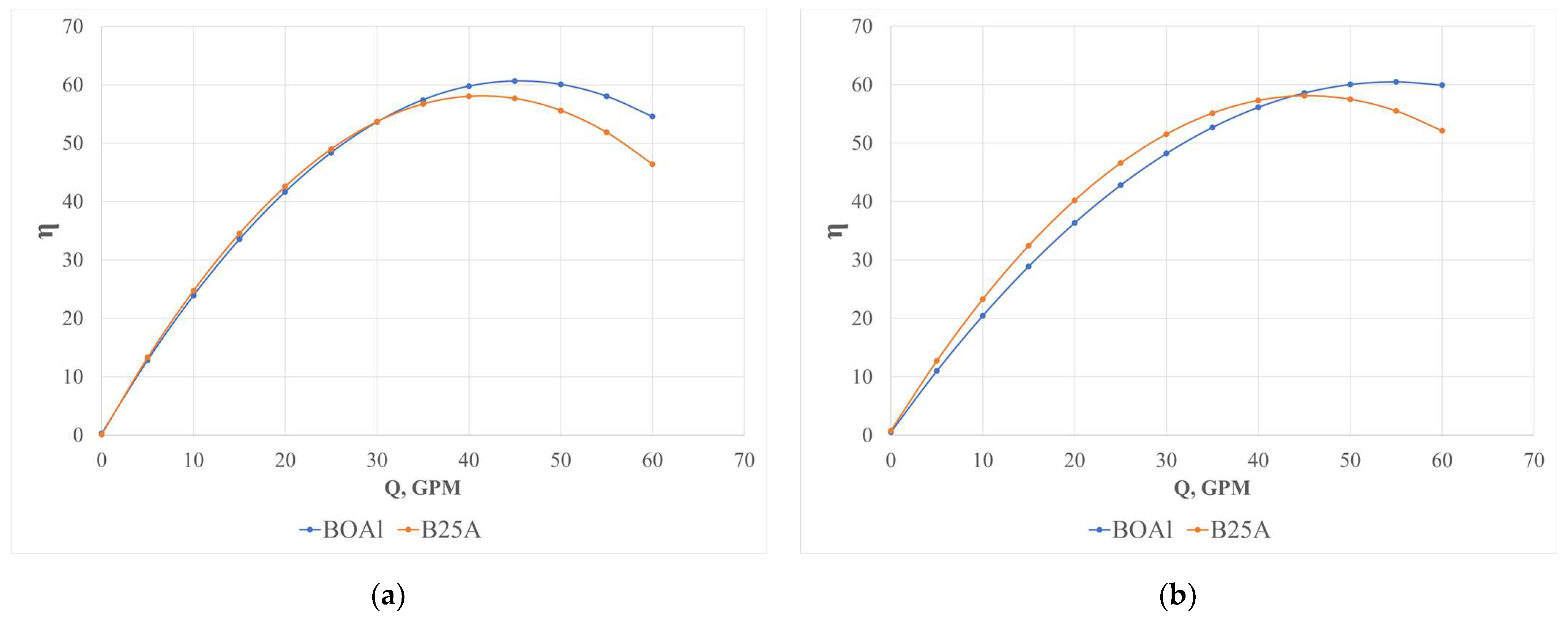
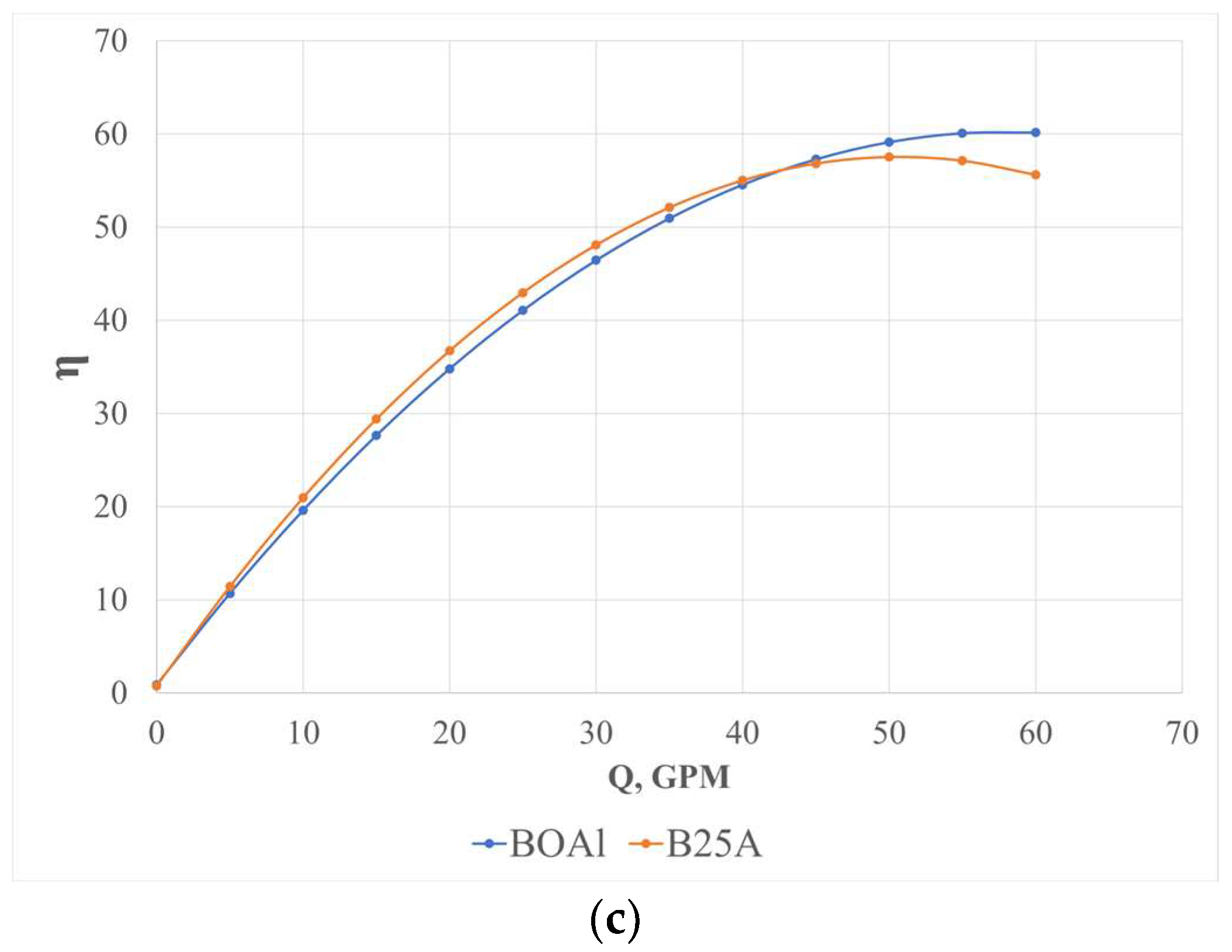
3.1.2. Performance–Flow Rate Curve
4. Discussion
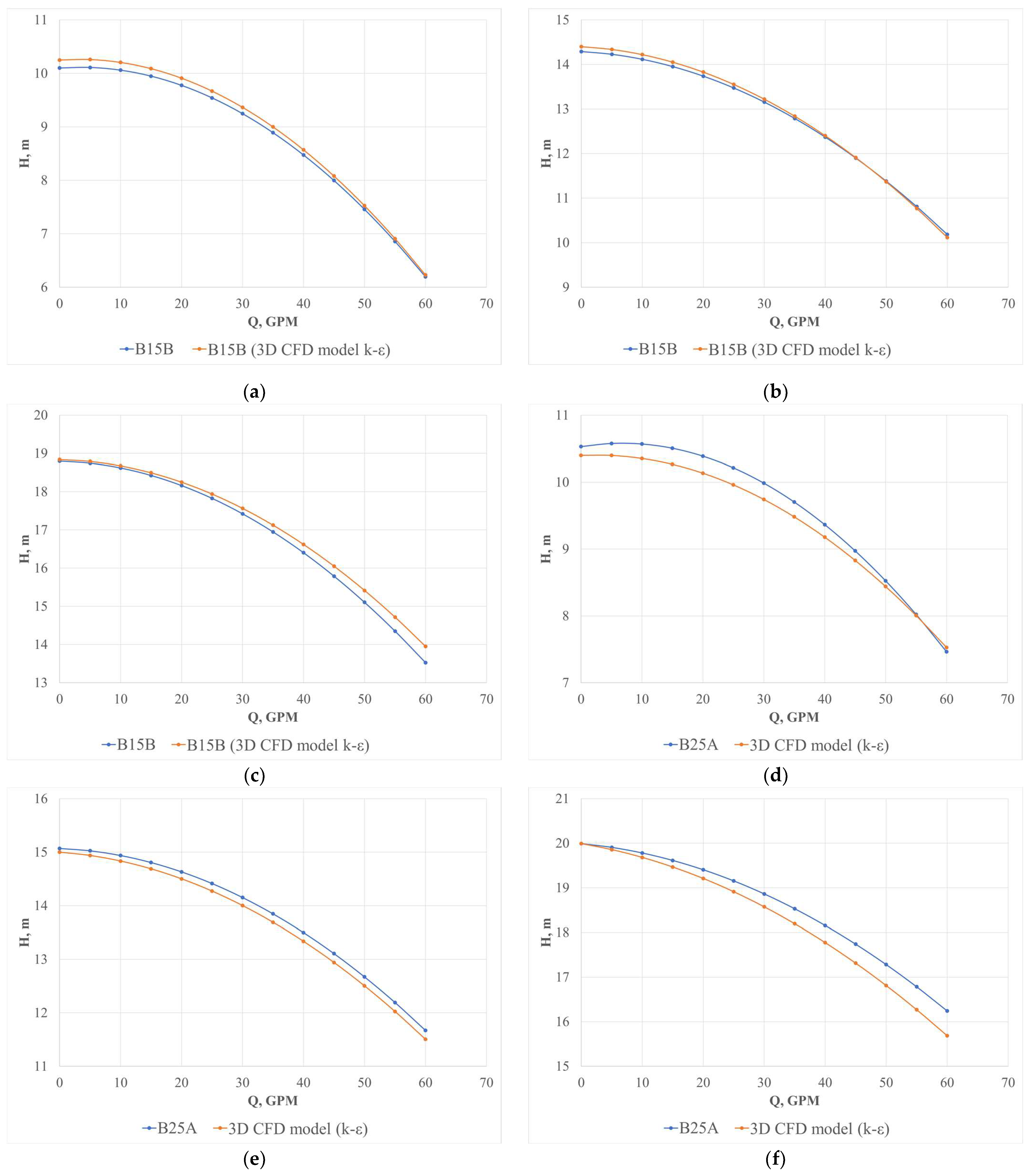
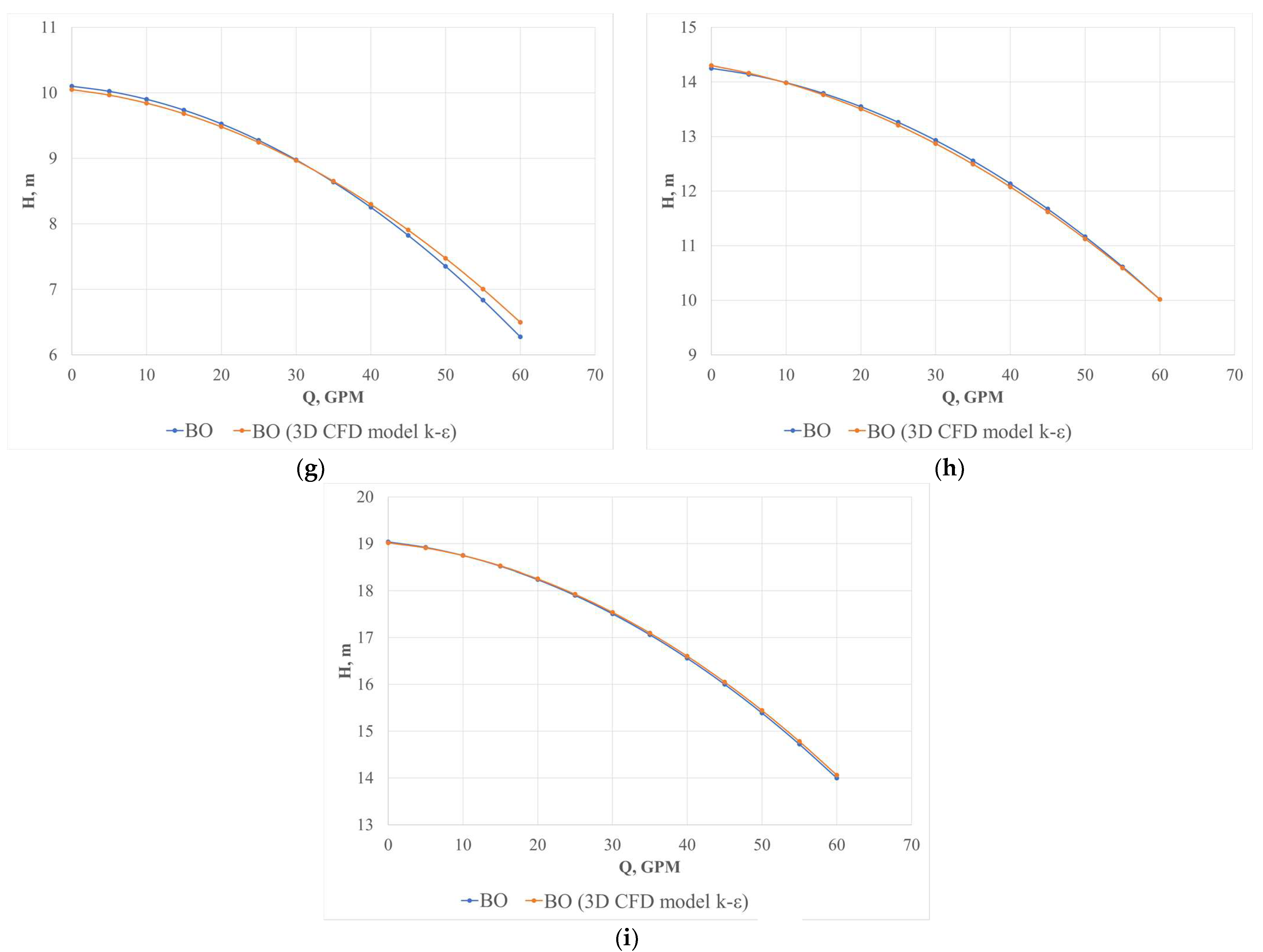
4.1. Head–Flow Rate Curves
4.2. Performance–Flow Rate Curve
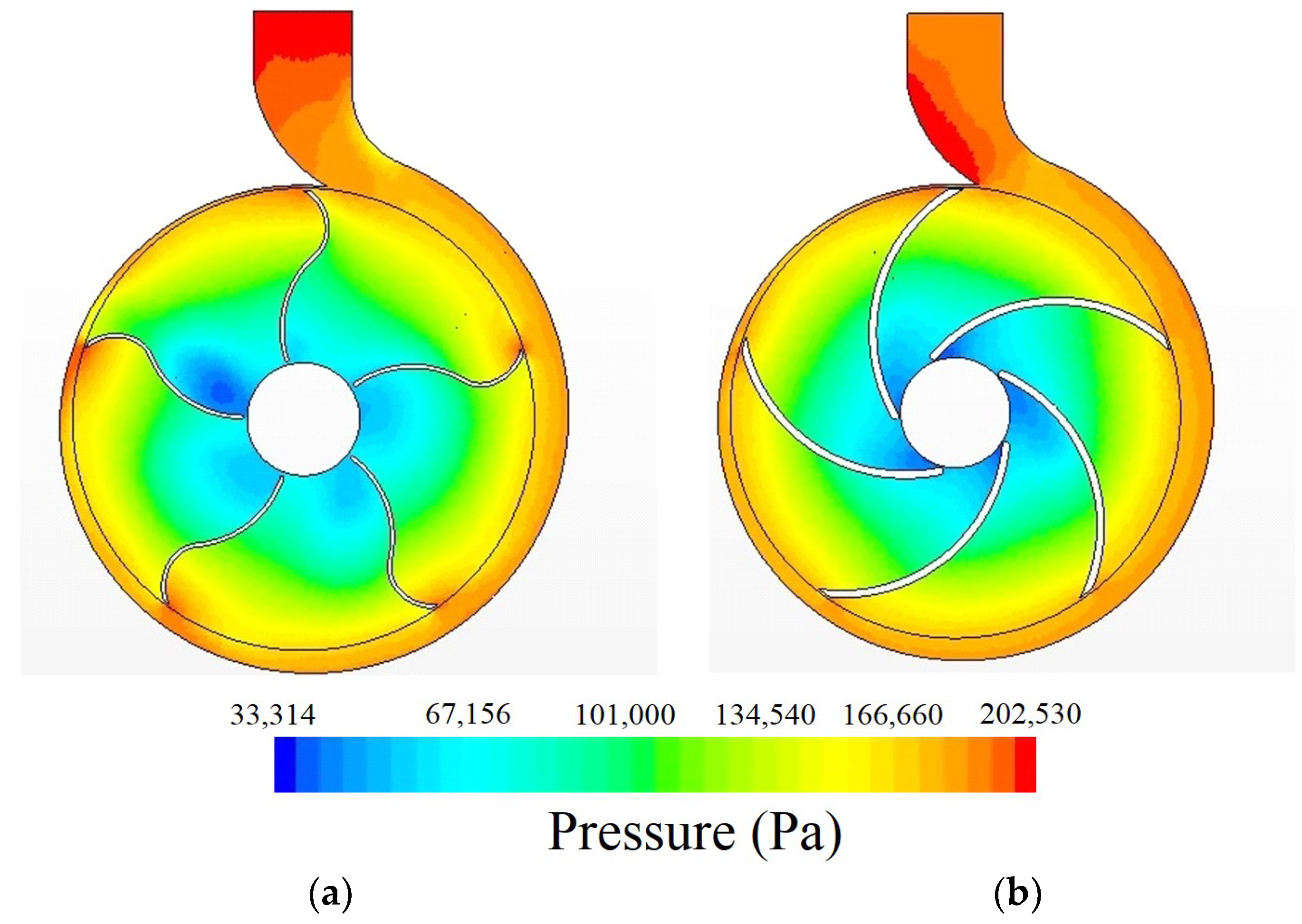
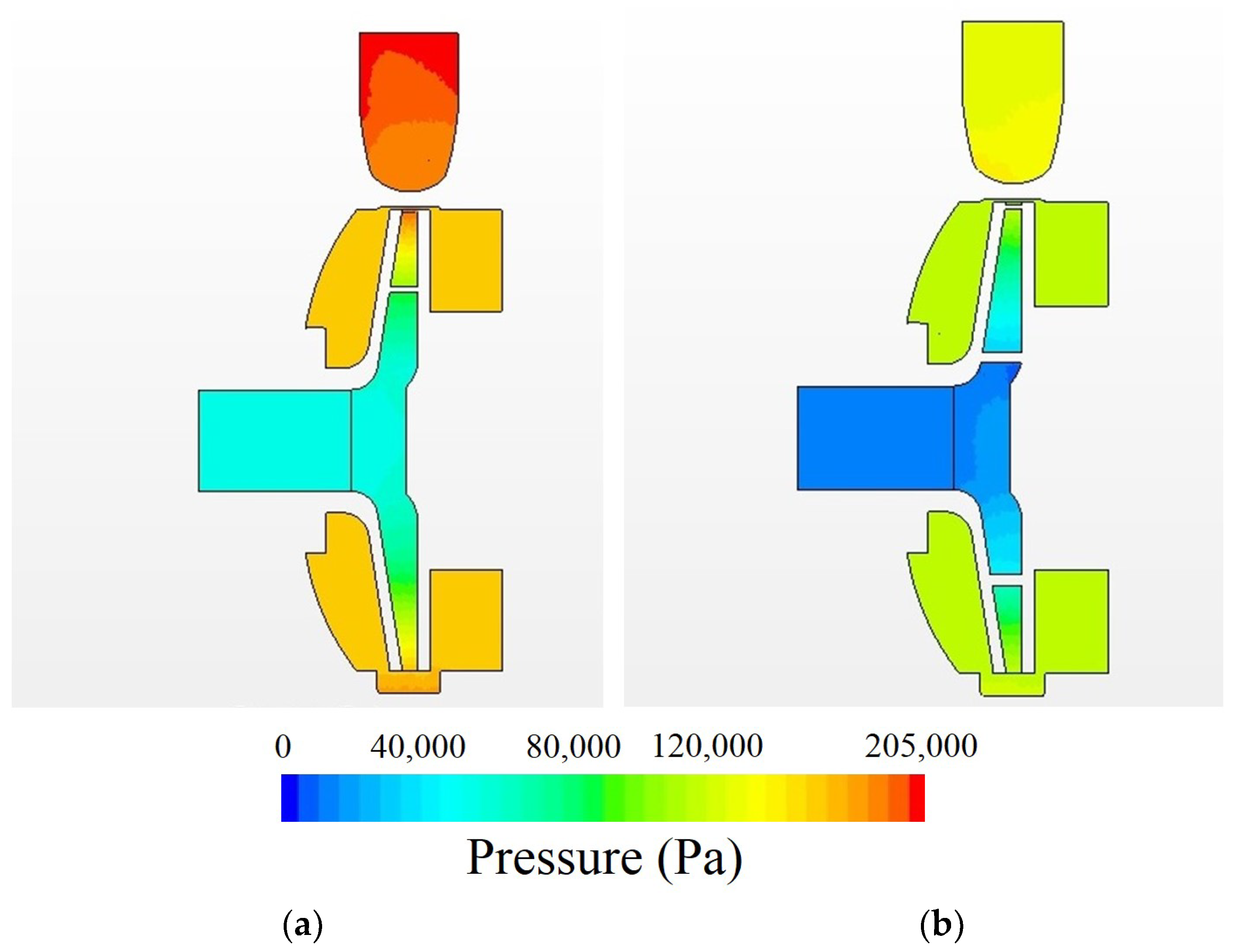
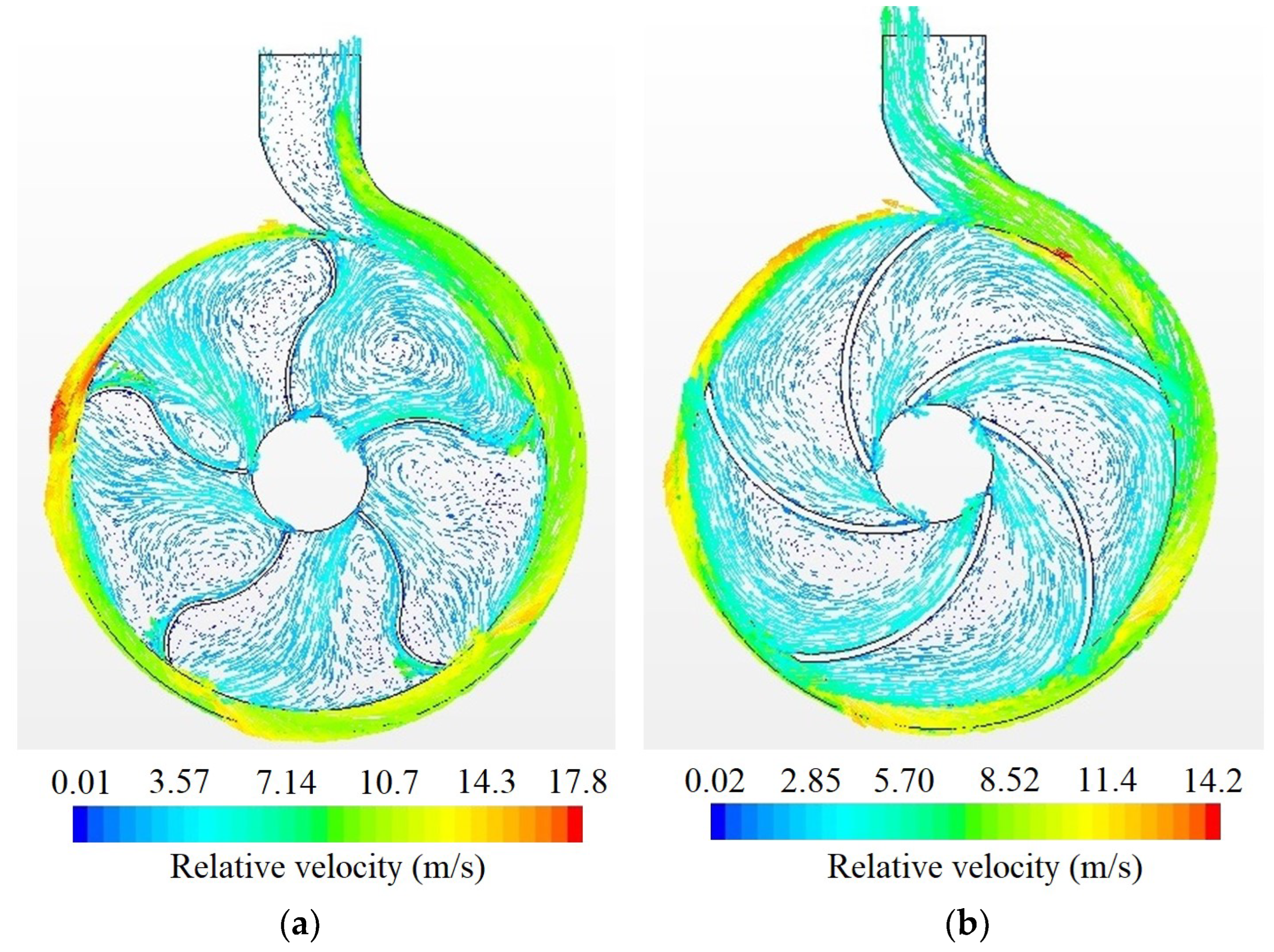
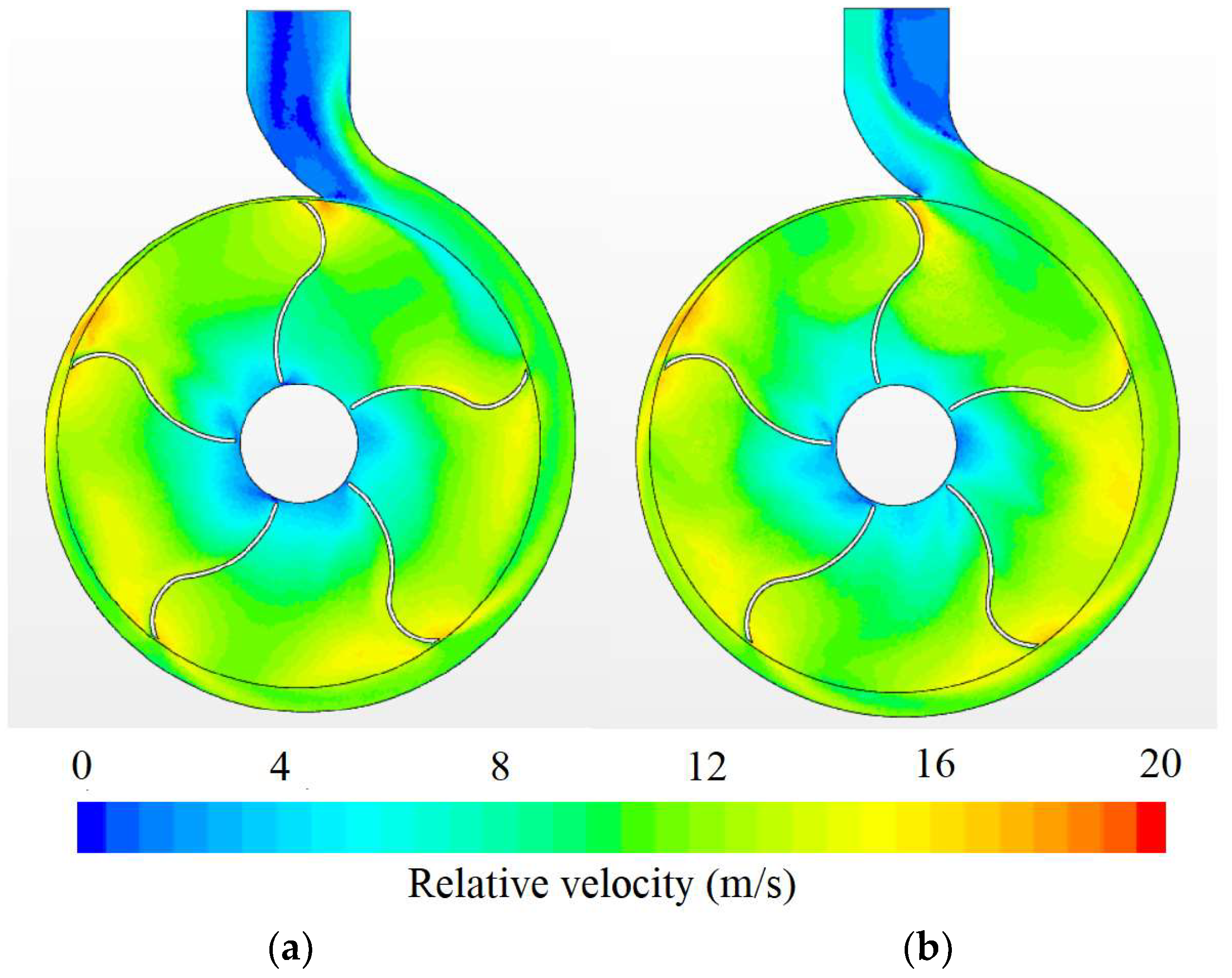
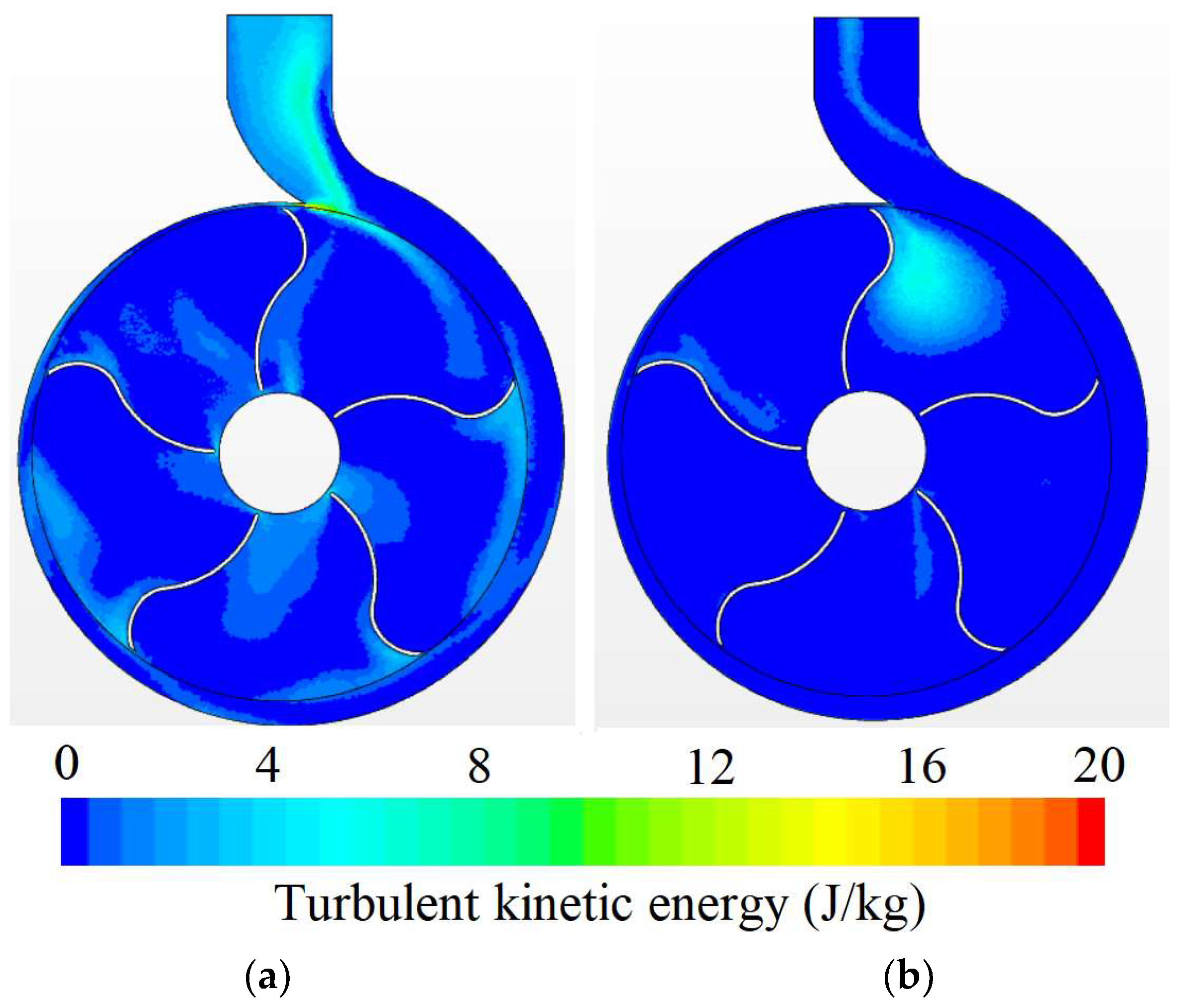
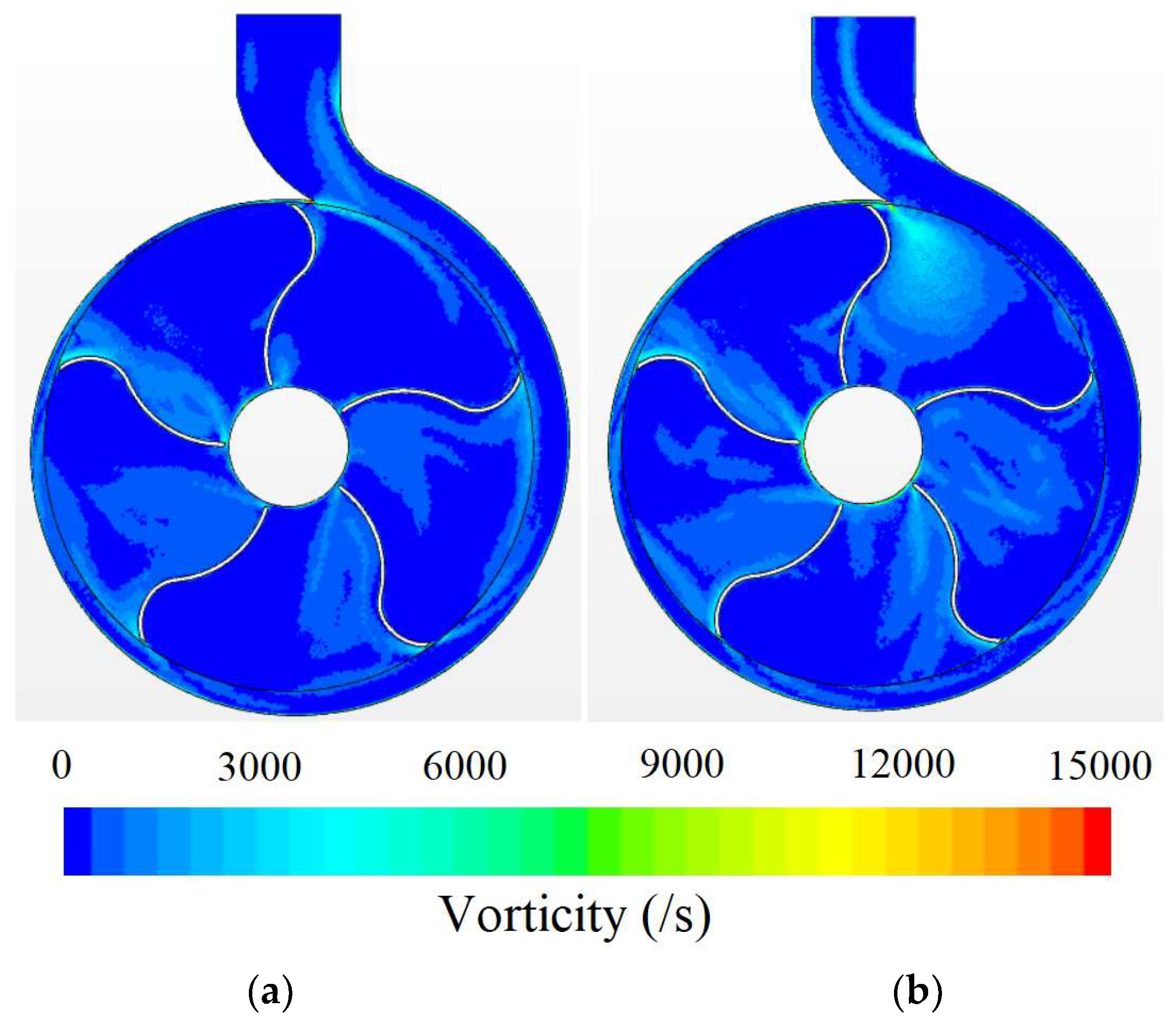
4.3. Phenomenon Description and CFD Validation
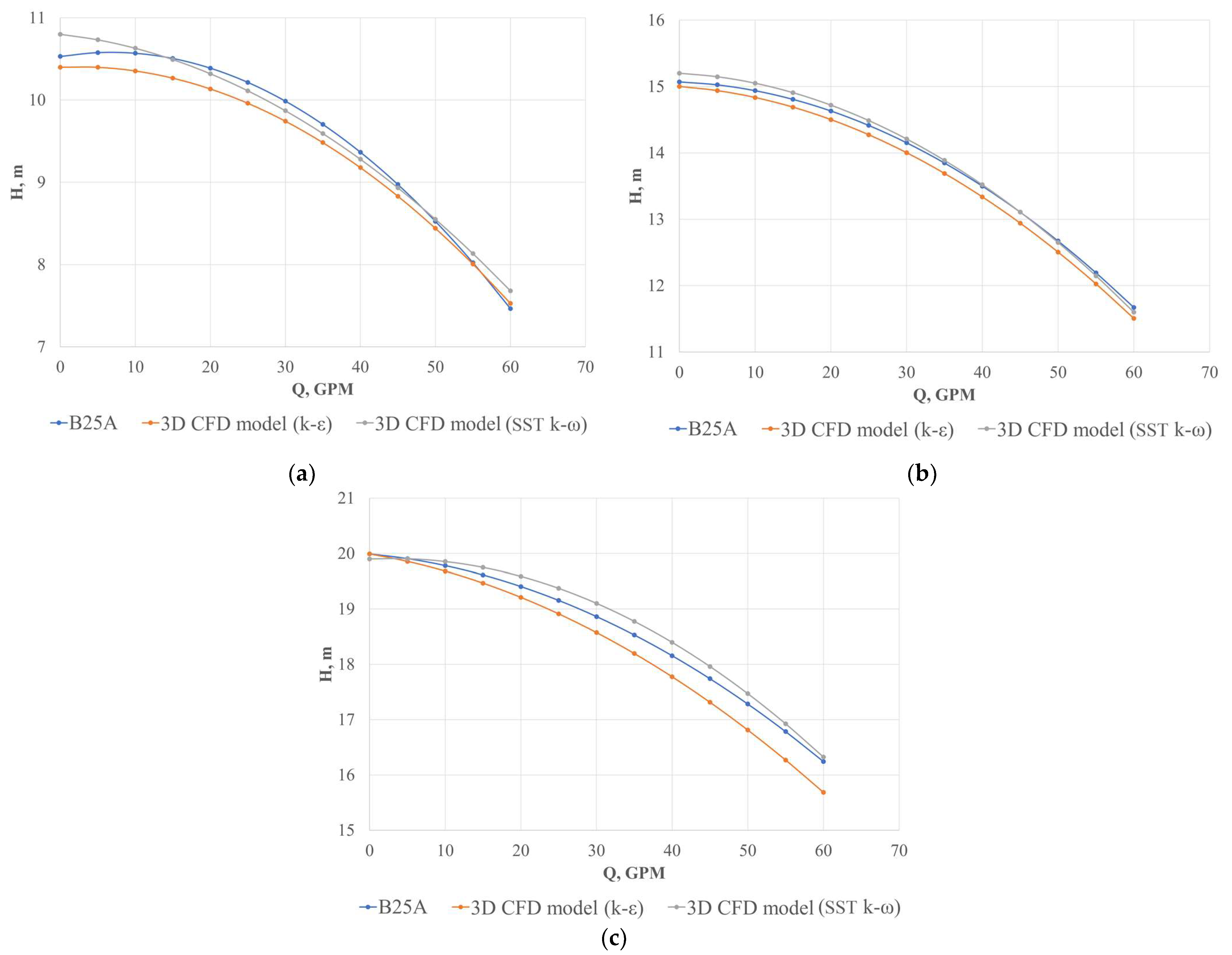
4.4. Comparison between k-ε and SST k-ω Turbulence Models
5. Conclusions
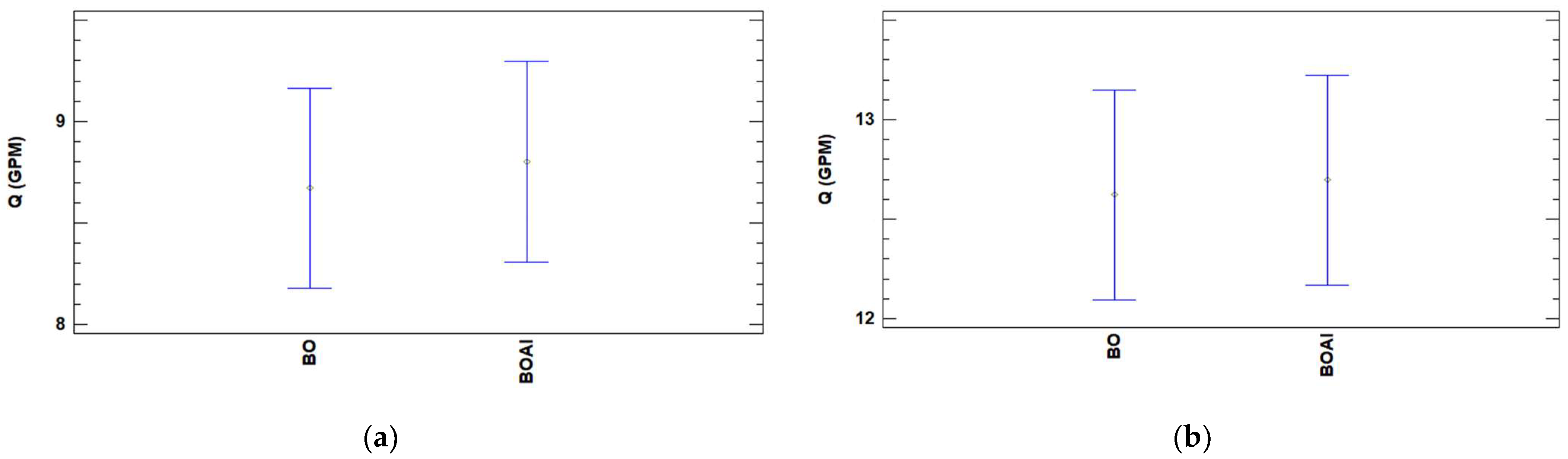
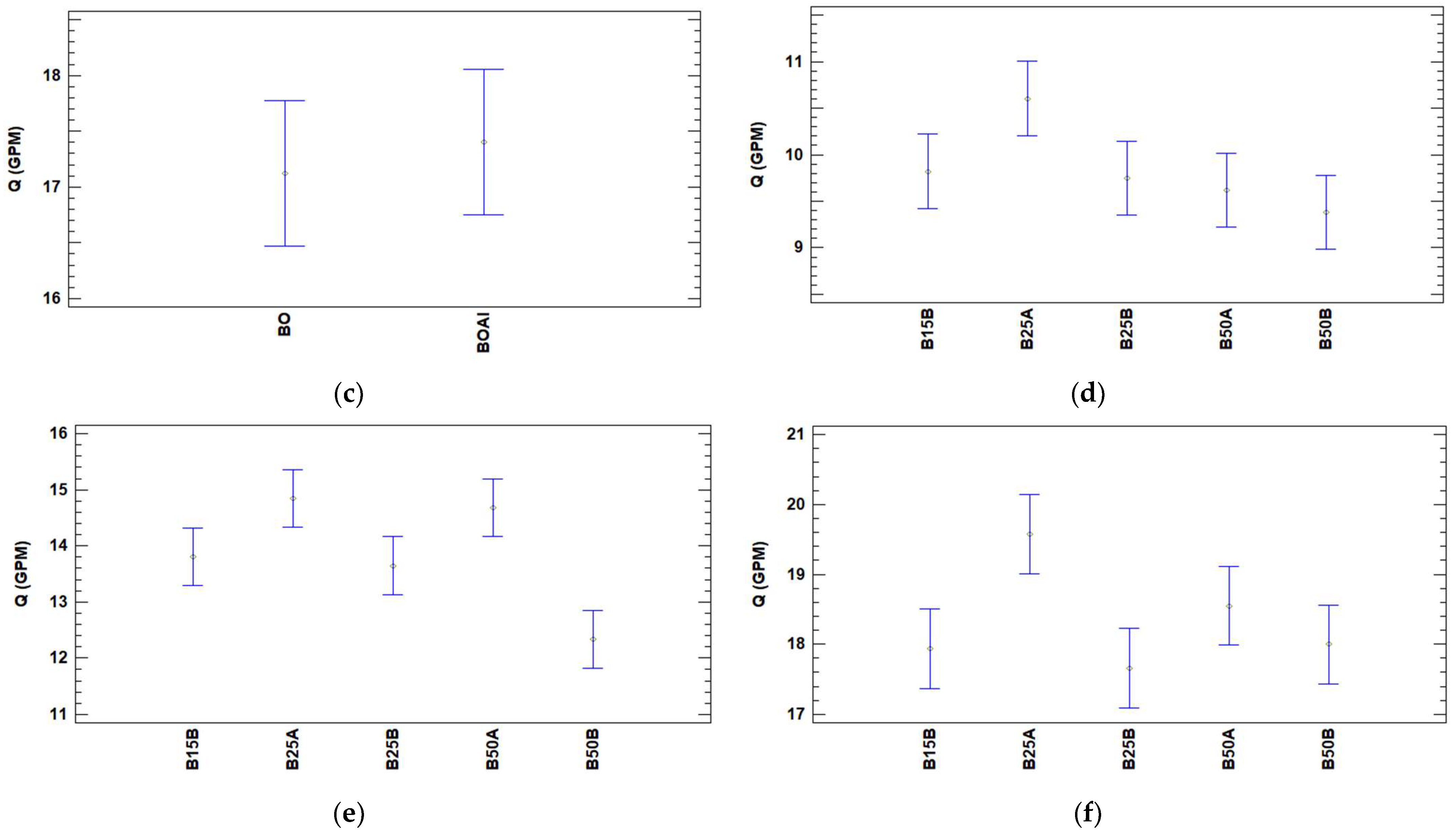
- The head–flow rate and performance–flow rate curves for the original aluminum impeller and original bronze impeller, which came with the pump, are not different; this result validates the comparison of the original bronze impeller with the double curvature impellers. Another important contribution of this study is the set of different head–flow rate and performance–flow rate equations obtained for each of the assessed impellers, both experimentally and by simulation.
- Double curvature impellers at 25% of the length from the exterior diameter in relation to the interior diameter deliver more head than the original impeller; impeller B25A performed better compared to impeller B25B. This difference can be observed not only in the head–flow rate curve figures but also in the Turkey’s test. The performance of the pump–motor unit with impeller B25A was better than the original impeller.
- The curves obtained experimentally and by simulation do not show a statistically significant difference with a 95% confidence interval.
- For a better understanding of the physical behavior of variables such as pressure and flow velocity in the impellers and at the outlet of the pumping system, several three-dimensional CFD models were developed, which were used to represent the scenarios described in Table 1. In the different tests carried out, flows at the inlet and outlet were in the range of the Reynolds number between 10,304 and 138,951, being in the turbulent flow regime; therefore, the use of turbulence models was considered for the modelling of the pumping system.
- For the validation process, a mesh independence analysis and comparison with experimental pumping characteristic curves was performed, where the curves obtained from the CFD model showed a similar trend to the experimental curves.
- It was identified, through CFD modelling, that the double curved blades generate higher pressure fronts when pushing the water towards the volute, leading to the generation of higher pressure compared to impellers without double curvature.
- The application of the k-ω SST and k-ε turbulence models was adequate to understand the physical behavior of the turbulence effects in impellers, where some numerical and spatial differences were identified concerning the generation of turbulent kinetic energy and the prediction of vorticity by summing the results of the velocity and pressure contours. However, it was found that the trend of the Q-H curves was similar using the different turbulence models. Finally, these turbulence models guarantee an adequate prediction of physical behavior concerning the Q-H ratio, and they have been used for similar analyses in previous research.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Patel, M.G.; Doshi, A.V. Effect of Impeller Blade Exit Angle on the Performance of Centrifugal Pump. Int. J. Emerg. Technol. Adv. Eng. 2013, 3, 702–706. [Google Scholar]
- Tuzson, J. Centrifugal Pump Design; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2000. [Google Scholar]
- Gulich, J.F. Centrifugal Pumps, 2nd ed.; Springer: New York, NY, USA, 2010. [Google Scholar]
- Srinivasan, K. Rotodynamic Pumps (Centrifugal and Axial); New Age International (P) Ltd.: Delhi, India, 2008. [Google Scholar]
- Spence, R.; Amaral-Teixeira, J. Investigation into pressure pulsations in a centrifugal pump using numerical methods supported by industrial tests. Comput. Fluids 2008, 37, 690–704. [Google Scholar] [CrossRef]
- Spence, R.; Amaral-Teixeira, J. A CFD parametric study of geometrical variations on the pressure pulsations and performance characteristics of a centrifugal pump. Comput. Fluids 2009, 38, 1243–1257. [Google Scholar] [CrossRef] [Green Version]
- Fontanals, A.; Guardo, A.; Coussirat, M.; Egusquiza, E. Numerical Study of the Fluid—Structure Interaction in the Diffuser Passage of a Centrifugal Pump. In Proceedings of the IV International Conference on Computational Methods for Coupled Problems in Science and Engineering, Kos, Greece, 20–22 June 2011. [Google Scholar]
- Savar, M.; Kozmar, H.; Sutlović, I. Improving centrifugal pump efficiency by impeller trimming. Desalination 2009, 249, 654–659. [Google Scholar] [CrossRef]
- Barrio, R.; Fern’andez, J.; Blanco, E.; Parrondo, J. Estimation of radial load in centrifugal pumps using computational fluid dynamics. Eur. J. Mech. B/Fluids 2011, 30, 316–324. [Google Scholar] [CrossRef]
- Houlin, L.; Yong, W.; Shouqi, Y.; Minggao, T.A.N.; Kai, W. Effects of Blade Number on Characteristics of Centrifugal Pumps. Chin. J. Mech. Eng. 2010, 23, 742. [Google Scholar]
- Li, W.-G. Influence of the Number of Impeller Blades on the Performance of Centrifugal Oil Pumps; World Pumps: Oxford, MS, USA, 2002. [Google Scholar]
- Rababa, K.S. The Effect of Blades Number and Shape on the Operating Characteristics of Groundwater Centrifugal Pumps. Eur. J. Sci. Res. 2011, 52, 243–251. [Google Scholar]
- Chakraborty, S.; Pandey, K.M. Numerical Studies on Effects of Blade Number Variations on Performance of Centrifugal Pumps at 4000 RPM. Int. J. Eng. Technol. 2011, 3, 410–416. [Google Scholar] [CrossRef] [Green Version]
- Pandey, K.M.; Singh, A.P.; Chakraborty, S.; Engineering, M.; Silchar, N.I.T. Numerical studies on effects of blade number variations on performance of centrifugal pumps at 2500 RPM. J. Environ. Res. Dev. 2012, 6, 863–868. [Google Scholar]
- Sanda, B.; Daniela, C.V. The Influence of the Inlet Angle Over the Radial Impeller Geometry Design Approach with ANSYS. J. Eng. Stud. Res. 2012, 18, 32–39. [Google Scholar] [CrossRef]
- Luo, X.; Zhang, Y.; Peng, J.; Xu, H.; Yu, W. Impeller inlet geometry effect on performance improvement for centrifugal pumps. J. Mech. Sci. Technol. 2008, 22, 1971–1976. [Google Scholar] [CrossRef]
- Shojaeefard, M.; Tahani, M.; Ehghaghi, M.; Fallahian, M.; Beglari, M. Numerical study of the effects of some geometric characteristics of a centrifugal pump impeller that pumps a viscous fluid. Comput. Fluids 2012, 60, 61–70. [Google Scholar] [CrossRef]
- Bacharoudis, E.C.; Filios, A.E.; Mentzos, M.D.; Margaris, D.P. Parametric Study of a Centrifugal Pump Impeller by Varying the Outlet Blade Angle. Open Mech. Eng. J. 2008, 2, 75–83. [Google Scholar] [CrossRef]
- Al-Qutub, A.M.; Khalifa, A.E.; Al-Sulaiman, F.A. Exploring the Effect of V-Shaped Cut at Blade Exit of a Double Volute Centrifugal Pump. J. Press. Vessel. Technol. 2012, 134, 8. [Google Scholar] [CrossRef]
- Patil, P.M.; Patil, S.S.; Todkar, R.G. Design, Development and Testing of an Impeller of Open Well Submersible Pump for Performance Improvement. Int. J. Sci. Res. 2014, 3, 2670–2675. [Google Scholar]
- Anagnostopoulos, J.S. A fast numerical method for flow analysis and blade design in centrifugal pump impellers. Comput. Fluids 2009, 38, 284–289. [Google Scholar] [CrossRef]
- Grapsas, V.A.; Anagnostopoulos, J.S.; Papantonis, D.E. Experimental and Numerical Study of a radial Flow Pump Impeller with 2D-Curved Blades. In Proceedings of the International Conference on Fluid Mechanics and Aerodynamics, Athens, Greece, 25–27 August 2007; pp. 175–180. [Google Scholar]
- Zhou, W.; Zhao, Z.; Lee, T.S.; Winoto, S.H. Investigation of Flow Through Centrifugal Pump Impellers Using Computational Fluid Dynamics. Int. J. Rotating Mach. 2003, 9, 49–61. [Google Scholar] [CrossRef] [Green Version]
- Yang, M.G.; Liu, D.; Gu, H.F.; Kang, C.; Li, H. Analysis of Turbulent Flow in the Impeller of a Chemical Pump. J. Eng. Sci. Technol. 2007, 2, 218–225. [Google Scholar]
- Shvindin, A.I.; Ivanyushin, A.A. Operation of centrifugal pumps in off-design conditions. Chem. Pet. Eng. 2009, 45, 148–151. [Google Scholar] [CrossRef]
- Cheah, K.W.; Lee, T.S.; Winoto, S.H.; Zhao, Z.M. Numerical Flow Simulation in a Centrifugal Pump at Design and Off-Design Conditions. Int. J. Rotating Mach. 2007, 2007, 083641. [Google Scholar] [CrossRef]
- Barrio, R.; Parrondo, J.; Blanco, E. Numerical analysis of the unsteady flow in the near-tongue region in a volute-type centrifugal pump for different operating points. Comput. Fluids 2010, 39, 859–870. [Google Scholar] [CrossRef]
- Ozturk, A.; Aydin, K.; Sahin, B.; Pinarbasi, A. Effect of impeller-diffuser radial gap ratio in a centrifugal pump. JSIR 2009, 68, 203–213. [Google Scholar]
- Gupta, M.; Kumar, S.; Kumar, A. Numerical Study of Pressure and Velocity Distribution Analysis of Centrifugal Pump. Int. J. Therm. Technol. 2011, 1, 114–118. [Google Scholar]
- Asuaje, M.; Bakir, F.; Kouidri, S.; Kenyery, F.; Rey, R. Numerical Modelization of the Flow in Centrifugal Pump: Volute Influence in Velocity and Pressure Fields. Int. J. Rotating Mach. 2005, 2005, 244–255. [Google Scholar] [CrossRef] [Green Version]
- Esfahani, J.A.; Moghadam, B.J.; Nouri, M.; Mahmoudi, A. Numerical and parametric study of a centrifugal pump. In Proceedings of the International Conference on Advances in Mechanical and Robotics Engineering—MRE 2014, Kuala Lumpur, Malaysia, 8–9 March 2014; pp. 35–39. [Google Scholar]
- Kulkarni, S.S. Parametric Study of Centrifugal Pump and its Performance Analysis using CFD. Int. J. Emerg. Technol. Adv. Eng. 2014, 4, 155–161. [Google Scholar]
- Shojaeefard, M.H.; Boyaghchi, F.A.; Ehghaghi, M.B. Experimental Study and Three-Dimensional Numerical Flow Simulation in a Centrifugal Pump when Handling Viscous Fluids. IUST Int. J. Eng. Sci. 2006, 17, 53–60. [Google Scholar]
- Fard, M.H.S.; Boyaghchi, F.A. Studies on the Influence of Various Blade Outlet Angles in a Centrifugal Pump when Handling Viscous Fluids. Am. J. Appl. Sci. 2007, 4, 718. [Google Scholar] [CrossRef]
- Pagalthivarthi, K.V.; Gupta, P.K.; Tyagi, V.; Ravi, M.R. CFD Predictions of Dense Slurry Flow in Centrifugal Pump Casings. Int. J. Aerosp. Mech. Eng. 2011, 5, 254–266. [Google Scholar]
- Gölcü, M.; Pancar, Y. Investigation of Performance Characteristics in a Pump Impeller with Low Blade Discharge Angle; World Pumps: Oxford, MS, USA, 2005. [Google Scholar]
- Baoling, C.; Zuchao, Z.; Jianci, Z.; Ying, C. The Flow Simulation and Experimental Study of Low Specific-Speed High-speed Complex Centrifugal Impellers. Chin. J. Mech. Eng. 2006, 14, 435–441. [Google Scholar]
- Kaya, D.; Yagmur, E.A.; Yigit, K.S.; Kilic, F.C.; Eren, A.S.; Celik, C. Energy efficiency in pumps. Energy Convers. Manag. 2008, 49, 1662–1673. [Google Scholar] [CrossRef]
- Yedidiah, S. A Study in the Use of CFD in the Design of Centrifugal Pumps. Eng. Appl. Comput. Fluid Mech. 2008, 2, 331–343. [Google Scholar] [CrossRef] [Green Version]
- Wu, K.-H.; Lin, B.-J.; Hung, C.-I. Novel Design of Centrifugal Pump Impellers Using Generated Machining Method and CFD. Eng. Appl. Comput. Fluid Mech. 2008, 2, 195–207. [Google Scholar] [CrossRef] [Green Version]
- Bachus, L. ADHD and NPSH; World Pumps: Oxford, MS, USA, 2005; pp. 26–29. [Google Scholar]
- Abbas, M.K. Cavitation in centrifugal pumps. Diyala J. Eng. Sci. 2010, 170–180. [Google Scholar]
- Černetič, J.; Čudina, M. Cavitation Noise Phenomena in Centrifugal Pumps. In Proceedings of the 5th Congress of Alps-Adria Acoustics Association, Petrcane, Croatia, 12–14 September 2012; pp. 1–6. [Google Scholar]
- Budea, S.; Ciocanea, A. The Influence of the Suction Vortex Over the NPSH Available of Centrifugal Pumps. U.P.B. Sci. Bull. 2008, 70, 1–10. [Google Scholar]
- Shah, S.R.; Jain, S.V.; Patel, R.N.; Lakhera, V.J. CFD for centrifugal pumps: A review of the state-of-the-art. Procedia Eng. 2013, 51, 715–720. [Google Scholar] [CrossRef] [Green Version]
- Cherkasski, V. Pumps, Fans, Compressors; MIRED: Moscow, Russia, 1980. [Google Scholar]
- Ke, Q.; Tang, L.; Luo, W.; Cao, J. Parameter Optimization of Centrifugal Pump Splitter Blades with Artificial Fish Swarm Algorithm. Water 2023, 15, 1806. [Google Scholar] [CrossRef]
- Hu, J.; Li, K.; Su, W.; Zhao, X. Numerical Simulation of Drilling Fluid Flow in Centrifugal Pumps. Water 2023, 15, 992. [Google Scholar] [CrossRef]
- PTC 8.2-1990; Centrifugal Pumps. ASME: New York, NY, USA, 1990.
- Greenshields, C.; Weller, H. Notes on Computational Fluid Dynamics: General Principles; CFD Direct Ltd.: Reading, UK, 2022. [Google Scholar]
- Launder, B.E.; Spalding, D.B. The Numerical Computation of Turbulent Flows. In Numerical Prediction of Flow, Heat Transfer, Turbulence and Combustion; Imperial College of Science and Technology, Department of Mechanical Engineering; Elsevier: London, UK, 1983; pp. 96–116. [Google Scholar]
- Liu, H.L.; Liu, M.M.; Dong, L.; Ren, Y.; Du, H. Effects of computational grids and turbulence models on numerical simulation of centrifugal pump with CFD. IOP Conf. Ser. Earth Environ. Sci. 2012, 15, 062005. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Menter, F.R. Review of the shear-stress transport turbulence model experience from an industrial perspective. Int. J. Comput. Fluid Dyn. 2009, 23, 305–316. [Google Scholar] [CrossRef]
- Kaewnai, S.; Chamaoot, M.; Wongwises, S. Predicting performance of radial flow type impeller of centrifugal pump using CFD. J. Mech. Sci. Technol. 2009, 23, 1620–1627. [Google Scholar] [CrossRef]
- Chima, R.; Liou, M.S. Comparison of the AUSM+ and H-CUSP Schemes for Turbomachinery Applications. In Proceedings of the 16th AIAA Computational Fluid Dynamics Conference, Orlando, FL, USA, 23–26 June 2003; p. 4120. [Google Scholar]
- Wu, J.; Shimmei, K.; Tani, K.; Niikura, K.; Sato, J. CFD-based design optimization for hydro turbines. J. Fluids Eng. 2007, 129, 159–168. [Google Scholar] [CrossRef]
- Mott, R.L. Applied Fluid Mechanics, 6th ed.; Pearson Education: London, UK, 2016. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments, 8th ed.; LWW: Philadelphia, PA, USA, 2012. [Google Scholar]
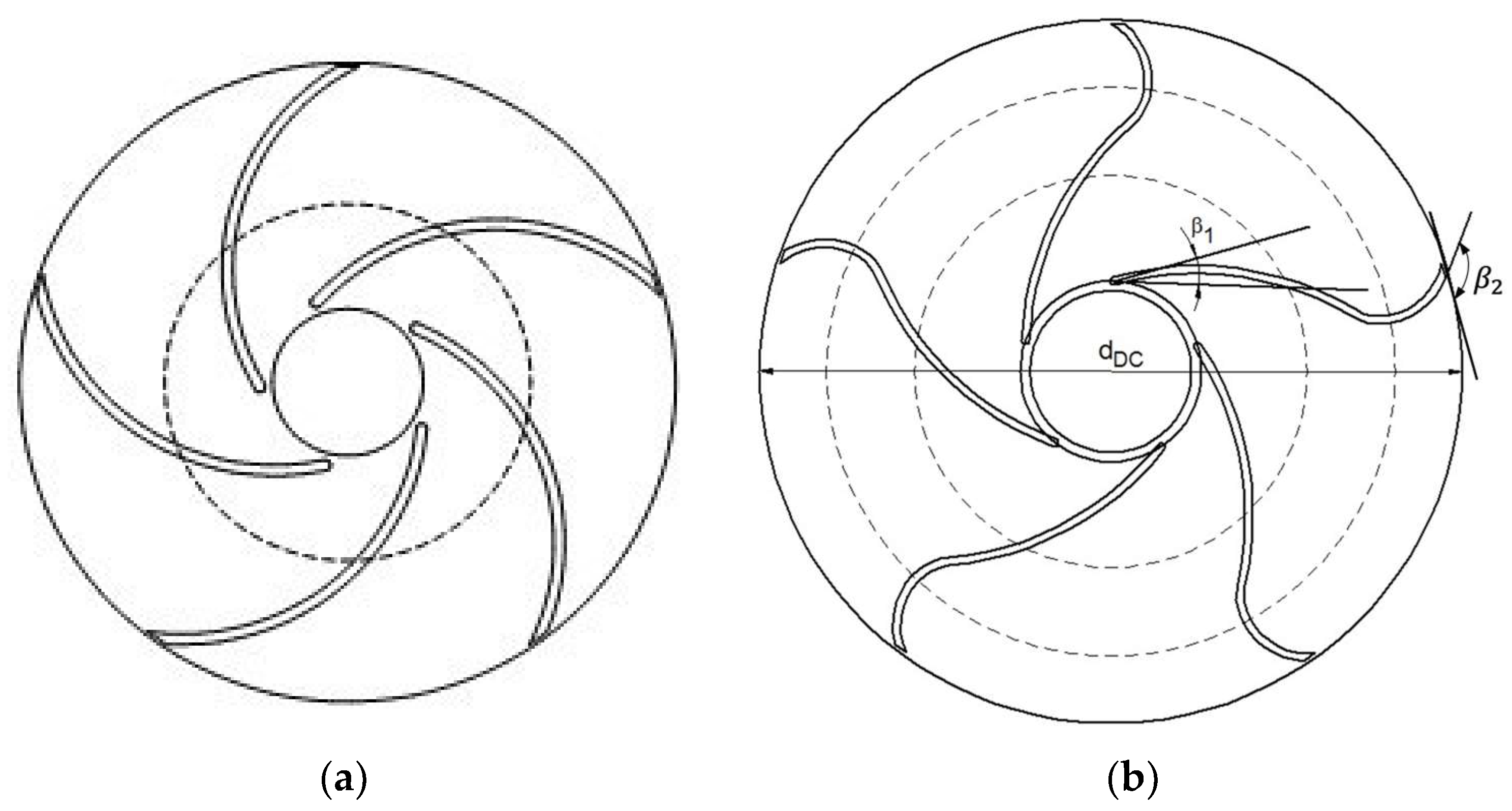


| Impeller | (°) | (°) | (%) | (mm) |
|---|---|---|---|---|
| BO | 17 | 30 | ||
| BOAl | 17 | 30 | ||
| B25A | 90 | 150 | 25 | 159.9 |
| B25B | 163 | 30 | 25 | 159.9 |
| B50A | 90 | 150 | 50 | 113.2 |
| B50B | 163 | 30 | 50 | 113.2 |
| B15B | 163 | 30 | 15 | 159.9 |
| Impeller | Fluid | Rotating Fluid | ||
|---|---|---|---|---|
| Cells | Nodes | Cells | Nodes | |
| BO/BOAl | 776,181 | 4,243,191 | 217,590 | 1,088,747 |
| B25A | 776,005 | 4,238,226 | 216,562 | 1,099,660 |
| B25B | 774,347 | 4,227,560 | 224,197 | 1,122,148 |
| B50A | 779,221 | 4,260,653 | 213,663 | 1,083,460 |
| B50B | 777,577 | 4,250,597 | 223,323 | 1,122,050 |
| B15B | 771,334 | 4,208,591 | 227,538 | 1,138,883 |
| Impeller | w (RPM) | R2 | |||
|---|---|---|---|---|---|
| BO | 1400 | −8.77 × 10−4 | −1.11 × 10−2 | 10.10 | 98.98 |
| 1700 | −8.86 × 10−4 | −1.74 × 10−2 | 14.25 | 99.76 | |
| 1900 | −1.10 × 10−3 | −1.80 × 10−2 | 19.04 | 99.80 | |
| BOAl | 1400 | −7.28 × 10−4 | −1.53 × 10−2 | 10.17 | 99.90 |
| 1700 | −5.37 × 10−4 | −2.81 × 10−2 | 14.21 | 99.93 | |
| 1900 | −7.23 × 10−4 | −3.51 × 10−2 | 19.36 | 99.94 | |
| B25A | 1400 | −1.10 × 10−3 | 1.49 × 10−2 | 10.53 | 98.83 |
| 1700 | −8.69 × 10−4 | −4.50 × 10−3 | 15.07 | 99.67 | |
| 1900 | −8.29 × 10−4 | −1.27 × 10−2 | 19.99 | 99.46 | |
| B25B | 1400 | −9.16 × 10−4 | 5.20 × 10−3 | 10.53 | 98.36 |
| 1700 | −1.37 × 10−3 | 4.75 × 10−3 | 14.86 | 98.37 | |
| 1900 | −1.00 × 10−3 | −2.28 × 10−2 | 19.81 | 99.80 | |
| B50A | 1400 | −5.81 × 10−4 | 4.09 × 10−3 | 9.84 | 97.61 |
| 1700 | −7.00 × 10−4 | −4.62 × 10−3 | 14.14 | 99.34 | |
| 1900 | −9.72 × 10−4 | −4.78 × 10−3 | 19.11 | 95.24 | |
| B50B | 1400 | −4.32 × 10−4 | −2.84 × 10−2 | 10.43 | 97.28 |
| 1700 | −1.15 × 10−4 | −4.88 × 10−2 | 14.82 | 96.59 | |
| 1900 | −1.25 × 10−3 | −2.50 × 10−2 | 19.73 | 99.55 | |
| B15B | 1400 | −1.22 × 10−3 | 8.15 × 10−3 | 10.10 | 98.06 |
| 1700 | −1.02 × 10−3 | −7.20 × 10−3 | 14.29 | 98.91 | |
| 1900 | −1.40 × 10−3 | −3.91 × 10−3 | 18.80 | 99.47 |
| Impeller | w (RPM) | ||
|---|---|---|---|
| 1400 | 1700 | 1900 | |
| BO | 37.95 | 45.33 | 51.82 |
| BOAl | 37.96 | 45.42 | 52.08 |
| B25A | 39.41 | 46.98 | 53.60 |
| B25B | 39.35 | 43.47 | 52.07 |
| B50A | 38.97 | 46.22 | 52.84 |
| B50B | 37.06 | 45.08 | 50.80 |
| B15B | 37.31 | 44.56 | 50.55 |
| Impeller | w (RPM) | D | E | F | R2 |
|---|---|---|---|---|---|
| BO | 1400 | −3.17 × 10−2 | 2.65 | 1.27 × 10−1 | 99.99 |
| 1700 | −2.32 × 10−2 | 2.29 | 4.01 × 10−1 | 99.97 | |
| 1900 | −1.88 × 10−2 | 2.02 | 3.71 × 10−1 | 99.98 | |
| BOAl | 1400 | −2.91 × 10−2 | 2.65 | 3.10 × 10−1 | 99.95 |
| 1700 | −2.00 × 10−2 | 2.19 | 5.46 × 10−1 | 99.95 | |
| 1900 | −1.77 × 10−2 | 2.05 | 8.68 × 10−1 | 99.90 | |
| B25A | 1400 | −3.38 × 10−2 | 2.80 | 1.22 × 10−1 | 99.71 |
| 1700 | −2.79 × 10−2 | 2.53 | 7.61 × 10−1 | 99.90 | |
| 1900 | −2.21 × 10−2 | 2.24 | 7.74 × 10−1 | 99.92 | |
| B25B | 1400 | −3.35 × 10−2 | 2.69 | 5.53 × 10−1 | 99.91 |
| 1700 | −3.06 × 10−2 | 2.47 | 5.17 × 10−1 | 99.86 | |
| 1900 | −2.25 × 10−2 | 2.09 | 9.85 × 10−1 | 99.73 | |
| B50A | 1400 | −2.58 × 10−2 | 2.31 | 6.18 × 10−1 | 99.93 |
| 1700 | −2.27 × 10−2 | 2.13 | 3.94 × 10−1 | 99.92 | |
| 1900 | −2.00 × 10−2 | 1.98 | 2.23 × 10−1 | 99.13 | |
| B50B | 1400 | −3.28 × 10−2 | 2.55 | 8.57 × 10−1 | 99.73 |
| 1700 | −2.48 × 10−2 | 2.30 | 1.08 | 99.55 | |
| 1900 | −2.36 × 10−2 | 2.15 | 4.88 × 10−1 | 99.89 | |
| B15B | 1400 | −2.67 × 10−2 | 2.26 | 8.55 × 10−1 | 99.40 |
| 1700 | −2.28 × 10−2 | 2.07 | 6.11 × 10−1 | 99.89 | |
| 1900 | −1.92 × 10−2 | 1.84 | 6.24 × 10−1 | 99.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abuchar-Curi, A.M.; Coronado-Hernández, O.E.; Useche, J.; Abuchar-Soto, V.J.; Palencia-Díaz, A.; Paternina-Verona, D.A.; Ramos, H.M. Improving Pump Characteristics through Double Curvature Impellers: Experimental Measurements and 3D CFD Analysis. Fluids 2023, 8, 217. https://doi.org/10.3390/fluids8080217
Abuchar-Curi AM, Coronado-Hernández OE, Useche J, Abuchar-Soto VJ, Palencia-Díaz A, Paternina-Verona DA, Ramos HM. Improving Pump Characteristics through Double Curvature Impellers: Experimental Measurements and 3D CFD Analysis. Fluids. 2023; 8(8):217. https://doi.org/10.3390/fluids8080217
Chicago/Turabian StyleAbuchar-Curi, Alfredo M., Oscar E. Coronado-Hernández, Jairo Useche, Verónica J. Abuchar-Soto, Argemiro Palencia-Díaz, Duban A. Paternina-Verona, and Helena M. Ramos. 2023. "Improving Pump Characteristics through Double Curvature Impellers: Experimental Measurements and 3D CFD Analysis" Fluids 8, no. 8: 217. https://doi.org/10.3390/fluids8080217
APA StyleAbuchar-Curi, A. M., Coronado-Hernández, O. E., Useche, J., Abuchar-Soto, V. J., Palencia-Díaz, A., Paternina-Verona, D. A., & Ramos, H. M. (2023). Improving Pump Characteristics through Double Curvature Impellers: Experimental Measurements and 3D CFD Analysis. Fluids, 8(8), 217. https://doi.org/10.3390/fluids8080217









