A Mock Circulation Loop to Characterize In Vitro Hemodynamics in Human Systemic Arteries with Stenosis
Abstract
1. Introduction
2. Materials and Methods
2.1. Medical Data
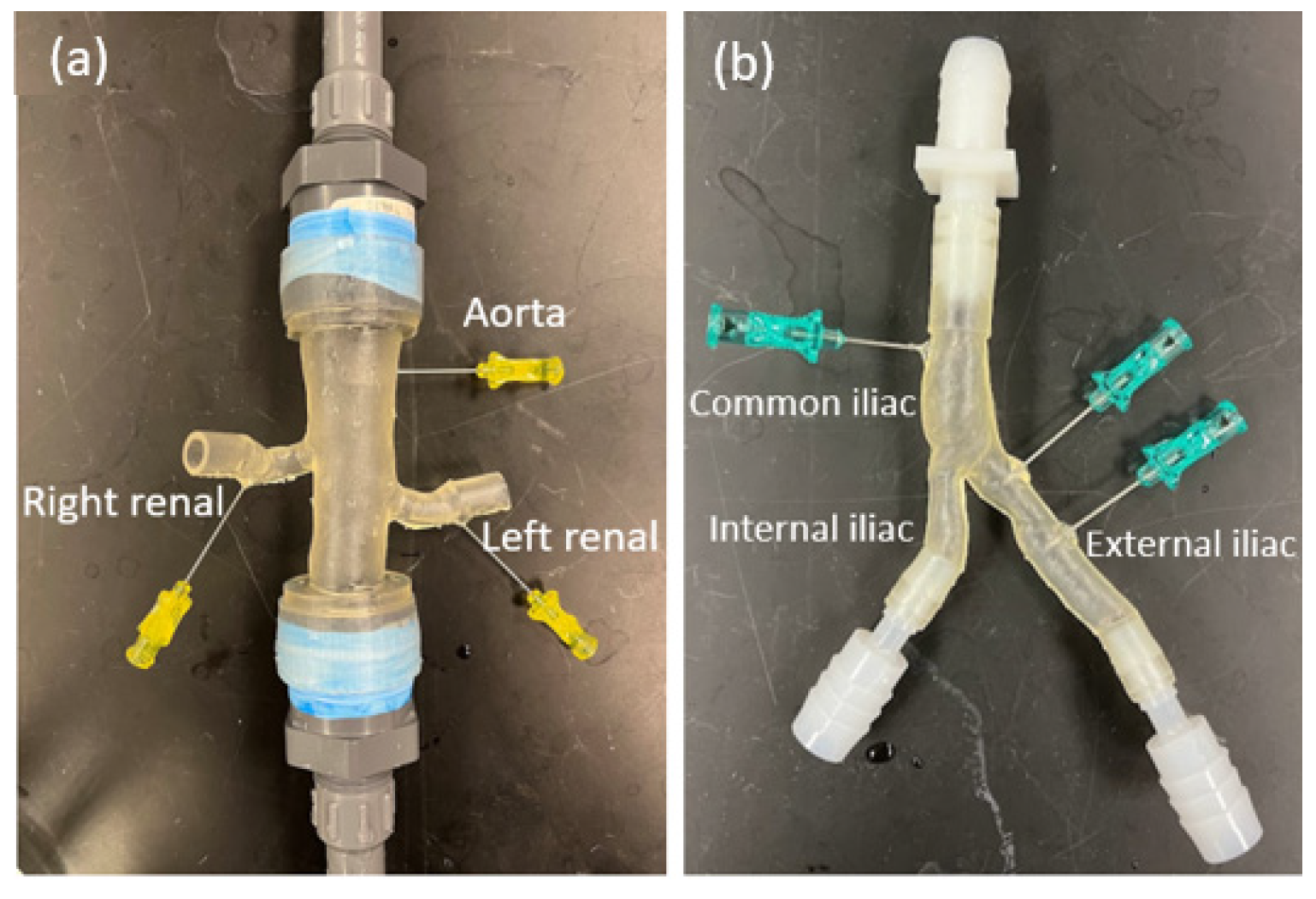
2.2. D-Printed Silicone Arterial Systems
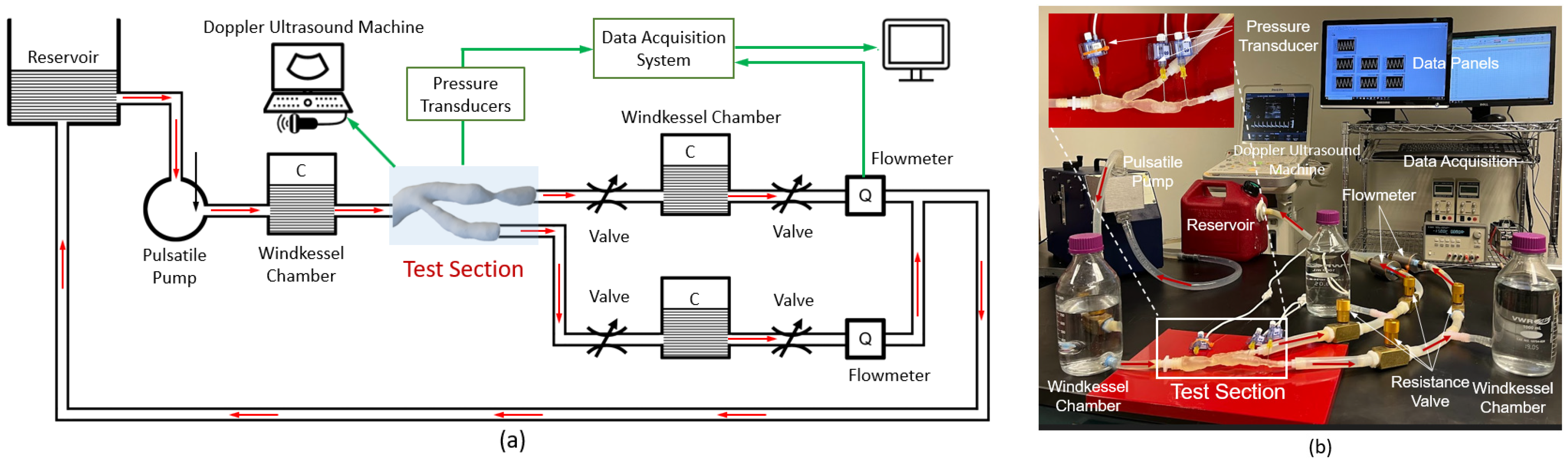
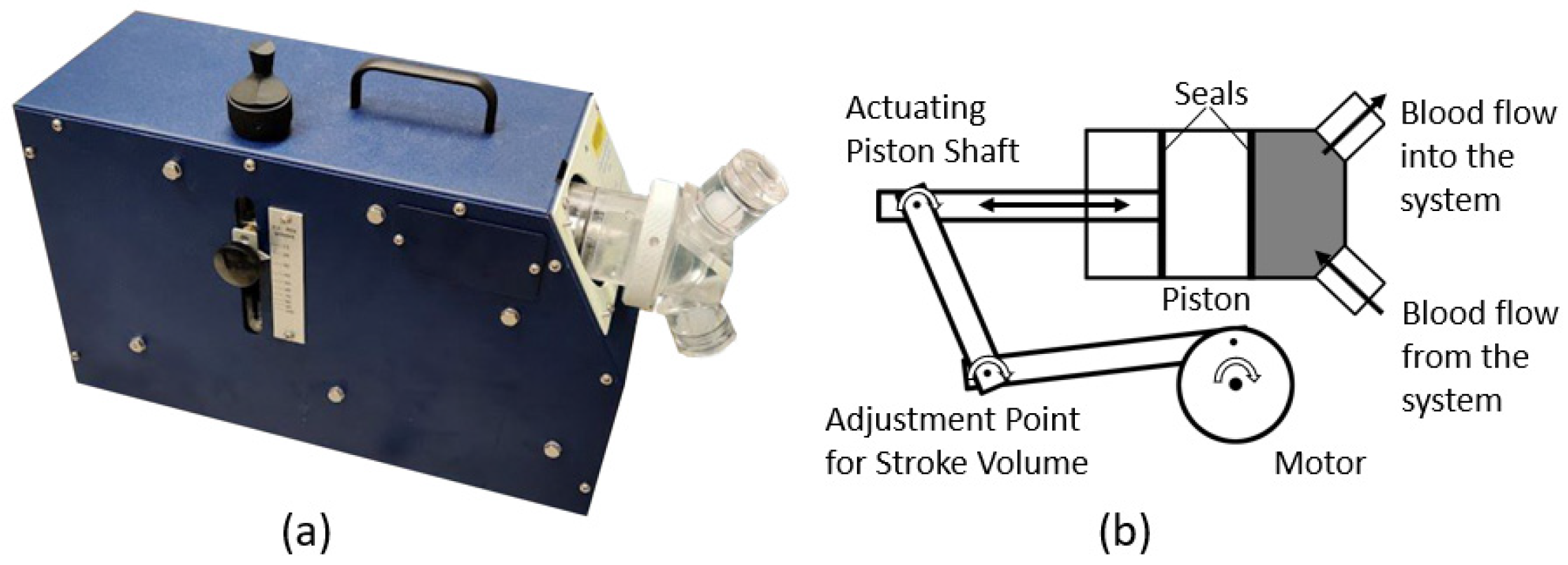
2.3. A Mock Circulation Loop for Human Systemic Arterial Systems
2.4. Instrumentations
3. Application Studies and Experimental Results
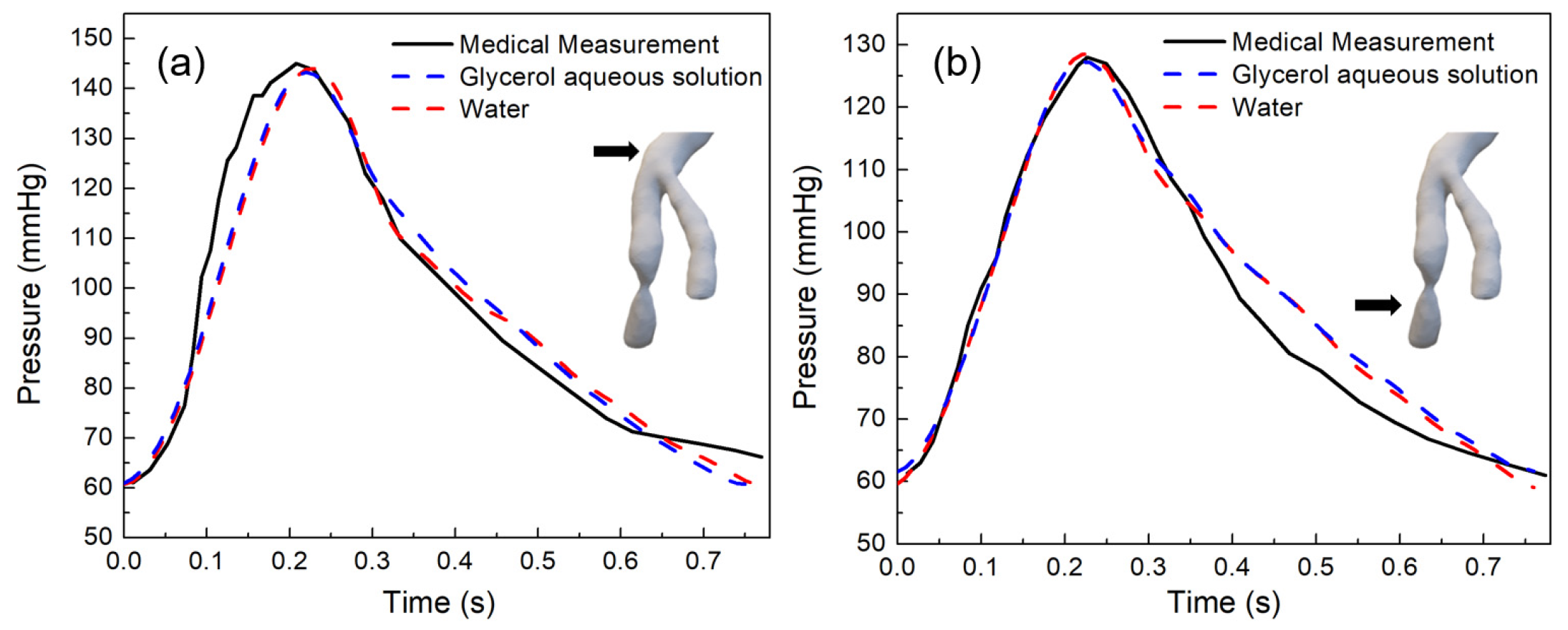
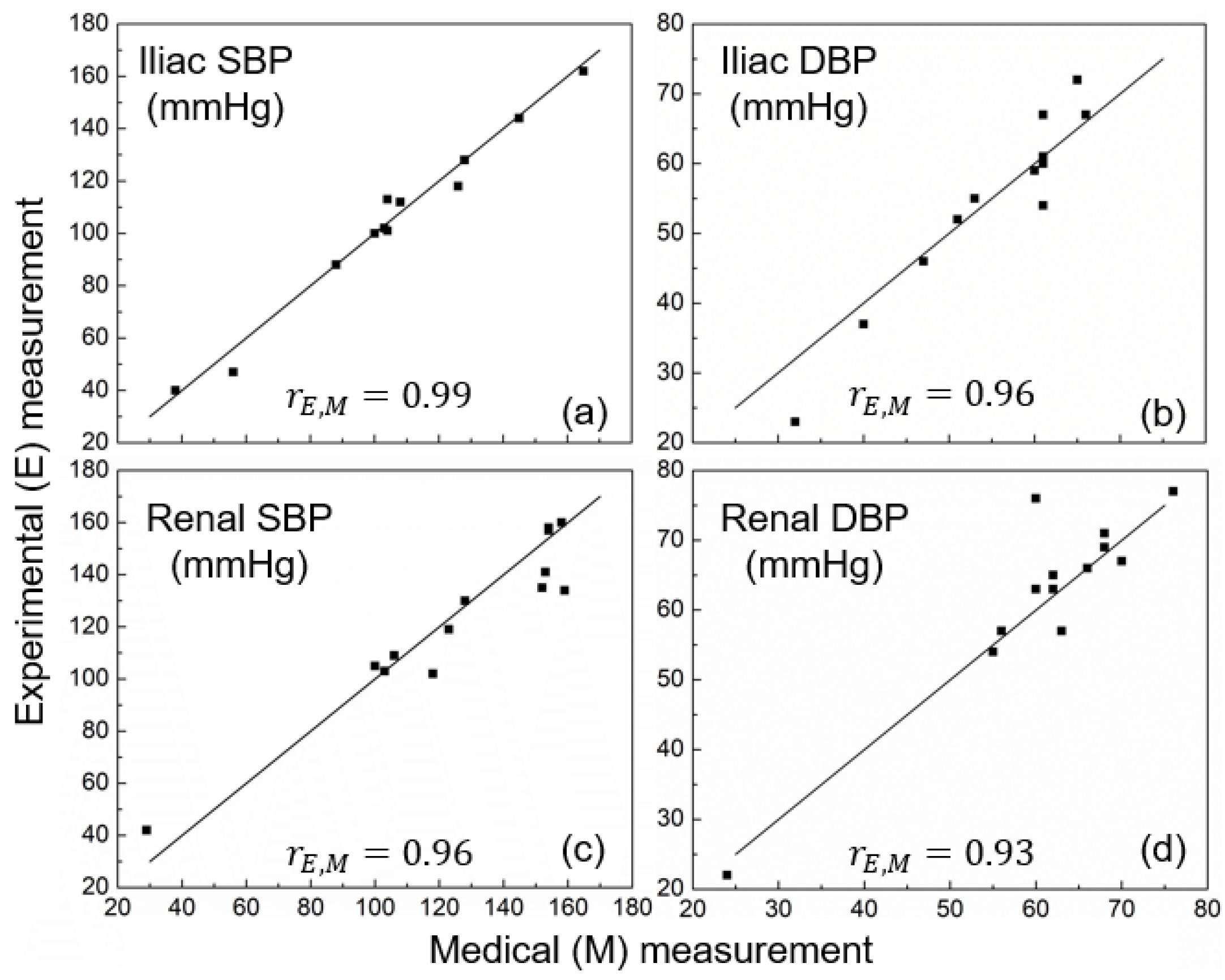
3.1. Reliability of In Vitro Pressure Measurement Using MCL
3.2. Parametric Studies and Experimental Results
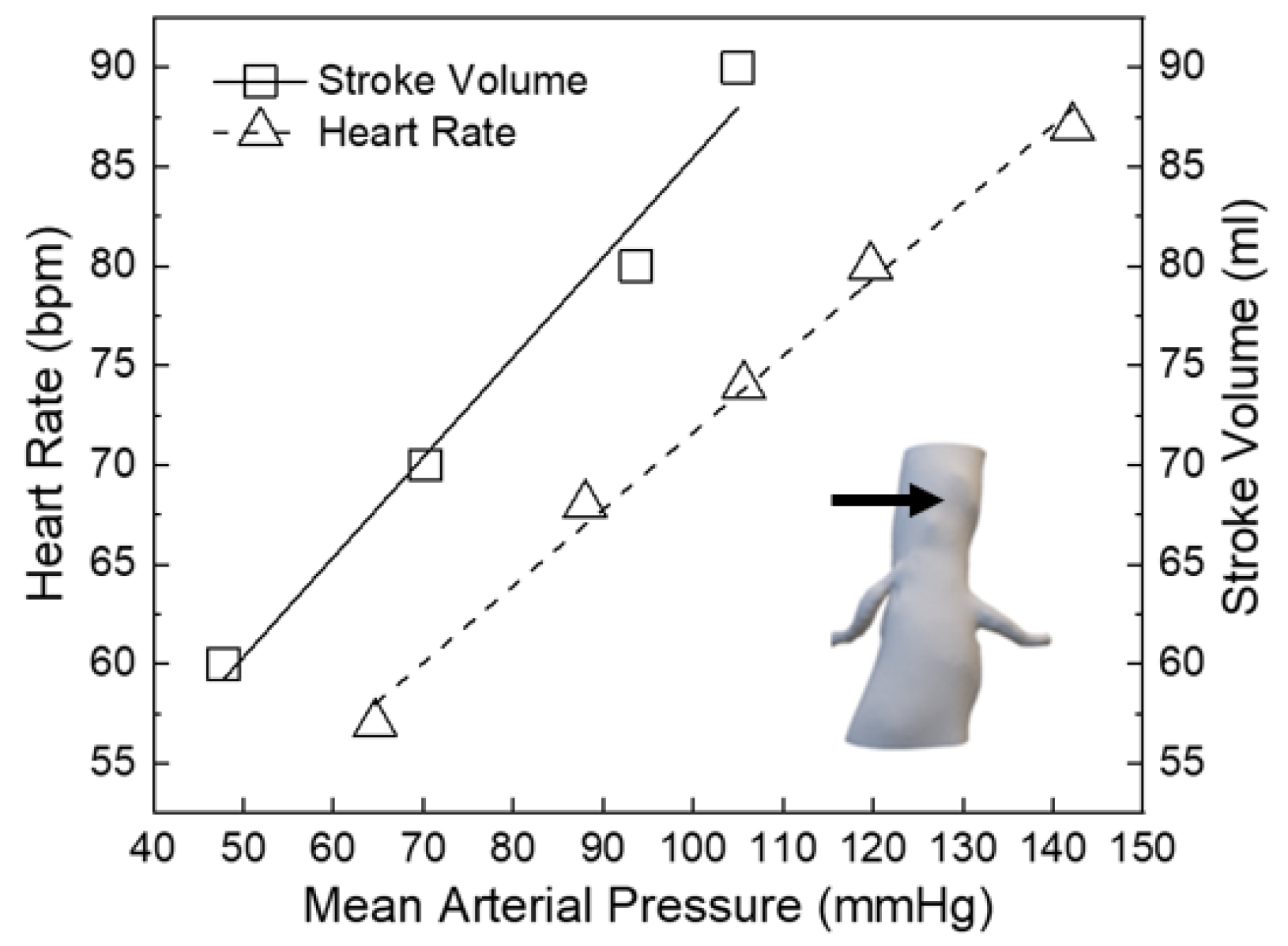
3.2.1. Cardiovascular Responses to MCL Parameters
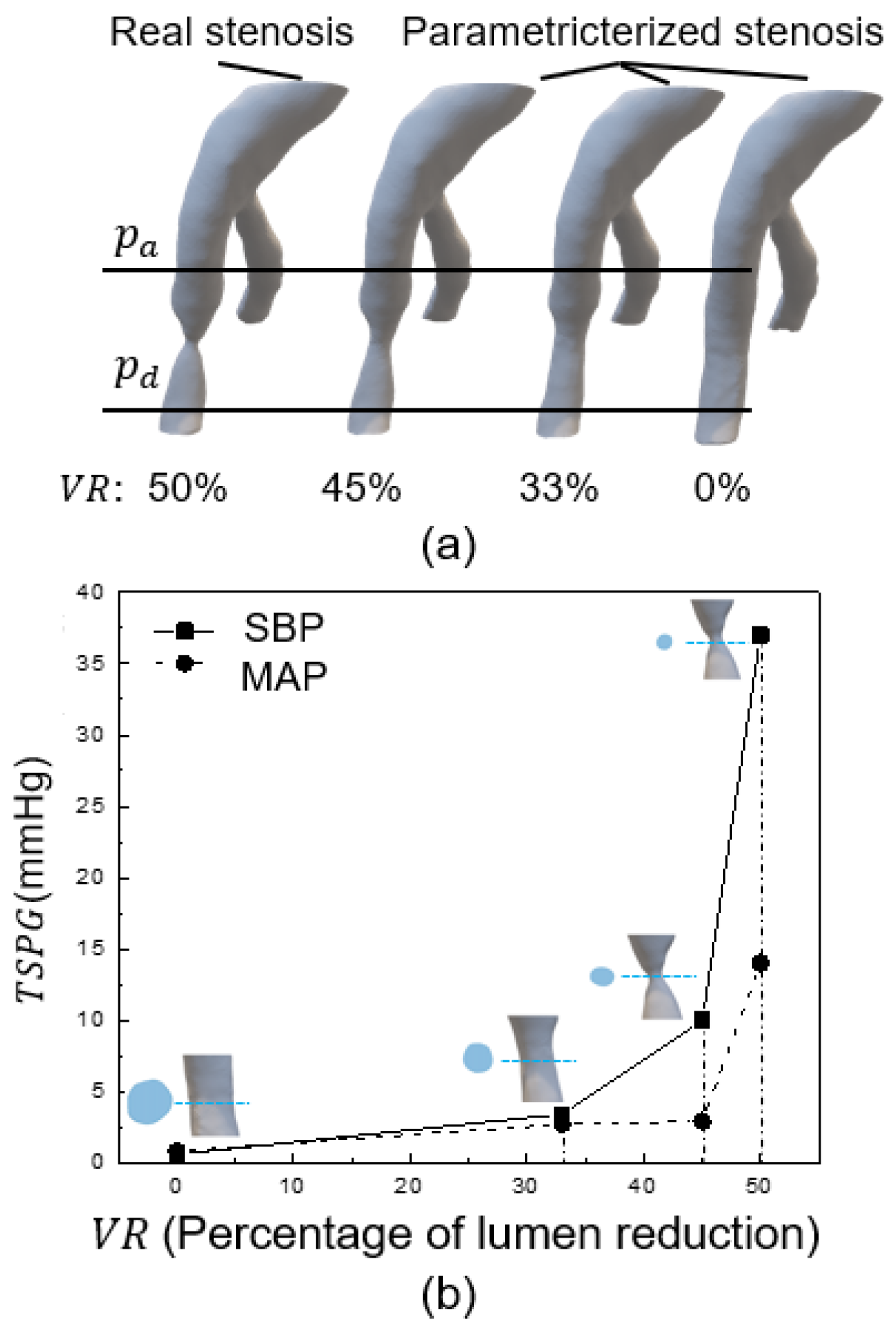
3.2.2. Effects of Stenosis Degree on TSPG
4. Summary and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclatures
| CO | Cardiac output |
| CTA | Computed Tomography angiogram |
| DAQ | Data acquisition system |
| DBP | Diastolic blood pressure |
| DICOM | Digital Imaging and Communications in Medicine |
| DUS | Doppler ultrasound sonography |
| FFR | Fractional flow reserve |
| HR | Heart Rate |
| ICHD | Image-based computational hemodynamics |
| IEHD | Image-based experimental hemodynamics |
| IRB | Institutional Review Board |
| MAP | Mean arterial pressure |
| MCL | Mock circulation loop |
| SBP | Systolic blood pressure |
| STL | Standard Tessellation Language |
| SV | Stroke volume |
| TSPG | Trans-stenotic pressure gradient |
| V&V | Verification and validation |
| WK3 | 3-element Windkessel model |
References
- Pijls, N.H.; de Bruyne, B.; Peels, K.; van der Voort, P.H.; Bonnier, H.J.; Bartunek, J.; Koolen, J.J. Measurement of fractional flow reserve to assess the functional severity of coronary-artery stenoses. N. Engl. J. Med. 1996, 334, 1703–1708. [Google Scholar] [CrossRef] [PubMed]
- Nørgaard, B.L.; Fairbairn, T.A.; Safian, R.D.; Rabbat, M.G.; Ko, B.; Jensen, J.M.; Nieman, K.; Chinnaiyan, K.M.; Sand, N.P.; Matsuo, H. Coronary CT angiography-derived fractional flow reserve testing in patients with stable coronary artery disease: Recommendations on interpretation and reporting. Radiol. Cardiothorac. Imaging 2019, 1, e190050. [Google Scholar] [CrossRef]
- Ahmad, Y.; Götberg, M.; Cook, C.; Howard, J.P.; Malik, I.; Mikhail, G.; Frame, A.; Petraco, R.; Rajkumar, C.; Demir, O. Coronary hemodynamics in patients with severe aortic stenosis and coronary artery disease undergoing transcatheter aortic valve replacement: Implications for clinical indices of coronary stenosis severity. JACC Cardiovasc. Interv. 2018, 11, 2019–2031. [Google Scholar] [CrossRef] [PubMed]
- Lu, M.T.; Ferencik, M.; Roberts, R.S.; Lee, K.L.; Ivanov, A.; Adami, E.; Mark, D.B.; Jaffer, F.A.; Leipsic, J.A.; Douglas, P.S. Noninvasive FFR derived from coronary CT angiography: Management and outcomes in the PROMISE trial. JACC Cardiovasc. Imaging 2017, 10, 1350–1358. [Google Scholar] [CrossRef]
- Mangiacapra, F.; Trana, C.; Sarno, G.; Davidavicius, G.; Protasiewicz, M.; Muller, O.; Ntalianis, A.; Misonis, N.; Van Vlem, B.; Heyndrickx, G.R.; et al. Translesional pressure gradients to predict blood pressure response after renal artery stenting in patients with renovascular hypertension. Circ. Cardiovasc. Interv. 2010, 3, 537–542. [Google Scholar] [CrossRef]
- Yu, H.; Khan, M.; Wu, H.; Zhang, C.; Du, X.; Chen, R.; Fang, X.; Long, J.; Sawchuk, A. Inlet and Outlet Boundary Conditions and Uncertainty Quantification in Volumetric Lattice Boltzmann Method for Image-Based Computational Hemodynamics. Fluids 2022, 7, 30. [Google Scholar] [CrossRef]
- Yu, H.; Khan, M.; Wu, H.; Du, X.; Chen, R.; Rollins, D.M.; Fang, X.; Long, J.; Xu, C.; Sawchuk, A.P. A new noninvasive and patient-specific hemodynamic index for assessing the severity of renal arterial stenosis. Int. J. Numer. Methods Biomed. Eng. 2022, 38, e3611. [Google Scholar] [CrossRef] [PubMed]
- Heinen, S.G.; van den Heuvel, D.A.; Huberts, W.; de Boer, S.W.; van de Vosse, F.N.; Delhaas, T.; de Vries, J.P. In Vivo Validation of Patient-Specific Pressure Gradient Calculations for Iliac Artery Stenosis Severity Assessment. J. Am. Heart Assoc. 2017, 6, e007328. [Google Scholar] [CrossRef]
- Kinney, T.B.; Rose, S.C. Intraarterial pressure measurements during angiographic evaluation of peripheral vascular disease: Techniques, interpretation, applications, and limitations. Am. J. Roentgenol. 1996, 166, 277–284. [Google Scholar] [CrossRef]
- de Boer, S.; Heinen, S.; van den Heuvel, D.; van de Vosse, F.; de Vries, J. How to define the hemodynamic significance of an equivocal iliofemoral artery stenosis: Review of literature and outcomes of an international questionnaire. J. Vascular. 2017, 25, 598–608. [Google Scholar] [CrossRef]
- Marshall, R.S.; Pavol, M.A.; Cheung, Y.K.; Asllani, I.; Lazar, R.M. Cognitive Impairment Correlates Linearly with Mean Flow Velocity by Transcranial Doppler below a Definable Threshold. Cerebrovasc. Dis. Extra 2020, 10, 21–27. [Google Scholar] [CrossRef] [PubMed]
- Koo, B.-K. The present and future of fractional flow reserve. Circ. J. 2014, 78, 1048–1054. [Google Scholar] [CrossRef] [PubMed]
- Marsden, A.L.; Esmaily-Moghadam, M. Multiscale Modeling of Cardiovascular Flows for Clinical Decision Support. Appl. Mech. Rev. 2015, 67, 030804. [Google Scholar] [CrossRef]
- Les, A.S.; Shadden, S.C.; Figueroa, C.A.; Park, J.M.; Tedesco, M.M.; Herfkens, R.J.; Dalman, R.L.; Taylor, C.A. Quantification of hemodynamics in abdominal aortic aneurysms during rest and exercise using magnetic resonance imaging and computational fluid dynamics. Ann. Biomed. Eng. 2010, 38, 1288–1313. [Google Scholar] [CrossRef]
- Antiga, L.; Piccinelli, M.; Botti, L.; Ene-Iordache, B.; Remuzzi, A.; Steinman, A.D. An image-based modeling framework for patient-specific computational hemodynamics. Med. Biol. Eng. Comput. 2008, 46, 1097–1112. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.D.; Kadri, O.E.; Voronov, R.S. An introductory overview of image-based computational modeling in personalized cardiovascular medicine. Front. Bioeng. Biotechnol. 2020, 8, 529365. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Zhao, Y.; Lin, C. Unified Computational Method and System for in vivo Patient-Specific Hemodynamics. U.S. Patent 10482215, 19 November 2019. [Google Scholar]
- Kim, H.; Vignon-Clementel, I.; Coogan, J.; Figueroa, C.; Jansen, K.; Taylor, C. Patient-specific modeling of blood flow and pressure in human coronary arteries. Ann. Biomed. Eng. 2010, 38, 3195–3209. [Google Scholar] [CrossRef] [PubMed]
- Yu, H. Non-invasive Functional Assessment Technique for Determining Hemodynamics Severity of an Arterial Stenosis. U.S. Patent 11538153, 19 November 2022. [Google Scholar]
- Murayama, Y.; Fujimura, S.; Suzuki, T.; Takao, H. Computational fluid dynamics as a risk assessment tool for aneurysm rupture. Neurosurg. Focus 2019, 47, E12. [Google Scholar] [CrossRef]
- Liang, L.; Steinman, D.A.; Brina, O.; Chnafa, C.; Cancelliere, N.M.; Pereira, V.M. Towards the Clinical utility of CFD for assessment of intracranial aneurysm rupture—A systematic review and novel parameter-ranking tool. J. Neurointerventional Surg. 2019, 11, 153–158. [Google Scholar] [CrossRef]
- Can, A.; Du, R. Association of hemodynamic factors with intracranial aneurysm formation and rupture: Systematic review and meta-analysis. Neurosurgery 2015, 78, 510–520. [Google Scholar] [CrossRef]
- Formaggia, L.; Lamponi, D.; Quarteroni, A. One-dimensional models for blood flow in arteries. J. Eng. Math. 2003, 47, 251–276. [Google Scholar] [CrossRef]
- Vignon-Clementel, I.E.; Figueroa, C.; Jansen, K.; Taylor, C. Outflow boundary conditions for 3D simulations of non-periodic blood flow and pressure fields in deformable arteries. Comput. Methods Biomech. Biomed. Eng. 2010, 13, 625–640. [Google Scholar] [CrossRef] [PubMed]
- Vignon-Clementel, I.E.; Figueroa, C.A.; Jansen, K.E.; Taylor, C.A. Outflow boundary conditions for three-dimensional finite element modeling of blood flow and pressure in arteries. Comput. Methods Appl. Mech. Eng. 2006, 195, 3776–3796. [Google Scholar] [CrossRef]
- Gallo, D.; De Santis, G.; Negri, F.; Tresoldi, D.; Ponzini, R.; Massai, D.; Deriu, M.; Segers, P.; Verhegghe, B.; Rizzo, G. On the use of in vivo measured flow rates as boundary conditions for image-based hemodynamic models of the human aorta: Implications for indicators of abnormal flow. Ann. Biomed. Eng. 2012, 40, 729–741. [Google Scholar] [CrossRef] [PubMed]
- Vignon-Clementel, I.E.; Marsden, A.L.; Feinstein, J.A. A primer on computational simulation in congenital heart disease for the clinician. Prog. Pediatr. Cardiol. 2010, 30, 3–13. [Google Scholar] [CrossRef]
- Alastruey, J.; Parker, K.; Peiró, J.; Sherwin, S. Lumped parameter outflow models for 1-D blood flow simulations: Effect on pulse waves and parameter estimation. Commun. Comput. Phys. 2008, 4, 317–336. [Google Scholar]
- Stergiopulos, N.; Young, D.; Rogge, T. Computer simulation of arterial flow with applications to arterial and aortic stenoses. J. Biomech. 1992, 25, 1477–1488. [Google Scholar] [CrossRef]
- Reymond, P.; Merenda, F.; Perren, F.; Rufenacht, D.; Stergiopulos, N. Validation of a one-dimensional model of the systemic arterial tree. Am. J. Physiol. Heart Circ. Physiol. 2009, 297, H208–H222. [Google Scholar] [CrossRef] [PubMed]
- Bonfanti, M.; Balabani, S.; Greenwood, J.P.; Puppala, S.; Homer-Vanniasinkam, S.; Díaz-Zuccarini, V. Computational tools for clinical support: A multi-scale compliant model for haemodynamic simulations in an aortic dissection based on multi-modal imaging data. J. R. Soc. Interface 2017, 14, 20170632. [Google Scholar] [CrossRef]
- Pirola, S.; Cheng, Z.; Jarral, O.; O’Regan, D.; Pepper, J.; Athanasiou, T.; Xu, X. On the choice of outlet boundary conditions for patient-specific analysis of aortic flow using computational fluid dynamics. J. Biomech. 2017, 60, 15–21. [Google Scholar] [CrossRef]
- Morbiducci, U.; Gallo, D.; Massai, D.; Consolo, F.; Ponzini, R.; Antiga, L.; Bignardi, C.; Deriu, M.A.; Redaelli, A. Outflow conditions for image-based hemodynamic models of the carotid bifurcation: Implications for indicators of abnormal flow. J. Biomech. Eng. 2010, 132, 091005. [Google Scholar] [CrossRef] [PubMed]
- Antonuccio, M.N.; Mariotti, A.; Fanni, B.M.; Capellini, K.; Capelli, C.; Sauvage, E.; Celi, S. Effects of uncertainty of outlet boundary conditions in a patient-specific case of aortic coarctation. Ann. Biomed. Eng. 2021, 49, 3494–3507. [Google Scholar] [CrossRef] [PubMed]
- Westerhof, N.; Elzinga, G.; Sipkema, P. An artificial arterial system for pumping hearts. J. Appl. Physiol. 1971, 31, 776–781. [Google Scholar] [CrossRef] [PubMed]
- Ohashi, Y.; De Andrade, A.; Nosé, Y. Hemolysis in an electromechanical driven pulsatile total artificial heart. Artif. Organs 2003, 27, 1089–1093. [Google Scholar] [CrossRef] [PubMed]
- Nestler, F.; Bradley, A.P.; Wilson, S.J.; Timms, D.L.; Frazier, O.H.; Cohn, W.E. A hybrid mock circulation loop for a total artificial heart. Artif. Organs 2014, 38, 775–782. [Google Scholar] [CrossRef] [PubMed]
- Gräf, F.; Finocchiaro, T.; Laumen, M.; Mager, I.; Steinseifer, U. Mock circulation loop to investigate hemolysis in a pulsatile total artificial heart. Artif. Organs 2015, 39, 416–422. [Google Scholar] [CrossRef]
- Koenig, S.C.; Pantalos, G.M.; Gillars, K.J.; Ewert, D.L.; Litwak, K.N.; Etoch, S.W. Hemodynamic and pressure–volume responses to continuous and pulsatile ventricular assist in an adult mock circulation. ASAIO J. 2004, 50, 15–24. [Google Scholar] [CrossRef]
- Pantalos, G.M.; Koenig, S.C.; Gillars, K.J.; Giridharan, G.A.; Ewert, D.L. Characterization of an adult mock circulation for testing cardiac support devices. ASAIO J. 2004, 50, 37–46. [Google Scholar] [CrossRef]
- Liu, Y.; Allaire, P.; Wood, H.; Olsen, D. Design and initial testing of a mock human circulatory loop for left ventricular assist device performance testing. Artif. Organs 2005, 29, 341–345. [Google Scholar] [CrossRef] [PubMed]
- Timms, D.; Hayne, M.; McNeil, K.; Galbraith, A. A complete mock circulation loop for the evaluation of left, right, and biventricular assist devices. Artif. Organs 2005, 29, 564–572. [Google Scholar] [CrossRef]
- Colacino, F.M.; Moscato, F.; Piedimonte, F.; Danieli, G.; Nicosia, S.; Arabia, M. A modified elastance model to control mock ventricles in real-time: Numerical and experimental validation. ASAIO J. 2008, 54, 563–573. [Google Scholar] [CrossRef] [PubMed]
- Schampaert, S.; Pennings, K.; Van de Molengraft, M.; Pijls, N.; Van de Vosse, F.; Rutten, M. A mock circulation model for cardiovascular device evaluation. Physiol. Meas. 2014, 35, 687. [Google Scholar] [CrossRef] [PubMed]
- Gregory, S.D.; Pauls, J.P.; Wu, E.L.; Stephens, A.; Steinseifer, U.; Tansley, G.; Fraser, J.F. An advanced mock circulation loop for in vitro cardiovascular device evaluation. Artif. Organs 2020, 44, E238–E250. [Google Scholar] [CrossRef] [PubMed]
- Rezaienia, M.; Paul, G.; Avital, E.; Mozafari, S.; Rothman, M.; Korakianitis, T. In-vitro investigation of the hemodynamic responses of the cerebral, coronary and renal circulations with a rotary blood pump installed in the descending aorta. Med. Eng. Phys. 2017, 40, 2–10. [Google Scholar] [CrossRef]
- Gehron, J.; Zirbes, J.; Bongert, M.; Schäfer, S.; Fiebich, M.; Krombach, G.; Böning, A.; Grieshaber, P.; EMPACS (Exploration of the Mixing Phenomena during Interaction of Internal and External circulations) Study Group. Development and Validation of a Life-Sized Mock Circulatory Loop of the Human Circulation for Fluid-Mechanical Studies. ASAIO J. 2019, 65, 788–797. [Google Scholar] [CrossRef]
- Ruiz, P.; Rezaienia, M.A.; Rahideh, A.; Keeble, T.R.; Rothman, M.T.; Korakianitis, T. In vitro cardiovascular system emulator (bioreactor) for the simulation of normal and diseased conditions with and without mechanical circulatory support. Artif. Organs 2013, 37, 549–560. [Google Scholar] [CrossRef] [PubMed]
- Sénage, T.; Février, D.; Michel, M.; Pichot, E.; Duveau, D.; Tsui, S.; Trochu, J.N.; Roussel, J.C. A mock circulatory system to assess the performance of continuous-flow left ventricular assist devices (LVADs): Does axial flow unload better than centrifugal LVAD? ASAIO J. 2014, 60, 140. [Google Scholar] [CrossRef]
- Pantalos, G.M.; Ionan, C.; Koenig, S.C.; Gillars, K.J.; Horrell, T.; Sahetya, S.; Colyer, J.; Gray, L.A., Jr. Expanded pediatric cardiovascular simulator for research and training. ASAIO J. 2010, 56, 67–72. [Google Scholar] [CrossRef]
- Giridharan, G.A.; Ising, M.; Sobieski, M.A.; Koenig, S.C.; Chen, J.; Frankel, S.; Rodefeld, M.D. Cavopulmonary assist for the failing Fontan circulation: Impact of ventricular function on mechanical support strategy. ASAIO J. 2014, 60, 707. [Google Scholar] [CrossRef]
- Giridharan, G.A.; Koenig, S.C.; Kennington, J.; Sobieski, M.A.; Chen, J.; Frankel, S.H.; Rodefeld, M.D. Performance evaluation of a pediatric viscous impeller pump for Fontan cavopulmonary assist. J. Thorac. Cardiovasc. Surg. 2013, 145, 249–257. [Google Scholar] [CrossRef]
- Van Poucke, S.; Stevens, K.; Kicken, C.; Simons, A.; Marcus, A.; Lancé, M. Platelet function during hypothermia in experimental mock circulation. Artif. Organs 2016, 40, 288–293. [Google Scholar] [CrossRef]
- Bleilevens, C.; Hill, A.; Grzanna, T.; Fechter, T.; Bohnen, M.; Weber, H.-J.; Beckers, C.; Borosch, S.; Zayat, R.; Benstoem, C. In vitro head-to-head comparison of anticoagulation properties of two heparin brands in a human blood miniature mock loop. Interact. Cardiovasc. Thorac. Surg. 2019, 28, 120–127. [Google Scholar] [CrossRef] [PubMed]
- Knoops, P.G.; Biglino, G.; Hughes, A.D.; Parker, K.H.; Xu, L.; Schievano, S.; Torii, R. A mock circulatory system incorporating a compliant 3D-printed anatomical model to investigate pulmonary hemodynamics. Artif. Organs 2017, 41, 637–646. [Google Scholar] [CrossRef] [PubMed]
- Conijn, M.; Wintermans, L.; Metselaar, R.; Ruisch, J.; Bax, E.; van Egmond, C.; Nieuwenstein, B.; Warmerdam, E.; Krings, G.J.B.P.; Express, E. A 3D printed pulmonary mock loop for hemodynamic studies in congenital heart disease. Biomed. Phys. Eng. Express 2022, 8, 065003. [Google Scholar] [CrossRef] [PubMed]
- Vignali, E.; Gasparotti, E.; Mariotti, A.; Haxhiademi, D.; Ait-Ali, L.; Celi, S. High-versatility left ventricle pump and aortic mock circulatory loop development for patient-specific hemodynamic in vitro analysis. ASAIO J. 2022, 68, 1272–1281. [Google Scholar] [CrossRef] [PubMed]
- Biglino, G.; Cosentino, D.; Steeden, J.A.; De Nova, L.; Castelli, M.; Ntsinjana, H.; Pennati, G.; Taylor, A.M.; Schievano, S. Using 4D cardiovascular magnetic resonance imaging to validate computational fluid dynamics: A case study. Front. Pediatr. 2015, 3, 107. [Google Scholar] [CrossRef]
- Shepard, L.; Sommer, K.; Izzo, R.; Podgorsak, A.; Wilson, M.; Said, Z.; Rybicki, F.J.; Mitsouras, D.; Rudin, S.; Angel, E. Initial simulated FFR investigation using flow measurements in patient-specific 3D printed coronary phantoms. In Proceedings of the Medical Imaging 2017: Imaging Informatics for Healthcare, Research, and Applications, Orlando, FL, USA, 15–16 February 2017; pp. 192–203. [Google Scholar]
- Sommer, K.N.; Shepard, L.; Karkhanis, N.V.; Iyer, V.; Angel, E.; Wilson, M.F.; Rybicki, F.J.; Mitsouras, D.; Rudin, S.; Ionita, C.N. 3D Printed Cardiovascular Patient Specific Phantoms Used for Clinical Validation of a CT-derived FFR Diagnostic Software. In Proceedings of the Medical Imaging 2018: Biomedical Applications in Molecular, Structural, and Functional Imaging, Houston, TX, USA, 11–13 February 2018; Volume 10578, p. 105780J. [Google Scholar]
- Rong, C.; Chen, R.; Yan, W.; Yu, H.; Xu, Y. Hemodynamic analysis of external iliac artery based on VLBM. J. Zhejiang Univ. Sci. Technol. 2022, 34, 7–16. [Google Scholar]
- Zhang, X.; Gomez-Paz, J.; Chen, X.; McDonough, J.M.; Islam, M.; Andreopoulos, Y.; Zhu, L.; Yu, H. Volumetric lattice Boltzmann method for wall stresses of image-based pulsatile flows. Sci. Rep. 2022, 12, 1697. [Google Scholar] [CrossRef]
- An, S.; Yu, H.; Yao, J. GPU-accelerated Volumetric Lattice Boltzmann Method for Porous Media Flow. J. Petro. Sci. Eng. 2017, 156, 546–552. [Google Scholar] [CrossRef]
- An, S.; Yu, H.; Wang, Z.; Chen, R.; Kapadia, B.; Yao, J. Unified Mesoscopic Modeling and GPU-accelerated Computational Method for Image-based Pore-scale Porous Media Flows. Int. J. Heat Mass Trans. 2017, 115, 1192–1202. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, Y.; Sawchuck, A.P.; Dalsing, M.C.; Yu, H. GPU acceleration of Volumetric Lattice Boltzmann Method for patient-specific computational hemodynamics. Comput. Fluids 2015, 115, 192–200. [Google Scholar] [CrossRef]
- Yu, H.; Chen, X.; Wang, Z.; Deep, D.; Lima, E.; Zhao, Y.; Teague, D.S. Mass-conserved volumetric lattice Boltzmann method for complex flows with willfully moving boundaries. Phys. Rev. E 2014, 89, 063304. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Rong, C.; Jin, X.; Xu, Y.; Murphy, M.; Motaganahalli, R.; Sawchuk, A. Fast and Noninvasive Evaluation of In Vivo Pressure in Stenosed Aortoiliac Arteries. J. Vasc. Surg. 2020, 72, e308–e309. [Google Scholar] [CrossRef]
- Monnet, X.; Letierce, A.; Hamzaoui, O.; Chemla, D.; Anguel, N.; Osman, D.; Richard, C.; Teboul, J.-L. Arterial pressure allows monitoring the changes in cardiac output induced by volume expansion but not by norepinephrine. Crit. Care Med. 2011, 39, 1394–1399. [Google Scholar] [CrossRef] [PubMed]
- Kluckow, M.; Evans, N. Relationship between blood pressure and cardiac output in preterm infants requiring mechanical ventilation. J. Pediatr. 1996, 129, 506–512. [Google Scholar] [CrossRef] [PubMed]
- Chapman, J.H.; Elliott, P. Cardiovascular effects of static and dynamic exercise. Eur. J. Appl. Physiol. Occup. Physiol. 1988, 58, 152–157. [Google Scholar] [CrossRef]
- Lind, A.; McNicol, G. Muscular factors which determine the cardiovascular responses to sustained and rhythmic exercise. Can. Med. Assoc. J. 1967, 96, 706. [Google Scholar]
- Lind, A.R. Cardiovascular responses to static exercise (Isometrics, anyone?). Circulation 1970, 41, 173–176. [Google Scholar] [CrossRef]


| Artery | Case | Age | Gender | Stenosis | Stenting |
|---|---|---|---|---|---|
| Renal (R) | I | 64 | Male | Yes | No |
| II | 87 | Male | Yes | Yes | |
| III | 83 | Male | Yes | No | |
| IV | 74 | Male | No | No | |
| V | 75 | Male | No | No | |
| Iliac (I) | I | 63 | Male | Yes | Yes |
| II | 61 | Female | Yes | Yes | |
| III | 64 | Female | Yes | Yes | |
| IV | 53 | Male | Yes | Yes | |
| V | 76 | Female | Yes | Yes | |
| VI | 69 | Male | Yes | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, W.; Yu, H.; Chen, J.; Talamantes, J.; Rollins, D.M.; Fang, X.; Long, J.; Xu, C.; Sawchuk, A.P. A Mock Circulation Loop to Characterize In Vitro Hemodynamics in Human Systemic Arteries with Stenosis. Fluids 2023, 8, 198. https://doi.org/10.3390/fluids8070198
Hong W, Yu H, Chen J, Talamantes J, Rollins DM, Fang X, Long J, Xu C, Sawchuk AP. A Mock Circulation Loop to Characterize In Vitro Hemodynamics in Human Systemic Arteries with Stenosis. Fluids. 2023; 8(7):198. https://doi.org/10.3390/fluids8070198
Chicago/Turabian StyleHong, Weichen, Huidan Yu, Jun Chen, John Talamantes, Dave M. Rollins, Xin Fang, Jianyun Long, Chenke Xu, and Alan P. Sawchuk. 2023. "A Mock Circulation Loop to Characterize In Vitro Hemodynamics in Human Systemic Arteries with Stenosis" Fluids 8, no. 7: 198. https://doi.org/10.3390/fluids8070198
APA StyleHong, W., Yu, H., Chen, J., Talamantes, J., Rollins, D. M., Fang, X., Long, J., Xu, C., & Sawchuk, A. P. (2023). A Mock Circulation Loop to Characterize In Vitro Hemodynamics in Human Systemic Arteries with Stenosis. Fluids, 8(7), 198. https://doi.org/10.3390/fluids8070198








