Blood Flow Simulation of Aneurysmatic and Sane Thoracic Aorta Using OpenFOAM CFD Software
Abstract
:1. Introduction
2. Mathematical and Numerical Method
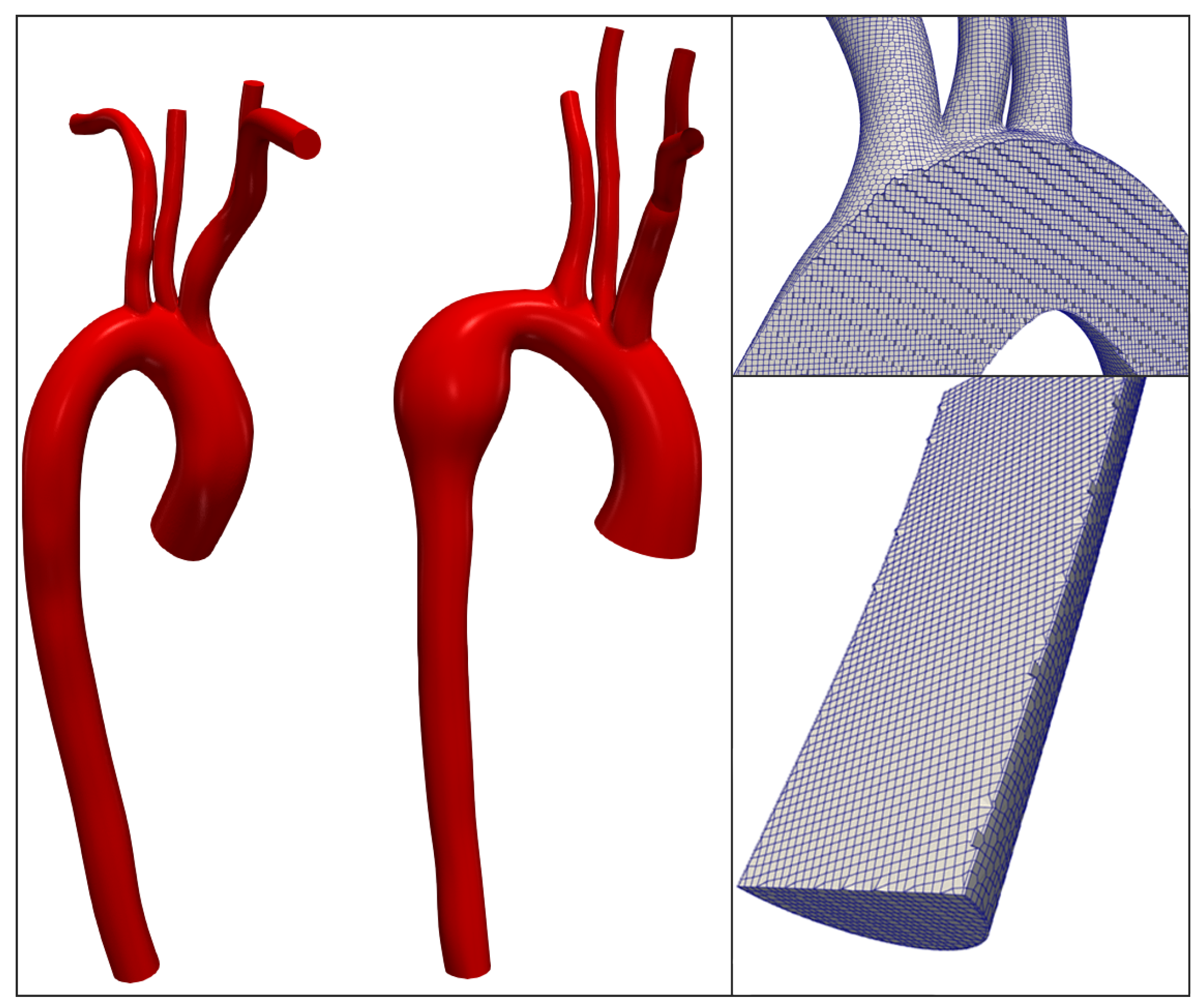
2.1. Geometries of Aorta and Generation of the Computational Domain
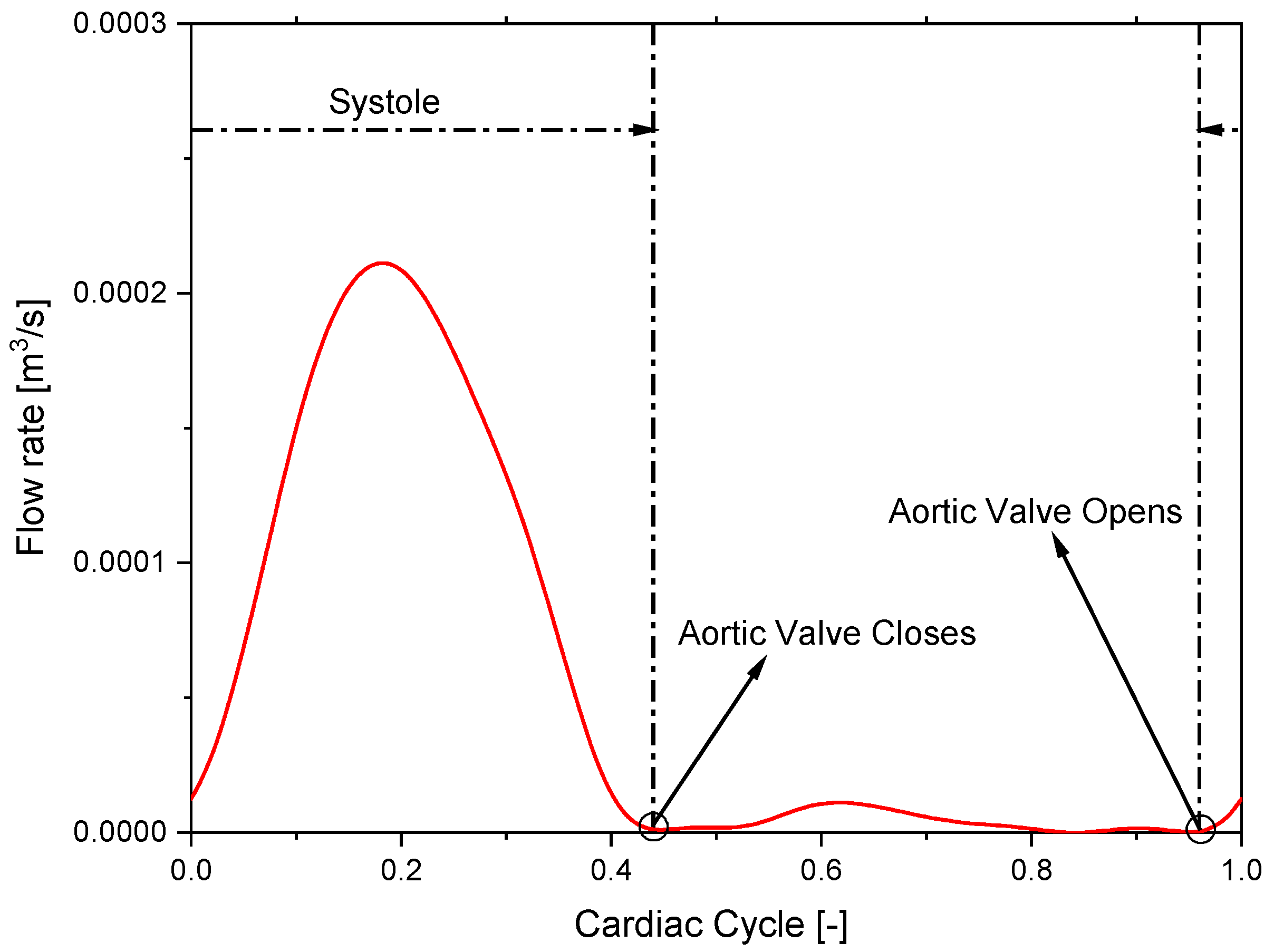
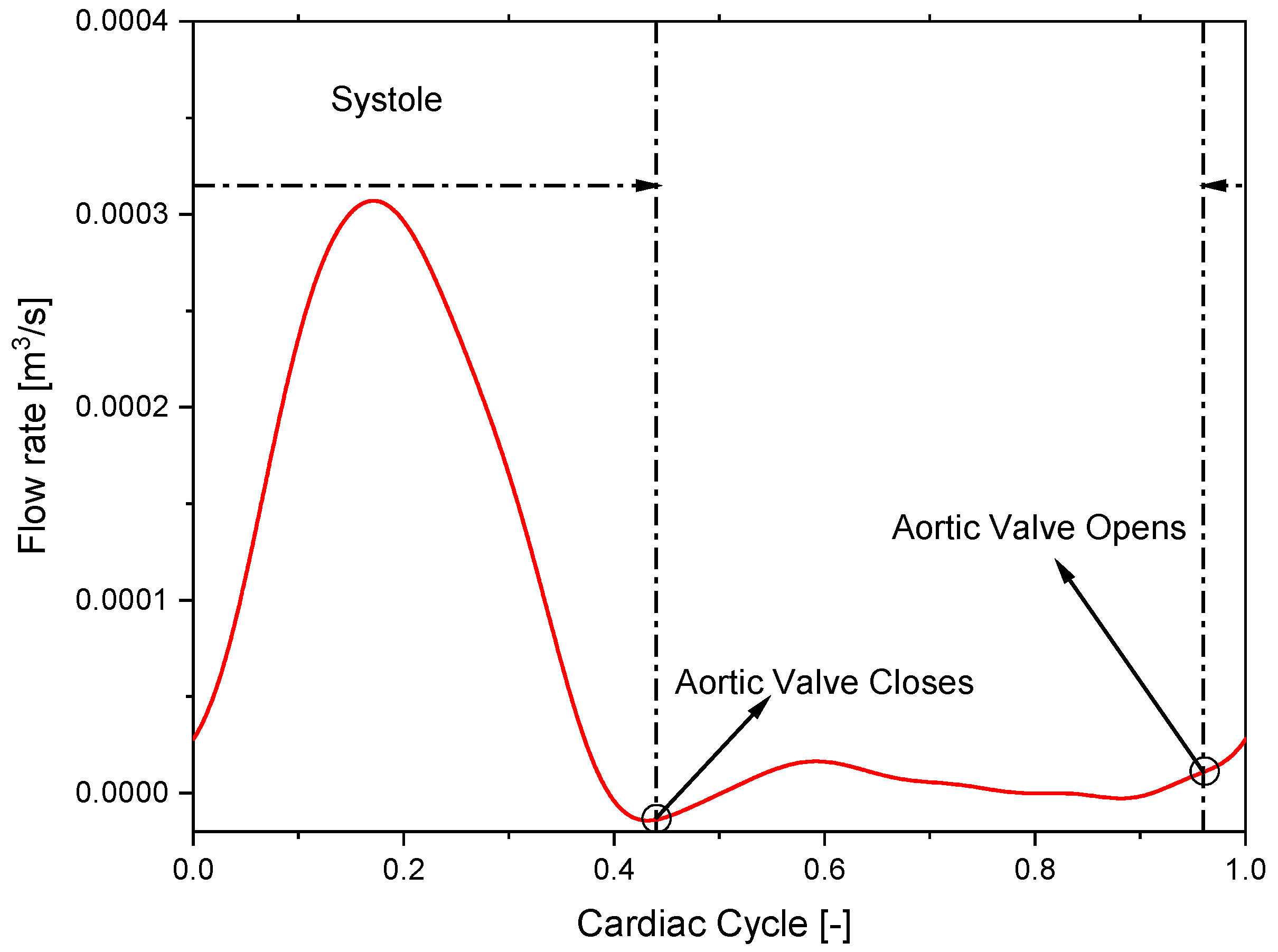
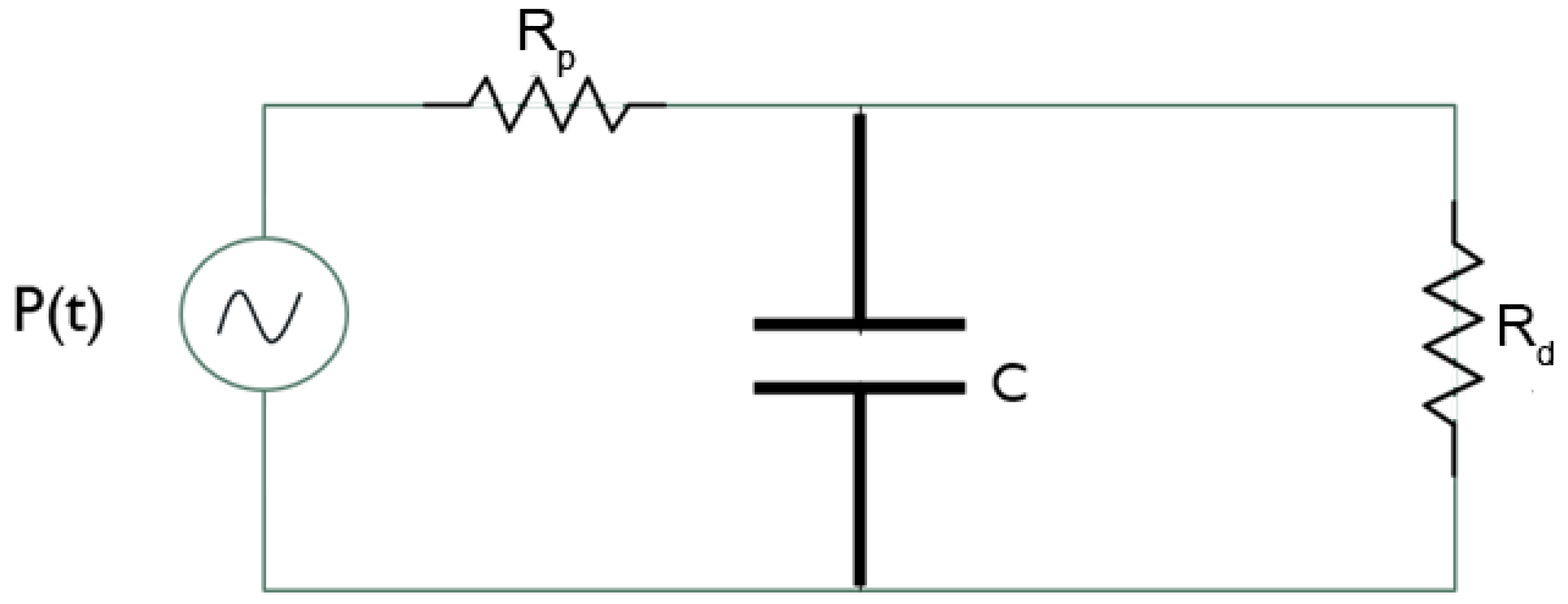
2.2. Model Setup
3. Results
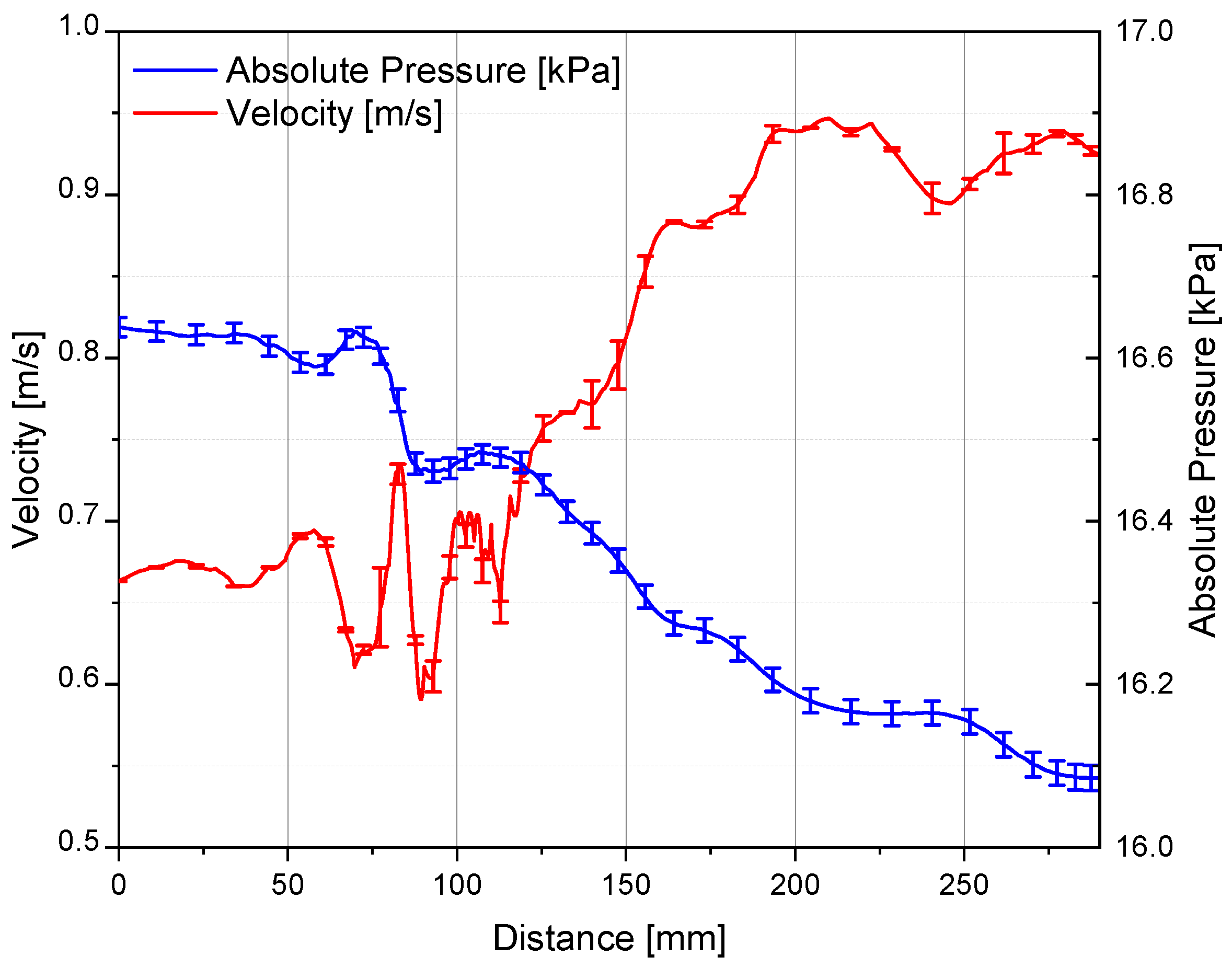
3.1. Convergence and Grid Sensibility Study: Preliminary Discussion
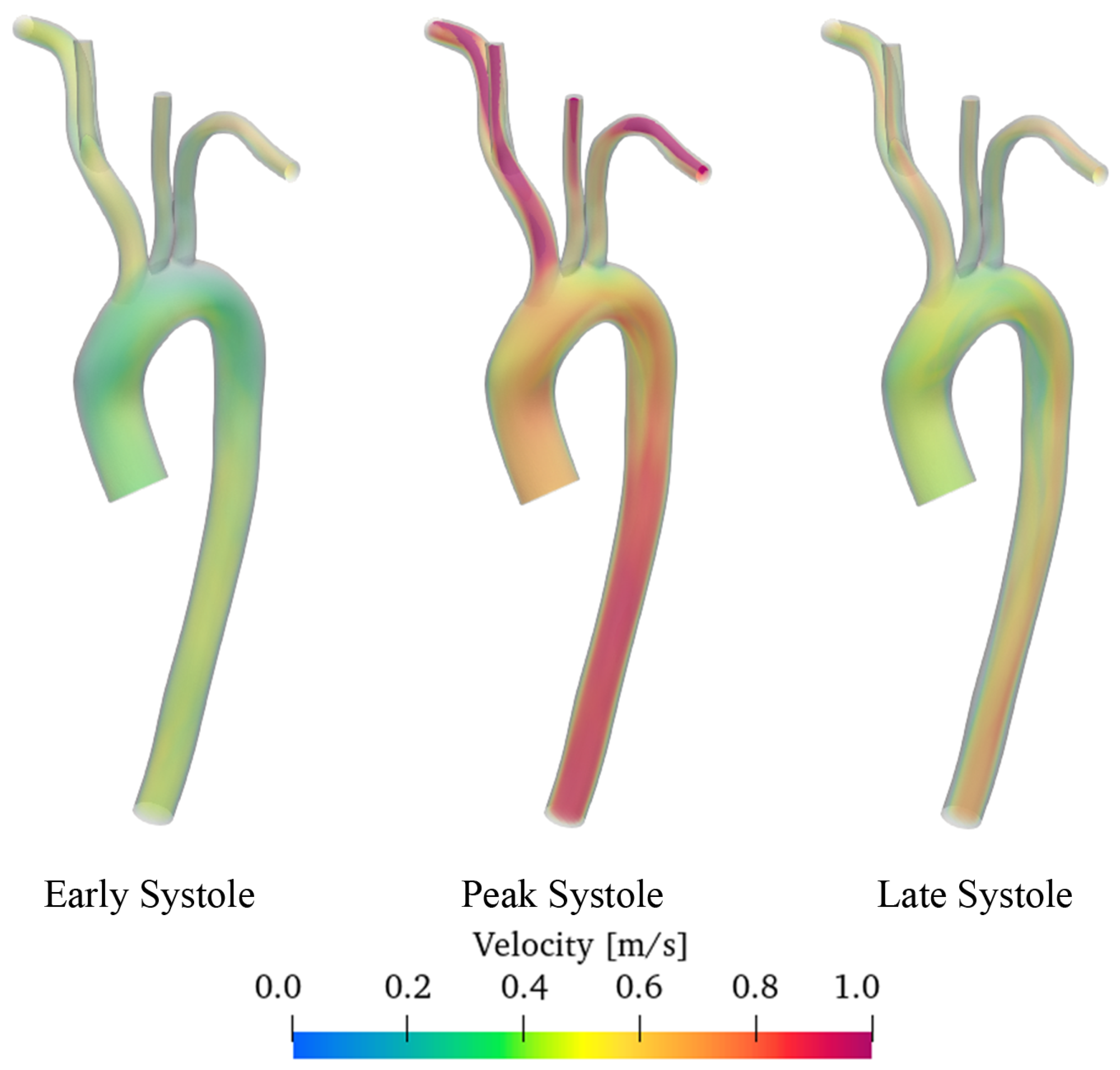
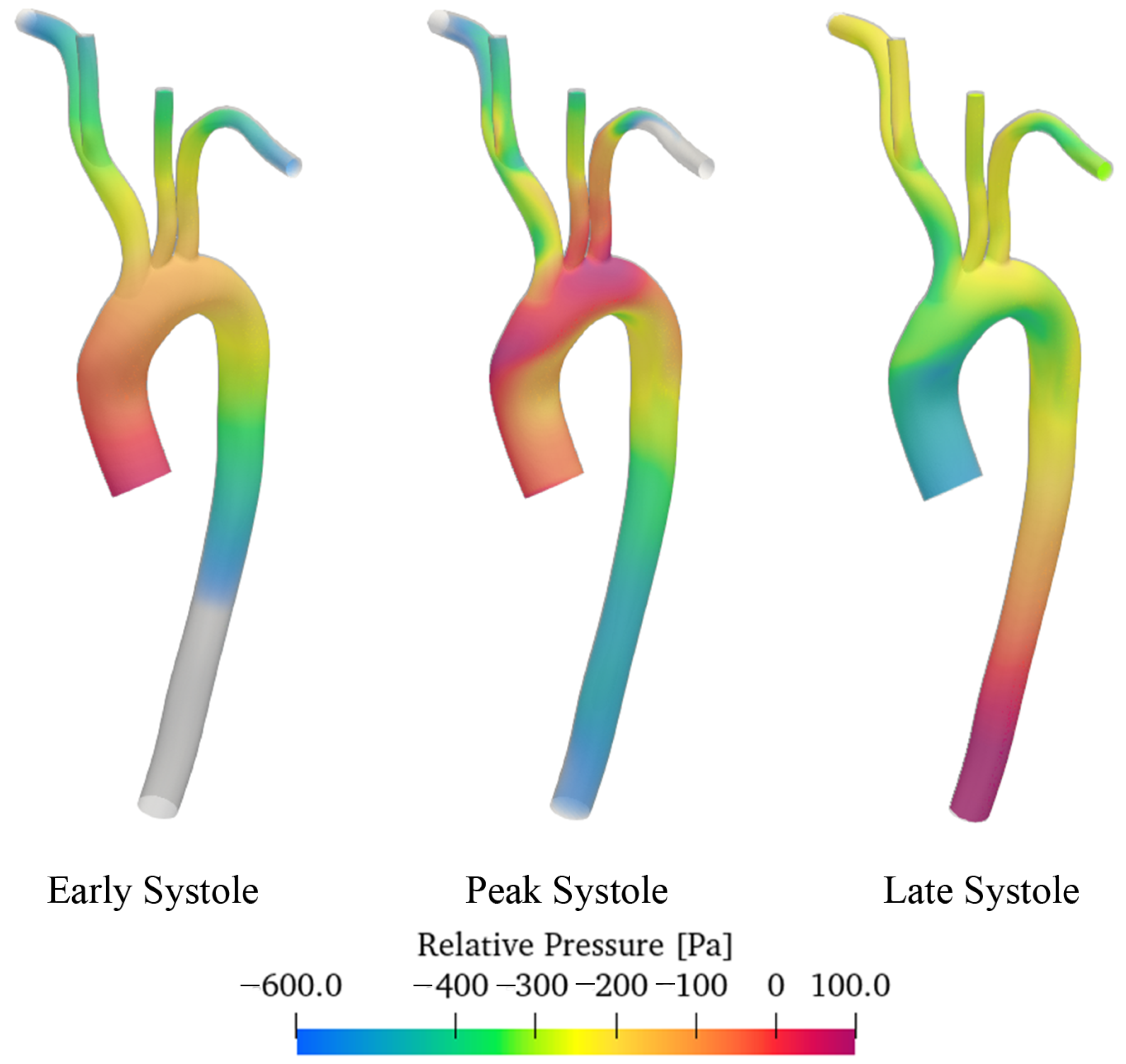
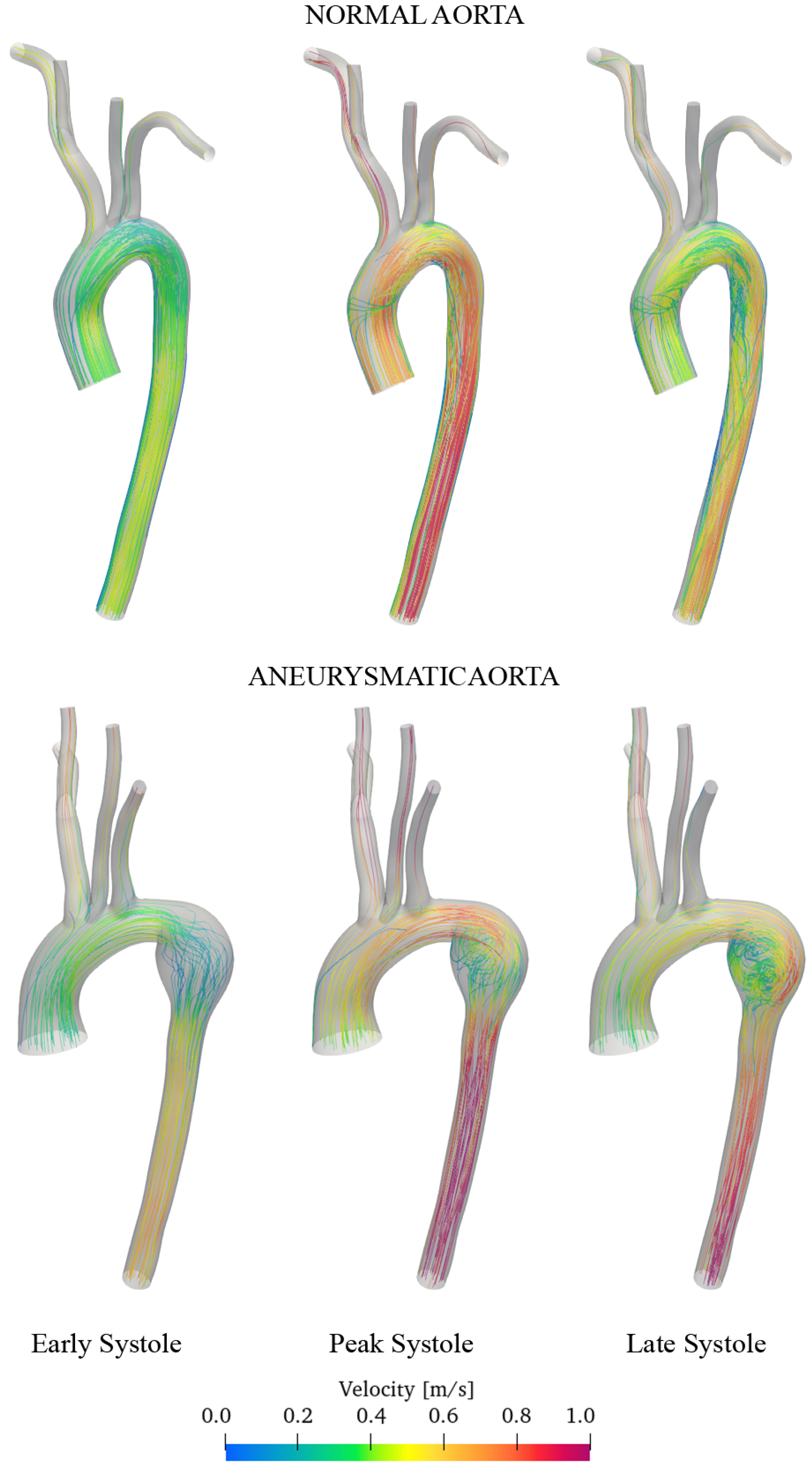
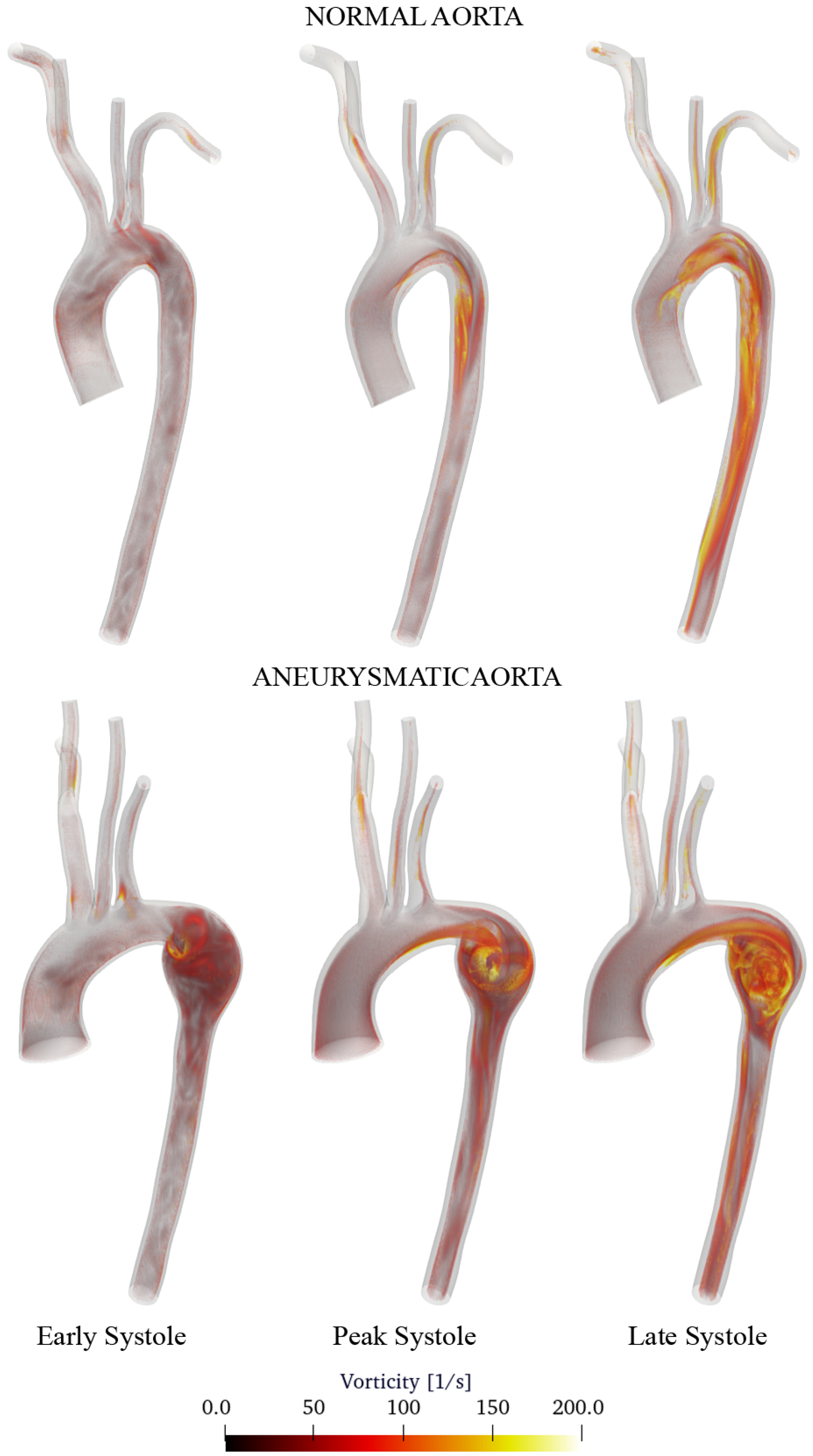
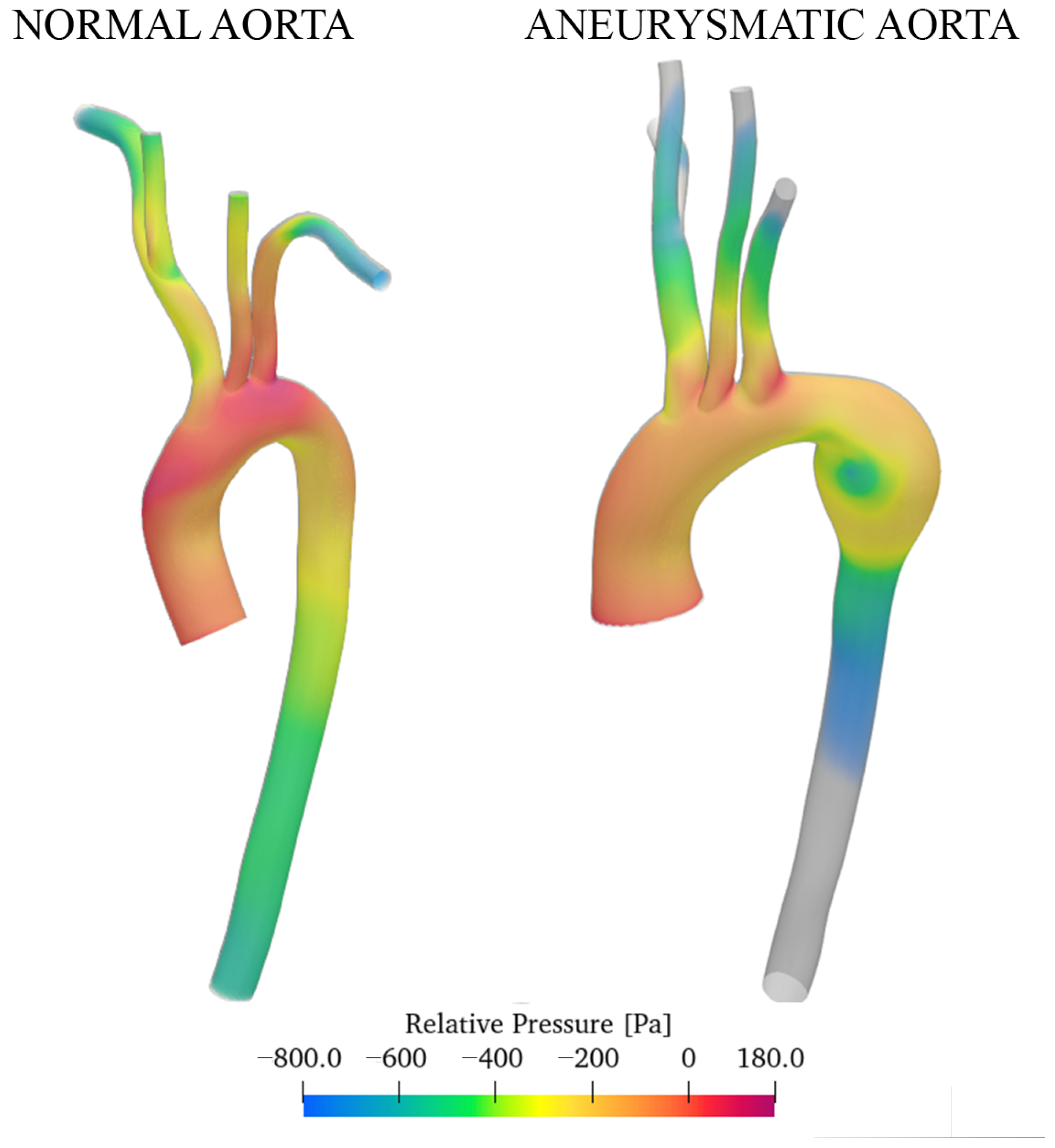
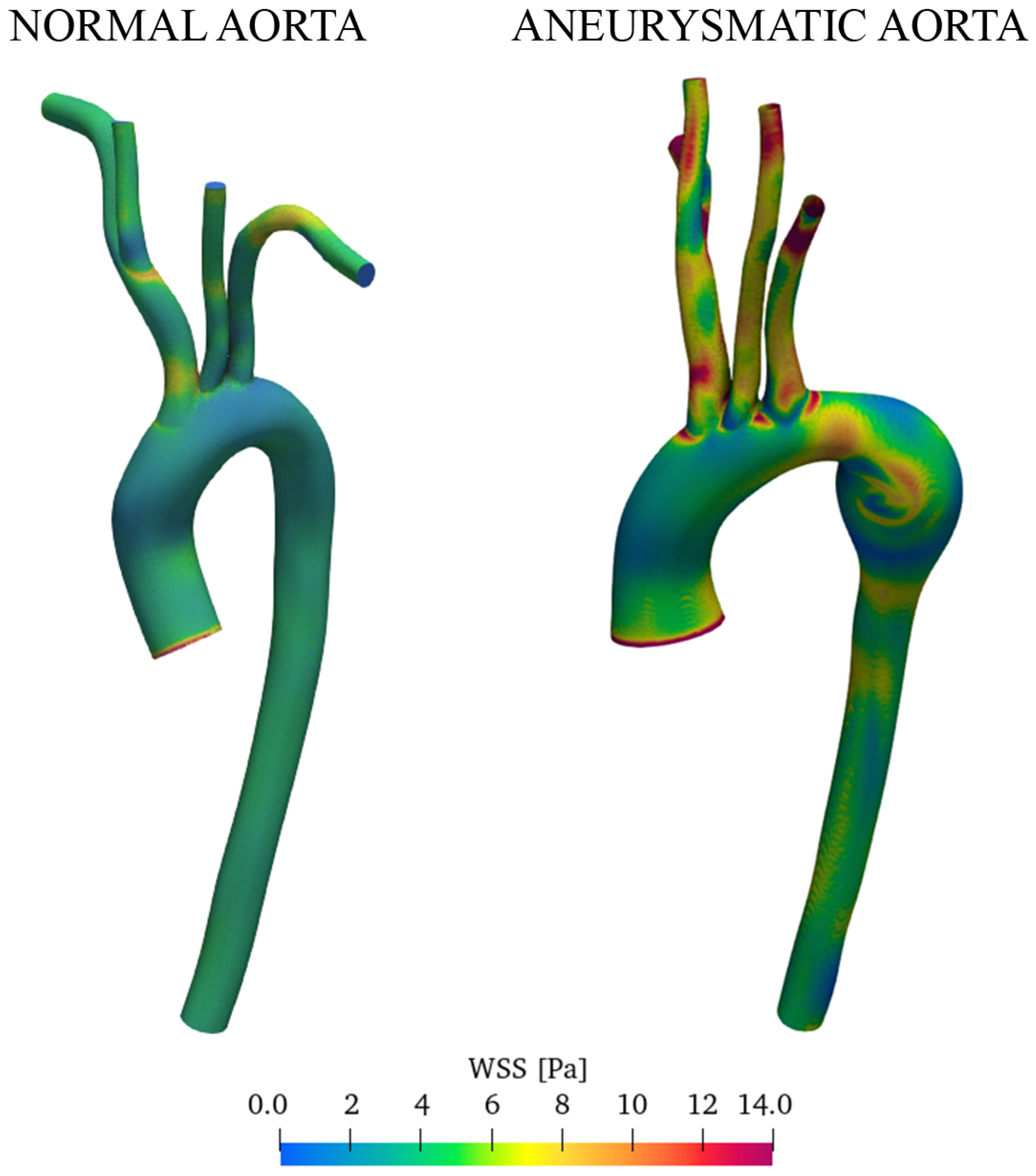
3.2. Discussion of Aneurysmatic and Sane Aorta Results
4. Conclusions
- The developed methodology with the implementation of the WK model is capable of reproducing the fluid-dynamic characteristics of the aortic flow, providing realistic pressure and velocity field values.
- In the thoracic aorta, blood velocity is on the order of 1 m/s, while the pressure varies by about 500/700 Pa crossing the aorta itself.
- Aneurysm onset causes the flow field to become unstable, and recirculation zones grow in the enlargement section with the consequent deposition of platelets and thrombus formation.
- CFD simulations allow identifying regions with WSS levels that may be more prone to dilatation or aneurysm formation. The magnitude of the WSS reaches the maximum values in the enlarged zone.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamic |
| CVD | Cardio-Vascular Diseases |
| CT | Computed Tomography |
| DES | Detached Eddy Simulation |
| MRI | Magnetic Resonance Imaging |
| PISO | Pressure Implicit with Splitting of Operator |
| LCCA | Left Common Carotid Artery; |
| LES | Large Eddy Simulation |
| LSA | Left Subclavian Artery |
| RCCA | Right Common Carotid Artery |
| RANS | Reynolds-Averaged Navier–Stokes |
| RSA | Right Subclavian Artery |
| WK | Windkessel |
| WSS | Wall Shear Stress |
References
- Gaidai, O.; Cao, Y.; Loginov, S. Global Cardiovascular Diseases Death Rate Prediction. Curr. Probl. Cardiol. 2023, 48, 101622. [Google Scholar] [CrossRef] [PubMed]
- Nerem, R. Hot film measurement of arterial blood flow and observation of flow disturbances. In Cardiovascular Flow Dynamics and Measurement; University Park Press: University Park, PA, USA, 1977; pp. 191–215. [Google Scholar]
- Smedby, Ö. Geometric risk factors for atherosclerosis in the aortic bifurcation: A digitized angiography study. Ann. Biomed. Eng. 1996, 24, 481–488. [Google Scholar] [CrossRef] [PubMed]
- Menichini, C.; Xu, X.Y. Mathematical modeling of thrombus formation in idealized models of aortic dissection: Initial findings and potential applications. J. Math. Biol. 2016, 73, 1205–1226. [Google Scholar] [CrossRef] [PubMed]
- Vasava, P.; Jalali, P.; Dabagh, M.; Kolari, P.J. Finite Element Modelling of Pulsatile Blood Flow in Idealized Model of Human Aortic Arch: Study of Hypotension and Hypertension. Comput. Math. Methods Med. 2012, 2012, 861837. [Google Scholar] [CrossRef] [PubMed]
- Voges, I.; Jerosch-Herold, M.; Hedderich, J.; Pardun, E.; Hart, C.; Gabbert, D.D.; Hansen, J.H.; Petko, C.; Kramer, H.H.; Rickers, C. Normal values of aortic dimensions, distensibility, and pulse wave velocity in children and young adults: A cross-sectional study. J. Cardiovasc. Magn. Reson. 2012, 14, 77. [Google Scholar] [CrossRef] [PubMed]
- Bouaou, K.; Bargiotas, I.; Dietenbeck, T.; Bollache, E.; Soulat, G.; Craiem, D.; Houriez-Gombaud-Saintonge, S.; De Cesare, A.; Gencer, U.; Giron, A.; et al. Analysis of aortic pressure fields from 4D flow MRI in healthy volunteers: Associations with age and left ventricular remodeling. J. Magn. Reson. Imaging 2019, 50, 982–993. [Google Scholar] [CrossRef]
- Lamata, P.; Pitcher, A.; Krittian, S.; Nordsletten, D.; Bissell, M.M.; Cassar, T.; Barker, A.J.; Markl, M.; Neubauer, S.; Smith, N.P. Aortic relative pressure components derived from four-dimensional flow cardiovascular magnetic resonance. Magn. Reson. Med. 2014, 72, 1162–1169. [Google Scholar] [CrossRef]
- Rengier, F.; Delles, M.; Eichhorn, J.; Azad, Y.J.; von Tengg-Kobligk, H.; Ley-Zaporozhan, J.; Dillmann, R.; Kauczor, H.U.; Unterhinninghofen, R.; Ley, S. Noninvasive 4D pressure difference mapping derived from 4D flow MRI in patients with repaired aortic coarctation: Comparison with young healthy volunteers. Int. J. Cardiovasc. Imaging 2015, 31, 823–830. [Google Scholar] [CrossRef]
- Yull Park, J.; Young Park, C.; Mo Hwang, C.; Sun, K.; Goo Min, B. Pseudo-organ boundary conditions applied to a computational fluid dynamics model of the human aorta. Comput. Biol. Med. 2007, 37, 1063–1072. [Google Scholar] [CrossRef]
- Madhavan, S.; Kemmerling, E.M.C. The effect of inlet and outlet boundary conditions in image-based CFD modeling of aortic flow. Biomed. Eng. Online 2018, 17, 66. [Google Scholar] [CrossRef]
- Pirola, S.; Cheng, Z.; Jarral, O.; O’Regan, D.; Pepper, J.; Athanasiou, T.; Xu, X. On the choice of outlet boundary conditions for patient-specific analysis of aortic flow using computational fluid dynamics. J. Biomech. 2017, 60, 15–21. [Google Scholar] [CrossRef] [PubMed]
- Hardman, D.; Semple, S.I.; Richards, J.M.; Hoskins, P.R. Comparison of patient-specific inlet boundary conditions in the numerical modelling of blood flow in abdominal aortic aneurysm disease. Int. J. Numer. Methods Biomed. Eng. 2013, 29, 165–178. [Google Scholar] [CrossRef] [PubMed]
- Antonuccio, M.N.; Mariotti, A.; Fanni, B.M.; Capellini, K.; Capelli, C.; Sauvage, E.; Celi, S. Effects of Uncertainty of Outlet Boundary Conditions in a Patient-Specific Case of Aortic Coarctation. Ann. Biomed. Eng. 2021, 49, 3494–3507. [Google Scholar] [CrossRef]
- Catanho, M.; Sinha, M.; Vijayan, V. Model of Aortic Blood Flow Using the Windkessel Effect; University of California of San Diego: San Diego, CA, USA, 2012. [Google Scholar]
- Westerhof, N.; Lankhaar, J.W.; Westerhof, B.E. The arterial Windkessel. Med Biol. Eng. Comput. 2009, 47, 131–141. [Google Scholar] [CrossRef] [PubMed]
- Wilson, N.M.; Ortiz, A.K.; Johnson, A.B. The Vascular Model Repository: A Public Resource of Medical Imaging Data and Blood Flow Simulation Results. J. Med. Device 2013, 7, 0409231. [Google Scholar] [CrossRef] [PubMed]
- Caballero, A.D.; Laín, S. A Review on Computational Fluid Dynamics Modelling in Human Thoracic Aorta. Cardiovasc. Eng. Technol. 2013, 4, 103–130. [Google Scholar] [CrossRef]
- Etli, M.; Canbolat, G.; Karahan, O.; Koru, M. Numerical investigation of patient-specific thoracic aortic aneurysms and comparison with normal subject via computational fluid dynamics (CFD). Med. Biol. Eng. Comput. 2021, 59, 71–84. [Google Scholar] [CrossRef]
- Duronio, F.; Di Mascio, A.; De Vita, A.; Innocenzi, V.; Prisciandaro, M. Eulerian–Lagrangian modeling of phase transition for application to cavitation-driven chemical processes. Phys. Fluids 2023, 35, 053305. [Google Scholar] [CrossRef]
- Dutta, H. Mathematical Methods in Engineering and Applied Sciences; Mathematics and Its Applications; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- De Vita, M.; Duronio, F.; De Vita, A.; De Berardinis, P. Adaptive Retrofit for Adaptive Reuse: Converting an Industrial Chimney into a Ventilation Duct to Improve Internal Comfort in a Historic Environment. Sustainability 2022, 14, 3360. [Google Scholar] [CrossRef]
- Duronio, F.; Mascio, A.D.; Villante, C.; Anatone, M.; Vita, A.D. ECN Spray G: Coupled Eulerian internal nozzle flow and Lagrangian spray simulation in flash boiling conditions. Int. J. Engine Res. 2023, 24, 1530–1544. [Google Scholar] [CrossRef]
- Berger, S.A.; Jou, L.D. Flows in Stenotic Vessels. Annu. Rev. Fluid Mech. 2000, 32, 347–382. [Google Scholar] [CrossRef]
- Pedley, T.J. The Fluid Mechanics of Large Blood Vessels; Cambridge University Press: Cambridge, UK, 1980. [Google Scholar] [CrossRef]
- Morris, L.; Delassus, P.; Callanan, A.; Walsh, M.; Wallis, F.; Grace, P.; McGloughlin, T. 3-D Numerical Simulation of Blood Flow through Models of the Human Aorta. J. Biomech. Eng. 2005, 127, 767–775. [Google Scholar] [CrossRef] [PubMed]
- Youssefi, P.; Gomez, A.; Arthurs, C.; Sharma, R.; Jahangiri, M.; Alberto Figueroa, C. Impact of Patient-Specific Inflow Velocity Profile on Hemodynamics of the Thoracic Aorta. J. Biomech. Eng. 2017, 140, 011002. [Google Scholar] [CrossRef]
- Qian, Y.; Liu, J.L.; Itatani, K.; Miyaji, K.; Umezu, M. Computational Hemodynamic Analysis in Congenital Heart Disease: Simulation of the Norwood Procedure. Ann. Biomed. Eng. 2010, 38, 2302–2313. [Google Scholar] [CrossRef] [PubMed]
- Zakaria, M.S.; Ismail, F.; Tamagawa, M.; Abdul Azi, A.F.; Wiriadidjaya, S.; Basri, A.A.; Ahmad, K.A. Computational Fluid Dynamics Study of Blood Flow in Aorta using OpenFOAM. J. Adv. Res. Fluid Mech. Therm. Sci. 2020, 43, 81–89. [Google Scholar]
- Boyd, J.; Buick, J.M. Comparison of Newtonian and non-Newtonian flows in a two-dimensional carotid artery model using the lattice Boltzmann method. Phys. Med. Biol. 2007, 52, 6215. [Google Scholar] [CrossRef]
- Otani, T.; Nakamura, M.; Fujinaka, T.; Hirata, M.; Kuroda, J.; Shibano, K.; Wada, S. Computational fluid dynamics of blood flow in coil-embolized aneurysms: Effect of packing density on flow stagnation in an idealized geometry. Med. Biol. Eng. Comput. 2013, 51, 901–910. [Google Scholar] [CrossRef]
- Antón, R.; Chen, C.Y.; Hung, M.Y.; Finol, E.; Pekkan, K. Experimental and computational investigation of the patient-specific abdominal aortic aneurysm pressure field. Comput. Methods Biomech. Biomed. Eng. 2015, 18, 981–992. [Google Scholar] [CrossRef]
- Spalart, P.R.; Deck, S.; Shur, M.L.; Squires, K.D.; Strelets, M.K.; Travin, A. A new version of detached-eddy simulation, resistant to ambiguous grid densities. Theor. Comput. Fluid Dyn. 2006, 20, 181–195. [Google Scholar] [CrossRef]
- Di Angelo, L.; Duronio, F.; De Vita, A.; Di Mascio, A. Cartesian Mesh Generation with Local Refinement for Immersed Boundary Approaches. J. Mar. Sci. Eng. 2021, 9, 572. [Google Scholar] [CrossRef]
- Safar, M.E.; Lévy, B.I. Chapter 13—Resistance Vessels in Hypertension. In Comprehensive Hypertension; Lip, G.Y., Hall, J.E., Eds.; Mosby: Philadelphia, PA, USA, 2007; pp. 145–150. [Google Scholar] [CrossRef]
- Pochet, T.; Gerard, P.; Marnette, J.M.; D’orio, V.; Marcelle, R.; Fatemi, M.; Fossion, A.; Juchmes, J. Identification of three-element windkessel model: Comparison of time and frequency domain techniques. Arch. Int. Physiol. Biochim. Biophys. 1992, 100, 295–301. [Google Scholar] [CrossRef] [PubMed]
- Tricarico, R.; Berceli, S.A.; Tran-Son-Tay, R.; He, Y. Non-invasive estimation of the parameters of a three-element windkessel model of aortic arch arteries in patients undergoing thoracic endovascular aortic repair. Front. Bioeng. Biotechnol. 2023, 11, 1127855. [Google Scholar] [CrossRef] [PubMed]
- Lungu, A.; Wild, J.; Capener, D.; Kiely, D.; Swift, A.; Hose, D. MRI model-based non-invasive differential diagnosis in pulmonary hypertension. J. Biomech. 2014, 47, 2941–2947. [Google Scholar] [CrossRef]
- Roache, P.J. Quantification of uncertainty in computational fluid dynamics. Annu. Rev. Fluid Mech. 1997, 29, 123–160. [Google Scholar] [CrossRef]
- Di Mascio, A.; Dubbioso, G.; Muscari, R. Vortex structures in the wake of a marine propeller operating close to a free surface. J. Fluid Mech. 2022, 949, A33. [Google Scholar] [CrossRef]
- Pope, S.B.; Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Garcia, J.; Barker, A.J.; Markl, M. The Role of Imaging of Flow Patterns by 4D Flow MRI in Aortic Stenosis. JACC Cardiovasc. Imaging 2019, 12, 252–266. [Google Scholar] [CrossRef]
- Soulat, G.; McCarthy, P.; Markl, M. 4D Flow with MRI. Annu. Rev. Biomed. Eng. 2020, 22, 103–126. [Google Scholar] [CrossRef]
- Bluestein, D.; Niu, L.; Schoephoerster, R.T.; Dewanjee, M.K. Steady Flow in an Aneurysm Model: Correlation Between Fluid Dynamics and Blood Platelet Deposition. J. Biomech. Eng. 1996, 118, 280–286. [Google Scholar] [CrossRef]
- Vinoth, R.; Kumar, D.; Adhikari, R.; Vijayapradeep, S.; Geetha, K.; Ilavarasi, R.; Mahalingam, S. Steady and Transient Flow CFD Simulations in an Aorta Model of Normal and Aortic Aneurysm Subjects. In Proceedings of the International Conference on Sensing and Imaging; Jiang, M., Ida, N., Louis, A.K., Quinto, E.T., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 29–43. [Google Scholar]
- Febina, J.; Sikkandar, M.Y.; Sudharsan, N.M. Wall Shear Stress Estimation of Thoracic Aortic Aneurysm Using Computational Fluid Dynamics. Comput. Math. Methods Med. 2018, 2018, 7126532. [Google Scholar] [CrossRef]

| [Pa · s/m] | [Pa · s/m] | C [m/Pa] | |
|---|---|---|---|
| OUTFLOW | |||
| LCCA | |||
| LSA | |||
| RCCA | |||
| RSA |
| [Pa · s/m] | [Pa · s/m] | C [m/Pa] | |
|---|---|---|---|
| OUTFLOW | |||
| LCCA | |||
| LSA | |||
| RCCA | |||
| RSA |
| Grid Convergence Index | Order of Convergence | |
|---|---|---|
| U | 0.72% | 2.03 |
| p | 0.23% | 2.83 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duronio, F.; Di Mascio, A. Blood Flow Simulation of Aneurysmatic and Sane Thoracic Aorta Using OpenFOAM CFD Software. Fluids 2023, 8, 272. https://doi.org/10.3390/fluids8100272
Duronio F, Di Mascio A. Blood Flow Simulation of Aneurysmatic and Sane Thoracic Aorta Using OpenFOAM CFD Software. Fluids. 2023; 8(10):272. https://doi.org/10.3390/fluids8100272
Chicago/Turabian StyleDuronio, Francesco, and Andrea Di Mascio. 2023. "Blood Flow Simulation of Aneurysmatic and Sane Thoracic Aorta Using OpenFOAM CFD Software" Fluids 8, no. 10: 272. https://doi.org/10.3390/fluids8100272
APA StyleDuronio, F., & Di Mascio, A. (2023). Blood Flow Simulation of Aneurysmatic and Sane Thoracic Aorta Using OpenFOAM CFD Software. Fluids, 8(10), 272. https://doi.org/10.3390/fluids8100272








