Modelling The Hemodynamics of Coronary Ischemia
Abstract
1. Introduction
- Devise and implement a 0D model and robust data handling protocols able to replicate in silico haemodynamic dysfunction;
- Make optimal use of appropriate haemodynamic data, collected in the clinical PCI pathway;
- Demonstrate our process’ ability to capture patient-specific (patho)physiological states in silico.
2. Background
- A coronary network topology conforming to the clinical pattern of atherosclerosis;
- Modelling that reflects diastolic dominance of myocardial flow;
- The ability to incorporate all available clinical patient data;
- Sufficient computational simplicity for clinical deployment.
3. Methods and Materials
3.1. Methods
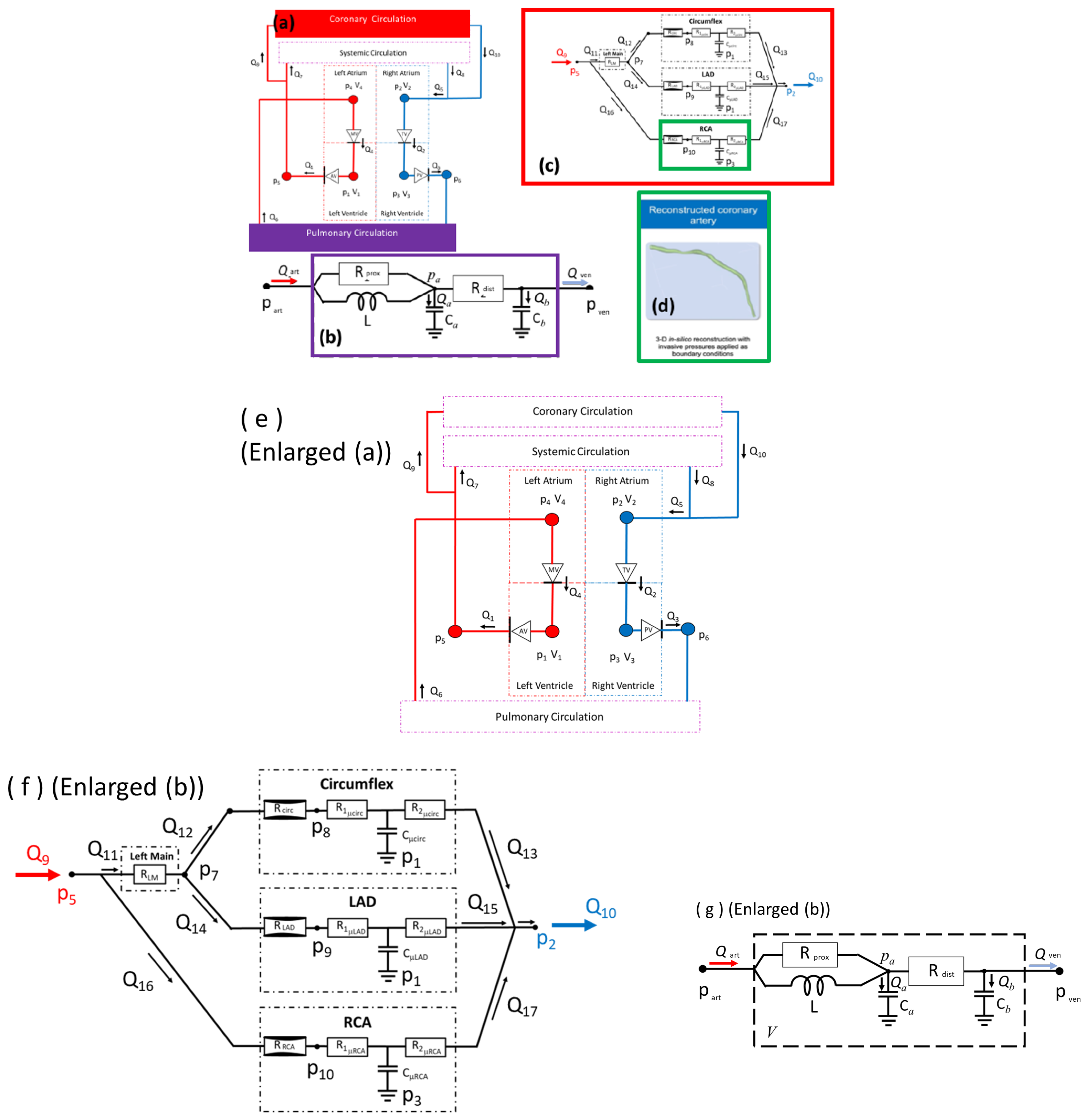
3.1.1. Low-Order Models
3.1.2. System Model
3.1.3. Input Parameters, Local Sensitivity and Orthogonality Analysis
3.1.4. Model Personalisation or Input Parameter Identification
3.1.5. 3D CFD Models
- Following VirtuQ methodology, apply measured proximal and distal average pressure on , , respectively,we compute the steady-state solution and deduce vessel flowthen, we use Ohm’s law and to compute a patient-specific MVR.
- Following VirtuHeart methodology, assume an MVR based on patient characteristics [6]; compute vessel inlet and outlet areasset two physiologically plausible inlet flows ( mL/s), find uniform inlet and outlet streamwise velocitiescompute the two corresponding pressure drops, , and hence infer the two Bernoulli resistance coefficients of the stenosis.
3.2. Materials
- Measured data (such as pressure and volume, expressed as time-series);
- Exercise and physical activity data (like patient 6mwt (exercise) and home monitoring (activity) measures).
- Functional form (qualitative data trends should accord with accepted physiology);
- Modality (pressure is measured directly, using a manometer; CMR volumes, in contradistinction, involve reciprocal space reconstruction).
3.2.1. Physical Data Processing
3.2.2. Exercise/Monitoring Data Processing
- Home activity monitoring. Fitbit Charge 4 wrist watches (Healthy Metrics Research Inc. San Francisco, CA, USA) and a smartphone were used. Data monitoring started at recruitment and extended up to six months post PCI. All data were uploaded to the Fitbit website simultaneously through a smartphone application and then exported as coarse-grained time-series (mechanical energy consumption, distance walked, minutes spent sedentary, light, fairly, and great activity). Concurrent HR data were also exported as downsampled HR data, which were simultaneously updated throughout the day as time-averaged values every 10–15 min.
- Formal six-minute walk tests (6MWT). These were performed at baseline before the PCI (ideally one day) with a repeat assessment after three and six months. In these standard clinical assessments, the data collected were cuff blood pressure, HR and distance walked.
4. Results
4.1. Elastance Function Evaluation

| Patient ID | A | B | C | |
|---|---|---|---|---|
| Co-Registration Rigid Shift | 1 | 5 | 2 | |
| double Hill LV elastance parameter | 0.29 | 0.54 | 0.82 | |
| 0.42 | 0.5 | 0.42 | ||
| 1.58 | 1.56 | 1.26 | ||
| 17.53 | 17.96 | 19.95 | ||
| 1.1 | 2.22 | 2.17 | ||
| 0.05 | 0.03 | 0.03 | ||
4.2. Tuning Protocol Evaluation
4.3. CFD Data Evaluation
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. System Model
Appendix A.1. System Model Dynamical Equations
Appendix A.2. Sub-Models—Chamber Elastances and Valve Characteristic Functions
Appendix B. Sensitivity and Orthogonality Analysis






| n | ||||
|---|---|---|---|---|
| 1 | Heart Rate | Cardiac Output | Heart Rate | Cardiac Output |
| 2 | Mean circ. filling press. | LV End Diastolic Volume | Mean circ. filling press. | Useful Cardiac Power |
| 3 | ELVmin | LV End Systolic Volume | ELVmin | LV End Diastolic Volume |
| 4 | ELVmax | LV Maximum Pressure | ELVmax | LV End Systolic Volume |
| 5 | n1LV | LV Minimum Pressure | n1LV | LV Stroke Volume |
| 6 | n2LV | Systemic Artery Systolic Press. | n2LV | LV Ejection Fraction |
| 7 | Tau1fLV | Systemic Artery Diastolic Pres. | Tau1fLV | LV Maximum Pressure |
| 8 | Tau2fLV | Systemic Artery True MAP | Tau2fLV | LV Minimum Pressure |
| 9 | LV fractional time shift | AV Opens | LV volume offset | LV End Diastolic Pressure |
| 10 | ELAmin | AV Closes | LV fractional time shift | LV dp/dt (peak) |
| 11 | ELAmax | MV Opens | ELAmin | LV Stroke Work per Beat |
| 12 | n1LA | MV Closes | ELAmax | LV Stroke Power (Mean) |
| 13 | n2LA | Mean Coronary Flow | n1LA | LV Stroke Power (Peak) |
| 14 | Tau1fLA | Maximum Coronary Flow | n2LA | LV Myocardial Power (mean) |
| 15 | Tau2fLA | Left Main Flow (mean) | Tau1fLA | LV Myocardial Power (peak) |
| 16 | LA fractional time shift | Left Main Flow (peak) | Tau2fLA | LV Wasted Myocardial Power (Suga) |
| 17 | Systemic Resistance (Prox.) | Left Main ’FFR’ (<Pd> / <Pa>) | LA volume offset | LA Maximum Volume |
| 18 | Systemic Resistance Distal | Cx Flow (mean) | LA fractional time shift | LA Minimum Volume |
| 19 | Systemic Art. Cap (Prox.) | Cx Flow (peak) | ERVmin | LA Maximum Pressure |
| 20 | Systemic Art. Inertance (Prox.) | Cx ’FFR’ (<Pd> / <Pa>) | ERVmax | LA Minimum Pressure |
| 21 | Mitral Valve quadratic coeff. | LAD Flow (mean) | n1RV | RV End Diastolic Volume |
| 22 | Mitral Valve linear coeff. | LAD Flow (peak) | n2RV | RV End Systolic Volume |
| 23 | Left main, quadratic coeff. | LAD ’FFR’ (<Pd>/<Pa>) | Tau1fRV | RV Stroke Volume |
| 24 | Left main, linear coeff. | RCA Flow (mean) | Tau2fRV | RV Ejection Fraction |
| 25 | Cx, quadratic coeff. | RCA Flow (peak) | RV volume offset | RV Maximum Pressure |
| 26 | Cx, linear coeff. | RCA ’FFR’ (<Pd> / <Pa>) | RV fractional time shift | RV Minimum Pressure |
| 27 | Cx, RCR total res. | ∼ | ERAmin | RV End Diastolic Pressure |
| 28 | Cx, RCR cap. | ∼ | ERAmax | RV dp/dt (peak) |
| 29 | Cx Cap. back press. fraction | ∼ | n1RA | RV Stroke Work per Beat |
| 30 | LAD, quadratic coeff. | ∼ | n2RA | RV Stroke Power Expenditure |
| 31 | LAD, linear coeff. | ∼ | Tau1fRA | RV Stroke Power (Peak) |
| 32 | LAD, RCR total resistance | ∼ | Tau2fRA | RV Myocardial Power (mean) |
| 33 | LAD, RCR cap, | ∼ | RA volume offset | RV Myocardial Power (peak) |
| 34 | LAD Cap. back press. fraction | ∼ | RA fractional time shift | RV Wasted Myocardial Power (Suga) |
| 35 | RCA, quadratic coeff. | ∼ | Systemic Resistance Prox. | RA End Diastolic Volume |
| 36 | RCA, linear coeff. | ∼ | Systemic Resistance Dist. | RA End Systolic Volume |
| 37 | RCA, RCR total resistance | ∼ | Systemic Arterial Prox. Cap. | RA Maximum Pressure |
| 38 | RCA, RCR capacitance | ∼ | Systemic Arterial Prox. Unstressed Vol. | RA Minimum Pressure |
| 39 | ∼ | ∼ | Systemic Arterial Distal Cap. | Systemic Artery Systolic Pressure |
| 40 | ∼ | ∼ | Systemic Arterial Distal Unstressed Vol. | Systemic Artery Diastolic Pressure |
| 41 | ∼ | ∼ | Systemic Arterial Inertance (Prox.l) | Systemic Artery Nominal MAP |
| 42 | ∼ | ∼ | Pulmonary Resistance Prox. | Systemic Artery True MAP |
| 43 | ∼ | ∼ | Pulmonary Resistance Distal | Systemic Artery Pulse Pressure |
| 44 | ∼ | ∼ | Pulmonary Arterial Proximal Cap. | Systemic Vein Mean Pressure |
| 45 | ∼ | ∼ | Pul. Art. Prox. Unstressed Vol. | Systemic Vein Pulse Pressure |
| 46 | ∼ | ∼ | Pul. Art. Distal Cap. | Pulmonary Artery Systolic Pressure |
| 47 | ∼ | ∼ | Pulmonary Arterial Distal Unstressed Vol. | Pulmonary Artery Diastolic Pressure |
| 48 | ∼ | ∼ | Pulmonary Arterial Inertance (Prox.) | Pulmonary Artery Nominal MAP |
| 49 | ∼ | ∼ | Aortic Valve quadratic coeff. | Pulmonary Artery True MAP |
| 50 | ∼ | ∼ | Aortic Valve linear coeff. | Pulmonary Artery Pulse Pressure |
| 51 | ∼ | ∼ | Aortic Valve regurgitant quadratic coeff. | Pulmonary Vein Mean Pressure |
| 52 | ∼ | ∼ | Aortic Valve regurgitant linear coeff. | Pulmonary Vein Pulse Pressure |
| 53 | ∼ | ∼ | Mitral Valve quadratic coeff. | AV Forward Flow [ml/beat] |
| 54 | ∼ | ∼ | Mitral Valve linear coeff. | AV Regurgitation [ml/beat] |
| 55 | ∼ | ∼ | Mitral Valve regurgitant quadratic coeff. | AV Regurgitant Fraction [-] |
| 56 | ∼ | ∼ | Mitral Valve regurgitant linear coeff. | AV Maximum Pressure Drop |
| 57 | ∼ | ∼ | PulmonaryValve quadratic coeff. | AV Mean Pressure Drop |
| 58 | ∼ | ∼ | Pulmonary Valve linear coeff. | (Stroke Power Lost):(AV Resistance) |
| 59 | ∼ | ∼ | Pulmonary Valve regurgitant quad. coeff. | (Stroke Power Lost):(AV Resistance) |
| 60 | ∼ | ∼ | Pulmonary Valve regurgitant linear coeff. | MV Forward Flow [ml/beat] |
| 61 | ∼ | ∼ | Tricuspid Valve quadratic coeff. | MV Regurgitation [ml/beat] |
| 62 | ∼ | ∼ | Tricuspid Valve linear coeff. | MV Regurgitant Fraction [-] |
| 63 | ∼ | ∼ | Tricuspid Valve regurgitant quad. coeff. | MV Maximum Pressure Drop |
| 64 | ∼ | ∼ | Tricuspid Valve regurgitant linear coeff. | MV Mean Pressure Drop |
| 65 | ∼ | ∼ | Left main, quadratic coeff. | Stroke Power Lost to MV Regurgitation |
| 66 | ∼ | ∼ | Left main, linear coeff. | (Stroke Power Lost):(MV Regurgitation) |
| 67 | ∼ | ∼ | Cx. quad. coefficient | AV Opens |
| 68 | ∼ | ∼ | Cx. linear coefficient | AV Closes |
| 69 | ∼ | ∼ | Cx. RCR total resistance | MV Opens |
| 70 | ∼ | ∼ | Cx. RCR cap. | MV Closes |
| 71 | ∼ | ∼ | Cx. RCR fraction proximal resistance | Period of Systole |
| 72 | ∼ | ∼ | Cx. cap. back pressure fraction | Period of Diastole |
| 73 | ∼ | ∼ | LAD, quadratic coefficient | Proportion of Heart Period in Systole |
| 74 | ∼ | ∼ | LAD, linear coefficient | Period of Isovolumetric Contraction |
| 75 | ∼ | ∼ | LAD, RCR total resistance | Period of Isovolumetric Relaxation |
| 76 | ∼ | ∼ | LAD, RCR capacitance | Mean Coronary Flow |
| 77 | ∼ | ∼ | LAD, RCR fraction proximal resistance | Maximum Coronary Flow |
| 78 | ∼ | ∼ | LAD cap. back pressure fraction | Left Main Flow (mean) |
| 79 | ∼ | ∼ | RCA, quadratic coefficient | Left Main Flow (peak) |
| 80 | ∼ | ∼ | RCA, linear coefficient | Left Main ’FFR’ (<Pd> / <Pa>) |
| 81 | ∼ | ∼ | RCA, RCR total resistance | Circumflex Flow (mean) |
| 82 | ∼ | ∼ | RCA, RCR capacitance | Circumflex Flow (peak) |
| 83 | ∼ | ∼ | RCA, RCR fraction proximal resistance | Circumflex ’FFR’ (<Pd>/ <Pa>) |
| 84 | ∼ | ∼ | LAD cap, back pressure fraction | LAD Flow (mean) |
| 85 | ∼ | ∼ | ∼ | LAD Flow (peak) |
| 86 | ∼ | ∼ | ∼ | LAD ’FFR’ (<Pd>/ <Pa>) |
| 87 | ∼ | ∼ | ∼ | RCA Flow (mean) |
| 88 | ∼ | ∼ | ∼ | RCA Flow (peak) |
| 88 | ∼ | ∼ | ∼ | RCA ’FFR’ (<Pd> / <Pa>) |
References
- Shi, Y.; Lawford, P.; Hose, D.R. Review of Zero-D and 1-D Models of Blood Flow in the Cardiovascular System. BioMed. Eng. 2011, 10, 33. [Google Scholar] [CrossRef] [PubMed]
- Hose, D.R.; Lawford, P.V.; Huberts, W.; Hellevik, L.R.; Omholt, S.; van de Vosse, W. Cardiovascular models for personalised medicine: Where now and where next? Med. Eng. Phys. 2019, 72, 38. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y. Lumped-Parameter Cardiovascular Model with Windkessel Afterload; CellML: Auckland, New Zealand, 2007; Available online: http://models.cellml.org/exposure/ea64608ab564ee085bef7cde3ed1731e (accessed on 1 May 2023).
- Korakianitis, T.; Shi, Y. A concentrated parameter model for the human cardiovascular system including heart valve dynamics and atrioventricular interaction. Med. Eng. Phys. 2006, 28, 613–628. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantole, S. Global Sensitivity Analysis: The Primer; John Wiley and Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Morris, P.D.; Ryan, D.; Morton, A.C.; Lycett, R.; Lawford, P.V.; Hose, D.R.; Gunn, J.P. Virtual Fractional Flow Reserve From Coronary Angiography: Modeling the Significance of Coronary Lesions: Results From the VIRTU-1 (VIRTUal Fractional Flow Reserve From Coronary Angiography). JACC Cardiovasc. Interv. 2013, 6, 149–157. [Google Scholar] [CrossRef]
- Morris, P.D.; Gosling, R.; Zwierzak, I.; Evans, H.; Aubiniere-Robb, L.; Czechowicz, K.; Evans, P.C.; Hose, D.R.; Lawford, P.V.; Narracott, A.J. A novel method for measuring absolute coronary blood flow and microvascular resistance in patients with ischaemic heart disease. Cardiovasc. Res. 2021, 117, 1567–1577. [Google Scholar] [CrossRef] [PubMed]
- Succi, S. The Lattice Boltzmann Equation for Fluid Dynamics and Beyond; Clarendon Press: Oxford, UK, 2001. [Google Scholar]
- Groen, D.; Richardson, R.; Coy, R.; Schiller, U.D.; Chandrashekar, H.; Robertson, F.; Coveney, P.V. Validation of Patient-Specific Cerebral Blood Flow Simulation Using Transcranial Doppler Measurements. Front. Physiol. 2018, 9, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Westerhof, N.; Lankhaar, J.W.; Westerhof, B.E. The arterial windkessel. Med. Biol. Eng. Comput. 2009, 47, 131–141. [Google Scholar] [CrossRef]
- Sagawa, K.R.; Lie, J. Schaefer, Translation of Otto Frank’s paper “Die Grundform des arteriellen Pulses” Zeitschrift fur Biologie 37: 483–526 (1899) [Translation of Otto Frank’s paper, The basic shape of the arterial pulse]. J. Mol. Cell. Cardiol. 1990, 22, 253–277. [Google Scholar] [CrossRef]
- Mynard, J.P.; Davidson, M.R.; Penny, D.J.; Smolich, J.J. A simple, versatile valve model for use in lumped parameter and one-dimensional cardiovascular models. Numer. Methods Biomed. Eng. 2012, 28, 626–641. [Google Scholar] [CrossRef]
- Walley, K.R. Left ventricular function: Time-varying elastance and left ventricular aortic coupling. Crit. Care 2016, 20, 626–641. [Google Scholar] [CrossRef]
- Seemann, F.; Arvidsson, P.; Nordlund, D.; Kopic, S.; Carlsson, M.; Arheden, H.; Heiberg, E. Noninvasive quantification of pressure-volume loops from brachial pressure and cardiovascular magnetic resonance. Circ. Cardiovasc. 2019, 12, e008493. [Google Scholar] [CrossRef] [PubMed]
- Available online: https://models.physiomeproject.org/welcome (accessed on 1 May 2023).
- Czechowicz, K.; Archer, G.; Franz, J.; Nowakowski, P.; Narracott, A.J.; Hose, D.R. Modelling the Aortic and Mitral valve replacement using personalised 0D and 3D Computational Models of Left Heart Circulation; To be submitted to Fluids; Multi-Disciplinary Publishing Institute: Basel, Switzerland, 2023. [Google Scholar]
- Hann, C.E.; Chase, J.G.; Desaive, T.; Froissart, C.; Revie, J.; Stevenson, D.; Lambermont, B.; Ghuysen, A.; Kohl, P.; Shaw, G.M. Unique parameter identification for cardiac diagnosis in critical care using minimal data sets. Comput. Methods Programs Biomed. 2010, 29, 75. [Google Scholar] [CrossRef]
- Ramanathan, T.; Skinner, H. Coronary blood flow. Contin. Educ. Anaesth. Crit. Care Pain 2005, 5, 61–64. [Google Scholar] [CrossRef]
- Wiggers, C. Modern Aspects of the Circulation in Health and Disease; Lea and Febiger: Philadelphia, PA, USA, 1923. [Google Scholar]
- Monge Garcia, M.I.; Santos, A. Understanding ventriculo-arterial coupling. Ann. Transl. Med. 2020, 8, 795–805. [Google Scholar] [CrossRef] [PubMed]
- Stergiopulos, N.; Westerhof, B.E.; Westerhof, N. Total arterial inertance as the fourth element of the windkessel model. Am. J. Physiol. 1999, 276, 81–88. [Google Scholar] [CrossRef] [PubMed]
- Bastos, M.B.; Burkhoff, D.; Maly, J.; Daemen, J.; den Ui, C.A.L.; Ameloot, K.; Lenzen, M.; Mahfoud, F.; Zijlstra, F.; Schreuder, J.J.; et al. Invasive left ventricle pressure-volume analysis: Overview and practical clinical implications. Eur. Heart J. 2020, 21, 1286–1297. [Google Scholar] [CrossRef]
- Kunkel, P.; Mehrmann, V.L. Differential-Algebraic Equations: Analysis and Numerical Solution; European Mathematical Society: Zurich, Switzerland, 2006; ISBN 978-3-03719-017-3. [Google Scholar]
- Jacobs, O.L.R. Introduction to Control Theory; Oxford University Press: Oxford, UK, 1984; ISBN 0-19-856148-2. [Google Scholar]
- Murray, C.D. The Physiological Principle of Minimum Work: I. The Vascular System and the Cost of Blood Volume. Proc. Natl. Acad. Sci. USA 1923, 12, 207–214. [Google Scholar] [CrossRef]
- Huo, Y.; Kassab, G.S. Intraspecific scaling laws of vascular trees. J. R. Soc. Interface 2012, 9, 190–200. [Google Scholar] [CrossRef]
- Gosling, R.C.; Study, J.; Morris, P.D.; Fossan, F.E.; Hellevik, L.R.; Lawford, P.; Hose, D.R.; Gunn, J.P. Effect of side branch flow upon physiological indices in coronary artery disease. J. Biomech. 2020, 103, 109698. [Google Scholar] [CrossRef]
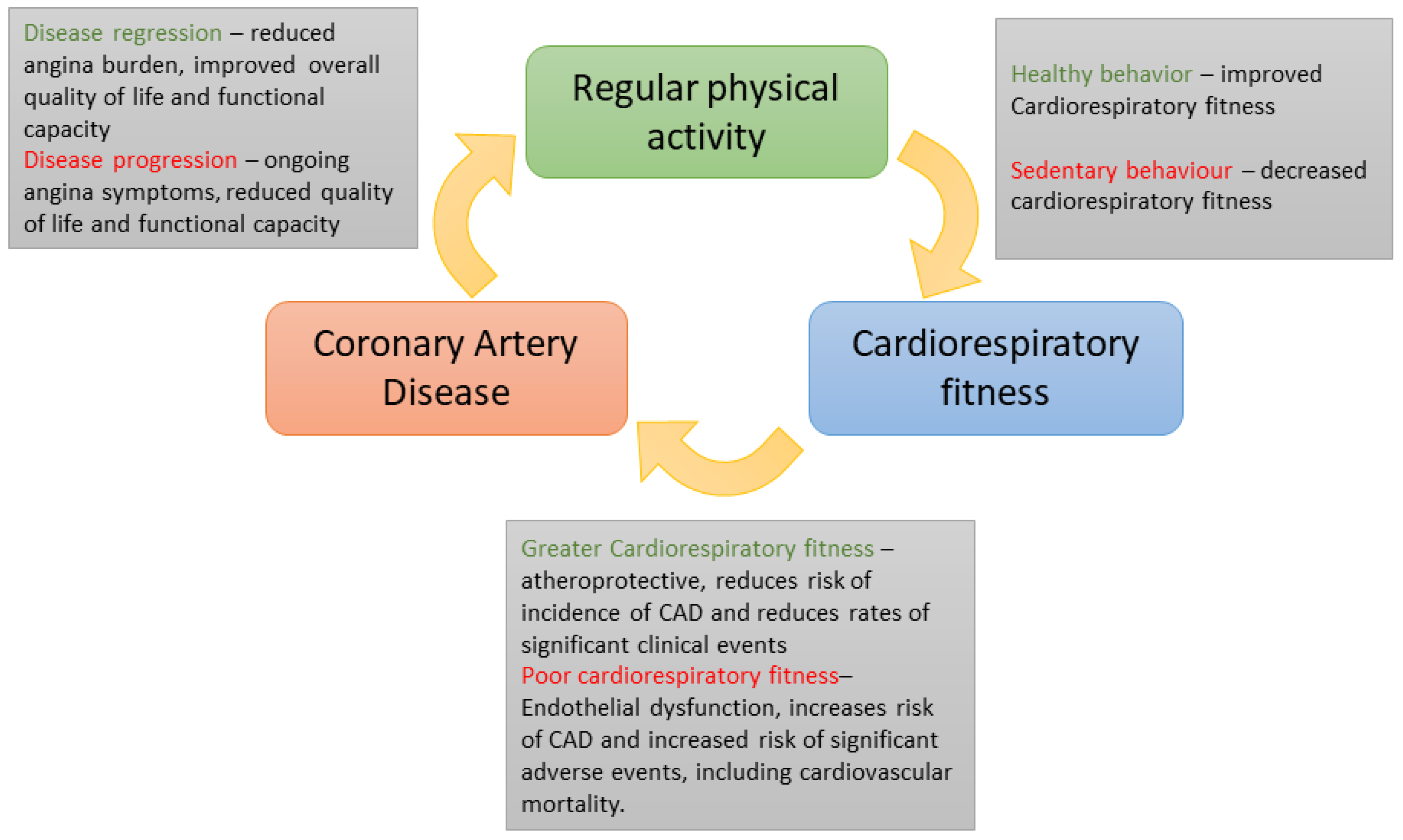
- Foerstermann, U.; Muenzel, T. Endothelial Nitric Oxide Synthase in Vascular Disease From Marvel to Menace. Circulation 2006, 113, 1708–1714. [Google Scholar] [CrossRef]
- Linke, A.; Erbs, S.; Hambrecht, R. Effects of exercise training upon endothelial function in patients with cardiovascular disease. Front Biosci. 2008, 13, 424–432. [Google Scholar] [CrossRef]
- Laufs, U.; Wassmann, S.; Czech, T.; Muenzel, T.; Eisenhauer, M.; Boehm, M.; Nickenig, G. Physical inactivity increases oxidative stress, endothelial dysfunction, and atherosclerosis, Arteriosclerosis. Thromb. Vasc. Biol. 2005, 25, 809–814. [Google Scholar] [CrossRef]
- Sattelmair, J.; Pertman, J.; Ding, E.L.; Kohl, H.W.; Haskell, W.; Lee, I.M. Dose response between physical activity and risk of coronary heart disease: A meta-analysis. Circulation 2011, 124, 789–795. [Google Scholar] [CrossRef]
- Hung, R.K.; Al-Mallah, M.H.; McEvoy, J.W.; Whelton, S.P.; Blumenthal, R.S.; Nasir, K.; Schairer, J.R.; Brawner, C.; Alam, M.; Keteyian, S.J.; et al. Prognostic value of exercise capacity in patients with coronary artery disease: The FIT (Henry Ford ExercIse Testing) project. Mayo Clin. Proc. 2014, 89, 1644–1654. [Google Scholar] [CrossRef] [PubMed]
- Hambrecht, R.; Walther, C.; Moebius-Winkler, S.; Gielen, S.; Linke, A.; Conradi, K.; Erbs, S.; Kluge, R.; Kendziorra, K.; Sabri, O.; et al. Percutaneous coronary angioplasty compared with exercise training in patients with stable coronary artery disease: A randomized trial. Circulation 2004, 109, 371–378. [Google Scholar] [CrossRef]
- Shi, Y.; Korakianitis, T. Numerical simulation of cardiovascular dynamics with left heart failure and in-series pulsatile ventricular assist device. Artif. Organs 2006, 30, 929–948. [Google Scholar] [CrossRef]
- Arts, T.; Bovendeerd, P.H.M.; Prinzen, F.W. Reneman, Relation between left ventricular cavity pressure and volume and systolic fiber stress and strain in the wall. Biophys. J. 1991, 59, 93–102. [Google Scholar] [CrossRef]
- Bovendeerd, P.H.; Borsje, P.; Arts, T.; van de Vosse, F.N. Dependence of intramyocardial pressure and coronary flow on ventricular loading and contractility, a model study. Ann. Biomed. Eng. 2006, 34, 133–1145. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Henson, M.A.; Kurtz, M.J. Selection of model parameters for off-line parameter estimation. IEEE Trans. Control. Syst. Technol. 2004, 12, 402–412. [Google Scholar] [CrossRef]
- Bjordalsbakke, N.I.; Sturdy, J.T.; Hose, D.R.; Hellevik, L.R. Parameter estimation for closed loop lumped parameter models in the systemic circulation using synthetic data. Math. Biosci. 2002, 343, 108731. [Google Scholar] [CrossRef] [PubMed]






| Step | Processing Tool | Physiology | Objective | Comment |
|---|---|---|---|---|
| 0 | statistical analysis | LV function | ensemble average, downsample time-series | synchronised to ECG1 R-R interval |
| 1 | elastance model | LV function | derive LV elastance; ingest into 0D model | characterised by double Hill LV parameters |
| 2 | 0D system model | LV–aortic coupling in systole | primary tune of 0D model systemic circulation windkessel parameters | large sub-space scanned by GA tuning |
| 3 | 0D system model | LV–atrial coupling and diastolic filling | ancillary tuning of 0D left atrial elastance and mitral valve resistances | uses gradient descent tuning. |
| 4 | CFD analysis | coronary flows | ingest into 0D model computed , MVR | use software VirtuHEART |
| 5 | 0D system model | system-coronary | in silico representation of the patient at rest |
| Subscript | ||
|---|---|---|
| Number | Name | |
| 1 | LV | ao val |
| 2 | RA | tri val |
| 3 | RV | pul val |
| 4 | LA | mit val |
| 5 | sys art | sys prox |
| 6 | pul art | pul prox |
| 7 | sys ven | sys dist |
| 8 | pul ven | pul dist |
| 9 | cor art | cor prox |
| 10 | cor ven | cor dist |
| Compartment | Index | Symbol | Description | Unit | Status | Base Value |
|---|---|---|---|---|---|---|
| NA | 1 | HR | Heart rate | bpm | Allocated | |
| NA | 2 | mcfp | Mean circulatory filling pressure | mmHg | tuned, step 3 | 7 |
| Left Ventricle (LV) | 3 | LV min. elastance (“compliance”) | mmHg/mL | assigned, step2 | 0.08 | |
| 4 | LV max. elastance (“contractility”) | mmHg/mL | assigned, step3 | 3 | ||
| 5 | LV contraction rate constant | - | tuned, step 2 | 1.32 | ||
| 6 | LV relaxation rate constant | - | tuned, step 2 | 27.4 | ||
| 7 | LV systolic time constant | - | tuned, step 2 | 0.269 | ||
| 8 | LV diastolic time constant | - | tuned, step 2 | 0.452 | ||
| 9 | LV volume offset | mL | fixed | 10 | ||
| 10 | LV fractional time shift | - | fixed | 0 | ||
| Left Atrium (LA) | 11 | LA max. elastance (“compliance”) | mmHg/mL | tuned, step 4 | 0.08 | |
| 12 | LA min. elastance (“contractility”) | mmHg/mL | tuned, step 4 | 0.17 | ||
| 13 | LA contraction rate constant | - | fixed | 1.32 | ||
| 14 | LA relaxation time constant | - | fixed | 13.1 | ||
| 15 | LA systolic time | - | tuned, step 4 | 0.11 | ||
| 16 | LA diastolic time | - | tuned, step4 | 0.18 | ||
| 17 | LA volume offset | mL | fixed | 3 | ||
| 18 | LA fractional time shift | - | fixed | 0.85 | ||
| Right Ventricle (RV) | 19 | RV min. elastance (“compliance”) | mmHg/mL | fixed | 0.04 | |
| 20 | RV max. elastance (“contractility”) | mmHg/mL | fixed | 0.6 | ||
| 21 | RV contraction rate constant | - | fixed | 1.32 | ||
| 22 | RV relaxation rate constant | - | fixed | 27.4 | ||
| 23 | RV systolic time | - | fixed | 0.269 | ||
| 24 | RV diastolic time | - | fixed | 0.452 | ||
| 25 | RV volume offset | mL | fixed | 55 | ||
| 26 | RV fractional time shift | -l | fixed | 0 | ||
| Right Atrium (RA) | 27 | RA max. elastance (“compliance”) | mmHg/mL | fixed | 0.04 | |
| 28 | RA min. elastance (“contractility”) | mmHg/mL | fixed | 0.15 | ||
| 29 | RA contraction rate constant | - | fixed | 1.32 | ||
| 30 | RA relaxation rate constant | - | fixed | 13.1 | ||
| 31 | RA systolic time | - | fixed | 0.11 | ||
| 32 | RA diastolic time | - | fixed | 0.18 | ||
| 33 | RA volume offset | mL | fixed | 17 | ||
| 34 | RA fractional time shift | - | fixed | 0.85 | ||
| Systemic Circulation LR CRC windkessel | 35 | Systemic Resistance Distal | mmHg·s/mL | tuned, step 3 | 0.033 | |
| 36 | Systemic Resistance Proximal | mmHg·s/mL | tuned, step 3 | 0.9 | ||
| 37 | Systemic Arterial Proximal Capacitance | mL/mmHg | tuned, step 3 | 1 | ||
| 38 | Systemic Arterial Proximal Unstressed Volume | mL | fixed | 720 | ||
| 39 | Systemic Arterial Distal Capacitance | mL/mmHg | fixed | 11 | ||
| 40 | Systemic Arterial Distal Unstressed Volume | mL | fixed | 3000 | ||
| 41 | Systemic Arterial Inertance (Proximal) | mmHg·s2/mL | tuned, step 3 | 0.005 | ||
| Pulmonary Circulation LR CRC windkessel | 42 | Pulmonary Resistance Distal | mmHg·s/mL | fixed | 0.01 | |
| 43 | Pulmonary Resistance Proximal | mmHg·s/mL | fixed | 0.05 | ||
| 44 | Pulmonary Arterial Proximal Capacitance | mL/mmHg | fixed | 10 | ||
| 45 | Pulmonary Arterial Proximal Unstressed Volume | mL | fixed | 180 | ||
| 46 | Pulmonary Arterial Distal Capacitance | mL/mmHg | fixed | 15 | ||
| 47 | Pulmonary Arterial Distal Unstressed Volume | mL | fixed | 720 | ||
| 48 | Pulmonary Arterial Inertance (Proximal) | mmHg·s2/mL | fixed | 0.0017 | ||
| Aortic Valve | 49 | Aortic Valve quadratic coefficient | mmHg·s/mL | fixed | 1.60 | |
| 50 | Aortic Valve linear coefficient | mmHg·s/mL | fixed | 0 | ||
| 51 | Aortic Valve regurgitant quadratic coefficient | mmHg·s/mL | fixed | 0 | ||
| 52 | Aortic Valve regurgitant linear coefficient | mmHg·s/mL | fixed | 0 | ||
| Mitral Valve | 53 | Mitral Valve quadratic coefficient | mmHg·s/mL | tuned, step 4 | 6.25 | |
| 54 | Mitral Valve linear coefficient | mmHg·s/mL | tuned, step 4 | 0 | ||
| 55 | Mitral Valve regurgitant quadratic coefficient | mmHg·s/mL | fixed | 0 | ||
| 56 | Mitral Valve regurgitant linear coefficient | mmHg·s/mL | fixed | 0 | ||
| Pulmonary Valve | 57 | Pulmonary Valve quadratic coefficient | mmHg·s/mL | fixed | 8.16 | |
| 58 | Pulmonary Valve linear coefficient | mmHg·s/mL | fixed | 0 | ||
| 59 | Pulmonary Valve regurgitant quadratic coefficient | mmHg·s/mL | fixed | 0 | ||
| 60 | Pulmonary Valve regurgitant linear coefficient | mmHg·s/mL | fixed | 0 | ||
| Tricuspid Valve | 61 | Tricuspid Valve quadratic coefficient | mmHg·s/mL | fixed | 6.25 | |
| 62 | Tricuspid Valve linear coefficient | mmHg·s/mL | fixed | 0 | ||
| 63 | Tricuspid Valve regurgitant quadratic coefficient | mmHg·s/mL | fixed | 0 | ||
| 64 | Tricuspid Valve regurgitant linear coefficient | mmHg·s/mL | fixed | 0 | ||
| Coronary Left Main | 65 | Left main stenosis, quadratic coefficient | mmHg·s/mL | assigned, step 5 | 0 | |
| 66 | Left main stenosis, linear coefficient | mmHg·s/mL | assigned, step 5 | 0 | ||
| Coronary Circumflex RCRC windkessel | 67 | Circumflex, quadratic coefficient | mmHg·s/mL | assigned, step 5 | 0 | |
| 68 | Circumflex, linear coefficient | mmHg·s/mL | assigned, step 5 | 0 | ||
| 69 | Circumflex, RCR total resistance | mmHg·s/mL | assigned, step 5 | 35 | ||
| 70 | Circumflex, RCR capacitance | mL/mmHg | tuned, step 5 | 0.25 | ||
| 71 | Circumflex, RCR fraction proximal resistance | - | tuned, step 5 | 0.9 | ||
| 72 | Circumflex unstressed volume | mL | tuned, step 5 | 8 | ||
| 73 | Circumflex capacitance back pressure fraction | - | fixed | 0.5 |
| Data Source | Compartment | Role | Unit | Data Form | Notation | State | Pathway Stage | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Rest | Exercise | Hyperemia | Pre PCI | Post PCI | ||||||
| six-minute walk test | all (general) | cardiac output proxy | ∼ | statistics | ∼ | yes | yes | no | yes | yes |
| activity monitoring | all (general) | cardiac output proxy | ∼ | statistics | ∼ | yes | yes | no | yes | yes |
| CMR scan | left ventricle | volume | ml | time-series | yes | no | no | yes | no | |
| coronary angiograms | coronaries | flow | mL/s | discrete | yes | no | yes | yes | yes | |
| coronary angiograms | coronaries | MVR | mmHg·s/mL | discrete | etc. | yes | no | yes | yes | yes |
| PCI pressure catheter | left ventricle | pressure | mmHg | time-series | yes | no | yes | yes | yes | |
| PCI pressure catheter | systemmic | pressure | mmHg | time-series | yes | no | yes | yes | no | |
| PCI pressure catheter | coronaries | pressure | mmHg | time-series | etc. | yes | no | yes | yes | yes |
| Source Data | Pre-Processing | Ingests into 0D System Model as |
|---|---|---|
| fit to double Hill elastance function | personal elastance function parameters | |
| extract extrema | personal LV volume extrema | |
| extract extrema | personal LV pressure extrema | |
| personal systemmic (aortic) pressure time-series | ||
| coronary angiograms | steady-state CFD simulations | personal MVRs for treated vessels |
| etc. | ||
| coronary angiograms | steady-state CFD simulation | personal stenotic Bernoulli resistance quadratic and linear coefficients in treated vessels |
| etc. | ||
| 6mwt | clinical interpretation | validation data |
| monitoring |
| Step | Personalisation Search Definition | |
|---|---|---|
| Input Parameters Adjusted | Output Metrics Targeted | |
| 3 | mcfp, L, , , | |
| 4 | to the above, add | |
| Valve | Time-Series | Valve Opening Signature | Difference | Notation |
|---|---|---|---|---|
| Aortic | pressure | mmHg | central | |
| volume | mL/s | forward | ||
| close to | ||||
| Mitral | pressure | central | ||
| mmHg | ||||
| volume | forward | |||
| Shift | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| double Hill LV elastance parameter | 1.91 | 1.83 | 1.78 | 1.68 | 1.52 | |
| 16.46 | 17.93 | 18.06 | 17.52 | 17.04 | ||
| 0.28 | 0.32 | 0.38 | 0.47 | 0.73 | ||
| 0.47 | 0.48 | 0.49 | 0.49 | 0.49 | ||
| 0.04 | 0.04 | 0.04 | 0.04 | 0.04 | ||
| 2.95 | 2.86 | 2.68 | 2.48 | 2.27 |
| Patient | Vessel | |||||
|---|---|---|---|---|---|---|
| LAD | LCx | RCA | ||||
| UNIT | mmHg | mmHg | mmHg | mmHg | mmHg | mmHg |
| A | 88.60 | 74.50 | ∼ | ∼ | ∼ | ∼ |
| B | 103.71 | 99.17 | 103.95 | 101.69 | ∼ | ∼ |
| C | 121.74 | 115.73 | ∼ | ∼ | 127.23 | 125.89 |
| Patient | Metric | Unit | Vessel | ||
|---|---|---|---|---|---|
| LAD | LCx | RCA | |||
| A | MVR | mmHg·s/mL | 1.50 | ∼ | ∼ |
| mmHg·s/mL | 28.45 | ∼ | ∼ | ||
| mmHg·s/mL | 28.58 | ∼ | ∼ | ||
| B | MVR | mmHg·s/mL | 0.77 | 1.10 | ∼ |
| mmHg·s/mL | 16.56 | 10.22 | ∼ | ||
| mmHg·s/mL | 22.34 | 14.33 | ∼ | ||
| C | MVR | mmHg·s/mL | 1.75 | ∼ | 1.01 |
| mmHg·s/mL | 22.34 | ∼ | 16.67 | ||
| mmHg·s/mL | 12.33 | ∼ | 14.11 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baraikan, A.A.; Czechowicz, K.; Morris, P.D.; Halliday, I.; Gosling, R.C.; Gunn, J.P.; Narracott, A.J.; Williams, G.; Garg, P.; Malawski, M.; et al. Modelling The Hemodynamics of Coronary Ischemia. Fluids 2023, 8, 159. https://doi.org/10.3390/fluids8050159
Baraikan AA, Czechowicz K, Morris PD, Halliday I, Gosling RC, Gunn JP, Narracott AJ, Williams G, Garg P, Malawski M, et al. Modelling The Hemodynamics of Coronary Ischemia. Fluids. 2023; 8(5):159. https://doi.org/10.3390/fluids8050159
Chicago/Turabian StyleBaraikan, Abdulaziz Al, Krzysztof Czechowicz, Paul D. Morris, Ian Halliday, Rebecca C. Gosling, Julian P. Gunn, Andrew J. Narracott, Gareth Williams, Pankaj Garg, Maciej Malawski, and et al. 2023. "Modelling The Hemodynamics of Coronary Ischemia" Fluids 8, no. 5: 159. https://doi.org/10.3390/fluids8050159
APA StyleBaraikan, A. A., Czechowicz, K., Morris, P. D., Halliday, I., Gosling, R. C., Gunn, J. P., Narracott, A. J., Williams, G., Garg, P., Malawski, M., Vosse, F. v. d., Lungu, A., Rafiroiu, D., & Hose, D. R. (2023). Modelling The Hemodynamics of Coronary Ischemia. Fluids, 8(5), 159. https://doi.org/10.3390/fluids8050159







