Hemodynamic Investigation of the Flow Diverter Treatment of Intracranial Aneurysm
Abstract
1. Introduction
2. Materials and Methods
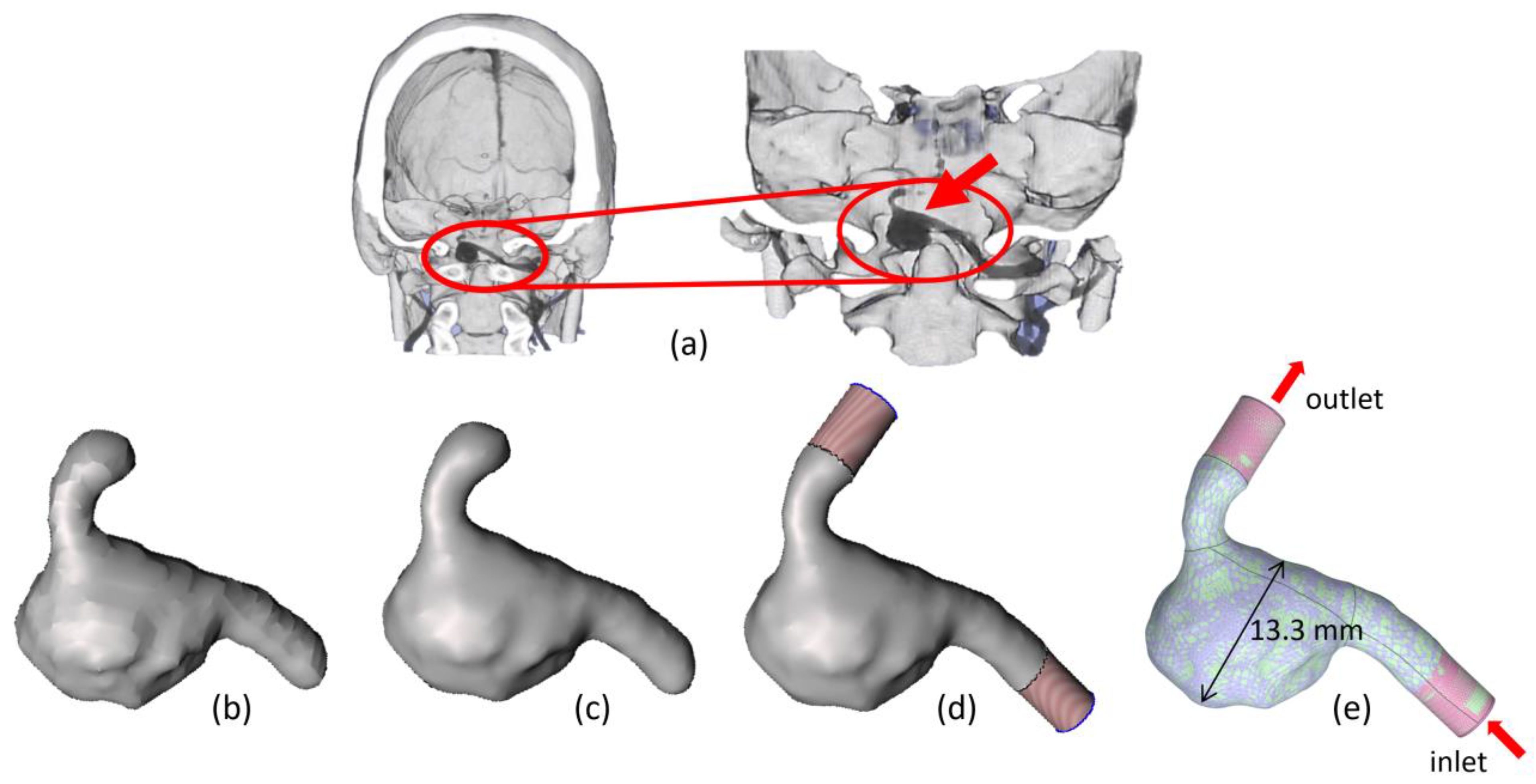
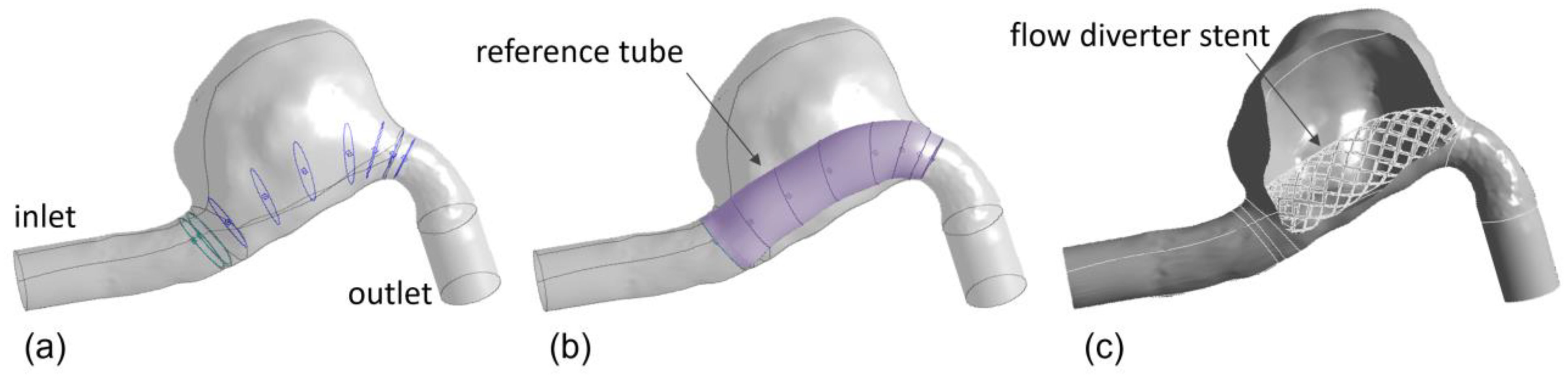
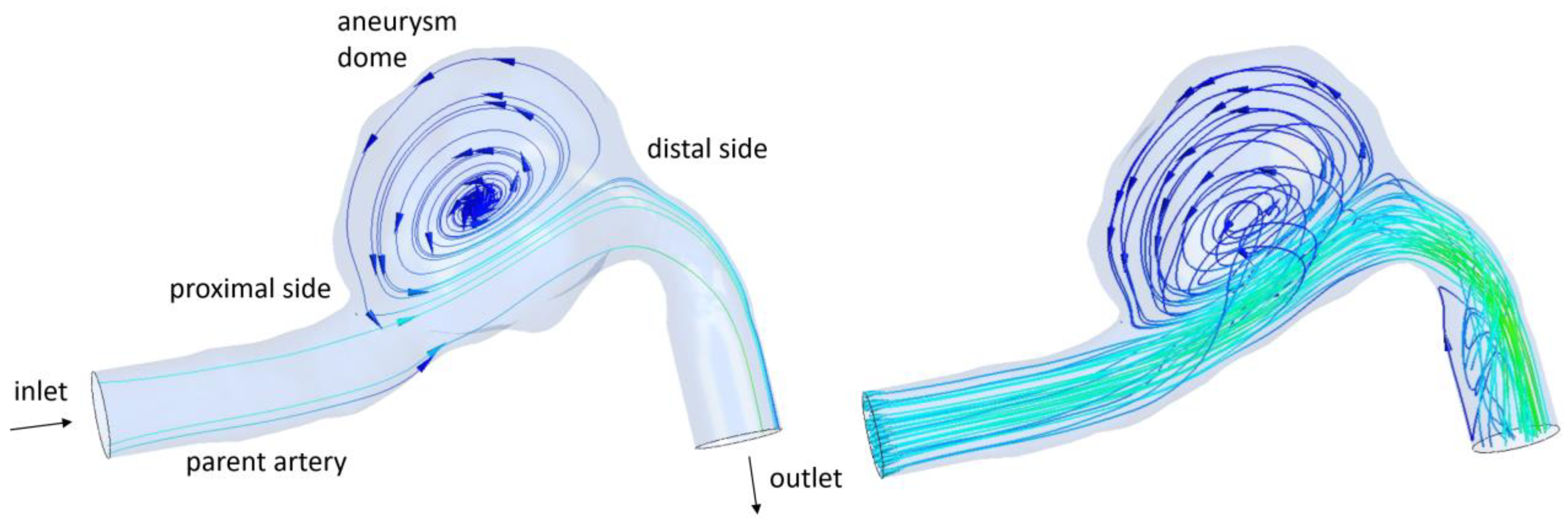
2.1. Intracranial Aneurysm and FDS Reconstruction Process
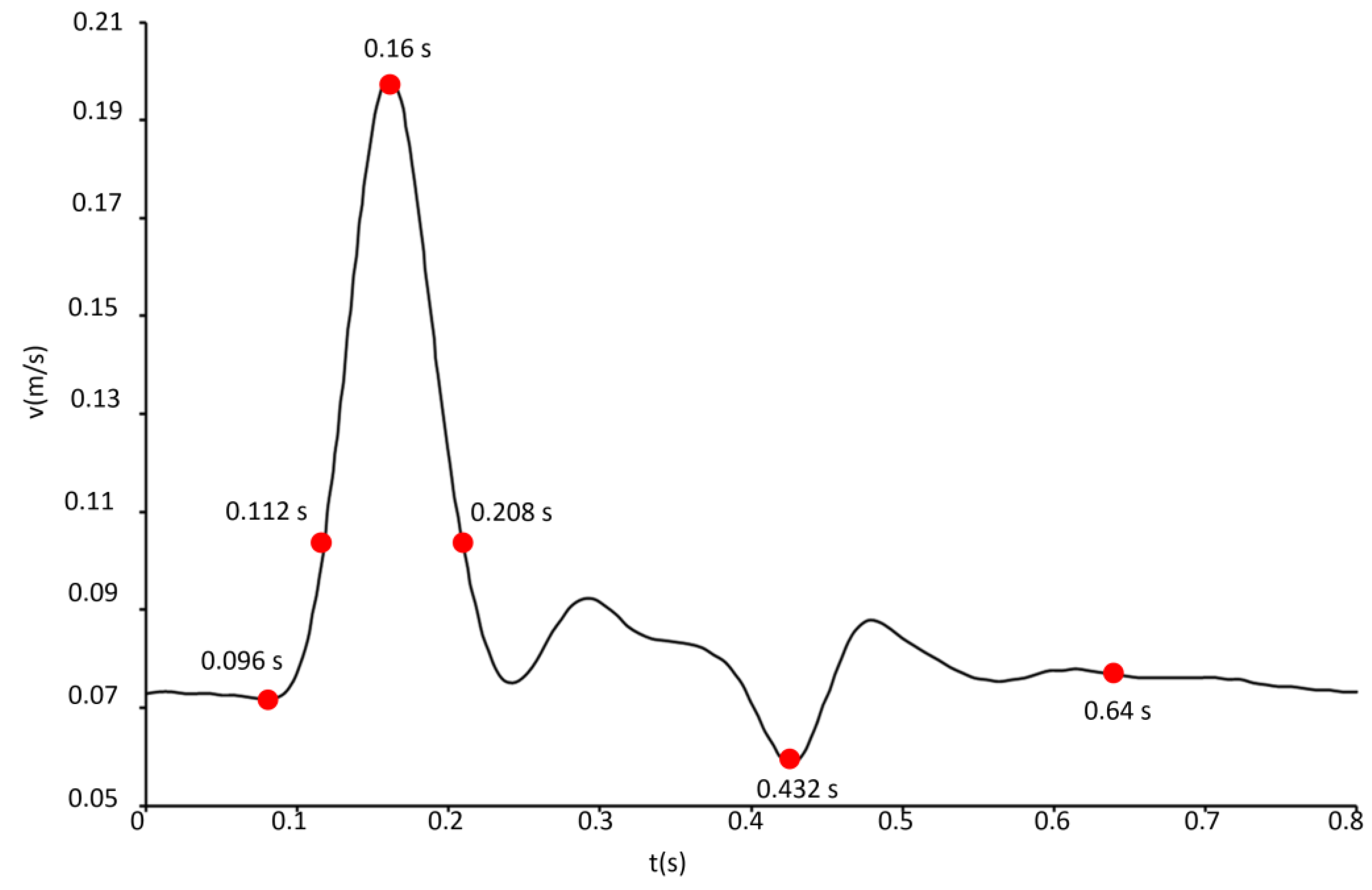
2.2. Governing Equations and Numerical Setup
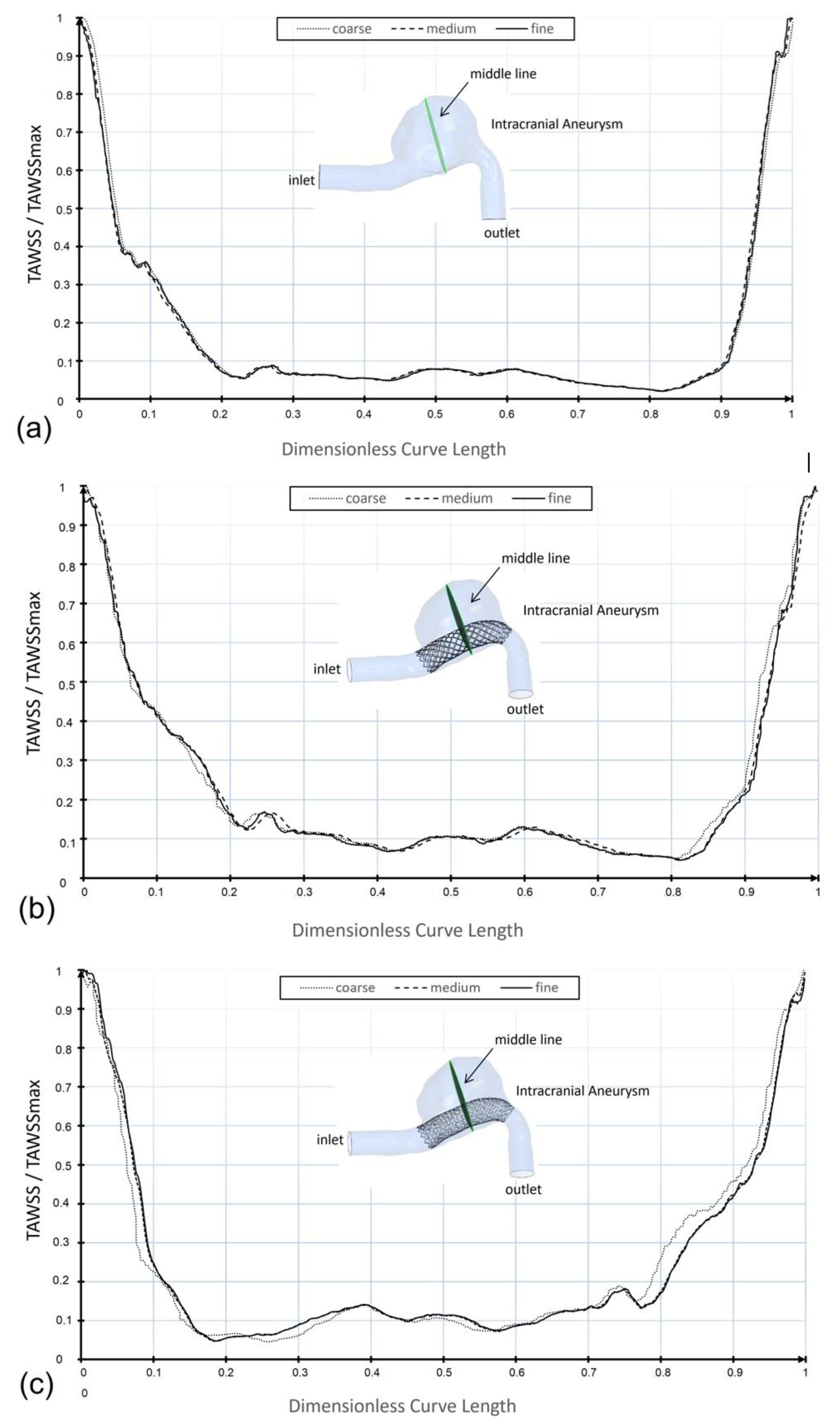
2.3. Mesh Convergence Analysis
2.4. Hemodynamic Parameters
3. Results and Discussion
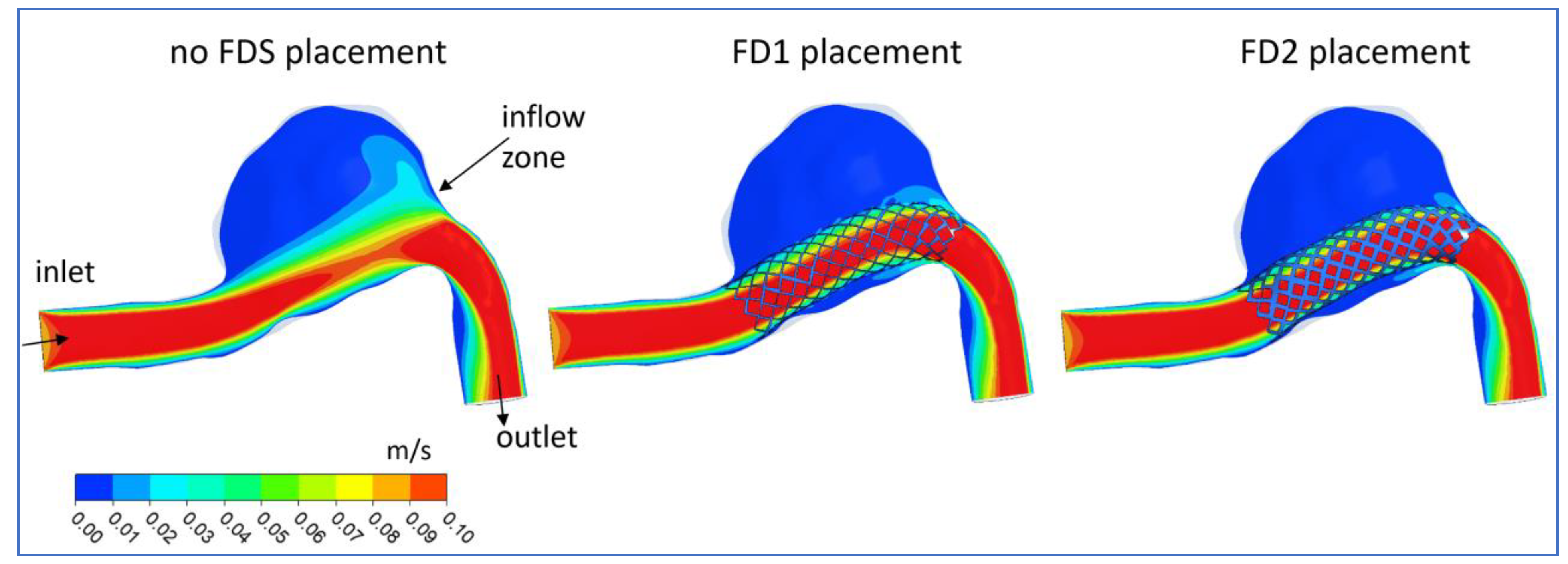
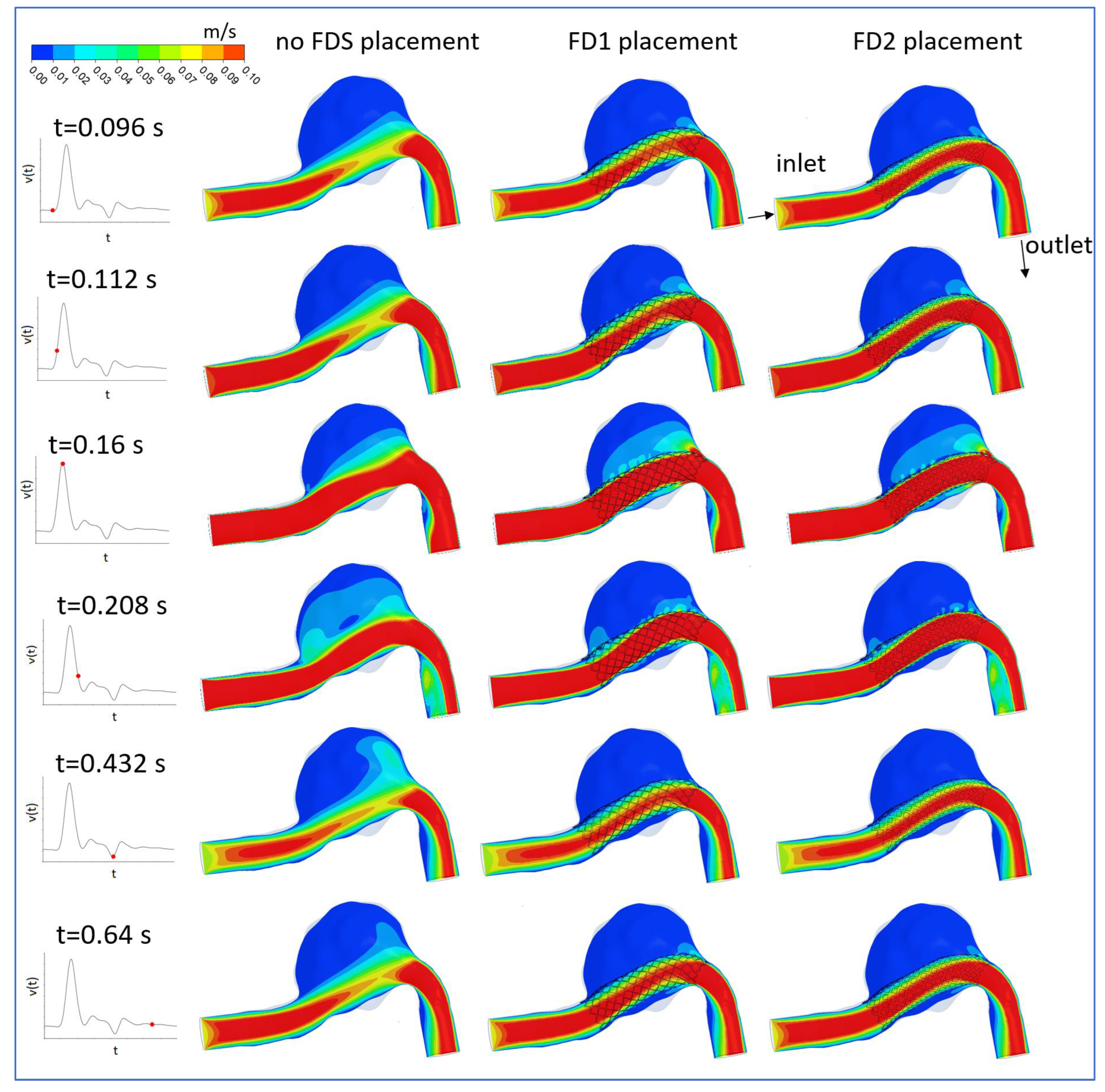
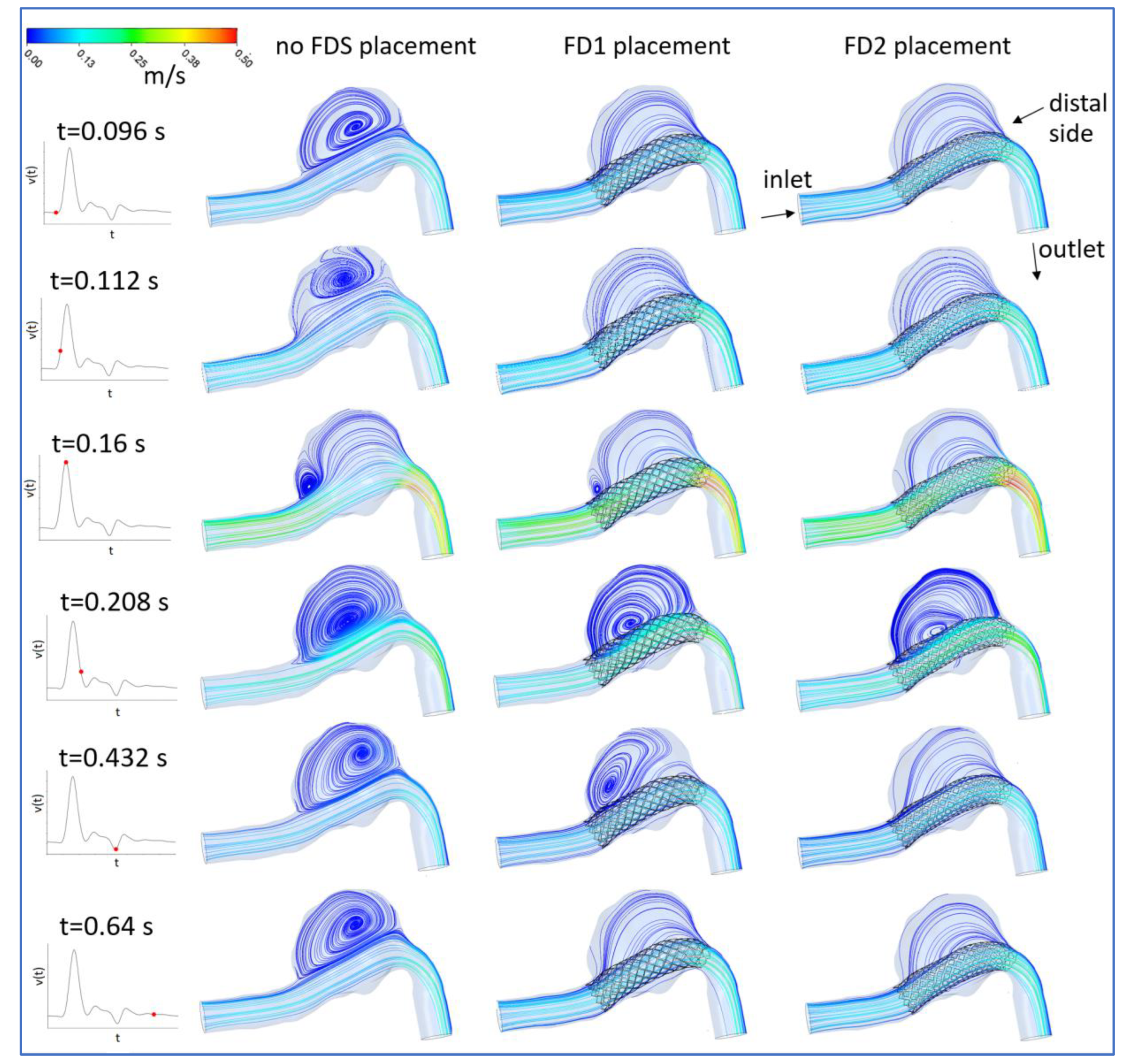
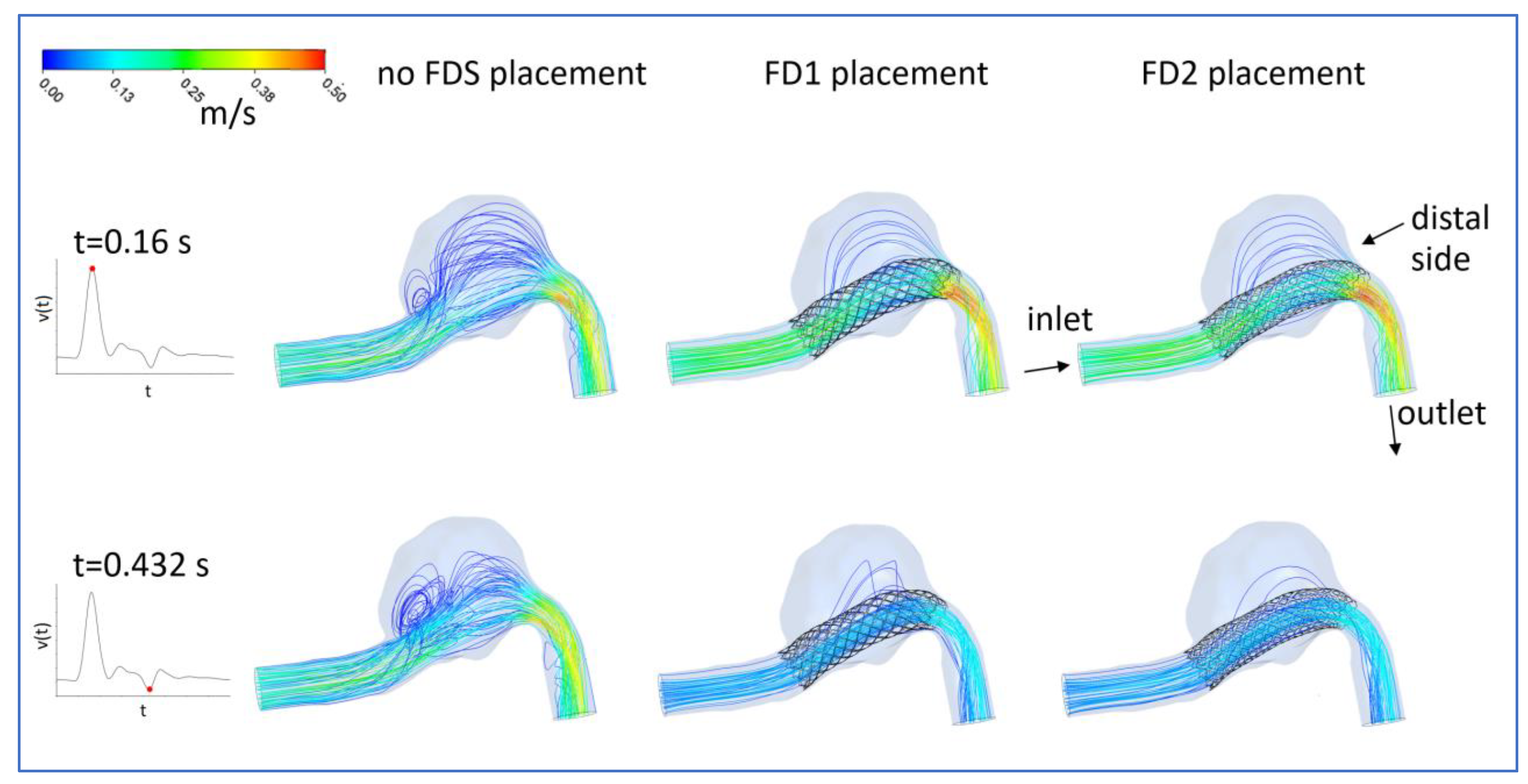
3.1. FDS Effects on Blood Flow
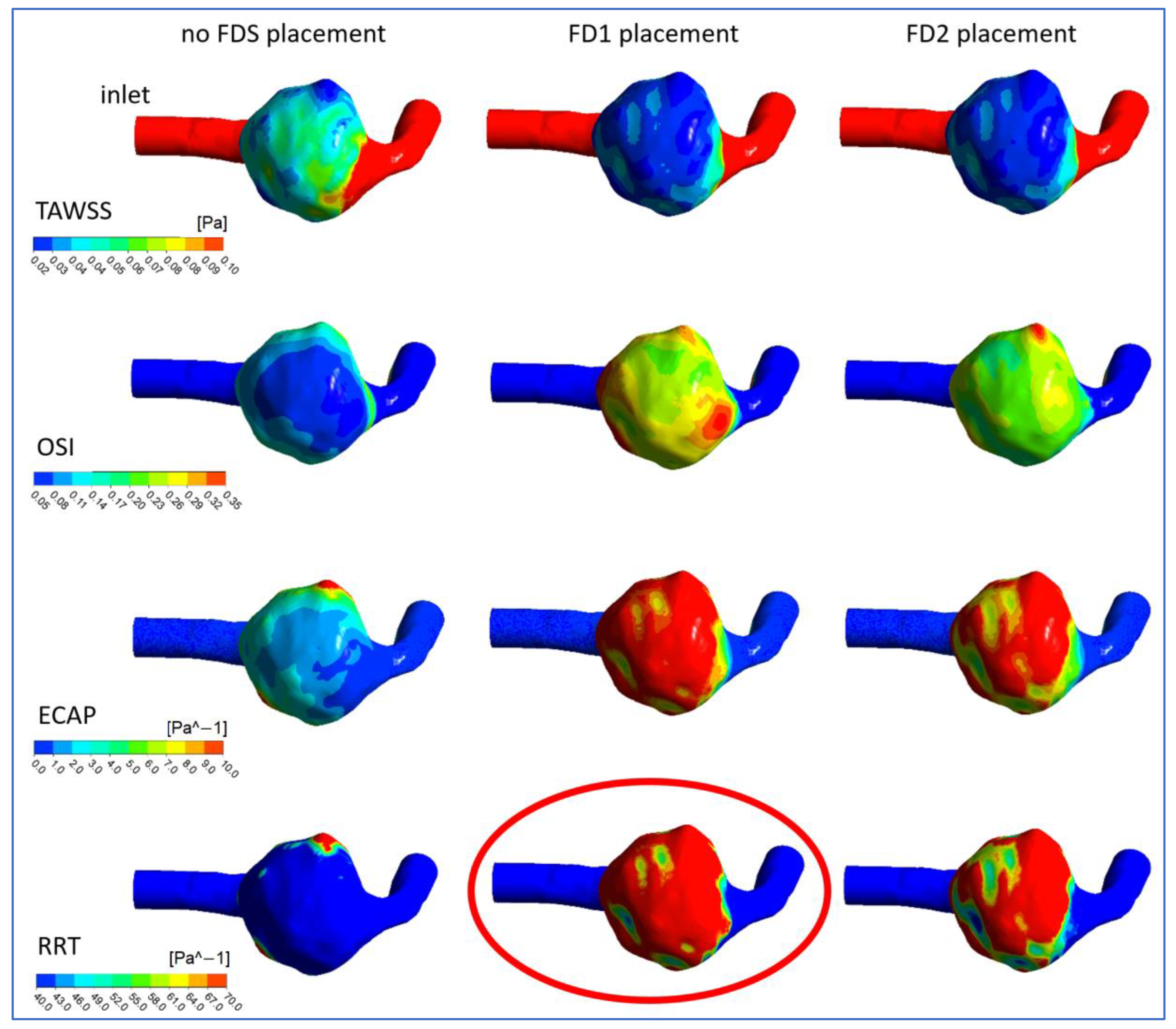
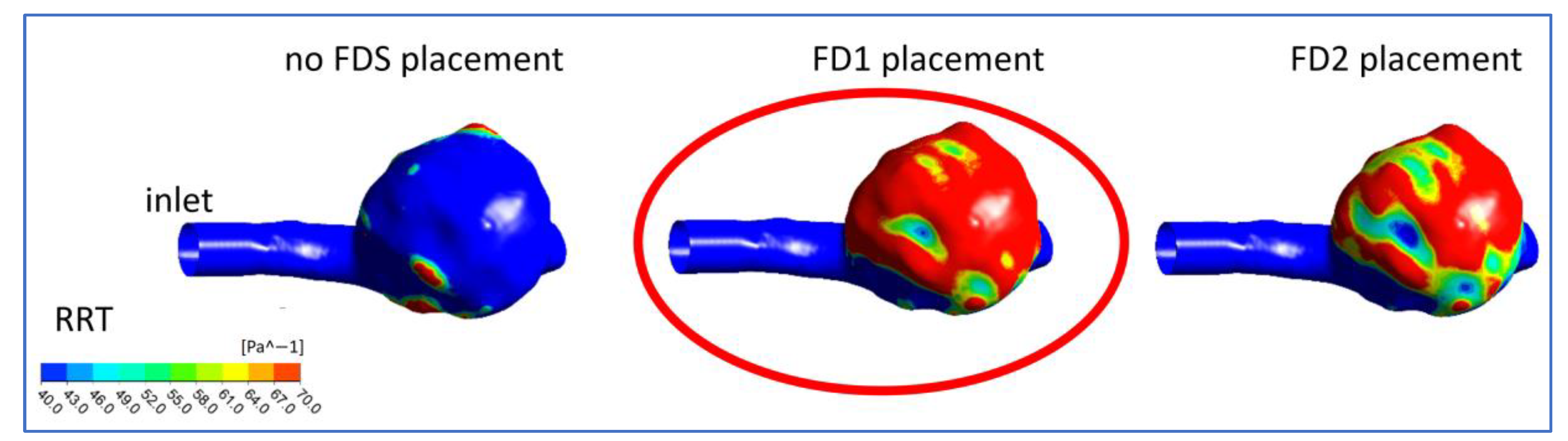
3.2. Hemodynamic Parameters
3.3. Study Limitations
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Etminan, N.; Rinkel, G.J. Unruptured intracranial aneurysms: Development, rupture and preventive management. Nat. Rev. Neurol. 2016, 12, 699–713. [Google Scholar] [CrossRef] [PubMed]
- Texakalidis, P.; Sweid, A.; Mouchtouris, N.; Peterson, E.C.; Sioka, C.; Rangel-Castilla, L.; Reavey-Cantwell, J.; Jabbour, P. Aneurysm Formation, Growth, and Rupture: The Biology and Physics of Cerebral Aneurysms. World Neurosurg. 2019, 130, 277–284. [Google Scholar] [CrossRef] [PubMed]
- Meng, H.; Tutino, V.M.; Xiang, J.; Siddiqui, A. High WSS or low WSS? Complex interactions of hemodynamics with intracranial aneurysm initiation, growth, and rupture: Toward a unifying hypothesis. AJNR Am. J. Neuroradiol. 2014, 35, 1254–1262. [Google Scholar] [CrossRef] [PubMed]
- Qiu, T.; Jin, G.; Xing, H.; Lu, H. Association between hemodynamics, morphology, and rupture risk of intracranial aneurysms: A computational fluid modeling study. Neurol. Sci. 2017, 38, 1009–1018. [Google Scholar] [CrossRef]
- Hsiai, T.K.; Cho, S.K.; Honda, H.M.; Hama, S.; Navab, M.; Demer, L.L.; Ho, C.M. Endothelial cell dynamics under pulsating flows: Significance of high versus low shear stress (d(tau)/dt). Ann. Biomed. Eng. 2002, 30, 646–656. [Google Scholar] [CrossRef] [PubMed]
- Murayama, Y.; Fujimura, S.; Suzuki, T.; Takao, H. Computational fluid dynamics as a risk assessment tool for aneurysm rupture. Neurosurg. Focus 2019, 47, E12. [Google Scholar] [CrossRef]
- Jin, Z.H.; Gerdroodbary, M.B.; Valipour, P.; Faraji, M.; Abu-Hamdeh, N.H. CFD investigations of the blood hemodynamic inside internal cerebral aneurysm (ICA) in the existence of coiling embolism. Alex. Eng. J. 2023, 66, 797–809. [Google Scholar] [CrossRef]
- Byrne, J.V.; Beltechi, R.; Yarnold, J.A.; Birks, J.; Kamran, M. Early experience in the treatment of intra-cranial aneurysms by endovascular flow diversion: A multicentre prospective study. PLoS ONE 2010, 5, e12492. [Google Scholar] [CrossRef]
- Venguru, S.; Nguyen, K.; Davidson, J. Intracranial Aneurysms: Evaluation of Braid Pore Configurations on Flow Disruption with Flow Diverter Devices. Biomed. Sci. Technol. 2019, 1, 18–26. [Google Scholar]
- Sadasivan, C.; Cesar, L.; Seong, J.; Rakian, A.; Hao, Q.; Tio, F.O.; Wakhloo, A.K.; Lieber, B.B. An original flow diversion device for the treatment of in-tracranial aneurysms: Evaluation in the rabbit elastase-induced model. Stroke 2009, 40, 952–958. [Google Scholar] [CrossRef] [PubMed]
- Mutlu, O.; Olcay, A.B.; Bilgin, C.; Hakyemez, B. Evaluating the Effectiveness of 2 Different Flow Diverter Stents Based on the Stagnation Region Formation in an Aneurysm Sac Using Lagrangian Coherent Structure. World Neurosurg. 2019, 127, e727–e737. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y.; Kao, E.; Flórez-Valencia, L.; Courbebaisse, G. Towards optimal flow diverter porosity for the treatment of intracranial aneurysm. J. Biomech. 2019, 82, 20–27. [Google Scholar] [CrossRef]
- Dholakia, R.; Sadasivan, C.; Fiorella, D.J.; Woo, H.H.; Lieber, B.B. Hemodynamics of flow diverters. J. Biomech. Eng. 2017, 139, 021002. [Google Scholar] [CrossRef]
- Suzuki, T.; Takao, H.; Fujimura, S.; Dahmani, C.; Ishibashi, T.; Mamori, H.; Fukushima, N.; Yamamoto, M.; Murayama, Y. Selection of helical braided flow diverter stents based on hemodynamic performance and mechanical properties. J. Neurointerv. Surg. 2017, 9, 999–1005. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Yang, H.; Hong, I.; Oh, J.H.; Kim, Y.B. Computational Study of Hemodynamic Changes Induced by Overlapping and Compacting of Stents and Flow Diverter in Cerebral Aneurysms. Front Neurol. 2021, 12, 705841. [Google Scholar] [CrossRef] [PubMed]
- Nada, A.; Hassan, M.A.; Fakhr, M.A.; El-Wakad, M.T.I. Studying the effect of stent thickness and porosity on post-stent implantation hemodynamics. J. Med. Eng. Technol. 2021, 45, 408–416. [Google Scholar] [CrossRef] [PubMed]
- Catalán-Echeverría, B.; Kelly, M.E.; Peeling, L.; Bergstrom, D.; Chen, X.; Malvè, M. CFD-Based Comparison Study of a New Flow Diverting Stent and Commercially-Available Ones for the Treatment of Cerebral Aneurysms. Appl. Sci. 2019, 9, 1341. [Google Scholar] [CrossRef]
- Bouillot, P.; Brina, O.; Ouared, R.; Yilmaz, H.; Lovblad, K.O.; Farhat, M.; Pereira, V.M. Computational fluid dynamics with stents: Quantitative comparison with particle image velocimetry for three commercial off the shelf intracranial stents. J. Neurointerv. Surg. 2016, 8, 309–315. [Google Scholar] [CrossRef]
- Saqr, K.M.; Mansour, O.; Tupin, S.; Hassan, T.; Ohta, M. Evidence for non-Newtonian behavior of intracranial blood flow from Doppler ultrasonography measurements. Med. Biol. Eng. Comput. 2019, 57, 1029–1036. [Google Scholar] [CrossRef]
- Abdehkakha, A.; Hammond, A.L.; Patel, T.R.; Siddiqui, A.H.; Dargush, G.F.; Meng, H. Cerebral aneurysm flow diverter modeled as a thin inhomogeneous porous medium in hemodynamic simulations. Comput. Biol. Med. 2021, 139, 104988.20. [Google Scholar] [CrossRef]
- Ngoepe, M.N.; Ventikos, Y. Computational modelling of clot development in pa-tient-specific cerebral aneurysm cases. J. Thromb Haemost. 2016, 14, 262–272. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Karmonik, C.; Yu, Y.; Lv, N.; Shi, Z.; Liu, J.M.; Huang, Q. Modeling flow diverters using a porous medium approach: A fast alternative to virtual flow diverter deployment. World Neurosurg. 2022, 164, e501–e508. [Google Scholar] [CrossRef] [PubMed]
- Rouchaud, A.; Brinjikji, W.; Lanzino, G.; Cloft, H.J.; Kadirvel, R.; Kallmes, D.F. Delayed Hemorrhagic Complications after Flow Diversion for Intracranial Aneurysms: A Literature Overview. Neuroradiology 2016, 58, 171–177. [Google Scholar] [CrossRef]
- Cebral, J.R.; Mut, F.; Raschi, M.; Scrivano, E.; Ceratto, R.; Lylyk, P.; Putman, C.M. Aneurysm rupture following treatment with flow diverting stents: Computational hemodynamics analysis of treatment. AJNR Am. J. Neuroradiol. 2011, 32, 27–33. [Google Scholar] [CrossRef] [PubMed]
- Himburg, H.A.; Grzybowski, D.M.; Hazel, A.L.; LaMack, J.A.; Li, X.M.; Friedman, M.H. Spatial comparison between wall shear stress measures and porcine arterial endothelial permeability. Am. J. Physiol. Heart Circ. Physiol. 2004, 286, H1916–H1922. [Google Scholar] [CrossRef]
- Rayz, V.; Boussel, L.; Ge, L.; Leach, J.; Martin, V.; Lawton, V.; McCulloch, V.; Saloner, D. Flow Residence Time and Regions of Intraluminal Thrombus Deposition in Intracranial Aneurysms. Ann. Biomed. Eng. 2010, 38, 3058–3069. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.W.; Antiga, L.; Steinman, D.A. Correlation among indicators of disturbed flow at the normal carotid bifurcation. J. Biomech. Ing. 2009, 131, 061013. [Google Scholar] [CrossRef]
- Schlichting, H. Boundary Layer Theory, 7th ed.; McGraw-Hill: New York, NY, USA, 1979. [Google Scholar]
- Reymond, P.; Merenda, F.; Perren, F.; Rüfenacht, D.; Stergiopulos, N. Validation of a one-dimensional model of the systemic arterial tree. Am. J. Physiol. Heart Circ. Physiol. 2009, 297, H208–H222. [Google Scholar] [CrossRef]
- Shibeshi, S.S.; Collins, W.E. The rheology of blood flow in a branched arterial system. Appl. Rheol. 2005, 15, 398–405. [Google Scholar] [CrossRef]
- ANSYS. Workbench User’s Guide, Release 2022 R1, January 2022; ANSYS, Inc.: Canonsburg, PA, USA, 2022. [Google Scholar]
- Ferziger, J.H.; Peric, M. Computational Methods for Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2001; ISBN 978-3-540-42074-3. [Google Scholar]
- He, X.; Ku, D.N. Pulsatile flow in the human left coronary artery bifurcation: Average conditions. J. Biomech. Eng. 1996, 118, 74–82. [Google Scholar] [CrossRef]
- Sorescu, G.P.; Song, H.N.; Tressel, S.L.; Hwang, J.; Dikalov, S.; Smith, D.A.; Boyd, N.L.; Platt, M.O.; Lassègue, B.; Griendling, K.K.; et al. Bone morphogenic protein 4 produced in endothelial cells by oscillatory shear stress induces monocyte adhesion by stimulating reactive oxygen species production from a nox1-based NADPH oxidase. Circ. Res. 2004, 95, 773–779. [Google Scholar] [CrossRef]
- Di Achille, P.; Tellides, G.; Figueroa, C.A.; Humphrey, J.D. A haemodynamic predictor of intraluminal thrombus formation in abdominal aortic aneurysms. Proc. R. Soc. Lond. Math. Phys. Eng. Sci. 2014, 470, 20140163. [Google Scholar] [CrossRef]
- Boniforti, M.A.; Cesaroni, M.C.; Magini, R.; Pasqui, E.; de Donato, G. Image-Based Numerical Investigation in an Impending Abdominal Aneurysm Rupture. Fluids 2022, 7, 269. [Google Scholar] [CrossRef]
- Cecchi, E.; Giglioli, C.; Valente, S.; Lazzeri, C.; Gensini, G.F.; Abbate, R.; Mannini, L. Role of hemodynamic shear stress in cardiovascular disease. Atherosclerosis. 2011, 214, 249–256. [Google Scholar] [CrossRef] [PubMed]
- Tarbell, J.M.; Shi, Z.D.; Dunn, J.; Jo, H. Fluid mechanics, arterial disease, and gene expression. Annu. Rev. Fluid Mech. 2014, 46, 591–614. [Google Scholar] [CrossRef]
- Boniforti, M.A.; Di Bella, L.; Magini, R. On the role of hemodynamics in predicting rupture of the abdominal aortic aneurysm. J. Zhejiang Univ. Sci. 2021, A 22, 957–978. [Google Scholar] [CrossRef]
- Xiang, J.; Siddiqui, A.H.; Meng, H. The effect of inlet waveforms on computational hemodynamics of patient-specific intracranial aneurysms. J. Biomech. 2014, 47, 3882–3890. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Wang, S.; Tian, Z.; Zhu, W.; Zhang, Y.; Zhang, Y.; Wang, Y.; Wang, K.; Yang, X.; Liu, J. Discrimination of intracranial aneurysm rupture status: Patient-specific inflow boundary may not be a must-have condition in hemodynamic simulations. Neuroradiology 2020, 62, 1485–1495. [Google Scholar] [CrossRef] [PubMed]
- Robertson, A.M.; Duan, X.; Aziz, K.M.; Hill, M.R.; Watkins, S.C.; Cebral, J.R. Diversity in the strength and structure of unruptured cerebral aneurysms. Ann. Biomed. Eng. 2015, 43, 1502–1515. [Google Scholar] [CrossRef] [PubMed]
- Rayz, V.L.; Cohen-Gadol, A.A. Hemodynamics of cerebral aneurysms: Connecting medical imaging and biomechanical analysis. Annu. Rev. Biomed. Eng. 2020, 22, 231–256. [Google Scholar] [CrossRef]
- Voß, S.; Glaßer, S.; Hoffmann, T.; Beuing, O.; Weigand, S.; Jachau, K.; Preim, B.; Thévenin, D.; Janiga, G. Berg, Fluid-structure simulations of a ruptured intracranial aneurysm: Constant versus patient-specific wall thickness. Comput. Math. Methods Med. 2016, 2016, 9854539. [Google Scholar] [CrossRef]

| No FDS Placement | FD1 Placement | FD2 Placement | |||
|---|---|---|---|---|---|
| Elements (approximate number) | WSS (Pa) | Elements (approximate number) | WSS (Pa) | Elements (approximate number) | WSS (Pa) |
| 1 × 106 | 1.24014 | 2 × 106 | 1.2718 | 2 × 106 | 1.22263 |
| 2 × 106 | 1.23136 | 3 × 106 | 1.23366 | 3 × 106 | 1.21016 |
| 3 × 106 | 1.24095 | 4 × 106 | 1.2331 | 4 × 106 | 1.2181 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boniforti, M.A.; Magini, R.; Orosco Salinas, T. Hemodynamic Investigation of the Flow Diverter Treatment of Intracranial Aneurysm. Fluids 2023, 8, 189. https://doi.org/10.3390/fluids8070189
Boniforti MA, Magini R, Orosco Salinas T. Hemodynamic Investigation of the Flow Diverter Treatment of Intracranial Aneurysm. Fluids. 2023; 8(7):189. https://doi.org/10.3390/fluids8070189
Chicago/Turabian StyleBoniforti, Maria Antonietta, Roberto Magini, and Tania Orosco Salinas. 2023. "Hemodynamic Investigation of the Flow Diverter Treatment of Intracranial Aneurysm" Fluids 8, no. 7: 189. https://doi.org/10.3390/fluids8070189
APA StyleBoniforti, M. A., Magini, R., & Orosco Salinas, T. (2023). Hemodynamic Investigation of the Flow Diverter Treatment of Intracranial Aneurysm. Fluids, 8(7), 189. https://doi.org/10.3390/fluids8070189









