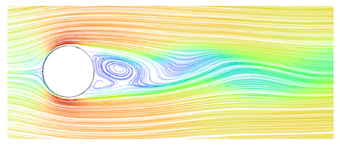
Abstract
Using unmanned aerial vehicles (UAVs) for bridge inspection is becoming increasingly popular due to its ability to improve efficiency and ensure the safety of monitoring personnel. Compared to traditional manual monitoring methods, UAV inspections are a safer and more efficient alternative. This paper examines the impact of meteorological conditions on UAV-based bridge monitoring during specific tasks, with the aim of enhancing the safety of the UAV’s costly components. The wake vortex behind a bridge structure can vary over time due to airflow, which can have a direct impact on the safety of UAV flights. To assess this impact, numerical analysis is conducted based on monitoring requirements specific to different tasks, taking into account wind speed, wind direction, and air temperature. In order to optimize UAV trajectory, it is important to consider the wake vortex intensity and its associated influence region, which can pose a potential danger to UAV flight. Additionally, the analysis should take into account the aerodynamic effects of different types of bridge columns on the wake vortex. An optimization algorithm was utilized to optimize the trajectory of a UAV during bridge inspections within the safe region affected by wind fields. This resulted in the determination of an effective and safe flight path. The study reveals that varying wind speeds have an impact on the safe flight zone of UAVs, even if they are below the operational requirements. Therefore, when monitoring bridges using UAVs, it is important to take into account the influence of meteorological conditions. Furthermore, it was observed that the flight path of UAVs during square cylinder column monitoring is longer and more time-consuming than round cylinder column monitoring. Determining an effective UAV inspection path is crucial for completing bridge monitoring tasks in windy conditions, establishing bridge inspection standards, and developing the Intelligent Bridge Inspection System (IBIS).
1. Introduction
China has an extensive bridge network of over 960,000 structures, covering a total distance exceeding 73 million kilometers [1]. Despite this, bridge collapse incidents are frequent due to design flaws, environmental decay, overload operations, and inherent lifespan limitations. Alarmingly, 70% of these accidents occur during operation, resulting in a 45% fatality rate [2]. Conventional inspection methods face challenges related to terrain [3], traffic, and diverse bridge types, necessitating the development of a new, safe, cost-effective, and time-efficient inspection approach.
In recent years, the use of UAVs for non-destructive analysis has gained popularity due to enhanced accessibility, cost efficiency, avoidance of traffic disruptions, and reduced safety hazards [4]. Notably, studies by Jeong et al. [5], Peng et al. [3], Jung et al. [6], Cano et al. [7], Mohammadi et al. [8], and Lee et al. [9] demonstrate the effectiveness of UAVs in quantifying damage, achieving precision in inspections, and proposing autonomous inspection methods. Drones offer advantages over conventional methods in terms of cost, time, and reduced risk for inspectors [10].
However, a critical gap exists in the analysis of UAV reliability and the shortest detection path in windy conditions. This necessitates a comprehensive understanding of potential danger regions during windy detection missions to enhance the overall effectiveness of UAV-based bridge inspections.
Several studies have addressed the impact of wind on UAV flight routes and stabilization. Shalyhin and Nerubatsky et al. [11] optimized UAV flight routes considering wind influence. Yang and Chen [12] proposed a joint estimation of aerodynamic parameters and wind disturbances. Barikbin and Fakharian [13] addressed wind disturbances in quadrotor stabilization using a combined backstepping and super-twisting integral sliding mode strategy. Xu et al. [14] enhanced UAV flight performance with a backstepping controller considering wind field disturbance. Reference [15] summarized different wind fields affecting UAVs, proposing a Lyapunov stability theory-based adaptive control system. Lee [16] suggested a linear acceleration control algorithm for accurate trajectory tracking in high-wind environments. Nobahari et al. [17] introduced an online tuning method for parameters under varying wind conditions based on fuzzy logic. Reference [18] concluded that reducing total wind force on piers with rounded corners depends on the corner design. Zhou et al. [19] considered the influence of static wind coefficient on beam section lift coefficient using Computational Fluid Dynamics (CFD), finding larger effects on wind speed and angle of attack. Cao et al. [20] simulated the response of long-span bridges to non-synoptic winds to assess vulnerability. Zhang et al. [21] obtained wind flow data around a bridge site using CFD technology. Wang et al. [22] studied the wind environment near an inverted Y-shaped pylon. Zheng et al. [23] suggested that long-span bridges with high piers have a low fundamental frequency, emphasizing the importance of inertial forces from fluctuating winds.
Due to the widespread use of UAVs and their structural limitations, environmental adaptability is crucial. Temperature, a primary factor affecting UAV battery consumption, is investigated in Reference [24] for cruising hybrid-powered fixed-wing UAVs. Fluctuations in temperature significantly impact fuel consumption, limiting UAV flight capabilities. Li et al. [25] explore UAV overall performance, noting a pronounced effect of low-temperature conditions on battery performance. Scrutinizing UAV operational states in low-temperature environments is thus imperative. Temperature variations also impact bridge structural integrity, leading to potential cracks. Hossain et al. [26] discovered that cumulative thermal stresses may surpass concrete tensile strength, causing cracks. Guo and Lu [27] assess temperature effects on concrete-filled steel tube arch bridges. Niu et al. [28] elucidate temperature-induced deformation mechanisms, emphasizing its significant influence on concrete truss combination arch bridges.
In UAV track planning, AlRaslan and AlKurdi [29] investigated Parallel Genetic Algorithms (PGA) and implemented a parallel path planner on multi-core processors using OpenMP, reducing execution time compared to sequential execution. Leng and Sun [30] found that genetic algorithms improve UAV performance in mountainous regions. Wang and Meng [31] proposed an enhanced genetic algorithm improving local search ability and efficiency. Zhang et al. [32] addressed the limitations of the 4-D trajectory-prediction model, proposing a 4-D trajectory combined prediction model based on a genetic algorithm for a safe drone flight. Zhou et al. [33] used an improved genetic algorithm and A* algorithm for trajectory planning, ensuring the shortest path with minimal error corrections. Hua et al. [34] introduced a genetic algorithm-based fault diagnosis and fault-tolerant control for a four-rotor UAV. Pehlivanoglu et al. [35] refined the vibrational genetic algorithm for path planning in 3D terrain environments. Yuan et al. [36] suggested a genetic algorithm for region coverage in fixed-wing UAVs, demonstrating improved convergence compared to conventional algorithms.
Roberge et al. [37] proposed a parallel genetic algorithm implementation on a graphics processing unit to minimize fuel consumption and improve range. Hu and Liu [38] introduced a Proportion Integral Differential (PID) control algorithm combined with a genetic algorithm for effective obstacle avoidance. Liu [39] presented an improved genetic algorithm for UAV swarm path planning problems.
Genetic algorithms have been successful in UAV obstacle avoidance and bridge inspection, considering wind-generated wake vortices. This study introduces models for bridges, UAV performance, vortex hazard zones, and optimization algorithm selection, aiming to demonstrate their validity and applicability. Utilizing UAVs for bridge inspection enables non-intrusive inspections, saving time and effort, with a focus on monitoring the bridge along the optimized flight path throughout the day, even in windy conditions.
2. Methods
2.1. Bridge Model
Bridges are strongly sensitive to wind, and the wind characteristic parameters (i.e., wind speed and turbulence intensity) vary greatly between directions [40]. For bridge modeling, we focus on UAV monitoring, prediction, and corresponding maintenance of the columns supporting the bridge deck as shown in Figure 1.

Figure 1.
Chongqing Yangtze River Bridge (local view).
The impact of wind on bridge structures is primarily concentrated on the bridge columns, making them a crucial highlighted focus of UAV monitoring. Establishing bridge models for subsequent numerical analysis proves to be a conveniently feasible approach. This is due to the fact that bridge columns, when exposed to wind, generate a wake vortex. Based on their cross-sectional shape, bridge models can be approximated as cylindrical or cubed columns. Numerical simulations were conducted on two types of bridge models—circular and square cylinders. These simulations contributed significantly to the effectiveness and accuracy of the subsequent analysis.
Table 1 displays the dimensions of some typical bridges in China. The main span refers to the maximum distance between two bridge columns. The characteristic scale is determined by the diameter of the circular cylinder section or the maximum length of the square cylinder section. The spacing ratio is obtained by dividing the characteristic scale by the main span.

Table 1.
Typical bridges over the Yangtze River.
For the purposes of this analysis, the Chongqing Yangtze River Bridge has been simplified and is represented in Figure 2. Additionally, Table 2 provides the two bridge column models used in the study.
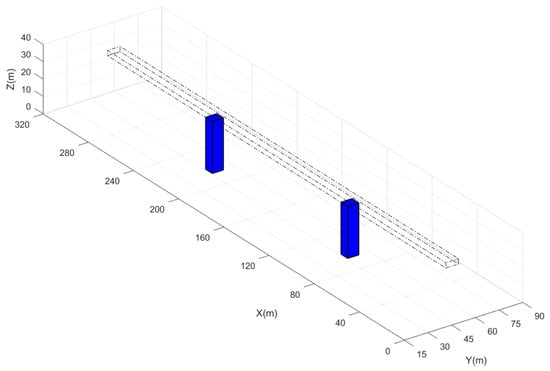
Figure 2.
The simplified model for Chongqing Yangtze River Bridge.

Table 2.
Main dimensions of models.
2.2. UAV Model
The analysis involves the utilization of a small-scale industry UAV, characterized by wind resistance capabilities ranging between levels 4 and 5. Due to the intricacies associated with various UAV models, this study specifically focused on employing a designated model as the subject of research. Furthermore, bridge detection was executed using a Hasselblad camera. Detailed information regarding specific operational performance and parameters is provided in Table 3 below.

Table 3.
Performance parameters of the UAVs.
The selection of the particular UAV model was based on its suitability for our research objectives, ensuring a standardized platform to maintain consistency in our methodology. Additionally, for bridge detection, we employed a Hasselblad camera, chosen for its high-quality imaging capabilities [46]. These equipment choices were made to enhance the accuracy and reliability of our data collection during experiments.
Based on the data presented in the aforementioned table, the UAV and camera are operating modestly for the detection mission. In windy conditions, where wind speed exceeds 12 m/s, the UAV is more susceptible to damage during takeoff and landing. Thus, it is not advisable to conduct the detection mission under such conditions due to the increased risk imposed on the UAV.
The field of view Angle (DFOV) is calculated as follows:
where is the horizontal distance from the shooting point to the subject, and is the diagonal length of the photographed picture.
The focal length is calculated by the formula:
where is the focal length of the camera, is the height of the sensor, and is the length of the subject.
Utilizing formulas 1 and 2, it can be deduced that the object being photographed by the UAV has a height of 0.6 m. Assuming that the UAV is flying at a speed of 10 m/s, the UAV must maintain a minimum distance of 5 m from the bridge column. If the actual flight speed of the UAV exceeds 10 m/s under tailwind conditions, an increase in safety distance is required. A 20 percent safety margin was applied herein, necessitating that the actual horizontal distance between the UAV and bridge pillar be at least 6 m above. In terms of the vertical direction, the UAV must maintain a flight path within the range of 0.6 m to 29.4 m.
2.3. Wind Model
The standard long-span bridges can withstand gusts of up to 28 m/s, according to the published data [47]. The wind resistance encountered by the UAV (in this study) provides the necessary information for deriving parameters that aid in simulating and evaluating wind activity. The selected air temperature was based on the average temperature of a Yangtze River bridge, and the source data were obtained from the Chongqing Meteorological Bureau. Wind direction was also taken into consideration, with specific initial values [48] shown in Table 4.

Table 4.
Meteorological condition for calculation.
The flow simulation module in the software version Fluent 2022 was utilized for numerical simulation in order to identify the hazardous regions near the bridge columns that endanger UAV flights. To validate the feasibility of using numerical simulation software, this paper compares it with the study conducted by Yu [49], which employed column circumference as the primary study object.
The accuracy of the simulation is verified by creating a flow field patterned after a single cylindrical column. Figure 3 illustrates the calculated region for the flow field around a single cylinder column. The field calculated for this validation example is 42D × 24D, where D denotes the cylinder’s length in the direction of incoming flow. Additionally, 12D represents the distance between the upper and lower limits, 30D represents the distance between the outlet and the aid center, and 12D is the distance between the center of the cylinder and the aid center [50].
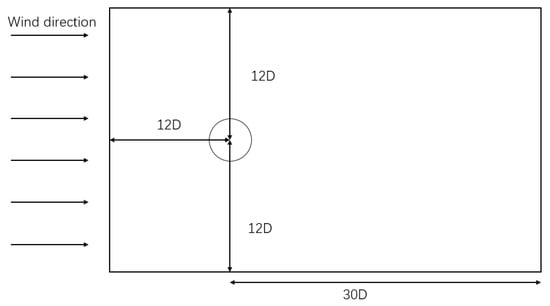
Figure 3.
Compute domain size.
Typical dimensionless coefficients for flow issues include the drag coefficient, lift coefficient, Storoha coefficient, and more. Chen et al. [49] comparatively analyzed the average drag coefficient at different Reynolds numbers. The results showed that different Reynolds numbers have a great influence on the wake vortices.
The time-averaged cylinder drag coefficient is defined as follows:
where is the drag force acting on the cylinder, is the incoming stream dynamic head, is the cylinder diameter, and is the cylinder length. The cylinder drag coefficient, predicted by Fluent, is compared to the well-known () experimental data [51] in Figure 4. The experimentally acquired data are presented with black markers, whereas the numerically simulated drag coefficients are depicted with red markers, as showed in Figure 4.
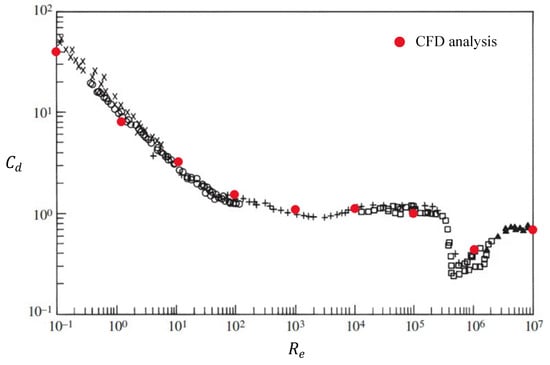
Figure 4.
Simulation results for comparison with experimental data.
To show the reliability of the Fluent program, an examination in comparison to other resources was conducted using high Reynolds numbers, and the results are presented in Table 5.

Table 5.
Comparisons of drag coefficients at different Reynolds numbers.
The results presented in Table 5 demonstrate good agreement between the current investigation and the literature for some Reynolds numbers, thereby validating the precision and dependability of the Fluent program. Moreover, the average drag coefficient observed in this study falls within the acceptable margin of error allowed by the literature values, further reinforcing the effectiveness of the numerical simulation software utilized in this research and paving the way for the numerical simulation of the wind field.
Given that the size of the computational domain can impact the results of numerical simulations, this study expanded the computational domain for wind field simulations to 40D × 60D × 9D to ensure the accuracy of the numerical simulation results for the simplified bridge model. Figure 5 illustrates the primary computational domain employed in this study.
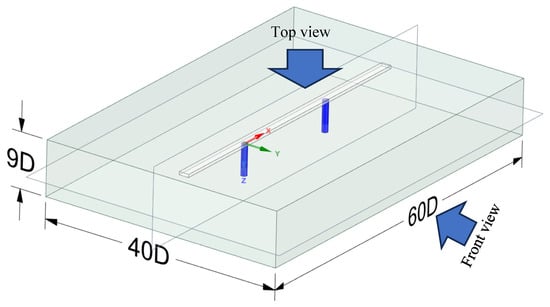
Figure 5.
Calculation domain for UAV bridge inspection.
3. Unsafe Zone Identification
We have performed numerical simulations under various conditions such as wind velocity, wind angle, and air temperature to obtain the influence range of the eddy current zone of various cylinder structures and determine the safe flight region for UAVs. This was performed in consideration of the unique environment such as variable wind speed and wind direction and the eddy current zone in real life. The k-omega (k-ω) model is applied because the numerical analysis of the bridge columns corresponds to the large Reynolds number, and the cylinder wall is smooth and untextured in this model. Moreover, the k-omega (k-ω) model is accurate for calculating wake and turbulence in the near-wall region. The computations and boundary conditions listed below are as follows:
- (1)
- The solution method uses the pressure-velocity coupled SIMPLE algorithm
- (2)
- The density of the set fluid (air) is 1.29 kg/m3, the specific heat capacity is 1006 J/(kg·K), the thermal conductivity is 0.0242 W/(m·K), and the viscosity is 1.8 × 10−5 kg/(m·s).
- (3)
- The average static pressure, P, is zero, and the outlet is on the right boundary.
- (4)
- Symmetric boundary conditions are applied at the two spanwise borders of the computing domain, and the components of each variable in the normal direction are all equal to zero.
3.1. Wind Speed Effects
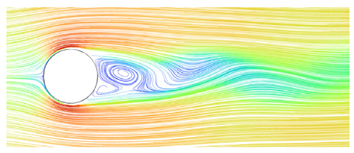
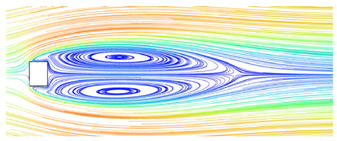
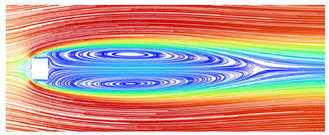
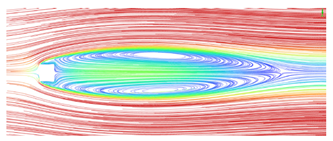
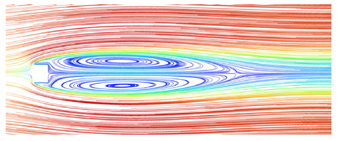
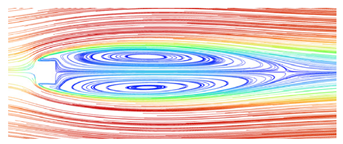
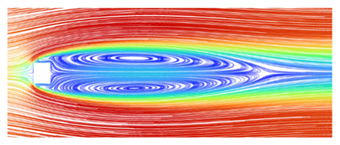
After ensuring the proper functioning of the software, experimental studies were conducted on the bridge column under various wind conditions, as outlined in Table 2. For this particular analysis, simulations were specifically performed for a wind speed of 12 m/s, an air temperature of 15 °C, and a wind angle of 0° (the angle between the incoming flow direction and the orientation of the bridge deck). Figure 5 illustrates the positions of the front view and top view in the flow field. The resulting flow patterns of the flow field for different types of bridge columns are illustrated in Figure 6 and Figure 7.

Figure 6.
Flow field simulation results for the bridge’s circular cylinder column (wind speed is 12 m/s). (a) Front view; (b) top view.
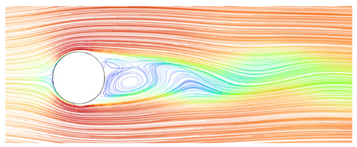
Figure 7.
Flow field simulation results for the bridge’s square cylinder column (wind speed is 12 m/s). (a) Front view; (b) top view.
As can be seen from Figure 6 and Figure 7, the wake vortices formed by square columns are significantly more complex than those formed by circular columns, and their scope is larger. This means that the danger of square columns is greater than that of circular columns when UAV is used for bridge detection. Whether it is a circular or square column, the increase in wind speed will increase the influence range of its wake vortex, and the threat to the UAV is greater. Therefore, when using UAVs for bridge detection, in addition to paying attention to the structure type of bridge column, attention should also be paid to whether UAVs can perform bridge detection under such wind speed.
After analyzing the impact of various wind conditions, it is important to take into account the changes in wind speed when carrying out bridge detection tasks. A higher wind speed leads to a more significant influence from wake vortices, which can have adverse effects on the UAV. However, changes in air temperature and wind direction can be taken into consideration appropriately.
3.2. Air Temperature Effects
Investigating the working environment of the UAV, we analyzed the wind field’s flow conditions at different temperatures. To minimize interference, the wind speed was maintained at a uniform 12 m/s, with a wind direction of 0°, and the air pressure was held at the typical standard atmospheric value. Given the heightened sensitivity of the UAV battery to low temperatures, Figure 8 and Figure 9 exclusively depict the flow conditions at a temperature of 40 °C.

Figure 8.
Flow field simulation results at 40 °C for the bridge’s circular cylinder column. (a) Front view; (b) top view.

Figure 9.
Flow field simulation results at 40 °C for the bridge’s square cylinder column. (a) Front view; (b) top view.
The flow streamlines for the same bridge structure at various temperatures and speeds are basically consistent, according to Figure 8 and Figure 9. The velocity change value near the circular cylinder column is significant at the extreme highest and lowest temperatures compared to the average temperature, but the square cylinder column essentially experiences no change. At all temperatures and wind speeds, the flow streamlines of the two bridge structure models are essentially symmetrical. In a word, the influence degree of the wake vortex caused by temperature is less than that caused by the wind speed change.
3.3. Wind Angle Effects
This paper examines the scenario when the wind shifts to a specific angle relative to the direction of the long-span bridge in the event of variable wind direction. To determine if there is any wake interference between bridge columns within a wind field, especially if the wake generated by the front column affects the rear column, additional analysis is required.
The numerical analysis presented here exclusively showcases the airflow conditions when the wind angle is 22.5°, as this angle is crucial for assessing the potential impact of the wake of the front column on the rear column. The current case analysis maintains a wind speed of 12 m/s and an air temperature of 15 °C.
When observed from the front, it appears that the wakes generated by the two columns are interfering with each other. However, a top view reveals that there is no airflow interference between the two columns in this type of long-span bridge. As illustrated in Figure 10, the airflow through both cylindrical columns appears to be quite similar. The impact of the tail vortex spreads out in the downwind direction, but its strength gradually diminishes until it becomes consistent with that of the mainstream airflow. The same physical phenomenon applies to square cylinder columns, as shown in Figure 11.
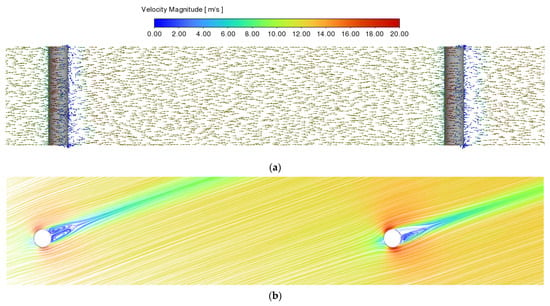
Figure 10.
Airflow pattern induced by circular cylinder columns with 22.5° wind angle. (a) Front view; (b) top view.
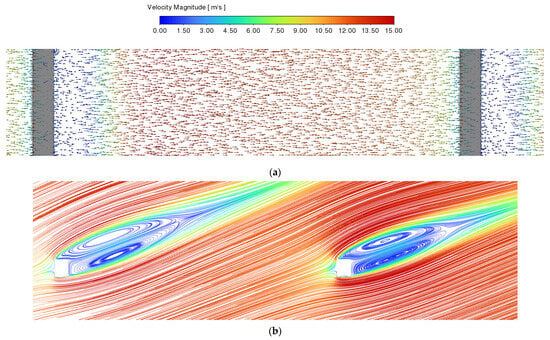
Figure 11.
Airflow pattern induced by square cylinder columns with 22.5° wind angle. (a) Front view; (b) top view.
After examining the wind direction in Figure 10b and Figure 11b, it was discovered that the trailing vortex produced by the front bridge column has a negligible impact on the fluid dynamics of the rear bridge column.
However, if the spacing between the columns is narrow and the wind angle is small, the aerodynamic interference between columns will become more apparent.
3.4. Unsafety Zone Model
At a wind speed of 12 m/s, Figure 12 depicts the velocity fluctuations and wake vortex characteristics at five monitoring points spaced at 1D intervals, starting from 0.5D away from the bridge column. The differences in features are illustrated for each point which identified by a series of digits ranging from 1 to 5.
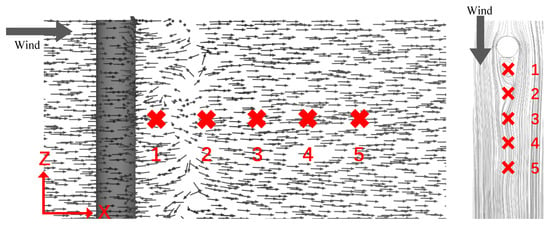
Figure 12.
Velocity vector field visualization and detection point positioning, 12 m/s.
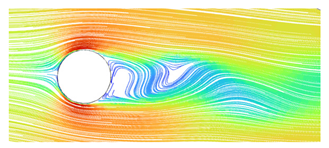
The fluid velocity decreases when it is closer to the bridge structure, whereas it increases as it approaches the center of the vortex in the flow field. The formation of a wake vortex behind the bridge structure can be distinctly observed.
The research shows that higher values of turbulent kinetic energy and a specific dissipation rate are found where well-formed circulation exists behind the bridge piers [53]. As shown in Table 6, the average turbulent kinetic energy and dissipation rates at identification points 1 and 2, which are located near the bridge column producing a smaller vortex, are considerably higher than those at other points. Based on the flow streamlines (Figure 13), it can be concluded that the formation of vortices occurs behind the structure, with tail vortices specifically forming at points 1 and 2. Between identification points 3 and 5, there is an increase in dissipation rate, energy loss, and tail vortex dissipation rate. As a result, the streamline transitions towards a straightened state. Hence, when the wind speed is 12 m/s, if the UAV flies between point 1 and point 2, it can be regarded as being in a dangerous region.

Table 6.
The relevant information at the identification points behind the bridge structure.

Figure 13.
Dangerous region when wind speed is 12 m/s.
This approach involves creating hazard zone models as a result of bridge column wake under different weather conditions. These models can then be used to prepare for the planning of UAV bridge monitoring paths. In essence, this helps to identify potential risks and enables better planning for safe and effective monitoring of the bridge using unmanned aerial vehicles.
By understanding the hazardous zones around bridge pillars, bridge maintenance teams can better plan safe UAV monitoring routes and identify potential risks associated with the operation.
Hence, based on the hazard zone’s most significant influence range, Table 7 and Table 8 present the non-safe zone model. This model can be used to identify and map the areas where potential danger exists when conducting UAV monitoring activities. By utilizing this information, we can plan safer and more efficient monitoring routes to ensure the overall safety of the inspection operation.

Table 7.
Influence of wake vortex on circular cylinder column and its non-safe zone.

Table 8.
Influence of wake vortex on square cylinder column and its non-safe zone.
4. Path Planning
4.1. Objective Function Design
The UAV detection route is split into beam and pier detection, or flying in a two-dimensional plane and three-dimensional space, in order to make sure that the UAV can detect the bridge in all directions.
A succession of practical points basically makes up a UAV’s flight in a two-dimensional plane. The eddy current region is considered the detection of obstacles based on the actual flight characteristics of the UAV in Table 3 and the eddy current’s effect range in Table 6. In this work, the location of the UAV is turned into every possible point, and the actual possible points of the UAV are established as follows:
where E is the set of all feasible points, and are all viable locations in the two-dimensional plane of the UAV.
Therefore, the path value of UAV is as follows:
where is the value of a feasible path formed by feasible points, and the genetic algorithm is used to process and calculate the feasible points. The specific algorithm process is shown in the following flow chart (see Figure 14).
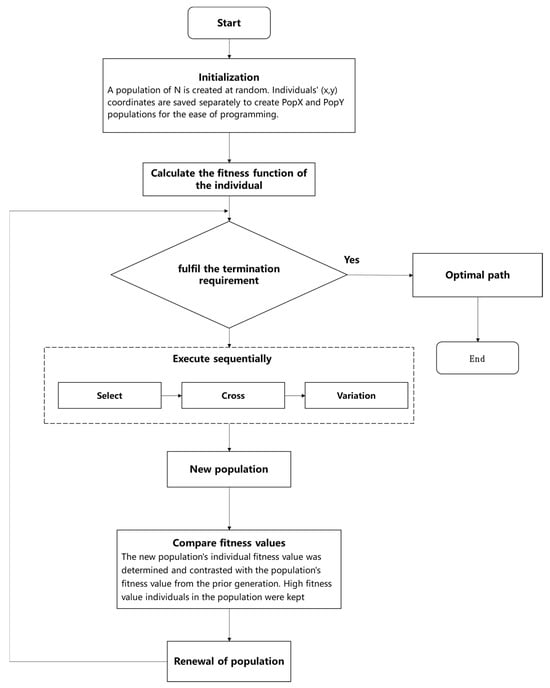
Figure 14.
Flow chart of genetic algorithm for flight path planning.
In order to ensure the safe flight of UAV while also conserving their energy consumption, the fitness function is defined based on the shortest path value, as shown in Equation (6). A higher fitness value indicates a shorter path, resulting in reduced energy consumption for the UAV. Consequently, individuals with feasible points along the path are considered more favorable and are more likely to be retained. Through operations such as selection, crossover, and mutation, the obtained path tends to converge towards the optimal detection path.
A 3D route is created by adding together many 2D plane pathways once the UAV’s 2D path planning is complete. The cylindrical spiral parameter equation (see Equation (8)) is presented, which enables UAVs to better regulate the distance in the vertical direction since the flying height of UAVs must meet certain specifications.
where , is the angular velocity, is the pitch, and is the helix Angle, where the right helix is positive and the left helix is negative. The above equation may be expressed as follows if the arc length s is used as the parameter:
Finally, the UAV bridge detection route planning is complete.
4.2. Flightpath Simulation
The UAV is treated as a particle in this research, and its own structure and flight attitude are disregarded in the flight path planning. The bridge’s fundamental design and tail vortex are built in accordance with Table 1, Table 2 and Table 6. Apart from visible structural obstacles, UAV obstacle avoidance flight also needs to take into account the danger area resulting from trailing vortex. In this case, the obstacles comprise two parts: the bridge column and the non-safety zone created by the invisible wake vortex. It is essential to take both these factors into account when planning the UAV’s flight path to ensure safe and efficient monitoring of the bridge.
Genetic algorithm is employed to optimize the trajectory of UAVs for monitoring bridges, taking into account both the UAV’s performance capabilities and the pilot’s operating skills. Under the assumption of no wind conditions, Figure 15 illustrates the optimized monitoring route for a specific light and small UAV when inspecting circular or square column bridges. By following this optimized route, the pilot’s workload is reduced, consequently minimizing the risk of accidents caused by human factors. Ultimately, this approach ensures the safe and efficient completion of bridge structure inspections by UAVs.
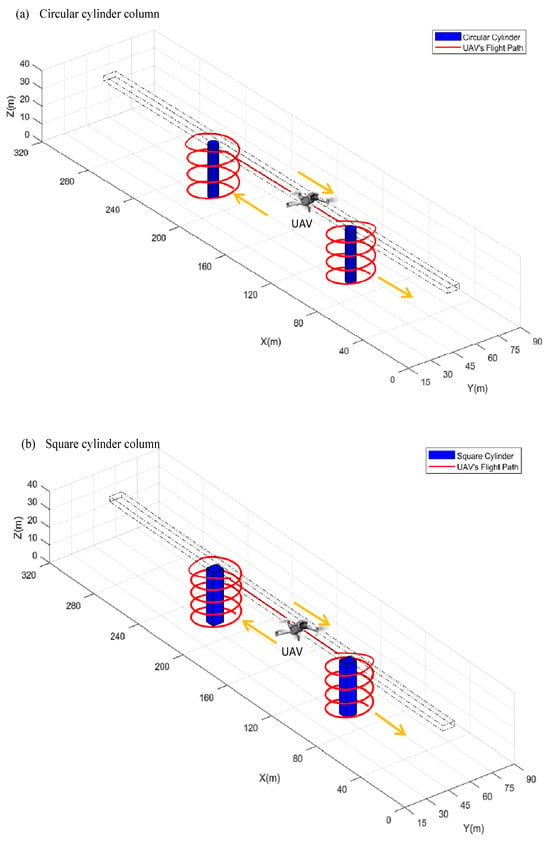
Figure 15.
Optimized route for UAV bridge monitoring in windless conditions.
When considering the danger zone generated by a trailing vortex at a wind speed of 12 m/s, the obstacles become larger, and factors such as the pilot’s driving skills must be considered. To address these challenges, the genetic algorithm optimization approach is employed for intelligent trajectory optimization. This algorithm takes into account the impact of wind on the UAV’s flight path and the size of the obstacle to ensure that the optimized path accounts for all potential risks.
Figure 16 and Figure 17 illustrate the optimized flight paths for UAV bridge inspection, considering two distinct bridge pillar structures. Employing a genetic algorithm optimization method, these paths account for the impact of wind and the size of obstacles. The figures offer a comprehensive comparison between paths considering wind effects and those without, providing a detailed showcase of the UAV’s optimized flight paths under varied conditions.
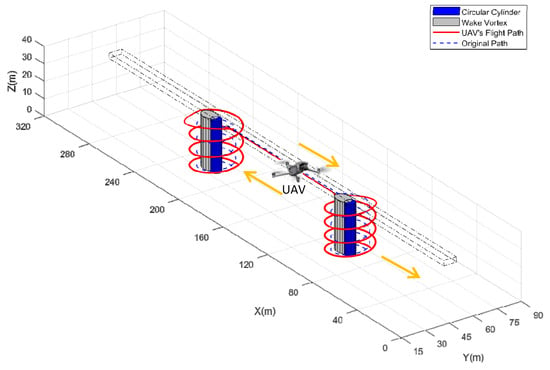
Figure 16.
Flight path of inspection for circular cylinder column bridge.
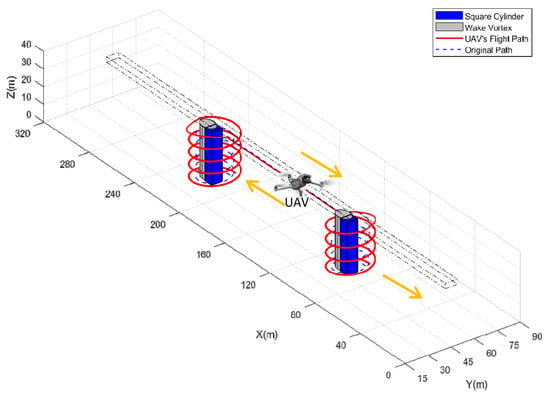
Figure 17.
Flight path of inspection for square cylinder column bridge.
For the working condition with a wind angle of 22.5 degrees, another calculation is carried out to determine the optimized flight path for the UAV bridge monitoring. Figure 18 and Figure 19 display the specific results of this calculation, which takes into account the impact of wind and the danger zone generated by the wake vortex.
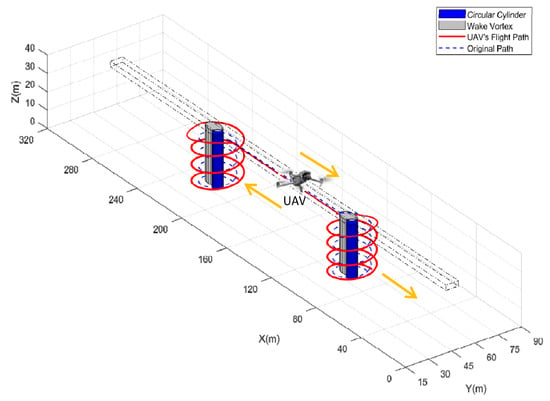
Figure 18.
Flight path of inspection for circular cylinder column bridge (wind angle is 22.5°).
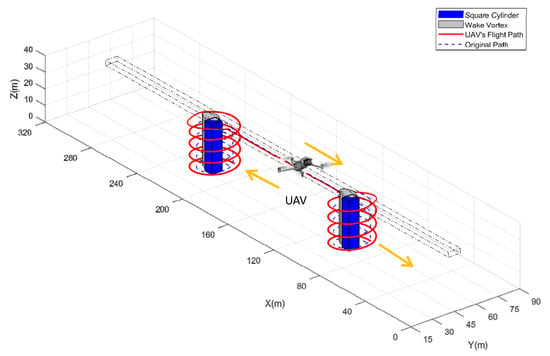
Figure 19.
Flight path of inspection for square cylinder column bridge (wind angle is 22.5°).
The wake vortex tilt under this condition causes the danger zone to incline sideways, resulting in a longer UAV flying path. Accounting for the effects of the wind field, the UAV monitoring path of the bridge must be completed while ensuring flight safety. Therefore, the optimized path needs to be adjusted to account for changes in the wind direction and the impact of the wake vortex. By conducting these calculations and optimizing the trajectory using intelligent algorithms, it is possible to ensure safe and efficient monitoring of the bridge, even under challenging weather conditions.
As highlighted in Figure 16 and Figure 17, an optimized route using intelligent algorithms enables a UAV to conduct safe monitoring of the bridge while successfully avoiding obstacles and flying around dangerous eddies. However, in the presence of windy weather conditions, the wake vortex can cause the flight path to be longer compared to the situation without wind effects. Nonetheless, by accounting for the impact of wind and using these algorithms, it is possible to create an optimized flight path.
The analysis in Figure 20 shows that the square cylinder column requires a longer route value than the round cylinder column due to the more complex wake vortex it generates and the larger effect zone. This effect results in a more extended optimized flight path for the UAV during bridge monitoring tasks. Based on this analysis, the full coverage detection route for the UAV takes almost a complete circle around the bridge pier and beam, effectively covering the entire bridge structure for maintenance purposes. It is worth noting that these modeling results accurately reflect potential real-life scenarios, enabling bridge maintenance teams to plan and execute safe and efficient monitoring operations.
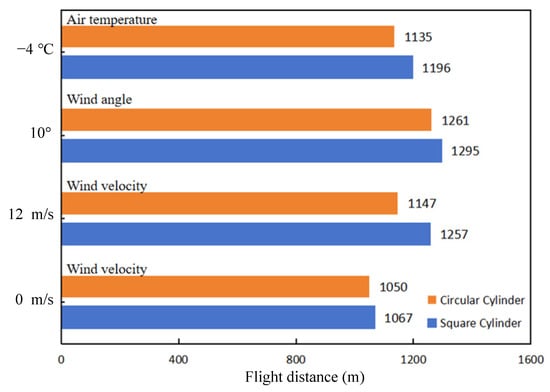
Figure 20.
Various pier constructions’ path values at different wind speeds.
5. Conclusions
The primary objective of this paper is to present a comprehensive all-daytime bridge inspection method utilizing general UAVs, with optimized flight paths that account for weather conditions. Notably, this study emphasizes the importance of considering the impact of wake vortex generated by air flowing through bridge structures, and accurately identifying unsafe zones that need to be avoided. However, given the limited range of the wake vortex produced by bridge column structures, this paper strictly focuses on analyzing the wake vortex generated by two bridge columns, i.e., circular cylinder and square cylinder. The results are as follows:
- (1)
- At different wind speeds, the larger the wind speed, the larger the wake vortex and the higher the risk for UAV flight operation. Moreover, the optimal path of UAV bridge monitoring is sensitive to meteorological conditions, especially wind speed factors. Therefore, it is crucial to accurately identify and account for these factors when creating flight plans for UAVs conducting bridge inspections in order to increase the efficiency and effectiveness of these operations.
- (2)
- The wake vortex generated by a square cylinder column is more intricate and complex than that generated by a circular cylinder column due to the different bridge structure types. Therefore, the UAV flight path optimization required for square cylinder columns tends to be larger. The strength and influence of the vortex generated by different bridge columns significantly impact the optimal path and flight safety of UAVs conducting bridge monitoring. Irregular columns have an even greater impact as they can result in creating a larger UAV flying danger zone. Therefore, it is of utmost importance to identify and consider these factors when designing flight plans for UAVs conducting bridge inspections.
- (3)
- Most of the focus of research right now is on using drones to monitor bridges with spans that stretch long distances. The primary emphasis of the current research is on the UAV surveillance of long-span bridges. Future research can be applied to small-span bridges because the close spacing of the bridge columns will affect the wake vortex of the bridge columns on the downwind side, resulting in an inconsistent wake danger zone and wind direction, which will complicate UAV bridge monitoring and even the best flight path for UAV bridge inspection. In the future, it would be beneficial to explore new approaches such as selecting professional analysis software like Fluent for a comprehensive examination of the wake vortex and their potential threats to UAV flight safety.
In addition, suggestions should be made to establish monitoring requirements specifically tailored for UAV bridge inspections. Such requirements should consider and address different factors, including the impact of wake vortices on UAV flight safety, bridge types and structures, and other potential environmental factors that may affect the accuracy, efficiency, and safety of UAV bridge monitoring. By advancing research in this direction, we can improve the effectiveness, safety, and reliability of UAV bridge inspections, which are essential for managing and maintaining critical infrastructure.
Author Contributions
Conceptualization, Y.W. and X.H.; methodology, Y.W. and X.H.; software, X.H. and C.D.; validation, X.H., J.Z. and R.Z.; investigation, Y.W., X.H. and J.Z.; data curation, X.H., H.L. and J.Z.; writing—original draft preparation, X.H. and C.D.; writing—review and editing, Y.W. and C.D.; funding acquisition, Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported in part by the Special Key Projects of Technological Innovation and Application Development of Chongqing (grant no. cstc2019jscx-fxydX0036), the Scientific Research Project of CQJTU (grant no. 19JDKJC-A012), and the Research and Innovation Program for Graduate Students in Chongqing (2022S0085).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ministry of Transport of the People’s Republic of China. Statistical Bulletin on the Development of the Transport Sector. 2021. Available online: https://xxgk.mot.gov.cn/2020/jigou/zhghs/202205/t20220524_3656659.html (accessed on 1 September 2023).
- Ruan, X.; Chen, A.; Shi, X. Bridge Engineering Risk Assessment; China Communications Press: Beijing, China, 2008. (In Chinese) [Google Scholar]
- Peng, X.; Zhong, X.G.; Zhao, C.; Chen, Y.F.; Zhang, T.Y. The Feasibility Assessment Study of Bridge Crack Width Recognition in Images Based on Special Inspection UAV. Adv. Civ. Eng. 2020, 2020, 17. [Google Scholar] [CrossRef]
- Seo, J.; Duque, L.; Wacker, J.P. Field Application of UAS-Based Bridge Inspection. Transp. Res. Rec. 2018, 2672, 72–81. [Google Scholar] [CrossRef]
- Jeong, E.; Seo, J.; Wacker, J.P. UAV-aided bridge inspection protocol through machine learning with improved visibility images. Expert Syst. Appl. 2022, 197, 14. [Google Scholar] [CrossRef]
- Jung, S.; Choi, D.; Song, S.; Myung, H. Bridge Inspection Using Unmanned Aerial Vehicle Based on HG-SLAM: Hierarchical Graph-Based SLAM. Remote Sens. 2020, 12, 3022. [Google Scholar] [CrossRef]
- Cano, M.; Pastor, J.L.; Tomas, R.; Riquelme, A.; Asensio, J.L. A New Methodology for Bridge Inspections in Linear Infrastructures from Optical Images and HD Videos Obtained by UAV. Remote Sens. 2022, 14, 1244. [Google Scholar] [CrossRef]
- Mohammadi, M.; Rashidi, M.; Mousavi, V.; Karami, A.; Yu, Y.; Samali, B. Quality Evaluation of Digital Twins Generated Based on UAV Photogrammetry and TLS: Bridge Case Study. Remote Sens. 2021, 13, 3499. [Google Scholar] [CrossRef]
- Lee, J.H.; Yoon, S.; Kim, B.; Gwon, G.H.; Kim, I.H.; Jung, H.J. A new image-quality evaluating and enhancing methodology for bridge inspection using an unmanned aerial vehicle. Smart. Struct. Syst. 2021, 27, 209–226. [Google Scholar] [CrossRef]
- Seo, J.; Duque, L.; Wacker, J. Drone-enabled bridge inspection methodology and application. Autom. Constr. 2018, 94, 112–126. [Google Scholar] [CrossRef]
- Shalyhin, A.; Nerubatsky, V.; Denysova, S. The UAV flight route optimization by taking into consideration the wind influence. Наука І Техніка Пoвітряних Сил Збрoйних Сил України 2018, 3, 20–24. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, Y. Wind disturbance rejection control based on the dynamic parameters estimation of quadrotors UAV. High Technol. Lett. 2019, 25, 443–451. [Google Scholar]
- Barikbin, B.; Fakharian, A. Trajectory tracking for quadrotor UAV transporting cable-suspended payload in wind presence. Trans. Inst. Meas. Control. 2019, 41, 1243–1255. [Google Scholar] [CrossRef]
- Xu, X.; Watanabe, K.; Nagai, I. Flight control system design for a tandem rotor UAV robot in the presence of wind field disturbances. Artif. Life Robot. 2021, 26, 457–464. [Google Scholar] [CrossRef]
- Wang, B.; Ali, Z.A.; Wang, D. Controller for UAV to Oppose Different Kinds of Wind in the Environment. J. Control. Sci. Eng. 2020, 2020, 5708970. [Google Scholar] [CrossRef]
- Lee, D. A Linear Acceleration Control for Precise Trajectory Tracking Flights of a Quadrotor UAV Under High-wind Environments. Int. J. Aeronaut. Space Sci. 2021, 22, 898–910. [Google Scholar] [CrossRef]
- Nobahari, H.; Asghari, J. A Fuzzy-PLOS Guidance Law for Precise Trajectory Tracking of a UAV in the Presence of Wind. J. Intell. Robot. Syst. Theory Appl. 2022, 105, 18. [Google Scholar] [CrossRef]
- Grandić, I.Š. Reduction in wind force in relation to corner design of bridge piers. Eng. Rev. 2020, 40, 88–100. [Google Scholar] [CrossRef]
- Zhipeng, Z.; Guangbiao, J. Numerical Simulation of Static Wind Coefficient and Flow Field of Box Girder of High Pier and Large Span Continuous Bridge. In Proceedings of the 2017 3rd International Forum on Energy, Environment Science and Materials (IFEESM 2017), Shenzhen, China, 25–26 November 2017; pp. 299–305. [Google Scholar]
- Cao, B.; Sarkar, P.P. Numerical simulation of dynamic response of a long-span bridge to assess its vulnerability to non-synoptic wind. Eng. Struct. 2015, 84, 67–75. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, M. Field investigation and wind-environment numerical simulation of cable-stayed bridge site in the west midlands region. In Proceedings of the 2011 International Conference on Civil Engineering and Building Materials, CEBM 2011, Kunming, China, 29–31 July 2011; pp. 4202–4206. [Google Scholar]
- Wang, D.; Zhang, Y.; Sun, M.; Chen, A. Characteristics of the Wind Environment above Bridge Deck near the Pylon Zone and Wind Barrier Arrangement Criteria. Appl. Sci. 2020, 10, 1437. [Google Scholar] [CrossRef]
- Ye, Z.-W.; Xiang, Y.-Q. Analysis and comparison on wind load of long span girder bridges with high pier. In Proceedings of the 2011 2nd International Conference on Challenges in Environmental Science and Computer Engineering, CESCE 2011, Haikou, China, 14–15 December 2011; pp. 322–327. [Google Scholar]
- Bayrak, Z.U.; Kaya, U.; Oksuztepe, E. Investigation of PEMFC performance for cruising hybrid powered fixed-wing electric UAV in different temperatures. Int. J. Hydrogen Energy 2020, 45, 7036–7045. [Google Scholar] [CrossRef]
- Li, N.; Liu, X.; Yu, B.; Li, L.; Xu, J.; Tan, Q. Study on the environmental adaptability of lithium-ion battery powered UAV under extreme temperature conditions. Energy 2021, 219, 119481. [Google Scholar] [CrossRef]
- Hossain, T.; Segura, S.; Okeil, A.M. Structural effects of temperature gradient on a continuous prestressed concrete girder bridge: Analysis and field measurements. Struct. Infrastruct. Eng. 2020, 16, 1539–1550. [Google Scholar] [CrossRef]
- Guo, C.; Lu, Z. Effect of temperature on CFST arch bridge ribs in harsh weather environments. Mech. Adv. Mater. Struct. 2020, 29, 732–747. [Google Scholar] [CrossRef]
- Niu, Y.; Wang, Y.; Tang, Y. Analysis of temperature-induced deformation and stress distribution of long-span concrete truss combination arch bridge based on bridge health monitoring data and finite element simulation. Int. J. Distrib. Sens. Netw. 2020, 16, 155014772094520. [Google Scholar] [CrossRef]
- Cekmez, U.; Ozsiginan, M.; Aydin, M.; Sahingoz, O. UAV Path Planning with Parallel Genetic Algorithms on CUDA Architecture. Lect. Notes Eng. Comput. Sci. 2014, 1, 551–557. [Google Scholar]
- Leng, S.; Sun, H. UAV Path Planning in 3D Complex Environments Using Genetic Algorithms. In Proceedings of the 33rd Chinese Control and Decision Conference, CCDC 2021, Kunming, China, 22–24 May 2021; pp. 1324–1330. [Google Scholar]
- Wang, X.; Meng, X. UAV online path planning based on improved genetic algorithm. In Proceedings of the 38th Chinese Control Conference, CCC 2019, Guangzhou, China, 27–30 July 2019; pp. 4101–4106. [Google Scholar]
- Zhang, H.; Yan, Y.; Li, S.; Hu, Y.; Liu, H. UAV Behavior-Intention Estimation Method Based on 4-D Flight-Trajectory Prediction. Sustainability 2021, 13, 12528. [Google Scholar] [CrossRef]
- Zhou, H.; Xiong, H.-L.; Liu, Y.; Tan, N.-D.; Chen, L. Trajectory Planning Algorithm of UAV Based on System Positioning Accuracy Constraints. Electronics 2020, 9, 250. [Google Scholar] [CrossRef]
- Hua, L.; Zhang, J.; Li, D.; Xi, X.; Shah, M.A. Sensor Fault Diagnosis and Fault Tolerant Control of Quadrotor UAV Based on Genetic Algorithm. J. Sens. 2022, 2022, 8626722. [Google Scholar] [CrossRef]
- Pehlivanoglu, Y.V.; Baysal, O.; Hacioglu, A. Path planning for autonomous UAV via vibrational genetic algorithm. Aircr. Eng. Aerosp. Technol. 2007, 79, 352–359. [Google Scholar] [CrossRef]
- Yuan, J.; Liu, Z.; Lian, Y.; Chen, L.; An, Q.; Wang, L.; Ma, B. Global Optimization of UAV Area Coverage Path Planning Based on Good Point Set and Genetic Algorithm. Aerospace 2022, 9, 86. [Google Scholar] [CrossRef]
- Roberge, V.; Tarbouchi, M.; Labonte, G. Fast genetic algorithm path planner for fixed-wing military UAV Using GPU. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 2105–2117. [Google Scholar] [CrossRef]
- Hu, X.; Liu, J. An obstacle avoidance design of UAV based on genetic algorithm. In Proceedings of the 3rd International Conference on Mechanical, Electric and Industrial Engineering, MEIE 2020, Virtual, Online, 18 June 2020. [Google Scholar]
- Liu, J. An Improved Genetic Algorithm for Rapid UAV Path Planning. In Proceedings of the 2021 3rd International Conference on Robotics, Intelligent Control and Artificial Intelligence, ICRICA 2021, Virtual, Online, 3–5 December 2021. [Google Scholar]
- Zhang, J.; Zhang, M.; Li, Y.; Jiang, F.; Wu, L.; Guo, D. Comparison of wind characteristics in different directions of deep-cut gorges based on field measurements. J. Wind Eng. Ind. Aerodyn. 2021, 212, 104595. [Google Scholar] [CrossRef]
- Zhan, S.; Qing, Z.; Guo, C. Brief introduction of Chongqing Yangtze River Bridge construction. Bridge Construction. 1981, 3, 1–35. (In Chinese) [Google Scholar]
- Гoлoдoв, Н.М. Wuhan Yangtze River Bridge Structure and Construction; Science and Technology Health Press: Beijing, China, 1958. (In Chinese) [Google Scholar]
- Yuan, M.; Ma, T.; You, L. Design of Changshou Changji ang River Bridge. Bridge Constr. 2005, 3, 40–43. (In Chinese) [Google Scholar]
- Wang, K. Introduction to the Design of the Sanjiang Highway Bridge of the Gezhouba Water Conservancy Hub. Highway 1982, 3, 1–6. (In Chinese) [Google Scholar]
- Zhu, P.F. Research on Key Construction Technologies of Yichang Yangtze River Bridge on the Yiwu Railway. Bridge Constr. 2004, 1, 62–65. (In Chinese) [Google Scholar]
- Liu, Y.; Han, K.; Rasdorf, W. Assessment and Prediction of Impact of Flight Configuration Factors on UAS-Based Photogrammetric Survey Accuracy. Remote Sens. 2022, 14, 4119. [Google Scholar] [CrossRef]
- JTG/T D60-01-2004; Highway Bridge Wind Resistance Design Code. Ministry of Transport of the People’s Republic of China: Beijing, China, 2004. (In Chinese)
- Bureau, C.M. Temperature Statistics by Month of the Year in Nanchuan District, Chongqing. Available online: https://www.tianqi24.com/nanchuan/history.html (accessed on 17 September 2023).
- Yu, C.; Qiang, L.; Ting, G. Numerical simulation of flow around a cylinder at different Reynolds numbers. China Water Transp. 2015, 15, 88–90. (In Chinese) [Google Scholar]
- 5Luo, Y.J.; Liang, L.; Wei, C.; Shui, L.Y.; Ying, L. Numerical simulation of flow around a circular cylinder with rough surface at subcritical Reynolds number. Chin. J. Appl. Mech. 2022, 39, 974–980. (In Chinese) [Google Scholar]
- Anderson, J. Fundamentals of Aerodynamics; McGraw-Hill Education: Columbus, OH, USA, 2016. [Google Scholar]
- Jun, Y.H. Two Dimensional Numerical Analysis of Flow over a Circular and Square Cylinder and Vortex-Induced Vibration of Rectangular Cylinder. Master’s Thesis, Tianjin University, Tianjin, China, 2012. [Google Scholar]
- Green, J.J.; Mott, J. Identification of Wind-Induced Hazard Zones Impacting UAS Bridge Inspection. Int. J. Aviat. Aeronaut. Aerosp. 2021, 8, 2. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).