Flight Dynamic Characteristics of Wide-Body Aircraft with Wind Gust and Turbulence
Abstract
1. Introduction
1.1. Stability and Performance Optimization—A Design Dilemma
1.2. Extended Flight Envelope and Unconventional Aircraft Design
1.3. Atmospheric Influence on Stability
1.4. Flight Dynamic Models
2. Aircraft Non-Linear Dynamics
2.1. Equations of Motion (EOMs)
2.2. COESA Atmospheric Models
2.3. Mathematical Representation of Turbulence Modeling
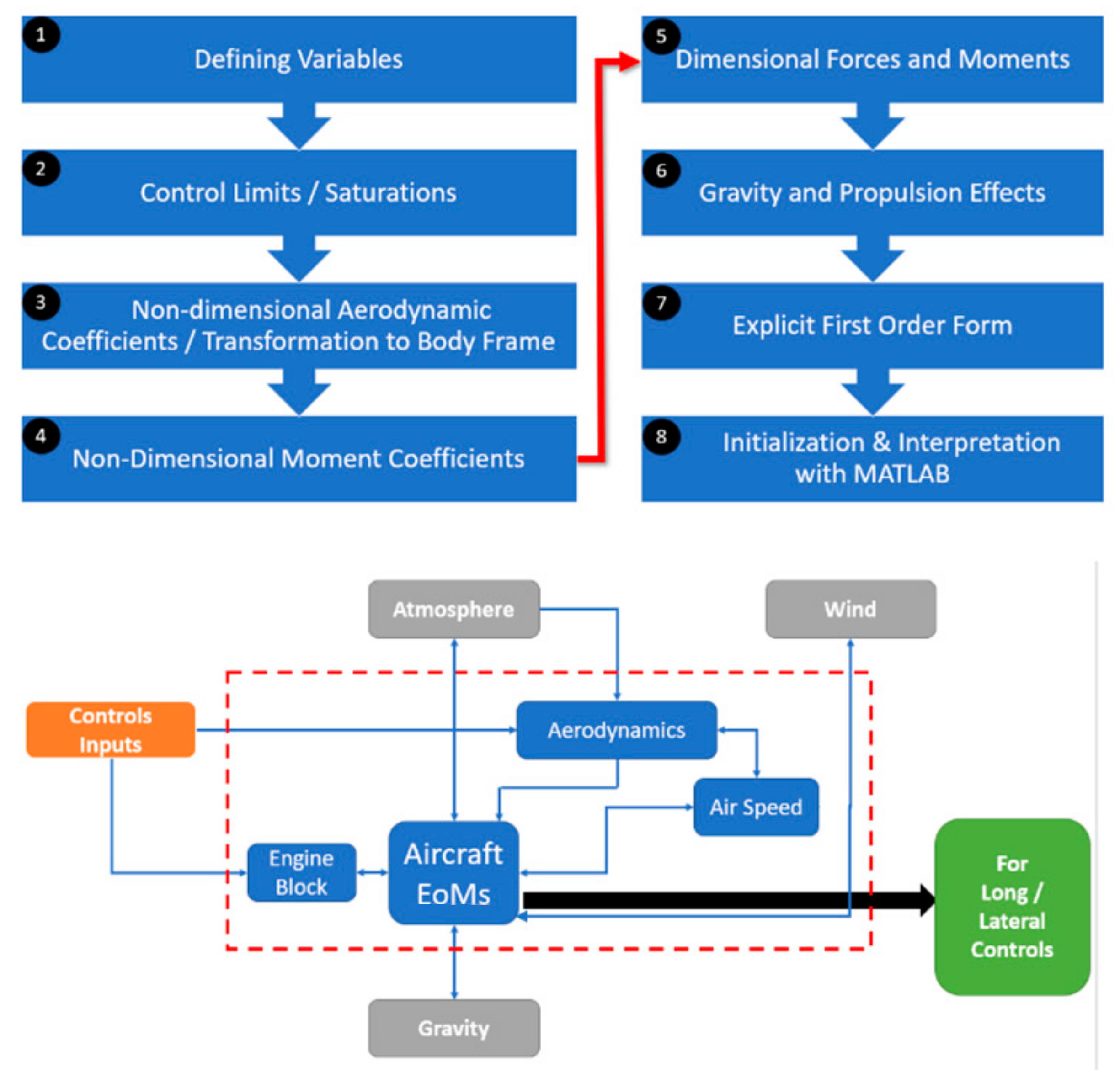
3. Modeling Methodology
3.1. Schematic of UDF
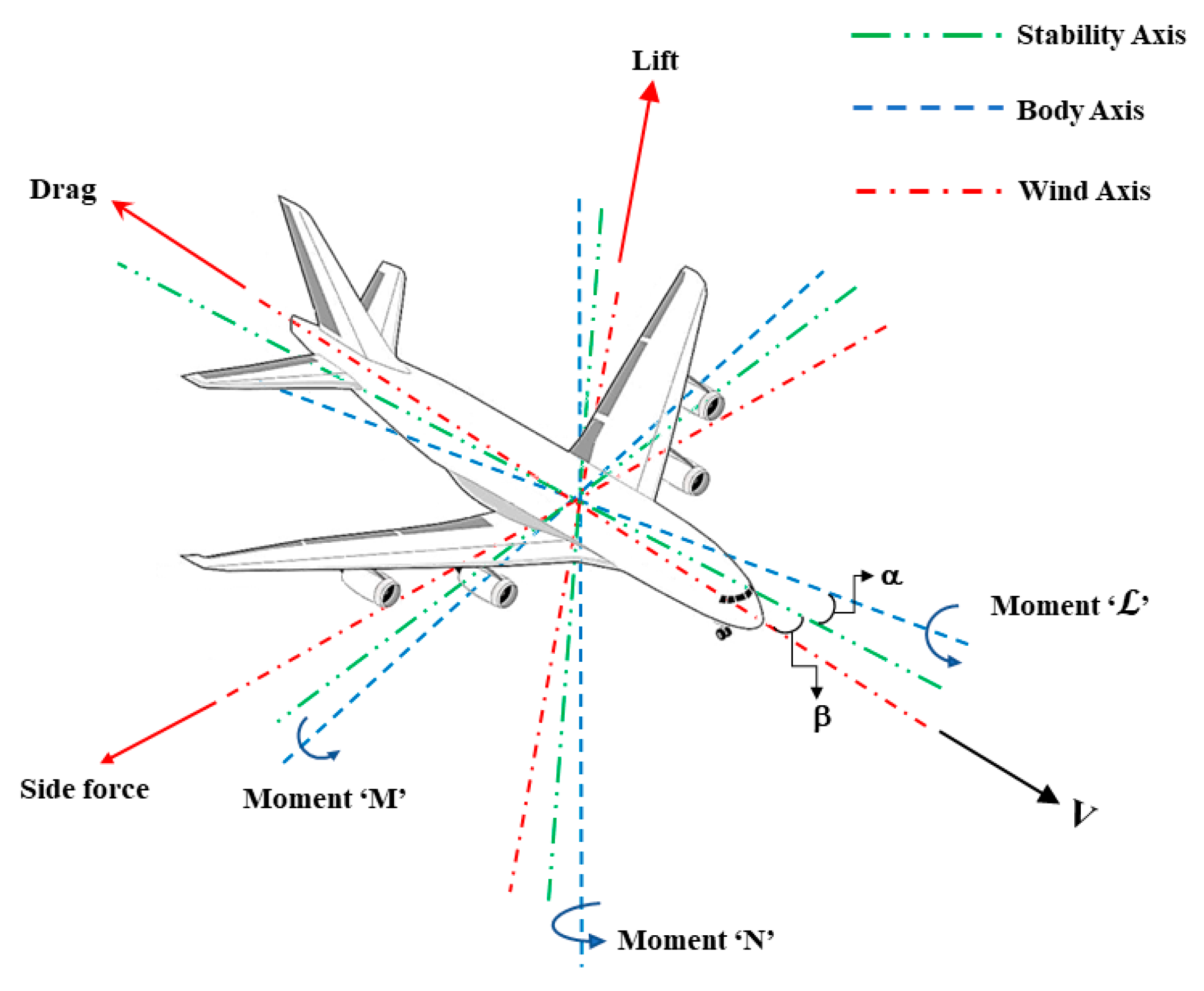
3.2. Axis System
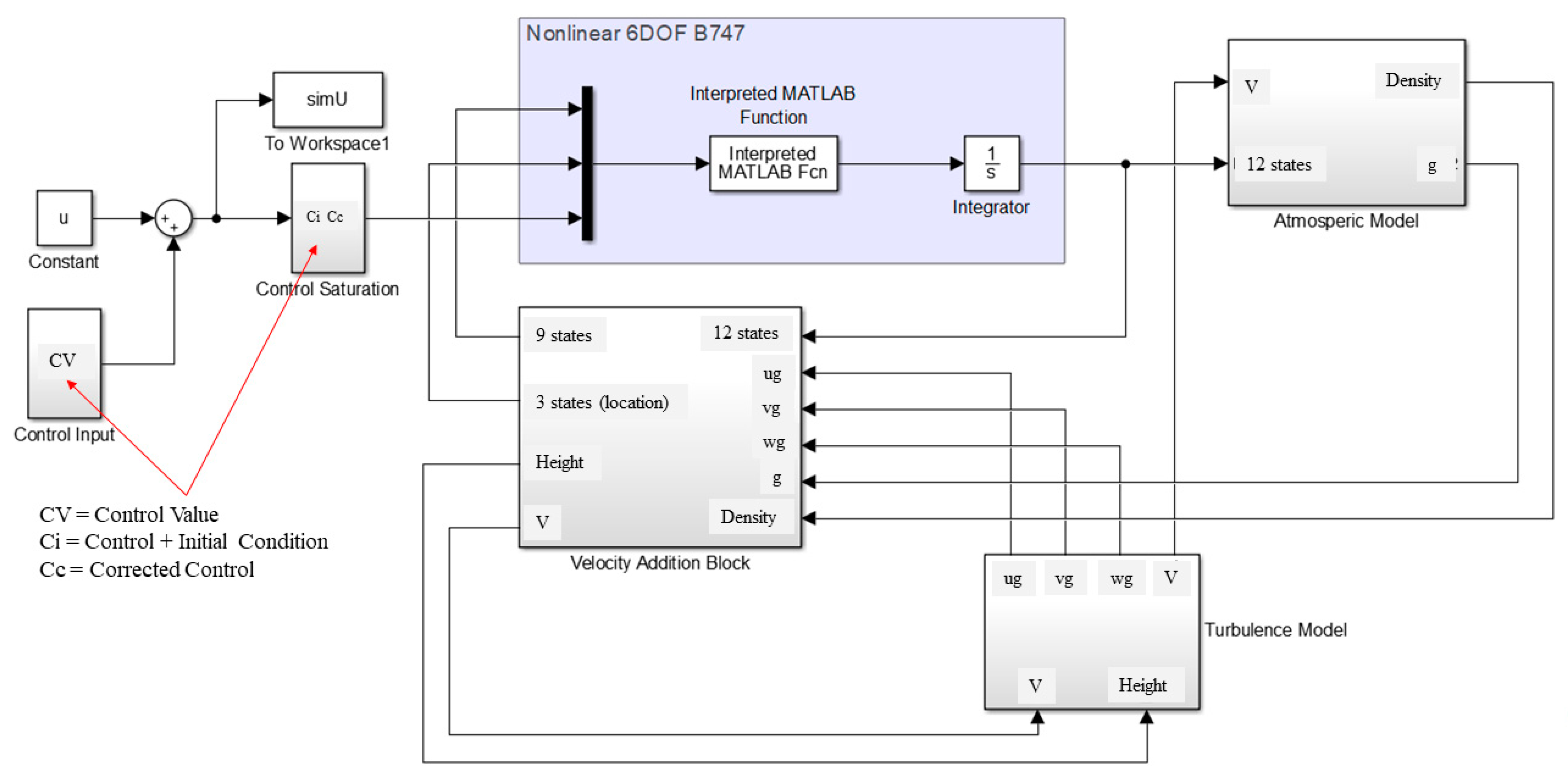
3.3. Designing of Simulink Canvas
3.4. Validation of Non-Linear Model
- Validation using the Boeing 747-200: A state–space model was built using the values for the Boeing 747-200 taken from [61]. The characteristic equation was formulated using frequencies and the damping ratio calculated for Phugoid and short periods. The frequencies were found to be in agreement with the frequencies captured during UDF simulations for the control input, thus validating the UDF accuracy (see Table 4). Moreover, the trim conditions calculated for the approach and cruise conditions were found to be in agreement with the data published in [61] and provide further authentication of the accuracy of the non-linear model. The time history plots obtained from the present canvas also predicted the same trim conditions under the same operating conditions as those mentioned in [61] and had a maximum error of 5.1%.
- 2.
- Validation using a Civil Airplane Model (RCAM): Further validation of the designed canvas was performed using RCAM (an open-source model from the Group of Aeronautical Research and Technology in Europe (GARTEUR) [62,63]). The non-linear UDF was updated with the RCAM model parameters; simulation results were found to be in agreement with the RCAM results available in [62]; this further validated the functionality and structure canvas for computing non-linear flight dynamics. After successful validation, simulations were carried out for two flight conditions: (i) at sea level and (ii) at 40,000 feet cruise flight conditions; the results are discussed in the subsequent sections.
4. Aircraft Trim Conditions and Control Response
4.1. Sea Level Flight Condition
- (1)
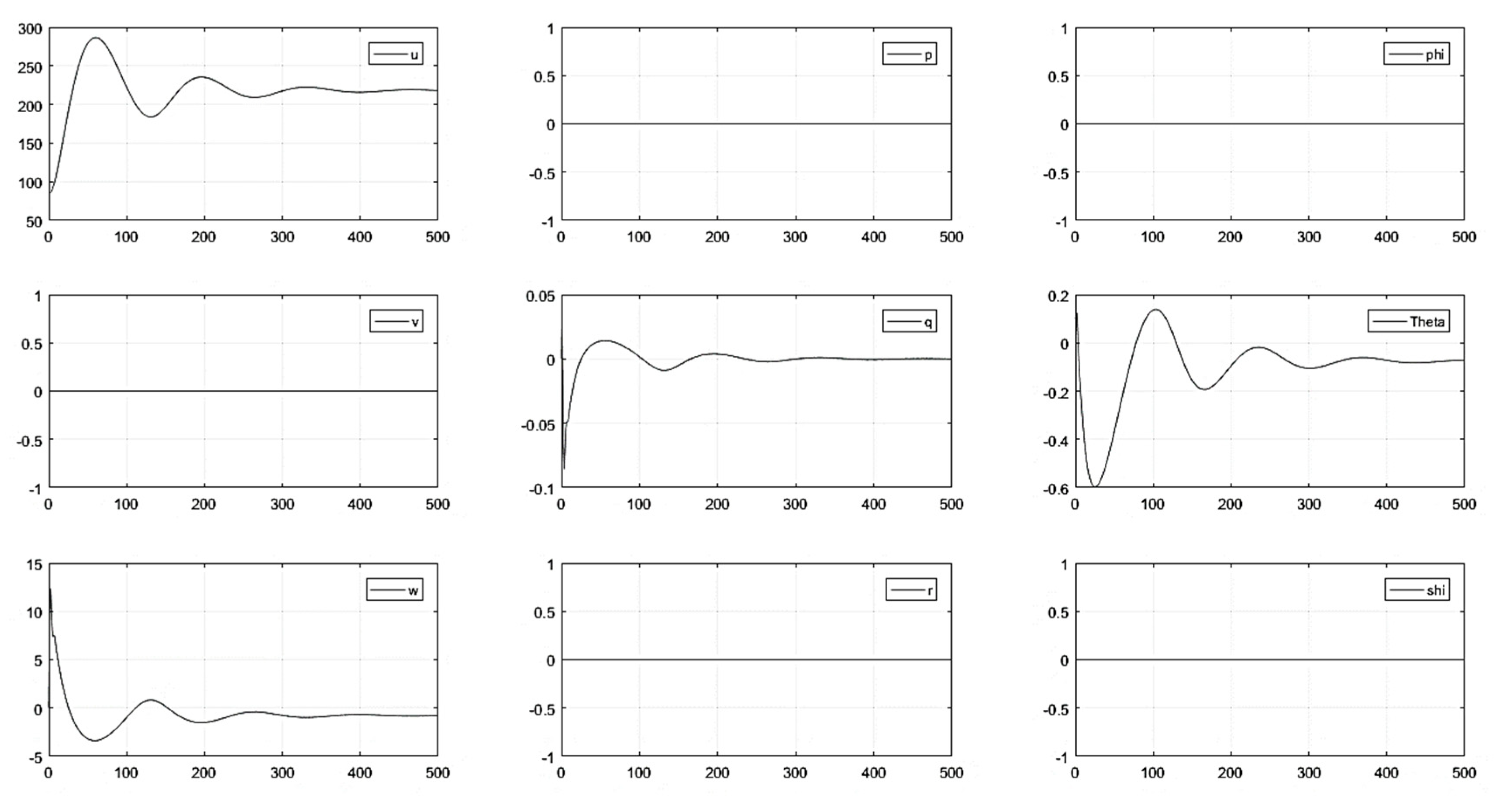
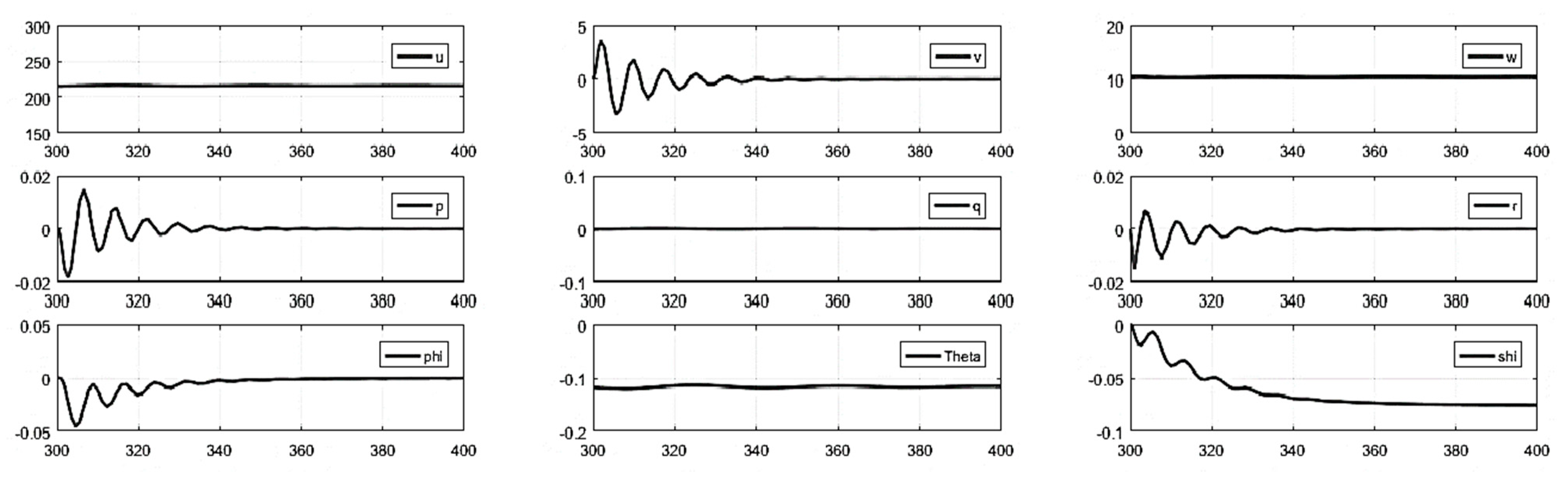
- Without control inputs: The model was updated using the sea level coefficients and was subjected to various initial conditions. The initial conditions acted as a disturbance in the system and the aircraft free response was captured; Figure 6 shows the variation in the longitudinal variables. The aircraft entered phugoid mode, which died out subsequently and the aircraft achieved trim conditions. The trim longitudinal velocity achieved was approximately 225 m/s (documented value of 221 m/s in literature [63]).
- (2)
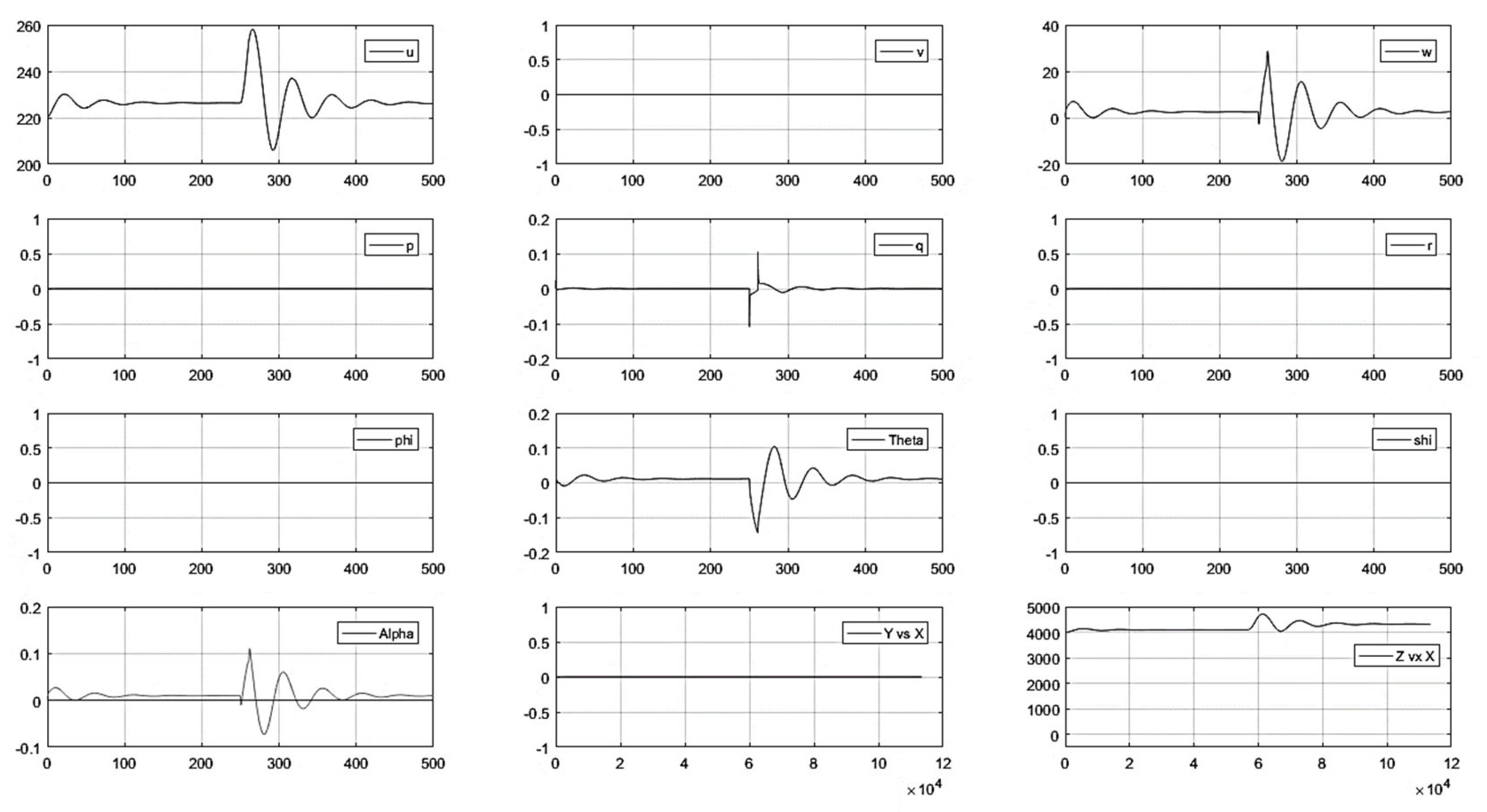
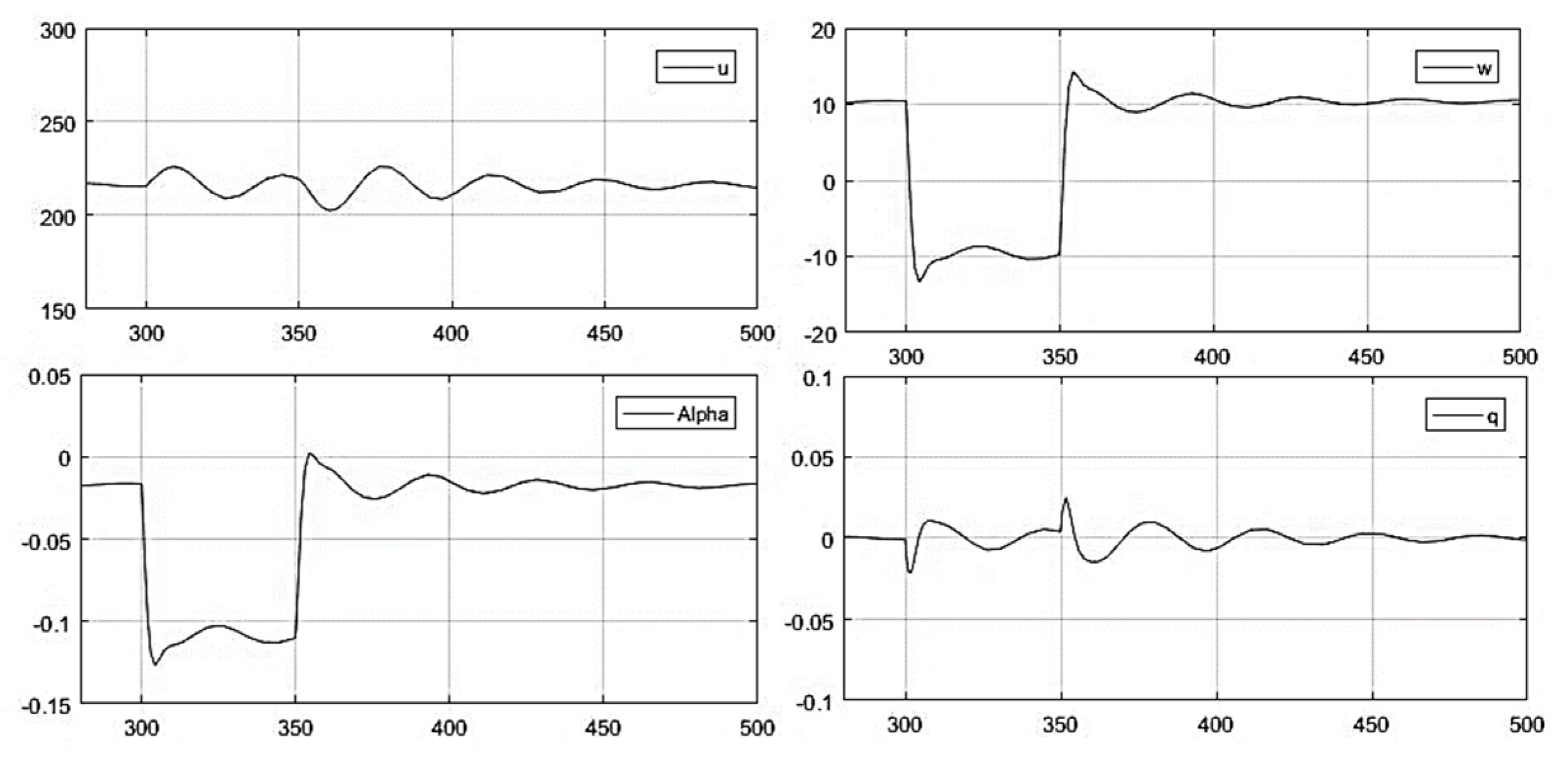
- With elevator control input: In order to evaluate the free response, a 5° impulse elevator input was initiated (acting as a longitudinal disturbance); the aircraft entered a long-period oscillation that subsequently died out; then, the aircraft returned to its trimmed state (see Figure A7 of Appendix B).
- (3)
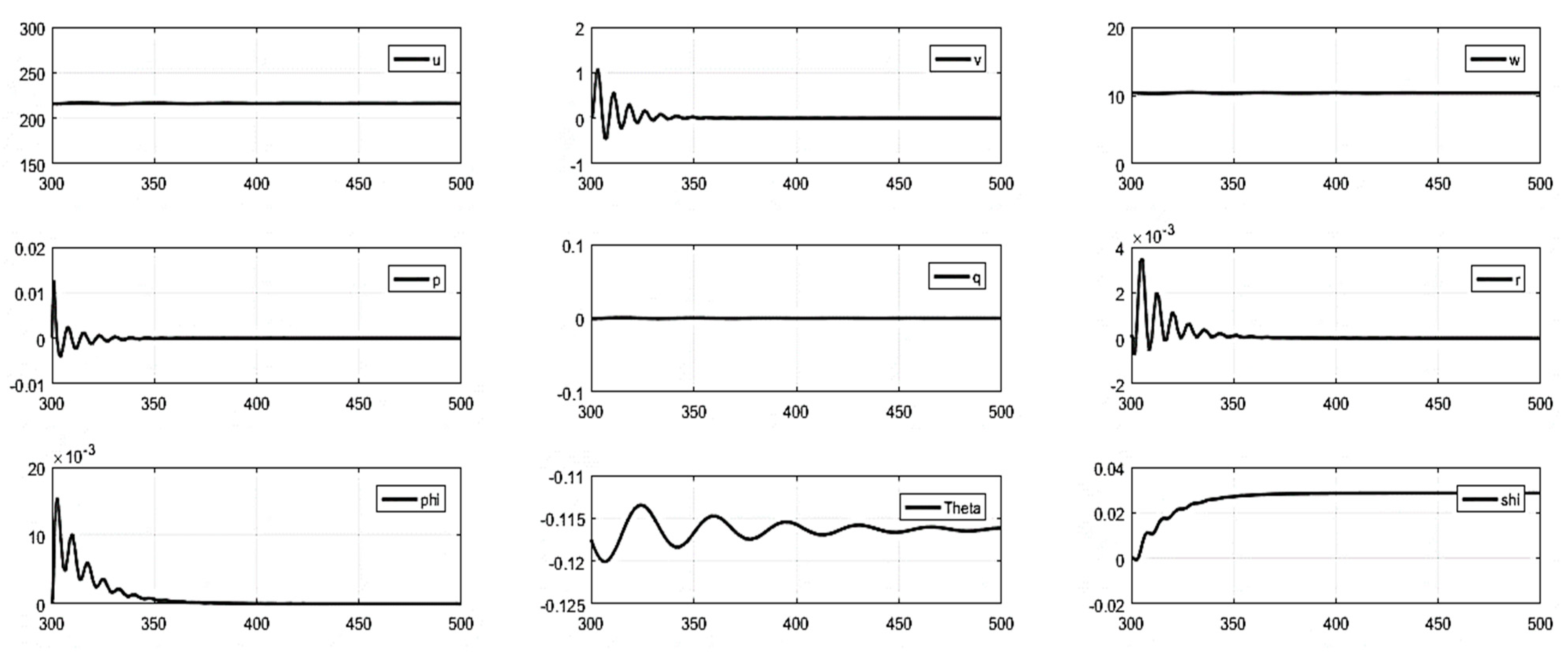
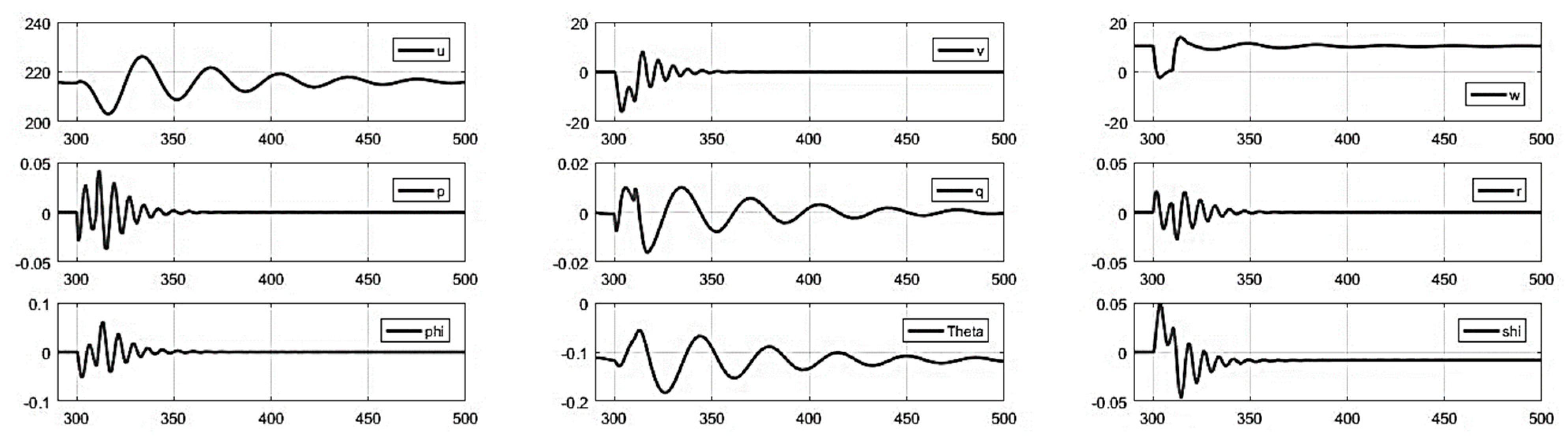
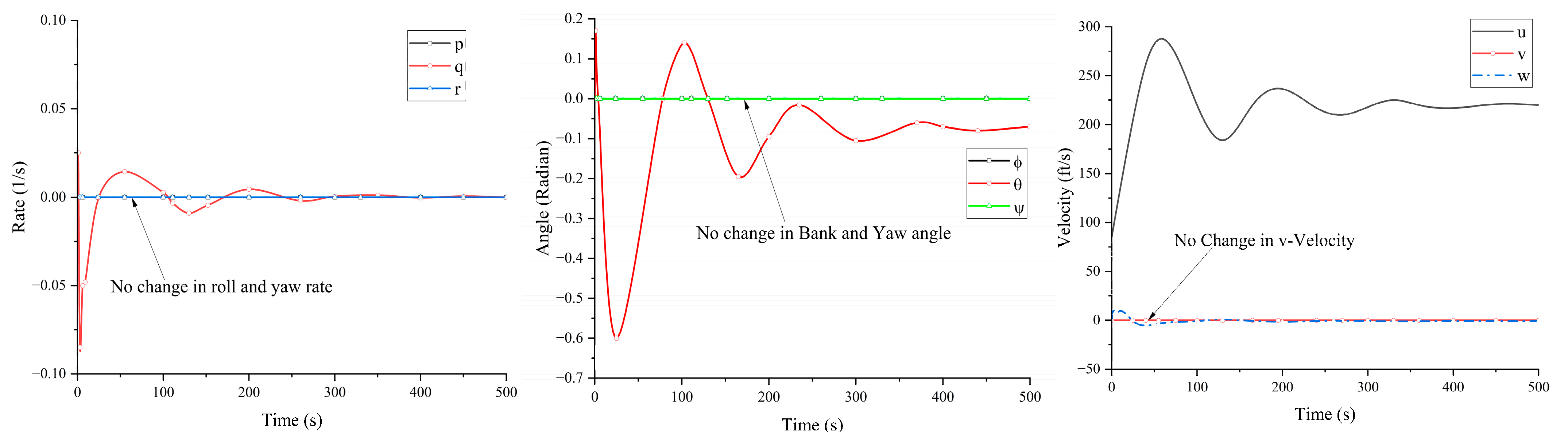
- With lateral control inputs: Under the influence of lateral controls (aileron and rudder impulse inputs), the longitudinal states remained unaffected; the lateral states depicted short-period oscillation as a response to lateral control deflection, which quickly died out and regained its original position. The bank angle ϕ recovered its original zero position; however, the yaw angle ψ reached a new trim position (as expected from theoretical knowledge—see Figure A9 and Figure A10 of Appendix B).
4.2. Cruise Flight Condition
5. Aircraft Response to Wind Turbulence and Wind Shear
- (1)
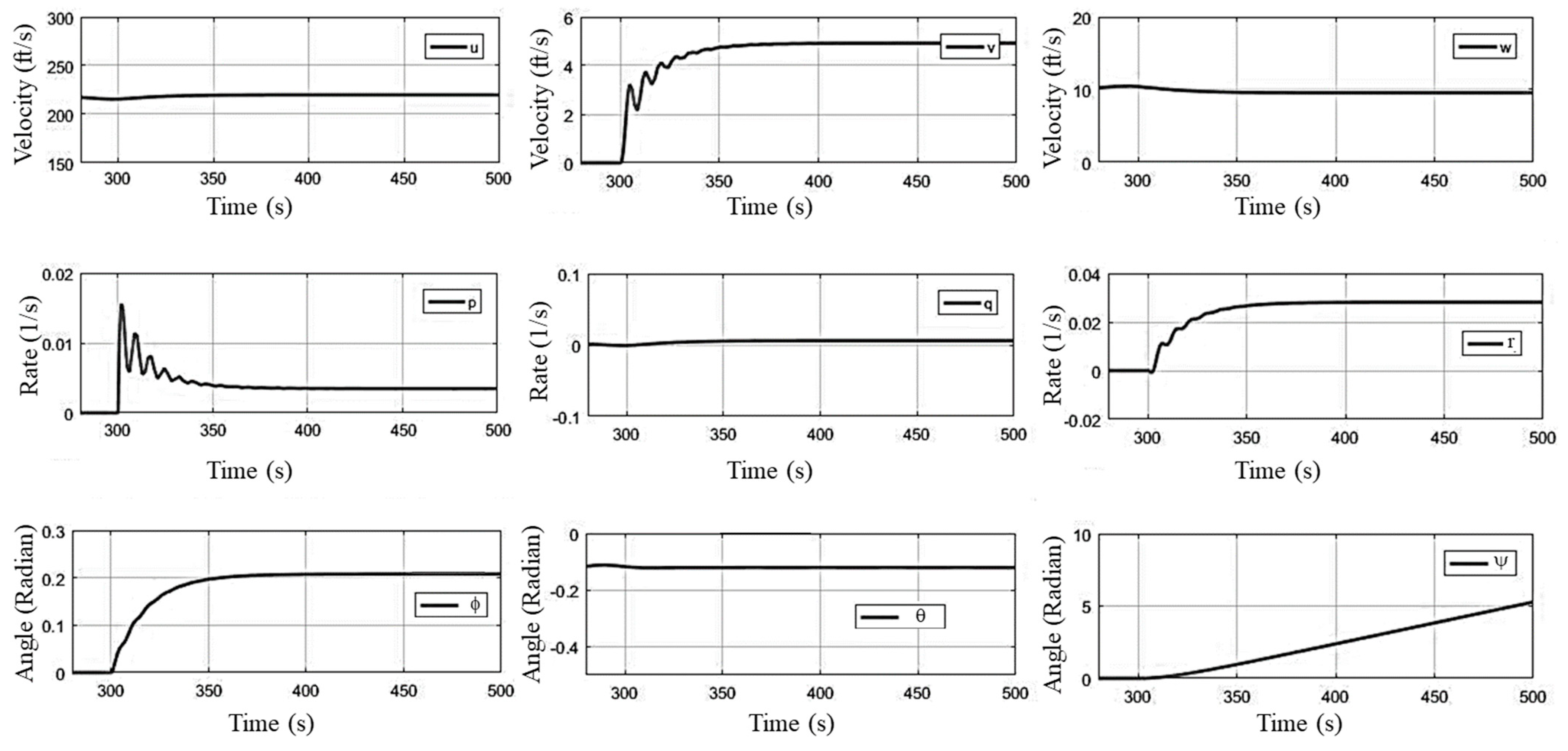
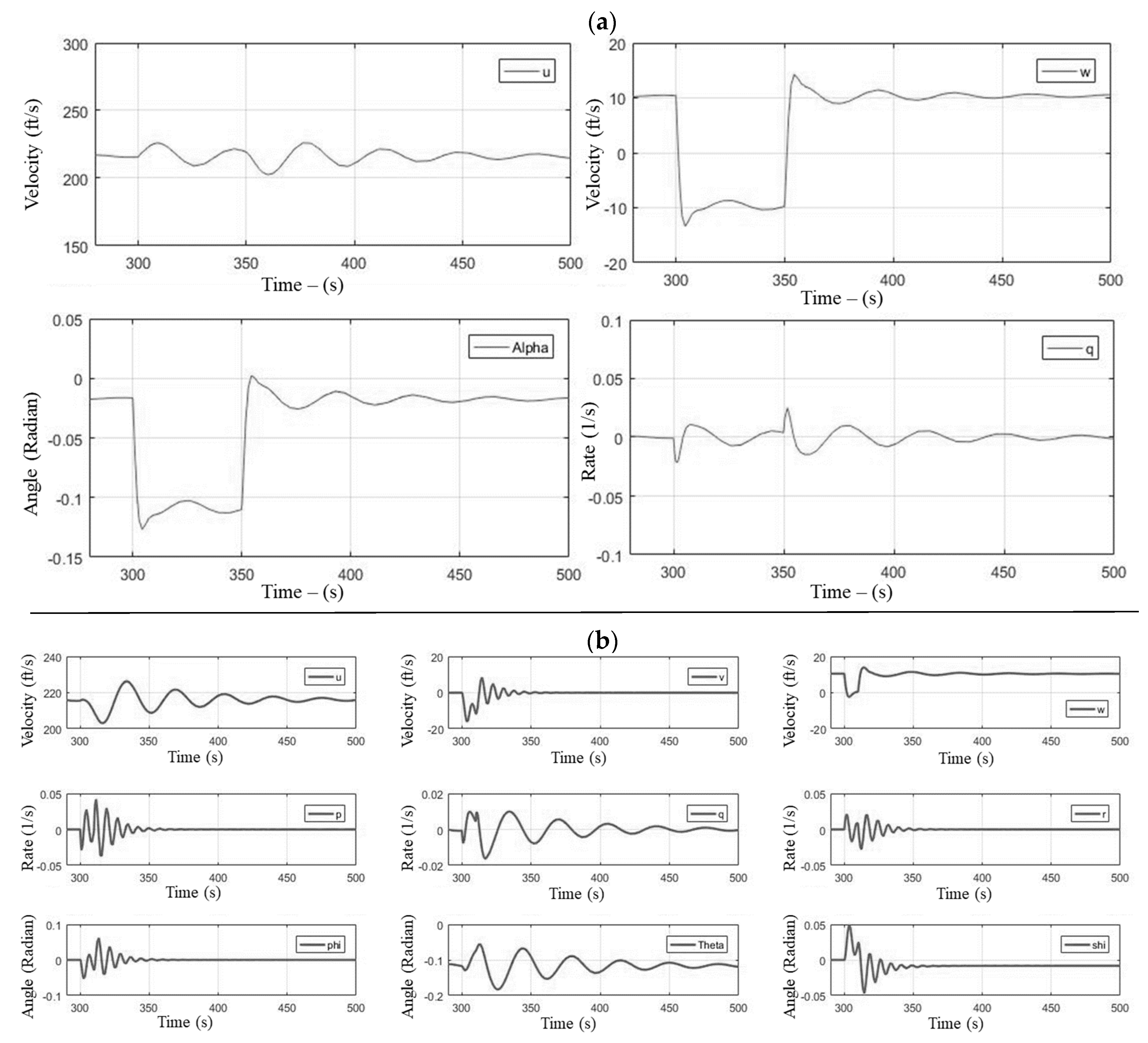
- Wind gust. In order to check the aircraft response to a wind gust, a constant velocity vertical wind gust of 20 ft/s was generated at sea level flight conditions for 50 s using the Simulink wind shear and gust blocks. As expected, the aircraft angle of attack was disturbed for the period of wind gust (see Figure 9a); once the gust was removed, the aircraft regained its trim conditions. The aircraft response to a 3D gust of 10 ft/s in all directions was also simulated; the response of the aircraft to the 3D gust is presented in Figure 9b. All the state variables were disturbed from its trim conditions for the period of gust, and once the gust was removed, the aircraft regained position.
- (2)
- Atmospheric turbulence. In order to analyze the behavior of the aircraft for atmospheric turbulence, the turbulence block was used during the simulations. As wind turbulence is a three-dimensional phenomenon, all the modes are affected. However, the random fluctuations were small in amplitude and continued for the entire duration of the simulation; therefore, all the modes kept fluctuating about their free-response behavior.
- (3)
- Atmospheric conditions at landing. As the landing approach is the most critical phase of flight and sudden changes in wind profile in the proximity of the ground have catastrophic effects on flight safety; therefore, a detailed analysis with a variety of wind gust profiles was conducted to ascertain the free response of the aircraft during landing conditions.
- (i)
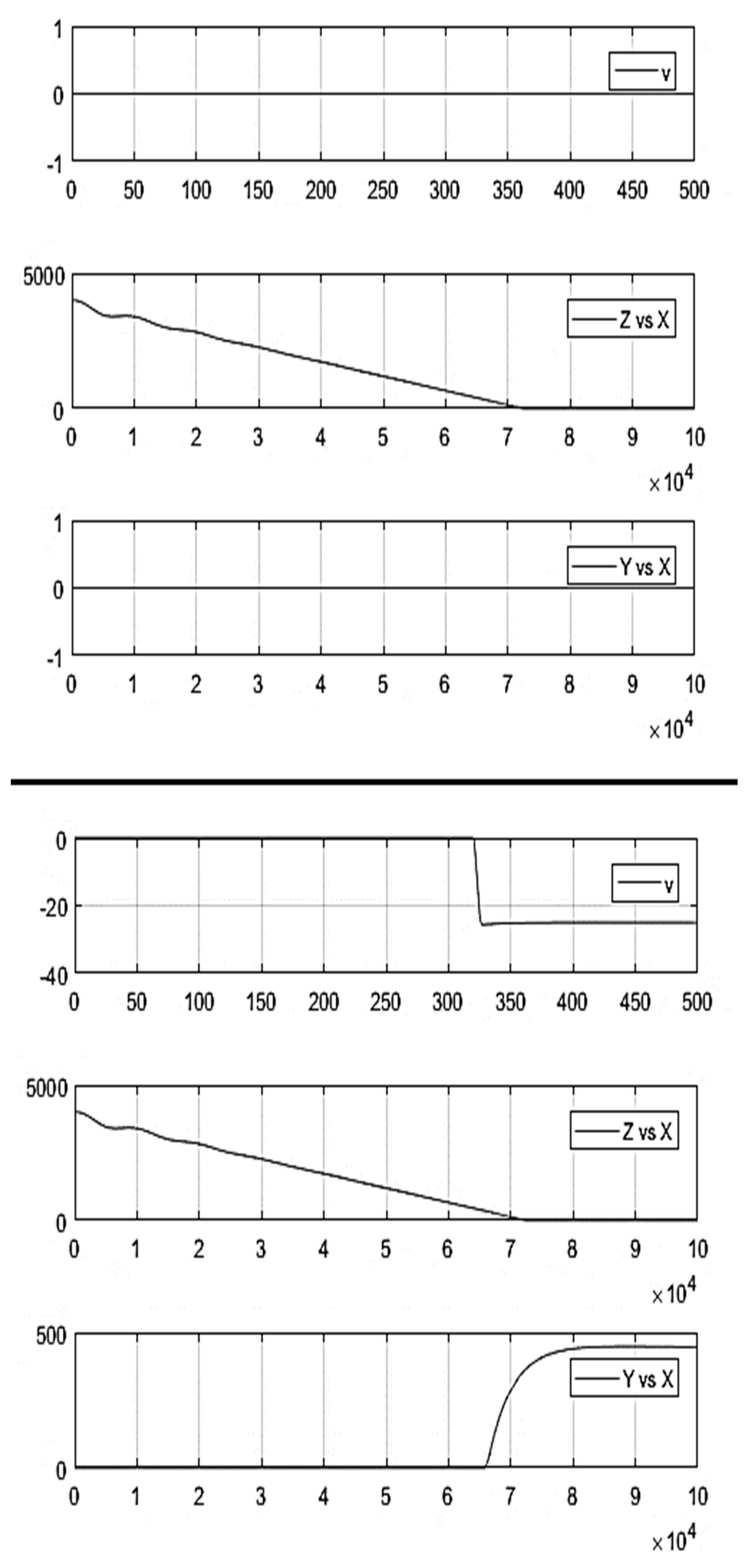
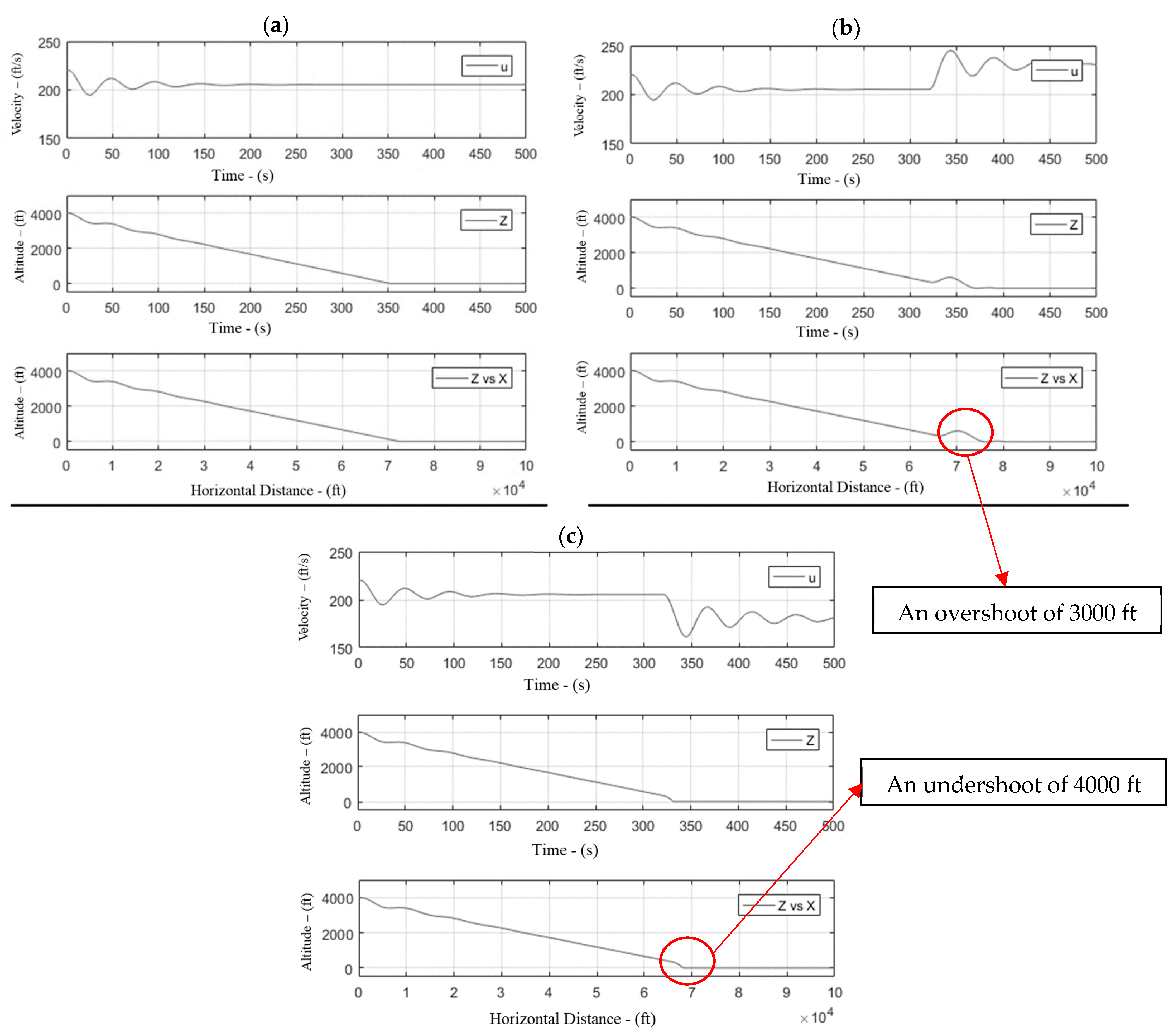
- Landing in headwind and tailwind conditions. When considering an aircraft on a standard 3° glide slope that was subjected to 25 ft/s headwinds (see Figure 10), the effective speed of the aircraft increased due to headwind and generated more lift. As a result, the aircraft gained height and was disturbed from its preset glide course. The aircraft experienced an overshoot of approximately 3000 ft from the touchdown point. Similarly, an undershoot of approximately 4000 ft was recorded for a 25 ft/s tailwind condition due to the reduction in the effective forward speed. The undershoot and overshoot were increased to approximately 6000 ft once the wind velocity was increased to 30 ft/s.
- (ii)
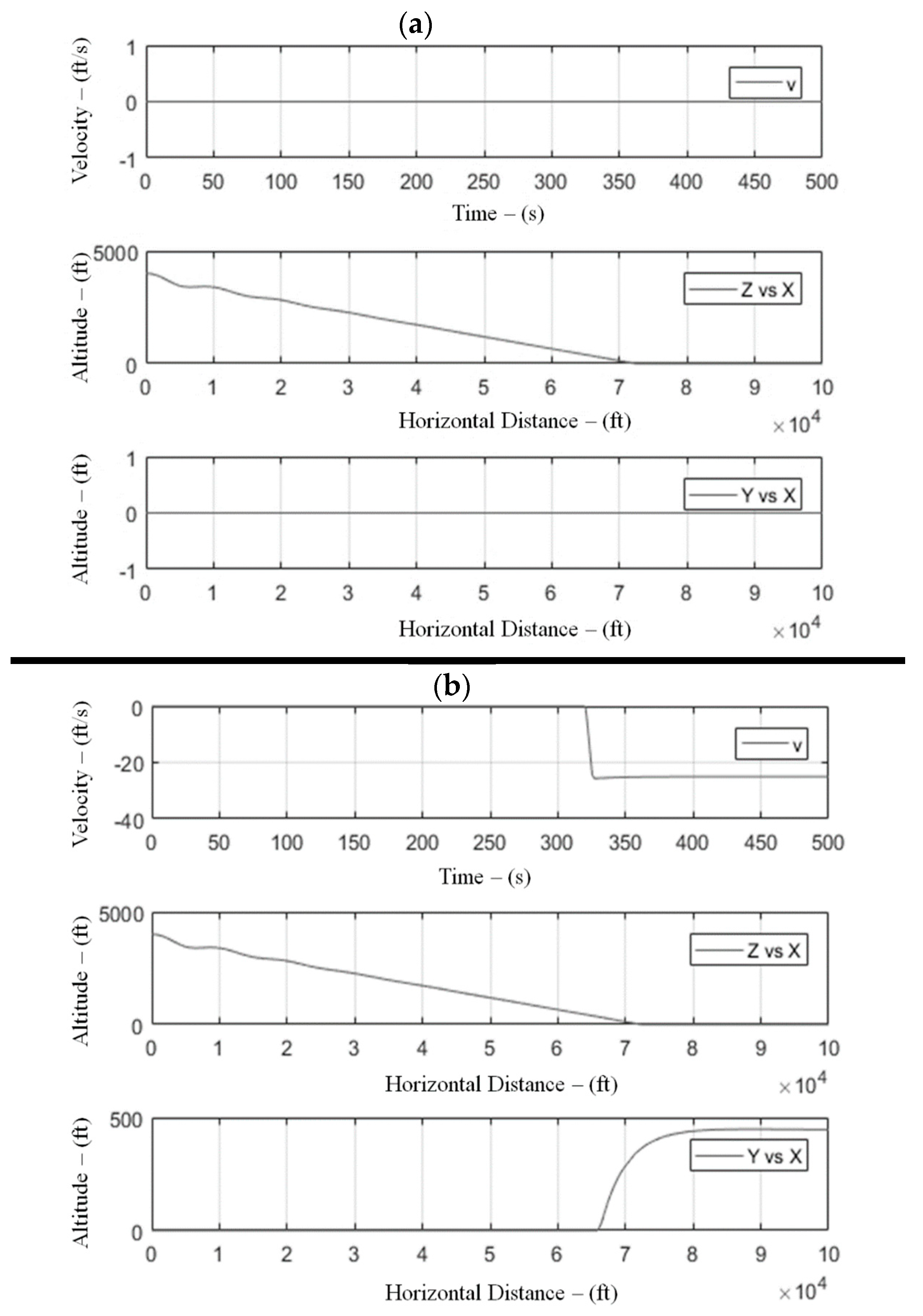
- Landing in crosswind conditions. A case of a 25 ft/s 90° crosswind condition was also simulated; as expected, the aircraft started drifting in the direction of the crosswind. Under the simulated conditions, the aircraft became offset from its landing approach by approximately 450 ft (see Figure 11), with the glide slope and touchdown point being negligibly affected. Due to inherent coupling, the roll and yaw rates along with the variation in roll and yaw angle were observed. Once the crosswind conditions were reduced to 10 ft/s, an offset was reduced to 180 ft from the initial course.
- (iii)
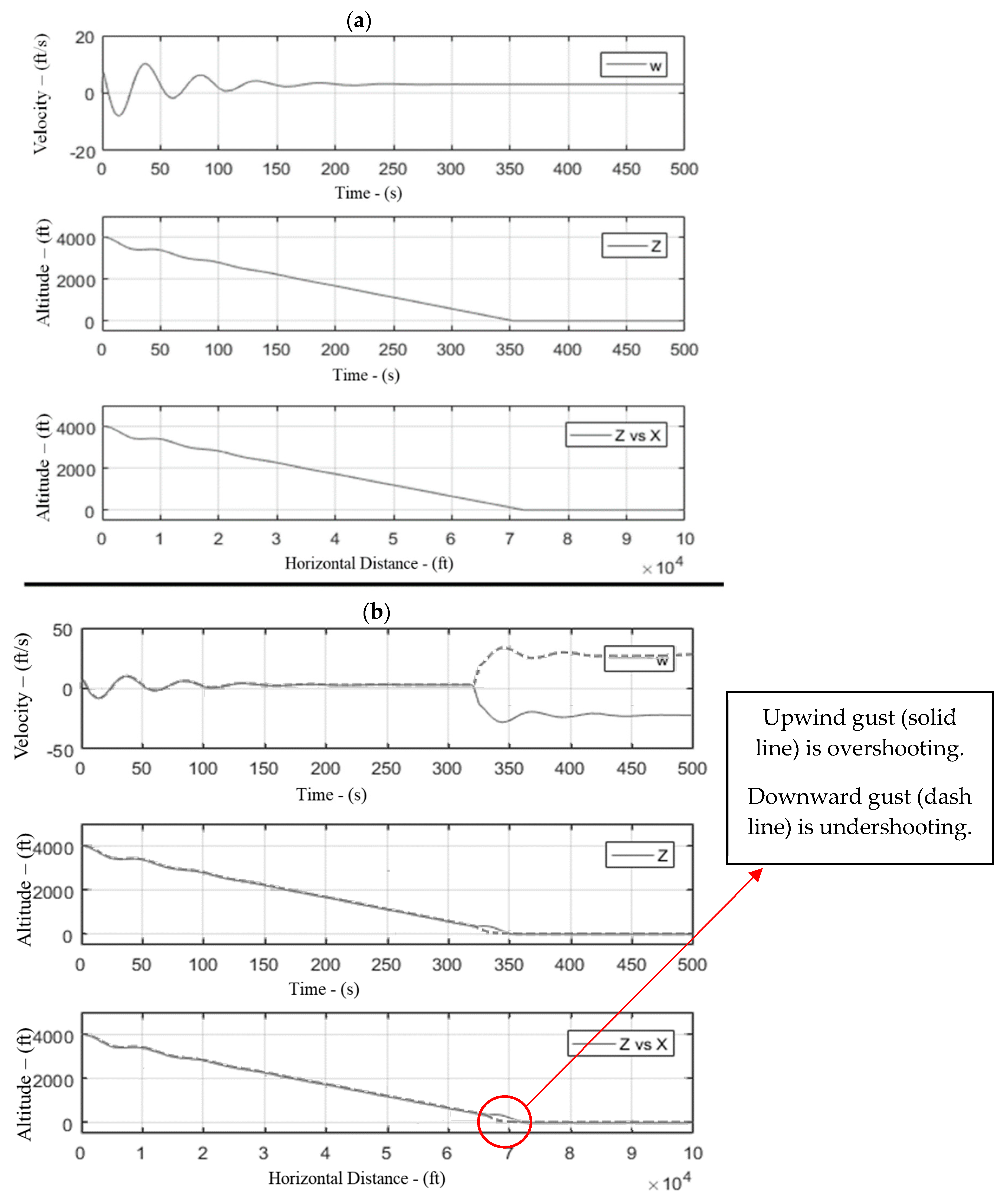
- Landing in vertical wind shear conditions. Vertical wind shear simulations were also conducted for a wind velocity of 25 ft/s. During an upward gust condition, the effective angle of attack increased for the aircraft, thus increasing the overall lift of the aircraft. The aircraft momentarily gained height, departing from its preset 3° glide slope before diving again to a glide slope of approximately 10° and overshooting the touchdown point by a couple of hundred feet (see Figure 12). In the case of a downward gust condition of 25 ft/s, the aircraft’s angle of attack decreased, and this put the aircraft into a steep glide slope of approximately 11~12° and undershot the touchdown point by approximately 4000 ft.
- (iv)
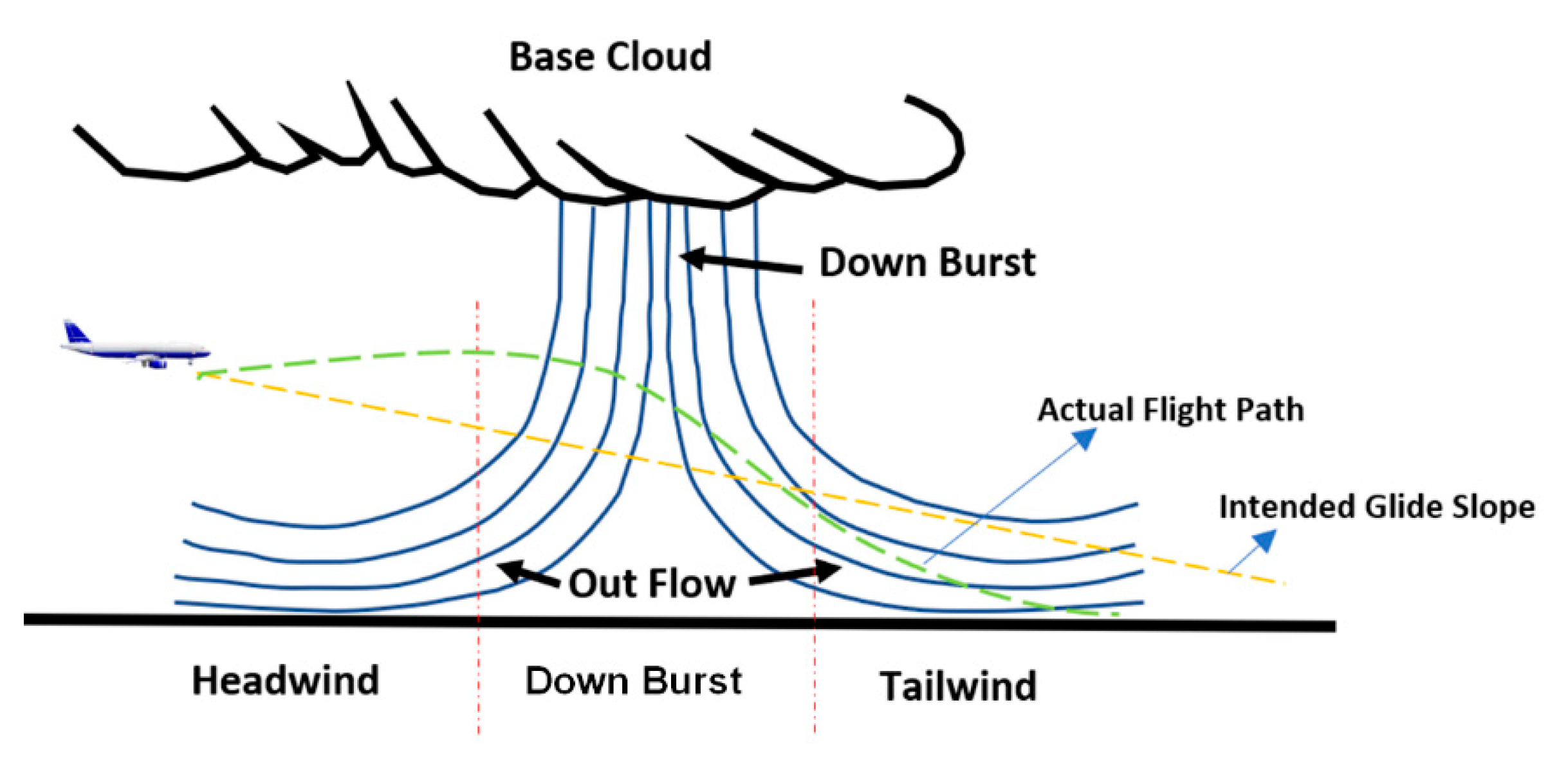
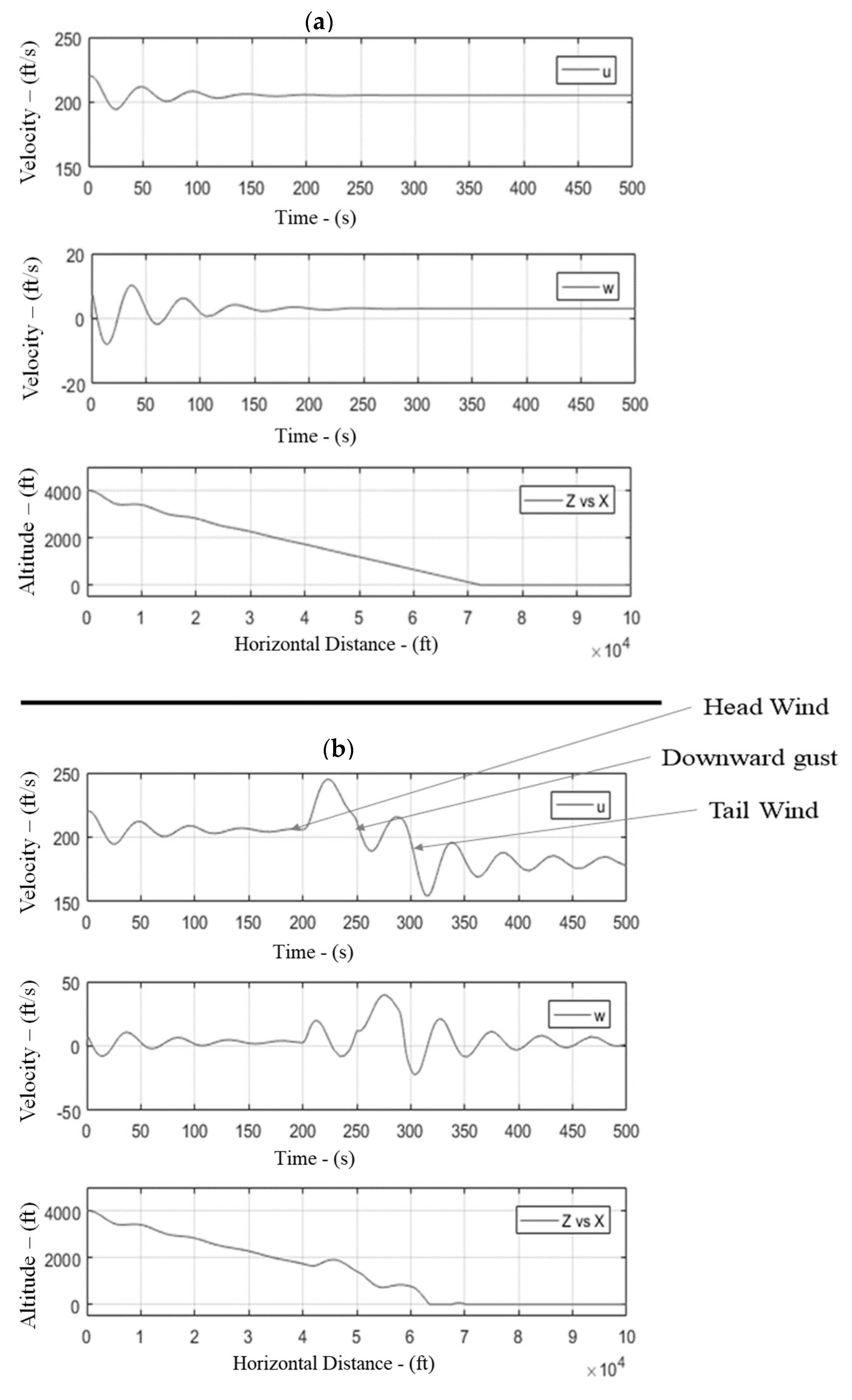
- Landing in microburst conditions. A microburst with a maximum velocity of 25 ft/s was also simulated. As the physical spread of the velocity profile was higher, the burst simulations were started at 32,000 ft short of the actual touch-down point. In the first phase, a headwind of 25 ft/s was built and sustained for 10,000 ft and then transitioned into a sustained downwind of 25 ft/s for another 10,000 ft. In the last phase, the downwind was transitioned into a tailwind of 25 ft/s, which continued until touchdown. As expected, initially, the aircraft gained height in the headwind condition due to an increase in the effective speed (departing from its 3° glide course), followed by a sharp dip under the influence of the sustained downwind. The aircraft momentarily leveled off while transitioning from a downwind condition to a tailwind condition; it then glided down at a sharp angle of ~14.5° under the influence of tailwind (as the aircraft’s forward speed was reduced). Aircraft touchdown was approximately 8000 ft short of the actual touchdown point (see Figure 13); additionally, the descent rate was also high. It was the high glide slope angles and higher descent rate that led to aircraft crashes while encountering microbursts short of the runway. This dangerous phenomenon associated with aircraft crashes encountering microbursts during the approach was successfully simulated and analyzed.
6. Conclusions
7. Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| I | Inertia tensor |
| Ix, Iy, Iz | Moment of inertia about axis (rotational inertia that resists change in the rotational velocity of an object on its axis |
| Ixz, Iyz, Ixy | Product of inertia (feature of an object that describes an imbalance relative to a defined set of coordinate axes) |
| , M, N | Moments about x, y, and z-axes in a body frame, respectively. corresponds to rolling, M corresponds to pitching, and N corresponds to yawing moment of the aircraft |
| Velocity components about x, y, and z-axes in a body frame | |
| Translational accelerations about x, y, and z-axes in a body frame | |
| Angular velocities about x, y, and z-axes in a body frame | |
| Rotational accelerations about x, y, and z-axes in a body frame | |
| Euler angles of aircraft about x, y, and z-axes of inertial frame | |
| Rate of change of Euler angles about x, y, and z-axes of inertial frame | |
| Position coordinates of the aircraft with respect to inertial frame | |
| Translational velocities of the aircraft with respect to inertial frame | |
| Direction cosines for transformation of vectors from body frame to inertial frame |
Appendix A
- Assumption. While formulating EoMs for aircraft (747-200), the following assumptions were made:
- (a)
- The aircraft is a rigid body.
- (b)
- The Earth is taken as an inertial frame—stationary flat surface.
- Formulation of non-linear EoMs: According to Newton’s second law, the motion of a rigid body in an inertial frame is governed by Equation (A1).
- 3.
- Calculation of external forces: To solve Equation (A5), we need to calculate external forces applied on the aircraft. External forces in a body frame are a combination of gravitational force, aerodynamics force, and propulsive forces acting on the aircraft.
- (A)
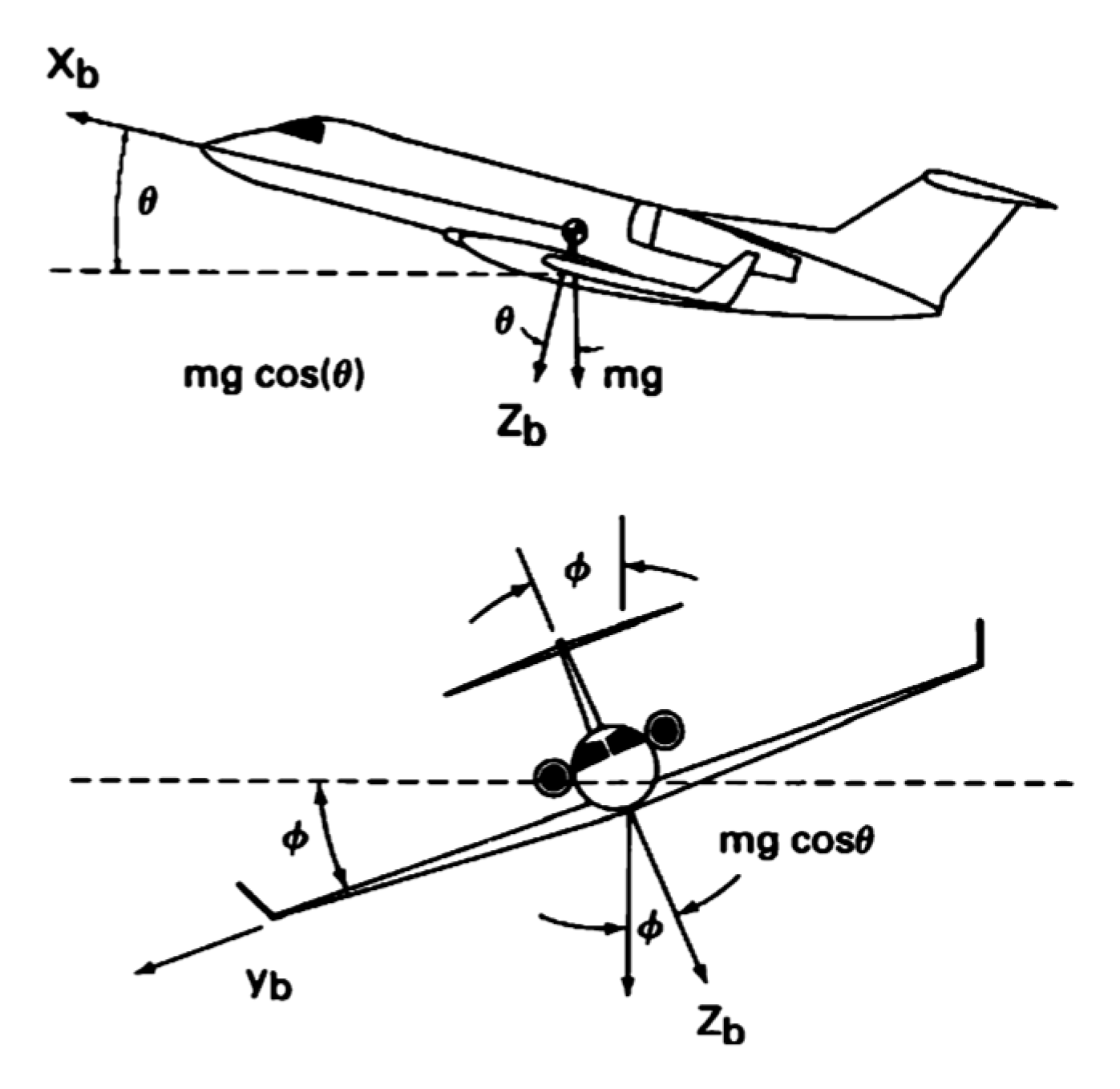
- Gravitational force: In an inertial frame, weight is always acting downward toward the center of the Earth (z-axis of inertial frame) and can be represented as Equation (A16). Gravitational force into the body frame can be calculated using direction cosines as shown in Equation (A17) using Figure A1.
- (B)
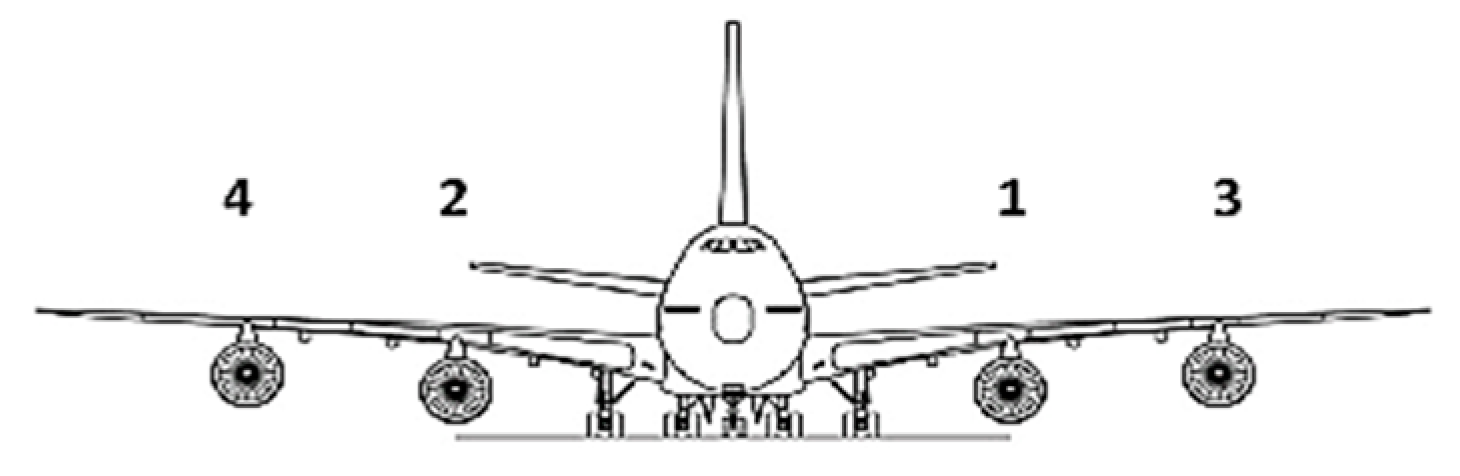
- Propulsion forces: The Boeing 747-200 has four engines installed on its wings, two on each side (ref. Figure A2). It is assumed that the thrust produced by all the engines is in line with the x-axis of the body frame. Therefore, a simple expression can be used to express the propulsion forces (ref. Equation (A18)). These propulsive forces are throttle-dependent forces and require the throttle position as an input condition.
- (C)
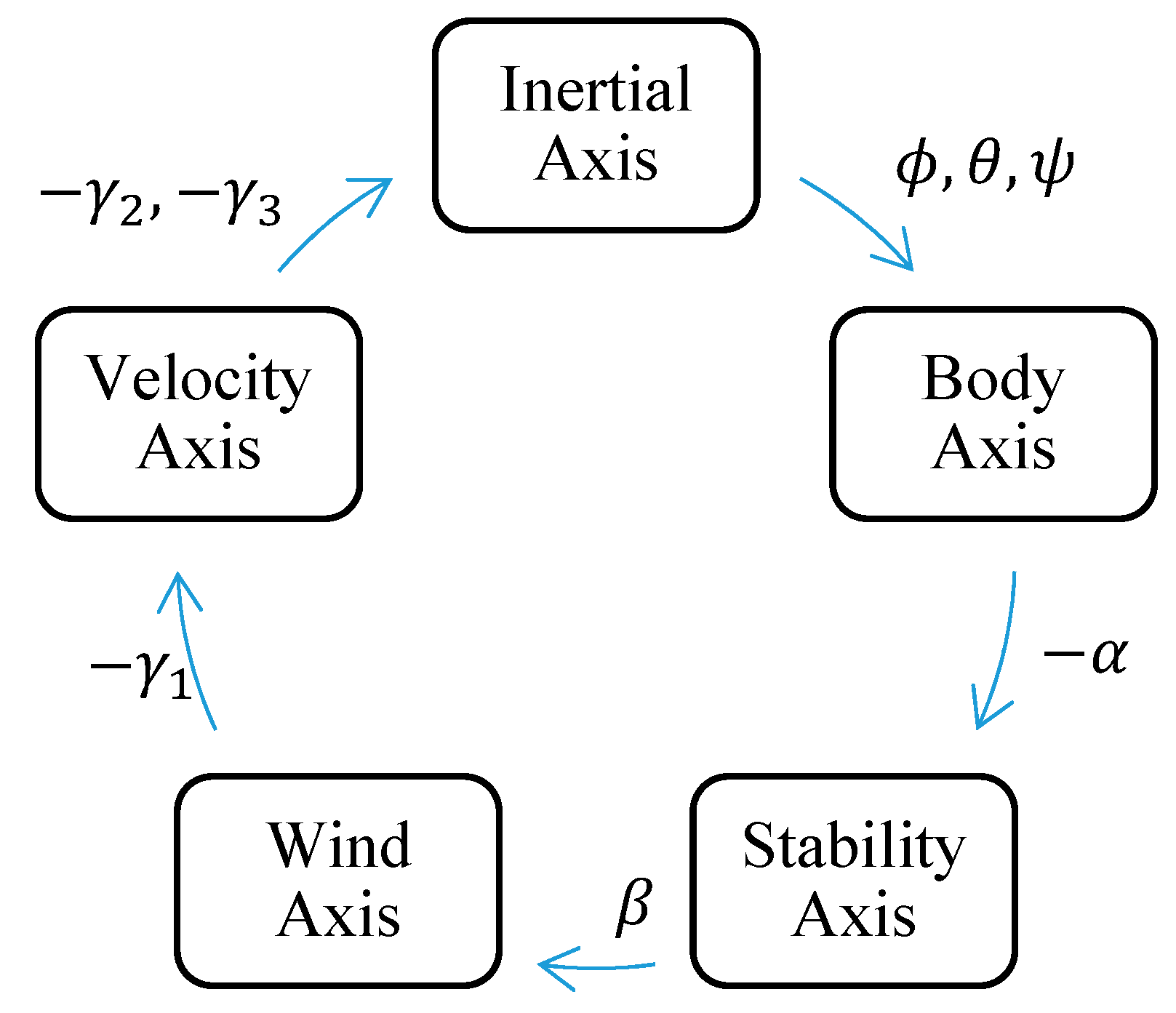
- Aerodynamics Forces: There are three forces acting along the axes of the body frame. These are normal, axial, and side forces. Generally, the forces are captured in the wind axes by definition and need to be transformed back to body axes using a transformation matrix (Ref Equation (A19)). The transformation variables are selected as per Figure A3.
Therefore, the sum of the external forces is presented in Equation (A20).
- 4.
- Calculation of External Moments: External moments in a body frame are a combination of moments generated by gravitational force, aerodynamics force, and propulsive forces.
- 5.
- Calculation of aerodynamics forces: Aerodynamic forces are a function of a lot of variables, which include translational velocities, angular velocities, the rates of change of velocities, control input, etc. The aerodynamic forces and moments can be expressed as a function of all the motion variables; however, only the significant variables are retained, and the rest are neglected.
- 6.
- State space representation: Equations (A5), (A10), (A12), and (A14) represent the equations of motion and can be easily represented in a state space notation. For ease, the input conditions and are placed in a separate column vector as per standard procedures of state space representation (ref. Equation (A27)).
- 7.
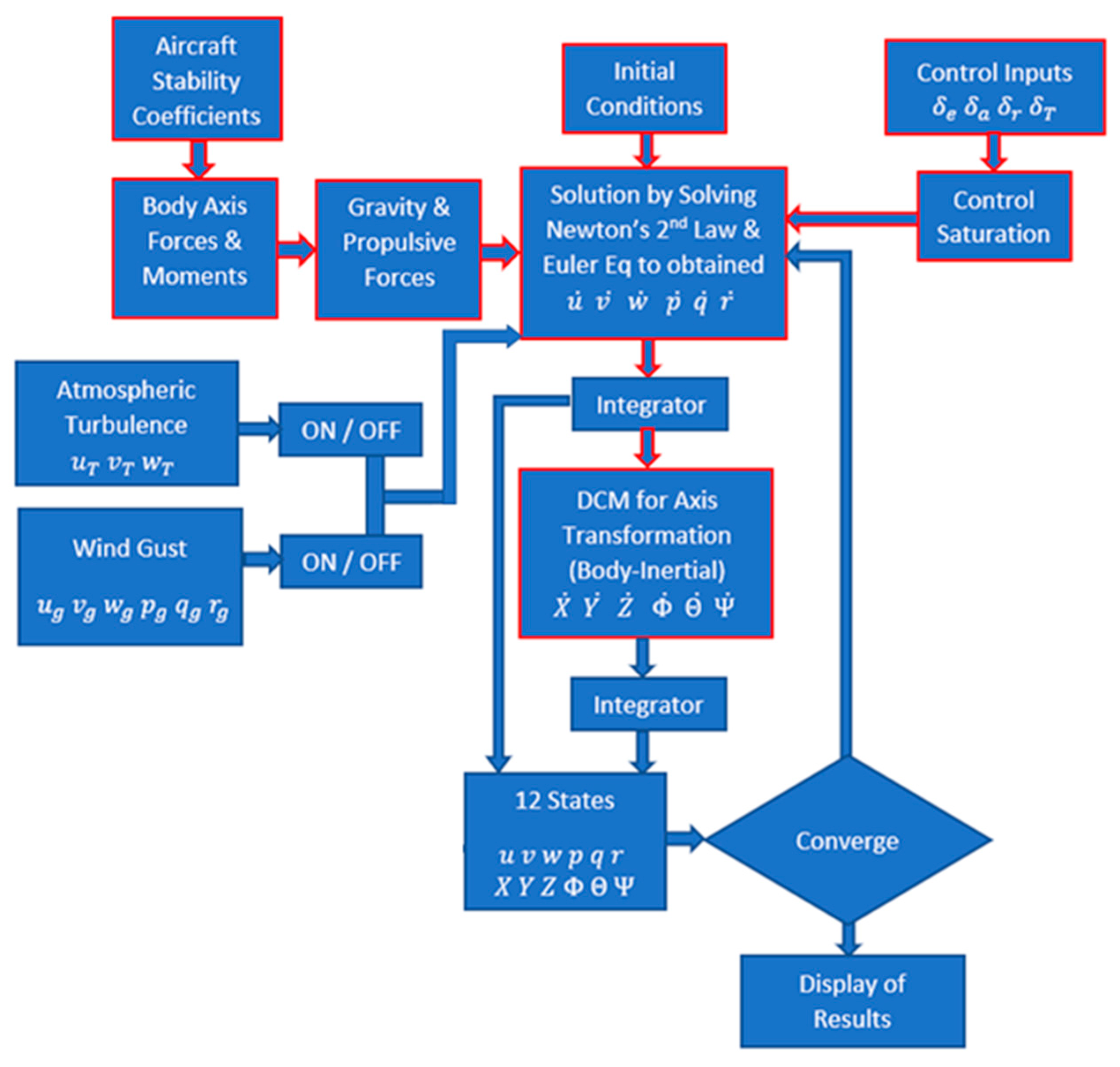
- Simulink modeling: The function formulated in Equation A27 was interpreted in a Simulink environment as a user-defined function. The sketch is shown in Figure A4. and are provided as inputs; the block calculates , which is passed through an integrator to obtain the state space . is routed again to the block as an input. The cycle continues until convergence is achieved.
- 8.
- Wind turbulence modeling: To introduce the effect of wind turbulence and atmospheric gust/shear, Simulink blocks are separated; the Dryden turbulence model, wind shear, and wind gust were incorporated into the canvas. The schematic of the improved canvas is shown in Figure A5. The density variation with height was captured through the COESA atmospheric block. The linear and angular wind velocities were summed up with the velocities obtained from the interpreted MATLAB function and rerouted to the interpreted MATLAB function block for subsequent iteration until the solution is converged.
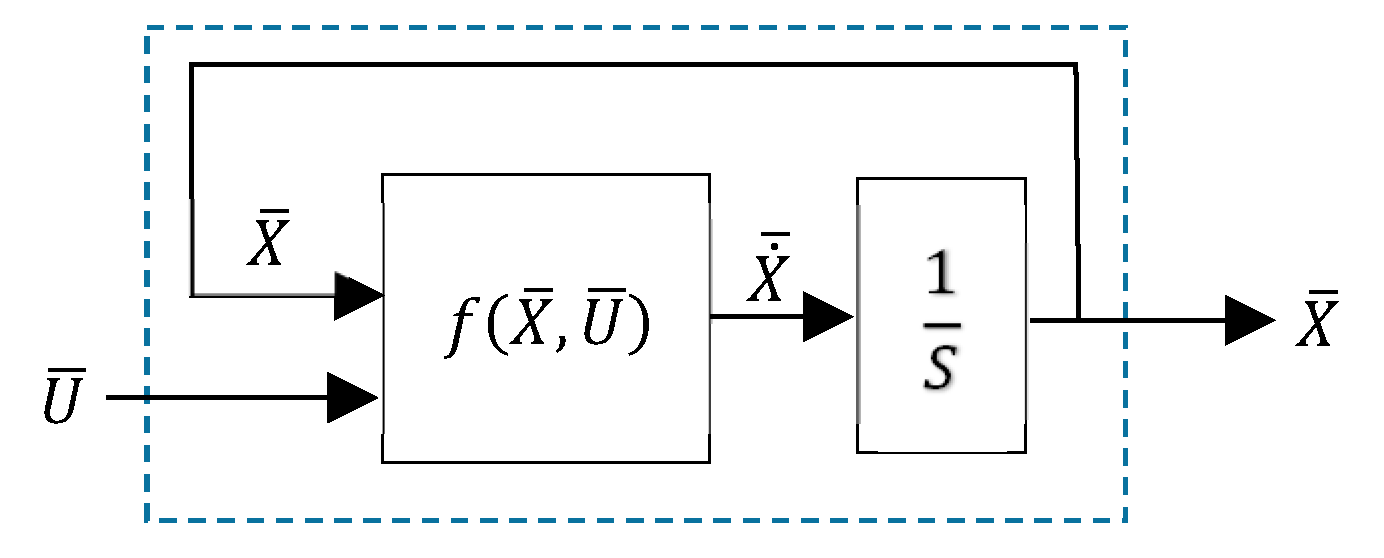
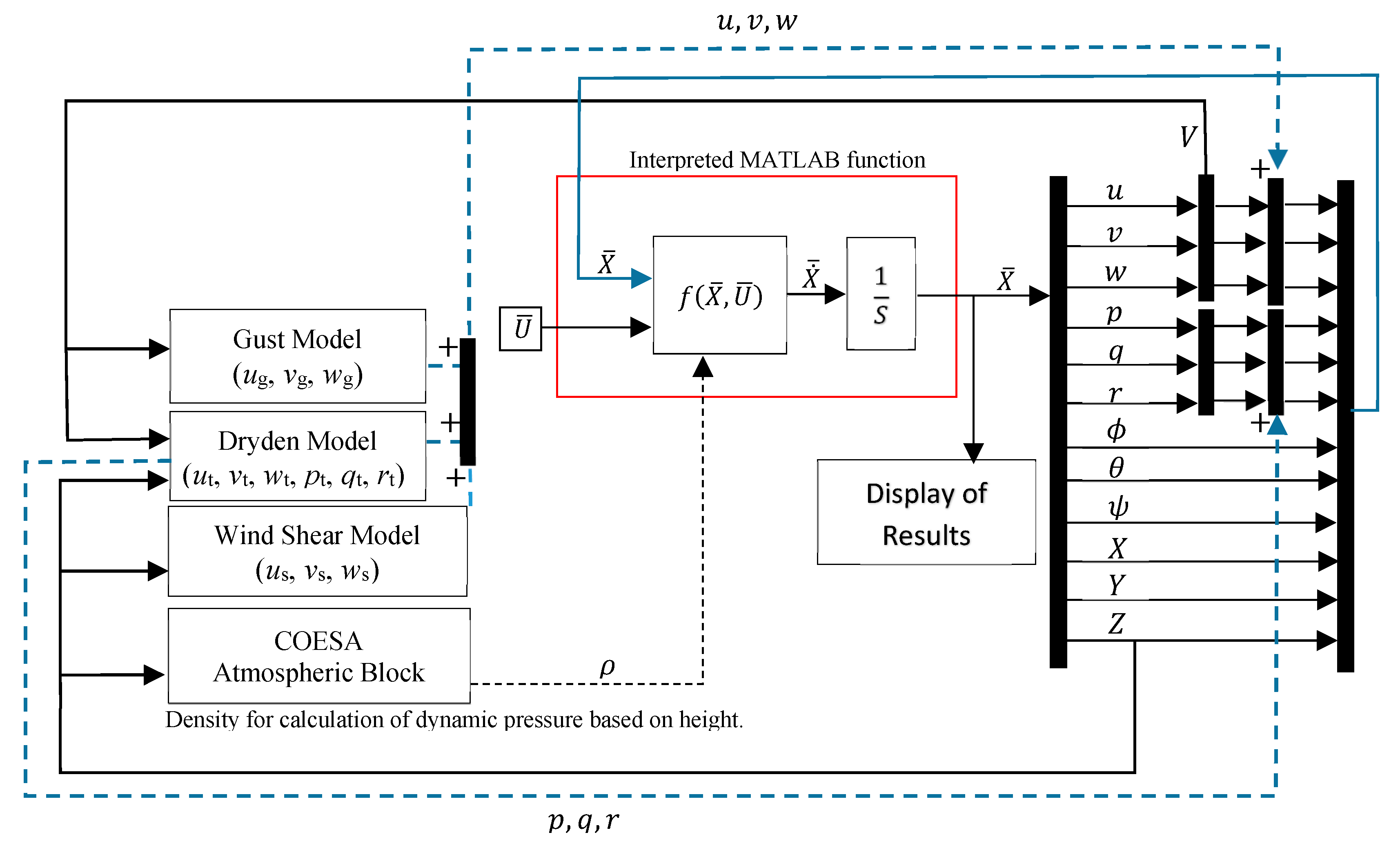
Appendix B
- (1)
- Without Control Inputs.
- (2)
- With Elevator Control Input.

- (3)
- With Aileron/Rudder Control Inputs.



- (1)
- Landing Under Headwind and Tailwind Conditions.
- (2)
- Landing Under Crosswind Conditions.
- (3)
- Landing Under Vertical Wind Shear Conditions.



References
- Rizzi, A. Modeling and simulating aircraft stability and control—The SimSAC project. Prog. Aerosp. Sci. 2011, 47, 573–588. [Google Scholar] [CrossRef]
- Mehra, R.K.; Kessel, W.C.; Carroll, J.V. Global stability and control analysis of aircraft at high angles of attack. In Annual Technical Reports 1/2/3, ONR-CR215-(1/2/3), 1977/1978/1979; Scientific Systems Inc.: Woburn, MA, USA, 1977. [Google Scholar]
- Carroll, J.V.; Mehra, R.K. Bifurcation analysis of nonlinear aircraft dynamics. J. Guid. Control Dyn. 1982, 5, 529–536. [Google Scholar] [CrossRef]
- Winslow, J.; Otsuka, H.; Govindarajan, B.; Chopra, I. Basic understanding of airfoil characteristics at low Reynolds numbers (104–105). J. Aircr. 2018, 55, 1050–1061. [Google Scholar] [CrossRef]
- Goman, M.G.; Khramtsovsky, A.V. Computational framework for investigation of aircraft nonlinear dynamics. Adv. Eng. Softw. 2008, 39, 167–177. [Google Scholar] [CrossRef][Green Version]
- Zagaynov, G.I.; Goman, M.G. Bifurcation analysis of critical aircraft flight regimes. In Proceedings of the 14th Congress of ICAS Paper, Toulouse, France, 9–14 September 1984; p. 84-4. [Google Scholar]
- Jahnke, C.C.; Culick, F.E.C. Application of bifurcation theory to the high-angle-of-attack dynamics of the F-14. J. Aircr. 1994, 31, 26–34. [Google Scholar] [CrossRef]
- Lowenberg, M.; Lowenberg, M. Bifurcation analysis as a tool for post-departure stability enhancement. In Proceedings of the 22nd Atmospheric Flight Mechanics Conference, New Orleans, LA, USA, 11–13 August 1997; p. 3716. [Google Scholar]
- Guicheteau, P. Bifurcation theory: A tool for nonlinear flight dynamics. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 356, 2181–2201. [Google Scholar] [CrossRef]
- Planeaux, J. Bifurcation analysis of a model fighter aircraft with control augmentation. In Proceedings of the 17th Atmospheric Flight Mechanics Conference, Portland, OR, USA, 20–22 August 1990; p. 2836. [Google Scholar]
- Avanzini, G.; Matteis, G.D. Bifurcation analysis of a highly augmented aircraft model. J. Guid. Control Dyn. 1997, 20, 754–759. [Google Scholar] [CrossRef]
- Goman, M.; Khramtsovsky, A.; Goman, M.; Khramtsovsky, A. Global stability analysis of nonlinear aircraft dynamics. In Proceedings of the 22nd Atmospheric Flight Mechanics Conference, New Orleans, LA, USA, 11–13 August 1997; p. 3721. [Google Scholar]
- Littleboy, D.; Smith, P. Bifurcation analysis of a high incidence aircraft with nonlinear dynamic inversion control. In Proceedings of the 22nd Atmospheric Flight Mechanics Conference, New Orleans, LA, USA, 11–13 August 1997; p. 3717. [Google Scholar]
- Garrard, W.L. Suboptimal feedback control for nonlinear systems. Automatica 1972, 8, 219–221. [Google Scholar] [CrossRef]
- Sannomiya, N.; Itakura, H. A method for suboptimal design of nonlinear feedback systems. Automatica 1971, 7, 703–712. [Google Scholar]
- Bras, M.; Vale, J.; Lau, F.; Suleman, A. Flight dynamics and control of a vertical tailless aircraft. J. Aeronaut. Aerosp. Eng. 2013, 2, 1–10. [Google Scholar]
- Morris, C.; Allison, D.; Sultan, C.; Schetz, J.; Kapania, R. Towards flying qualities constraints in the multidisciplinary design optimization of a supersonic tailless aircraft. In Proceedings of the 12th AIAA Aviation Technology, Integration, and Operations (ATIO) Conference and 14th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Indianapolis, IN, USA, 17–19 September 2012; p. 5517. [Google Scholar]
- Finck, R.D. USAF Stability and Control DATCOM, AFWAL-TR-83-3048; McDonnel Douglas Corporation: Long Beach, CA, USA, 1978. [Google Scholar]
- Goetzendorf-Grabowski, T.; Antoniewski, T. Three surface aircraft (TSA) configuration–flying qualities evaluation. Aircr. Eng. Aerosp. Technol. Int. J. 2016, 88, 277–284. [Google Scholar] [CrossRef]
- Goetzendorf-Grabowski, T.; Figat, M. Aerodynamic and stability analysis of personal vehicle in tandem-wing configuration. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2017, 231, 2146–2162. [Google Scholar] [CrossRef]
- Mader, C.A.; Martins, J.R. Stability-constrained aerodynamic shape optimization of flying wings. J. Aircr. 2013, 50, 1431–1449. [Google Scholar] [CrossRef]
- National Research Council. Low-Altitude Wind Shear and Its Hazard to Aviation; National Academies Press: Washington, DC, USA, 1983. [Google Scholar]
- Moser, W. Ted Fujita, Chicago’s Mr. Tornado, and The Super Outbreak of 1974. Online Chicago Magazine. Available online: https://www.chicagomag.com/city-life/april-2011/ted-fujita-chicagos-mr-tornado/ (accessed on 28 April 2011).
- Miele, A.; Wang, T.; Melvin, W.W. Guidance strategies for near-optimum take-off performance in a windshear. J. Optim. Theory Appl. 1986, 50, 1–47. [Google Scholar] [CrossRef]
- Bryson, A.E.; Zhao, Y. Feedback control for penetrating a downburst. In Proceedings of the Guidance, Navigation and Control Conference, Monterey, CA, USA, 17–19 August 1987; p. 2343. [Google Scholar]
- Leitmann, G.; Pandey, S. Aircraft control for flight in an uncertain environment: Takeoff in windshear. J. Optim. Theory Appl. 1991, 70, 25–55. [Google Scholar] [CrossRef]
- Seube, N.; Moitie, R.; Leitmann, G. Aircraft take-off in windshear: A viability approach. In Dynamical Systems and Control; CRC Press: Boca Raton, FL, USA, 2004; pp. 139–156. [Google Scholar]
- Chu, P.; Bryson, A., Jr. Control of aircraft landing approach in wind shear. In Proceedings of the 25th AIAA Aerospace Sciences Meeting, Reno, NV, USA, 24–26 March 1987; p. 632. [Google Scholar]
- Martynov, K.; Botkin, N.; Turova, V.; Diepolder, J. Real-time control of aircraft take-off in wind shear. Part I: Aircraft model and control schemes. In Proceedings of the IEEE 2017 25th Mediterranean Conference on Control and Automation (MED), Valletta, Malta, 3–6 July 2017; pp. 277–284. [Google Scholar]
- Avrenli, K.A.; Dempsey, B.J. A kinematic methodology to optimize the landing trajectory for the Boeing 737 jet undergoing total loss of thrust. J. Transp. Saf. Secur. 2017, 9, 82–104. [Google Scholar] [CrossRef]
- Nguyen, N.; Krishnakumar, K.; Kaneshige, J.; Nespeca, P. Flight dynamics and hybrid adaptive control of damaged aircraft. J. Guid. Control Dyn. 2008, 31, 751–764. [Google Scholar] [CrossRef]
- Dat, N.T.; Son, T.N.; Tra, D.A. Development of a flight dynamics model for fixed wing aircraft. In Proceedings of the 10th International Conference on Computer Modeling and Simulation, Sydney, Australia, 8–10 January 2018; pp. 202–205. [Google Scholar]
- Shah, G.; Hill, M. Flight dynamics modeling and simulation of a damaged transport aircraft. In Proceedings of the AIAA Modeling and Simulation Technologies Conference, Minneapolis, MN, USA, 13–16 August 2012; p. 4632. [Google Scholar]
- Sharma, U.; Nadda, S. Analysis and Control of Civilian Aircraft Model Using Simulink [PECS] 2020. In Modeling, Simulation and Optimization: Proceedings of CoMSO 2020; Springer: Singapore, 2021; pp. 613–622. [Google Scholar]
- Ahmad, M.; Hussain, Z.L.; Shah, S.I.A.; Shams, T.A. Estimation of stability parameters for wide body aircraft using computational techniques. Appl. Sci. 2021, 11, 2087. [Google Scholar] [CrossRef]
- Shams, T.A.; Shah, S.I.A.; Shahzad, A.; Javed, A.; Mehmood, K. Experimental investigation of propeller induced flow on flying wing micro aerial vehicle for improved 6DOF modeling. IEEE Access 2020, 8, 179626–179647. [Google Scholar] [CrossRef]
- Siddiqui, B.A.; Khushnood, A. Improving USAF DATCOM predictions of aircraft nonlinear aerodynamics. In Canadian Aeronautics and Space Institute AERO’09 Conference, Aerodynamics Symposium; Canadian Aeronautics and Space Institute: Kanata, ON, Canada, 2009; pp. 1–11. [Google Scholar]
- Shams, T.A.; Shah, S.I.A.; Ahmad, M.A. Study of Low Reynolds Number Aerodynamics for Low Aspect Ratio MAV Wing. In Proceedings of the 2018 IEEE 21st International Multi-Topic Conference (INMIC), Karachi, Pakistan, 1–2 November 2018; pp. 1–8. [Google Scholar]
- Tumse, S.; Tasci, M.O.; Karasu, I.; Sahin, B. Effect of ground on flow characteristics and aerodynamic performance of a non-slender delta wing. Aerosp. Sci. Technol. 2021, 110, 106475. [Google Scholar] [CrossRef]
- Zhang, X.; Zerihan, J. Off-surface aerodynamic measurements of a wing in ground effect. J. Aircr. 2003, 40, 716–725. [Google Scholar] [CrossRef]
- Tumse, S.; Karasu, I.; Sahin, B. Experimental investigation of ground effect on the vortical flow structure of a 40° swept delta wing. J. Aerosp. Eng. 2022, 35, 04022055. [Google Scholar] [CrossRef]
- Qu, Q.; Zuo, P.; Wang, W.; Liu, P.; Agarwal, R.K. Numerical investigation of the aerodynamics of an airfoil in mutational ground effect. AIAA J. 2015, 53, 3144–3154. [Google Scholar] [CrossRef]
- Tasci, M.O.; Pektas, M.C.; Tumse, S.; Karasu, I.; Sahin, B.; Akilli, H. The impact of the pitching motion on the structure of the vortical flow over a slender delta wing under sideslip angle. J. Vis. 2021, 24, 437–442. [Google Scholar] [CrossRef]
- Nuhait, A.O.; Zedan, M.F. Numerical simulation of unsteady flow induced by a flat plate moving near ground. J. Aircr. 1993, 30, 611–617. [Google Scholar] [CrossRef]
- Coesa, U.S. Standard Atmosphere, 1976; US Government Printing Office: Washington, DC, USA, 1976; Volume 40, p. 56. [Google Scholar]
- Mohamed, A.; Massey, K.; Watkins, S.; Clothier, R. The attitude control of fixed-wing MAVS in turbulent environments. Prog. Aerosp. Sci. 2014, 66, 37–48. [Google Scholar] [CrossRef]
- Jones, T. Statistical Data for the Boeing-747-400 Aircraft in Commercial Operations. Report No DOT/FAA/AR-04/44, Published by US Department of Transportation, Federal Aviation Administration, Office of Aviation Research. 2005. Available online: https://www.tc.faa.gov/its/worldpac/techrpt/ar04-44.pdf (accessed on 26 August 2020).
- Balatti, D.; Khodaparast, H.H.; Friswell, M.I.; Manolesos, M.; Castrichini, A. Aircraft turbulence and gust identification using simulated in-flight data. Aerosp. Sci. Technol. 2021, 115, 106805. [Google Scholar] [CrossRef]
- Wu, Z.; Cao, Y.; Ismail, M. Gust loads on aircraft. Aeronaut. J. 2019, 123, 1216–1274. [Google Scholar] [CrossRef]
- Liepmann, H.W. On the application of statistical concepts to the buffeting problem. J. Aeronaut. Sci. 1952, 19, 793–800. [Google Scholar] [CrossRef]
- De Karman, T.; Howarth, L. On the statistical theory of isotropic turbulence. Proc. R. Soc. Lond. Ser. A-Math. Phys. Sci. 1938, 164, 192–215. [Google Scholar] [CrossRef]
- Hakim, T.M.I.; Arifianto, O. Implementation of Dryden continuous turbulence model into simulink for LSA-02 flight test simulation. In Journal of Physics: Conference Series; IOP Publishing: Medan, Indonesia, 2018; Volume 1005, p. 012017. [Google Scholar]
- Dongli, M. An improvement of the digital simulation method for atmospheric turbulence. J. Beijing Univ. Aeronaut. Astronaut. 1990, 3, 57–63. [Google Scholar]
- Jing, P.; Chang, J.J. Research on the Numerical Simulation of Aircraft Carrier Air Wake. J. Beijing Univ. Aeronaut. Astronaut. 2000, 26, 340–343. [Google Scholar]
- Etkin, B. Turbulent wind and its effect on flight. J. Aircr. 1981, 18, 327–345. [Google Scholar] [CrossRef]
- Dryden, H.L. A review of the statistical theory of turbulence. Q. Appl. Math. 1943, 1, 7–42. [Google Scholar] [CrossRef]
- Xiao, Y. Digital generation of two-dimensional field of turbulence for flight simulation. Chin. J. Aeronaut. 1990, 3, 239–245. [Google Scholar]
- Beal, T.R. Digital simulation of atmospheric turbulence for Dryden and von Karman models. J. Guid. Control Dyn. 1993, 16, 132–138. [Google Scholar] [CrossRef]
- MIL-STD-1797A; Fling Qualities of Piloted Aircraft. Military Standard 1797A; Government Printing Office: Washington, DC, USA, 1990; p. 678.
- Nelson, R.C. Flight Stability and Automatic Control; WCB/McGraw Hill: New York, NY, USA, 1998; Volume 2. [Google Scholar]
- Roskam, J. Airplane Flight Dynamics and Automatic Flight Controls; DAR Corporation: Lawrence, KS, USA, 1998. [Google Scholar]
- Lambrechts, P.F.; Terlouw, J.C.; Doorn, J.T.M. Robust Flight Control Design Challenge Problem Formulation and Manual: The Research Civil Aircraft Model (RCAM). Garteur/TP-088-3. 1996. Available online: https://garteur.org/wp-content/reports/FM/FM_AG-08_TP-088-3.pdf (accessed on 26 August 2020).
- Irving, J.P. Robust Flight Control in a Computational Aircraft Control Engineering Environment. Garteur FM(AG08)/TP-088-2. 1995. Available online: https://garteur.org/wp-content/reports/FM/FM_AG-08_TP-088-2.pdf (accessed on 26 August 2020).

| Input/Output | Definition | Remarks |
|---|---|---|
| U(1) | Aileron deflection for roll control | Input |
| U(2) | Elevator deflection for pitch control | Input |
| U(3) | Rudder deflection for yaw control | Input |
| U(4), U(5) | Throttle controls for engines | Input |
| du/dt, dv/dt, dw/dt | Rate of change of linear velocities | Output |
| dϕ/dt, dθ/dt, dψ/dt | Rate of change of Euler velocities | Output |
| Parameter | Approach | Cruise | Units | ||
|---|---|---|---|---|---|
| W | 564,000 (255,826) | 636,636 (288,773) | Ib (kg) | ||
| S | 5500 (~510.9) | 5500 (~510.9) | ft2 (m2) | ||
| c | 27.3 (8.3) | 27.3 (8.3) | ft (m) | ||
| cg | 0.25 | 0.25 | |||
| Ixx | 13,700,000 (18,574,705) | 18,200,000(24,675,886) | Slug-ft2 (kg-m2) | ||
| Iyy | 30,500,000 (41,352,447) | 33,100,000 (44,877,574) | Slug-ft2 (kg-m2) | ||
| Izz | 43,100,000 (58,435,753) | 49,700,000 (67,384,152) | Slug-ft2 (kg-m2) | ||
| Ixz | 830,000 (1,125,328) | 970,000 (1,315,143) | Slug-ft2 (kg-m2) | ||
| Longitudinal Coefficients | Lateral Coefficients | ||||
| Coeff | Approach | Cruise | Coeff | Approach | Cruise |
| CL1 | 1.76 | 0.52 | Clb | −0.281 | −0.095 |
| CD1 | 0.263 | 0.045 | Clp | −0.502 | −0.32 |
| CM1 | 0 | 0 | Clr | 0.195 | 0.2 |
| CD0 | 0.0751 | 0.0305 | Cyb | −1.08 | −0.9 |
| Cdu | 0 | 0.22 | Cyp | 0 | 0 |
| Cda | 1.13 | 0.5 | Cyr | 0 | 0 |
| CL0 | 0.92 | 0.29 | Cnb | 0.184 | 0.21 |
| CLu | −0.22 | −0.23 | Cnp | −0.222 | 0.02 |
| CLa | 5.67 | 5.5 | Cnr | −0.36 | −0.33 |
| CLa. | 6.7 | 8 | Clda | 0.053 | 0.014 |
| CLq | 5.65 | 7.8 | Clδr | 0 | 0.005 |
| Cmu | 0.071 | −0.09 | Cyδa | 0 | 0 |
| Cma | −1.45 | −1.6 | Cyδr | 0.179 | 0.06 |
| Cma. | −3.3 | −9 | Cnδa | 0.0083 | −0.0028 |
| Cmq | −21.4 | −25.5 | Cnδr | −0.113 | −0.095 |
| CDδe | 0 | 0 | |||
| CLδe | 0.36 | 0.3 | |||
| Cmδe | −1.4 | −1.2 | |||
| Parameter | Units | Approach | Cruise |
|---|---|---|---|
| H | ft (m) | 0 | 40,000 (12,192) |
| M | - | 0.198 | 0.9 |
| TAS | ft/s (m/s) | 221.0 (67.4) | 870.91 (265.24) |
| ρ ρ | Slug/ft3 (kg/m3) | 0.0023769 (4.6 × 10−6) | 0.0005873 (1.14 × 10−6) |
| Q | Ib/ft2 (N/m-) | 58.0 (2777) | 222.72 (10,664) |
| α | Deg | 8.5 | 2.4 |
| Parameter | Literature Value [61] | Present Work | Error |
|---|---|---|---|
| Approach Velocity | 221 ft/s | 225 ft/s | 1.8% |
| Cruise Velocity | 871 ft/s | 882 ft/s | 1.2% |
| Time Period (Phugoid) | 45.9 s | 43.5 s | 4.3% |
| Time Period (SP) | 9.13 s | 9.6 s | 5.1% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehmood, K.; Ali Shah, S.I.; Ali Shams, T.; Mumtaz Qadri, M.N.; Khan, T.A.; Kukulka, D. Flight Dynamic Characteristics of Wide-Body Aircraft with Wind Gust and Turbulence. Fluids 2023, 8, 320. https://doi.org/10.3390/fluids8120320
Mehmood K, Ali Shah SI, Ali Shams T, Mumtaz Qadri MN, Khan TA, Kukulka D. Flight Dynamic Characteristics of Wide-Body Aircraft with Wind Gust and Turbulence. Fluids. 2023; 8(12):320. https://doi.org/10.3390/fluids8120320
Chicago/Turabian StyleMehmood, Kashif, Syed Irtiza Ali Shah, Taimur Ali Shams, Muhammad Nafees Mumtaz Qadri, Tariq Amin Khan, and David Kukulka. 2023. "Flight Dynamic Characteristics of Wide-Body Aircraft with Wind Gust and Turbulence" Fluids 8, no. 12: 320. https://doi.org/10.3390/fluids8120320
APA StyleMehmood, K., Ali Shah, S. I., Ali Shams, T., Mumtaz Qadri, M. N., Khan, T. A., & Kukulka, D. (2023). Flight Dynamic Characteristics of Wide-Body Aircraft with Wind Gust and Turbulence. Fluids, 8(12), 320. https://doi.org/10.3390/fluids8120320









