Surface Roughness in RANS Applied to Aircraft Ice Accretion Simulation: A Review
Abstract
1. Introduction
2. Roughness Geometrical Characterization in Aerodynamics
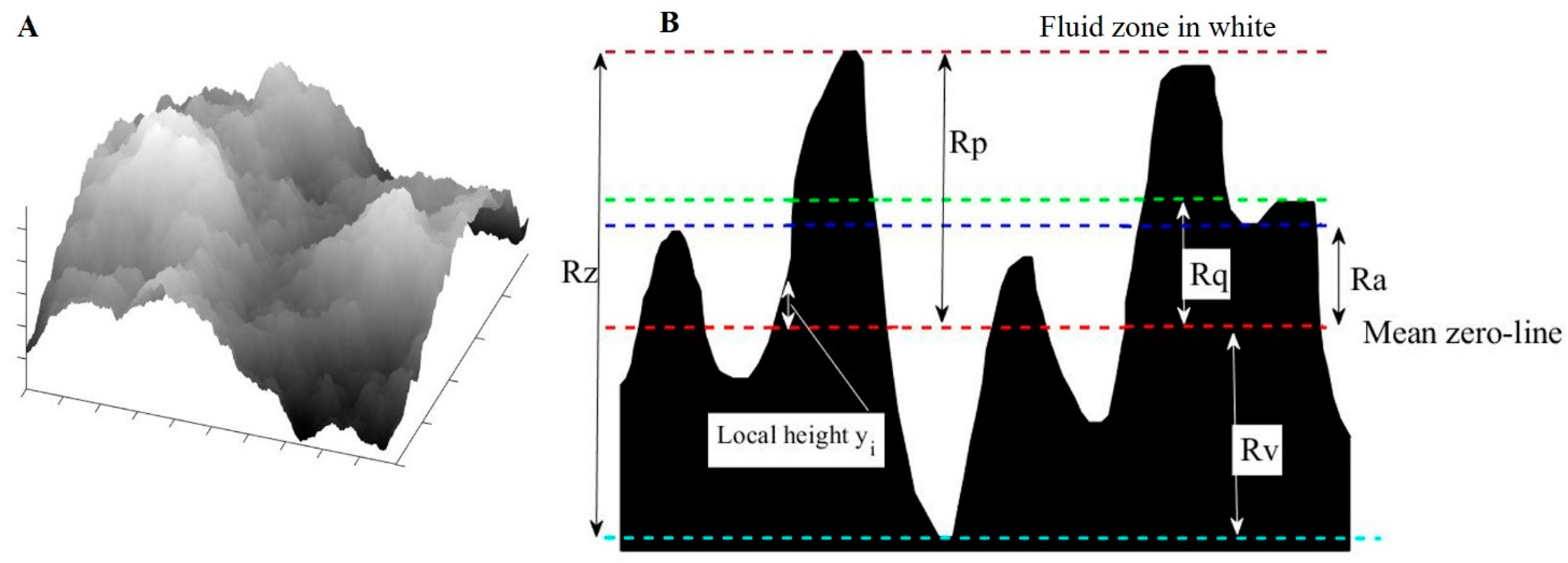
2.1. Geometrical Parameters
- Ra, the arithmetic mean height;
- Rq, the root mean square height;
- Rv, the maximum valley depth;
- Rp, the maximum peak height;
- Rz, the maximum peak to valley height;
- Sk, the skewness;
- Ku, the kurtosis.
2.2. The Equivalent Sand Grain Roughness (ESGR)
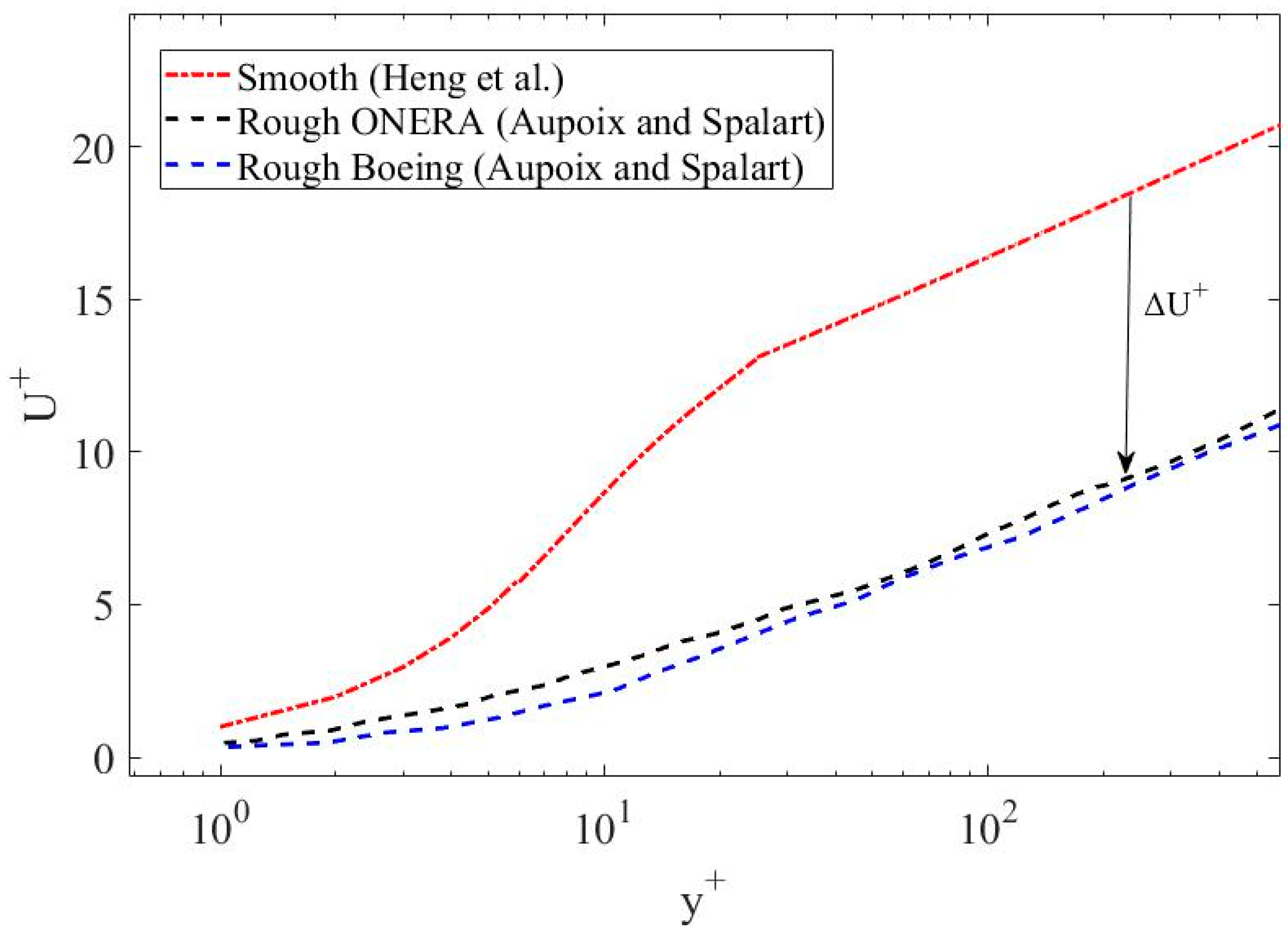
3. Roughness Regimes and Rough Turbulence Models
3.1. The Rough Flow Regimes
- The hydraulically smooth regime if
- The transitionally rough regime if
- The fully rough regime if
- Roughness elements small compared to the viscous sublayer thickness (hydraulically smooth);
- Roughness elements in the same order of thickness as the viscous sublayer thickness (transitionally rough); and
- Nikuradse: and
- Ligrani and Moffat: and
- Langelandsvik et al.: and
- Schultz and Flack: and
3.2. RANS Implementations to Account for Roughness
4. The Specific Case of Aircraft Icing
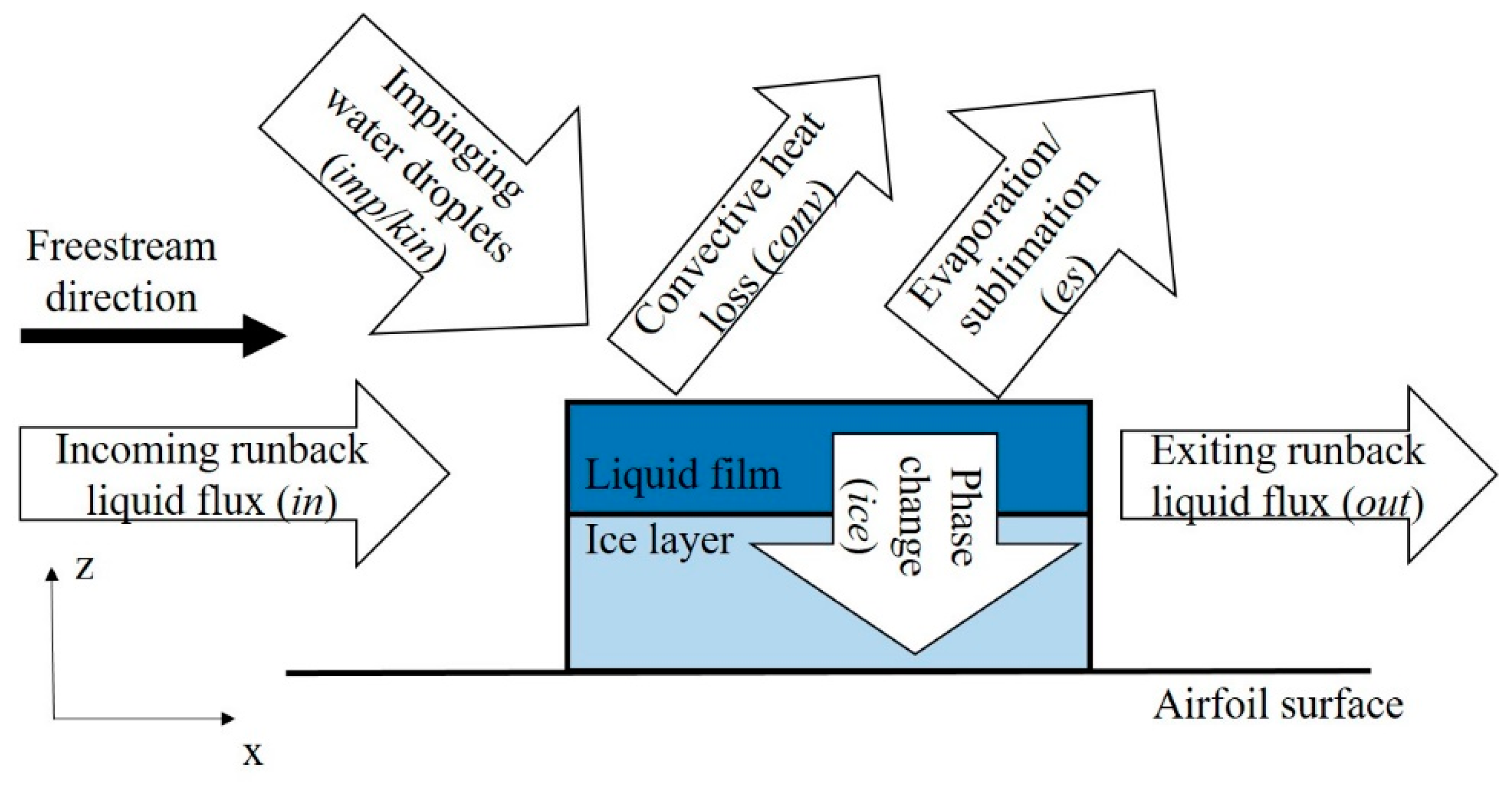
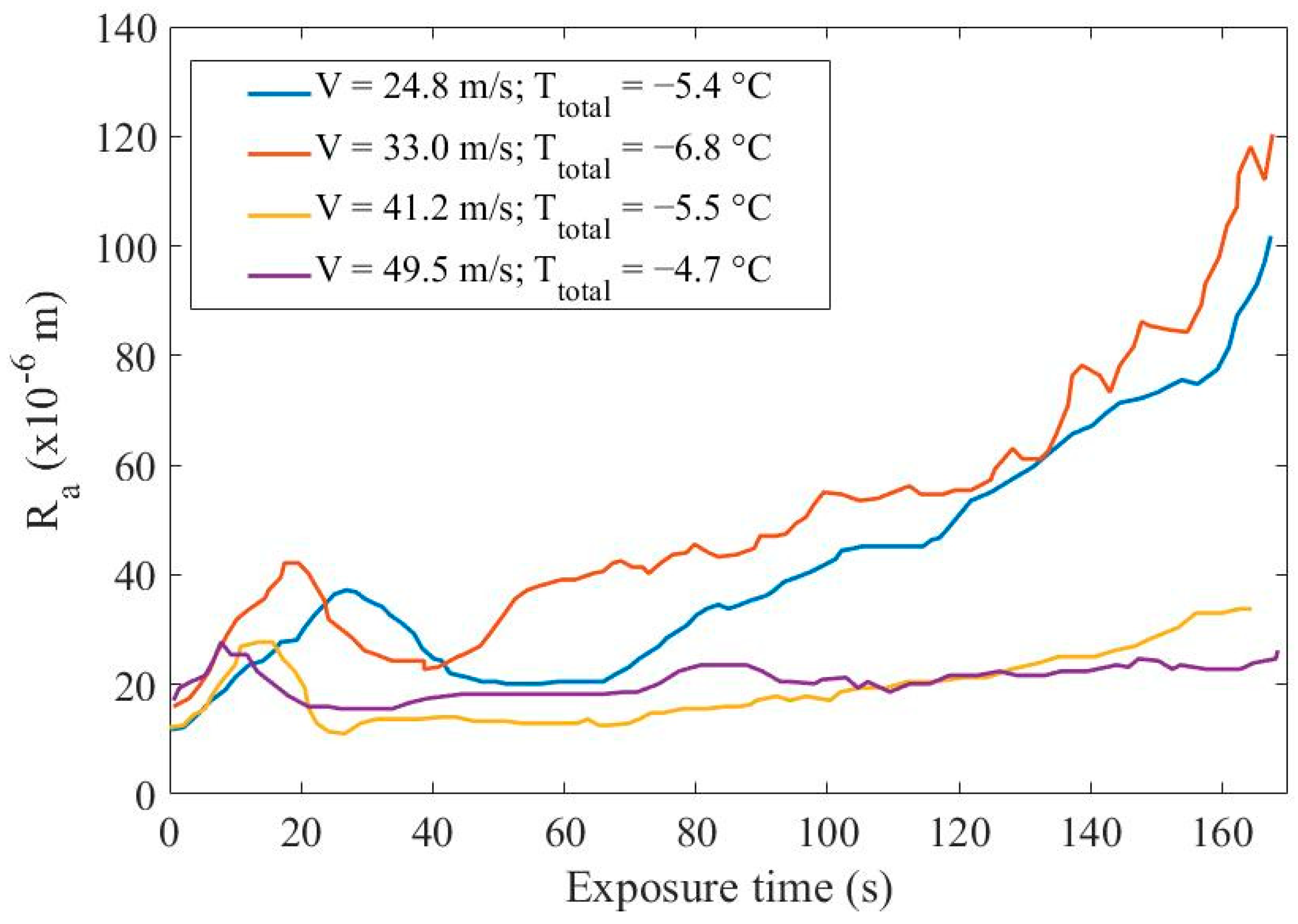
The Ice Accretion Process: A Roughness-Dependent Phenomenon
- The evaporation/sublimation mass and energy variables depend on the heat transfer coefficient [99];
- The convective heat loss is a function of the heat transfer coefficient;
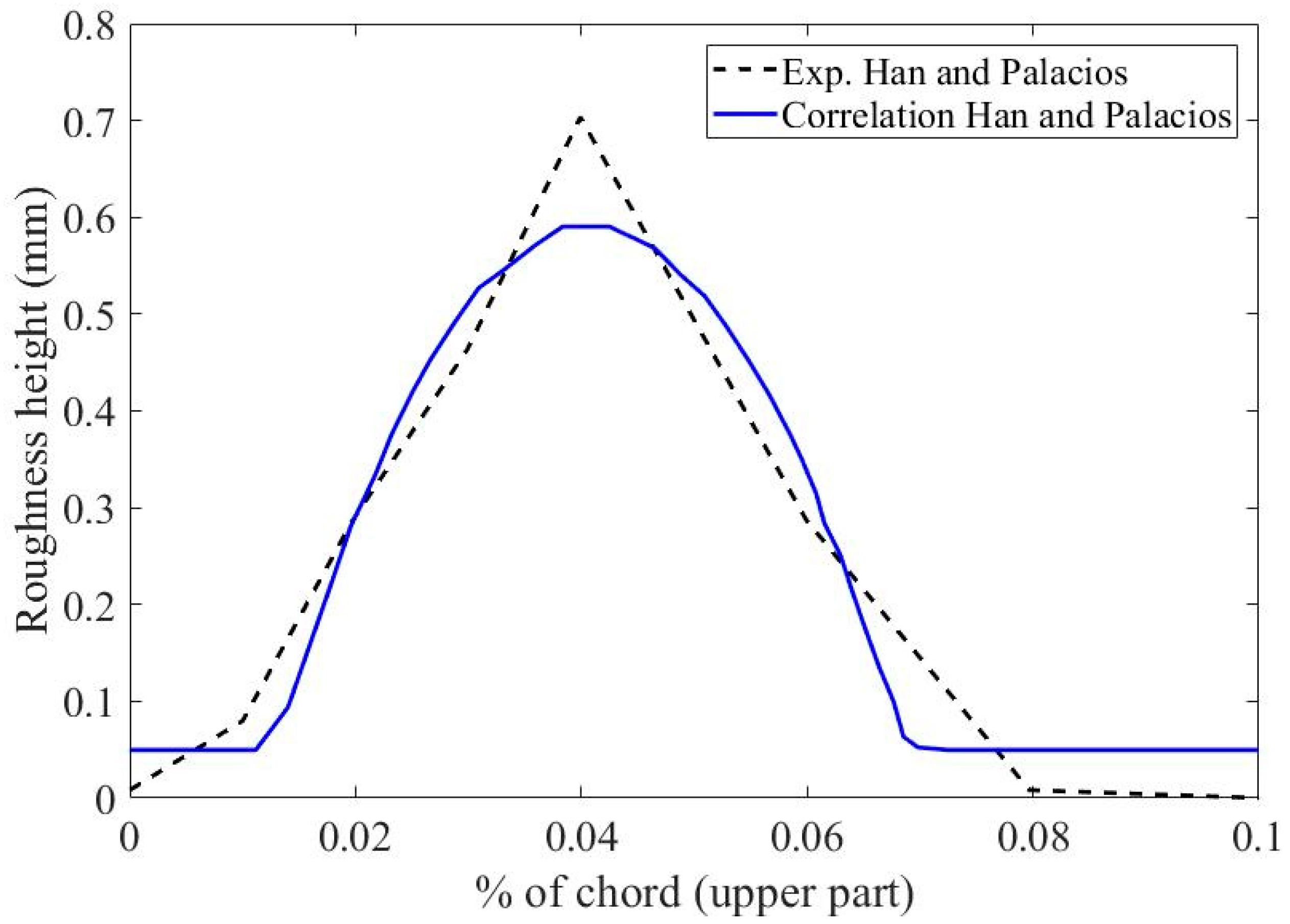
5. Empirical Roughness Correlations in Ice Accretion Simulations
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Gao, H.; Li, X.; Nezhad, A.H.; Behshad, A. Numerical simulation of the flow in pipes with numerical models. Struct. Eng. Mech. 2022, 81, 523–527. [Google Scholar] [CrossRef]
- Marquet, O.; Leontini, J.S.; Zhao, J.; Thompson, M.C. Hysteresis of two-dimensional flows around a NACA0012 airfoil at Re=5000 and linear analyses of their mean flow. Int. J. Heat Fluid Flow 2022, 94, 108920. [Google Scholar] [CrossRef]
- Howell, J.; Forbes, D.; Passmore, M.; Page, G. The Effect of a Sheared Crosswind Flow on Car Aerodynamics. SAE Int. J. Passeng. Cars-Mech. Systems 2017, 10, 278–285. [Google Scholar] [CrossRef]
- Jafari, M.; Alipour, A. Review of approaches, opportunities, and future directions for improving aerodynamics of tall buildings with smart facades. Sustain. Cities Soc. 2021, 72, 102979. [Google Scholar] [CrossRef]
- Kaya, M.N.; Kok, A.R.; Kurt, H. Comparison of aerodynamic performances of various airfoils from different airfoil families using CFD. Wind. Struct. Int. J. 2021, 32, 239–248. [Google Scholar] [CrossRef]
- Omoware, W.D.; Maheri, A.; Azimov, U. Aerodynamic analysis of flapping-pitching flat plates. In Proceedings of the 3rd International Symposium on Environmental Friendly Energies and Applications (EFEA), Paris, France, 19–21 November 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Bons, J.P. A review of surface roughness effects in gas turbines. J. Turbomach. 2010, 132, 021004. [Google Scholar] [CrossRef]
- Kontogiannis, A.; Prakash, A.; Laurendeau, E.; Moens, F. Sensitivity of Glaze Ice Accretion and Iced Aerodynamics Prediction to Roughness. In Proceedings of the 26th Annual Conference of the Computational Fluid Dynamics Society of Canada, Winnipeg, MB, Canada, 10–12 June 2018. [Google Scholar]
- Hosni, M.H.; Coleman, H.W.; Garner, J.W.; Taylor, R.P. Roughness element shape effects on heat transfer and skin friction in rough-wall turbulent boundary layers. Int. J. Heat Mass Transf. 1993, 36, 147–153. [Google Scholar] [CrossRef]
- Kadivar, M.; Tormey, D.; McGranaghan, G. A review on turbulent flow over rough surfaces: Fundamentals and theories. Int. J. Thermofluids 2021, 10, 100077. [Google Scholar] [CrossRef]
- Suga, K.; Craft, T.J.; Iacovides, H. An analytical wall-function for turbulent flows and heat transfer over rough walls. Int. J. Heat Fluid Flow 2006, 27, 852–866. [Google Scholar] [CrossRef]
- Schlichting, H. Experimental Investigation of the Problem of Surface Roughness; NACA-TM-823; National Advisory Commitee for Aeronautics: Edwards, CA, USA, 1937. [Google Scholar]
- Botros, K.K. Experimental Investigation into the Relationship between the Roughness Height in Use with Nikuradse or Colebrook Roughness Functions and the Internal Wall Roughness Profile for Commercial Steel Pipes. J. Fluids Eng. Trans. ASME 2016, 138, 081202. [Google Scholar] [CrossRef]
- Javanappa, S.K.; Narasimhamurthy, V.D. DNS of plane Couette flow with surface roughness. Int. J. Adv. Eng. Sci. Appl. Math. 2019, 11, 288–300. [Google Scholar] [CrossRef]
- Forooghi, P.; Stroh, A.; Schlatter, P.; Frohnapfel, B. Direct numerical simulation of flow over dissimilar, randomly distributed roughness elements: A systematic study on the effect of surface morphology on turbulence. Phys. Rev. Fluids 2018, 3, 044605. [Google Scholar] [CrossRef]
- Rao, V.N.; Jefferson-Loveday, R.; Tucker, P.G.; Lardeau, S. Large eddy simulations in turbines: Influence of roughness and free-stream turbulence. Flow Turbul. Combust. 2014, 92, 543–561. [Google Scholar] [CrossRef]
- De Marchis, M. Large eddy simulations of roughened channel flows: Estimation of the energy losses using the slope of the roughness. Comput. Fluids 2016, 140, 148–157. [Google Scholar] [CrossRef]
- Blazek, J. Computational Fluid Dynamics: Principles and Applications, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Spalart, P.; Allmaras, S. A one-equation turbulence model for aerodynamic flows. In 30th Aerospace Sciences Meeting and Exhibit; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1992. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Aupoix, B.; Spalart, P.R. Extensions of the Spalart–Allmaras turbulence model to account for wall roughness. Int. J. Heat Fluid Flow 2003, 24, 454–462. [Google Scholar] [CrossRef]
- Chedevergne, F. A double-averaged Navier-Stokes k -ω turbulence model for wall flows over rough surfaces with heat transfer. J. Turbul. 2021, 22, 713–734. [Google Scholar] [CrossRef]
- Morency, F.; Beaugendre, H. Comparison of turbulent Prandtl number correction models for the Stanton evaluation over rough surfaces. Int. J. Comput. Fluid Dyn. 2020, 34, 278–298. [Google Scholar] [CrossRef]
- Chedevergne, F. Analytical wall function including roughness corrections. Int. J. Heat Fluid Flow 2018, 73, 258–269. [Google Scholar] [CrossRef]
- Aupoix, B. Improved heat transfer predictions on rough surfaces. Int. J. Heat Fluid Flow 2015, 56, 160–171. [Google Scholar] [CrossRef]
- Hanson, D.R.; Kinzel, M.P.; McClain, S.T. Validation of the discrete element roughness method for predicting heat transfer on rough surfaces. Int. J. Heat Mass Transf. 2019, 136, 1217–1232. [Google Scholar] [CrossRef]
- Hanson, D.R.; Kinzel, M.P. Application of the discrete element roughness method to ice accretion geometries. In Proceedings of the 46th AIAA Fluid Dynamics Conference, Washington, DC, USA, 13–17 June 2016; American Institute of Aeronautics and Astronautics Inc, AIAA: Las Vegas, NV, USA, 2016. [Google Scholar]
- Aupoix, B. Revisiting the Discrete Element Method for Predictions of Flows over Rough Surfaces. J. Fluids Eng. Trans. ASME 2016, 138, 031205. [Google Scholar] [CrossRef]
- Chedevergne, F. Modeling rough walls from surface topography to double averaged Navier-Stokes computation. J. Turbul. 2023, 24, 36–56. [Google Scholar] [CrossRef]
- Jayabarathi, S.B.; Ratnam, M.M. Comparison of Correlation between 3D Surface Roughness and Laser Speckle Pattern for Experimental Setup Using He-Ne as Laser Source and Laser Pointer as Laser Source. Sensors 2022, 2, 6003. [Google Scholar] [CrossRef] [PubMed]
- Mejia-Alvarez, R.; Christensen, K.T. Wall-parallel stereo particle-image velocimetry measurements in the roughness sublayer of turbulent flow overlying highly irregular roughness. Phys. Fluids 2013, 25, 115109. [Google Scholar] [CrossRef]
- Kuwata, Y.; Yamamoto, Y.; Tabata, S.; Suga, K. Scaling of the roughness effects in turbulent flows over systematically-varied irregular rough surfaces. Int. J. Heat Fluid Flow 2023, 101, 109130. [Google Scholar] [CrossRef]
- Leach, R. Characterisation of Areal Surface Texture, 1st ed.; Leach, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; p. 353. [Google Scholar] [CrossRef]
- Nikuradse, J. Laws of flow in rough pipes. VDI Forschungsheft 1933, 4, 63. [Google Scholar]
- Dirling, R. A method for computing roughwall heat transfer rates on reentry nosetips. In Proceedings of the 8th Thermophysics Conference, Palm Springs, CA, USA, 16–18 July 1973. [Google Scholar] [CrossRef]
- Sigal, A.; Danberg, J.E. New correlation of roughness density effect on the turbulent boundary layer. AIAA J. 1990, 28, 554–556. [Google Scholar] [CrossRef]
- McClain, S.T.; Vargas, M.; Jen-Ching, T. Characterization of Ice Roughness Variations in Scaled Glaze Icing Conditions. In Proceedings of the 8th AIAA Atmospheric and Space Environments Conference, Reston, VA, USA, 13–17 June 2016; AIAA—American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2016; p. 14. [Google Scholar]
- Liu, Y.; Hu, H. An experimental investigation on the unsteady heat transfer process over an ice accreting airfoil surface. Int. J. Heat Mass Transf. 2018, 122, 707–718. [Google Scholar] [CrossRef]
- Bourgault-Cote, S.; Docampo-Sánchez, J.; Laurendeau, E. Multi-Layer Ice Accretion Simulations Using a Level-Set Method with B-Spline Representation. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Akbal, O.; Ayan, E.; Murat, C.; Ozgen, S. Flight Ice Shape Prediction with Data Fit Surrogate Models; SAE International: Minneapolis, MN, USA, 2023. [Google Scholar] [CrossRef]
- Radenac, E.; Gaible, H.; Bezard, H.; Reulet, P. IGLOO3D Computations of the Ice Accretion on Swept-Wings of the SUNSET2 Database. In Proceedings of the International Conference on Icing of Aircraft, Engines, and Structures, Minneapolis, MN, USA, 17–21 June 2019; SAE International: Minneapolis, MN, USA, 2019. [Google Scholar] [CrossRef]
- Shannon, T.; McClain, S.T. An Assessment of LEWICE Roughness and Convection Enhancement Models. SAE Int. J. Adv. Curr. Pract. Mobil. 2019, 2, 128–139. [Google Scholar] [CrossRef]
- Fortin, G. Equivalent Sand Grain Roughness Correlation for Aircraft Ice Shape Predictions; SAE International: Minneapolis, MN, USA, 2019. [Google Scholar] [CrossRef]
- Ruff, G.A.; Berkowitz, B.M. Users Manual for the NASA Lewis Ice Accretion Prediction Code (LEWICE); NASA CR-185129; National Aeronautics and Space Administration: Washington, DC, USA, 1990. [Google Scholar]
- Shin, J.; Bond, T.H. Results of an icing test on a NACA 0012 airfoil in the NASA Lewis Icing Research Tunnel. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992. [Google Scholar] [CrossRef]
- Shin, J.; Berkowitz, B.; Chen, H.H.; Cebeci, T. Prediction of ice shapes and their effect on airfoil performance. In Proceedings of the AIAA 29th Aerospace Sciences Meeting, Reno, NV, USA, 7–10 January 1991. [Google Scholar]
- Lavoie, P.; Pena, D.; Hoarau, Y.; Laurendeau, E. Comparison of thermodynamic models for ice accretion on airfoils. Int. J. Numer. Methods Heat Fluid Flow 2018, 28, 1004–1030. [Google Scholar] [CrossRef]
- Hansman, R.; Yamaguchi, K.; Berkowitz, B.; Potapczuk, M. Modeling of Surface Roughness Effects on Glaze Ice Accretion. J. Thermophys. Heat Transf. 1989, 5, 54–60. [Google Scholar] [CrossRef][Green Version]
- Baghel, A.P.; Sotomayor-Zakharov, D.; Knop, I.; Ortwein, H.-P. Detailed Study of Photogrammetry Technique as a Valid Ice Accretion Measurement Method; SAE International: Minneapolis, MN, USA, 2023. [Google Scholar] [CrossRef]
- Han, Y.; Palacios, J. Surface Roughness and Heat Transfer Improved Predictions for Aircraft Ice-Accretion Modeling. AIAA J. 2017, 55, 1318–1331. [Google Scholar] [CrossRef]
- Laurendeau, E.; Bourgault-Cote, S.; Ozcer, I.A.; Hann, R.; Radenac, E.; Pueyo, A. Summary from the 1st AIAA Ice Prediction Workshop. In Proceedings of the AIAA AVIATION 2022 Forum, Chicago, IL, USA, 27 June–1 July 2022. [Google Scholar] [CrossRef]
- Caccia, F.; Guardone, A. Numerical simulations of ice accretion on wind turbine blades: Are performance losses due to ice shape or surface roughness? Wind. Energy Sci. 2023, 8, 341–362. [Google Scholar] [CrossRef]
- Ravenna, R.; Song, S.; Shi, W.; Sant, T.; De Marco Muscat-Fenech, C.; Tezdogan, T.; Demirel, Y.K. CFD analysis of the effect of heterogeneous hull roughness on ship resistance. Ocean. Eng. 2022, 258, 111733. [Google Scholar] [CrossRef]
- Committee, S.E. Surface Texture; SAE International: Warrendale, PA, USA, 2023. [Google Scholar] [CrossRef]
- Leach, R. Introduction to Surface Topography. In Characterisation of Areal Surface Texture; Leach, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 1–13. [Google Scholar] [CrossRef]
- Heldt, E. Measurement of component surface roughness. Qual. Und Zuverlaessigkeit 2006, 51, 80–84. [Google Scholar]
- Todhunter, L.D.; Leach, R.K.; Lawes, S.D.A.; Blateyron, F. Industrial survey of ISO surface texture parameters. CIRP J. Manuf. Sci. Technol. 2017, 19, 84–92. [Google Scholar] [CrossRef]
- Flack, K.A.; Schultz, M.P. Review of Hydraulic Roughness Scales in the Fully Rough Regime. J. Fluids Eng. 2010, 132, 041203. [Google Scholar] [CrossRef]
- Schlichting, H.; Gersten, K. Boundary-Layer Theory, 9th ed.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- van Rij, J.A.; Belnap, B.J.; Ligrani, P.M. Analysis and Experiments on Three-Dimensional, Irregular Surface Roughness. J. Fluids Eng. 2002, 124, 671–677. [Google Scholar] [CrossRef]
- Colebrook, C.F.; White, C.M.; Taylor, G.I. Experiments with fluid friction in roughened pipes. Proc. R. Soc. London. Ser. A-Math. Phys. Sci. 1937, 161, 367–381. [Google Scholar] [CrossRef]
- Bons, J.P. St and cf Augmentation for Real Turbine Roughness with Elevated Freestream Turbulence. J. Turbomach. 2002, 124, 632–644. [Google Scholar] [CrossRef]
- Von Kármán, T. Mechanical Similitude and Turbulence; NACA-TM-611; National Advisory Committee for Aeronautics: Washington, DC, USA, 1931. [Google Scholar]
- Reichardt, H. Vollständige Darstellung der turbulenten Geschwindigkeitsverteilung in glatten Leitungen. ZAMM-J. Appl. Math. Mech./Z. Für Angew. Math. Und Mech. 1951, 31, 208–219. [Google Scholar] [CrossRef]
- Heng, L.; Duo, W.; Hongyi, X. Improved Law-of-the-Wall Model for Turbulent Boundary Layer in Engineering. AIAA J. 2020, 58, 3308–3319. [Google Scholar] [CrossRef]
- Ghanadi, F.; Djenidi, L. Study of a rough-wall turbulent boundary layer under pressure gradient. J. Fluid Mech. 2022, 938, A17. [Google Scholar] [CrossRef]
- Ligrani, P.M.; Moffat, R.J. Structure of transitionally rough and fully rough turbulent boundary layers. J. Fluid Mech. 1986, 162, 69–98. [Google Scholar] [CrossRef]
- Langelandsvik, L.I.; Kunkel, G.; Smits, A. Flow in a commercial steel pipe. J. Fluid Mech. 2008, 595, 323–339. [Google Scholar] [CrossRef]
- Schultz, M.P.; Flack, K.A. The rough-wall turbulent boundary layer from the hydraulically smooth to the fully rough regime. J. Fluid Mech. 2007, 580, 381–405. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modeling for CFD; DCW Industries: La Cañada Flintridge, CA, USA, 2006. [Google Scholar]
- Patel, V.C.; Yoon, J.Y. Application of Turbulence Models to Separated Flow Over Rough Surfaces. J. Fluids Eng. 1995, 117, 234–241. [Google Scholar] [CrossRef]
- Hellsten, A.; Laine, S. Extension of the k-omega-SST turbulence model for flows over rough surfaces. In Proceedings of the AIAA 22nd Atmospheric Flight Mechanics Conference, New Orleans, LA, USA, 11–13 August 1997. [Google Scholar]
- Knopp, T.; Eisfeld, B.; Calvo, J.B. A new extension for k–ω turbulence models to account for wall roughness. Int. J. Heat Fluid Flow 2009, 30, 54–65. [Google Scholar] [CrossRef]
- Durbin, P.A.; Medic, G.; Seo, J.M.; Eaton, J.K.; Song, S. Rough wall modification of two-layer k-ε. Trans. ASME J. Fluids Eng. 2001, 123, 16–21. [Google Scholar] [CrossRef]
- Kays, W.M.; Crawford, M.E. Convective Heat and Mass Transfer; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
- Grigson, C. Drag Losses of New Ships Caused by Hull Finish. J. Ship Res. 1992, 36, 182–196. [Google Scholar] [CrossRef]
- Radenac, E.; Kontogiannis, A.; Bayeux, C.; Villedieu, P. An extended rough-wall model for an integral boundary layer model intended for ice accretion calculations. In Proceedings of the 2018 Atmospheric and Space Environments Conference, AIAA, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar] [CrossRef]
- Orych, M.; Werner, S.; Larsson, L. Roughness effect modelling for wall resolved RANS—Comparison of methods for marine hydrodynamics. Ocean. Eng. 2022, 266, 112778. [Google Scholar] [CrossRef]
- Andersson, J.; Oliveira, D.R.; Yeginbayeva, I.; Leer-Andersen, M.; Bensow, R.E. Review and comparison of methods to model ship hull roughness. Appl. Ocean. Res. 2020, 99, 102119. [Google Scholar] [CrossRef]
- Ligrani, P.M.; Moffat, R.J.; Kays, W.M. The Thermal and Hydrodynamic Behavior of Thick, Rough-Wall, Turbulent Boundary Layers; Stanford University: Stanford, CA, USA, 1979. [Google Scholar]
- Dipprey, D.F.; Sabersky, R.H. Heat and momentum transfer in smooth and rough tubes at various prandtl numbers. Int. J. Heat Mass Transf. 1963, 6, 329–353. [Google Scholar] [CrossRef]
- Owen, P.R.; Thomson, W.R. Heat transfer across rough surfaces. J. Fluid Mech. 1963, 15, 321–334. [Google Scholar] [CrossRef]
- International Air Transport Association. Safety Report 2015; International Air Transport Association: Montreal, QC, Canada, 2016. [Google Scholar]
- Cao, Y.; Tan, W.; Wu, Z. Aircraft icing: An ongoing threat to aviation safety. Aerosp. Sci. Technol. 2018, 75, 353–385. [Google Scholar] [CrossRef]
- Bragg, M.B.; Broeren, A.P.; Blumenthal, L.A. Iced-airfoil aerodynamics. Prog. Aerosp. Sci. 2005, 41, 323–362. [Google Scholar] [CrossRef]
- Esmaeilifar, E.; Prince Raj, L.; Myong, R.S. Computational simulation of aircraft electrothermal de-icing using an unsteady formulation of phase change and runback water in a unified framework. Aerosp. Sci. Technol. 2022, 130, 107936. [Google Scholar] [CrossRef]
- Bennani, L.; Villedieu, P.; Salaun, M.; Trontin, P. Numerical simulation and modeling of ice shedding: Process initiation. Comput. Struct. 2014, 142, 15–27. [Google Scholar] [CrossRef]
- Ignatowicz, K.; Morency, F.; Lopez, P. Dynamic Moment Model for Numerical Simulation of a 6-DOF Plate Trajectory around an Aircraft. J. Aerosp. Eng. 2019, 32. [Google Scholar] [CrossRef]
- Dukhan, N.; Masiulaniec, K.C.; Witt, K.J.D.; Fossen, G.J.V. Experimental Heat Transfer Coefficients from Ice-Roughened Surfaces for Aircraft Deicing Design. J. Aircr. 1999, 36, 948–956. [Google Scholar] [CrossRef]
- Gori, G.; Bellosta, T.; Guardone, A. Numerical Simulation of In-Flight Icing Under Uncertain Conditions. In Handbook of Numerical Simulation of In-Flight Icing; Habashi, W.G., Ed.; Springer International Publishing: Cham, Switzerland, 2023; pp. 1–34. [Google Scholar] [CrossRef]
- Fujiwara, G.E.C.; Bragg, M.B.; Broeren, A.P. Comparison of Computational and Experimental Ice Accretions of Large Swept Wings. J. Aircr. 2020, 57, 342–359. [Google Scholar] [CrossRef]
- Messinger, B.L. Equilibrium Temperature of an Unheated Icing Surface as a Function of Air Speed. J. Aeronaut. Sci. 1953, 20, 29–42. [Google Scholar] [CrossRef]
- Myers, T.G. Extension to the Messinger Model for Aircraft Icing. AIAA J. 2001, 39, 211–218. [Google Scholar] [CrossRef]
- Zhu, C.; Fu, B.; Sun, Z.; Zhu, C. 3D Ice Accretion Simulation For Complex Configuration Basing On Improved Messinger Model. Int. J. Mod. Phys. Conf. Ser. 2012, 19, 341–350. [Google Scholar] [CrossRef]
- Ayan, E.; Ozgen, S. Modification of the Extended Messinger Model for Mixed Phase Icing and Industrial Applications with TAICE. In Proceedings of the 9th AIAA Atmospheric and Space Environments Conference, Denver, CO, USA, 5–9 June 2017; p. 3759. [Google Scholar]
- Bourgault, Y.; Beaugendre, H.; Habashi, W.G. Development of a Shallow-Water Icing Model in FENSAP-ICE. J. Aircr. 2000, 37, 640–646. [Google Scholar] [CrossRef]
- Ignatowicz, K.; Morency, F.; Beaugendre, H. Extension of SU2 CFD capabilities to 3D aircraft icing simulation. In Proceedings of the 29th Annual Conference of the Computational Fluid Dynamics Society of Canada (CFDSC2021), Online, 27–29 July 2021. [Google Scholar]
- Özgen, S.; Canıbek, M. Ice accretion simulation on multi-element airfoils using extended Messinger model. Heat Mass Transf. 2008, 45, 305. [Google Scholar] [CrossRef]
- Macarthur, C.; Keller, J.; Luers, J. Mathematical modeling of ice accretion on airfoils. In Proceedings of the 20th Aerospace Sciences Meeting, Orlando, FL, USA, 11–14 January 1982. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, K.; Tian, W.; Hu, H. An experimental investigation on the dynamic ice accretion and unsteady heat transfer over an airfoil surface with embedded initial ice roughness. Int. J. Heat Mass Transf. 2020, 146, 118900. [Google Scholar] [CrossRef]
- Han, Y.; Palacios, J. Transient Heat Transfer Measurements of Surface Roughness due to Ice Accretion. In Proceedings of the 6th AIAA Atmospheric and Space Environments Conference, Reston, VA, USA, 16–20 June 2014; p. 22. [Google Scholar]
- Wang, Y.; Zhang, Y.; Wang, Y.; Zhu, D.; Zhao, N.; Zhu, C. Quantitative Measurement Method for Ice Roughness on an Aircraft Surface. Aerospace 2022, 9, 739. [Google Scholar] [CrossRef]
- Fossati, M.; Khurram, R.A.; Habashi, W.G. An ALE mesh movement scheme for long-term in-flight ice accretion. Int. J. Numer. Methods Fluids 2012, 68, 958–976. [Google Scholar] [CrossRef]
- de Rosa, D.; Capizzano, F.; Cinquegrana, D. Multi-Step Ice Accretion by Immersed Boundaries; SAE International: Minneapolis, MN, USA, 2023. [Google Scholar] [CrossRef]
- Ignatowicz, K.; Morency, F.; Beaugendre, H. Numerical simulation of ice accretion using Messinger-based approach: Effects of surface roughness. In Proceedings of the CASI AERO 2019, CASI, Laval, QC, Canada, 14–16 May 2019. [Google Scholar]
- Wright, W.B.; Gent, R.W.; Guffond, D. DRA/NASA/ONERA Collaboration on Icing Research. Part II—Prediction of Airfoil Ice Accretion; NASA: Washington, DC, USA, 1997. [Google Scholar]
- Gent, R.; Markiewicz, R.; Cansdale, J. Further Studies of Helicopter Rotor Ice Accretion and Protection. Vertica 1987, 11, 473–492. [Google Scholar]
- Cinquegrana, D.; D’Aniello, F.; de Rosa, D.; Carozza, A.; Catalano, P.; Mingione, G. A CIRA 3D Ice Accretion Code for Multiple Cloud Conditions Simulations; SAE International: Minneapolis, MN, USA, 2023. [Google Scholar] [CrossRef]
- Beaugendre, H.; Morency, F.; Habashi, W.G.; Benquet, P. Roughness Implementation in FENSAP-ICE: Model Calibration and Influence on Ice Shapes. J. Aircr. 2003, 40, 1212–1215. [Google Scholar] [CrossRef]
- Martini, F.; Ibrahim, H.; Contreras Montoya, L.T.; Rizk, P.; Ilinca, A. Turbulence Modeling of Iced Wind Turbine Airfoils. Energies 2022, 15, 8325. [Google Scholar] [CrossRef]
- Ozcer, I.A.; Baruzzi, G.S.; Reid, T.; Habashi, W.G.; Fossati, M.; Croce, G. FENSAP-ICE: Numerical Prediction of Ice Roughness Evolution, and Its Effects on Ice Shapes; SAE International: Minneapolis, MN, USA, 2011. [Google Scholar] [CrossRef]
- Croce, G.; Candido, E.D.; Habashi, W.; Aubé, M.; Baruzzi, G. FENSAP-ICE: Numerical Prediction of In-flight Icing Roughness Evolution. In Proceedings of the 1st AIAA Atmospheric and Space Environments Conference, San Antonio, TX, USA, 22–25 June 2009. [Google Scholar] [CrossRef]
- ANSYS. ANSYS FENSAP-ICE User Manual; ANSYS: Canonsburg, PA, USA, 2020. [Google Scholar]
- Yan, L.; Chao, W.; Shi-nan, C.; Du, C. Simulation of Ice Accretion Based on Roughness Distribution. Procedia Eng. 2011, 17, 160–177. [Google Scholar] [CrossRef]
- Fortin, G.; Laforte, J.-L.; Ilinca, A. Heat and mass transfer during ice accretion on aircraft wings with an improved roughness model. Int. J. Therm. Sci. 2006, 45, 595–606. [Google Scholar] [CrossRef]
- Anderson, D.; Shin, J.; Anderson, D.; Shin, J. Characterization of ice roughness from simulated icing encounters. In Proceedings of the AIAA 35th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1997. [Google Scholar] [CrossRef][Green Version]
- Wright, W. User’s Manual for LEWICE Version 3.2; QSS Group, Inc.: Cleveland, OH, USA, 2008. [Google Scholar]
- Wright, W.; Rigby, D.; Ozoroski, T. Roughness Parameter Optimization of the McClain Model in GlennICE; SAE International: Minneapolis, MN, USA, 2023. [Google Scholar] [CrossRef]
- Aghaei Jouybari, M.; Junlin, Y.; Brereton, G.J.; Murillo, M.S. Data-driven prediction of the equivalent sand-grain height in rough-wall turbulent flows. J. Fluid Mech. 2021, 912, A8. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ignatowicz, K.; Morency, F.; Beaugendre, H. Surface Roughness in RANS Applied to Aircraft Ice Accretion Simulation: A Review. Fluids 2023, 8, 278. https://doi.org/10.3390/fluids8100278
Ignatowicz K, Morency F, Beaugendre H. Surface Roughness in RANS Applied to Aircraft Ice Accretion Simulation: A Review. Fluids. 2023; 8(10):278. https://doi.org/10.3390/fluids8100278
Chicago/Turabian StyleIgnatowicz, Kevin, François Morency, and Héloïse Beaugendre. 2023. "Surface Roughness in RANS Applied to Aircraft Ice Accretion Simulation: A Review" Fluids 8, no. 10: 278. https://doi.org/10.3390/fluids8100278
APA StyleIgnatowicz, K., Morency, F., & Beaugendre, H. (2023). Surface Roughness in RANS Applied to Aircraft Ice Accretion Simulation: A Review. Fluids, 8(10), 278. https://doi.org/10.3390/fluids8100278