Pipe Flow of Suspensions of Cellulose Nanocrystals
Abstract
:1. Introduction
2. Background
2.1. Friction Factor vs. Reynolds Number for Newtonian Fluids
2.2. Friction Factor vs. Reynolds Number for Non-Newtonian Power-Law Fluids
3. Materials and Methods
3.1. Materials
3.2. Flow Loop
3.3. Viscometry
3.4. Preparation of CNC Suspensions
3.5. Calibration of Pipeline Test-Sections
4. Results and Discussion
4.1. Particle Size Distribution of CNC Suspensions
4.2. Rheology of CNC Suspensions
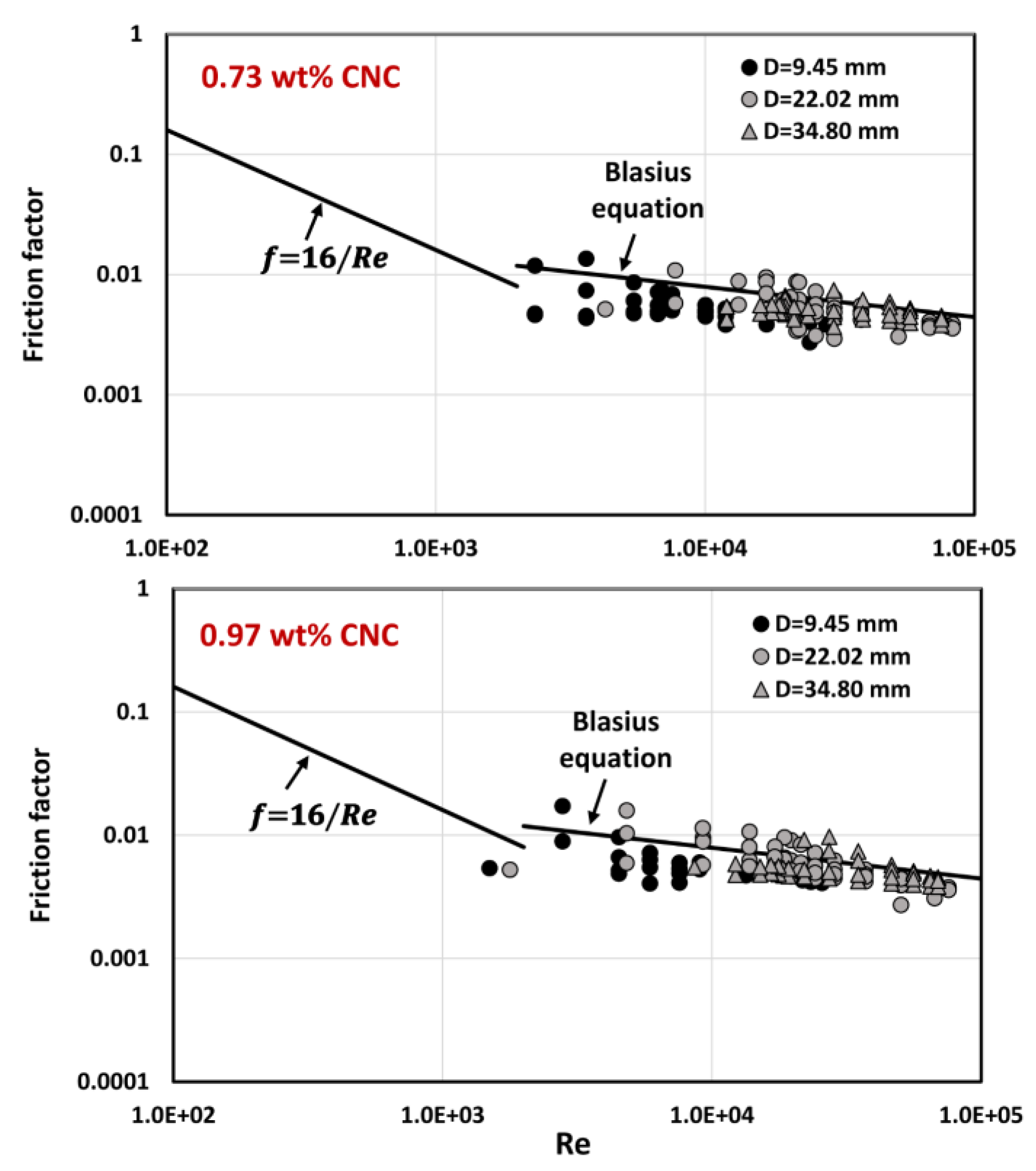
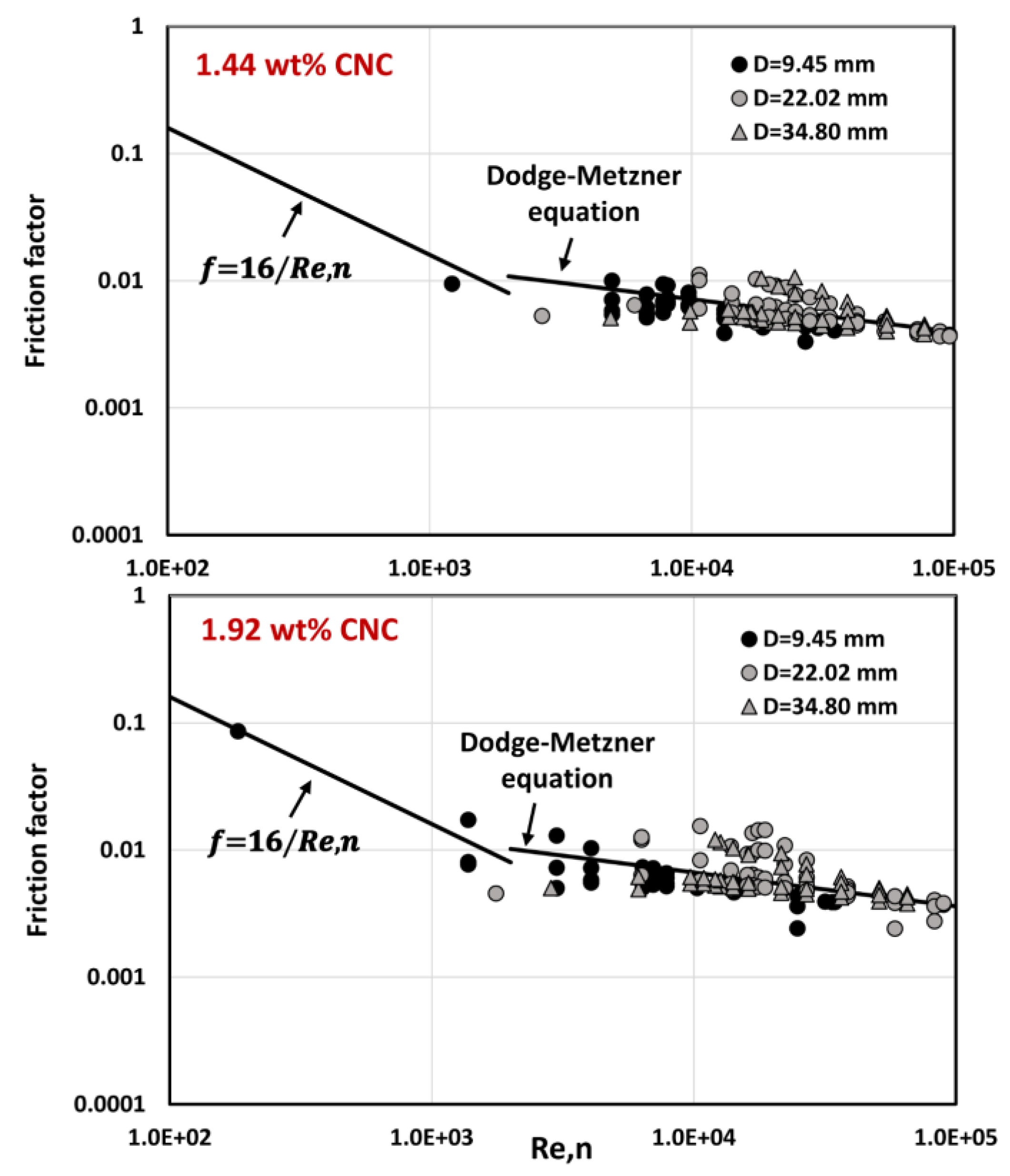
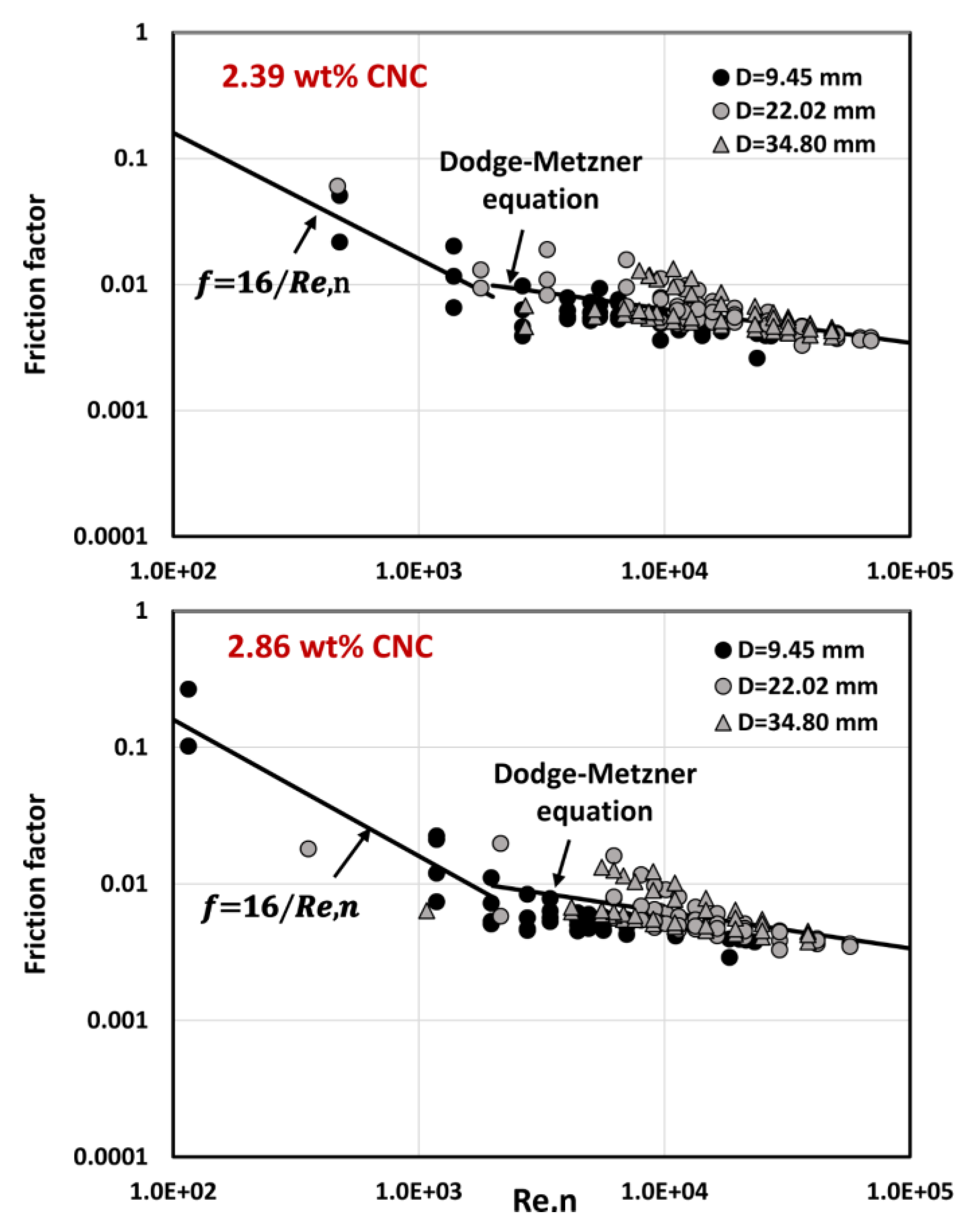
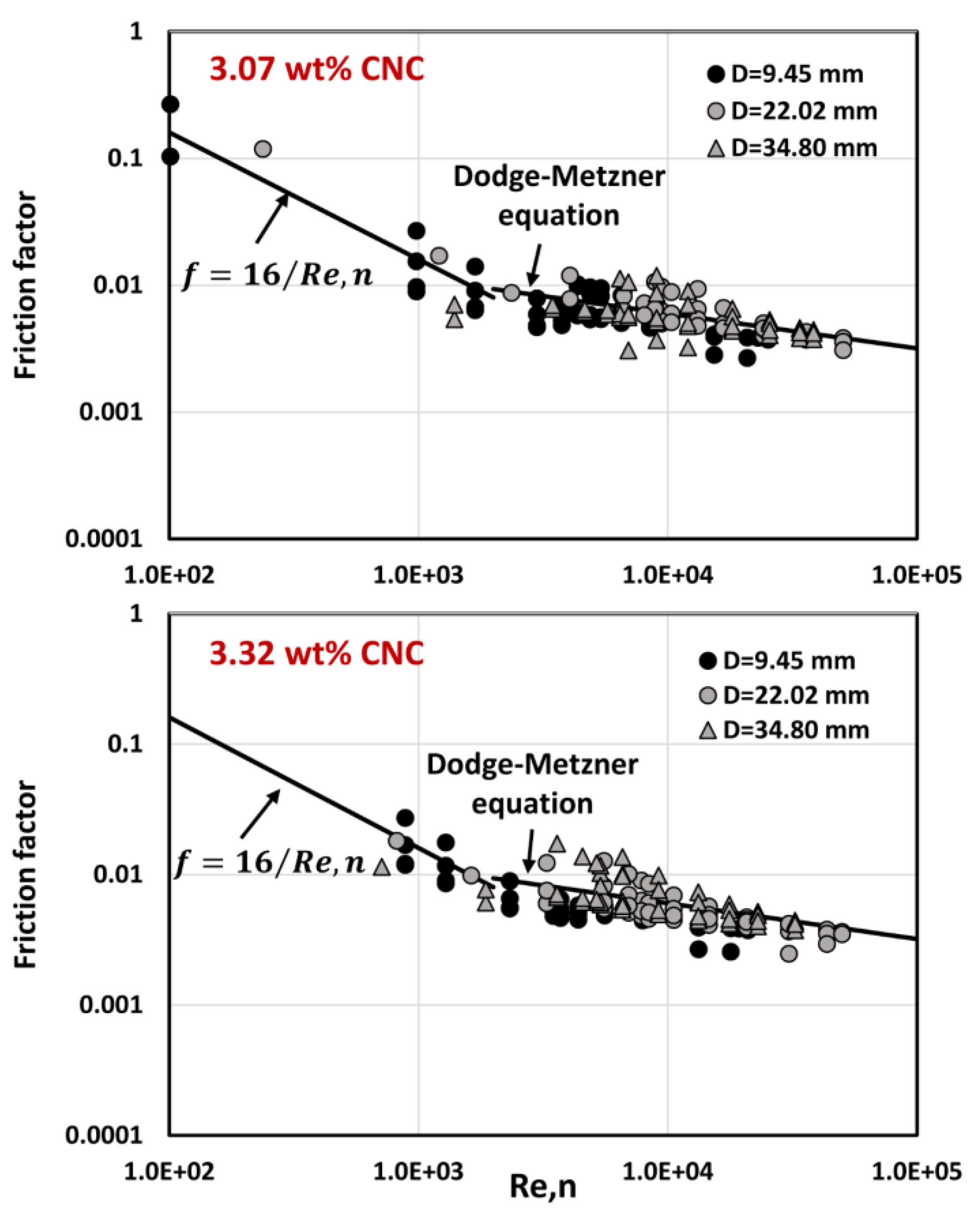
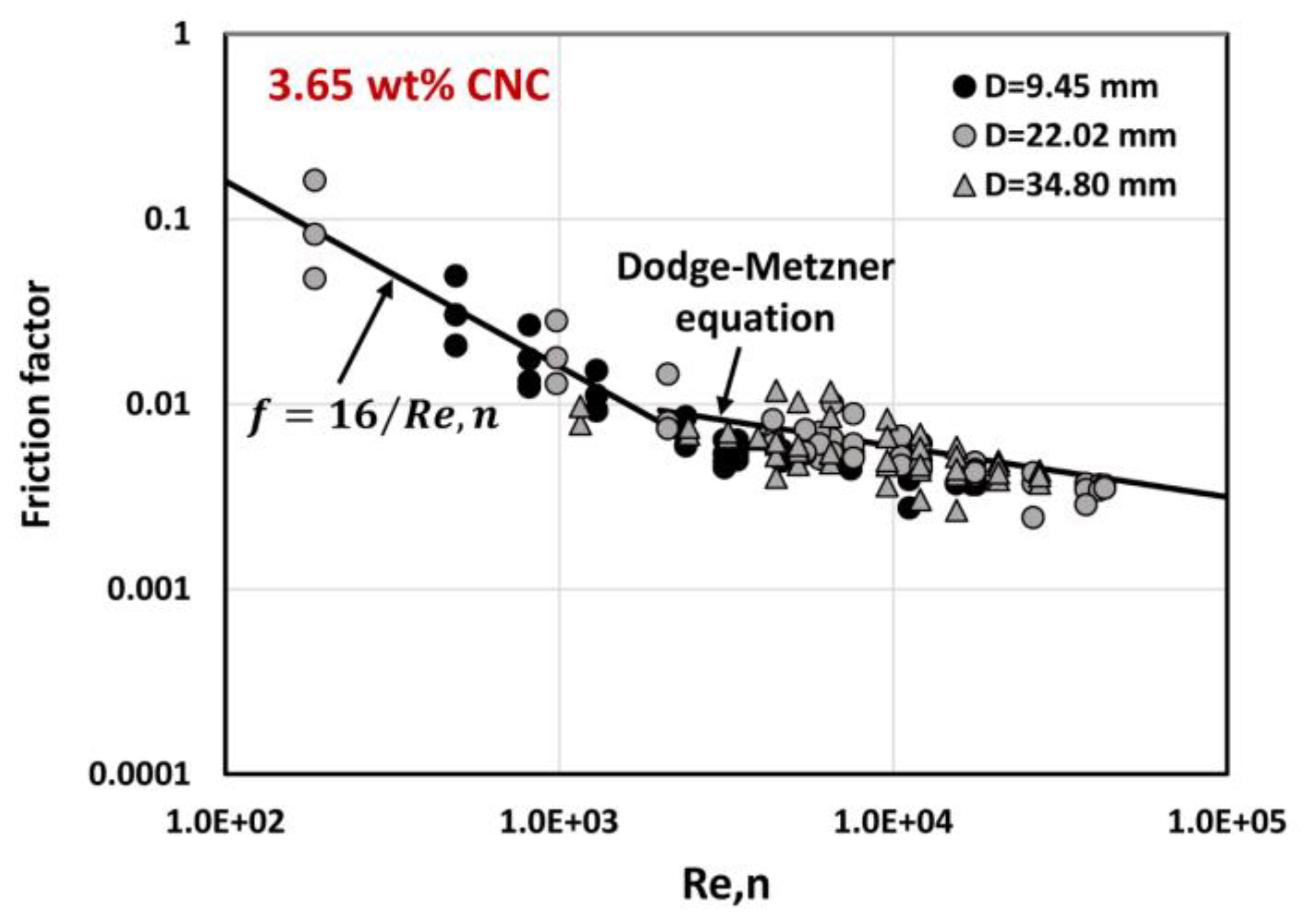
4.3. Pipeline Flow Behavior of CNC Suspensions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Girard, M.; Vidal, D.; Bertrand, F.; Tavares, J.R.; Heuzey, M. Evidence-based guidelines for the ultrasonic dispersion of cellulose nanocrystals. Ultrason. Sonochem. 2021, 71, 105378. [Google Scholar] [CrossRef]
- Shojaeiarani, J.; Bajwa, D.S.; Chanda, S. Cellulose nanocrystal-based composites: A review. Compos. Part C Open Access 2021, 5, 100164. [Google Scholar] [CrossRef]
- Prathapan, R.; Thapa, R.; Garnier, G.; Tabor, R.F. Modulating the zeta potential of cellulose nanocrystals using salts and surfactants. Colloids Surf. A Physicochem. Eng. Asp. 2016, 509, 11–18. [Google Scholar] [CrossRef]
- Lu, P.; Hsieh, Y. Preparation and properties of cellulose nanocrystals: Rods, spheres, and network. Carbohydr. Polym. 2010, 82, 329–336. [Google Scholar] [CrossRef]
- Yang, X.; Biswas, S.K.; Han, J.; Tanpichai, S.; Li, M.; Chen, C.; Zhu, S.; Das, A.K.; Yano, H. Surface and interface engineering for nanocellulosic advanced materials. Adv. Mater. 2021, 33, 2002264. [Google Scholar] [CrossRef] [PubMed]
- Aziz, T.; Ullah, A.; Fan, H.; Ullah, R.; Haq, F.; Khan, F.U.; Iqbal, M.; Wei, J. Cellulose nanocrystals applications in health, medicine, and catalysis. J. Polym. Environ. 2021, 29, 2062–2071. [Google Scholar] [CrossRef]
- Dufresne, A. Nanocellulose processing properties and potential applications. Curr. For. Rep. 2019, 5, 76–89. [Google Scholar] [CrossRef]
- Trache, D.; Hussin, M.H.; Haafiz, M.K.M.; Thakur, V.K. Recent progress in cellulose nanocrystals: Sources and production. Nanoscale 2017, 9, 1763–1786. [Google Scholar] [CrossRef]
- Aziz, T.; Fan, H.; Zhang, X.; Haq, A.; Ullah, R.; Khan, F.U.; Iqbal, M. Advance study of cellulose nanocrystals properties and applications. J. Polym. Environ. 2020, 28, 1117–1128. [Google Scholar] [CrossRef]
- Vanderfleet, O.M.; Cranston, E.D. Production routes to tailor the performance of cellulose nanocrystals. Nat. Rev. Mater. 2021, 6, 124–144. [Google Scholar] [CrossRef]
- Zhang, H.; Dou, C.; Pal, L.; Hubbe, M.A. Review of electrically conductive composites and films containing cellulosic fibers or nanocellulose. BioResources 2019, 14, 7494–7542. [Google Scholar] [CrossRef]
- Panchal, P.; Ogunsona, E.; Mekonnen, T. Trends in advanced functional material applications of nanocellulose. Processes 2019, 10, 1–27. [Google Scholar] [CrossRef]
- Gupta, A.; Mekonnen, T.H. Cellulose nanocrystals enabled sustainable polycaprolactone based shape memory polyurethane bionanocomposites. J. Colloid Interface Sci. 2022, 611, 726–738. [Google Scholar] [CrossRef] [PubMed]
- Cellulose Nanocrystals (CNC). Available online: https://celluforce.com/cellulose-nanocrystals-cnc/ (accessed on 26 February 2023).
- Lu, Y.; Yue, Y.; Ding, Q.; Mei, C.; Xu, X.; Wu, Q.; Xiao, H.; Han, J. Self-recovery, fatigue-resistant, and multifunctional sensor assembled by a nanocellulose/carbon nanotube nanocomplex-mediated hydrogel. Appl. Mater. Interfaces 2021, 13, 50281–50297. [Google Scholar] [CrossRef] [PubMed]
- Zhu, S.; Sun, H.; Lu, Y.; Wang, S.; Yue, Y.; Xu, X.; Mei, C.; Xiao, H.; Fu, Q.; Han, J. Inherently conductive poly(dimethylsiloxane) elastomers synergistically mediated by nanocellulose/carbon nanotube nanohybrids toward highly sensitive, stretchable, and durable strain sensors. Appl. Mater. Interfaces 2021, 13, 59142–59153. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Yu, H.; Xu, X.; Han, F.; Lubineau, G. Ultrasensitive, stretchable strain sensors based on fragmented carbon nanotube papers. Appl. Mater. Interfaces 2017, 9, 4835–4842. [Google Scholar] [CrossRef] [PubMed]
- Zhu, S.; Lu, Y.; Wang, S.; Sun, H.; Yue, Y.; Xu, X.; Mei, C.; Xiao, H.; Fu, Q.; Han, J. Interface design of stretchable and environment-tolerant strain tensors with hierarchical nanocellulose-supported graphene nanocomplexes. Compos. Part A 2023, 164, 107313. [Google Scholar] [CrossRef]
- Sun, H.; Lu, Y.; Chen, Y.; Yue, Y.; Jiang, S.; Xu, X.; Mei, C.; Xiao, H.; Han, J. Flexible environment-tolerant electroluminescent devices based on nanocellulose-mediated transparent electrodes. Carbohydr. Polym. 2022, 296, 119891. [Google Scholar] [CrossRef] [PubMed]
- Niu, Z.; Cheng, W.; Cao, M.; Wang, D.; Wang, Q.; Han, J.; Long, Y.; Han, G. Recent advances in cellulose-based flexible triboelectric nanogenerators. Nano Energy 2021, 87, 106175. [Google Scholar] [CrossRef]
- Wang, J.; Euring, M.; Ostendorf, K.; Zhang, K. Biobased materials for food packaging. J. Bioresour. Bioprod. 2022, 7, 1–13. [Google Scholar] [CrossRef]
- Dodge, D.W.; Metzner, A.B. Turbulent flow of non-Newtonian systems. AIChE J. 1959, 5, 189–204. [Google Scholar] [CrossRef]
- Pal, R. Entropy generation in flow of highly concentrated non-Newtonian emulsions in smooth tubes. Entropy 2014, 16, 5178–5197. [Google Scholar] [CrossRef]
- Kinra, S.; Pal, R. Rheology of Pickering emulsions stabilized and thickened by cellulose nanocrystals over broad ranges of oil and nanocrystal concentrations. Colloids Interfaces 2023, 7, 36. [Google Scholar] [CrossRef]
- Niskanen, I.; Suopajarvi, T.; Liimatainen, H.; Fabritius, T.; Heikkila, R.; Thungstrom, G. Determining the complex refractive index of cellulose nanocrystals by combination of Beer-Lambert and immersion matching methods. J. Quant. Spectrosc. Radiat. Transf. 2019, 235, 1–6. [Google Scholar] [CrossRef]





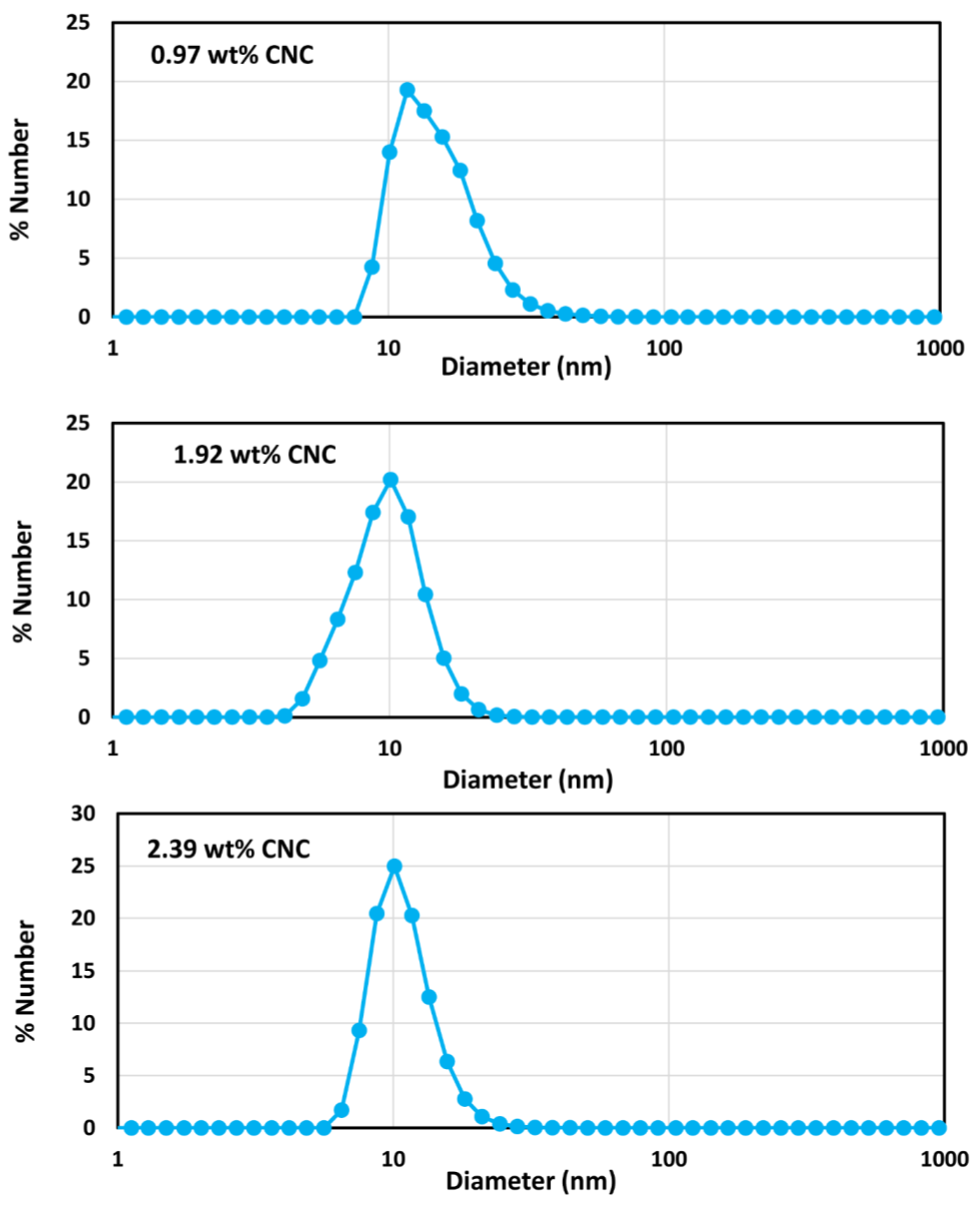
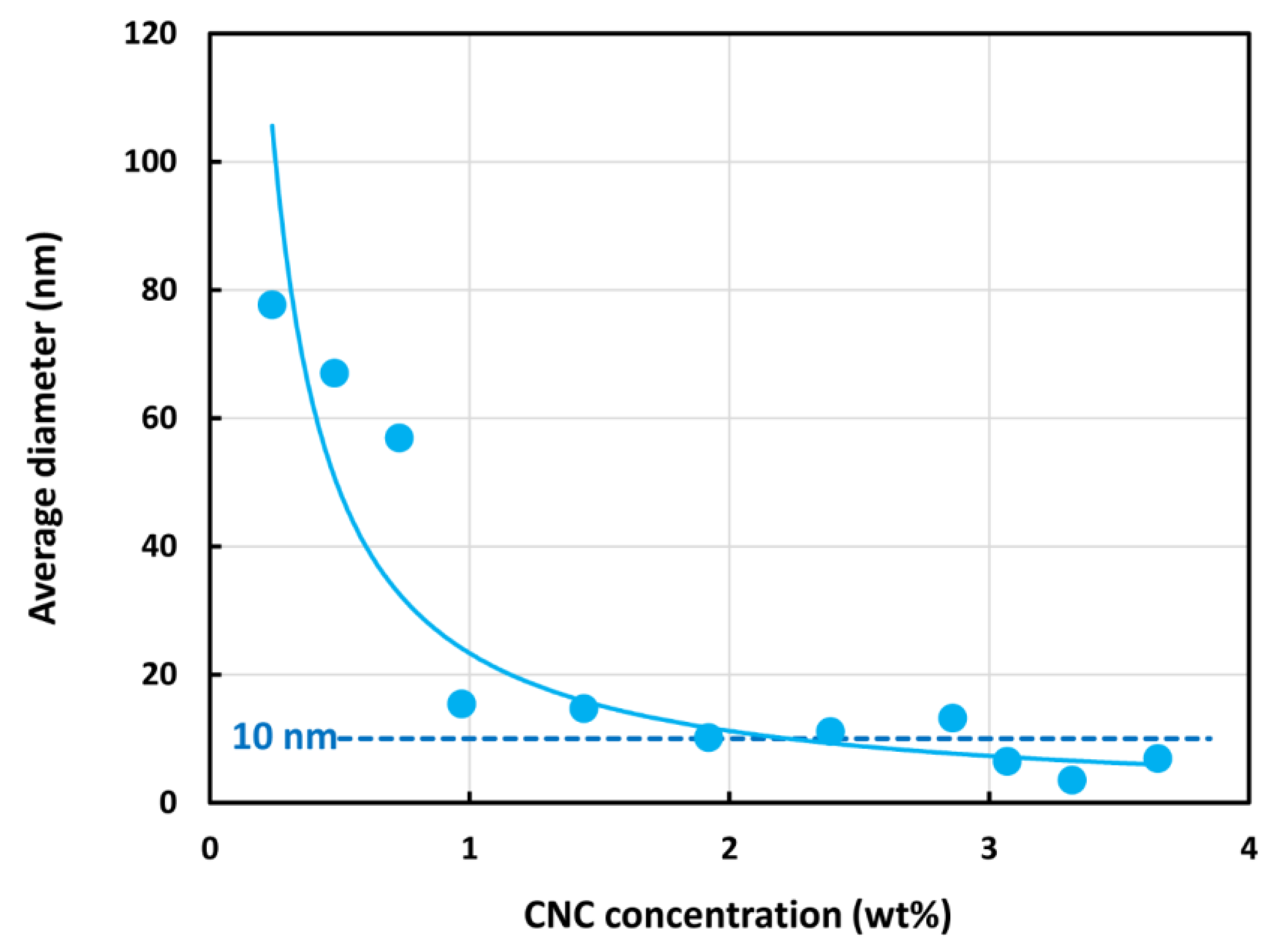
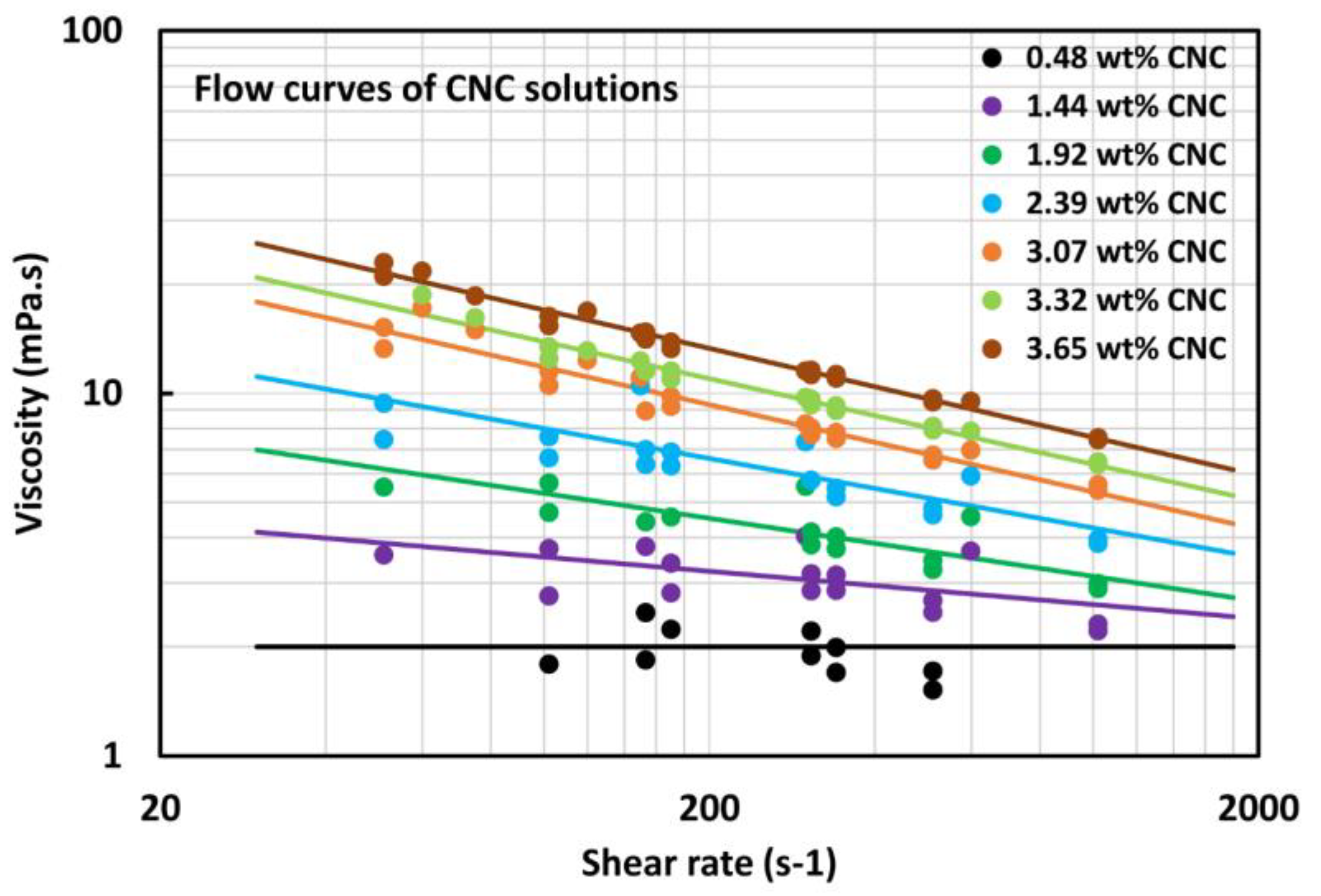
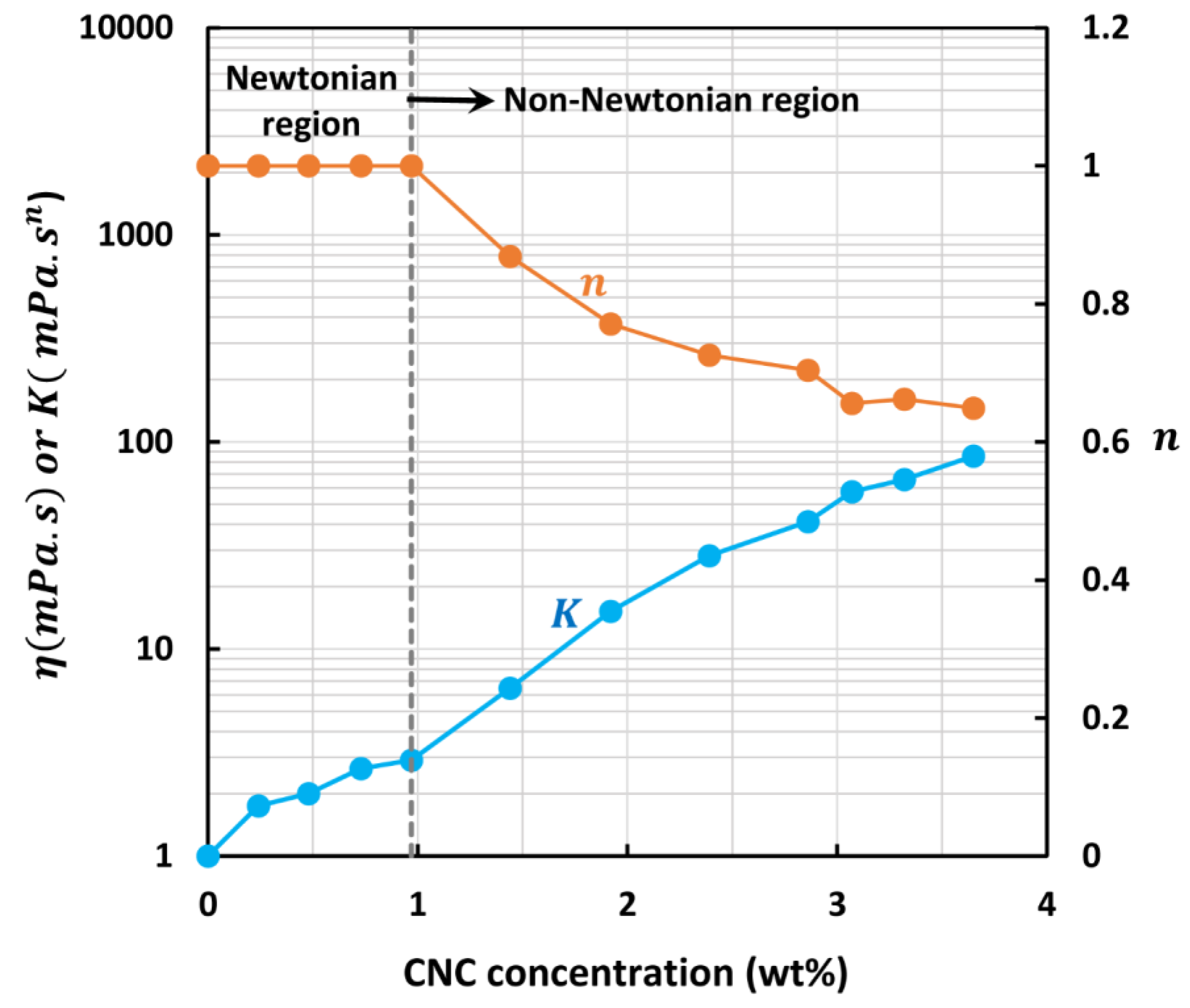

| Nominal Diameter (inch) | Inside Diameter (mm) | Test Section Lengths (m) |
|---|---|---|
| 0.5 | 9.45 | 1.22, 3.667 |
| 1.0 | 22.02 | 0.92, 3.048 |
| 1.5 | 34.80 | 1.52, 3.048 |
| Device | Length of Inner Cylinder | Gap-Width | ||
|---|---|---|---|---|
| Fann 35A/SR-12 viscometer | 1.72 cm | 1.84 cm | 3.8 cm | 0.12 cm |
| Haake Roto-visco RV 12 with MV I | 2.00 cm | 2.1 cm | 6.0 cm | 0.10 cm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kinra, S.; Pal, R. Pipe Flow of Suspensions of Cellulose Nanocrystals. Fluids 2023, 8, 275. https://doi.org/10.3390/fluids8100275
Kinra S, Pal R. Pipe Flow of Suspensions of Cellulose Nanocrystals. Fluids. 2023; 8(10):275. https://doi.org/10.3390/fluids8100275
Chicago/Turabian StyleKinra, Saumay, and Rajinder Pal. 2023. "Pipe Flow of Suspensions of Cellulose Nanocrystals" Fluids 8, no. 10: 275. https://doi.org/10.3390/fluids8100275
APA StyleKinra, S., & Pal, R. (2023). Pipe Flow of Suspensions of Cellulose Nanocrystals. Fluids, 8(10), 275. https://doi.org/10.3390/fluids8100275







