Numerical Simulation of the Conjugate Heat Transfer of a “Fluid–Solid Body” System on an Unmatched Grid Interface

Abstract

Recently, when modeling transient problems of conjugate heat transfer, the independent construction of grid models for fluid and solid subdomains is increasingly being used. Such grid models, as a rule, are unmatched and require the development of special grid interfaces that match the heat fluxes at the interface. Currently, the most common sequential approach to modeling problems of conjugate heat transfer requires the iterative matching of boundary conditions, which can significantly slow down the process of the convergence of the solution in the case of modeling transient problems with fast processes. The present study is devoted to the development of a direct method for solving conjugate heat transfer problems on grid models consisting of inconsistent grid fragments on adjacent boundaries in which, in the general case, the number and location of nodes do not coincide. A conservative method for the discretization of the heat transfer equation by the direct method in the region of inconsistent interface boundaries between liquid and solid bodies is proposed. The proposed method for matching heat fluxes at mismatched boundaries is based on the principle of forming matched virtual boundaries, proposed in the GGI (General Grid Interface) method. A description of a numerical scheme is presented, which takes into account the different scales of cells and the sharply different thermophysical properties at the interface between liquid and solid media. An algorithm for constructing a conjugate matrix, the form of matrix coefficients responsible for conjugate heat transfer, and methods for calculating them are described. The operability of the presented method is demonstrated by the example of calculating conjugate heat transfer problems, the grid models of which consist of inconsistent grid fragments. The use of the direct conjugation method makes it possible to effectively solve both stationary and non-stationary problems using inconsistent meshes, without the need to modify them in the conjugation region within a single CFD solver.

1. Introduction

Conjugate heat transfer simulation is one of the most important classes of production problems. These problems play a key role in the design and optimization process of products, whose operation needs to consider thermal limitations (e.g., supersonic aerodynamics problems [1]), the stability of thermal processes, the thermal stress level, thermal effectiveness, etc. The importance of such numerical solution problems is primarily determined by the necessity of the spatial and time distribution of temperatures, as well as in spotting problem areas when simulating emergency situations in the designed structures for which a natural experiment is often impossible or entails considerable financial expenses [2,3,4].

When solving industrial problems involving conjugate heat transfer, in most cases, the grid model is formed by individual segments containing fluid flow and solid body subareas. The form and density of the grid for each segment are selected according to their physical processes. Such approach simplifies the process of optimizing individual regions of the model, since it allows for re-meshing only in desired subdomains, and also makes it possible to perform a more accurate solution without a significant increase in the number of cells in the mesh model.

As usual, grid models consist of unmatched grid segments, with the number and location of cells on their adjacent boundaries mismatching in general. The key feature of the numerical simulation of conjugate heat transfer problems on such grid models is the necessity to match thermal flows in the coupling area of fluid and solid body subareas by means of special grid interfaces.

In order to calculate conjugate heat transfer problems, several methods can be applied [5], each having its own application area, advantages, and disadvantages. The least computationally expensive is the approach under which fluid flow field calculation is carried out in a steady-state arrangement and only in key points, used to form thermal boundary conditions on a fluid and solid body interface [6]. Hypotheses, based on empirical data and engineering expertise, commonly underlie such calculations. This may lead to significant errors in estimating the temperature field in geometrically complex structures.

According to the sequential approach [7,8], temperature fields in fluid and solid body subareas are calculated by separate calculation modules. This approach implies a distinct boundary detection in the coupling area and a boundary conditions exchange mechanism between calculation modules. At each calculation step, coupling takes place between different calculation methods until the required residual level is reached. When unmatched grids are present in the fluid and solid body coupling area, various interpolation techniques of boundary conditions are applied. The major disadvantage of the sequential approach is the necessity of the iterative matching of changing boundary conditions, which considerably slows down the convergence process. This is most noticeable when solving non-stationary problems.

The direct coupling method [9,10,11] allows for building a numerical scheme, which is capable of simultaneously discretizing heat-transfer equations for fluid and solid body subareas and constructing a system of linear algebraic equations (SLAE) relative to temperature. The direct method is the most computationally expensive, having the biggest SLAE size, which considerably speeds up the convergence process; it is also the most universal one, as it allows for efficiently calculating both steady and transient problems in the conjugation area within a single CFD solver. Most articles [12,13,14,15,16] devoted to the direct coupling method do not cover the issue of calculating problems on the models, containing unmatched grid segments on the fluid and solid body interface. Unmatched grids on the fluid and solid body interface require conservatively matching thermal flows in the coupling area, which is a nontrivial task and requires developing special interfaces.

The present study is devoted to the development of a direct conjugation method for problems containing arbitrary, inconsistent meshes at the interface between liquid and solid regions. The work is an extension of the possibilities of the mass flow matching method in solving the Navier–Stokes equations in the liquid–liquid interface proposed in [17,18], which is based on the principle of forming virtual boundaries that form a virtual matched interface, which is the basis of the matching method of heat fluxes presented in the article. The proposed method does not require the modification of the original unmatched mesh in the interface area, allows for the use of a single principle of matching heat and mass flows, and can be implemented within a single CFD solver. At the same time, the presence of an inconsistent grid should not worsen the solution in comparison with the solution on a consistent grid.

The structure of the work is organized as follows: first, the article describes the classical form of the discretization of the analog of the heat transfer equation and the method of obtaining the matrix coefficients of a single matrix with respect to the temperature for the case of a consistent grid in the area of conjugation of a liquid and a solid body, followed by a description of the modification of the components of the discrete analog of the heat transfer equations and the coefficients of the matrix in the interface area for the case of using an inconsistent grid model in the interface area. The last section shows the applicability of the presented method for the example of conjugate heat transfer problems, the grid models of which consist of inconsistent grid fragments. The results of the simulation of test problems show that the presence of mismatched meshes at the interface between liquid and solid blocks does not significantly affect the temperature field.

2. Mathematical Model and Numerical Method

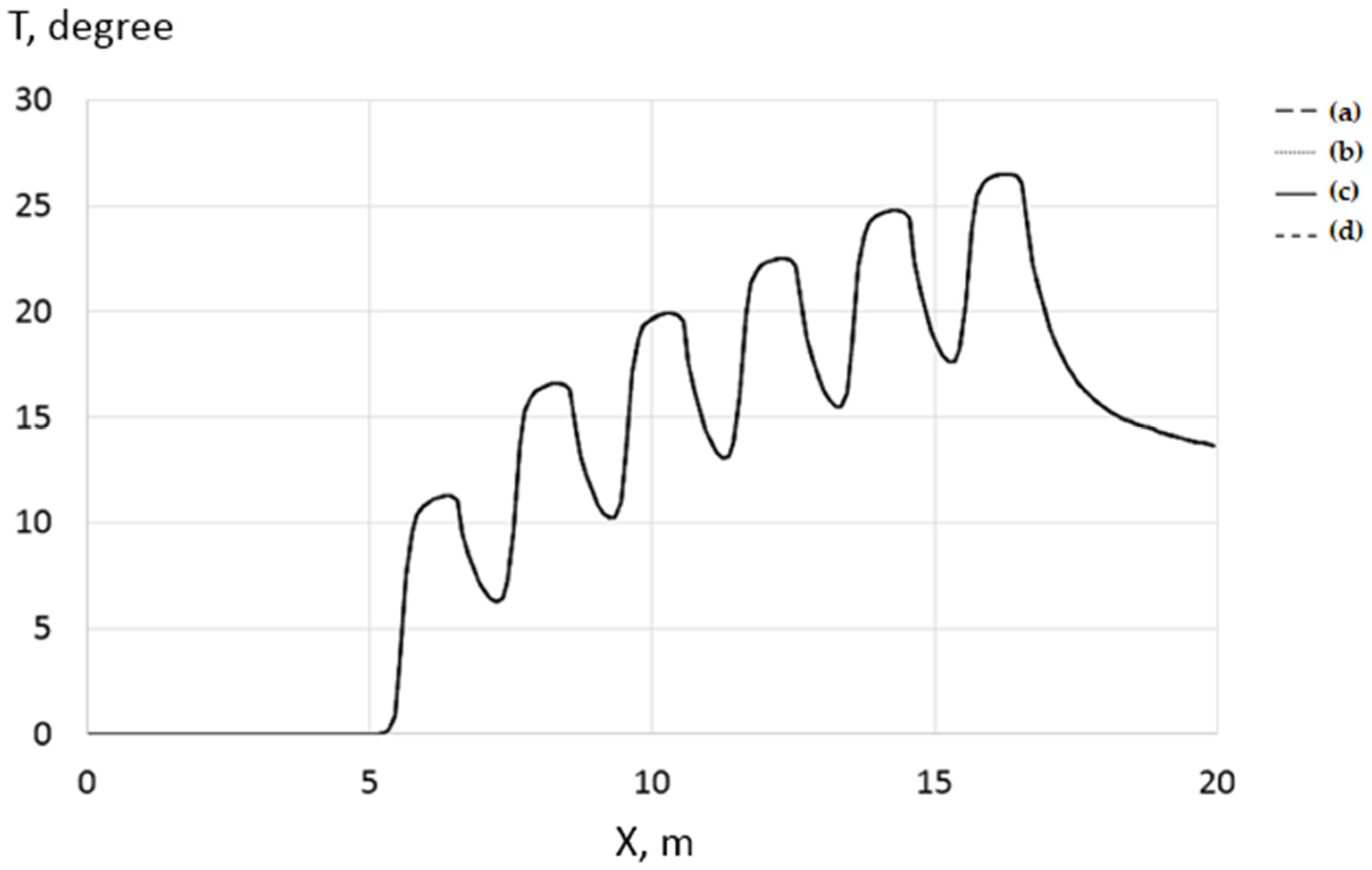
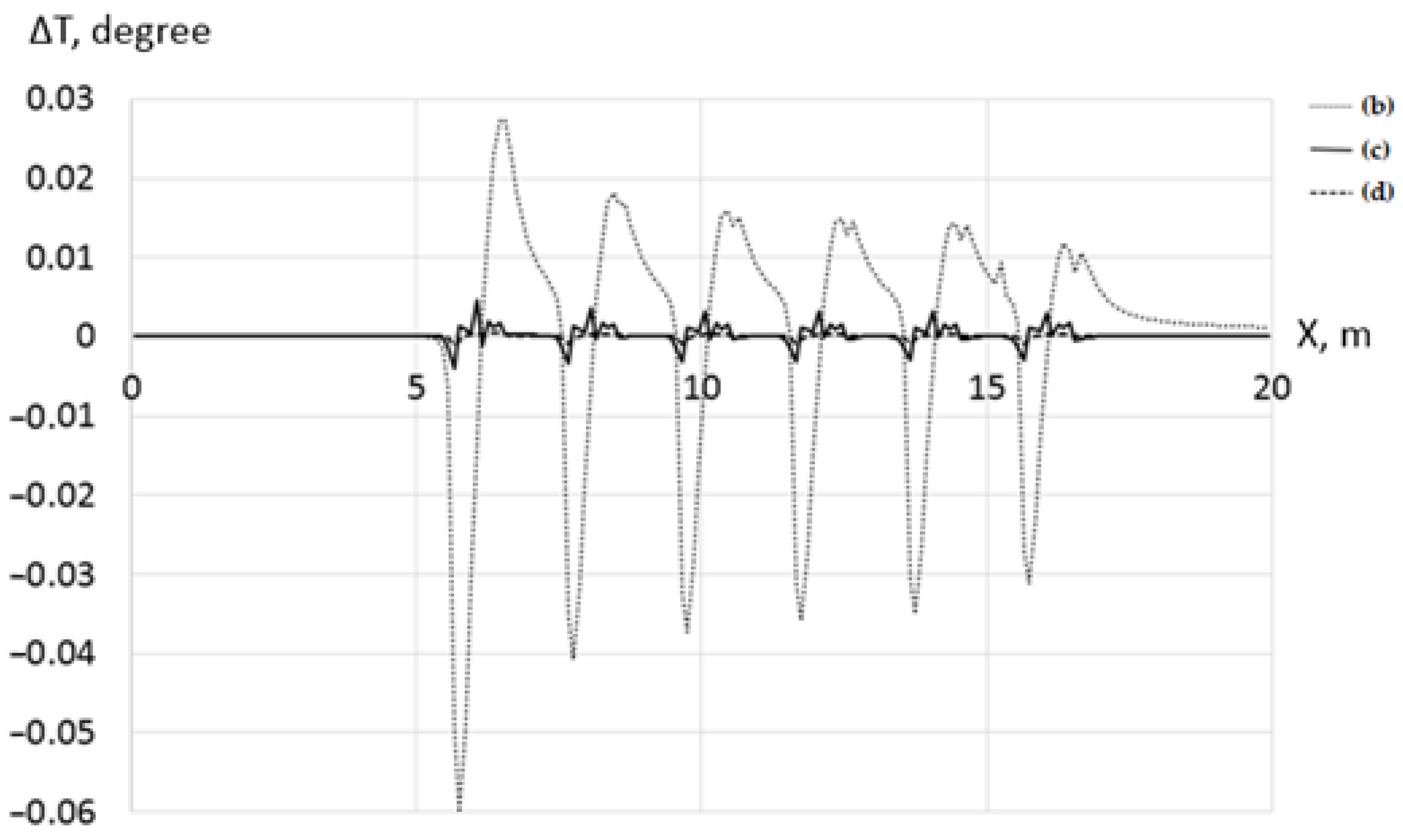
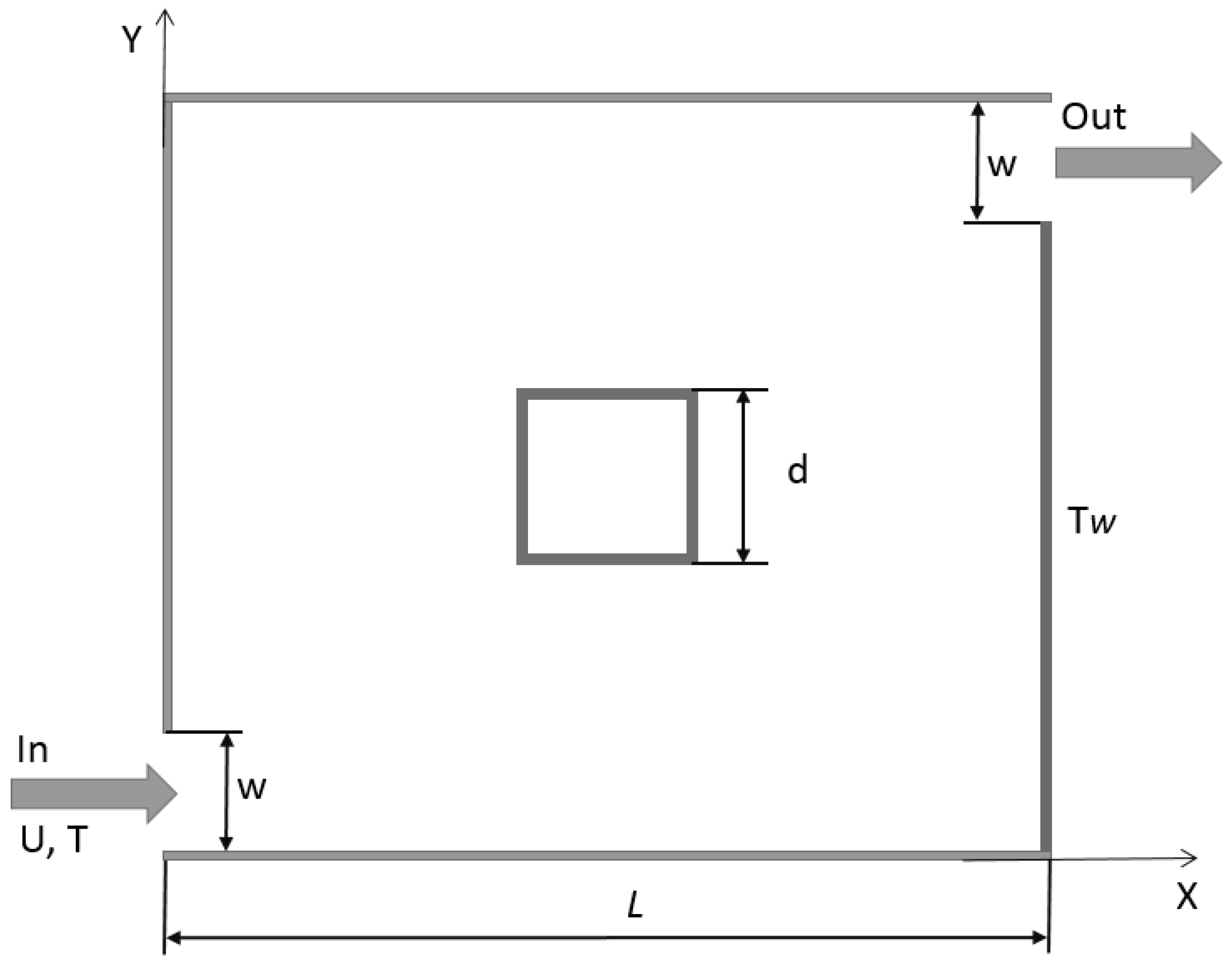
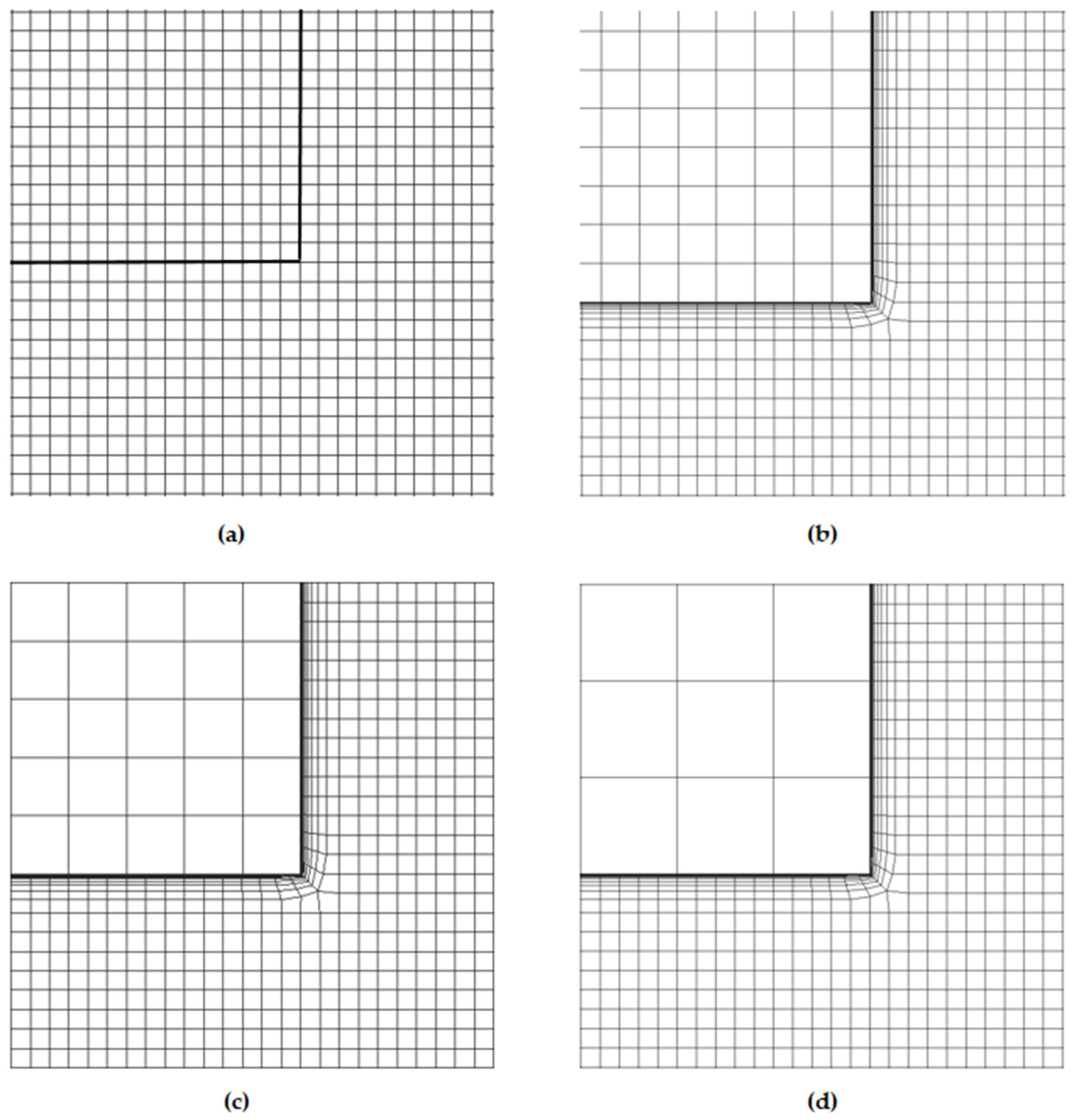
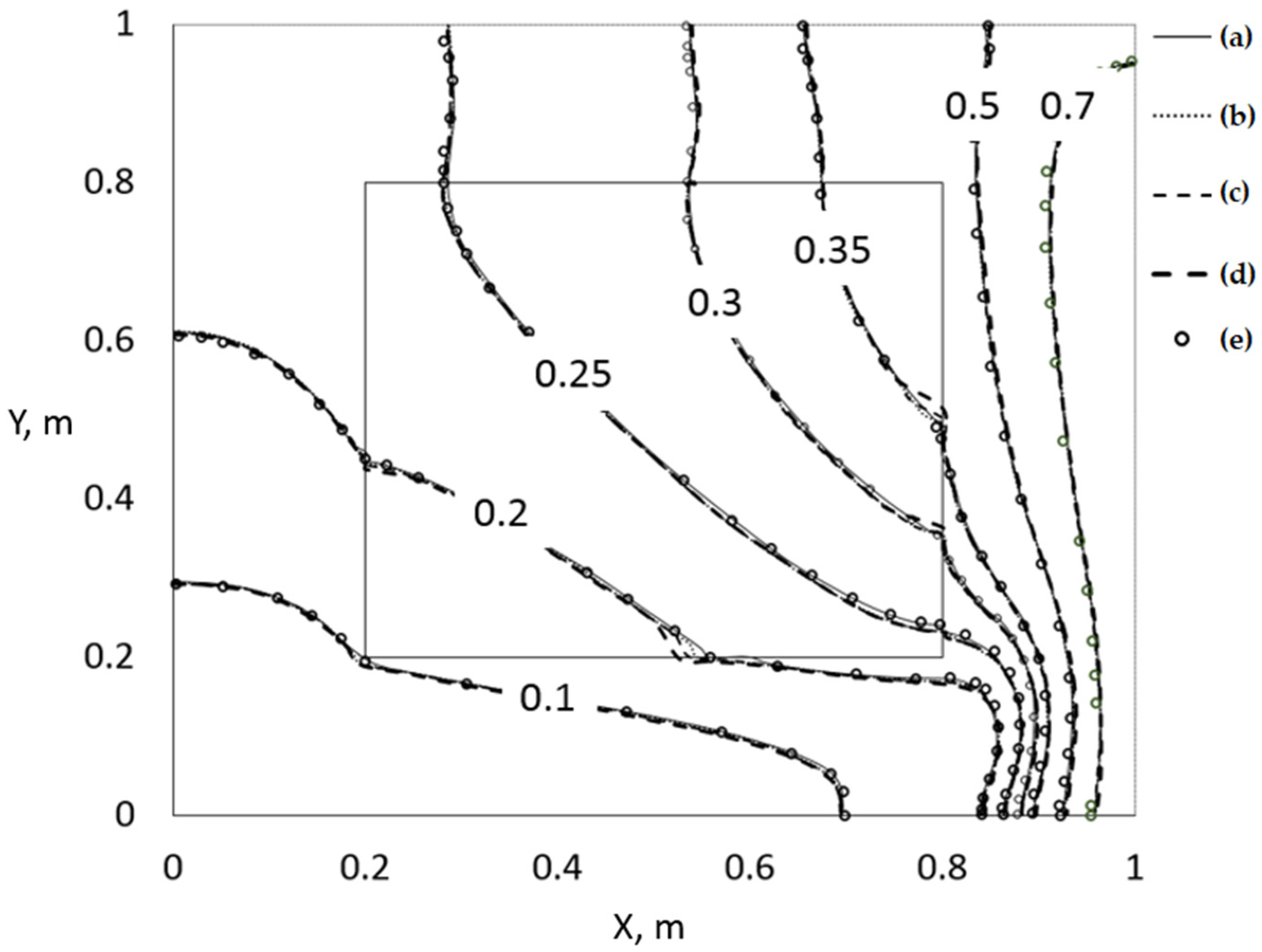
2.1. Mathematical Model

In conjugate heat transfer problems, the numerical simulation area is divided into solid and fluid substance subareas (Figure 1).

We consider a mathematical model, in which the subarea (Figure 1) is a laminar incompressible fluid having a constant thermal conductivity coefficient, with heat sources (including dissipative ones) being absent. Taking into account the above assumptions, the heat transfer equation for a subarea written with respect to the temperature takes the following form:

$${\rho }_F{C}_F\frac{\partial T}{\partial t}+{\rho }_F{C}_F\nabla \cdot \left(uT\right)=\nabla \cdot \left(k_F\nabla T\right),$$

(1)

where ρ_F—fluid density, C_F—fluid heat capacity, u—fluid phase velocity vector, k_F—fluid thermal conductivity coefficient, and t—time.

In Equation (1), the fluid phase velocity vector u is determined by solving the Navier–Stokes equation system—for example, by the well-known SIMPLE algorithm [19,20,21]; meanwhile, a no-slip boundary condition on the side of the fluid is accepted on the interface boundary.

Subarea S (Figure 1) is a fixed solid body with a constant thermal conductivity coefficient without heat sources. Taking into account the above assumptions, the heat transfer equation for subarea S, written with respect to the temperature, takes the following form:

$${\rho }_S{C}_S\frac{\partial T}{\partial t}=\nabla \cdot \left(k_s\nabla T\right),$$

(2)

where ρ_S—solid body density, C_S—solid body thermal capacity, k_S—solid body thermal conductivity coefficient, and t—time.

A necessary condition of coupling Equations (1) and (2) is following the energy conservation law, i.e., thermal flows equality on the fluid and solid body boundary:

$${\mathbf{q}}_F={\mathbf{q}}_S,$$

(3)

where q_F—thermal flow on the side of fluid and q_S—thermal flow on the side of the solid body.

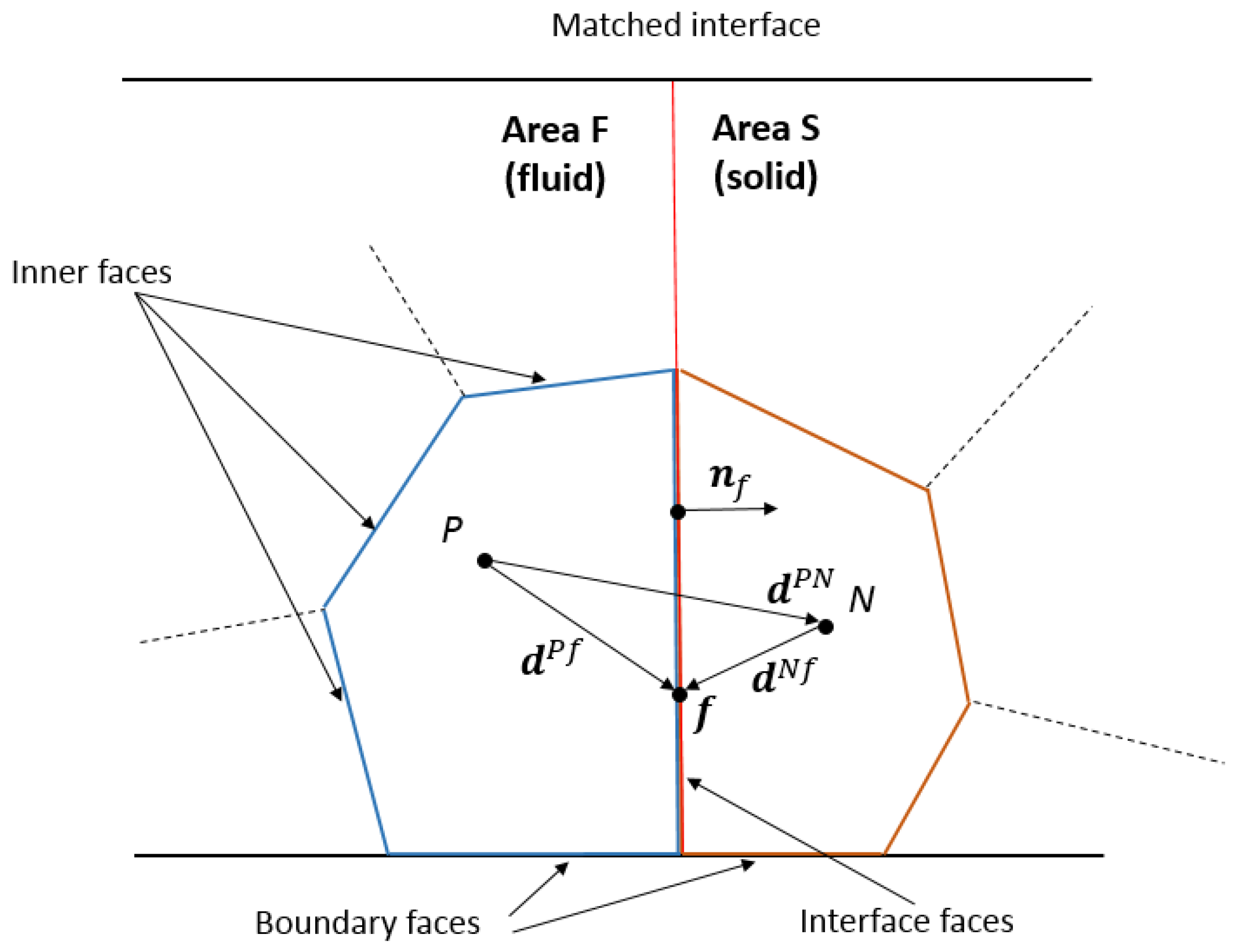
Finite-volume discretization of the direct coupling method is considered by the example of heat transfer discretization (Equations (1) and (2)), considering coupling condition (3) for matched grids on the interface boundary, which form a consistent interface. As an example, we examine the modeling region, comprising two control volumes of the fluid and solid substance, respectively (Figure 2).

In general, the complete form of discrete analogs of differential heat transfer (Equations (1) and (2)) for cells P and N (Figure 2), with the transient term approximated by the Euler implicit scheme [22], is determined by the following expressions:

$${\rho }_F{C}_F\frac{T_P-T_P^{t-1}}{\Delta t}{V}_P+Con{v}_P-D_P=0,$$

(4)

$${\rho }_S{C}_S\frac{T_N-T_N^{t-1}}{\Delta t}{V}_N-D_N=0,$$

(5)

where T_P, T_N—temperature values in P and N cell centers at the current time step, $T_P^{t-1}$, $T_N^{t-1}$—temperature values in P and N cell centers at the previous time step, Conv_P—convective term for cell P at the current time step, and D_P, D_N—diffusive terms for cells P and N at the current time step.

The diffusive terms D_P and D_N in (4) and (5) at the current time step are determined by the following expressions:

$$D_P={\displaystyle \sum _{f=face(P_{inner},P_{bound})}{k}_F(\nabla T_f\cdot S_f)}+{\displaystyle \sum _{f=face(P_{interface})}{k}_f(\nabla T_f\cdot S_f)},$$

(6)

$$D_N={\displaystyle \sum _{f=face(N_{inner},N_{bound})}{k}_S(\nabla T_f\cdot S_f)}+{\displaystyle \sum _{f=face(N_{interface})}{k}_f(\nabla T_f\cdot S_f)},$$

(7)

where S_f—area vector with its normal orientation toward the face f, S_f—face area f, T_f—temperature in the face center f at the current time step, $\nabla$T_f—temperature gradient on the face f at the current time step, k_f—thermal conductivity coefficient on interface faces, f = face(P_inner, P_bound)—summing over all internal and external faces, constraining cell P, f = face(P_interface)—summing over all interface faces of the P cell, f = face(N_inner, N_bound)—summing over all internal and external faces, constraining the N cell, and f = face(N_interface)—summing over all interface faces of the N cell.

The temperature gradient on internal and interface faces for arbitrary unstructured grids, considering a correction for nonorthogonality [23] at the n-th iteration of the current time step, is determined by the following expression:

$$\nabla T_f^n=(T_{A_i}^n-T_{A_j}^n)\frac{S_f}{S_f\cdot d^{A_i{A}_j}}+\overline{\nabla T_f^{n-1}}-(\overline{\nabla T_f^{n-1}}\cdot d^{A_i{A}_j})\frac{S_f}{S_f\cdot d^{A_i{A}_j}},$$

(8)

where A_i and A_j—adjacent cells over the face f, $d^{A_i{A}_j}$—A_i and A_j cells center-to-center vector (Figure 2), $T_{A_i}^n$, $T_{A_j}^n$—temperature value in adjacent cells centers at the n iteration, and $\overline{\nabla T_f^{n-1}}$ = λ_f $\nabla T_{A_i}^{n-1}$ + (1 − λ_f)$\nabla T_{A_j}^{n-1}$—interpolated temperature value on the f face at the n − 1 iteration.

Temperature gradient values in the centers of cells can be calculated by the Green–Gauss algorithm [20]:

$$\nabla T_{A_i}=\frac{1}{V_{A_i}}{\displaystyle \sum _{f=face(A_i)}{T}_f{S}_f},$$

(9)

In the convective term of the discrete analog of the differential heat transfer equation in subarea F (4) on the interface faces, featuring a coupling boundary, a no-slip boundary condition is accepted. As a result, all velocity components u_f on the interface faces in subarea F are zeros, and the convective term of the discrete analog of the differential heat transfer equation for cell P at the current time step takes the following form:

$$Con{v}_P={\rho }_F{C}_F{\displaystyle \sum _{f=face(P_{inner},P_{bound})}{T}_f(u_f\cdot S_f)},$$

(10)

where u_f—velocity in the face center f at the current time step, T_f—temperature on the face f at the current time step, and f = face(P_inner, P_bound)—summing over all internal and external faces constraining cell P.

The values of the unknown variables T_f and u_f in expression (10) for external faces are determined by calculation model boundary conditions, whereas for internal faces, they can be calculated by any well-known approximation scheme [20]. For example, when approximation scheme CD is used, the values of the variables T_f and u_f on internal faces are determined by the weighted interpolation method:

$$T_f={\lambda }_f{T}_{A_i}+(1-{\lambda }_f)T_{A_j},$$

(11)

$$u_f={\lambda }_f{u}_{A_i}+(1-{\lambda }_f)u_{A_j},$$

(12)

where A_i and A_j—adjacent cells over the internal face f, λ_f—geometric interpolation coefficient value for the face f, $T_{A_i}$, $T_{A_j}$—temperature values in adjacent A_i and A_j cells’ centers at the current time step, and $u_{A_i}$, $u_{A_j}$—velocities in adjacent A_i and A_j cells’ centers at the current time step.

Geometric interpolation coefficient value λ_f for cells A_i and A_j over the face f (Figure 2) is determined by the following expression:

$${\lambda }_f=\frac{\left|n_f\cdot d^{A_{i}f}\right|}{\left|n_f\cdot d^{A_{i}f}\right|+\left|n_f\cdot d^{A_{j}f}\right|},$$

(13)

where $d^{A_{i}f}$ and $d^{A_{j}f}$—vectors constructed between the centers of the A_i and A_j cells and the face f (Figure 2).

For the adjacent cells P and N over the interface (Figure 2), taking into consideration (3) and the temperature match T_f on the interface faces, the expression for thermal flows can be written as follows:

$$q_P=q_N=-k_F\frac{T_P-T_f}{d^{Nf}}=-k_S\frac{T_f-T_N}{d^{Pf}}=-k_f\frac{T_P-T_N}{d^{PN}},$$

(14)

where k_f—thermal conductivity coefficient on the interface face f, q_P, q_N—thermal flows on the side of cells P and N, T_P and T_N—temperature values in P and N cells’ centers, and d^PN—vector, constructed between P and N cells’ centers (Figure 2).

When calculating the average coefficient value k_f on the interface faces, differences in the thermal conductivity coefficients and geometric parameters of cells in the coupling area should be taken into consideration. In the case of media coupling with significantly different thermophysical properties, common methods of interpolating thermal conductivity on faces in the coupling area, such as geometric mean or arithmetic mean averaging, can cause excessive error, and their application is limited by slight changes in coefficients of fluid and solid body thermal conductivity. As shown in [24,25,26], the most accurate and universal method, which takes into consideration thermal–physical property differences and the coupling media grid model nonuniformity, is the harmonic-average method of calculating the thermal conductivity coefficient considering the grid model nonuniformity:

$$k_f=\frac{1}{\frac{{\lambda }_f}{k_F}+\frac{1-{\lambda }_f}{k_S}},$$

(15)

where k_F and k_S—thermal conductivity coefficients of fluid and solid substances, respectively, and λ_f—geometric interpolation coefficient value for the interface face f (13).

Equation (14) allows for simultaneously solving the system of Equations (1) and (2), taking the same approach to thermal conductivity equation discretization on the side of both the fluid and solid body.

The finite-volume discretization of thermal conductivity Equations (1) and (2) considering (14) will result in a general system of algebraic equations, solved simultaneously in fluid and solid body subareas. For instance, for an arbitrary cell P (Figure 2), the following equation is composed:

$$a_P{T}_P+a_{PN}{T}_N+{\displaystyle \sum _{i=nb(P)}{a}_i{T}_i}=b_P,$$

(16)

where a_P—diagonal coefficient of cell P, a_PN—off-diagonal coefficient determining the connection between cell P and cell N over the matched interface faces in the fluid and solid body coupling area, a_i—off-diagonal coefficients determining the connection of cell P with cells of the calculated subarea F over the common (internal) faces, b_P—the right side, and i = nb(P)—summing over all adjacent cells i with common faces with cell P.

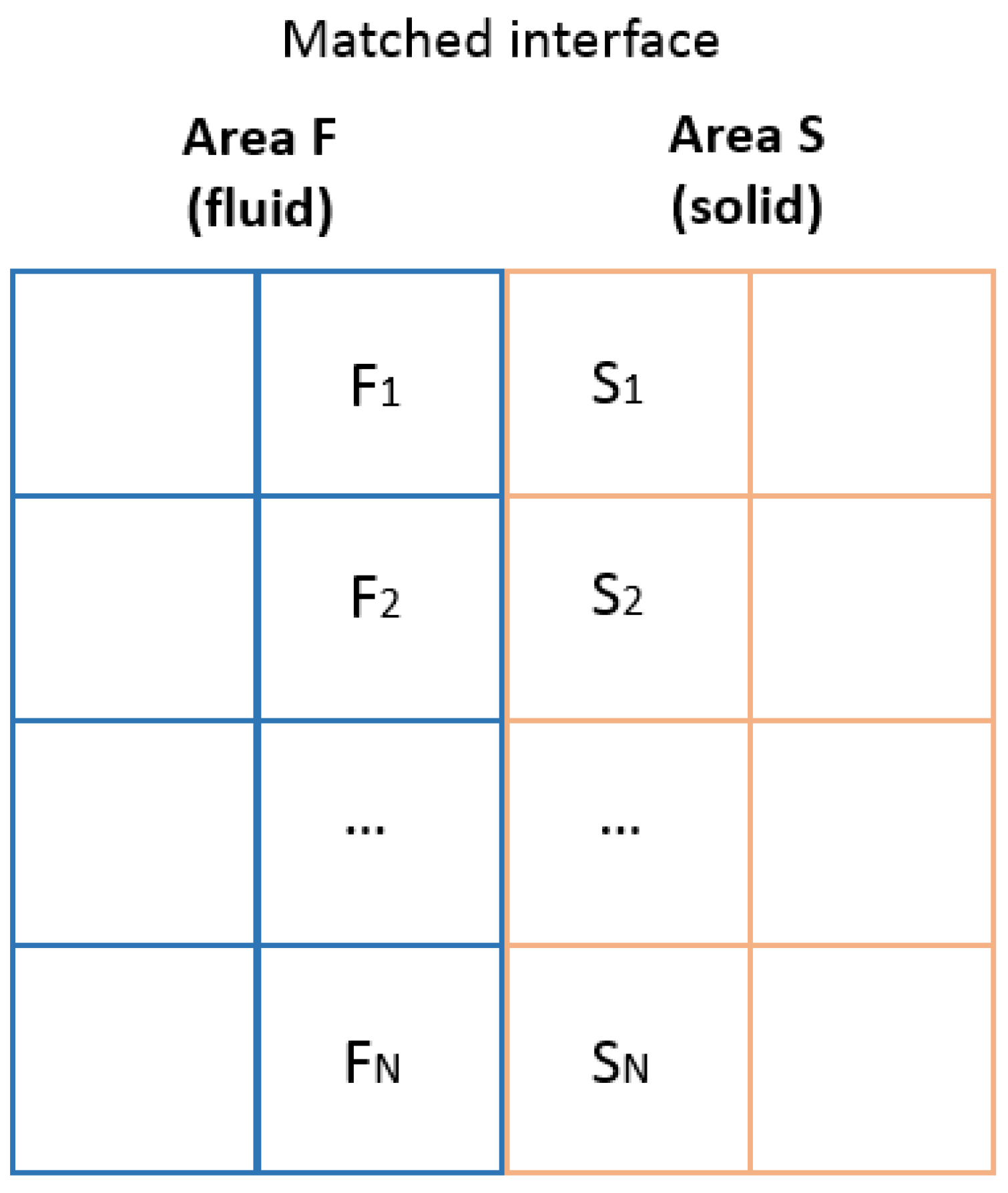
As a result, for a grid model comprising the two matched calculated subareas F and S (Figure 3), SLAE (17) is formed, which can be solved by one of the methods detailed in [20,27,28].

$$\left(\begin{array}{cccccc}{a}_{F_1}& \cdots & 0& a_{F_1,S_1}& \cdots & 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0& \cdots & a_{F_N}& 0& \cdots & a_{F_N,S_N}\\ a_{F_1,S_1}& \cdots & 0& a_{S_1}& \cdots & 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0& \cdots & a_{F_N,S_N}& 0& \cdots & a_{S_N}\end{array}\right)(T)=(b),$$

(17)

where $a_{F_i}$, i$\in$[1…N]—diagonal coefficients of cells in subarea F, $a_{S_i}$, i$\in$[1…N]—diagonal coefficients of cells in subarea S, $a_{F_i{S}_i}$—off-diagonal coefficients determining the connection between cells F_i and S_i over the interface faces, (T)—vector of sought temperatures in the cell centers, and (b)—the right-side vector.

For simplification purposes, SLAE (17) does not show off-diagonal coefficients, determining the connection of cells over internal faces. Further, we write the matrix SLAE (17) coefficients’ form at the n-th iteration of the current time step, disregarding boundary conditions.

The form of SLAE (17) diagonal coefficients for cells of subarea F is:

$$a_{F_i}=\frac{{\rho }_F{C}_F}{\Delta t}{V}_{F_i}+a_{F_i}^{inner}+a_{F_i}^{interface}.$$

(18)

Term $a_{F_i}^{inner}$ in (18) is formed due to cell F_i being adjacent to cells of subarea F over the internal face f:

$$a_{F_i}^{inner}={\displaystyle \sum _{f=face(F_i^{inner})}\left(C_F{\rho }_F{\lambda }_f{u}_f^n\cdot S_f-k_F\frac{S_f}{n_f\cdot d^{F_i{F}_j}}\right)},$$

(19)

where f = face($F_i^{inner}$)—summing over all internal faces of cell F_i, and F_j—cell adjacent to cell F_i over the internal face f.

Term $a_{F_i}^{interface}$ in (18) is formed due to cell F_i being adjacent to cells of subarea S over interface faces f:

$$a_{F_i}^{interface}={\displaystyle \sum _{f=face(F_i^{interface})}\left(-k_f\frac{S_f}{n_f\cdot d^{F_i{S}_i}}\right)},$$

(20)

where f = face($F_i^{interface}$)—summing over all interface faces of cell F_i, and S_i—cell adjacent to cell F_i over the interface face f.

The form of SLAE (17) diagonal coefficients for cells of subarea S is:

$$a_{S_i}=\frac{{\rho }_S{C}_S}{\Delta t}{V}_{S_i}+a_{S_i}^{inner}+a_{S_i}^{interface}.$$

(21)

Term $a_{S_i}^{inner}$ in (21) is formed due to cell S_i being adjacent to cells of subarea S over internal faces f:

$$a_{S_i}^{inner}={\displaystyle \sum _{f=face(S_i^{inner})}\left(-k_S\frac{S_f}{n_f\cdot d^{S_i{S}_j}}\right)},$$

(22)

where S_i—cell adjacent to cell S_j over the internal face f.

Term $a_{S_i}^{interface}$ is formed due to cell S_i being adjacent to cell F_i over interface faces f:

$$a_{S_i}^{interface}={\displaystyle \sum _{f=face(S_i^{interface})}\left(-k_f\frac{S_f}{n_f\cdot d^{S_i{F}_i}}\right)}.$$

(23)

The form of SLAE (17) off-diagonal coefficients determining the connection between cells in subarea F over internal faces f is:

$$a_{F_i{F}_j}={\displaystyle \sum _{f=face(F_i^{inner})}\left(C_F{\rho }_F(1-{\lambda }_f)u_f^n\cdot S_f+k_F\frac{S_f}{n_f\cdot d^{F_i{F}_j}}\right)}.$$

(24)

The form of SLAE (17) off-diagonal coefficients determining the connection of cells from subarea F with cells of subarea S over interface faces f is:

$$a_{F_i{S}_i}=a_{S_i{F}_i}={\displaystyle \sum _{f=face(F_i^{interface})}{k}_f\frac{S_f}{n_f\cdot d^{F_i{S}_i}}}.$$

(25)

The form of SLAE (17) off-diagonal coefficients determining the connection between cells of subarea S over internal faces f is:

$$a_{S_i{S}_j}={\displaystyle \sum _{f=face(S_i^{inner})}{k}_S\frac{S_f}{n_f\cdot d^{S_i{S}_j}}}.$$

(26)

The form of SLAE (17) right-hand side coefficients for cells of subarea F is:

$$b_{F_i}=\frac{{\rho }_F{C}_F}{\Delta t}{V}_{F_i}+b_{F_i}^{inner}+b_{F_i}^{interface},$$

(27)

where the terms $b_{F_i}^{inner}$и $b_{F_i}^{interface}$ have the following form:

$$b_{F_i}^{inner}=k_F{S}_f{{\displaystyle \sum _{f=face(F_i^{inner})}\left[\overline{\nabla T_f}\cdot n_f-\frac{\overline{\nabla T_f}\cdot d^{F_i{F}_j}}{n_f\cdot d^{F_i{F}_j}}\right]}}^{n-1},$$

(28)

$$b_{F_i}^{interface}=k_f{S}_f{{\displaystyle \sum _{f=face(F_i^{interface})}\left[\overline{\nabla T_f}\cdot n_f-\frac{\overline{\nabla T_f}\cdot d^{F_i{S}_i}}{n_f\cdot d^{F_i{S}_i}}\right]}}^{n-1}.$$

(29)

The form of SLAE (17) right-hand side coefficients for cells of subarea S is:

$$b_{S_i}=\frac{{\rho }_S{C}_S}{\Delta t}{V}_{S_i}+b_{S_i}^{inner}+b_{S_i}^{interface},$$

(30)

where terms $b_{S_i}^{inner}$ и $b_{S_i}^{interface}$ have the following form:

$$b_{S_i}^{inner}=k_S{S}_f{{\displaystyle \sum _{f=face(S_i^{inner})}\left[\overline{\nabla T_f}\cdot n_f-\frac{\overline{\nabla T_f}\cdot d^{S_i{S}_j}}{n_f\cdot d^{S_i{S}_j}}\right]}}^{n-1},$$

(31)

$$b_{S_i}^{interface}=k_f{S}_f{{\displaystyle \sum _{f=face(S_i^{interface})}\left[\overline{\nabla T_f}\cdot n_f-\frac{\overline{\nabla T_f}\cdot d^{S_i{F}_i}}{n_f\cdot d^{S_i{F}_i}}\right]}}^{n-1}.$$

(32)

The direct method described can be applied to calculate conjugate heat transfer problems on models of any dimension. However, the application of the described discretization algorithm of the original Equations (1) and (2) considering (3) is possible only on the models containing matched grids on adjacent boundaries of fluid and solid body subareas. This limitation considerably complicates this method’s applicability in solving most conjugate heat transfer industrial-type problems, their grid models generally consisting of unmatched grid segments, which are independently built for fluid areas and for solid body constructions. In order to solve such problems, it is necessary to ensure that thermal flows match on the unmatched interface boundary with consideration of adjacent cells. Next, a way to modify the direct coupling method is presented, considering the discretization features of Equations (1) and (2) as well as providing conservative thermal flows matching on the unmatched boundaries’ area of fluid and solid body coupling.

2.2. Direct Coupling Method of Fluid and Solid Body Unmatched Subareas

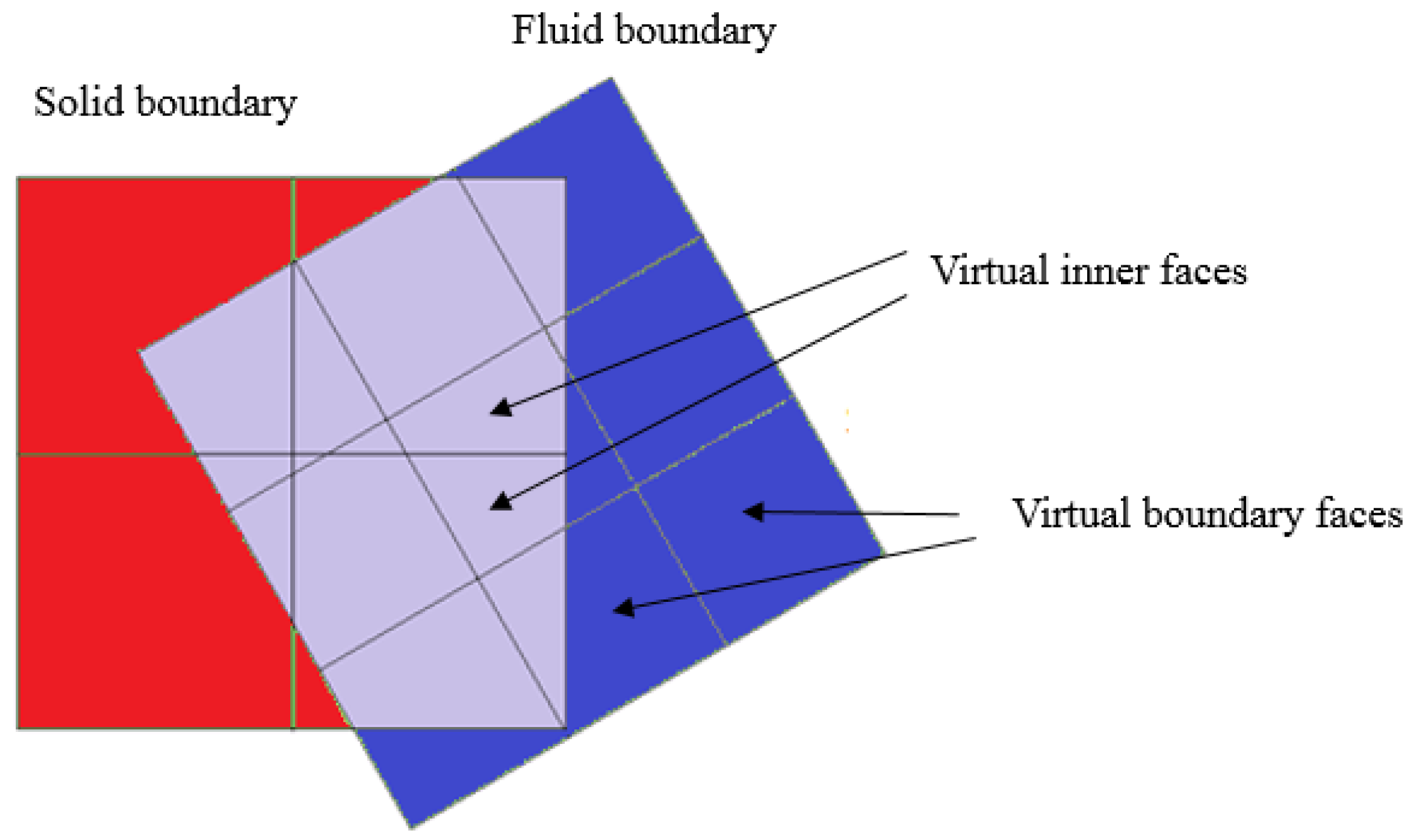
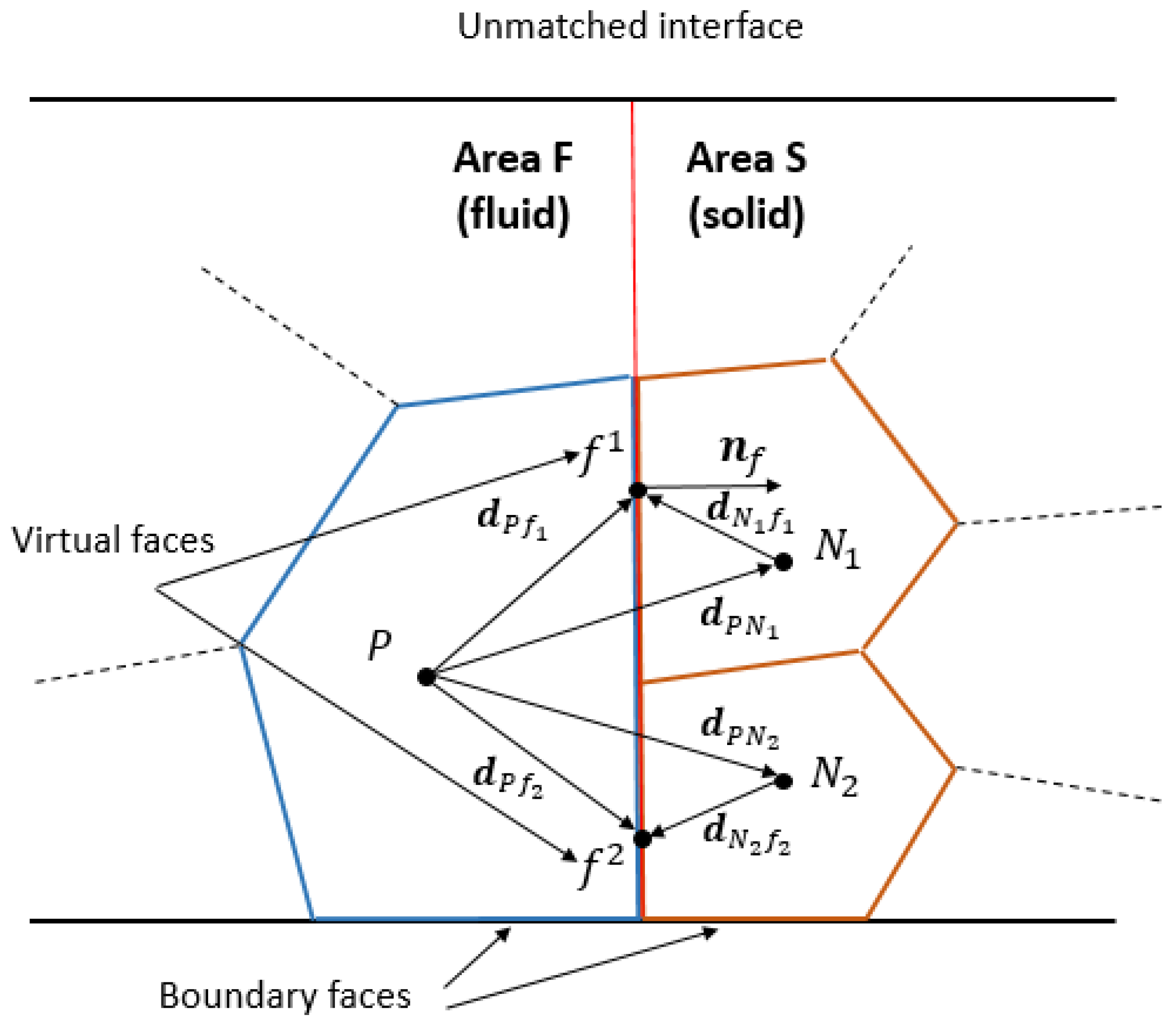
Let us consider a mathematical model of a conjugate heat transfer problem, in which the numerical simulation region consists of unmatched grid segments, featuring calculated subareas of fluid F and solid body S, their adjacent boundaries forming an inconsistent (unmatched) interface (Figure 4). Unmatched interfaces mean adjacent boundaries of unmatched grid segments, the number and position of points and edges on them generally being mismatched.

For coupling unmatched interfaces, the set of initial faces, which are part of an inconsistent interface, is substituted for a set of virtual faces, forming a matched virtual interface. The virtual faces’ geometrical parameters are determined as a result of successively projecting the initial interface faces of subarea F onto all initial interface faces of subarea S. In order to determine the points’ coordinates, formed as a result of face intersection, any algorithm of polygons’ intersections can be applied [29]. The obtained set of virtual faces forms a pair of matched virtual boundaries, through which the connection between cells of unmatched adjacent grid subareas is established (Figure 4).

In general, a virtual interface consists of a set of internal and external virtual faces (Figure 5). Internal virtual faces form the connection between adjacent cells on the interface boundaries. External virtual faces without any connection with cells on the adjacent interface boundary should be processed according to selected boundary conditions.

Finite-volume discretization of the direct coupling method is considered by the example of heat transfer equations discretization (1) and (2) considering coupling condition (3) for the case of unmatched grids on the interface boundary, featuring an inconsistent (unmatched) interface. As an example of an unmatched interface, we examine a calculating area, comprising one control volume of fluid subarea F, adjacent with several control volumes of solid body subarea S (Figure 6).

As in the case of a matched interface, on interface faces in subarea F, featuring the boundary, a no-slip boundary condition is assumed, and a convective term of a discrete analog of a differential heat transfer equation for cell P (4) at the current time step is determined by expression (10).

Further, we examine the diffusive terms modification (6) and (7) of discrete analogs of differential heat transfer equations for subarea F and subarea S on an unmatched interface, considering the transition from initial faces to virtual ones (Figure 6).

A discrete analog of diffusive component (6) for cell P when transferring from initial faces to virtual ones is written as follows:

$$D_P={\displaystyle \sum _{f=face(P_{inner},P_{bound})}{k}_F(\nabla T_f\cdot S_f)}+{\displaystyle \sum _{f=face(P_{interface})}{\displaystyle \sum _v{k}_{f^v}(\nabla T_{f^v}\cdot S_{f^v})}},$$

(33)

where $\nabla T_{f^v}$—scalar quantity gradient value on the virtual face f^v, $k_{f^v}$—thermal conductivity coefficient on the virtual face f^v, and $S_{f^v}$—virtual face area f^v, normally oriented toward the initial face f.

A discrete analog of diffusive component (7) for cell N when transferring from initial faces to virtual ones will be written as follows:

$$D_N={\displaystyle \sum _{f=face(N_{inner},N_{bound})}{k}_S(\nabla T_f\cdot S_f)}+{\displaystyle \sum _{f=face(N_{interface})}{\displaystyle \sum _v{k}_{f^v}(\nabla T_{f^v}\cdot S_{f^v})}},$$

(34)

The thermal conductivity coefficient value on virtual faces $k_{f^v}$ is calculated by analogy with (15).

$$k_{f^v}=\frac{1}{\frac{{\lambda }_{f^v}}{k_F}+\frac{1-{\lambda }_{f^v}}{k_S}},$$

(35)

where ${\lambda }_{f^v}$—geometric interpolation coefficient value for cell P, adjacent to cell N_v over the virtual face f^v (Figure 6), which is determined by the following expression:

$${\lambda }_{f^v}=\frac{\left|n_f\cdot d^{N_v{f}^v}\right|}{\left|n_f\cdot d^{N_v{f}^v}\right|+\left|n_f\cdot d^{P{f}^v}\right|}.$$

(36)

The gradient value $\nabla T_{f^v}$ on the virtual face f^v, formed between the adjacent cells P and N_v (Figure 6), considering nonorthogonal correction at n-th iteration of the current time step, equals:

$$\nabla T_{f^v}=(T_N^n-T_P^n)\frac{S_{f^v}}{S_{f^v}\cdot d^{P{N}_v}}+\overline{\nabla T_{f^v}^{n-1}}-(\overline{\nabla T_{f^v}^{n-1}}\cdot d^{P{N}_v})\frac{S_{f^v}}{S_{f^v}\cdot d^{P{N}_v}},$$

(37)

where $T_N^n$, $T_P^n$—temperature value in adjacent cells centers at the n iteration, $d^{PN}$—P and N_v cells’ center-to-center vector (Figure 6), and $\overline{\nabla T_{f^v}^{n-1}}={\lambda }_{f^v}\nabla T_P^{n-1}+(1-{\lambda }_{f^v})\nabla T_{N_v}^{n-1}$—interpolated temperature gradient value on the virtual face f^v, obtained at the previous iteration.

The temperature gradient value $\nabla T_P$ in the cell center P, positioned on an unmatched interface (Figure 6), is calculated by the Green–Gauss algorithm:

$$\nabla T_P=\frac{1}{V_P}\left({\displaystyle \sum _{f=face(P_{inner},P_{bound})}{T}_f{S}_f}+{\displaystyle \sum _{f=face(P_{interface})}{T}_f^{av}{S}_f}\right),$$

(38)

where $T_f^{av}=\frac{{\displaystyle \sum _v{T}_{f^v}{S}_{f^v}}}{{\displaystyle \sum _v{S}_{f^v}}}$—averaged temperature value on the interface face f.

For the cell N_v, which is positioned on an unmatched interface (Figure 6), the temperature gradient value $\nabla T_{N_v}$ is found by analogy with (38).

As a result of the above transformations of diffusive components into discrete analogs (7) and (8), the terms, considering the connection of adjacent cells over virtual faces, are added to each cell, which is positioned on an unmatched interface (Figure 6).

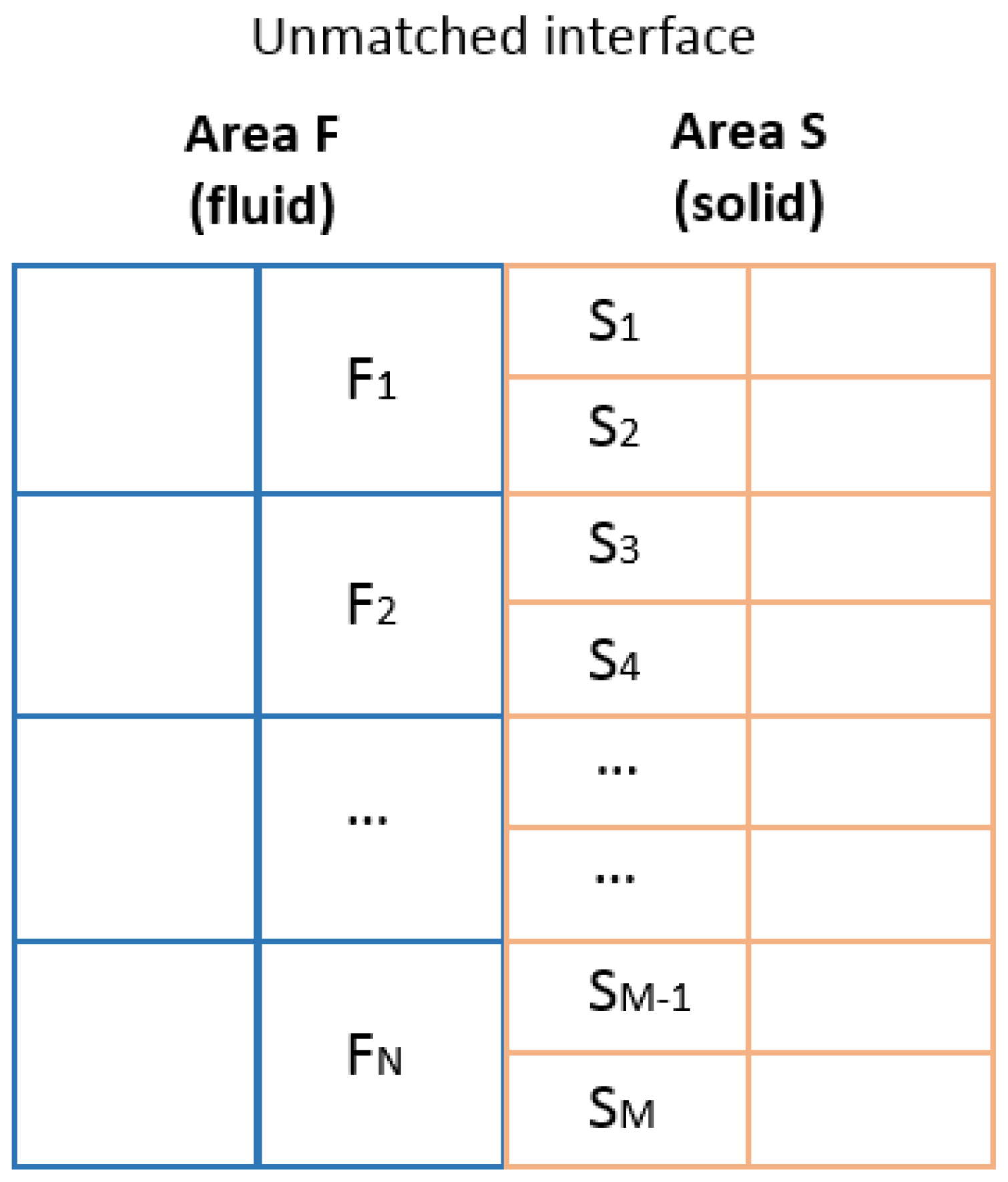
In general, for a grid model consisting of two unmatched calculated subareas F and S (Figure 7), SLAE (39) is formed, which can be solved by one of the methods specified in [20,27,28].

$$\left(\begin{array}{cccccccc}{a}_{F_1}& \cdots & 0& a_{F_1,S_1}& a_{F_1,S_2}& \cdots & 0& 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0& \cdots & a_{F_N}& 0& 0& \cdots & a_{F_N,S_{M-1}}& a_{F_N,S_M}\\ a_{F_1,S_1}& \cdots & 0& a_{S_1}& \cdots & \cdots & 0& 0\\ a_{F_1,S_2}& \cdots & 0& \cdots & a_{S_2}& \cdots & 0& 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0& \cdots & a_{F_N,S_{M-1}}& 0& 0& \cdots & a_{S_{M-1}}& 0\\ 0& \cdots & a_{F_N,S_M}& 0& 0& \cdots & 0& a_{S_M}\end{array}\right)(T)=(b),$$

(39)

where $a_{F_i}$, i$\in$[1…N]—diagonal coefficients of cells in subarea F, $a_{S_j}$, j$\in$[1…M]—diagonal coefficients of cells in subarea S, $a_{F_i{S}_j}$—off-diagonal coefficients determining the connection between cells F_i and S_j over virtual faces, (T)—vector of sought temperatures in the cells’ centers, and (b)—the right-side vector.

For simplification purposes, a system of Equations (39) does not show off-diagonal coefficients, determining the connection of cells over internal faces. Next, we write the form of matrix SLAE (39) coefficients at the n-th iteration of the current time step, disregarding boundary conditions.

The form of SLAE (39) diagonal coefficients for cells of subarea F is:

$$a_{F_i}=\frac{{\rho }_F{C}_F}{\Delta t}{V}_{F_i}+a_{F_i}^{inner}+a_{F_i}^{interface},$$

(40)

Term $a_{F_i}^{inner}$ in (40) is formed due to cell F_i being adjacent to cells of subarea F over internal faces f, similarly to (19). Term $a_{F_i}^{interface}$ is formed due to cell F_i being adjacent to cells of subarea S over virtual faces f^v:

$$a_{F_i}^{interface}={\displaystyle \sum _{f=face(F_{interface})}{\displaystyle \sum _v\left(-k_{f^v}\frac{S_{f^v}}{n_f\cdot d^{F_i{S}_j}}\right)}}.$$

(41)

The form of SLAE (39) diagonal coefficients for cells of subarea S is:

$$a_{S_i}=\frac{{\rho }_S{C}_S}{\Delta t}{V}_{S_i}+a_{S_i}^{inner}+a_{S_i}^{interface}.$$

(42)

Term $a_{S_i}^{inner}$ in (42) is formed due to cell S_i being adjacent to cells of subarea S over internal faces f, similarly to (22). Term $a_{S_i}^{interface}$ is formed due to cell S_i being adjacent to cells of subarea F over virtual faces f^v:

$$a_{S_i}^{interface}={\displaystyle \sum _{f=face(S_{interface})}{\displaystyle \sum _v\left(-k_{f^v}\frac{S_{f^v}}{n_f\cdot d^{S_i{F}_j}}\right)}}.$$

(43)

SLAE (39) off-diagonal coefficients $a_{F_i{F}_j}$, determining the connection between cells in subarea F over internal faces f, are formed by analogy with (24). The form of SLAE (39) off-diagonal coefficients, determining the connection of cells in subarea F with cells in subarea S over virtual faces f^v, is the following:

$$a_{F_i{S}_j}=a_{S_i{F}_j}={\displaystyle \sum _{f=face(F_{interface})}{\displaystyle \sum _v\left(k_{f^v}\frac{S_{f^v}}{n_{f^v}\cdot d^{F_i{S}_j}}\right)}}.$$

(44)

SLAE (39) off-diagonal coefficients, determining the connection between cells in subarea S over internal faces f, are formed by analogy with (26).

The form of SLAE (39) right-hand side coefficients for cells of subarea F is:

$$b_{F_i}=\frac{{\rho }_F{C}_F}{\Delta t}{V}_{F_i}+b_{F_i}^{inner}+b_{F_i}^{interface},$$

(45)

where term $b_{F_i}^{inner}$ is formed by analogy with (28), while term $b_{F_i}^{interface}$ is written as:

$$b_{F_i}^{interface}={{\displaystyle \sum _{f=face(F_{interface})}{\displaystyle \sum _v{k}_{f^v}{S}_{f^v}}\left[\overline{\nabla T_{f^v}}\cdot n_f-\frac{\overline{\nabla T_{f^v}}\cdot d^{F_i{S}_j}}{n_f\cdot d^{F_i{S}_j}}\right]}}^{n-1}.$$

(46)

The form of SLAE (39) right-hand side coefficients for cells of subarea S is:

$$b_{S_i}=\frac{{\rho }_S{C}_S}{\Delta t}{V}_{S_i}+b_{S_i}^{inner}+b_{S_i}^{interface},$$

(47)

where term $b_{S_i}^{inner}$ is formed by analogy with (31), while term $b_{S_i}^{interface}$ is written as:

$$b_{S_i}^{interface}={{\displaystyle \sum _{f=face(S_{interface})}{\displaystyle \sum _v{k}_{f^v}{S}_{f^v}}\left[\overline{\nabla T_{f^v}}\cdot n_f-\frac{\overline{\nabla T_{f^v}}\cdot d^{S_i{F}_j}}{n_f\cdot d^{S_i{F}_j}}\right]}}^{n-1}.$$

(48)

The described direct coupling method allows for the simultaneous discretization of heat transfer equations for fluid and solid body subareas as well as building a uniform “coupled” SLAE relative to the temperature variable on grid models, containing unmatched boundaries in the fluid and solid body coupling area. The resulting virtual interface provides conservatism and conserves the total energy across planar and curved interfaces, because the heat flux flowing out of one side of the interface will always be equal to the heat flux flowing in from the opposite side of the interface. Curvilinear interfaces can affect the accuracy of the calculation of the effective area, which affects the heat transfer coefficient and is most pronounced in non-stationary problems. The method does not require the initial grid modification and allows for matching thermal flows on unmatched interface boundaries, considering the adjacent cells’ connection over the set of virtual faces, thus forming additional terms in the SLAE calculation model. The method application considerably enhances the ability to calculate conjugate heat transfer industrial-type problems, their grid models consisting of a set of unmatched segments containing fluid flow and solid body subareas.

The described method was realized on the basis of the national software suite LOGOS, aimed at modeling 3D problems of computational hydrodynamics, aerodynamics and heat transfer [30,31,32]. The method efficiency is shown by examples of the numerical simulation of conjugate heat transfer problems [33,34], their grid models built of unstructured, unmatched segments.

3. Numerical Experiments

3.1. Solid Blocks’ Cooling in a Flat Channel

The method implementation is shown by the example of the numerical simulation of cooling six solid blocks with a volumetric heat source, which are mounted in a flat rectangular channel, by a laminar flow of incompressible fluid under forced convection [33]. Previously, we presented this problem’s numerical simulation results on a matched grid model in the LOGOS software suite [18], which showed good agreement of the results obtained with the results listed in [33].

Computational region geometry is outlined in Figure 8.

A flat rectangular channel has a height H = 1 m and a length L = 20H. Six identical solid blocks of a length H and a height h = 0.25H are located inside the channel directly against the lower wall. The first block left bound is located at a distance of 5.6H from the input. The gaps between the blocks are identical and equal to H. Each block is heated by a volume heat source with a Q = 71.4 W/m³ specific capacity. The channel walls are immovable, impermeable, and thermally insulated. A no-slip boundary condition is set for upper and lower walls, and a symmetry condition is set for front and back walls. On the left side of the channel, an input flow is set with a zero temperature and a unit velocity vector, directed along the X axis. On the right boundary, the pressure boundary condition is set. When calculating, the media physical parameters were set in such a way as to make the values of the non-dimensional quantities listed in [33] equal to: Re = 100 and Pr = 0.7. The aim of this numerical experiment is to compare the results obtained on four grid models, built with the gradual refinement of the grid in the solid blocks’ region (Figure 9). One of the grid models has matched grids on adjacent fluid and solid blocks’ boundaries (Figure 9a); the rest of the grid models are unmatched.

The problems were calculated in parallel mode on 12 processors. The boundary coupling of adjacent subarea boundaries of fluid and solid blocks was carried out by the interface, realized according to the above method. Figure 10 shows the calculated profiles of the temperature distribution along the channel at the y = 0.275 m level (in the fluid region above the solid blocks) for grids shown in Figure 9.

Figure 11 shows the profiles of the absolute values of design temperature deviations on unmatched grids (Figure 9b–d) relative to the design temperatures on the matched grid (Figure 9a).

The design temperature profiles and profiles of temperature deviations shown in Figure 10 and Figure 11, which were obtained by the above coupling method, demonstrate that unmatched grids on the fluid and solid blocks’ boundary do not have any considerable impact on the temperature field pattern.

3.2. Mixed Convection in a Square Cavity

The method efficiency is considered by the example of the numerical simulation of a mixed convection problem in a square cavity with a solid block [34]. The computational region geometry is outlined in Figure 12.

In the selected calculation model, the square cavity side length is L = 1 m. The cavity contains a solid block with a side length d = 0.6 m, placed in the center, as well as an inlet and outlet w = 0.1 m in size.

The constant dimensionless temperature T_w = 1 is set on the right vertical cavity wall, the other walls being thermally insulated. At the cavity input, the temperature T = 0 is set and the input flow velocity U = 1 m/s is directed along the X axis. Viscous laminar incompressible flow disregarding viscous dissipation is considered in the problem. When calculating, the media physical parameters were set in such a way as to make the values of the non-dimensional quantities listed in [33] equal to: Re = 100 and Pr = 0.71.

The calculations were made on four grid models, built with the gradual refinement of the grid in the solid blocks’ region. The computational grid segments are shown in Figure 13. The grid model, shown in Figure 13a, has matched grids on adjacent fluid and solid blocks’ boundaries; the rest of the grid models, shown in Figure 13b–d, are unmatched.

The problems were calculated in parallel mode on 12 processors. The boundary coupling of adjacent subarea boundaries of fluid and solid blocks was carried out by the interface, realized according to the above method. Figure 14 shows the calculated distribution of temperature isolines, obtained on computational grids, which are shown in Figure 13, as well as the distribution of the temperature isolines obtained in [34].

The obtained temperature isolines distribution (Figure 14), found as a result of numerical simulation using the above method on unmatched grid models (diagrams b, c, d, Figure 14), demonstrates good agreement with the results obtained on the matched grid model (diagram a, Figure 14), as well as with the results listed in [34].

4. Conclusions

This paper presents a description of a numerical method that takes into account the features of the discretization of the heat transfer equation by the finite volume method when solving conjugate heat transfer problems containing arbitrary unmatched grids at the interface between liquid and solids. The method does not require modification of the original grid in the interface area and allows for combining adjacent, inconsistent fragments of the unstructured grid into a single computational area using virtual interfaces that take into account the connections of neighboring cells through virtual faces. The discretization of the heat transfer equation takes into account the different scales of the cells and the sharply different thermophysical properties of liquid and solid media. A unified approach to the matching of mass (presented in previous works) and heat fluxes in the area of conjugation of inconsistent grid subdomains has been worked out. The algorithm of the method was implemented as part of the LOGOS software package in terms of the hydrodynamics solver, with the help of test calculations that were carried out. The results of the modeling test problems of conjugate heat transfer using this method on grid models containing unstructured inconsistent grids in the area of conjugation of a liquid and a solid showed good agreement with the results obtained on a consistent grid model. The implementations of the numerical scheme presented in this paper may be of interest to a wide range of CFD code developers and researchers in the field of conjugate heat transfer. The further development of the method will make it possible to use it in solving problems with partial intersection in the conjugation region, as well as problems with moving bodies and sliding meshes.