Grid-Characteristic Method for Calculation of Discontinuous Non-Steady Flows of a Multicomponent Reacting Gas in Channels

Abstract

This paper is devoted to the description of computational algorithms for modeling quasi-one-dimensional non-steady flows of a multicomponent reacting gas. The particularity of the developed modeling technique is that the paths of strong and weak discontinuities are mobile computational nodes, and the parameters for them are calculated using special algorithms. A set of programs has been developed, which can be used to solve the problems of the reacting gas dynamics that are of applied importance, as well as serve as an illustrator for physical gas dynamics training courses. The paper provides the results of the numerical modeling of the supersonic flow in a flat channel simulating the operation of experimental facilities of the Institute for Problems in Mechanics and the Institute of Physics and Technology. A satisfactory correlation between the calculated and experimental data has been obtained.

1. Introduction

When solving many applied problems, numerically examining unsteady flows of multicomponent gas mixture with physicochemical transformations is required. In this case, in the flow field, there may be zones of rapid changes in the flow parameters or their gradients; they may include shock waves, contact discontinuities (strong discontinuities), and boundary characteristics of expansion wave fans (weak discontinuities) [1,2,3,4,5,6,7,8]. Moreover, the works [1,2,3,4,5,6,7] describe methods in which shock waves and contact discontinuities are clearly distinguished. Work [8] is a typical representative of a large number of works, in which reacting flows with shock waves and contact discontinuities are simulated using the shock-capturing method with the condensation of grid lines in areas with a large gradient of parameters. The number of discontinuities can change as a result of the interaction of existing ones and the emergence of new ones. To model such flows, it is necessary to use special methods. This paper presents the application of the original grid-characteristic method, which allows tracking the parameter positions and differences for all types of discontinuities.

Methods with explicit isolation of discontinuity surfaces, unlike the shock-capturing method [1,2,3,4,5,6], allow one to construct adaptive difference grids consisting of both fixed and mobile nodes that can move along the paths of the indicated strong and weak discontinuities, gas trajectories, moving boundaries, etc. This approach provides high-precision results on relatively coarse grids.

The computing algorithms developed by the authors were implemented as a set of programs, including subsystems designed for setting initial data and defining the thermodynamic properties of substances and the mechanisms of chemical transformations, as well as a system for visualizing the results of calculations, which have no analogues. The original visualization system allows one to track the distribution of flow parameters not only at fixed times but also along arbitrary grid lines, the number of which can change during the calculation process.

For the first time, it was proposed to use the self-similar problem of G. M. Bam-Zelikovich as a test problem when modeling both one-dimensional and multidimensional flows of a multicomponent detonating gas behind incident and reflected shock waves. The solution of the system of partial differential equations describing the flow of detonating gas, on average, asymptotically tends to the solution of the problem of G. M. Bam-Zelikovich, which allows one to instantly determine the parameters characterizing plane detonation waves before carrying out multidimensional calculations.

2. Mathematical Model

A quasi-one-dimensional non-steady approximation is used, and the effects of viscosity, heat conduction, and diffusion are neglected. The model is based on the equations of mass, momentum, and energy transfer, written in differential form within the regions of the solution smoothness, and in integral form, namely in the form of dynamic and kinematic compatibility conditions, at the areas of strong and weak discontinuities. The corresponding hyperbolic system of quasilinear differential equations in partial derivatives in the regions of flow continuity can be stated in the characteristic form, as follows [6,9]:

$$dx=(u\pm a)dt,du\pm \frac{1}{\rho a}dp\pm \left(ua\frac{d\ln F}{dx}+{\displaystyle \sum _{i=1}^N\frac{{\rho }_{{\gamma }_i}^{}{h}_T^{}-h_{{\gamma }_i}^{}{\rho }_T^{}}{{\rho }^2{h}_T}}{W}_i\right)dt=0$$

(1)

$$dx=udt, dh-\frac{1}{\rho }dp=0, d{\gamma }_i-\frac{1}{\rho }{W}_{i}dt=0, i=1,\dots ,N$$

(2)

Here, t is time, x is the spatial coordinate, ρ, u, p, and h are density, velocity, pressure, and specific enthalpy of the mixture, respectively, F = F(x) is the channel area, γ_j—are molar mass concentrations of the j-th chemical component, N is the number of components taken into account, W_j is the rate of change in the concentrations of the j-th component per unit volume of the mixture, and

$$a=\sqrt{h_T{\left({\rho }_P{h}_T-{\rho }_T(h_P-1/\rho )\right)}^{-1}}$$

is the speed of sound. The indices “T”, “P”, and “γ_j” denote partial differentiation per the corresponding parameter.

When passing through a shock wave (SW) and a contact discontinuity (CD), the following Rankine–Hugoniot relations are followed [9,10]:

$$\begin{gathered} {\mathsf{\rho }}_1(D-u_1)={\mathsf{\rho }}_2(D-u_2) \\ {p}_1+{\rho }_1{(D-u_1)}^2=p_2+{\rho }_2{(D-u_2)}^2 \\ {\rho }_1(D-u_1)\left(h_1+\frac{{(D-u_1)}^2}{2}\right)={\rho }_2(D-u_2)\left(h_2+\frac{{(D-u_2)}^2}{2}\right) \end{gathered}$$

(3)

Here, D is the SW velocity (for CD, D = u₁ = u₂), the index “1” marks the parameters prior to the wave, and the index “2” marks the parameters after the wave. When passing through the shock wave in a non-equilibrium flow, the ratios are supplemented by the concentration constancy conditions:

$${\gamma }_{1i}={\gamma }_{2i}.$$

The thermodynamic properties of the reacting gas are defined using the model of a multicomponent perfect gas under the assumption of an equilibrium population of the energy levels corresponding to all internal degrees of freedom of molecules and atoms [11]. In the indicated case, the specific thermodynamic Gibbs potential has the following form:

$$G(p,T,\gamma )={\displaystyle \sum _{(i)}{\gamma }_i[RT\ln (p{\gamma }_i}/p_0{\displaystyle \sum _{(j)}{\gamma }_j})+G_i^0(T)].$$

(4)

Here, R is the universal gas constant, p₀ = 101,325 Pa is the standard pressure, $G_i^0(T)$ are the known functions, which are the temperature parts of the standard Gibbs molar potentials for the individual components of the mixture [11]. Other thermodynamic values can be expressed via the Gibbs potential and its partial derivatives. In particular, the thermal and caloric equations of state have the following form:

$$\mathsf{\rho }=p/(RT{\displaystyle \sum _{i=1}^N{\gamma }_i)}, h={\displaystyle \sum _{i=1}^N{\gamma }_i{H}_i^0(T)}$$

(5)

where

$$H_i^0(T)=G_i^0(T)-T\frac{d{G}_i^0(T)}{dT}.$$

In the case of a nonequilibrium course of chemical transformations, an arbitrary mechanism of chemical reactions can be formulated as follows [9]:

$${\displaystyle \sum _{i=1}^N{\overrightarrow{\nu }}_i^{(r)}{M}_i{ }_{\underset{{\overleftarrow{W}}^{(r)}}{\leftarrow }}^{\stackrel{{\overrightarrow{W}}^{(r)}}{\to }}{\displaystyle \sum _{i=1}^N{\overleftarrow{\nu }}_i^{(r)}{M}_i}}, r=1,\dots ,N_r.$$

(6)

Here, ${\nu }_i^{(r)}$ are stoichiometric coefficients, and M_i is the symbol of the molecule of the i-th substance. The number of elementary reactions per time unit within a volume unit ${\overrightarrow{\overleftarrow{W}}}^{(r)}$ depends on the temperature, pressure, and volumetric concentrations of the reagents:

$${\overrightarrow{\overleftarrow{W}}}^{(r)}={\overrightarrow{\overleftarrow{K}}}^{(r)}(p,T){\displaystyle \prod _{(i)}{(\rho {\gamma }_i)}^{{\overrightarrow{\overleftarrow{\nu }}}_i^{(r)}}}$$

(7)

To approximate the dependence of the rate constants of direct reactions on temperature and pressure, the generalized Arrhenius formula is used:

$$\overrightarrow{K}(p,T)=A{(T/T_0)}^n{(p/p_0)}^m\exp (-\frac{E}{T})$$

(8)

To ensure that the entropy is non-decreasing in nonequilibrium processes and to ensure the correct calculation of heat release, the relationship between the rate constants of direct and reverse reactions is used [11]:

$$\frac{{\overleftarrow{K}}^{(r)}(p,T)}{{\overrightarrow{K}}^{(r)}(p,T)}=\exp \left[{\displaystyle \sum _{i=1}^N({\overleftarrow{\nu }}_i^{(r)}-{\overrightarrow{\nu }}_i^{(r)})\left(\frac{G_i^0(T)}{RT}+\ln \frac{RT}{P_0}\right)}\right]$$

(9)

Here, A, n, m, and E are the given constants. The number of moles of the i-th substance formed per time unit within a volume unit of the mixture is written in the traditional way, as follows:

$$W_i={\displaystyle \sum _{r=1}^{N_r}({\overleftarrow{\nu }}_i^{(r)}-{\overrightarrow{\nu }}_i^{(r)})({\overrightarrow{W}}^{(r)}-{\overleftarrow{W}}^{(r)})}$$

(10)

In the case of an equilibrium course of chemical transformations, the concentrations are implicitly defined via the functions of temperature and pressure and can be calculated by solving the equations of chemical equilibrium and the conservation of elemental composition:

$$\ln (\rho RT{\gamma }_i/p_0)+\frac{G_i^0(T)}{RT}={\displaystyle \sum _{K=1}^{N_e}{A}_K^i{Z}_K} , i=1,\dots ,N,{\displaystyle \sum _{i=1}^N{A}_K^i{\gamma }_i}={\gamma }_K^0 , K=1,\dots ,N_e$$

(11)

Here, N_e is the number of elements in the mixture; $A_K^i$ is the composition matrix, and Z_K are unknown values.

To solve the system of Equations (1) and (2), supplemented by Relations (3)–(11), the grid-characteristic method is used with an explicit isolation of all discontinuities formed in the flow field [6,7]. The applied grid lines (design points) can belong to one of the following types: gas trajectory (GT); fixed point (FP); shock wave (SW); contact discontinuity (CD); characteristic of the C+ family (PC+); characteristic of the C− family (PC−); discontinuous characteristics (DC+, DC−); rigid wall (RW); or left (LH) and right (RH) boundaries of the computational domain.

Let us briefly describe the features of the proposed modeling technique.

• Firstly, the calculation is carried out by the marching grid-characteristic method for layers t = const. The flow parameters at a point are determined iteratively until the predetermined accuracy is reached. If convergence is not achieved within the maximum allowable number of iterations, the time step is reduced.
• The flow region being reviewed is divided into sub-regions of the solution smoothness, the boundaries of which are formed by the lines of strong and weak discontinuities, as well as the by left and right boundaries of the computational domain. When interpolating parameters, only points from a single smoothness sub-region are used; they can be located both on the previous layer and on the selected discontinuities.
• The finite difference grid consists of grid lines, each of which is characterized by a unique number, type, coordinate, velocity, and gas parameters. A strong discontinuity (SW, CD) corresponds to two grid lines with the same coordinates and speed of movement and different parameters that satisfy the Rankine–Hugoniot relations. The CD can be the boundary of regions with different chemical compositions and models of the ongoing processes.
• If an intersection of grid lines is detected, the layer is calculated with a variable time step. In this case, the integration step at each iteration is chosen so that the intersection point lies on the calculated layer. After the layer calculation is completed, the intersection is processed depending on its type (

  Table 1. Interaction between grid lines. RP—“the Riemann problem”; T—“transfer of parameters”; TCC—“transfer of parameters” with a change of the characteristic family; RF—shock wave reflection from the wall; RFC—reflection of the characteristic with a change of its family; R—removal of the grid line; SWO—SW origination.

  	№	1	2	3	4	5	6	7	8	9	10
  №	Line	SW+	SW−	CD	PC+	PC−	GT	LHW	RHW	LHB	RHB
  1	SW+	+RP	+RP	+RP	+R, TCC	+T	T	−	+RF	−	+R, RFC
  2	SW−	−	+RP	−	−	+RFC	−	−	−	−	+R
  3	CD	−	+RP	−	−	+T	−	−	−	−	+R, RFC
  4	PC+	+RFC	+T	+T, RFC	−SWO	+T	T	−	+RFC	−	+R, RFC
  5	PC−	−	+R, TCC	−SWO	−	−SWO	−	+RFC	−	−	+R
  6	GT		+T	−	−	+T	−	−	−	+R	+R
  7	LHW	−	+RF	−	−	+RFC	−	−	−	−	+R
  8	RHW	+RF	−	−	+RFC	−	−	−	−	−	−
  9	LHB	+R	+R, RFC	+R, RFC	+R	+R, RFC	+R	−	+R	−	−
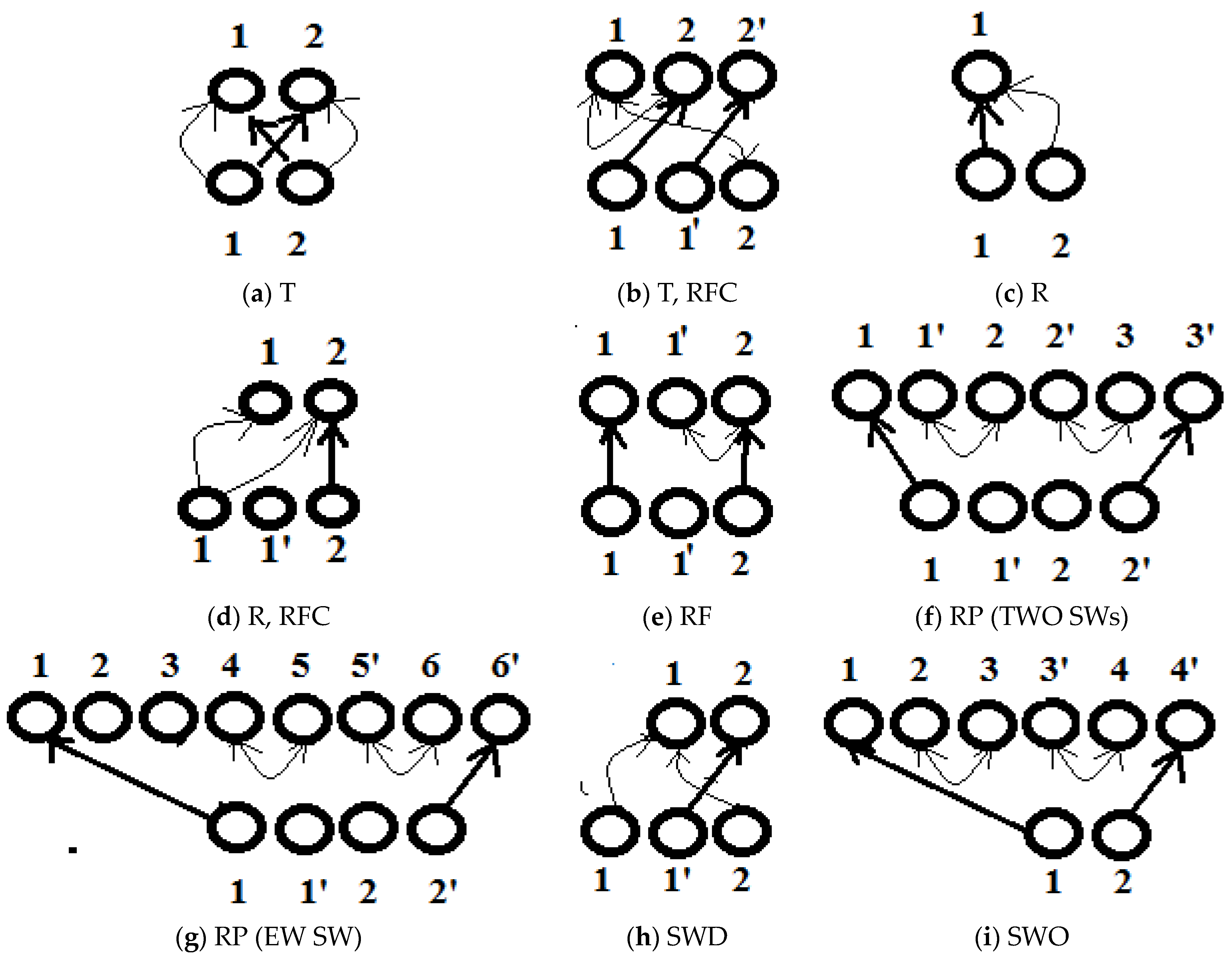
  10	RHB	−	−	−	−	−	+R	−	−	−	−

  ) using a special algorithm; during this process, new grid lines may “emerge”, and old ones may “disappear”.

The algorithm for calculating the next layer in time can be represented as a sequence of the following elementary steps:

(a)

determination of the integration step from the Courant criterion, which ensures stability and the control of the error in the approximation of the chemical kinetics equations;

(b)

determination of the coordinates of moving nodes on the new layer and analysis of the presence of intersections of the discontinuity lines with each other and with gas trajectories. If an intersection is present, then the time of the earliest intersection becomes the time of the new layer, and the integration step is recalculated;

(c)

one iteration is performed to find the parameters of the gas field and the concentrations of chemical components at all nodes of the grid;

(d)

the accuracy of the fulfillment of finite-difference equations is verified: if the specified accuracy is achieved at all points of the difference grid, then go to step (e), and if at least at a single point it is not achieved, then another iteration is performed, meaning a return to step (b);

(e)

if an intersection of discontinuities was detected (see step b), then, depending on the physical nature of interacting discontinuities, the structure of the materialized flow at the intersection point is determined (for example, if two strong discontinuities intersect, then the Riemann problem is to be solved);

(f)

transition to the calculation for the next time layer.

Let us dwell in more detail for steps (b) and (c). Any node of the computational grid belongs to one of the following types: rigid walls—right and left (RHW and LHW), shock wave (SW), contact discontinuity (CD), point on the characteristic (PC), or gas trajectory (GT). The parameters are calculated using the grid-characteristic method. Figure 1 provides templates for point calculations, and a description of computational algorithms is given in [1,6,9].

When the grid lines intersect, the calculation of the layer is followed by the processing of the intersection with the correction of the grid lines used and the flow parameters (Figure 2).

Parameter transfer (“T”) is the most commonly applied algorithm for grid line interactions, which is used in two versions. The first case is when the grid lines are not discontinuity lines for the flow parameters (Figure 2a). It should be noted that, in this description and further on, the coordinates (time and spatial coordinate) of all points before and after the interaction are equal to each other, while the speeds of the grid line movements are different. In the lower part, there are the calculated points before the interaction is processed, and, in the upper part, there are the points after interaction processing. Grid lines (1, 2) and (2, 1), indicated by bold arrows, are interchanged, while, in some cases, in order to avoid rounding errors, a number of parameters at points 1 and 2 are retained. For example, if line (1-2) is the gas trajectory and line (2-1) is characteristic (C−), then the concentrations of chemical components at points 1 and 2 after intersection processing are exactly equal to the concentrations of chemical components at point 1 before intersection processing. The second case (Figure 2b) is when one of the grid lines is a discontinuity line for the flow parameters. For example, the line (1-2, 1′-2′) is the C+ family SW, and the line (2-1) is the gas trajectory; in this case, the flow parameters at points 1 and 2 after the intersection processing coincide with each other, while the speed, pressure, temperature, and other parameters along the trajectory change abruptly from the parameters at point 2 to the parameters at point 1 (including the complexes included in the right-hand sides of the characteristic relations), and the concentrations of chemical components remain unchanged. In the case of the interaction of a shock wave with a characteristic line, the processing of the intersection depends on the families to which they belong. For example, the configuration shown in Figure 2b can materialize when SW (1-2, 1′-2′) and characteristic (1-2) belong to the C+ family. In this case, two types of processing algorithms are used. The first one is the transfer of the characteristic to point 1 to the left of the shock wave, in which case the characteristic changes its type from C+ to C− (there is no C+ characteristic to the left of the SW, directed forward in time) and, accordingly, its propagation velocity changes. The second one is the removal of the C+ characteristic. Line 1-2 in Figure 2b can constitute a C− characteristic. In this case, the standard parameter transfer described above is performed.

Figure 2c demonstrates the case of intersection between the free boundary and the grid line (GT, PC−). When the grid line crosses the free boundary of the computational domain, the grid line is removed, and some of the parameters of the removed grid line are transferred to the boundary point.

When a shock wave (or a contact discontinuity) interacts with a free boundary (Figure 2d, SW C+ or CR (1, 1′) and RHB (2-2) line 1 after processing—PC−), the SW (CD) are removed (R), and a new calculation point emerges on the new time layer: the C− characteristic, in the case of the right free boundary, or the C+ characteristic, in the case of the left free boundary.

Figure 2e demonstrates the case of SW+ reflection from RHW. After reflection, the SW becomes a wave of the C− family (SW−) while the flow parameters at point 1 are retained (except for the grid line velocity), and the parameters at points 1′ and 2, along with the SW velocity, are calculated by solving the problem of SW reflection from the wall. In the case of reflecting a characteristic, the characteristic changes its type (from C+ to C− or from C− to C+) and movement speed, while the rest of the parameters remain unchanged.

In the case of interaction between shock waves and contact discontinuities, the Riemann problem is to be solved. In this case, the parameters to the left side of the left one of the interacting discontinuities are taken as parameters to the left of the discontinuity breakdown, and the parameters to the right side of the right one of the interacting discontinuities are taken as the parameters to the right of the discontinuity breakdown. The number of computational points after the calculation of the interaction depends on the configuration emerging as a result of solving the Riemann problem and on the initial difference in parameters. Figure 2f shows the case of the interaction of two strong discontinuities (two SWs or SW and CD) defined by points (1, 1′) and (2, 2′) before the interaction. As a result of the interaction, the “Two SWs” configuration emerged, which corresponds to 3 grid lines (or 6 computational points) tracked at the following time points: (1, 1′)—SW−; (2, 2′)—CD; (3, 3′)—SW+; moreover, the values of the flow parameters at points 1′ and 2, as well as at points 2′ and 3, coincide.

Figure 2g provides the case of the interaction of two SWs or SW and CD, defined by points (1, 1′) and (2, 2′) before the interaction. As a result of their interaction, the “DF to the left, SW to the right” configuration materialized. It corresponds to 6 grid lines (or 8 computational points) tracked at the following points in time: 1, 2, 3, 4—PC+, (5, 5′)—CD; and (6, 6′)—SW+; moreover, the values of the flow parameters at points 4 and 5, as well as at points 5′ and 6, coincide. Four tracked characteristics in the fan indicate that the fan is of medium intensity. Typically, the number of characteristics to be tracked after the discontinuity breakdown is proportional to the pressure gradient in the fan and ranges from two to twenty.

It should be noted that the modeling technique provides for the cases of degeneration of shock waves and contact discontinuities (Figure 2h) if the difference in parameters observed at them is less than 0.001%. In this case, shock waves degenerate into characteristics, and contact discontinuities degenerate into gas trajectories.

The case of intersection of the characteristics belonging to a single family, which is inadmissible from the point of view of the applied system of equations in partial derivatives, is used in the numerical implementation to describe the origination of shock waves in an initially shockless flow (Figure 2i). Here, 1 and 2 are characteristics of the C+ family. The flow parameters obtained at points 1 and 2 as a result of solving the finite-difference system of equations differ. To resolve the kinematically incompatible situation that has arisen, the Riemann problem has to be solved. In the case shown (Figure 2i), a shock wave that propagates to the right SW+ (4, 4′), a contact discontinuity (3, 3′), and a weak expansion wave fan described by two characteristics 1 and 2 are formed. It should be noted that, in real problems modeled via the detailed finite-difference grids, the difference in parameters at the expansion wave fan and at the contact discontinuity is often below the degeneration threshold, and they are not taken into account in the calculation.

In principle, the Riemann problem can be used to resolve any of the interactions between the internal grid lines from the table, which are marked with the “-” sign. However, in order to avoid cases of loss of gas mass located between the initially defined grid lines (gas trajectories), if an intersection between the trajectories and contact discontinuities is detected, the algorithm is interrupted with the appropriate diagnostics.

In mathematical modeling, 18 types of grid line intersections are considered. In the case of SW + SW or SW + CD interaction, the structure and parameters of the realizing flow are determined through the solution of the Riemann problem, which, for the case of gas with constant adiabatic exponents, is described in detail in [12]. This paper considers the case when the thermodynamic properties of gas mixtures to the left and right of the discontinuity depend on pressure and temperature, and the concentrations of the components can either be fixed or satisfy the conditions of thermodynamic equilibrium. Therefore, the generalized solver of the Riemann problem is applied [13].

In SW + PW (point on the wall) interactions, the parameters of the reflected shock wave are determined via Rankine–Hugoniot type relations for a multicomponent gas using the condition that the velocity behind it is equal to zero, supplemented, if necessary, by the conditions of thermodynamic equilibrium.

3. Results

The authors have developed a software package that includes a system for preparing initial data (geometry of the computational domain, initial gas-dynamic parameters, grid parameters, thermodynamic properties of substances and kinetic mechanisms), a computational module, and a system for visualization and storage of the results [7].

The grid-characteristic method described above has been tried on a large number of test problems [6] and has demonstrated its effectiveness.

When studying a supersonic flow in a flat channel simulating the operation of the experimental facility of the IPMech RAS Hypersonic Shock Wind Tunnel in the mode with a closed inlet of the nozzle block [14], it became necessary to refine the structure of the flow in the near-wall region. In the setup, air was used as the working and pushing gas, the pressures in the sections at the moment of opening of the membrane separating the chambers of high pressure (HPC) and low pressure (LPC) were 2.1 MPa (0 < X < 2 m) and 0.1 MPa (2 < X < 10 m), and the pressure sensors were located on the left end of the HPC and in the middle of the LPC.

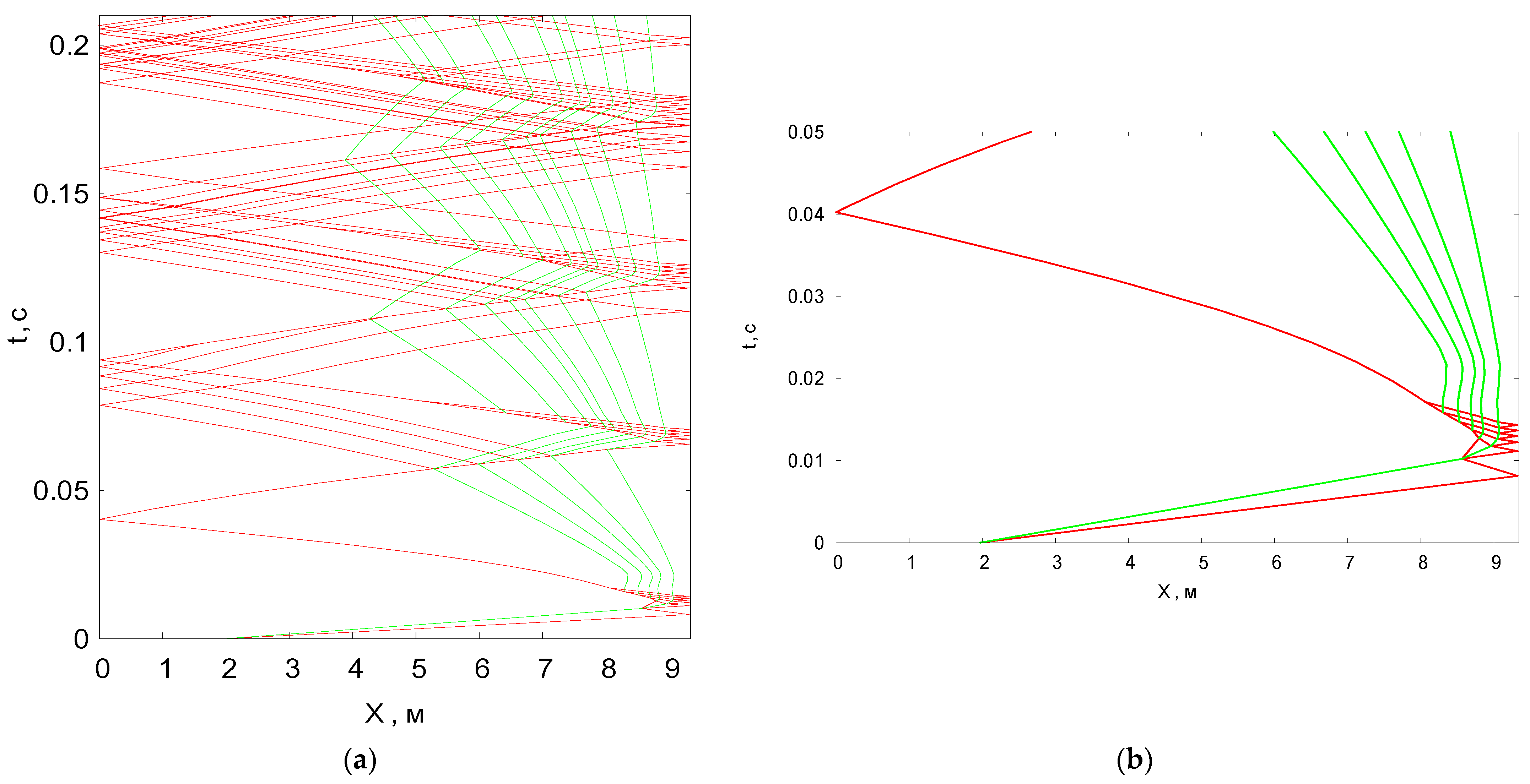
As a result of numerical simulation, the flow structure presented in Figure 1 was obtained. Here, the red lines indicate the trajectories of shock waves, and the green lines indicate contact discontinuities. During the observation time, which was ~0.2 s, the initial shock wave managed to be reflected four times from the ends of the installation (Figure 3a). Figure 3b shows an enlarged fragment of a complex shock wave structure that appears when the incident shock wave is first reflected from the wall and interacts with the initial contact discontinuity. The flow structure includes a set of secondary shock waves and contact discontinuities of varying intensity. It should be noted that, in contrast to the shock-capturing method, all generated shock waves and contact discontinuities are clearly distinguished; they are double computational grid nodes, which are interconnected by the exact fulfillment of the Rankine–Hugoniot relations. When these computational nodes interact with each other, the Riemann problem is solved with high accuracy. The shock waves and contact discontinuities formed as a result of the solution become new grid nodes.

The numerical modeling resulted in the flow structure presented in Figure 3. Here, “thick solid” lines denote SWs, “dotted” lines denote CDs, and “thin solid” lines denote characteristics. During the observation time, which was ~0.2 s, the initial SW managed to reflect four times from the ends of the setup.

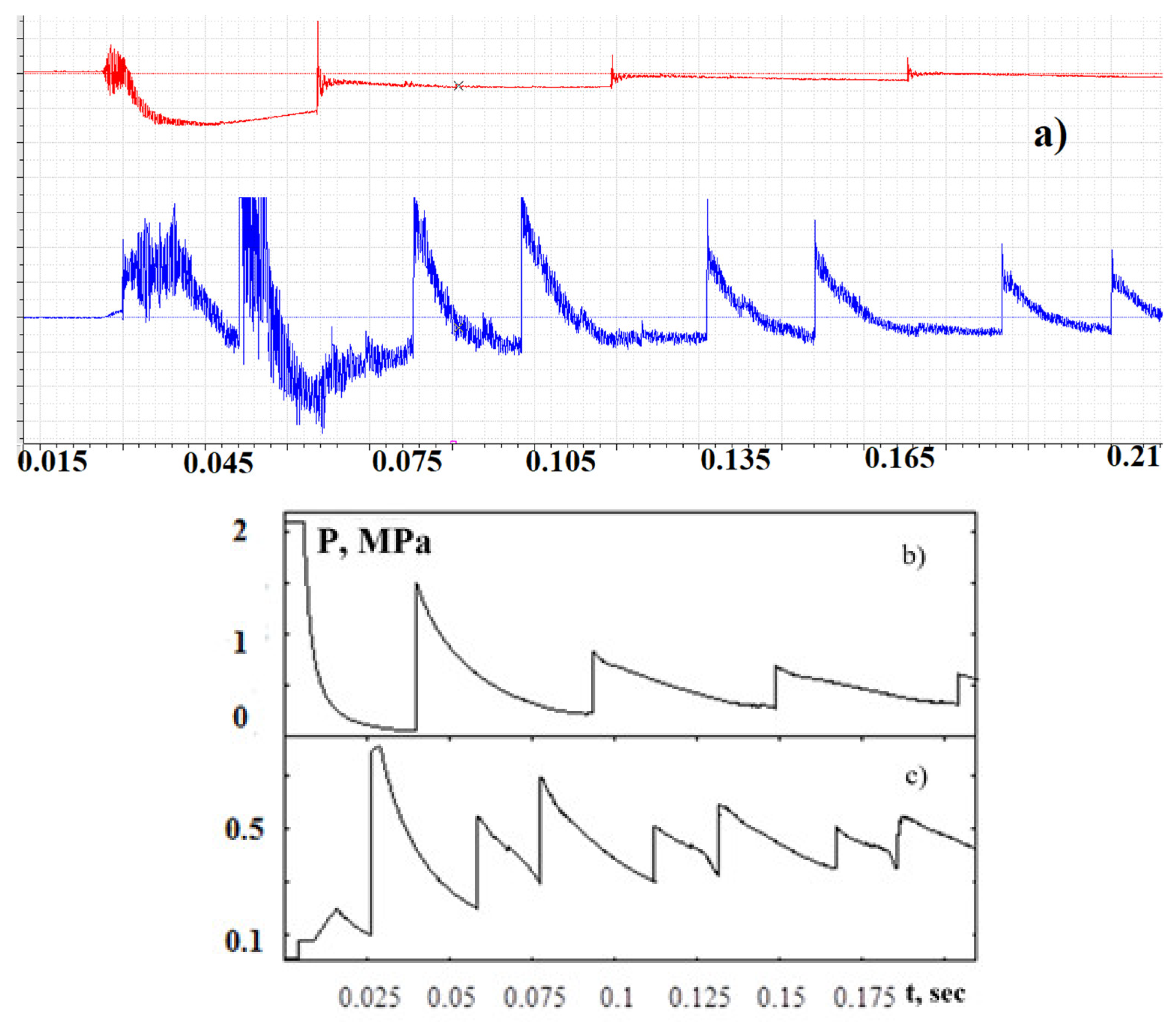
Figure 4 provides a comparison of pressure sensor readings typical for this series of experiments with the results of the numerical modeling. Figure 4a demonstrates the readings of the pressure sensors located at the HPC end (the upper curve) and in the middle of the LPC (the lower curve). Figure 4b,c demonstrate the results of numerical modeling of the flow in the installation: the graph of the pressure at the LHW, which corresponds to the readings of the HPC end sensor, and the graph of the pressure in the middle of the LPC. The modeling technique under consideration makes it possible to “take” the readings of the sensors. To perform this, fixed nodes with coordinates corresponding to the location of the pressure sensors along the setup length are introduced into the computational grid.

The experimenters were interested in the flow pattern adjacent to the right closed end of the setup. Figure 3b shows that, in the area of the closed nozzle block, a complex shock-wave structure of the flow emerges. It is important to note that the reflected SW observed in the experiments is the result of a series of SW reflections and interactions with the CD instead of a pure SW reflection from the wall, which must be taken into account when analyzing the experimental data. The developed method of numerical modeling makes it possible to visually study such effects. Moreover, not only qualitative but also quantitative alignment between the results of numerical calculations and experimental data is observed (Figure 4), despite the fact that the numerical simulation does not take into account viscous effects.

To test the computational algorithms for the numerical modeling of high-speed flows with exothermic chemical transformations, it is worth reviewing the self-similar modeling Riemann problem in a combustible mixture [15,16] (Bam-Zelikovich problem), the solution of which can be found from a system of nonlinear algebraic equations, including those applied for the thermodynamic model used in the present paper. A special case [15], which is the problem of the reflection of a plane shock wave from a wall in a combustible mixture, is considered. It should be noted that this test example is valid for both one-dimensional and two- and three-dimensional non-steady flows.

Let us consider the flow of a stoichiometric methane–air combustible mixture behind a reflected shock wave, which simulates the experimental studies of detonation carried out using a shock tube at the Institute of Physics and Technology [17,18] (the pressure in front of the incident shock wave was 10,132.5 Pa, and the temperature was 298.15 K). To simulate chemical transformations, a simplified kinetic mechanism was used (

Table 2. Kinetic mechanism of methane combustion [19,20]. Parameter n from (8) is equal to 0.

	Reactions	A; m3, mole, c	m	E, K
1	CH4 + O2 = 2/3CO + 4/3H2O + 1/3CH4	6 × 108	−0.2264	22,660
2	H2 + H2 + O2 → H2O + H2O	7 × 107	−0.5	10,574
3	CO + CO + H2 → CO2 + CO2	8.5 × 106	−1.5	10,574
4	CO2 + H2 = CO + H2O	1 × 109	−1	20,998

), which includes four reversible stages; the rate constants of direct reactions were borrowed from [19].

This kinetic mechanism was tested by the authors in [20], which presented the results of calculations of more than 100 experiments [17] to determine the ignition delay time of a combustible mixture behind reflected shock waves.

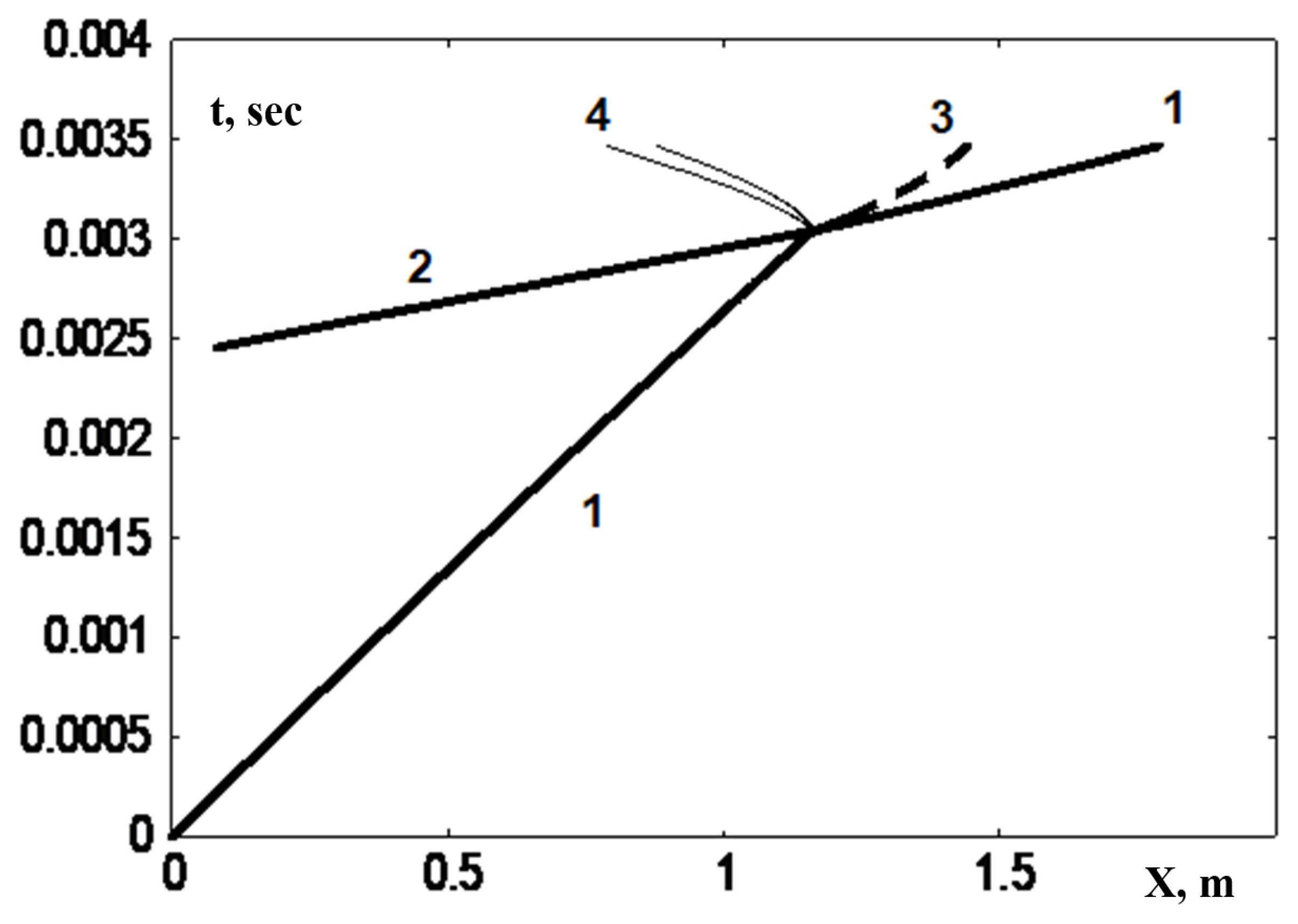
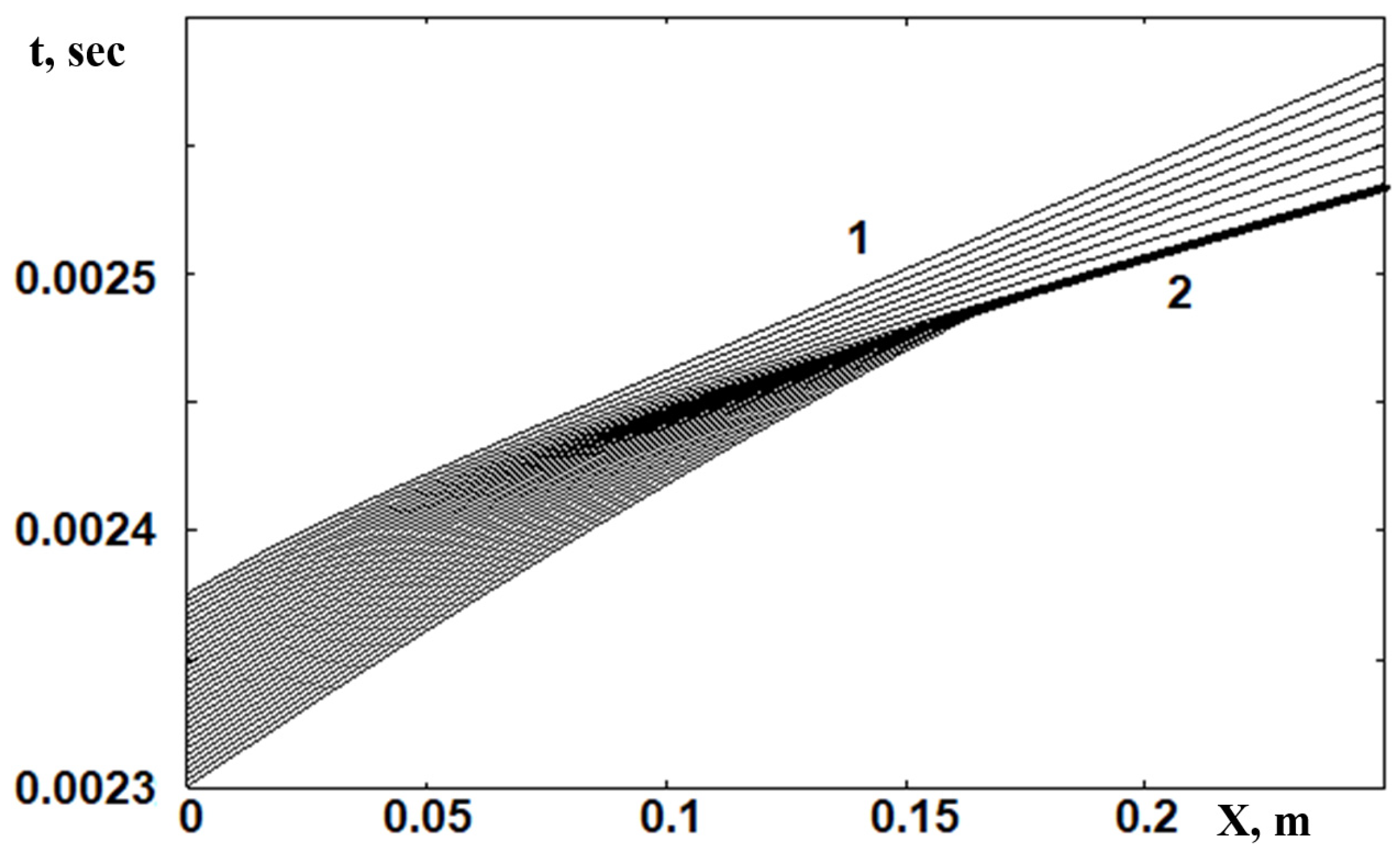
The Mach number of the incident SW varied. Figure 5 shows a typical time sweep of the process. In contrast to the results presented in [20], the case was considered when the incident wave propagates with a Mach number equal to M_i = 3 through a combustible mixture having a temperature T₀ = 298.15 and P₀ = 1.01325 × 10⁴ Πa. Figure 6 shows a detailed picture of the flow during the formation of a hanging shock (HSW, Figure 5 line 2), which is a consequence of the intersection of the C+ family sound characteristics, the trajectories of which are grid lines.

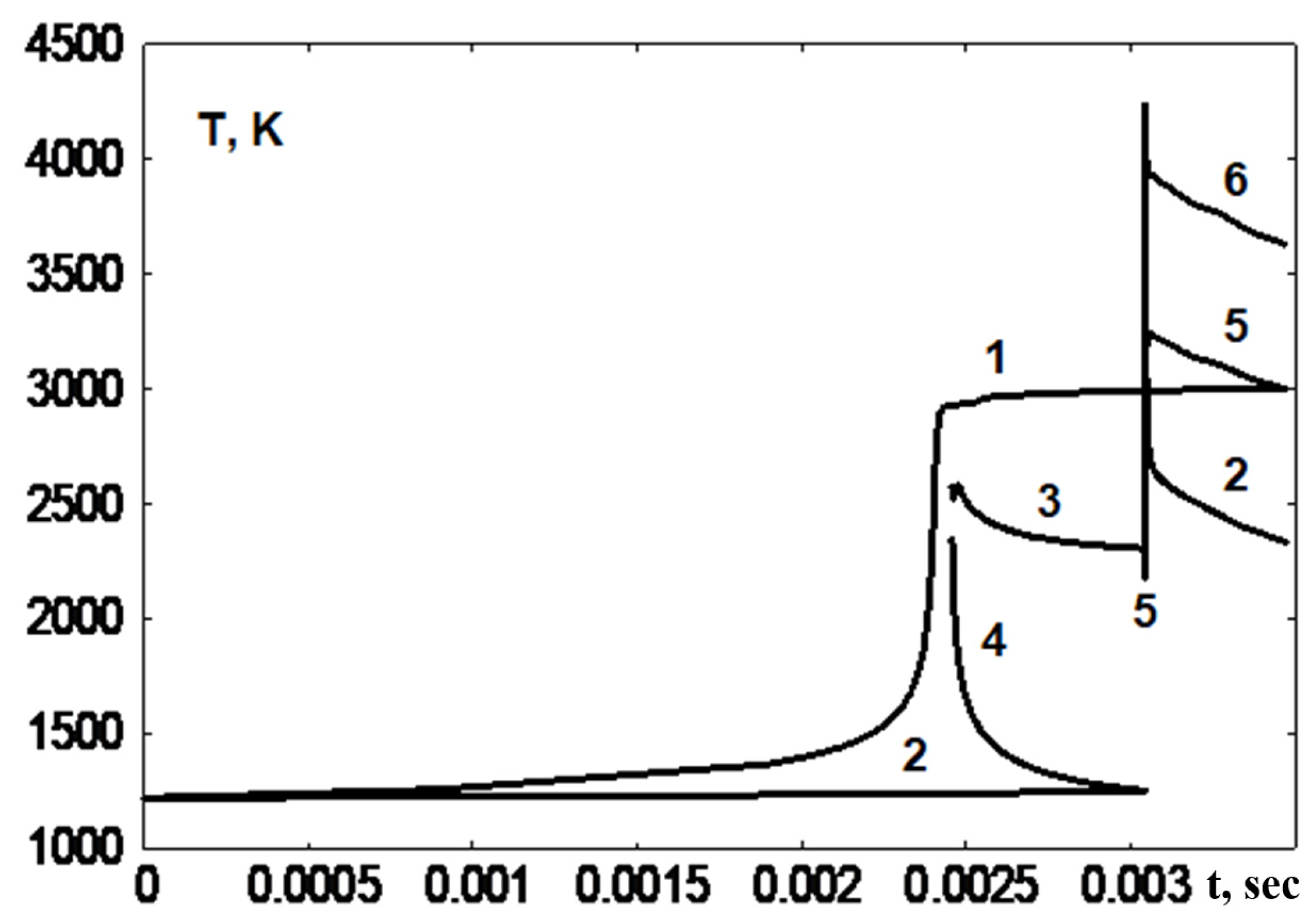
The temperature behind the reflected SW exceeds the self-ignition temperature of the combustible mixture, and ignition occurs at the left wall (Figure 7, curve 1). An increase in temperature and pressure leads to the appearance of a compression wave, which, at t ~ 0.00245, forms a “hanging” shock wave (Figure 5 and Figure 6). It should be noted that the temperature drop at the hanging SW at the moment of its origination depends on the computational grid; in the calculation, it is less than 100 K (Figure 7, curves 2, 3). At subsequent time stamps, the hanging SW intensity increases, and a detonation wave is formed (Figure 7), which propagates behind the reflected shock wave. At t ~ 0.0031, the waves interact; an overcompressed detonation wave, a contact discontinuity, and a fan of expansion waves are generated (Figure 5). Over time, the intensity of the detonation wave decreases, and it enters the propagation regime with parameter fluctuations around a certain stationary state.

The results of quantitative studies of the stationary state around which the plane detonation wave oscillates have shown compliance with the solution of the self-similar problem of the Riemann problem in a combustible mixture [15], obtained for the thermodynamic model being applied, provided that the conditions of chemical equilibrium in the combustion products behind the detonation wave are fulfilled. 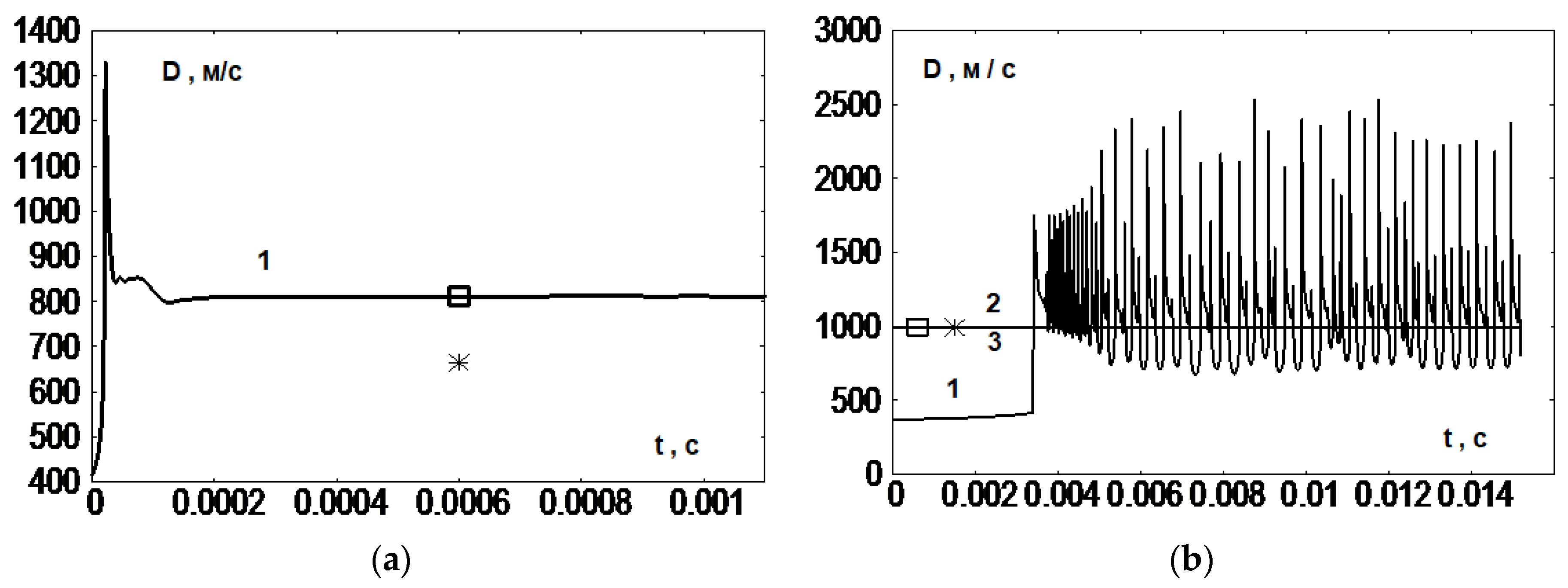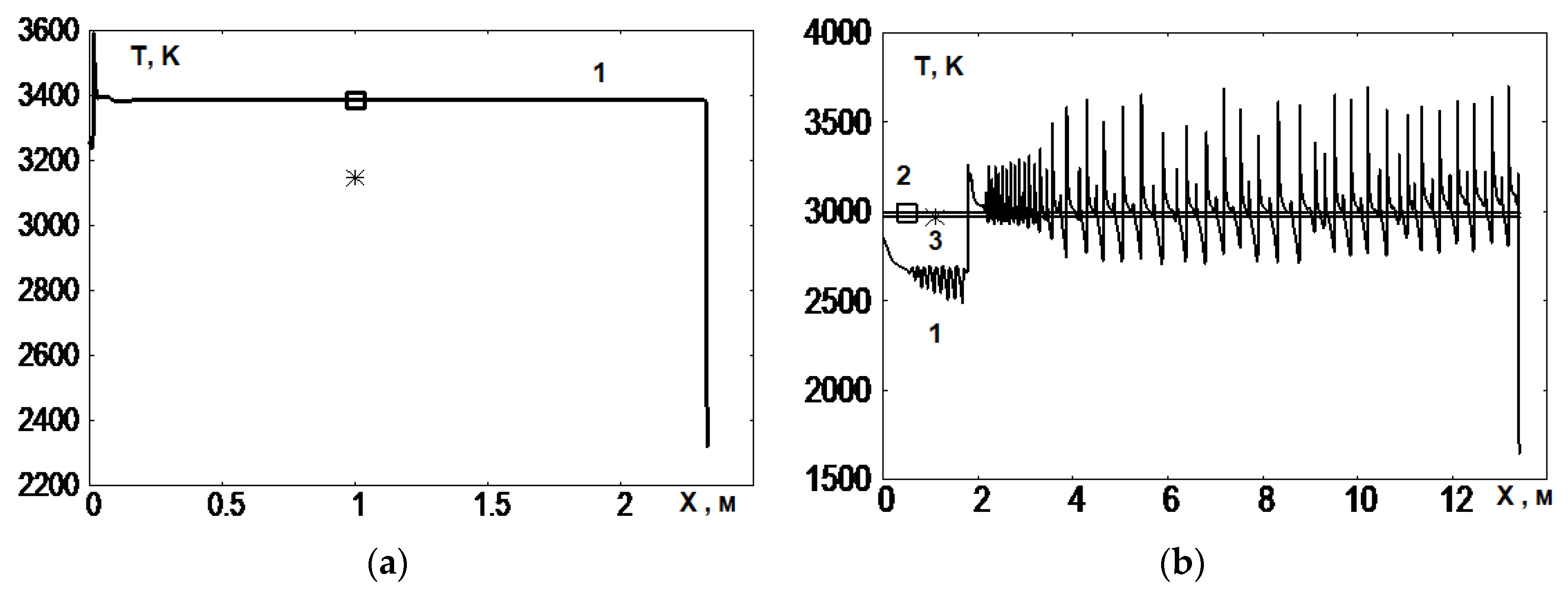Figure 8 and Figure 9 show two typical cases of detonation wave propagation. The case of a stationary detonation wave takes place at the Mach number of the incident shock wave equal to 4 (Figure 8a and Figure 9a). The obtained solution corresponds, with high accuracy, to the solution of the Bam-Zelikovich problem [15], while the parameters of the Chapman–Jouguet wave differ significantly. The case of a detonation wave propagating in an oscillatory mode takes place when the Mach number of the incident SW is equal to 3 (Figure 8b and Figure 9b). The resulting solution oscillates regularly around the solution of the problem [15], while the parameters of the Chapman–Jouguet wave (D = 992.5 m/s, T = 2968.3 K) and the reflected equilibrium wave (D = 995.5 m/s, T = 2992 K) are similar.

4. Conclusions

A grid-characteristic method has been developed that makes it possible to calculate quasi-one-dimensional flows of a reacting gas; the grid lines in this method are the gas trajectories, shock waves, contact discontinuities, and sound characteristics.

Examples of calculation of flows in experimental setups have been provided and demonstrate the effectiveness of the developed method.

The use of the self-similar Riemann problem in a combustible gas mixture (Bam-Zelikovich, 1949) [15] as a test problem for modeling flows with exothermic reactions has been proposed. It has been shown that the parameters of detonation waves in plane channels propagating in stationary or oscillatory modes correspond, on average, to the solution of this problem.