Numerical Study of Indoor Oil Mist Particle Concentration Distribution in an Industrial Factory Using the Eulerian–Eulerian and Eulerian–Lagrangian Methods

Abstract

The transport and prediction of the concentration of particles in confined spaces are crucial for human well-being; this has become particularly evident during the current worldwide pandemic. Computational fluid dynamics (CFD) has been widely used for such predictions, relying on Eulerian–Eulerian (EE) and Eulerian–Lagrangian (EL) models to study particle flow. However, there is a lack of research on industrial factories. In this study, a scaled laboratory in an industrial factory was established for oil mist particles in a machining factory, and oil mist dispersion experiments were conducted under roof exhaust and mixed ventilation conditions. After that, the oil mist concentration distribution in the factory under the same working conditions was calculated by Eulerian and Lagrangian methods, and the corresponding calculation errors and resource consumption were compared. It was found that the simulation results of both methods are acceptable for mixed ventilation and roof exhaust ventilation systems. When there are more vortices in the factory, the Lagrangian method increases the computation time by more than 53% to satisfy the computational accuracy, and the computational error between the Eulerian and Lagrangian methods becomes about 10% larger. For oil mist particles with an aerodynamic diameter of 0.5 μm, both Eulerian and Lagrangian methods have reliable accuracy. Based on the same flow field, the Lagrangian method consumes more than 400 times more computational resources than the Eulerian method. This study can provide a reference for the simulation of indoor particulate transport in industrial factories.

1. Introduction

In industrial factories, the intensive use of machining equipment poses significant health risks and indoor environmental concerns. One particular issue arises from the utilization of cutting fluid during the machining process. This fluid generates oil mist particles that are continuously emitted into the air through various mechanisms, including impact centrifugation, atomization, evaporation, and condensation [1]. Unfortunately, production workers unavoidably come into close contact with these harmful oil mist particles, ranging from sub-micron to micron scales [2,3,4]. The adverse effects on human health are well-documented, especially when exposed to high concentrations of oil mist particles [5,6,7,8,9].

Consequently, it becomes imperative to control the indoor air quality (IAQ) in industrial settings. Computational fluid dynamics (CFD) has emerged as a valuable tool in assessing and managing IAQ, enabling early prediction and prevention of contaminant dispersion. CFD enables the analysis of gas phase and particle contaminant concentration distributions in two-phase flows, as well as particle deposition [10]. The significance of IAQ, both in industrial and general settings, has become increasingly evident during the current pandemic, along with the numerous health risk assessments associated with the novel human coronavirus SARS-CoV-2 [11,12,13,14,15,16]. By leveraging CFD tools to study aerosol and particle dispersion, researchers have gained insights into the effective control and management of industrial indoor air quality. This knowledge has broader implications for public health and has the potential to improve preventive measures in similar health crises in the future.

The Eulerian–Eulerian method (EE) and Eulerian–Lagrangian method (EL) are the two main numerical simulation methods for particle propagation and deposition. The EE regards the particle phase as a continuous medium, including passive containment treatment (also known as the single fluid model) [17], drift flux mode [18], mixture model [19], and two-phase model [20]. For instance, Murakami et al. categorized particles smaller than 4.5 μm as passive pollutants [17]. Gao et al. [21] determined that sub-micron particles can be treated as tracer gases, disregarding the influence of ventilation conditions and air exchange rates on deposition rates. Additionally, Zhao et al. [22] observed that the distribution patterns of non-passive and passive contaminants were quite similar for particles measuring 20 μm and 10 μm under mixed and displacement ventilation, respectively. Zhang and Chen [23] found that when the particle size is less than 5 μm, the passive scalar method can predict indoor particle propagation well. In conclusion, the prediction of smaller particles (e.g., ≤5 μm) can be treated as passive containment. The EL model regards particles as a discrete phase, offering a semi-direct approach to predicting particle concentration by tracking individual particles over time. While considerable research has been conducted on both the EE and EL approaches, a consensus regarding their accuracy and suitability has yet to be reached, and the understanding of aerosol and particle dispersion remains incomplete. EE models have found extensive application in studying the concentration distribution of particulate matter in indoor environments [17,22]. Meanwhile, EL models have primarily been employed to forecast particle trajectories and dispersion within a confined space [24].

Regarding indoor aerosol dispersion and deposition, Zhang et al. [23] reported the suitability of passive scalar EL over EE for unsteady analysis of indoor particles between 0.3 and 1 μm, assuming a single-phase coupling and neglecting deposition. Yan et al. [20] compared two fluid EE and EL models to transport micron particles in a displacement ventilation chamber. According to Li et al. [25], the two-phase EE model has higher accuracy than the EL model when calculating steady-state and transient indoor particle distributions. A literature review comparing EE and EL for indoor particle dispersion and deposition is presented in

Table 1. Literature review of EE and EL models for indoor particle.

Author	Turbulence Model	PT Model	Diameter [μm]	EE Type	EL Type	EE WBC	EL WBC
Lai et al. [18]	RNG k-ε	EE/EL	0.3, 1, 3, 7	Drift flux	-	Particle deposition flux	Trap + turbulence correction
Zhang and Chen, [23]	Standard k-ε	EE/EL	0.31, 1	Passive scalar	One-way coupling	Zero flux	Full-bouncing
Zhao et al. [19]	RNG k-ε, Zero-eq. model	EE/EL	10	Drift flux, mixture model	One-way coupling	Particle deposition flux	Trap
Wang et al. [26]	RNG k-ε, LES, DES, Real. k-ε, semi-v2f/LES	EE/EL	0.31, 0.7, 1~5	Passive scalar treatment	-	-	-
Li et al. [25]	RNG k-ε, Std. k-ε	EE/EL	0.2, 0.77, 10	Two-phase flow	Two-way coupling	Free-slip	Full-bouncing
Chen et al. [27]	RNG k-ε	EE/EL	1, 2, 3	Drift flux	-	Zero flux	Reflect
Xu et al. [28]	RSM, RNG k-ε	EE/EL	1, 3, 5, 9, 16	Drift flux	One-way coupling	Particle deposition flux	Critical deposition velocity
Yan et al. [20]	RNG k-ε	EE/EL	0.2, 0.77, 2.5	Two-phase flow model	Two-way coupling	Free-slip	Full-bouncing
Wei et al. [29]	RNG k-ε	EE/EL	-	Passive scalar	One-way coupling	-	-
Murakami et al. [17]	k-ε model	EE	0.31, 1, 4.5, 10, 50, 100	Passive scalar, drift flux	-	Zero flux	-
Zhao et al. [22]	Zero equation model	EE	2.5, 5, 7.5, 10, 20	Passive scalar, drift flux	-	Zero flux	-
Chen et al. [30]	RNG k-ε	EE	10	Drift flux	-	Particle deposition flux	-
Zhao et al. [31]	-	EE	0.01, 0.05, 0.1, 5	Improved drift flux	-	Particle deposition flux	-
Zhang et al. [32]	v2f-dav	EL	0.01~50	-	-	-	Trap + turbulence correction
Zhang and Chen, [33]	Standard k-ε	EL	0.31, 1, 4.5	-	One-way coupling	-	Restitution coefficient
Cao et al. [34]	RNG k-ε, Real. k-ε, SST k-ω	EL	8.1	-	One-way coupling	-	Trap + turbulence correction

PT: particle transport; WBC: wall boundary conditions.

. From Table 1, two types of boundary conditions can be summarized for EE: zero flux (deposition is not considered) and settling flux (sedimentation is considered). EL has four types of boundary conditions: (i) trap, (ii) trap + turbulence correction, (iii) rebound, and (iv) rebound with a determined coefficient.

Industrial factories are known for their high concentration of pollutants, with particulate matter being one of the most prevalent types. The complex indoor environment and vast spatial layout of industrial factories pose significant challenges to effective indoor pollutant control. Conducting experimental studies to devise pollutant control strategies is often costly and limited in scope. As a result, CFD has emerged as the primary method for investigating indoor environmental control in industrial factories [35,36,37,38,39,40]. However, existing research primarily focuses on particle transmission in residential buildings, with limited attention given to industrial factory settings. Furthermore, the simulation methods and accuracy of particle transmission in industrial factories remain largely unexplored. In addition, there is a lack of detailed experimental data to validate the numerical simulation results. This paper aims to bridge this gap by investigating the transmission of particulate matter in an industrial shop with simulations and experiments, utilizing oil mist particles in a machining factory as a representative case study.

This study presents a comparative analysis of simulation methods, focusing on the accuracy and cost-effectiveness of modeling oil mist particles in machining factories. Specifically, two commonly employed ventilation systems, roof exhaust and mixed ventilation, are evaluated. To validate the CFD results, a scaled experimental bench is established. Additionally, the study compares the advantages and disadvantages of Eulerian and Lagrangian methods under identical operating conditions. The findings of this research provide a valuable reference for simulating indoor particulate matter transmission in industrial factories.

2. Experimental Method

2.1. Factory Model

To simplify the experimental conditions, reduce uncertainties (e.g., limitations of measurement points, opening and closing of doors, worker activity), and reduce experimental costs, a scale model of a real workshop (1:10) was designed to analyze the velocity field [41]. The relationship between the dimensions of the scale model and the original model follows the Equation (1):

$$x^{*}=\frac{x}{h_o},y^{*}=\frac{y}{h_o},z^{*}=\frac{z}{h_o}$$

(1)

where x, y, and z are coordinates of the model; h_o is a characteristic length, and, in this study, h_o is the characteristic length of the roof exhaust area.

Figure 1a shows a schematic diagram of the scale laboratory bench with dimensions of length (X) 1.2 m, width (Y) 0.9 m, and height (Z) 0.8 m. The model contains the ventilation system, production equipment, and contamination sources. The ventilation system is a roof exhaust and ducted air supply system. In this case, the roof vent size is 0.04 m × 0.04 m, two ducts are installed at Z = 0.5 m, and there are three air outlets under each duct with a size of 0.04 m × 0.05 m. The machine equipment in the model is an LA-type CNC lathe shown in Figure 1b with dimensions of 0.23 m × 0.13 m × 0.21 m. The front is a transparent operating door, and the bottom pipe is used to discharge the waste chips and fluids generated during the machining process. Figure 1c shows a simplified model of this study, and a circle (d = 0.01 m) on the operation door is used to simulate the source of contamination.

The heat was neglected inside the factory model, and the flow was regarded as isothermal. The Reynolds number [42] is used as the dimensionless criterion number and is defined as follows:

$$R\mathrm{e}=\frac{ud}{\nu }$$

(2)

where u is the air velocity, m/s; v is the air kinematic viscosity coefficient, m²/s; and d is the characteristic size of the outlet, m.

2.2. Experimental System

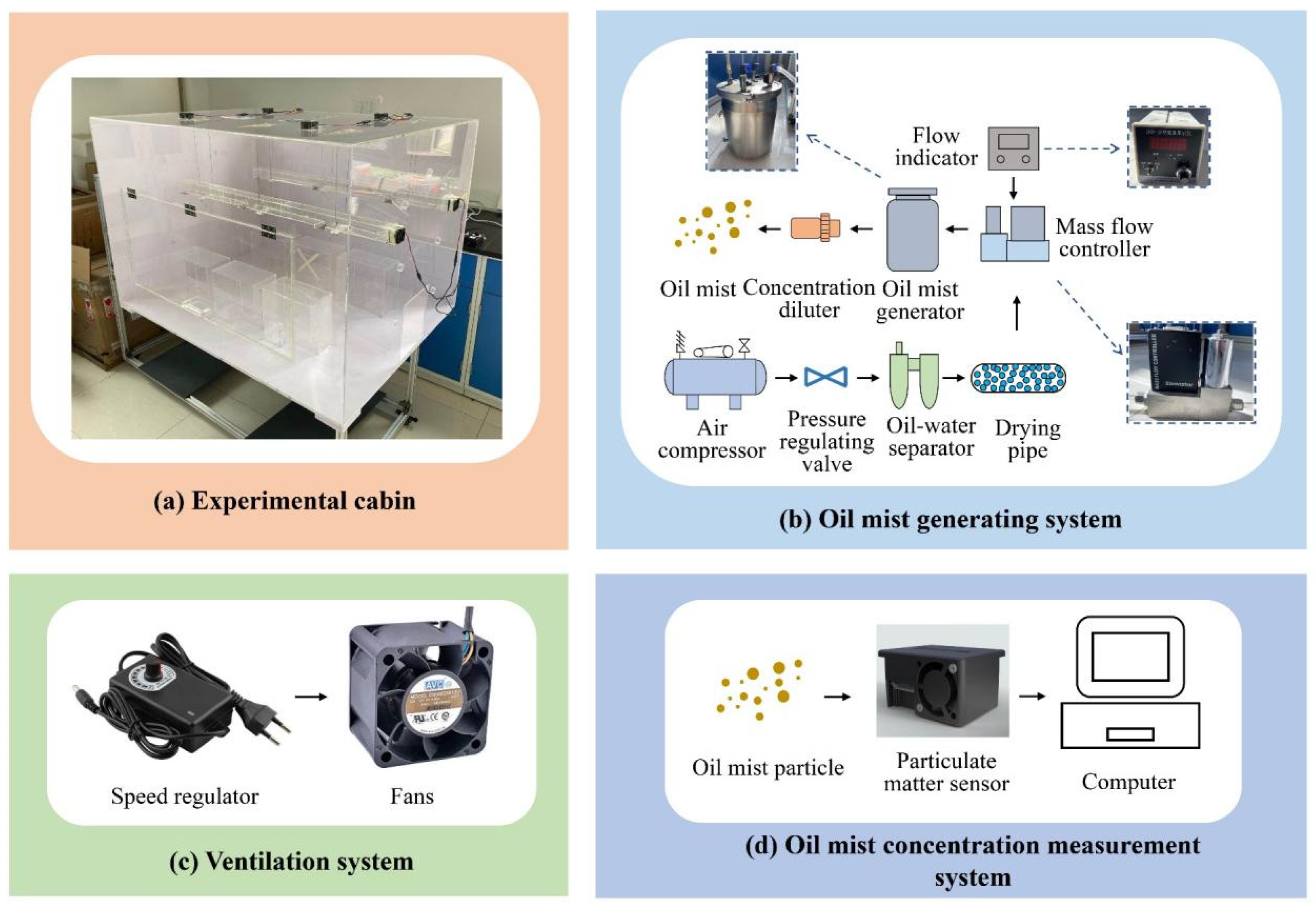
The experimental system is shown in Figure 2, which mainly includes (a) an experimental cabin, (b) an oil mist generating system, (c) a ventilation system, and (d) an oil mist concentration measurement system. In the oil mist generation system, the high-pressure air is generated by the air compressor. The compressed air is treated by the water–oil separator and drying tube and then enters the oil mist generator. The aerosol is released through a nozzle in the generator. To ensure a stable air flow, the compressed air is controlled by a mass flow controller (range: 0 to 50 L/min). A concentration diluter is connected to the outlet of the oil mist generator. By adjusting the value of the mass flow controller, the airflow into the aerosol generator can be controlled at a low flow rate to ensure a stable amount of oil mist emission. The ventilation system consists of a fan and a speed controller. The speed controller changes the fan speed to control the ventilation volume.

Particle concentration in the chamber was measured by a particulate matter (PM) A4-CG PM sensor, which uses a laser light scattering method and has a built-in laser transmitter as well as a photoelectric receiving element.

Table 2. Parameters of the PM sensor.

Object	Value
Rated Voltage	5 V
Operating Temperature	−10~50 °C
Measuring Range	0.3~10 μm
Range	0~6000 μg/m3
Resolution	1 μg/m3
Concentration Consistency	±10% of the display number or ±10 μg
Size	45 × 36 × 23 mm

shows the parameters of the PM sensors, and Figure 1a shows the measurement positions. In addition, a hot wire anemometer type Testo405i (Testo SE & Co. KGaA, Titisee-Neustadt, Germany) was used to measure air velocity, and the measurement positions are also shown in Figure 1a. Dioctyl sebacate (DOS) was used as the particle type in this research. DOS is a colorless or yellowish-transparent oily liquid that is not volatile and has a density of 913 kg/m³ at 20 °C. It maintained a stable shape and particle size during the experiment.

2.3. Experimental Procedure and Setup

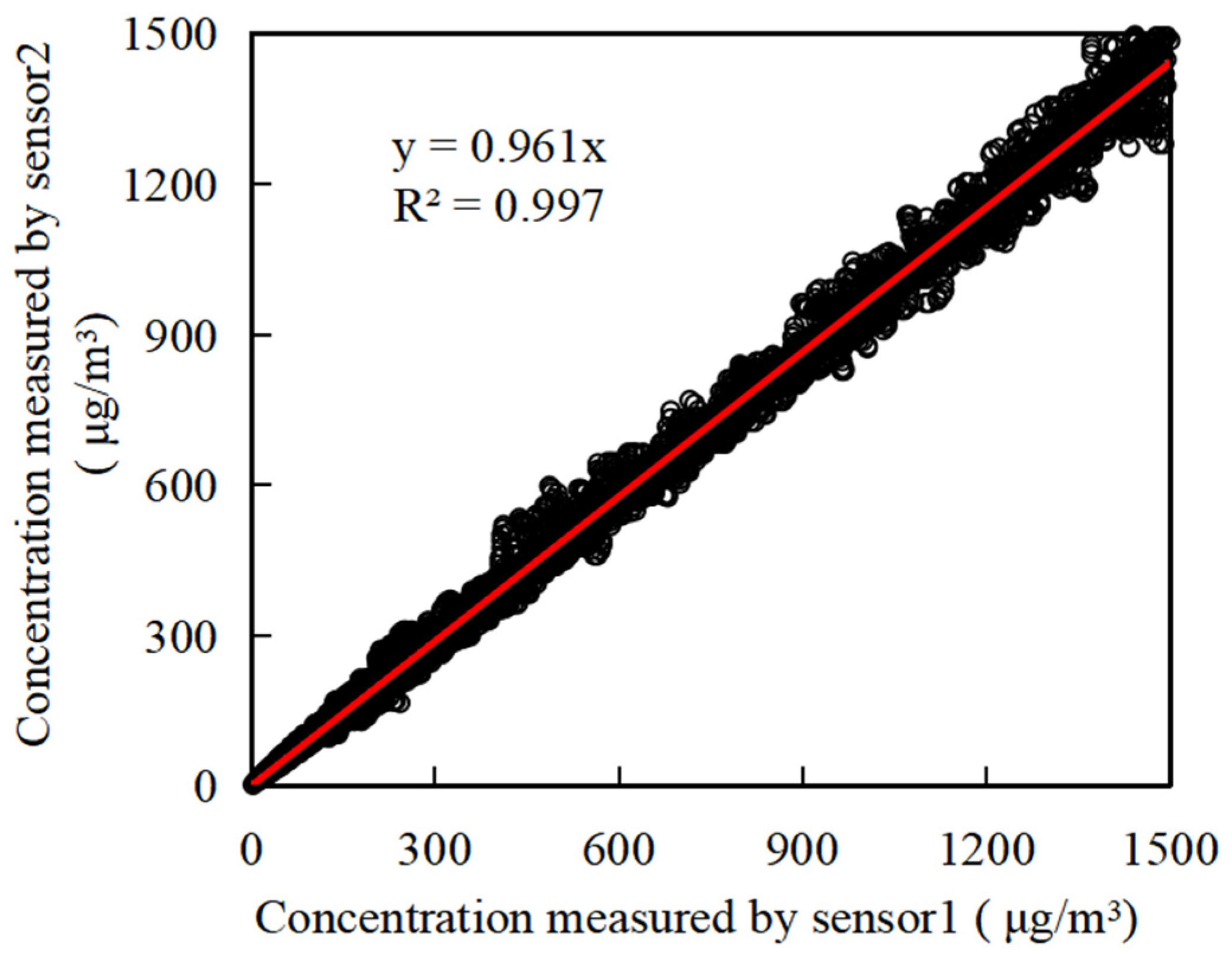
To perform simultaneous multi-point measurements, it is necessary to ensure the consistency of the measurement results from each sensor. During the measurement, the ambient temperature was set at 24 °C and the relative humidity was 20%. The instruments and calibration methods used were consistent with those of Zhang et al. [43]. Sensor 1 was used as a reference to measure the deviation degree of other sensors relative to Sensor 1. Figure 3 shows the comparison of measurement results from Sensors 1 and 2, where 0.961 is the consistency parameter. More measurements are shown in

Table 3. Sensor consistency.

Sensor	1	2	3	4	5	6	7	8	9
Consistency Parameter	1	0.96	0.93	0.99	0.99	0.92	0.96	1.04	1.08
R2	-	0.997	0.92	0.98	0.99	0.95	0.96	0.96	0.96

.

The particle concentration in the room satisfies the following Equation (3). The rate of oil mist emission can be obtained by measuring the corresponding concentration.

$$V\frac{dC}{dt}=E$$

(3)

where V is the chamber volume, m³; C is particle concentration, mg/m³; and E is the particle emission rate, mg/s. Due to the small particle size and low settling velocity, particle deposition is neglected.

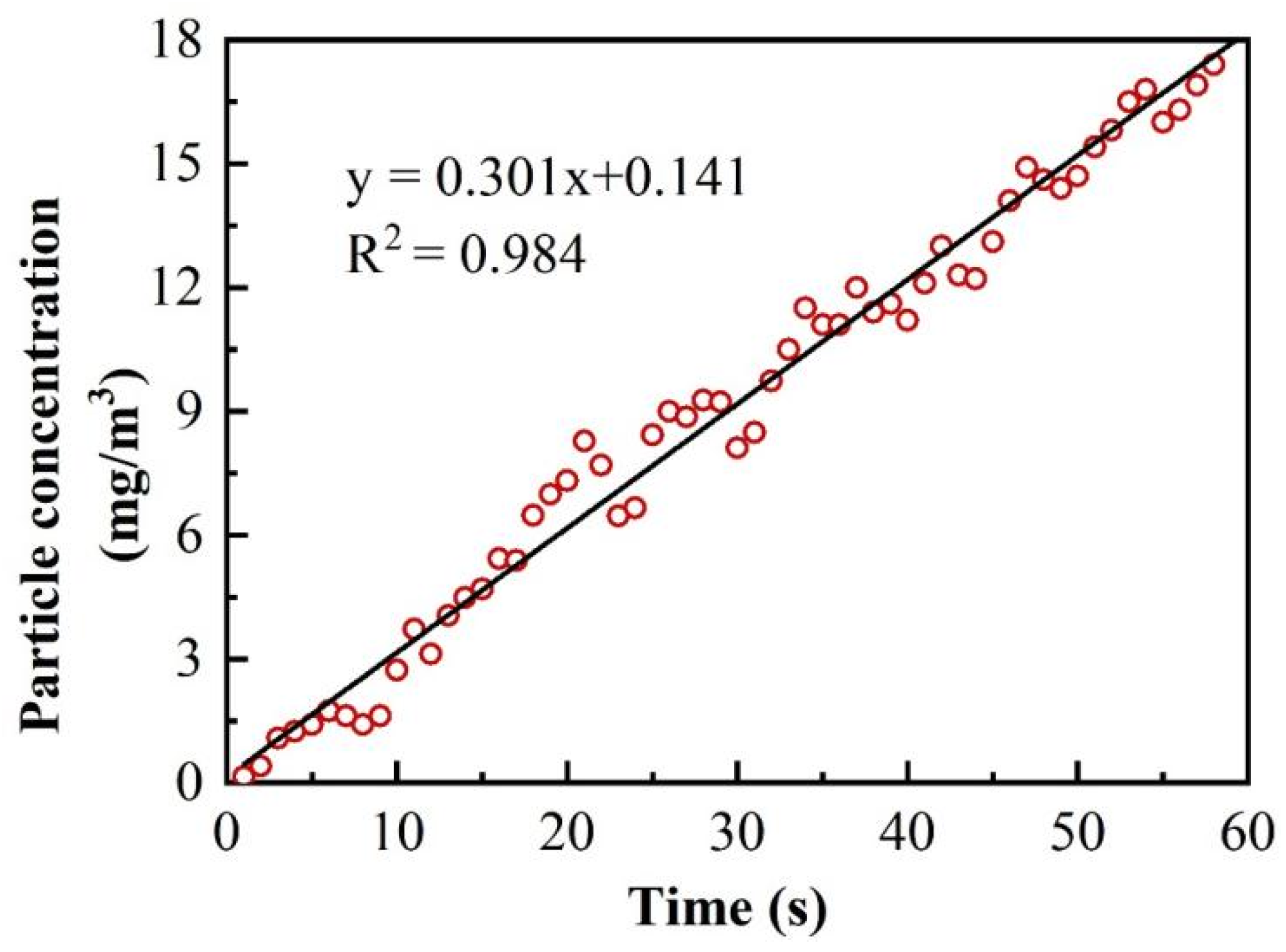
To measure the rate of oil mist emission, an experimental chamber was first closed, and a fan was used for mixing inside to ensure adequate mixing of the particles inside the chamber. Figure 4 shows the emission rate results from Equation (3) and the aerosol detector. The slope of the fitting curve was 0.3, the volume of the test bench was 0.028 m³, and the emission rate was calculated as 0.0085 mg/s. The lathe’s oil mist emission ranges from 0.007 mg/s to 0.114 mg/s.

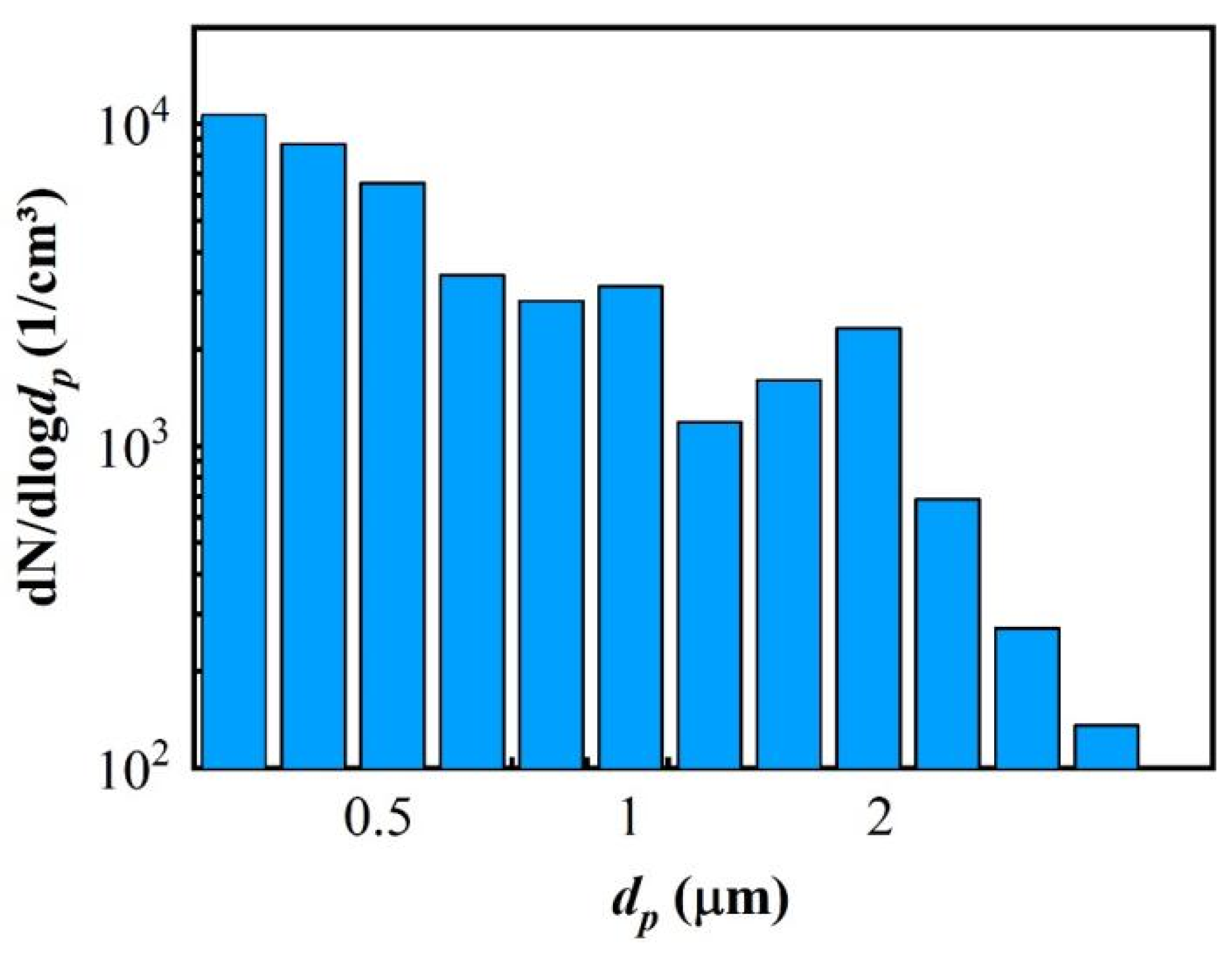
In addition, the particle size distribution was measured by a TSI DustTrak II 8530 aerosol detector at the same rate of oil mist emission, and the results are shown in Figure 5. It shows particle size distribution during emission: roughly less than 1 µm, with a median diameter of 0.5 µm, which is similar to the on-site measurements that the aerodynamic diameters of the oil particles are in the range of 0.5–0.8 µm [1]. The experiments were conducted under roof exhaust and mixed ventilation conditions, both of which are commonly used in factories. Under roof exhaust conditions, the exhaust air velocity is 3.25 m/s, and under mixed ventilation conditions, the exhaust air velocity is 3.75 m/s, and the air supply volume of each air duct is 30 m³/h. During the experiment, the corresponding experimental data were recorded when the whole system reached stability. The air velocity is measured at line 1 (X = 0.3 m, Y = 0.45 m), line 2 (X = 0.6 m, Y = 0.45 m) and line 3 (X = 0.9 m, Y = 0.45 m). The oil mist concentration is measured by 9 sensor located in three vertical lines (line 4: X = 0.3 m, Y = 0.6 m; line 5: X = 0.6 m, Y = 0.6 m; line 6: X = 0.9 m, Y = 0.6 m).

3. Numerical Method

For oil mist transport in a machining factory, the oil volume is usually only a small fraction of the total air volume. Therefore, the effect of oil mist on the flow field is negligible. In this study, the Eulerian–Eulerian (EE) and Eulerian–Lagrangian (EL) models were used to study the distribution of oil mist in the factory.

3.1. Eulerian-Based Flow Model

In this study, the RNG k-ε model was selected to study the airflow and the governing equation can be written in a general form as follows:

$$\frac{\partial }{\partial t}(\rho \overline{\phi })+\frac{\partial }{\partial x_i}(\rho \overline{u_i}\overline{\phi })=\frac{\partial }{\partial x_i}\left({\Gamma }_{\phi }\frac{\partial \overline{\phi }}{\partial x_i}\right)+S_{\phi }$$

(4)

where ρ is the fluid density, kg/m³; u_i is the fluid velocity, m/s; ϕ is a generalized variable (velocity, temperature, concentration); Γ_ϕ is the diffusion coefficient; and S_ϕ is the source term. The parameters of this model are summarized in

Table 4. Coefficients for RNG k-ε model.

Term	ϕ	Γϕ	Sϕ	Constants
Continuity	1	0	0
Momentum	uj	μ + μt	$-\frac{\partial p}{\partial x_i}$
RNG k-ε	k	$\mu +\frac{{\mu }_t}{{\sigma }_k}$	$G_k+G_b-\rho \epsilon$	${\mu }_t=\rho C_{\mu }\frac{k^2}{\epsilon },G_k={\mu }_t{S}^2$$,G_b=\beta g_i\frac{\partial {\mu }_t}{\partial {\sigma }_{T,t}}\frac{\partial \stackrel{—}{T}}{\partial x_i}$ $S=\sqrt{2S_{ij}{S}_{ij}}$$,R_{\epsilon }=\frac{C_{\mu }\rho {\eta }^3(1-\eta /{\eta }_0)}{1+\beta {\eta }^3}\frac{{\epsilon }^2}{k}$
	ε	$\mu +\frac{{\mu }_t}{{\sigma }_{\epsilon }}$	$C_{1\epsilon }{G}_k\frac{\epsilon }{k}-G_2\rho \frac{{\epsilon }^2}{k}-R_{\epsilon }^{}$	$\eta =Sk/\epsilon$, η0 = 4.38, β = 0.012, σk = 1.0, Cμ = 0.0845, C1,ε = 1.42, C2,ε = 1.68

.

3.1.1. Eulerian–Eulerian Model

For the Eulerian–Eulerian method, the particle phase is treated as a continuous phase. The governing equation of convection diffusion was considered as:

$$\frac{\partial }{\partial t}{\displaystyle \underset{\tilde{V}}{\int }\rho {\phi }_i}dV+{\displaystyle {\oint }_A\rho {\phi }_i}\overrightarrow{u}\cdot d\mathrm{a}={{\displaystyle {\oint }_A\mathrm{j}}}_i\cdot d\mathrm{a}+{\displaystyle \underset{V}{\int }{S}_{{\phi }_i}}dV$$

(5)

where i is the component index, V is the volume, j_i is the diffusion flux; a is the area vector; $\overrightarrow{u}$ is the velocity, m/s; Sϕi is the source item.

3.1.2. Eulerian–Lagrangian Model

For the Eulerian–Lagrangian model, particles are tracked using the Lagrangian method while airflow is analyzed using Eulerian equations. Particle motion is defined as:

$$\frac{d{\overrightarrow{u}}_p}{d_t}=\frac{18\mu }{{\rho }_p{d}_p^2{C}_c}(\overrightarrow{u}-{\overrightarrow{u}}_p)+\frac{\overrightarrow{g}({\rho }_p-\rho )}{{\rho }_p}+{\overrightarrow{F}}_a$$

(6)

where $\overrightarrow{u}$ and ${\overrightarrow{u}}_p$ are the local air and particle velocity, m/s; μ is air viscosity, kg/(m·s); ρ and ρ_p and the air and particle density, respectively, kg/m³; d_p is the particle diameter, m; C_c is the Cunningham factor; $\overrightarrow{g}$ is the gravity acceleration, m/s²; ${\overrightarrow{F}}_a$ is additional forces acting on the particle.

The $\overrightarrow{u}$ includes two components: average velocity and instantaneous velocity. The former is obtained by solving the RANS equations, and the latter needs to be modeled by the discrete random walk (DRW) model. In the DRW model, the interaction of a particle with a fluid-phase turbulent eddy is simulated [44]. The instantaneous velocities follow the Gaussian distribution, and they are correlated with the flow of turbulent kinetic energy and the concentration distribution obtained by the particle trajectories.

$$u{\prime }_i={\xi }_i\sqrt{2k/3}$$

(7)

where $u{\prime }_i$ is the instantaneous velocity, ξ is the Gaussian random number, and k is the turbulent kinetic energy.

3.2. Boundary Conditions

The air supply inlet and exhaust outlet were set at constant positive and negative velocities, respectively. The door was set up as a pressure outlet. The wall was considered a no-slip boundary. The deposition velocity of particles (diameter = 0.5 μm) was 1.0 × 10⁻⁵ and the deposition rate was 0.24 h⁻¹, about two orders of magnitude lower than the air exchange rate [45]. Therefore, particle deposition was ignored in Lagrangian and Eulerian models, adopting complete rebound and zero flux (gradient zero condition) at the wall, respectively. Other boundary conditions are shown in

Table 5. CFD boundary settings.

	Item	Specific Value
Roof Exhaust Ventilation System	Exhaust air velocity	−3.25 m/s
Mixed Ventilation System	Exhaust air velocity	−3.75 m/s
	Duct air volume	30 m3/h
Lagrangian Method	Wall boundary condition	Reflect
	Particle density	913 kg/m3
	Emission source	8.5 × 10−6 g/s, 1.6 m/s
	Particle size	0.5 μm
Eulerian Method	Emission source	Specified scalar value: 1.0, Velocity: 1.6 m/s
	Wall boundary condition	Zero flux (gradient zero)

.

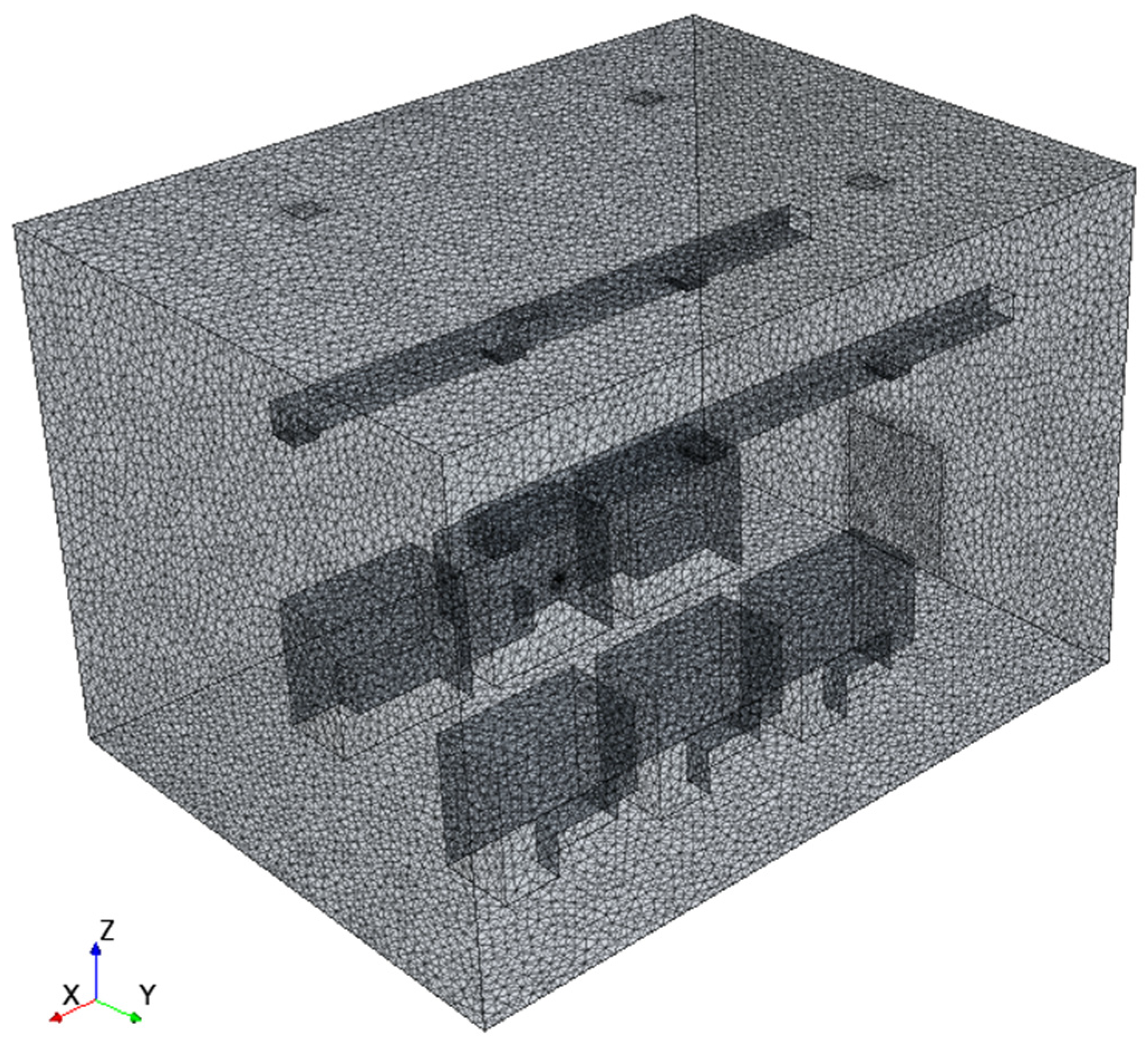
3.3. Grid and Numerical Schemes

In this study, a tetrahedral grid was used and fine mesh was used for the air inlet and outlet, as shown in Figure 6. The wall function was set as the standard wall function, so the y* was greater than 11.225 [46,47]. The model was divided into different grid numbers, namely, 0.36 million, 0.69 million, 1.43 million, and 2.80 million. The details of the calculations are shown in Section 4. This investigation used the finite volume method to discretize the governing equations and the semi-implicit method for pressure linked equations (SIMPLE) algorithm to couple the pressure and velocity. The pressure staggering option (PRESTO!) scheme was adopted for pressure discretization, and the second-order upwind discretization scheme was used for iterations for all variables except pressure to achieve higher accuracy. Convergence was reached when the residuals were less than 10⁻⁶ or air velocity and oil mist concentration varied within a limited range at some monitoring sites. In the Lagrangian model, the quantity concentration of particles below 2.5 μm in the machining workshop is maintained at 400~800 P/cm³ and accounts for more than 98% [2]. Converted to volume fractions, it is approximately 1.4 × 10⁻⁸~2.7 × 10⁻⁸. Since indoor particulate matter usually occupies a very low volume fraction, the effect of airflow on the distribution of oil mist is usually studied, rather than the other way around [48]. Thus, the effect of discrete relatively continuous phases is not considered in this paper, i.e., a single-phase coupling approach is adopted.

3.4. Calculation Error Analysis

In this study, the CFD results were compared with experimental data, and the computational results of different CFD also be compared. This study used dimensionless variables that were defined as Equation (8).

$${\mathit{u}}^{*}=\frac{\mathit{u}}{u_o},C^{*}=\frac{C-C_o}{C_R-C_o}$$

(8)

where u is the velocity at the measurement point, m/s; u_o is the supply velocity, m/s. C_o is the supply concentration, mg/m³; C_R is the return concentration, mg/m³. In this study, C_R is the concentration at the exhaust outlet. C_o is the concentration at the inlet.

The standard deviation was used to express the error, and the errors are calculated as follows:

$${\sigma }_u=\sqrt{\frac{{\displaystyle {\sum }_{i=1}^n\left(u_i-\overline{u}\right)}}{n}},{\sigma }_c=\sqrt{\frac{{\displaystyle {\sum }_{i=1}^n\left(C_i-\overline{C}\right)}}{n}}$$

(9)

where σ_u, σ_c are the errors of velocity and oil mist concentration, respectively; n is the number of sampled data; $\overline{u}$ and $\overline{C}$ are the average values of velocity and oil mist concentration, respectively; u_i and C_i are the results values of velocity and oil mist concentration, respectively.

4. Results

4.1. Flowfield Distribution

4.1.1. Roof Exhaust Condition

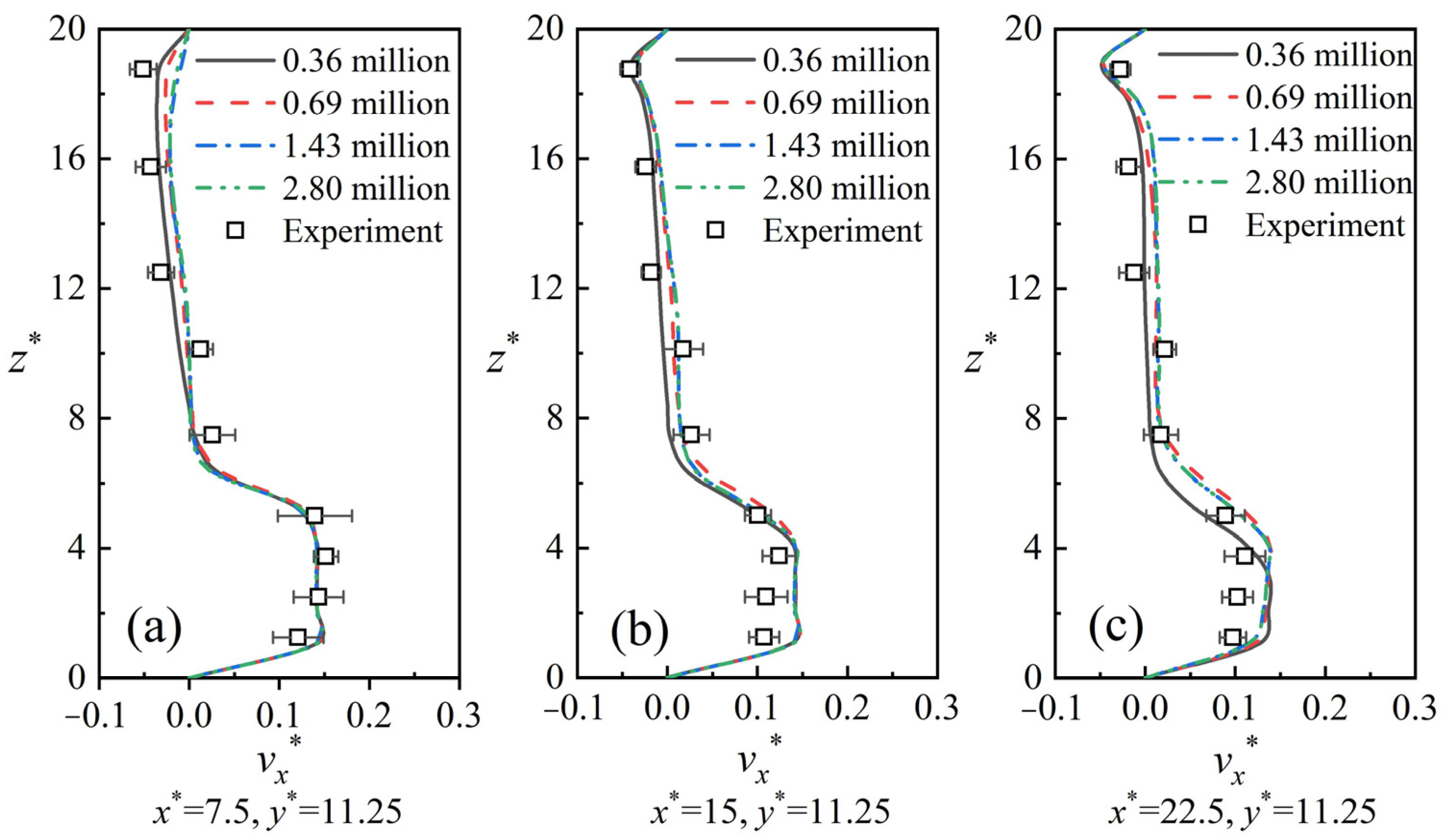
This section compares the simulated and experimental results of air velocity for the roof exhaust condition and measures the computational error for different numbers of grids. Figure 7 shows the comparison of experimental and measured results for different measurement positions with different grid numbers.

Table 6. Computational error of different grid numbers.

Grid Number (Million)	Velocity v*x
	x* = 7.5, y* = 11.25	x* = 15, y* = 11.25	x* = 22.5, y* = 11.25
0.36/0.69	49.10%	112.62%	560.78%
0.69/1.43	25.81%	34.54%	26.13%
1.43/2.80	6.74%	2.57%	3.86%

shows the relative errors of the calculation results under different grid numbers.

From Table 6, it can be found that the computational error on each line is less than 6.74% when the grid number is increased from 1.43 million to 2.80 million, while the computational error on each line is 20–30% when the grid is increased from 0.69 million to 1.43 million. Therefore, this study continues the follow-up study at the grid number of 1.43 million. Figure 7 shows that the experimental data and the simulation results are in good agreement, which also indicates that the numerical model used in this study is feasible.

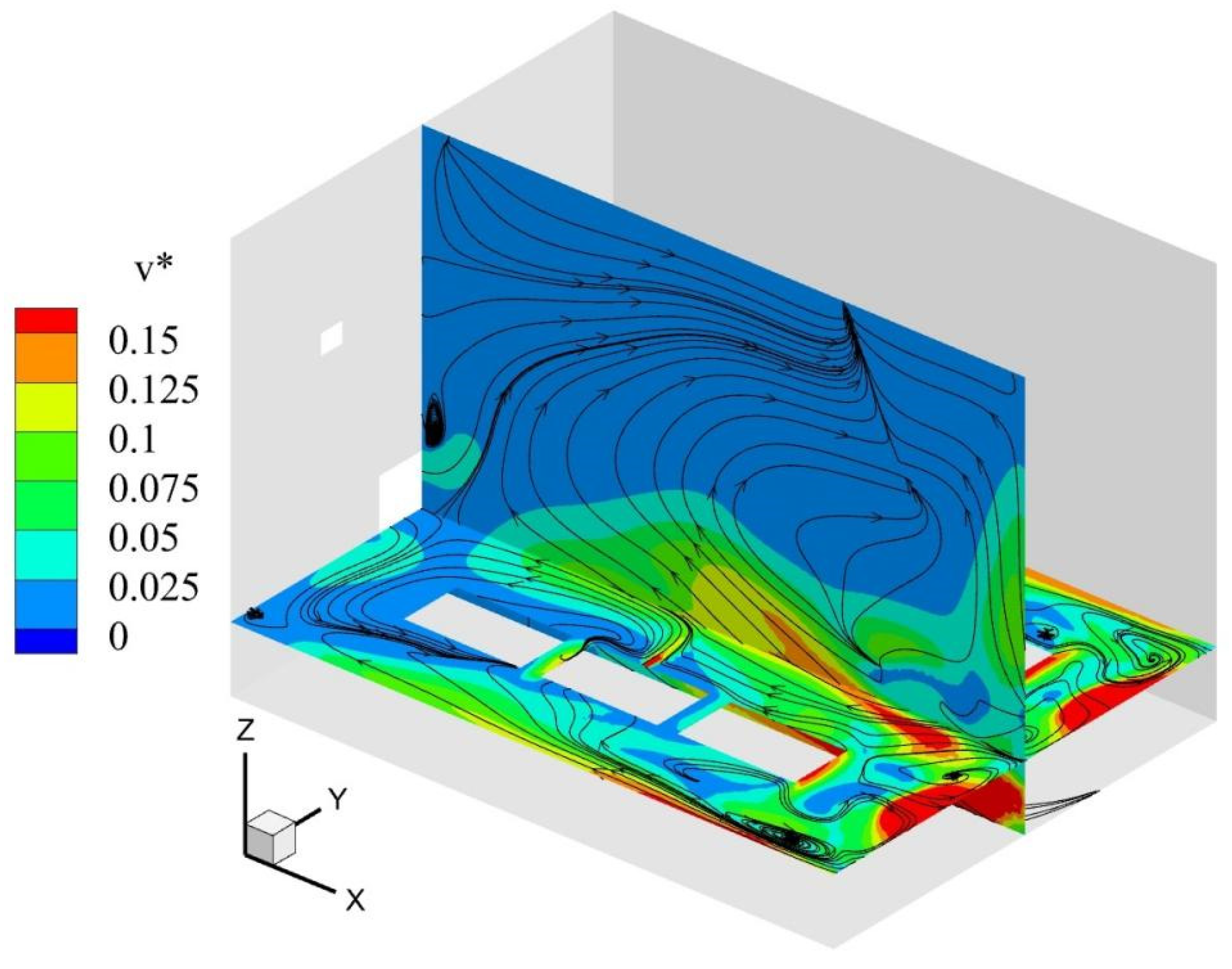
Figure 8 shows the distribution of the flow field in the exhaust condition of the Z plane (Z = 0.13 m) and Y plane (Y = 0.45 m), which shows that the aisle between the two rows of equipment has high air velocity, and some vortices are distributed inside the factory space, mainly between the equipment and the wall and near the roof. The presence of many vortices in the space and the direction of the airflow is not always towards the exhaust air outlet, which may lead to high pollutant concentrations in the factory.

4.1.2. Mixed Ventilation Conditions

Referring to the results in the previous section, this section uses the same grid strategy for the calculation of the flow field under mixed ventilation conditions. Figure 9 shows the comparison of experimental and measured results in mixed ventilation conditions. Figure 10 shows the distribution of the flow field in mixed ventilation conditions. From Figure 9, it can be seen that the numerical results are more consistent with the experimental results at lower altitudes. When the altitude increases, the difference between the experimental and numerical results is greater due to the smaller airflow velocity. In general, the experimental and numerical results are in agreement. Figure 10 shows that due to the influence of the ducted air supply system, there are fewer vortices in the room compared to when only the roof exhaust is available. While there is more airflow directed to the roof vents, the higher airflow velocity is more concentrated in the lower part of the factory, which may lead to excessive concentrations of pollutants in certain parts.

4.2. Particle Transport under Roof Exhaust Ventilation

In this section, indoor pollutant transport under roof exhaust conditions is investigated, and the results of the Eulerian and Lagrangian methods are compared.

4.2.1. Quality Control of the Lagrangian Method

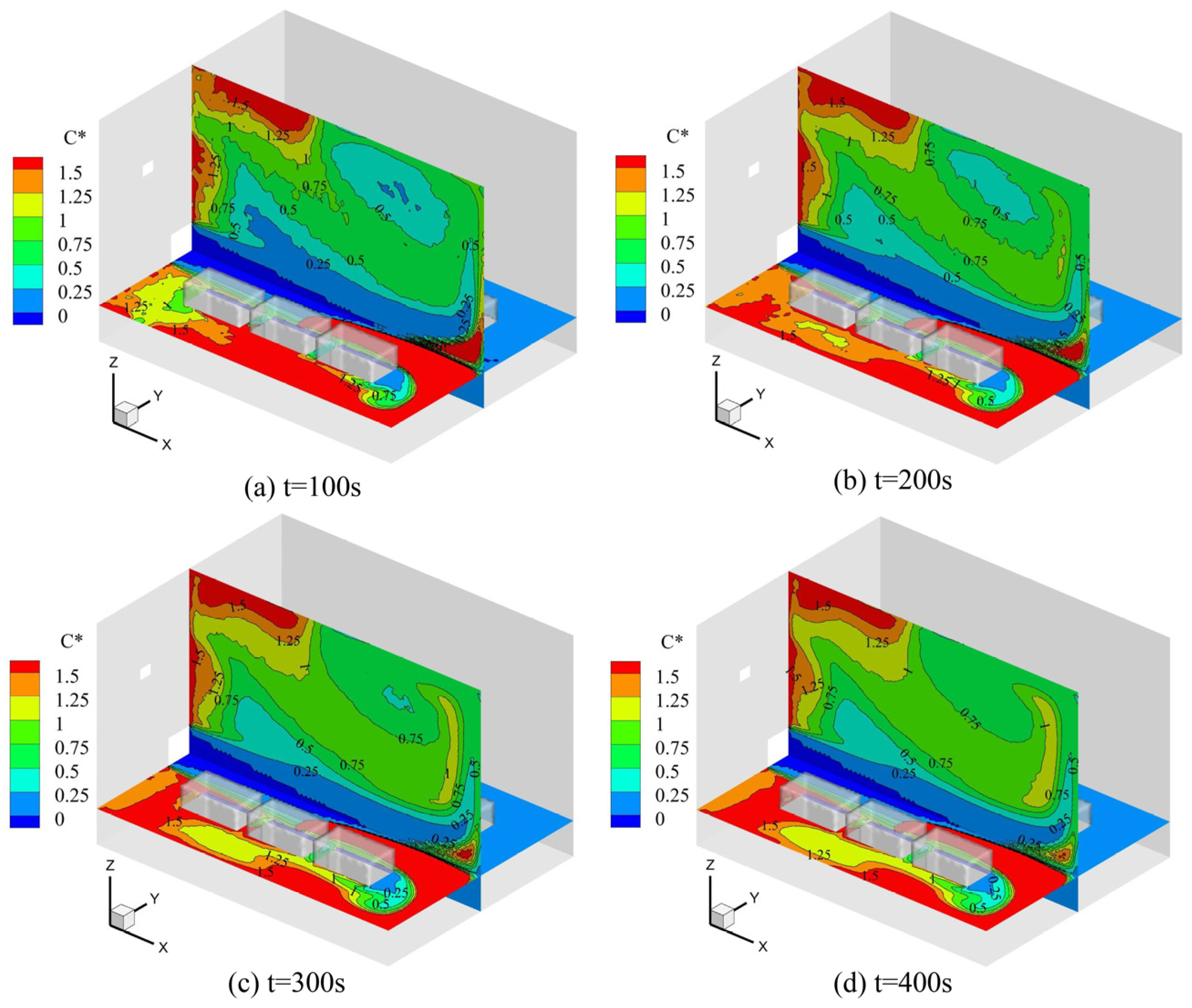
Many factors affect the calculation results of the Lagrangian method, among which the most obvious influence is the calculation time. Therefore, this section first investigates the concentration distributions at different calculation times. Figure 11 shows the concentration distribution at different calculation times. It can be found that when the calculation time is short, such as t = 100 s, the spatial concentration distribution is not continuous, and as time increases, the concentration distribution gradually becomes continuous. Moreover, the change in particle concentration distribution from t = 300 s to t = 400 s is not obvious.

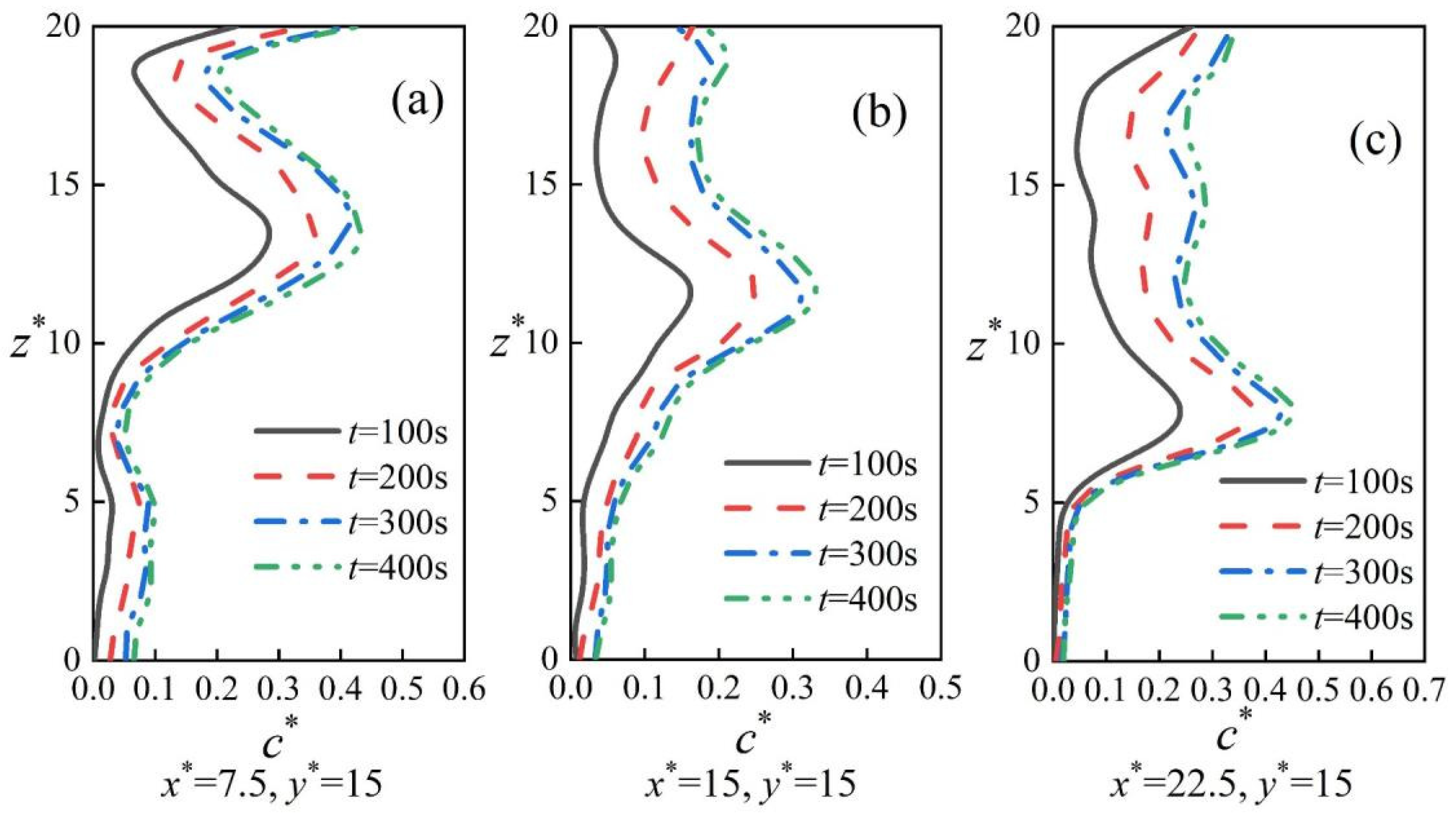
Figure 12 shows the oil mist concentration on the monitoring line at different times, and it can be found that the oil mist concentration rises as time increases. When the time increases from t = 300 s to t = 400 s, the pollutant concentration changes are no longer obvious. The average calculation error of t = 100 s and t = 300 s is about 200%, while the average error of t = 300 s and t = 400 s is less than 10%. Considering the computation time, for a computer with a 128-core CPU, the computation time for t = 100 s, t = 200 s, t = 300 s, and t = 400 s is 2 h, 7.5 h, 15 h, and 25 h, respectively, provided that the boundary conditions are consistent. Therefore, t = 300 s was chosen as the final result.

4.2.2. Comparison of Eulerian and Lagrangian Calculation Results

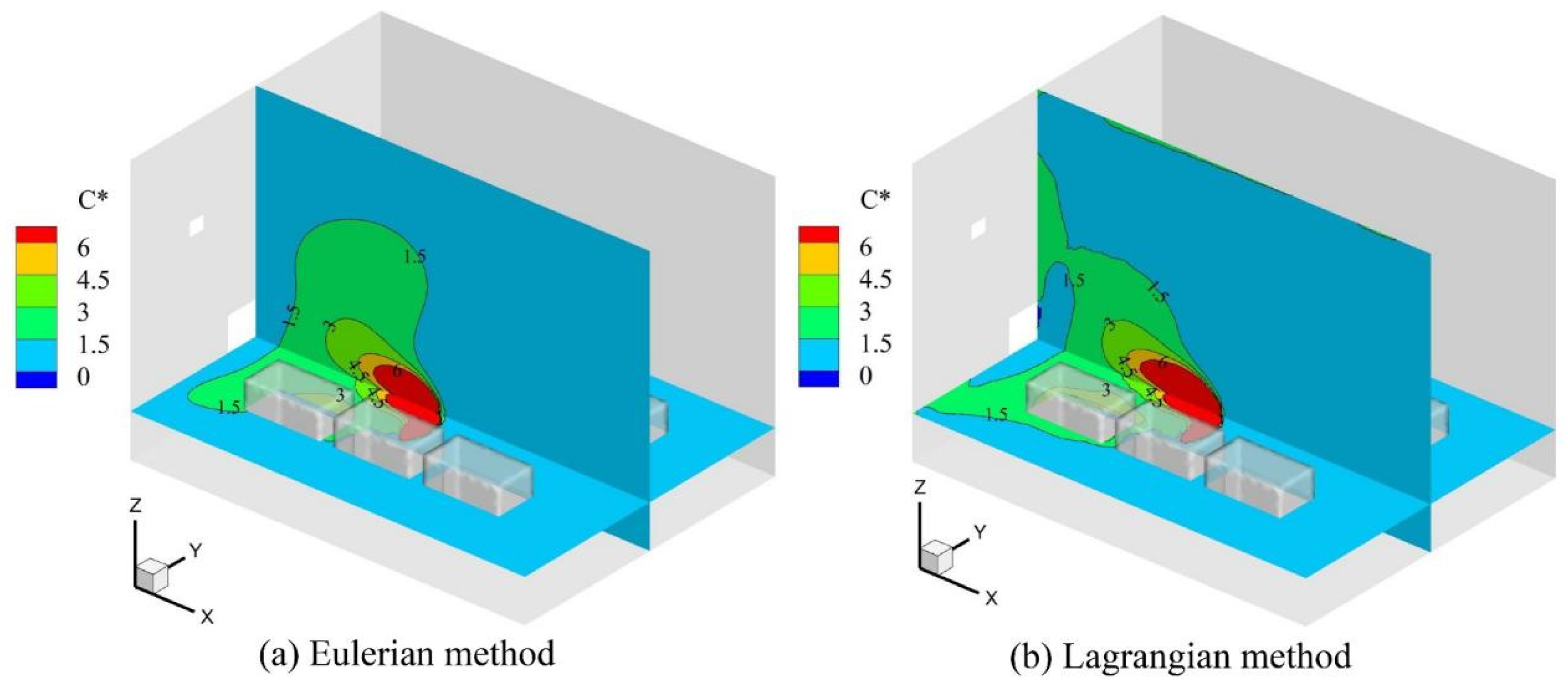
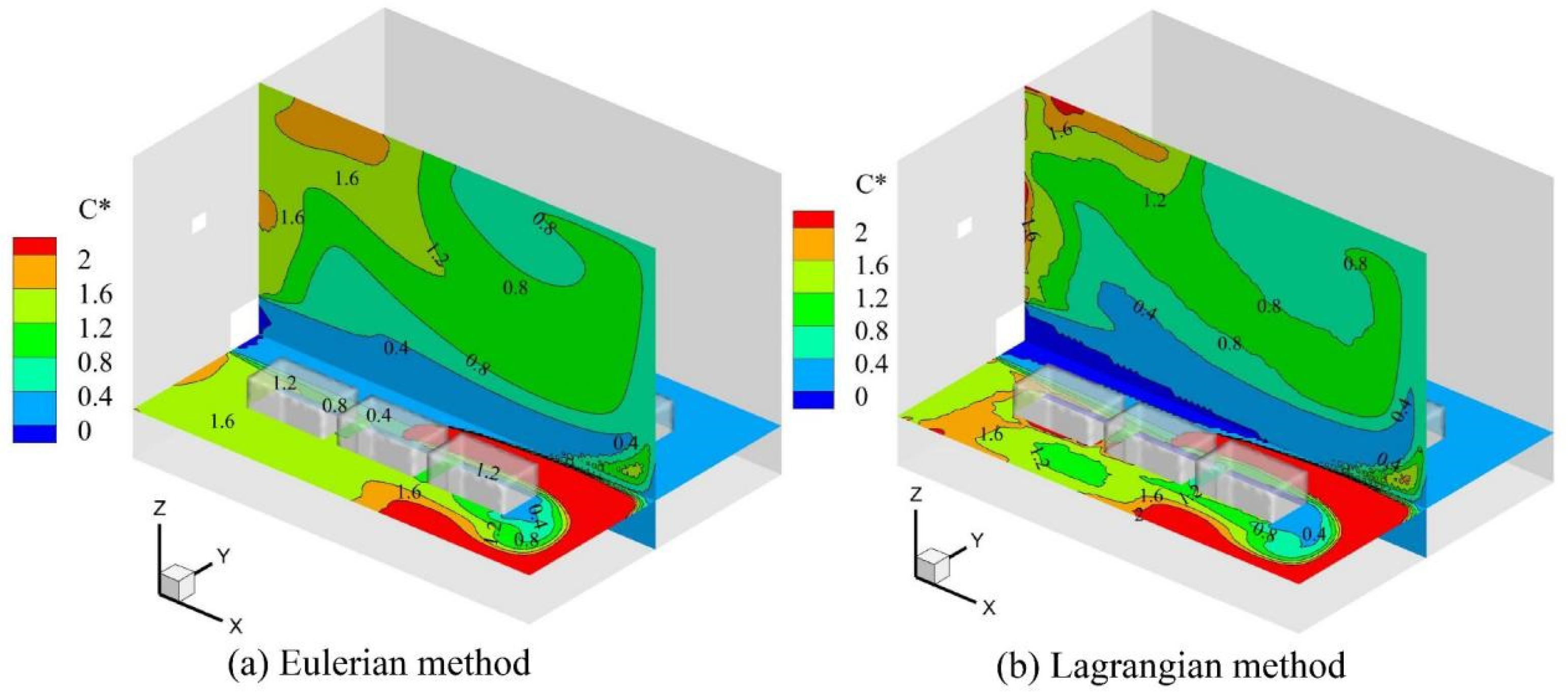
Figure 13 shows the distribution of oil mist concentration calculated by different methods, where Figure 13a,b are the results of the Eulerian and Lagrangian methods, respectively. Combined with the flow field shown in Figure 8, it can be found that the Lagrangian result has a higher oil mist concentration near the vortex at the wall, while the Eulerian method shows a stronger “diffusion effect”. In general, the difference between the two concentration distributions is not significant. 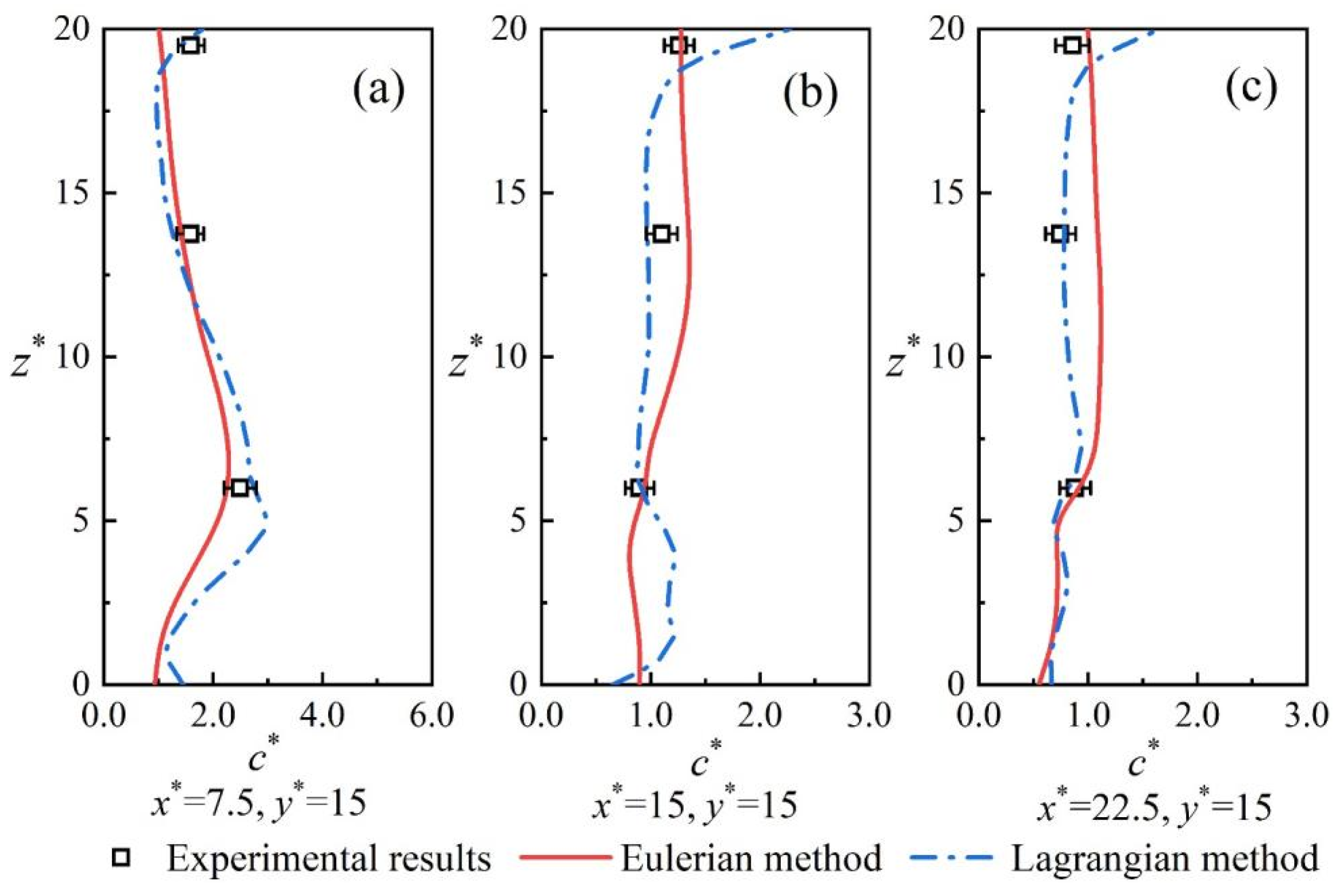Figure 14 shows the simulation results of the Eulerian and Lagrangian methods compared with the experimental results at different locations. The average error of the two methods is about 20%, and the two methods’ results are acceptable compared with the experimental results.

4.3. Particle Transport under Mixed Ventilation

4.3.1. Quality Control of the Lagrangian Method

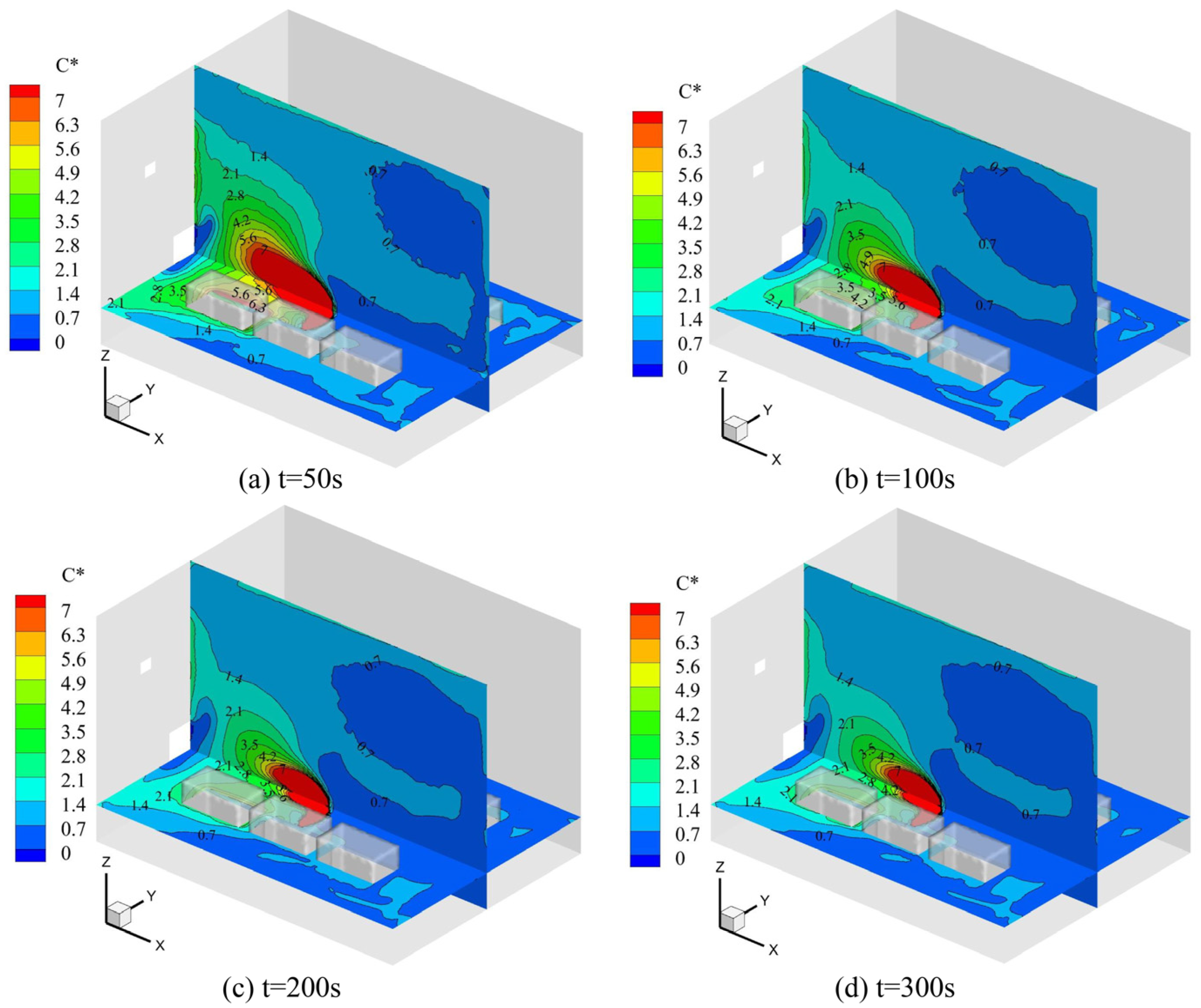
The difference between the flow fields under mixed ventilation and roof exhaust is large. To obtain more accurate Lagrangian calculation results, the calculated oil mist concentration at different times is compared under mixed ventilation conditions. Figure 15 shows the distribution of oil mist concentration at different times. Different from the roof exhaust conditions, the space reaches stability faster at a greater distance from the pollution source because there are fewer vortices in the room, which reduces the residence time of particles in the space. 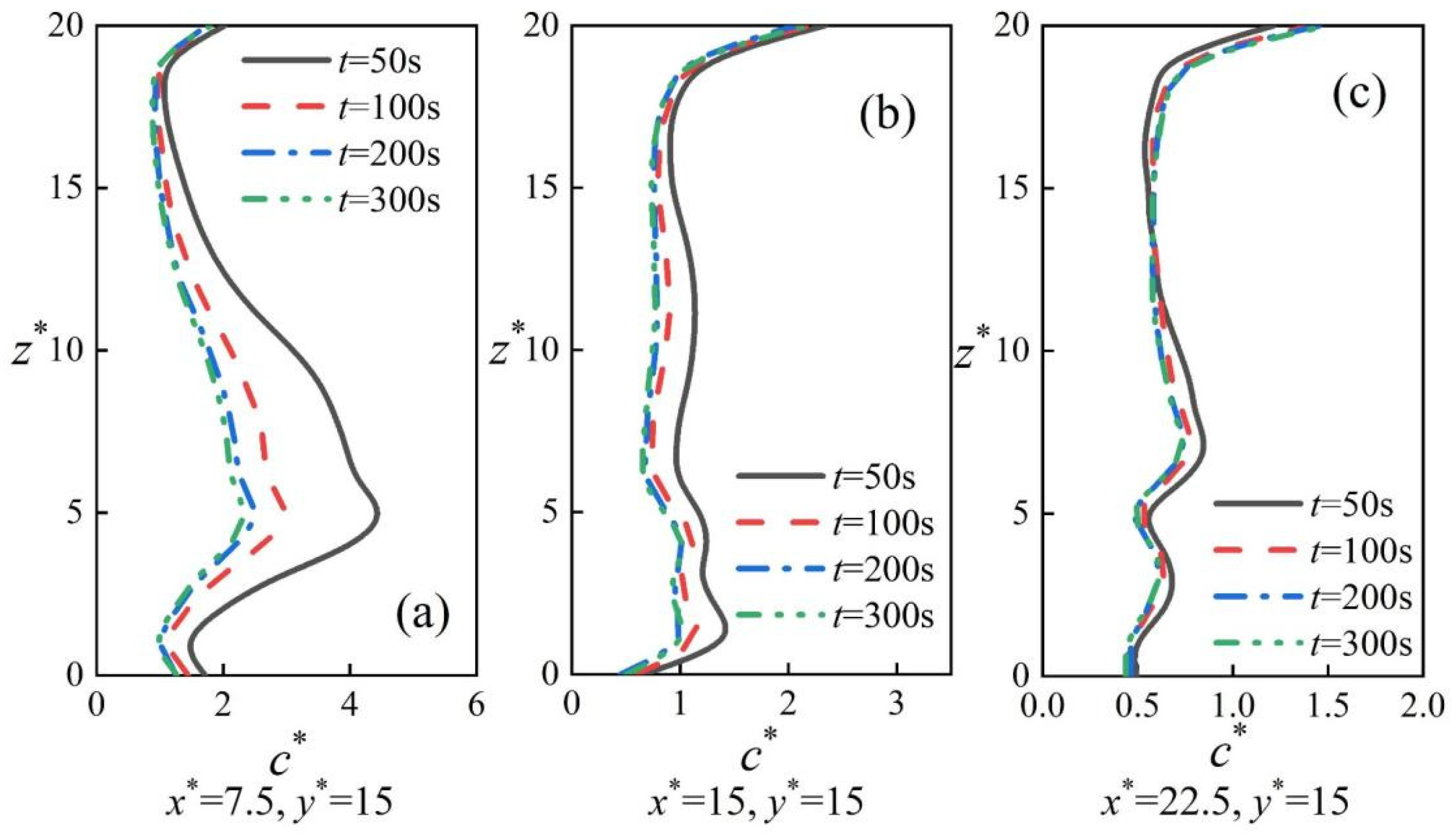Figure 16 shows the simulation results of the Eulerian and Lagrangian methods compared with the experimental results at different locations. From the figure, it can be found that the average error of t = 50 s and t = 200 s is about 20%, and the average error of t = 200 s and t = 300 s is less than 5%. In addition, t = 100 s, t = 200 s, and t = 300 s took 2 h, 7 h, and 14.5 h, respectively, on a computer with the same 128-core CPU. Therefore, t = 200 s was chosen as the calculation time for the Lagrangian method.

4.3.2. Comparison of Eulerian and Lagrangian Calculation Results

Figure 17 shows the oil mist concentration distributions calculated by different methods under mixed ventilation conditions, where Figure 17a and Figure 18b show the results of the Eulerian and Lagrangian methods, respectively. The differences between these two concentration distributions are mainly concentrated in the position near the roof. According to the flow field in Figure 10, it can be seen that although most of the flow lines are toward the roof, some of them flow near the left wall. Where there is a vortex that causes the particles to collide with the wall several times and reduce the total distance traveled in the Lagrangian model, the Eulerian method does not have the same problem. Figure 17a,b show similar conclusions, with the Lagrangian method calculating higher concentrations near the left wall, while the Eulerian method has higher concentrations in the upper part near the roof. Figure 18 shows the comparison between the calculation results of the Eulerian method and the Lagrangian method with the experiment. The average error of the calculation of the two methods is about 10%, and both methods can better match the concentration trend compared with the experimental results.

5. Discussion

The calculation of the Lagrangian method needs to consider a variety of factors to ensure the accuracy of the calculation, among which the calculation time has the greatest impact. From the above calculation results, it can be found that the calculation error of oil mist concentration is about 200% for t = 100 s and t = 300 s and less than 10% for t = 300 s and t = 400 s under roof exhaust conditions. Under mixed ventilation conditions, the calculation error is about 20% for t = 50 s and t = 200 s, and the calculation error of oil mist concentration is about 5% for t = 200 s and t = 300 s. This may be because the flow field in roof exhaust conditions in this study is more complex and there are many vortices in the space, resulting in a more difficult diffusion of particulate matter, therefore more time is needed to reach the steady state. In addition, the errors in the calculation of oil mist concentration were 20% and 10% for the Eulerian and Lagrangian methods for roof exhaust conditions and mixed ventilation conditions, respectively. This is due to the presence of more vortices under roof exhaust conditions in this study, which makes it more difficult for the particles to disperse. Indoor oil mist concentration calculations using the Lagrangian method can take longer when the factory flow field environment is more complex and has more vortices than a simple flow field.

For the roof exhaust and mixed ventilation conditions, oil mist concentrations were calculated using the Eulerian and Lagrangian methods based on the same flow field results. Using the same computer, with a 128-core CPU, the calculation time for the Eulerian method is about 1 min for the roof vent conditions, while the Lagrangian method takes 7.5 h. In the mixed ventilation case, the calculation time of the Eulerian method is also about 1 min, while that of the Lagrangian method is 7 h. Overall, the Lagrangian method consumes about 400 times more computational resources than the Eulerian method. Therefore, when simulating oil mist pollutants in industrial factories, the Eulerian method needs to be considered in the first place. In addition, the factory model in this paper is an ideal simplified model with a small volume, and the difference in resource consumption and calculation error between the Eulerian and Lagrangian methods may further increase when calculating the oil mist in a real industrial factory.

In this study, only isothermal conditions were considered. In future studies, humidity should also be included in the particle transport analysis. For particles with an aerodynamic diameter of 0.5 µm, the effects of Brownian diffusion and gravitational settling are relatively small, so a “passive scalar” can be assumed. For particles significantly deviating from this aerodynamic diameter, it is fundamental to model the various forces acting anisotropically on particles. Furthermore, the scalar transport equation for the Eulerian method has not been sufficiently discussed and should be further studied.

6. Conclusions

In this study, a scaled experimental chamber of an industrial factory was built and oil mist dispersion experiments under roof exhaust and mixed ventilation conditions were conducted. Afterward, the oil mist concentration distribution in the factory was calculated using the Eulerian and Lagrangian methods under the same working conditions, and the corresponding calculation errors and resource consumption were compared. This study can provide a reference for the numerical simulation of oil mist concentration in the industrial factory. The main conclusions of the study are as follows.

For oil mist particles with an aerodynamic diameter of 0.5 μm, both Eulerian and Lagrangian methods have a reliable accuracy.

The simulation results of Eulerian and Lagrangian methods for oil mist distribution under mixed ventilation and roof exhaust systems are consistent with the experimental results. The error of the results between the Eulerian and the Lagrangian methods under different conditions is about 10–20%.

When there are more vortices in the factory, the Lagrangian method increases the computation time by more than 53% to satisfy the computational accuracy, and the computational error between the Eulerian and Lagrangian methods becomes about 10% larger.

Based on the same flow field, the Lagrangian method consumes more than 400 times more computational resources than the Eulerian method.