The Effects of Mainstream Reynolds Number and Blowing Ratio on Film Cooling of Gas Turbine Vanes
Abstract
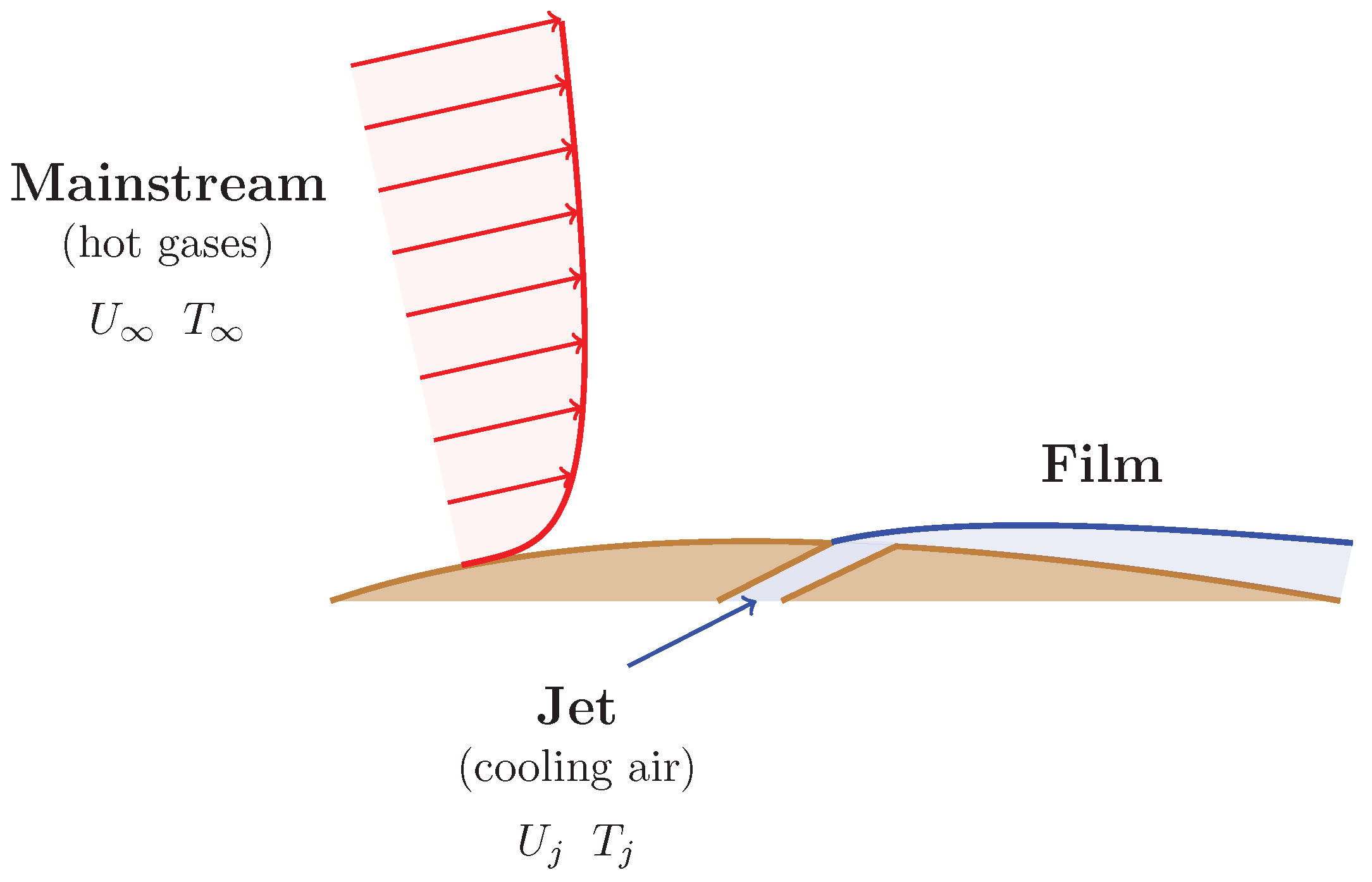
:1. Introduction
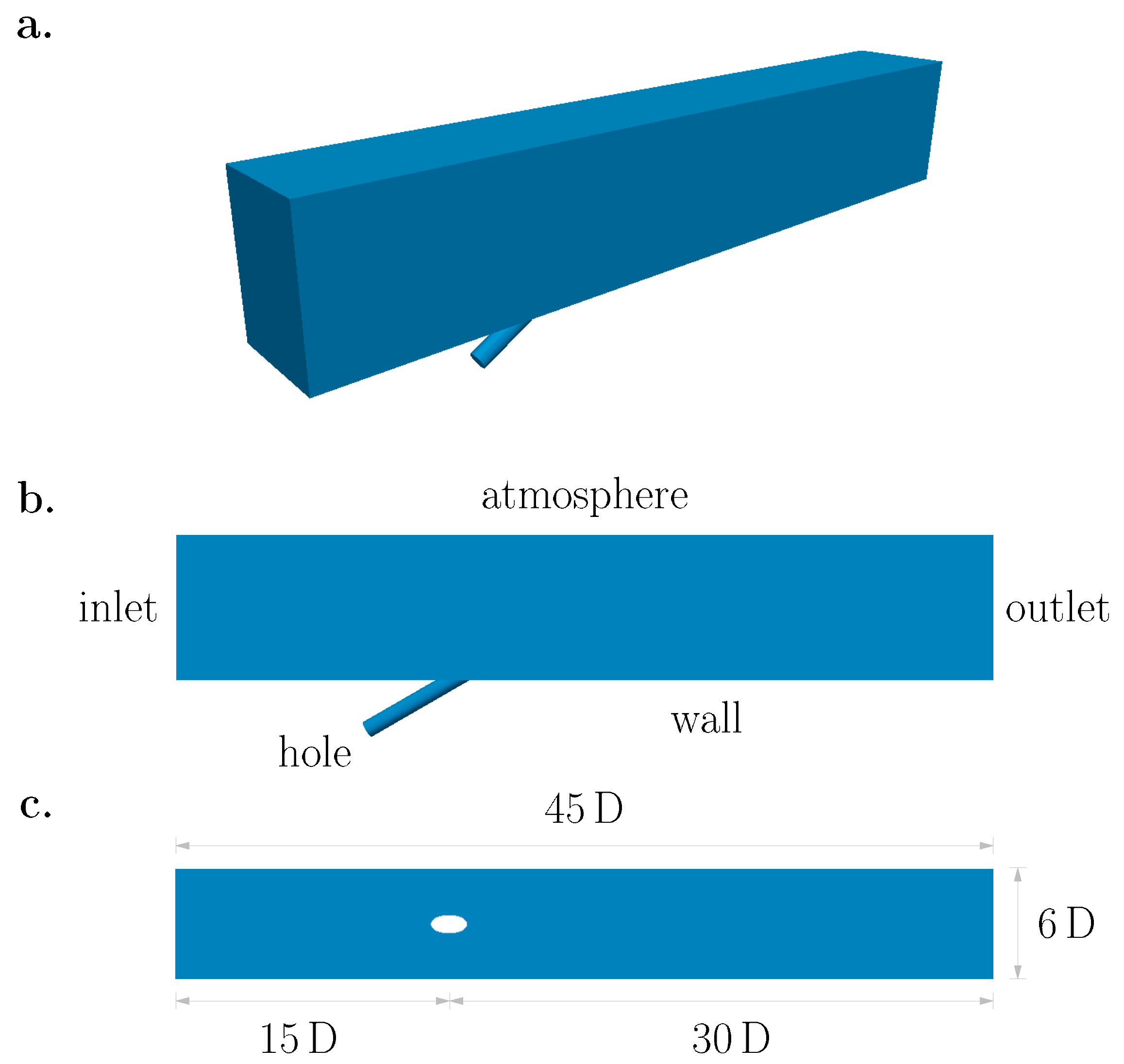
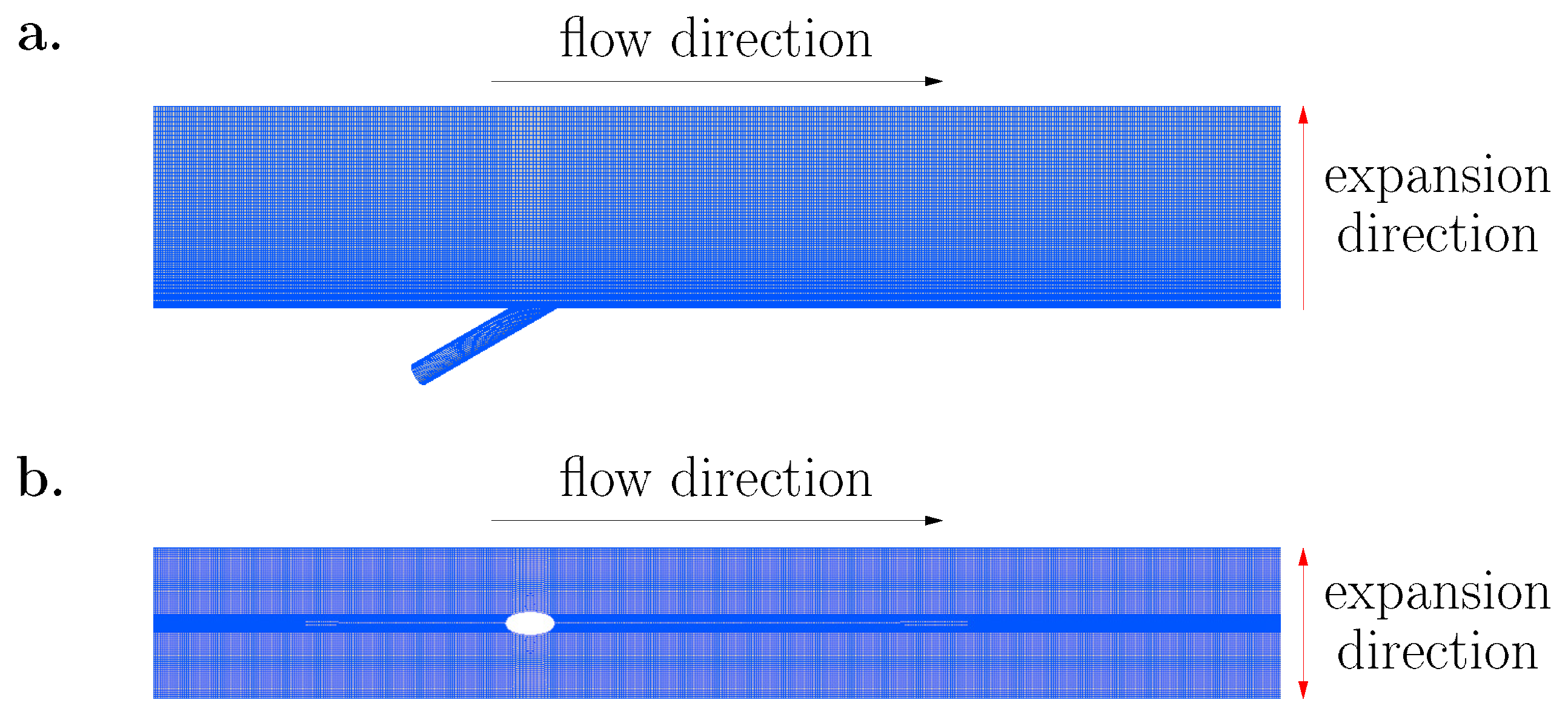
2. Numerical and Computational Methods
3. Results and Discussion
3.1. Validation on a Flat Plate
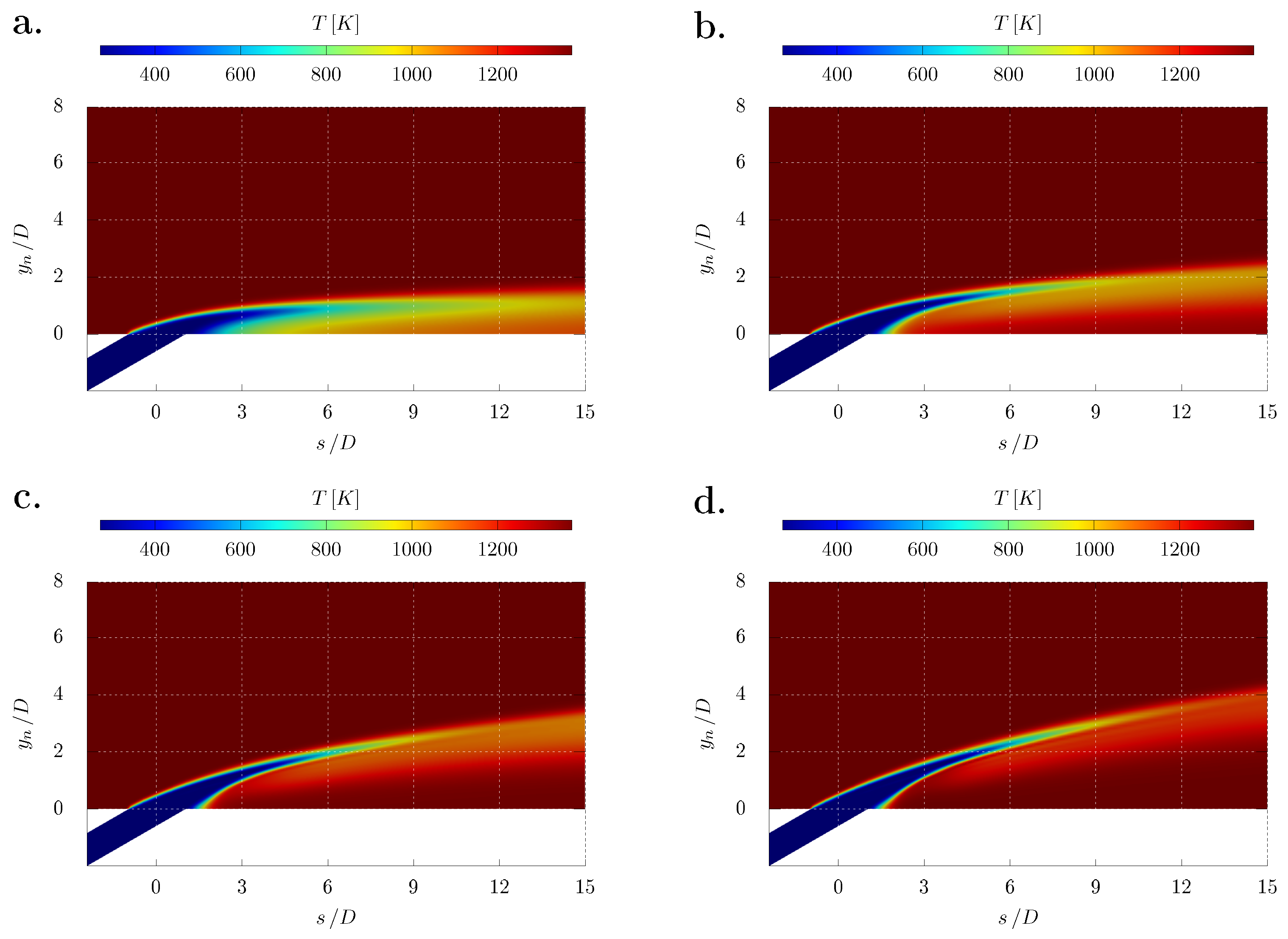
3.1.1. Adiabatic Temperature
3.1.2. Film Effectiveness
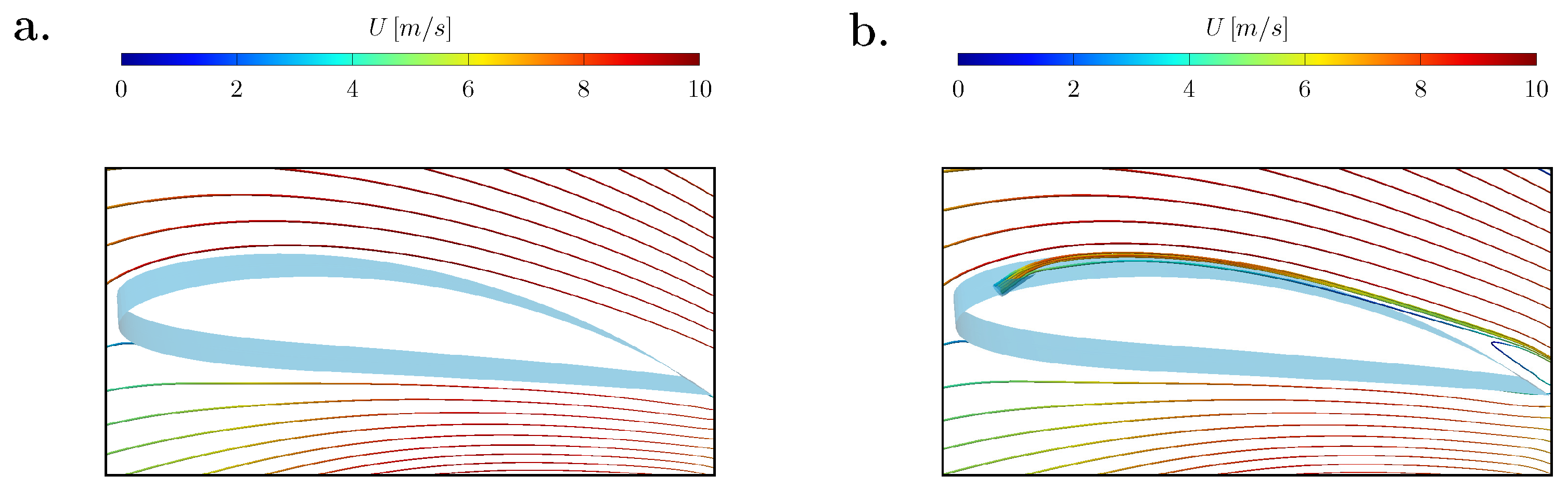
3.2. Simulations over a NACA 4412 Cascade Vane
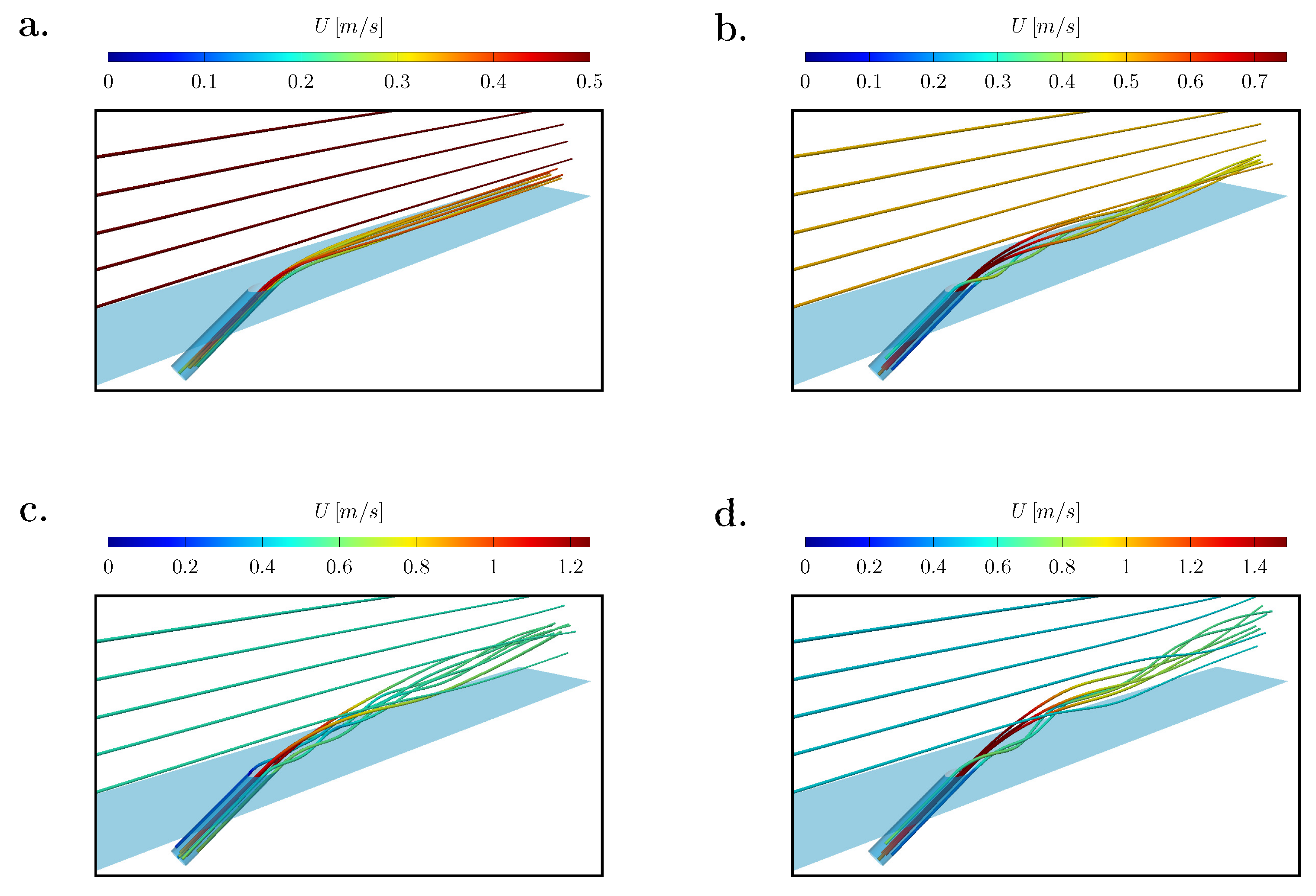
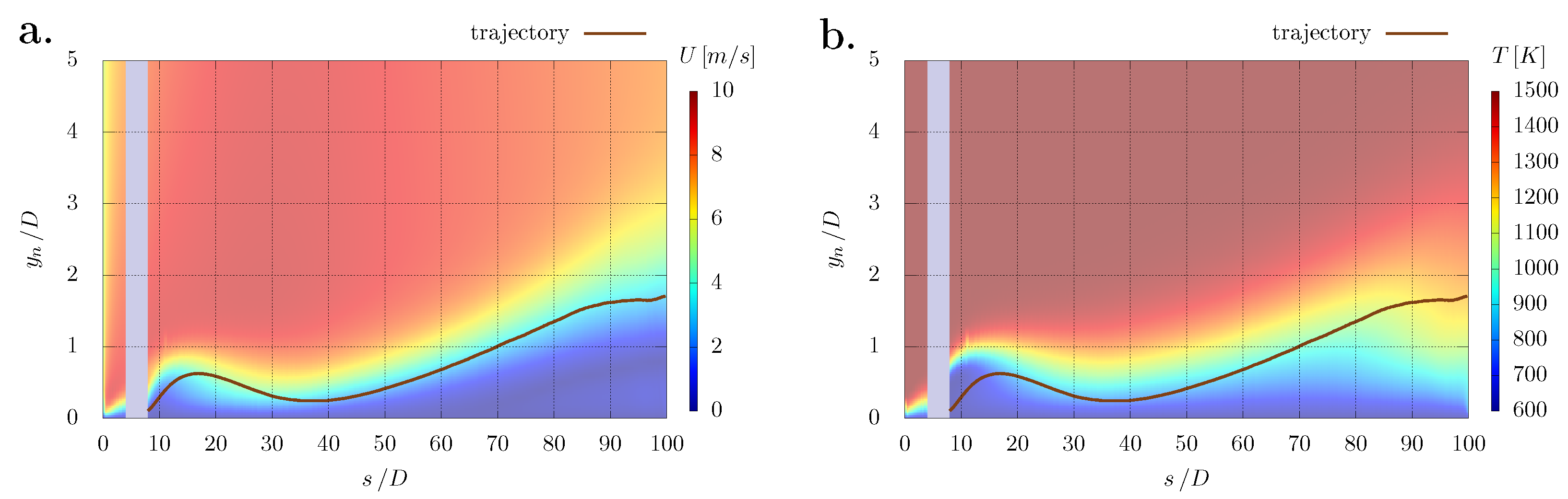
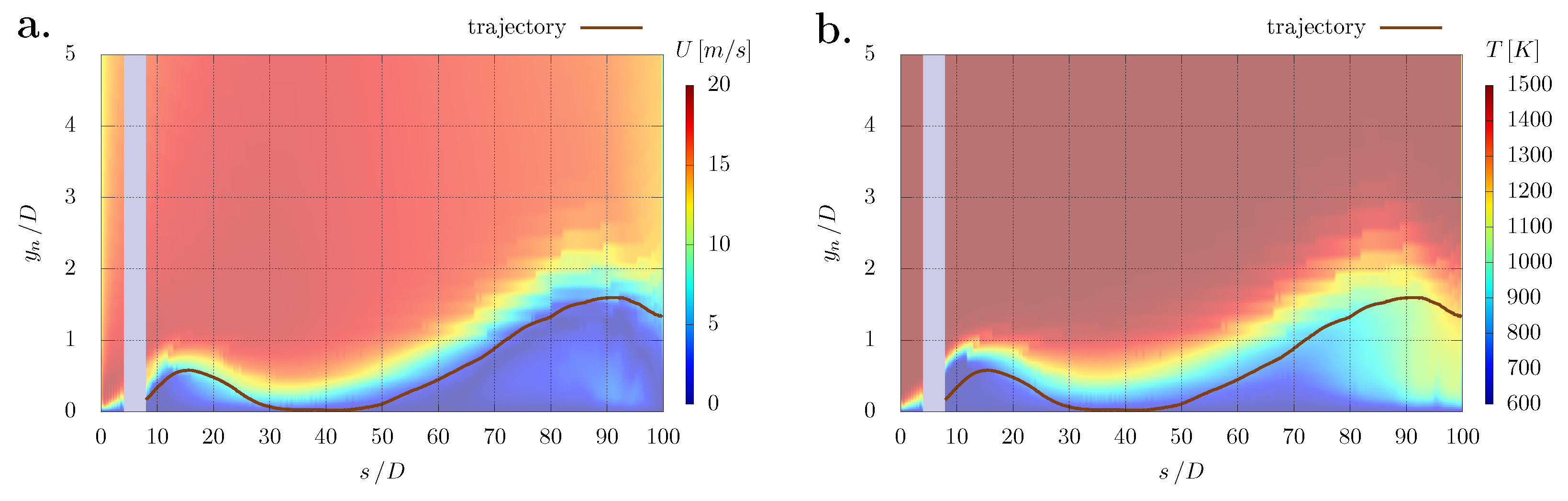
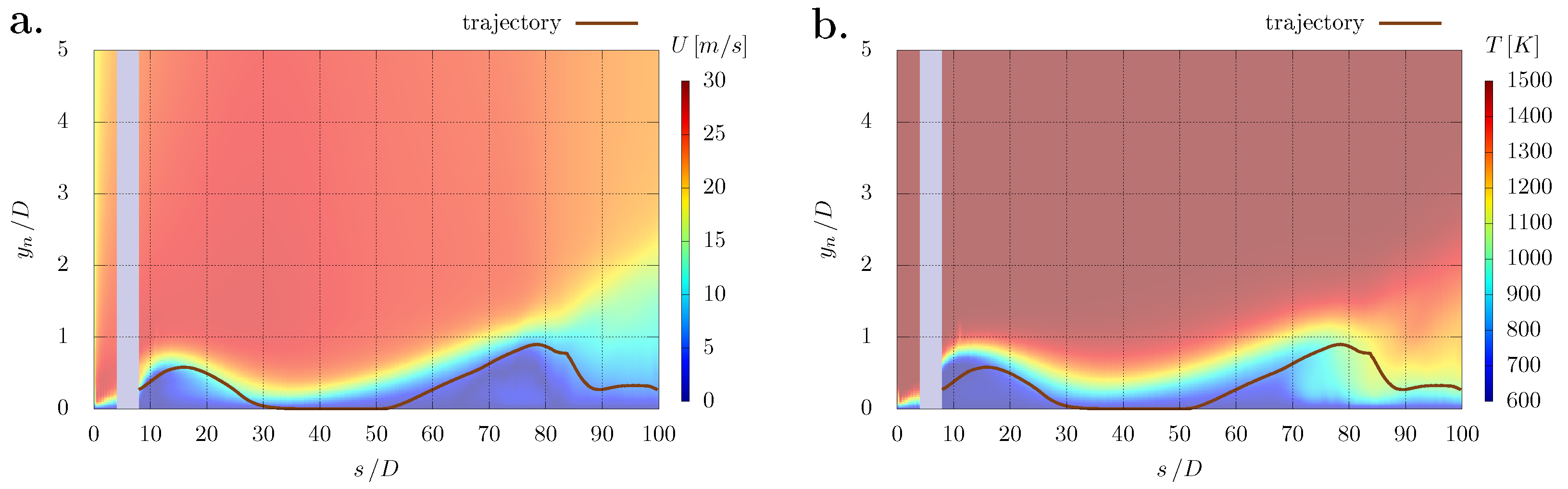
3.2.1. Jet Trajectory
3.2.2. Film Effectiveness
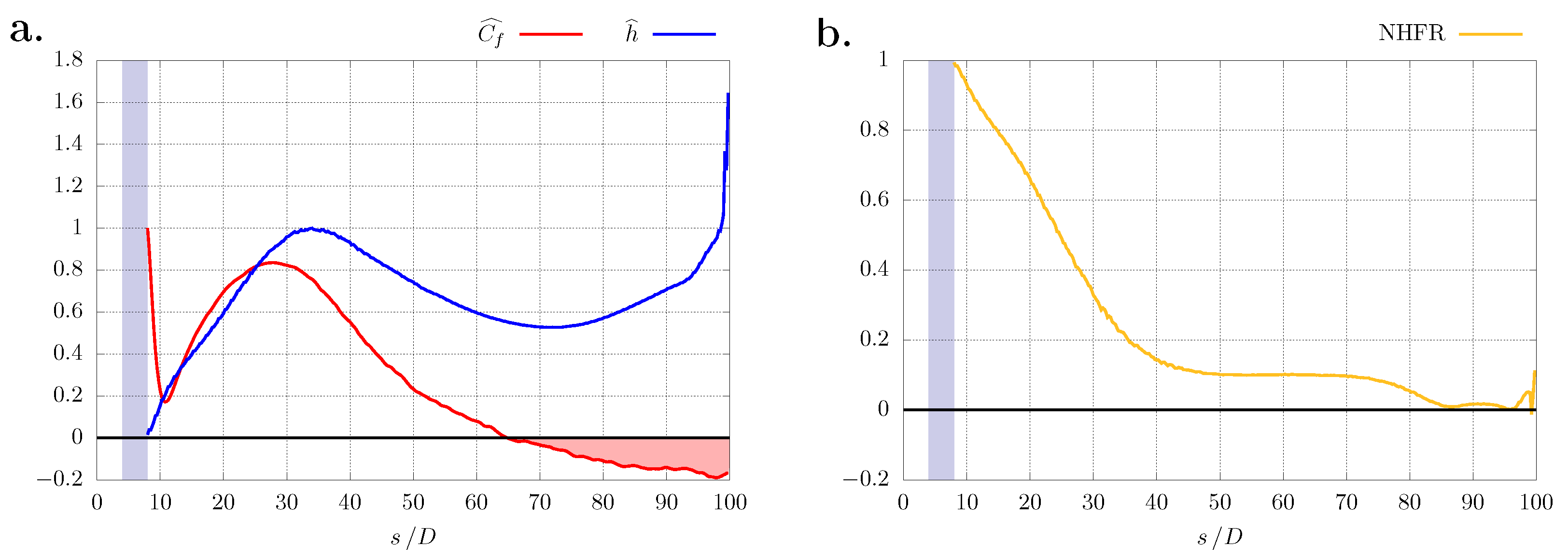
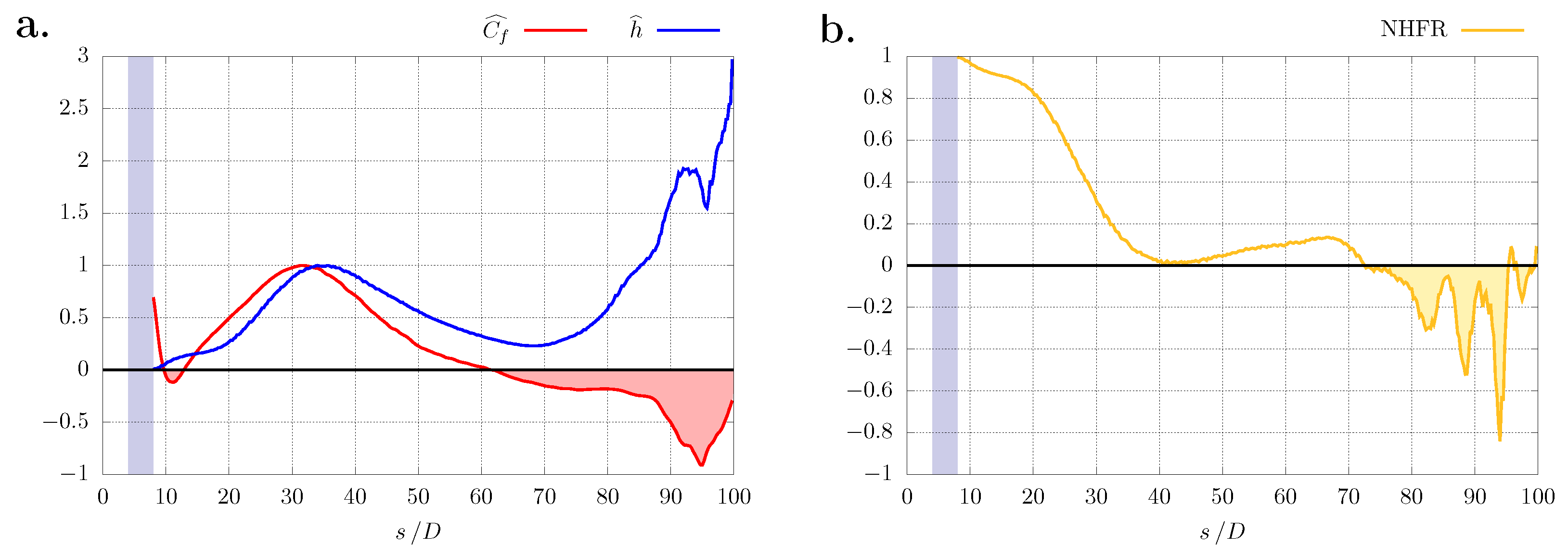
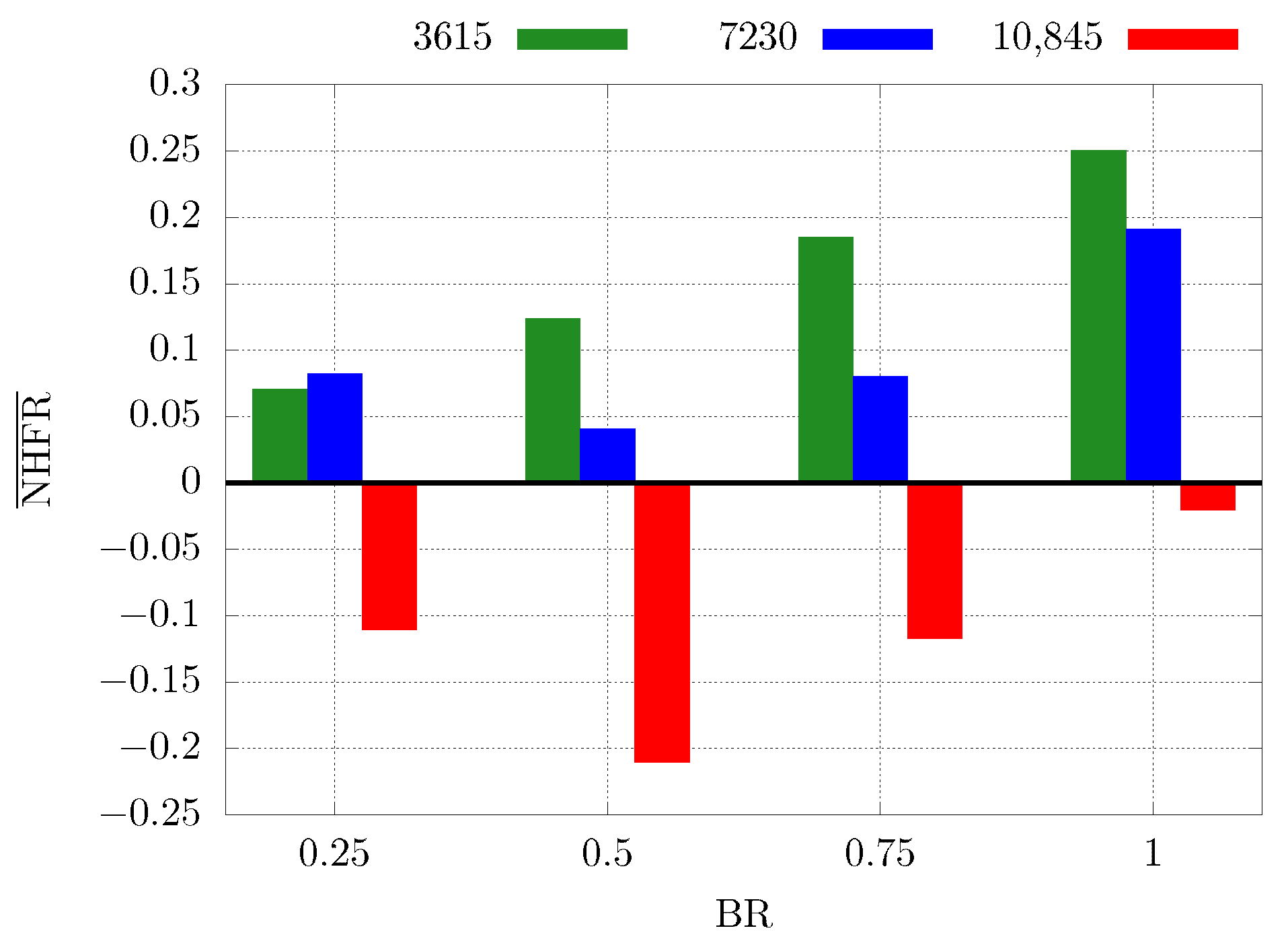
3.2.3. Net Heat Flux Reduction
4. Conclusions
5. Future Research
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BR | Blowing ratio |
| CMC | Ceramic matrix composite |
| DLN | Dry low NOx |
| EBC | Environmental barrier coating |
| FVM | Finite volume method |
| LES | Large eddy simulation |
| NHFR | Net heat flux reduction |
| PISO | Pressure-implicit with operator splitting |
| RANS | Reynolds-averaged Navier–Stokes equations |
| RIT | Rotor inlet temperature |
| SGS | Subgrid-scale model |
| SIMPLE | Semi-implicit method for pressure-linked equations |
| TBC | Thermal barrier coating |
| TIT | Turbine inlet temperature |
| WALE | Wall-adapting local eddy-viscosity |
References
- Soares, C. Gas Turbines: An Introduction and Applications. In Gas Turbines; Butterworth-Heinemann: Oxford, UK, 2015; Volume 1. [Google Scholar] [CrossRef]
- National Academies of Sciences, Engineering, and Medicine, Aggressive goals for gas turbine development: Aviation. In Advanced Technologies for Gas Turbines; The National Academies Press: Washington, DC, USA, 2020; Volume 2.2. [CrossRef]
- Cohen, H. Teoría de las Turbinas de Gas; Marcombo: Barcelona, Spain, 1982; p. 433. [Google Scholar]
- Boyce, M.P. An Overview of Gas Turbines. In Gas Turbine Engineering Handbook; Butterworth-Heinemann: Oxford, UK, 2006; Volume 1. [Google Scholar] [CrossRef]
- Banihabib, R.; Assadi, M. The Role of Micro Gas Turbines in Energy Transition. Energies 2022, 15, 8084. [Google Scholar] [CrossRef]
- Farhat, H.; Salvini, C. Novel Gas Turbine Challenges to Support the Clean Energy Transition. Energies 2022, 15, 5474. [Google Scholar] [CrossRef]
- Gil García, G. Turbinas y Compresores de Gas. Los Motores del Siglo XXI; Alfaomega: Benito Juarez, CDMX, Mexico, 2013; p. 600. [Google Scholar]
- Min Kwon, H.; Won Moon, S.; Seop Kim, T.; Won Kang, D. Performance enhancement of the gas turbine combined cycle by simultaneous reheating, recuperation, and coolant inter-cooling. Energy 2020, 207, 118271. [Google Scholar] [CrossRef]
- Faqih, M.; Omar, M.B.; Ibrahim, R.; Omar, B.A.A. Dry-Low Emission Gas Turbine Technology: Recent Trends and Challenges. Appl. Sci. 2022, 12, 10922. [Google Scholar] [CrossRef]
- Ishikawa, M.; Terauchi, M.; Komori, T.; Yasuraoka, J. Development of High Efficiency Gas Turbine Combined Cycle Power Plant; Technical Review (TR) 2008-451015; Mitsubishi Heavy Industries, Ltd.: Tokyo, Japan, 2008. [Google Scholar]
- Puspitasari, P.; Andoko, A.; Kurniawan, P. Failure analysis of a gas turbine blade: A review. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1034, 12156. [Google Scholar] [CrossRef]
- Fathyunes, L.; Mohtadi-Bonab, M.A. A Review on the Corrosion and Fatigue Failure of Gas Turbines. Metals 2023, 13, 701. [Google Scholar] [CrossRef]
- Wee, S.; Do, J.; Kim, K.; Lee, C.; Seok, C.; Choi, B.G.; Choi, Y.; Kim, W. Review on Mechanical Thermal Properties of Superalloys and Thermal Barrier Coating Used in Gas Turbines. Appl. Sci. 2020, 10, 5476. [Google Scholar] [CrossRef]
- Krishna Anand, V.G.; Parammasivam, K.M. Thermal barrier coated surface modifications for gas turbine film cooling: A review. J. Therm. Anal. Calorim. 2021, 146, 545–580. [Google Scholar] [CrossRef]
- Zhu, D. Aerospace Ceramic Materials: Thermal, Environmental Barrier Coatings and SiC/SiC Ceramic Matrix Composites for Turbine Engine Applications; Technical Memorandum (TM) 2018-219884; NASA Glenn Research Center: Cleveland, OH, USA, 2018. [Google Scholar]
- Lv, B.; Jin, X.; Cao, J.; Xu, B.; Wang, Y.; Fang, D. Advances in numerical modeling of environmental barrier coating systems for gas turbines. J. Eur. Ceram. Soc. 2020, 40, 3363–3379. [Google Scholar] [CrossRef]
- Han, J.C.; Dutta, S.; Ekkad, S. Gas Turbine Heat Transfer and Cooling Technology; CRC Press: Boca Raton, FL, USA, 2013; p. 887. [Google Scholar] [CrossRef]
- El-Damaty, W.; Gadalla, M. Exergoeconomic Analysis of Intercooled, Reheated and Recuperated Gas Turbine Cycles With Air Film Blade Cooling. In Proceedings of the ASME 2018 International Mechanical Engineering Congress and Exposition, Pittsburgh, PA, USA, 9–15 November 2018. [Google Scholar] [CrossRef]
- Filinov, E.P.; Kuz’michev, V.S.; Tkachenko, A.Y.; Ostapyuk, Y.A.; Krupenich, I.N. Estimation of cooling flow rate for conceptual design stage of a gas turbine engine. Proc. Inst. Mech. Eng. Part A J. Power Energy 2021, 235, 2014–2021. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, S.; Wang, C.; Tan, X. Recent advances in film cooling enhancement: A review. Chin. J. Aeronaut. 2020, 33, 1119–1136. [Google Scholar] [CrossRef]
- Chang, J.; Du, Y.; Shao, X.; Zhao, Y.; Zheng, S. Investigation and analysis of vortex and application of jet in crossflow. Case Stud. Therm. Eng. 2019, 14, 100459. [Google Scholar] [CrossRef]
- Li, W.; Li, X.; Ren, J.; Jiang, H. Length to diameter ratio effect on heat transfer performance of simple and compound angle holes in thin-wall airfoil cooling. Int. J. Heat Mass Transf. 2018, 127, 867–879. [Google Scholar] [CrossRef]
- Li, W.; Lu, X.; Li, X.; Ren, J.; Jiang, H. High resolution measurements of film cooling performance of simple and compound angle cylindrical holes with varying hole length-to-diameter ratio–Part I: Adiabatic film effectiveness. Int. J. Therm. Sci. 2018, 124, 146–161. [Google Scholar] [CrossRef]
- El-Damaty, W.; Gadalla, M. Assessment of Gas Turbine’s Cooling Systems Integrated With Bottoming Cycle. In Proceedings of the ASME 2018 Power Conference, Lake Buena Vista, FL, USA, 24–28 June 2018. [Google Scholar] [CrossRef]
- Bogard, D.G. Airfoil Film Cooling. In The Gas Turbine Handbook; U.S. Department of Energy’s National Energy Technology Laboratory (NETL): Pittsburgh, PA, USA, 2006; Volume 4.2.2.1. [Google Scholar]
- Khalatov, A.; Shi-Ju, E.; Wang, D.; Borisov, I. Film cooling evaluation of a single array of triangular craters. Int. J. Heat Mass Transf. 2020, 159, 120055. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, Z.; Tian, L.; Ren, X.; Sundén, B. Effects of hole configuration on film cooling effectiveness and particle deposition on curved surfaces in gas turbines. Appl. Therm. Eng. 2021, 190, 116861. [Google Scholar] [CrossRef]
- Zhu, R.; Xie, G.; Simon, T.W. New Designs of Novel Holes Based on Cylindrical Configurations for Improving Film Cooling Effectiveness. In Proceedings of the ASME Turbo Expo 2018: Turbomachinery Technical Conference and Exposition, Oslo, Norway, 11–15 June 2018. [Google Scholar] [CrossRef]
- Hou, R.; Wen, F.; Luo, Y.; Tang, X.; Wang, S. Large eddy simulation of film cooling flow from round and trenched holes. Int. J. Heat Mass Transf. 2019, 144, 118631. [Google Scholar] [CrossRef]
- He, J.; Deng, Q.; Feng, Z. Film Cooling Performance Enhancement by Upstream V-shaped Protrusion/Dimple Vortex Generator. Int. J. Heat Mass Transf. 2021, 180, 121784. [Google Scholar] [CrossRef]
- Zhou, W.; Peng, D.; Wen, X.; Liu, Y.; Hu, H. Unsteady analysis of adiabatic film cooling effectiveness behind circular, shaped, and sand-dune-inspired film cooling holes: Measurement using fast-response pressure-sensitive paint. Int. J. Heat Mass Transf. 2018, 125, 1003–1016. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Perić, M. Computational Methods for Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2012; p. 426. [Google Scholar] [CrossRef]
- Nicoud, F.; Ducros, F. Subgrid-Scale Stress Modelling Based on the Square of the Velocity Gradient Tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Hou, R.; Wen, F.; Wang, S.; Luo, Y.; Tang, X. Large eddy simulation of the trenched film cooling hole with different compound angles and coolant inflow orientation effects. Appl. Therm. Eng. 2019, 163, 114397. [Google Scholar] [CrossRef]
- Zamiri, A.; Chung, J.T. Large eddy simulation of internal coolant crossflow orientation effects on film-cooling effectiveness of fan-shaped holes. Int. J. Heat Mass Transf. 2022, 190, 122778. [Google Scholar] [CrossRef]
- Kang, Y.S.; Rhee, D.H.; Song, Y.J.; Kwak, J.S. Large Eddy Simulations on Film Cooling Flow Behaviors with Upstream Turbulent Boundary Layer Generated by Circular Cylinder. Energies 2021, 14, 7227. [Google Scholar] [CrossRef]
- Moukalled, F.; Mangani, L.; Darwish, M. The Finite Volume Method in Computational Fluid Dynamics; Springer: Cham, Switzerland, 2016; p. 791. [Google Scholar] [CrossRef]
- Issa, R.I. Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Caretto, L.S.; Gosman, A.D.; Patankar, S.V.; Spalding, D.B. Two calculation procedures for steady, three-dimensional flows with recirculation. In Proceedings of the Third International Conference on Numerical Methods in Fluid Mechanics, Paris, France, 3–7 July 1972; Springer: Berlin/Heidelberg, Germany, 1973. [Google Scholar] [CrossRef]
- Holzmann, T. Mathematics, Numerics, Derivations and OpenFOAM (R); Holzmann CFD: Leoben, Austria, 2019; p. 159. [Google Scholar]
- Marić, T.; Höpken, J.; Mooney, K.G. The OpenFOAM (R) Technology Primer; European Organisation for Nuclear Research (CERN): Geneva, Switzerland, 2021; p. 423. [Google Scholar] [CrossRef]
- Baagherzadeh Hushmandi, N. Large Eddy simulation of flat plate film cooling at high blowing ratio using OpenFOAM. Heat Mass Transf. 2018, 54, 1603–1611. [Google Scholar] [CrossRef]
- Greenshields, C.; Weller, H. Notes on Computational Fluid Dynamics: General Principles; CFD Direct: Reading, UK, 2022; p. 291. [Google Scholar]
- Thurman, D.R.; El-Gabry, L.A.; Poinsatte, P.E.; Heidmann, J.D. Turbulence and Heat Transfer Measurements in an Inclined Large Scale Film Cooling Array: Part II–Temperature and Heat Transfer Measurements. In Proceedings of the ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition, Vancouver, BC, Canada, 6–10 June 2011. [Google Scholar] [CrossRef]
- Dhivya, S.; Karthikeyan, A. Design and Analysis of Gas Turbine Blade with Cooling. EAI Endorsed Trans. Energy Web Inf. Technol. 2018, 5, 12. [Google Scholar] [CrossRef]
- El-Sayed, A.F. Blade Profile Selection. In Aircraft Propulsion and Gas Turbine Engines; CRC Press: Boca Raton, FL, USA, 2017; Volume 14.5.3. [Google Scholar]
- Zhao, W.; Chi, Z.; Zang, S. Numerical and experimental study of scaling criteria accuracy for film cooling using CO2 coolant. Int. J. Heat Mass Transf. 2021, 181, 121984. [Google Scholar] [CrossRef]







| Boundary | U | p |
|---|---|---|
| atmosphere (inflow) | ||
| atmosphere (outflow) | ||
| inlet | ||
| hole | ||
| outlet | ||
| wall | ||
| front/back |
| Boundary | |||
|---|---|---|---|
| atmosphere (inflow) | |||
| atmosphere (outflow) | |||
| inlet | |||
| hole | |||
| outlet | |||
| wall | |||
| front/back |
| BR | [m3/s] | [m/s] | Re |
|---|---|---|---|
| 0.5 | 0.5 | 330 | |
| 1 | 1 | 660 | |
| 1.5 | 1.5 | 990 | |
| 2 | 2 | 1320 |
| BR | [m3/s] | [m/s] | Re | [m3/s] | [m/s] | Re |
|---|---|---|---|---|---|---|
| 0.25 | 5 | 3615 | 1.25 | 52 | ||
| 0.5 | 2.5 | 105 | ||||
| 0.75 | 3.75 | 157 | ||||
| 1 | 5 | 209 | ||||
| 0.25 | 10 | 7230 | 2.5 | 105 | ||
| 0.5 | 5 | 209 | ||||
| 0.75 | 7.5 | 314 | ||||
| 1 | 10 | 418 | ||||
| 0.25 | 15 | 10,845 | 3.75 | 157 | ||
| 0.5 | 7.5 | 314 | ||||
| 0.75 | 11.25 | 471 | ||||
| 1 | 15 | 628 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sierra-Vargas, G.; Garzón-Alvarado, D.; Duque-Daza, C. The Effects of Mainstream Reynolds Number and Blowing Ratio on Film Cooling of Gas Turbine Vanes. Fluids 2023, 8, 263. https://doi.org/10.3390/fluids8100263
Sierra-Vargas G, Garzón-Alvarado D, Duque-Daza C. The Effects of Mainstream Reynolds Number and Blowing Ratio on Film Cooling of Gas Turbine Vanes. Fluids. 2023; 8(10):263. https://doi.org/10.3390/fluids8100263
Chicago/Turabian StyleSierra-Vargas, Germán, Diego Garzón-Alvarado, and Carlos Duque-Daza. 2023. "The Effects of Mainstream Reynolds Number and Blowing Ratio on Film Cooling of Gas Turbine Vanes" Fluids 8, no. 10: 263. https://doi.org/10.3390/fluids8100263
APA StyleSierra-Vargas, G., Garzón-Alvarado, D., & Duque-Daza, C. (2023). The Effects of Mainstream Reynolds Number and Blowing Ratio on Film Cooling of Gas Turbine Vanes. Fluids, 8(10), 263. https://doi.org/10.3390/fluids8100263







