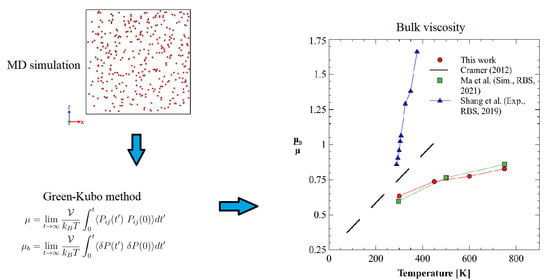
Bulk Viscosity of Dilute Gases and Their Mixtures
Abstract
1. Introduction
2. Mechanism of Bulk Viscosity
2.1. Apparent Bulk Viscosity
2.2. Intrinsic Bulk Viscosity
3. Applications of Bulk Viscosity
4. Molecular Model and Simulation Details
4.1. Green–Kubo Method
4.2. Molecular Model
| Gas | Source | [K] | [Å] | Bond-Length [Å] |
|---|---|---|---|---|
| Nitrogen | Tokumasu et al. [65] | 47.202 | 3.17 | 1.098 |
| Neon | Vrabec et al. [4] | 33.921 | 2.8010 | – |
| Argon | Vrabec et al. [4] | 116.79 | 3.3952 | – |
| Krypton | Vrabec et al. [4] | 162.58 | 3.6274 | – |
| Source | [K] | [Å] | Bond-Length [Å] |
|---|---|---|---|
| CHARM [66] | 60.389 | 3.029 | 1.208 |
| CHARM-2 [66] | 60.389 | 3.029 | 1.12 |
| Javananien et al. [67] | 48.458 | 3.13 | 1.016 |
| Bouanich et al. [68] | 52.583 | 3.0058 | 1.21 |
| Cordeiro et al. [69] | 35.0 | 2.6 | 1.21 |
| Fishcher et al. [70] | 43.659 | 3.09 | 1.016 |
| Porrini et al. [71] | 52.331 | 2.96 | 1.12 |
| Victor et al. [72] | 67.0 | 3.57 | 1.214 |
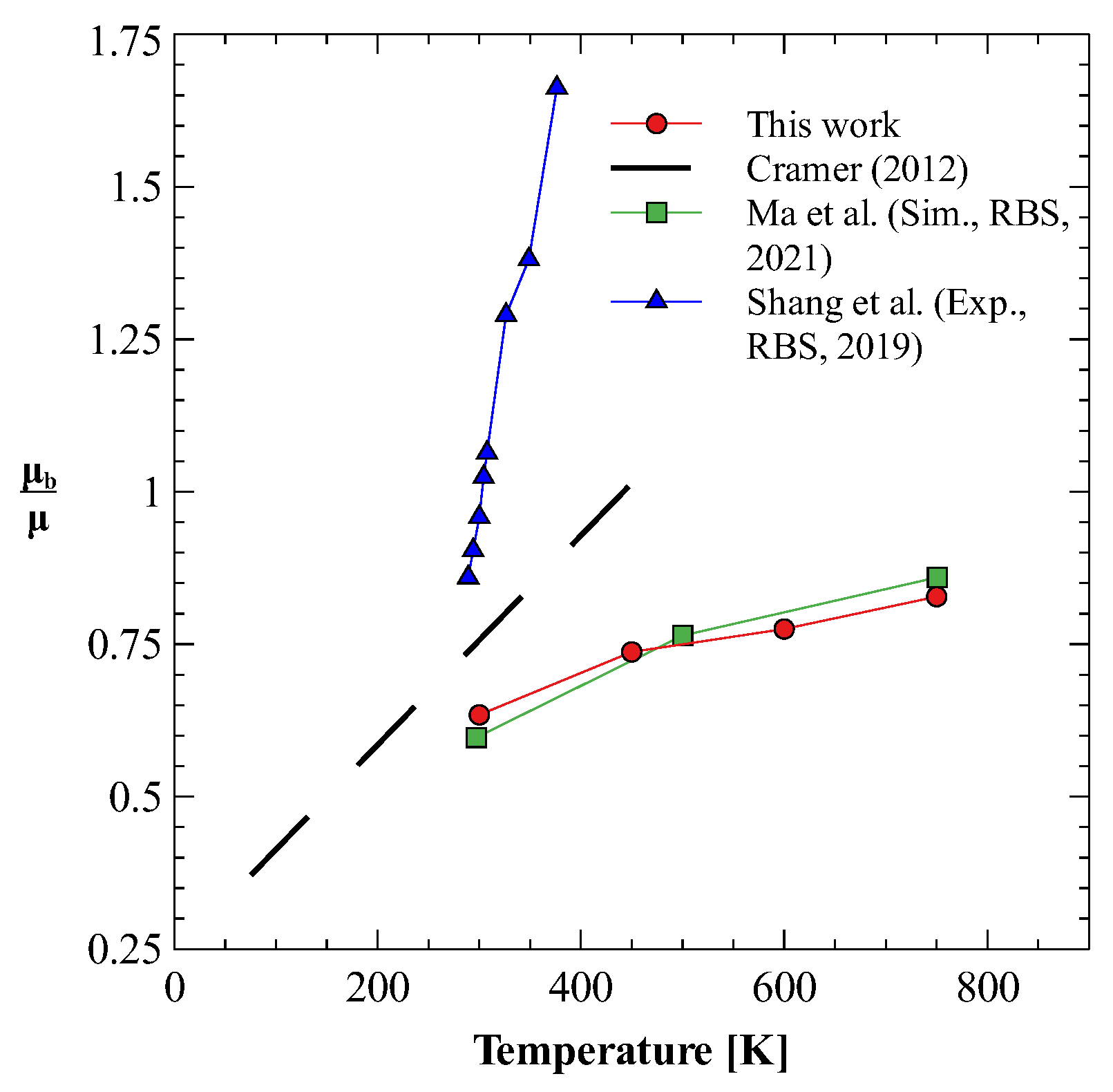
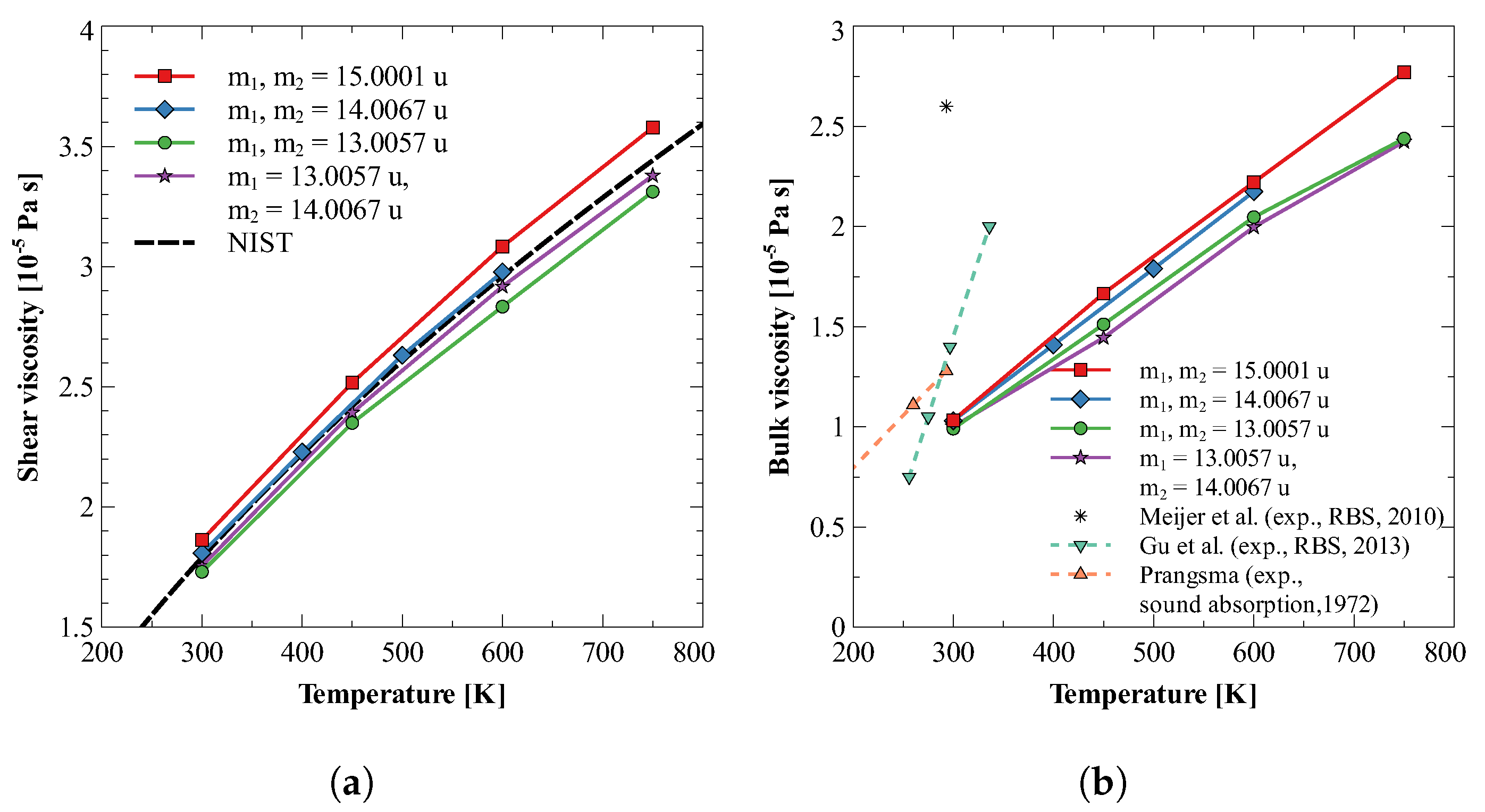
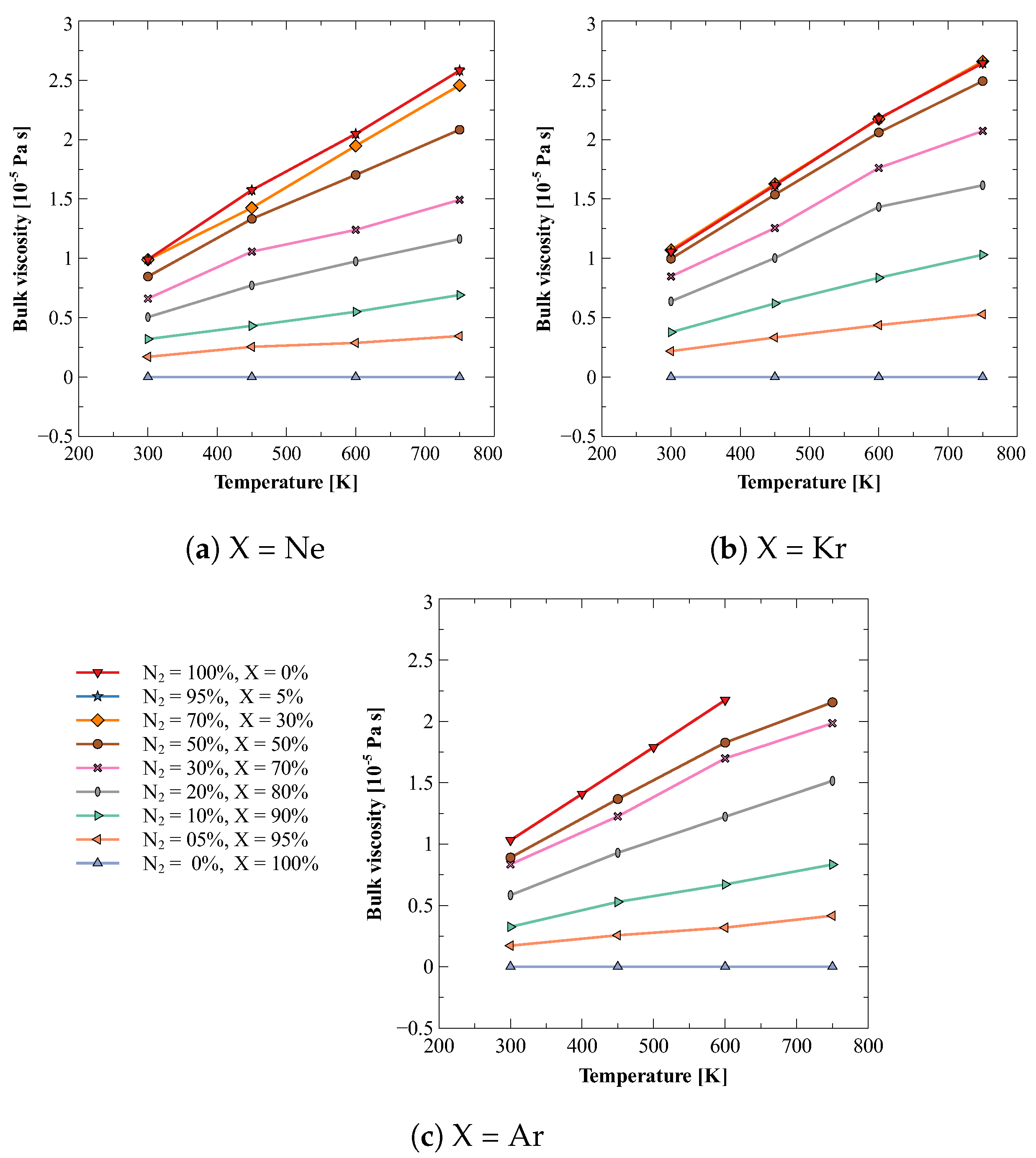
5. Results and Discussion
5.1. Effect of Atomic Mass: Bulk Viscosity of Isotopes of N2
5.2. Bulk Viscosity of Mixture of Nitrogen with Noble Gas
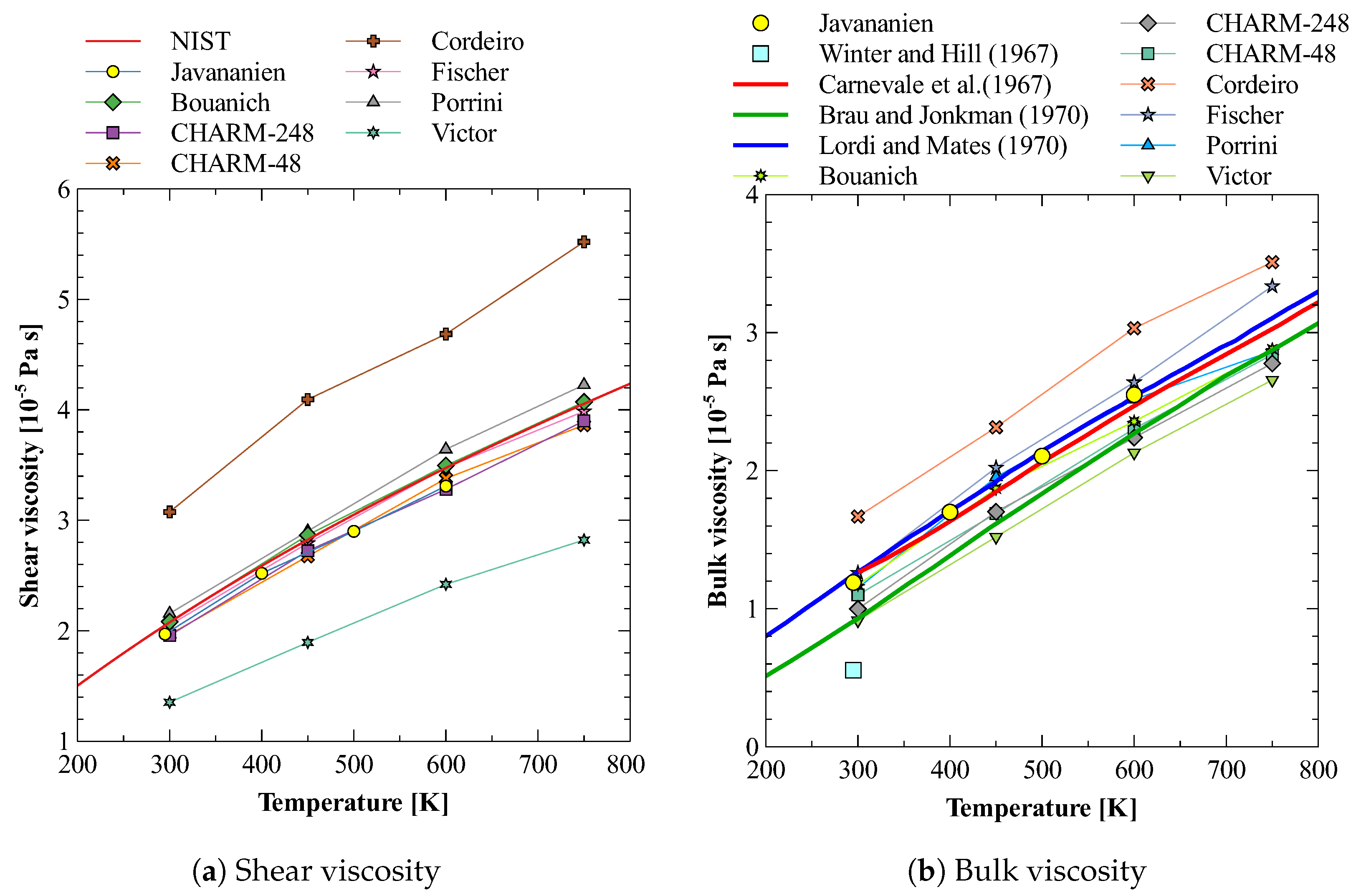
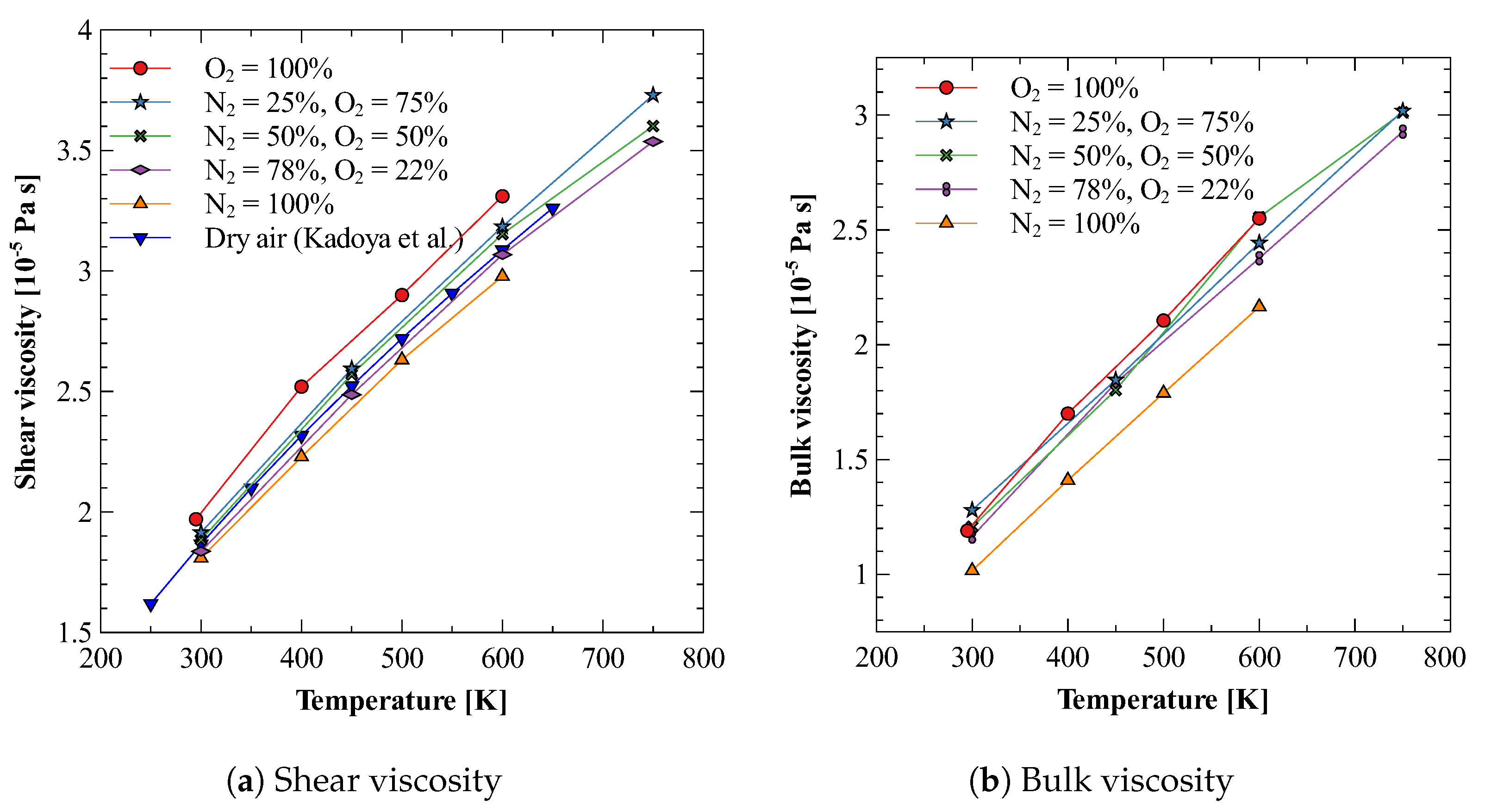
5.3. Bulk Viscosity of O2
5.4. Bulk Viscosity of N2 + O2Mixture
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Heyes, D.M. Thermal conductivity and bulk viscosity of simple fluids. A molecular-dynamics study. J. Chem. Soc. Faraday Trans. Mol. Chem. Phys. 1984, 80, 1363–1394. [Google Scholar] [CrossRef]
- Hoheisel, C.; Vogelsang, R.; Schoen, M. Bulk viscosity of the Lennard-Jones fluid for a wide range of states computed by equilibrium molecular dynamics. J. Chem. Phys. 1987, 87, 7195–7198. [Google Scholar] [CrossRef]
- Hoheisel, C. Bulk viscosity of model fluids. A comparison of equilibrium and nonequilibrium molecular dynamics results. J. Chem. Phys. 1987, 86, 2328–2333. [Google Scholar] [CrossRef]
- Fernez, G.; Vrabec, J.; Hasse, H. A molecular simulation study of shear and bulk viscosity and thermal conductivity of simple real fluids. Fluid Phase Equilibria 2004, 221, 157–163. [Google Scholar]
- Meador, W.E.; Miner, G.A.; Townsend, L.W. Bulk viscosity as a relaxation parameter: Fact or fiction? Phys. Fluids 1996, 8, 258–261. [Google Scholar] [CrossRef]
- Meier, K.; Laesecke, A.; Kabelac, S. Transport coefficients of the Lennard-Jones model fluid. III. Bulk viscosity. J. Chem. Phys. 2005, 122, 014513. [Google Scholar] [CrossRef]
- Baidakov, V.G.; Protsenko, S.P. Metastable Lennard-Jones fluids. III. Bulk viscosity. J. Chem. Phys. 2014, 141, 114503. [Google Scholar] [CrossRef]
- Rah, K.; Eu, B.C. Density and temperature dependence of the bulk viscosity of molecular liquids: Carbon dioxide and nitrogen. J. Chem. Phys. 2001, 114, 10436–10447. [Google Scholar] [CrossRef]
- Guo, G.-J.; Zhang, Y.-G. Equilibrium molecular dynamics calculation of the bulk viscosity of liquid water. Mol. Phys. 2001, 99, 283–289. [Google Scholar] [CrossRef]
- Tisza, L. Supersonic absorption and Stokes’ viscosity relation. Phys. Rev. 1942, 61, 531. [Google Scholar] [CrossRef]
- Sharma, B.; Kumar, R. Estimation of bulk viscosity of dilute gases using a nonequilibrium molecular dynamics approach. Phys. Rev. E 2019, 100, 013309. [Google Scholar] [CrossRef]
- Sharma, B.; Kumar, R.; Gupta, P.; Pareek, S.; Singh, A. On the estimation of bulk viscosity of dilute nitrogen gas using equilibrium molecular dynamics approach. Phys. Fluids 2022, 34, 057104. [Google Scholar] [CrossRef]
- Madigosky, W. Density dependence of the bulk viscosity in argon. J. Chem. Phys. 1967, 46, 4441–4444. [Google Scholar] [CrossRef]
- Kistemaker, P.; Tom, A.; Vries, A.D. Rotational relaxation numbers for the isotopic molecules of N2 and CO. Physica 1970, 48, 414–424. [Google Scholar] [CrossRef]
- Prangsma, G.J.; Alberga, A.H.; Beenakker, J. Ultrasonic determination of the volume viscosity of N2, CO, CH4 and CD4 between 77 and 300 K. Physica 1973, 64, 278–288. [Google Scholar] [CrossRef]
- Pan, X.; Shneider, M.N.; Miles, R.B. Coherent Rayleigh-Brillouin scattering in molecular gases. Phys. Rev. A 2004, 69, 033814. [Google Scholar] [CrossRef]
- Pan, X.; Shneider, M.N.; Miles, R.B. Power spectrum of coherent Rayleigh-Brillouin scattering in carbon dioxide. Phys. Rev. A 2005, 71, 045801. [Google Scholar] [CrossRef]
- Vieitez, M.O.; VanDuijn, E.J.; Ubachs, W.; Witschas, B.; Meijer, A.; DeWijn, A.S.; Dam, N.J.; van de Water, W. Coherent and spontaneous Rayleigh-Brillouin scattering in atomic and molecular gases and gas mixtures. Phys. Rev. A 2010, 82, 043836. [Google Scholar] [CrossRef]
- Meijer, A.; deWijn, A.; Peters, M.; Dam, N.; van de Water, W. Coherent Rayleigh–Brillouin scattering measurements of bulk viscosity of polar and nonpolar gases, and kinetic theory. J. Chem. Phys. 2010, 133, 164315. [Google Scholar] [CrossRef]
- Gu, Z.; Ubachs, W. Temperature-dependent bulk viscosity of nitrogen gas determined from spontaneous Rayleigh–Brillouin scattering. Opt. Lett. 2013, 38, 1110–1112. [Google Scholar] [CrossRef]
- Gu, Z.; Ubachs, W. A systematic study of Rayleigh-Brillouin scattering in air, N2, and O2 gases. J. Chem. Phys. 2014, 141, 104320. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Ubachs, W.; Van DeWater, W. Bulk viscosity of CO2 from Rayleigh-Brillouin light scattering spectroscopy at 532 nm. J. Chem. Phys. 2019, 150, 154502. [Google Scholar] [CrossRef]
- Ma, Q.; Yang, C.; Bruno, D.; Zhang, J. Molecular simulation of Rayleigh-Brillouin scattering in binary gas mixtures and extraction of the rotational relaxation numbers. Phys. Rev. E 2021, 104, 035109. [Google Scholar] [CrossRef]
- Herzfeld, K.; Rice, F. Dispersion and absorption of high frequency sound waves. Phys. Rev. 1928, 31, 691. [Google Scholar] [CrossRef]
- Marcy, S.J. Evaluating the second coefficient of viscosity from sound dispersionor absorption data. AIAA J. 1990, 28, 171–173. [Google Scholar] [CrossRef]
- Dukhin, A.S.; Goetz, P.J. Bulk viscosity and compressibility measurement using acoustic spectroscopy. J. Chem. Phys. 2009, 130, 124519. [Google Scholar] [CrossRef]
- Claes, L.; Hülskämper, L.M.; Baumhögger, E.; Feldmann, N.; Chatwell, R.S.; Vrabec, J.; Henning, B. Acoustic absorption measurement for the determination of the volume viscosity of pure fluids/Messverfahren für die akustischen Absorption zur Bestimmung der Volumenviskosität reiner Fluide. Tech. Mess. 2019, 86, 2–6. [Google Scholar] [CrossRef]
- Holmes, M.; Parker, N.; Povey, M. Temperature dependence of bulk viscosity in water using acoustic spectroscopy. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2011; Volume 269, p. 012011. [Google Scholar]
- Zuckerwar, A.J.; Ash, R.L. Volume viscosity in fluids with multiple dissipative processes. Phys. Fluids 2009, 21, 033105. [Google Scholar] [CrossRef]
- Kosuge, S.; Aoki, K. Shock-wave structure for a polyatomic gas with large bulk viscosity. Phys. Rev. Fluids 2018, 3, 023401. [Google Scholar] [CrossRef]
- Singh, S.; Myong, R. A computational study of bulk viscosity effects on shock-vortex interaction using discontinuous Galerkin method. J. Comput. Fluids Eng. 2017, 22, 86–95. [Google Scholar] [CrossRef]
- Singh, S.; Battiato, M.; Myong, R. Impact of bulk viscosity on flow morphology of shock-accelerated cylindrical light bubble in diatomic and polyatomic gases. Phys. Fluids 2021, 33, 066103. [Google Scholar] [CrossRef]
- Pan, S.; Johnsen, E. The role of bulk viscosity on the decay of compressible, homogeneous, isotropic turbulence. J. Fluid Mech. 2017, 833, 717–744. [Google Scholar] [CrossRef]
- Szemberg O’Connor, T. Bulk Viscosity Effects in Compressible Turbulent Couette Flow. Ph.D. Thesis, Imperial College London, London, UK, 2018. [Google Scholar]
- Touber, E. Small-scale two-dimensional turbulence shaped by bulk viscosity. J. Fluid Mech. 2019, 875, 974–1003. [Google Scholar] [CrossRef]
- Boukharfane, R.; Ferrer, P.J.M.; Mura, A.; Giovangigli, V. On the role of bulk viscosity in compressible reactive shear layer developments. Eur. J. Mech. B/Fluids 2019, 77, 32–47. [Google Scholar] [CrossRef]
- Nazari-Mahroo, H.; Pasandideh, K.; Navid, H.; Sadighi-Bonabi, R. How important is the liquid bulk viscosity effect on the dynamics of a single cavitation bubble? Ultrason. Sonochem. 2018, 49, 47–52. [Google Scholar] [CrossRef]
- Lin, J.; Scalo, C.; Hesselink, L. High-fidelity simulation of an ultrasonic standing-wave thermoacoustic engine with bulk viscosity effects. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017; p. 0929. [Google Scholar]
- Lin, J.; Scalo, C.; Hesselink, L. Bulk viscosity model for near-equilibrium acoustic wave attenuation. arXiv 2017, arXiv:1707.05876. [Google Scholar]
- Singh, S.; Karchani, A.; Myong, R. Non-equilibrium effects of diatomic and polyatomic gases on the shock-vortex interaction based on the second-order constitutive model of the Boltzmann-Curtiss equation. Phys. Fluids 2018, 30, 016109. [Google Scholar] [CrossRef]
- Chen, S.; Wang, X.; Wang, J.; Wan, M.; Li, H.; Chen, S. Effects of bulk viscosity on compressible homogeneous turbulence. Phys. Fluids 2019, 31, 085115. [Google Scholar]
- Chen, T.; Wen, X.; Wang, L.-P.; Guo, Z.; Wang, J.; Chen, S. Simulation of three-dimensional compressible decaying isotropic turbulence using a redesigned discrete unified gas kinetic scheme. Phys. Fluids 2020, 32, 125104. [Google Scholar] [CrossRef]
- Nettleton, R. Intrinsic Bulk Viscosity in Monatomic and Diatomic Gases. J. Appl. Phys. 1958, 29, 204–212. [Google Scholar] [CrossRef]
- Okumura, H.; Yonezawa, F. New formula for the bulk viscosity constructed from the interatomic potential and the pair distribution function. J. Chem. Phys. 2002, 116, 7400–7410. [Google Scholar] [CrossRef]
- Hall, L. The origin of ultrasonic absorption in water. Phys. Rev. 1948, 73, 775. [Google Scholar] [CrossRef]
- Yahya, A.; Tan, L.; Perticaroli, S.; Mamontov, E.; Pajerowski, D.; Neuefeind, J.; Ehlers, G.; Nickels, J.D. Molecular origins of bulk viscosity in liquid water. Phys. Chem. Chem. Phys. 2020, 22, 9494–9502. [Google Scholar] [CrossRef] [PubMed]
- Buresti, G. A note on Stokes’ hypothesis. Acta Mech. 2015, 226, 3555–3559. [Google Scholar] [CrossRef]
- Emanuel, G. Effect of bulk viscosity on a hypersonic boundary layer. Phys. Fluids A Fluid Dyn. 1992, 4, 491–495. [Google Scholar] [CrossRef]
- Sengupta, T.K.; Sengupta, A.; Sharma, N.; Sengupta, S.; Bhole, A.; Shruti, K. Roles of bulk viscosity on Rayleigh-Taylor instability: Non-equilibrium thermodynamics due to spatio-temporal pressure fronts. Phys. Fluids 2016, 28, 094102. [Google Scholar] [CrossRef]
- Emanuel, G. Bulk viscosity of a dilute polyatomic gas. Phys. Fluids Fluid Dyn. 1990, 2, 2252–2254. [Google Scholar] [CrossRef]
- Emanuel, G.; Argrow, B.M. Linear dependence of the bulk viscosity on shock wave thickness. Phys. Fluids 1994, 6, 3203–3205. [Google Scholar] [CrossRef]
- Emanuel, G. Bulk viscosity in the Navier–Stokes equations. Int. J. Eng. Sci. 1998, 36, 1313–1323. [Google Scholar] [CrossRef]
- Chikitkin, A.; Rogov, B.; Tirsky, G.; Utyuzhnikov, S. Effect of bulk viscosity in supersonic flow past spacecraft. Appl. Numer. Math. 2015, 93, 47–60. [Google Scholar] [CrossRef]
- Shevelev, Y.D.; Syzranova, N.; Nagnibeda, E.; Kustova, E. Bulk-viscosity effect on CO2 hypersonic flow around blunt bodies. Dokl. Phys. 2015, 60, 207–209. [Google Scholar] [CrossRef]
- Elizarova, T.G.; Khokhlov, A.A.; Montero, S. Numerical simulation of shock wave structure in nitrogen. Phys. Fluids 2007, 19, 068102. [Google Scholar] [CrossRef]
- Claycomb, A.; Greendyke, R. Extending CFD Modeling to the Transition Regime by Enhanced Thermophysical Modeling. In Proceedings of the 40th Thermophysics Conference, Seattle, WA, USA, 23–26 June 2008; p. 3930. [Google Scholar]
- Bahmani, F.; Cramer, M. Suppression of shock-induced separation in fluids having large bulk viscosities. J. Fluid Mech. 2014, 756, R2. [Google Scholar] [CrossRef]
- Riabov, V.V. Limitations of the bulk viscosity approach in modeling the expanding nitrogen flows. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2019; Volume 2132, p. 150003. [Google Scholar]
- Fru, G.; Janiga, G.; Thévenin, D. Direct numerical simulations of the impact of high turbulence intensities and volume viscosity on premixed methane flames. J. Combust. 2011, 2011, 746719. [Google Scholar] [CrossRef]
- Fru, G.; Janiga, G.; Thévenin, D. Impact of volume viscosity on the structure of turbulent premixed flames in the thin reaction zone regime. Flow Turbul. Combust. 2012, 88, 451–478. [Google Scholar] [CrossRef]
- Billet, G.; Giovangigli, V.; DeGassowski, G. Impact of volume viscosity on a shock–hydrogen-bubble interaction. Combust. Theory Model. 2008, 12, 221–248. [Google Scholar] [CrossRef]
- Zhang, Y.; Otani, A.; Maginn, E.J. Reliable viscosity calculation from equilibrium molecular dynamics simulations: A time decomposition method. J. Chem. Theory Comput. 2015, 11, 3537–3546. [Google Scholar] [CrossRef]
- Plimpton, S.; Crozier, P.; Thompson, A. LAMMPS-large-scale atomic/molecular massively parallel simulator. Sandia Natl. Lab. 2007, 18, 43. [Google Scholar]
- Sanders, J. Veusz—A Scientific Plotting Package, VERSION: 3.3.1. 2008. Available online: https://veusz.github.io/ (accessed on 1 December 2022).
- Tokumasu, T.; Matsumoto, Y. Dynamic molecular collision (DMC) model for rarefied gas flow simulations by the DSMC method. Phys. Fluids 1999, 11, 1907–1920. [Google Scholar] [CrossRef]
- MacKerell, A.D., Jr.; Bashford, D.; Bellott, M.; Dunbrack, R.L., Jr.; Evanseck, J.D.; Field, M.J.; Fischer, S.; Gao, J.; Guo, H.; Ha, S.; et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B 1998, 102, 3586–3616. [Google Scholar] [CrossRef]
- Javanainen, M.; Vattulainen, I.; Monticelli, L. On atomistic models for molecular oxygen. J. Phys. Chem. B 2017, 121, 518–528. [Google Scholar] [CrossRef]
- Bouanich, J.-P. Site-site Lennard-Jones potential parameters for N2, O2, H2, CO and CO2. J. Quant. Spectrosc. Radiat. Transf. 1992, 47, 243–250. [Google Scholar] [CrossRef]
- Cordeiro, R.M. Reactive oxygen species at phospholipid bilayers: Distribution, mobility and permeation. Biochim. Biophys. Acta-(Bba)-Biomembr. 2014, 1838, 438–444. [Google Scholar] [CrossRef] [PubMed]
- Fischer, J.; Lago, S. Thermodynamic perturbation theory for molecular liquid mixtures. J. Chem. Phys. 1983, 78, 5750–5758. [Google Scholar] [CrossRef]
- Porrini, M.; Daskalakis, V.; Farantos, S.C. Exploring the topography of free energy surfaces and kinetics of cytochrome c oxidases interacting with small ligands. RSC Adv. 2012, 2, 5828–5836. [Google Scholar] [CrossRef]
- Victor, B.L.; Baptista, A.M.; Soares, C.M. Dioxygen and nitric oxide pathways and affinity to the catalytic site of rubredoxin: Oxygen oxidoreductase from Desulfovibrio gigas. JBIC J. Biol. Inorg. Chem. 2009, 14, 853–862. [Google Scholar] [CrossRef]
- Lemmon, E.W.; McLinden, M.O.; Friend, D.G. Thermophysical Properties of Fluid Systems. In The NIST Chemistry WebBook, NIST Standard Reference Database; Linstrom, P.J., Mallard, W.G., Eds.; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1998; p. 20899. [Google Scholar]
- Winter, T.G.; Hill, G.L. High-Temperature Ultrasonic Measurements of Rotational Relaxation in Hydrogen, Deuterium, Nitrogen, and Oxygen. J. Acoust. Soc. Am. 1967, 42, 848–858. [Google Scholar] [CrossRef]
- Carnevale, E.; Carey, C.; Larson, G. Ultrasonic determination of rotational collision numbers and vibrational relaxation times of polyatomic gases at high temperatures. J. Chem. Phys. 1967, 47, 2829–2835. [Google Scholar] [CrossRef]
- Brau, C.; Jonkman, R. Classical theory of rotational relaxation in diatomic gases. J. Chem. Phys. 1970, 52, 477–484. [Google Scholar] [CrossRef]
- Lordi, J.A.; Mates, R.E. Rotational relaxation in nonpolar diatomic gases. Phys. Fluids 1970, 13, 291–308. [Google Scholar] [CrossRef]
- Kadoya, K.; Matsunaga, N.; Nagashima, A. Viscosity and thermal conductivity of dry air in the gaseous phase. J. Phys. Chem. Ref. Data 1985, 14, 947–970. [Google Scholar] [CrossRef]
- Cramer, M.S. Numerical estimates for the bulk viscosity of ideal gases. Phys. Fluids 2012, 24, 066102. [Google Scholar] [CrossRef]
- Shang, J.; Wu, T.; Wang, H.; Yang, C.; Ye, C.; Hu, R.; Tao, J.; He, X. Measurement of temperature-dependent bulk viscosities of nitrogen, oxygen and air from spontaneous Rayleigh-Brillouin scattering. IEEE Access 2019, 7, 136439–136451. [Google Scholar] [CrossRef]
| m [u] | m [u] | I [u-Å] |
|---|---|---|
| 13.0057 | 13.0057 | 7.83986197 |
| 14.0067 | 14.0067 | 8.44326677 |
| 15.0001 | 15.0001 | 9.04209028 |
| 13.0057 | 14.0067 | 8.17510498 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharma, B.; Kumar, R.; Pareek, S. Bulk Viscosity of Dilute Gases and Their Mixtures. Fluids 2023, 8, 28. https://doi.org/10.3390/fluids8010028
Sharma B, Kumar R, Pareek S. Bulk Viscosity of Dilute Gases and Their Mixtures. Fluids. 2023; 8(1):28. https://doi.org/10.3390/fluids8010028
Chicago/Turabian StyleSharma, Bhanuday, Rakesh Kumar, and Savitha Pareek. 2023. "Bulk Viscosity of Dilute Gases and Their Mixtures" Fluids 8, no. 1: 28. https://doi.org/10.3390/fluids8010028
APA StyleSharma, B., Kumar, R., & Pareek, S. (2023). Bulk Viscosity of Dilute Gases and Their Mixtures. Fluids, 8(1), 28. https://doi.org/10.3390/fluids8010028