Scalable Simulation of Pressure Gradient-Driven Transport of Rarefied Gases in Complex Permeable Media Using Lattice Boltzmann Method
Abstract
:1. Introduction
2. Lattice Boltzmann
2.1. Fundamentals
2.2. Regularization
2.3. Wall Boundary Treatment
2.4. Open Flow Boundary Conditions
2.5. Constant Pressure Inlet-Outlet Condition
2.6. Periodic Boundary Conditions
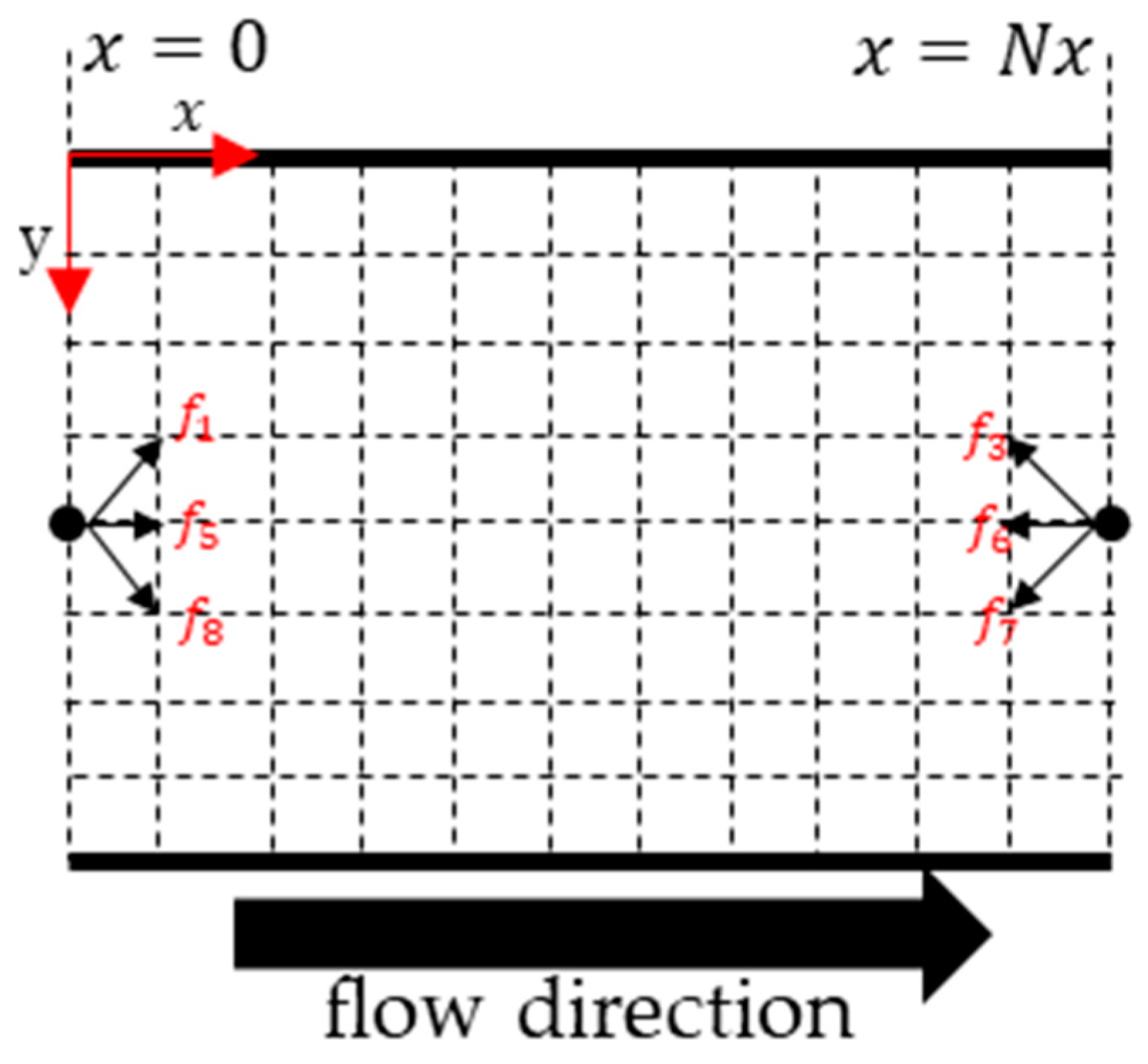
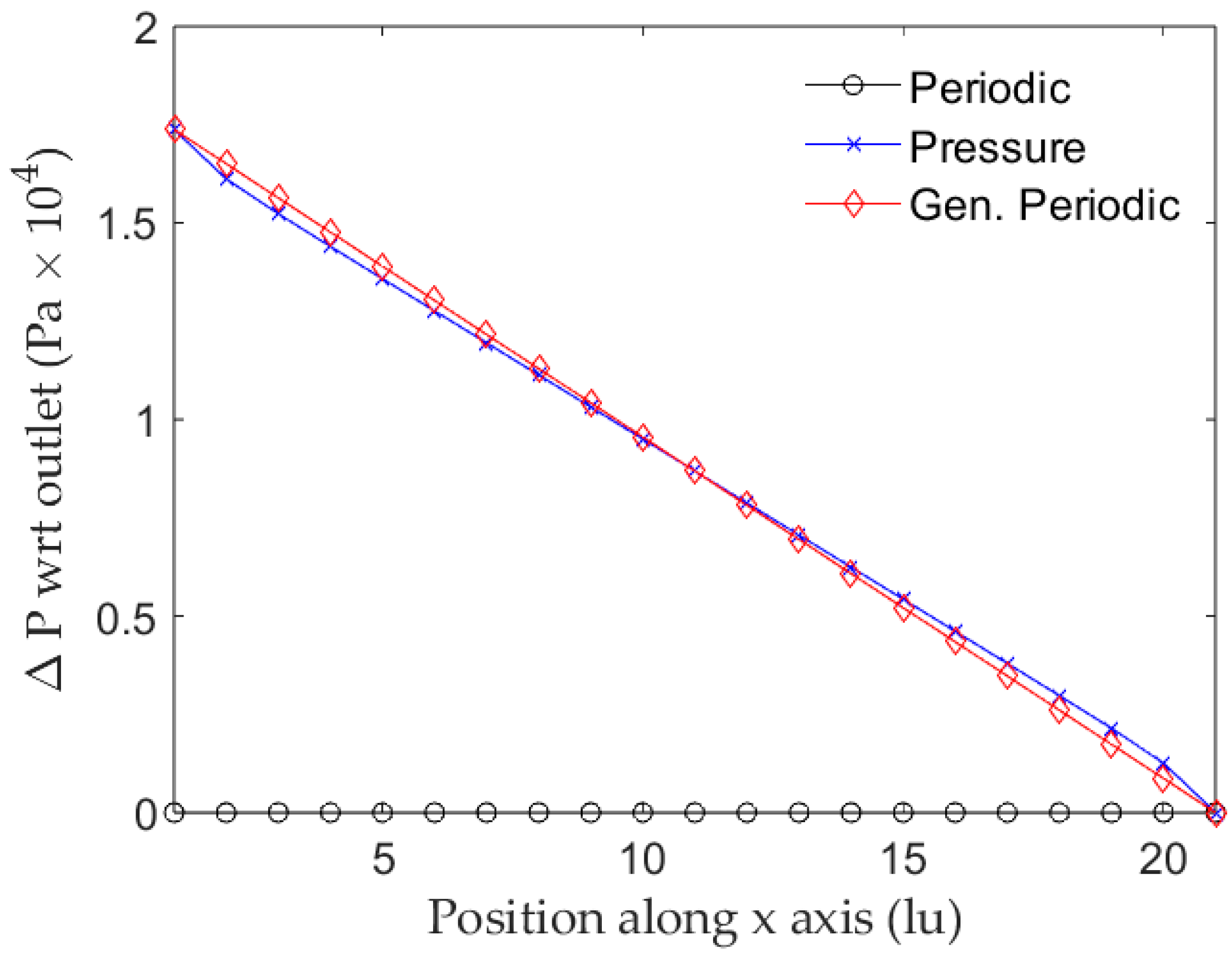
2.7. Generalized Periodic Inlet–Outlet Condition
3. Implementation Strategies
| Algorithm 1. Computation of equilibrium distribution with direct addressing—vector “pore” stores domain information, vector “feq” stores equilibrium distribution, and “argin” is for additional variables, such as density and velocity distributions. | |
| 1 | void computeEquilibrium(vector <double> &feq, vector <int> &pore, argin) { |
| 2 | for (int i = 0; i < pore.size(); i++) |
| 3 | if (pore[i] ==1) |
| 4 | feq[i] = getEquilibrium(argin); |
| 5 | } |
| Algorithm 2. Pseudo-code for non-local operation with direct addressing—vector “f” stores distribution functions, “pore” stores domain information, and “argin” is for additional variables, such as local pore size and velocity vectors used in D2Q9; the subroutine “findNeighbor” is used for mapping of 1D indices onto 2D and finding the corresponding neighbors and mapping them back onto 1D. | |
| 1 | void streamBB(vector <double> &f, vector <int> &pore, argin) { |
| 2 | for (int i = 0; i<pore.size(); i++) |
| 3 | if (pore[i] == 1) |
| 4 | for (int c = 0; c < 9; c++) |
| 5 | pore_neighbor_id = findNeighbor(i, c, argin); |
| 6 | if (pore[pore_neighbor_id] == 1) |
| 7 | stream(vector <double> &f, argin); |
| 8 | else |
| 9 | bounceBack(vector <double> &f, argin);} |
| Algorithm 3. Finding pore indices before the start of simulation—“ids_pores” stores all the indices of pore nodes, “stream_from_ids” stores current indices where particles are streaming from, “stream_to_ids” stores the corresponding neighbors, and “bounceback_ids” stores lattices where bounce back is to be executed. | |
| 1 | Vector <int> ids_pores; |
| 2 | for (int i = 0; i < pore.size(); i++) |
| 3 | if (pore[i] == 1) |
| 4 | ids_pores.push_back(i); |
| 5 | vector <int > stream_from_ids; |
| 6 | vector <int> stream_to_ids; |
| 7 | vector <int> bounceback_ids; |
| 8 | for (int i = 0; i < pore.size(); i ++) |
| 9 | if (pore[i] == 1) |
| 10 | for (int c = 0; c < 9; c++) |
| 11 | pore_neighbor_id = findNeighbor(i, c); |
| 12 | if (pore[pore_neighbor_id] == 1) |
| 13 | stream_from_ids.push_back(i); |
| 14 | stream_to_ids.push_back(pore_neighbor_id); |
| 15 | else |
| 16 | bounceback_ids.push_back(i); |
| Algorithm 4. Local operation with direct addressing. | |
| 1 | void computeEquilibrium(vector <double> &feq, vector <int> &ids_pores, *argin) { |
| 2 | for (int i = 0; i< ids_pores.size(); i++) |
| 3 | feq[ids_pores[i]] = getEquilibrium(*argin); |
| 4 | } |
| Algorithm 5. Non-local operation with indirect addressing. | |
| 1 | void streamBB(vector <double> &f, vector <int> & stream_from_ids, vector <int> & stream_to_ids, vector <int> & boundary_ids, argin) { |
| 2 | for (int i = 0; i < stream_from_ids.size(); i++) |
| 3 | stream(f, stream_from_ids[i], stream_to_ids[i], argin); |
| 4 | for (int i = 0; i < boundary_ids.size(); i++) |
| 5 | bounceback(f, boundary_ids[i], argin); } |
4. Validation
5. Results and Discussion
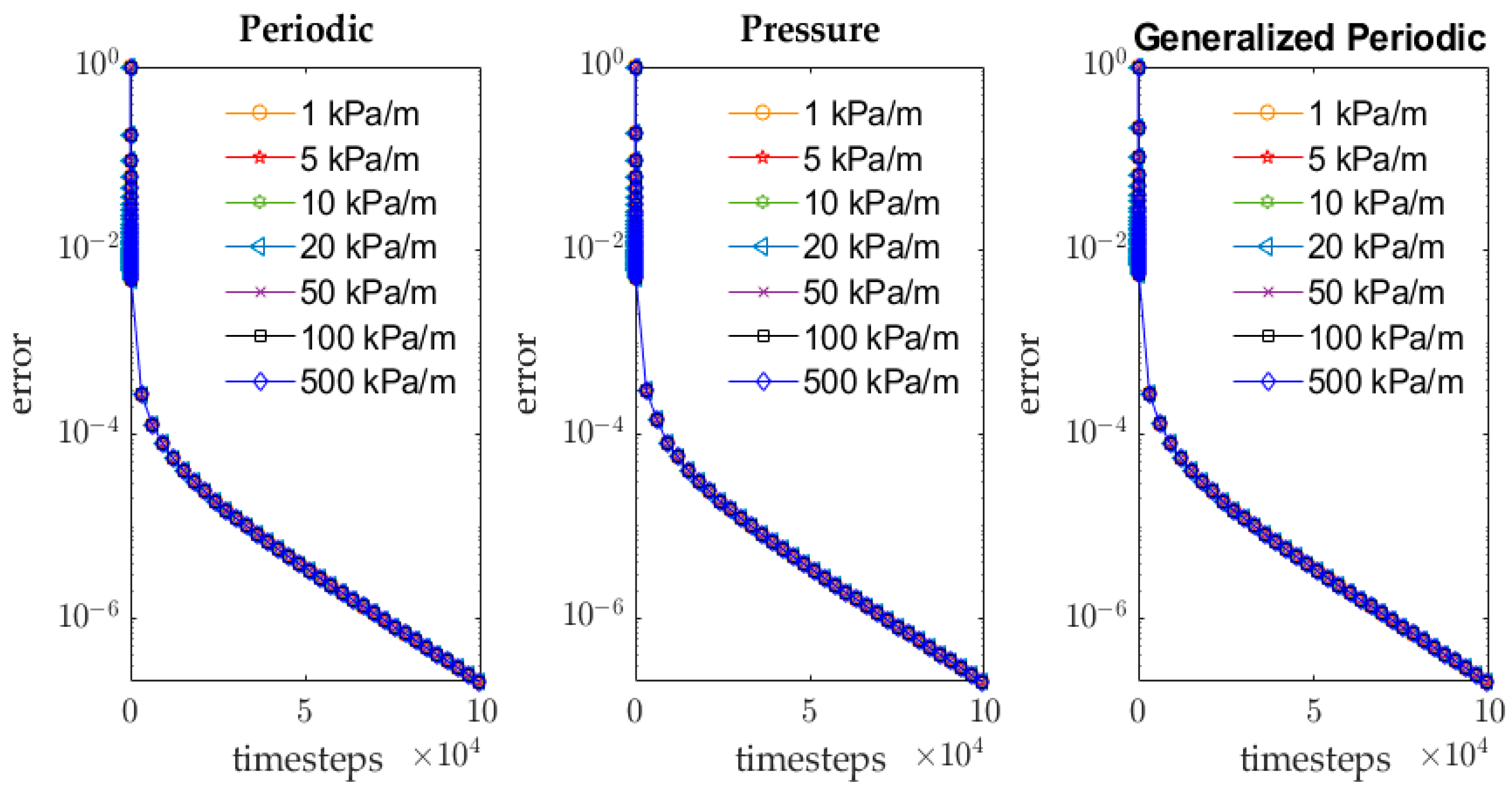
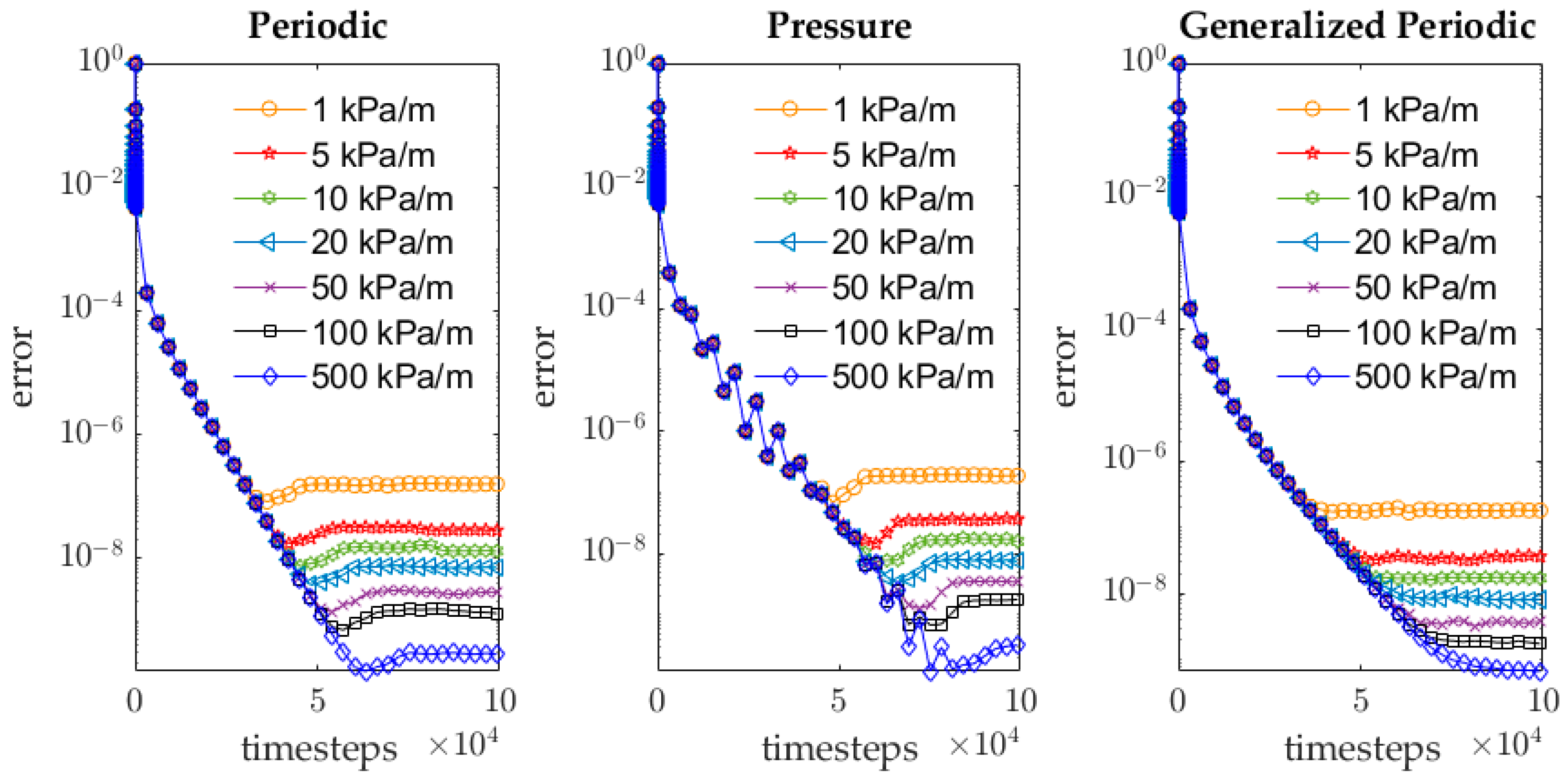
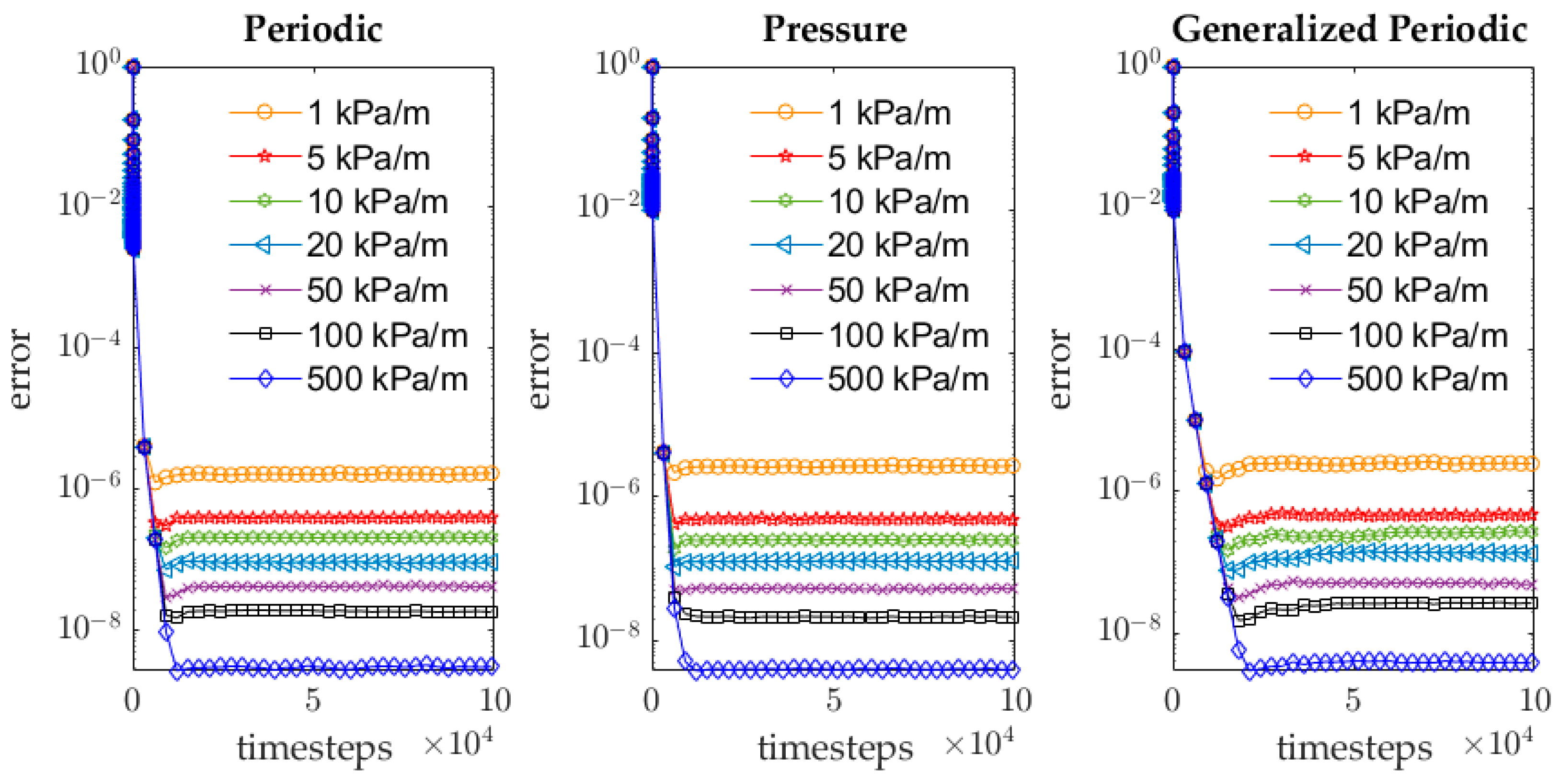
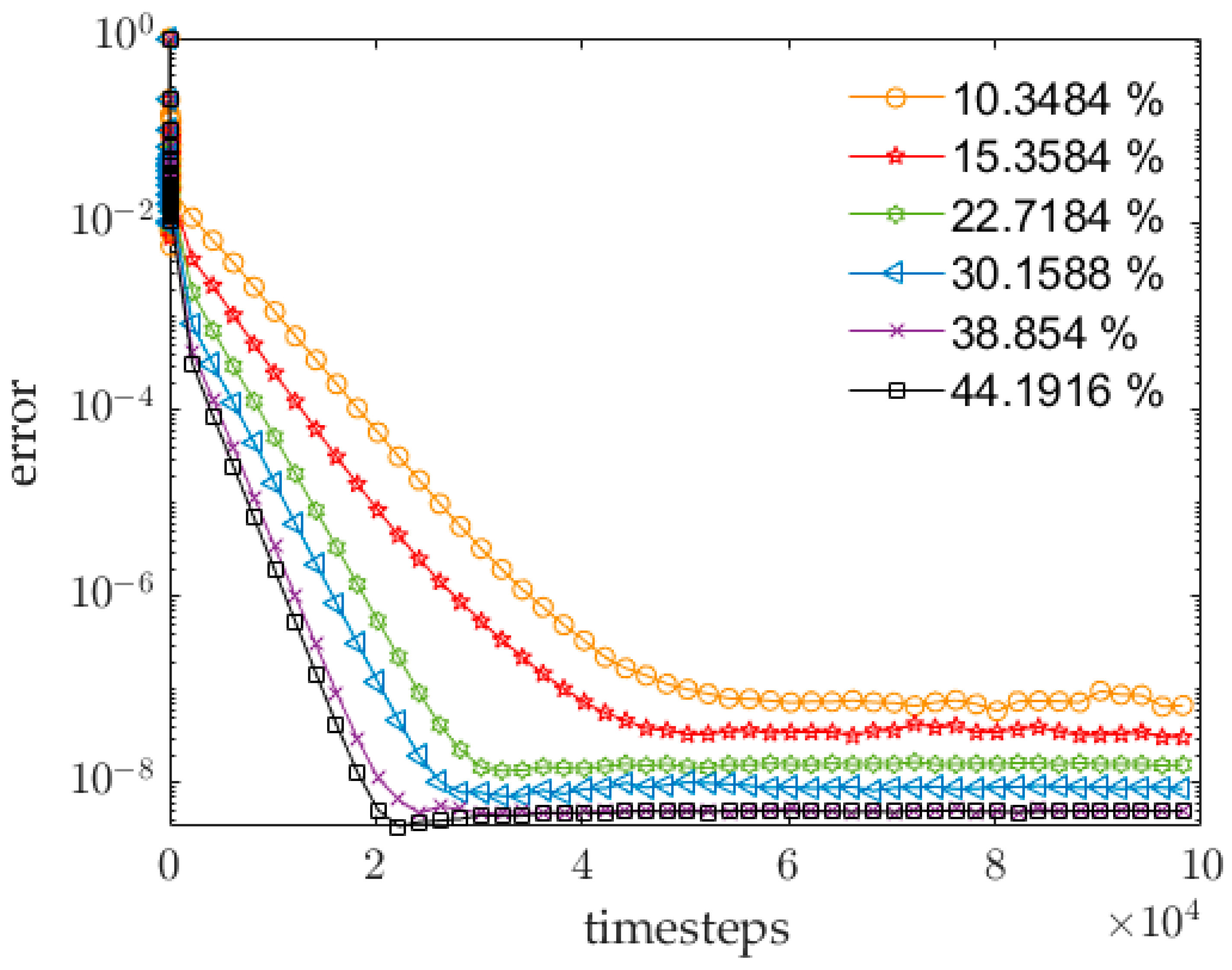
5.1. Convergence Behavior Sensitivity to Pressure Gradient and Complexity
5.2. Mass Conservation
6. Problem Significance and Future Work
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Simulation Domains
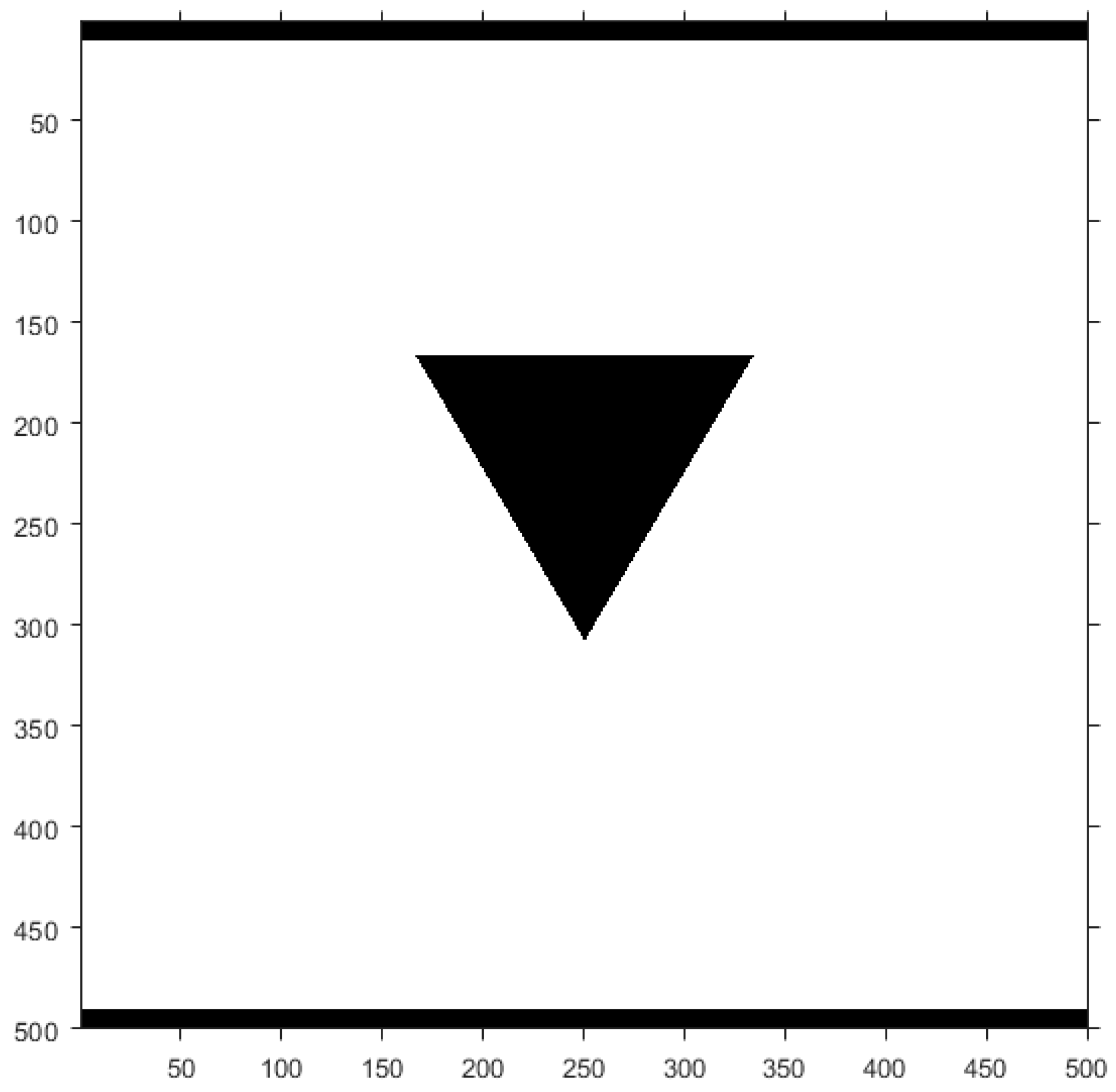

Appendix B. Mass Conservation
| D1 | D2 | D3 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Gradient (kPa/m) | Inlet Mass (kg/s) | Outlet Mass (kg/s) | Absolute Difference | Inlet Mass (kg/s) | Outlet Mass (kg/s) | Absolute Difference | Inlet Mass (kg/s) | Outlet Mass (kg/s) | Absolute Difference | |
| Periodic | 1 | 8.18 × | 8.18 × | 0.0 | 1.57 × | 1.57 × | 3.44 × | 3.77 × | 3.77 × | 6.19 × |
| 5 | 4.09 × | 4.09 × | 0.0 | 7.84 × | 7.84 × | 4.84 × | 1.88 × | 1.88 × | 3.06 × | |
| 10 | 8.18 × | 8.18 × | 0.0 | 1.57 × | 1.57 × | 6.88 × | 3.77 × | 3.77 × | 6.11 × | |
| 20 | 1.64 × | 1.64 × | 0.0 | 3.13 × | 3.13 × | 1.14 × | 7.54 × | 7.54 × | 1.22 × | |
| 50 | 4.09 × | 4.09 × . | 0.0 | 7.84 × | 7.84 × | 1.97 × | 1.88 × | 1.88 × | 3.05 × | |
| 100 | 8.18 × | 8.18 × | 0.0 | 1.57 × | 1.57 × | 4.77 × | 3.77 × | 3.77 × | 6.10 × | |
| 500 | 4.09 × | 4.09 × | 0.0 | 7.84 × | 7.84 × | 2.45 × | 1.88 × | 1.88 × | 3.05 × | |
| Pressure | 1 | 6.79 × | 6.79 × | 6.37 × | 1.30 × | 1.30 × | 7.23 × | 3.06 × | 3.06 × | 4.10 × |
| 5 | 3.40 × | 3.40 × | 7.88 × | 6.51 × | 6.51 × | 6.06 × | 1.53 × | 1.53 × | 1.33 × | |
| 10 | 6.79 × | 6.79 × | 7.32 × | 1.30 × | 1.30 × | 6.86 × | 3.06 × | 3.06 × | 3.04 × | |
| 20 | 1.36 × | 1.36 × | 7.28 × | 2.60 × | 2.60 × | 7.66 × | 6.12 × | 6.13 × | 6.47 × | |
| 50 | 3.40 × | 3.40 × | 8.27 × | 6.51 × | 6.51 × | 7.09 × | 1.53 × | 1.53 × | 1.68 × | |
| 100 | 6.79 × | 6.79 × | 5.75 × | 1.30 × | 1.30 × | 6.40 × | 3.06 × | 3.06 × | 3.39 × | |
| 500 | 3.40 × | 3.40 × | 1.60 × | 6.51 × | 6.51 × | 2.86 × | 1.53 × | 1.53 × | 1.71 × | |
| Generalized Periodic | 1 | 6.81 × | 6.81 × | 0.0 | 1.30 × | 1.30 × | 0.0 | 3.13 × | 3.13 × | 0.0 |
| 5 | 3.41 × | 3.41 × | 0.0 | 6.51 × | 6.51 × | 0.0 | 1.57 × | 1.57 × | 0.0 | |
| 10 | 6.81 × | 6.81 × | 0.0 | 1.30 × | 1.30 × | 0.0 | 3.13 × | 3.13 × | 0.0 | |
| 20 | 1.36 × | 1.36 × | 0.0 | 2.61 × | 2.61 × | 0.0 | 6.27 × | 6.27 × | 0.0 | |
| 50 | 3.41 × | 3.41 × | 0.0 | 6.51 × | 6.51 × | 1.08 × | 1.57 × | 1.57 × | 0.0 | |
| 100 | 6.81 × | 6.81 × | 1.04 × | 1.30 × | 1.30 × | 0.0 | 3.13 × | 3.13 × | 0.0 | |
| 500 | 3.41 × | 3.41 × | 0.0 | 6.51 × | 6.51 × | 0.0 | 1.57 × | 1.57 × | 0.0 | |
References
- Deng, H.; Hu, X.; Li, H.A.; Luo, B.; Wang, W. Improved pore-structure characterization in shale formations with FESEM technique. J. Nat. Gas Sci. Eng. 2016, 35, 309–319. [Google Scholar] [CrossRef]
- Li, X.; Fan, J.; Yu, H.; Zhu, Y.; Wu, H. Lattice Boltzmann method simulations about shale gas flow in contracting nano-channels. Int. J. Heat Mass Transf. 2018, 122, 1210–1221. [Google Scholar] [CrossRef]
- Chambre, P.A.; Schaaf, S.A. Flow of Rarefied Gases; Princeton University Press: Princeton, NJ, USA, 2017. [Google Scholar]
- Wang, Y.; Aryana, S.A. Pore-scale simulation of gas flow in microscopic permeable media with complex geometries. J. Nat. Gas Sci. Eng. 2020, 81, 103441. [Google Scholar] [CrossRef]
- Wu, H.; Chen, J.; Liu, H. Molecular Dynamics Simulations about Adsorption and Displacement of Methane in Carbon Nanochannels. J. Phys. Chem. C 2015, 119, 13652–13657. [Google Scholar] [CrossRef]
- Yu, H.; Zhu, Y.; Jin, X.; Liu, H.; Wu, H. Multiscale simulations of shale gas transport in micro/nano-porous shale matrix considering pore structure influence. J. Nat. Gas Sci. Eng. 2019, 64, 28–40. [Google Scholar] [CrossRef]
- Hanasoge, S.M.; Succi, S.; Orszag, S.A. Lattice Boltzmann method for electromagnetic wave propagation. EPL Europhys. Lett. 2011, 96, 14002. [Google Scholar] [CrossRef] [Green Version]
- Mehmani, Y.; Anderson, T.; Wang, Y.; Aryana, S.A.; Battiato, I.; Tchelepi, H.A.; Kovscek, A.R. Striving to translate shale physics across ten orders of magnitude: What have we learned? Earth-Sci. Rev. 2021, 223, 103848. [Google Scholar] [CrossRef]
- Liu, H.; Kang, Q.; Leonardi, C.R.; Schmieschek, S.; Narváez, A.; Jones, B.D.; Williams, J.R.; Valocchi, A.J.; Harting, J. Multiphase lattice Boltzmann simulations for porous media applications: A review. Comput. Geosci. 2016, 20, 777–805. [Google Scholar] [CrossRef] [Green Version]
- Guo, S.; Feng, Y.; Jacob, J.; Renard, F.; Sagaut, P. An efficient lattice Boltzmann method for compressible aerodynamics on D3Q19 lattice. J. Comput. Phys. 2020, 418, 109570. [Google Scholar] [CrossRef]
- Mishra, S.C.; Roy, H.K. Solving transient conduction and radiation heat transfer problems using the lattice Boltzmann method and the finite volume method. J. Comput. Phys. 2007, 223, 89–107. [Google Scholar] [CrossRef]
- Ramstad, T. Simulation of Two-Phase Flow in Reservoir Rocks Using a Lattice Boltzmann Method. SPE J. 2010, 15, 917–927. [Google Scholar] [CrossRef]
- Ramstad, T.; Idowu, N.; Nardi, C.; Øren, P.E. Relative Permeability Calculations from Two-Phase Flow Simulations Directly on Digital Images of Porous Rocks. Transp. Porous Media 2012, 94, 487–504. [Google Scholar] [CrossRef]
- Xu, M.; Liu, H. Prediction of immiscible two-phase flow properties in a two-dimensional Berea Sandstone using the pore-scale lattice Boltzmann simulation. Eur. Phys. J. E 2018, 41, 124. [Google Scholar] [CrossRef] [PubMed]
- Guiltinan, E.J.; Santos, J.E.; Cardenas, M.B.; Espinoza, D.N.; Kang, Q. Two-phase fluid flow properties of rough fractures with heterogeneous wettability: Analysis with lattice Boltzmann simulations. Water Resour. Res. 2020, 56, e2020WR027943. [Google Scholar] [CrossRef]
- Ghasemi, S.; Moradi, B.; Rasaei, M.R.; Rahmati, N. Near miscible relative permeability curves in layered porous media- investigations via diffuse interface lattice Boltzmann method. J. Pet. Sci. Eng. 2022, 209, 109744. [Google Scholar] [CrossRef]
- Li, Z.; Galindo-Torres, S.; Yan, G.; Scheuermann, A.; Li, L. A lattice Boltzmann investigation of steady-state fluid distribution, capillary pressure and relative permeability of a porous medium: Effects of fluid and geometrical properties. Adv. Water Resour. 2018, 116, 153–166. [Google Scholar] [CrossRef]
- Nemer, M.N.; Rao, P.R.; Schaefer, L. Wettability alteration implications on pore-scale multiphase flow in porous media using the lattice Boltzmann method. Adv. Water Resour. 2020, 146, 103790. [Google Scholar] [CrossRef]
- An, S.; Zhan, Y.; Mahani, H.; Niasar, V. Kinetics of wettability alteration and droplet detachment from a solid surface by low-salinity: A lattice-boltzmann method. Fuel 2022, 329, 125294. [Google Scholar] [CrossRef]
- Akai, T.; Blunt, M.J.; Bijeljic, B. Pore-scale numerical simulation of low salinity water flooding using the lattice Boltzmann method. J. Colloid Interface Sci. 2020, 566, 444–453. [Google Scholar] [CrossRef]
- Viberti, D.; Peter, C.; Salina Borello, E.; Panini, F. Pore structure characterization through path-finding and lattice Boltzmann simulation. Adv. Water Resour. 2020, 141, 103609. [Google Scholar] [CrossRef]
- Zhao, J.; Qin, F.; Derome, D.; Kang, Q.; Carmeliet, J. Improved pore network models to simulate single-phase flow in porous media by coupling with lattice Boltzmann method. Adv. Water Resour. 2020, 145, 103738. [Google Scholar] [CrossRef]
- Cheng, Z.; Ning, Z.; Wang, Q.; Zeng, Y.; Qi, R.; Huang, L.; Zhang, W. The effect of pore structure on non-Darcy flow in porous media using the lattice Boltzmann method. J. Pet. Sci. Eng. 2018, 172, 391–400. [Google Scholar] [CrossRef] [Green Version]
- Guo, F.; Aryana, S.A.; Wang, Y.; McLaughlin, J.F.; Coddington, K. Enhancement of storage capacity of CO2 in mega porous saline aquifers using nanoparticle-stabilized CO2 foam. Int. J. Greenh. Gas Control 2019, 87, 134–141. [Google Scholar] [CrossRef]
- Frouté, L.; Wang, Y.; McKinzie, J.; Aryana, S.; Kovscek, A. Transport Simulations on Scanning Transmission Electron Microscope Images of Nanoporous Shale. Energies 2020, 13, 6665. [Google Scholar] [CrossRef]
- Nie, X.; Doolen, G.D.; Chen, S. Lattice-Boltzmann Simulations of Fluid Flows in MEMS. J. Stat. Phys. 2002, 107, 279–289. [Google Scholar] [CrossRef]
- Lim, C.Y.; Shu, C.; Niu, X.D.; Chew, Y.T. Application of lattice Boltzmann method to simulate microchannel flows. Fluids 2002, 14, 2299–2308. [Google Scholar] [CrossRef]
- Ansumali, S.V.; Karlin, I. Kinetic boundary conditions in the lattice Boltzmann method. Phys. Rev. E 2002, 66, 026311. [Google Scholar] [CrossRef] [Green Version]
- Ziarani, A.S.; Aguilera, R. Knudsen’s Permeability Correction for Tight Porous Media. Transp. Porous Media 2011, 91, 239–260. [Google Scholar] [CrossRef]
- Krüger, T.; Kusumaatmaja, H.; Kuzmin, A.; Shardt, O.; Silva, G.; Viggen, E.M. The Lattice Boltzmann Method: Principles and Practice; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Zou, Q.; He, X. On pressure and velocity boundary conditions for the lattice Boltzmann BGK model. Phys. Fluids 1997, 9, 1591–1598. [Google Scholar] [CrossRef]
- Gräser, O.; Grimm, A. Adaptive generalized periodic boundary conditions for lattice Boltzmann simulations of pressure-driven flows through confined repetitive geometries. Phys. Rev. E 2010, 82, 016702. [Google Scholar] [CrossRef]
- Kim, S.H.; Pitsch, H. A generalized periodic boundary condition for lattice Boltzmann method simulation of a pressure driven flow in a periodic geometry. Phys. Fluids 2007, 19, 108101. [Google Scholar] [CrossRef]
- Zhang, R.; Shan, X.; Chen, H. Efficient kinetic method for fluid simulation beyond the Navier-Stokes equation. Phys. Rev. E 2006, 74, 046703. [Google Scholar] [CrossRef] [Green Version]
- He, X.; Luo, L.S. Theory of the lattice Boltzmann method: From the Boltzmann equation to the lattice Boltzmann equation. Phys. Rev. E 1997, 56, 6811–6817. [Google Scholar] [CrossRef] [Green Version]
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A Model for Collision Processes in Gases. I. Small Amplitude Processes in Charged and Neutral One-Component Systems. Phys. Rev. 1954, 94, 511–525. [Google Scholar] [CrossRef]
- Qian, Y.H.; D’Humières, D.; Lallemand, P. Lattice BGK Models for Navier-Stokes Equation. EPL Europhys. Lett. 1992, 17, 479–484. [Google Scholar] [CrossRef]
- Lallemand, P.; Luo, L.S. Theory of the lattice Boltzmann method: Dispersion, dissipation, isotropy, Galilean invariance, and stability. Phys. Rev. E 2000, 61, 6546–6562. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- D’Humières, D.; Ginzburg, I.; Krafczyk, M.; Lallemand, P.; Luo, L.-S. Multiple–relaxation–time lattice Boltzmann models in three dimensions. Philos. Trans. R Soc. Lond Ser. Math. Phys. Eng. Sci. 2002, 360, 437–451. [Google Scholar] [CrossRef]
- Guo, Z.; Zheng, C.; Shi, B. Lattice Boltzmann equation with multiple effective relaxation times for gaseous microscale flow. Phys. Rev. E 2008, 77, 036707. [Google Scholar] [CrossRef]
- Li, Q.; He, Y.L.; Tang, G.H.; Tao, W.Q. Lattice Boltzmann modeling of microchannel flows in the transition flow regime. Nanofluidics 2011, 10, 607–618. [Google Scholar] [CrossRef]
- Chen, H.; Chen, S.; Matthaeus, W.H. Recovery of the Navier-Stokes equations using a lattice-gas Boltzmann method. Phys. Rev. A 1992, 45, R5339–R5342. [Google Scholar] [CrossRef]
- Suga, K. Lattice Boltzmann methods for complex micro-flows: Applicability and limitations for practical applications. Fluid Dyn. Res. 2013, 45, 034501. [Google Scholar] [CrossRef]
- Latt, J.; Chopard, B. Lattice Boltzmann method with regularized pre-collision distribution functions. Math. Comput. Simul. 2006, 72, 165–168. [Google Scholar] [CrossRef]
- Shan, X.; Yuan, X.F.; Chen, H. Kinetic theory representation of hydrodynamics: A way beyond the Navier–Stokes equation. J. Fluid Mech. 2006, 550, 413–441. [Google Scholar] [CrossRef]
- Chai, Z. Gas Flow Through Square Arrays of Circular Cylinders with Klinkenberg Effect: A Lattice Boltzmann Study. Commun. Comput. Phys. 2010, 8, 1052–1073. [Google Scholar] [CrossRef]
- Mohamad, A.A. Lattice Boltzmann Method: Fundamentals and Engineering Applications with Computer Codes, 2nd ed.; Springer: London, UK, 2019. [Google Scholar]
- Zhang, J.; Kwok, D.Y. Pressure boundary condition of the lattice Boltzmann method for fully developed periodic flows. Phys. Rev. E 2006, 73, 047702. [Google Scholar] [CrossRef] [PubMed]
- Maier, R.S.; Bernard, R.S.; Grunau, D.W. Boundary conditions for the lattice Boltzmann method. Phys. Fluids 1996, 8, 1788–1801. [Google Scholar] [CrossRef]
- Narváez, A.; Harting, J. Evaluation of pressure boundary conditions for permeability calculations using the lattice-Boltzmann method. arXiv 2010, arXiv:1005.2322. [Google Scholar]
- Rostamzadeh, A.; Razavi, S.E.; Mirsajedi, S.M. Towards multidimensional artificially characteristic-based scheme for incompressible thermo-fluid problems. Mechanics 2018, 23, 826–834. [Google Scholar] [CrossRef] [Green Version]
- Guo, F.; Aryana, S.A. An Experimental Investigation of Flow Regimes in Imbibition and Drainage Using a Microfluidic Platform. Energies 2019, 12, 1390. [Google Scholar] [CrossRef]









| D1 | D2 | D3 | |
|---|---|---|---|
| Periodic | 1.99 × | 2.86 × | 2.99 × |
| Pressure | 1.96 × | 3.19 × | 3.97 × |
| Generalized Periodic | 1.96 × | 6.73 × | 3.74 × |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rustamov, N.; Douglas, C.C.; Aryana, S.A. Scalable Simulation of Pressure Gradient-Driven Transport of Rarefied Gases in Complex Permeable Media Using Lattice Boltzmann Method. Fluids 2023, 8, 1. https://doi.org/10.3390/fluids8010001
Rustamov N, Douglas CC, Aryana SA. Scalable Simulation of Pressure Gradient-Driven Transport of Rarefied Gases in Complex Permeable Media Using Lattice Boltzmann Method. Fluids. 2023; 8(1):1. https://doi.org/10.3390/fluids8010001
Chicago/Turabian StyleRustamov, Nijat, Craig C. Douglas, and Saman A. Aryana. 2023. "Scalable Simulation of Pressure Gradient-Driven Transport of Rarefied Gases in Complex Permeable Media Using Lattice Boltzmann Method" Fluids 8, no. 1: 1. https://doi.org/10.3390/fluids8010001
APA StyleRustamov, N., Douglas, C. C., & Aryana, S. A. (2023). Scalable Simulation of Pressure Gradient-Driven Transport of Rarefied Gases in Complex Permeable Media Using Lattice Boltzmann Method. Fluids, 8(1), 1. https://doi.org/10.3390/fluids8010001






