Influence of Sill on the Hydraulic Regime in Sluice Gates: An Experimental and Numerical Analysis
Abstract
:1. Introduction
2. Materials and Methods
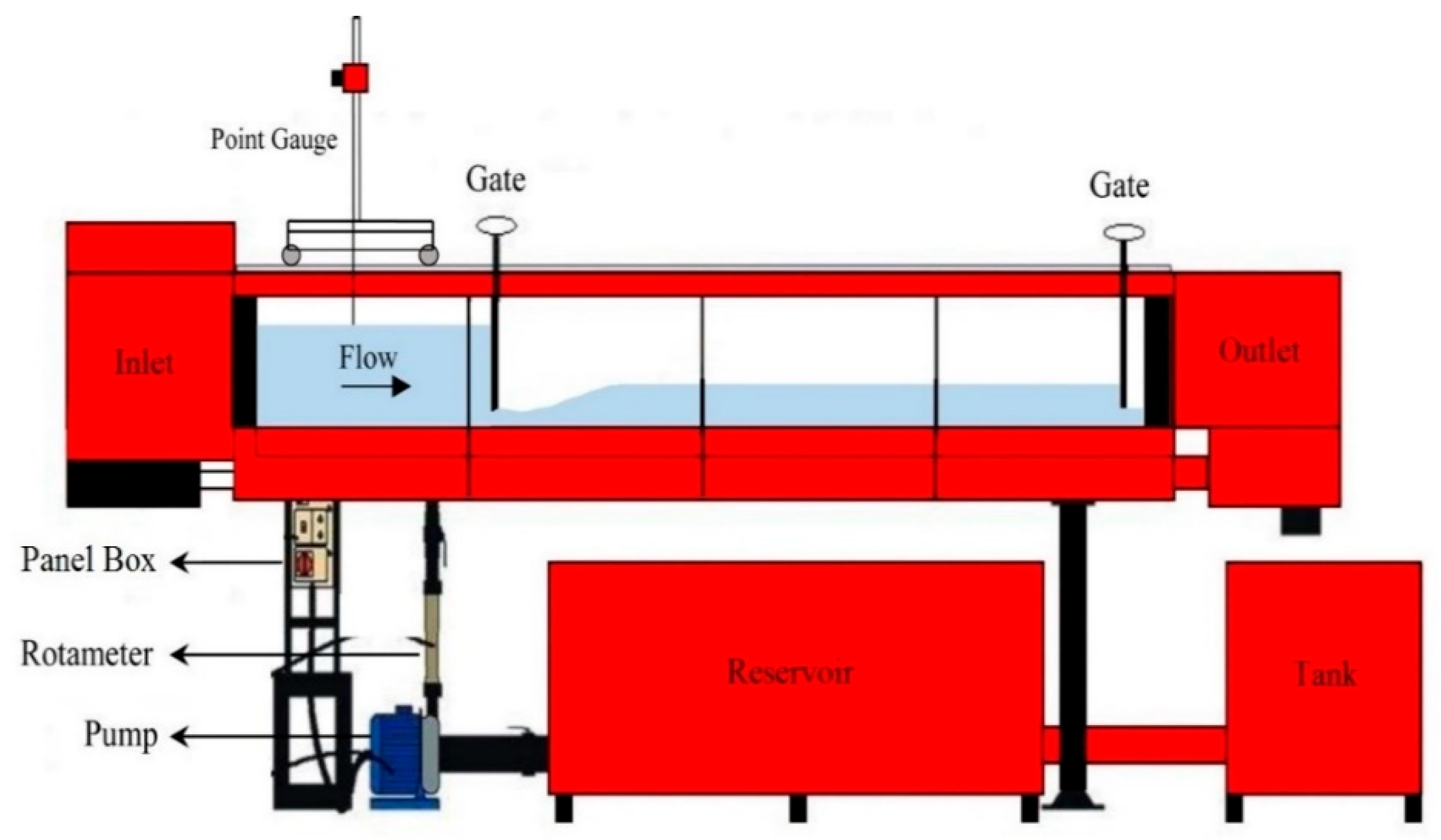
2.1. Experimental Equipment
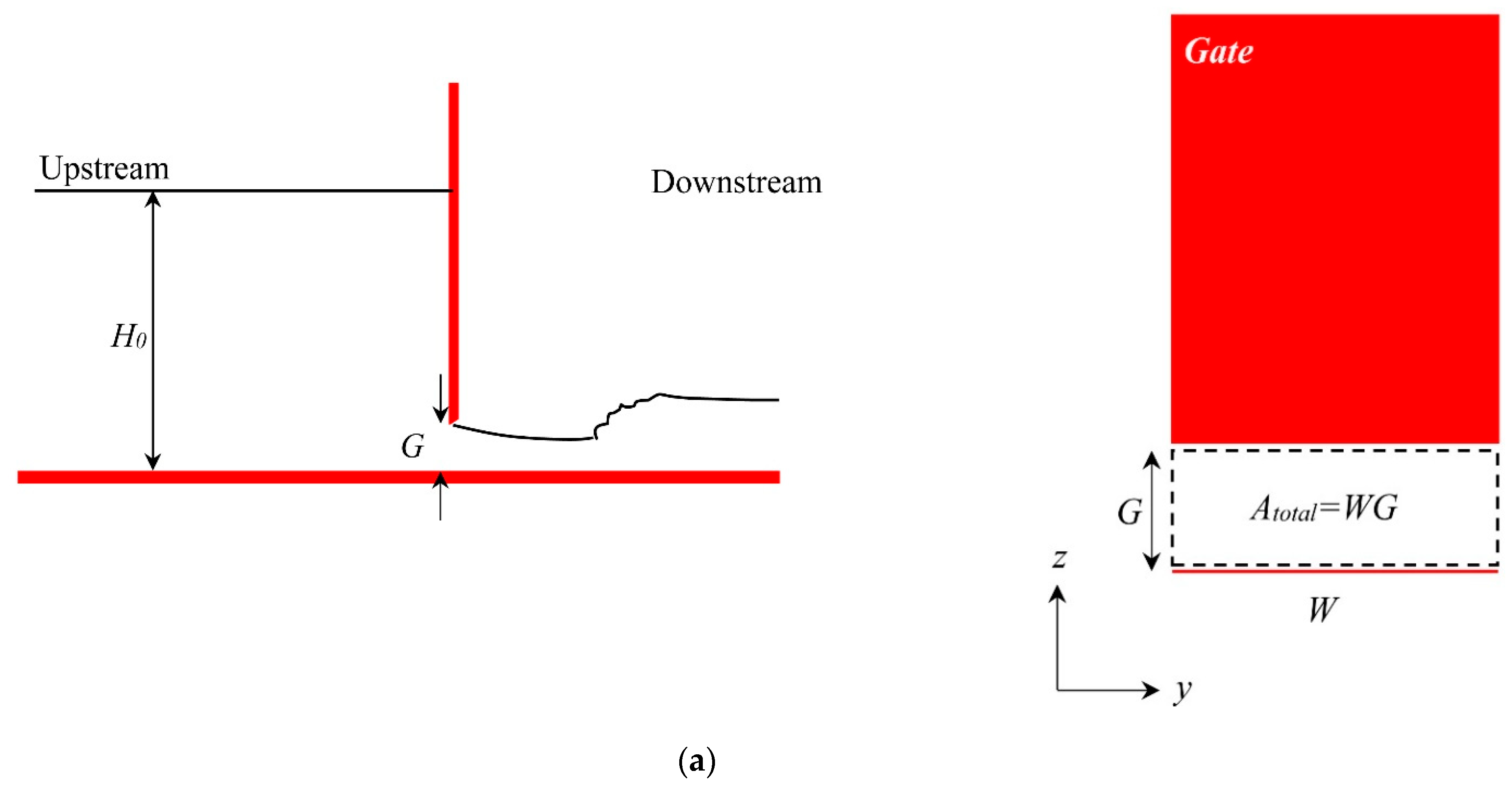
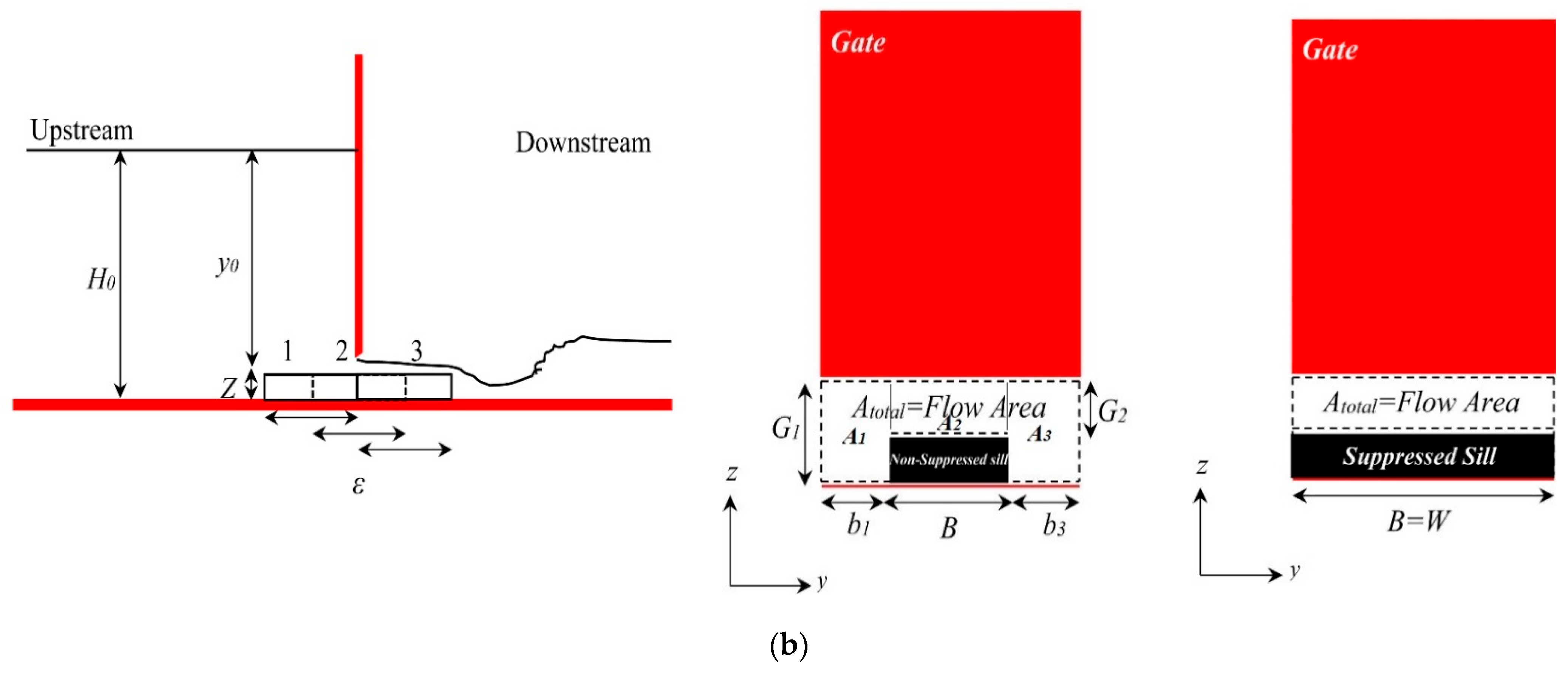
2.2. Relation Related to Flow Passing through the Sluice Gate
2.3. Flow Governing Equations
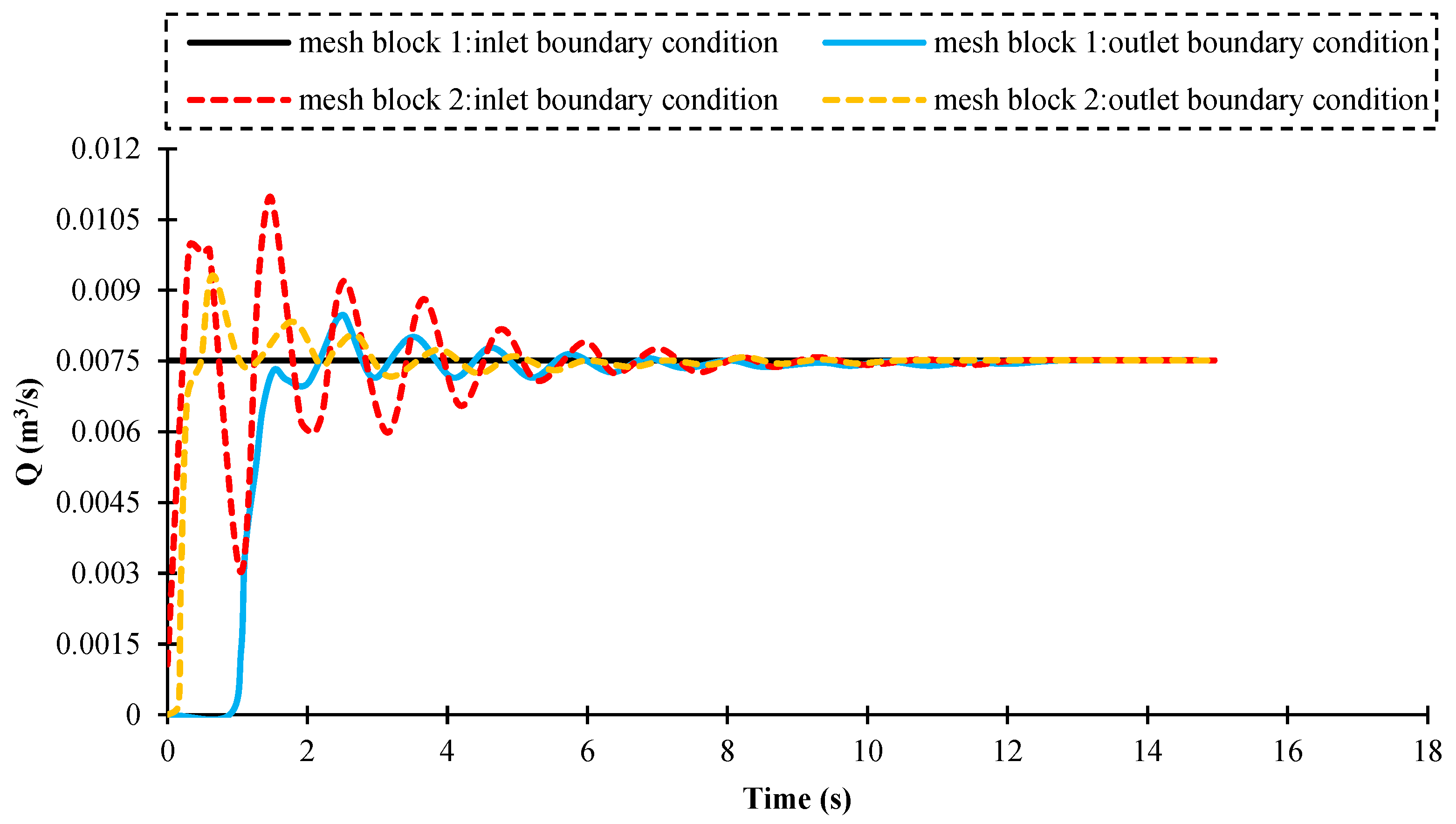
2.4. Defining the Solution Network, Boundary Conditions, and Selecting the Turbulence Model
3. Results and Discussion
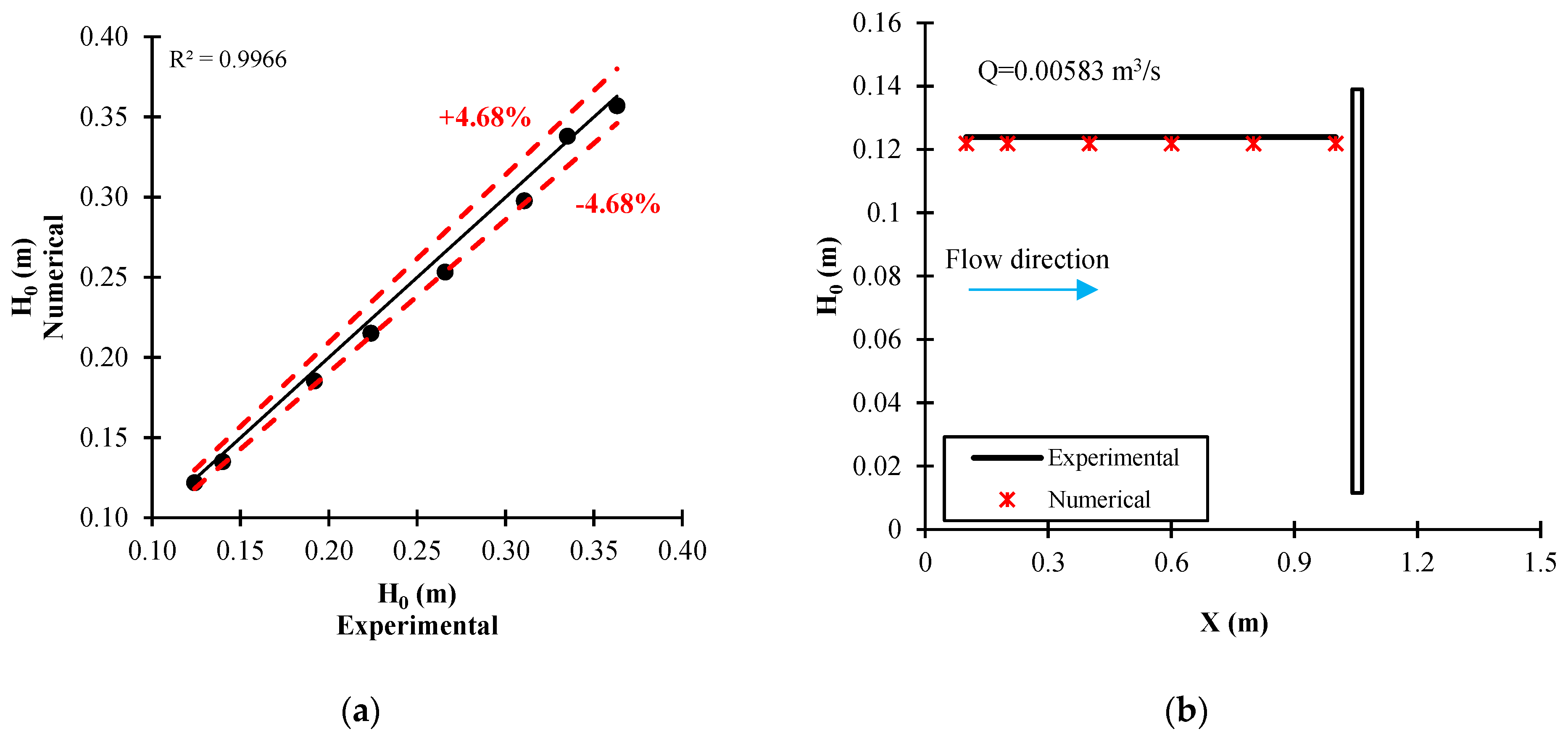
3.1. Validation Results
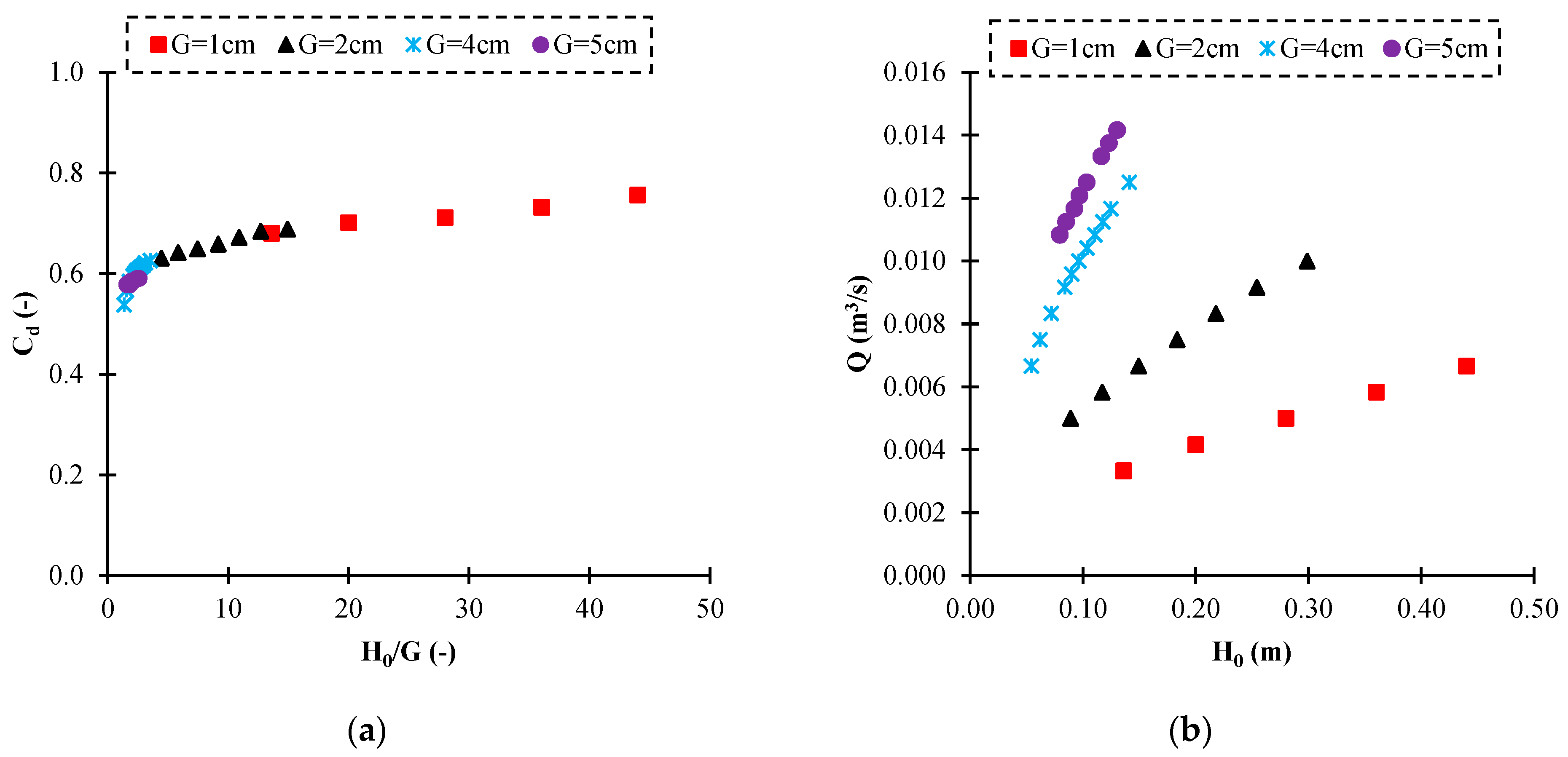
3.2. Discharge Coefficient of the Gate with No-Sill Case
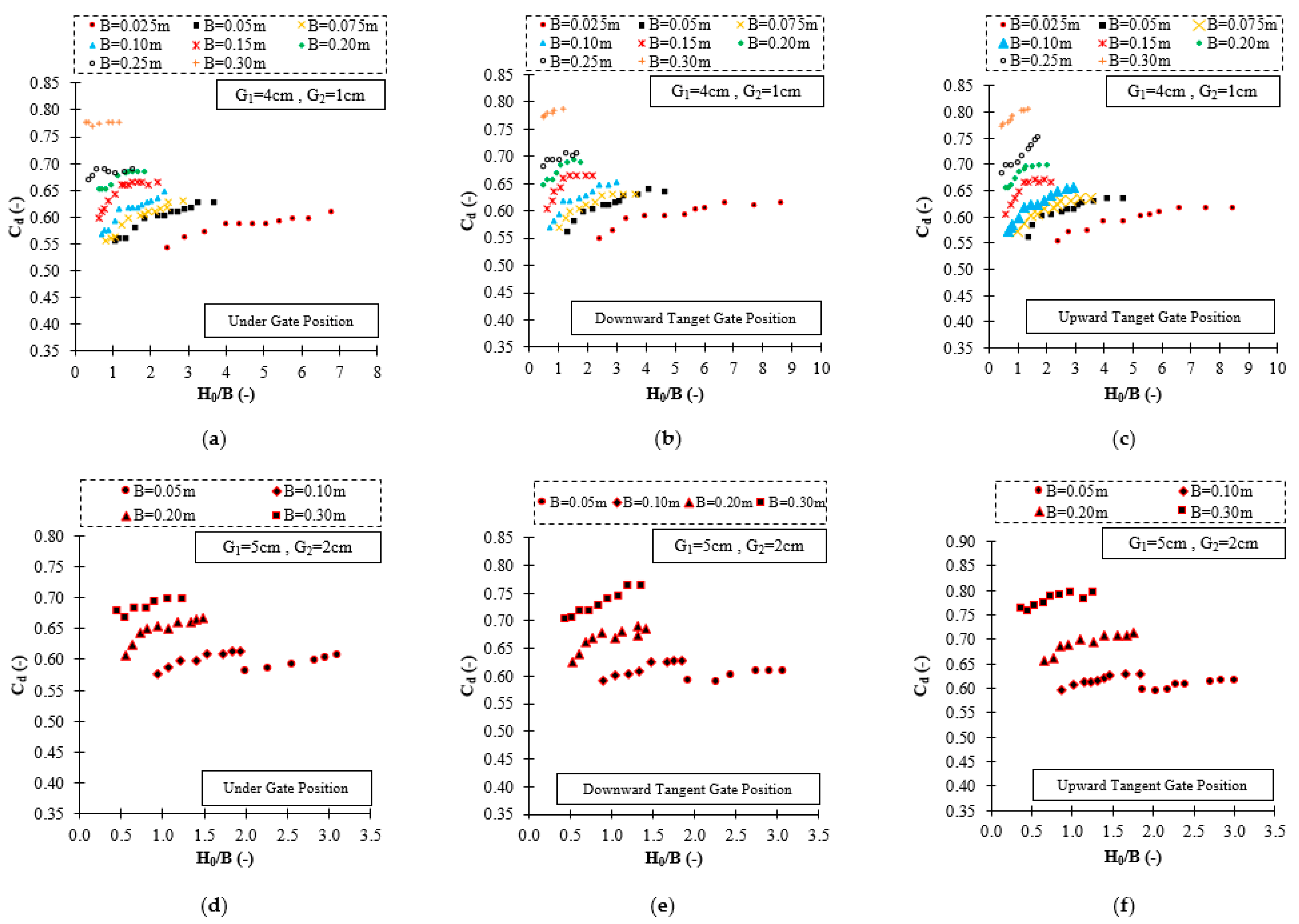
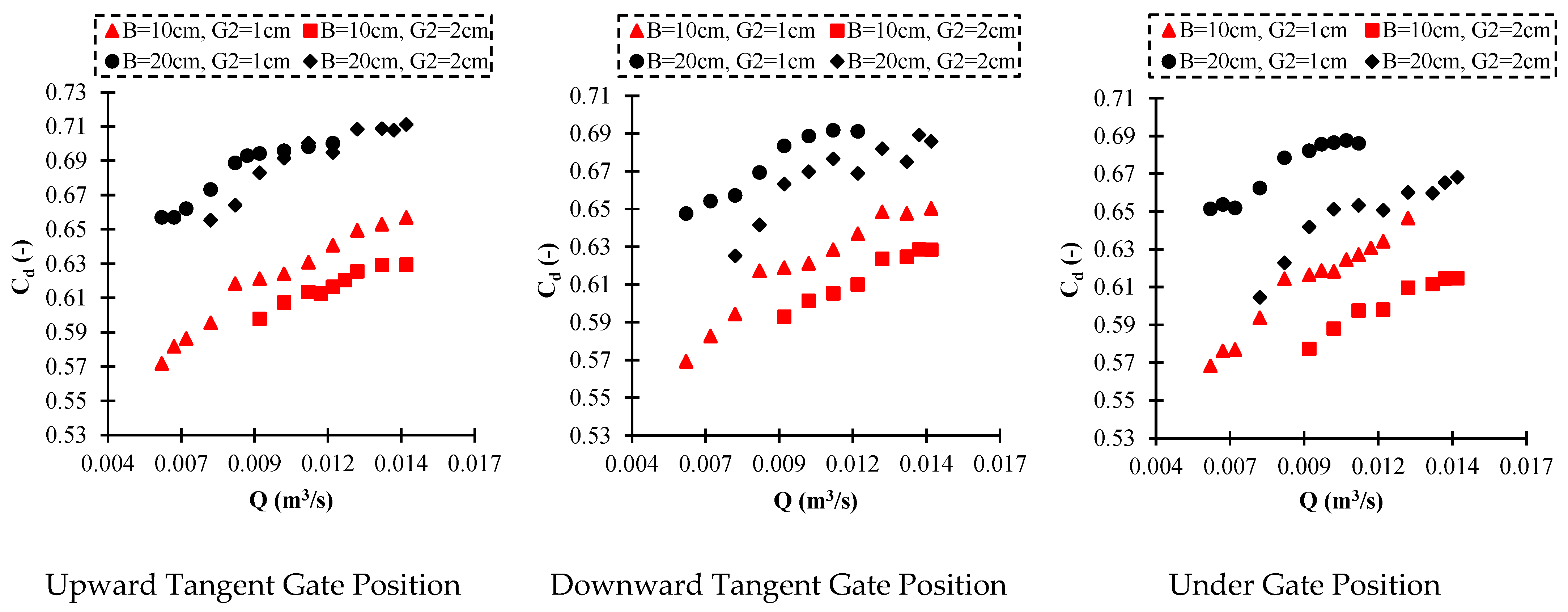
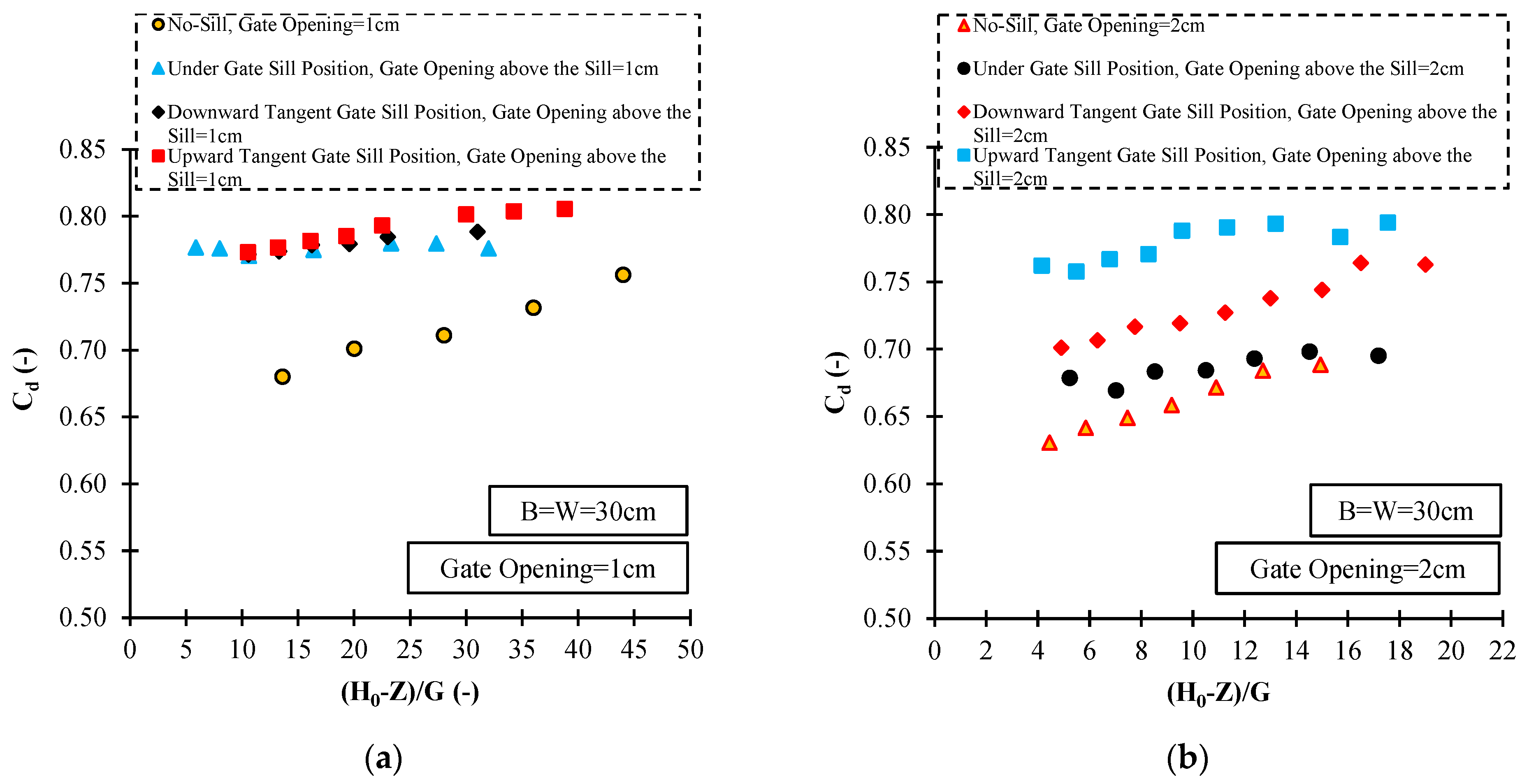
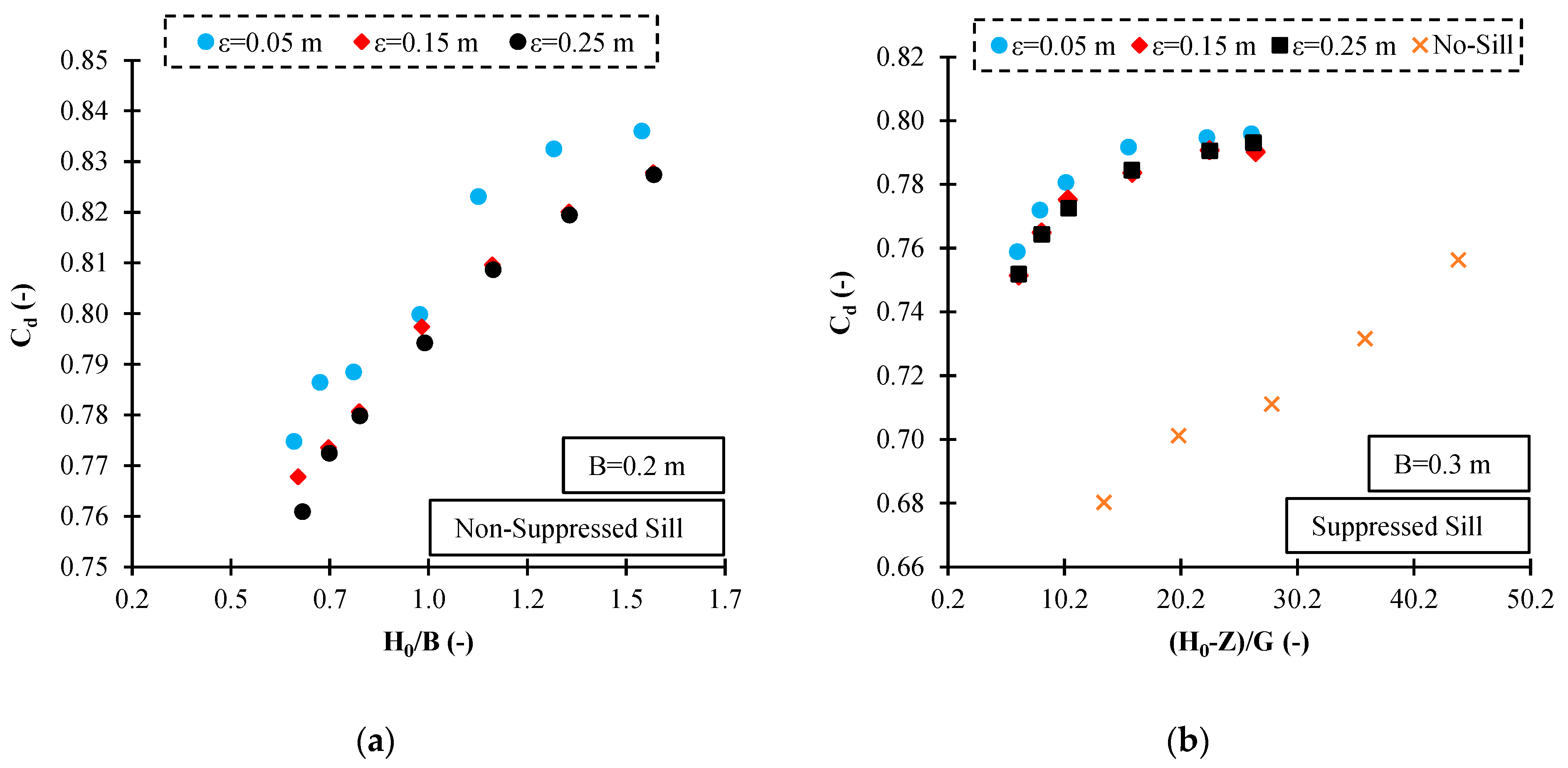
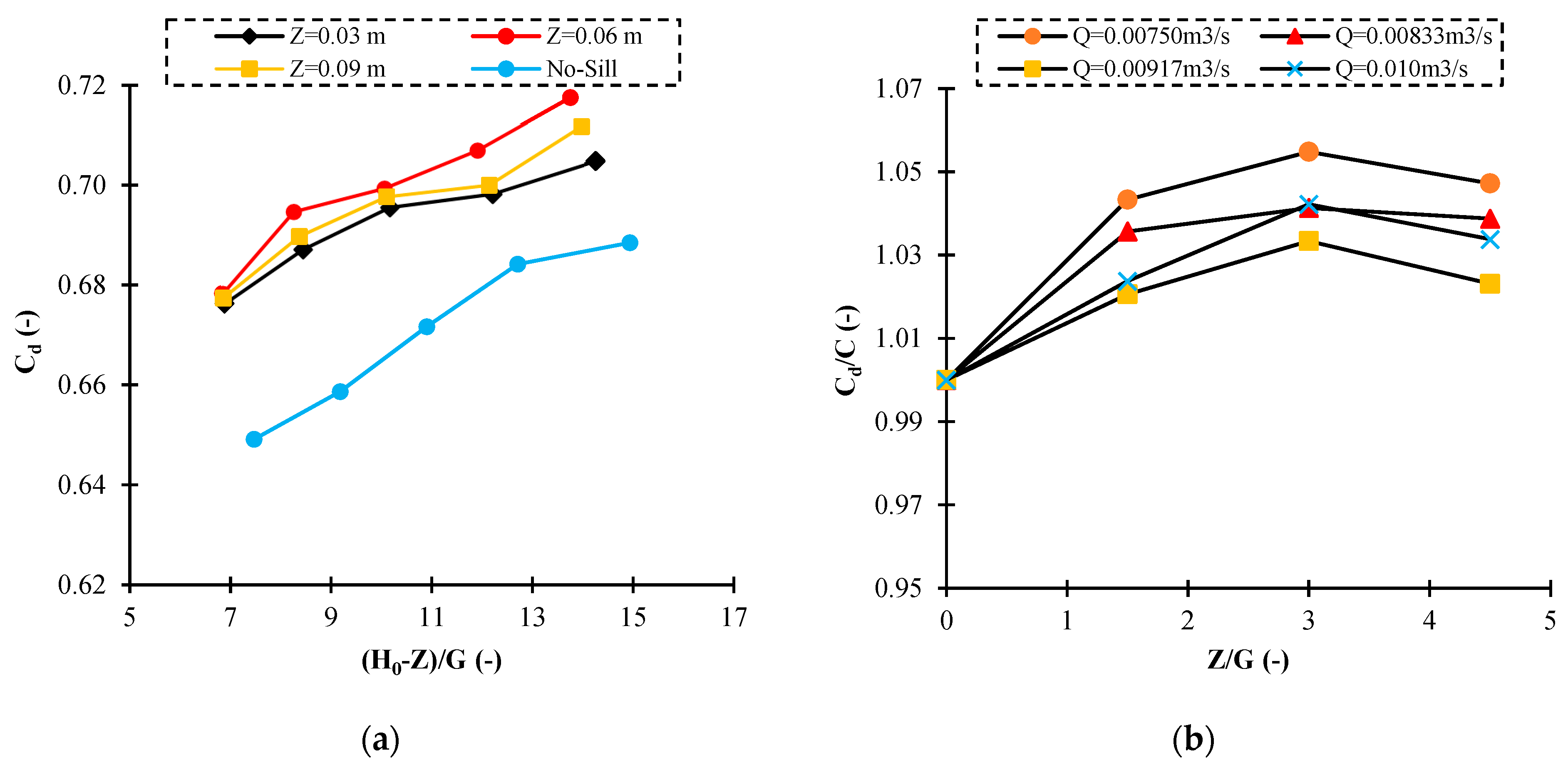
3.3. Discharge Coefficient of the Gate with Suppressed and Non-Suppressed Sill Case
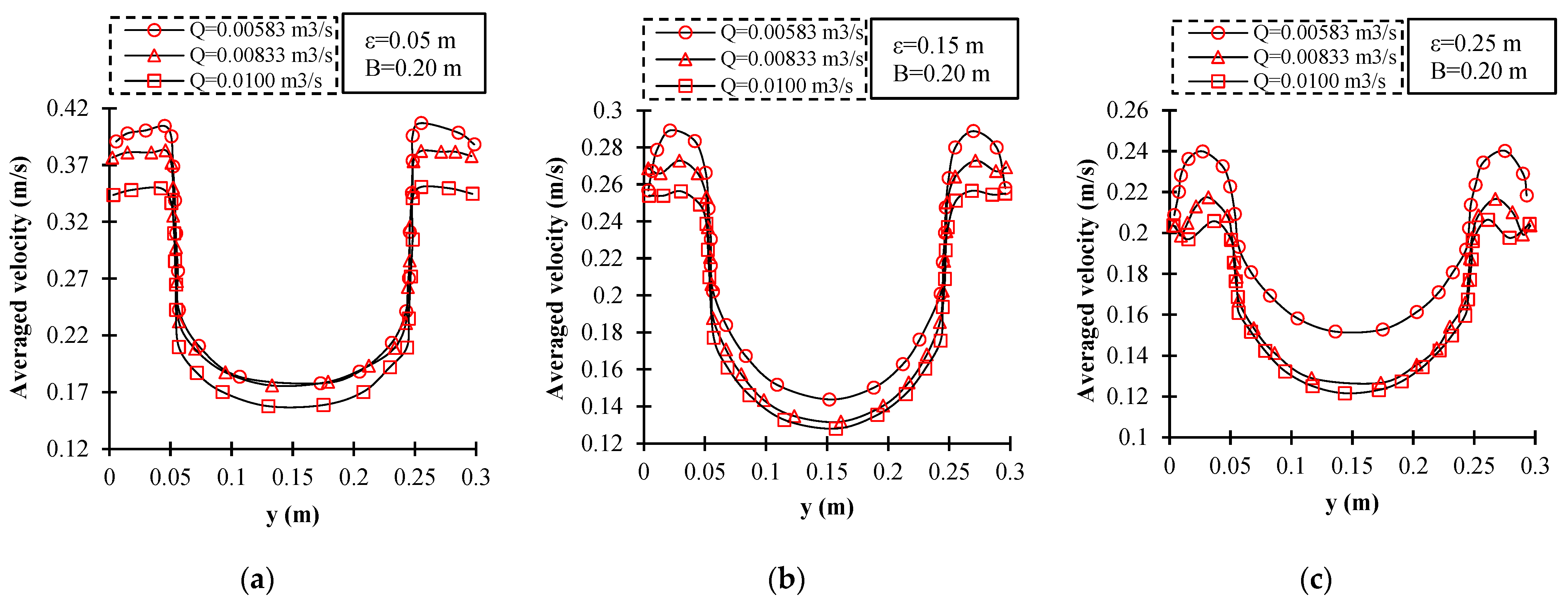
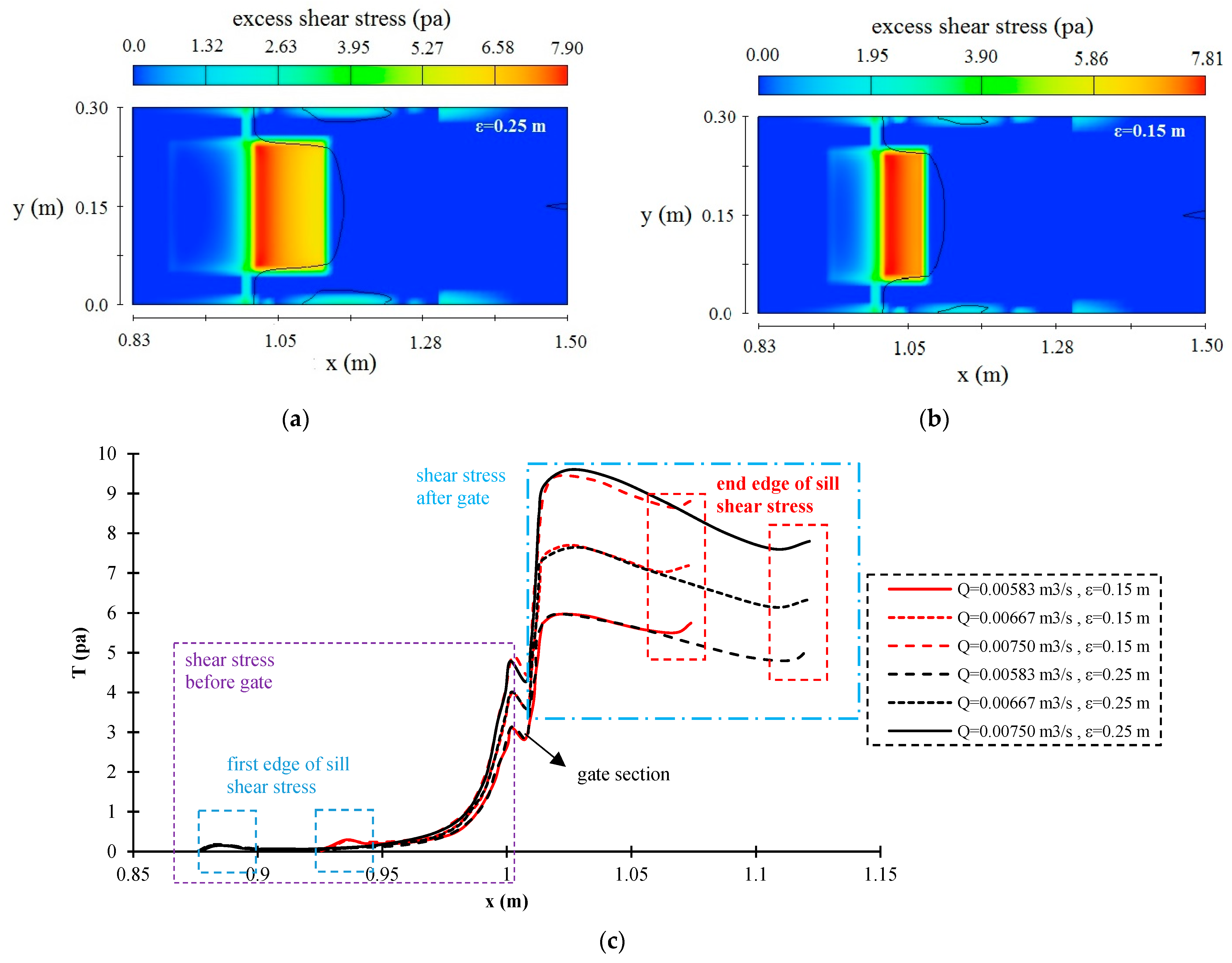
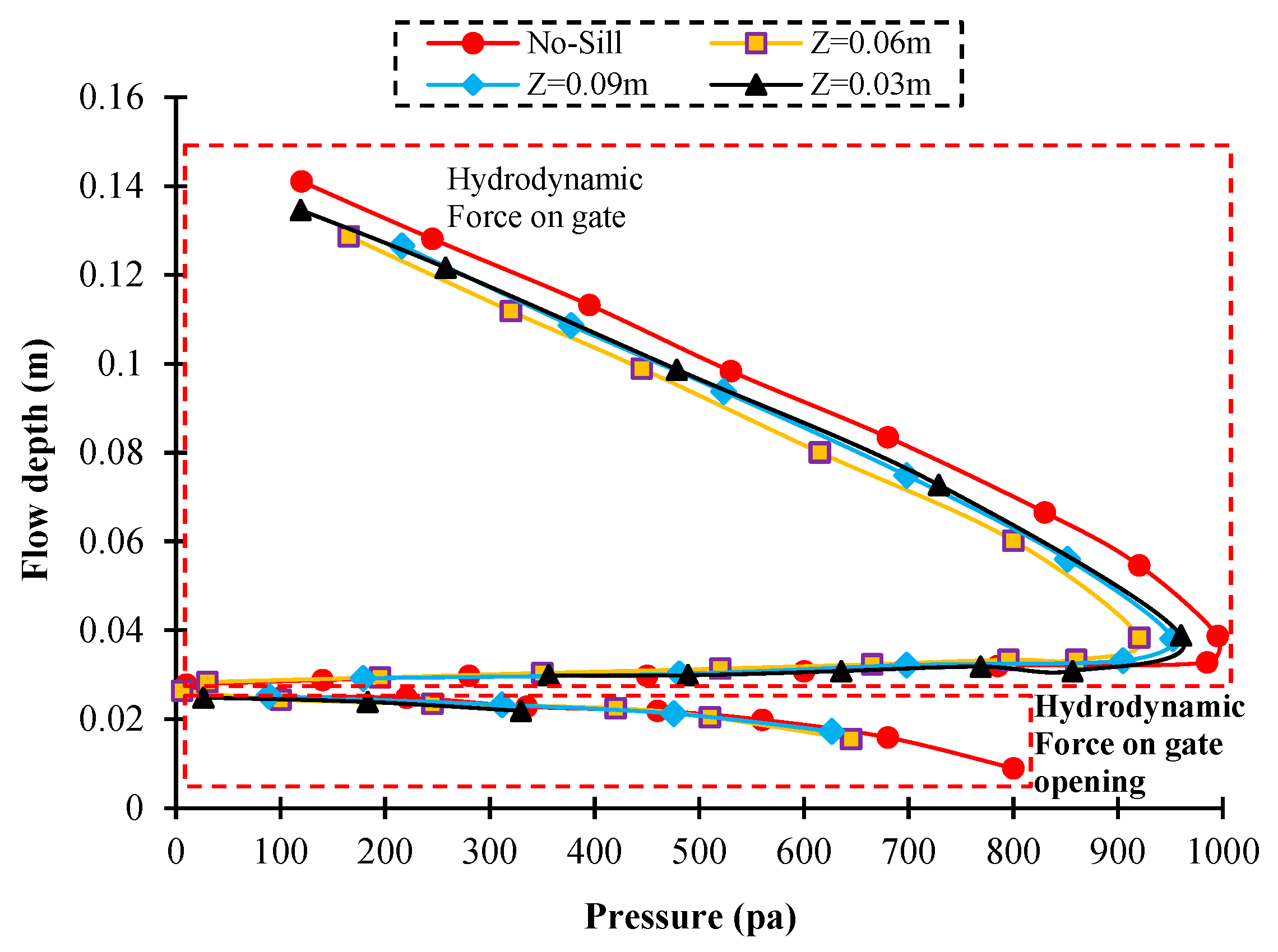
3.4. Hydraulic Parameters of the Gate with Various Geometry of the Sill
4. Conclusions
- Out of the three studied sill positions, the under-gate sill case has a lower discharge coefficient than other sill positions.
- A comparison of discharge coefficients obtained from the application of sills showed that the highest value of discharge coefficients is related to the tangential model upstream of the gate. In the suppressed sill case, on average, the value of discharge coefficient for the upward tangential sill, downward tangential sill, and under gate sill positions are 0.779, 0.731, and 0.686, respectively.
- The flow depth upstream of the gate in the tangential upward position has the lowest value compared to other sill positions, leading to an increased discharge coefficient.
- The discharge coefficient is higher when the suppressed sill is broader and thicker until specified thicknesses and then begins to decrease. This conclusion is based on using various sill dimensions as well as the constant ratio of upstream fluid depth to the gate opening.
- By increasing the length of the suppressed and non-suppressed sill, the shear stress increases, and the value of the discharge coefficient decreases.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Negm, A.M.; Alhamid, A.A.; El-Saiad, A.A. Submerged flow below sluice gate with sill. In Proceedings of the International Conference on Hydro-Science and Engineering Hydro-Science and Engineering ICHE98, Cottbus/Berlin, Germany, 31 August–3 September 1998; University of Mississippi: Oxford, MS, USA, 1998. Advances in Hydro-Science and Engineering. Volume 3. [Google Scholar]
- Henry, H.R. Discussion on “Diffusion of submerged jets” by Albertson, M.L. et al. Trans. Am. Soc. Civ. Eng. 1950, 115, 687. [Google Scholar]
- Rajaratnam, N.; Subramanya, K. Flow Equation for the Sluice Gate. J. Irrig. Drain. Div. 1967, 93, 167–186. [Google Scholar] [CrossRef]
- Rajaratnam, N. Free Flow Immediately Below Sluice Gates. J. Hydraul. Div. 1977, 103, 345–351. [Google Scholar] [CrossRef]
- Swamee, P.K. Sluice Gate Discharge Equations. J. Irrig. Drain. Eng. 1992, 118, 56–60. [Google Scholar] [CrossRef]
- Alhamid, A.A. Coefficient of Discharge for Free Flow Sluice Gates. J. King Saud Univ. Eng. Sci. 1999, 11, 33–47. [Google Scholar] [CrossRef]
- Shivapur, A.V.; Shesha Prakash, M.N. Inclined sluice gate for flow measurement. ISH J. Hydraul. Eng. 2005, 11, 46–56. [Google Scholar] [CrossRef]
- Mohammed, A.; Moayed, K. Gate Lip Hydraulics under Sluice gate. Mod. Instrum. 2013, 2, 16–19. [Google Scholar] [CrossRef] [Green Version]
- Daneshfaraz, R.; Ghahramanzadeh, A.; Ghaderi, A.; Joudi, A.R.; Abraham, J. Investigation of the Effect of Edge Shape on Characteristics of Flow Under Vertical Gates. J. Am. Water Work. Assoc. 2016, 108, E425–E432. [Google Scholar] [CrossRef]
- Reda, A.E.R. Modeling of flow characteristics beneath vertical and inclined sluice gates using artificial neural networks. Ain Shams Eng. J. 2016, 7, 917–924. [Google Scholar]
- Salmasi, F.; Norouzi Sarkarabad, R. Investigation of different geometric shapes of sills on discharge coefficient of vertical sluice gate. Amirkabir J. Civ. Eng. 2020, 52, 21–36. [Google Scholar] [CrossRef]
- Karami, S.; Heidari, M.M.; Adib Rad, M.H. Investigation of Free Flow under the Sluice Gate with the Sill Using Flow-3D Model. Iran. J. Sci. Technol. Trans. Civ. Eng. 2020, 44, 317–324. [Google Scholar] [CrossRef]
- Salmasi, F.; Abraham, J. Prediction of discharge coefficients for sluice gates equipped with different geometric sills under the gate using multiple non-linear regression (MNLR). J. Hydrol. 2020, 597, 125728. [Google Scholar] [CrossRef]
- Pástor, M.; Bocko, J.; Lengvarský, P.; Sivák, P.; Šarga, P. Experimental and Numerical Analysis of 60-Year-Old Sluice Gate Affected by Long-Term Operation. Materials 2020, 13, 5201. [Google Scholar] [CrossRef]
- Ghorbani, M.A.; Salmasi, F.; Saggi, M.K.; Bhatia, A.S.; Kahya, E.; Norouzi, R. Deep learning under H2O framework. A novel approach for quantitative analysis of discharge coefficient in sluice gates. J. Hydroinformatics 2020, 22, 1603–1619. [Google Scholar] [CrossRef]
- Daneshfaraz, R.; Abbaszadeh, H.; Gorbanvatan, P.; Abdi, M. Application of Sluice Gate in Different Positions and Its Effect on Hydraulic Parameters in Free-Flow Conditions. J. Hydraul. Struct. 2021, 7, 72–87. [Google Scholar] [CrossRef]
- Kubrak, E.; Kubrak, J.; Kiczko, A.; Kubrak, M. Flow Measurements Using a Sluice Gate; Analysis of Applicability. Water 2020, 12, 819. [Google Scholar] [CrossRef] [Green Version]
- Salmasi, F.; Nouri, M.; Sihag, P.; Abraham, J. Application of SVM, ANN, GRNN, RF, GP and RT Models for Predicting Discharge Coefficients of Oblique Sluice Gates Using Experimental Data. Water Supply 2021, 21, 232–248. [Google Scholar] [CrossRef]
- Lauria, A.; Calomino, F.; Alfonsi, G.; D’Ippolito, A. Discharge Coefficients for Sluice Gates Set in Weirs at Different Upstream Wall Inclinations. Water 2020, 12, 245. [Google Scholar] [CrossRef] [Green Version]
- Salmasi, F.; Abraham, J. Expert System for Determining Discharge Coefficients for Inclined Slide Gates Using Genetic Programming. J. Irrig. Drain. Eng. 2020, 146, 06020013. [Google Scholar] [CrossRef]
- Silva, C.O.; Rijo, M. Flow rate measurements under sluice gates. J. Irrig. Drain. Eng. 2017, 143, 06017001. [Google Scholar] [CrossRef] [Green Version]
- Flow Science Inc. FLOW-3D V 11.2 User’s Manual; Flow Science Inc.: Santa Fe, NM, USA, 2016. [Google Scholar]
- Cassan, L.; Belaud, G. Experimental and Numerical Investigation of Flow under Sluice Gates. J. Hydraul. Eng. 2012, 138, 367–373. [Google Scholar] [CrossRef] [Green Version]
- Gorman, J.; Bhattacharya, S.; Abraham, J.; Cheng, L. Turbulence Models Commonly Used in CFD, Computational Fluid Dynamics; Bhattacharya, S., Ed.; IntechOpen: London, UK, 2021. [Google Scholar] [CrossRef]
- Daneshfaraz, R.; Norouzi, R.; Ebadzadeh, P. Experimental and numerical study of sluice gate flow pattern with non- suppressed sill and its effect on discharge coefficient in free-flow conditions. J. Hydraul. Struct. 2022, 8, 1–20. [Google Scholar]
- Kim, D.G. Numerical analysis of free flow past a sluice gate. KSCE J. Civ. Eng. 2007, 11, 127–132. [Google Scholar] [CrossRef]
- Ghaderi, A.; Dasineh, M.; Aristodemo, F.; Aricò, C. Numerical Simulations of the Flow Field of a Submerged Hydraulic Jump over Triangular Macroroughnesses. Water 2021, 13, 674. [Google Scholar] [CrossRef]



| Hydraulic Characteristics | ||||
| Q (L/min) | Upstream Water Depth (m) | Froude Number (-) | Reynolds Number (-) | |
| 150–850 | 0.05–0.44 | 0.024–0.515 | 11,111–47,222 | |
| Geometric Characteristics | ||||
| Gate opening | Sill height (m) | Sill length (m) | Sill width (m) | Sill position |
| 0.01–0.02 0.04–0.05 | 0.03–0.06–0.09 | 0.05–0.15–0.25 | 0.025–0.05–0.075–0.10 0.15–0.20–0.25–0.30 | Under gate, upward, and downward tangent gate positions |
| Test No. | Size of Cells (m) | Assumed Turbulence Model | Mean RE% | RMSE | KGE | |||
|---|---|---|---|---|---|---|---|---|
| H0 | Cd | H0 (m) | Cd (-) | H0 (m) | Cd (-) | |||
| 1 | Mesh block 1: 0.014 Mesh block 2: 0.007 | RNG | 14.12 | 9.28 | 0.0735 | 0.0914 | good | good |
| 2 | Mesh block 1: 0.013 Mesh block 2: 0.0065 | 6.35 | 5.72 | 0.0285 | 0.0348 | Very good | Very good | |
| 3 | Mesh block 1: 0.012 Mesh block 2: 0.007 | 3.9 | 2.95 | 0.0185 | 0.0245 | Very good | Very good | |
| 4 | Mesh block 1: 0.012 Mesh block 2: 0.006 | 2.94 | 1.60 | 0.0079 | 0.0117 | Very good | Very good | |
| 5 | Mesh block 1: 0.010 Mesh block 2: 0.005 | 2.86 | 1.50 | 0.0076 | 0.0114 | Very good | Very good | |
| Optimal Mesh Size | Turbulence Models | RMSE | |
|---|---|---|---|
| H0 (m) | Cd (-) | ||
| Test No. 4 | RNG | 0.0079 | 0.0117 |
| k-ε | 0.0085 | 0.0123 | |
| k-ω | 0.0094 | 0.0128 | |
| LES | 0.0083 | 0.0120 | |
| Q (m3/s) | Cd (-) Exp | Cd (-) Num | RE (%) | H0 (m) Exp | H0 (m) Num | RE (%) |
|---|---|---|---|---|---|---|
| 0.00583 | 0.6515 | 0.6575 | 0.93 | 0.124 | 0.122 | 1.67 |
| 0.00625 | 0.6538 | 0.6661 | 1.89 | 0.140 | 0.135 | 3.39 |
| 0.00750 | 0.6625 | 0.6743 | 1.77 | 0.192 | 0.185 | 3.27 |
| 0.00833 | 0.6786 | 0.6927 | 2.09 | 0.224 | 0.215 | 3.86 |
| 0.00917 | 0.6823 | 0.6995 | 2.53 | 0.266 | 0.253 | 4.68 |
| 0.01000 | 0.6865 | 0.7016 | 2.16 | 0.311 | 0.298 | 4.10 |
| 0.01042 | 0.6877 | 0.6845 | 0.46 | 0.335 | 0.338 | 0.90 |
| 0.01083 | 0.6862 | 0.6921 | 0.86 | 0.363 | 0.357 | 1.65 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Daneshfaraz, R.; Norouzi, R.; Abbaszadeh, H.; Kuriqi, A.; Di Francesco, S. Influence of Sill on the Hydraulic Regime in Sluice Gates: An Experimental and Numerical Analysis. Fluids 2022, 7, 244. https://doi.org/10.3390/fluids7070244
Daneshfaraz R, Norouzi R, Abbaszadeh H, Kuriqi A, Di Francesco S. Influence of Sill on the Hydraulic Regime in Sluice Gates: An Experimental and Numerical Analysis. Fluids. 2022; 7(7):244. https://doi.org/10.3390/fluids7070244
Chicago/Turabian StyleDaneshfaraz, Rasoul, Reza Norouzi, Hamidreza Abbaszadeh, Alban Kuriqi, and Silvia Di Francesco. 2022. "Influence of Sill on the Hydraulic Regime in Sluice Gates: An Experimental and Numerical Analysis" Fluids 7, no. 7: 244. https://doi.org/10.3390/fluids7070244
APA StyleDaneshfaraz, R., Norouzi, R., Abbaszadeh, H., Kuriqi, A., & Di Francesco, S. (2022). Influence of Sill on the Hydraulic Regime in Sluice Gates: An Experimental and Numerical Analysis. Fluids, 7(7), 244. https://doi.org/10.3390/fluids7070244










