Two Models for 2D Deep Water Waves

Abstract

In this paper we propose two Hamiltonian models to describe two-dimensional deep water waves propagating on the surface of an ideal incompressible three-dimensional fluid. The idea is based on taking advantage of the Zakharov equation for one-dimensional waves which can be written in the form of so-called compact equations. We generalize these equations to the case of two-dimensional waves. As a test of our models, we perform numerical simulations of the dynamics of standing waves in a channel with smooth vertical walls. The results obtained in the proposed models are comparable, indicating that the models are similar to the original Zakharov equation.

1. Introduction

Physical phenomena related to deep water waves, for instance, the overturning of waves or the formation of so-called rogue waves, raise many questions for researchers. It is impossible to list all the efforts devoted to studying this field. In the general case, the dynamics of deep water waves propagating on the free surface can be described by the Laplace equation with nonlinear kinematic and dynamic boundary conditions at the surface. Solving these equations is a non-trivial task. Therefore, researchers use various simplified models.

At present, in the context of studying the dynamics of one-dimensional deep water waves, the only approximate model that is integrable in terms of the inverse scattering problem [1] is the well-known nonlinear Schrödinger equation (NLSE) [2]. Unfortunately, despite numerous advantages the model contains significant limitations that do not allow one to adequately describe the mentioned physical processes. Among the more accurate models one can highlight the Zakharov Equation [3]. Like the NLSE, it is based on perturbation theory where the small parameter is the wave steepness. It should be noticed that in the one-dimensional case the Zakharov equation can be rewritten in compact forms [4,5]. Another widely used method for solving the original equations, which is based on the expansion of velocity potential, is a high-order spectral method (HOSM) [6]. Finally, there is an exact model for describing the dynamics of one-dimensional deep water waves, a system of nonlinear equations written in conformal variables [7,8].

The problem becomes more complicated when considering two-dimensional waves propagating on the surface of a three-dimensional fluid. Exact equations in conformal variables can no longer be used in such geometry. Nevertheless, these equations with weak three-dimensional effects were considered in [9], and their corresponding numerical simulations were given in [10,11,12]. One straightforward variant is to use some two-dimensional version of the NLSE [13,14], but it is still very limited in its applicability [15]. Moreover, it is no longer an integrable model. A more accurate modification of the NLSE softening its limitations is in [16]. Intermediate model between the NLSE and the Zakharov equation can be found in [17]. Several studies on the physical phenomena and statistical properties of two-dimensional deep water waves using HOSM can be found in [18,19]. The Zakharov equation can also be used in the case of two-dimensional waves. However, there is considerable difficulty here that makes working with it quite challenging. The original Zakharov equation has a complex form that cannot be written in the way of some “compact” equations, as it was done in the one-dimensional case. Nevertheless, this equation is used to derive kinetic equations, in the manner of the Hasselmann equation [20], that allows studying weak turbulence in wind-driven sea [21,22].

This paper proposes two approximate Hamiltonian models to describe two-dimensional deep water waves propagating on the surface of a three-dimensional ideal incompressible fluid in a gravity field. The idea is based on using the advantages of the one-dimensional Zakharov equation. As mentioned earlier in this case it can be written in simple form of so-called compact equations. Then, these equations can be generalized to the case of two-dimensional waves. To verify the models for adequacy in describing deep water waves, we consider the dynamics of standing waves in a channel with smooth vertical walls.

The article is presented in the following way: the theoretical part, including the derivation of the proposed models from the Zakharov equation and their detailed description, will be shown in Section 2. Then, in Section 3, we present a description of the methods used in numerical simulations and the results obtained within the framework of the derived models. Finally, Section 4 will be devoted to a discussion of the results.

2. Hamiltonian Formalism for Deep Water Waves

Since the starting point for the proposed models is the Zakharov equation, we consider it necessary to briefly recall its derivation.

The 3D potential flow of an ideal incompressible deep fluid in the presence of a gravity field can be described by the following equations:

$$\begin{array}{ccc}\hfill & & ▵\varphi =0,\hfill \\ & & \frac{\partial \varphi }{\partial t}+\frac{1}{2}{|\nabla \varphi |}^2+g\eta =0{\mid }_{z=\eta },\hfill \\ & & \frac{\partial \eta }{\partial t}+\nabla \eta \nabla \varphi =\frac{\partial \varphi }{\partial z}{\mid }_{z=\eta }\hfill \end{array}$$

(1)

Here, the $\overrightarrow{r}=(x,y)$, z axis is directed away from the undisturbed surface coinciding with xy plane, t is time, g is the free-fall acceleration, $\eta (\overrightarrow{r},t)$ is the shape of the surface, $\varphi (\overrightarrow{r},z,t)$ is the hydrodynamic potential inside the fluid, and $\psi (\overrightarrow{r},t)=\varphi (\overrightarrow{r},z=\eta ,t)$ is the potential at the surface.

The system is Hamiltonian and $\eta$, $\psi$ is Hamiltonian variables [3]:

$$\begin{array}{ccc}\hfill & & \frac{\partial \eta }{\partial t}=\frac{\delta H}{\delta \psi },\hfill \\ & & \frac{\partial \psi }{\partial t}=-\frac{\delta H}{\delta \eta },\hfill \\ & & H=\frac{1}{2}\int d\overrightarrow{r}{\int }_{-\infty }^{\eta }{(\nabla \varphi )}^{2}dz+\frac{g}{2}\int {\eta }^{2}d\overrightarrow{r}\hfill \end{array}$$

(2)

The expansion of the Hamiltonian in power series of $\eta$ and $\psi$ up to the fourth-order is as follows:

$$\begin{array}{c}\hfill H=\frac{1}{2}\int (g{\eta }^2+\psi \widehat{k}\psi )d\overrightarrow{r}-\frac{1}{2}\int \{{\left(\widehat{k}\psi \right)}^2-{(\nabla \psi )}^2\}\eta d\overrightarrow{r}+\frac{1}{2}\int \{▵\psi {\eta }^2\widehat{k}\psi +\psi \widehat{k}\left(\eta \widehat{k}\left(\eta \widehat{k}\psi \right)\right)\}d\overrightarrow{r}.\end{array}$$

(3)

Here, operator $\widehat{k}$ means multiplication by $|\overrightarrow{k}|$ in k space.

Applying canonical transformation (also see [3] for details) from $\eta$ and $\psi$ to the variables of b and $b^{*}$, one can remove all non-resonant terms and drastically simplify the Hamiltonian:

$$\begin{array}{c}\hfill H(b,b^{*})=\int {\omega }_{\overrightarrow{k}}{b}_{\overrightarrow{k}}{b}_{\overrightarrow{k}}^{*}d\overrightarrow{k}+\frac{1}{2}\int T_{\overrightarrow{k},{\overrightarrow{k}}_1}^{{\overrightarrow{k}}_2,{\overrightarrow{k}}_3}{b}_{\overrightarrow{k}}^{*}{b}_{{\overrightarrow{k}}_1}^{*}{b}_{{\overrightarrow{k}}_2}{b}_{{\overrightarrow{k}}_3}{\delta }_{\overrightarrow{k}+{\overrightarrow{k}}_1-{\overrightarrow{k}}_2-{\overrightarrow{k}}_3}d\overrightarrow{k}d{\overrightarrow{k}}_{1}d{\overrightarrow{k}}_{2}d{\overrightarrow{k}}_3\end{array}$$

(4)

Here, ${\omega }_{\overrightarrow{k}}=\sqrt{g|\overrightarrow{k}|}$. The equation of motion in this case is a traditional Zakharov equation:

$$\begin{array}{ccc}\hfill & & \frac{\partial b_{\overrightarrow{k}}}{\partial t}+i\frac{\delta H}{\delta {b_{\overrightarrow{k}}}^{*}}=0\hfill \\ & & i\frac{\partial b_{\overrightarrow{k}}}{\partial t}={\omega }_{\overrightarrow{k}}{b}_{\overrightarrow{k}}+\int T_{\overrightarrow{k},{\overrightarrow{k}}_1}^{{\overrightarrow{k}}_2,{\overrightarrow{k}}_3}{b}_{{\overrightarrow{k}}_1}^{*}{b}_{{\overrightarrow{k}}_2}{b}_{{\overrightarrow{k}}_3}{\delta }_{\overrightarrow{k}+{\overrightarrow{k}}_1-{\overrightarrow{k}}_2-{\overrightarrow{k}}_3}d{\overrightarrow{k}}_{1}d{\overrightarrow{k}}_{2}d{\overrightarrow{k}}_3\hfill \end{array}$$

(5)

Here $T_{\overrightarrow{k},{\overrightarrow{k}}_1}^{{\overrightarrow{k}}_2,{\overrightarrow{k}}_3}$ represents the coefficient of four-wave interactions. Despite the explicit expression [23], it does not allow writing the Zakharov equation in x space. Direct use of Equation (5) to describe the evolution of two-dimensional waves is quite challenging because it requires the calculation of four-dimensional integrals over $\overrightarrow{k}$. Applying a canonical transformation that would simplify the original equation is also a non-trivial problem.

However, such transformations can be performed in the one-dimensional case since the one-dimensional version of the Zakharov equation has some exciting property. Our work will take advantage of this property to derive approximate models for describing two-dimensional deep water waves, which can be written in x space and are therefore suitable for numerical simulations.

The original canonical transformations removing all the non-resonant terms mentioned above are also valid in the one-dimensional case. One can obtain a one-dimensional version of the Zakharov equation:

$$\begin{array}{c}\hfill i\frac{\partial b_k}{\partial t}={\omega }_k{b}_k+\int T_{k,k_1}^{k_2,k_3}{b}_{k_1}^{*}{b}_{k_2}{b}_{k_3}{\delta }_{k+k_1-k_2-k_3}d{k}_{1}d{k}_{2}d{k}_3\end{array}$$

(6)

In this case, all wave vectors simply become wave numbers, and variables b, $b^{*}$ and operator ${\omega }_k$ also become one-dimensional.

Recently, an explicit and simple form was obtained for the 1D coefficient of four-wave interactions in the case of resonance $k+k_1=k_2+k_3$ [24].

$$T_{k,k_1}^{k_2,k_3}=\left\{\begin{array}{c}\frac{|k{k}_1{k}_2{k}_3{|}^{\frac{1}{4}}}{8\pi }\left[L_{-k{k}_1}+L_{-k_2{k}_3}\right]D_{k,k_1}^{k_2,k_3},\mathrm{if}\mathrm{all}k\mathrm{are}\mathrm{positive}(\mathrm{or}\mathrm{negative})\hfill \\ \frac{|k{k}_1{k}_2{k}_3{|}^{\frac{1}{4}}}{8\pi }\left[-L_{k{k}_2}-L_{k{k}_3}-L_{k_1{k}_2}-L_{k_1{k}_3}\right]D_{k,k_1}^{k_2,k_3},\mathrm{if}k{k}_1<0\mathrm{and}{k}_2{k}_3<0\hfill \\ 0,\mathrm{if}k{k}_1{k}_2{k}_3<0\hfill \end{array}\right.$$

(7)

Here,

$$\begin{array}{ccc}& & L_{k{k}_1}=\frac{|k{k}_1|-k{k}_1}{\sqrt{|k{k}_1|}}\hfill \\ & & D_{k,k_1}^{k_2,k_3}=\left\{\begin{array}{c}min\left(\right|k|,|k_1|,|k_2|,|k_3\left|\right),k{k}_1{k}_2{k}_3>0\hfill \\ 0\hfill \end{array}\right.\hfill \end{array}$$

There is an explicit formula for $D_{k,k_1}^{k_2,k_3}$:

$$\begin{array}{ccc}\hfill D_{k,k_1}^{k_2,k_3}& =& \frac{1}{2}\left(\left|k\right|+|k_1|+|k_2|+|k_3|\right)-\frac{1}{4}\left(|k+k_1|+|k_2+k_3|\right)-\hfill \\ & -& \frac{1}{4}\left(|k-k_2|+|k-k_3|+|k_1-k_2|+|k_1-k_3|\right)\hfill \end{array}$$

(8)

Coefficient $T_{k,k_1}^{k_2,k_3}$ has a special property:

$$\begin{array}{c}\hfill T_{k,k_1}^{k_2,k_3}=0\mathrm{if}k{k}_1{k}_2{k}_3<0,\end{array}$$

(9)

which is very important for further simplification of the Hamiltonian by applying canonical transformations. The transformation simplifying the four-order term in the Hamiltonian has the following form (we will use the same notations for new canonical variable $b_k$):

$$b_k\to b_k-i\int {\mathbf{B}}_{{\mathbf{kk}}_{\mathbf{1}}}^{{\mathbf{k}}_{\mathbf{2}}{\mathbf{k}}_{\mathbf{3}}}{b}_{k_1}^{*}{b}_{k_2}{b}_{k_3}{\delta }_{k+k_1-k_2-k_3}d{k}_{1}d{k}_{2}d{k}_3$$

(10)

Here, ${\mathbf{B}}_{{\mathbf{kk}}_{\mathbf{1}}}^{{\mathbf{k}}_{\mathbf{2}}{\mathbf{k}}_{\mathbf{3}}}$ is an arbitrary coefficient of the canonical transformation with the following symmetry relations:

$$\begin{array}{c}\hfill {\mathbf{B}}_{{\mathbf{kk}}_{\mathbf{1}}}^{{\mathbf{k}}_{\mathbf{2}}{\mathbf{k}}_{\mathbf{3}}}={\mathbf{B}}_{{\mathbf{k}}_{\mathbf{1}}\mathbf{k}}^{{\mathbf{k}}_{\mathbf{2}}{\mathbf{k}}_{\mathbf{3}}}={\mathbf{B}}_{{\mathbf{kk}}_{\mathbf{1}}}^{{\mathbf{k}}_{\mathbf{3}}{\mathbf{k}}_{\mathbf{2}}}={\left({\mathbf{B}}_{{\mathbf{k}}_{\mathbf{2}}{\mathbf{k}}_{\mathbf{3}}}^{{\mathbf{kk}}_{\mathbf{1}}}\right)}^{*}.\end{array}$$

Now, we plug this transformation into the Hamiltonian of the 1D Zakharov equation and obtain the new Hamiltonian:

$$\begin{array}{ccc}\hfill H=\int {\omega }_k{b}_k{b}_k^{*}dk& +& \frac{1}{2}\int \left[T_{k{k}_1}^{k_2{k}_3}-i({\omega }_k+{\omega }_{k_1}-{\omega }_{k_2}-{\omega }_{k_3}){\mathbf{B}}_{{\mathbf{kk}}_{\mathbf{1}}}^{{\mathbf{k}}_{\mathbf{2}}{\mathbf{k}}_{\mathbf{3}}}\right]\times \hfill \\ & \times & b_k^{*}{b}_{k_1}^{*}{b}_{k_2}{b}_{k_3}{\delta }_{k+k_1-k_2-k_3}dkd{k}_{1}d{k}_{2}d{k}_3+\cdots \hfill \end{array}$$

(11)

To replace Zakharov’s $T_{k{k}_1}^{k_2{k}_3}$ by the simpler ${\tilde{T}}_{k{k}_1}^{k_2{k}_3}$, the coefficient ${\mathbf{B}}_{{\mathbf{kk}}_{\mathbf{1}}}^{{\mathbf{k}}_{\mathbf{2}}{\mathbf{k}}_{\mathbf{3}}}$ has to be equal to

$${\mathbf{B}}_{{\mathbf{kk}}_{\mathbf{1}}}^{{\mathbf{k}}_{\mathbf{2}}{\mathbf{k}}_{\mathbf{3}}}=i\frac{{\tilde{T}}_{k{k}_1}^{k_2{k}_3}-T_{k{k}_1}^{k_2{k}_3}}{{\omega }_k+{\omega }_{k_1}-{\omega }_{k_2}-{\omega }_{k_3}}.$$

(12)

Any canonical transformation applied to the Hamiltonian system keeps a value of the wave interaction coefficient unchanged (${\tilde{T}}_{k{k}_1}^{k_2{k}_3}\equiv T_{k{k}_1}^{k_2{k}_3}$) on the resonant manifold:

$$\begin{array}{ccc}\hfill k+k_1& =& k_2+k_3,\hfill \\ \hfill {\omega }_k+{\omega }_{k_1}& =& {\omega }_{k_2}+{\omega }_{k_3}.\hfill \end{array}$$

(13)

Therefore, the coefficient ${\mathbf{B}}_{{\mathbf{kk}}_{\mathbf{1}}}^{{\mathbf{k}}_{\mathbf{2}}{\mathbf{k}}_{\mathbf{3}}}$ has no singularities at $k+k_1=k_2+k_3$. In the 1D case, all solutions of Equation (13) can be divided into two parts: so-called “trivial” and “non-trivial”. The “non-trivial” solution can be solved as follows:

$$\begin{array}{ccc}\hfill k& =& a{(1+\zeta )}^2,\hfill \\ \hfill k_1& =& a{(1+\zeta )}^2{\zeta }^2,\hfill \\ \hfill k_2& =& -a{\zeta }^2,\hfill \\ \hfill k_3& =& a{(1+\zeta +{\zeta }^2)}^2,\hfill \end{array}$$

(14)

and $0<\zeta <1$. Notice the product $k{k}_1{k}_2{k}_3<0$ and $T_{k,k_1}^{k_2,k_3}\equiv 0$. The “trivial” solution is obvious:

$$\begin{array}{c}\hfill k=k_2,k_1=k_3(\mathrm{plus}\mathrm{permutations}).\end{array}$$

Hence, on the resonant manifold

$$\begin{array}{c}\hfill T_{k,k_1}^{k,k_1}=\left\{\begin{array}{c}\frac{1}{2\pi }k{k}_{1}min\left(\right|k|,|k_1\left|\right),\mathrm{if}k{k}_1{k}_2{k}_3>0\hfill \\ 0\mathrm{if}k{k}_1{k}_2{k}_3<0\hfill \end{array}\right.\end{array}$$

(15)

Thus, we can apply some canonical transformation to replace $T_{k,k_1}^{k_2,k_3}$ by the new four-wave interaction coefficient ${\tilde{T}}_{k,k_1}^{k_2,k_3}$ which coincides on the resonant manifold:

$$\begin{array}{c}\hfill {\tilde{T}}_{k,k_1}^{k_2,k_3}=\left\{\begin{array}{c}\frac{1}{4\pi }\left(k{k}_1+k_2{k}_3\right)min\left(\right|k|,|k_1|,|k_2|,|k_3\left|\right),\mathrm{if}k{k}_1{k}_2{k}_3>0\hfill \\ 0,\mathrm{if}k{k}_1{k}_2{k}_3<0\hfill \end{array}\right.\end{array}$$

(16)

Using expression (8) we finally obtain:

$$\begin{array}{ccc}\hfill {\tilde{T}}_{k,k_1}^{k_2,k_3}& =& \frac{1}{4\pi }\left(k{k}_1+k_2{k}_3\right)D_{k,k_1}^{k_2,k_3}\hfill \end{array}$$

(17)

The Hamiltonian and the dynamical equation for b in k space are now the following:

$$\begin{array}{ccc}& & H(b,b^{*})=\int {\omega }_k{b}_k{b}_k^{*}dk+\frac{1}{2}\int {\tilde{T}}_{k,k_1}^{k_2,k_3}{b}_k^{*}{b}_{k_1}^{*}{b}_{k_2}{b}_{k_3}{\delta }_{k+k_1-k_2-k_3}dkd{k}_{1}d{k}_{2}d{k}_3\hfill \\ & & i\frac{\partial b_k}{\partial t}={\omega }_k{b}_k+\int {\tilde{T}}_{k,k_1}^{k_2,k_3}{b}_{k_1}^{*}{b}_{k_2}{b}_{k_3}{\delta }_{k+k_1-k_2-k_3}d{k}_{1}d{k}_{2}d{k}_3.\hfill \end{array}$$

Using operators $\widehat{k}$ and ${\widehat{\omega }}_k$ which are multiplication by $\left|k\right|$ and by $\sqrt{g\left|k\right|}$ in Fourier space, the equation of motion in the x space takes the form:

$$\begin{array}{ccc}\hfill i\frac{\partial b}{\partial t}& =& {\widehat{\omega }}_{k}b-\frac{1}{4}[2b_x{b}^{*}\widehat{k}\left(b_x\right)+b_x{b}_x\widehat{k}\left(b^{*}\right)+\widehat{k}\left(b_x{b}_x{b}^{*}\right)-\frac{\partial }{\partial x}(bb\widehat{k}\left(b_x^{*}\right))-\frac{\partial }{\partial x}\widehat{k}\left(bb{b}_x^{*}\right)\hfill \\ & -& 2\frac{\partial }{\partial x}(b_x^{*}b\widehat{k}\left(b\right))]+\frac{1}{4}\left[b^{*}\widehat{k}\left(b_x{b}_x\right)-\frac{\partial }{\partial x}(b_x^{*}\widehat{k}\left(bb\right))\right]+\frac{1}{2}\left[b_x\widehat{k}\left(b_x{b}^{*}\right)-\frac{\partial }{\partial x}(b\widehat{k}\left(b_x^{*}b\right))\right]\hfill \end{array}$$

(18)

Equation of motion (18) corresponding to the Hamiltonian with a four-wave interaction coefficient (17) is the first one-dimensional model of the two considered in this article. Section 2.1 will show how a two-dimensional equation for waves on the surface of a three-dimensional fluid can be obtained from this model.

Obviously, this is not the only possible canonical transformation. One can accomplish this in many ways, thereby obtaining different forms of the compact equation. Therefore, we present another model called “the system of super-compact equations” for deep water waves.

The diagonal part of the four-wave interaction coefficient on the resonant manifold can be represented by (compare with (15)):

$$\begin{array}{c}\hfill T_{k,k_1}^{k,k_1}=\left\{\begin{array}{c}\frac{1}{2\pi }\left|k\right||k_1|min(\left|k\right|,|k_1\left|\right),\mathrm{if}\mathrm{all}k\mathrm{are}\mathrm{positive}(\mathrm{or}\mathrm{negative})\hfill \\ -\frac{1}{2\pi }\left|k\right||k_1|min(\left|k\right|,|k_1\left|\right),\mathrm{if}k{k}_1<0\mathrm{and}{k}_2{k}_3<0\hfill \\ 0\mathrm{if}k{k}_1{k}_2{k}_3<0\hfill \end{array}\right.\end{array}$$

(19)

Using expression (19) we can apply a canonical transformation ($b\to c$) to replace $T_{k,k_1}^{k_2,k_3}\to {\tilde{\tilde{T}}}_{k,k_1}^{k_2,k_3}$ which allows to simplify the Hamiltonian and divide waves into two groups: waves running to the left and to the right ($c(x,t)=c^{+}(x,t)+c^{-}(x,t)$). The details of this transformation can be found in [24] so here we only present the final result. The Hamiltonian in new variables $c^{+}(x,t)$ and $c^{-}(x,t)$ has the following form:

$$\begin{array}{c}\hfill H=\int {c^{+}}^{*}\widehat{V}{c}^{+}dx+\frac{1}{2}\int \left[\frac{i}{4}({c^{+}}^2\frac{\partial }{\partial x}{{c^{+}}^{*}}^2-{{c^{+}}^{*}}^2\frac{\partial }{\partial x}{c^{+}}^2)-|c^{+}{|}^2\widehat{k}{|c^{+}|}^2\right]dx\\ \hfill +\int {c^{-}}^{*}\widehat{V}{c}^{-}dx+\frac{1}{2}\int \left[\frac{i}{4}({{c^{-}}^{*}}^2\frac{\partial }{\partial x}{c^{-}}^2-{c^{-}}^2\frac{\partial }{\partial x}{{c^{-}}^{*}}^2)-|c^{-}{|}^2\widehat{k}{|c^{-}|}^2\right]dx\\ \hfill +\int \left[|c^{+}{|}^2\widehat{k}{|c^{-}|}^2+{c^{+}}^{*}{c^{-}}^{*}\widehat{k}\left(c^{+}{c}^{-}\right)+i\left({c^{+}}^{*}{c}^{-}\right)\frac{\partial }{\partial x}\left(c^{+}{c^{-}}^{*}\right)\right]dx\end{array}$$

(20)

Here, $\widehat{V}=\widehat{\omega }/\widehat{k}$, $\widehat{k}$ and $\widehat{\omega }$ correspond to multiplication by $\left|k\right|$ and $\sqrt{g\left|k\right|}$ in k space. The functions $c^{+}(x,t)$ and $c^{-}(x,t)$ only contain positive and negative k, respectively, and satisfy the following equations:

$$\begin{array}{ccc}& & \frac{\partial c^{+}}{\partial t}+{\partial }_x^{+}\frac{\delta H}{\delta {c^{+}}^{*}}=0,\hfill \\ & & \frac{\partial c^{-}}{\partial t}-{\partial }_x^{-}\frac{\delta H}{\delta {c^{-}}^{*}}=0,\hfill \end{array}$$

Here, ${\partial }_x^{+}$, ${\partial }_x^{-}$ correspond to multiplication by $ik{\theta }_k$ and $ik{\theta }_{-k}$ where ${\theta }_k$ denotes the Heaviside step function. Then, the motion equations in x space take the form:

$$\begin{array}{c}\hfill \frac{\partial c^{+}}{\partial t}+i\widehat{\omega }{c}^{+}={\partial }_x^{+}\left[i(|c^{+}{|}^2-|c^{-}{|}^2)c_x^{+}+c^{+}\widehat{k}(|c^{+}{|}^2-|c^{-}{|}^2)-i{c}^{+}{c}^{-}{c}_x^{-*}-c^{-*}\widehat{k}\left(c^{+}{c}^{-}\right)\right]\\ \hfill \frac{\partial c^{-}}{\partial t}+i\widehat{\omega }{c}^{-}={\partial }_x^{-}\left[i(|c^{-}{|}^2-|c^{+}{|}^2)c_x^{-}-c^{-}\widehat{k}(|c^{-}{|}^2-|c^{+}{|}^2)-i{c}^{-}{c}^{+}{c}_x^{+*}+c^{+*}\widehat{k}\left(c^{+}{c}^{-}\right)\right]\end{array}$$

(21)

We call the equations in (21) for the functions $c^{+}(x,t)$ and $c^{-}(x,t)$ “the system of supercompact equations” because one of the equations vanishes when considering unidirectional waves, and the remaining one is nothing but a “supercompact equation” obtained earlier in [5].

System of Equation (21) with Hamiltonian (20) is the second of the models considered in our article. Its generalization to the case of two-dimensional waves will be considered in Section 2.2.

We would like to again note that Equation (18) and system of Equation (21) are equivalent up to the expansion of original Hamiltonian (4). One model can be obtained from another one and vice versa by applying corresponding canonical transformations. Nevertheless, system of Equation (21) is more suitable for numerical simulations because these equations are of lower order in comparison to Equation (18).

2.1. Generalization to Two-Dimensional Waves in b Variable Model

Recall again that four-wave interaction coefficient (17) has a compact form, unlike the original Zakharov coefficient. It allows to write equation of motion (18) in x space. The equation can be easily used for studying the dynamics of one-dimensional deep water waves with conventional pseudo-spectral numerical algorithms.

We now generalize the coefficient to the case of two-dimensional waves by replacing wave numbers by vectors $k\to \overrightarrow{k}$, coefficient $D_{k,k_1}^{k_2,k_3}\to D_{\overrightarrow{k},{\overrightarrow{k}}_1}^{{\overrightarrow{k}}_2,{\overrightarrow{k}}_3}$ and the products of wave numbers by scalar products, and thus taking into account angular dependence:

$$\begin{array}{ccc}\hfill {\tilde{T}}_{\overrightarrow{k},{\overrightarrow{k}}_1}^{{\overrightarrow{k}}_2,{\overrightarrow{k}}_3}& =& \frac{1}{4\pi }\left(\overrightarrow{k}·{\overrightarrow{k}}_1+{\overrightarrow{k}}_2·{\overrightarrow{k}}_3\right)D_{\overrightarrow{k},{\overrightarrow{k}}_1}^{{\overrightarrow{k}}_2,{\overrightarrow{k}}_3}\hfill \end{array}$$

(22)

We highlight that coefficient (22) exactly coincides with the original Zakharov coefficient on the resonance manifold for one-dimensional waves.

We would like to emphasize the crucial point of this procedure. We propose another way to study the dynamics of 2D deep water waves with the help of approximate models, the derivation of which is based on the Zakharov equation. This allows overcoming the problems related to direct calculations of Equation (5). This is not a canonical transformation, therefore, this generalized ${\tilde{T}}_{\overrightarrow{k},{\overrightarrow{k}}_1}^{{\overrightarrow{k}}_2,{\overrightarrow{k}}_3}$ is not equivalent to the original Zakharov coefficient $T_{\overrightarrow{k},{\overrightarrow{k}}_1}^{{\overrightarrow{k}}_2,{\overrightarrow{k}}_3}$ on the resonance manifold. Thus, this procedure does not have rigorous mathematical proof. Nonetheless, as discussed below, these coefficients turned out to be very similar on the resonant manifold.

A comparison of the original two-dimensional Zakharov coefficient $T_{\overrightarrow{k},{\overrightarrow{k}}_1}^{{\overrightarrow{k}}_2,{\overrightarrow{k}}_3}$ with the generalized coefficient ${\tilde{T}}_{\overrightarrow{k},{\overrightarrow{k}}_1}^{{\overrightarrow{k}}_2,{\overrightarrow{k}}_3}$ on the resonance manifold was carried out by Dr. V.V. Geogjaev. Panels (a) and (b) in Figure 1 show the behavior of coefficients on the Phillips curve, respectively. In all curves, the coefficients are normalized: $T_{\overrightarrow{k},\overrightarrow{k}}^{\overrightarrow{k},\overrightarrow{k}}=2$ ($k_B=\frac{1}{2}(\overrightarrow{k}+{\overrightarrow{k}}_1)=\frac{1}{2}({\overrightarrow{k}}_2+{\overrightarrow{k}}_3)=1$). A quadruplet is defined by choosing two points P and $P_2$ on the Phillips curve. The curves in panels are built depending on the x coordinate of point $P_2$ while P is fixed for each curve.

Since the models are equivalent in the one-dimensional case, we assume that discrepancies in the dynamics between the proposed two-dimensional models and the Zakharov equation will appear when the dependence on the parameter $k_y$ increases. Nevertheless, the comparison showed that these discrepancies are small, and the coefficients are very similar, which justifies the generalization. The feature is that it is still possible to write the equation of motion in x space using ${\tilde{T}}_{\overrightarrow{k},{\overrightarrow{k}}_1}^{{\overrightarrow{k}}_2,{\overrightarrow{k}}_3}$, which is not possible if using the original Zakharov coefficient.

Now function $b(x,y,t)$ depends on two space variables and time, operator $\widehat{k}$ corresponds to multiplication by $|\overrightarrow{k}|=\sqrt{k_x^2+k_y^2}$, $\widehat{\omega }$—to multiplication by $\sqrt{g|\overrightarrow{k}|}$ in k space, and partial derivatives are replaced by ∇ operators.

$$\begin{array}{ccc}\hfill i\frac{\partial b}{\partial t}& =& {\widehat{\omega }}_{\overrightarrow{k}}b-\frac{1}{4}[2(\nabla b)·\widehat{k}(\nabla b)b^{*}+(\nabla b)·(\nabla b)\widehat{k}\left(b^{*}\right)+\widehat{k}((\nabla b)·(\nabla b)b^{*})\hfill \\ & -& \nabla ·(bb\widehat{k}(\nabla b^{*}))-\nabla ·(\widehat{k}\left(bb(\nabla b^{*})\right))-2\nabla ·((\nabla b^{*})b\widehat{k}\left(b\right))]\hfill \\ & +& \frac{1}{4}\left[b^{*}\widehat{k}((\nabla b)·(\nabla b))-\nabla ·((\nabla b^{*})\widehat{k}\left(bb\right))\right]\hfill \\ & +& \frac{1}{2}\left[(\nabla b)·\widehat{k}\left((\nabla b)b^{*}\right)-\nabla ·(b\widehat{k}\left((\nabla b^{*})b\right))\right]\hfill \end{array}$$

(23)

Furthermore, in Section 3.1, we present the results obtained using this equation.

2.2. Generalization to Two-Dimensional Waves in Variables $c^{+}$ and $c^{-}$

Let us generalize Hamiltonian (20) to the case of two-dimensional waves. For this purpose, we need to redefine all one-dimensional operators in the Hamiltonian. Recall that in the one-dimensional case, operator $\widehat{k}$ acts as a multiplication by $\left|k\right|$ in Fourier-space while $\frac{\partial }{\partial x}$ acts as a multiplication by $ik$. Now we replace scalar k with a vector $\overrightarrow{k}=(k_x,k_y)$. Then, the operators are redefined as follows: $\widehat{k}\to \left|\overrightarrow{k}\right|=\sqrt{k_x^2+k_y^2}$, $\widehat{\omega }\to \sqrt{g|\overrightarrow{k}|}$, and $\frac{\partial }{\partial x}\to i\left|\overrightarrow{k}\right|sign\left(k_x\right)$ in k space. Operators ${\partial }_x^{+}$ and ${\partial }_x^{-}$ now turn to $i\widehat{k}{\theta }_{k_x}$ or $i{\widehat{k}}^{+}$ and $-i\widehat{k}{\theta }_{-k_x}$ or $-i{\widehat{k}}^{-}$, respectively. Furthermore, considering that $c^{+}=c^{+}(x,y)$, $c^{-}=c^{-}(x,y)$, now the Hamiltonian is:

$$\begin{array}{c}\hfill H=\int {c^{+}}^{*}\widehat{V}{c}^{+}dxdy+\frac{1}{2}\int \left[\frac{1}{4}({c^{+}}^2\widehat{k}{{c^{+}}^{*}}^2+{{c^{+}}^{*}}^2\widehat{k}{c^{+}}^2)-|c^{+}{|}^2\widehat{k}{\left|c^{+}\right|}^2\right]dxdy\\ \hfill +\int {c^{-}}^{*}\widehat{V}{c}^{-}dxdy+\frac{1}{2}\int \left[\frac{1}{4}({{c^{-}}^{*}}^2\widehat{k}{c^{-}}^2+{c^{-}}^2\widehat{k}{{c^{-}}^{*}}^2)-|c^{-}{|}^2\widehat{k}{\left|c^{-}\right|}^2\right]dxdy\\ \hfill +\int \left[|c^{+}{|}^2\widehat{k}{\left|c^{-}\right|}^2+{c^{+}}^{*}{c^{-}}^{*}\widehat{k}\left(c^{+}{c}^{-}\right)-i\left({c^{+}}^{*}{c}^{-}\right)\widehat{k}\left(c^{+}{c^{-}}^{*}\right)\right]dxdy\end{array}$$

(24)

The corresponding equations of motion are:

$$i\frac{\partial c^{+}}{\partial t}={\widehat{k}}^{+}\frac{\delta H}{\delta {c^{+}}^{*}},i\frac{\partial c^{-}}{\partial t}=-{\widehat{k}}^{-}\frac{\delta H}{\delta {c^{-}}^{*}}$$

After taking the variation of the Hamiltonian, one can obtain a system of supercompact equations generalized for two-dimensional waves:

$$\begin{array}{c}\hfill \frac{\partial c^{+}}{\partial t}=-i\widehat{\omega }{c}^{+}-i{\widehat{k}}^{+}\left[\frac{1}{2}{c^{+}}^{*}\widehat{k}\left({c^{+}}^2\right)-c^{+}\widehat{k}\left(\right|c^{+}{|}^2-|c^{-}{|}^2)-c^{-}\widehat{k}\left(c^{+}{c^{-}}^{*}\right)+c^{-*}\widehat{k}\left(c^{+}{c}^{-}\right)\right]\\ \hfill \frac{\partial c^{-}}{\partial t}=-i\widehat{\omega }{c}^{-}+i{\widehat{k}}^{-}\left[\frac{1}{2}{c^{-}}^{*}\widehat{k}\left({c^{-}}^2\right)-c^{-}\widehat{k}\left(\right|c^{-}{|}^2-|c^{+}{|}^2)-c^{+}\widehat{k}\left({c^{+}}^{*}{c}^{-}\right)+c^{+*}\widehat{k}\left(c^{+}{c}^{-}\right)\right]\end{array}$$

(25)

In addition to Hamiltonian (24), this system of equations has the following integrals of motion: the number of waves propagating to the “left” $N^{-}$ and to the “right” $N^{+}$ (with respect to $k_x$), longitudinal $P_x$ and transverse $P_y$ momentum.

$$N^{+}=\int \frac{|c_{\overrightarrow{k}}^{+}{|}^2}{|\overrightarrow{k}|}d\overrightarrow{k},N^{-}=\int \frac{|c_{\overrightarrow{k}}^{-}{|}^2}{|\overrightarrow{k}|}d\overrightarrow{k}$$

(26)

$$P_x=\int \frac{k_x}{|\overrightarrow{k}|}(|c_{\overrightarrow{k}}^{+}{|}^2+|c_{\overrightarrow{k}}^{-}{|}^2)d\overrightarrow{k},P_y=\int \frac{k_y}{|\overrightarrow{k}|}(|c_{\overrightarrow{k}}^{+}{|}^2+|c_{\overrightarrow{k}}^{-}{|}^2)d\overrightarrow{k}$$

(27)

The results of numerical simulations obtained by using Equation (25) will be shown in Section 3.2.

3. Numerical Simulations

The validity of the models is also confirmed by using the method of frozen coefficients. One can easily show that equations do not have instability at small scales, which is important in numerical simulations because of rounding errors. Both models (23) and (25) contain non-local terms with operator $\widehat{k}$. Recall that this operator can be easily calculated in Fourier-space as multiplication by $|\overrightarrow{k}|$. Therefore, it seems reasonable to use pseudo-spectral Fourier methods to calculate the right-hand side of the equations. We use the standard fourth-order Runga–Kutta method for time integration. The correctness of the calculations is carried out by checking the conservation of the integrals of motion. The FFTW3 library [25] was used for the fast Fourier transform procedure. The multiplication of grid functions was carried out in x space, and the direct and inverse Fourier transforms were used to calculate derivatives and non-local terms. OpenMP tools were used to parallelize the numerical algorithm, and the 2D Fourier transforms paralleling was performed using the fftw3-threads.

To test the proposed models for adequacy in describing the dynamics of two-dimensional deep water waves, we consider the physical problem of standing waves in a channel with smooth vertical walls in our numerical simulations. For this purpose, we consider the periodic domain in the water channel with sizes $L_x\times L_y=300$ m $\times 1000$ m. A perturbed one-dimensional standing wave with a characteristic wavelength ${\lambda }_0=20$ m was considered as the initial condition. Average steepness $\mu =|\overrightarrow{\nabla }\eta |\approx 0.26$. The perturbation was performed in the region around the basic harmonic ${\overrightarrow{k}}_0=(k_x=\frac{\pi }{10};k_y=0)$. To prevent wave overturning, damping concentrated in the region of short wave harmonics was used.

Considering perturbed standing waves in a water channel with smooth vertical walls, it is necessary to make the surface derivative equal to zero at the walls. This means that the expansion of ${\eta }_k$ has to only contain cosines.

$$\frac{\partial \eta }{\partial x}{|}_{x=0,L}=0;{\eta }_k=\sum _k{a}_{k}cos\left(kx\right)$$

(28)

In terms of b and $c^{+},c^{-}$, the surface can be recovered by the following canonical transformations:

$${\eta }_k=\frac{|\overrightarrow{k}{|}^{\frac{1}{4}}}{\sqrt{2}{g}^{\frac{1}{4}}}\left[b_{\overrightarrow{k}}+b_{\overrightarrow{k}}^{*}\right];{\eta }_k=\frac{|\overrightarrow{k}{|}^{-\frac{1}{4}}}{\sqrt{2}{g}^{\frac{1}{4}}}\left[c_{\overrightarrow{k}}^{+}+c_{\overrightarrow{k}}^{-}+{c_{\overrightarrow{k}}^{+}}^{*}+{c_{\overrightarrow{k}}^{-}}^{*}\right]$$

(29)

This results in the following conditions for variables:

$$b(-k_x,k_y)=b(k_x,k_y);c^{-}(-k_x,k_y)=c^{+}(k_x,k_y)$$

(30)

Thus, condition (30) for b variables is maintained at each time step while calculating in Equation (23). In the case of variables $c^{+},c^{-}$, one can only use the first equation in (25) with condition (30) for $c^{+},c^{-}$ variables:

$$\frac{\partial c^{+}}{\partial t}=-i\widehat{\omega }{c}^{+}-i{\widehat{k}}^{+}\left[\frac{1}{2}{c^{+}}^{*}\widehat{k}\left({c^{+}}^2\right)-c^{+}\widehat{k}(|c^{+}{|}^2-|c^{-}{|}^2)-c^{-}\widehat{k}\left(c^{+}{c^{-}}^{*}\right)+c^{-*}\widehat{k}\left(c^{+}{c}^{-}\right)\right]$$

The following sections will show the results of numerical simulations obtained within the framework of the proposed models.

3.1. Numerical Results Obtained in b Variable Model

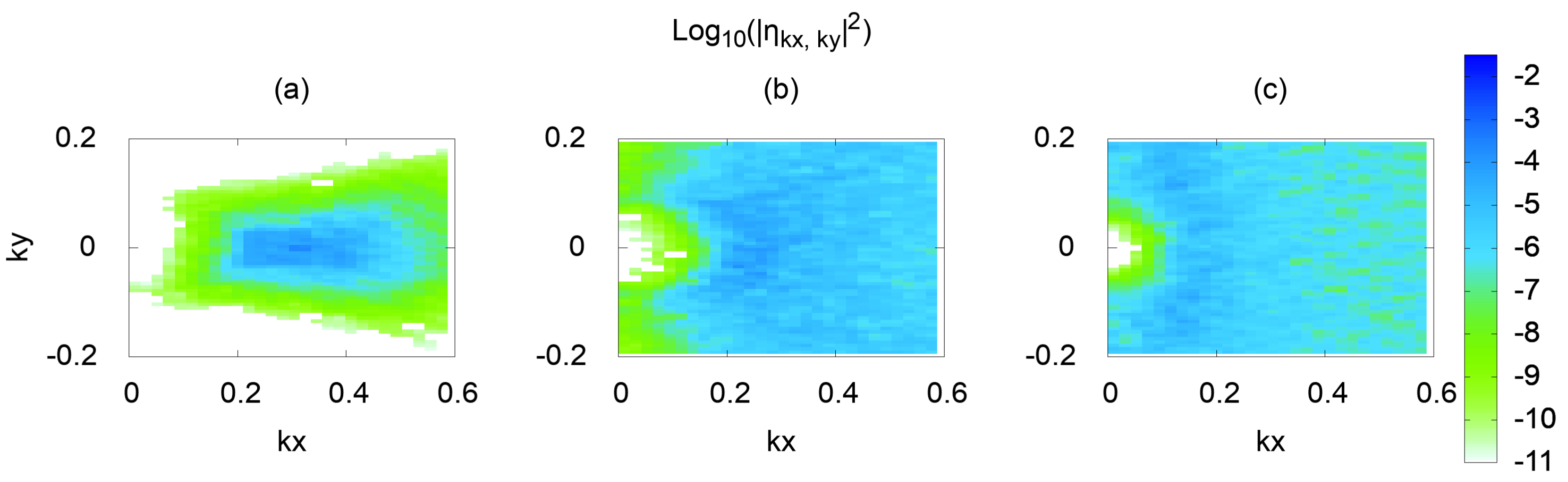
Figure 2 shows the two-dimensional spectra of $|{\eta }_{k_x,k_y}{|}^2$ at different times. The spectrum is symmetric with respect to the vertical line at $k_x=0$ since considering standing waves. That is why we do not show the part of the spectrum with negative $k_x$. As it mentioned previously, initially (panel a) it is a one-dimensional standing wave with $k_{x0}=\frac{\pi }{10}{m}^{-1},k_{y0}=0$ and small perturbation around it. In the process of time evolution, the spectrum expands (panel b) and eventually becomes almost isotropic (ring formation) after a long time (panel c).

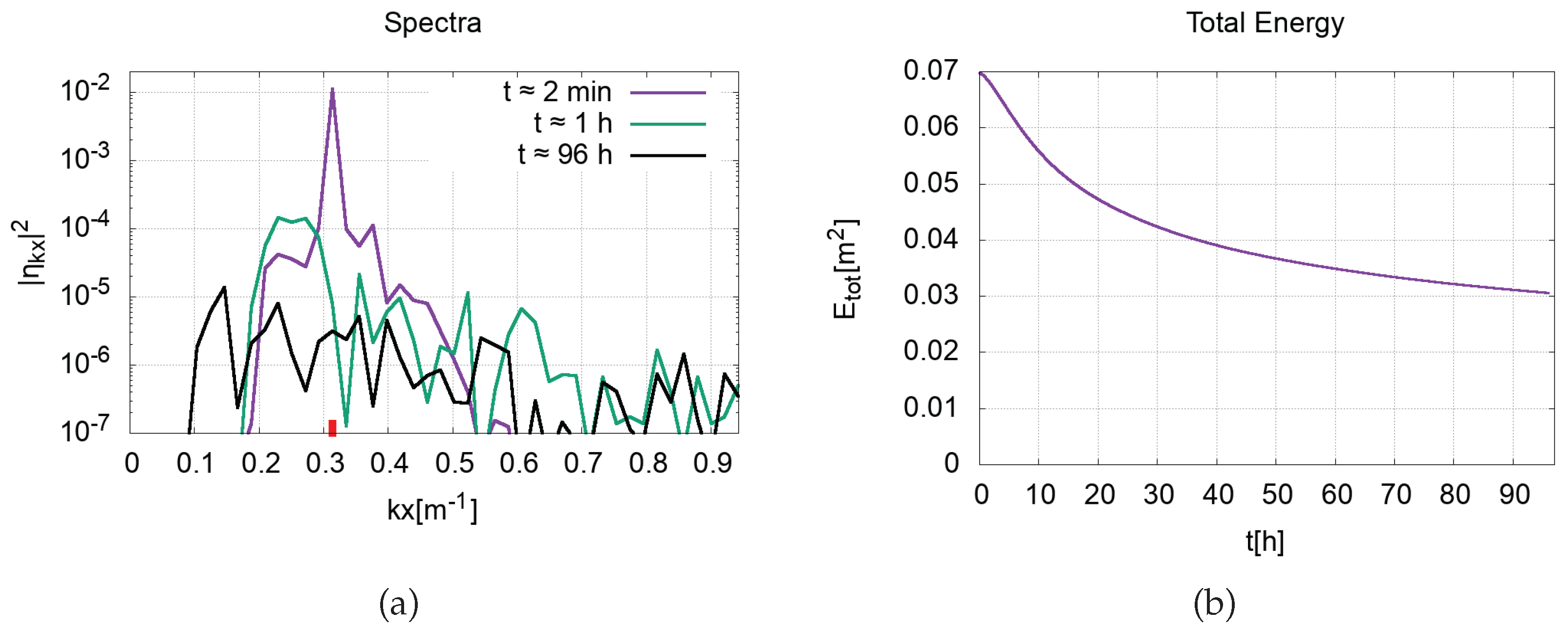
Figure 3 shows one-dimensional spectra $|{\eta }_{k_x}{|}^2$ at $k_y=0$ (panel a) and the dependence of total energy on time (panel b). It can be seen that the spectrum shifts to the region of long-wave harmonics with time; that is, the waves in the channel become longer along the x axis. Taken together with the two-dimensional spectrum, one can conclude that the waves become slightly longer in the x axis direction and significantly longer in the y axis direction. The total energy of the system gradually decreases due to the damping concentrated in the region of short-wave harmonics. It can be seen that the energy was almost halved in 96 h.

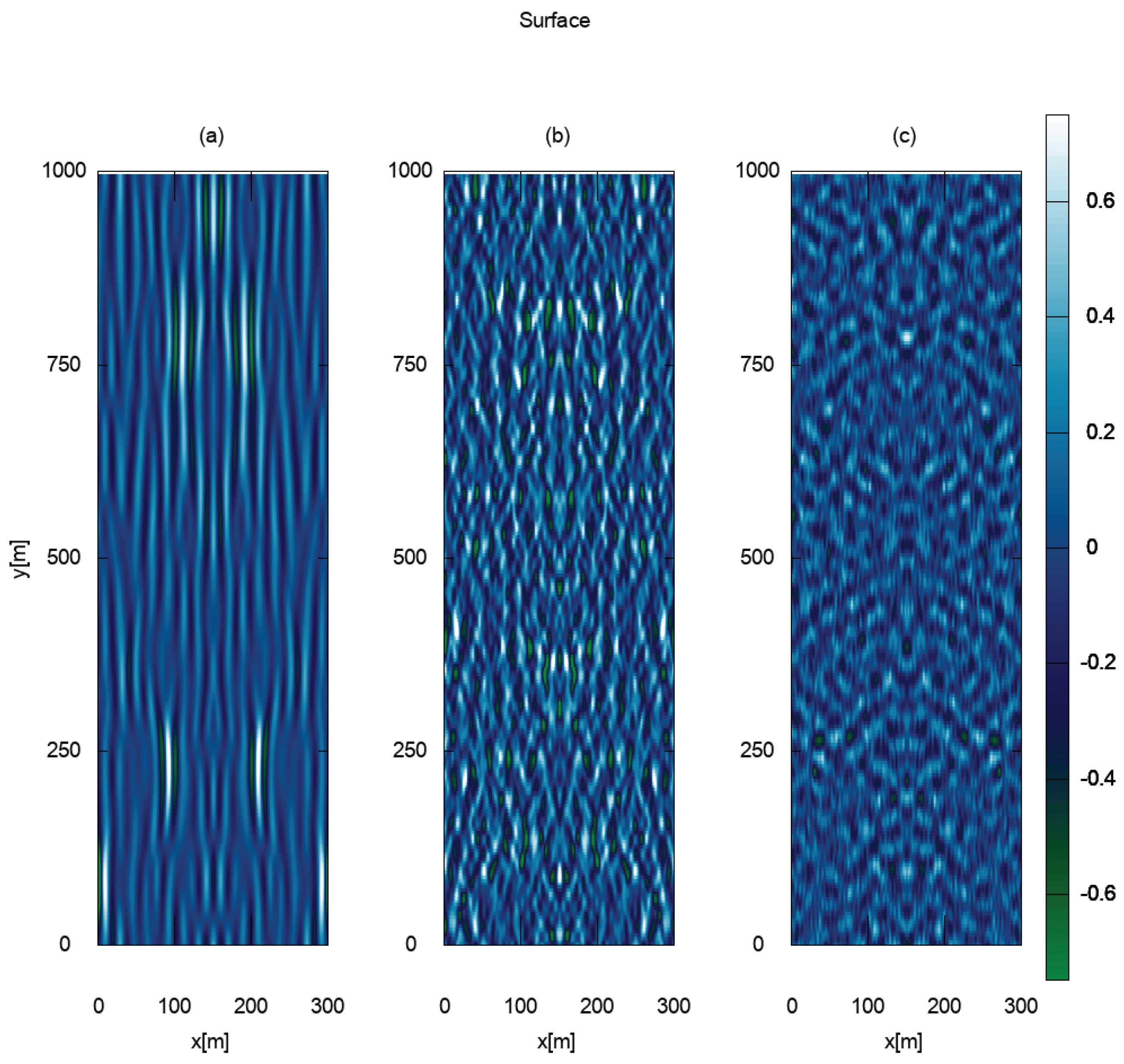
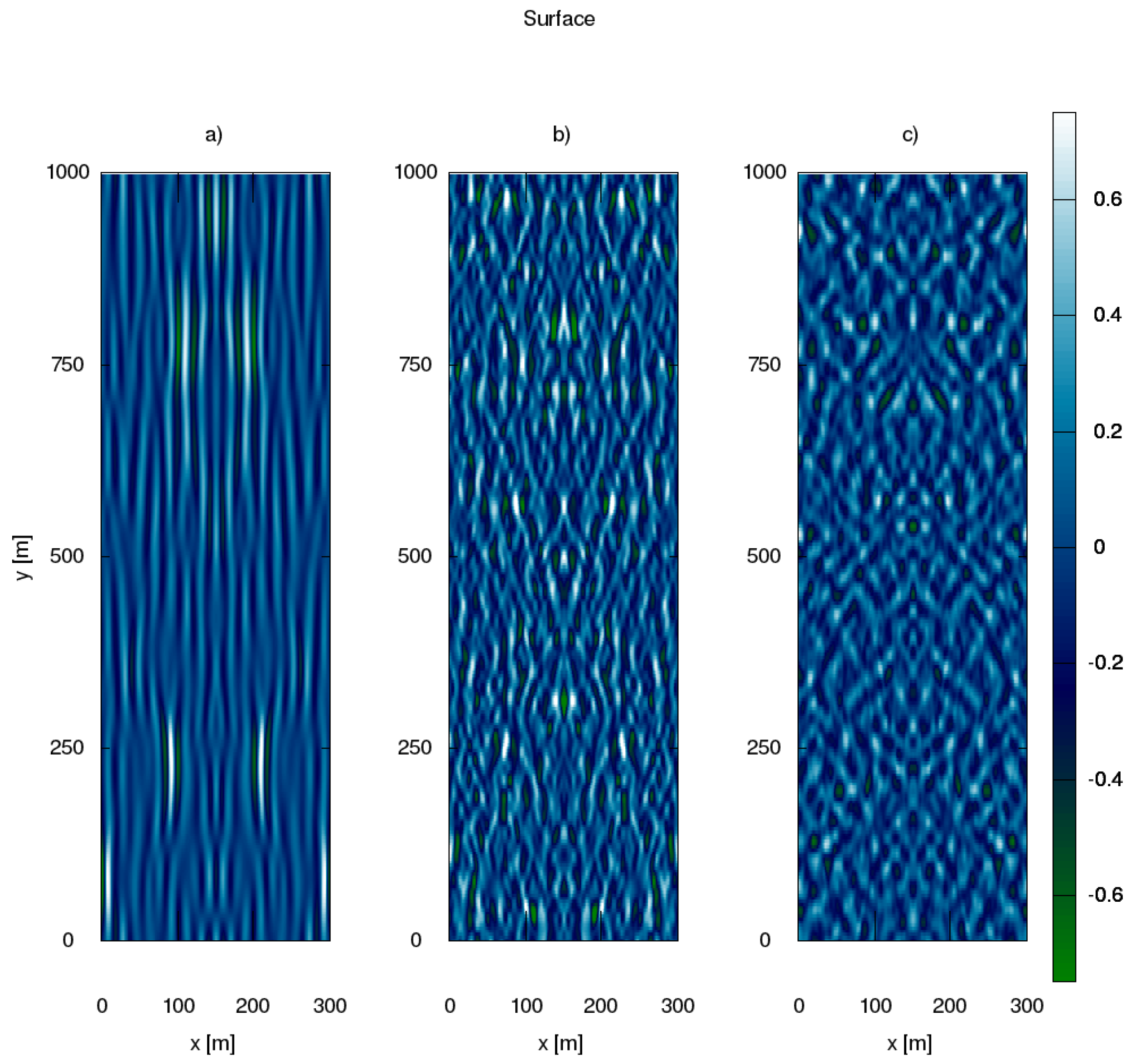
The time evolution of the surface is presented in Figure 4. The pictures are symmetrical around the central vertical line at $x=150$ m. In the beginning, the waves look quasi-one-dimensional. Then, the waves begin to bend over time. Finally, after a long time, the isotropization of the spectrum results in waves pointed in all directions.

Several films are available for more information:

A film with the dynamics of the one-dimensional spectrum can be viewed here: http://kachulin.itp.ac.ru/mdpi-2022-films/spectrum-1d.avi (accessed on 25 April 2022).

A film with the dynamics of the two-dimensional spectrum can be viewed here: http://kachulin.itp.ac.ru/mdpi-2022-films/spectrum-2d-zoom.avi (accessed on 25 April 2022).

Short films with surface dynamics are presented here.

At initial time: http://kachulin.itp.ac.ru/mdpi-2022-films/surface-0s.avi (accessed on 25 April 2022).

At final time: http://kachulin.itp.ac.ru/mdpi-2022-films/surface-96h.avi (accessed on 25 April 2022).

3.2. Numerical Results Obtained in the Model of $c^{+}$ and $c^{-}$ Variables

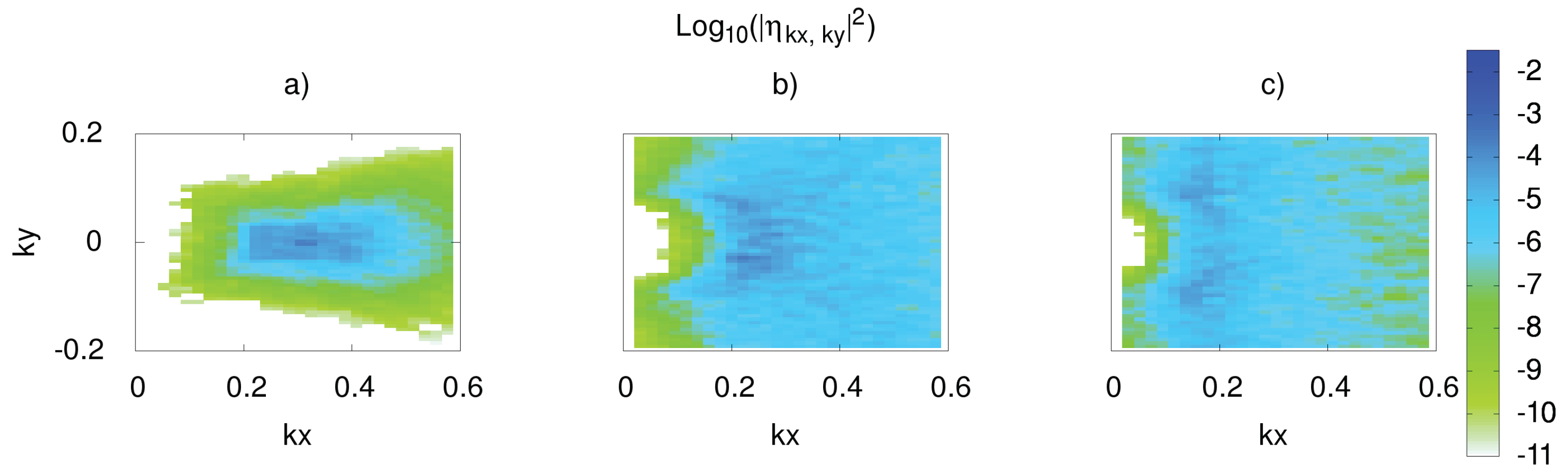
The model in terms of ${}^{+}c$ and $c^{-}$ slightly differs from the one in terms of b. Nevertheless, the detailed discussion of the results in Section 3.1 maintains its validity here as well. In Figure 5, one can also see the process of spectrum isotropization with time. Despite the differences, in general, the dynamics remain the same.

The same can be said about the one-dimensional spectrum shown in Figure 6 (panel a). Since the equations of motion in the $c^{+}$ and $c^{-}$ variables are different, the damping function is also different. This results in a change in energy dependence. It decreased more in the shorter computation time (panel b), but it did not again affect the overall dynamics.

Figure 7 presents the time evolution of the surface. Comparing panels (a) and (b) in Figure 4 and Figure 7, one can see that they are almost indistinguishable. Since there were no changes in the dynamics, the final computation time in this model was shorter.

A similar problem was considered in [26] in the framework of the equations in physical variables $\eta$ and $\psi$ corresponding to the Hamiltonian (3). It was shown that the initial spectrum of the perturbed standing wave becomes isotropic over time, and a specific ”ring” is formed. We observe very similar dynamics in proposed equations which can be clearly seen in Figure 2c and Figure 5c.

4. Conclusions

This work was devoted to the study of the hydrodynamics of two-dimensional waves propagating on the surface of a three-dimensional ideal incompressible fluid. Two new Hamiltonian models were proposed to describe the dynamics of such waves. The derivation of the models was based on the use of compact forms of the Zakharov equation for one-dimensional waves. Furthermore, we considered the dynamics of standing waves in a channel with smooth vertical walls as a physical problem. The results of numerical simulations showed an isotropization of the spectrum over time in both proposed models, which is entirely consistent with the studies carried out earlier. Furthermore, similarities in the overall dynamics in both models allowed us to conclude that the system of super-compact equations, which is the simplest form of the Zakharov equation, can be successfully applied to numerical simulations of two-dimensional deep water waves as well.