Transient CFD Modelling of Air–Water Two-Phase Annular Flow Characteristics in a Small Horizontal Circular Pipe
Abstract
1. Introduction
2. Numerical Method
2.1. Governing Equations of Two-Phase Flow Using the Eulerian–Eulerian Approach
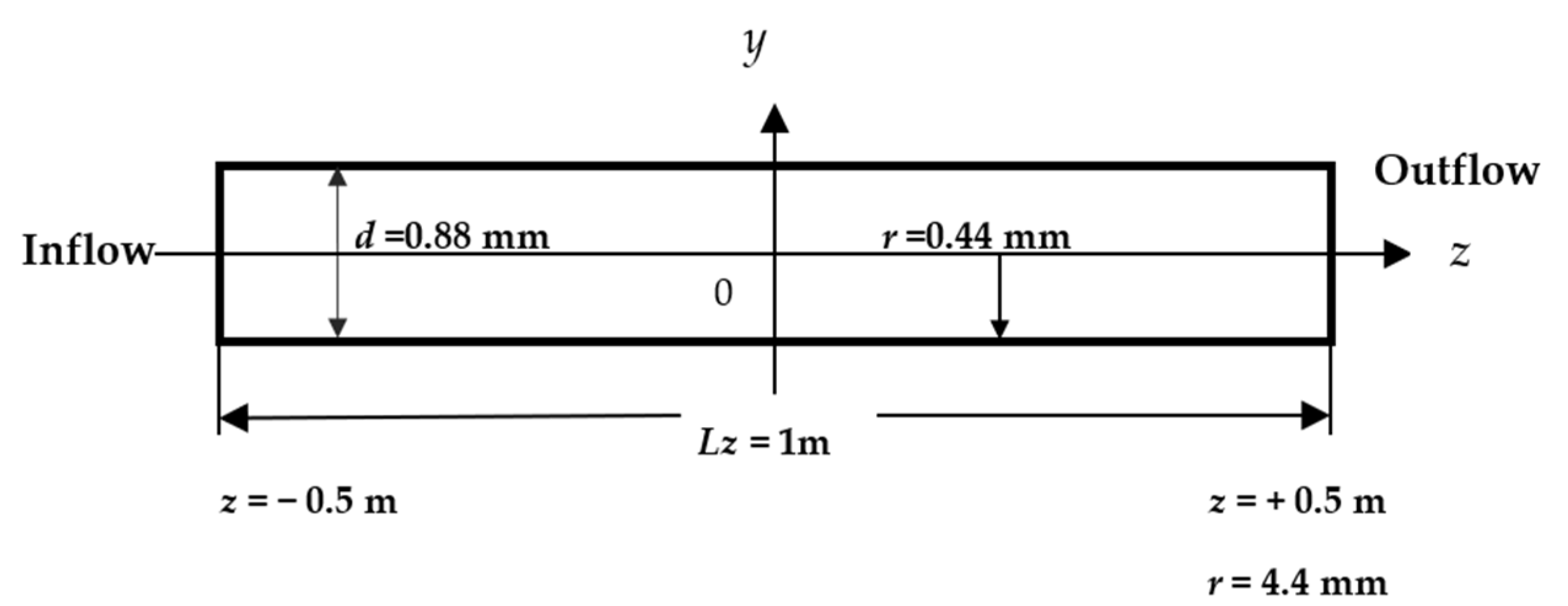
2.2. Problem Definition
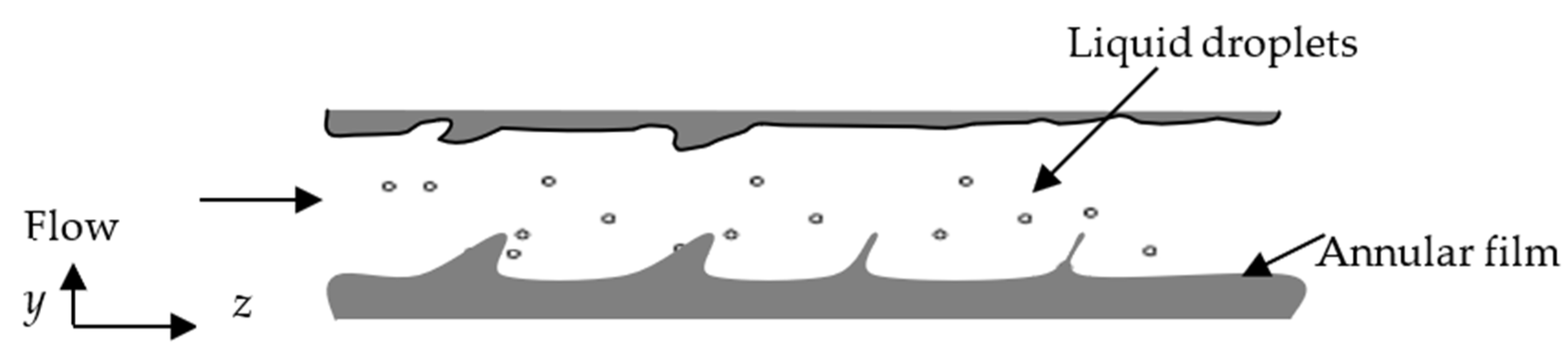
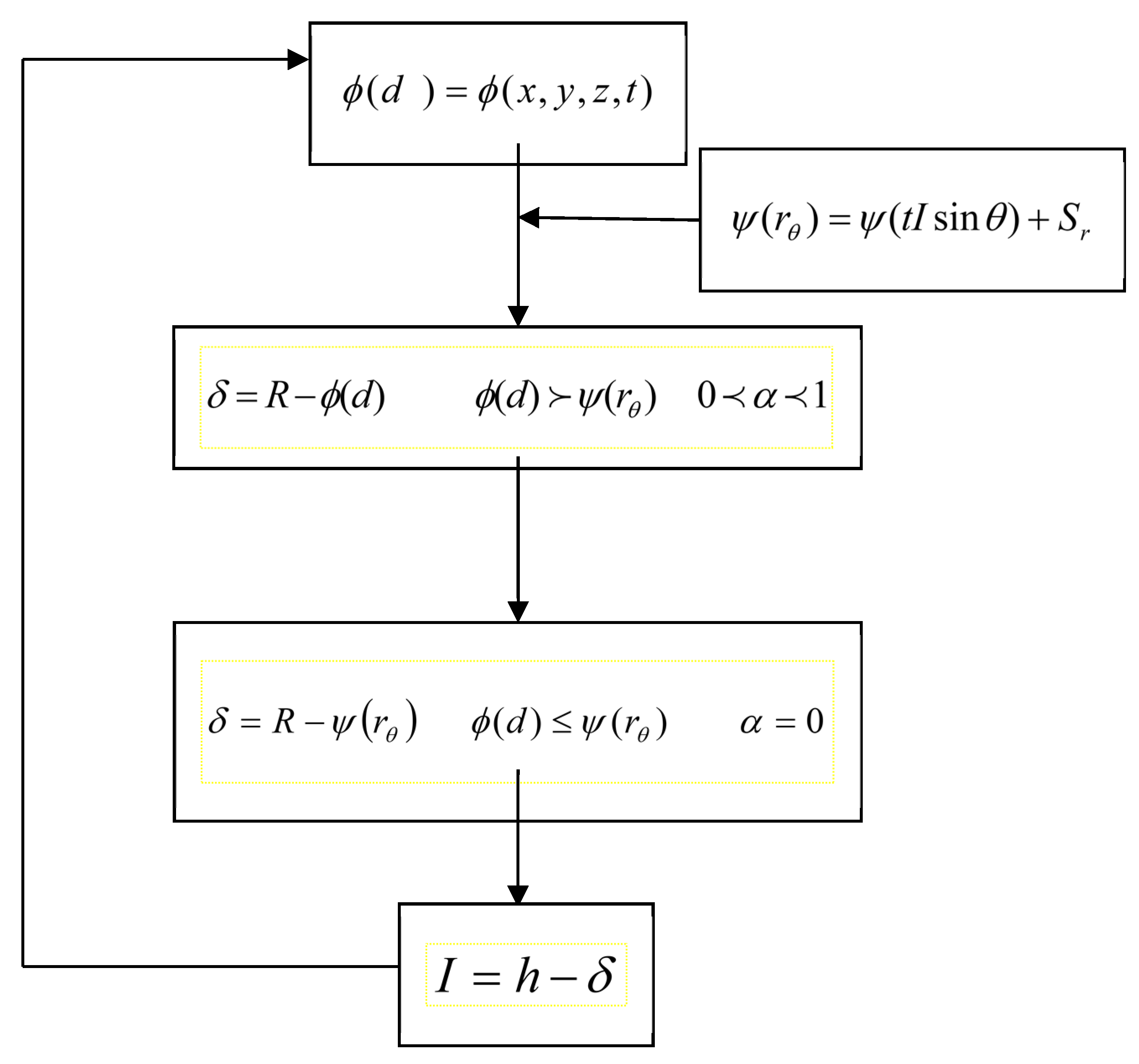
2.3. Mathematical Model for Predicting Liquid Annular Film Distributions
3. Flow Problem and CFD Settings
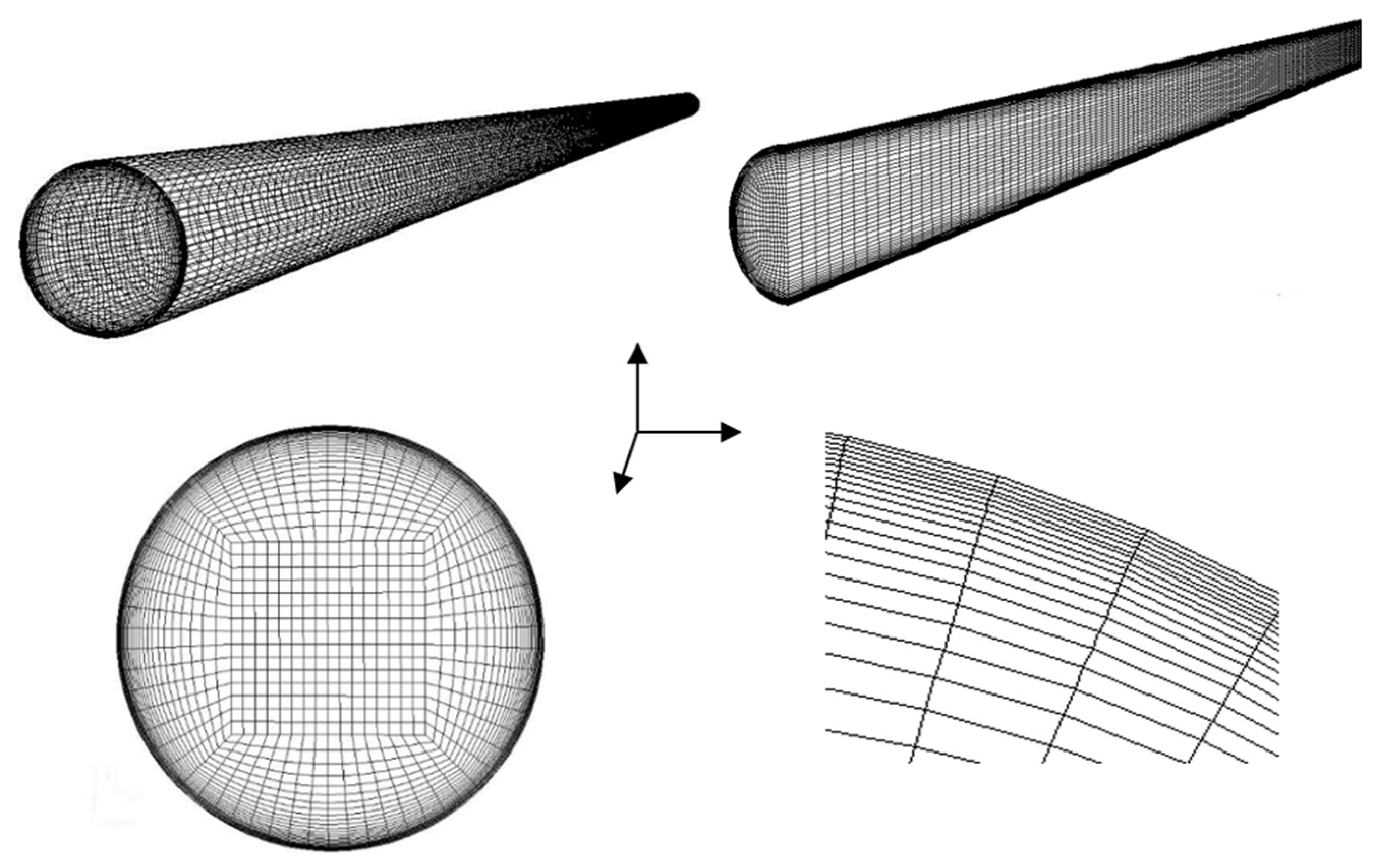
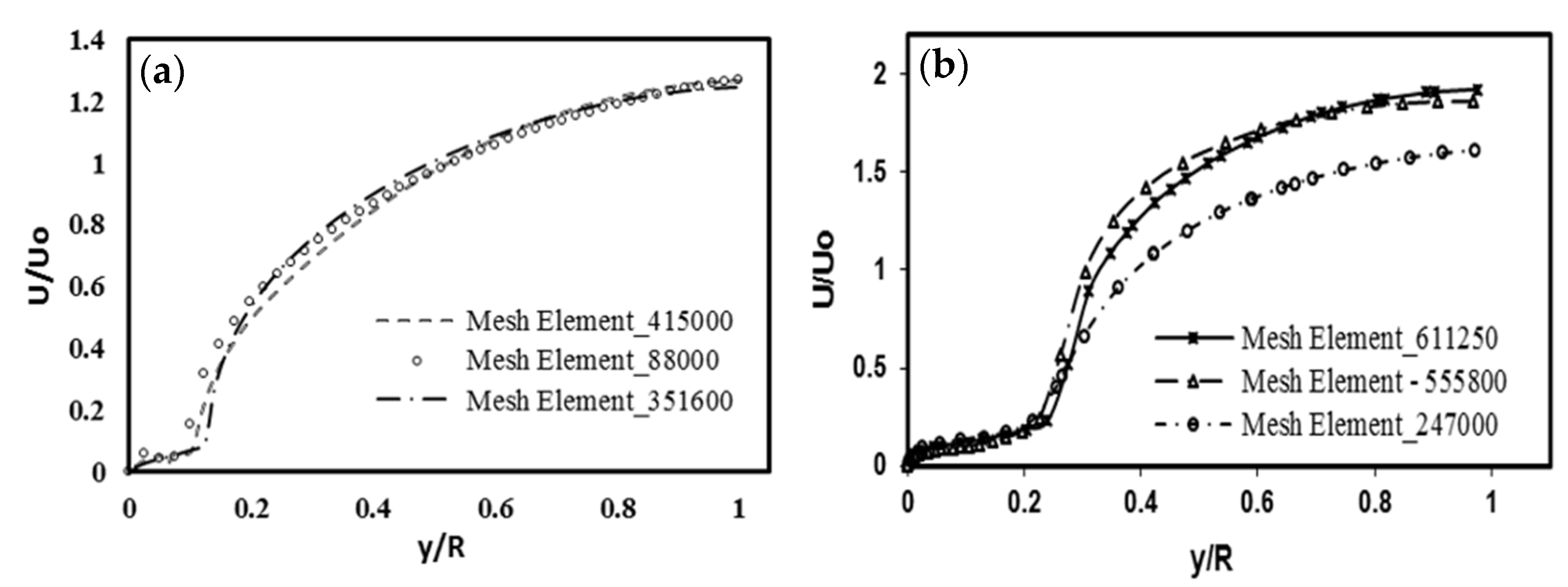
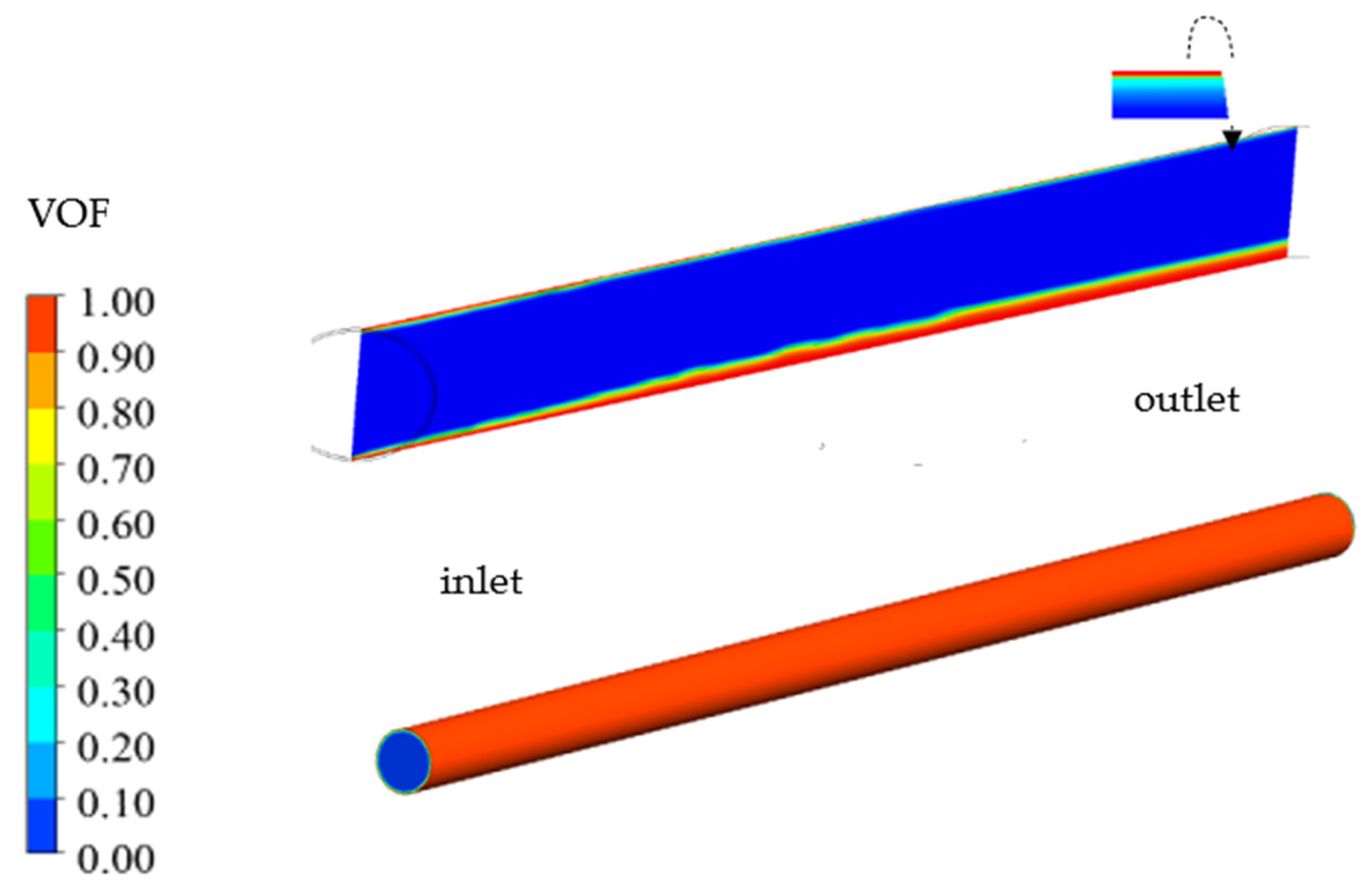
3.1. Computational Domain and Mesh
3.2. Boundary Condition and Simulation Setup
4. Results and Discussion
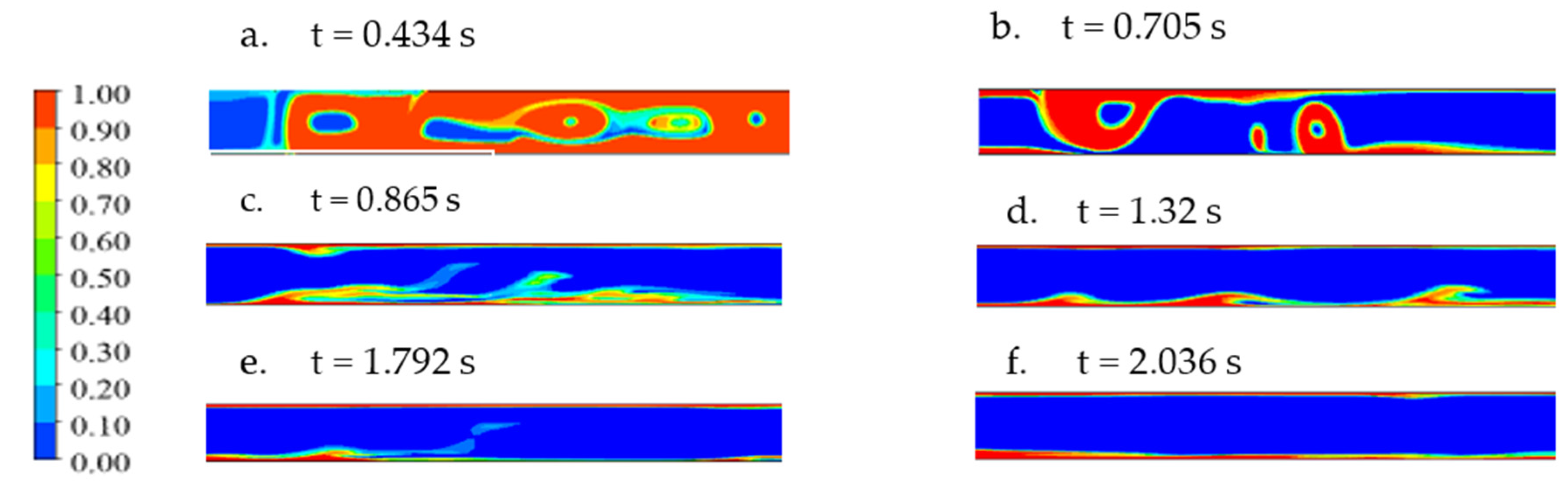
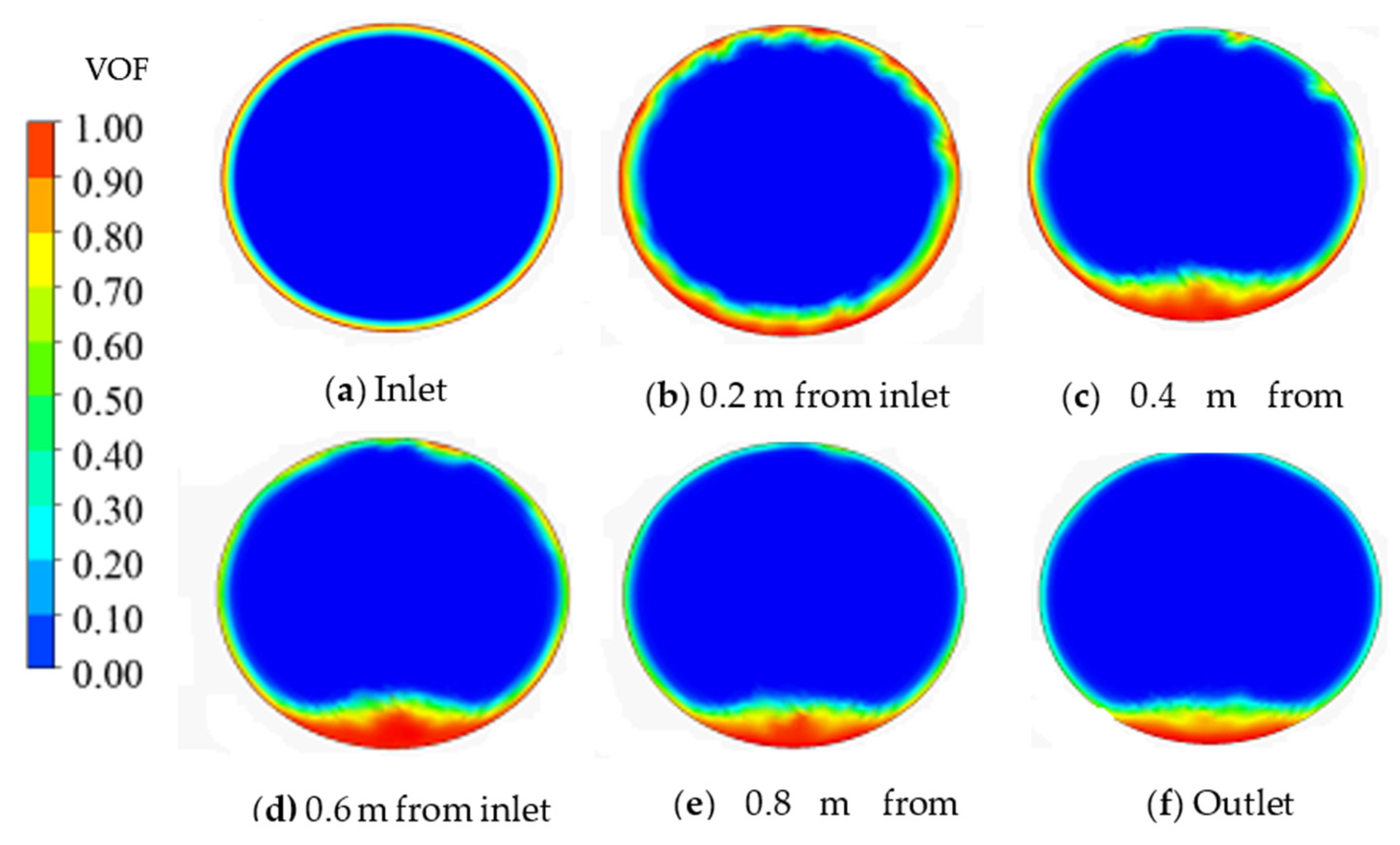
4.1. The Liquid Film Distribution Characterisation
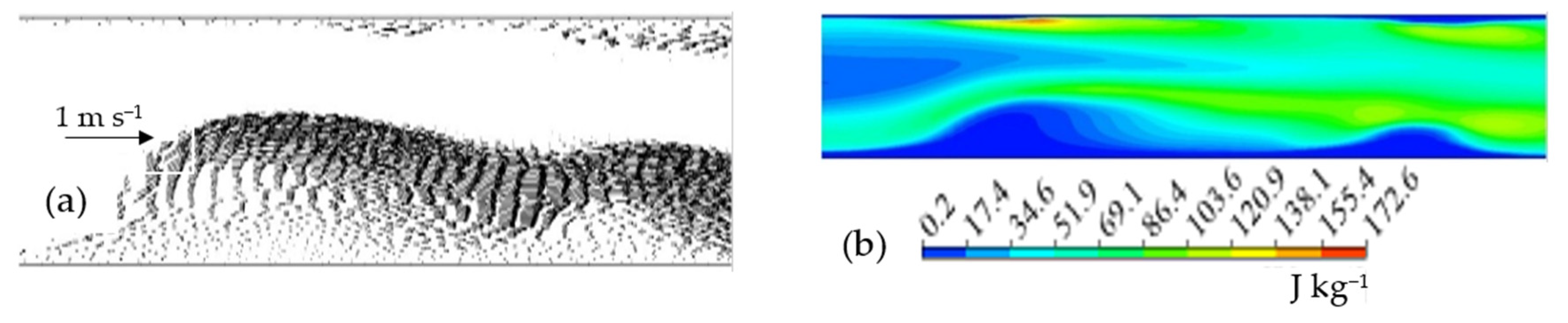
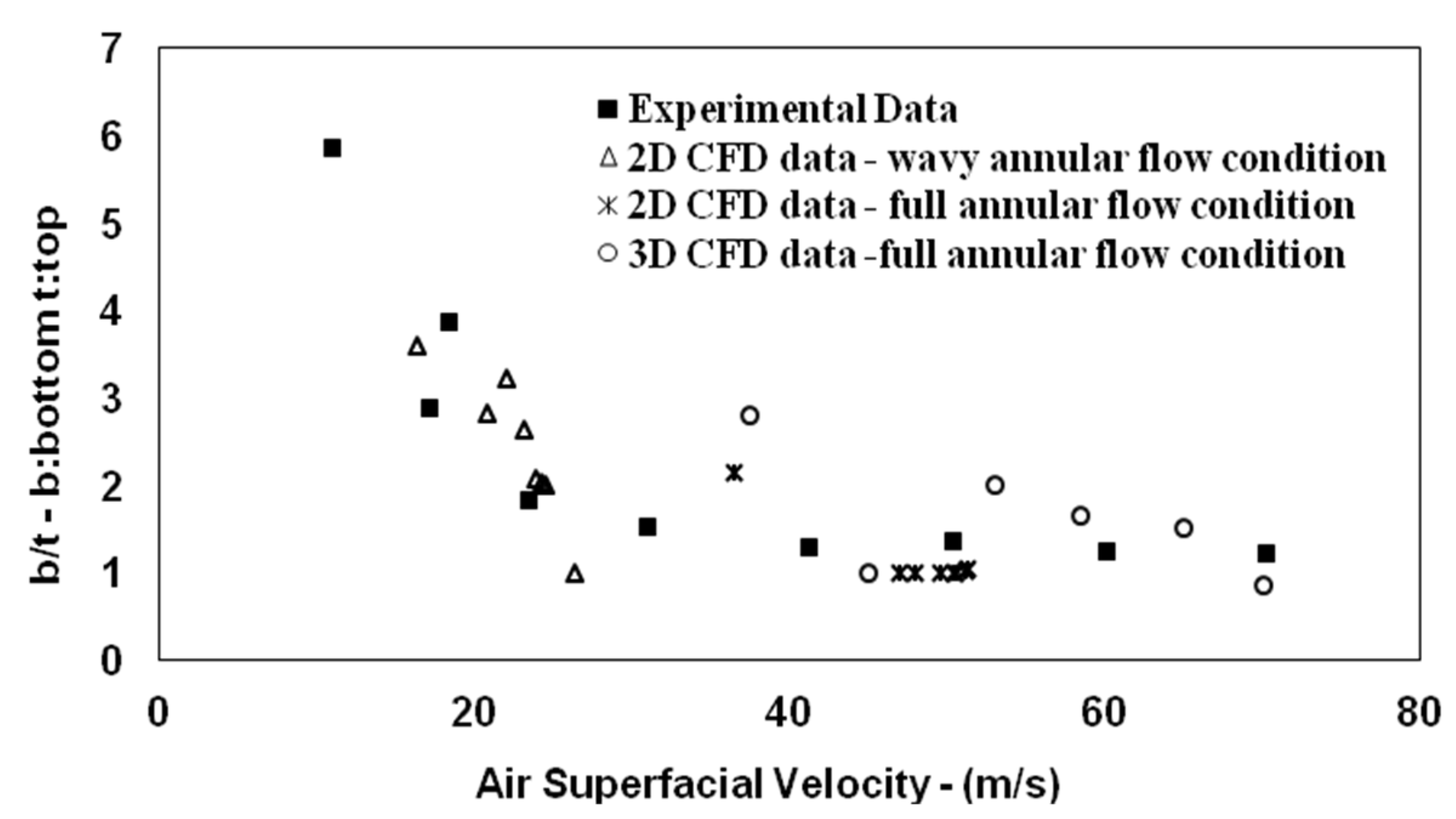
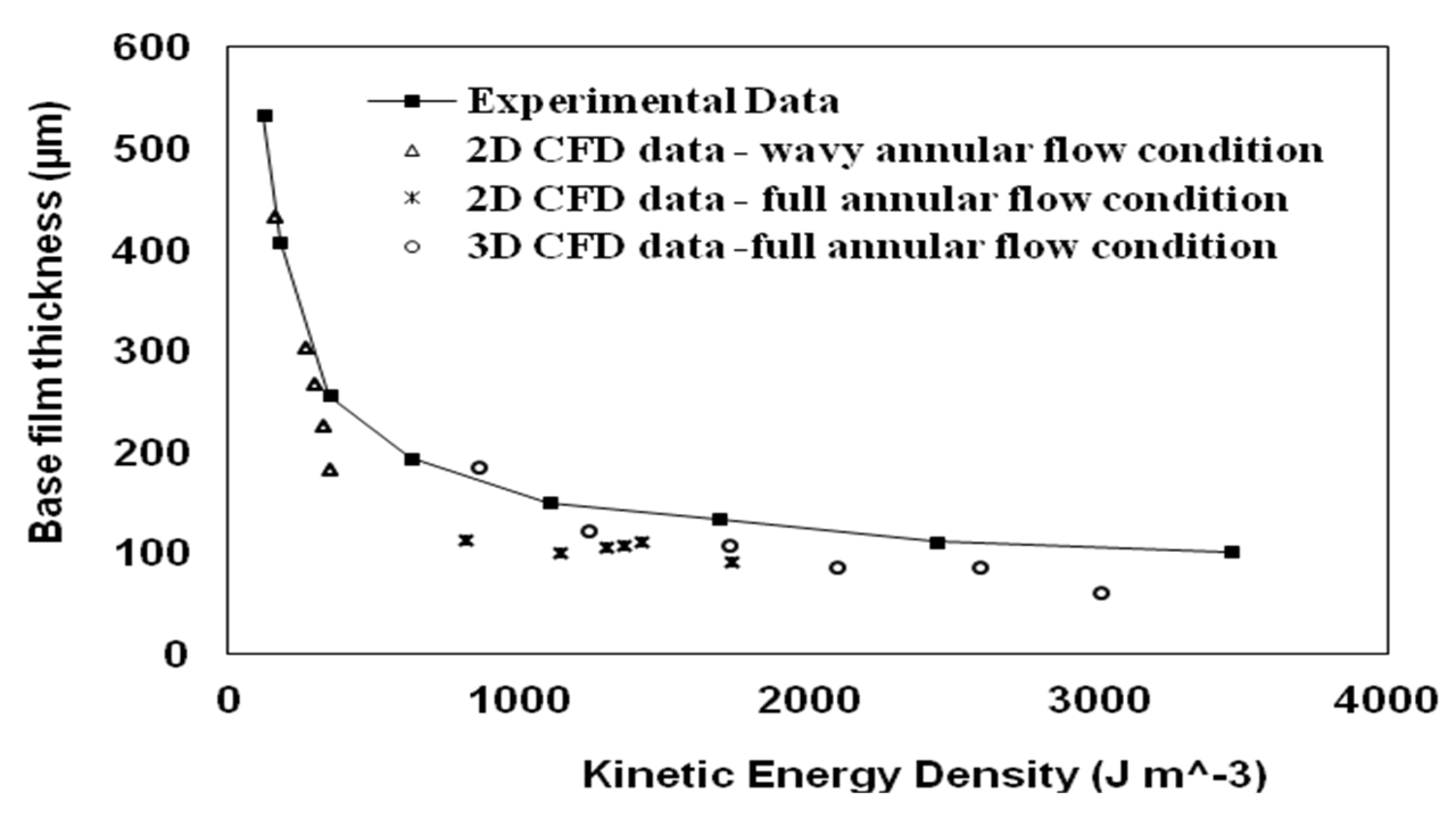
4.2. The Dynamic Performance of Water Film
4.3. Correlations
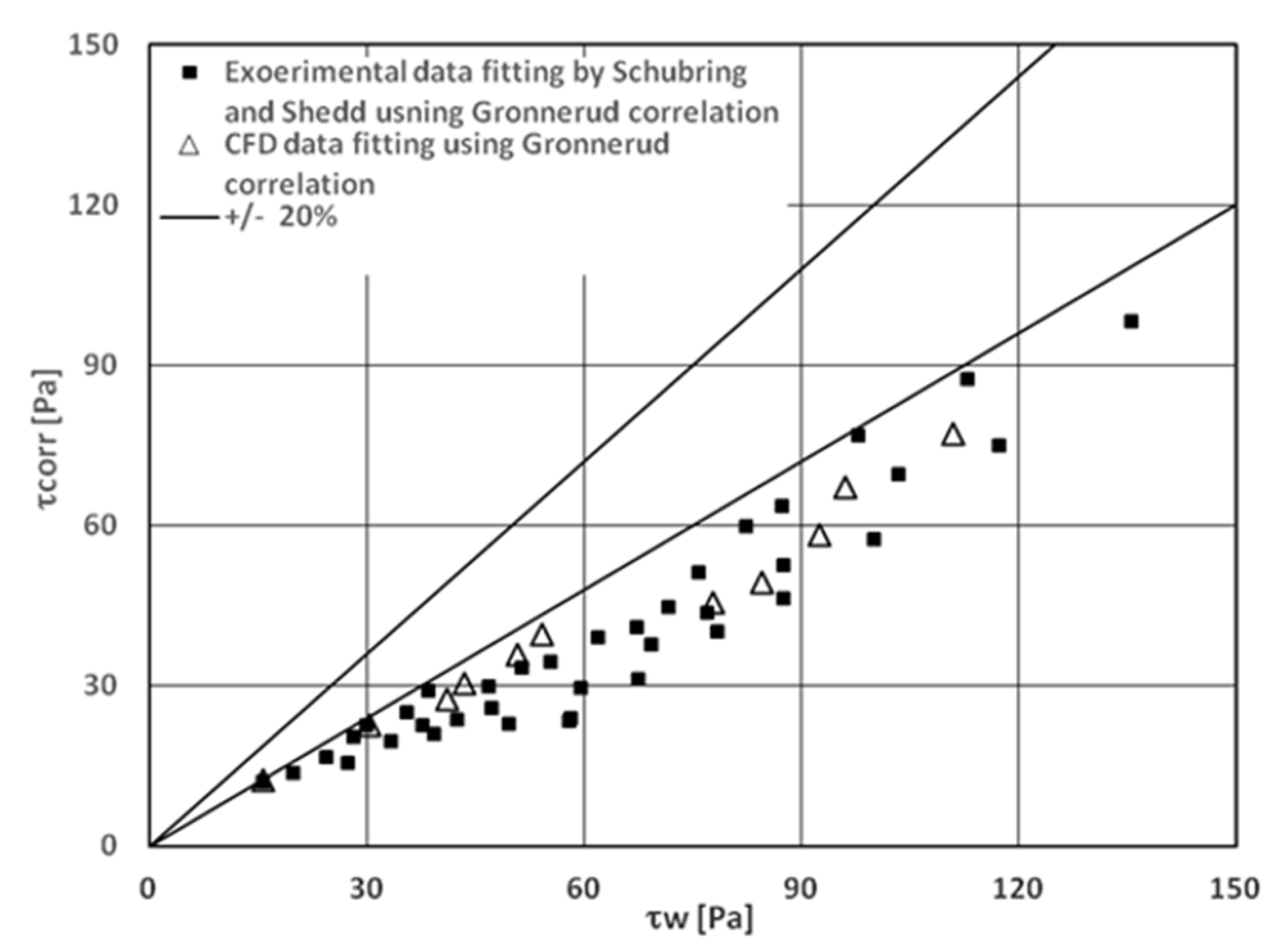
4.3.1. GrÖnnerud Correlation
4.3.2. Chisholm Correlation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Layssac, T.; Capo, C.; Lips, S.; William, A.; Revellin, R. Prediction of symmetry during intermittent and annular horizontal two-phase flows. Int. J. Multiph. Flow 2017, 95, 91–100. [Google Scholar] [CrossRef]
- Bestion, D. The difficult challenge of a two-phase CFD modelling flow all flow. Regimes. Nucl. Eng. Des. 2014, 279, 116–125. [Google Scholar] [CrossRef]
- Pourahmad, S.; Pesteei, S.M.; Ravaeei, H.; Khorasani, S. Experimental study of heat transfer and pressure drop analysis of the air/water two-phase flow in a double tube heat exchanger equipped with dual twusted tape turbulator: Simultanepous usage of active and passive methods. J. Energy Storage 2021, 44, 103408. [Google Scholar] [CrossRef]
- Pletcher, R.H.; McManus, H.N. The fluid dynamics of three dimensional liquid films with free surface shear: A finite difference approach. In Proceedings of the 9th Mid-Western Conference on Mechanics (Developments in Mechanics), Madison, WI, USA, 16–18 August 1965; pp. 305–318. [Google Scholar]
- Laurinat, J.E.; Hanratty, T.J.; Dallman, J.C. Pressure drop and film height measurements for annular gas-liquid flow. Int. J. Multiph. Flow 1984, 10, 341–356. [Google Scholar] [CrossRef]
- Lin, T.F.; Block, R.C.; Jone, Q.C.; Lahey, R.T.; Murase, M. Horizontal annular flow measurements using pulsed photon activation and film thickness distribution modelling. Nucl. Eng. Des. 1986, 95, 353–363. [Google Scholar] [CrossRef]
- Butterworth, D. Air-water annular flow in a horizontal tube. Progs. Heat Mass Transf. 1972, 6, 235–251. [Google Scholar]
- Jayanti, S.; Hewitt, G.F.; White, S.P. Time-dependent behaviour of the liquid film in horizontal annular flow. Int. J. Multiph. Flow 1990, 16, 1097–1116. [Google Scholar] [CrossRef]
- Schubring, D.; Shedd, T.A. Two-phase wavy-annular flow in small tubes. Int. J. Heat Mass Transf. 2009, 52, 1619–1622. [Google Scholar] [CrossRef]
- Schubring, D.; Shedd, T.A. Prediction of wall shear for horizontal annular air-water flow. Int. J. Heat Mass Transf. 2009, 52, 200–209. [Google Scholar] [CrossRef]
- Schubring, D.; Shedd, T.A. Critical fraction factor modelling of horizontal annular base film thickness. Int. J. Multiph. Flow 2009, 35, 389–397. [Google Scholar] [CrossRef]
- Schubring, D.; Shedd, T.A. Wave behaviour in horizontal annular air-water flow. Int. J. Multiph. Flow 2008, 34, 636–646. [Google Scholar] [CrossRef]
- William, L.R.; Dykhno, L.A.; Hanratty, T.J. Droplet Flux distribution and entrainment in horizontal gas-liquid flow. Int. J. Multiph. Flow 1996, 22, 1–18. [Google Scholar] [CrossRef]
- Donniacuo, A.; Charnay, R.; Mauro, A.W.; Revellin, R. Film thickness measurements for annular flow in minichannel: Description of the optical techniques and experimental results. Exp. Them. Fluid Sci. 2015, 69, 73–85. [Google Scholar] [CrossRef]
- O’Neill, L.E.; Mudaear, I. Review of two-phase flow instabilities in macro- and micro-channel system (Review). Int. J. Heat Mass Transf. 2020, 157, 119738. [Google Scholar] [CrossRef]
- Ruspini, L.C.; Marcel, C.P.; Clausse, A. Two-phase flow instabilities: A review. Int. J. Heat Transf. Mass Transf. 2014, 71, 521–548. [Google Scholar] [CrossRef]
- Boure, J.; Mihaila, A. The oscillatory behaviour of heated channel. In Proceedings of the EUROATOM, Symposium of Two-Phase Flow Dynamics, Eindhoven, The Netherlands, 4–9 September 1967; pp. 695–720. [Google Scholar]
- Mayinger, F. Status of thermohydraulic research in nuclear safety and new challenges. In Proceedings of the Eight International Topical Meeting on Nuclear Reactor Thermal-Hydraulics, Kyoto, Japan, 30 September–4 October 1997; pp. 1508–1518. [Google Scholar]
- Ishii, M. Study of Flow Instabilities in Two-Phase Mixtures; ANL-76-23; Argonne National Lab., III: Lemont, IL, USA, 1976. [Google Scholar]
- Lahey, R.; Podowski, M. On the analysis of various instabilities in two-phase flow. Multiph. Sci. Technol. 1989, 4, 183–371. [Google Scholar] [CrossRef]
- Prasad, G.; Pandley, M.; Kalra, M. Review of research on flow instabilities in natural circulation boiling systems. Progr. Nucl. Energy 2007, 49, 429–451. [Google Scholar] [CrossRef]
- Boure, J.; Bergles, A.; Tong, L. Review of two-phase flow instabilities. Nucl. Eng. Des. 1973, 25, 165–192. [Google Scholar] [CrossRef]
- Rouhani, S.Z.; Sohal, M.S. Two-phase flow patterns: A review of research results. Prog. Nucl. Energy 1982, 11, 219–259. [Google Scholar] [CrossRef]
- Dobson, M.K.; Chato, J.C.; Wattelet, J.P.; Gaibel, J.A.; Ponchner, M.; Kenney, P.J.; Shimon, R.L.; Villaneuva, T.C.; Rhines, N.L.; Sweeney, K.A.; et al. Heat Transfer and Flow Regimes during Condensation in Horizontal Tubes; ACRC Technical Report 57; University of Illinois at Urbana-Champaign: Urbana, IL, USA, 1994. [Google Scholar]
- Thome, J. Engineering Data Book III; Wolverine Tube Inc.: Huntsville, AL, USA, 2004. [Google Scholar]
- Monni, G.; Salve, M.; De Panella, C. Horizontal two-phase flow pattern recognition. Exp. Therm. Fluid Sci. 2014, 59, 213–221. [Google Scholar] [CrossRef][Green Version]
- Li, H.; Anglart, H. Modelling of annular two-phase flow using a unified CFD approach. Nucl. Eng. Des. 2016, 303, 17–24. [Google Scholar] [CrossRef]
- Li, H.; Anglart, H. CFD model of adiabatic annular two-phase flow using the Eulerian—Lagrangian approach. Annals. Nucl. Energy 2015, 77, 415–424. [Google Scholar] [CrossRef]
- Bai, C.; Gosman, A.D. Mathematical modelling of wall films formed by impinging spray. SAE Tech. Pap. 1996, 105, 782–796. [Google Scholar]
- Adechy, D.; Issa, R.I. Modelling of annular flow through pipes and T-junctions. Comput. Fluids 2004, 33, 289–313. [Google Scholar] [CrossRef]
- Meredith, K.; Xin, Y.; De Vires, J. A numerical model for simulation of thin-film water transport over solid fuel surface. Fire Saf. Sci. 2011, 10, 415–428. [Google Scholar] [CrossRef]
- Ishii, M.; Hibiki, T. Thermo-Fluid Dynamics of Two-Phase Flow; Springer: New York, NY, USA, 2011. [Google Scholar]
- Caraghiaur, D.; Anglart, H. Drop deposition in annular two-phase flow calculated with Lagrangian Particle Tracking. Nucl. Eng. Des. 2013, 265, 856–866. [Google Scholar] [CrossRef]
- Westende van’t, J.M.C.; Belt, R.J.; Portela, L.M.; Mudde, R.F.; Oliemans, R.V.A. Effect of secondary flow on droplet distribution and deposition in horizontal annular pipe flow. Int. J. Multiph. Flow 2007, 33, 67–85. [Google Scholar] [CrossRef]
- Grönnerud, R. Investigation of liquid hold-up, flow-resistance and heat transfer in circulation type evaporators. Part IV: Two-Phase Flow Resistance in Boiling Refrigerants. In Proceedings of the IIR Conference “Heat and Mass Transfer in Refrigeration System and in Air Conditioning”, Freudenstadt, Germany, January 1972; pp. 127–138. [Google Scholar]
- Chisholm, D. Pressure gradients due to friction during the flow of evaporating two phase mixtures in smooth tubes and channels. Int. J. Heat Mass Transf. 1973, 16, 47–58. [Google Scholar] [CrossRef]
- ANSYS FLUENT Theory Guide v18; ANSYS, Inc.: Canonsburg, PA, USA, 2011.
- Anderson, T.B.; Jackson, R. A fluid mechanical description of fluidized beds. Ind. Eng. Chem. Fundam. 1967, 6, 527–534. [Google Scholar] [CrossRef]
- Bowen, R.M. Theory of Mixture, in Continuum Physics; Eringen, A.C., Ed.; Academic Press: New York, NY, USA, 1976; pp. 1–127. [Google Scholar]
- Schiller, L.; Naumann, Z. A drag coefficient Correlation. VDI Zeitung Zeitschrift des Vereins Deutscher Ingenieure 1935, 77, 318–320. [Google Scholar]
- Choudhury, D. Introduction to the Renormalization Group Method and Turbulence Modeling; Technical Memorandum TM-107; Fluent Inc.: Lebanon, NH, USA, 1993. [Google Scholar]
- Orszag, S.A.; Yakhot, V.; Flannery, W.S.; Boysan, F.; Choudhury, D.; Maruzewski, J.; Patel, B. Renormalization Group Modeling and Turbulence Simulations. In Proceedings of the International Conference on Near-Wall Turbulent Flows, Tempe, AZ, USA, 15–17 March 1993. [Google Scholar]
- Collier, J.G.; Thome, J.R. Convective Boiling and Condensation, 3rd ed.; Oxford Science Publications; Clarendon Press: Oxford, UK, 2002. [Google Scholar]
- Yao, J.; Yao, Y.F.; Arini, A.; Gordon, T. Modelling air and water two-phase annular flow in small horizontal pipe. Int. J. Mod. Phys. Conf. Ser. 2016, 42, 1660158–1660161. [Google Scholar] [CrossRef]
- Mandhane, J.M.; Gregory, G.A.; Aziz, K. A flow pattern map for gas–liquid flow in horizontal pipes. Int. J. Multiph. Flow 1974, 1, 537–553. [Google Scholar] [CrossRef]
- Ishii, M.; Grolmes, M.A. Inception criteria for droplet entrainment in two-phase concurrent film flow. AIChE J. 1975, 21, 308–318. [Google Scholar] [CrossRef]
- Flores, A.G.; Crowe, K.E.; Griffith, P. Gas-phase secondary flow in horizontal, stratified and annular two-phase flow. Int. J. Multiph. Flow 1995, 21, 207–221. [Google Scholar] [CrossRef]
- Berna, C.; Escrivá, A.; Muñoz-Cobo, J.L.; Herranz, L.E. Review of droplet entrainment in annular flow, Interfacial waves and onset of entrainment. Prog. Nucl. Energy 2014, 74, 14–43. [Google Scholar] [CrossRef]
- Muzaferija, S.; Peric, M.; Sames, P.; Schellin, T. A Two-Fluid Navier-Stokes Solver to Simulate Water Entry. In Proceedings of the 22nd Symposium on Naval Hydrodynamics, Washington, DC, USA, 9–14 August 1989; pp. 277–289. [Google Scholar]
- Barth, T.J.; Jespersen, D. The design and application of upwind schemes on unstructured meshes. In Proceedings of the AIAA 27th Aerospace Sciences Meeting, Technical Report AIAA-89-0366, Reno, NV, USA, 9–12 January 1989. [Google Scholar]
- Styrikovich, M.A.; Shitsman, M.E.; Miropolski, Z.I. Certain Data on the temperature region of vertical boiler pipes at near critical pressures. Teploenergetka 1956, 3, 32. [Google Scholar]
- Abdulkadir, M.; Zhao, D.; Azzi, A.; Lowndes, I.S.; Azzopardi, B.J. Two-phase air-water flow through a large diameter vertical 180o return bend. Chem. Eng. Sci. 2012, 79, 138–152. [Google Scholar] [CrossRef]
- Ould, M.B.; Kattan, N.; Thome, J.R. Prediction of two-phase pressure gradients of refrigerants inside horizontal tubes. Int. J. Refrig. 2002, 25, 935–947. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, J.; Yao, Y. Transient CFD Modelling of Air–Water Two-Phase Annular Flow Characteristics in a Small Horizontal Circular Pipe. Fluids 2022, 7, 191. https://doi.org/10.3390/fluids7060191
Yao J, Yao Y. Transient CFD Modelling of Air–Water Two-Phase Annular Flow Characteristics in a Small Horizontal Circular Pipe. Fluids. 2022; 7(6):191. https://doi.org/10.3390/fluids7060191
Chicago/Turabian StyleYao, Jun, and Yufeng Yao. 2022. "Transient CFD Modelling of Air–Water Two-Phase Annular Flow Characteristics in a Small Horizontal Circular Pipe" Fluids 7, no. 6: 191. https://doi.org/10.3390/fluids7060191
APA StyleYao, J., & Yao, Y. (2022). Transient CFD Modelling of Air–Water Two-Phase Annular Flow Characteristics in a Small Horizontal Circular Pipe. Fluids, 7(6), 191. https://doi.org/10.3390/fluids7060191





