Three-Phase-Lag Bio-Heat Transfer Model of Cardiac Ablation
Abstract
:1. Introduction
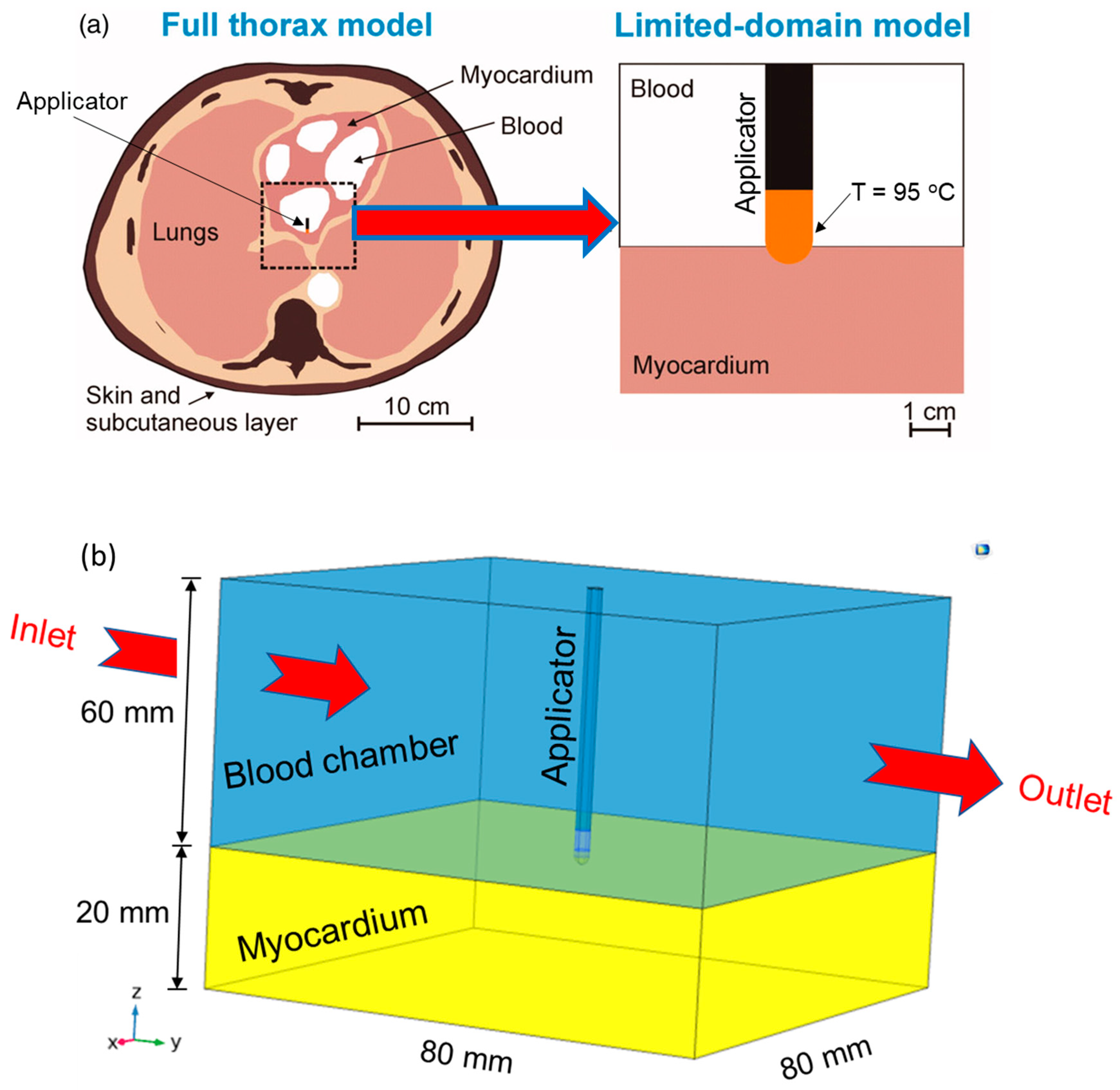
2. Materials and Methods
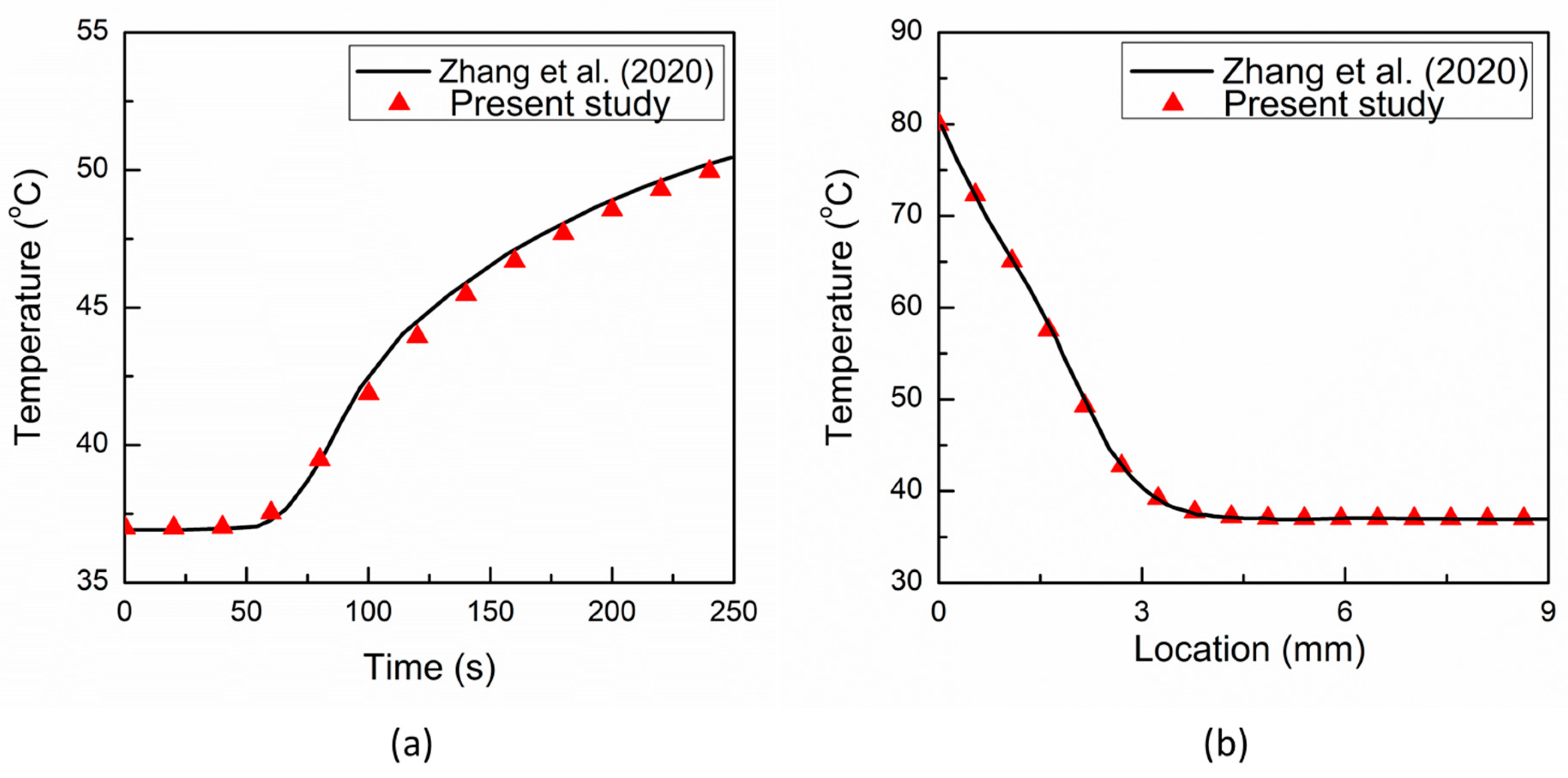
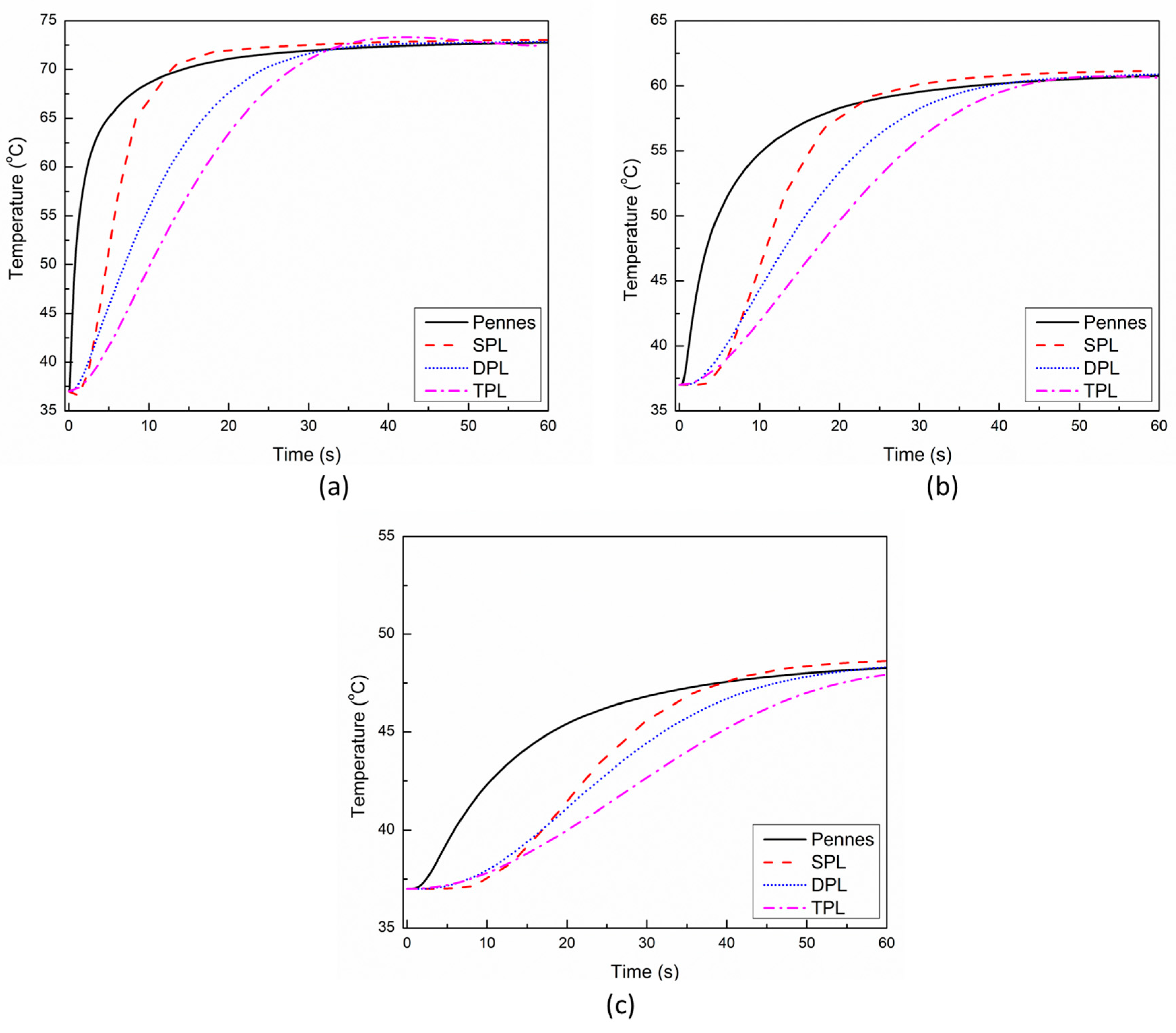
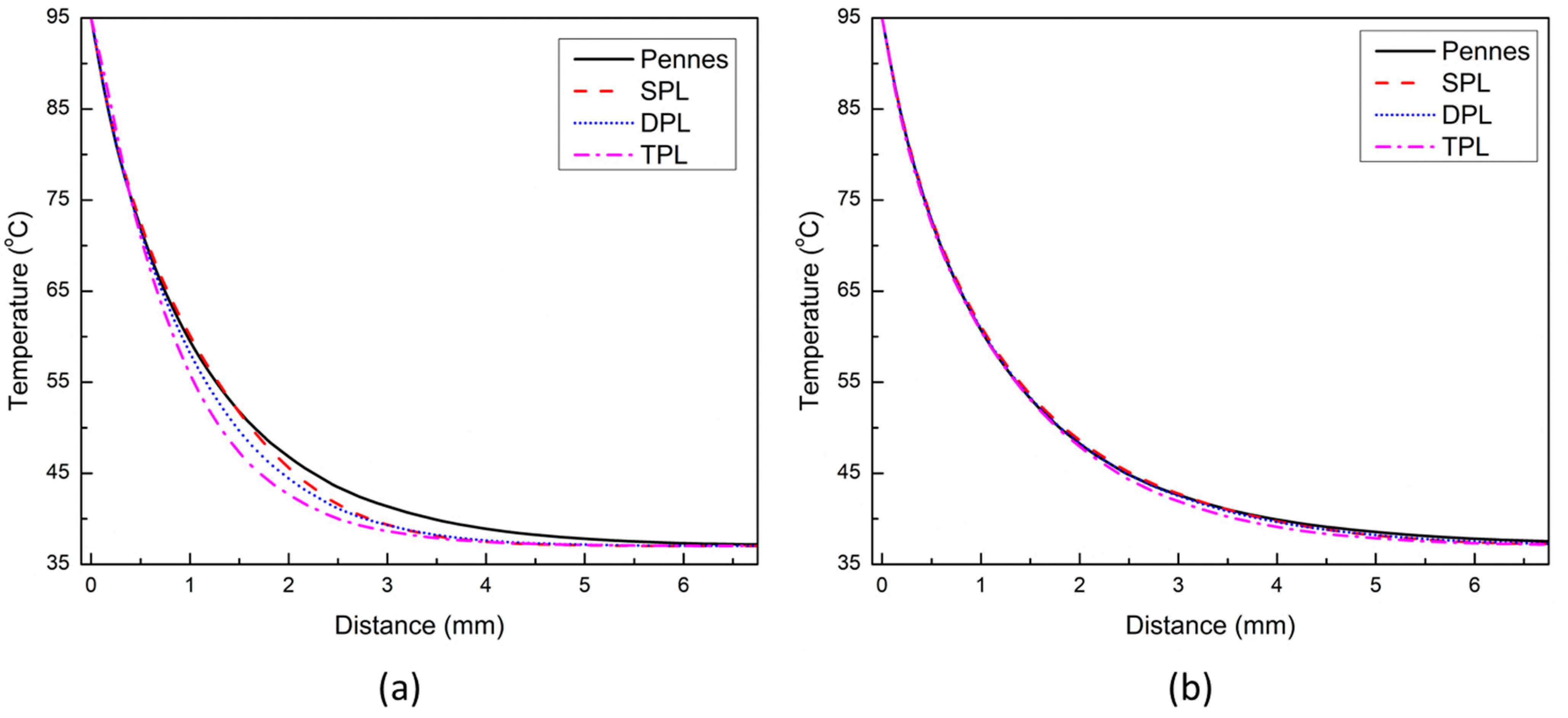
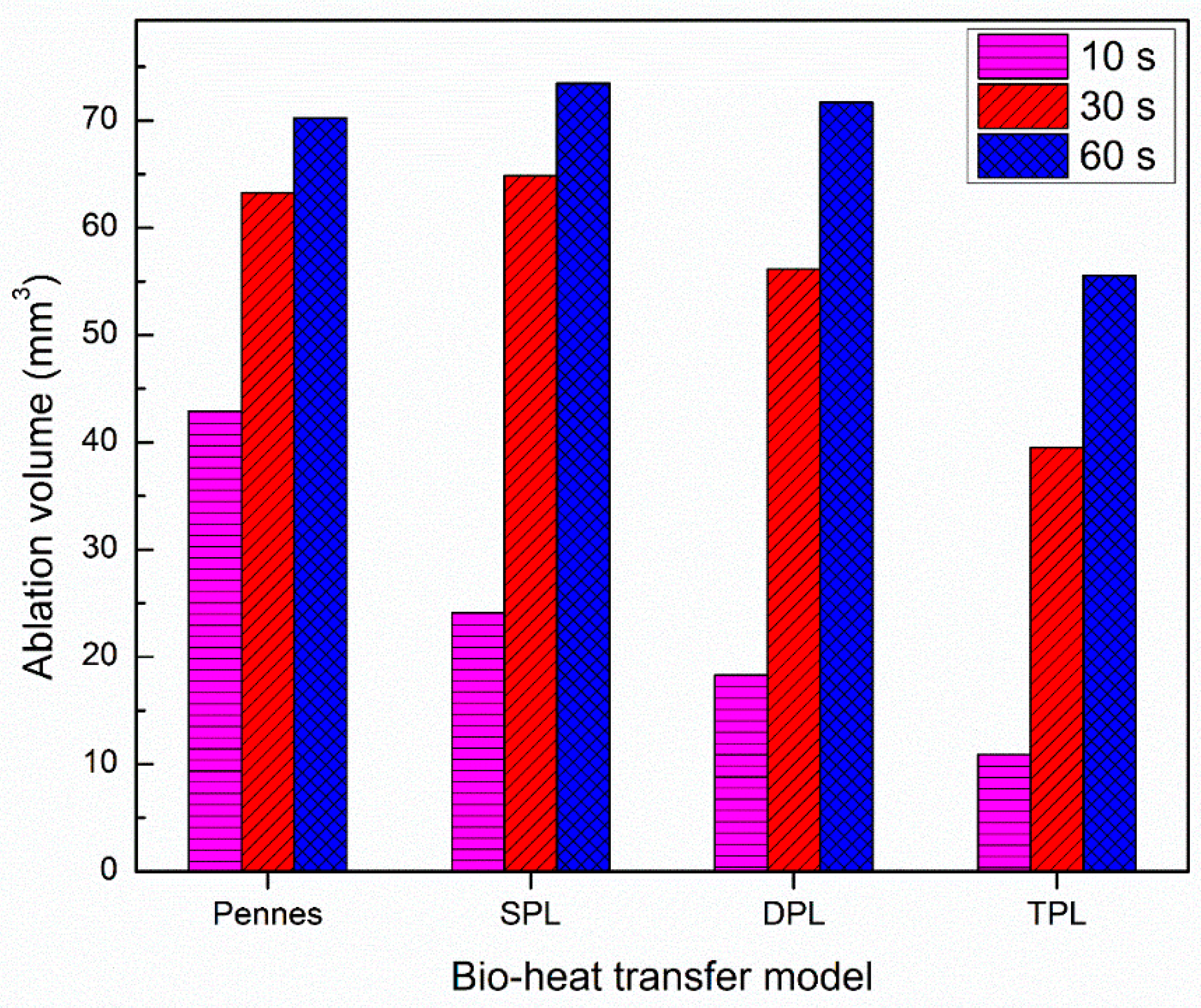
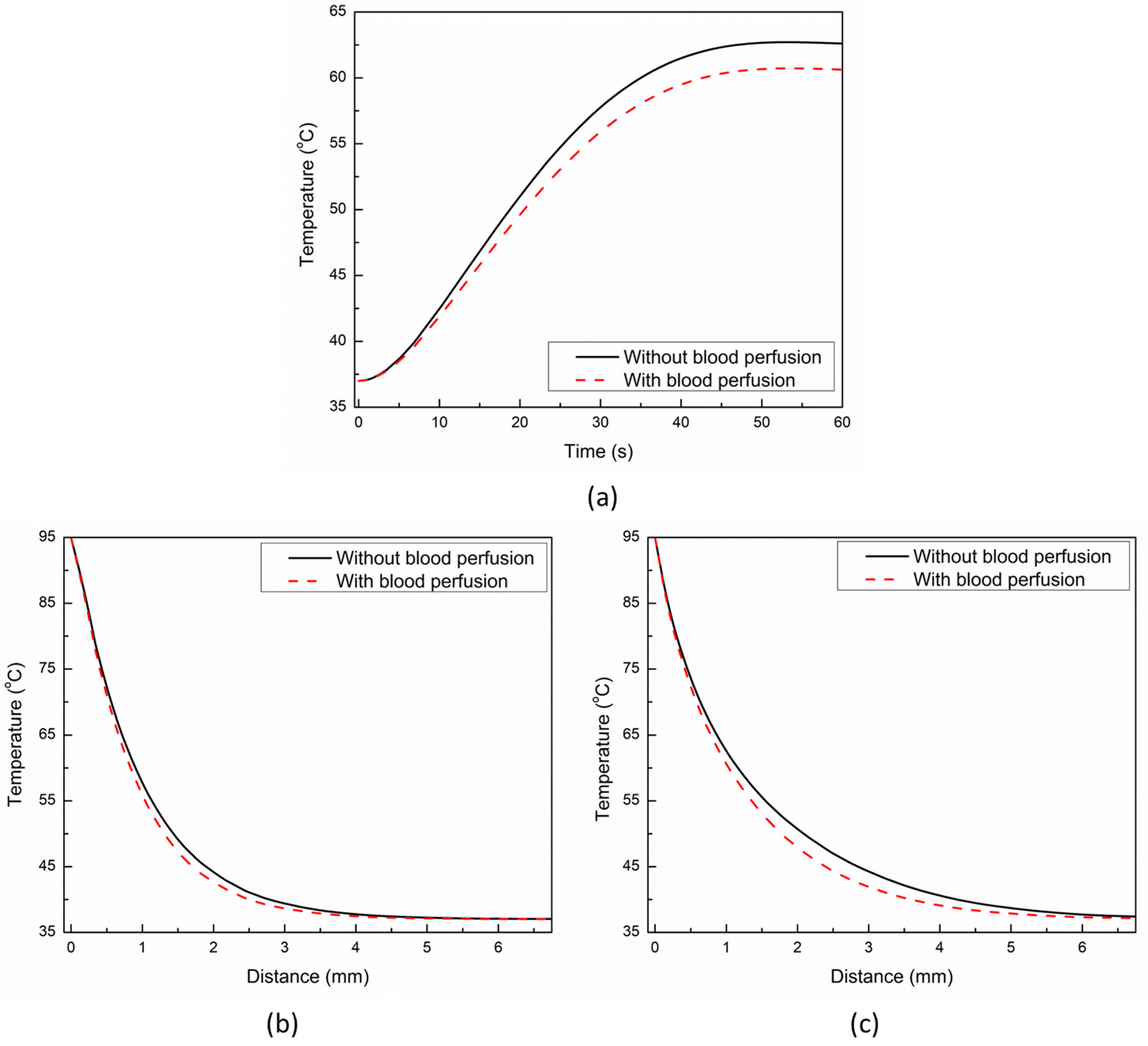
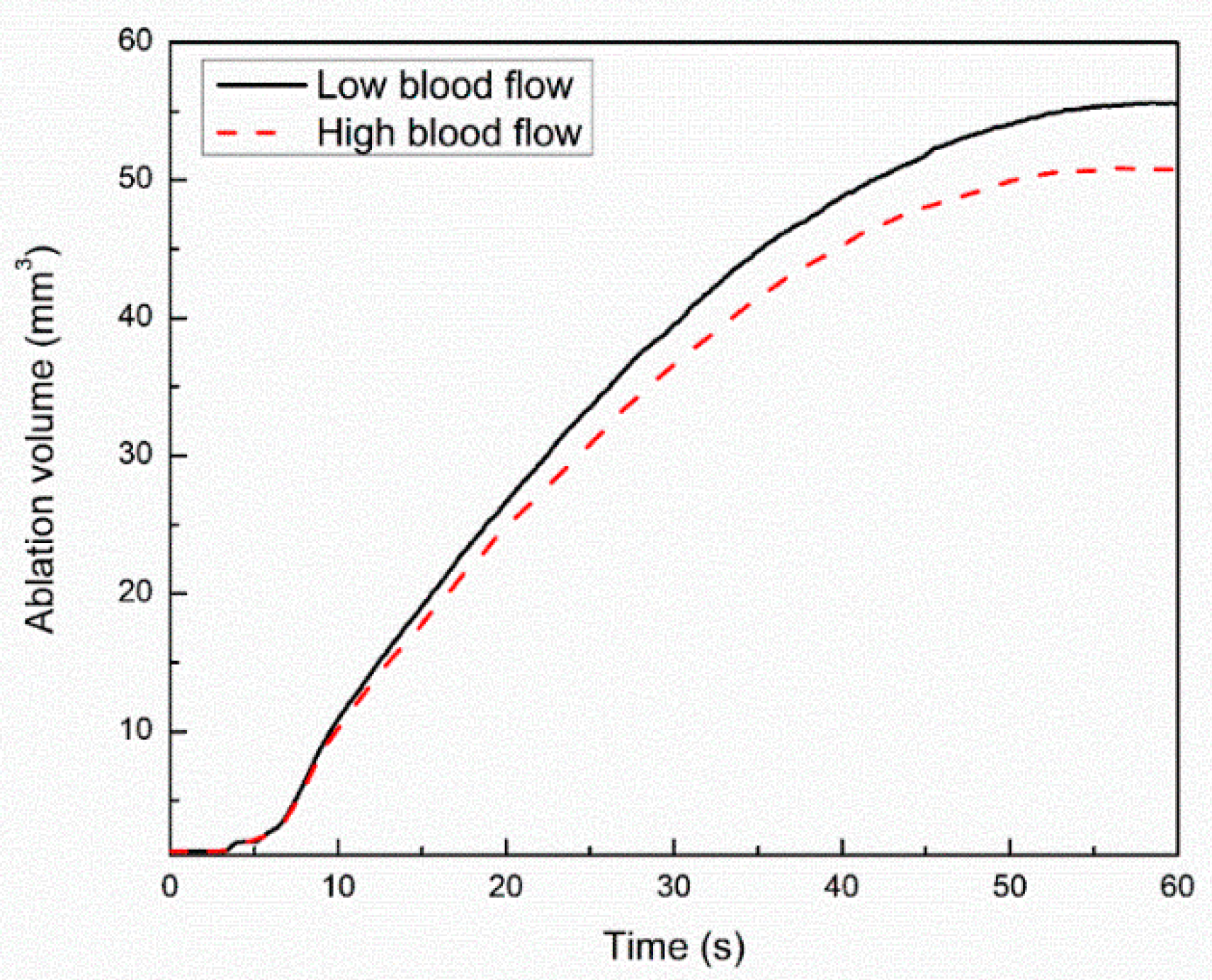
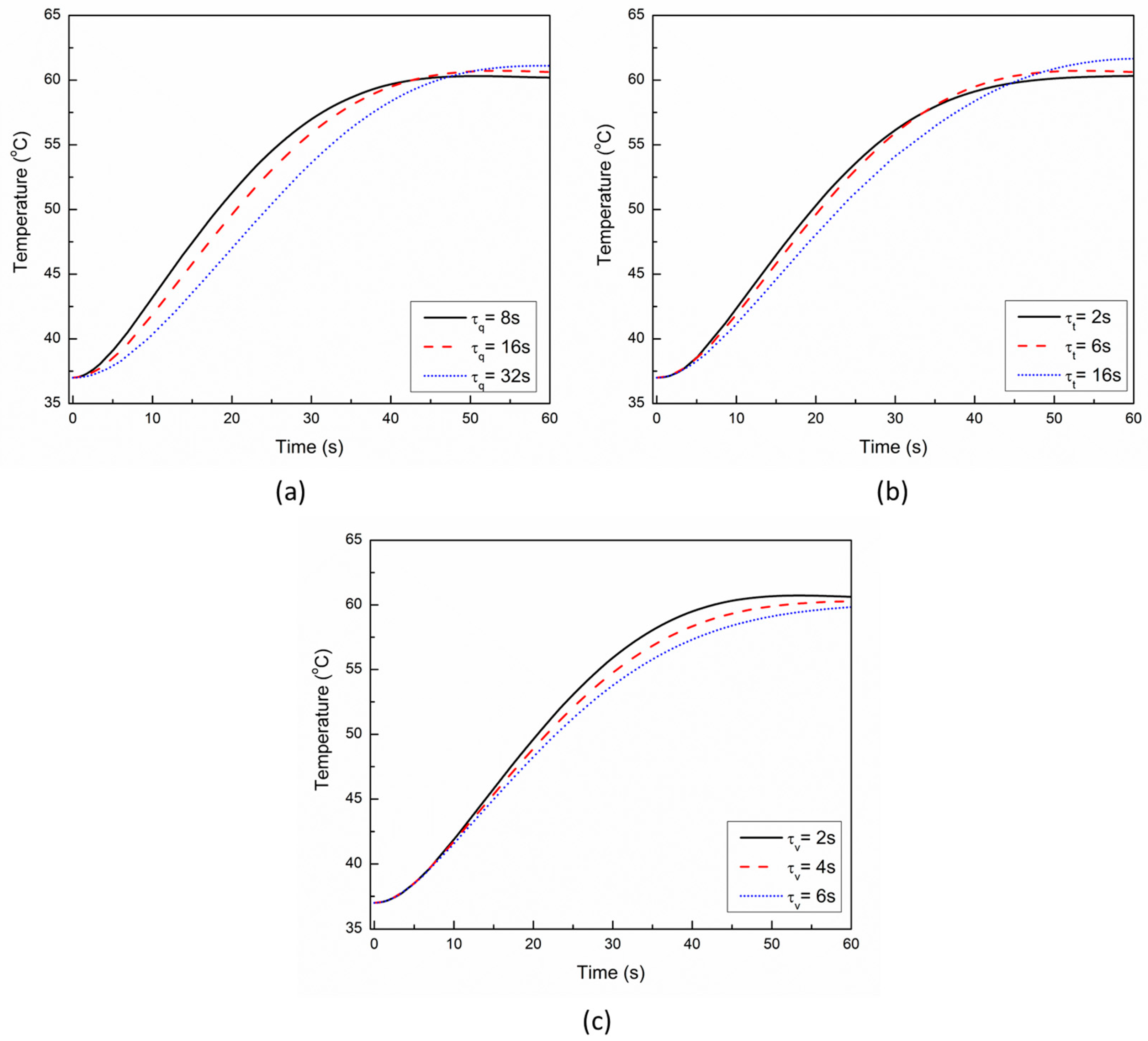
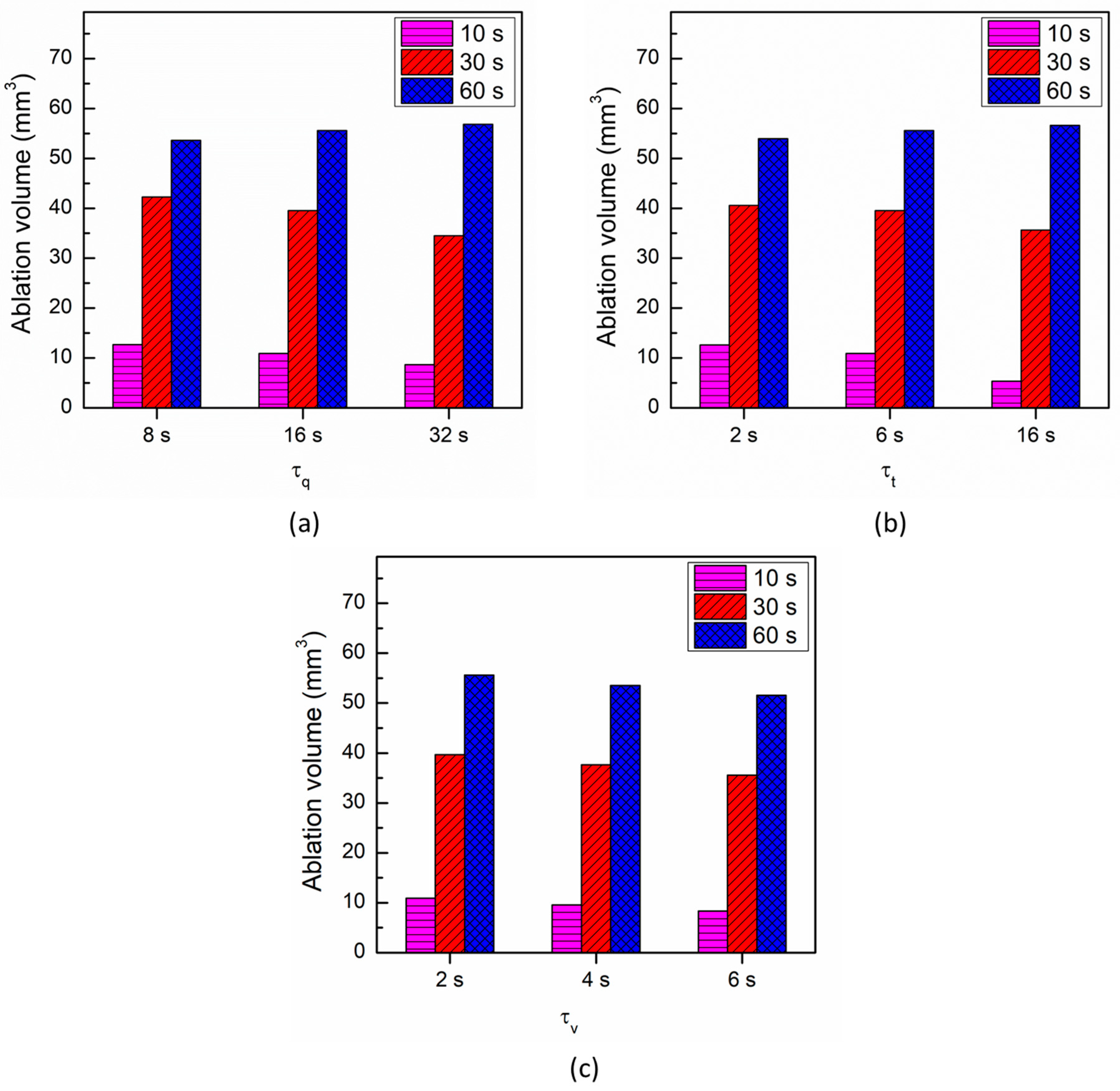
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Almekkawy, M.; Chen, J.; Ellis, M.D.; Haemmerich, D.; Holmes, D.R.; Linte, C.A.; Panescu, D.; Pearce, J.; Prakash, P.; Zderic, V. Therapeutic systems and technologies: State-of-the-art applications, opportunities, and challenges. IEEE Rev. Biomed. Eng. 2019, 13, 325–339. [Google Scholar] [CrossRef]
- Chu, K.F.; Dupuy, D.E. Thermal ablation of tumours: Biological mechanisms and advances in therapy. Nat. Rev. Cancer 2014, 14, 199–208. [Google Scholar] [CrossRef]
- Kok, H.P.; Cressman, E.N.; Ceelen, W.; Brace, C.L.; Ivkov, R.; Grüll, H.; Ter Haar, G.; Wust, P.; Crezee, J. Heating technology for malignant tumors: A review. Int. J. Hyperth. 2020, 37, 711–741. [Google Scholar] [CrossRef]
- Huang, S.K.S.; Miller, J.M. Catheter Ablation of Cardiac Arrhythmias; Elsevier: Philadelphia, PA, USA, 2020. [Google Scholar]
- Prakash, P.; Srimathveeravalli, G. Principles and Technologies for Electromagnetic Energy Based Therapies; Academic Press: Cambridge, MA, USA, 2021. [Google Scholar]
- Haemmerich, D.; Laeseke, P. Thermal tumour ablation: Devices, clinical applications and future directions. Int. J. Hyperth. 2005, 21, 755–760. [Google Scholar] [CrossRef]
- Andreozzi, A.; Brunese, L.; Iasiello, M.; Tucci, C.; Vanoli, G.P. Modeling heat transfer in tumors: A review of thermal therapies. Ann. Biomed. Eng. 2019, 47, 676–693. [Google Scholar] [CrossRef]
- Bianchi, L.; Cavarzan, F.; Ciampitti, L.; Cremonesi, M.; Grilli, F.; Saccomandi, P. Thermophysical and mechanical properties of biological tissues as a function of temperature: A systematic literature review. Int. J. Hyperth. 2022, 39, 297–340. [Google Scholar] [CrossRef]
- Singh, S.; Melnik, R. Thermal ablation of biological tissues in disease treatment: A review of computational models and future directions. Electromagn. Biol. Med. 2020, 39, 49–88. [Google Scholar] [CrossRef]
- González-Suárez, A.; Pérez, J.J.; Irastorza, R.M.; D’Avila, A.; Berjano, E. Computer modeling of radiofrequency cardiac ablation: 30 years of bioengineering research. Comput. Methods Programs Biomed. 2021, 214, 106546. [Google Scholar] [CrossRef]
- Mohammadi, A.; Bianchi, L.; Korganbayev, S.; De Landro, M.; Saccomandi, P. Thermomechanical Modeling of Laser Ablation Therapy of Tumors: Sensitivity Analysis and Optimization of Influential Variables. IEEE Trans. Biomed. Eng. 2021, 69, 302–313. [Google Scholar] [CrossRef]
- Pennes, H.H. Analysis of tissue and arterial blood temperatures in the resting human forearm. J. Appl. Physiol. 1948, 1, 93–122. [Google Scholar] [CrossRef]
- Maillet, D. A review of the models using the Cattaneo and Vernotte hyperbolic heat equation and their experimental validation. Int. J. Therm. Sci. 2019, 139, 424–432. [Google Scholar] [CrossRef]
- Mitra, K.; Kumar, S.; Vedevarz, A.; Moallemi, M. Experimental evidence of hyperbolic heat conduction in processed meat. J. Heat Transf. 1995, 117, 568–573. [Google Scholar] [CrossRef]
- Cattaneo, C. A form of heat-conduction equations which eliminates the paradox of instantaneous propagation. Comptes Rendus 1958, 247, 431. [Google Scholar]
- Vernotte, P. Les paradoxes de la theorie continue de l’equation de la chaleur. Comptes Rendus 1958, 246, 3154–3155. [Google Scholar]
- Tzou, D.Y. The generalized lagging response in small-scale and high-rate heating. Int. J. Heat Mass Transf. 1995, 38, 3231–3240. [Google Scholar] [CrossRef]
- Singh, S.; Melnik, R. Coupled thermo-electro-mechanical models for thermal ablation of biological tissues and heat relaxation time effects. Phys. Med. Biol. 2019, 64, 245008. [Google Scholar] [CrossRef] [Green Version]
- Singh, S.; Melnik, R. Fluid–structure interaction and non-fourier effects in coupled electro-thermo-mechanical models for cardiac ablation. Fluids 2021, 6, 294. [Google Scholar] [CrossRef]
- Singh, S.; Repaka, R. Thermal characterization using fourier and non-fourier conduction during radiofrequency ablation of breast tumor. Multiph. Sci. Technol. 2018, 30, 207–219. [Google Scholar] [CrossRef]
- Youssef, H.M.; Alghamdi, N.A. The exact analytical solution of the dual-phase-lag two-temperature bioheat transfer of a skin tissue subjected to constant heat flux. Sci. Rep. 2020, 10, 15946. [Google Scholar] [CrossRef]
- Askarizadeh, H.; Ahmadikia, H. Analytical analysis of the dual-phase-lag model of bioheat transfer equation during transient heating of skin tissue. Heat Mass Transf. 2014, 50, 1673–1684. [Google Scholar] [CrossRef]
- Askarizadeh, H.; Ahmadikia, H. Analytical study on the transient heating of a two-dimensional skin tissue using parabolic and hyperbolic bioheat transfer equations. Appl. Math. Model. 2015, 39, 3704–3720. [Google Scholar] [CrossRef]
- Kabiri, A.; Talaee, M.R. Theoretical investigation of thermal wave model of microwave ablation applied in prostate Cancer therapy. Heat Mass Transf. 2019, 55, 2199–2208. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, S.; Rai, K. Analysis of classical Fourier, SPL and DPL heat transfer model in biological tissues in presence of metabolic and external heat source. Heat Mass Transf. 2016, 52, 1089–1107. [Google Scholar] [CrossRef]
- Li, X.; Li, Y.; Luo, P.; Tian, X. Relationship between the nonlocal effect and lagging behavior in bioheat transfer. J. Heat Transf. 2021, 143, 051201. [Google Scholar] [CrossRef]
- Sahoo, N.; Ghosh, S.; Narasimhan, A.; Das, S.K. Investigation of non-Fourier effects in bio-tissues during laser assisted photothermal therapy. Int. J. Therm. Sci. 2014, 76, 208–220. [Google Scholar] [CrossRef]
- Shih, T.-C.; Horng, T.-L.; Huang, H.-W.; Ju, K.-C.; Huang, T.-C.; Chen, P.-Y.; Ho, Y.-J.; Lin, W.-L. Numerical analysis of coupled effects of pulsatile blood flow and thermal relaxation time during thermal therapy. Int. J. Heat Mass Transf. 2012, 55, 3763–3773. [Google Scholar] [CrossRef]
- Zhang, Y. Generalized dual-phase lag bioheat equations based on nonequilibrium heat transfer in living biological tissues. Int. J. Heat Mass Transf. 2009, 52, 4829–4834. [Google Scholar] [CrossRef]
- Choudhuri, S.R. On a thermoelastic three-phase-lag model. J. Therm. Stresses 2007, 30, 231–238. [Google Scholar] [CrossRef]
- Green, A.; Naghdi, P. On undamped heat waves in an elastic solid. J. Therm. Stresses 1992, 15, 253–264. [Google Scholar] [CrossRef]
- Green, A.; Naghdi, P. Thermoelasticity without energy dissipation. J. Elast. 1993, 31, 189–208. [Google Scholar] [CrossRef]
- Zhang, Q.; Sun, Y.; Yang, J. Bio-heat response of skin tissue based on three-phase-lag model. Sci. Rep. 2020, 10, 16421. [Google Scholar] [CrossRef] [PubMed]
- Hobiny, A.; Alzahrani, F.; Abbas, I. Analytical estimation of temperature in living tissues using the TPL bioheat model with experimental verification. Mathematics 2020, 8, 1188. [Google Scholar] [CrossRef]
- Kumar, D.; Rai, K. Three-phase-lag bioheat transfer model and its validation with experimental data. Mech. Based Des. Struct. Mach. 2020, 1–15. [Google Scholar] [CrossRef]
- Verma, R.; Kumar, S. Computational Study on Skin Tissue Freezing Using Three-Phase Lag Bioheat Model. J. Heat Transf. 2021, 143, 111201. [Google Scholar] [CrossRef]
- Irastorza, R.M.; Gonzalez-Suarez, A.; Pérez, J.J.; Berjano, E. Differences in applied electrical power between full thorax models and limited-domain models for RF cardiac ablation. Int. J. Hyperth. 2020, 37, 677–687. [Google Scholar] [CrossRef] [PubMed]
- Quintanilla, R.; Racke, R. A note on stability in three-phase-lag heat conduction. Int. J. Heat Mass Transf. 2008, 51, 24–29. [Google Scholar] [CrossRef] [Green Version]
- Korganbayev, S.; Orrico, A.; Bianchi, L.; Paloschi, D.; Wolf, A.; Dostovalov, A.; Saccomandi, P. PID controlling approach based on FBG array measurements for laser ablation of pancreatic tissues. IEEE Trans. Instrum. Meas. 2021, 70, 1–9. [Google Scholar] [CrossRef]
- Singh, S.; Melnik, R. Domain heterogeneity in radiofrequency therapies for pain relief: A computational study with coupled models. Bioengineering 2020, 7, 35. [Google Scholar] [CrossRef] [Green Version]
- Singh, S.; Repaka, R. Temperature-controlled radiofrequency ablation of different tissues using two-compartment models. Int. J. Hyperth. 2017, 33, 122–134. [Google Scholar] [CrossRef] [Green Version]
- Singh, S.; Repaka, R. Numerical study to establish relationship between coagulation volume and target tip temperature during temperature-controlled radiofrequency ablation. Electromagn. Biol. Med. 2018, 37, 13–22. [Google Scholar] [CrossRef]
- González-Suárez, A.; Pérez, J.J.; Berjano, E. Should fluid dynamics be included in computer models of RF cardiac ablation by irrigated-tip electrodes? Biomed. Eng. Online 2018, 17, 1–14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- González-Suárez, A.; Berjano, E. Comparative analysis of different methods of modeling the thermal effect of circulating blood flow during RF cardiac ablation. IEEE Trans. Biomed. Eng. 2015, 63, 250–259. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- González-Suárez, A.; Berjano, E.; Guerra, J.M.; Gerardo-Giorda, L. Computational modeling of open-irrigated electrodes for radiofrequency cardiac ablation including blood motion-saline flow interaction. PLoS ONE 2016, 11, e0150356. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Johnston, B.M.; Johnston, P.R.; Corney, S.; Kilpatrick, D. Non-Newtonian blood flow in human right coronary arteries: Steady state simulations. J. Biomech. 2004, 37, 709–720. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rossmann, C.; Motamarry, A.; Panescu, D.; Haemmerich, D. Computer simulations of an irrigated radiofrequency cardiac ablation catheter and experimental validation by infrared imaging. Int. J. Hyperth. 2021, 38, 1149–1163. [Google Scholar] [CrossRef] [PubMed]
- Formaggia, L.; Quarteroni, A.; Veneziani, A. Cardiovascular Mathematics: Modeling and Simulation of the Circulatory System; Springer Science & Business Media: Berlin, Germany, 2010; Volume 1. [Google Scholar]
- Quarteroni, A.; Manzoni, A.; Vergara, C. Mathematical Modelling of the Human Cardiovascular System: Data, Numerical Approximation, Clinical Applications; Cambridge University Press: Cambridge, UK, 2019; Volume 33. [Google Scholar]
- Quarteroni, A.; Veneziani, A.; Vergara, C. Geometric multiscale modeling of the cardiovascular system, between theory and practice. Comput. Methods Appl. Mech. Eng. 2016, 302, 193–252. [Google Scholar] [CrossRef] [Green Version]
- Hessenthaler, A.; Falgout, R.D.; Schroder, J.B.; de Vecchi, A.; Nordsletten, D.; Röhrle, O. Time-periodic steady-state solution of fluid-structure interaction and cardiac flow problems through multigrid-reduction-in-time. Comput. Methods Appl. Mech. Eng. 2022, 389, 114368. [Google Scholar] [CrossRef]
- Kadem, M.; Garber, L.; Abdelkhalek, M.; Al-Khazraji, B.K.; Keshavarz-Motamed, Z. Hemodynamic modeling, medical imaging, and machine learning and their applications to cardiovascular interventions. IEEE Rev. Biomed. Eng. 2022. [Google Scholar] [CrossRef]
- Le, T.B.; Usta, M.; Aidun, C.; Yoganathan, A.; Sotiropoulos, F. Computational Methods for Fluid-Structure Interaction Simulation of Heart Valves in Patient-Specific Left Heart Anatomies. Fluids 2022, 7, 94. [Google Scholar] [CrossRef]
- Mittal, R.; Seo, J.H.; Vedula, V.; Choi, Y.J.; Liu, H.; Huang, H.H.; Jain, S.; Younes, L.; Abraham, T.; George, R.T. Computational modeling of cardiac hemodynamics: Current status and future outlook. J. Comput. Phys. 2016, 305, 1065–1082. [Google Scholar] [CrossRef]
- Viola, F.; Spandan, V.; Meschini, V.; Romero, J.; Fatica, M.; de Tullio, M.D.; Verzicco, R. FSEI-GPU: GPU accelerated simulations of the fluid–structure–electrophysiology interaction in the left heart. Comput. Phys. Commun. 2022, 273, 108248. [Google Scholar] [CrossRef]
- Parés, C.; Berjano, E.; González-Suárez, A. Effect of intracardiac blood flow pulsatility during radiofrequency cardiac ablation: Computer modeling study. Int. J. Hyperth. 2021, 38, 316–325. [Google Scholar] [CrossRef] [PubMed]
- Pérez, J.J.; Nadal, E.; Berjano, E.; González-Suárez, A. Computer modeling of radiofrequency cardiac ablation including heartbeat-induced electrode displacement. Comput. Biol. Med. 2022, 144, 105346. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.; Melnik, R. Computational modeling of cardiac ablation incorporating electrothermomechanical interactions. J. Eng. Sci. Med. Diagn. Ther. 2020, 3, 041004. [Google Scholar] [CrossRef]
- Pérez, J.J.; González-Suárez, A.; Berjano, E. Numerical analysis of thermal impact of intramyocardial capillary blood flow during radiofrequency cardiac ablation. Int. J. Hyperth. 2018, 34, 243–249. [Google Scholar] [CrossRef] [Green Version]
- COMSOL Multiphysics v. 6; COMSOL AB: Stockholm, Sweden, 2022.
- Amestoy, P.R.; Duff, I.S.; L’excellent, J.-Y. Multifrontal parallel distributed symmetric and unsymmetric solvers. Comput. Methods Appl. Mech. Eng. 2000, 184, 501–520. [Google Scholar] [CrossRef] [Green Version]
- Singh, S.; Krishnaswamy, J.A.; Melnik, R. Biological cells and coupled electro-mechanical effects: The role of organelles, microtubules, and nonlocal contributions. J. Mech. Behav. Biomed. Mater. 2020, 110, 103859. [Google Scholar] [CrossRef]
- Singh, S.; Melnik, R. Microtubule biomechanics and the effect of degradation of elastic moduli. In Proceedings of the 20th International Conference on Computational Science, Lecture Notes in Computer Science, Amsterdam, The Netherlands, 3–5 June 2020; Springer: Cham, Switzerland, 2020; Volume 12142. [Google Scholar] [CrossRef]
- Singh, S.; Melnik, R. Coupled Electro-mechanical Behavior of Microtubules. In Proceedings of the 8th International Work-Conference on Bioinformatics and Biomedical Engineering, Lecture Notes in Computer Science, Granada, Spain, 6–8 May 2020; Springer: Cham, Switzerland, 2020; Volume 12108. [Google Scholar] [CrossRef]
- Singh, S.; Melnik, R. Coupled thermo-electro-mechanical models of cardiac ablation at tissue-cellular scales and a role of microtubules. In Proceedings of the 14th WCCM-ECCOMAS Congress 2020, Web, 11–15 January 2021; p. 400. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, S.; Saccomandi, P.; Melnik, R. Three-Phase-Lag Bio-Heat Transfer Model of Cardiac Ablation. Fluids 2022, 7, 180. https://doi.org/10.3390/fluids7050180
Singh S, Saccomandi P, Melnik R. Three-Phase-Lag Bio-Heat Transfer Model of Cardiac Ablation. Fluids. 2022; 7(5):180. https://doi.org/10.3390/fluids7050180
Chicago/Turabian StyleSingh, Sundeep, Paola Saccomandi, and Roderick Melnik. 2022. "Three-Phase-Lag Bio-Heat Transfer Model of Cardiac Ablation" Fluids 7, no. 5: 180. https://doi.org/10.3390/fluids7050180
APA StyleSingh, S., Saccomandi, P., & Melnik, R. (2022). Three-Phase-Lag Bio-Heat Transfer Model of Cardiac Ablation. Fluids, 7(5), 180. https://doi.org/10.3390/fluids7050180







