Computational Methods for Fluid-Structure Interaction Simulation of Heart Valves in Patient-Specific Left Heart Anatomies
Abstract
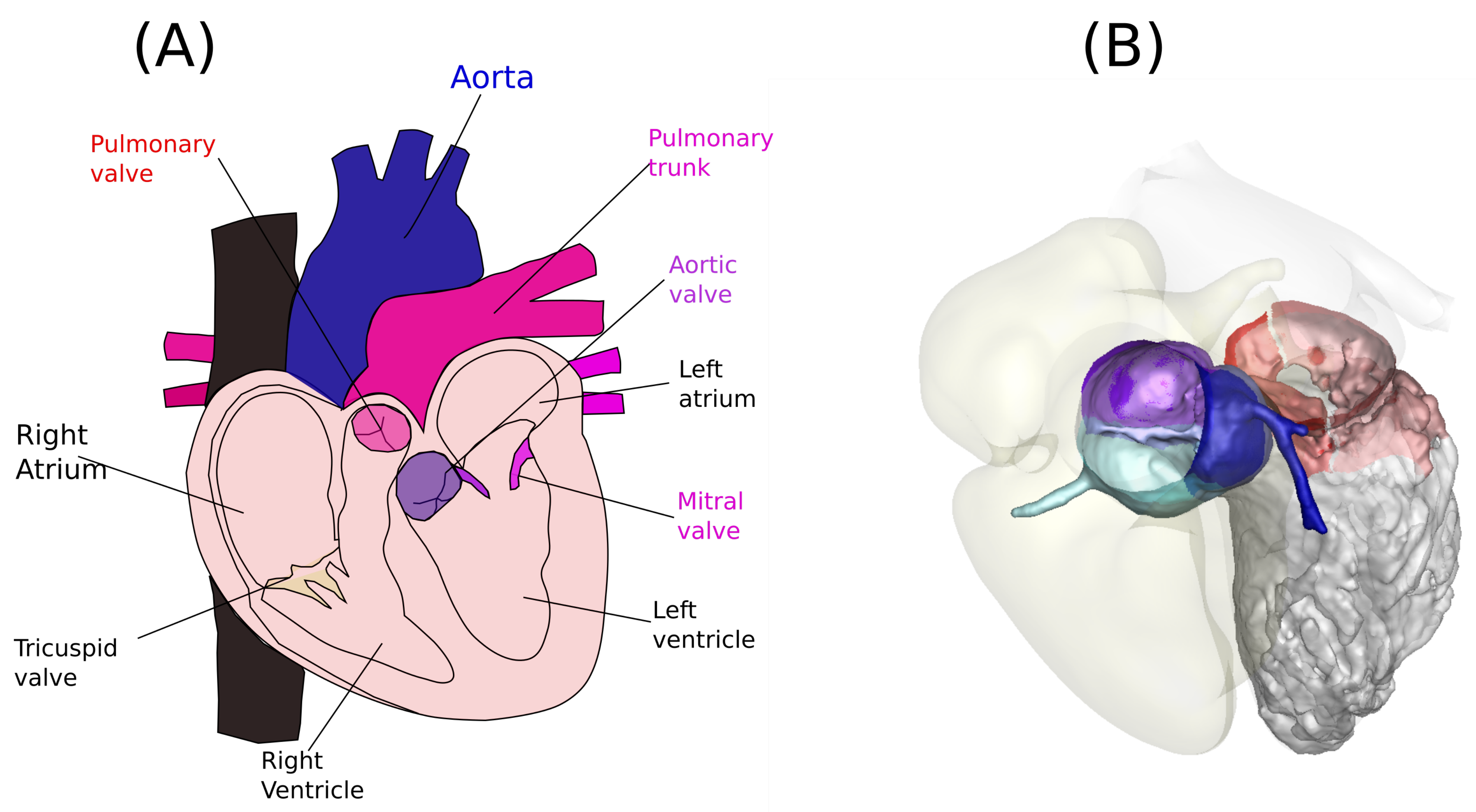
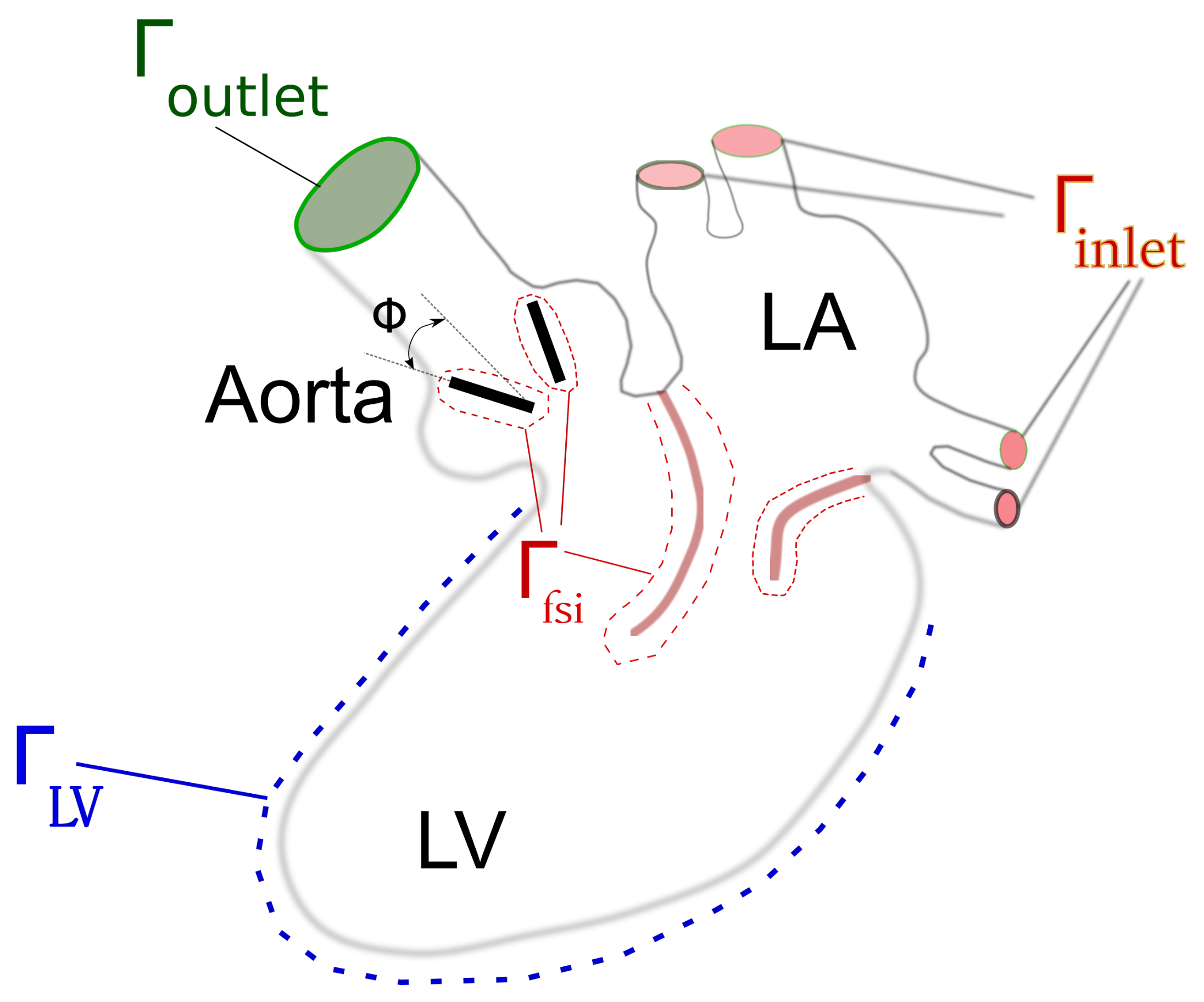
1. Problem Formulation
2. Prosthetic Heart Valves
2.1. Mechanical Valves
2.2. Bioprosthetic Valves
3. Fluid–Structure Interaction of Valves and Blood Flows
| Algorithm 1: Fixed-point iteration algorithm to solve the Equation (25) |
|
while do end while |
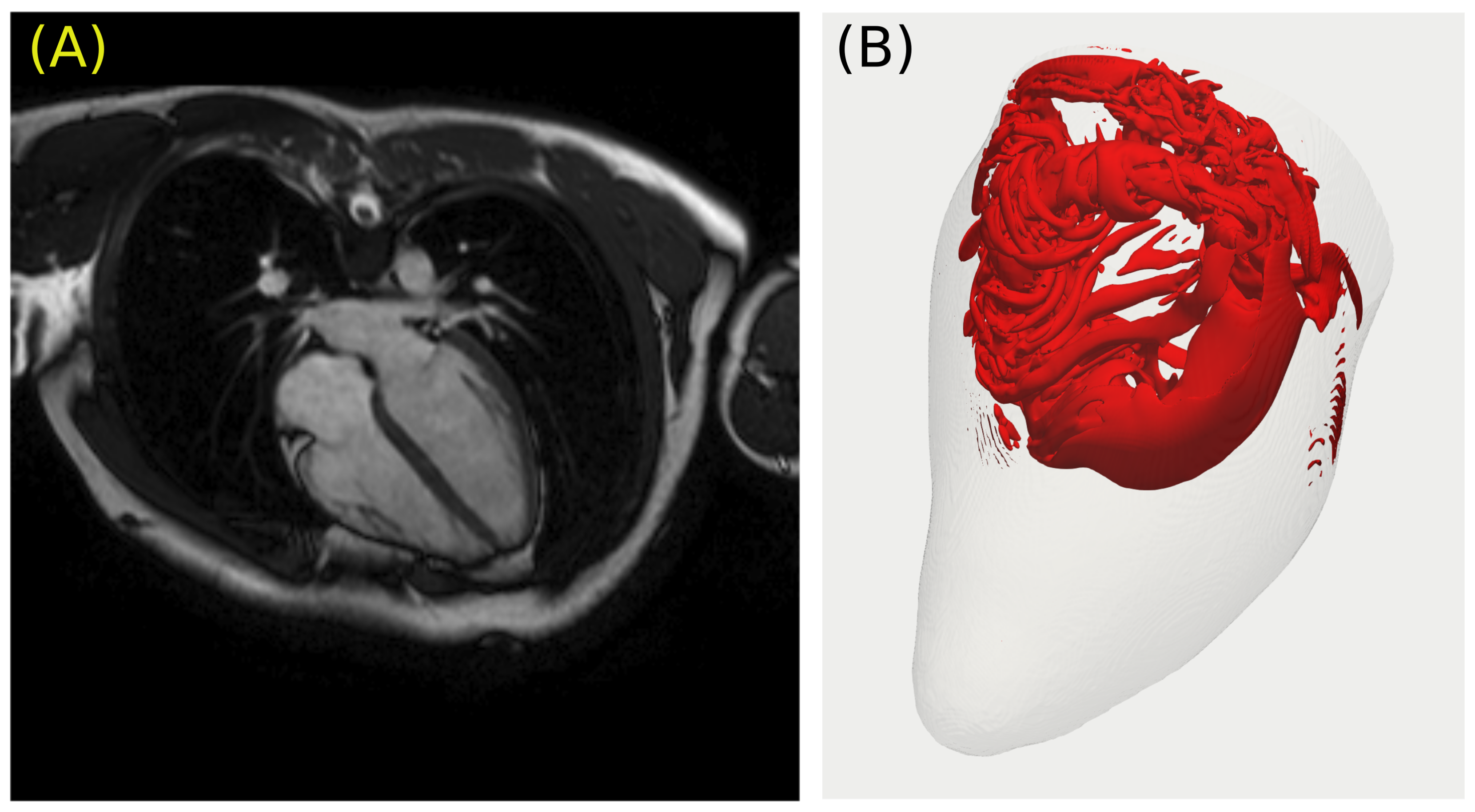
4. Patient-Specific Anatomy and the Dynamics of
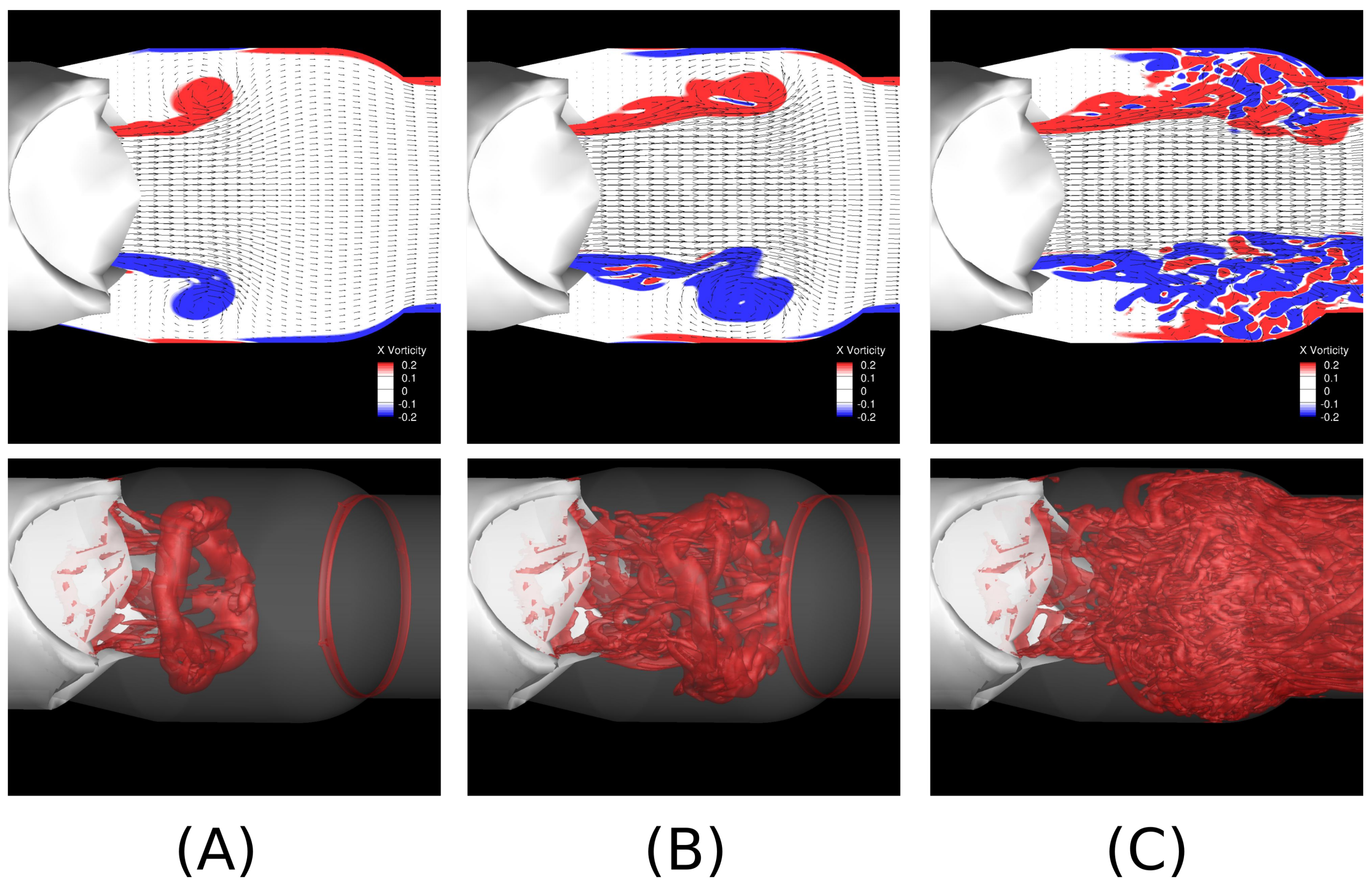
5. Continuum Approaches for Solving the Flow Dynamics in Ωf
5.1. Governing Equations for the Fluid Domain
5.2. Finite Difference Methods
5.3. Immersed Finite Element Methods
6. Particle Methods
7. Current Challenges and Future Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ALE | Arbitrary Lagrangian–Eulerian |
| BMHV | Bi-leaflet Mechanical Heart Valve |
| BGK | Bhatnagar–Gross–Krook |
| BDI | Blood Damage Index |
| CT | Computed Tomography |
| DNS | Direct Numerical Simulation |
| ELB | Entropic Lattice Boltzmann |
| EBF | External Boundary Force |
| FSI | Fluid–Structure Interaction |
| IBM | Immersed Boundary Method |
| LV | Left Ventricle |
| LVOT | Left Ventricle Outflow Tract |
| LCA | Left Coronary Artery |
| NCA | Non-Cusp Coronary Artery |
| LBM | Lattice Boltzmann Method |
| MRI | Magnetic Resonance Imaging |
| PSM | Patient-Specific Modeling |
| RCA | Right Coronary Artery |
| SIB | Sharp-Interface Immersed Boundary |
| SBB | Standard Bounce Back |
References
- Dasi, L.P.; Simon, H.A.; Sucosky, P.; Yoganathan, A.P. Fluid mechanics of artificial heart valves. Clin. Exp. Pharmacol. Physiol. 2009, 36, 225–237. [Google Scholar] [CrossRef] [PubMed]
- Votta, E.; Le, T.B.; Stevanella, M.; Fusini, L.; Caiani, E.G.; Redaelli, A.; Sotiropoulos, F. Toward patient-specific simulations of cardiac valves: State-of-the-art and future directions. J. Biomech. 2013, 46, 217–228. [Google Scholar] [CrossRef] [PubMed]
- Sotiropoulos, F.; Le, T.B.; Gilmanov, A. Fluid mechanics of heart valves and their replacements. Annu. Rev. Fluid Mech. 2016, 48, 259–283. [Google Scholar] [CrossRef]
- Baiocchi, M.; Barsoum, S.; Khodaei, S.; de la Torre Hernandez, J.M.; Valentino, S.E.; Dunford, E.C.; MacDonald, M.J.; Keshavarz-Motamed, Z. Effects of Choice of Medical Imaging Modalities on a Non-invasive Diagnostic and Monitoring Computational Framework for Patients with Complex Valvular, Vascular, and Ventricular Diseases Who Undergo Transcatheter Aortic Valve Replacement. Front. Bioeng. Biotechnol. 2021, 389. [Google Scholar] [CrossRef] [PubMed]
- Peirlinck, M.; Costabal, F.S.; Yao, J.; Guccione, J.; Tripathy, S.; Wang, Y.; Ozturk, D.; Segars, P.; Morrison, T.; Levine, S.; et al. Precision medicine in human heart modeling. Biomech. Model. Mechanobiol. 2021, 20, 803–831. [Google Scholar] [CrossRef] [PubMed]
- Khodaei, S.; Henstock, A.; Sadeghi, R.; Sellers, S.; Blanke, P.; Leipsic, J.; Emadi, A.; Keshavarz-Motamed, Z. Personalized intervention cardiology with transcatheter aortic valve replacement made possible with a non-invasive monitoring and diagnostic framework. Sci. Rep. 2021, 11, 1–28. [Google Scholar]
- Griffith, B.E.; Patankar, N.A. Immersed Methods for Fluid–Structure Interaction. Annu. Rev. Fluid Mech. 2020, 52, 421–448. [Google Scholar] [CrossRef]
- Rufaihah, A.J.; Chen, C.K.; Yap, C.H.; Mattar, C.N. Mending a broken heart: In vitro, in vivo and in silico models of congenital heart disease. Dis. Model. Mech. 2021, 14, dmm047522. [Google Scholar] [CrossRef]
- Avazmohammadi, R.; Soares, J.S.; Li, D.S.; Raut, S.S.; Gorman, R.C.; Sacks, M.S. A contemporary look at biomechanical models of myocardium. Annu. Rev. Biomed. Eng. 2019, 21, 417–442. [Google Scholar] [CrossRef]
- Sacks, M.S.; David Merryman, W.; Schmidt, D.E. On the biomechanics of heart valve function. J. Biomech. 2009, 42, 1804–1824. [Google Scholar] [CrossRef]
- Johnson, E.L.; Wu, M.C.; Xu, F.; Wiese, N.M.; Rajanna, M.R.; Herrema, A.J.; Ganapathysubramanian, B.; Hughes, T.J.; Sacks, M.S.; Hsu, M.C. Thinner biological tissues induce leaflet flutter in aortic heart valve replacements. Proc. Natl. Acad. Sci. USA 2020, 117, 19007–19016. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Gao, H.; Griffith, B.E.; Berry, C.; Luo, X. Image-based fluid–structure interaction model of the human mitral valve. Comput. Fluids 2013, 71, 417–425. [Google Scholar] [CrossRef]
- Moore, B.; Dasi, L.P. Spatiotemporal complexity of the aortic sinus vortex. Exp. Fluids 2014, 55, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Hatoum, H.; Lilly, S.; Maureira, P.; Crestanello, J.; Dasi, L.P. Sinus hemodynamics after transcatheter aortic valve in transcatheter aortic valve. Ann. Thorac. Surg. 2020, 110, 1348–1356. [Google Scholar] [CrossRef] [PubMed]
- Gooden, S.C.M.; Hatoum, H.; Zhang, W.; Boudoulas, K.D.; Dasi, L.P. Multiple MitraClips: The balancing act between pressure gradient and regurgitation. J. Thorac. Cardiovasc. Surg. 2020, in press. [Google Scholar] [CrossRef]
- Le, T.B.; Borazjani, I.; Kang, S.; Sotiropoulos, F. On the structure of vortex rings from inclined nozzles. J. Fluid Mech 2011, 686, 451–483. [Google Scholar] [CrossRef]
- Le, T.B.; Sotiropoulos, F.; Coffey, D.; Keefe, D. Vortex formation and instability in the left ventricle. Phys. Fluids 2012, 24, 091110. [Google Scholar] [CrossRef]
- Le, T.B.; Elbaz, M.S.; Van Der Geest, R.J.; Sotiropoulos, F. High resolution simulation of diastolic left ventricular hemodynamics guided by four-dimensional flow magnetic resonance imaging data. Flow Turbul. Combust. 2019, 102, 3–26. [Google Scholar] [CrossRef]
- Elbaz, M.S.; Calkoen, E.E.; Westenberg, J.J.; Lelieveldt, B.P.; Roest, A.A.; van der Geest, R.J. Vortex flow during early and late left ventricular filling in normal subjects: Quantitative characterization using retrospectively-gated 4D flow cardiovascular magnetic resonance and three-dimensional vortex core analysis. J. Cardiovasc. Magn. Reson. 2014, 16, 78. [Google Scholar] [CrossRef]
- Elbaz, M.S.; van der Geest, R.J.; Calkoen, E.E.; de Roos, A.; Lelieveldt, B.P.; Roest, A.A.; Westenberg, J.J. Assessment of viscous energy loss and the association with three-dimensional vortex ring formation in left ventricular inflow: In vivo evaluation using four-dimensional flow MRI. Magn. Reson. Med. 2017, 77, 794–805. [Google Scholar] [CrossRef]
- Dasi, L.P.; Ge, L.; Simon, H.A.; Sotiropoulos, F.; Yoganathan, A.P. Vorticity dynamics of a bileaflet mechanical heart valve in an axisymmetric aorta. Phys. Fluids 2007, 19, 067105. [Google Scholar] [CrossRef]
- Raghav, V.; Midha, P.; Sharma, R.; Babaliaros, V.; Yoganathan, A. Transcatheter aortic valve thrombosis: A review of potential mechanisms. J. R. Soc. Interface 2021, 18, 20210599. [Google Scholar] [CrossRef]
- Hatoum, H.; Dasi, L.P. Spatiotemporal complexity of the aortic sinus vortex as a function of leaflet calcification. Ann. Biomed. Eng. 2019, 47, 1116–1128. [Google Scholar] [CrossRef]
- Kheradvar, A.; Groves, E.M.; Falahatpisheh, A.; Mofrad, M.K.; Alavi, S.H.; Tranquillo, R.; Dasi, L.P.; Simmons, C.A.; Grande-Allen, K.J.; Goergen, C.J.; et al. Emerging trends in heart valve engineering: Part IV. Computational modeling and experimental studies. Ann. Biomed. Eng. 2015, 43, 2314–2333. [Google Scholar] [CrossRef]
- Reasor, D.; Clausen, J.; Aidun, C. Rheological characterization of cellular blood in shear. J. Fluid Mech. 2013, 726, 497–516. [Google Scholar] [CrossRef]
- Borazjani, I.; Ge, L.; Sotiropoulos, F. Curvilinear immersed boundary method for simulating fluid structure interaction with complex 3D rigid bodies. J. Comput. Phys. 2008, 227, 7587–7620. [Google Scholar] [CrossRef]
- Liu, Z.L.; Clausen, J.R.; Wagner, J.L.; Butler, K.S.; Bolintineanu, D.S.; Lechman, J.B.; Rao, R.R.; Aidun, C.K. Heterogeneous partition of cellular blood-borne nanoparticles through microvascular bifurcations. Phys. Rev. E 2020, 102, 013310. [Google Scholar] [CrossRef]
- Bäumler, K.; Vedula, V.; Sailer, A.M.; Seo, J.; Chiu, P.; Mistelbauer, G.; Chan, F.P.; Fischbein, M.P.; Marsden, A.L.; Fleischmann, D. Fluid–structure interaction simulations of patient-specific aortic dissection. Biomech. Model. Mechanobiol. 2020, 19, 1607–1628. [Google Scholar] [CrossRef]
- Kaiser, A.D.; Shad, R.; Hiesinger, W.; Marsden, A.L. A design-based model of the aortic valve for fluid–structure interaction. Biomech. Model. Mechanobiol. 2021, 20, 2413–2435. [Google Scholar] [CrossRef]
- Vedula, V.; Seo, J.H.; Lardo, A.C.; Mittal, R. Effect of trabeculae and papillary muscles on the hemodynamics of the left ventricle. Theor. Comput. Fluid Dyn. 2016, 30, 3–21. [Google Scholar] [CrossRef]
- Ghosh, R.P.; Marom, G.; Bianchi, M.; D’souza, K.; Zietak, W.; Bluestein, D. Numerical evaluation of transcatheter aortic valve performance during heart beating and its post-deployment fluid–structure interaction analysis. Biomech. Model. Mechanobiol. 2020, 19, 1725–1740. [Google Scholar] [CrossRef]
- Chnafa, C.; Mendez, S.; Nicoud, F. Image-based large-eddy simulation in a realistic left heart. Comput. Fluids 2014, 94, 173–187. [Google Scholar] [CrossRef]
- Gilmanov, A.; Sotiropoulos, F. A hybrid Cartesian/immersed boundary method for simulating flows with 3D, geometrically complex, moving bodies. J. Comput. Phys. 2005, 207, 457. [Google Scholar] [CrossRef]
- Yoganathan, A.; Chandran, K.; Sotiropoulos, F. Flow in Prosthetic Heart Valves: State-of-the-Art and Future Directions. Ann. Biomed. Eng. 2005, 33, 1689–1694. [Google Scholar] [CrossRef]
- Kheradvar, A.; Groves, E.M.; Goergen, C.J.; Alavi, S.H.; Tranquillo, R.; Simmons, C.A.; Dasi, L.P.; Grande-Allen, K.J.; Mofrad, M.R.; Falahatpisheh, A.; et al. Emerging trends in heart valve engineering: Part II. Novel and standard technologies for aortic valve replacement. Ann. Biomed. Eng. 2015, 43, 844–857. [Google Scholar] [CrossRef][Green Version]
- Dasi, L.P.; Grande-Allen, J.; Kunzelman, K.; Kuhl, E. The pursuit of engineering the ideal heart valve replacement or repair: A special issue of the annals of biomedical engineering. Ann. Biomed. Eng. 2017, 45, 307–309. [Google Scholar] [CrossRef] [PubMed]
- Masuda, M.; Kado, H.; Tatewaki, H.; Shiokawa, Y.; Yasui, H. Late results after mitral valve replacement with bileaflet mechanical prosthesis in children: Evaluation of prosthesis-patient mismatch. Ann. Thorac. Surg. 2004, 77, 913–917. [Google Scholar] [CrossRef]
- Bark, D.L.; Vahabi, H.; Bui, H.; Movafaghi, S.; Moore, B.; Kota, A.K.; Popat, K.; Dasi, L.P. Hemodynamic performance and thrombogenic properties of a superhydrophobic bileaflet mechanical heart valve. Ann. Biomed. Eng. 2017, 45, 452–463. [Google Scholar] [CrossRef] [PubMed]
- Zakaria, M.S.; Ismail, F.; Tamagawa, M.; Aziz, A.F.A.; Wiriadidjaja, S.; Basri, A.A.; Ahmad, K.A. Review of numerical methods for simulation of mechanical heart valves and the potential for blood clotting. Med. Biol. Eng. Comput. 2017, 55, 1519–1548. [Google Scholar] [CrossRef] [PubMed]
- Li, C.P.; Chen, S.F.; Lo, C.W.; Lu, P.C. Turbulence characteristics downstream of a new trileaflet mechanical heart valve. Asaio J. 2011, 57, 188–196. [Google Scholar] [CrossRef] [PubMed]
- Schubert, K.; Schaller, T.; Stojenthin, E.; Stephan, C.; Sievers, H.H.; Scharfschwerdt, M. A novel trileaflet mechanical heart valve: First in vitro results. Interact. Cardiovasc. Thorac. Surg. 2018, 28, 689–694. Available online: https://academic.oup.com/icvts/article-pdf/28/5/689/28532707/ivy337.pdf (accessed on 10 January 2022). [CrossRef]
- Hedayat, M.; Asgharzadeh, H.; Borazjani, I. Platelet activation of mechanical versus bioprosthetic heart valves during systole. J. Biomech. 2017, 56, 111–116. [Google Scholar] [CrossRef]
- Hedayat, M.; Borazjani, I. Comparison of platelet activation through hinge vs. bulk flow in bileaflet mechanical heart valves. J. Biomech. 2019, 83, 280–290. [Google Scholar] [CrossRef]
- Hedayat, M.; Patel, T.R.; Kim, T.; Belohlavek, M.; Hoffmann, K.R.; Borazjani, I. A hybrid echocardiography-CFD framework for ventricular flow simulations. Int. J. Numer. Methods Biomed. Eng. 2020, 36, e3352. [Google Scholar] [CrossRef]
- Sadrabadi, M.S.; Hedayat, M.; Borazjani, I.; Arzani, A. Fluid–structure coupled biotransport processes in aortic valve disease. J. Biomech. 2021, 117, 110239. [Google Scholar] [CrossRef]
- Tallec, P.L.; Mouro, J. Fluid structure interaction with large structural displacements. Comput. Methods Appl. Mech. Eng. 2001, 190, 3039–3067. [Google Scholar] [CrossRef]
- Dasi, L.P.; Hatoum, H.; Kheradvar, A.; Zareian, R.; Alavi, S.H.; Sun, W.; Martin, C.; Pham, T.; Wang, Q.; Midha, P.A.; et al. On the mechanics of transcatheter aortic valve replacement. Ann. Biomed. Eng. 2017, 45, 310–331. [Google Scholar] [CrossRef]
- Rotman, O.M.; Kovarovic, B.; Chiu, W.C.; Bianchi, M.; Marom, G.; Slepian, M.J.; Bluestein, D. Novel polymeric valve for transcatheter aortic valve replacement applications: In vitro hemodynamic study. Ann. Biomed. Eng. 2019, 47, 113–125. [Google Scholar] [CrossRef]
- Piatti, F.; Sturla, F.; Marom, G.; Sheriff, J.; Claiborne, T.E.; Slepian, M.J.; Redaelli, A.; Bluestein, D. Hemodynamic and thrombogenic analysis of a trileaflet polymeric valve using a fluid–structure interaction approach. J. Biomech. 2015, 48, 3641–3649. [Google Scholar] [CrossRef]
- Bianchi, M.; Marom, G.; Ghosh, R.P.; Rotman, O.M.; Parikh, P.; Gruberg, L.; Bluestein, D. Patient-specific simulation of transcatheter aortic valve replacement: Impact of deployment options on paravalvular leakage. Biomech. Model. Mechanobiol. 2019, 18, 435–451. [Google Scholar] [CrossRef]
- Ge, L.; Sotiropoulos, F. A numerical method for solving the 3D unsteady incompressible Navier–Stokes equations in curvilinear domains with complex immersed boundaries. J. Comput. Phys. 2007, 225, 1782. [Google Scholar] [CrossRef]
- Küttler, U.; Wall, W.A. Vector extrapolation for strong coupling fluid–structure interaction solvers. J. Appl. Mech. Mar. 2009, 76, 021205. [Google Scholar] [CrossRef]
- Sotiropoulos, F.; Yang, X. Immersed boundary methods for simulating fluid–structure interaction. Prog. Aerosp. Sci. 2014, 65, 1–21. [Google Scholar] [CrossRef]
- Gilmanov, A.; Le, T.B.; Sotiropoulos, F. A numerical approach for simulating fluid structure interaction of flexible thin shells undergoing arbitrarily large deformations in complex domains. J. Comput. Phys. 2015, 300, 814–843. [Google Scholar] [CrossRef]
- Kuttler, U.; Wall, W. Fixed-point fluid structure interaction solvers with dynamic relaxation. Comput. Mech. 2008, 43, 61–72. [Google Scholar] [CrossRef]
- Le, T.B.; Christenson, A.; Calderer, T.; Stolarski, H.; Sotiropoulos, F. A thin-walled composite beam model for light-weighted structures interacting with fluids. J. Fluids Struct. 2020, 95, 102968. [Google Scholar] [CrossRef]
- Morganti, S.; Auricchio, F.; Benson, D.; Gambarin, F.; Hartmann, S.; Hughes, T.; Reali, A. Patient-specific isogeometric structural analysis of aortic valve closure. Comput. Methods Appl. Mech. Eng. 2015, 284, 508–520. [Google Scholar] [CrossRef]
- Li, C.P.; Lu, P.C. Numerical comparison of the closing dynamics of a new trileaflet and a bileaflet mechanical aortic heart valve. J. Artif. Organs 2012, 15, 364–374. [Google Scholar] [CrossRef]
- Griffith, B.E. Immersed boundary model of aortic heart valve dynamics with physiological driving and loading conditions. Int. J. Numer. Methods Biomed. Eng. 2012, 28, 317–345. [Google Scholar] [CrossRef]
- Le, T.B.; Sotiropoulos, F. Fluid–structure interaction of an aortic heart valve prosthesis driven by an animated anatomic left ventricle. J. Comput. Phys. 2013, 244, 41–62. [Google Scholar] [CrossRef]
- Yun, B.M.; Dasi, L.; Aidun, C.; Yoganathan, A. Computational modelling of flow through prosthetic heart valves using the entropic lattice-Boltzmann method. J. Fluid Mech. 2014, 743, 170–201. [Google Scholar] [CrossRef]
- Okafor, I.; Raghav, V.; Condado, J.F.; Midha, P.A.; Kumar, G.; Yoganathan, A.P. Aortic regurgitation generates a kinematic obstruction which hinders left ventricular filling. Ann. Biomed. Eng. 2017, 45, 1305–1314. [Google Scholar] [CrossRef] [PubMed]
- Redaelli, A.; Votta, E. Cardiovascular patient-specific modeling: Where are we now and what does the future look like? APL Bioeng. 2020, 4, 040401. [Google Scholar] [CrossRef] [PubMed]
- Vellguth, K.; Brüning, J.; Goubergrits, L.; Tautz, L.; Hennemuth, A.; Kertzscher, U.; Degener, F.; Kelm, M.; Sündermann, S.; Kuehne, T. Development of a modeling pipeline for the prediction of hemodynamic outcome after virtual mitral valve repair using image-based CFD. Int. J. Comput. Assist. Radiol. Surg. 2018, 13, 1795–1805. [Google Scholar] [CrossRef] [PubMed]
- Mittal, R.; Seo, J.H.; Vedula, V.; Choi, Y.J.; Liu, H.; Huang, H.H.; Jain, S.; Younes, L.; Abraham, T.; George, R.T. Computational modeling of cardiac hemodynamics: Current status and future outlook. J. Comput. Phys. 2016, 305, 1065–1082. [Google Scholar] [CrossRef]
- Boccadifuoco, A.; Mariotti, A.; Celi, S.; Martini, N.; Salvetti, M. Impact of uncertainties in outflow boundary conditions on the predictions of hemodynamic simulations of ascending thoracic aortic aneurysms. Comput. Fluids 2018, 165, 96–115. [Google Scholar] [CrossRef]
- Crandon, S.; Elbaz, M.S.; Westenberg, J.J.; van der Geest, R.J.; Plein, S.; Garg, P. Clinical applications of intra-cardiac four-dimensional flow cardiovascular magnetic resonance: A systematic review. Int. J. Cardiol. 2017, 249, 486–493. [Google Scholar] [CrossRef]
- Zhong, L.; Schrauben, E.M.; Garcia, J.; Uribe, S.; Grieve, S.M.; Elbaz, M.S.; Barker, A.J.; Geiger, J.; Nordmeyer, S.; Marsden, A.; et al. Intracardiac 4D flow MRI in congenital heart disease: Recommendations on behalf of the ISMRM flow & motion study group. J. Magn. Reson. Imaging 2019, 50. [Google Scholar] [CrossRef]
- Faurie, J.; Baudet, M.; Assi, K.C.; Auger, D.; Gilbert, G.; Tournoux, F.; Garcia, D. Intracardiac vortex dynamics by high-frame-rate Doppler vortography—In vivo comparison with vector flow mapping and 4-D flow MRI. IEEE Trans. Ultrason. Ferroelectr. Freq. control 2016, 64, 424–432. [Google Scholar] [CrossRef]
- Gomez, A.; De Vecchi, A.; Jantsch, M.; Shi, W.; Pushparajah, K.; Simpson, J.M.; Smith, N.P.; Rueckert, D.; Schaeffter, T.; Penney, G.P. 4D blood flow reconstruction over the entire ventricle from wall motion and blood velocity derived from ultrasound data. IEEE Trans. Med Imaging 2015, 34, 2298–2308. [Google Scholar] [CrossRef]
- Faurie, J.; Baudet, M.; Porée, J.; Cloutier, G.; Tournoux, F.; Garcia, D. Coupling myocardium and vortex dynamics in diverging-wave echocardiography. IEEE Trans. Ultrason. Ferroelectr. Freq. control 2018, 66, 425–432. [Google Scholar] [CrossRef]
- Kim, T.; Hedayat, M.; Vaitkus, V.V.; Belohlavek, M.; Krishnamurthy, V.; Borazjani, I. Automatic segmentation of the left ventricle in echocardiographic images using convolutional neural networks. Quant. Imaging Med. Surg. 2021, 11, 1763. [Google Scholar] [CrossRef]
- JCR, H.; Wray, A.; Moin, P. Eddies, stream, and convergence zones in turbulent flows. In Studying Turbulence Using Numerical Simulation Databases-I1; NASA Ames Research Center: Moffet Field, CA, USA, 1988; Volume 193. [Google Scholar]
- Su, B.; Wang, X.; Kabinejadian, F.; Chin, C.; Le, T.T.; Zhang, J.M. Effects of left atrium on intraventricular flow in numerical simulations. Comput. Biol. Med. 2019, 106, 46–53. [Google Scholar] [CrossRef]
- Seo, J.H.; Vedula, V.; Abraham, T.; Lardo, A.C.; Dawoud, F.; Luo, H.; Mittal, R. Effect of the mitral valve on diastolic flow patterns. Phys. Fluids 2014, 26, 121901. [Google Scholar] [CrossRef]
- Vedula, V.; George, R.; Younes, L.; Mittal, R. Hemodynamics in the left atrium and its effect on ventricular flow patterns. J. Biomech. Eng. 2015, 137, 111003. [Google Scholar] [CrossRef]
- Lantz, J.; Bäck, S.; Carlhäll, C.J.; Bolger, A.; Persson, A.; Karlsson, M.; Ebbers, T. Impact of prosthetic mitral valve orientation on the ventricular flow field: Comparison using patient-specific computational fluid dynamics. J. Biomech. 2021, 116, 110209. [Google Scholar] [CrossRef]
- Mao, W.; Caballero, A.; McKay, R.; Primiano, C.; Sun, W. Fully-coupled fluid–structure interaction simulation of the aortic and mitral valves in a realistic 3D left ventricle model. PLoS ONE 2017, 12, e0184729. [Google Scholar] [CrossRef]
- Viola, F.; Meschini, V.; Verzicco, R. Fluid–Structure-Electrophysiology interaction (FSEI) in the left-heart: A multi-way coupled computational model. Eur. J. Mech. B/Fluids 2020, 79, 212–232. [Google Scholar] [CrossRef]
- Grinberg, L.; Karniadakis, G. Outflow Boundary Conditions for Arterial Networks with Multiple Outlets. Ann. Biomed. Eng. 2008, 36, 1496–1514. [Google Scholar] [CrossRef]
- Le, T.B.; Sotiropoulos, F. On the three-dimensional vortical structure of early diastolic flow in a patient-specific left ventricle. Eur. J. Mech. B/Fluids 2012, 35, 20–24. [Google Scholar] [CrossRef]
- Peskin, C.S. The immersed boundary method. Acta Numer. 2002, 11, 479–517. [Google Scholar] [CrossRef]
- Griffith, B.E.; Luo, X.; McQueen, D.M.; Peskin, C.S. Simulating the fluid dynamics of natural and prosthetic heart valves using the immersed boundary method. Int. J. Appl. Mech. 2009, 1, 137–177. [Google Scholar] [CrossRef]
- Fadlun, E.; Verzicco, R.; Orlandi, P.; Mohd-Yusof, J. Combined immmersed-boundary finite-difference methods for three-dimensional complex flow simulations. J. Comput. Phys. 2000, 161, 35–60. [Google Scholar] [CrossRef]
- Kolahdouz, E.M.; Bhalla, A.P.; Scotten, L.N.; Craven, B.A.; Griffith, B.E. A sharp interface Lagrangian–Eulerian method for rigid-body fluid–structure interaction. J. Comput. Phys. 2021, 443, 110442. [Google Scholar] [CrossRef]
- Nestola, M.G.C.; Becsek, B.; Zolfaghari, H.; Zulian, P.; De Marinis, D.; Krause, R.; Obrist, D. An immersed boundary method for fluid–structure interaction based on variational transfer. J. Comput. Phys. 2019, 398, 108884. [Google Scholar] [CrossRef]
- Borazjani, I. Fluid–structure interaction, immersed boundary-finite element method simulations of bio-prosthetic heart valves. Comput. Methods Appl. Mech. Eng. 2013, 257, 103–116. [Google Scholar] [CrossRef]
- Gilmanov, A.; Sotiropoulos, F. Comparative hemodynamics in an aorta with bicuspid and trileaflet valves. Theor. Comput. Fluid Dyn. 2016, 30, 67–85. [Google Scholar] [CrossRef]
- Sigüenza, J.; Pott, D.; Mendez, S.; Sonntag, S.J.; Kaufmann, T.A.; Steinseifer, U.; Nicoud, F. Fluid–structure interaction of a pulsatile flow with an aortic valve model: A combined experimental and numerical study. Int. J. Numer. Methods Biomed. Eng. 2018, 34, e2945. [Google Scholar] [CrossRef]
- Chen, Y.; Luo, H. A computational study of the three-dimensional fluid–structure interaction of aortic valve. J. Fluids Struct. 2018, 80, 332–349. [Google Scholar] [CrossRef]
- Bao Le, T.; Gilmanov, A.; Sotiropoulos, F. High Resolution Simulation of Tri-Leaflet Aortic Heart Valve in an Idealized Aorta. J. Med. Devices 2013, 7, 030930. Available online: https://asmedigitalcollection.asme.org/medicaldevices/article-pdf/7/3/030930/6235047/med_007_03_030930.pdf (accessed on 10 January 2022). [CrossRef]
- Hasler, D.; Landolt, A.; Obrist, D. Tomographic PIV behind a prosthetic heart valve. Exp. Fluids 2016, 57, 80. [Google Scholar] [CrossRef]
- Seo, J.H.; Abd, T.; George, R.T.; Mittal, R. A coupled chemo-fluidic computational model for thrombogenesis in infarcted left ventricles. Am. J. Physiol.-Heart Circ. Physiol. 2016, 310, H1567–H1582. [Google Scholar] [CrossRef]
- Imanparast, A.; Fatouraee, N.; Sharif, F. The impact of valve simplifications on left ventricular hemodynamics in a three dimensional simulation based on in vivo MRI data. J. Biomech. 2016, 49, 1482–1489. [Google Scholar] [CrossRef]
- Gao, H.; Qi, N.; Feng, L.; Ma, X.; Danton, M.; Berry, C.; Luo, X. Modelling mitral valvular dynamics–current trend and future directions. Int. J. Numer. Methods Biomed. Eng. 2017, 33, e2858. [Google Scholar] [CrossRef]
- Sacks, M.S.; Drach, A.; Lee, C.H.; Khalighi, A.H.; Rego, B.V.; Zhang, W.; Ayoub, S.; Yoganathan, A.P.; Gorman, R.C.; Gorman, J.H. On the simulation of mitral valve function in health, disease, and treatment. J. Biomech. Eng. 2019, 141, 0708041–07080422. [Google Scholar] [CrossRef]
- Khalighi, A.H.; Rego, B.V.; Drach, A.; Gorman, R.C.; Gorman, J.H.; Sacks, M.S. Development of a functionally equivalent model of the mitral valve chordae tendineae through topology optimization. Ann. Biomed. Eng. 2019, 47, 60–74. [Google Scholar] [CrossRef]
- Gilmanov, A.; Stolarski, H.; Sotiropoulos, F. Flow–Structure Interaction Simulations of the Aortic Heart Valve at Physiologic Conditions: The Role of Tissue Constitutive Model. J. Biomech. Eng. 2018, 140, 041003. Available online: https://asmedigitalcollection.asme.org/biomechanical/article-pdf/140/4/041003/6096301/bio_140_04_041003.pdf (accessed on 10 January 2022). [CrossRef]
- Cheng, R.; Lai, Y.G.; Chandran, K.B. Three-Dimensional Fluid-Structure Interaction Simulation of Bileaflet Mechanical Heart Valve Flow Dynamics. Ann. Biomed. Eng. 2004, 32, 1471–1483. [Google Scholar] [CrossRef]
- Larsson, D.; Spühler, J.H.; Petersson, S.; Nordenfur, T.; Colarieti-Tosti, M.; Hoffman, J.; Winter, R.; Larsson, M. Patient-specific left ventricular flow simulations from transthoracic echocardiography: Robustness evaluation and validation against ultrasound Doppler and magnetic resonance imaging. IEEE Trans. Med Imaging 2017, 36, 2261–2275. [Google Scholar] [CrossRef]
- Luraghi, G.; Migliavacca, F.; García-González, A.; Chiastra, C.; Rossi, A.; Cao, D.; Stefanini, G.; Matas, J.F.R. On the modeling of patient-specific transcatheter aortic valve replacement: A fluid–structure interaction approach. Cardiovasc. Eng. Technol. 2019, 10, 437–455. [Google Scholar] [CrossRef]
- Lavon, K.; Halevi, R.; Marom, G.; Ben Zekry, S.; Hamdan, A.; Joachim Schäfers, H.; Raanani, E.; Haj-Ali, R. Fluid–structure interaction models of bicuspid aortic valves: The effects of nonfused cusp angles. J. Biomech. Eng. 2018, 140, 031010. [Google Scholar] [CrossRef] [PubMed]
- Luraghi, G.; Migliavacca, F.; Matas, J.F.R. Study on the accuracy of structural and FSI heart valves simulations. Cardiovasc. Eng. Technol. 2018, 9, 723–738. [Google Scholar] [CrossRef] [PubMed]
- Kohli, K.; Wei, Z.A.; Sadri, V.; Netto, T.; Lisko, J.C.; Greenbaum, A.B.; Babaliaros, V.; Oshinski, J.N.; Yoganathan, A.P. A Simplified In Silico Model of Left Ventricular Outflow in Patients After Transcatheter Mitral Valve Replacement with Anterior Leaflet Laceration. Ann. Biomed. Eng. 2021, 49, 1449–1461. [Google Scholar] [CrossRef] [PubMed]
- Spühler, J.H.; Jansson, J.; Jansson, N.; Hoffman, J. 3D fluid–structure interaction simulation of aortic valves using a unified continuum ALE FEM model. Front. Physiol. 2018, 9, 363. [Google Scholar] [CrossRef]
- Xu, F.; Kenjereš, S. Numerical simulations of flow patterns in the human left ventricle model with a novel dynamic mesh morphing approach based on radial basis function. Comput. Biol. Med. 2021, 130, 104184. [Google Scholar] [CrossRef]
- Kamensky, D.; Hsu, M.C.; Schillinger, D.; Evans, J.A.; Aggarwal, A.; Bazilevs, Y.; Sacks, M.S.; Hughes, T.J. An immersogeometric variational framework for fluid–structure interaction: Application to bioprosthetic heart valves. Comput. Methods Appl. Mech. Eng. 2015, 284, 1005–1053. [Google Scholar] [CrossRef]
- Farhat, C.; Lakshminarayan, V. An ALE formulation of embedded boundary methods for tracking boundary layers in turbulent fluid–structure interaction problems. J. Comput. Phys. 2014, 263, 53–70. [Google Scholar] [CrossRef]
- Zakerzadeh, R.; Hsu, M.C.; Sacks, M.S. Computational methods for the aortic heart valve and its replacements. Expert Rev. Med. Devices 2017, 14, 849–866. [Google Scholar] [CrossRef]
- Fedele, M.; Faggiano, E.; Dedè, L.; Quarteroni, A. A patient-specific aortic valve model based on moving resistive immersed implicit surfaces. Biomech. Model. Mechanobiol. 2017, 16, 1779–1803. [Google Scholar] [CrossRef]
- Takizawa, K.; Tezduyar, T.E.; Terahara, T.; Sasaki, T. Heart valve flow computation with the integrated space–time VMS, slip interface, topology change and isogeometric discretization methods. Comput. Fluids 2017, 158, 176–188. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Hsu, M.C.; Scott, M. Isogeometric fluid–structure interaction analysis with emphasis on non-matching discretizations, and with application to wind turbines. Comput. Methods Appl. Mech. Eng. 2012, 249, 28–41. [Google Scholar] [CrossRef]
- Hsu, M.C.; Kamensky, D.; Bazilevs, Y.; Sacks, M.S.; Hughes, T.J. Fluid–structure interaction analysis of bioprosthetic heart valves: Significance of arterial wall deformation. Comput. Mech. 2014, 54, 1055–1071. [Google Scholar] [CrossRef]
- Kamensky, D.; Evans, J.A.; Hsu, M.C.; Bazilevs, Y. Projection-based stabilization of interface Lagrange multipliers in immersogeometric fluid–thin structure interaction analysis, with application to heart valve modeling. Comput. Math. Appl. 2017, 74, 2068–2088. [Google Scholar] [CrossRef]
- Mao, W.; Li, K.; Sun, W. Fluid–structure interaction study of transcatheter aortic valve dynamics using smoothed particle hydrodynamics. Cardiovasc. Eng. Technol. 2016, 7, 374–388. [Google Scholar] [CrossRef]
- Pasta, S.; Cannata, S.; Gentile, G.; Di Giuseppe, M.; Cosentino, F.; Pasta, F.; Agnese, V.; Bellavia, D.; Raffa, G.M.; Pilato, M.; et al. Simulation study of transcatheter heart valve implantation in patients with stenotic bicuspid aortic valve. Med. Biol. Eng. Comput. 2020, 58, 815–829. [Google Scholar] [CrossRef]
- Caballero, A.; Mao, W.; McKay, R.; Sun, W. The impact of balloon-expandable transcatheter aortic valve replacement on concomitant mitral regurgitation: A comprehensive computational analysis. J. R. Soc. Interface 2019, 16, 20190355. [Google Scholar] [CrossRef]
- Lluch, È.; De Craene, M.; Bijnens, B.; Sermesant, M.; Noailly, J.; Camara, O.; Morales, H.G. Breaking the state of the heart: Meshless model for cardiac mechanics. Biomech. Model. Mechanobiol. 2019, 18, 1549–1561. [Google Scholar] [CrossRef]
- Caballero, A.; Mao, W.; McKay, R.; Hahn, R.T.; Sun, W. A comprehensive engineering analysis of left heart dynamics after MitraClip in a functional mitral regurgitation patient. Front. Physiol. 2020, 11, 432. [Google Scholar] [CrossRef]
- Qin, T.; Caballero, A.; Mao, W.; Barrett, B.; Kamioka, N.; Lerakis, S.; Sun, W. Patient-specific analysis of bicuspid aortic valve hemodynamics using a fully coupled fluid–structure interaction (FSI) model. medRxiv 2021. [Google Scholar] [CrossRef]
- Mayo, R.P.; Yaakobovich, H.; Finkelstein, A.; Shadden, S.C.; Marom, G. Impact of BASILICA on the thrombogenicity potential of valve-in-valve implantations. J. Biomech. 2021, 118, 110309. [Google Scholar] [CrossRef]
- Mutlu, O.; Salman, H.E.; Yalcin, H.C.; Olcay, A.B. Fluid flow characteristics of healthy and calcified aortic valves using three-dimensional Lagrangian coherent structures analysis. Fluids 2021, 6, 203. [Google Scholar] [CrossRef]
- Aidun, C.K.; Clausen, J.R. Lattice-Boltzmann method for complex flows. Annu. Rev. Fluid Mech. 2010, 42, 439–472. [Google Scholar] [CrossRef]
- Keating, B.; Vahala, G.; Yepez, J.; Soe, M.; Vahala, L. Entropic lattice Boltzmann representations required to recover Navier–Stokes flows. Phys. Rev. E 2007, 75, 036712. [Google Scholar] [CrossRef] [PubMed]
- Aidun, C.K.; Lu, Y. Lattice Boltzmann simulation of solid particles suspended in fluid. J. Stat. Phys. 1995, 81, 49–61. [Google Scholar] [CrossRef]
- Aidun, C.K.; Lu, Y.; Ding, E.J. Direct analysis of particulate suspensions with inertia using the discrete Boltzmann equation. J. Fluid Mech. 1998, 373, 287–311. [Google Scholar] [CrossRef]
- Ziegler, D.P. Boundary conditions for lattice Boltzmann simulations. J. Stat. Phys. 1993, 71, 1171–1177. [Google Scholar] [CrossRef]
- Ginzbourg, I.; Adler, P. Boundary flow condition analysis for the three-dimensional lattice Boltzmann model. J. Phys. II 1994, 4, 191–214. [Google Scholar] [CrossRef]
- Noble, D.R.; Chen, S.; Georgiadis, J.G.; Buckius, R.O. A consistent hydrodynamic boundary condition for the lattice Boltzmann method. Phys. Fluids 1995, 7, 203–209. [Google Scholar] [CrossRef]
- Pan, C.; Luo, L.S.; Miller, C.T. An evaluation of lattice Boltzmann schemes for porous medium flow simulation. Comput. Fluids 2006, 35, 898–909. [Google Scholar] [CrossRef]
- Wu, J.; Aidun, C.K. Simulating 3D deformable particle suspensions using lattice Boltzmann method with discrete external boundary force. Int. J. Numer. Methods Fluids 2010, 62, 765–783. [Google Scholar] [CrossRef]
- Yun, B.M.; Wu, J.; Simon, H.A.; Arjunon, S.; Sotiropoulos, F.; Aidun, C.K.; Yoganathan, A.P. A numerical investigation of blood damage in the hinge area of aortic bileaflet mechanical heart valves during the leakage phase. Ann. Biomed. Eng. 2012, 40, 1468–1485. [Google Scholar] [CrossRef]
- Wu, J.; Aidun, C.K. A method for direct simulation of flexible fiber suspensions using lattice Boltzmann equation with external boundary force. Int. J. Multiph. Flow 2010, 36, 202–209. [Google Scholar] [CrossRef]
- Wang, C.H.; Ho, J.R. A lattice Boltzmann approach for the non-Newtonian effect in the blood flow. Comput. Math. Appl. 2011, 62, 75–86. [Google Scholar] [CrossRef]
- Gabbanelli, S.; Drazer, G.; Koplik, J. Lattice Boltzmann method for non-Newtonian (power-law) fluids. Phys. Rev. E 2005, 72, 046312. [Google Scholar] [CrossRef]
- Min Yun, B.; Aidun, C.K.; Yoganathan, A.P. Blood damage through a bileaflet mechanical heart valve: A quantitative computational study using a multiscale suspension flow solver. J. Biomech. Eng. 2014, 136, 101009. [Google Scholar] [CrossRef]
- Yun, B.M.; Dasi, L.; Aidun, C.; Yoganathan, A. Highly resolved pulsatile flows through prosthetic heart valves using the entropic lattice-Boltzmann method. J. Fluid Mech. 2014, 754, 122–160. [Google Scholar] [CrossRef]
- Dumont, K.; Vierendeels, J.; Kaminsky, R.; Van Nooten, G.; Verdonck, P.; Bluestein, D. Comparison of the hemodynamic and thrombogenic performance of two bileaflet mechanical heart valves using a CFD/FSI model. J. Biomech. Eng. 2007, 129, 558–565. [Google Scholar] [CrossRef]
- Mamalakis, M.; Garg, P.; Nelson, T.; Lee, J.; Wild, J.M.; Clayton, R.H. MA-SOCRATIS: An automatic pipeline for robust segmentation of the left ventricle and scar. Comput. Med. Imaging Graph. 2021, 93, 101982. [Google Scholar] [CrossRef]
- Kong, F.; Shadden, S.C. Whole Heart Mesh Generation For Image-Based Computational Simulations by Learning Free-From Deformations. arXiv 2021, arXiv:2107.10839. [Google Scholar]
- Assi, K.C.; Gay, E.; Chnafa, C.; Mendez, S.; Nicoud, F.; Abascal, J.F.; Lantelme, P.; Tournoux, F.; Garcia, D. Intraventricular vector flow mapping—A Doppler-based regularized problem with automatic model selection. Phys. Med. Biol. 2017, 62, 7131. [Google Scholar] [CrossRef]
- Lantz, J.; Gupta, V.; Henriksson, L.; Karlsson, M.; Persson, A.; Carlhäll, C.J.; Ebbers, T. Intracardiac flow at 4D CT: Comparison with 4D flow MRI. Radiology 2018, 289, 51–58. [Google Scholar] [CrossRef] [PubMed]
- Seo, J.H.; Vedula, V.; Abraham, T.; Mittal, R. Multiphysics computational models for cardiac flow and virtual cardiography. Int. J. Numer. Methods Biomed. Eng. 2013, 29, 850–869. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.; Seo, J.H.; Mittal, R. Computational modeling and analysis of murmurs generated by modeled aortic stenoses. J. Biomech. Eng. 2019, 141, online ahead of print. [Google Scholar] [CrossRef] [PubMed]
- Bailoor, S.; Seo, J.H.; Dasi, L.; Schena, S.; Mittal, R. Prosthetic Valve Monitoring via In Situ Pressure Sensors: In Silico Concept Evaluation using Supervised Learning. Cardiovasc. Eng. Technol. 2021, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Habibi, M.; D’Souza, R.M.; Dawson, S.T.; Arzani, A. Integrating multi-fidelity blood flow data with reduced-order data assimilation. Comput. Biol. Med. 2021, 135, 104566. [Google Scholar] [CrossRef]
- Arzani, A.; Dawson, S.T. Data-driven cardiovascular flow modelling: Examples and opportunities. J. R. Soc. Interface 2021, 18, 20200802. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Sun, L.; Gao, H.; Pan, S.; Wang, J.X. Surrogate modeling for fluid flows based on physics-constrained deep learning without simulation data. Comput. Methods Appl. Mech. Eng. 2020, 361, 112732. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le, T.B.; Usta, M.; Aidun, C.; Yoganathan, A.; Sotiropoulos, F. Computational Methods for Fluid-Structure Interaction Simulation of Heart Valves in Patient-Specific Left Heart Anatomies. Fluids 2022, 7, 94. https://doi.org/10.3390/fluids7030094
Le TB, Usta M, Aidun C, Yoganathan A, Sotiropoulos F. Computational Methods for Fluid-Structure Interaction Simulation of Heart Valves in Patient-Specific Left Heart Anatomies. Fluids. 2022; 7(3):94. https://doi.org/10.3390/fluids7030094
Chicago/Turabian StyleLe, Trung Bao, Mustafa Usta, Cyrus Aidun, Ajit Yoganathan, and Fotis Sotiropoulos. 2022. "Computational Methods for Fluid-Structure Interaction Simulation of Heart Valves in Patient-Specific Left Heart Anatomies" Fluids 7, no. 3: 94. https://doi.org/10.3390/fluids7030094
APA StyleLe, T. B., Usta, M., Aidun, C., Yoganathan, A., & Sotiropoulos, F. (2022). Computational Methods for Fluid-Structure Interaction Simulation of Heart Valves in Patient-Specific Left Heart Anatomies. Fluids, 7(3), 94. https://doi.org/10.3390/fluids7030094





