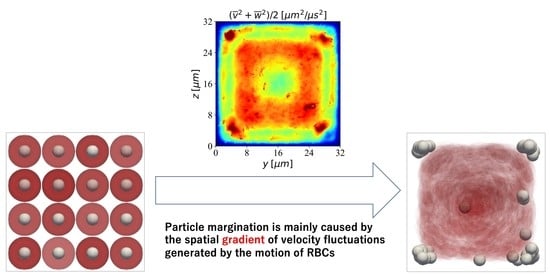
Numerical Study of Particle Margination in a Square Channel Flow with Red Blood Cells
Abstract
1. Introduction
2. Numerical Methods
2.1. Governing Equations for Fluid–Membrane Interaction Problems
2.2. Discretization
2.3. Simulation Conditions
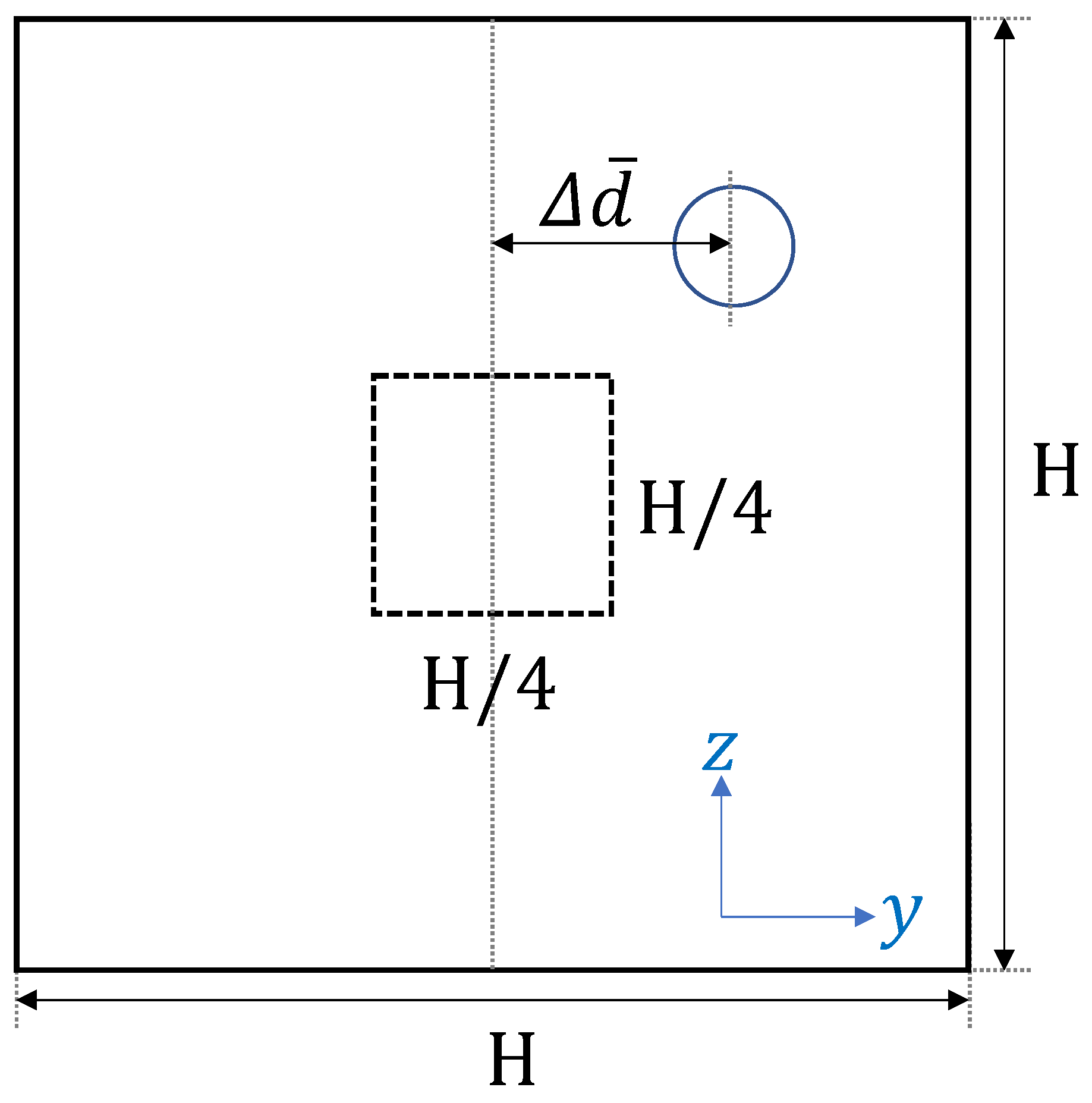
2.4. Evaluation of Particle Migration toward the Near-Wall Region
3. Results
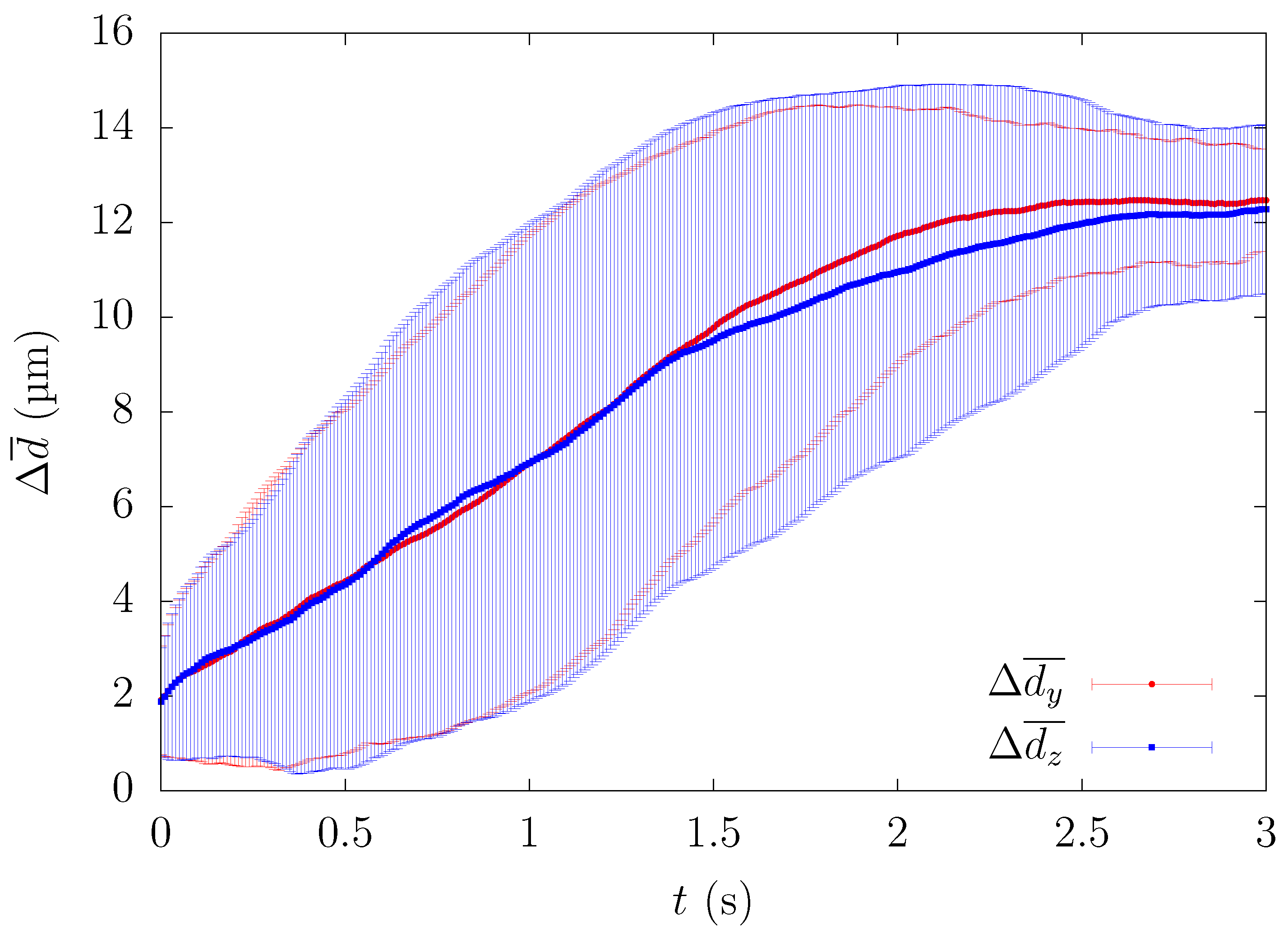
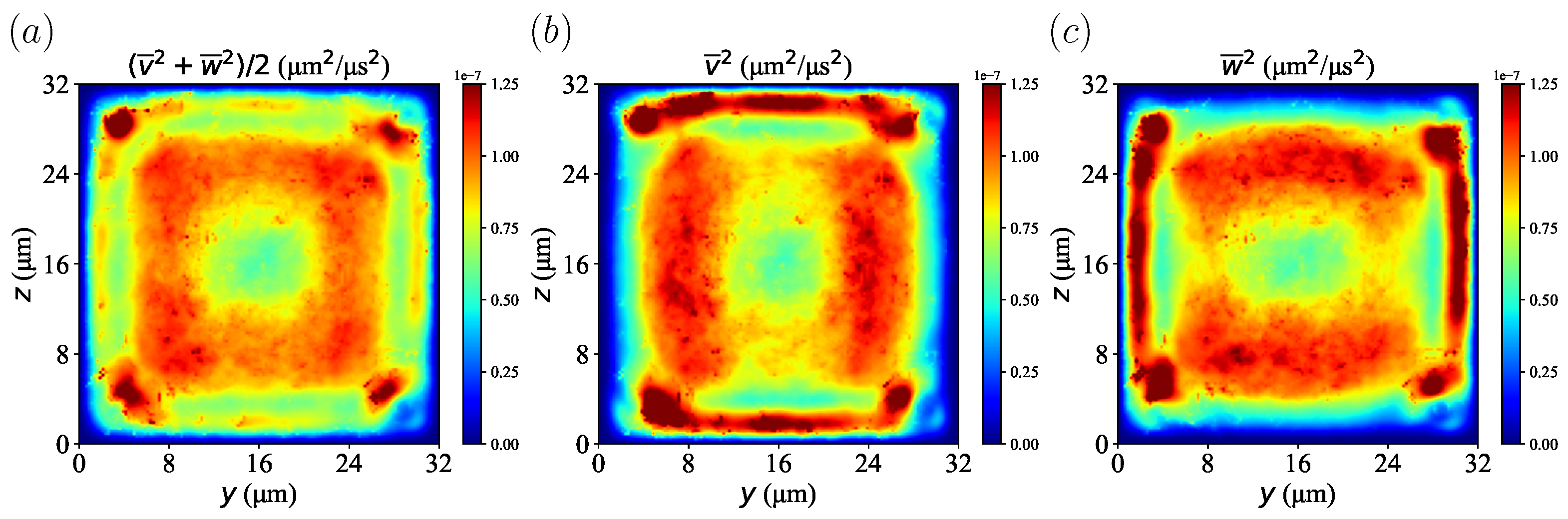
3.1. Direction Dependency of Particle Migration
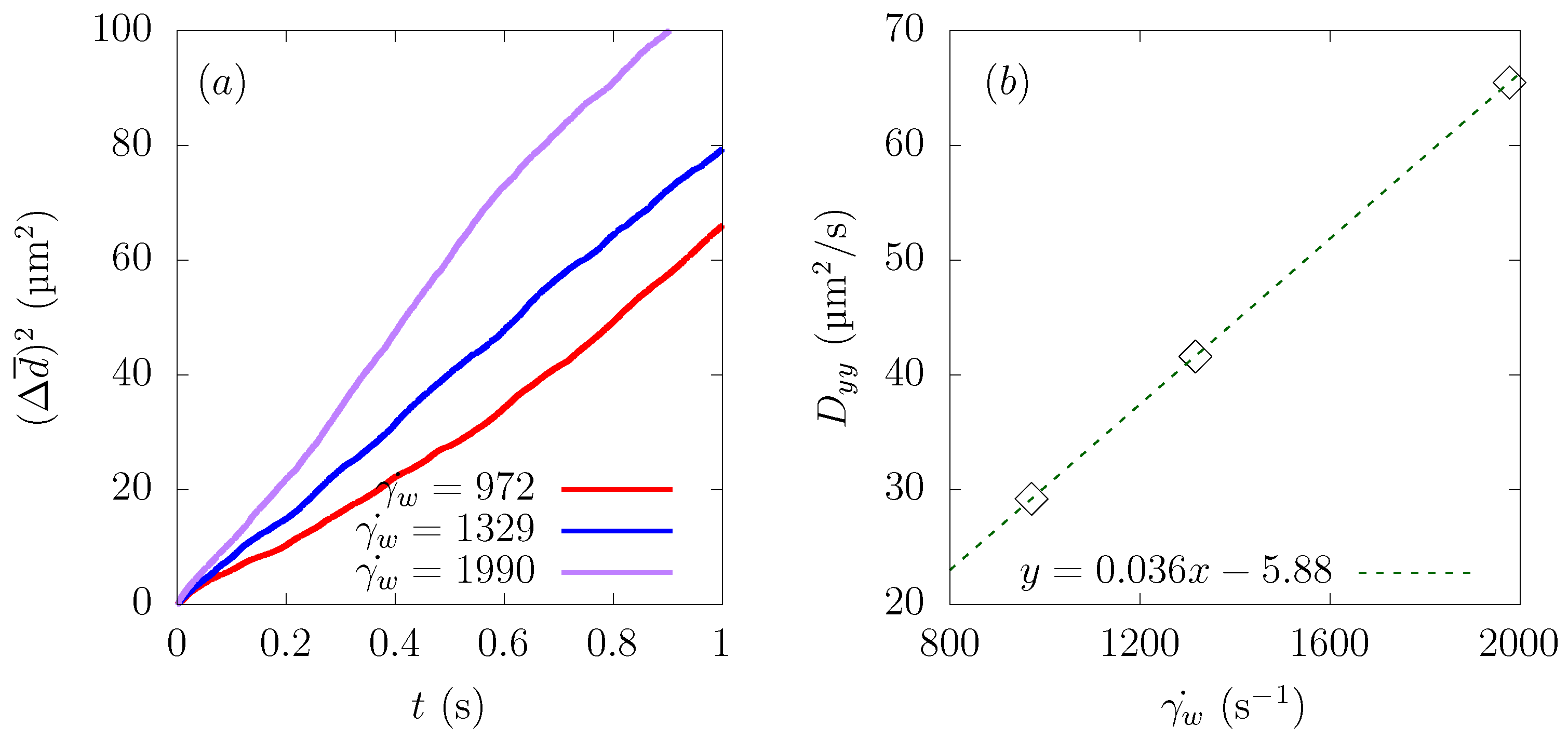
3.2. Shear Rate Dependency
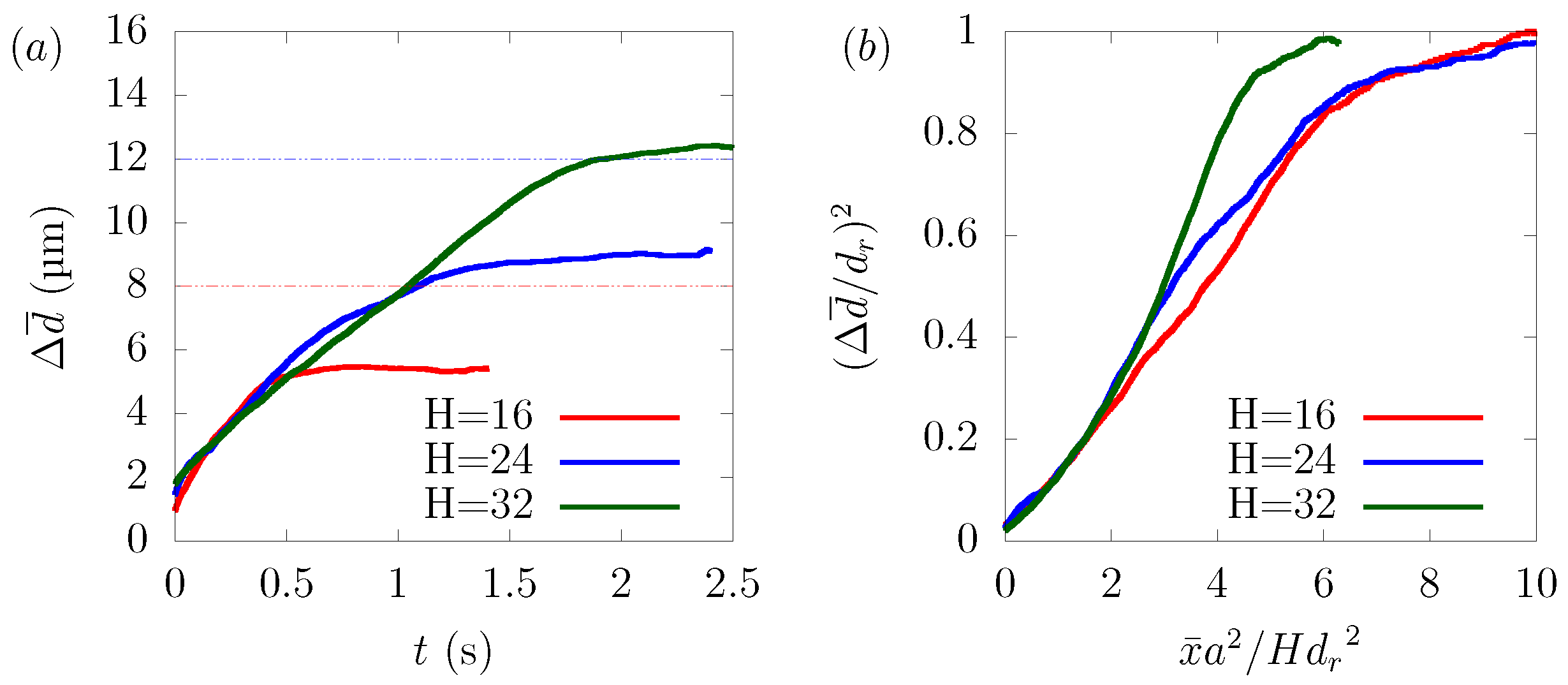
3.3. Channel Size Dependency
3.4. Hematocrit Dependency
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
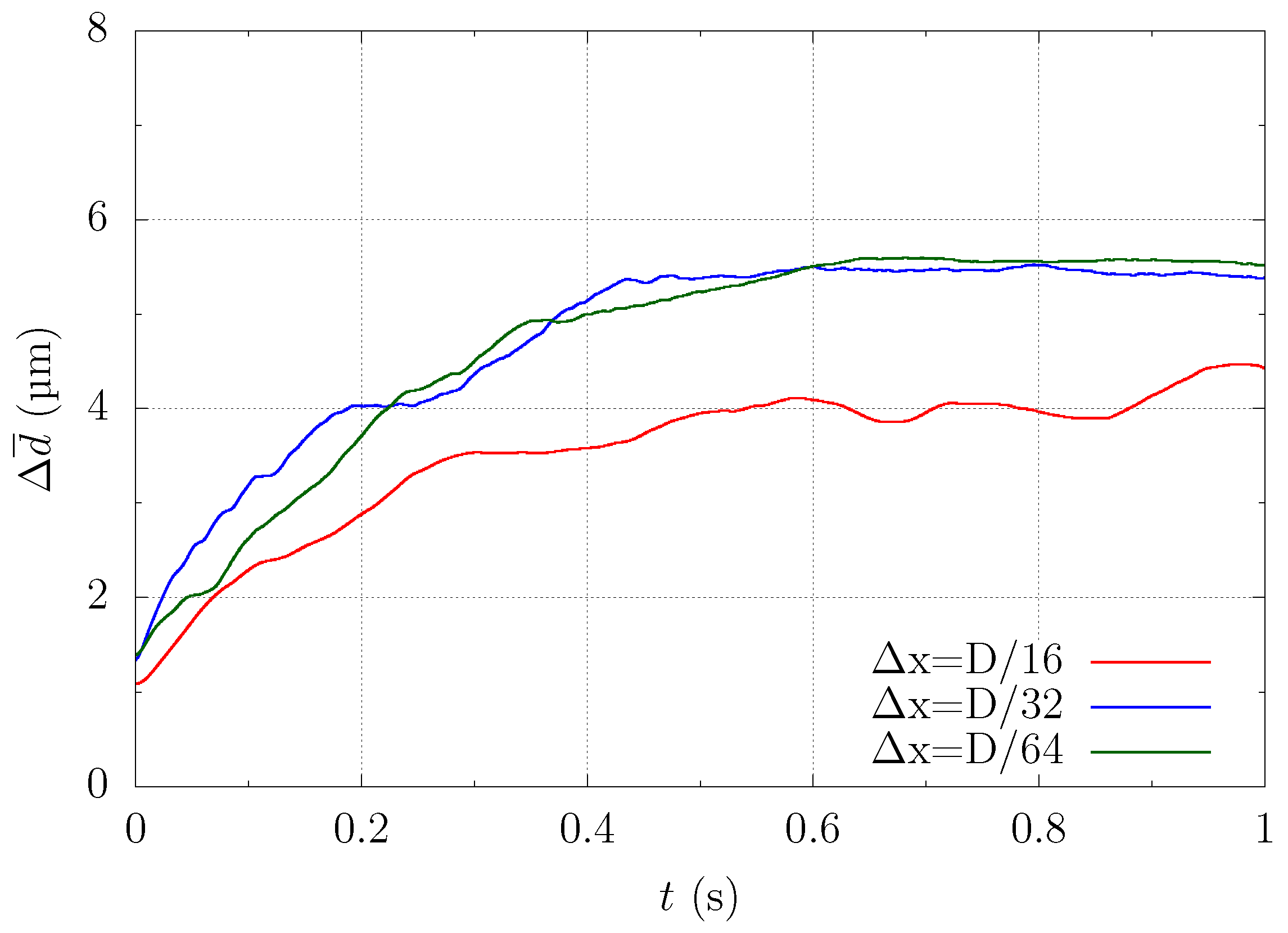
Appendix A. Grid Size Dependency

References
- Grandchamp, X.; Coupier, G.; Srivastav, A.; Minetti, C.; Podgorski, T. Lift and down-gradient shear-induced diffusion in red blood cell suspensions. Phys. Rev. Lett. 2013, 110, 108101. [Google Scholar] [CrossRef]
- Fåhræus, R.; Lindqvist, T. The viscosity of the blood in narrow capillary tubes. Am. J. Physiol.-Leg. Content 1931, 96, 562–568. [Google Scholar] [CrossRef]
- Pries, A.R.; Neuhaus, D.; Gaehtgens, P. Blood viscosity in tube flow: Dependence on diameter and hematocrit. Am. J. Physiol.-Heart Circ. Physiol. 1992, 263, H1770–H1778. [Google Scholar] [CrossRef]
- Radmacher, M.; Fritz, M.; Kacher, C.M.; Cleveland, J.P.; Hansma, P.K. Measuring the viscoelastic properties of human platelets with the atomic force microscope. Biophys. J. 1996, 70, 556–567. [Google Scholar] [CrossRef]
- Pozrikidis, C. Orbiting motion of a freely suspended spheroid near a plane wall. J. Fluid Mech. 2005, 541, 105–114. [Google Scholar] [CrossRef]
- Goto, S.; Hasebe, T.; Takagi, S. Platelets: Small in Size But Essential in the Regulation of Vascular Homeostasis. Circ. J. 2015, 79, 1871–1881. [Google Scholar] [CrossRef]
- Yeh, C.; Eckstein, E.C. Transient lateral transport of platelet-sized particles in flowing blood suspensions. Biophys. J. 1994, 66, 1706–1716. [Google Scholar] [CrossRef]
- Tokarev, A.A.; Butylin, A.A.; Ermakova, E.A.; Shnol, E.E.; Panasenko, G.P.; Ataullakhanov, F.I. Finite platelet size could be responsible for platelet margination effect. Biophys. J. 2011, 101, 1835–1843. [Google Scholar] [CrossRef][Green Version]
- Tangelder, G.J.; Teirlinck, H.C.; Slaaf, D.W.; Reneman, R.S. Distribution of blood platelets flowing in arterioles. Am. J. Physiol.-Heart Circ. Physiol. 1985, 248, H318–H323. [Google Scholar] [CrossRef]
- Tilles, A.W.; Eckstein, E.C. The near-wall excess of platelet-sized particles in blood flow: Its dependence on hematocrit and wall shear rate. Microvasc. Res. 1987, 33, 211–223. [Google Scholar] [CrossRef]
- Aarts, P.A.; Steendijk, P.; Sixma, J.J.; Heethaar, R.M. Fluid shear as a possible mechanism for platelet diffusivity in flowing blood. J. Biomech. 1986, 19, 799–805. [Google Scholar] [CrossRef]
- Sugihara-Seki, M.; Onozawa, T.; Takinouchi, N.; Itano, T.; Seki, J. Development of margination of platelet-sized particles in red blood cell suspensions flowing through Y-shaped bifurcating microchannels. Biorheology 2020, 57, 101–116. [Google Scholar] [CrossRef]
- Eckstein, E.C.; Belgacem, F. Model of platelet transport in flowing blood with drift and diffusion terms. Biophys. J. 1991, 60, 53–69. [Google Scholar] [CrossRef]
- AlMomani, T.; Udaykumar, H.S.; Marshall, J.S.; Chandran, K.B. Micro-scale dynamic simulation of erythrocyte-platelet interaction in blood flow. Ann. Biomed. Eng. 2008, 36, 905–920. [Google Scholar] [CrossRef]
- Crowl, L.; Fogelson, A.L. Analysis of mechanisms for platelet near-wall excess under arterial blood flow conditions. J. Fluid Mech. 2011, 676, 348–375. [Google Scholar] [CrossRef]
- Mehrabadi, M.; Ku, D.N.; Aidun, C.K. Effects of shear rate, confinement, and particle parameters on margination in blood flow. Phys. Rev. E 2016, 93, 023109. [Google Scholar] [CrossRef]
- Chang, H.Y.; Yazdani, A.; Li, X.; Douglas, K.A.; Mantzoros, C.S.; Karniadakis, G.E. Quantifying Platelet Margination in Diabetic Blood Flow. Biophys. J. 2018, 115, 1371–1382. [Google Scholar] [CrossRef]
- Czaja, B.; Gutierrez, M.; Závodszky, G.; de Kanter, D.; Hoekstra, A.; Eniola-Adefeso, O. The influence of red blood cell deformability on hematocrit profiles and platelet margination. PLoS Comput. Biol. 2020, 16, e1007716. [Google Scholar] [CrossRef]
- Krüger, T. Effect of tube diameter and capillary number on platelet margination and near-wall dynamics. Rheol. Acta 2016, 55, 511–526. [Google Scholar] [CrossRef]
- Kumar, A.; Graham, M.D. Mechanism of margination in confined flows of blood and other multicomponent suspensions. Phys. Rev. Lett. 2012, 109, 108102. [Google Scholar] [CrossRef]
- Sugihara-Seki, M.; Takinouchi, N. Margination of platelet-sized particles in the red blood cell suspension flow through square microchannels. Micromachines 2021, 12, 1175. [Google Scholar] [CrossRef]
- Zhao, H.; Shaqfeh, E.S.; Narsimhan, V. Shear-induced particle migration and margination in a cellular suspension. Phys. Fluids 2012, 24, 011902. [Google Scholar] [CrossRef]
- Ii, S.; Shimizu, K.; Sugiyama, K.; Takagi, S. Continuum and stochastic approach for cell adhesion process based on Eulerian fluid-capsule coupling with Lagrangian markers. J. Comput. Phys. 2018, 374, 769–786. [Google Scholar] [CrossRef]
- Zhao, H.; Shaqfeh, E.S. Shear-induced platelet margination in a microchannel. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2011, 83, 061924. [Google Scholar] [CrossRef]
- Takeishi, N.; Imai, Y.; Wada, S. Capture event of platelets by bolus flow of red blood cells in capillaries. J. Biomech. Sci. Eng. 2019, 14, 18–00535. [Google Scholar] [CrossRef]
- Peskin, C.S. Flow patterns around heart valves: A numerical method. J. Comput. Phys. 1972, 10, 252–271. [Google Scholar] [CrossRef]
- Unverdi, S.O.; Tryggvason, G. A front-tracking method for viscous, incompressible, multi-fluid flows. J. Comput. Phys. 1992, 100, 25–37. [Google Scholar] [CrossRef]
- Skalak, R.; Tozeren, A.; Zarda, R.P.; Chien, S. Strain Energy Function of Red Blood Cell Membranes. Biophys. J. 1973, 13, 245–264. [Google Scholar] [CrossRef]
- Pozrikidis, C. Effect of membrane bending stiffness on the deformation of capsules in simple shear flow. J. Fluid Mech. 2001, 440, 269–291. [Google Scholar] [CrossRef]
- Walter, J.; Salsac, A.V.; Barthès-Biesel, D.; le Tallec, P. Coupling of finite element and boundary integral methods for a capsule in a Stokes flow. Int. J. Numer. Methods Eng. 2010, 83, 829–850. [Google Scholar] [CrossRef]
- Amsden, A.; Harlow, F. A simplified MAC technique for incompressible fluid flow calculations. J. Comput. Phys. 1970, 6, 322–325. [Google Scholar] [CrossRef]
- Jing, P.; Ii, S.; Wang, X.; Sugiyama, K.; Noda, S.; Gong, X. Effects of fluid-cell-vessel interactions on the membrane tensions of circulating tumor cells in capillary blood flows. Phys. Fluids 2022, 34, 031904. [Google Scholar] [CrossRef]
- Takeishi, N.; Imai, Y.; Nakaaki, K.; Yamaguchi, T.; Ishikawa, T. Leukocyte margination at arteriole shear rate. Physiol. Rep. 2014, 2, e12037. [Google Scholar] [CrossRef] [PubMed]
- Evans, E.A.; La Celle, P.L. Intrinsic material properties of the erythrocyte membrane indicated by mechanical analysis of deformation. Blood 1975, 45, 29–43. [Google Scholar] [CrossRef] [PubMed]
- Evans, E.A.; Waugh, R.; Melnik, L. Elastic area compressibility modulus of red cell membrane. Biophys. J. 1976, 16, 585–595. [Google Scholar] [CrossRef]
- Evans, E.A. Bending elastic modulus of red blood cell membrane derived from buckling instability in micropipet aspiration tests. Biophys. J. 1983, 43, 27–30. [Google Scholar] [CrossRef]
- Frojmovic, M.M.; Milton, J.G. Human platelet size, shape, and related functions in health and disease. Physiol. Rev. 1982, 62, 185–261. [Google Scholar] [CrossRef]
- Miller, C. Predicting Non-Newtonian Flow Behavior in Ducts of Unusual Cross Section. Ind. Eng. Chem. Fundam. 1972, 11, 524–528. [Google Scholar] [CrossRef]
- Katanov, D.; Gompper, G.; Fedosov, D.A. Microvascular blood flow resistance: Role of red blood cell migration and dispersion. Microvasc. Res. 2015, 99, 57–66. [Google Scholar] [CrossRef]
- Vahidkhah, K.; Diamond, S.L.; Bagchi, P. Platelet dynamics in three-dimensional simulation of whole blood. Biophys. J. 2014, 106, 2529–2540. [Google Scholar] [CrossRef]
- Leighton, D.; Acrivos, A. Measurement of shear induced self diffusion in concentrated suspensions of spheres. J. Fluid Mech. 1987, 177, 109–131. [Google Scholar] [CrossRef]
- Závodszky, G.; Van Rooij, B.; Czaja, B.; Azizi, V.; De Kanter, D.; Hoekstra, A.G. Red blood cell and platelet diffusivity and margination in the presence of cross-stream gradients in blood flows. Phys. Fluids 2019, 31, 031903. [Google Scholar] [CrossRef]
- Talbot, L.; Cheng, R.K.; Schefer, R.W.; Willis, D.R. Thermophoresis of particles in a heated boundary layer. J. Fluid Mech. 1980, 101, 737–758. [Google Scholar] [CrossRef]
- Reeks, M.W. The transport of discrete particles in inhomogeneous turbulence. J. Aerosol Sci. 1983, 14, 729–739. [Google Scholar] [CrossRef]
- Caporaloni, M.; Tampieri, F.; Trombetti, F.; Vittori, O. Transfer of particles in nonisotropic air turbulence. J. Atmos. Sci. 1975, 32, 565–568. [Google Scholar] [CrossRef]
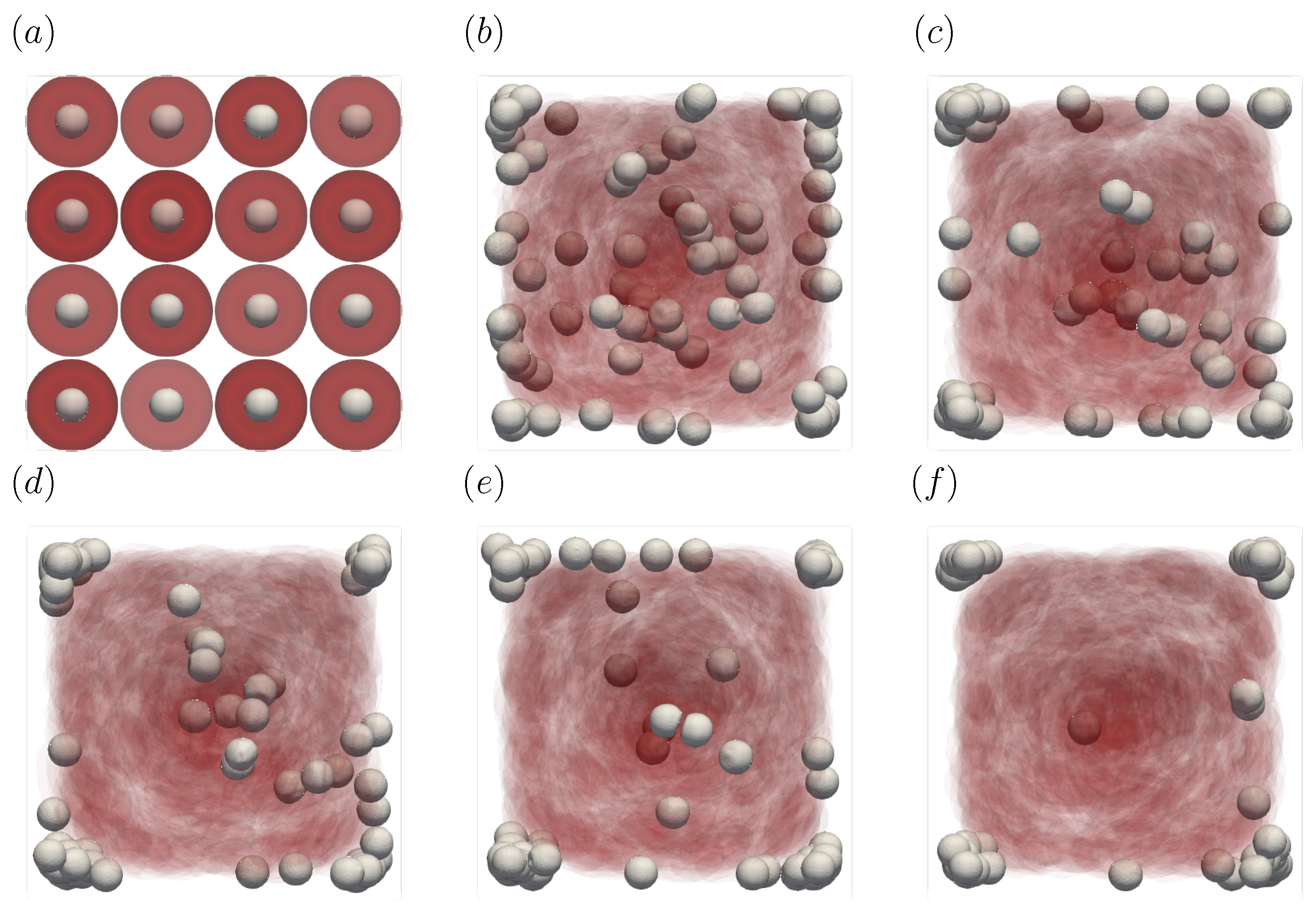
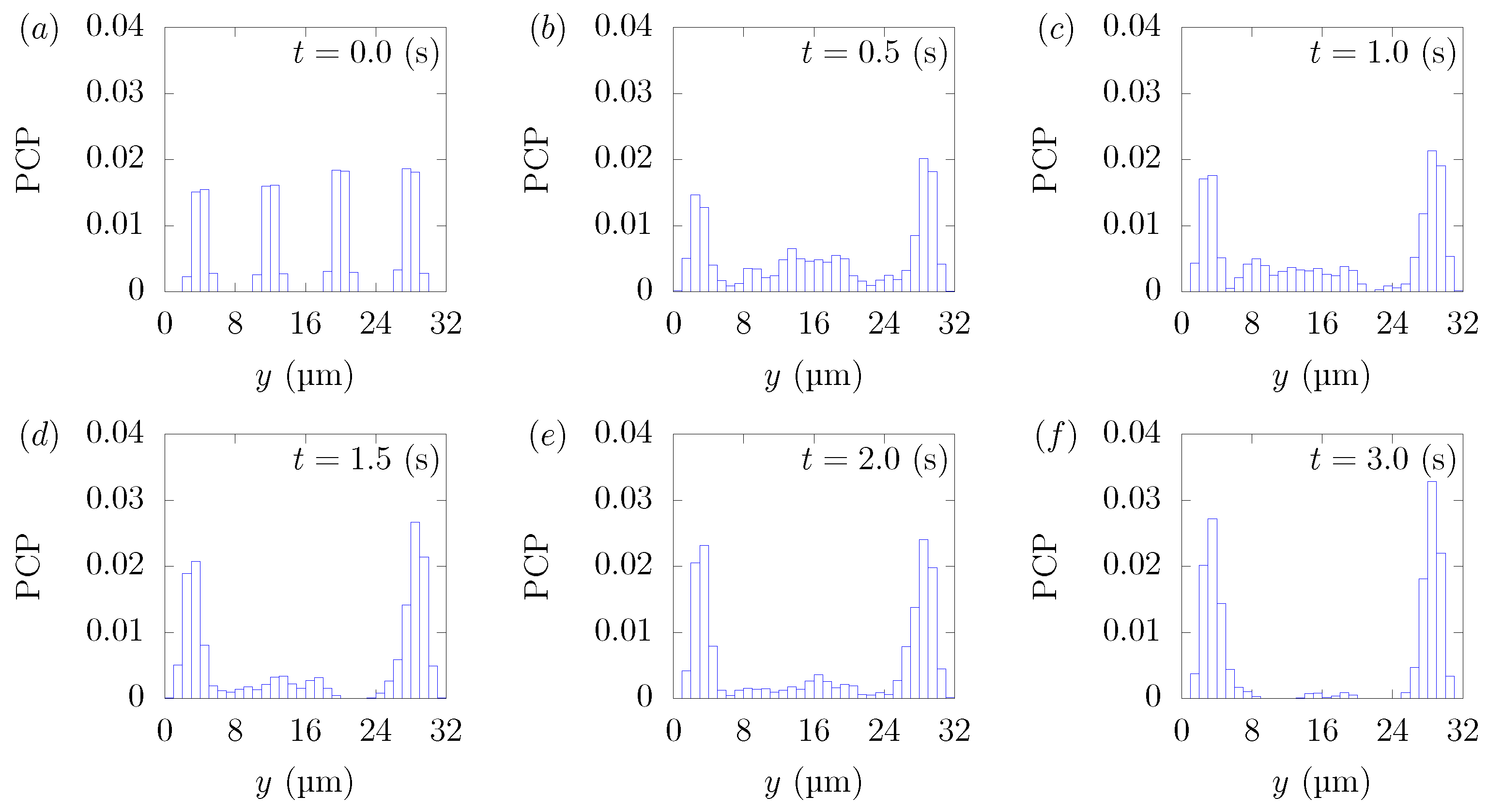
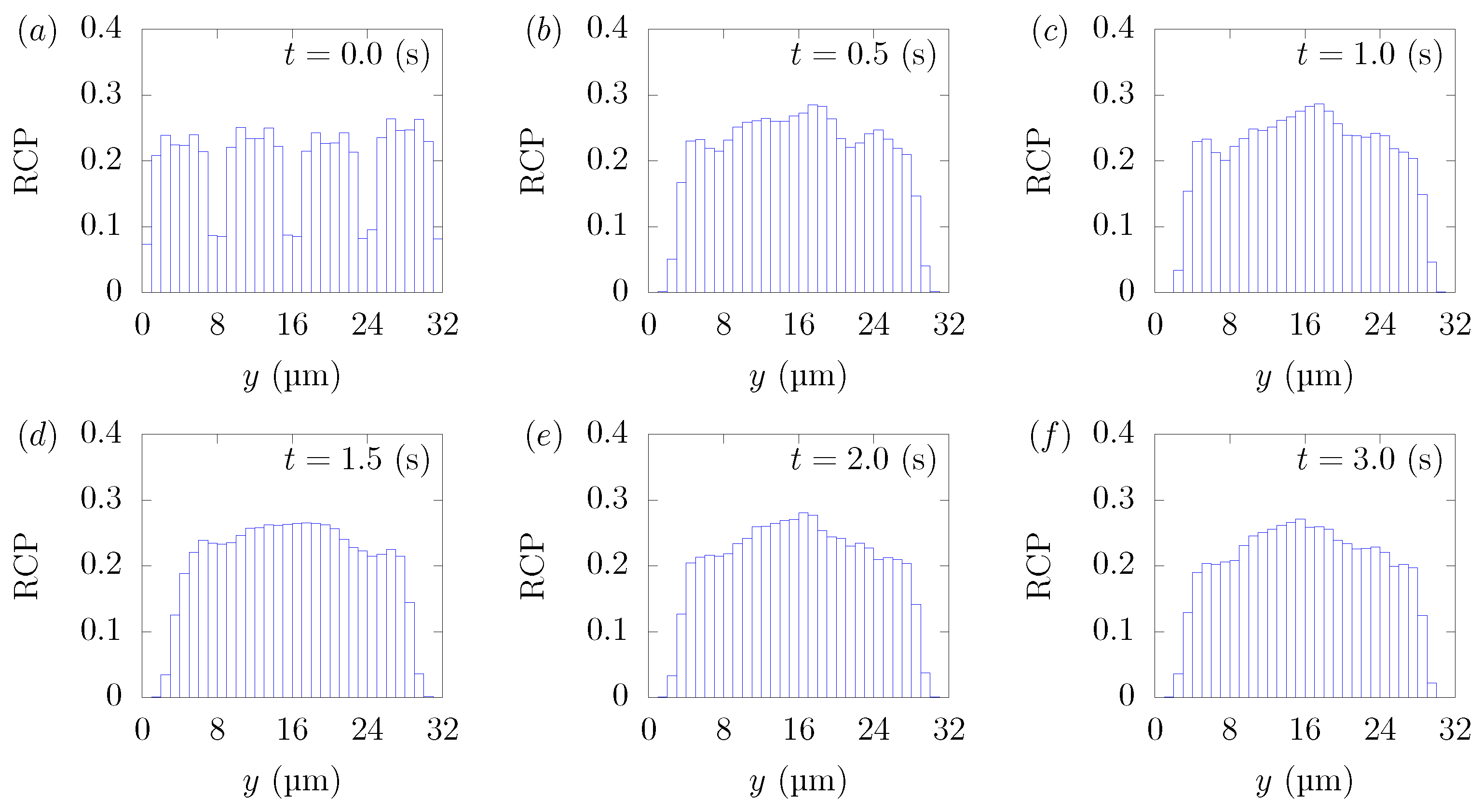
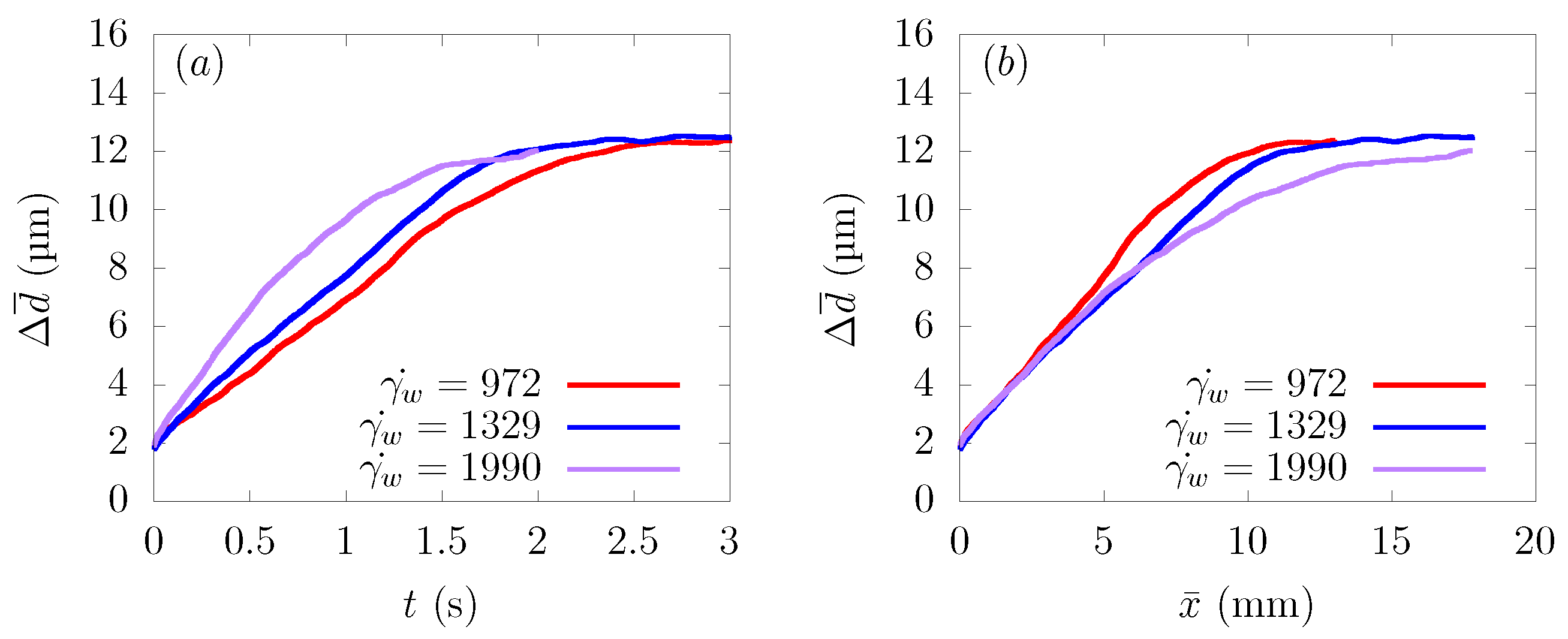
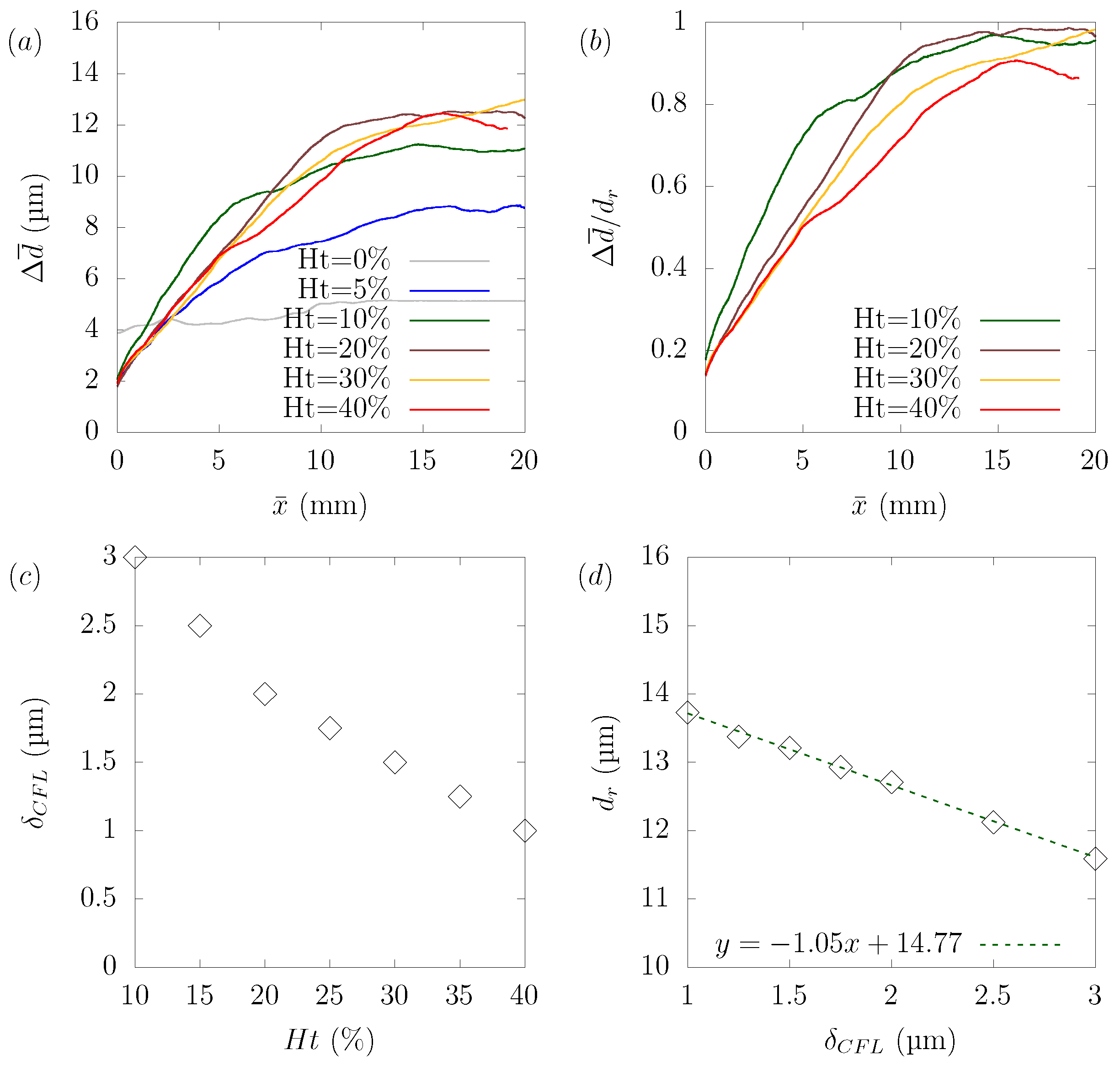


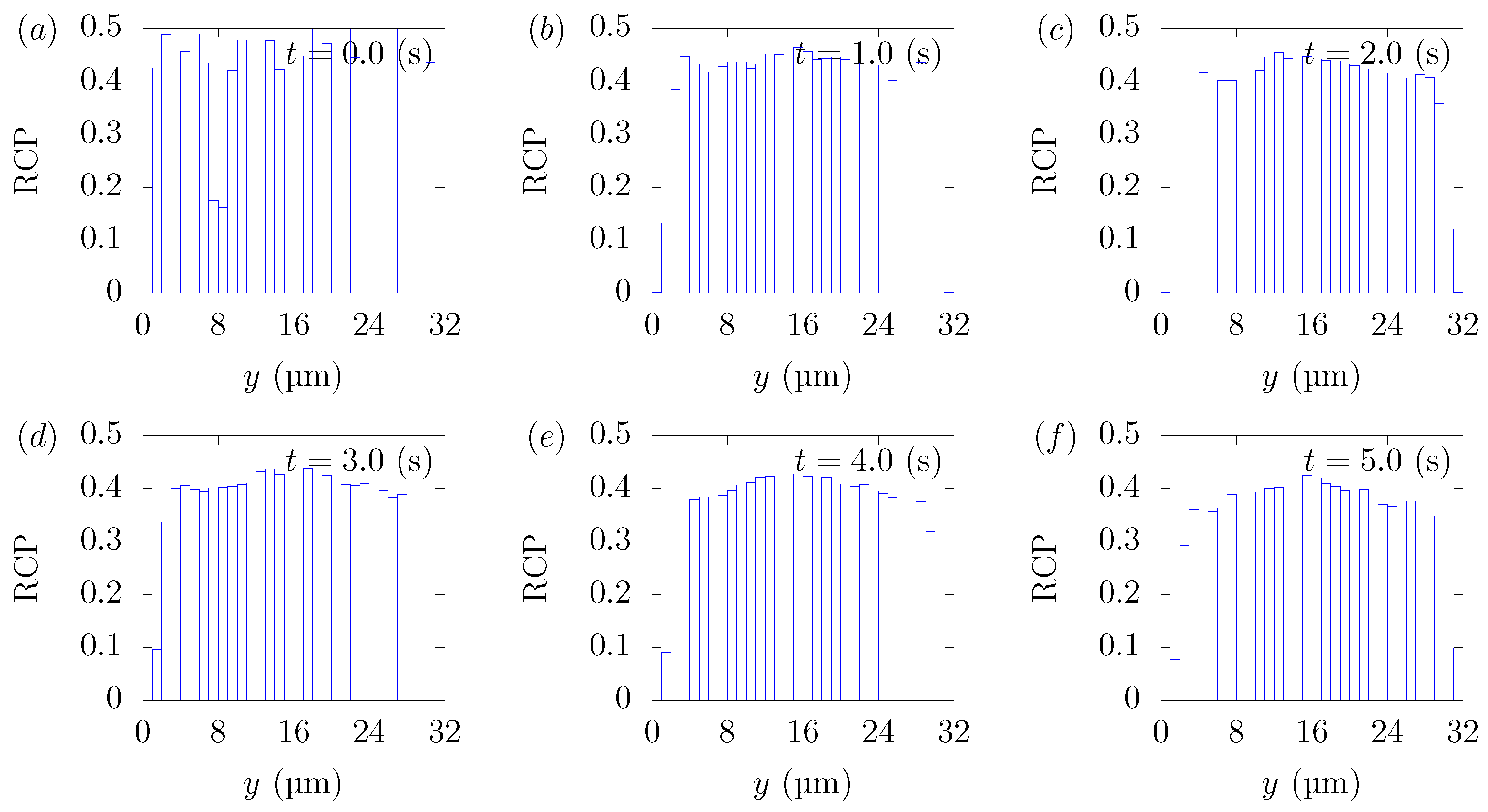

| U (m/s) | (s) | ||
|---|---|---|---|
| 0.0044 | 0.66 | 0.116 | 972 |
| 0.0059 | 0.90 | 0.159 | 1329 |
| 0.0089 | 1.35 | 0.238 | 1990 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oh, D.; Ii, S.; Takagi, S. Numerical Study of Particle Margination in a Square Channel Flow with Red Blood Cells. Fluids 2022, 7, 96. https://doi.org/10.3390/fluids7030096
Oh D, Ii S, Takagi S. Numerical Study of Particle Margination in a Square Channel Flow with Red Blood Cells. Fluids. 2022; 7(3):96. https://doi.org/10.3390/fluids7030096
Chicago/Turabian StyleOh, Dongig, Satoshi Ii, and Shu Takagi. 2022. "Numerical Study of Particle Margination in a Square Channel Flow with Red Blood Cells" Fluids 7, no. 3: 96. https://doi.org/10.3390/fluids7030096
APA StyleOh, D., Ii, S., & Takagi, S. (2022). Numerical Study of Particle Margination in a Square Channel Flow with Red Blood Cells. Fluids, 7(3), 96. https://doi.org/10.3390/fluids7030096