From Two-Equation Turbulence Models to Minimal Error Resolving Simulation Methods for Complex Turbulent Flows
Abstract
1. Introduction
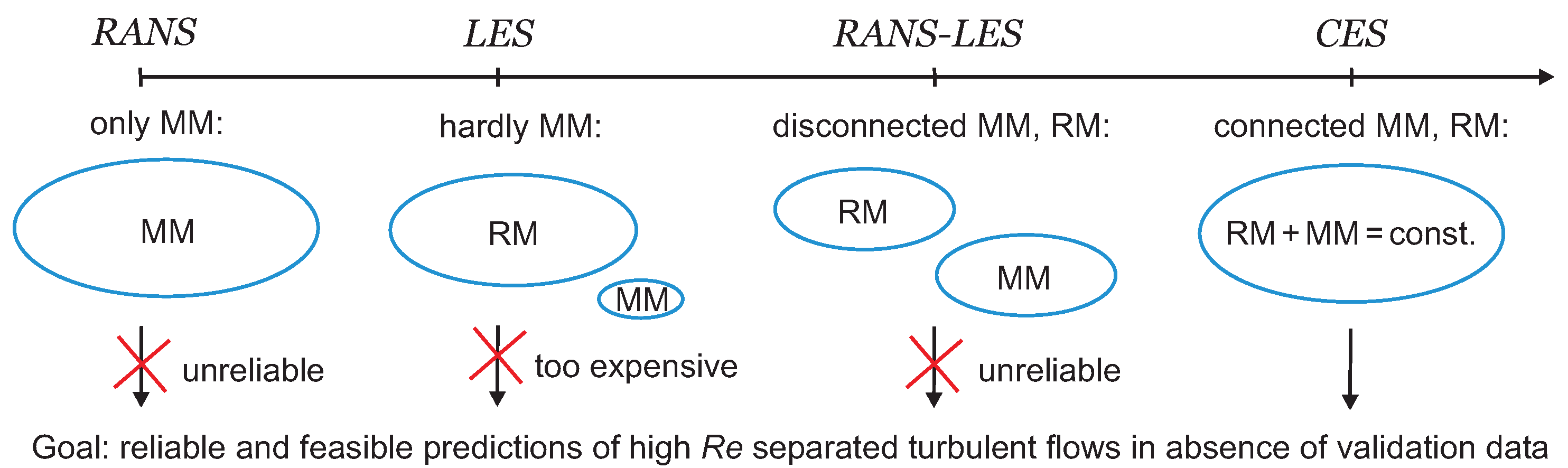
2. Basic Problems of Existing Hybrid RANS-LES Methods
3. Challenges
3.1. NASA’s CFD 2030 Vision
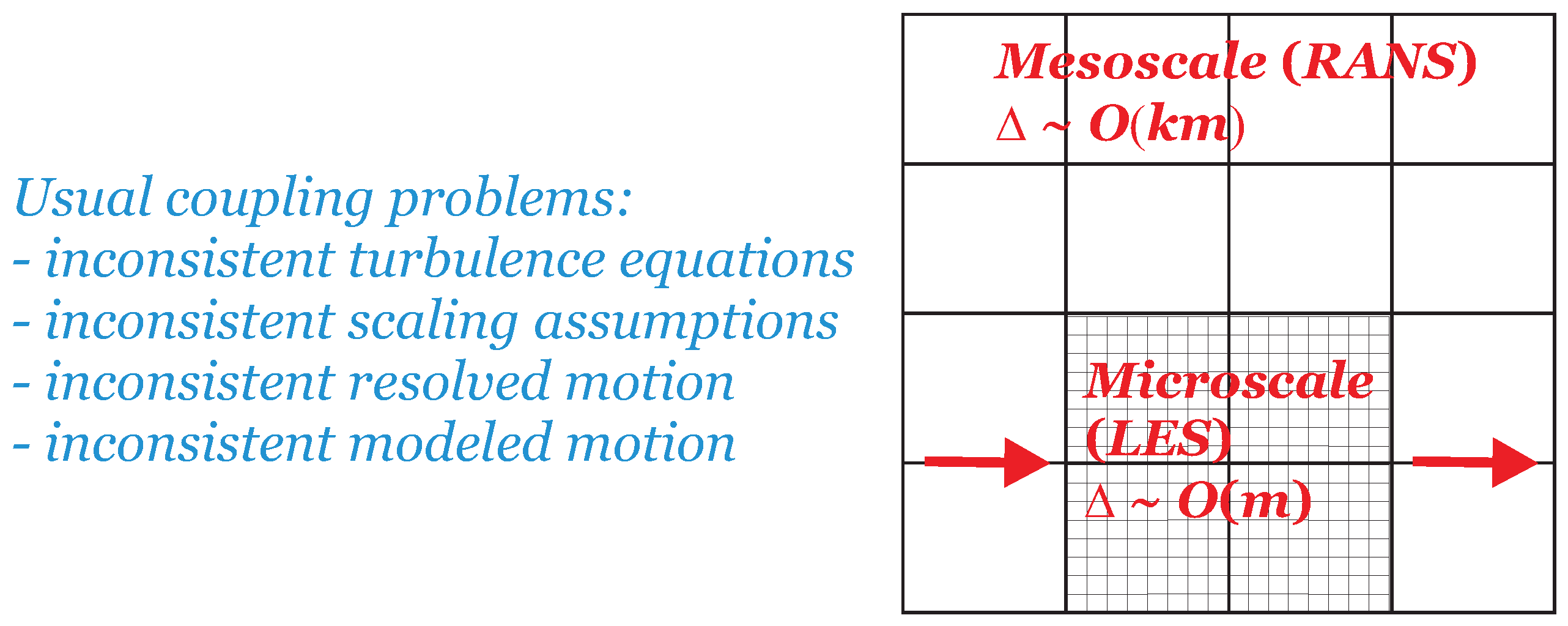
3.2. Atmospheric Mesoscale to Microscale Coupling
3.3. High Angle of Attack Supersonic and Hypersonic Flow Predictions
4. Minimal Error Methods
4.1. Incompressible Flows
4.2. Stratified Flows
4.3. Compressible Flows
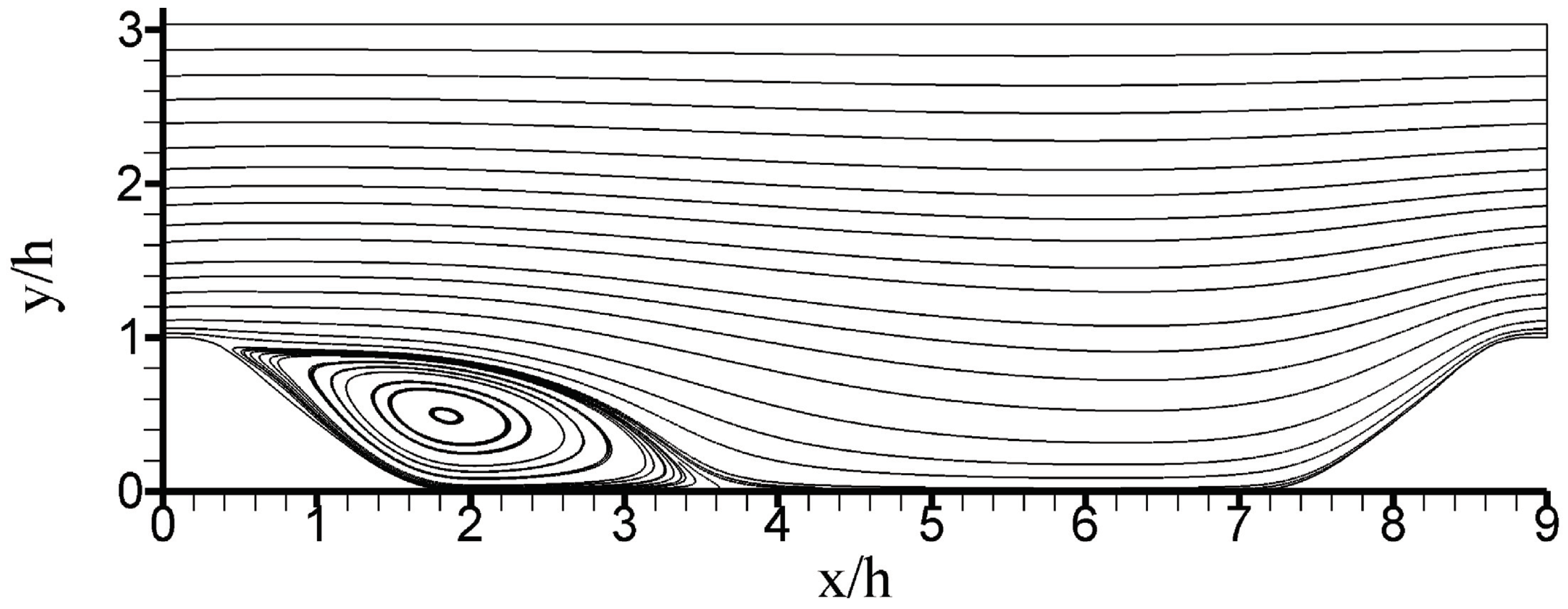
5. Applications: Periodic Hill Flow Simulations
- Problem : The most relevant fact is the conclusion that the “RANS-LES swing” was fully functional. There was a stable redistribution between the resolved and modeled motions, depending on the grid and variations. In particular, a spatially relatively uniform mode variation reflected by the resolution indicator was found.
- Problem : In regard to the almost RANS regime, a stable generation mechanism of turbulent velocity fluctuations was observed. In particular, fluctuations were not extinguished even for very high values and very coarse grids. In regard to the almost LES regime, it was found that the characteristic length scale provided by CES, which was independent of the LES filter width , properly worked. The LES simulations performed on this basis (with grid points) showed better performance than almost resolving LES using 20 million grid points.
- Problem : Another relevant observation is that different model hybridization options worked equally well; there were hardly differences regarding the simulation results obtained. This fact confirms the applicability of the CES approach to at least several turbulence model structures, as long as the “RANS-LES swing” is functional.
6. Summary
- 1.
- The minimal error approach presented here (which generalizes CES methods) minimizes the hybridization error among many other hybrid RANS-LES methods. It provides a theoretical solution to the problems , , and . Applications demonstrated the excellent performance of such simulation methods (see Section 5). It is essential to note that these methods represent a relatively minor extension of standard two-equation turbulence models.
- 2.
- An essential observation presented here is that minimal error methods for incompressible flows [32] can be extended to stratified and compressible flows. This opens the way to addressing relevant atmospheric science problems (mesoscale to microscale coupling) and aerospace problems (supersonic and hypersonic flow predictions) (see the discussions in Section 3). It was argued that such simulations need, in particular, the ability to perform reliable predictions under almost RANS and almost LES conditions.
- 3.
- Hybrid RANS-LES models are based on RANS equations, and such RANS equations face relevant modeling questions, particularly for stratified and compressible flows. Minimal error methods are in line with standard modeling options, and they exclude many other options. Thus, minimal error methods can provide valuable contributions to the design of consistent turbulence models. In regard to compressible flows, models are excluded that include a variety of compressibility effects in the equation [40,41]. In regard to stratified flows, a welcome byproduct of considering the hybridization of the closure model of Mellor and Yamada [49] (see Appendix B) is the correct specification of the length scales involved, which is seen as a major issue of such simulations.
- 4.
- From a more general view point, the relevance of the minimal error methods presented is the following. We need reliable methods to simulate high flows. LES models and experiments are restricted by resolution requirements, and popular hybrid RANS-LES models are known to be unreliable. In this situation, minimal error methods can provide an error-free simulation contribution in response to the flow resolution (see the illustration in Figure 2). The latter is the essential requirement for providing reliable predictions under conditions where validation data are unavailable.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Wilcox, D.C. Turbulence Modeling for CFD, 2nd ed.; DCW Industries: La Canada, CA, USA, 1998. [Google Scholar]
- Fröhlich, J.; Terzi, D.V. Hybrid LES/RANS methods for the simulation of turbulent flows. Prog. Aerosp. Sci. 2008, 44, 349–377. [Google Scholar] [CrossRef]
- Chaouat, B. The state of the art of hybrid RANS/LES modeling for the simulation of turbulent flows. Flow Turbul. Combust. 2017, 99, 279–327. [Google Scholar] [CrossRef] [PubMed]
- Heinz, S. A review of hybrid RANS-LES methods for turbulent flows: Concepts and applications. Prog. Aerosp. Sci. 2020, 114, 100597. [Google Scholar] [CrossRef]
- Piomelli, U. Large eddy simulations in 2030 and beyond. Philos. Trans. R. Soc. A 2014, 372, 20130320. [Google Scholar] [CrossRef] [PubMed]
- Larsson, J.; Kawai, S.; Bodart, J.; Bermejo-Moreno, I. Large eddy simulation with modeled wall-stress: Recent progress and future directions. Mech. Eng. Rev. 2016, 3, 15-00418. [Google Scholar] [CrossRef]
- Bose, S.T.; Park, G.I. Wall-modeled large-eddy simulation for complex turbulent flows. Annu. Rev. Fluid Mech. 2018, 50, 535–561. [Google Scholar] [CrossRef]
- Spalart, P.R.; Jou, W.H.; Strelets, M.; Allmaras, S.R. Comments on the feasibility of LES for wings, and on a hybrid RANS/LES approach. In Advances in DNS/LES; Liu, C., Liu, Z., Eds.; Greyden Press: Dayton, OH, USA, 1997; pp. 137–147. [Google Scholar]
- Spalart, P.R. Detached-eddy simulation. Annu. Rev. Fluid Mech. 2009, 41, 181–202. [Google Scholar] [CrossRef]
- Friess, C.; Manceau, R.; Gatski, T.B. Toward an equivalence criterion for hybrid RANS/LES methods. Comput. Fluids 2015, 122, 233–246. [Google Scholar] [CrossRef]
- Menter, F.R.; Egorov, Y. The scale-adaptive simulation method for unsteady turbulent flow prediction: Part 1: Theory and model description. Flow Turbul. Combust. 2010, 78, 113–138. [Google Scholar] [CrossRef]
- Jakirlić, S.; Maduta, R. Extending the bounds of "steady" RANS closures: Toward an instability-sensitive Reynolds stress model. Int. J. Heat Fluid Flow 2015, 51, 175–194. [Google Scholar] [CrossRef]
- Li, J.; Zhong, C.; Pan, D.; Zhuo, C. A gas-kinetic scheme coupled with SST model for turbulent flows. Comput. Math. Appl. 2019, 78, 1227–1242. [Google Scholar] [CrossRef]
- Chen, S.; Xia, Z.; Pei, S.; Wang, J.; Yang, Y.; Xiao, Z.; Shi, Y. Reynolds-stress-constrained large-eddy simulation of wall-bounded turbulent flows. J. Fluid Mech. 2012, 703, 1–28. [Google Scholar] [CrossRef]
- Heinz, S. Statistical Mechanics of Turbulent Flows; Springer: Berlin, Germany, 2003. [Google Scholar]
- Heinz, S. Comment on “A dynamic nonlinear subgrid-scale stress model” [Phys. Fluid 17, 035109 (2005)]. Phys. Fluids 2005, 17, 099101. [Google Scholar] [CrossRef]
- Heinz, S. Unified turbulence models for LES and RANS, FDF and PDF simulations. Theor. Comput. Fluid Dyn. 2007, 21, 99–118. [Google Scholar] [CrossRef]
- Gopalan, H.; Heinz, S.; Stöllinger, M. A unified RANS-LES model: Computational development, accuracy and cost. J. Comput. Phys. 2013, 249, 249–279. [Google Scholar] [CrossRef]
- Mokhtarpoor, R.; Heinz, S.; Stoellinger, M. Dynamic unified RANS-LES simulations of high Reynolds number separated flows. Phys. Fluids 2016, 28, 095101. [Google Scholar] [CrossRef]
- Mokhtarpoor, R.; Heinz, S. Dynamic large eddy simulation: Stability via realizability. Phys. Fluids 2017, 29, 105104. [Google Scholar] [CrossRef]
- Stöllinger, M.; Heinz, S.; Zemtsop, C.; Gopalan, H.; Mokhtarpoor, R. Stochastic-based RANS-LES simulations of swirling turbulent jet flows. Int. J. Nonlinear Sci. Numer. Simul. 2017, 18, 351–369. [Google Scholar] [CrossRef]
- Girimaji, S. Partially-averaged Navier-Stokes method for turbulence: A Reynolds-averaged Navier-Stokes to direct numerical simulation bridging method. ASME J. Appl. Mech. 2006, 73, 413–421. [Google Scholar] [CrossRef]
- Chaouat, B.; Schiestel, R. A new partially integrated transport model for subgrid-scale stresses and dissipation rate for turbulent developing flows. Phys. Fluids 2005, 17, 065106. [Google Scholar] [CrossRef]
- Chaouat, B.; Schiestel, R. Analytical insights into the partially integrated transport modeling method for hybrid Reynolds averaged Navier-Stokes equations-large eddy simulations of turbulent flows. Phys. Fluids 2012, 24, 085106. [Google Scholar] [CrossRef]
- Heinz, S. The large eddy simulation capability of Reynolds-averaged Navier-Stokes equations: Analytical results. Phys. Fluids 2019, 31, 021702. [Google Scholar] [CrossRef]
- Heinz, S.; Mokhtarpoor, R.; Stoellinger, M.K. Theory-Based Reynolds-Averaged Navier-Stokes Equations with Large Eddy Simulation Capability for Separated Turbulent Flow Simulations. Phys. Fluids 2020, 32, 065102. [Google Scholar] [CrossRef]
- Heinz, S. The Continuous Eddy Simulation Capability of Velocity and Scalar Probability Density Function Equations for Turbulent Flows. Phys. Fluids 2021, 33, 025107. [Google Scholar] [CrossRef]
- Heinz, S. Theory-Based Mesoscale to Microscale Coupling for Wind Energy Applications. Appl. Math. Model. 2021, 98, 563–575. [Google Scholar] [CrossRef]
- Heinz, S.; Peinke, J.; Stoevesandt, B. Cutting-Edge Turbulence Simulation Methods for Wind Energy and Aerospace Problems. Fluids 2021, 6, 288. [Google Scholar] [CrossRef]
- Fagbade, A.; Heinz, S. Application of Mode-Controlled Hybrid RANS-LES to the NASA Wall-Mounted Hump Flow. In Proceedings of the 2022 AIAA SciTech Forum, San Diego, CA, USA, 3–7 January 2022; AIAA Paper 22-0180. pp. 1–16. [Google Scholar]
- Heinz, S. Minimal error partially resolving simulation methods for turbulent flows: A dynamic machine learning approach. Phys. Fluids 2022, 34, 051705. [Google Scholar] [CrossRef]
- Slotnick, J.; Khodadoust, A.; Alonso, J.; Darmofal, D.; Gropp, W.; Lurie, E.; Mavriplis, D. CFD Vision 2030 Study: A Path to Revolutionary Computational Aerosciences. NASA/CR-2014-218178. 2014. Available online: https://ntrs.nasa.gov/search.jsp?R=20140003093 (accessed on 10 October 2022).
- Slotnick, J.P.; Khodadoust, A.; Alonso, J.J.; Darmofal, D.L.; Gropp, W.D.; Lurie, E.A.; Mavriplis, D.J.; Venkatakrishnan, V. Enabling the environmentally clean air transportation of the future: A vision of computational fluid dynamics in 2030. Philos. Trans. R. Soc. A 2014, 372, 20130317. [Google Scholar] [CrossRef]
- Probst, A.; Knopp, T.; Grabe, C.; Jägersküpper, J. HPC requirements of high-fidelity flow simulations for aerodynamic applications. In Proceedings of the European Conference on Parallel Processing, Warsaw, Poland, 24–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 375–387. [Google Scholar]
- Goc, K.A.; Lehmkuhl, O.; Park, G.I.; Bose, S.T.; Moin, P. Large eddy simulation of aircraft at affordable cost: A milestone in computational fluid dynamics. Flow 2021, 1, E14. [Google Scholar] [CrossRef]
- Slotnick, J.P.; Mavriplis, D. A Grand Challenge for the Advancement of Numerical Prediction of High Lift Aerodynamics. In Proceedings of the AIAA SciTech Forum, Virtual, 11–15 & 19–21 January 2021; AIAA Paper 22-0955. pp. 1–21. [Google Scholar]
- Wyngaard, J.C. Toward numerical modeling in the “Terra Incognita”. J. Atmos. Sci. 2004, 61, 1816–1826. [Google Scholar] [CrossRef]
- Cummings, R.M.; Forsythe, J.R.; Morton, S.A.; Squires, K.D. Computational challenges in high angle of attack flow prediction. Prog. Aerosp. Sci. 2003, 39, 369–384. [Google Scholar] [CrossRef]
- Chassaing, P. The modeling of variable density turbulent flows. A review of first-order closure schemes. Flow Turb. Combust. 2001, 66, 293–332. [Google Scholar] [CrossRef]
- Chassaing, P.; Antonia, R.A.; Anselmet, F.; Joly, L.; Sarkar, S. Variable Density Fluid Turbulence; Springer Science & Business Media: Dordrecht, The Netherlands, 2002; Volume 69. [Google Scholar]
- Park, N.; Mahesh, K. Numerical and modeling issues in LES of compressible turbulence on unstructured grids. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007; AIAA Paper 07-0722. pp. 1–18. [Google Scholar]
- Temel, O.; Porchetta, S.; Bricteux, L.; van Beeck, J. RANS closures for non-neutral microscale CFD simulations sustained with inflow conditions acquired from mesoscale simulations. Appl. Math. Model. 2018, 53, 635–652. [Google Scholar] [CrossRef]
- Heinz, S. Nonlinear Lagrangian equations for turbulent motion and buoyancy in inhomogeneous flows. Phys. Fluids 1997, 9, 703–716. [Google Scholar] [CrossRef][Green Version]
- Heinz, S. Connections between Lagrangian stochastic models and the closure theory of turbulence for stratified flows. Int. J. Heat Fluid Flow 1998, 19, 193–200. [Google Scholar] [CrossRef]
- Heinz, S.; van Dop, H. Buoyant plume rise described by a Lagrangian turbulence model. Atmos. Environ. 1999, 33, 2031–2043. [Google Scholar] [CrossRef]
- Baumert, H.; Peters, H. Second-moment closures and length scales for weakly stratified turbulent shear flows. J. Geophys. Res. Oceans 2000, 105, 6453–6468. [Google Scholar] [CrossRef]
- Sogachev, A. A note on two-equation closure modelling of canopy flow. Bound. Layer Meteorol. 2009, 130, 423–435. [Google Scholar] [CrossRef]
- Mellor, G.L.; Yamada, T. Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. 1982, 20, 851–875. [Google Scholar] [CrossRef]
- Muñoz-Esparza, D.; Kosović, B.; Mirocha, J.; van Beeck, J. Bridging the transition from mesoscale to microscale turbulence in numerical weather prediction models. Bound. Layer Meteorol. 2014, 153, 409–440. [Google Scholar] [CrossRef]
- Sanz Rodrigo, J.; Chavez Arroyo, R.A.; Moriarty, P.; Churchfield, M.; Kosović, B.; Réthoré, P.E.; Hansen, K.S.; Hahmann, A.; Mirocha, J.D.; Rife, D. Mesoscale to microscale wind farm flow modeling and evaluation. Wires Energy Environ. 2017, 6, e214. [Google Scholar] [CrossRef]
- Veers, P.; Dykes, K.; Lantz, E.; Barth, S.; Bottasso, C.L.; Carlson, O.; Clifton, A.; Green, J.; Green, P.; Holttinen, H.; et al. Grand challenges in the science of wind energy. Science 2019, 366, eaau2027. [Google Scholar] [CrossRef] [PubMed]
- Meneveau, C. Big wind power: Seven questions for turbulence research. J. Turbul. 2019, 20, 2–20. [Google Scholar] [CrossRef]
- Haupt, S.E.; Berg, L.; Churchfield, M.; Kosović, B.; Mirocha, J.; Shaw, W. Mesoscale to Microscale Coupling for Wind Energy Applications: Addressing the Challenges. J. Phys. Conf. Ser. 2020, 1452, 012076. [Google Scholar] [CrossRef]
- Detering, H.W.; Etling, D. Application of the E-ε turbulence model to the atmospheric boundary layer. Bound. Layer Meteorol. 1985, 33, 113–133. [Google Scholar] [CrossRef]
- Duynkerke, P.; Driedonks, A. A model for the turbulent structure of the stratocumulus–topped atmospheric boundary layer. J. Atmos. Sci. 1987, 44, 43–64. [Google Scholar] [CrossRef]
- Duynkerke, P.G. Application of the E–ε turbulence closure model to the neutral and stable atmospheric boundary layer. J. Atmos. Sci. 1988, 45, 865–880. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Y.; Xue, M. Evaluation of an E–ε and three other boundary layer parameterization schemes in the WRF model over the Southeast Pacific and the Southern Great Plains. Mon. Weather Rev. 2020, 148, 1121–1145. [Google Scholar] [CrossRef]
- Tran, V.; Ng, E.Y.K.; Skote, M. CFD simulation of dense gas dispersion in neutral atmospheric boundary layer with OpenFOAM. Meteorol. Atmos. Phys. 2020, 132, 273–285. [Google Scholar] [CrossRef]
- Juliano, T.W.; Kosović, B.; Jiménez, P.A.; Eghdami, M.; Haupt, S.E.; Martilli, A. “Gray Zone” simulations using a three-dimensional planetary boundary layer parameterization in the Weather Research and Forecasting Model. Mon. Weather Rev. 2022, 150, 1585–1619. [Google Scholar] [CrossRef]
- Hong, S.Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Nakanishi, M.; Niino, H. Development of an improved turbulence closure model for the atmospheric boundary layer. J. Meteorol. Soc. Jpn. Ser. II 2009, 87, 895–912. [Google Scholar] [CrossRef]
- Sarkar, S. The pressure–dilatation correlation in compressible flows. Phys. Fluids A 1992, 4, 2674–2682. [Google Scholar] [CrossRef]
- Suzen, Y.; Hoffmann, K. Investigation of supersonic jet exhaust flow by one-and two-equation turbulence models. In Proceedings of the 36th AIAA Aerospace Sciences Meeting and Exhibit, Las Vegas, NV, USA, 24–28 July 1998; AIAA Paper 98-0322. pp. 1–18. [Google Scholar]
- Forsythe, J.R.; Hoffmann, K.A.; Cummings, R.M.; Squires, K.D. Detached-eddy simulation with compressibility corrections applied to a supersonic axisymmetric base flow. J. Fluids Eng. 2002, 124, 911–923. [Google Scholar] [CrossRef]
- Openfoam Documentation; Technical Report. 2009. Available online: https://openfoam.org/release/1-6/ (accessed on 10 May 2020).
- Rapp, C.; Manhart, M. Flow over periodic hills—An experimental study. Exp. Fluids 2011, 51, 247–269. [Google Scholar] [CrossRef]
- Warhaft, Z. Passive scalars in turbulent flows. Annu. Rev. Fluid Mech. 2000, 32, 203–240. [Google Scholar] [CrossRef]
- Das, S.K.; Durbin, P.A. A Lagrangian stochastic model for dispersion in stratified turbulence. Phys. Fluids 2005, 17, 025109. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heinz, S. From Two-Equation Turbulence Models to Minimal Error Resolving Simulation Methods for Complex Turbulent Flows. Fluids 2022, 7, 368. https://doi.org/10.3390/fluids7120368
Heinz S. From Two-Equation Turbulence Models to Minimal Error Resolving Simulation Methods for Complex Turbulent Flows. Fluids. 2022; 7(12):368. https://doi.org/10.3390/fluids7120368
Chicago/Turabian StyleHeinz, Stefan. 2022. "From Two-Equation Turbulence Models to Minimal Error Resolving Simulation Methods for Complex Turbulent Flows" Fluids 7, no. 12: 368. https://doi.org/10.3390/fluids7120368
APA StyleHeinz, S. (2022). From Two-Equation Turbulence Models to Minimal Error Resolving Simulation Methods for Complex Turbulent Flows. Fluids, 7(12), 368. https://doi.org/10.3390/fluids7120368





