Measurement of Mass Transfer Intensity in Gas–Liquid Medium of Bioreactor Circuit Using the Thermometry Method
Abstract
1. Introduction
2. Materials and Methods
2.1. Theory of the Thermometry Method
- 1.
- Averaged and turbulent (pulsation) kinetic energy of the flow,
- 2.
- Change in the potential energy of the fluid in the gravitational field,
- 3.
- Enthalpy change (heating of liquid due to thermal dissipation),
- 4.
- Heat of gas dissolution (negative),
- 5.
- External heat losses of the circuit,
- 6.
- Interfacial “liquid–gas” energy.
2.2. Design and Procedure of the Experiment
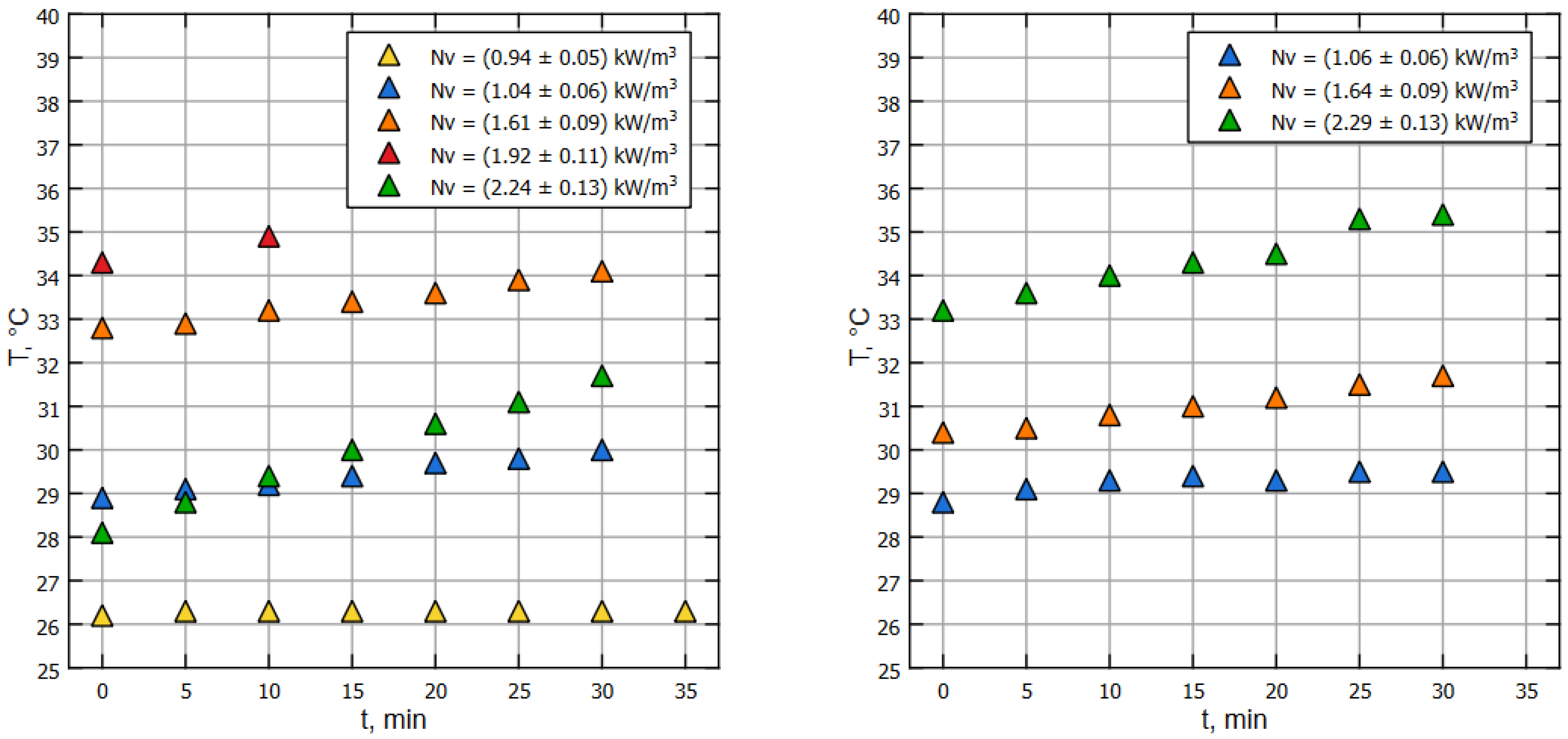
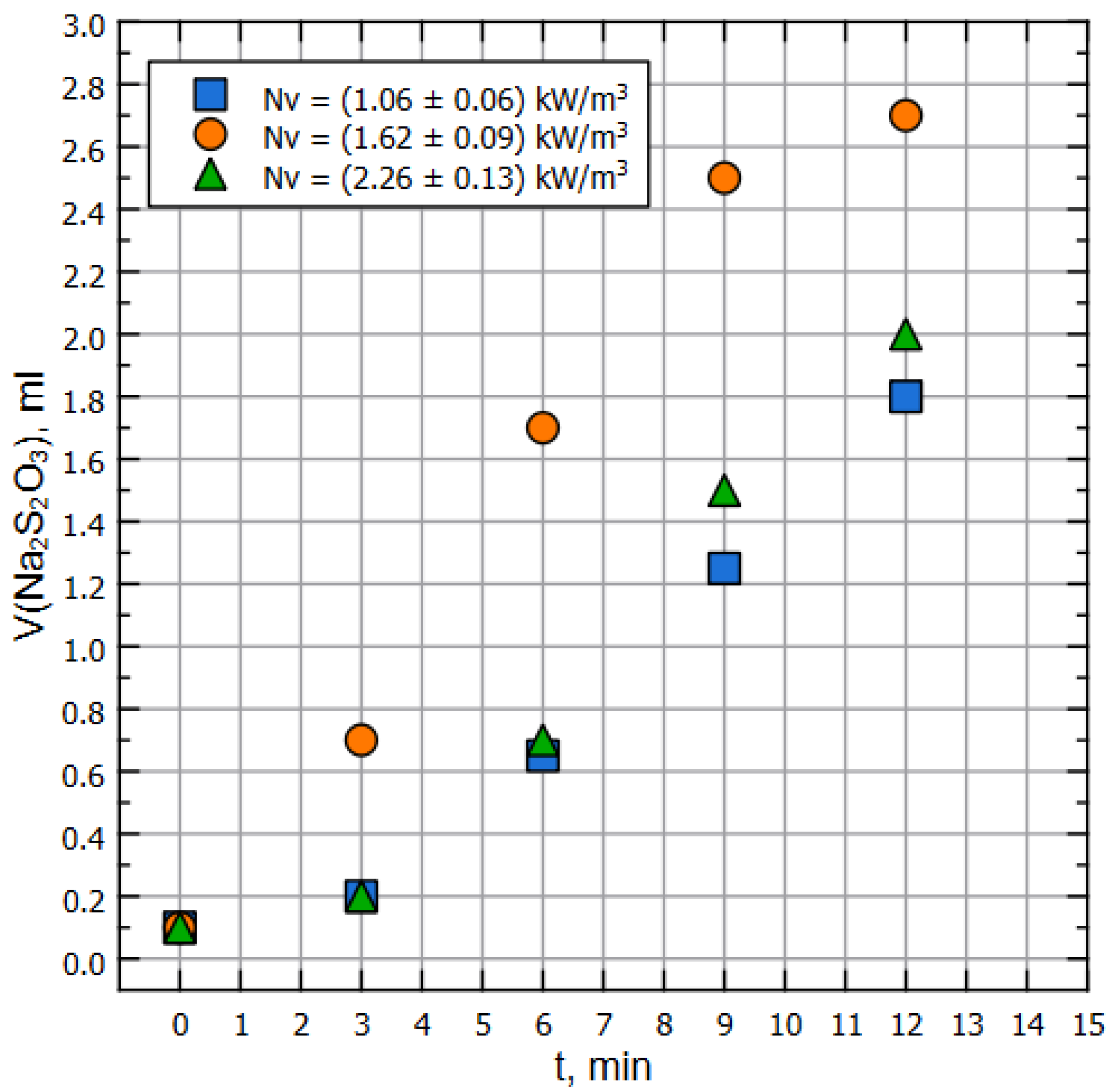
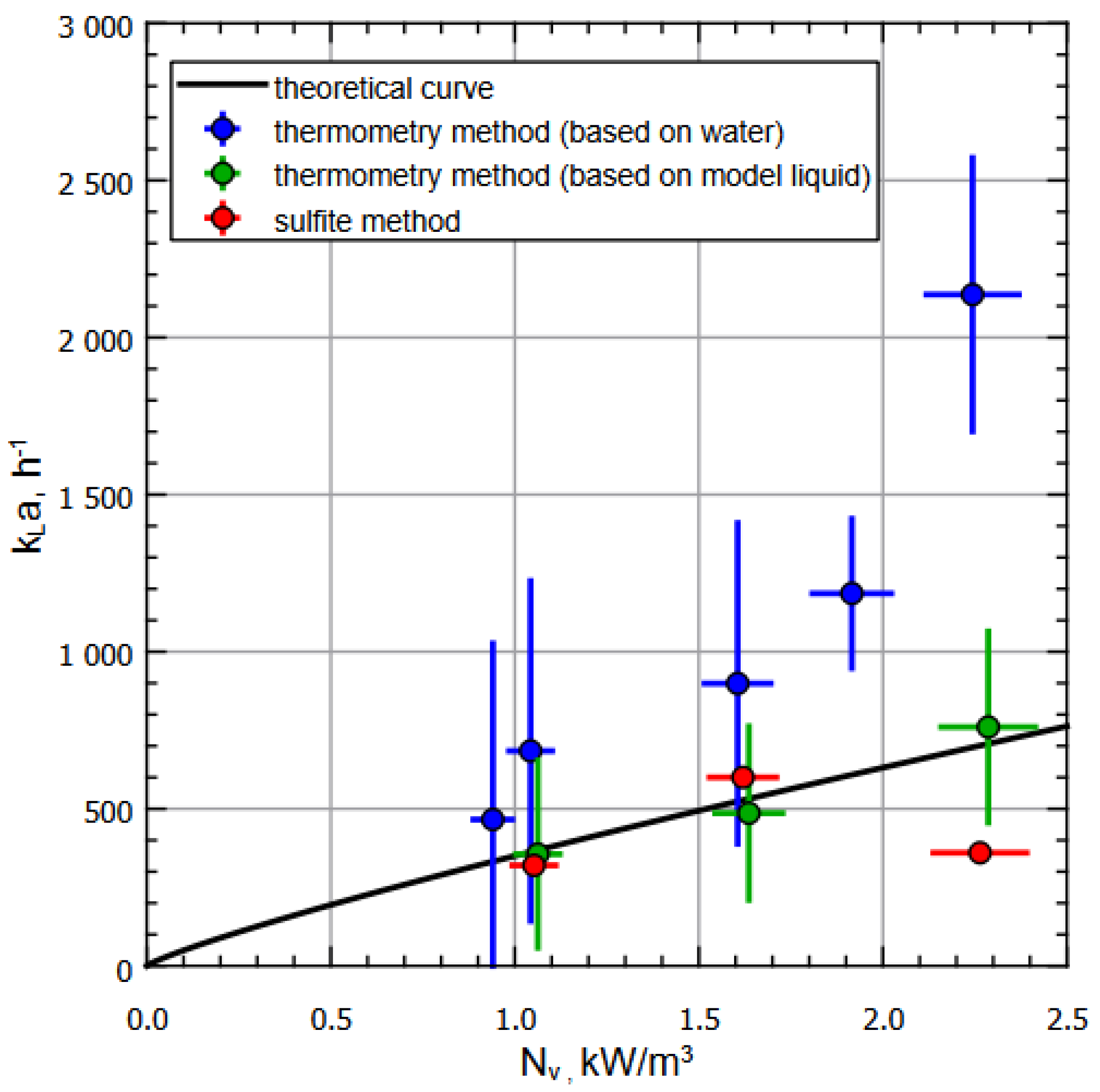
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| density of the liquid, | |
| dissolved oxygen concentration in the liquid, (kg/L) | |
| equilibrium dissolved oxygen concentration in the liquid, (kg/L) | |
| heat loss, (J) | |
| total coefficient of heat transfer by radiation and convection, (W/(m | |
| heat exchange surface area, (m) | |
| surface temperature of the apparatus, () | |
| ambient temperature, () | |
| measurement period, (s) | |
| temperature of the liquid, | |
| liquid temperature difference during the measurement, | |
| specific heat capacity of the liquid, | |
| specific input power (thermal), | |
| specific input power (at the pump impeller), , calculated taking into account pump and liquid specific characteristics | |
| volumetric mass transfer coefficient, |
References
- Guseva, E.M.N.; Safarov, R.; Boudrant, J. An approach to modeling, scaling and optimizing the operation of bioreactors based on computational fluid dynamics. Int. J. Softw. Prod. Syst. 2015, 112, 249–255. [Google Scholar]
- Petersen, L.A.; Villadsen, J.; Jørgensen, S.B.; Gernaey, K.V. Mixing and mass transfer in a pilot scale U-loop bioreactor. Biotechnol. Bioeng. 2017, 114, 344–354. [Google Scholar] [CrossRef] [PubMed]
- Prasser, H.M.; Häfeli, R. Signal response of wire-mesh sensors to an idealized bubbly flow. Nucl. Eng. Des. 2018, 336, 3–14. [Google Scholar] [CrossRef]
- Krychowska, A.; Kordas, M.; Konopacki, M.; Grygorcewicz, B.; Musik, D.; Wójcik, K.; Jędrzejczak-Silicka, M.; Rakoczy, R. Mathematical modeling of hydrodynamics in bioreactor by means of CFD-based compartment model. Processes 2020, 8, 1301. [Google Scholar] [CrossRef]
- Yao, Y.; Fringer, O.B.; Criddle, C.S. CFD-accelerated bioreactor optimization: Reducing the hydrodynamic parameter space. Environ. Sci. Water Res. Technol. 2022, 8, 456–464. [Google Scholar] [CrossRef]
- Panunzi, A.; Moroni, M.; Mazzelli, A.; Bravi, M. Industrial Case-Study-Based Computational Fluid Dynamic (CFD) Modeling of Stirred and Aerated Bioreactors. ACS Omega 2022, 7, 25152–25163. [Google Scholar] [CrossRef]
- Ramírez, L.A.; Pérez, E.L.; García Díaz, C.; Camacho Luengas, D.A.; Ratkovich, N.; Reyes, L.H. CFD and Experimental Characterization of a Bioreactor: Analysis via Power Curve, Flow Patterns and kLa. Processes 2020, 8, 878. [Google Scholar] [CrossRef]
- Cappello, V.; Plais, C.; Vial, C.; Augier, F. Scale-up of aerated bioreactors: CFD validation and application to the enzyme production by Trichoderma reesei. Chem. Eng. Sci. 2021, 229, 116033. [Google Scholar] [CrossRef]
- Nizovtseva, I.G.; Starodumov, I.O.; Schelyaev, A.Y.; Aksenov, A.A.; Zhluktov, S.V.; Sazonova, M.L.; Kashinsky, O.N.; Timkin, L.S.; Gasenko, V.G.; Gorelik, R.S.; et al. Simulation of two-phase air–liquid flows in a closed bioreactor loop: Numerical modeling, experiments, and verification. Math. Methods Appl. Sci. 2022, 45, 8216–8229. [Google Scholar] [CrossRef]
- Biessey, P.; Bayer, H.; Theßeling, C.; Hilbrands, E.; Grünewald, M. Prediction of Bubble Sizes in Bubble Columns with Machine Learning Methods. Chem. Ing. Tech. 2021, 93, 1968–1975. [Google Scholar] [CrossRef]
- Cruz, I.A.; Chuenchart, W.; Long, F.; Surendra, K.; Andrade, L.R.S.; Bilal, M.; Liu, H.; Figueiredo, R.T.; Khanal, S.K.; Ferreira, L.F.R. Application of machine learning in anaerobic digestion: Perspectives and challenges. Bioresour. Technol. 2022, 345, 126433. [Google Scholar] [CrossRef] [PubMed]
- Hessenkemper, H.; Starke, S.; Atassi, Y.; Ziegenhein, T.; Lucas, D. Bubble identification from images with machine learning methods. arXiv 2022, arXiv:2202.03107. [Google Scholar]
- Yu, S.I.; Rhee, C.; Cho, K.H.; Shin, S.G. Comparison of different machine learning algorithms to estimate liquid level for bioreactor management. Environ. Eng. Res. 2022, 28, 220037. [Google Scholar] [CrossRef]
- Rathore, A.S.; Kanwar Shekhawat, L.; Loomba, V. Computational Fluid Dynamics for Bioreactor Design. In Bioreactors: Design, Operation and Novel Applications; Wiley Online Library: Hoboken, NJ, USA, 2016; pp. 295–322. [Google Scholar]
- Ansoni, J.L.; Seleghim, P., Jr. Optimal industrial reactor design: Development of a multiobjective optimization method based on a posteriori performance parameters calculated from CFD flow solutions. Adv. Eng. Softw. 2016, 91, 23–35. [Google Scholar] [CrossRef]
- Charles, M. Fermentation scale-up: Problems and possibilities. Trends Biotechnol. 1985, 3, 134–139. [Google Scholar] [CrossRef]
- Gill, N.; Appleton, M.; Baganz, F.; Lye, G. Quantification of power consumption and oxygen transfer characteristics of a stirred miniature bioreactor for predictive fermentation scale-up. Biotechnol. Bioeng. 2008, 100, 1144–1155. [Google Scholar] [CrossRef]
- Petříček, R.; Labík, L.; Moucha, T.; Rejl, F.J.; Valenz, L.; Haidl, J. Volumetric Mass Transfer Coefficient in Fermenters: Scale-up Study in Viscous Liquids. Chem. Eng. Technol. 2017, 40, 878–888. [Google Scholar] [CrossRef]
- Schügerl, K. Comparison of different bioreactor performances. Bioprocess Eng. 1993, 9, 215–223. [Google Scholar] [CrossRef]
- Moser, A. Bioreactor Performance: Process Design Methods. In Bioprocess Technology; Springer: Berlin/Heidelberg, Germany, 1988; pp. 307–405. [Google Scholar]
- Stanbury, P.F.; Whitaker, A.; Hall, S.J. Principles of Fermentation Technology; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Halme, A.; Kiviranta, H.; Kiviranta, M. Study of a single-cell protein fermentation process for computer control. Ifac Proc. Vol. 1977, 10, 407–415. [Google Scholar] [CrossRef]
- Pilarek, M.; Sobieszuk, P.; Wierzchowski, K.; Dąbkowska, K. Impact of operating parameters on values of a volumetric mass transfer coefficient in a single-use bioreactor with wave-induced agitation. Chem. Eng. Res. Des. 2018, 136, 1–10. [Google Scholar] [CrossRef]
- Šulc, R.; Dymák, J. Hydrodynamics and Mass Transfer in a Concentric Internal Jet-Loop Airlift Bioreactor Equipped with a Deflector. Energies 2021, 14, 4329. [Google Scholar] [CrossRef]
- Bun, S.; Wongwailikhit, K.; Chawaloesphonsiya, N.; Lohwacharin, J.; Ham, P.; Painmanakul, P. Development of modified airlift reactor (MALR) for improving oxygen transfer: Optimize design and operation condition using ‘design of experiment’methodology. Environ. Technol. 2020, 41, 2670–2682. [Google Scholar] [CrossRef] [PubMed]
- Hibiki, T.; Goda, H.; Kim, S.; Ishii, M.; Uhle, J. Experimental study on interfacial area transport of a vertical downward bubbly flow. Exp. Fluids 2003, 35, 100–111. [Google Scholar] [CrossRef]
- Kreitmayer, D.; Gopireddy, S.R.; Matsuura, T.; Aki, Y.; Katayama, Y.; Nakano, T.; Eguchi, T.; Kakihara, H.; Nonaka, K.; Profitlich, T.; et al. CFD-Based and Experimental Hydrodynamic Characterization of the Single-Use Bioreactor XcellerexTM XDR-10. Bioengineering 2022, 9, 22. [Google Scholar] [CrossRef] [PubMed]
- Vaidheeswaran, A.; Hibiki, T. Bubble-induced turbulence modeling for vertical bubbly flows. Int. J. Heat Mass Transf. 2017, 115, 741–752. [Google Scholar] [CrossRef]
- Ohba, K.; Yuhara, T.; Matsuyama, H. Simultaneous measurements of bubble and liquid velocities in two-phase bubbly flow using laser Doppler velocimeter. Bull. JSME 1986, 29, 2487–2493. [Google Scholar] [CrossRef]
- Maischberger, T. Optimized process and bioreactor characterization. Chem. Ing. Tech. 2019, 91, 1719–1723. [Google Scholar] [CrossRef]
- Bun, S.; Chawaloesphonsiya, N.; Ham, P.; Wongwailikhit, K.; Chaiwiwatworakul, P.; Painmanakul, P. Experimental and empirical investigation of mass transfer enhancement in multi-scale modified airlift reactors. Multiscale Multidiscip. Model. Exp. Des. 2020, 3, 89–101. [Google Scholar] [CrossRef]
- Richard, H.; Irina, N.; Dmitri, C.; Kalyuzhnaya, M.G. C1-Proteins Prospect for Production of Industrial Proteins and Protein-Based Materials from Methane. In Algal Biorefineries and the Circular Bioeconomy; CRC Press: Boca Raton, FL, USA, 2022; pp. 251–276. [Google Scholar]
- Strong, P.; Kalyuzhnaya, M.; Silverman, J.; Clarke, W. A methanotroph-based biorefinery: Potential scenarios for generating multiple products from a single fermentation. Bioresour. Technol. 2016, 215, 314–323. [Google Scholar] [CrossRef]
- Listov, E.L.; Chernushkin, D.V.; Burov, S.N.; Dibtsov, V.P.; Sorokin, A.G.; Butorova, I.A.; Aksyutin, O.E.; Ishkov, A.G.; Bondarenko, K.N.; Shajkhutdinov, A.Z.; et al. Method for Determining Mass-Exchange Apparatus Efficiency. RUS Patent RU 2702539 C1, 20 February 2019. [Google Scholar]
- Wallis, G. One-Dimensional Two-Phase Flow; McGraw Hill: New York, NY, USA, 1969. [Google Scholar]
- Levich, V. Physicochemical Hydrodynamics; Prentice-Hall: Upper Saddle River, NJ, USA, 2017. [Google Scholar]
- Viestur, U.; Kuznetsov, A.; Savenkov, B. Sistemy Fermentacii; Zinatne: Riga, Latvia, 1986. [Google Scholar]
- Kirillin, V.; Sychev, V.; Sheindlin, A. Technical Thermodynamics; Izdatel Energiia: Moscow, Russia, 1974. [Google Scholar]
- Nazarov, V. Processes and devices of microbiological productions. J. Tech. Res. 2016, 2, 4. [Google Scholar]
- Vinogradova, A.; Anashkina, E. Obshchaya Biotekhnologiya; Perm University Press: Perm Krai, Russia, 2008. [Google Scholar]
- Khabibrahmanov, R.; Muhachev, S. Issledovanie massoobmennyh harakteristik apparatov s perforirovannymi meshalkami sul’fitnym metodom. Vestn. Kazan. Tekhnologicheskogo Univ. 2014, 17, 140–143. [Google Scholar]
- Mironov, M.; Tokareva, M. Metody Rascheta Oborudovaniya Biotekhnologicheskih Proizvodstv; Urals University Press: Chelyabinsk, Russia, 2017. [Google Scholar]


| Specific Input Power (Experimental Setup Regime), kW/m | Liquid Type | Heat Capacity, | Density, | Air Temperature, |
|---|---|---|---|---|
| Thermometry method | ||||
| Water | 1.17 | 1000 | ||
| Water | 1.17 | 1000 | ||
| Water | 1.17 | 1000 | ||
| Water | 1.17 | 1000 | ||
| Water | 1.17 | 1000 | 30 | |
| Model liquid | 0.56 | 1020 | ||
| Model liquid | 0.56 | 1020 | 28 | |
| Model liquid | 0.56 | 1020 | 28 | |
| Sulfite method | ||||
| Water | 1.17 | 1000 | 29 | |
| Water | 1.17 | 1000 | 29 | |
| Water | 1.17 | 1000 | 29 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Starodumov, I.; Nizovtseva, I.; Lezhnin, S.; Vikharev, S.; Svitich, V.; Mikushin, P.; Alexandrov, D.; Kuznetsov, N.; Chernushkin, D. Measurement of Mass Transfer Intensity in Gas–Liquid Medium of Bioreactor Circuit Using the Thermometry Method. Fluids 2022, 7, 366. https://doi.org/10.3390/fluids7120366
Starodumov I, Nizovtseva I, Lezhnin S, Vikharev S, Svitich V, Mikushin P, Alexandrov D, Kuznetsov N, Chernushkin D. Measurement of Mass Transfer Intensity in Gas–Liquid Medium of Bioreactor Circuit Using the Thermometry Method. Fluids. 2022; 7(12):366. https://doi.org/10.3390/fluids7120366
Chicago/Turabian StyleStarodumov, Ilya, Irina Nizovtseva, Sergey Lezhnin, Sergey Vikharev, Vladislav Svitich, Pavel Mikushin, Dmitri Alexandrov, Nikolay Kuznetsov, and Dmitri Chernushkin. 2022. "Measurement of Mass Transfer Intensity in Gas–Liquid Medium of Bioreactor Circuit Using the Thermometry Method" Fluids 7, no. 12: 366. https://doi.org/10.3390/fluids7120366
APA StyleStarodumov, I., Nizovtseva, I., Lezhnin, S., Vikharev, S., Svitich, V., Mikushin, P., Alexandrov, D., Kuznetsov, N., & Chernushkin, D. (2022). Measurement of Mass Transfer Intensity in Gas–Liquid Medium of Bioreactor Circuit Using the Thermometry Method. Fluids, 7(12), 366. https://doi.org/10.3390/fluids7120366









