Strong Viscosity Increase in Aqueous Solutions of Cationic C22-Tailed Surfactant Wormlike Micelles
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
2.2.1. Rheology
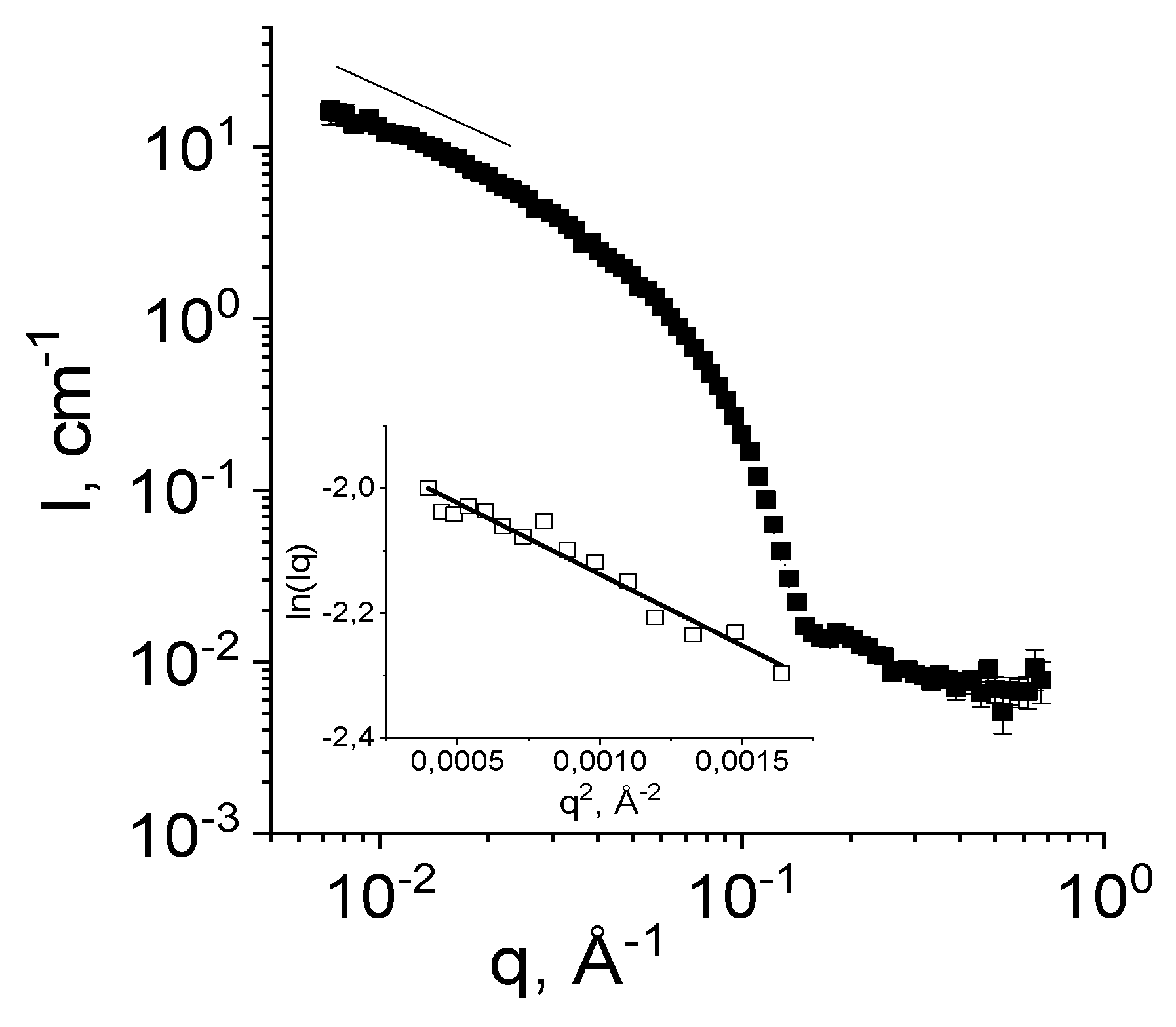
2.2.2. Small-Angle Neutron Scattering (SANS)
3. Results and Discussion
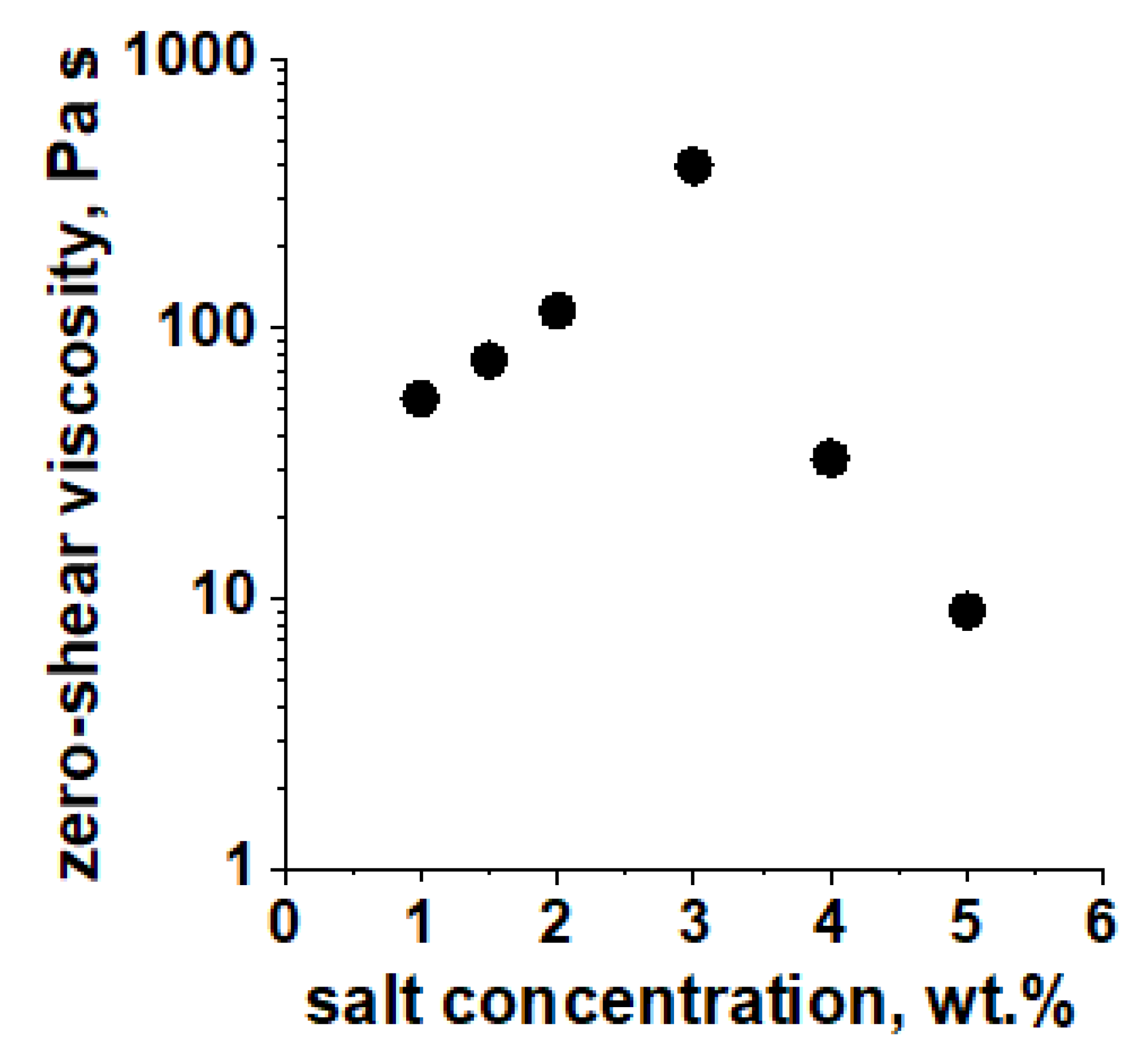
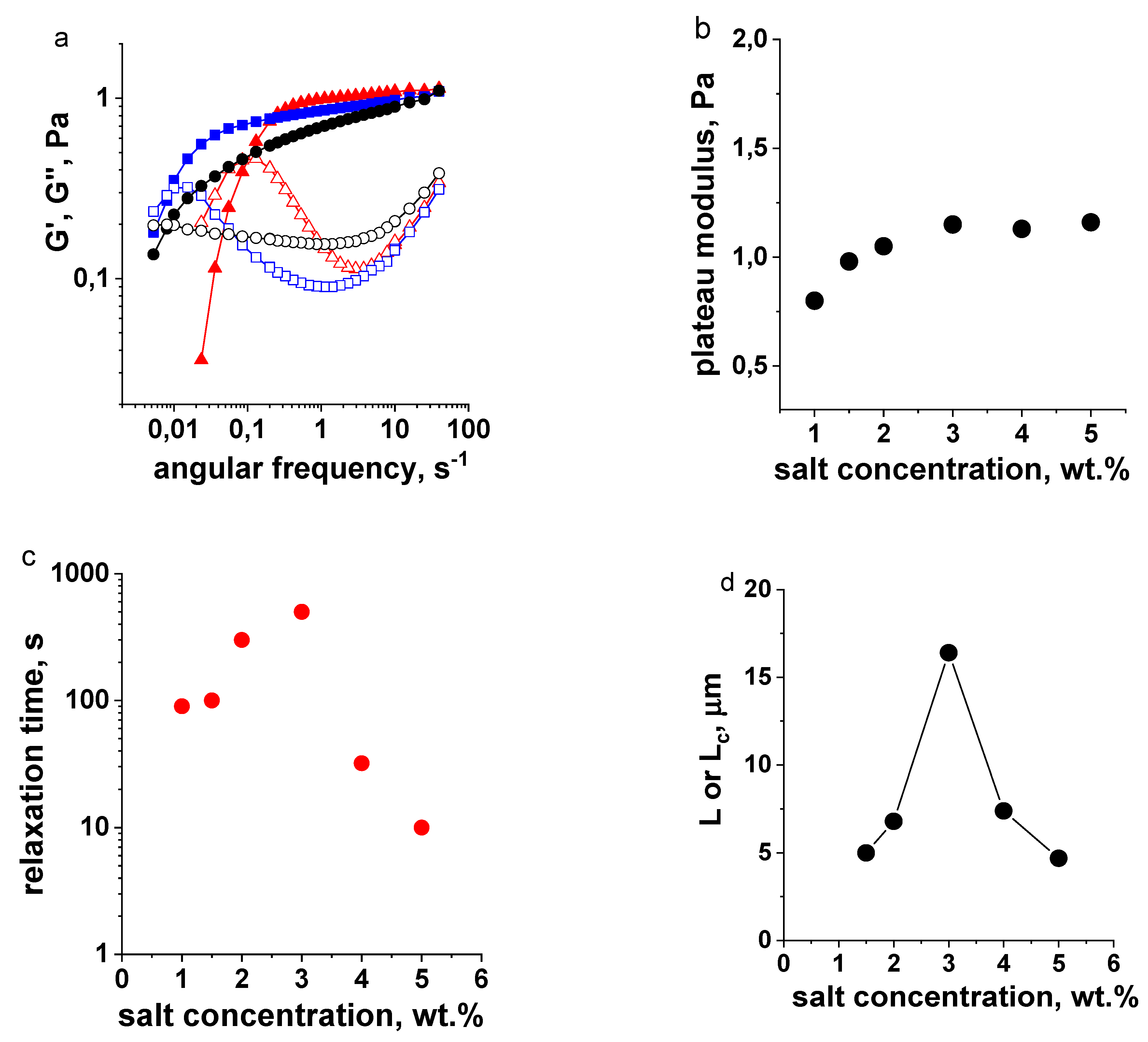
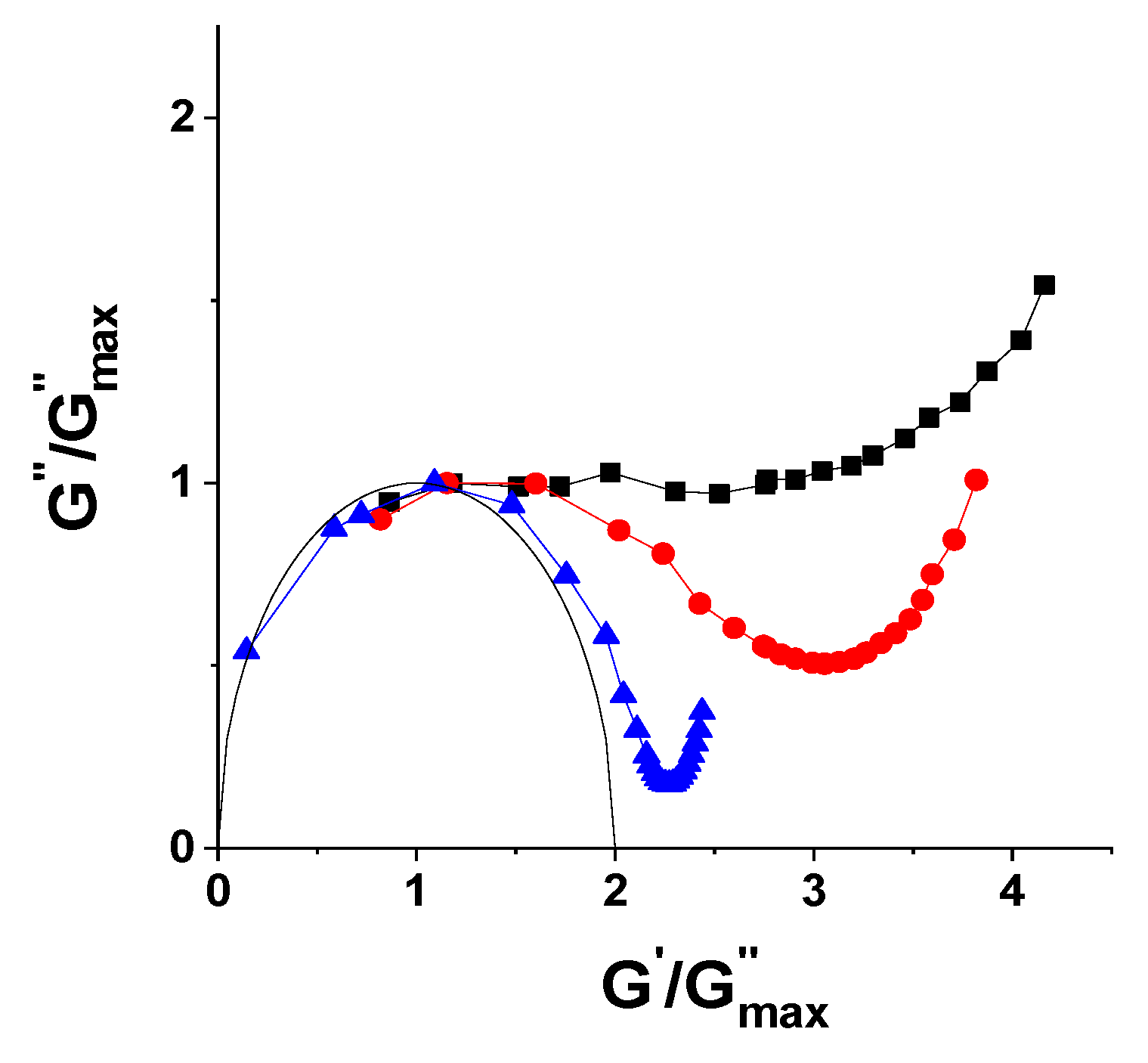
3.1. Effect of Salt Concentration
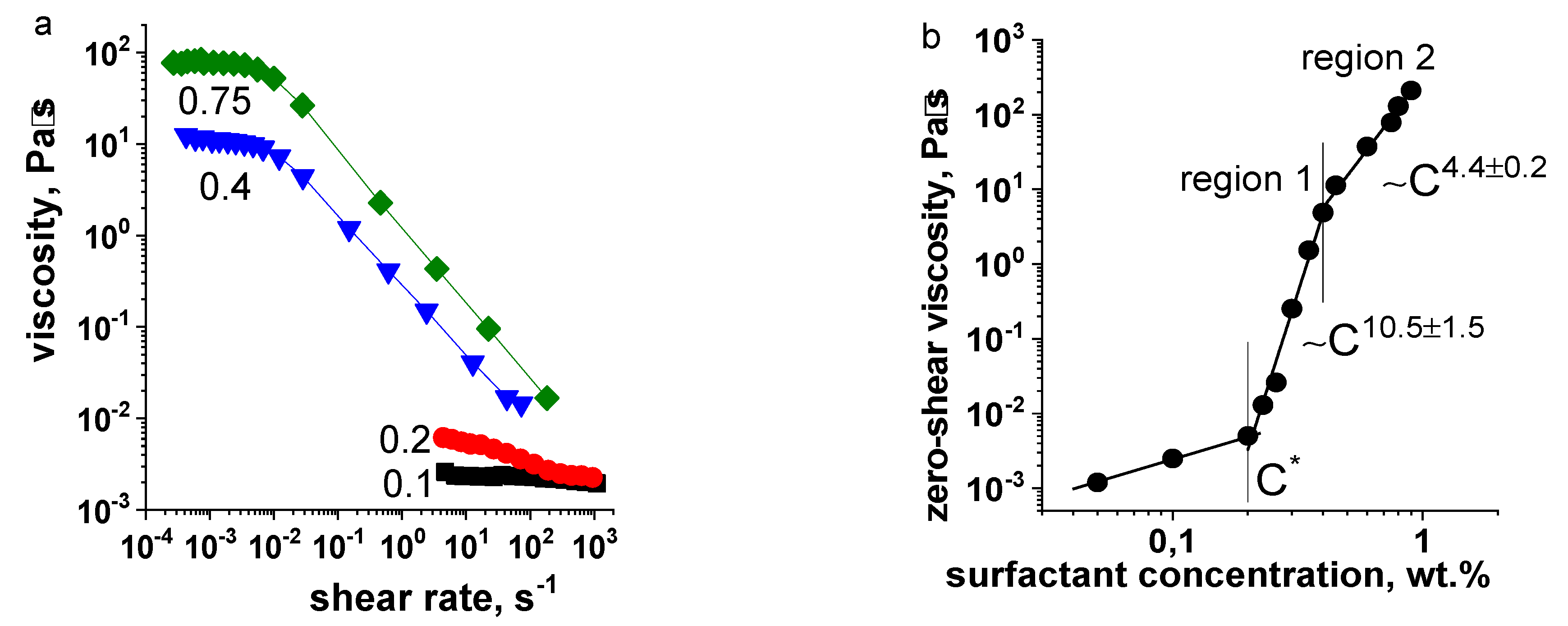
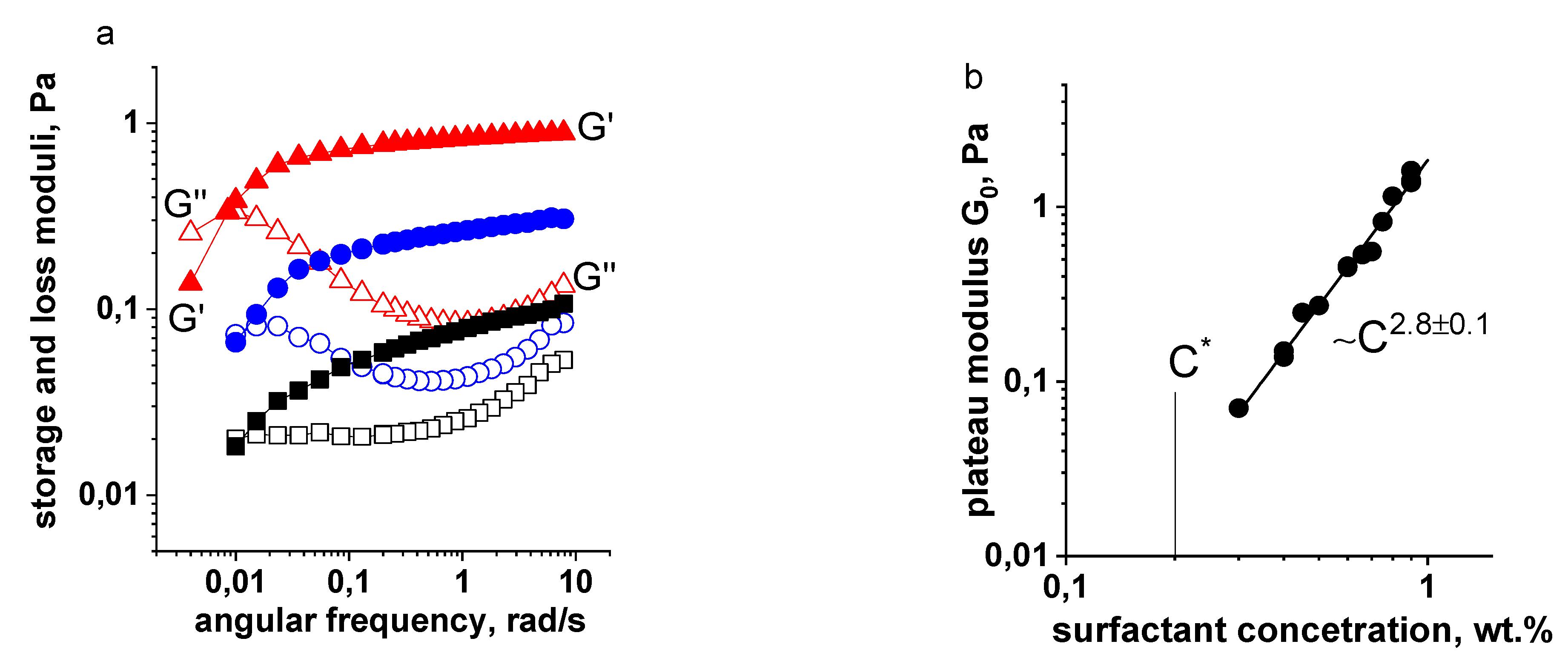
3.2. Surfactant Concentration Dependencies
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Table of Symbols
| Symbol | Definition | Units |
| η0 | zero-shear viscosity | Pa·s |
| storage modulus | Pa | |
| loss modulus | Pa | |
| plateau modulus | Pa | |
| minimum of loss modulus | Pa | |
| maximum of loss modulus | Pa | |
| le | average contour length | nm |
| ξ | mesh size | nm |
| relaxation time | s | |
| breaking time | s | |
| L | contour length between entanglements | nm |
| lp | persistence length | nm |
| Rg | gyration radius | nm |
| k | breaking rate constant | (nm·s)−1 |
| C* | overlap concentration | wt.% |
References
- Israelachvili, J.N.; Mitchell, D.J.; Ninham, B.W. Theory of self-assembly of hydrocarbon amphiphiles into micelles and bilayers. J. Chem. Soc. Faraday Trans. 2 Mol. Chem. Phys. 1976, 72, 1525–1568. [Google Scholar] [CrossRef]
- Magid, L.J. The Surfactant—Polyelectrolyte Analogy. J. Phys. Chem. B 1998, 5647, 4064–4074. [Google Scholar] [CrossRef]
- Molchanov, V.S.; Kuklin, A.I.; Orekhov, A.S.; Arkharova, N.A.; Philippova, O.E. Temporally persistent networks of long-lived mixed wormlike micelles of zwitterionic and anionic surfactants. J. Mol. Liq. 2021, 342, 116955. [Google Scholar] [CrossRef]
- Molchanov, V.S.; Philippova, O.E. Effects of concentration and temperature on viscoelastic properties of aqueous potassium oleate solutions. Colloid J. 2009, 71, 249–255. [Google Scholar] [CrossRef]
- Dreiss, C.A. Wormlike micelles: Where do we stand? Recent developments, linear rheology and scattering techniques. Soft Matter 2007, 3, 956–970. [Google Scholar] [CrossRef]
- Yang, J.C.; Li, F.C.; He, Y.R.; Huang, Y.M.; Jiang, B.C. Experimental study on the characteristics of heat transfer and flow resistance in turbulent pipe flows of viscoelastic-fluid-based Cu nanofluid. Int. J. Heat Mass Transf. 2013, 62, 303–313. [Google Scholar] [CrossRef]
- Cates, M.E.; Fielding, S.M. Rheology of giant micelles. Adv. Phys. 2006, 55, 799–879. [Google Scholar] [CrossRef]
- Couillet, I.; Hughes, T.; Maitland, G.; Candau, F. Synergistic effects in aqueous solutions of mixed wormlike micelles and hydrophobically modified polymers. Macromolecules 2005, 38, 5271–5282. [Google Scholar] [CrossRef]
- Shashkina, J.A.; Philippova, O.E.; Zaroslov, Y.D.; Khokhlov, A.R.; Pryakhina, T.A.; Blagodatskikh, I.V. Rheology of viscoelastic solutions of cationic surfactant. Effect of added associating polymer. Langmuir 2005, 21, 1524–1530. [Google Scholar] [CrossRef]
- Qi, Y.; Zakin, J.L. Chemical and rheological characterization of drag-reducing cationic surfactant systems. Ind. Eng. Chem. Res. 2002, 41, 6326–6336. [Google Scholar] [CrossRef]
- Yavrukova, V.I.; Radulova, G.M.; Danov, K.D.; Kralchevsky, P.A.; Xu, H.; Ung, Y.W.; Petkov, J.T. Rheology of mixed solutions of sulfonated methyl esters and betaine in relation to the growth of giant micelles and shampoo applications. Adv. Colloid Interface Sci. 2019, 275, 102262. [Google Scholar] [CrossRef] [PubMed]
- Cates, M.E.; Candau, S.J. Statics and dynamics of worm-like surfactant micelles. J. Phys. Condens. Matter 1990, 2, 6869–6892. [Google Scholar] [CrossRef]
- Khatory, A.; Kern, F.; Lequeux, F.; Appell, J.; Porte, G.; Morie, N.; Ott, A.; Urbach, W. Entangled versus multiconnected network of wormlike micelles. Langmuir 1993, 9, 933–939. [Google Scholar] [CrossRef]
- Kern, F.; Lamarechal, P.; Candau, S.J.; Cates, M.E. Rheological properties of semidilute and concentrated aqueous solutions of cetyltrimethylammonium bromide in the presence of potassium bromide. Langmuir 1992, 8, 437–440. [Google Scholar] [CrossRef]
- Molchanov, V.S.; Philippova, O.E.; Khokhlov, A.R.; Kovalev, Y.A.; Kuklin, A.I. Self-assembled networks highly responsive to hydrocarbons. Langmuir 2007, 23, 105–111. [Google Scholar] [CrossRef]
- MacKintosh, F.C.; Safran, S.A.; Pincus, P.A. Self-assembly of linear aggregates: The effect of electrostatics on growth. Europhys. Lett. 1990, 12, 697–702. [Google Scholar] [CrossRef][Green Version]
- Odijk, T. Growth of linear charged micelles. Biophys. Chem. 1991, 41, 23–29. [Google Scholar] [CrossRef][Green Version]
- Croce, V.; Cosgrove, T.; Dreiss, A.; King, S.; Maitland, G.; Hughes, T. Giant micellar worms under shear: A rheological study using SANS. Langmuir 2005, 6762–6768. [Google Scholar] [CrossRef]
- Khatory, A.; Lequeux, F.; Kern, F.; Candau, S.J. Linear and nonlinear viscoelasticity of semidilute solutions of wormlike micelles at high salt content. Langmuir 1993, 9, 1456–1464. [Google Scholar] [CrossRef]
- Ospennikov, A.S.; Gavrilov, A.A.; Artykulnyi, O.P.; Kuklin, A.I.; Novikov, V.V.; Shibaev, A.V.; Philippova, O.E. Transformations of wormlike surfactant micelles induced by a water-soluble monomer. J. Colloid Interface Sci. 2021, 602, 590–601. [Google Scholar] [CrossRef]
- Kwiatkowski, A.L.; Molchanov, V.S.; Orekhov, A.S.; Vasiliev, A.L.; Philippova, O.E. Impact of salt co- and counterions on rheological properties and structure of wormlike micellar solutions. J. Phys. Chem. B 2016, 120, 2547–12556. [Google Scholar] [CrossRef]
- Yesilata, B.; Clasen, C.; Mckinley, G.H. Nonlinear shear and extensional flow dynamics of wormlike surfactant solutions. J. Non-Newtonian Fluid Mech. 2006, 133, 73–90. [Google Scholar] [CrossRef]
- Raghavan, S.R.; Kaler, E.W. Highly viscoelastic wormlike micellar solutions formed by cationic surfactants with long unsaturated tails. Langmuir 2001, 300–306. [Google Scholar] [CrossRef]
- Croce, V.; Cosgrove, T.; Dreiss, C.A.; Maitland, G.; Hughes, T.; Karlsson, G. Impacting the length of wormlike micelles using mixed surfactant systems. Langmuir 2004, 20, 7984–7990. [Google Scholar] [CrossRef]
- Search, H.; Journals, C.; Contact, A.; Iopscience, M.; Address, I.P. Neutronographic investigations of supramolecular structures on upgraded small-angle spectrometer YuMO. J. Phys. Conf. Ser. 2017, 848, 012010. [Google Scholar]
- Andreeva, A.S.; Philippova, O.E.; Khokhlov, A.R.; Islamov, A.K.; Kuklin, A.I. Effect of the mobility of charged units on the microphase separation in amphiphilic polyelectrolyte hydrogels. Langmuir 2005, 21, 1216–1222. [Google Scholar] [CrossRef]
- Padding, J.T.; Boek, E.S.; Briels, W.J. Dynamics and rheology of wormlike micelles emerging from particulate computer simulations. J. Chem. Phys. 2008, 129. [Google Scholar] [CrossRef]
- Calabrese, M.A.; Rogers, S.A.; Murphy, R.P.; Wagner, N.J. The rheology and microstructure of branched micelles under shear. J. Rheol. 2015, 59, 1299–1328. [Google Scholar] [CrossRef]
- Lerouge, S.; Berret, J.-F. Shear-induced transitions and instabilities in surfactant wormlike micelles. Adv. Polym. Sci. 2009, 230, 1–71. [Google Scholar]
- Turner, M.S.; Marques, C.; Cates, M.E. Dynamics of wormlike micelles: The “bond-interchange” reaction scheme. Langmuir 1993, 9, 695–701. [Google Scholar] [CrossRef]
- Granek, R.; Cates, M.E. Stress relaxation in living polymers: Results from a Poisson renewal model. J. Chem. Phys. 1992, 96, 4758–4767. [Google Scholar] [CrossRef]
- Molchanov, V.S.; Pletneva, V.A.; Kuklin, A.I.; Philippova, O.E. Nanocomposite composed of charged wormlike micelles and magnetic particles. J. Phys. Conf. Ser. 2017, 848, 012013. [Google Scholar] [CrossRef]
- Kern, F.; Lequeux, F.; Zana, R.; Candau, S.J. Dynamical properties of salt-free viscoelastic micellar solutions. Langmuir 1994, 10, 1714–1723. [Google Scholar] [CrossRef]
- Gaudino, D.; Pasquino, R.; Grizzuti, N. Adding salt to a surfactant solution: Linear rheological response of the resulting morphologies. J. Rheol. 2015, 59, 1363–1375. [Google Scholar] [CrossRef]
- Rogers, S.A.; Calabrese, M.A.; Wagner, N.J. Rheology of branched wormlike micelles. Curr. Opin. Colloid Interface Sci. 2014, 19, 530–535. [Google Scholar] [CrossRef]
- Kwiatkowski, A.L.; Molchanov, V.S.; Sharma, H.; Kuklin, A.I.; Dormidontova, E.E.; Philippova, O.E. Growth of wormlike micelles of surfactant induced by embedded polymer: Role of polymer chain length. Soft Matter 2018, 14, 4792–4804. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Molchanov, V.S.; Rostovtsev, A.V.; Shishkhanova, K.B.; Kuklin, A.I.; Philippova, O.E. Strong Viscosity Increase in Aqueous Solutions of Cationic C22-Tailed Surfactant Wormlike Micelles. Fluids 2022, 7, 8. https://doi.org/10.3390/fluids7010008
Molchanov VS, Rostovtsev AV, Shishkhanova KB, Kuklin AI, Philippova OE. Strong Viscosity Increase in Aqueous Solutions of Cationic C22-Tailed Surfactant Wormlike Micelles. Fluids. 2022; 7(1):8. https://doi.org/10.3390/fluids7010008
Chicago/Turabian StyleMolchanov, Vyacheslav S., Andrei V. Rostovtsev, Kamilla B. Shishkhanova, Alexander I. Kuklin, and Olga E. Philippova. 2022. "Strong Viscosity Increase in Aqueous Solutions of Cationic C22-Tailed Surfactant Wormlike Micelles" Fluids 7, no. 1: 8. https://doi.org/10.3390/fluids7010008
APA StyleMolchanov, V. S., Rostovtsev, A. V., Shishkhanova, K. B., Kuklin, A. I., & Philippova, O. E. (2022). Strong Viscosity Increase in Aqueous Solutions of Cationic C22-Tailed Surfactant Wormlike Micelles. Fluids, 7(1), 8. https://doi.org/10.3390/fluids7010008






