Numerical Investigation of Conjugate Natural Convection in a Cavity with a Local Heater by the Lattice Boltzmann Method

Abstract

A numerical study of conjugate thermogravitational convection in a closed cavity with a local heater of square or triangular shape placed on a heat-conducting substrate using the double distribution function of the lattice Boltzmann method has been carried out. The side walls of the research area are maintained at a constant minimum temperature. The influence of the geometric shape of the heating element, the Rayleigh number, and the material of the heat-removing substrate on the thermohydrodynamic parameters has been studied. As a result of the research, the joint effect of these mentioned parameters on the efficiency of heat removal from the heater surface has been established. It has been found that a rise of the bottom wall thermal conductivity causes an increase in the average Nusselt number at the heater surface.

1. Introduction

Conjugate thermogravitational convection attracts the attention of many scientists from all over the world due to the extensive range of tasks where it can be applied. One of such tasks is the convective–conductive cooling of radio-electronic units with the presence of heating elements. These tasks are particularly relevant due to the intensive development of the micro and radio electronics industry, while the power of such devices is also growing, and therefore the energy consumption and heat load of the active elements are also increasing. In this connection, the development of the active and passive cooling systems is required. The analysis of passive cooling systems is not so spread compared to active cooling systems, where many published results can be found [1,2,3,4,5]. To study the efficiency of passive cooling systems, it is proposed to consider the influence of the geometric shape of the heating element and the thermal conductivity of the substrate material where this local energy source is placed. The lattice Boltzmann method (LBM) has been used as the main method of numerical research.

A crucial challenge for scientists is the conjugate heat exchange in cavities of various configurations with heating elements [6,7,8,9,10] to try to intensify the heat removal from the heaters. Thus, Joshi et al. [6] have examined conjugate natural convection in a closed square cavity having a local heater inside the heat-conducting substrate in the middle part of the region. Authors have conducted studies for a wide range of Rayleigh and Prandtl numbers. The reduction of the maximum heated surface temperature has been observed in the case of low and moderate thermal conductivity ratios. Madhavan and Sastri [7] have numerically investigated the conjugate natural convective heat transfer in the closed cavity. Three heating elements have been located on the heat-conducting substrate, and the distance between the heaters has been varied. It was found that the Rayleigh and Prandtl numbers, as well as the chamber border restrictions, have an essential influence on the heat transfer performance and fluid flow structure within the cavity. Desrayaud et al. [8] investigated laminar natural convection in a channel with a heat-conducting substrate and a local energy source. The authors analyzed the influence of the thermal conductivity of the substrate and its thickness, as well as the width of the channel. It was shown that the growth of the substrate thickness decreases the heater temperature.

Now there are many different works which analyze of conjugate convection energy transport using the lattice Boltzmann method. Thus, Wang et al. [11] proposed an improved lattice Boltzmann model that takes into account the influence of heat capacity. The influence of the Rayleigh number, the thermophysical properties of the wall and the wall thickness on the streamlines, isotherms and the Nusselt number was analyzed. It was established that an increase in the thickness of the external wall tends to decrease the heat transfer rate. Suzuki et al. [12] proposed the immersed boundary-lattice Boltzmann method for heat transfer with moving-boundary flows. The proposed approach consists of the lattice Boltzmann method for the temperature field, and the immersed boundary methods have been used for the thermal boundary conditions. Zhang et al. [13] studied the conjugate heat transfer of nanofluids within a fibrous medium. A random-walk-based stochastic model was offered to create the fibrous medium made up of interrelated fibers. The developed conjugate scheme allows for an efficient and correct approach to simulate conjugate thermal interfaces at pore scales. Imani [14] used the lattice Boltzmann method to simulate conjugate natural convection in a closed square cavity in the presence of a heat-conducting insert in the center of the region. The author proposed a scheme based on the Taylor series expansion and the least square-based lattice Boltzmann method. Mohebbi et al. [15] investigated the conjugate heat transfer of the laminar flow in a cavity with two conductive ribs and filled with water/Al₂O₃ nanofluid using the lattice Boltzmann method. The influence of rectangular partitions on the thermohydrodynamics in the cavity was determined. Yue et al. [16] developed a new lattice Boltzmann model for the conjugate heat transfer problems where the evolution equation with an updated equilibrium distribution function and a source term was considered. It was shown that the results obtained from the present lattice Boltzmann model are in good agreement with the analytical solutions. Korba et al. [17] compared the common interface schemes proposed in the literature by focusing on their numerical accuracy and approximation orders. Nouri et al. [18] proposed an innovative formulation of the lattice Boltzmann method for solving the conjugate heat transfer problems in heterogeneous media. The developed model was validated using various unsteady heat conduction problems in heterogeneous media. Lu et al. [19] offered the optimal two-relaxation-time (OTRT) thermal lattice Boltzmann equation (TLBE) for the analysis of conjugate heat transfer. As a result, the authors found that this developed technique is very effective for the modeling of conjugate heat transfer problems with both planar and curved interfaces for both transient and steady modes. Lu et al. [20] suggested a simple difference method for the lattice Boltzmann model to simulate the conjugate heat transfer problems. They noted that the developed method is not difficult and is viable for both steady and transient heat transfer problems.

This brief review shows the meaningfulness and necessity of analyzing conjugate heat transfer in different cavities with local heaters. The development of the lattice Boltzmann method for this purpose is a very good technique, that allows for the reduction of the computational time and programming efforts. Therefore, the objective of this research is an implementation of the lattice Boltzmann method for the numerical analysis of natural convection in a square cavity with a heat-conducting bottom solid wall and a local isothermal heater placed on this wall. In addition, the considered passive cooling technique for the heated element based on the temperature difference between the heater and cooled vertical walls, the heat-conducting substrate material and the shape of this local unit can help improve the understanding of the features of the temperature evolution in electronics devices. Such analysis is performed for the first time taking into account previously published papers.

2. Mathematical Model

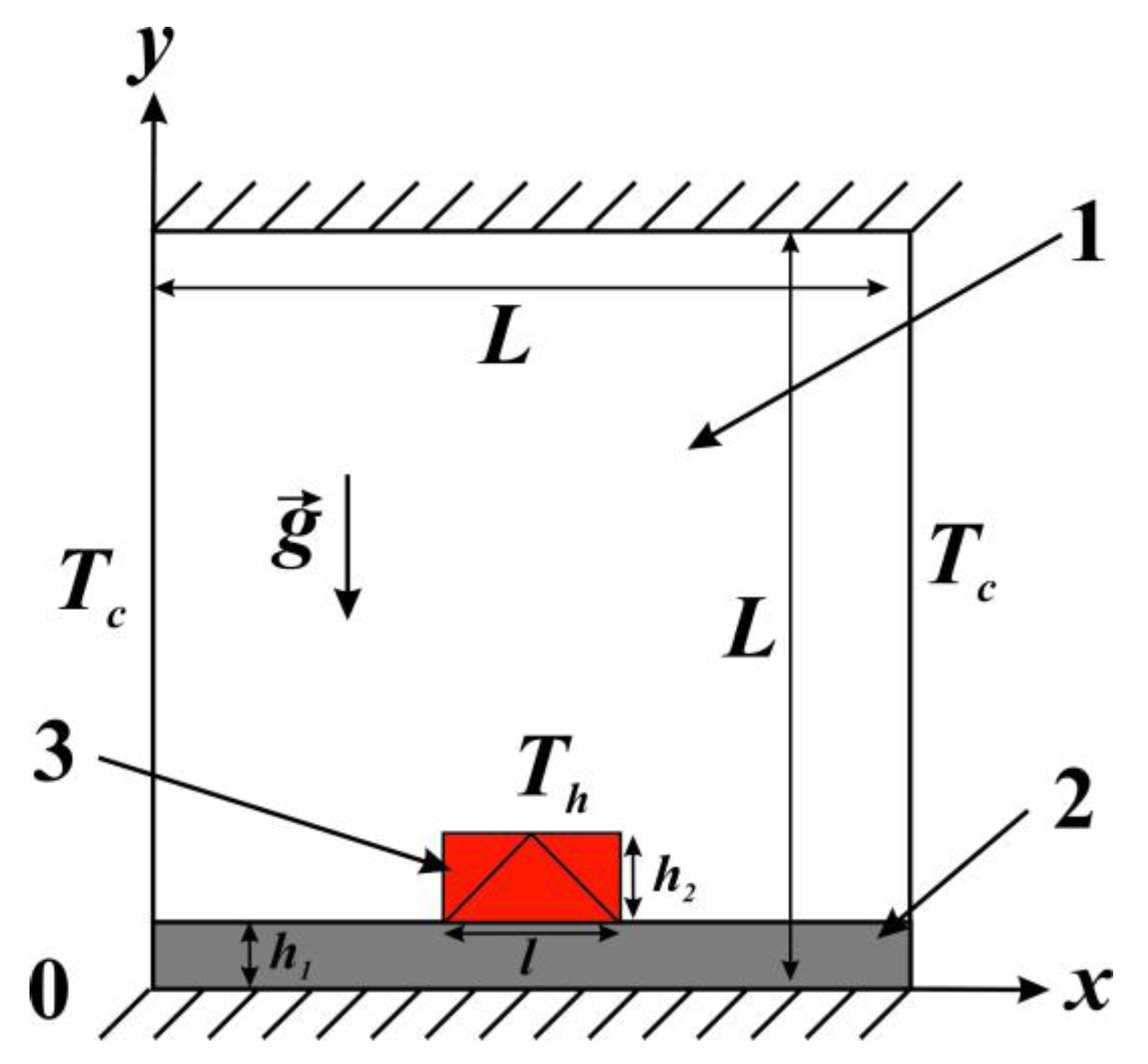
The research configuration is shown in Figure 1. A local heater of length l and height h₂ having a rectangular or triangular shape is placed on a heat-conducting substrate of height h₁ within a closed square cavity filled with air. The vertical walls are maintained at a constant minimum temperature T_c, and the remaining boundaries of the region are considered to be adiabatic. The temperature of the energy source is constant (T_h) and has a maximum within the cavity.

The numerical study of the considered problem has been carried out on the basis of the double distribution function lattice Boltzmann method using the D2Q9 scheme. The main equation for describing transport processes in LBM is the kinetic Boltzmann equation. This equation can be written using dimensionless variables as follows [21]

$$\begin{array}{c}{f}_i\left(X+C_{x_i}\Delta \tau ,Y+C_{y_i}\Delta \tau ,\tau +\Delta \tau \right)=\left(1-{\omega }_f\right)f_i\left(X,Y,\tau \right)+\hspace{1em}\left(i=0,1,\dots ,8\right)\\ +{\omega }_f{f}_i^{eq}\left(X,Y,\tau \right)+F_{y_i}\left(X,Y,\tau \right)\Delta \tau \end{array}$$

(1)

$$g_i\left(X+C_{x_i}\Delta \tau ,Y+C_{y_i}\Delta \tau ,\tau +\Delta \tau \right)=\left(1-{\omega }_g\right)g_i\left(X,Y,\tau \right)+{\omega }_g{g}_i^{eq}\left(X,Y,\tau \right) \left(i=0,1,\dots ,8\right)$$

(2)

$$h_i\left(X+C_{x_i}\Delta \tau ,Y+C_{y_i}\Delta \tau ,\tau +\Delta \tau \right)=\left(1-{\omega }_h\right)h_i\left(X,Y,\tau \right)+{\omega }_h{h}_i^{eq}\left(X,Y,\tau \right) \left(i=0,1,\dots ,8\right)$$

(3)

Here f_i, g_i, h_i are the density distribution function, the energy distribution function for the fluid and the energy distribution function for the solid wall, respectively; X and Y are the dimensionless Cartesian coordinates, τ and Δτ are the dimensionless time and time step, respectively. Solving these equations, the computational process is divided into the two steps:

• Collision (relaxation):

$$f_i\left(X,Y,\tau \right)=\left(1-{\omega }_f\right)f_i\left(X,Y,\tau \right)+{\omega }_f{f}_i^{eq}\left(X,Y,\tau \right)+F_{y_i}\left(X,Y,\tau \right)\Delta \tau \hspace{1em}\left(i=0,1,\dots ,8\right)$$

(4)

$$g_i\left(X,Y,\tau \right)=\left(1-{\omega }_g\right)g_i\left(X,Y,\tau \right)+{\omega }_g{g}_i^{eq}\left(X,Y,\tau \right)\hspace{1em}\left(i=0,1,\dots ,8\right)$$

(5)

$$h_i\left(X,Y,\tau \right)=\left(1-{\omega }_h\right)h_i\left(X,Y,\tau \right)+{\omega }_h{h}_i^{eq}\left(X,Y,\tau \right)\hspace{1em}\left(i=0,1,\dots ,8\right)$$

(6)

2.

Streaming (propagation):

$$f_i\left(X+C_{y_i}\Delta \tau ,Y+C_{y_i}\Delta \tau ,\tau +\Delta \tau \right)=f_i\left(X,Y,\tau \right)\hspace{1em}\left(i=0,1,\dots ,8\right)$$

(7)

$$g_i\left(X+C_{y_i}\Delta \tau ,Y+C_{y_i}\Delta \tau ,\tau +\Delta \tau \right)=g_i\left(X,Y,\tau \right)\hspace{1em}\left(i=0,1,\dots ,8\right)$$

(8)

$$h_i\left(X+C_{y_i}\Delta \tau ,Y+C_{y_i}\Delta \tau ,\tau +\Delta \tau \right)=h_i\left(X,Y,\tau \right)\hspace{1em}\left(i=0,1,\dots ,8\right)$$

(9)

To determine the equilibrium distribution functions, the following relations are used:

$$f_i^{eq}=w_i\rho \left(1+\frac{\mathit{V}{\mathit{C}}_i}{C_s^2}+\frac{{\left(\mathit{V}{\mathit{C}}_i\right)}^2}{2C_s^4}-\frac{\mathit{V}\mathit{V}}{2C_s^2}\right)$$

(10)

$$g_i^{eq}=w_i\mathsf{\Theta }\left(1+\frac{\mathit{V}{\mathit{C}}_i}{C_s^2}+\frac{{\left(\mathit{V}{\mathit{C}}_i\right)}^2}{2C_s^4}-\frac{\mathit{V}\mathit{V}}{2C_s^2}\right)$$

(11)

$$h_i^{eq}=w_i\mathsf{\Theta }\left(1+\frac{\mathit{V}{\mathit{C}}_i}{C_s^2}+\frac{{\left(\mathit{V}{\mathit{C}}_i\right)}^2}{2C_s^4}-\frac{\mathit{V}\mathit{V}}{2C_s^2}\right)$$

(12)

Here $f_i^{eq}$ is the equilibrium distribution function for density, $g_i^{eq}$ is the equilibrium distribution function for the temperature of the fluid, $h_i^{eq}$ is the equilibrium distribution function for the temperature of the solid wall, ρ is the dimensionless density, Θ is the dimensionless temperature, w_i is the weight function $\left({\displaystyle \sum _i{w}_i}=1\right)$, V is the macroscopic velocity vector, C_i is the discrete velocity vector, $C_s=1/\sqrt{3}$ is the speed of sound, $F_{y_i}=\left\{w_i\rho g\beta \left(\mathsf{\Theta }-{\mathsf{\Theta }}_0\right)C_{y_i}\right\}/C_s^2$ is the force of gravity, g is the acceleration of gravity and β is the coefficient of volumetric thermal expansion. The relaxation frequency for each equation can be defined as follows:

$${\omega }_f=\frac{1}{0.5+\frac{\nu }{\Delta \tau C_s^2}}$$

(13)

$${\omega }_g=\frac{1}{0.5+\frac{\alpha }{\Delta \tau C_s^2}}$$

(14)

$${\omega }_h=\frac{1}{0.5+k\frac{\alpha }{\Delta \tau C_s^2}}$$

(15)

here $k=\frac{k_{wall}}{k_{fluid}}$ is the thermal conductivity ratio.

The density and the macroscopic velocity vector are calculated as

$$\rho ={\displaystyle \sum _{i=0}^8{f}_i}$$

(16)

$$\rho V={\displaystyle \sum _{i=0}^8{f}_i{C}_i}$$

(17)

All calculations have been performed using the D2Q9 lattice type. The link-wise bounce back scheme has been chosen as the type of boundary conditions [21].

The initial conditions are $\mathit{V}\left(X,Y,0\right)=\mathsf{\Theta }\left(X,Y,0\right)=0$ and for the local heater Θ = 1.

The boundary conditions are

$\mathit{V}\left(X,Y\right)=0$ on the walls of the cavity and heat source,

$\mathsf{\Theta }\left(X,Y\right)=1$ for the local heater;

$\mathsf{\Theta }\left(0,Y\right)=\mathsf{\Theta }\left(1,Y\right)=\frac{\partial \mathsf{\Theta }}{\partial Y}\left(X,0\right)=\frac{\partial \mathsf{\Theta }}{\partial Y}\left(X,1\right)=0$.

Verification

The developed computational technique has been validated using both conjugate and non-conjugate problems for natural convection in differentially-heated cavities. The first benchmark problem is the classical de Vahl Davis problem [22,23] on air natural convection in a differentially-heated square chamber.

Table 1. Average Nusselt number at the heated wall with the Rayleigh number.

Ra	Present Results	[23]	[24]	[25]
103	1.117	1.118	1.074	1.073
104	2.241	2.243	2.084	2.155
105	4.509	4.519	4.3	4.352
106	8.841	8.8	8.743	8.632

shows the average Nusselt number values on the heated wall compared to numerical data of other authors [23,24,25].

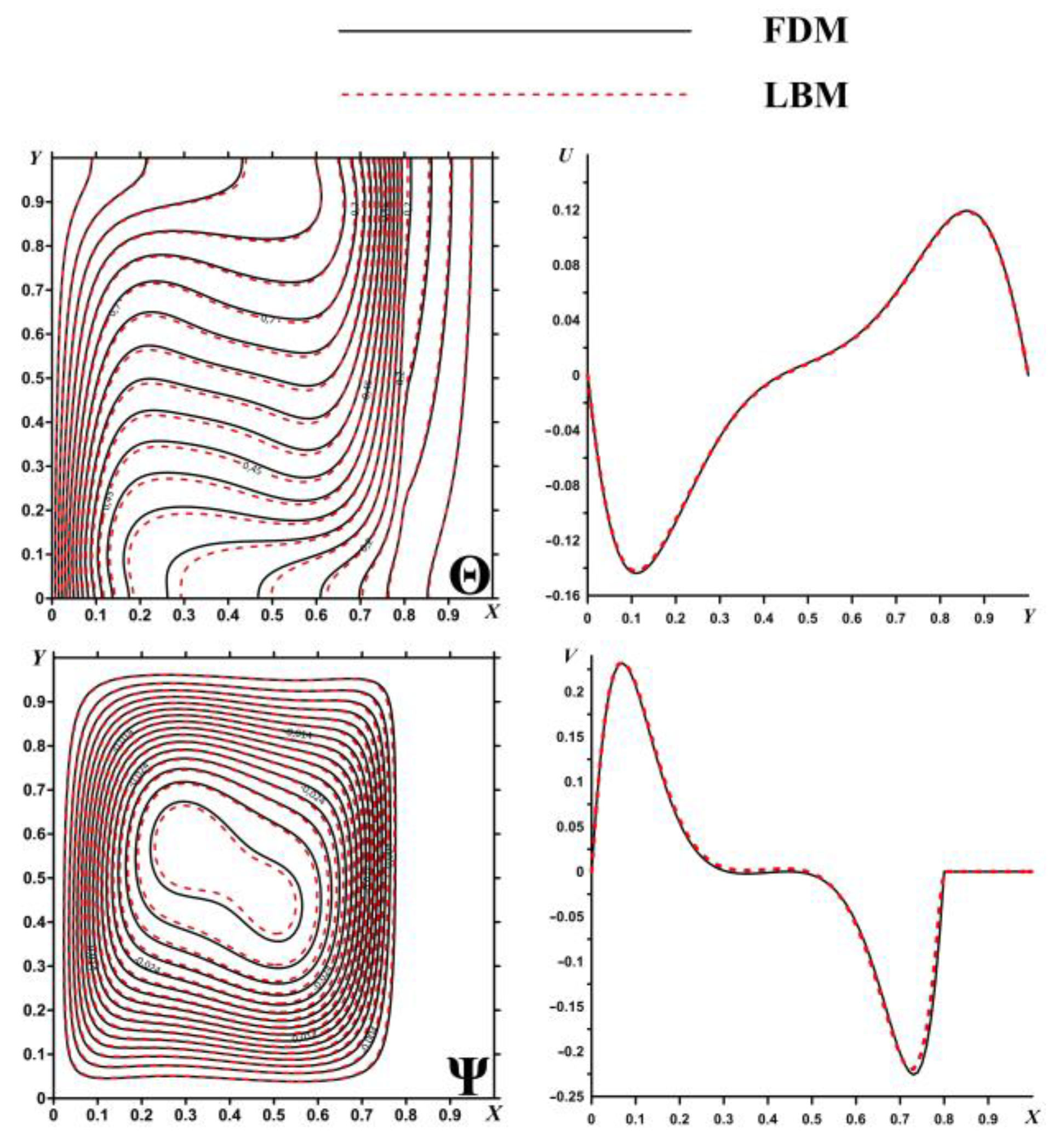
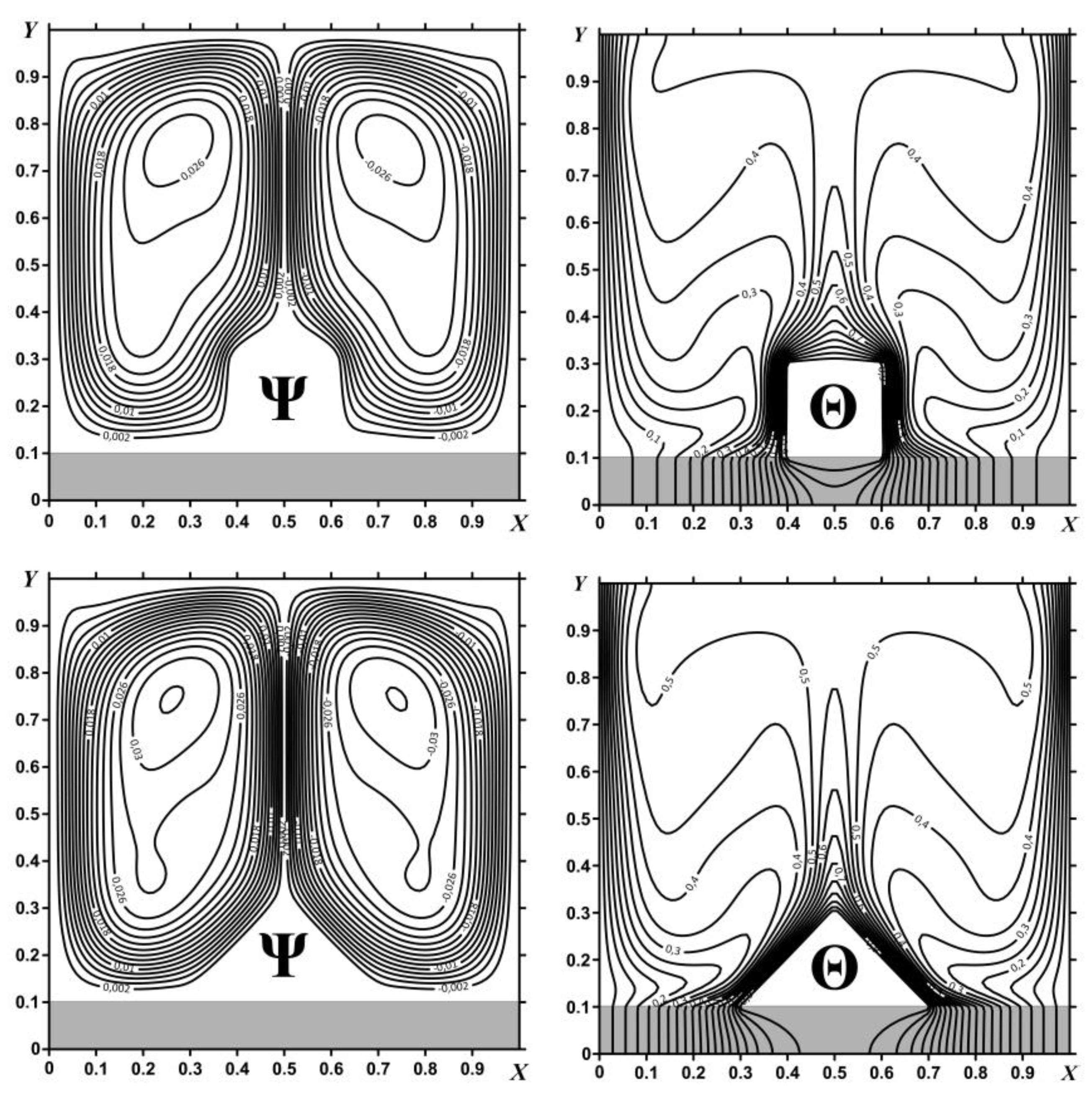
The second benchmark problem is a conjugate free convection in an enclosure with a right heat-conducting solid wall of finite thickness. A differentially-heated cavity has been considered, namely, the left wall is isothermally heated with non-dimensional temperature Θ = 1, while the right one is isothermally cooled from the outside with non-dimensional temperature Θ = 0; at the same time, the thermal conductivity ratio as a ratio between the thermal conductivity of the solid wall and the thermal conductivity of the inner medium was equal to 5. This benchmark problem has been considered to compare flow and thermal patterns obtained using the developed codes based on the lattice Boltzmann and finite difference methods. Thus, Figure 2 shows isotherms Θ, streamlines Ψ, horizontal U and vertical V velocity profiles at the middle cross-sections obtained using these two numerical techniques. As can be seen from this figure, a good agreement of various computational methods has been obtained.

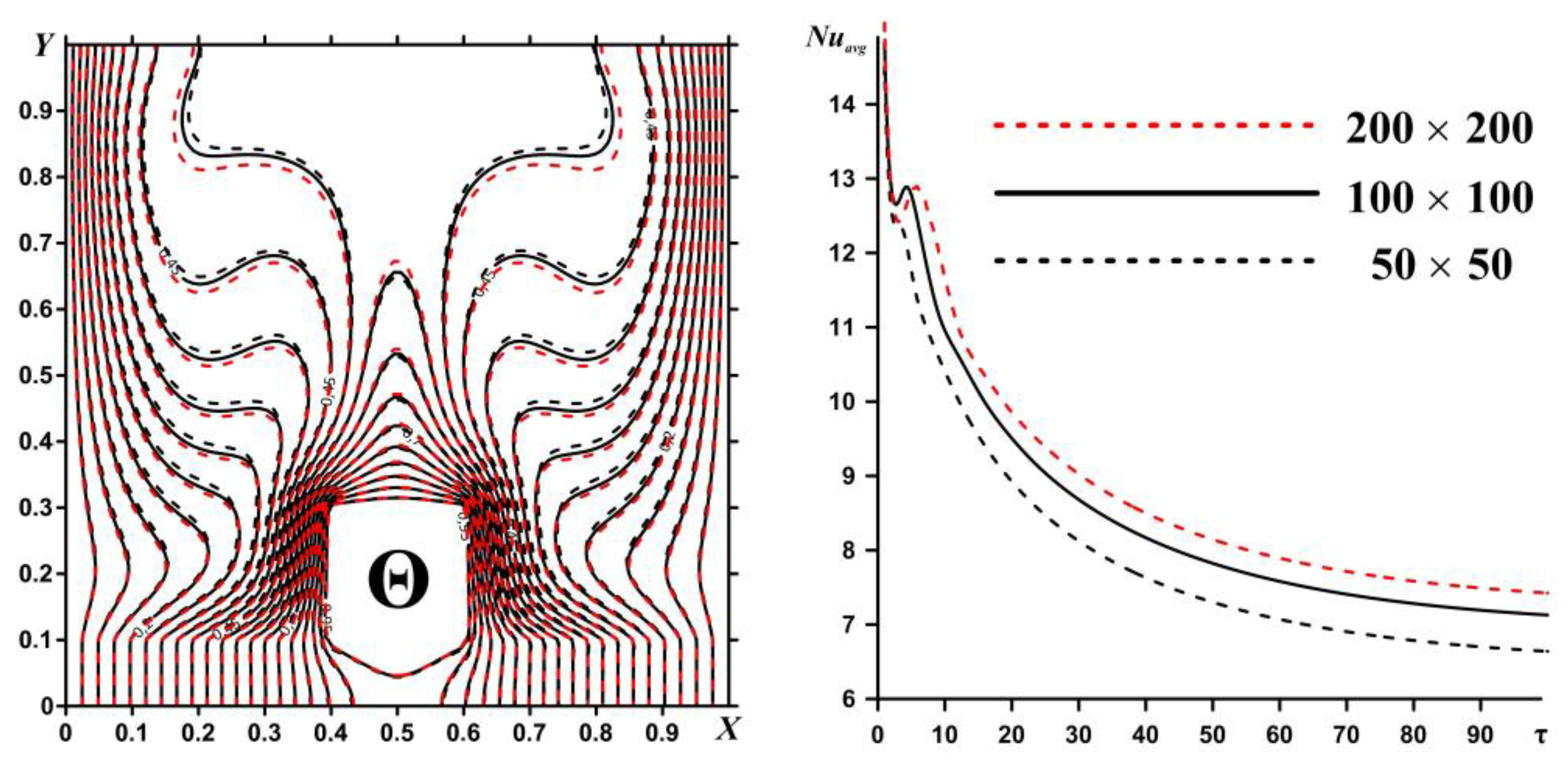
Another stage of validation is the analysis of the grid independence of calculations for the considered problem shown in Figure 1. Figure 3 shows the influence of mesh parameters on the isotherms and average Nusselt number at the local heater surface at Ra = 10⁵ for structured grids of 50 × 50, 100 × 100 and 200 × 200 elements. The optimal dimension for this problem is 100 × 100 elements, and, as a result, further calculations have been carried out using this mesh.

3. Results and Discussion

The numerical investigation of conjugate thermogravitational convection in a closed cavity with a local heater of square or triangular shape has been carried out at the following values of the governing parameters: 10⁴ ≤ Ra ≤ 10⁶, Pr = 0.7. Two materials for solid wall have been studied, namely, textolite, with a thermal conductivity ratio k = 18.2, and steel, with a thermal conductivity ratio k = 631.8. The considered time interval is 0 ≤ τ ≤ 100. Rectangular and triangular shapes for the heating elements have been studied. The height of the heat-conducting substrate is equal to h₁/L = 0.1, while the height of the heat source is equal to h₂/L = 0.2. The sizes of the energy sources have been chosen so that their areas are equal to each other, namely, S_triangle = S_rectangle (therefore l/L = 0.4 is for the heater of triangular shape and l/L = 0.2 is for the heater of rectangular shape). It has been assumed that the energy source is isothermal. Additionally, the case of equal lengths of the heater of rectangular and triangular shapes has been studied, namely, l/L = 0.4 and h₂/L = 0.2.

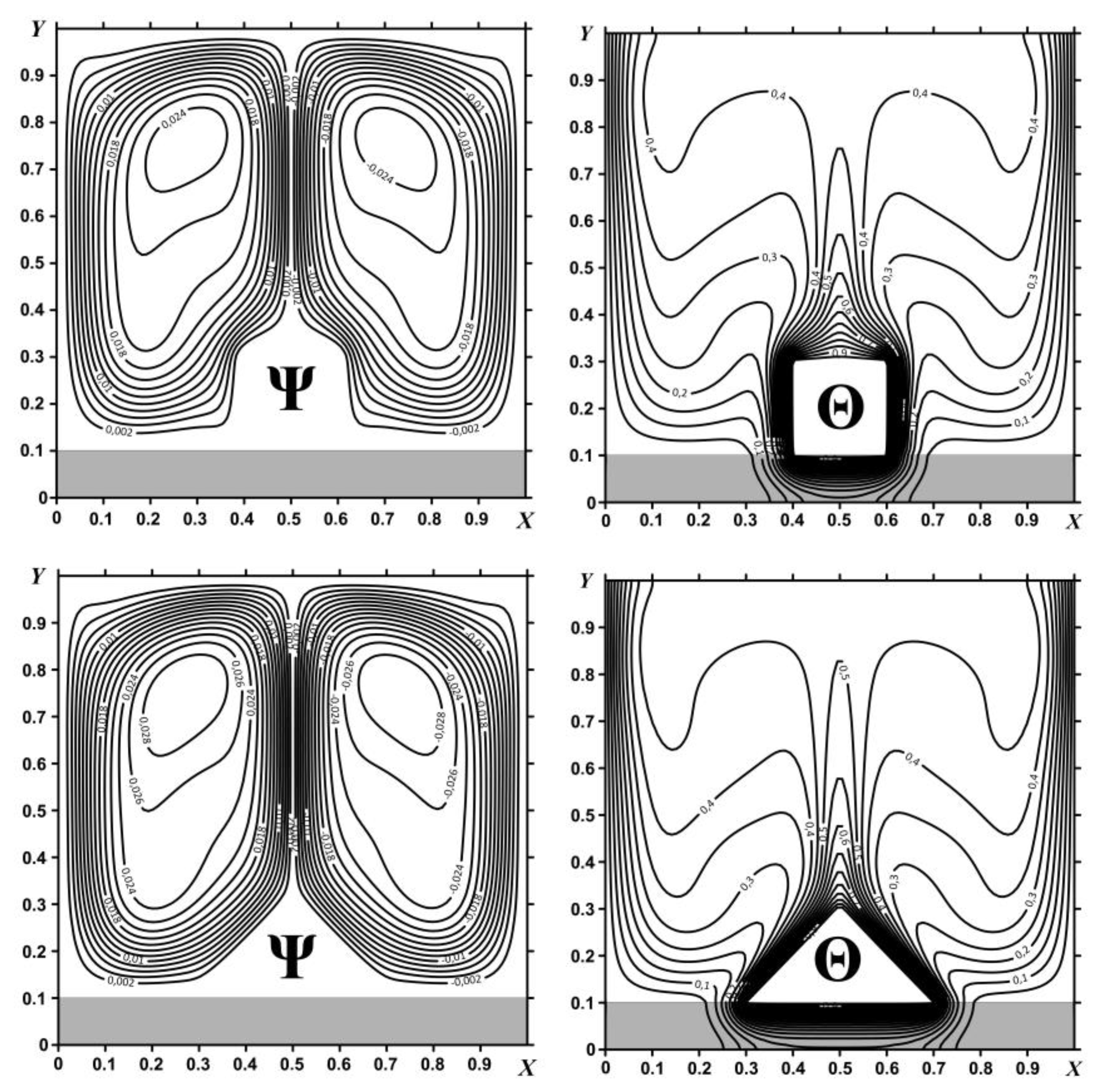
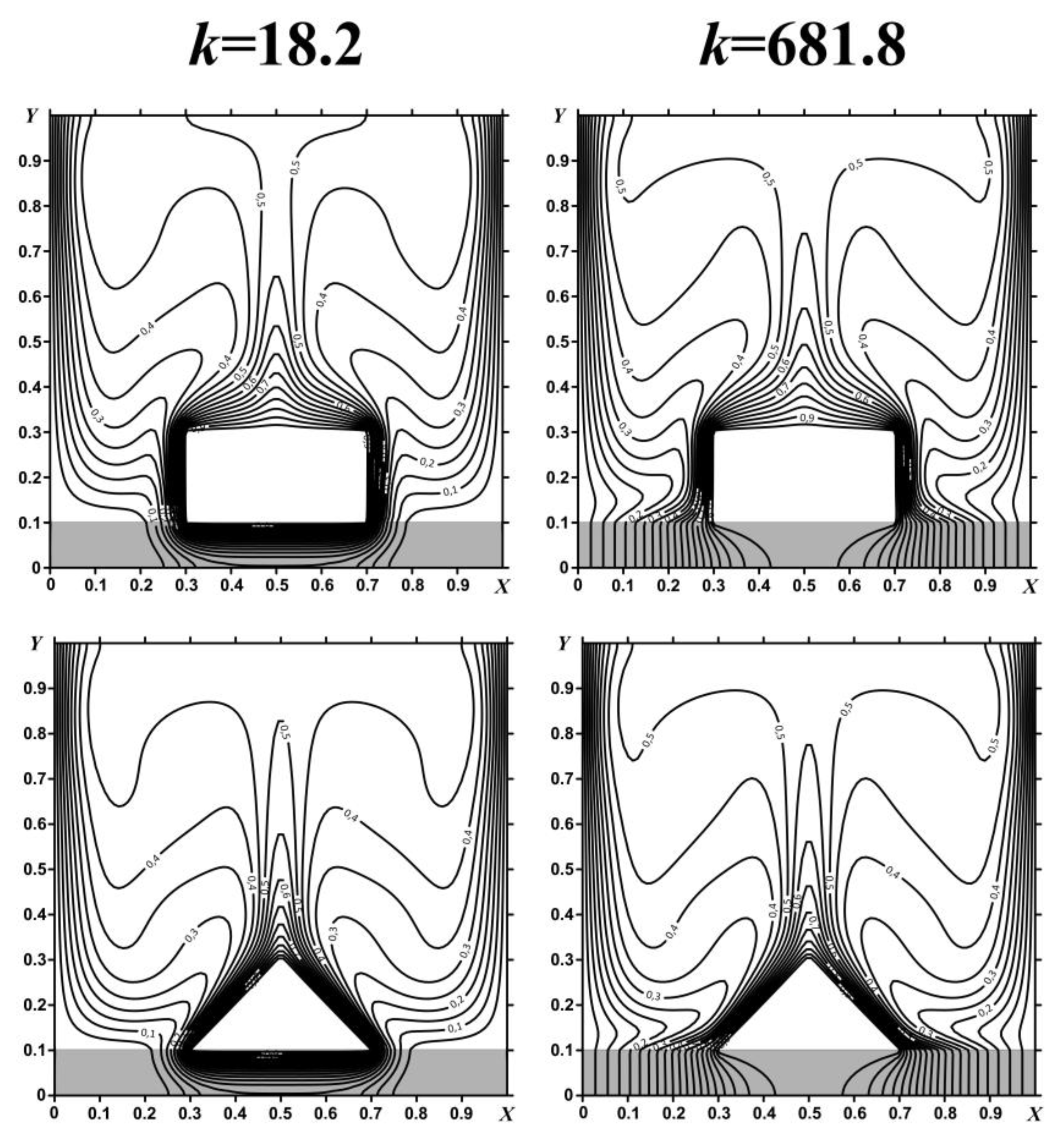
Figure 4 and Figure 5 show the streamlines and isotherms at Ra = 10⁶ and different thermal conductivity ratios for τ = 100. Two zones of recirculation flow are formed in the cavity with the cores in the upper part of these areas. In the case of a square-shaped source, the streamlines are deformed near the surface of the heater, and with an increase in the thermal conductivity ratio, an influence of the upper corner points of the square source increases. In the case of a triangular heater, the streamlines have a smoother structure, and the cores of convective cells are more elongated. An increase in the thermal conductivity ratio has less influence on the flow structure for this heater shape. The structures of isotherms for various forms of source are distinguished mainly near the surface of the heater and inside the heat-conducting bottom wall. Due to the fact that the triangular shape of the heater is more elongated along the lower heat-conducting wall, it has a higher contact surface area with the bottom wall. As a result, the temperature inside the wall and cavity is higher for a heater with a triangular shape.

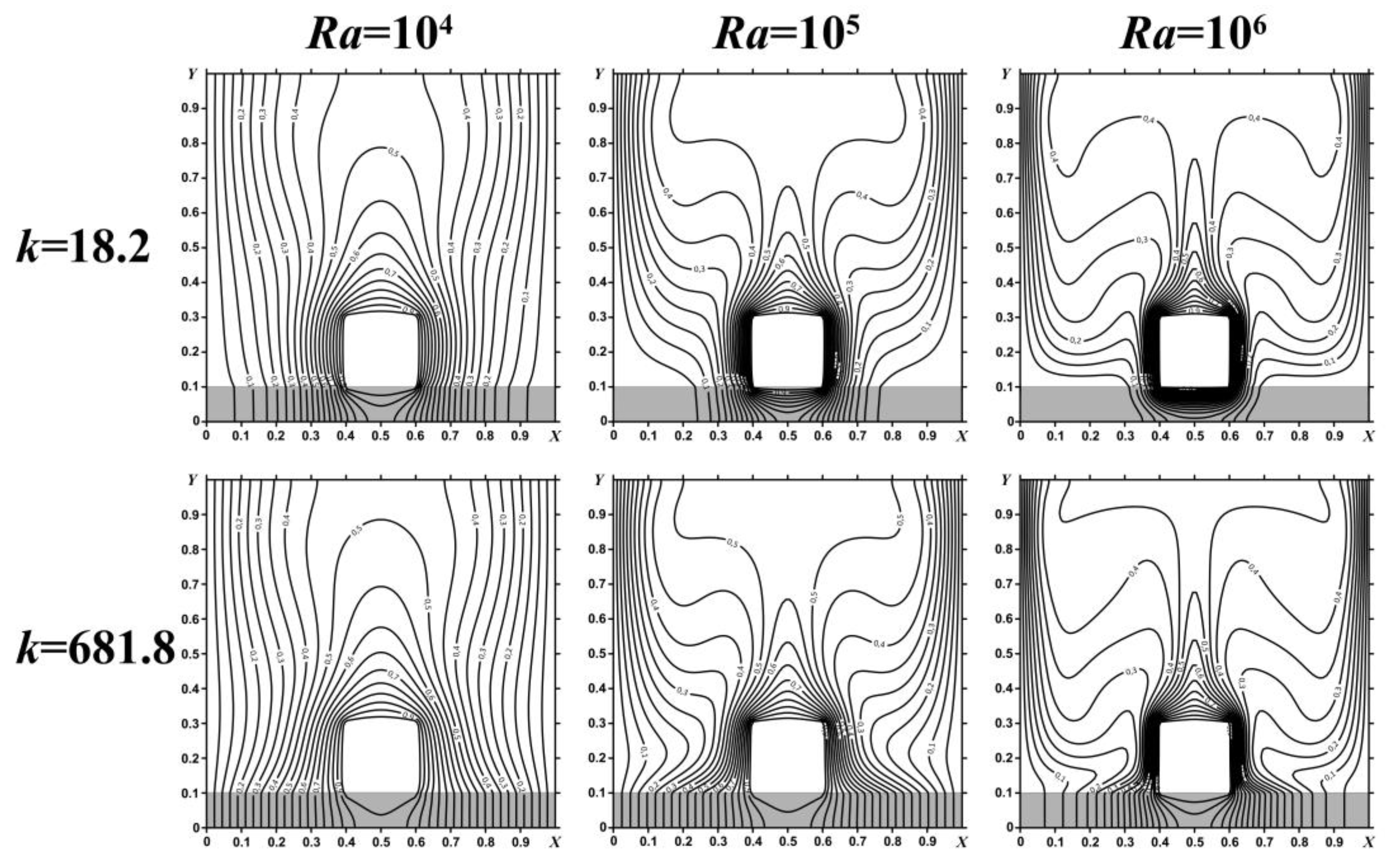
Figure 6 shows the temperature fields for various values of thermal conductivity ratio and Rayleigh number in the case of a square heater. For k = 18.2 (textolite material for the bottom wall) and Ra = 10⁴, the conductive mode of heat transfer is predominant. As a result, the air region and the heat-conducting wall are heated near the energy source. With an increase in the Rayleigh number, a transition from a conductive mode to a convective one is observed, and the cold air front comes close to the side walls of the energy source. The sealing of the isotherms near the vertical walls of a square source characterizes the development of the thermal boundary layers. In the case of k = 631.8 (steel material for the bottom wall), due to the high thermal conductivity of the substrate material, with an increase in the Rayleigh number, both the temperatures inside the cavity and inside the heat-removing wall increase. At Ra = 10⁶, the heated part of the air is shifted upwards from the source, and the cold front of the air reaches the heater as close as possible to the side walls.

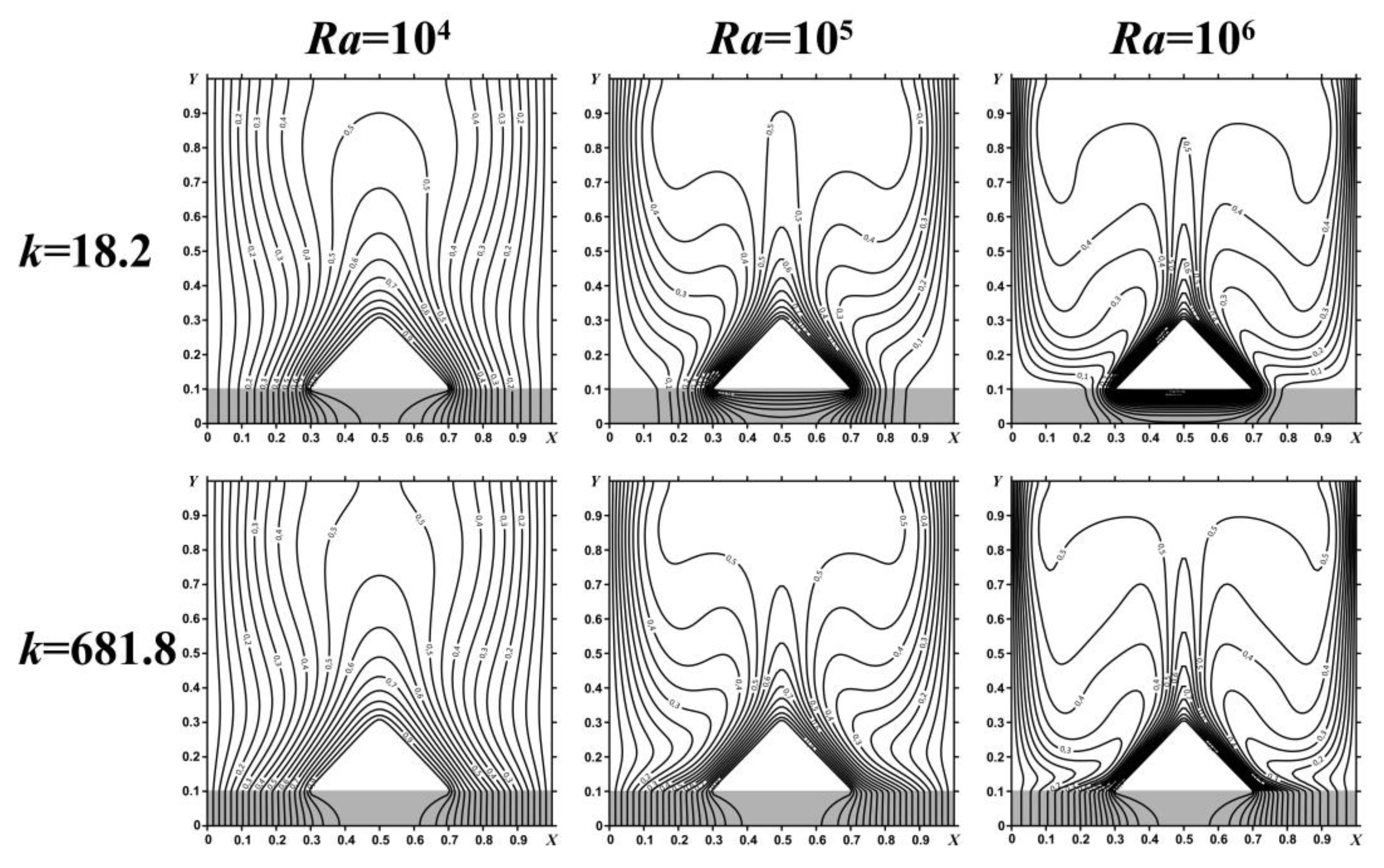
Figure 7 shows the temperature distributions in the case of a triangular heater. As already mentioned above, as the Rayleigh number increases, there is a transition from the dominant conductive mode to the convective heat exchange mode. In the case of k = 631.8 (steel material for the bottom wall), due to the large length of the base of the triangular energy element, the heat-conducting substrate warms up significantly. 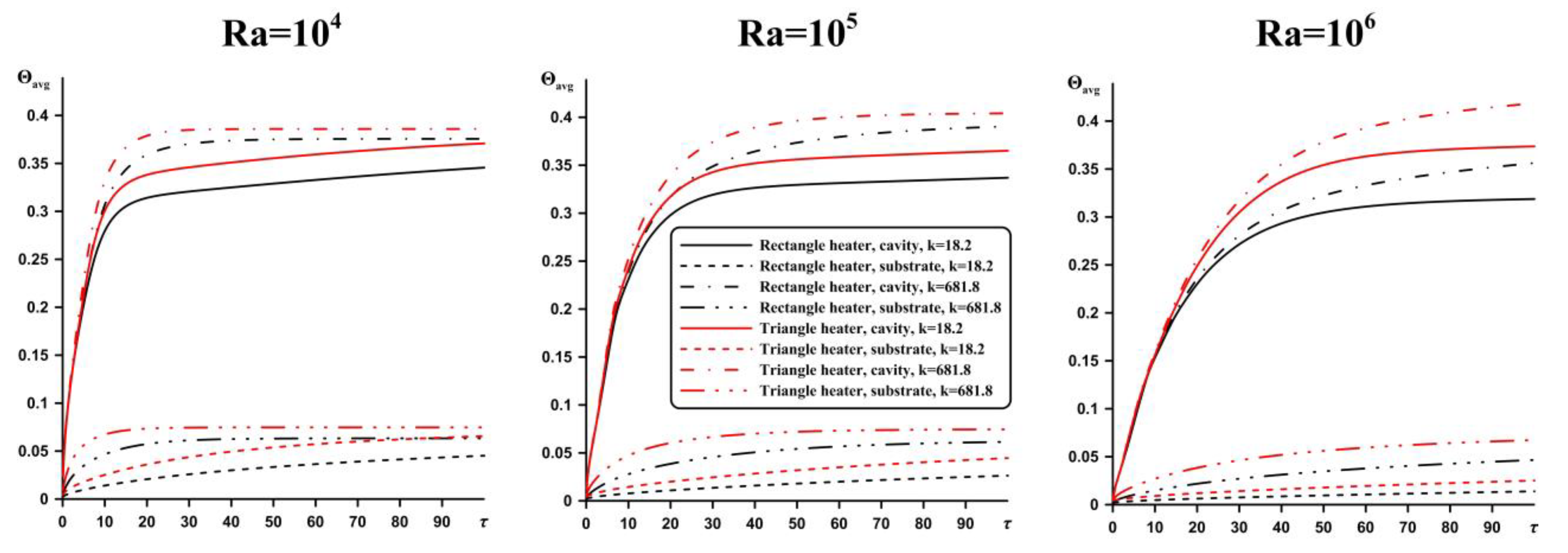As a result, the temperature increases both in the area and in the wall, which can be seen in Figure 8. In addition, it can be highlighted that the average temperature in the bottom wall at Ra = 10⁴ and τ = 100 has a maximum value for a triangular source, regardless of the substrate material. With an increase in the Rayleigh number, the average temperature in the cavity has the maximum value in the case of a triangular heater compared to the square one.

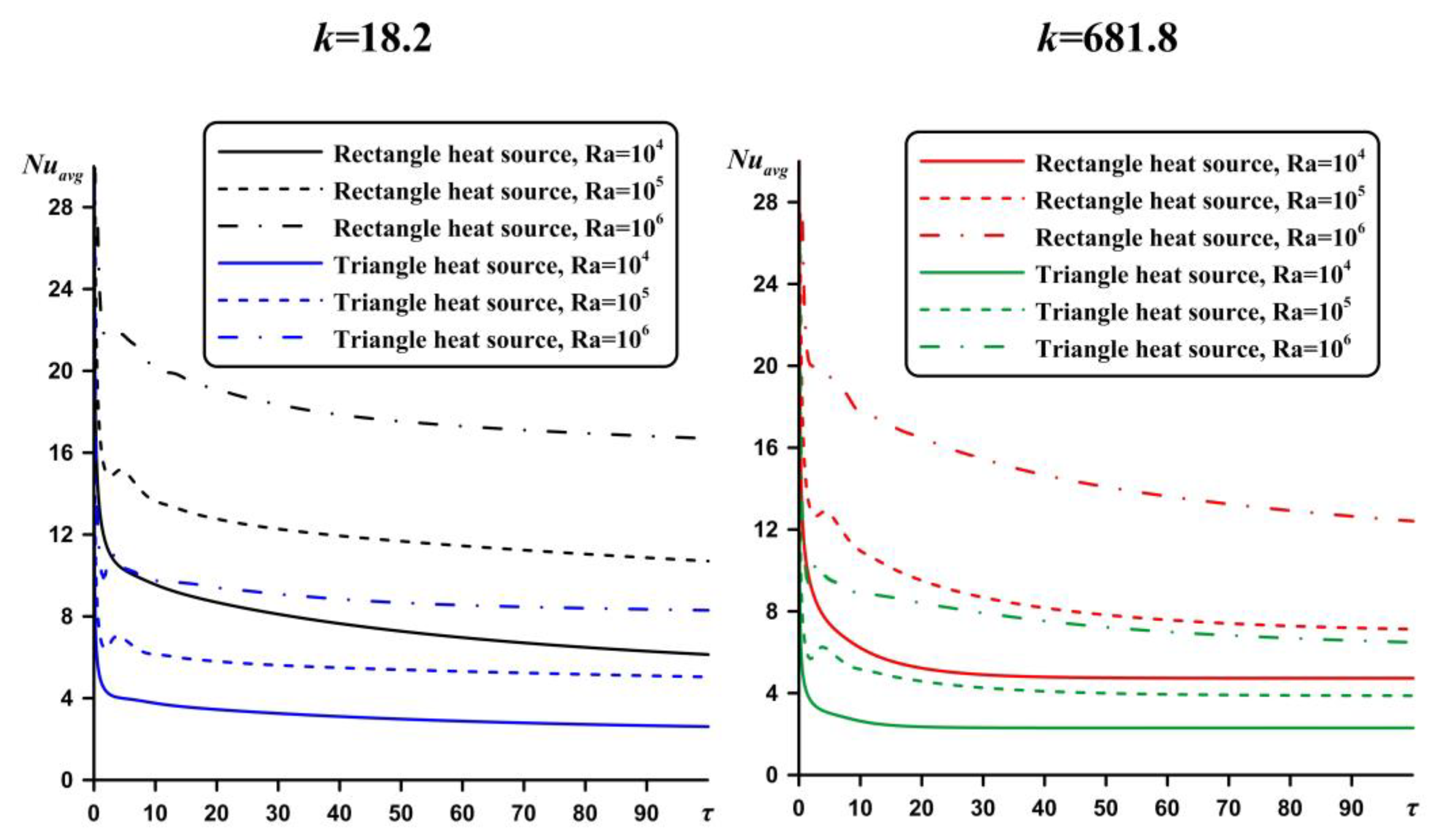
Figure 9 shows the average Nusselt numbers at the heater surface for various substrate materials, depending on the shape of the source and the Rayleigh number. The highest values have been observed in the case of a square energy source, regardless of the material of the heat-removing wall. The heat exchange on the surface of a square energy source is most effective due to the more active interaction of the cold air coming from the cooling walls with the heating element. At the same time, this analysis has been performed for the case of equal heater areas, but different perimeters. Therefore, one can find here different heated surface areas.

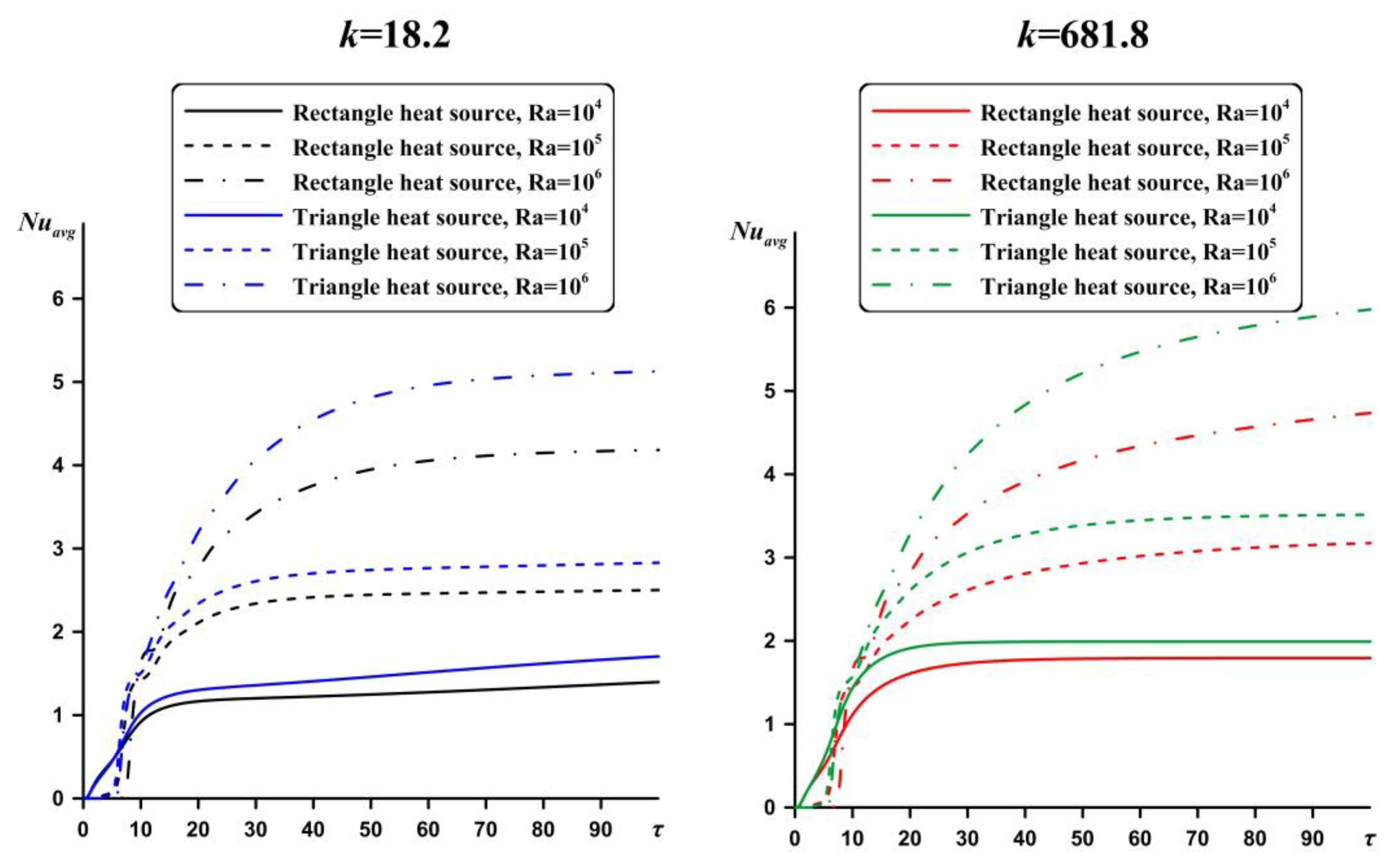
Figure 10 shows the average Nusselt numbers at the cooled vertical wall of the cavity. In this case, the maximum value of the Nusselt number can be found for the triangular shape of the source, due to a great temperature difference in this case, as has been mentioned above.

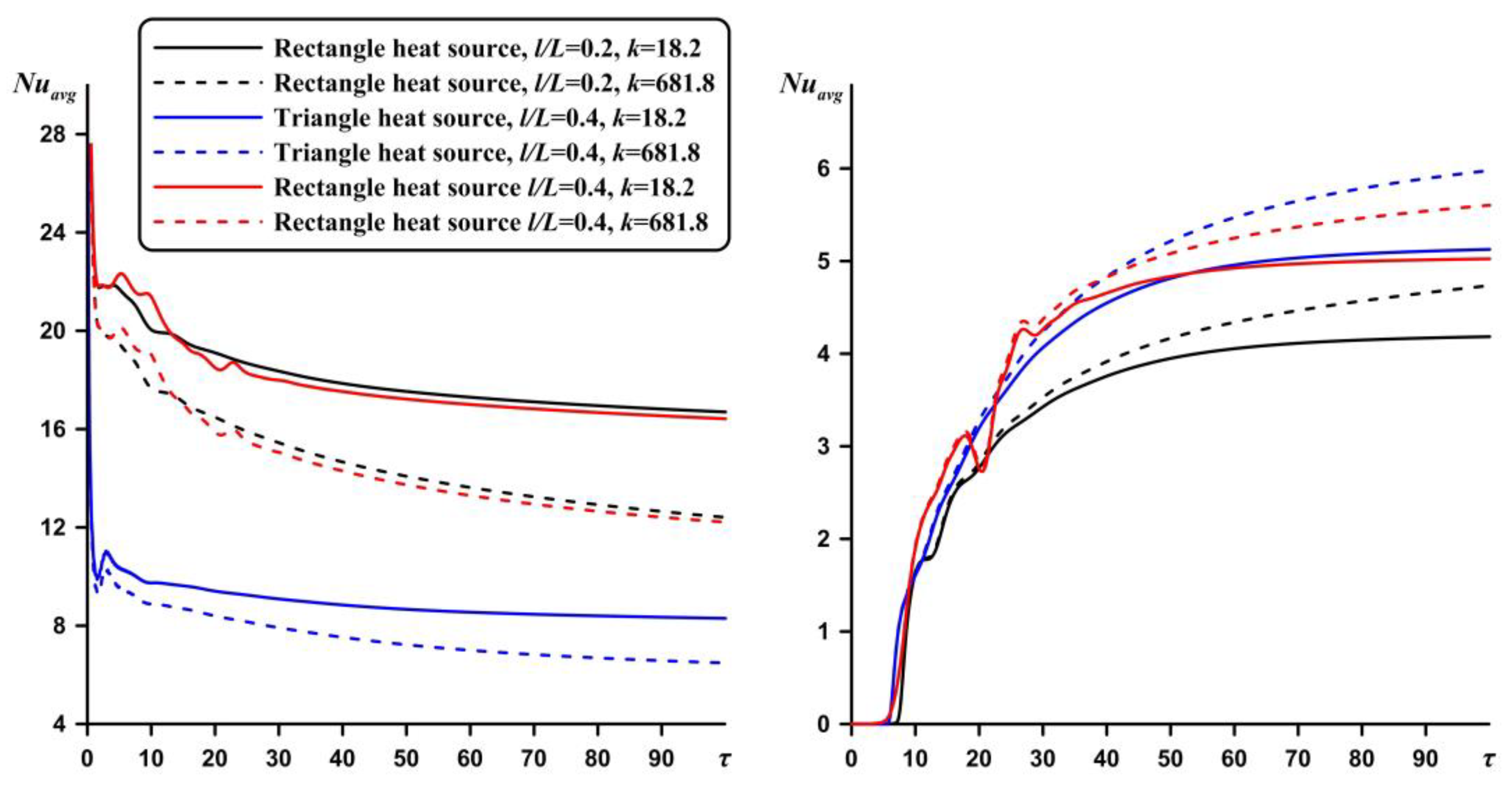
Figure 11 shows the temperature fields for triangular and rectangular heaters with the same length of the bottom wall of the heater (l/L = 0.4). It can be seen that the temperature in the cavity and the substrate in the case of a rectangular source exceeds the temperature in the case of a triangular one. A comparison of the efficiency of heat transfer from the surface of the energy source and the cooling walls (Figure 12) indicates that a triangular-shaped heating element cools less well than a rectangular one, but at the same time the circulation in a closed cavity is more intense due to the high temperature difference between the average cavity temperature and the low temperature of the vertical walls. An additional factor that should be taken into account for designing the electronics equipment is the material of a heat-conducting substrate. The combined influence of the temperature difference, the shape of the heating element and the material of the heat-conducting components of the system allows one to maximize the efficiency of the passive cooling system.

4. Conclusions

The conjugate thermogravitational convection in a closed cavity in the presence of local energy sources of various geometric shapes has been numerically investigated. The double Distribution Function Lattice Boltzmann Method has been chosen as the numerical method. The analysis has been performed for two different materials of the cavity substrate, namely, textolite and steel. It was established that the shape of the local energy source, the substrate material and the Rayleigh number have a significant effect on the temperature evolution in the region. An increase in the base area of a rectangular energy source leads to insignificant changes in the efficiency of the heat transfer from its surface. To increase the efficiency of the passive cooling system, it is necessary to take into account the combined influence of the shape of the heater, the material of the heat-removing walls, as well as the temperature difference. Moreover, a rectangular heater is characterized by a high average Nusselt number compared to the triangular shape, and therefore the rectangular shape is more effective for the implementation of the passive cooling system. At the same time, a rise of the thermal conductivity of the substrate material causes a reduction of the heat transfer strength at the heater surface. Another idea of the present research is a comparison of two wide-spread numerical techniques, namely, the lattice Boltzmann method and the finite difference method for the test problem. Such analysis has shown that the accuracy of the obtained data is comparable for these methods, but the lattice Boltzmann method has an advantage in the speed of calculation for the transient problems.