Abstract
Calcification and bicuspid valve formation are important aortic valve disorders that disturb the hemodynamics and the valve function. The detailed analysis of aortic valve hemodynamics would lead to a better understanding of the disease’s etiology. We computationally modeled the aortic valve using simplified three-dimensional geometry and inlet velocity conditions obtained via echocardiography. We examined various calcification severities and bicuspid valve formation. Fluid-structure interaction (FSI) analyses were adapted using ANSYS Workbench to incorporate both flow dynamics and leaflet deformation accurately. Simulation results were validated by comparing leaflet movements in B-mode echo recordings. Results indicate that the biomechanical environment is significantly changed for calcified and bicuspid valves. High flow jet velocities are observed in the calcified valves which results in high transvalvular pressure difference (TPG). Wall shear stresses (WSS) increased with the calcification on both fibrosa (aorta side) and ventricularis (left ventricle side) surfaces of the leaflet. The WSS distribution is regular on the ventricularis, as the WSS values proportionally increase from the base to the tip of the leaflet. However, WSS patterns are spatially complex on the fibrosa side. Low WSS levels and spatially complex WSS patterns on the fibrosa side are considered as promoting factors for further calcification and valvular diseases.
1. Introduction
Aortic valve disease is one of the most common cardiovascular disorders, affecting 25% of the population over 65 years of age [1,2]. Valve disorders may be innate as in the case of a bicuspid valve formation or may develop later in a lifetime as the leaflet calcification. The aortic valve separates the left ventricle from the aortic vessel and consists of three half-moon-shaped leaflets and three slot-like sinus cavities on the aortic root. The valve leaflets are the most dynamic structures in the valve, and the sinuses are the gaps corresponding to the back of the leaflets. Aortic valve leaflets are thin structures that allow the transport of nutrients, oxygen, and waste through diffusion [3]. The aortic root acts as a bridge between the left ventricle and the ascending aorta, creating a region for the blood to be pumped out of the heart. An aortic valve opens and closes approximately 3 billion times throughout its lifetime [4]. During each cardiac cycle, the leaflets are subjected to various hemodynamic forces due to the blood flow. The aortic valve is opened during the ventricle contraction and closed during the ventricle relaxation.
Calcification occurs predominantly on the back side of the leaflet which is known as fibrosa surface [5]. On the front side of the leaflet, the ventricularis surface is exposed to jet-type flows. An oscillatory flow develops in the sinuses during the leaflet opening and in the root during the leaflet closing. Therefore, it has been suggested that one of the main contributing factors for the calcification is the oscillatory flows acting on the fibrosa surfaces [2,6,7]. Another important finding regarding the hemodynamic forces is related to congenital bicuspid aortic valves. In the bicuspid valves, two of the leaflets are fused to each other, and the unfused leaflet moves separately. Bicuspid valves are more prone to calcification compared to the normal tricuspid valves [8], suggesting that the disturbed hemodynamics in the bicuspid valves influence the valve calcification [9]. The detailed hemodynamic assessment of the defected aortic valves will provide a better understanding of the contribution of hemodynamic factors to the valve disease.
Conventionally, the diagnosis of the valve disease is performed by examining the medical images of the patient [10]. The diagnosis is crucial as it determines the type of treatment such as the surgery through the valve repair or the replacement with an artificial valve. The most commonly used diagnostic technique is echocardiography performed with the aid of sound waves. During the diagnosis, the clinician examines the images and evaluates the valve function, thereby enabling the qualitative determination of the severity of the disease [2,11]. However, this qualitative examination can often differ from clinician to clinician. Therefore, it is clear that there is a need for precise techniques that allow quantitative evaluation of the aortic valve function. With the help of computational modeling approaches, it is possible to accurately simulate the aortic valve motion and extract information for qualitative and quantitative assessment of the valve function [12].
Computational studies provided important findings to understand the progression of the aortic valve disease [2,13], and for the decision of the repair method [14,15]. Computational fluid dynamics (CFD) and fluid-structure interaction (FSI) simulations enable detailed investigations on the complex flow patterns and the leaflet motions in aortic valves [15,16,17,18,19,20]. Two-dimensional (2D) FSI studies have some limitations due to the highly turbulent nature of the aortic valve and these 2D models need to be adapted to realistic 3D model geometries [21,22,23,24]. It is reported that calcification results in deteriorated leaflet motion, lowered hemodynamic performance, and increased structural stresses on the leaflets [25].
The etiology and biological markers of the aortic valve diseases are investigated [7,26,27,28,29] and it is reported that calcification can be related to the shear stresses on the leaflets, and unsteadiness of the shear stress can trigger inflammation [30]. Shear stresses exerted on the endothelial cells of the aortic valve changed the gene expression patterns, where the calcification-associated gene level was higher on the aortic fibrosa surface, and the inflammation-associated gene level was dominating on the ventricularis side of the leaflet [6,31]. The aforementioned results show that disturbed hemodynamic forces and altered shear stress environment are influential on the initiation and progression of the aortic valve calcification [2,32,33].
Modeling the complex fluid dynamics and leaflet motion of the aortic valve requires the implementation of the FSI approach. The hemodynamic forces generated by the left ventricular pressure results in the opening of the aortic valve leaflets. The vortices generated in the sinuses during the ventricular relaxation ensure the closure of the valve leaflets. These interactions between the blood and the aortic valve should be investigated to determine the shear stresses exerted on the leaflets during the opening and closing configurations. In this study, we used ANSYS Workbench 19.2, to model this complex behavior between the blood and the valve by employing FSI modeling. We provided the details of our modeling approach using a commercial solver, which can be adapted easily by other researchers. Our results show that calcification leads to increased wall shear stress (WSS) on both sides of the leaflets and the disruption of regular WSS patterns on the aortic fibrosa side might contribute to further calcification.
2. Materials and Methods
In this study, we investigated the effect of valve calcification and bicuspid valve formation on the hemodynamics of aortic valve leaflets. A simplified 3D model geometry is generated based on the main dimensions of an aortic valve. Fluid and solid domains are modeled separately, and the solution is obtained by the 2-way coupling of these two domains using the ANSYS Workbench system coupling module. In the following sections, we explain the modeling and solution steps in detail.
2.1. Echocardiography Imaging
Echocardiography images (using a GE Vivid 7 Ultrasound Machine, GE Healthcare, Milwaukee, WI, USA) of a healthy adult are used to define the main dimensions of the 3D aortic valve model [25]. The dimensions of the inlet, outlet, root, and sinus diameters are determined using the short axis B-mode images. Time-dependent velocity magnitude through the valve inlet is measured via pulsed Doppler mode as presented in Figure 1a,b. In the Doppler waveform shown in Figure 1a, the systolic phases of two cardiac cycles can be seen. The systolic phases with the peak blood flow rates are observed within the first 0.3 s of each cardiac cycle. Therefore, the maximum valve deformations are expected between 0 and 0.3 s of each cardiac cycle. Since the inlet flow rates after 0.3 s are not significant in the pulsed Doppler waveform, the backflow in the valve is neglected due to its small amount in the B-mode echo measurements, and the inlet flow rate is set to zero between 0.3 s to 1.0 s as shown in Figure 1b. The waveform presented in Figure 1b covers one full cardiac cycle. The inlet flow profile presented in Figure 1b is employed for both the healthy and calcified aortic valve models. In order to apply the inlet flow waveform in the FLUENT software, a UDF (user-defined function) file is generated. The UDF file covers the inlet flow velocities at 400-time points between 0 and 1 s with 0.0025 s time increments.
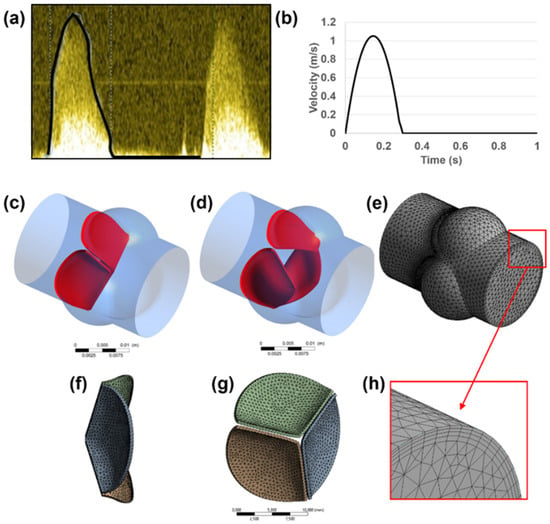
Figure 1.
(a) Time-dependent inlet velocity profile measured via pulsed Doppler mode. (b) Transient velocity profile applied at the inlet boundary. Generated 3D aortic valve model is shown in (c–h). Closed (c) and opened (d) configurations of the leaflets are indicated in red. Fluid (e) and solid (f,g) domains are modeled and meshed separately. For the fluid mesh, inflation layers (h) are used on the wall boundaries.
2.2. Numerical Model
The aortic root diameter of 18 mm is used as the flow domain, and three sinuses around the valve leaflets are modeled with a diameter of 14 mm. The leaflets are modeled as single-layered structures with a uniform thickness of 0.4 mm [34]. A generated 3D aortic valve model is presented in Figure 1c–h. A simplified geometry is adapted by measuring the main dimensions from a 2D medical image, in order to elucidate the main conclusions depending on the basic geometrical parameters of the aortic valve.
Both the fluid and solid domains are meshed using tetrahedral elements. In the fluid domain, wall boundaries are meshed using 4 inflation layers to provide a better mesh resolution on the wall boundaries as presented in Figure 1f. The leaflet surfaces are defined as FSI boundaries, and the fluid mesh density is increased at the proximity of the FSI boundaries for enhancing the accuracy of the solution.
A mesh convergence study is performed by employing two different mesh densities. The first mesh is used as a coarse mesh with approximately 150,000 and 20,000 tetrahedral elements for the fluid and solid domains, respectively. The second mesh, which is used for further computational analyses, is composed of approximately 400,000 and 50,000 tetrahedral elements for the fluid and solid domains, respectively. The maximum flow velocity in the fluid domain is compared for the first and second meshes, and a difference of less than 4% is achieved. For further improvement of the solution accuracy, a denser mesh can be used for the fluid and solid domains, but the convergence issues of the FSI coupling procedures limited the use of a denser mesh. For the selected fluid mesh, the maximum and average skewness values are determined around 0.84 and 0.21, respectively. The effect of gravity and the heat transfer between the blood and aortic valve are neglected in the model due to their insignificant effect on the leaflet deformation [35,36,37].
In the fluid domain, there are four different boundary conditions as inlet, outlet, wall, and FSI boundaries. At the inlet boundary, the transient velocity profile provided in Figure 1b is applied as plug flow, which defines the spatially averaged blood flow rate entering the valve from the left ventricle [36,38]. At the outlet boundary, zero pressure is defined. It is worth noting that assuming zero pressure at the outlet is a primitive approach due to ignoring the flow resistance of arteries in the body. In order to improve the model, a clinically measured pressure waveform at the outlet of the aortic valve can be applied. Since we could not clinically measure the outlet pressure profile, we preferred to use zero-pressure boundary conditions at the outlet of the aortic valve. The zero-pressure assumption can lead to an increased valve closure period, but this increase is not expected to change the WSS patterns on the valve surfaces. A no-slip boundary condition is applied on the wall and FSI boundaries of the fluid domain. In the solid domain, the circular edges of the inlet and outlet surfaces are fixed with zero displacements. The rest of the solid domain boundaries are set as FSI boundaries which interact with the blood flow. All of the boundary conditions applied in the aortic valve model are shown on a cross-sectional plane in Figure 2.
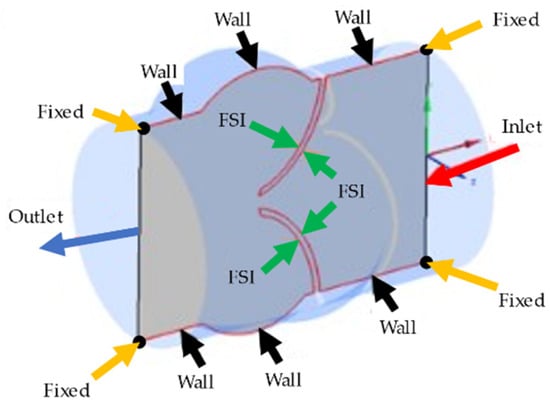
Figure 2.
Representation of the boundary conditions applied in the aortic valve model. Inlet, outlet, wall, and FSI boundary conditions are shown on the longitudinal cross-sectional plane. The black points on the corners of the cross-sectional plane are shown by yellow arrows and fixed with no displacement.
2.3. Solution of the Fluid Domain
The flow equations are solved using the CFD software package, FLUENT. The governing equations of Navier-Stokes and continuity are solved to obtain the flow velocity, pressure, and WSS. The Navier-Stokes and continuity equations are defined in Equations (1) and (2), respectively, for an incompressible and homogeneous fluid medium.
In Equation (1), the fluid velocity vector is denoted by ; time is denoted by ; the velocity due to the change of geometry in the fluid domain (i.e., the velocity of fluid mesh primarily due to FSI) is denoted by ; and the fluid stress tensor is denoted by .The fluid stress tensor is defined in Equation (3), in terms of fluid pressure (), Kronecker delta (), dynamic viscosity (), and strain rate (). The strain rate can be written in terms of the velocity vector () as given in Equation (4).
For the large arteries, the shear strain rate in the flow exceeds 50 s−1 and the blood viscosity is nearly constant due to the high shear rate [39]. Therefore, the blood is assumed as a Newtonian fluid with a constant density of 1056 kg/m3 and a dynamic viscosity of 0.0035 Pa∙s [15].
The pulsatile nature of the flow and large leaflet deformation result in turbulent activity especially downstream of the valve leaflets. For modeling the turbulent nature in the aortic valve, the realizable k–ε model is employed which is a 2-equations Reynolds averaged Navier-Stokes (RANS) model. Compared to the standard k–ε model, the realizable k–ε model provides higher solution accuracy for cases involving flow separation and circulatory flows [40] by introducing an improved transfer equation for turbulent dissipation rate [25].
It should be noted that the large eddy simulation (LES) approach provides a better prediction of the unsteady flow variables compared to the RANS-based turbulence models. However, LES requires high computational power, because the element dimensions in the mesh should be small enough to resolve even the tiny rotating vortex structures in the flow domain. In addition, the time increments in the flow analysis should be small enough to provide the solution stability in the LES approach. As consequence, we preferred to use the RANS-based realizable k–ε turbulence model due to our limitations in the computational power. The adaptation of LES or direct numerical simulation (DNS) approaches in the flow simulations would result in enhanced solution accuracy in the investigations.
A pressure-based transient solver is used in FLUENT to obtain the flow solution due to the incompressible nature of the blood flow. The SIMPLEC solution scheme with no skewness correction is used for the pressure-velocity coupling. For the flow solution convergence, the residual of the continuity equation is used as 10−5. Standard wall functions are employed near wall boundaries to accurately model the physical behavior in the viscous boundary layers. The second-order upwind scheme is used for spatial discretization of the momentum equations, and the first-order upwind scheme is used for the turbulent kinetic energy and turbulent dissipation rate [41]. The initialization process in FLUENT is performed using hybrid initialization with 10 iterations.
2.4. Solution of the Solid Domain
ANSYS Mechanical APDL module is used to determine the dynamic response of the valve leaflets. The governing equation in the solid domain is the momentum conservation given in Equation (5).
In Equation (5), is the solid stress tensor; is the mass density of the leaflets; and is the local acceleration in the solid domain. The Newmark time integration method is used to solve the governing equations at discrete time points. The leaflets are modeled as linearly elastic isotropic structures with a constant mass density [17] of 1100 kg/m3 and Poisson’s ratio [42] of 0.45. The elastic modulus of the leaflets is defined depending on the calcification level. For a healthy aortic valve, the leaflets have an elastic modulus [43] of 1 MPa. For the moderately and severely calcified aortic valve leaflets, elastic modulus [25] is used as 10 MPa and 20 MPa, respectively. For the bicuspid valve, elastic modulus [22] is employed as 5 MPa.
In reality, the valve structure has nonlinear elasticity with anisotropic material characteristics. Therefore, using a nonlinearly elastic material model is more realistic for the aortic valve and would provide an improved solution accuracy. However, it is more difficult to achieve a solution convergence for the FSI model by using a nonlinear valve structure. Using a linearly elastic valve material model is a limitation of the current study. We employed the linearly elastic material model due to the easier solution convergence. The maximum opening states of the valves are compared between the linearly elastic valve models and B-mode echo images in Figure 3. Since an agreement is observed for the maximum opening configurations of the linearly elastic models and the medical images, the linearly elastic valve models are employed in the further numerical analyses.
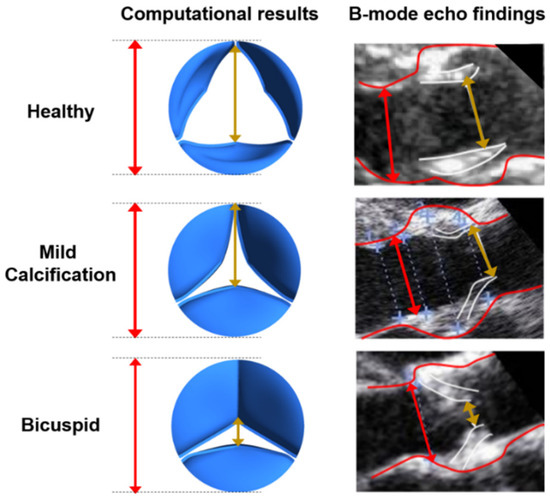
Figure 3.
Leaflet deformations at the instant of maximum valve opening state for the healthy, mildly calcified, and bicuspid valves. Red lines depict the aortic diameter. The gold lines show the peak orifice length at the instant of maximum valve opening configuration.
2.5. FSI Coupling
There is a strong interaction between the flowing blood and the aortic valve leaflets. The blood flow results in unsteady forces causing complex dynamic structural motion, whereas the deformed state in the solid domain affects the flow field geometry which changes the blood flow patterns. If these counter-interacting effects between the solid and fluid domains are ignored, the leaflet deformations cannot be predicted accurately. For the problems including strong physical interactions as in the aortic valves, implicit 2-way coupling is recommended to accurately predict the solid deformation [44]. In this work, the ANSYS Coupling module is used to couple the solutions of fluid and solid domains using the iterative implicit 2-way coupling method.
During the coupling process, first, the hemodynamic forces are transferred from the fluid domain to the leaflets. The deformed geometric configuration of the leaflets is then transferred to the fluid domain for the new time step. Particular attention is required during matching the FSI boundary surfaces of solid and fluid domains, otherwise, incompatibility problems may arise due to the mismatch of FSI boundary surfaces. On the FSI boundaries, the solutions of fluid and solid domains are coupled considering the displacement compatibility and traction equilibrium equations [45] given in Equations (6) and (7). The solid and fluid displacement vectors are denoted by and ; solid and fluid unit normal vectors are denoted by and , respectively.
The geometry of the fluid domain is deteriorated due to the large leaflet deformation. For this reason, the fluid domain is remeshed at each time step to enhance the mesh quality. A time step of 2.5 × 10−3 s is employed for the simulations by dividing one cardiac cycle into 400 equal time steps. Spring-based smoothing and remeshing algorithms are used in FLUENT to minimize the solution instabilities. This way, the cells that violate the size criteria are locally remeshed and updated using additional cells. Unless the remeshing algorithms are used in the FSI models with large structural deformations, the cells in the fluid mesh may become degenerative and lead to convergence problems [25].
FSI simulations are performed for one full cardiac cycle between 0 and 1 s. At each time step, three FSI iterations are performed to converge a solution for the system coupling. For the data transfer between the fluid and solid domains, the under relaxation factor is used as 1, in order to guarantee that the hemodynamic forces generated by the fluid flow are fully transferred to the solid domain. No ramping is used during the system coupling and the root mean squared (RMS) convergence target is used as 0.01.
3. Results
In this section, the velocity, pressure, and WSS fields are investigated considering the healthy, calcified, and bicuspid aortic valves. The biomechanical environment on the leaflets is analyzed to clarify the effect of WSS patterns on the leaflet calcification.
3.1. Validation of Results
B-mode echo recordings are used for the validation of the simulation results by comparing the opening rates of the leaflets as shown in Figure 3. At the instant of maximum valve opening, the peak orifice length is divided by the aortic diameter to determine the percent opening ratios. For the healthy valve, opening ratios are determined as 71.74% and 79.31% for the computational model and B-mode echo image, respectively. For the mild calcification, these opening ratios are found as 62.17% and 69.03% for the computational model and B-mode echo image. The lowest opening rate is observed for the bicuspid valve, where the opening ratios are 21.74% and 30.68% for the computational model and B-mode echo image, respectively. The valve opening ratios of computational results and B-mode images are in agreement, and the differences are tolerable since the exact determination of the leaflet borders is challenging and prone to error in 2D B-mode echo images. Compared to a valve with healthy leaflets, the effective blood flow area at the valve orifice is decreased by approximately 60% and 80% for mildly calcified and bicuspid valves, respectively.
The opening rates are similar for the medical images and the simulation results; therefore, a realistic flow field is expected for the flow simulations. The in-vivo determination of the entire flow field is a challenging task using clinical tools, and the flow velocities can only be measured at specific points using the Doppler ultrasound measurements. In order to compare the entire flow fields, an experimental setup that mimics the clinical conditions is required to measure the 3D flow field. Using the particle image velocimetry (PIV) technique, the flowing particles can be tracked experimentally, and the 3D flow field can be determined. Since our study is only limited to numerical modeling, the entire flow fields are not compared for the computational model and the clinical case. Therefore, the flow fields could not be validated since we could not measure the 3D flow distribution of the clinical case. We could only measure the flow velocities at specific points on the inlet boundary, and we used these velocities as the inlet flow conditions in the computational simulations. Due to the similarity in the opening configuration and the ratio of the maximum opening state between the clinical case and the computational simulations, we expect similar flow fields for the simulations and the clinical case. The agreement in the opening rates of the valve leaflets shows the close resemblance between the clinical and computational flow fields.
3.2. Velocity Field
The inlet velocity profile given in Figure 1b has positive flow rates within 0–0.3 s with a peak flow rate of 1.05 m/s at the time point of 0.15 s. In Figure 4, the velocity streamlines are presented on the longitudinal mid-plane of the aortic valve. For the healthy valve, the flow jet velocity at the valve orifice reaches 2.25 m/s at 0.17 s. The peak velocities at the inlet and valve orifice are observed at similar time points. For the mild and severe calcification, the peak orifice velocity increases to 3.71 m/s and 3.82 m/s at the time points of 0.22 s and 0.25 s, respectively, which is indicating a time lag in the peak orifice velocity and peak inlet velocity [21,46].
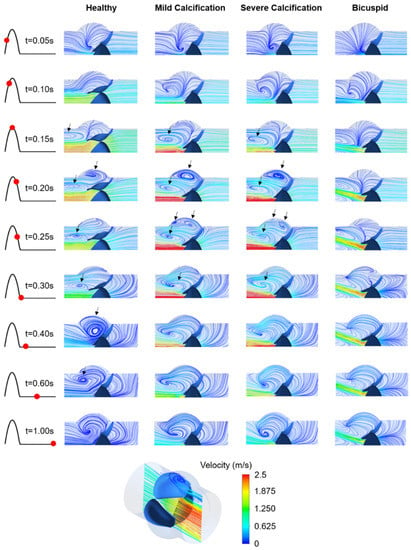
Figure 4.
Velocity streamlines for the healthy, mildly calcified, severely calcified, and bicuspid valves. Time points are shown by red dots on the cardiac cycle. The recirculating vortices are indicated by arrows. Contour plots are obtained in the longitudinal cross-sectional plane of the aortic valve, and only the upper half of the plot is provided due to the symmetry. Flow is from right to left.
For the bicuspid valve, the flow jet has an angle of approximately 20 degrees with the longitudinal axis of the aortic valve (see Figure 4). The peak orifice velocity is measured as 2.43 m/s at 0.25 s, showing a time lag with the peak inlet velocity. Compared to the healthy valve, the peak orifice velocities are increased by 64.9%, 69.8%, and 8.0% for mild calcification, severe calcification, and bicuspid valve formation, respectively.
For the healthy valve, the circulatory flow emerges in the aortic sinuses at 0.2 s, right after the instant of peak inlet velocity, and slowly diminishes while moving towards the central axis of the valve. For the calcified valves, the flow recirculation initiates at 0.15 s, which is earlier than the instant of peak orifice velocity. In the case of mild calcification, three different recirculating vortices are observed at 0.25 s, indicating a highly turbulent flow downstream of the leaflets. For severe calcification, the movement of the leaflets is quite limited, resulting in two distinct recirculating vortices. For the bicuspid valve, the flow behavior is significantly different compared to tricuspid valves. At 0.4 s, only the healthy valve has circulatory flow in the aortic sinuses which helps the complete closure of the leaflets [25]. This circulation in the aortic sinus continues until 0.6 s for the healthy valve. The duration of recirculation inside the aortic sinus is also critical in terms of development of the valve thrombosis [47].
3.3. WSS Patterns on the Ventricularis and Fibrosa Surfaces
WSS patterns are determined on the ventricularis and aortic fibrosa surfaces of the leaflets as presented in Figure 5 and Figure 6, respectively. Calcification altered the WSS distribution on both the ventricularis and fibrosa surfaces, as the leaflets are exposed to much higher WSS in calcified cases. The area-weighted average (within 0–0.3 s) WSS plots are presented in Figure 7. For the healthy ventricularis, the area-weighted average WSS (within 0–0.3 s) and maximum WSS values are determined as 14.31 Pa and 23.16 Pa, respectively. The area-weighted average WSS (within 0–0.3 s) and maximum WSS on ventricularis are determined as 18.77 Pa and 27.74 Pa for the mild calcification. Area-weighted average WSS and maximum WSS values are measured as 18.92 Pa and 27.68 Pa for severe calcification. Interestingly, mild and severely calcified valves resulted in similar WSS values on the ventricularis, indicating that WSS magnitude on the venticularis surface is not sensitive to the level of calcification. The highest WSS is observed on the ventricularis of the bicuspid valve, as the area-weighted average WSS (within 0–0.3 s) and maximum WSS values are determined as 19.53 Pa and 31.74 Pa.
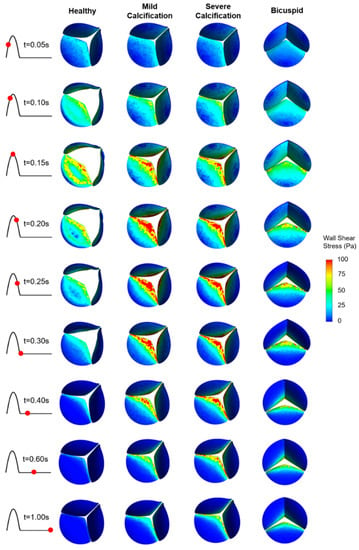
Figure 5.
WSS patterns on the ventricularis surface of the leaflets. The view of the valve is provided at an oblique angle to visualize the WSS distribution. For the bicuspid valve, the unfused leaflet is at the bottom.
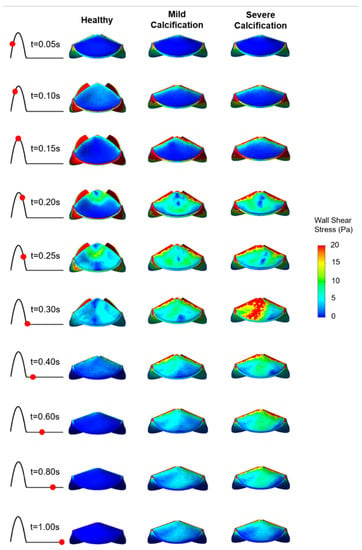
Figure 6.
WSS patterns on the fibrosa surface of the leaflets. The view of the valve is provided from the top of the model.
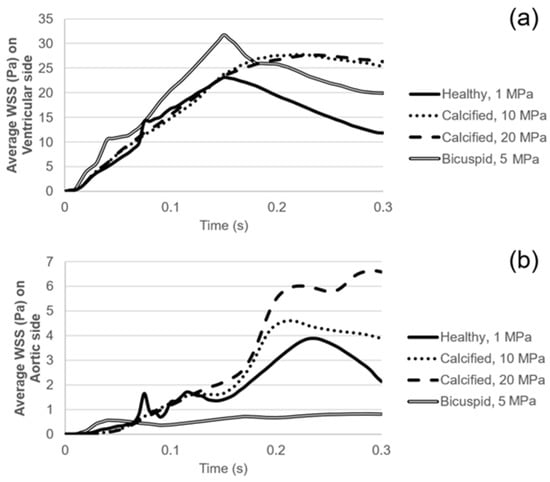
Figure 7.
(a) Area-weighted average WSS on the ventricularis surface. (b) Area-weighted average WSS on the fibrosa surface.
On the fibrosa surface of the leaflets, the area-weighted average WSS (within 0–0.3 s) and maximum WSS values are within the range of 0.57–2.99 Pa and 0.82–6.63 Pa, respectively. For the healthy valve, the average and maximum WSS are 1.85 Pa and 3.88 Pa on the fibrosa surface. Mild and severe calcification leads to an average WSS of 2.29 Pa and 2.99 Pa, and a maximum WSS of 4.61 Pa and 6.63 Pa, respectively. Opposing the ventricularis, the level of calcification significantly altered the WSS magnitudes on the fibrosa surface. For the bicuspid valve, relatively lower WSS levels are observed with an average WSS of 0.57 Pa and maximum WSS of 0.81 Pa. Results of fused and unfused leaflets are combined during the determination of the average WSS on the bicuspid valve. The average WSS on the unfused leaflet is approximately four times greater than the fused leaflet. Therefore, relatively low average WSS for the bicuspid valve is attributed to the low shear stresses on the fused leaflet. In general, WSS magnitudes on the ventricularis are much higher compared to the fibrosa surface of the leaflets in any kind of valve configuration.
On the fibrosa surface, fused and unfused leaflets of the bicuspid valve are exposed to significantly different shear environments as shown in Figure 8. WSS levels are relatively higher within the range of 0.4–1.0 s, particularly on the unfused fibrosa surface. The fused fibrosa surface is exposed to relatively lower shear stresses with a maximum WSS of about 1.25 Pa.
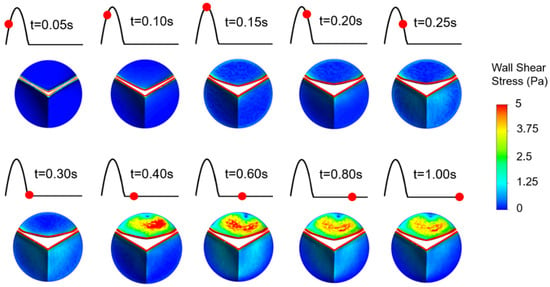
Figure 8.
WSS patterns on the fibrosa surface of the bicuspid valve leaflets. The unfused leaflet is at the top and the fused leaflet is at the bottom.
Valve calcification is mostly observed in two specific patterns known as coaptation and radial patterns [48]. In the coaptation pattern, the calcific deposits spread along the leaflet coaptation line as shown in Figure 9. In the radial pattern, the calcific deposits are spreading from the leaflet attachment region to the tip of the leaflet. Calcification mostly occurs on the fibrosa side which is exposed to an unsteady shear stress field. The ventricularis surface is exposed to a relatively regular shear environment. Therefore, specific WSS patterns on the fibrosa surface are of the main interest to investigate the similarity with the calcific deposit patterns. In Figure 9, we presented relatively high WSS regions to clearly distinguish the spatial distribution of the shear patterns on the fibrosa side for the healthy and diseased valves.
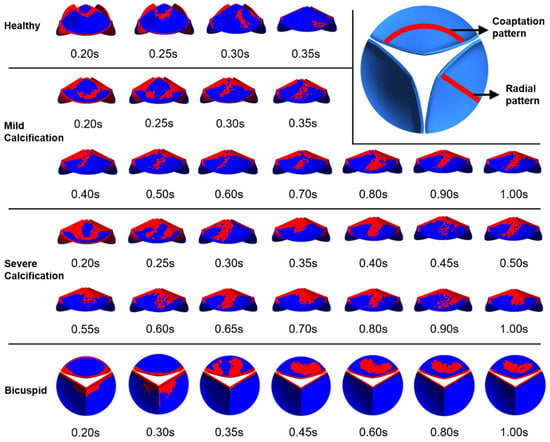
Figure 9.
Specific WSS patterns observed on the fibrosa surface. Relatively higher WSS regions are shown in red.
For the healthy valve, high WSS regions have the coaptation pattern at time points of 0.2 s and 0.25 s. At 0.3 s and 0.35 s, the radial pattern is observed. After the instant of 0.35 s, there is no apparent calcific pattern until the end of the cardiac cycle. For the mild calcification, the coaptation pattern is seen at 0.2 s and 0.25 s. For the time range within 0.3–1.0 s, the radial WSS pattern is dominant on the fibrosa surface. Similarly, severe calcification leads to the radial patterns within 0.3–1.0 s. This shows that radial WSS patterns become more dominant in the cardiac cycle as the stiffness of the leaflet increases. WSS patterns on the fibrosa surface demonstrate heterogeneous and locally distributed behavior rather than a smooth and homogenous pattern, which is similar to the patterns of clinically observed calcific deposits on the leaflets.
3.4. Pressure Contours
Pressure contours are presented in Figure 10. Calcification resulted in a higher transvalvular pressure gradient (TPG) as expected, which is the pressure difference between the inlet and outlet of the aortic valve. For the calcified valves, high TPG is observed as presented in Figure 11, suggesting an adverse effect of the prolonged pressure on the leaflets. For the healthy valve, a maximum TPG of 16.23 mmHg is observed around the time point of 0.15 s, and TPG immediately scales down after experiencing the peak value. The maximum TPG values are determined as 48.96 mmHg and 57.04 mmHg for the mild and severe calcification, respectively. TPG reduction in the calcified valves is much slower compared to the healthy valve. Our computational results are in agreement with the previously reported TPG values [49]. At the time point of 0.3 s, TPG values in the calcified valves are approximately 10-times greater than the healthy valve. For the bicuspid valve, a maximum TPG of 21.43 mmHg is measured, and this peak value is 32% higher than the healthy valve. Opposing to the healthy valve, TPG does not immediately start to scale down in the bicuspid valve, and it maintains around 20 mmHg. All hemodynamic findings are tabulated in Table 1.
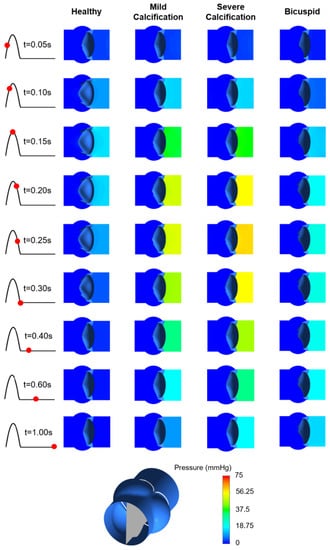
Figure 10.
Pressure contours for the healthy, mildly calcified, severely calcified, and bicuspid valves. Time points are shown by red dots on the cardiac cycle. Contour plots are obtained in the longitudinal cross-sectional plane of the aortic valve. Flow is from right to left.
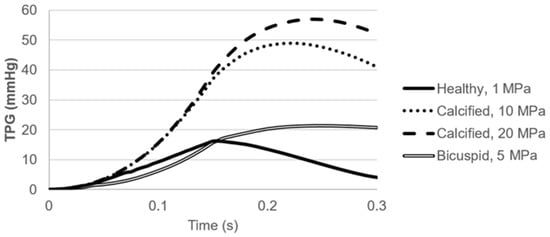
Figure 11.
Transvalvular pressure gradient (TPG) for the healthy, calcified, and bicuspid valves.

Table 1.
The hemodynamic findings of the computational models for the healthy, mildly calcified, severely calcified, and bicuspid aortic valves.
4. Discussion
CFD modeling is an important tool to investigate the complicated flow patterns in the body such as in the aortic valve. The complex motion of the leaflets and strong interactions between the valve and the flowing blood make the modeling approach challenging. In order to capture the accurate inflow hemodynamics, the FSI approach must be adapted. We used ANSYS Workbench for coupling the solutions of the fluid and solid domains for simulating a realistic aortic valve behavior. Calcification significantly changes the mechanical behavior of the aortic valve leaflets, resulting in functional deterioration. In this study, WSS patterns on the leaflets are investigated considering the calcification and bicuspid valve formation.
The change in the blood flow directly affects the WSS distribution on the leaflets that can be important for the progression of calcification [26,50]. The stiffening of the leaflets results in limited valve opening and decreases the efficiency of the blood transport, leading to an excessive left ventricle load consistent with the clinical observations. A flow jet forms at the valve orifice due to the limited valve opening and constricts the flow area in the calcified valves. The formation of a high-speed flow jet initiates circulatory flow and increases the turbulent behavior in the aortic sinuses. Altered hemodynamics in calcified valves leads to a high pressure difference between the inlet and outlet of the aortic valve. High TPG exposure may deteriorate the structural form of the leaflets and may lead to excessive strains [51,52,53].
Abnormal shear stresses may initiate inflammation of the leaflets. According to our simulations, the calcified leaflets are exposed to significantly high WSS compared to the healthy leaflets. At the base region of the leaflet (region close to the aortic root), WSS is relatively low and insensitive to calcification. However, the tip of the calcified leaflet is exposed to high WSS for longer periods and is significantly affected by the calcification level. For the calcified valves, the peak WSS values are not observed at the instant of peak inlet velocity, because the maximum orifice velocity is observed with a time delay due to the poor valve functioning.
On the healthy leaflet, spatial WSS distribution is relatively uniform when compared to the diseased ones. With the increasing calcification rates and presence of bicuspid valve formation, spatially complex shear stresses are generated on the leaflets, and the WSS difference between the tip and base regions becomes more prominent. In case of severe calcification, the tip of the leaflets is exposed to significantly high shear stresses. On the ventricularis surface of the leaflet, both mild and severe calcification led to similar WSS levels, indicating that WSS on the ventricularis is not sensitive to the severity of calcification. On the other hand, the calcification level significantly changed the WSS patterns on the fibrosa surface. The fibrosa side is exposed to much lower WSS compared to the ventricularis. This WSS difference between the fibrosa and ventricularis increased with the increasing calcification level and presence of bicuspid valve formation.
In previous studies, it is reported that the fibrosa side is more prone to calcification compared to the ventricularis [6,7,17]. Our findings support this fact, as the lower WSS levels on the fibrosa promote the deposition of calcific particles on the fibrosa layer. As mentioned, the WSS pattern is spatially simple and regular (i.e., uniformly increasing from the base to the tip of the leaflet) in the ventricularis. However, a spatially heterogeneous distribution is observed on the fibrosa. The spatially degenerated WSS pattern on the fibrosa indicates a highly dynamic behavior due to the turbulent effects. The low WSS magnitudes and high temporal alterations in the WSS levels are considered as factors that increase the risk of calcification on the fibrosa surface. Ge and Sotiropoulos [54] reported that nearly constant WSS levels on the ventricular side are not damaging the endothelial cells, on the other hand, a highly unsteady shear stress environment on the ventricularis side leads to serious risk factors. Similar to the TPG behavior, the WSS values for the calcified valves decrease more slowly compared to the healthy valve. For a healthy leaflet, WSS levels start to scale down immediately after experiencing the peak WSS value.
To summarize the clinical implications of our study, the numerically obtained patterns of high WSS regions on the fibrosa side show a similarity to the previously reported calcific deposit patterns [48]. For the healthy valves, coaptation patterns are observed at the instant of peak flow velocity, and no specific pattern dominated the cardiac cycle. Interestingly, the radial pattern is mostly observed on the calcified leaflets within 0.3–1.0 s. This fact showed that high WSS patterns on the fibrosa side can be related to the calcific deposits, and the calcification takes the form of a coaptation pattern as the leaflet stiffness increases. The numerically determined WSS patterns on the fibrosa are locally distributed as observed in the clinical investigations of the calcified leaflets. The focalized distribution of calcified lesions can be evidence for the link between the WSS and valve leaflet calcification, as a heterogeneous WSS field is observed on the fibrosa surface [54].
There are a few limitations within our study. In the geometric models, the aortic valve is completely isolated. The leaflets are modeled as single-layered elastic structures and the aortic valve is modeled in an axisymmetric way. The aortic root is assumed as a rigid structure with no displacements. For further improvement, the leaflets can be modeled considering the multiple layers and hyperelastic material properties. The non-homogeneous nature of calcification and the anisotropic behavior of the leaflets can also be considered. A patient-specific geometric model can be introduced with a flexible aortic root. The blood flow can be simulated including the non-Newtonian properties. The computationally demanding LES approach can be adapted for increased accuracy in predicting the unsteady behavior of the flow [55]. The RANS-based turbulence modeling may result in poor WSS estimation especially on the fibrosa side due to their time-averaged nature. Nevertheless, our results provide the main conclusions about the altered hemodynamics and WSS environment on the leaflets due to the calcification and bicuspid valve formation. These results have importance in terms of clarifying the mechanobiological mechanisms that are playing a role in the initiation and progression of aortic valve diseases.
Author Contributions
Conceptualization, H.E.S. and H.C.Y.; methodology, H.E.S. and H.C.Y.; software, H.E.S.; validation, H.E.S., L.S. and H.C.Y.; formal analysis, H.E.S.; investigation, H.E.S., L.S. and H.C.Y.; resources, L.S. and H.C.Y.; data curation, H.E.S.; writing—original draft preparation, H.E.S.; writing—review and editing, H.E.S., L.S. and H.C.Y.; visualization, H.E.S.; supervision, H.C.Y.; project administration, H.C.Y.; funding acquisition, H.C.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by Qatar National Research Fund (QNRF), National Priority Research Program NPRP 10-0123-170222 and NPRP13S-0108-200024, and Qatar University International Research Collaboration Co-Fund (IRCC) program IRCC-2020-002. The publication of this article was covered with a generous support from BARZAN HOLDINGS.
Institutional Review Board Statement
The study was conducted according to the guidelines of the Declaration of Helsinki, and approved by the Ethics Committee of ISTANBUL UNIVERSITY CERRAHPASA MEDICAL SCHOOL, TURKEY (protocol code: B.30.2.İST.0.30.90.00/18991, date of approval: 3 July 2012).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Stewart, B.F.; Siscovick, D.; Lind, B.K.; Gardin, J.M.; Gottdiener, J.S.; Smith, V.E.; Kitzman, D.W.; Otto, C.M. Clinical factors associated with calcific aortic valve disease. J. Am. Coll. Cardiol. 1997, 29, 630. [Google Scholar] [CrossRef] [Green Version]
- Halevi, R.; Hamdan, A.; Marom, G.; Mega, M.; Raanani, E.; Haj-Ali, R. Progressive aortic valve calcification: Three-dimensional visualization and biomechanical analysis. J. Biomech. 2015, 48, 489–497. [Google Scholar] [CrossRef]
- Weind, K.L.; Boughner, D.R.; Rigutto, L.; Ellis, C.G. Oxygen diffusion and consumption of aortic valve cusps. Am. J. Physiol. Heart Circ. Physiol. 2001, 281, H2604–H2611. [Google Scholar] [CrossRef] [PubMed]
- Sarah, T.G.; Srigunapalan, S.; Simmons Craig, A.; Kristi, S.A. Hemodynamic and cellular response feedback in calcific aortic valve disease. Circ. Res. 2013, 113, 186–197. [Google Scholar] [CrossRef] [Green Version]
- Balachandran, K.; Sucosky, P.; Yoganathan, A.P. Hemodynamics and mechanobiology of aortic valve inflammation and calcification. Int. J. Inflam. 2011, 2011, 263870. [Google Scholar] [CrossRef] [Green Version]
- Mahler, G.J.; Frendl, C.M.; Cao, Q.; Butcher, J.T. Effects of shear stress pattern and magnitude on mesenchymal transformation and invasion of aortic valve endothelial cells. Biotechnol. Bioeng. 2014, 111, 2326–2337. [Google Scholar] [CrossRef] [Green Version]
- Weinberg, E.J.; Mack, P.J.; Schoen, F.J.; García-Cardeña, G.; Mofrad, M.R.K. Hemodynamic environments from opposing sides of human aortic valve leaflets evoke distinct endothelial phenotypes in vitro. Cardiovasc. Eng. 2010, 10, 5–11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Otto, C.M. Calcification of bicuspid aortic valves. Heart 2002, 88, 321. [Google Scholar] [CrossRef] [Green Version]
- Yap, C.H.; Saikrishnan, N.; Tamilselvan, G.; Vasilyev, N.; Yoganathan, A.P. The congenital bicuspid aortic valve can experience high-frequency unsteady shear stresses on its leaflet surface. Am. J. Physiol. Heart Circ. Physiol. 2012, 303, H721–H731. [Google Scholar] [CrossRef] [Green Version]
- Maganti, K.; Rigolin, V.H.; Sarano, M.E.; Bonow, R.O. Valvular heart disease: Diagnosis and management. Mayo Clinic Proc. 2010, 85, 483–500. [Google Scholar] [CrossRef] [Green Version]
- Arjunon, S.; Rathan, S.; Jo, H.; Yoganathan, A.P. Aortic valve: Mechanical environment and mechanobiology. Ann. Biomed. Eng. 2013, 41, 1331–1346. [Google Scholar] [CrossRef] [Green Version]
- Votta, E.; Le, T.B.; Stevanella, M.; Fusini, L.; Caiani, E.G.; Redaelli, A.; Sotiropoulos, F. Toward patient-specific simulations of cardiac valves: State-of-the-art and future directions. J. Biomech. 2013, 46, 217–228. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Weinberg, E.J.; Mofrad, M.R.K. A multiscale computational comparison of the bicuspid and tricuspid aortic valves in relation to calcific aortic stenosis. J. Biomech. 2008, 41, 3482–3487. [Google Scholar] [CrossRef]
- Liu, A.C.; Gotlieb, A.I. Transforming growth factor-β regulates in vitro heart valve repair by activated valve interstitial cells. Am. J. Pathol. 2008, 173, 1275–1285. [Google Scholar] [CrossRef] [Green Version]
- Mao, W.; Caballero, A.; McKay, R.; Primiano, C.; Sun, W. Fully-coupled fluid-structure interaction simulation of the aortic and mitral valves in a realistic 3D left ventricle model. PLoS ONE 2017, 12, e0184729. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Spühler, J.H.; Jansson, J.; Jansson, N.; Hoffman, J. 3D fluid-structure interaction simulation of aortic valves using a unified continuum ALE FEM Model. Front. Physiol. 2018, 9, 9. [Google Scholar] [CrossRef] [Green Version]
- Halevi, R.; Hamdan, A.; Marom, G.; Lavon, K.; Ben-Zekry, S.; Raanani, E.; Bluestein, D.; Haj-Ali, R. Fluid-structure interaction modeling of calcific aortic valve disease using patient-specific three-dimensional calcification scans. Med. Biol. Eng. Comput. 2016, 54, 1683–1694. [Google Scholar] [CrossRef] [PubMed]
- Chandran, K.B.; Vigmostad, S.C. Patient-specific bicuspid valve dynamics: Overview of methods and challenges. J. Biomech. 2013, 46, 208–216. [Google Scholar] [CrossRef] [Green Version]
- Hart, J.D.; Peters, G.W.M.; Schreurs, P.J.G.; Baaijens, F.P.T. A three-dimensional computational analysis of fluid–structure interaction in the aortic valve. J. Biomech. 2003, 36, 103–112. [Google Scholar] [CrossRef]
- Haj-Ali, R.; Dasi, L.P.; Kim, H.-S.; Choi, J.; Leo, H.W.; Yoganathan, A.P. Structural simulations of prosthetic tri-leaflet aortic heart valves. J. Biomech. 2008, 41, 1510–1519. [Google Scholar] [CrossRef]
- Hart, J.D.; Peters, G.W.M.; Schreurs, P.J.G.; Baaijens, F.P.T. A two-dimensional fluid–structure interaction model of the aortic value. J. Biomech. 2000, 33, 1079–1088. [Google Scholar] [CrossRef]
- Kuan, M.Y.S.; Espino, D.M. Systolic fluid–structure interaction model of the congenitally bicuspid aortic valve: Assessment of modelling requirements. Comput. Methods Biomech. Biom. Eng. 2015, 18, 1305–1320. [Google Scholar] [CrossRef] [PubMed]
- Hsu, M.-C.; Kamensky, D.; Bazilevs, Y.; Sacks, M.S.; Hughes, T.J.R. Fluid–structure interaction analysis of bioprosthetic heart valves: Significance of arterial wall deformation. Comput. Mech. 2014, 54, 1055–1071. [Google Scholar] [CrossRef] [PubMed]
- Luraghi, G.; Wu, W.; Gaetano, F.D.; Matas, J.F.R.; Moggridge, G.D.; Serrani, M.; Stasiak, J.; Costantino, M.L.; Migliavacca, F. Evaluation of an aortic valve prosthesis: Fluid-structure interaction or structural simulation? J. Biomech. 2017, 58, 45–51. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Amindari, A.; Saltik, L.; Kirkkopru, K.; Yacoub, M.; Yalcin, H.C. Assessment of calcified aortic valve leaflet deformations and blood flow dynamics using fluid-structure interaction modeling. Inform. Med. Unlocked 2017, 9, 191–199. [Google Scholar] [CrossRef]
- Sun, L.; Chandra, S.; Sucosky, P. Ex vivo evidence for the contribution of hemodynamic shear stress abnormalities to the early pathogenesis of calcific bicuspid aortic valve disease. PLoS ONE 2012, 7, e48843. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yip, C.Y.Y.; Simmons, C.A. The aortic valve microenvironment and its role in calcific aortic valve disease. Cardiovasc. Pathol. 2011, 20, 177–182. [Google Scholar] [CrossRef]
- Ruiz, J.L.; Hutcheson, J.D.; Aikawa, E. Cardiovascular calcification: Current controversies and novel concepts. Cardiovasc. Pathol. 2015, 24, 207–212. [Google Scholar] [CrossRef]
- Rajamannan, N.M.; Evans, F.J.; Aikawa, E.; Grande-Allen, K.J.; Demer, L.L.; Heistad, D.D.; Simmons, C.A.; Masters, K.S.; Mathieu, P.; O’Brien, K.D.; et al. Calcific aortic valve disease: Not simply a degenerative process: A review and agenda for research from the National Heart and Lung and Blood Institute Aortic Stenosis Working Group. Executive summary: Calcific aortic valve disease–2011 update. Circulation 2011, 124, 1783–1791. [Google Scholar] [CrossRef] [Green Version]
- Sun, L.; Rajamannan, N.M.; Sucosky, P. Defining the role of fluid shear stress in the expression of early signaling markers for calcific aortic valve disease. PLoS ONE 2013, 8, e84433. [Google Scholar] [CrossRef] [Green Version]
- Bäck, M.; Gasser, T.C.; Michel, J.-B.; Caligiuri, G. Biomechanical factors in the biology of aortic wall and aortic valve diseases. Cardiovasc. Res. 2013, 99, 232–241. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chandra, S.; Rajamannan, N.M.; Sucosky, P. Computational assessment of bicuspid aortic valve wall-shear stress: Implications for calcific aortic valve disease. Biomech. Model. Mechanobiol. 2012, 11, 1085–1096. [Google Scholar] [CrossRef]
- Barannyk, O.; Fraser, R.; Oshkai, P. A correlation between long-term in vitro dynamic calcification and abnormal flow patterns past bioprosthetic heart valves. J. Biol. Phys. 2017, 43, 279–296. [Google Scholar] [CrossRef]
- Chester, A.H.; El-Hamamsy, I.; Butcher, J.T.; Latif, N.; Bertazzo, S.; Yacoub, M.H. The living aortic valve: From molecules to function. Glob. Cardiol. Sci. Pract. 2014. [Google Scholar] [CrossRef] [Green Version]
- Garcia, D.; Pibarot, P.; Durand, L.-G. Analytical modeling of the instantaneous pressure gradient across the aortic valve. J. Biomech. 2005, 38, 1303–1311. [Google Scholar] [CrossRef]
- Sotiropoulos, F.; Borazjani, I. A review of state-of-the-art numerical methods for simulating flow through mechanical heart valves. Med. Biol. Eng. Comput. 2009, 47, 245–256. [Google Scholar] [CrossRef] [Green Version]
- Yao, J.; Liu, G.R.; Narmoneva, D.A.; Hinton, R.B.; Zhang, Z.-Q. Immersed smoothed finite element method for fluid–structure interaction simulation of aortic valves. Comput. Mech. 2012, 50, 789–804. [Google Scholar] [CrossRef]
- Borazjani, I. Fluid–structure interaction, immersed boundary-finite element method simulations of bio-prosthetic heart valves. Comput. Methods Appl. Mech. Eng. 2013, 257, 103–116. [Google Scholar] [CrossRef]
- Young, D.F. Fluid mechanics of arterial stenoses. J. Biomech. Eng. 1979, 101, 157–175. [Google Scholar] [CrossRef]
- Meslem, A.; Bode, F.; Croitoru, C.; Nastase, I. Comparison of turbulence models in simulating jet flow from a cross-shaped orifice. Eur. J. Mech. B Fluids 2014, 44, 100–120. [Google Scholar] [CrossRef]
- Barth, T.; Jespersen, D. The Design and Application of Upwind Schemes on Unstructured Meshes. In Proceedings of the 27th Aerospace Sciences Meeting, American Institute of Aeronautics and Astronautics, Reno, NV, USA, 9–12 January 1989. [Google Scholar] [CrossRef]
- Grande, K.J.; Cochran, R.P.; Reinhall, P.G.; Kunzelman, K.S. Stress variations in the human aortic root and valve: The role of anatomic asymmetry. Ann. Biomed. Eng. 1998, 26, 534–545. [Google Scholar] [CrossRef] [PubMed]
- Conti, C.A.; Votta, E.; Corte, A.D.; Viscovo, L.D.; Bancone, C.; Cotrufo, M.; Redaelli, A. Dynamic finite element analysis of the aortic root from MRI-derived parameters. Med. Eng. Phys. 2010, 32, 212–221. [Google Scholar] [CrossRef]
- Benra, F.-K.; Dohmen, H.J.; Pei, J.; Schuster, S.; Wan, B. A comparison of one-way and two-way coupling methods for numerical analysis of fluid-structure interactions. J. Appl. Math. 2011, 2011, 16. [Google Scholar] [CrossRef]
- Bathe, K.-J.; Hou, Z.; Ji, S. Finite element analysis of fluid flows fully coupled with structural interactions. Comput. Struct. 1999, 72, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Yap, C.H.; Saikrishnan, N.; Tamilselvan, G.; Yoganathan, A.P. Experimental measurement of dynamic fluid shear stress on the aortic surface of the aortic valve leaflet. Biomech. Model. Mechanobiol. 2012, 11, 171–182. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stiehm, M.; Borowski, F.; Kaule, S.; Ott, R.; Pfensig, S.; Siewert, S.; Schmitz, K.-P.; Öner Alper, Ö.; Grabow, N. Computational flow analysis of the washout of an aortic valve by means of Eulerian transport equation. Curr. Dir. Biomed. Eng. 2019, 5, 123. [Google Scholar] [CrossRef]
- Thubrikar, M.J.; Aouad, J.; Nolan, S.P. Patterns of calcific deposits in operatively excised stenotic or purely regurgitant aortic valves and their relation to mechanical stress. Am. J. Cardiol. 1986, 58, 304–308. [Google Scholar] [CrossRef]
- Benevento, E.; Djebbari, A.; Keshavarz-Motamed, Z.; Cecere, R.; Kadem, L. Hemodynamic changes following aortic valve bypass: A mathematical approach. PLoS ONE 2015, 10, e0123000. [Google Scholar] [CrossRef] [Green Version]
- Cao, K.; Sucosky, P. Computational comparison of regional stress and deformation characteristics in tricuspid and bicuspid aortic valve leaflets. Int. J. Numer. Method Biomed. Eng. 2017, 33. [Google Scholar] [CrossRef]
- Fisher, C.I.; Chen, J.; Merryman, W.D. Calcific nodule morphogenesis by heart valve interstitial cells is strain dependent. Biomech. Modeling Mechanobiol. 2013, 12, 5–17. [Google Scholar] [CrossRef]
- Szeto, K.; Pastuszko, P.; Álamo, J.C.D.; Lasheras, J.; Nigam, V. Bicuspid aortic valves experience increased strain as compared to tricuspid aortic valves. World J. Pediatric Congenit. Heart Surg. 2013, 4, 362–366. [Google Scholar] [CrossRef] [PubMed]
- Arzani, A.; Mofrad, M.R.K. A strain-based finite element model for calcification progression in aortic valves. J. Biomech. 2017, 65, 216–220. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ge, L.; Sotiropoulos, F. Direction and magnitude of blood flow shear stresses on the leaflets of aortic valves: Is there a link with valve calcification? J. Biomech. Eng. 2009, 132. [Google Scholar] [CrossRef] [PubMed]
- Andersson, M.; Karlsson, M. Characterization of anisotropic turbulence behavior in pulsatile blood flow. Biomech. Model. Mechanobiol. 2021, 20, 491–506. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).