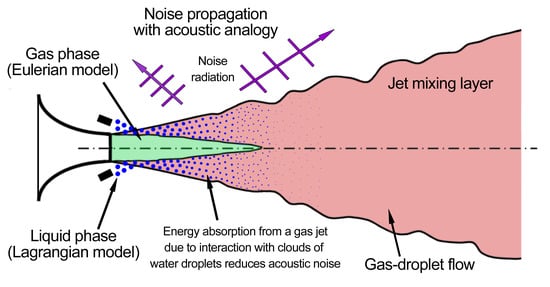
The Eulerian–Lagrangian Approach for the Numerical Investigation of an Acoustic Field Generated by a High-Speed Gas-Droplet Flow
Abstract
1. Introduction
2. Governing Equations
2.1. Gas Phase
2.2. Liquid Phase
2.3. Gas and Liquid Phase Coupling
2.4. Acoustic Prediction
3. Verification and Validation
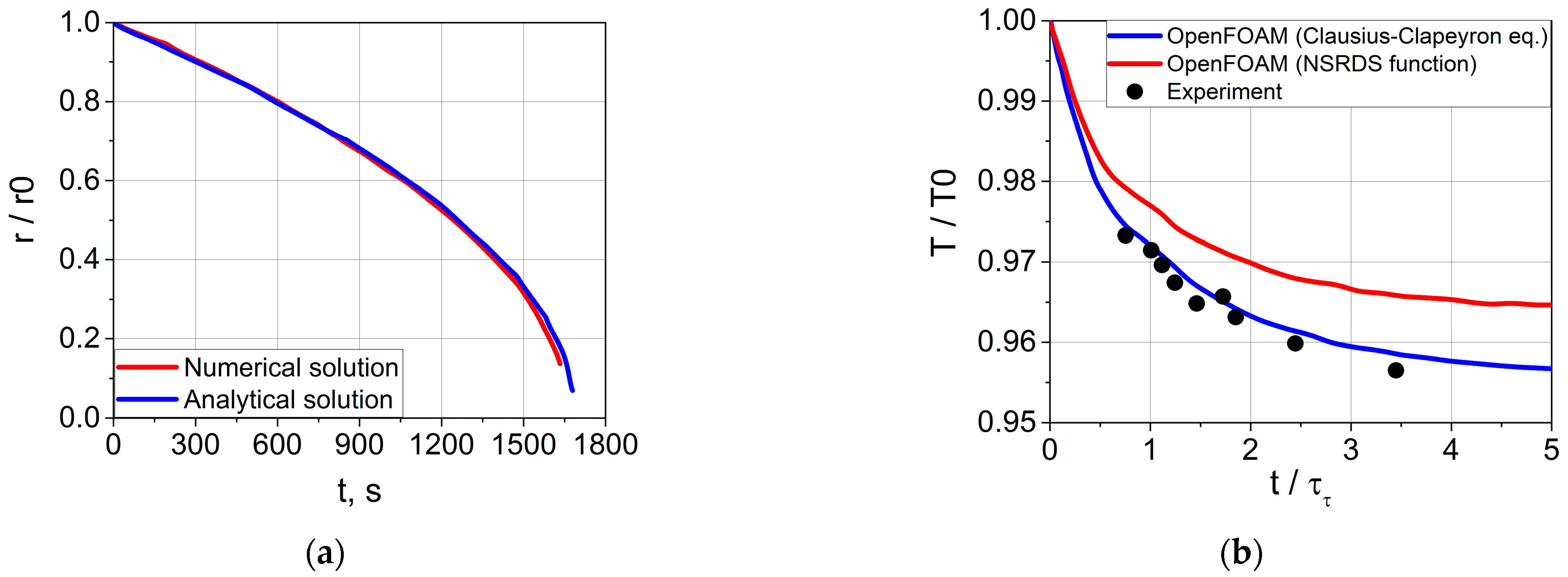
3.1. Droplet Evaporation
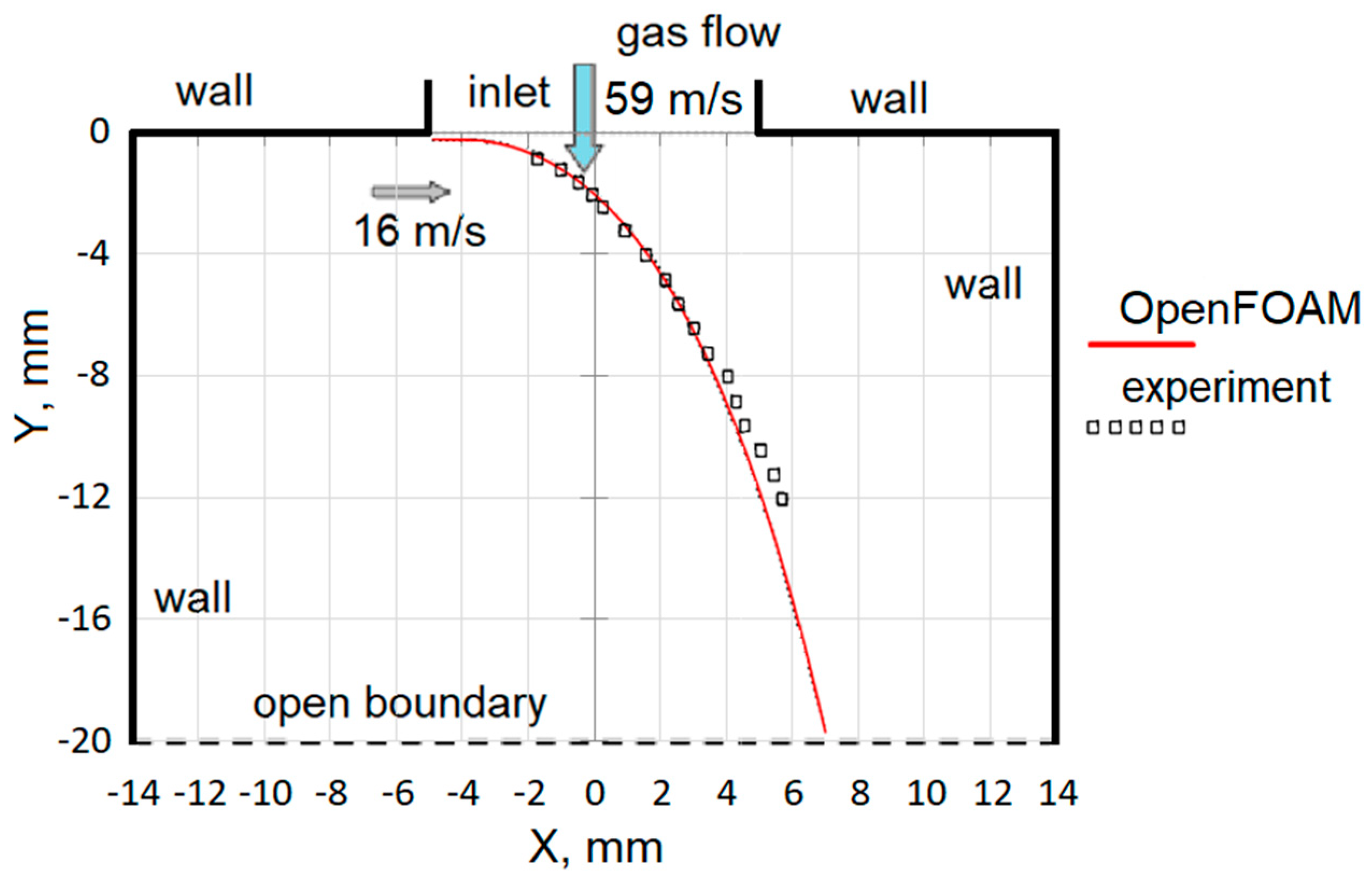
3.2. Droplet Movement
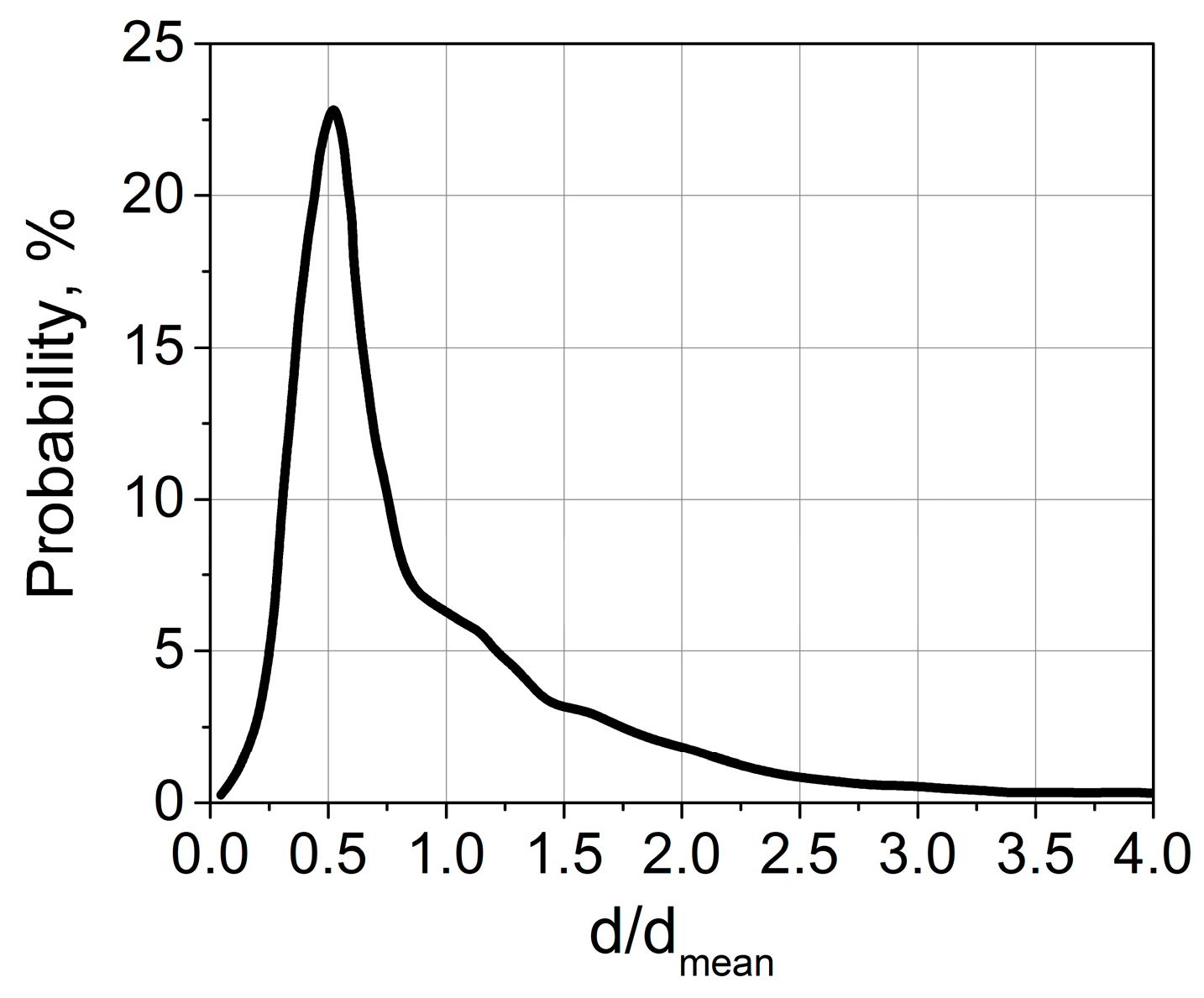
4. Jet-Noise Prediction with Water Microjet Injection
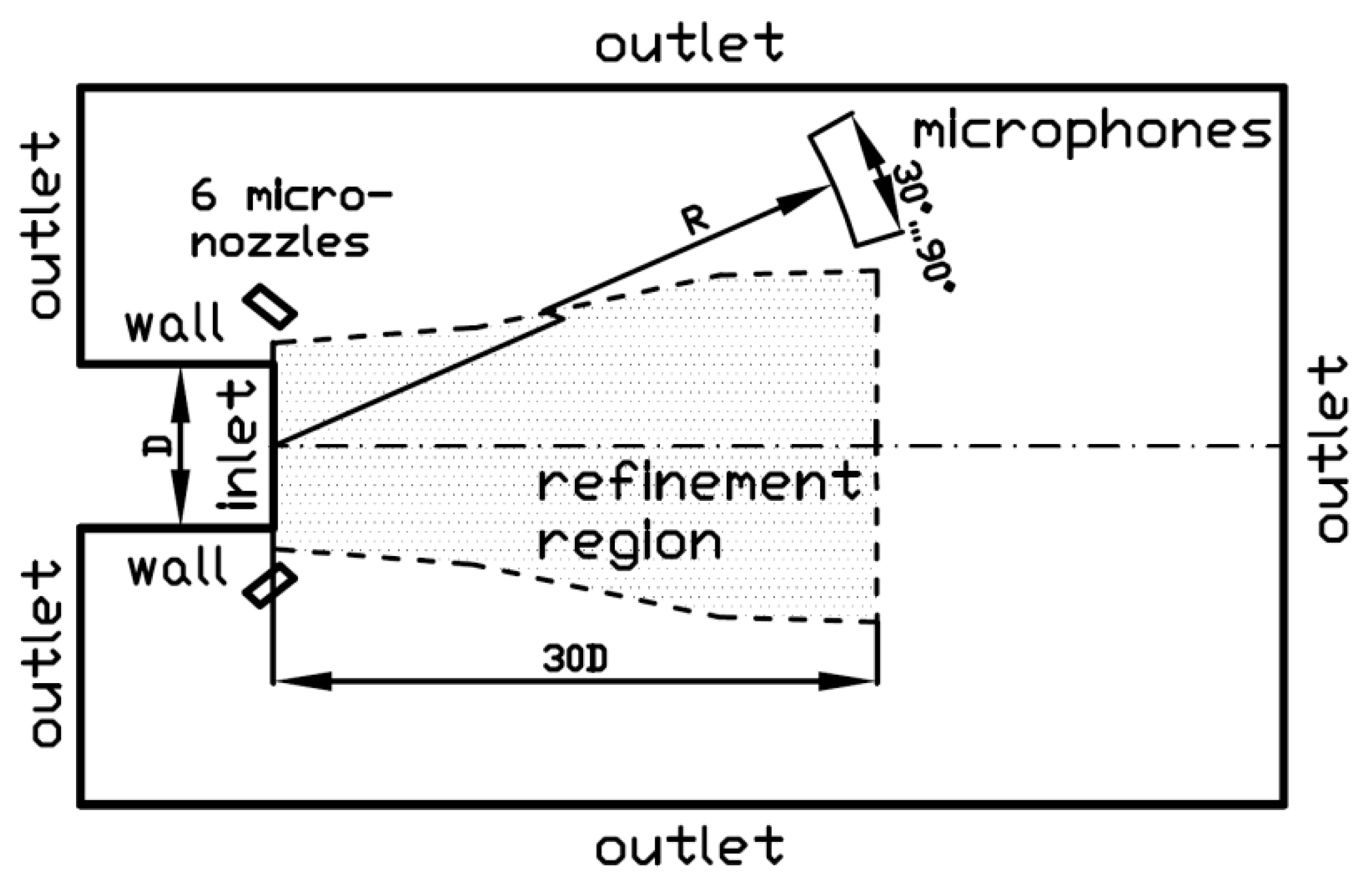
4.1. Computational Setup
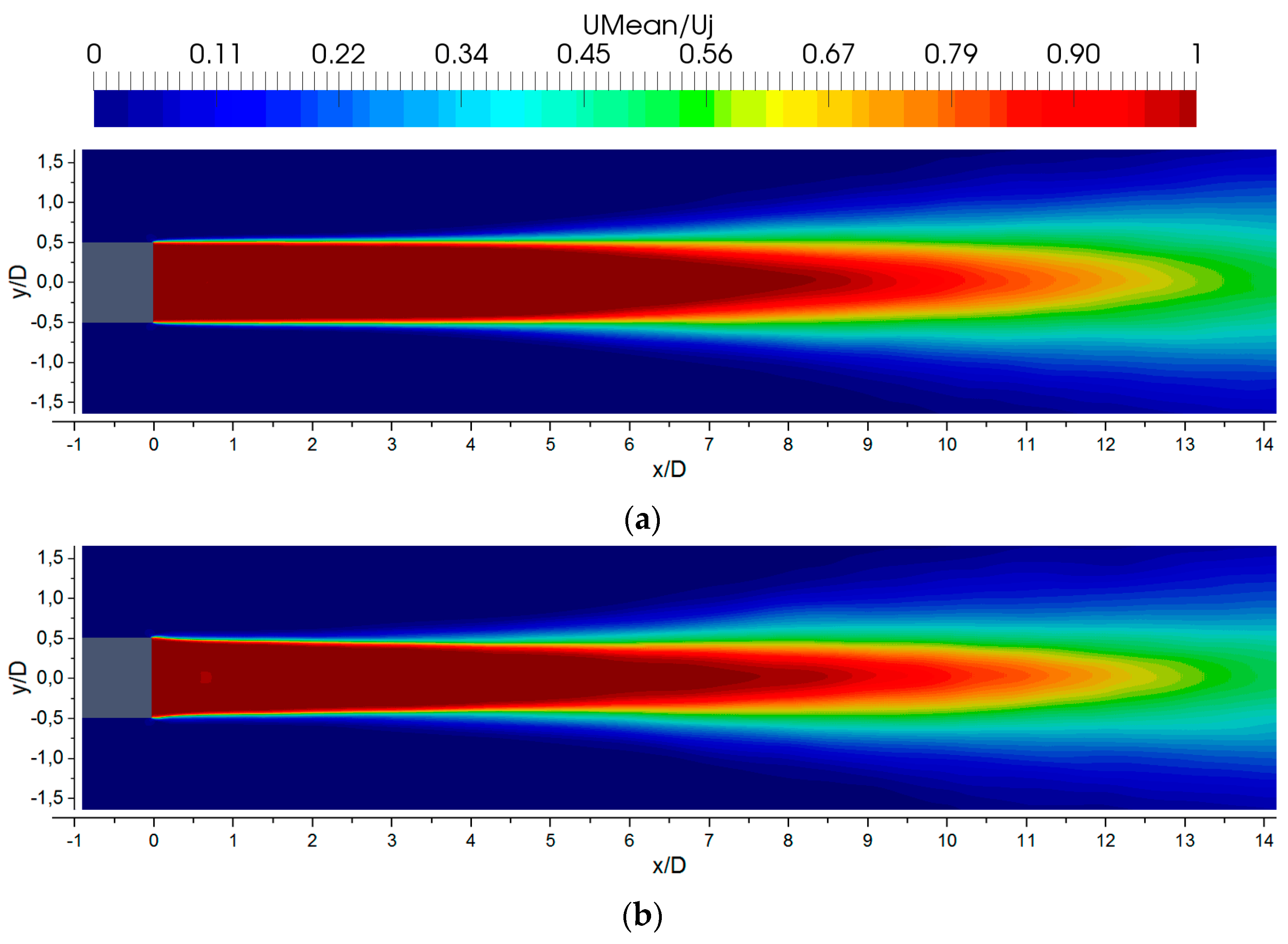
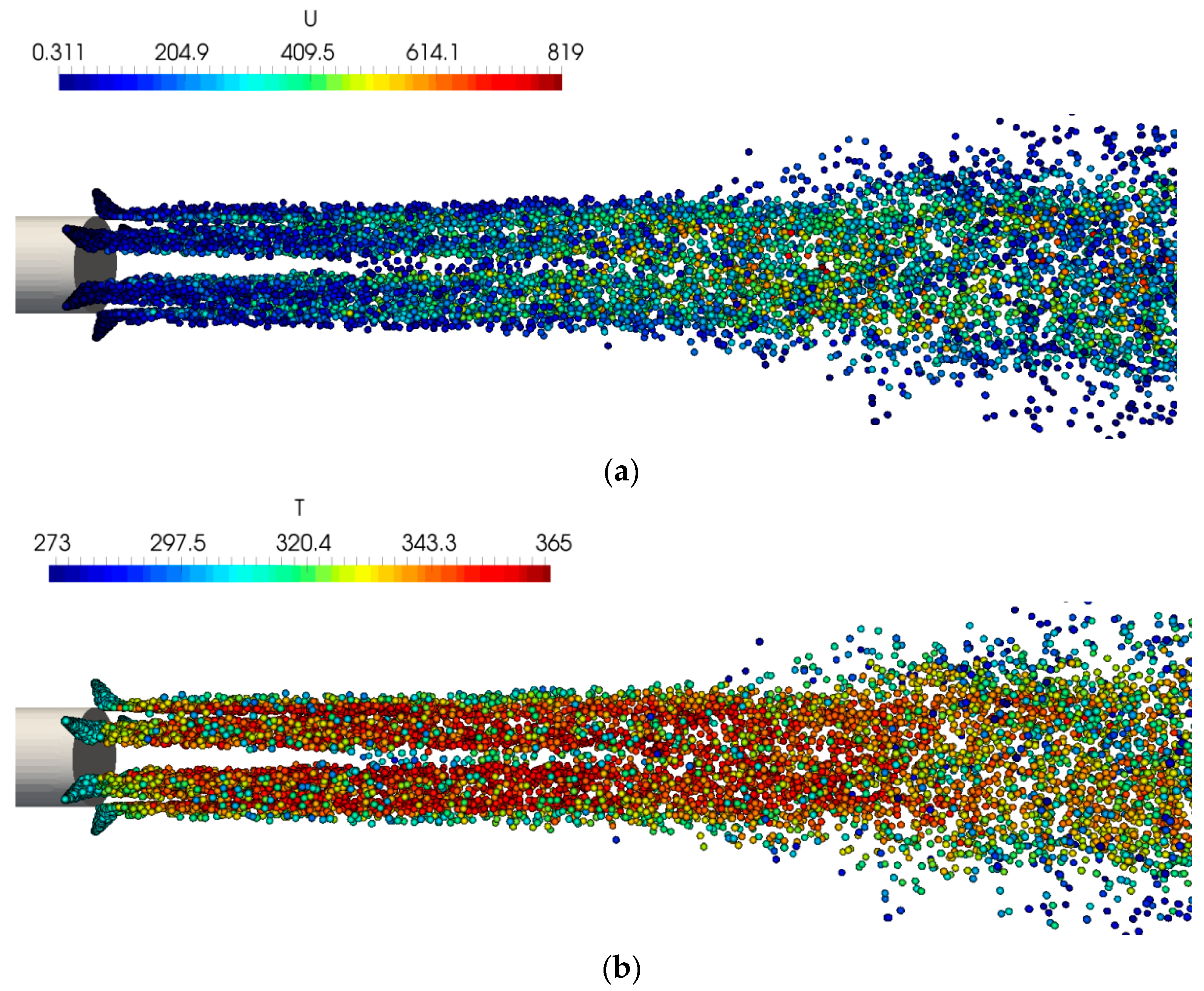
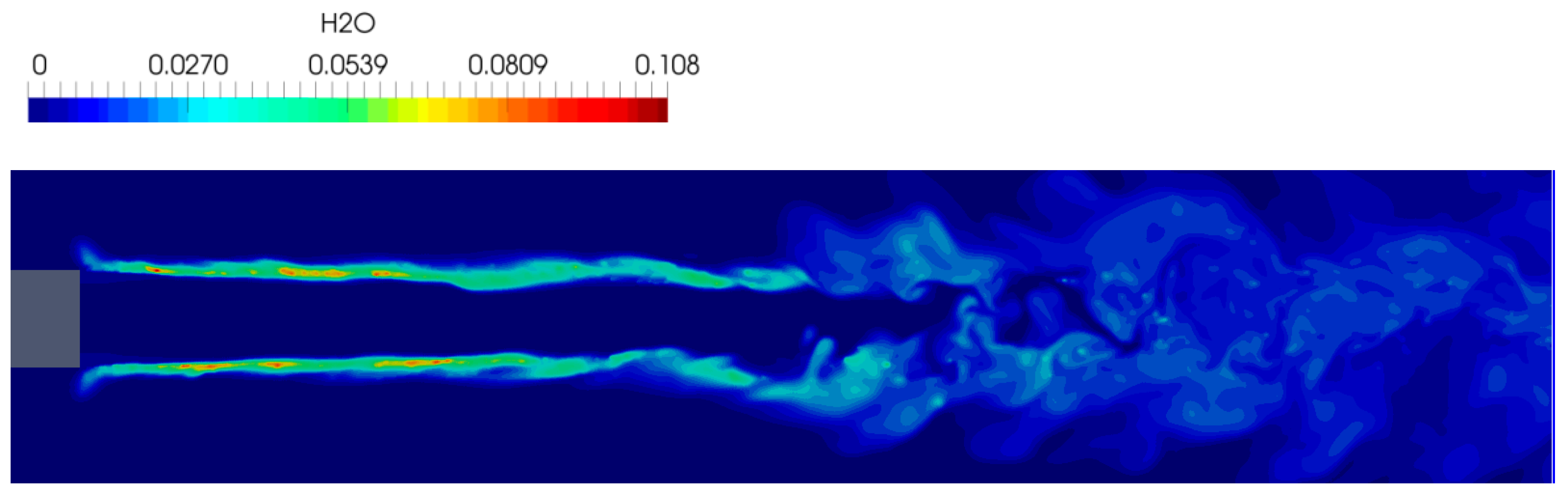
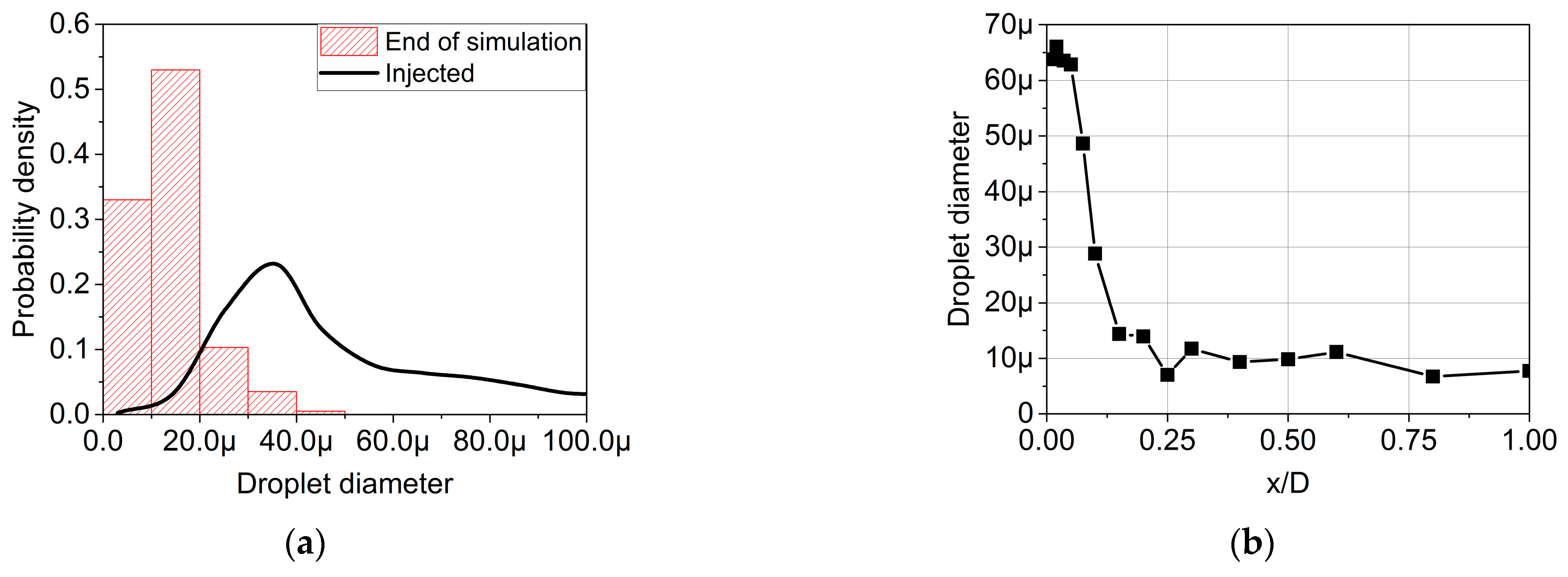
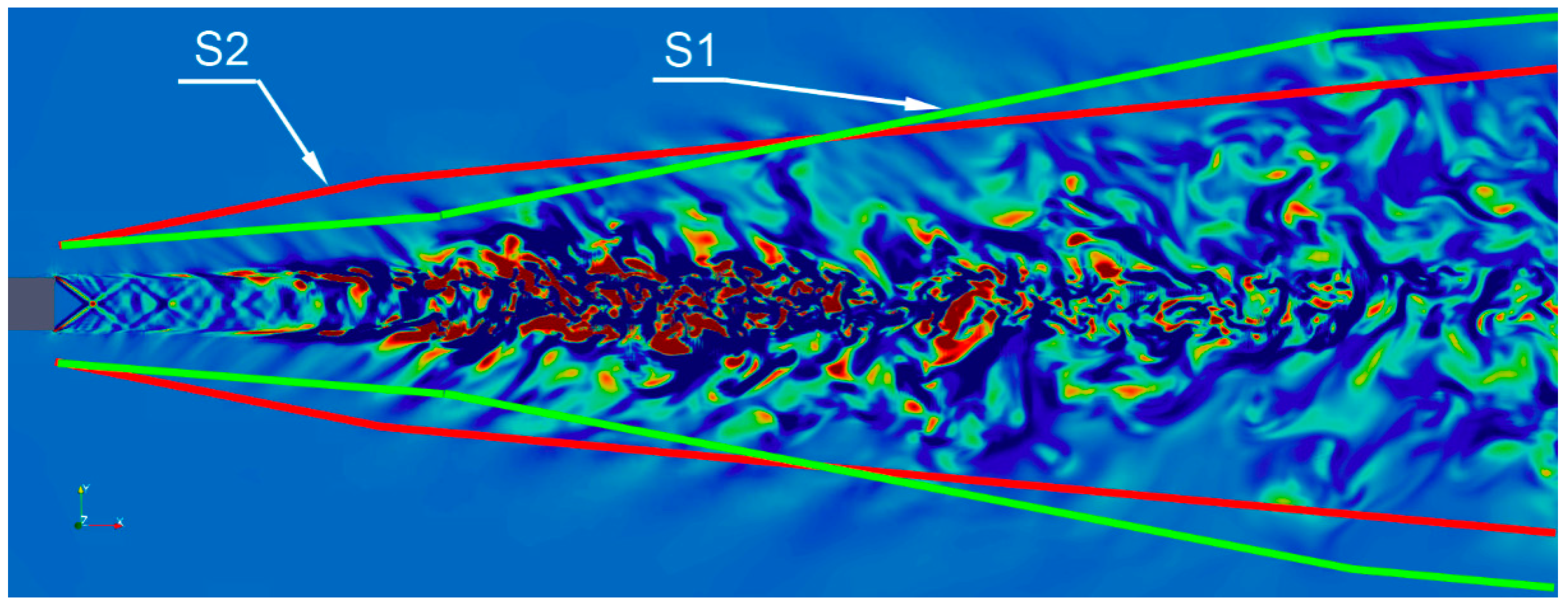
4.2. Near-Field Results
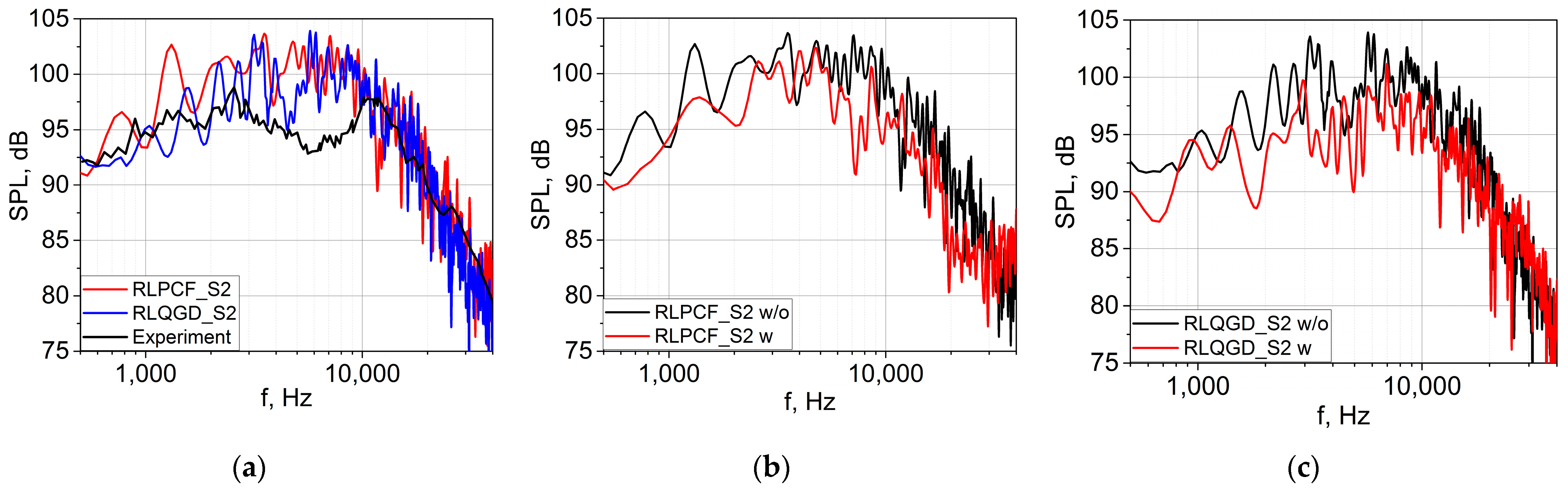
4.3. Acoustic Far-Field
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Casalino, D.; Diozzi, F.; Sannino, R.; Paonessa, A. Aircraft noise reduction technologies: A bibliographic review. Aerosp. Sci. Technol. 2008, 12, 1–17. [Google Scholar] [CrossRef]
- Crighton, D.G. Basic principles of aerodynamic noise generation. Prog. Aerosp. Sci. 1975, 16, 31–96. [Google Scholar] [CrossRef]
- Tam, C.K.W.; Viswanathan, K.; Ahuja, K.K.; Panda, J. The sources of jet noise: Experimental evidence. J. Fluid Mech. 2008, 615, 253–292. [Google Scholar] [CrossRef]
- Tam, C.K.W.; Shen, H.; Raman, G. Screech tones of supersonic jets from bevelled rectangular nozzles. AIAA J. 1997, 35, 1119–1125. [Google Scholar] [CrossRef]
- Tam, C.K.W. Mach wave radiation from high-speed jets. AIAA J. 1984, 47, 2440–2448. [Google Scholar] [CrossRef]
- Ignatius, J.; Sankaran, S.; Kumar, R.; Satyanarayana, T.; Chakravarthy, S. Suppression of jet noise during launch vehicle lift-off by water injection. Int. J. Aeroacoustics 2008, 7, 223–241. [Google Scholar] [CrossRef]
- Washington, D.; Krothapalli, A. The role of water injection on the mixing noise supersonic jet. In Proceedings of the 4th AIAA/CEAS Aeroacoustics Conference, Toulouse, France, 2–4 June 1998; p. 2205. [Google Scholar]
- Zoppellari, E.; Juvé, D. Reduction of supersonic jet noise by water injection. In Proceedings of the 4th AIAA/CEAS Aeroacoustics Conference, Toulouse, France, 2–4 June 1998; p. 2204. [Google Scholar]
- Marchesse, Y.; Gervais, Y.; Foulon, H. Water injection effect on hot supersonic jet noise. Comptes Rendus Mécanique 2002, 330, 1–8. [Google Scholar] [CrossRef]
- Krothapalli, A.; Venkatakrishnan, L.; Lourenco, L.; Greska, B.; Elavarasan, R. Turbulence and noise suppression of a high-speed jet by water injection. J. Fluid Mech. 2003, 491, 131–159. [Google Scholar] [CrossRef]
- Norum, T.D. Reduction in multi component jet noise by water injection. In Proceedings of the 10th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10–12 May 2004; p. 2976. [Google Scholar]
- Labergue, A.; Gradeck, M.; Lemoine, F. Comparative study of the cooling of a hot temperature surface using sprays and liquid jets. Int. J. Heat Mass Transf. 2015, 81, 889–900. [Google Scholar] [CrossRef]
- Kooij, S.; Sijs, R.; Denn, M.M.; Villermaux, E.; Bonn, D. What determines the drop size in sprays? Phys. Rev. X 2018, 8, 031019. [Google Scholar] [CrossRef]
- Trang, C.; Ahmed, R.; Kaosar, M.G. Effect of density ratio on the dispersion of particles in a submerged liquid jet. Comput. Part. Mech. 2019, 6, 581–589. [Google Scholar] [CrossRef]
- Kandula, M. Prediction of turbulent jet mixing noise reduction by water injection. AIAA J. 2008, 46, 2714–2722. [Google Scholar] [CrossRef]
- Yin, C. Transient heating and evaporation of moving fuel droplets. Energy Procedia 2014, 61, 37–40. [Google Scholar] [CrossRef][Green Version]
- Zahoor, R.; Regvar, R.; Bajt, S.; Šarler, B. A numerical study on the influence of liquid properties on gas-focused micro-jets. Prog. Comput. Fluid Dyn. 2020, 20, 71–83. [Google Scholar] [CrossRef]
- Barba, F.D.; Picano, F. Evaporation of dilute droplets in a turbulent jet: Clustering and entrainment effects. arXiv 2017, arXiv:1703.05927v1. [Google Scholar]
- Garcia-Oliver, J.M.; Pastor, J.M.; Pandal, A.; Trask, N.; Baldwin, E.; Schmidt, D.P. Diesel Spray CFD Simulation Based on the Σ-Y Eulerian Atomization Model. At. Sprays 2013, 23, 71–95. [Google Scholar] [CrossRef]
- Jordan, P.; Colonius, T. Wave Packets and Turbulent Jet Noise. Annu. Rev. Fluid Mech. 2013, 45, 173–195. [Google Scholar] [CrossRef]
- Kalugin, M.D.; Korchagova, V.N.; Kraposhin, M.V.; Marchevsky, I.K.; Moreva, V.S. Using big analytics tools in performance of gas dynamics and acoustics tasks. Her. Bauman Mosc. State Tech. Univ. Ser. Nat. Sci. 2018, 3, 32–47. [Google Scholar] [CrossRef]
- Salehian, S.; Mankbadi, R.R. Simulation of rocket launch noise suppression with water injection from impingement pad. Int. J. Aeroacoustics 2020, 19, 207–239. [Google Scholar] [CrossRef]
- Pourhashem, H.; Kumar, S.; Kalkhoran, I.M. Flow field characteristics of a supersonic jet influenced by downstream microjet fluidic injection. Aerosp. Sci. Technol. 2019, 93, 105281. [Google Scholar] [CrossRef]
- Rajput, P.; Kumar, S. Use of downstream fluid injection to reduce subsonic jet noise. Int. J. Aeroacoustics 2019, 18, 554–574. [Google Scholar] [CrossRef]
- Fukuda, K.; Tsutsumi, S.; Shimizu, T.; Takaki, R.; Ui, K. Examination of sound suppression by water injection at lift-off of launch vehicles. In Proceedings of the 17th AIAA/CEAS Aeroacoustics Conference, Portland, OR, USA, 5–8 June 2011. [Google Scholar]
- Lew, P.; Najafi-Yazdi, A.; Mongeau, L. Unsteady numerical simulation of a round jet with imping microjets for noise suppression. J. Acoust. Soc. Am. 2013, 134, 1982–1989. [Google Scholar] [CrossRef]
- Kraposhin, M.V.; Banholzer, M.; Pfitzner, M.; Marchevsky, I.K. A hybrid pressure-based solver for nonideal single-phase fluid flows at all speeds. Int. J. Numer. Meth. Fluids 2018, 88, 79–99. [Google Scholar] [CrossRef]
- Kraposhin, M.V.; Smirnova, E.V.; Elizarova, T.G.; Istomina, M.A. Development of a new OpenFOAM solver using regularized gas dynamic equations. Comput. Fluids 2018, 166, 163–175. [Google Scholar] [CrossRef]
- Elizarova, T.G. Quasi-Gas Dynamic Equations; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Elizarova, T.G.; Zlotnik, A.A.; Shil’nikov, E.V. Regularized equations for numerical simulation of flows of homogeneous binary mixtures of viscous compressible gases. Comput. Math. Math. Phys. 2019, 59, 1832–1847. [Google Scholar] [CrossRef]
- Balashov, V.; Savenkov, E.; Zlotnik, A. Numerical method for 3D two-component isothermal compressible flows with application to digital rock physics. Russ. J. Numer. Anal. Math. Model. 2019, 34, 1–13. [Google Scholar] [CrossRef]
- Putnam, A. Integrable form of droplet drag coefficient. ARS J. 1961, 31, 1467. [Google Scholar]
- O’Rourke, P.J.; Amsden, A.A. The TAB Method for Numerical Calculation of Spray Droplet Breakup; SAE: Warrendale, PA, USA, 1987. [Google Scholar]
- Aissa, A.; Abdelouahab, M.; Noureddine, A.; Elganaoui, M.; Pateyron, B. Ranz and Marshall correlations limits on heat flow between a sphere and its surrounding gas at high temperature. Therm. Sci. VINČA Inst. Nucl. Sci. 2015, 19, 1521–1528. [Google Scholar] [CrossRef]
- Brentner, K.; Farassat, F. An analytical comparison of the acoustic analogy and Kirchhoff formulations formoving surfaces. AIAA J. 1998, 36, 1379–1386. [Google Scholar] [CrossRef]
- Brès, G.A.; Pérot, F.; Freed, D. A ffowcs Williams-Hawkings solver for lattice Boltzmann based computational aeroacoustics. In Proceedings of the 16th AIAA/CEAS aeroacoustics conference, Stockholm, Sweden, 7–9 June 2010; p. 3711. [Google Scholar]
- Epikhin, A.; Evdokimov, I.; Kraposhin, M.; Kalugin, M.; Strijhak, S. Development of a dynamic library for computational aeroacoustics applications using the OpenFOAM open source package. Procedia Comput. Sci. 2015, 66, 150–157. [Google Scholar] [CrossRef]
- libAcoustics Library. Available online: https://github.com/unicfdlab/libAcoustics (accessed on 10 June 2021).
- Kraposhin, M.; Bovtrikova, A.; Strijhak, S. Adaptation of Kurganov-Tadmor numerical scheme for applying in combination with the PISO method in numerical simulation of flows in a wide range of mach numbers. Procedia Comput. Sci. 2015, 66, 43–52. [Google Scholar] [CrossRef]
- Epikhin, A.; Kraposhin, M.; Vatutin, K. The numerical simulation of compressible jet at low Reynolds number using OpenFOAM. E3S Web Conf. 2019, 128, 3. [Google Scholar] [CrossRef]
- Epikhin, A.; Kraposhin, M. Prediction of the free jet noise using quasi-gas dynamic equations and acoustic analogy. Lect. Notes Comput. Sci. 2020, 12143, 217–227. [Google Scholar]
- Liu, A.B.; Mather, D.; Reitz, R.D. Modeling the effects of drop drag and breakup on fuel sprays. J. Engines 1993, 102, 83–95. [Google Scholar]
- Greska, B.; Krothapalli, A. Jet noise reduction using aqueous microjet injection. In Proceedings of the 10th AIAA/CEAS Aeroacoustics Conference, Manchester, UK, 10–12 May 2004; p. 1928. [Google Scholar]
- Askarishahi, M.; Salehi, M.; Radl, S. Voidage correction algorithm for unresolved Euler–Lagrange simulations. Comput. Part. Mech. 2018, 5, 607–625. [Google Scholar] [CrossRef]
- Baars, W.; Tinney, C.; Murray, N.; Jansen, B.; Panickar, P. The effect of heat on turbulent mixing noise in supersonic jets. In Proceedings of the 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2011. AIAA 2011–1029. [Google Scholar]
- Uzun, A.; Lyrintzis, A.S.; Blaisdell, G.A. Coupling of integral acoustics methods with LES for jet noise prediction. Int. J. Aeroacoustics 2004, 3, 297–346. [Google Scholar] [CrossRef]
- Shur, M.; Spalart, P.; Strelets, M. Noise prediction for increasingly complex jets. Part I: Methods and tests. Int. J. Aeroacoustics 2005, 4, 213–246. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Melnikova, V.G.; Epikhin, A.S.; Kraposhin, M.V. The Eulerian–Lagrangian Approach for the Numerical Investigation of an Acoustic Field Generated by a High-Speed Gas-Droplet Flow. Fluids 2021, 6, 274. https://doi.org/10.3390/fluids6080274
Melnikova VG, Epikhin AS, Kraposhin MV. The Eulerian–Lagrangian Approach for the Numerical Investigation of an Acoustic Field Generated by a High-Speed Gas-Droplet Flow. Fluids. 2021; 6(8):274. https://doi.org/10.3390/fluids6080274
Chicago/Turabian StyleMelnikova, Valeriia G., Andrey S. Epikhin, and Matvey V. Kraposhin. 2021. "The Eulerian–Lagrangian Approach for the Numerical Investigation of an Acoustic Field Generated by a High-Speed Gas-Droplet Flow" Fluids 6, no. 8: 274. https://doi.org/10.3390/fluids6080274
APA StyleMelnikova, V. G., Epikhin, A. S., & Kraposhin, M. V. (2021). The Eulerian–Lagrangian Approach for the Numerical Investigation of an Acoustic Field Generated by a High-Speed Gas-Droplet Flow. Fluids, 6(8), 274. https://doi.org/10.3390/fluids6080274