A Study of RANS Turbulence Models in Fully Turbulent Jets: A Perspective for CFD-DEM Simulations
Abstract
1. Introduction
2. Numerical Methodology
2.1. Background
2.2. Numerical Model
2.2.1. Turbulence Models
2.2.2. k- Turbulence Models
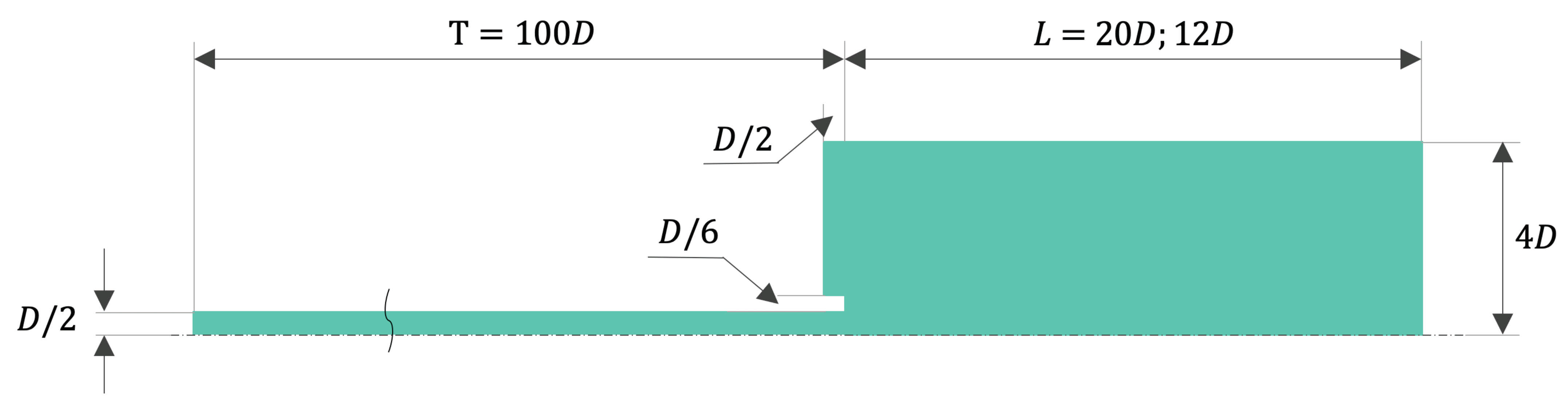
3. Simulation Setup
3.1. Hardalupas et al. Test Case
3.2. Bogusławki and Popiel Test Case
3.3. Model Setup
3.4. Wall Modelling Concerns and Mesh Resolution
4. Results and Discussion
4.1. Grid Independence
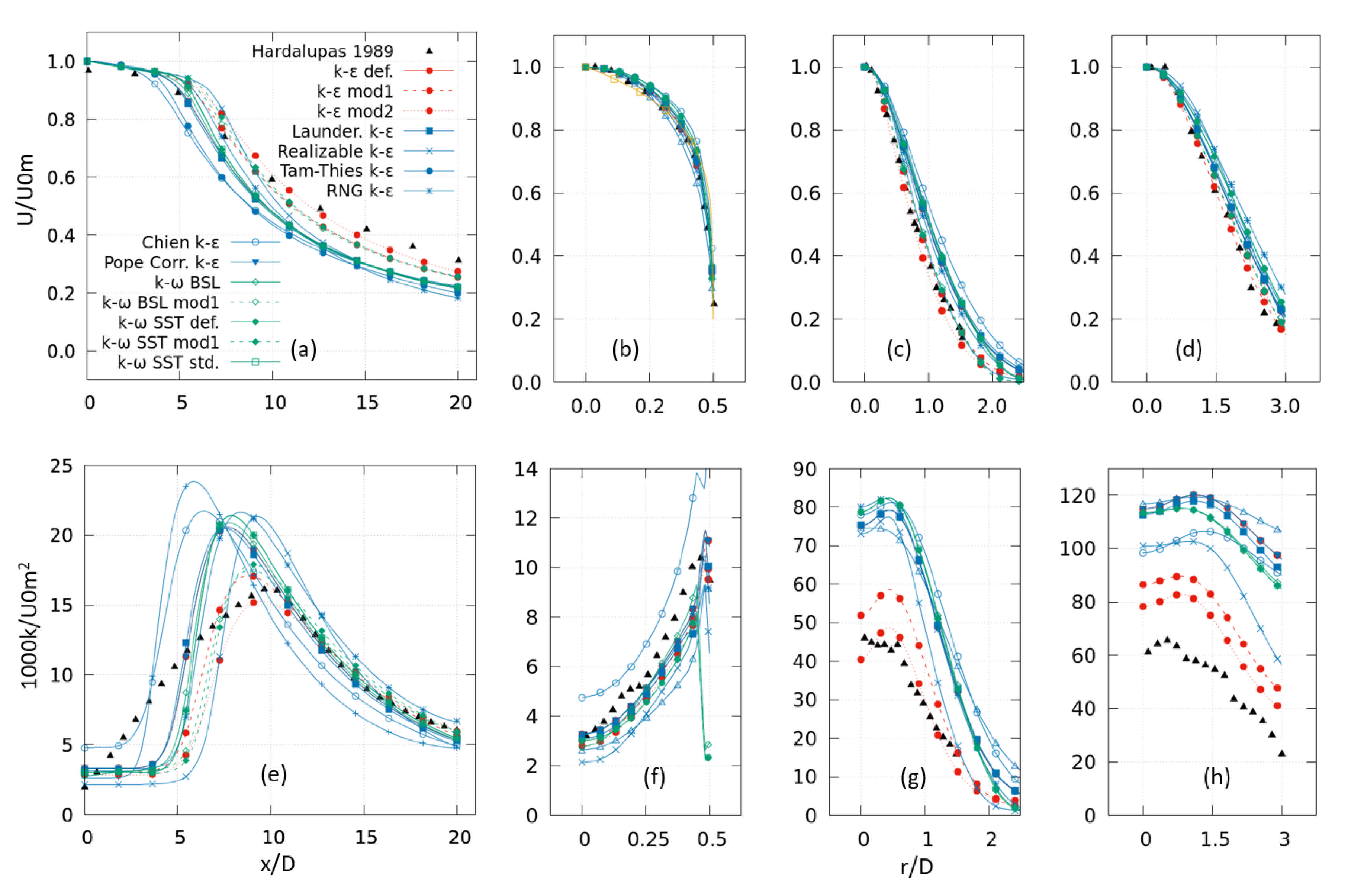
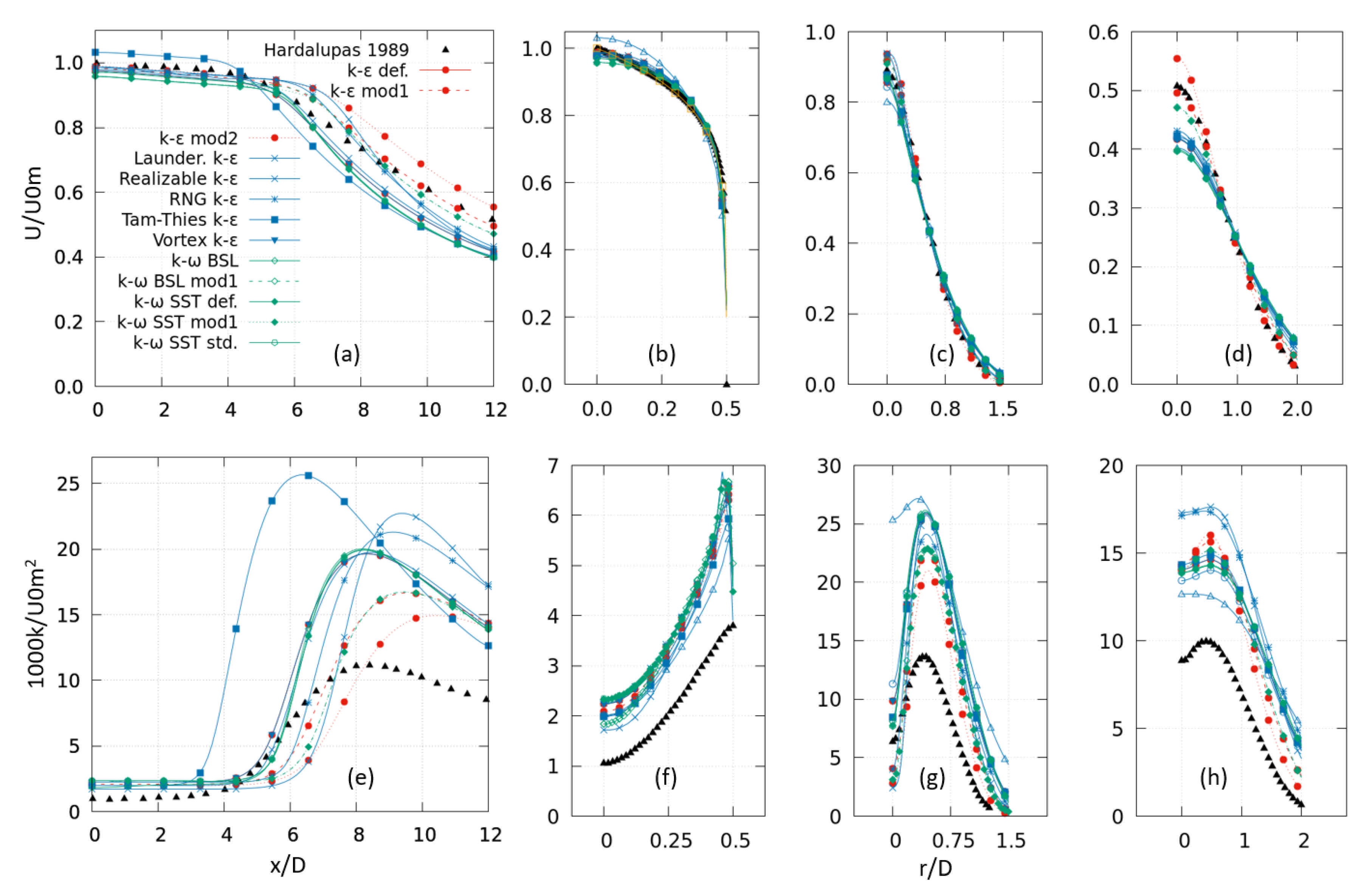
4.2. Fluid Velocity
4.3. Turbulence Properties
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hardalupas, Y.; Taylor, A.; Whitelaw, J. Velocity and particle-flux characteristics of turbulent particle-laden jets. Proc. R. Soc. Lond. A Math. Phys. Sci. 1989, 426, 31–78. [Google Scholar] [CrossRef]
- Lau, T.C.; Nathan, G.J. Influence of Stokes number on the velocity and concentration distributions in particle-laden jets. J. Fluid Mech. 2014, 757, 432–457. [Google Scholar] [CrossRef]
- Modarress, D.; Wuerer, J.; Elghobashi, S. An Experimental Study of a Turbulence Round Two-Phase Jet. Chem. Eng. Commun. 1984, 28, 341–354. [Google Scholar] [CrossRef]
- Lau, T.C.W.; Nathan, G.J. The effect of Stokes number on particle velocity and concentration distributions in a well-characterised, turbulent, co-flowing two-phase jet. J. Fluid Mech. 2016, 809, 72–110. [Google Scholar] [CrossRef]
- Fan, J.; Zhang, X.; Cen, K. Laser Diffraction Method Measurements of Particle-Gas Dispersion Effects in a Coaxial Jet. Aerosol Sci. Technol. 1997, 26, 447–458. [Google Scholar] [CrossRef][Green Version]
- Prevost, F.; Boree, J.; Nuglisch, H.J.; Charnay, G. Measurements of fluid/particle correlated motion in the far field of an axisymmetric jet. Int. J. Multiph. Flow 1996, 22, 685–701. [Google Scholar] [CrossRef]
- Sheen, H.; Jou, B.; Lee, Y. Effect of particle size on a two-phase turbulent jet. Exp. Therm. Fluid Sci. 1994, 8, 315–327. [Google Scholar] [CrossRef]
- Shuen, J.S. A Theoretical and Experimental Investigation of Dilute Particle-Laden Turbulent Gas Jets (Two-Phase Flow). Ph.D. Thesis, The Pennsylvania State University, State College, PA, USA, 1984. [Google Scholar]
- Tsuji, Y.; Morikawa, Y.; Tanaka, T.; Karimine, K.; Nishida, S. Measurement of an axisymmetric jet laden with coarse particles. Int. J. Multiph. Flow 1988, 14, 565–574. [Google Scholar] [CrossRef]
- Ashforth-Frost, S.; Jambunathan, K.; Whitney, C. Velocity and turbulence characteristics of a semiconfined orthogonally impinging slot jet. Exp. Therm. Fluid Sci. 1997, 14, 60–67. [Google Scholar] [CrossRef]
- Quinn, W.; Militzer, J. Effects of nonparallel exit flow on round turbulent free jets. Int. J. Heat Fluid Flow 1989, 10, 139–145. [Google Scholar] [CrossRef]
- Faeth, G. Mixing, transport and combustion in sprays. Prog. Energy Combust. Sci. 1987, 13, 293–345. [Google Scholar] [CrossRef]
- Pope, S.B. An explanation of the turbulent round-jet/plane-jet anomaly. AIAA J. 1978, 16, 279–281. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modeling for CFD, 3rd ed.; Number Book, Whole; DCW Industries: La Cãnada, CA, USA, 2006. [Google Scholar]
- Givi, P.; Ramos, J. On the calculation of heat and momentum transport in a round jet. Int. Commun. Heat Mass Transf. 1984, 11, 173–182. [Google Scholar] [CrossRef]
- Kim, K.Y.; Chung, M.K. Calculation of a strongly swirling turbulent round jet with recirculation by an algebraic stress model. Int. J. Heat Fluid Flow 1988, 9, 62–68. [Google Scholar] [CrossRef]
- Morgans, R.C.; Dally, B.B.; Nathan, G.J.; Lanspeary, P.V.; Fletcher, D.F. Applications of the Revised Wilcox 1998 K-Omega Turbulence Model to a Jet in Co-Flow. In Proceedings of the 2nd International Conference on CFD in the Minerals and Process Industries, Melbourne, Australia, 6–8 December 1999; pp. 479–484. [Google Scholar]
- Post, S.; Iyer, V.; Abraham, J. A Study of Near-Field Entrainment in Gas Jets and Sprays Under Diesel Conditions. J. Fluids Eng. 2000, 122, 385–395. [Google Scholar] [CrossRef]
- Georgiadis, N.J.; Yoder, D.A.; Engblom, W.A. Evaluation of Modified Two-Equation Turbulence Models for Jet Flow Predictions. AIAA J. 2006, 44, 3107–3114. [Google Scholar] [CrossRef]
- Faghani, E.; Saemi, S.D.; Maddahian, R.; Farhanieh, B. On the effect of inflow conditions in simulation of a turbulent round jet. Arch. Appl. Mech. 2011, 81, 1439–1453. [Google Scholar] [CrossRef]
- Wang, C.; Barghi, S.; Zhu, J. Hydrodynamics and reactor performance evaluation of a high flux gas-solids circulating fluidized bed downer: Experimental study. AIChE J. 2014, 60, 3412–3423. [Google Scholar] [CrossRef]
- Bonelli, F.; Viggiano, A.; Magi, V. High-speed turbulent gas jets: An LES investigation of Mach and Reynolds number effects on the velocity decay and spreading rate. Flow Turbul. Combust. 2021. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Rubel, A. On the vortex stretching modification of the k-epsilon turbulence model—Radial jets. AIAA J. 1985, 23, 1129–1130. [Google Scholar] [CrossRef]
- Wilcox, D.C. Formulation of the k-w Turbulence Model Revisited. AIAA J. 2008, 46, 2823–2838. [Google Scholar] [CrossRef]
- Menter, F.R. Influence of freestream values on k-omega turbulence model predictions. AIAA J. 1992, 30, 1657–1659. [Google Scholar] [CrossRef]
- Bogusławski, L.; Popiel, C.O. Flow structure of the free round turbulent jet in the initial region. J. Fluid Mech. 1979, 90, 531–539. [Google Scholar] [CrossRef]
- Weaver, D.; Miskovic, S. Analysis of Coupled CFD-DEM Simulations in Dense Particle-Laden Turbulent Jet Flow. In Proceedings of the ASME 2020 Fluids Engineering Division Summer Meeting, 13–15 July 2020. Virtual, Online. [Google Scholar] [CrossRef]
- Peng, Z.; Doroodchi, E.; Luo, C.; Moghtaderi, B. Influence of void fraction calculation on fidelity of CFD-DEM simulation of gas-solid bubbling fluidized beds. AIChE J. 2014, 60, 2000–2018. [Google Scholar] [CrossRef]
- Chien, K.Y. Predictions of Channel and Boundary-Layer Flows with a Low-Reynolds-Number Turbulence Model. AIAA J. 1982, 20, 33–38. [Google Scholar] [CrossRef]
- Arbiter, N. Development and scale-up of large flotation cells. Min. Eng. 2000, 52, 28. [Google Scholar]
- Launder, B.E.; Sharma, B.I. Application of the energy-dissipation model of turbulence to the calculation of flow near a spinning disc. Lett. Heat Mass Transf. 1974, 1, 131–137. [Google Scholar] [CrossRef]
- Thies, A.T.; Tam, C.K.W. Computation of turbulent axisymmetric and nonaxisymmetric jet flows using the K-epsilon model. AIAA J. 1996, 34, 309–316. [Google Scholar] [CrossRef]
- Wallin, S.; Johansson, A.V. An explicit algebraic Reynolds stress model for incompressible and compressible turbulent flows. J. Fluid Mech. 2000, 403, 89–132. [Google Scholar] [CrossRef]
- Tam, C.K.W.; Ganesan, A. Modified kappa-epsilon Turbulence Model for Calculating Hot Jet Mean Flows and Noise. AIAA J. 2004, 42, 26–34. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Equations of turbulent motion in an incompressible fluid. Dokl. Akad. Nauk SSSR 1941, 30, 299–303. [Google Scholar]
- Saffman, P.G. A Model for Inhomogeneous Turbulent Flow. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1970, 317, 417–433. [Google Scholar] [CrossRef]
- Wilcox, D.C. Reassessment of the scale-determining equation for advanced turbulence models. AIAA J. 1988, 26, 1299–1310. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten Years of Industrial Experience with the SST Turbulence Model. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620. [Google Scholar] [CrossRef]
- Issa, R. Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Spalding, D.B. A Single Formula for the “Law of the Wall”. J. Appl. Mech. 1961, 28, 455–458. [Google Scholar] [CrossRef]
- Kalitzin, G.; Medic, G.; Iaccarino, G.; Durbin, P. Near-wall behavior of RANS turbulence models and implications for wall functions. J. Comput. Phys. 2005, 204, 265–291. [Google Scholar] [CrossRef]
- Popovac, M.; Hanjalic, K. Compound Wall Treatment for RANS Computation of Complex Turbulent Flows and Heat Transfer. Flow Turbul. Combust. 2007, 78, 177–202. [Google Scholar] [CrossRef]
- Celik, I.B. Procedure for Estimation and Reporting of Uncertainty Due to Discretization in CFD Applications. J. Fluids Eng. 2008, 130, 078001. [Google Scholar] [CrossRef]
- Rajaratnam, N. Chapter 2 The Circular Turbulent Jet. In Turbulent Jets; Developments in Water Science; Elsevier: Amsterdam, The Netherlands, 1976; Volume 5, pp. 27–49. ISSN 0167-5648. [Google Scholar] [CrossRef]
- Rodriguez, G.; Weheliye, W.; Anderlei, T.; Micheletti, M.; Yianneskis, M.; Ducci, A. Mixing time and kinetic energy measurements in a shaken cylindrical bioreactor. Chem. Eng. Res. Des. 2013, 91, 2084–2097. [Google Scholar] [CrossRef]

| Study | Reynolds Number | Geometry | Nozzle Type | Turbulence Models | Key Features |
|---|---|---|---|---|---|
| Pope [13] | NA | Axi-Symmetric | Round jet | Modified k-epsilon | Suggested changing = 1.6 and proposed vortex stretching term |
| Givi and Ramos [15] | 373,000 | Axi-Symmetric | Round jet | Modified standard k- and k- turbulence models | Tested k-epsilon constants and = 1.52 with = 1.90 provided most agreeable spreading rates |
| Kim and Chung [16] | 11,600 | Axi-Symmetric | Edge fixed value set from experiments | Standard k-epsilon, algebraic stress model | Highly agreement results for swirling jets |
| Morgans et al. [17] | 50,000 | Axi-Symmetric | Fully developed straight tube round jet nozzle | Modified k-epsilon ( = 1.6), k- Wilcox | Comparable results between k- Wilcox and modified k-epsilon |
| Quinn and Militzer [11] | 208,000 | Axi-Symmetric | Sharp Edged and Smoothly Contoured | Modified k-epsilon ( = 1.48) | Comparable results between experiments for velocity but not turbulence quantities. |
| Post et al. [18] | 10,000 | Axi-Symmetric | Edge fixed value | Launder and Spalding, WF | Acheived results of lower entertainment from experiment |
| Georgiadis et al. [19] | 610,950 | Axi-Symmetric | Convergent contraction | Many two-equation RANS turbulence models | Tam-Thies k-epsilon model demonstrated greatest agreement |
| Faghani et al. [20] | 20,800 | Axi-Symmetric | Sharp edge, round, and contoured nozzles with edge fixed value set to experimental data nozzle exit conditions | Modified k-epsilon with = 1.5 | Significant differences in velocity, turbulence intensity, and turbulence kinetic energy with a change in nozzle shape |
| Wang et al. [21] | 20,000 | Impingement Three-Dimensional | Round jet with fully developed flow inlet | Many two-equation RANS turbulence models | k- SST demonstrated greatest agreement |
| Term | Launder and Spalding [23], mod1, mod2 | Chien [30] | RNG Arbiter [31] | Launder and Sharma [32] | Thies and Tam [33] |
|---|---|---|---|---|---|
| 1.44, 1.50, 1.52 | 1.35 | 1.42 | 1.44 | 1.40 | |
| 1.92, 1.92, 1.90 | 1.80 | 1.68 | 1.92 | 2.02 | |
| 1.0 | 1.0 | 1.0 | |||
| 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | |
| 1.0 | 1.0 | ||||
| 1.0 | 1.0 | 0.7194 | 1.0 | 0.324 | |
| 1.3 | 1.3 | 1.3 | 0.7194 | 0.377 | |
| 0.0 | 0.0 | 0.0 | |||
| 0.0 | 0.0 | 0.0 |
| Location | Velocity | Pressure | Eddy Viscosity | Kinetic Energy | Epsilon | Omega |
|---|---|---|---|---|---|---|
| Wall | No Slip | Zero Gradient | Spalding Wall Function | Zero Gradient | Epsilon Wall Function | Omega Wall Function |
| Inlet | Zero Gradient | Calculated | ||||
| Outlet | Entrainment Velocity | Total Pressure | Calculated | Zero Gradient | Zero Gradient | Zero Gradient |
| Initial free-stream | Uniform 0.0 | Uniform 0.0 | 0 | 1597 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weaver, D.S.; Mišković, S. A Study of RANS Turbulence Models in Fully Turbulent Jets: A Perspective for CFD-DEM Simulations. Fluids 2021, 6, 271. https://doi.org/10.3390/fluids6080271
Weaver DS, Mišković S. A Study of RANS Turbulence Models in Fully Turbulent Jets: A Perspective for CFD-DEM Simulations. Fluids. 2021; 6(8):271. https://doi.org/10.3390/fluids6080271
Chicago/Turabian StyleWeaver, Dustin Steven, and Sanja Mišković. 2021. "A Study of RANS Turbulence Models in Fully Turbulent Jets: A Perspective for CFD-DEM Simulations" Fluids 6, no. 8: 271. https://doi.org/10.3390/fluids6080271
APA StyleWeaver, D. S., & Mišković, S. (2021). A Study of RANS Turbulence Models in Fully Turbulent Jets: A Perspective for CFD-DEM Simulations. Fluids, 6(8), 271. https://doi.org/10.3390/fluids6080271






