Comparison of Semi-Empirical Single Point Wall Pressure Spectrum Models with Experimental Data

Abstract

This study presents an evaluation of semi-empirical single-point wall pressure spectrum models by comparing model predictions with wind tunnel and flight test data. The mean squared error was used to compare the power spectral density of the wall pressure fluctuations predicted by semi-empirical models with a large amount of experimental data. Results show that the models proposed by Goody and Smol’yakov have the lowest mean squared error when predicting the power spectral density for wind tunnel experiments and the Rackl and Weston model has the lowest mean squared error when predicting the power spectral density for flight test data. In addition, although current studies of the power spectra obtained in the wind tunnel are similar, they are not generally an accurate representation of flight test experiments.

1. Introduction

Pressure fluctuations caused by the turbulent boundary layer (TBL) in fluid flows are a source of noise and vibration. These surface pressure fluctuations may cause problems such as structure fatigue and the generation of acoustic noise radiation [1]. Controlling TBL pressure fluctuations and limiting radiated noise can reduce excess noise within the cabin of aircraft, acoustic interference in communication, the malfunction of sensitive equipment, and adverse health effects [2,3].

There have been many studies over the years on determining and describing the sound generated in the TBL to better understand, predict, and possibly control it. Bull provides a good summary of the different studies on the subject [1]. In 1962, Willmarth and Wooldridge were the first to comprehensively measure the pressure fluctuations in the turbulent boundary layer of a wind tunnel by placing pressure transducers flush with the flow through the test section [4]. They were also the first to notice that the power spectral density (PSD) of the wall pressure fluctuations was found to scale with certain flow parameters such as the free stream velocity and the boundary-layer displacement thickness. They found that the energy density of the wall pressure fluctuations was highest at low frequencies and that it decayed with higher frequencies. They also showed that a small increase in surface roughness causes a profound effect on the fluctuating wall pressure in the immediate vicinity. Farabee and Casarella later showed that the PSD is separated into four regions; a low frequency, medium frequency, overlap, and high-frequency range, as confirmed by Bull [5]. The low frequency range is defined as $\omega \delta /u_{\tau }<5$, the medium frequency as $5<\omega \delta /u_{\tau }<100$, the high region as $\omega v/u_{\tau }^2<0.3$, and the overlap region is defined as the region between the medium frequency region and the high frequency region. The distinct frequency regions are often used to describe the PSD since they have distinct power-law features, and the approximate slope of the pressure spectrum in these regions is the common method for comparing experimental data. The slope measured for each region from different studies was tabulated by Blitterswyk [6].

Since Bull, there have been several new wind tunnel studies performed on wall pressure fluctuations, such as by Goody and Simpson [7], Blitterswyck and Rocha [8], Miller [9] and Salze et al. [10], as well as flight test experiments from the National Aeronautics and Space Administration (NASA), using a Tuplov 144 [11] and a Gulfstream G550 [12], which include PSD data. The flight test data were obtained in both experiments by mounting an array of microphones flush with the fuselage of the aircraft, and then measuring the surface pressure fluctuations at different altitudes and velocities.

TBL PSD models are used by researchers to compare with individual experiments, generally, one at a time, to verify whether the obtained experimental data are in good agreement with experimental work previously done, as found in the literature. The present work compares how several TBL PSD wall pressure fluctuation models predict some of these experiments and investigates which model is the most reliable in its predictions of the PSD, as well as when certain models are preferable. Another key contribution of the current study is the comparison between models designed from wind tunnel experiments and models designed from flight tests. The models compared in this study are Efimtsov [13,14,15], Rackl and Weston [11,15], Lowson [16], Robertson [17], Lagnelli [18], Goody [19] and Smol’yakov [20].

Studies by Hwang et al. [21] and Blittersyck and Rocha [6,8] have compared existing semi-empirical models used to describe the acoustic response. Blittersyck and Rocha found that models by Efmitsov, and Rackl and Weston best predicted the low to medium frequency; while models by Goody and Smol’yakov best predicted the overlap and high-frequency ranges. The work by Hwang et al. concluded that Goody provided the best overall prediction of the pressure spectra for flows in air and water [21].

2. Materials and Methods

2.1. Data

The different experimental PSD datasets sampled are in Figure 1 and Figure 2 and are scaled on the inner and outer boundary layer variables, respectively. The naming convention used in the figures and tables is the name of the first researcher presented in the paper, followed by the momentum thickness Reynolds number, and by either a “w” denoting a wind tunnel, or “f” for a flight test. The boundary layer variables used to scale the experimental data are in

Table A1. Experiment variables.

Experiments	x	$\mathit{\delta }$ (mm)	$\mathit{\theta }$ (mm)	${\mathit{\delta }}^{+}$ (mm)	${\mathit{Re}}_{\mathit{x}}$	${\mathit{Re}}_{\mathit{\theta }}$	${\mathit{R}}_{\mathit{T}}$
Goody7300w	3.86	39.06	4.55	6.2	6,195,958	7300	82
Goody23400w	10.73	134.07	12.41	15.8	20,228,285	23,400	274
Blake8200w	2.26	45.72	5.82	7.85	3,194,738	8210	95
Blake10200w	2.69	43.18	5.79	7.24	4,736,029	10,200	104
Blake13200w	4.12	42.93	5.74	7.19	9,341,395	13,200	119
Gravante2953w	3.25	54.8	6.3	7.98	1,523,373	2953	42
Gravante4972w	2.49	44.9	5	6.19	2,476,056	4972	65
Gravante6241	3.25	53.9	6.2	7.2	3,271,492	6241	75
Gravante7076w	3.86	62.9	7	8.25	3,901,909	7076	89
McGrath7010w	3.52	59.53	4.9	6.58	5,046,549	7010	117
McGrath18820w	6.51	91.04	9.44	11.88	12,975,910	18,820	208
Farabee3386w	1.71	27.9	3.26	4.5	1,772,915	3386	47
Farabee4487w	1.74	27.4	3.13	4.29	2,489,277	4487	60
Farabee6025w	1.87	27.8	3.13	4.29	3,603,538	6025	77
Schewe1400w	1.5	30	3.3	4.6	622,917	1400	25
Blitterswyck1866w	1.1	32.6	3.5	5.1	592,743	1886	35
Blitterswyck2546w	1.1	32.5	3.5	5	800,171	2546	43
Rackl419848f	18.9	191.27	39.14	60.1	202,736,906	419,848	1598
Rackl617153f	32.6	327.57	57.53	88.34	349,694,346	617,153	2544
Rackl823168f	49.3	494.32	76.74	117.83	528,832,248	823,168	3639
Rocha239216f	6.7	75	37.42	53.69	42,832,000	239,216	444
Rocha151407f	6.7	77	24.75	37.39	40,982,000	151,407	440
Rocha92037f	6.7	82	21.14	33.3	29,170,000	92,037	353
Miller12933w	3	50.68	5.24	6.9	7,403,216	12,933	165
Miller28562w	3	43.77	4.29	5.52	19,963,978	28,562	328
Miller44899w	3	40.4	3.85	4.9	34,958,975	44,899	489
Salze1642w	0.75	20.44	2.31	3.1	532,258	1642	28
Salze5962w	0.75	20.5	2.46	3.2	1,734,375	5692	67
Salze10687w	0.75	24.97	2.75	3.6	2,916,667	10,687	117

in Appendix A.

Scaling is based on the concept of self-similarity and is done to describe the boundary layer shape over different conditions, collapsing the data into a similar range with other experiments [1,19]. When scaled on the inner variables, the different wind tunnel datasets collapsed to show general agreement between each other, including a good collapse in the high-frequency range. It is pertinent to note how the flight test PSD data from the Tu144 experiment by Rackl, Rizzi and Andianov [11] and the Gulf Stream PSD data by Rocha and Palumbo [12] collapse with each other but not with the wind tunnel data. This is somewhat unexpected since Miller [9] performed an experiment at a similar Mach number and Reynolds number in the wind tunnel as the flight test for Rocha239216f; however, the Miller data collapsed with the other wind tunnel experiments and Rocha239216f did not. Some variation between wind tunnel and flight test data is expected since wall pressure fluctuations in the wind tunnel are observed for controlled conditions with known roughness and pressure gradients. Flight test data can be subject to error since the boundary layer can be disturbed by rivets and have pressure gradient fluctuations [3]. Wind tunnel experiments also tend to have a smaller boundary layer, as the length for the boundary layer to develop is restricted by the size of the test section, whereas for a flight test the boundary layer begins at the nose of the aircraft. The high-frequency ranges do not collapse well when scaled on outer boundary layer variables, this is expected since the high-frequency range is caused by small inner boundary layer vortices and because a wide range of different transducers was used. Experiments with a small $d^{+}$ do not properly capture the high-frequency roll-off due to attenuation, this causes the slope of the roll-off to increase.

Each of these studies made different design choices to have a fully developed boundary layer. Schewe [22], Goody and Simpson [7], and Blake [23] allowed the flow to develop naturally into a fully developed boundary layer, whereas Farabee and Casarella [24], McGrath and Simpson [25], Gravante et al. [26] and Blitterswyk and Rocha [8] used either trip wires or sandpaper strips to artificially trip the flow into a fully developed turbulent boundary layer. A fully developed boundary layer causes the flow conditions to become steady and predictable with increased stream-wise distance, ensuring accurate prediction and repeatability in experiments. The wind tunnel data compared in this study are for a zero pressure gradient, two-dimensional flow, with a single-sided power spectrum.

Each of the experiments must contend with two issues concerning measuring the PSD. At low frequencies, there is often background noise that contaminates the data. At high frequencies, there is attenuation caused by the finite size of the microphone. Anechoic chambers and noise filtering techniques have been used to correct background noise. Anechoic chambers absorb the noise radiated outward and prevent it from reflecting, as well as absorbing noise from outside the test section from entering the chamber and contaminating the data [27]. Anechoic chambers were used by Blake, Farabee and Casarella, Schewe, and Blitterswyck and Rocha. Noise cancellation techniques can also be used to reduce undesired noise. A common approach to filtering out background noise is a temporal subtraction of two spanwise transducer signals that can be assumed to be uncorrelated by having them separated by a couple of boundary layer thicknesses [28,29]. Noise cancellation techniques were used by Farabee and Casarella, Gravante et al., Goody and Simpson, McGrath and Simpson, Blitterswyck and Rocha, and Miller.

The size of the microphone used has a significant impact on the ability to measure high-frequency noise. If the contribution to the pressure fluctuation from a source is smaller than the sensing diameter of the transducer then it will be attenuated, effectively acting as a low-pass filter. This is caused by the contribution of the source being spatially integrated and sources smaller than the sensing diameter are attenuated since their mean value will be zero by definition [26,30]. It was shown by Schewe [22] and Gravante [26] that the effective size of the pressure transducer to reduce attenuation should be $12<d^{+}<19$. A way to reduce the effective size is to use a pinhole capped microphone as opposed to a grid capped microphone.

Another way to reduce high-frequency attenuation is by applying the Corcos correction [31]. This is a table that can be used to try to recover high-frequency spectral values and has been shown to have favorable results in several studies. Nevertheless, other studies have raised concerns that the Corcos correction can lead to over correction at high frequencies [22,30]. Since it is unclear when it is appropriate to apply the Corcos correction, the data in this work are as reported by the original authors of each study.

Several of the authors sampled in this study commented on the uncertainty of hotwire measurements for TBL parameters and on the uncertainty of microphone measurements. TBL parameters’ measurements, such as mean velocity, had a low uncertainty of approximately 1–3% as measured by McGrath and Simpson, and Blake. Goody and Simpson, Blake, McGrath and Simpson, Rocha and Palumbo, and Gravante et al. commented on the uncertainty of the microphones in their experiments, in which the amount of uncertainty was between 1–3 dB. Rocha and Palumbo, and Gravante et al. also commented on how the uncertainty varied with frequency range. Gravante et al. found that the uncertainty of the measured turbulent wall pressure spectra was highest above 10,000 Hz where it was approximately 7%. Miller, Salze, Schewe, Farabee and Casarella did not mention uncertainty; however, they used similar instrumentation as the other authors, and so it would be reasonable to hypothesize that uncertainty is also low.

2.2. Single Point Wall Pressure Spectrum Models

Single point wall pressure spectrum semi-empirical models have been used to predict the PSD of wall pressure fluctuations for zero pressure gradient flows. By using the TBL parameters measured in wind tunnels and flight tests as input parameters to the TBL semi-empirical models, the PSD of the wall pressure fluctuations can be predicted. These models are generally constructed by using the observed scaling behavior of existing data as a starting form, and then by adjusting the constants of those scaling parameters to better match the existing data. This section describes each of the TBL semi-empirical models used in the present investigation. The single-sided PSD is defined as follows:

$$\overline{p^2}={\int }_0^{\infty }\mathsf{\Phi }\left(\omega \right)d\omega$$

(1)

$$\mathsf{\Phi }\left(f\right)=2\pi \mathsf{\Phi }\left(\omega \right),[p{a}^2,Hz]$$

(2)

$$PSD=10lo{g}_{10}\left(\frac{\mathsf{\Phi }\left(f\right)}{P_{ref}^2}\right),\left[DB\right]$$

(3)

in which $\mathsf{\Phi }\left(\omega \right)$ is the single point wall pressure spectrum, either provided by the respective TBL semi-empirical model or from the experimental data.

2.2.1. Efimtsov Model

Efimtsov created two models from flight tests using a Tupolev TU-22 (Soviet twin-engined, supersonic military aircraft) and additional wind tunnel experiments [13,14,15]. According to Efimtsov, a single point wall pressure spectrum model should be based around Mach Number, Reynolds number, and Strouhal number. The second of Efimtsov’s equations is shown in Equation (1).

$$\mathsf{\Phi }\left(w\right)=\frac{2\pi \alpha u_{\tau }^3{\rho }^2\delta \beta }{{(1+8{\alpha }^3{\left(\frac{\omega \delta }{u_{\tau }}\right)}^2)}^{1/3}+\alpha \beta R{e}_{\tau }{(\left(\frac{\omega \delta }{u_{\tau }}\right)/R{e}_{\tau })}^{10/3}},$$

(4)

where:

$$R{e}_{\tau }=\frac{\delta u_{\tau }}{{\nu }_w}$$

(5)

$$\beta ={[1+{\left(\frac{R{e}_{\tau 0}}{R{e}_{\tau }}\right)}^3]}^{1/3}$$

(6)

$$\alpha =0.01,$$

(7)

$${\nu }_w=\nu \frac{\rho }{{\rho }_w}{\left(\frac{T_w}{T}\right)}^{0.89}$$

(8)

$$T_w=T(1+0.89\frac{\gamma -1}{2}{M}^2)$$

(9)

$${\rho }_w=\rho \frac{T}{T_w}.$$

(10)

2.2.2. Rackl and Weston

Rackl and Weston used data collected from a TU144 to adjust Efimtsov to better predict a broadband peak around a Strouhal number of 0.6 and to adjust the high-frequency roll-off of the PSD. They did this by creating two semi-empirical corrective functions that add to the Efimtsov model [11,15].

The equation becomes:

$$\mathsf{\Phi }\left(f\right)=\mathsf{\Phi }{\left(f\right)}_{Efimtsov}+x_1\left(f\right)+x_2\left(f\right),$$

(11)

where the corrective functions are:

$$x_1\left(f\right)=1/4[tanh(lo{g}_{10}(\frac{f}{1000}))+1][M-1.65]lo{g}_{10}\left(f\right)$$

(12)

$$x_2\left(f\right)=2.5e^{(-{(ln(\frac{2\pi {\delta }^{\ast }}{U_{\infty }}\left(f\right))-ln\left(0.6\right))}^2)}.$$

(13)

2.2.3. Lowson Model

The semi-empirical model developed by Lowson was done for both supersonic and subsonic equilibrium boundary layers and tries to relate the power spectral density (PSD) to the Mach number and other TBL parameters [16]. This model was intended to be used directly for structural response calculations with the goal of being simple, related to physical parameters of the flow, and having a good agreement with available data.

$$\mathsf{\Phi }\left(f\right)=\frac{q^2\left(\frac{\overline{P^2}}{q^2}\right)}{{\omega }_0{(1+{\left(\frac{2\pi f}{{\omega }_0}\right)}^2)}^{3/2}},$$

(14)

where:

$${\omega }_0=\frac{8U_{\infty }}{\delta }$$

(15)

$$\frac{\overline{P^2}}{q^2}=\frac{{0.006}^2}{{(1+0.14M^2)}^2}.$$

(16)

2.2.4. Robertson Model

Robertson built on Lowson to try to improve upon the high-frequency roll-off and an overestimation of the low-frequency range [17]. This model was intended to be used for aerospace vehicles such as the space shuttle and a major portion of the investigation Robertson performed was for transonic speed conditions and the launch phase of the shuttle’s mission (0.60 ≤ M ≤ 1.6).

$$\mathsf{\Phi }\left(f\right)=\frac{q^2\left(\frac{\overline{P^2}}{q^2}\right)}{{\omega }_0{(1+{\left(\frac{2\pi f}{{\omega }_0}\right)}^{0.9})}^2},$$

(17)

where:

$${\omega }_0=\frac{U_{\infty }}{2{\delta }^{\ast }}.$$

(18)

2.2.5. Lagnelli Model

Through further subsonic and supersonic wind tunnel tests, Lagnelli proposed a further update of Robertson. Lagnelli accounts for viscous, compressibility and wall heat transfer effects and is based on the work by Lowson, Robertson and Blake [18]. Based on the availability of information, the ratio of $h_w/h_{aw}$ was assumed to be unity in this study. While this assumption has little effect for low Mach number flows, it leads to error at higher Mach numbers.

$$\mathsf{\Phi }\left(f\right)=\frac{q^2{\delta }^{\ast }(2.293\times {10}^{-5})F_c^{-0.5733}}{U_{\infty }[1+F_c^{2.867}{\left(\frac{2\pi f{\delta }^{\ast }}{U_{\infty }}\right)}^2]},$$

(19)

where $F_c$ is a transformation function for compressible to compressible flow states.

$$F_c=\frac{1}{2}+\frac{h_w}{h_{aw}}(\frac{1}{2}+\left(0.89\right)\frac{\gamma -1}{2}{M}^2)+0.22\left(0.89\right)\frac{\gamma -1}{2}{M}^2.$$

(20)

2.2.6. Goody Model

Goody decided to modify the Chase–Howe model [32,33] based on experimental data from Goody and Simpson [7], Farabee and Casarella [24], Gravante et al. [26], McGrath and Simpson [25], Olivero-Bally et al. [34] and Blake [23]. The Goody model tries to improve the Chase-Howe model in the prediction of the low-frequency response and the roll-off at high frequencies. This was done by adding a term to the denominator so that the spectral levels decay at ${\omega }^{-5}$, changing exponents in the denominator to better agree at middle frequencies, and adding a multiplicative constant to raise the spectral levels at all frequencies to better agree with the experimental data.

$$\mathsf{\Phi }\left(f\right)=\frac{3{\left(2\pi f{\tau }_w\right)}^2{\left(\frac{\delta }{U_{\infty }}\right)}^3}{{({\left(\frac{2\pi f\delta }{U_{\infty }}\right)}^{3/4}+0.5)}^{3.7}+{\left(1.1R_T^{-0.57}\frac{2\pi f\delta }{U_{\infty }}\right)}^7}.$$

(21)

2.2.7. Smol’yakov Model

Smol’yakov used several datasets to create a piece wise function model that has different equations for the low, overlap and high frequency ranges [20]. The method is based on modelling of the wave-number spectrum of the sources caused by the interaction of the turbulence–mean shear type.

$$\mathsf{\Phi }\left(f\right)=\frac{1}{u_{\tau }^2}1.49x{10}^{-}5{\tau }_w^2\nu R{e}_{\theta }^{2.74}\overline{f^2}(1-0.117R{e}_{\theta }^0.44\overline{f^{1/2}}),$$

(22)

for $\overline{f}<\overline{f_0}$

$$\mathsf{\Phi }\left(f\right)=\frac{2.75{\tau }_w^2\nu }{u_{\tau }^2{\overline{f}}^{1.11}}(1-0.82exp[-0.51(\frac{\overline{f}}{\overline{f_0}}-1)]),$$

(23)

for $\overline{f_0}<\overline{f}<0.2$

$$\mathsf{\Phi }\left(f\right)=\frac{{\tau }_w^2\nu \left(3.89exp\right(-8.35\overline{f}+18.6exp(-3.58\overline{f})+0.31exp(-2.14\overline{f})}{1-0.82exp(-0.51(\frac{\overline{f}}{\overline{f_0}}-1))}$$

(24)

for $\overline{f}>0.2$ where:

$$\overline{f}=\frac{2\pi f\nu }{u_{\tau }^2}$$

(25)

$$\overline{f_0}=49.35R{e}_{\theta }^{-0.88}.$$

(26)

3. Results and Discussion

The comparison between models and the different experiments was done by determining the mean squared error (MSE) between the PSD of the wall pressure fluctuations predicted by the semi-empirical single point models and the PSD of wall pressure fluctuations measured in each of the experiments. The MSE is then defined for this application as follows:

$$MSE=\frac{1}{N}\sum _{n=1}^N{(PS{D}_{experimental,n}-PS{D}_{predicted,n})}^2,$$

(27)

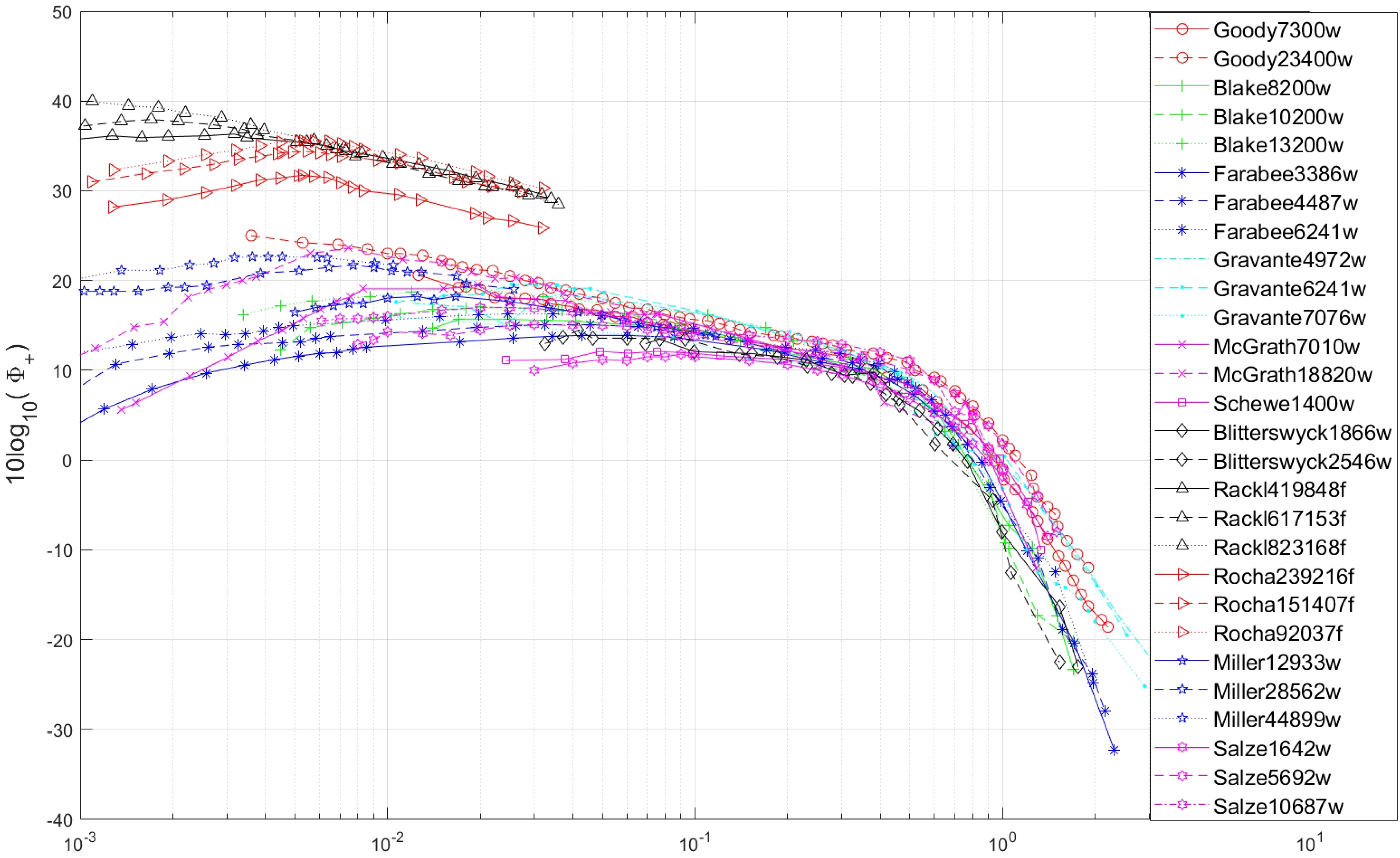
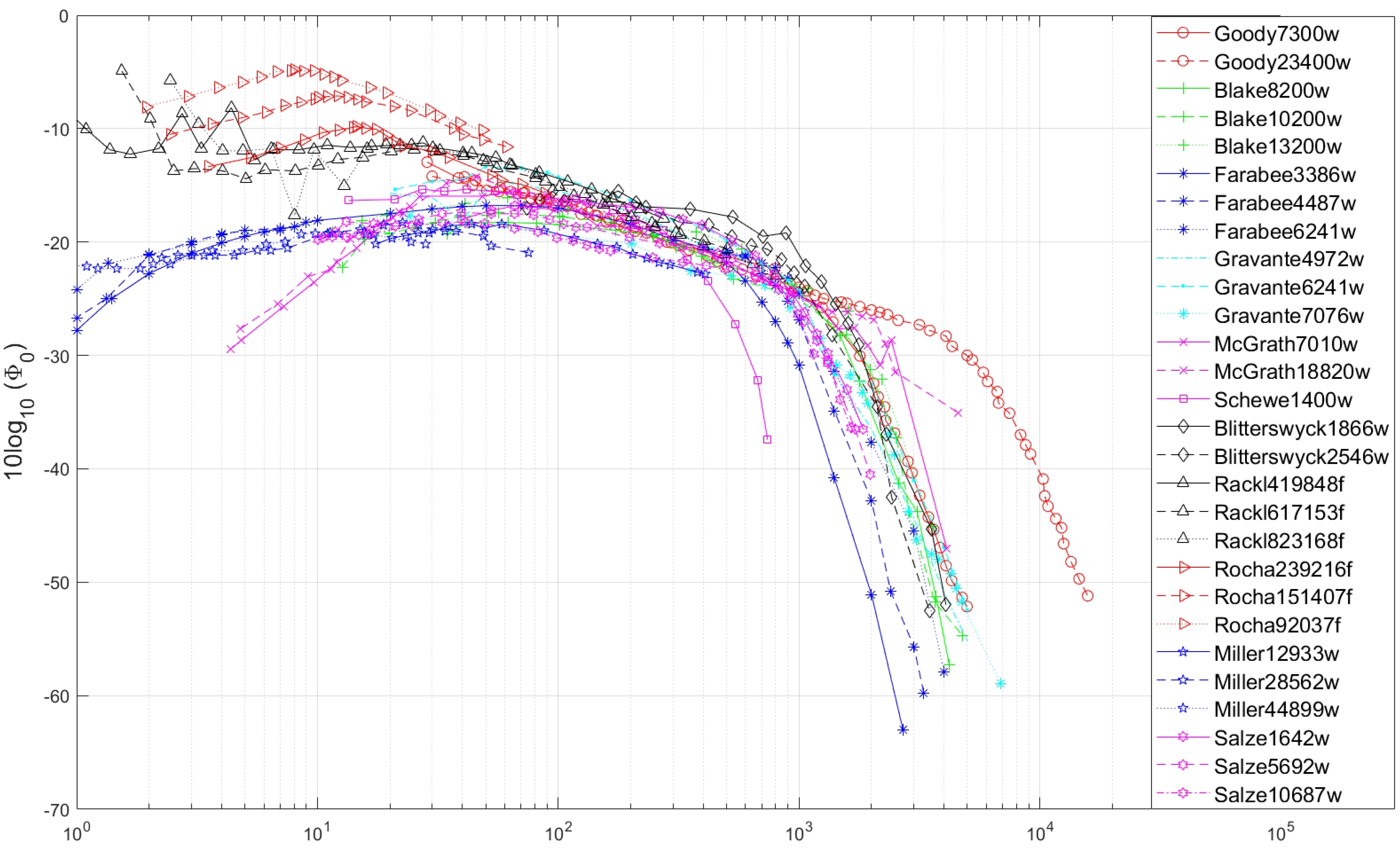
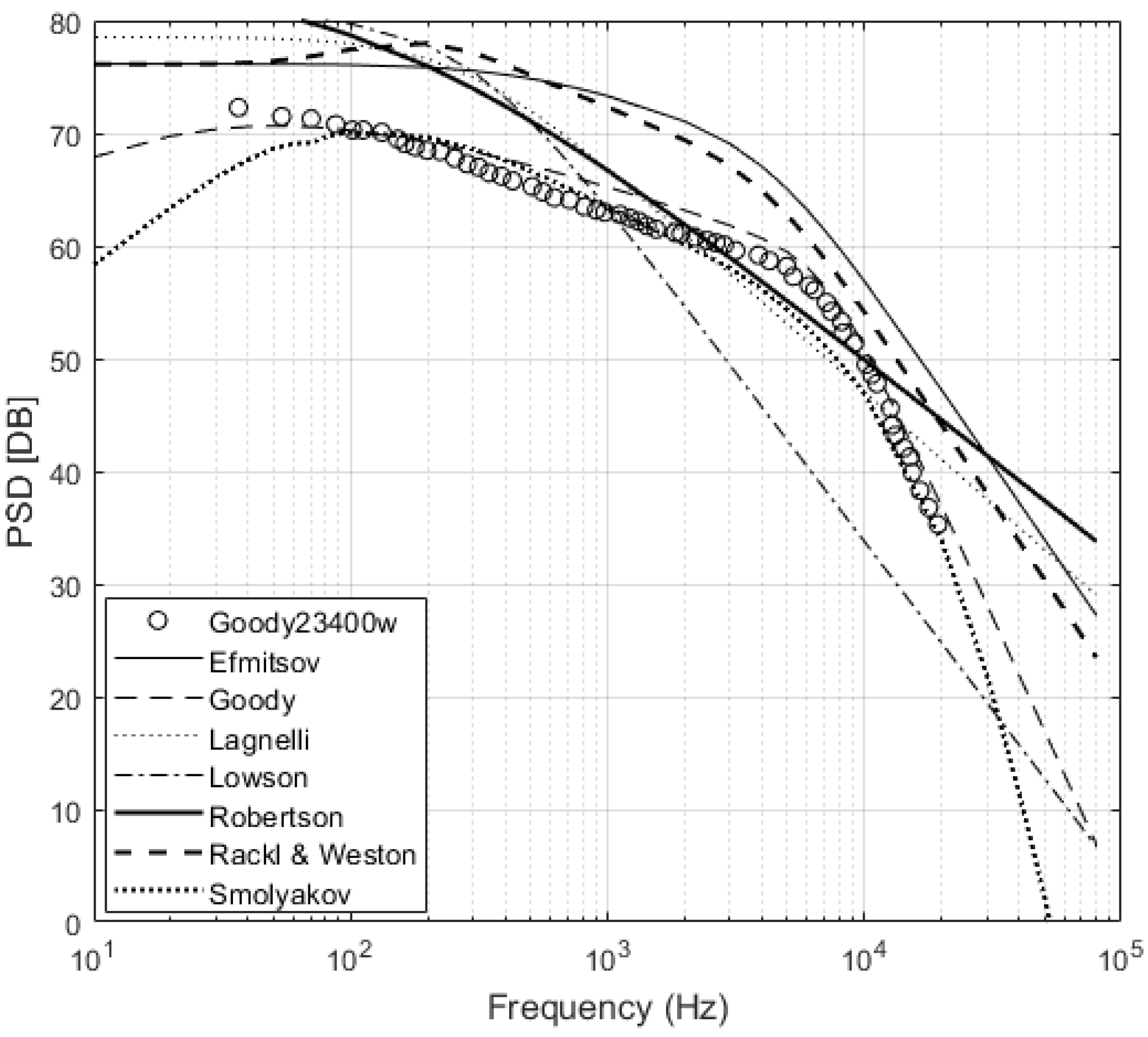
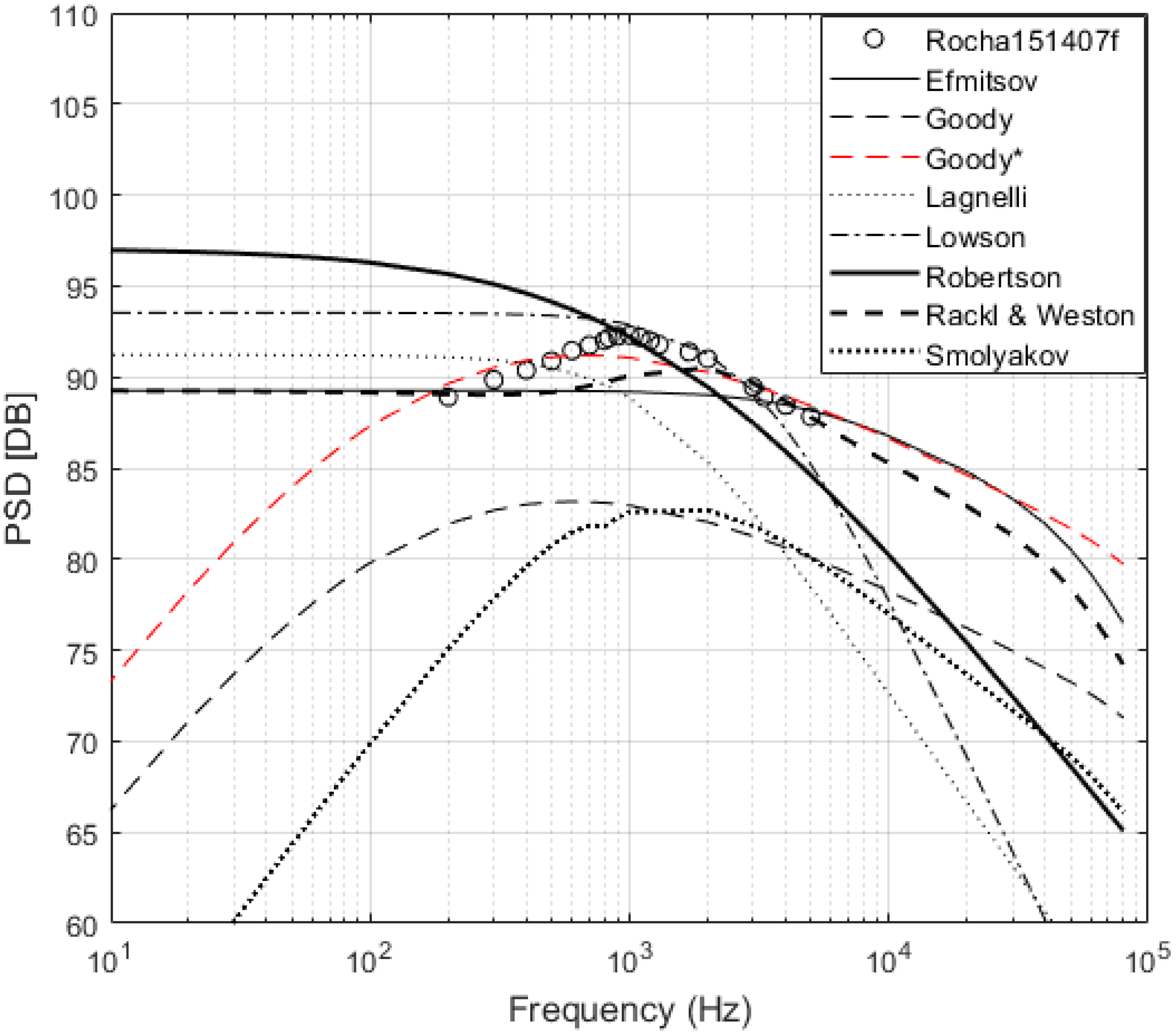
in which n is the PSD sampled at a specific frequency, and N is the total number of samples taken. In previous studies found in the literature, the evaluation of models and experiments are made either by visual inspection or by comparing the slope of the PSD for the low, medium, overlap and high-frequency ranges. Comparing the models based solely on the slope of PSD at different frequencies fails to account for a difference in magnitude. Ideally, both the shape and magnitude of the PSD should be compared when evaluating a model so that accurate estimations of the sound produced can be determined. 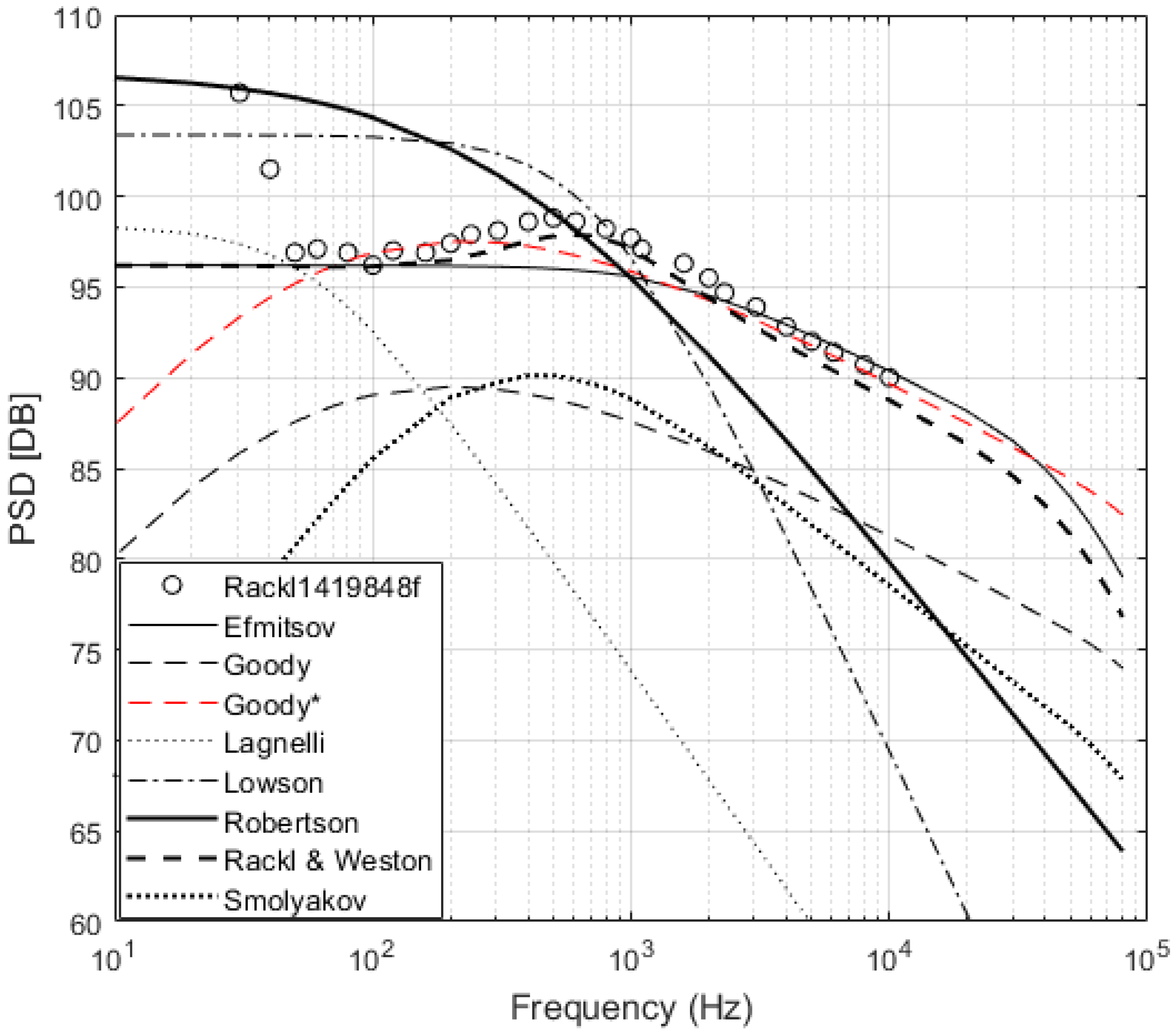The PSD for Goody23400w and Rackl419848f can be seen in Figure 3 and Figure 4, respectively, along with the semi-empirical model predictions for the same flow conditions. From visual inspection of Figure 3, it is not apparent which model best describes Goody23400w. However, it can be seen by looking at the MSE that the Goody model has the lowest MSE with 1.3 closely followed by the Smol’yakov model with 8.9, while the Efimtsov and Rackl and Weston models perform poorly. For the Rackl1419848f, the Rackl and Weston model has the lowest MSE, followed by the Efimtsov model, while the Goody and Smol’yakov models perform poorly, as seen in Figure 4.

The MSE of the PSD between each model and experiment is shown in Appendix B in

Table A2. Experiment variables continued.

Experiments	v (×${10}^5$)	M	U	${\mathit{u}}_{\mathit{t}}$	q	${\mathit{\tau }}_{\mathit{w}}$	${\mathit{d}}^{+}$	${\mathit{C}}_{\mathit{f}}$
Goody7300w	1.69	0.08	27.1	0.98	399	1.04	29.5	0.0026
Goody23400w	1.66	0.09	31.3	1.03	543	1.17	31.5	0.0022
Blake8200w	1.58	0.07	22.3	0.85	286.6	0.84	43	0.0029
Blake10200w	1.63	0.08	28.8	1.06	462.4	1.27	51	0.0027
Blake13200w	1.67	0.11	37.9	1.33	785.8	1.93	63	0.0025
Gravante2953w	1.54	0.02	7.2	0.29	30.8	0.1	6	0.0033
Gravante4972w	1.58	0.05	15.7	0.58	142.5	0.39	12.1	0.0031
Gravante6241	1.56	0.05	15.7	0.57	144.2	0.38	11.9	0.0029
Gravante7076w	1.51	0.04	15.3	0.57	141.1	1.16	11.9	0.0028
McGrath7010w	1.56	0.07	22.3	0.84	295	0.83	27.3	0.0027
McGrath18820w	1.63	0.09	32.5	1.09	597.2	1.35	35.5	0.0023
Farabee3386w	1.49	0.05	15.5	0.62	146.9	0.48	33	0.0033
Farabee4487w	1.49	0.06	21.3	0.83	278.5	0.85	44	0.0031
Farabee6025w	1.47	0.08	28.3	1.07	496.9	1.43	57	0.0029
Schewe1400w	1.51	0.02	6.3	0.28	24	0.09	19	0.004
Blitterswyck1866w	1.41	0.02	7.6	0.34	37.4	0.15	12.1	0.004
Blitterswyck2546w	1.43	0.03	10.4	0.44	69	0.25	15.4	0.0038
Rackl419848f	2.21	0.74	237.2	6.62	20,713.1	32.26	559.7	0.0016
Rackl617153f	2.21	0.74	237.2	6.38	20,713.1	30	539.8	0.0014
Rackl823168f	2.21	0.74	237.2	6.21	20,713.1	28.43	525.5	0.0014
Rocha239216f	2.72	0.56	174.2	5.18	8631.4	15.27	95.1	0.0019
Rocha151407f	3.44	0.7	210.4	6.3	9435.3	16.92	91.6	0.002
Rocha92037f	5.42	0.8	236.1	7.29	15,859.1	13.93	67.2	0.0021
Miller12933w	1.45	0.11	35.8	1.32	764.3	2.08	71.9	0.0025
Miller28562w	1.5	0.29	99.8	3.41	5951.6	13.91	179.8	0.0022
Miller44899w	1.5	0.51	174.7	5.75	18,244.6	39.47	302.8	0.002
Salze1642w	1.55	0.03	11	0.48	71.2	0.27	15.5	0.0038
Salze5962w	1.56	0.11	36	1.35	759.7	2.14	43.4	0.0028
Salze10687w	1.52	0.17	59	2.05	2093.7	5.06	67.6	0.0024

. The MSE of the PSD at different frequency ranges is also included in Appendix A to show how the models performed in certain ranges.

Table A3. Spectrum mean squared error.

Experiments	Efmitsov	Goody	Goody*	Lagnelli	Lowson	Robertson	Rackl and Weston	Smolyakov
Goody7300w	115.7	15.9	143	53.8	47.5	67.8	93	4.3
Goody23400w	74.9	3	97.5	27.3	114.1	28.1	60.3	4.1
Blake8200w	140.5	35.6	177.7	77.7	43.7	94.8	116	17.6
Blake10200w	131.9	34.4	176	77.3	66	104.7	111	16.2
Blake13200w	98.6	19.4	142.1	56	80.8	82	81	6.8
Gravante2953w	136.1	33.4	191.8	46	13	46.7	126.2	9.4
Gravante4972w	77.9	6.7	102.6	37.8	21.9	51	64.7	4.7
Gravante6241	70.3	7	95.6	27.7	19.7	39.2	58.6	5.7
Gravante7076w	21	20.6	22	24.9	99.5	30.3	8.8	61.7
McGrath7010w	86.7	12.1	114.3	65.7	96.2	102.1	83	10.3
McGrath18820w	93.2	10.4	114.6	69.3	102.7	104.9	87.3	7.6
Farabee3386w	216.3	16.9	124.5	184.3	199.3	275.8	205.4	101.6
Farabee4487w	203.5	14.9	111.4	175.2	184.2	262.6	187.7	116.7
Farabee6025w	201.5	7.6	82.5	184.7	215.7	281.3	190.4	141
Schewe1400w	56.6	5	103.7	20.9	19.1	27.7	61.1	6.8
Blitterswyck1866w	99.7	20.3	134.4	58.1	26.9	59.2	89.8	12.3
Blitterswyck2546w	101.6	28.7	147.4	52.2	31.5	55.4	93.1	22.3
Rackl419848f	8.1	117.1	12.2	234.1	41	25.8	7.5	201.1
Rackl617153f	6.5	98	8.9	467	71.8	33.3	5.4	148.5
Rackl823168f	8.7	102.3	9.1	781.3	99.7	33.9	6.8	137.4
Rocha239216f	4.5	27.4	9.9	5.7	20.2	18.7	5.6	37
Rocha151407f	4.4	71.5	0.6	21.1	3.6	7.3	2.4	93.3
Rocha92037f	16.1	110.3	6.4	56.1	4.1	8.8	11.4	145.5
Miller12933w	65.9	3.9	102	53.7	71.3	68.1	70.6	1.5
Miller28562w	60.4	1.8	83.1	87.9	123.8	138.9	62.6	19.8
Miller44899w	60.5	1.5	65.3	98.8	138.2	170.3	59.2	52.6
Salze1642w	66.2	9.1	121.7	22.8	20.6	27.8	62.9	5.2
Salze5962w	61.2	4.9	104.8	27	38.2	42.6	47.3	10.9
Salze10687w	61.7	5.9	105	29.1	45.1	44.8	45.4	12.1
Averages	81	29.2	93.4	107.7	71	80.5	72.6	48.7

is the MSE for the low-frequency range,

Table A4. Spectrum mean squared error for the low frequency range.

Experiments	Efimtsov	Goody	Lagnelli	Lowson	Robertson	Rackl and Weston	Smolyakov
McGrath7010w	321.2	69	347.3	424	534	320.7	21.6
McGrath18820w	295.3	47.6	360.8	439.6	552.8	294.8	26.8
Farabee3386w	401.5	5.8	382	459	584.9	401.4	234.5
Farabee4487w	365.9	1	361.2	435.3	557.7	365.7	287.8
Farabee6025w	396.1	3.3	406.3	483.7	612.4	395.9	331.4
Miller44899w	78.2	7.3	129.1	172.9	255.9	75.8	213.9

is the medium frequency range,

Table A5. Spectrum mean squared error for the medium frequency range.

Experiments	Efimtsov	Goody	Lagnelli	Lowson	Robertson	Rackl and Weston	Smolyakov
Goody7300w	48	1.9	52	76.9	58	72.5	2
Goody23400w	25.7	0.8	50.5	79.8	72.7	36.4	6.3
Blake8200w	54.1	5.9	53.9	83.9	81.9	67.6	0.7
Blake10200w	76	12.2	86.5	125	143.5	80.3	3.3
Blake13200w	74.4	9.9	98.5	139	152.5	80.5	2.1
Gravante2953w	53.9	4.6	35.6	56.5	37.1	93.8	0.5
Gravante4972w	27.3	1.3	23.7	43.9	41.8	40.7	10.9
Gravante6241	18.9	1.3	18.3	36.5	34.6	30.4	13
Gravante7076w	4.9	52.1	3.5	0	1	4.1	151
McGrath7010w	68.2	9.1	77.8	112.6	137.6	73.2	15.8
McGrath18820w	77.9	9.1	109.3	151.2	186.3	80.4	15.7
Farabee3386w	61.1	4.5	50.5	79.7	99.2	70.4	40.1
Farabee4487w	57.2	3.3	53.4	84.3	106.1	63.5	42.7
Farabee6025w	57.2	2.2	59.7	92.3	118.4	61.1	49.6
Schewe1400w	38	3.1	16.9	34.8	34.2	57.7	11.5
Blitterswyck1866w	16	0.4	3	11.7	6.9	35.4	16
Blitterswyck2546w	19.7	0.2	7.4	20.5	20.8	31.1	21
Rackl419848f	12.2	134.2	20.9	11.3	21.8	11.9	301.9
Rackl617153f	11.8	111	59	30	38.8	11.5	226.9
Rackl823168f	17.8	122.2	153	31.5	35.7	17.5	217.1
Rocha239216f	2	30.8	7.9	27.1	31.1	1.7	52.1
Rocha151407f	5.7	72.8	6.9	4.6	8.5	3.4	107.9
Rocha92037f	20.7	117.3	31.2	3	5.4	15.5	171.4
Miller12933w	55.7	5.2	69.8	104.5	111.5	61.2	1.7
Miller28562w	64.4	2.4	100.2	141	173.9	62	28
Miller44899w	60.1	0.9	100.8	140.4	173.6	57.2	39.8
Salze1642w	39	3.9	16.6	34.5	34.6	54.8	10.7
Salze5962w	50.6	4	42.6	70.5	88.2	49.9	27.8
Salze10687w	47	2	47.1	76.3	101.1	40.9	36.6

is the overlap range, and

Table A6. Spectrum mean squared error for the overlap frequency range.

Experiments	Efimtsov	Goody	Lagnelli	Lowson	Robertson	Rackl and Weston	Smolyakov
Goody7300w	86.7	5.3	48.3	49.3	34.3	98.8	3.3
Goody23400w	85.4	3.3	32.7	46.5	27.4	84.7	1.2
Blake8200w	63.5	2.2	28.2	33.2	21.3	73.2	0.4
Blake10200w	75.5	4	36	39.4	28.3	80.8	1.3
Blake13200w	75.3	1.8	19.6	25.3	16	63	1.2
Gravante2953w	77.5	6.2	25.9	28	16.6	96.4	2.2
Gravante4972w	46.1	0.5	11.6	13.5	6.9	53.8	0.9
Gravante6241	45.5	0.5	9.3	10.6	5.2	50.3	1.6
Gravante7076w	0.7	42.8	17.3	32.2	25.8	0.8	59.5
McGrath7010w	55.9	0.8	25.4	31.6	17.9	68.5	0.2
McGrath18820w	83.4	4.6	30.8	42.6	26.1	81.5	0.6
Farabee3386w	59.8	1.1	8.7	5.7	3.2	54.7	0.1
Farabee4487w	56.7	0.8	13.6	15.3	8.4	55.2	0.2
Farabee6025w	56	0.4	11.3	15.6	7.4	46.2	1.4
Schewe1400w	40.2	0.7	8.3	14.6	4	63.4	0.3
Blitterswyck1866w	24.5	0.2	2.1	6.1	0.8	41.6	4
Blitterswyck2546w	44.7	1	8.8	13.1	4.1	57.7	0.3
Rackl419848f	4.1	99.9	447.3	70.6	29.7	3.2	100.2
Rackl617153f	2.5	88.5	766.1	102.4	29.2	0.9	91
Rackl823168f	3.8	91.7	1114	135.7	33	1.2	95.2
Rocha239216f	7.3	23.6	3.3	12.5	4.9	9.9	20.2
Rocha151407f	1.6	68.7	51.9	1.5	4.7	0.2	61.7
Rocha92037f	6.3	95.3	110	6.6	16.2	2.3	89.5
Miller12933w	75.1	2.8	39.2	41.5	29	79.1	1.3
Miller28562w	51.3	0.6	59.2	83.6	57.3	64.1	0.9
Miller44899w	46.1	0	51.9	85.5	56.2	60.3	0.4
Salze1642w	47.6	2	9.6	15.2	4.7	60.2	0
Salze5962w	56.6	2.5	24.3	33.9	20.4	57.6	0.4
Salze10687w	57.8	2.3	29.8	41	27.4	52.7	0.9

is the high-frequency range.

Except for Goody, the PSD compared in this report does not provide an accurate prediction of the low-frequency range. The low-frequency range is a difficult range for experiments to capture due to noise from the fan and structural vibration leading to a contamination of the data. An increase seen in the pressure spectrum below 10 Hz can also be the result of pressure fluctuations from the irrotational motion of the flow above the boundary layer [24]. Farabee and Casarella had a significant amount of experimental data in the low-frequency range and were used in the creation of the Goody model [19].

The mid-frequency range and the overlap frequency range are well predicted and have a low MSE between the models and the experiments. This can be attributed to this being the range where the majority of data points were taken during experiments and therefore used in the creation of the models.

The high-frequency range is a function of the inner variables of the boundary layer and should be scaled based on the viscosity as the inner region is dominated by viscous forces. The difficulty in this region is that frequency attenuation is problematic for obtaining reliable data. Focusing on Gravante, Schewe, Blitterswyck and Salze1642w as the studies with the smallest $d^{+}$, the MSE is much smaller when compared to each model, and the Goody and Smol’yakov models have the lowest MSE. This is expected as Schewe demonstrated how a larger $d^{+}$ causes a steeper roll-off of the high-frequency response [22].

The results show that the models proposed by Efimtsov [14] and Rackl and Weston [15] both performed well when compared to the flight test PSD measurements, but poorly when compared to the PSD measured in wind tunnel experiments. Furthermore, when comparing against all the different data sets, the model proposed by Rackl and Weston consistently outperforms the model by Efimtsov, which indicates that the changes added to the Efimtsov model by Rackl and Weston better represent the PSD.

The models proposed by Goody [19] and Smol’ yakov [20] have the lowest MSE when predicting the PSD. However, when compared to the flight test data they did not perform as well. It is worth noting that when Goody and Smol’yakov proposed their respective models they postulated these would be effective even at high Reynolds numbers. This is confirmed from the comparison of their models to the experiments by Miller. Goody and Smol’yakov both predict the shape of the PSD from the flight tests well, with a decay of the overlap region being approximately ${\omega }^{-0.7}$, meaning that an adjustment only needs to be made to the magnitude.

The initial functional form of the Goody model is [19]:

$$\mathsf{\Phi }\left(f\right)=\frac{C_2{\left(2\pi f{\tau }_w\right)}^2{\left(\frac{\delta }{U_{\infty }}\right)}^3}{{({\left(\frac{2\pi f\delta }{U_{\infty }}\right)}^{3/4}+C_1)}^{3.7}+{\left(C_3^{-0.57}\frac{2\pi f\delta }{U_{\infty }}\right)}^7},$$

(28)

with parameters $C_1$, $C_2$, and/or $C_3$ varying with the Reynolds number. $C_1$ and $C_3$ determine the slope of the low and high frequency ranges, respectively, and also determine the size of the overlap region. $C_2$ acts as a multiplicative constant that increases the spectral levels at all frequencies so that the model better agrees with experimental data. Goody used the values $C_1=0.5$, $C_2=3.0$ and $C_3=1.1R_T^{-0.57}$ to agree with a selection of wind tunnel experiments.

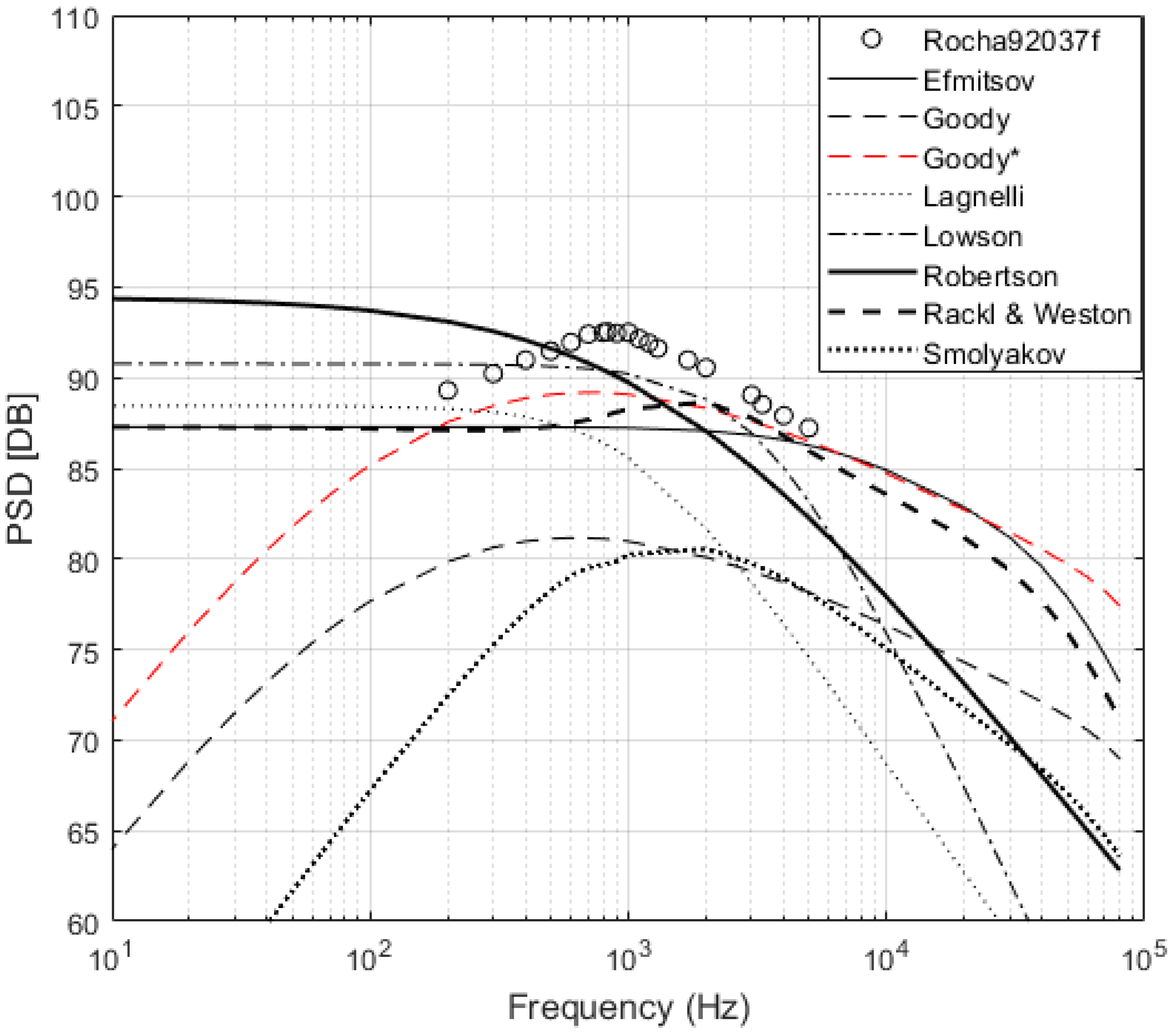
To update the Goody model to fit the flight test pressure spectra data in this study, the parameters were modified to $C_1=0.55$ and $C_2=21$, as displayed in red in Figure 4, Figure 5 and Figure 6. These values provide a local minimum for the MSE between the Goody model and the flight test experiments, the results of which are comparable to Efimtsov and Rackl and Weston. To create a universal model for flight test PSD, a $C_2$ parameter that scales effectively would be desirable. Goody suggested that $C_2$ should scale on the Reynolds number; however, Goody predicted Miller44899w well but not Rocha239216f, which has a similar Reynolds number. The adjusted Goody model does well predicting the magnitude and the shape of the pressure spectra for the four flight test experiments that are near Mach 0.7, as can be seen in Figure 4 and Figure 5. However, the adjusted Goody model overpredicts Rocha239216f, which is at a lower Mach number, and underpredicts Rocha92037f, which is at a higher Mach number, as shown in Figure 6. This suggests that a $C_2$ scaling parameter should include a velocity component as well. Other possible scaling parameters are the shear velocity and momentum thickness, given that the flight test data display much higher values for these parameters than the wind tunnel PSD data. However, currently there are not enough variety in high-speed and flight test PSD experiments to define a clear trend.

The findings from this study support that future work needs to be undertaken to improve current wall pressure fluctuation PSD prediction. Further high-speed wind tunnel and flight test experiments should be undertaken to better determine what factors cause the appearance of a broadband peak, and also to improve the understanding of the differences between wind tunnel and flight test experiments.

4. Conclusions

Existing semi-empirical models have been compared with experimental flight tests and wind tunnel data to better understand what methods of prediction are effective for determining the wall pressure fluctuation PSD. The MSE of the PSD between semi-empirical models and experimental data has been proposed as a comparison method since it provides insight into the effectiveness of the existing models. It was found that existing flight test and wind tunnel data do not collapse with each other for the same scaling values, and the best models for predicting the PSD for flight test and wind tunnel experiments are not the same. Goody or Smol’yakov are more accurate for the prediction of wind tunnel results or the for the validation of wind tunnel results. Rackl and Weston are more accurate for the prediction of in-flight PSD. This study also shows that Goody could be altered to better predict flight test PSD; however, a universal scaling parameter still needs to be found. Further high-speed wind tunnel testing is required to better represent the results measured from flight tests and to improve the prediction of existing wall pressure fluctuation PSD models. The authors are in the process of performing wind tunnel testing to better understand the inaccuracies of existing semi-empirical models and to improve the accuracy of PSD predictions.