Numerical Simulation of Pressure Fluctuation near an Expansion Corner in a Supersonic Flow of M = 3.01

Abstract

The influence of the expansion corner on pressure fluctuation is an important subject in supersonic flow around high-speed vehicles. Past studies have clarified how the expansion corner alters the root-mean-square of the fluctuating pressure coefficient ($C{p}_{rms}$) and the power spectral density (PSD) without considering how these fluctuating properties are related to compressible waves. In this paper, we use characteristics to determine the direction of wave propagation and identified three zones—U-zone, M-zone and D-zone—within which both $C{p}_{rms}$ and PSD are likely to display different behaviors across the boundary layer. The U-zone is upstream of the characteristic line of the second family and passing through the corner. The D-zone is downstream of the characteristic line of the first family and passing through the corner. The middle zone lies between the U-zone and D-zone. The results of $C{p}_{rms}$ and PSD at different layers within the boundary layer are obtained using numerical computation through a Detached Eddy Simulation (DES). It is found that in the U-zone and D-zone, both $C{p}_{rms}$ and PSD are the same in different layers within the boundary layer. In the M-zone, however, both $C{p}_{rms}$ and PSD may vary in different layers and this variation occurs in the high-frequency band upstream of the corner and mid-frequency band downstream of the corner. A feedback mechanism is tentatively used to explain the difference of spatial distribution of fluctuation properties inside the M-zone.

1. Introduction

The fluctuating pressure acting on the surface of the vehicle induces structural vibration, which may cause damage to the aircraft structure and a strong noise environment that affects the normal operation of airborne instruments, including the reliability and safety of weapons and equipment [1]. The intensity of the pressure fluctuations is commonly characterized by the root-mean-square fluctuating pressure coefficient ($C{p}_{rms}$), Power Spectral Density (PSD) and correlation coefficient [2]. Pressure fluctuation beneath a supersonic turbulent boundary layer (c.f. S. Beresh and J. Henfling and R. Spillers and B. Pruett [2]) may be amplified by shock–boundary layer interaction (c.f. M. Holden [3], H. Babinsky and J. Harvey [4]) and altered by geometry, such as forward step (V.Bibko and B. Efimtsov and V. Kuznetsov [5]) and expansion corners (c.f. [6]). Here in this paper, we consider pressure fluctuations due to expansion corners, which are typical geometric configurations that change the local flow properties, leading to the formation of a complex fluctuating environment [6]. This topic has received a number of studies.

Fluctuating pressure for subsonic flow around expansion corners has been studied experimentally by J. Robertson [7], who measured the surface fluctuating pressure in the vicinity of the expansion corner and found that the peak of the fluctuating pressure exists at the reattachment point, and this point moves backwards when the Mach number increases. Moreover, the fluctuating pressure of the expansion corner has been studied analytically by K. Plotkin and J. Roberson [6] based on the experimental data on the wall, and they found the relationship between the $C{p}_{rms}$ and the local Mach number of the separated flow caused by several expansion corners (cone-cylinder, back step, etc.). They found that the $C{p}_{rms}$ is closely related to the local Mach number and that the fluctuating pressure is stronger at low Mach numbers and decreases at high Mach numbers. Later, X. Ligong and L. Zhenhuan [8] also used the same formula to predict the $C{p}_{rms}$ at the expansion corner, he took the characteristic length as the displacement thickness of the local boundary layer and obtained results that are more consistent with the previous experiment. Furthermore, the surface pressure fluctuations of subsonic turbulent flow downstream of small expansion corners were found to be normally distributed through the expansion process but were severely attenuated [9]. In addition, the fluctuating pressure on an expansion corner has been investigated numerically using the Detached Eddy Simulation (DES) method by S. Deck and P. Thorigny [10]. They focused on the surface fluctuating pressure statistical properties and found that the spectral analysis of the pressure fluctuations has shown different frequency contributions depending on the location considered in the recirculation bubble. Close to the expansion corner, the spectrum displays a peak near a normalized frequency, which has been shown to represent the footprint of the vertical motion of the bubble.

Fluctuating pressure for transonic flow around expansion corners has been studied experimentally by D. Depres and P. Reijasse and J. Dussauge [11]. The experiments have been carried out to investigate the unsteady fluctuating surface-pressure field on afterbodies of revolution at transonic speeds with a freestream Mach number 0.85, and it was found that the spectra of fluctuating pressure in the whole region exhibit a well-defined periodicity that corresponds to the formation of large-scale structures in the wake, and when the shear layer reattaches near the end of the protruding wall, the rms pressure fluctuations reach their maximum value. Moreover, Z. Rui, R. Jili and R. Fang [12] used the large eddy simulation (LES) method to simulate the structure of a typical expansion corner numerically, and they recorded data on how pressure changes over time on the surface. Additionally, they found that the fluctuating pressure in the turbulent boundary layer, separation zone and other flow structures changes significantly with space; the fluctuating pressure in the separation zone is generally higher than the turbulent boundary layer; and the separation reaction on the shock wave will cause a stronger fluctuating pressure environment and shock waves to self-oscillate [13]. Then, based on previous experimental data, they provided an empirical formula for the $PSD$ of the fluctuating pressure of the expansion-reflection separation flow. Combining the calculation results of LES, they introduced spatial-related information based on the empirical formula published by K. Plotkin and J. Roberson [6], which improved the prediction accuracy of engineering algorithms for fluctuating pressure [14].

Fluctuating pressure for supersonic flow around expansion corners has been studied experimentally by C. Kungming and F. Lu [9]. In this work, surface pressure fluctuations of Mach 8 turbulent flow past a 2.5- and a 4.25-deg expansion corner maintained a Gaussian distribution but were severely attenuated by the expansion process. The pressure fluctuations did not recover to those of an equilibrium turbulent flow even though the mean pressure reached downstream inviscid values in four to six boundary-layer thicknesses. The fluctuations were convected with a velocity comparable to that on a flat plate, and they maintained their identities longer for the stronger expansion. The damping of pressure fluctuations at hypersonic Mach numbers, even by small corner angles, may be exploited in fatigue design. Moreover, fluctuating pressure near expansion corners has been studied experimentally by J. Dawson and M. Samimy [15], wherein multipoint wall pressure measurements were used to investigate the response of a Mach 3.01, fully developed, compressible, turbulent boundary layer to centered and gradual expansions of both 7- and 14-deg deflection. Furthermore, they found that although rms fluctuation levels decrease across the expansions, the rms normalized by the local static pressure remains nominally constant. Just downstream of the expansions, normalized power spectra are more concentrated at low frequencies than upstream, suggesting small-scale turbulence is quenched. This spectra alteration is more prominent for centered expansions and larger deflections. The spectra evolve very quickly after the centered expansions and very slowly after the gradual expansions. In the area near the expansion corner, there are separation points and reattachment points, a shock wave will appear at each location, and the fluctuating pressure environment will be more complicated [16].

K. Plotkin and J. Roberson [6] analyzed the typical subsonic, transonic and supersonic flow field and its fluctuating pressure of the reentry body with two shapes: cone-cylinder and cone-cylinder-skirt. They pointed out that at subsonic speeds, fluctuating pressure is caused by the appearance of the separation zone, and at transonic speeds, the airflow behind the cone-cylinder shoulder may reach supersonic speed, and shock waves will induce the separation of the boundary layer and cause strong fluctuating pressure. At supersonic speeds, there is a certain degree of separation after the expansion corner, and the fluctuating pressure environment will be more complicated.

Past studies have focused on fluctuating pressure on the surface. Here in this paper, we consider the spatial distribution of fluctuation properties in the vicinity of the expansion corner when the flow is supersonic. The problem we will use is the experimental model of J. Dawson and M. Samimy [15]. In Section 2, we will give the details of this model and present the method we use to obtain the pressure fluctuation properties. We will use characteristic lines to split the region near the corner into three zones—the U-zone, M-zone and D-zone—and study how Cprms and PSD change across the boundary layer in different zones. The description of characteristics and definition of the U-zone, M-zone and D-zone will be given in Section 3. The computed spatial distribution of Cprms and PSD in three zones around the expansion corner is presented in Section 4. The behavior of spatial distribution of fluctuating properties in the three zones will be summarized in Section 5, where we tentatively provide a possible feedback mechanism to explain the observed behavior. The conclusion will be summarized in Section 6.

2. The Expansion Corner Problem and Numerical Method for Simulation

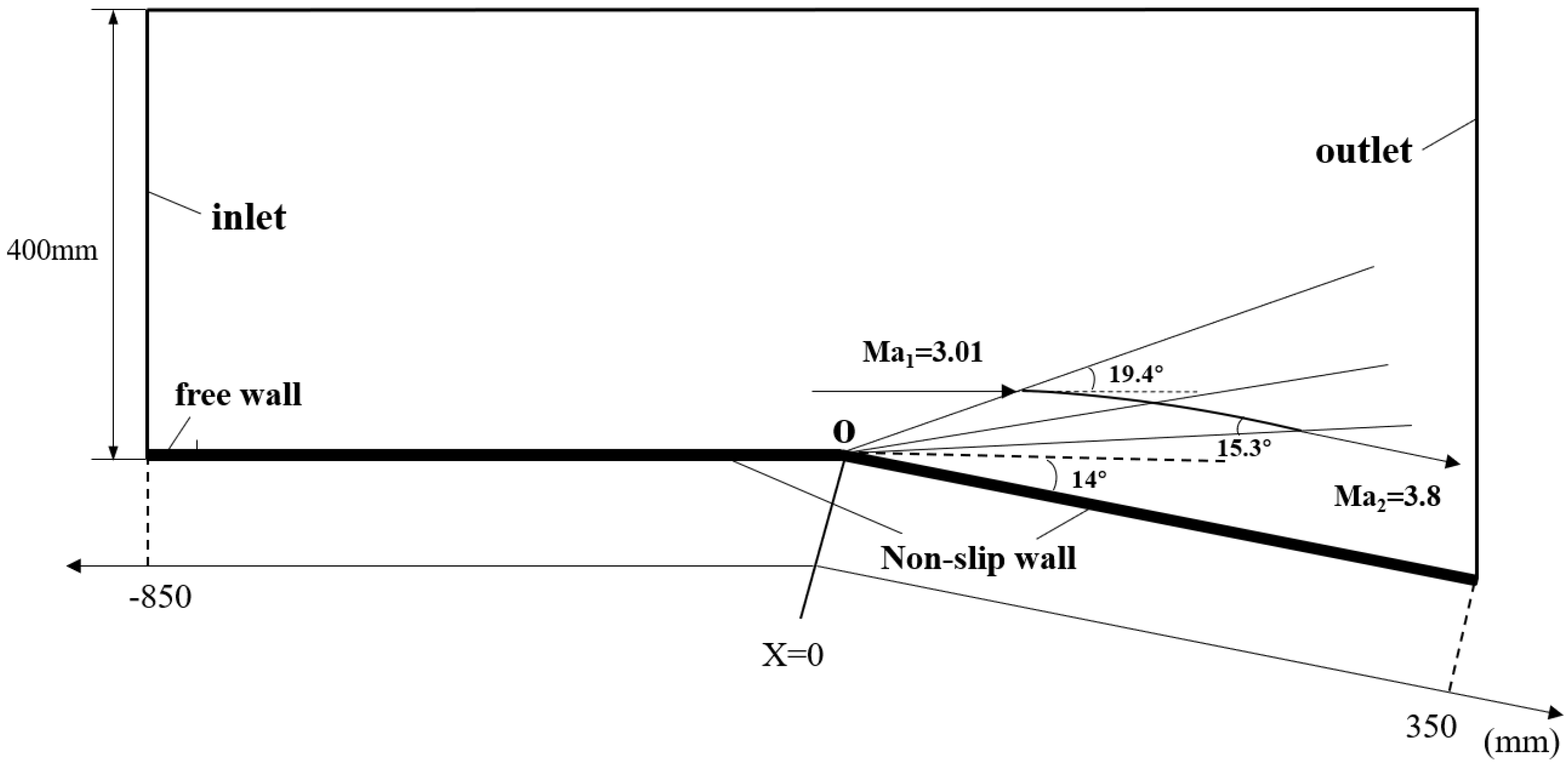
In this paper, the experimental model of J. Dawson and M. Samimy [15], with an expansion of 14 deg, as shown in Figure 1, is used. The upstream flow is supersonic, with a freestream Mach number $M{a}_{\infty }=$$3.01$. The Reynolds number based on the momentum thickness (${\delta }_2=0.37$ mm) is $R{e}_{{\delta }_2}=$ 24,700. The incoming pressure is $p_{\infty }=$ 22 KPa. J. Dawson and M. Samimy [15] measured the normalized rms pressure fluctuations and power spectra on the body surface.

Since we are interested in spatial distribution of the pressure fluctuation properties, we need numerical simulation to obtain these properties. Note that pressure fluctuation for flow around an expansion corner has been considered numerically using Reynolds Averaged Navier–Stokes (e.g., R. Soni and N. Arya and A. De [17]), Detached Eddy Simulation (DES) (e.g., S. Deck and P. Thorigny [10]), large eddy simulation (LES) (e.g., M. Grilli and S. Hickel and N. Adams [18]), and direct numerical simulation (DNS) (e.g., M. Kopera and R. Kerr and H. Blackburn and D. Barkley [19]).

To balance the accuracy and time requirement, we use the well-established DES method, which combines the features of the classical RANS formulations [20] with elements of LES method.

The domain and boundary conditions are shown in Figure 1. The left side is supersonic inlet, and the right boundary is a supersonic exit. The wall has a no-slip condition. A small segment of the free-sliding wall is set at the front edge of the non-slip wall. The calculation results are compared with J. Dawson and M. Samimy [15] in the paper to verify the accuracy and reliability of the CFD calculation method we chose.

The flow equation is solved by means of the second-order-accurate scheme of implicit Roe using finite difference simulation. The time step is fixed to $\Delta t=$$5e^{-7}$ s, which corresponds to ${10}^4$ time steps for one passage of the model at freestream velocity. The freestream turbulent in tensity is $Tu=3\%$, and there are three grids containing 7.5, 10.36 and 23.6 million nodes for computation, respectively. Several grid spaces have been considered in successive refinement to study the influence of the mesh density on the fluctuating pressure of the expansion corner. Based on the results of analysis, a grid of 10.36 million nodes with refinement inside the boundary and near the expansion corner is finally used. The grid has a wall normal resolution $y^{+}$ ~ 0.5 and $x^{+}$ ~ 0.5 in the densified area (similarly as in the work of [21]), and the increasing rate is 1.1. A study on the time independence is performed and the results of fluctuating pressure at four different times are given in Figure 2. In the early stage of the calculation, the PSD keeps changing with time. Until 0.37 s, the PSD does not vary in time. Thus, we will extract the data of 0.45 s.

As displayed in Figure 3, the numerical results of static pressure are comparable with the experimental results of J. Dawson and M. Samimy [15].

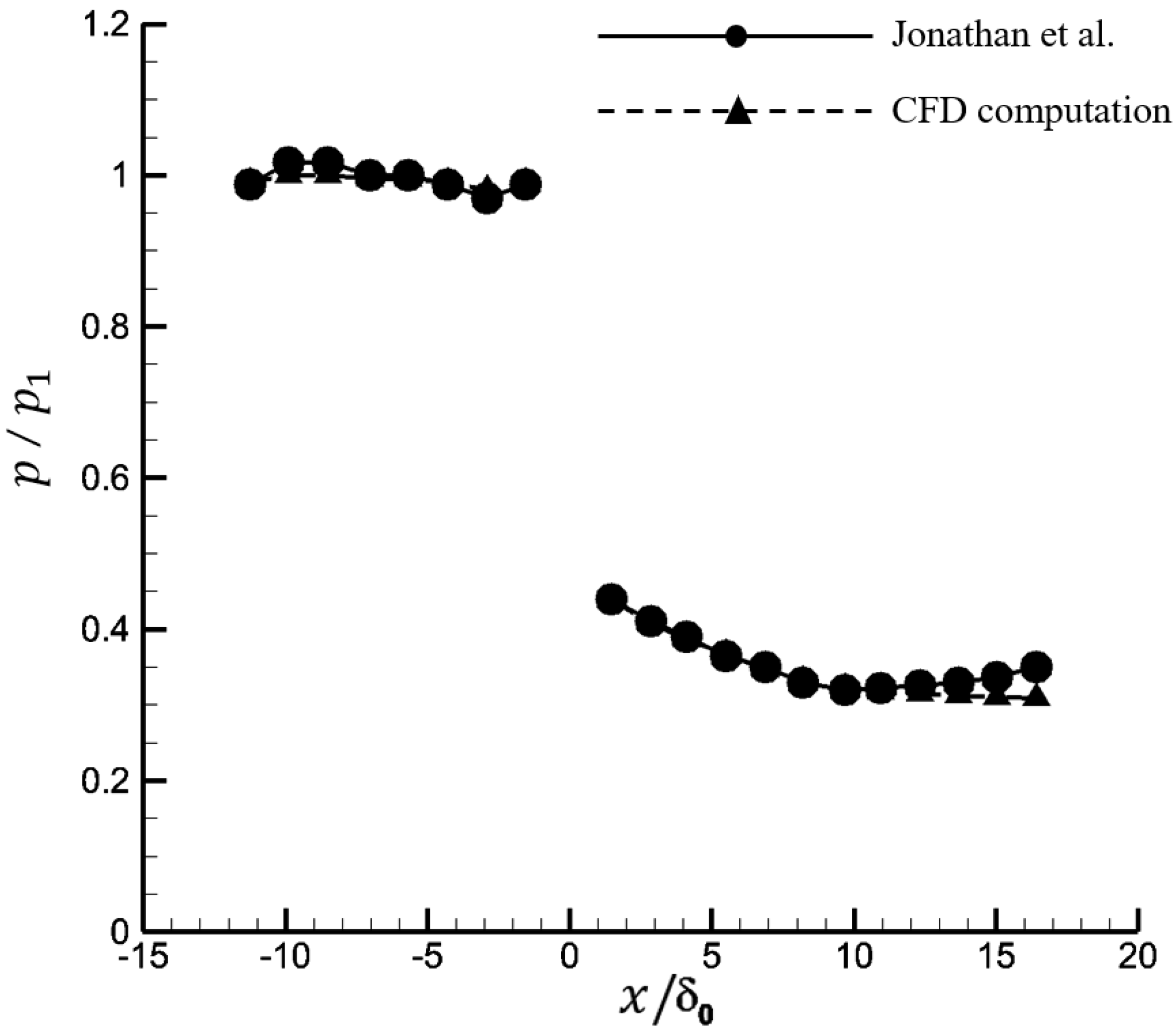
As displayed in Figure 4, the numerical results of the normalized fluctuating pressure on the wall are comparable with the experimental results of J. Dawson and M. Samimy [15]. In Figure 4, x is the position of flow direction, $\sqrt{{\overline{p}}^2}$ is the root-mean-square fluctuating pressure, p is the static pressure, $x/{\delta }_0=0$ is the location of the expansion corner, and the thickness of the boundary layer ${\delta }_0$ at the starting point of the expansion is $9.2$ mm.

Here, we use a Detached Eddy Simulation (DES) to obtain the instantaneous flow field. The instantaneous pressure $p\left(t\right)$ at a given point in the flow field (not just on the body surface) is recorded, and $C{p}_{rms}$ is computed as $C{p}_{rms}=\frac{\sqrt{{\overline{p}}^2}}{0.5{\rho }_{\infty }{U}_{\infty }^2}$, $\sqrt{{\overline{p}}^2}=\sqrt{\frac{1}{T}{\int }_0^T(p\left(t\right)-p_{avg})dt}$, where T is the time interval for sampling, $p_{avg}$ is the average pressure during the entire sampling process, and $\sqrt{{\overline{p}}^2}$ is the root-mean-square (rms) of the pressure fluctuation, which represents the total intensity of pressure. The power spectral density (PSD) (named $\varphi \left(\omega \right)$) is obtained by the Fourier transform of the pressure change in the time domain $\varphi \left(\omega \right)=\frac{1}{T}{\int }_0^{T}p\left(t\right)e^{i\omega t}dt$, where $\omega$ is the frequency (Hz).

3. Characteristics and Definition of U-Zone, M-Zone and D-Zone

Characteristics are well defined for inviscid and isentropic flow. Outside the boundary layer, the flow may be regarded as inviscid and isentropic. For inviscid and isentropic flow, the characteristic line is defined by

$$\frac{dy}{dx}={\displaystyle \frac{1}{\lambda }}$$

(1)

where $\lambda$ is the eigenvalue. For the characteristic line of the first family, $\lambda ={\lambda }_1$, and for characteristic line of the second family, $\lambda =$${\lambda }_2$, where

$$\left\{\begin{array}{c}{\lambda }_1={\displaystyle \frac{uv-a^2\sqrt{M{a}^2-1}}{v^2-a^2}}\hfill \\ {\lambda }_2={\displaystyle \frac{uv+a^2\sqrt{M{a}^2-1}}{v^2-a^2}}\hfill \end{array}\right.$$

(2)

Here, u and v are the local flow velocity components; $Ma$ is the local Mach number; a is the local sound speed.

One way to obtain the characteristic lines is to use the local flow parameters obtained by inviscid CFD and then use Equations (1) and (2) to integrate the characteristic lines. Here, we use the local flow parameters from CFD results and apply Equations (1) and (2) to find the characteristic lines as if the flow is inviscid. Note that inside the boundary layer and very close to the wall, $Ma<1$ so that we have no real values of ${\lambda }_1$ and ${\lambda }_2$. In such regions, we simply extend the characteristic lines to the wall using straight lines.

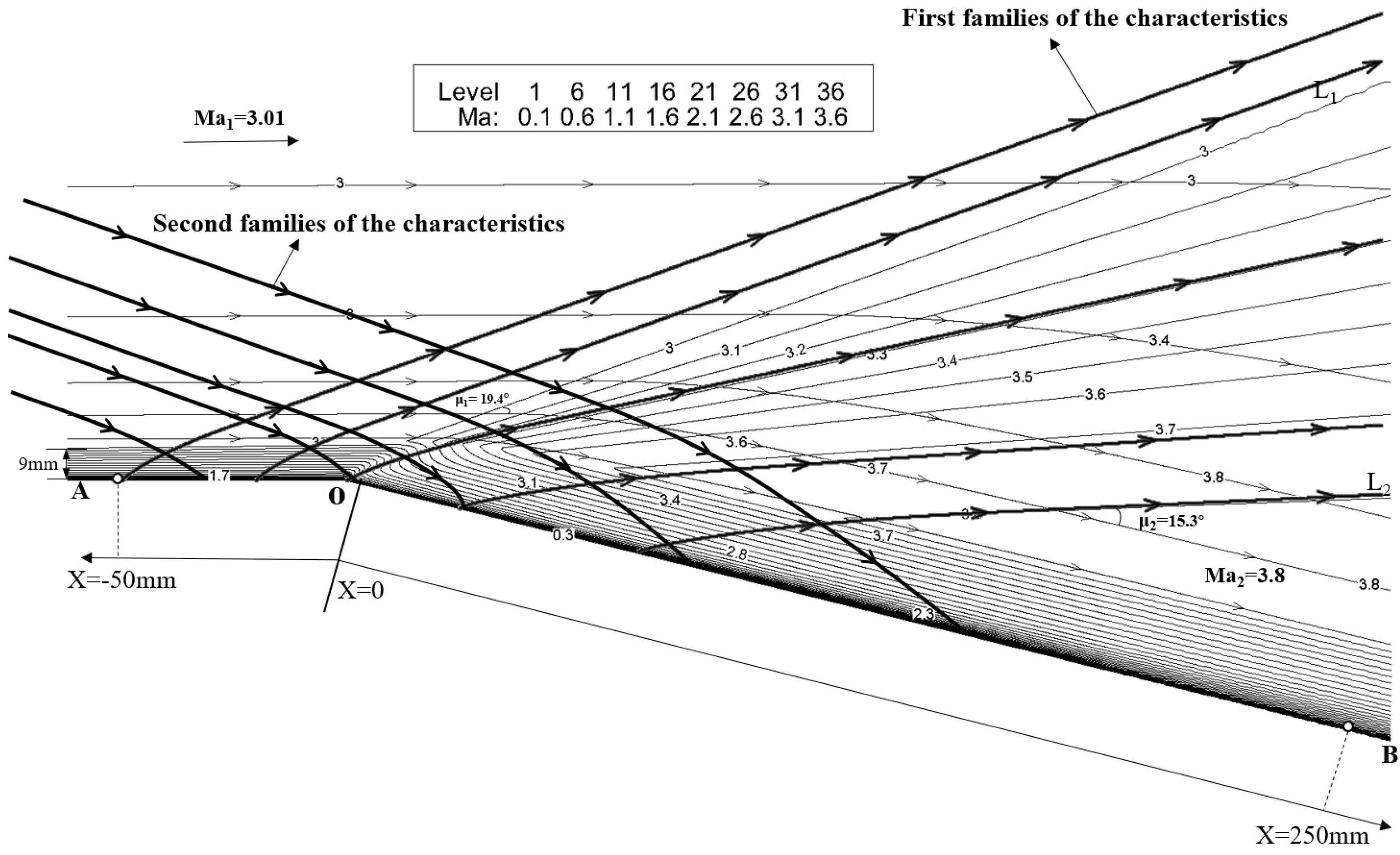
The characteristic lines and Mach contours in the vicinity of the expansion corner are displayed in Figure 5. Not surprisingly, the Mach number is constant along the characteristic line of the second family and connecting the expansion corner.

Now we define three zones using the two characteristic lines of the first and second families connecting the expansion corner O. These two characteristic lines, “$C_U$”and “$C_D$”, are shown in Figure 6. The intersection of $C_U$ and the edge of the boundary layer is denoted by “U”; the intersection of $C_D$ and the edge of the boundary layer are denoted by “D”.

The region near the expansion corner is divided into three zones:

(1)

U-zone is the region upstream of the characteristic line $C_U$.

(2)

M-zone is the region between the characteristic lines $C_U$ and $C_D$.

(3)

D-zone is the region downstream of the characteristic line $C_D$.

In the next section, we will display how $C{p}_{rms}$ and PSD vary across the boundary layer inside these three zones.

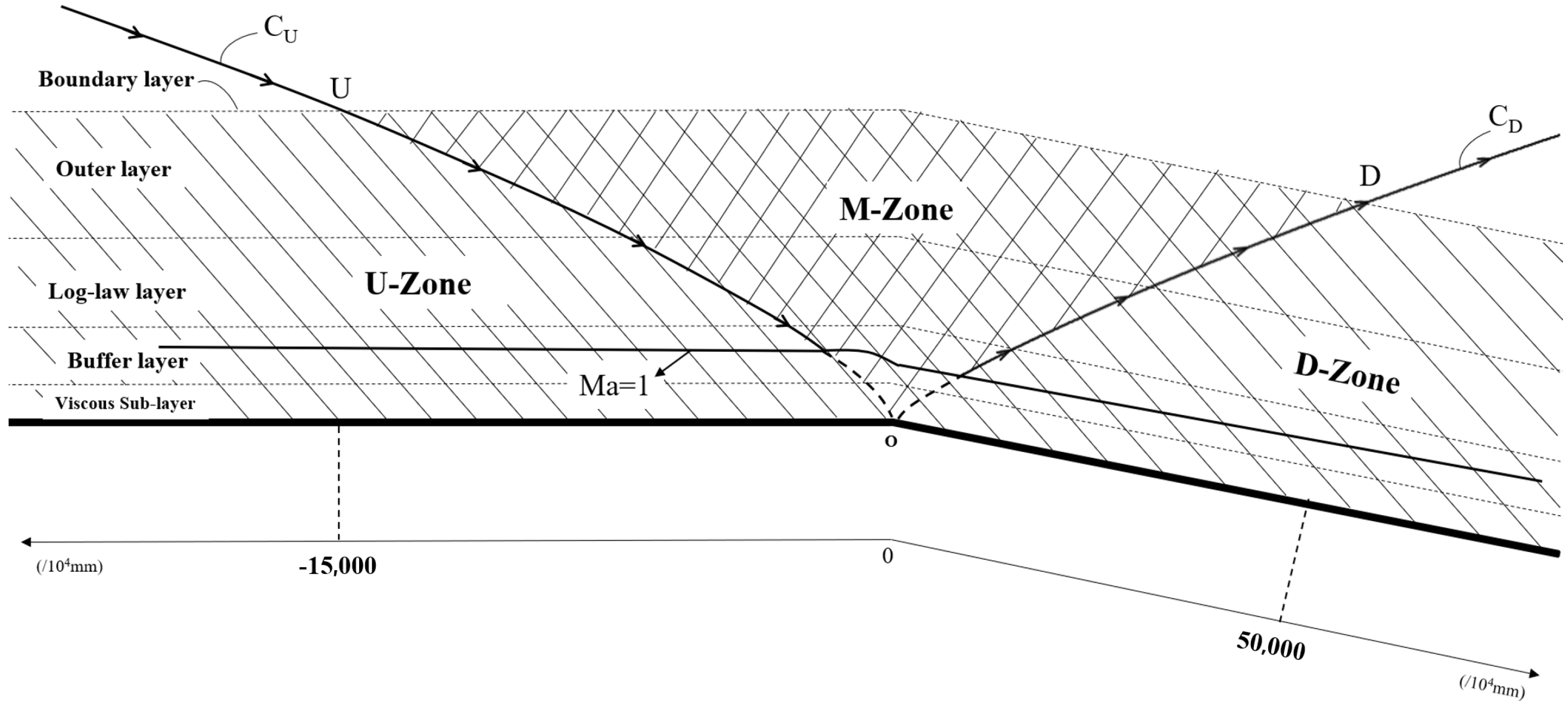
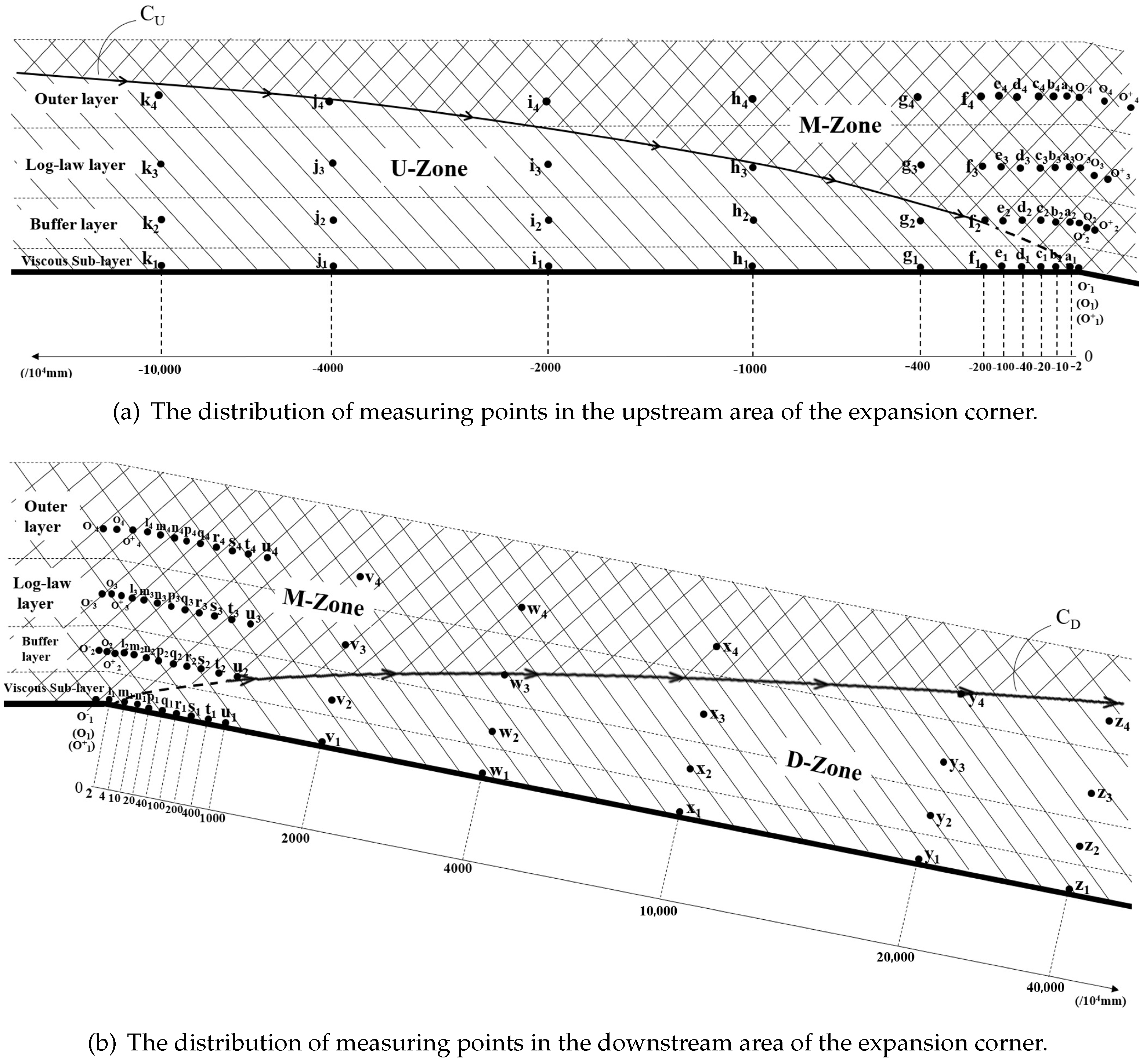
The distribution of the measuring points is shown in Figure 7a,b. Measuring points are evenly distributed in U-zone, D-zone, M-zone, and along the vertical direction of the wall surface. The measuring points are arranged at different layers within the boundary layer in these three zones:

(a)

wall surface, with $y^{+}=0$ and labelled point “1”.

(b)

buffer layer, with $y^{+}\approx 30$ and labelled point “2”.

(c)

log-law layer, with $y^{+}\approx 300$ and labelled point “3”.

(d)

outer layer, with $y^{+}>1000$ and labelled point “4”.

For each layer, position “o” is at the expansion corner, positions “o−”, “a”, “b”, “c”, “d”, “e”, “f”, “g”, “h”, “i”, “j” and “k” are upstream of the expansion corner, and positions “o+”, “l”, “m”, “n”, “o”, “p”, “q”, “r”, “s”, “t”, “u”, “v”, “w”, “x”, “y” and “z” are downstream of the expansion corner. The subscripts $1,2,3$ and 4 for these points correspond to the four layers.

For positions “j” and “k”, all the four layer points ($1,2,3,4$) are upstream of $C_U$ and are inside the U-zone. For positions “y” and “z”, the four layer points ($1,2,3,4$) are downstream of $C_D$ and are inside the D-zone.

Usually, the pressure fluctuation properties on the wall surfaces were considered. Here, we consider these properties at the four different layers. They have the same values at these four layers at a fixed horizontal location in the case of a pure boundary layer. We wonder if they may have different values in the vicinity of the expansion corner, and this will become clear in the next section.

4. The ${\mathbf{Cp}}_{\mathbf{rms}}$ and PSD in the U-Zone, M-Zone and D-Zone

Now we display the pressure fluctuation properties $C{p}_{rms}$ and $PSD$ at the four different layers (wall, buffer layer, log-law layer and outer layer) in the U-zone, M-zone and D-zone.

4.1. The Distribution of $C{p}_{rms}$ in Various Zones

The distribution of $C{p}_{rms}$ at the four layers are displayed in Figure 8. The abscissa in Figure 8 corresponds to the different positions in Figure 7a,b. The ordinate corresponds to the value of $C{p}_{rms}$. The four curves correspond to the four layers.

Looking at the positions of the points, as shown in Figure 7a,b, we observe that for points below the characteristic line $C_U$, i.e., inside the U-zone, the $C{p}_{rms}$ is almost constant in the vertical direction, i.e., they are the same at different layers of the boundary layers. For points below the characteristic line $C_D$, i.e., inside the D-zone, the $C{p}_{rms}$ is almost constant in the vertical direction, i.e., they are the same at different layers of the boundary layers.

In the M-zone, the $C{p}_{rms}$ changes in different layers of the boundary layer. Inside the M-zone, the $C{p}_{rms}$ is the highest in the buffer zone (point “2”) and is the lowermost in the outer layer (point “4”).

In approaching the expansion corner from the upstream along the flow direction, starting from position i for the measuring points that lie between characteristic line “$C_U$” and characteristic line “$C_D$”, the values of $C{p}_{rms}$ began to differ across the vertical direction of the boundary layer, and the difference gradually increased along the flow direction. After the expansion corner, the difference of $C{p}_{rms}$ gradually decreases at different layers in the direction normal to the surface within boundary layer. Until position x, this difference almost shrinks to zero and continues to develop downstream along the flow direction. The values of $C{p}_{rms}$ across the vertical direction of the boundary layer do not change.

4.2. The $PSD$ in Various Zones

The distribution of the $PSD$ at position “d~k” (sufficiently far upstream from the expansion corner) is displayed in Figure 9. For positions k and j, where all the four layer points are inside the U-zone, the curves of the $PSD$ at $y^{+}=0$ (wall surface), $y^{+}=30$ (buffer layer), $y^{+}=300$ (log-law layer) and $y^{+}>1000$ (outer layer) almost overlap; that is, the frequency properties of fluctuating pressure do not change much in the vertical direction within the U-zone. For positions i and h, the values of $PSD$ at $y^{+}>1000$ (outer layer) is lower than other layers in the high-frequency band, while for positions g~d, the values of $PSD$ in the high-frequency band gradually decrease when the distance from the wall surface increases.

The distribution of $PSD$ at positions “c~m” (in the vicinity of the expansion corner) is displayed in Figure 10. For positions c~o−, the $PSD$ in the high-frequency band gradually decreases with the increasing distance from the wall surface. In approaching the expansion corner along the flow direction, the difference of PSD in the high-frequency band gradually increases, and at position o−, this difference reaches the maximum value. In return, along the streamwise direction starting from position o, the $PSD$ becomes to show obvious differences in the mid-frequency band, and with increasing distance from the wall surface, the $PSD$ in the mid-frequency band gradually decreases.

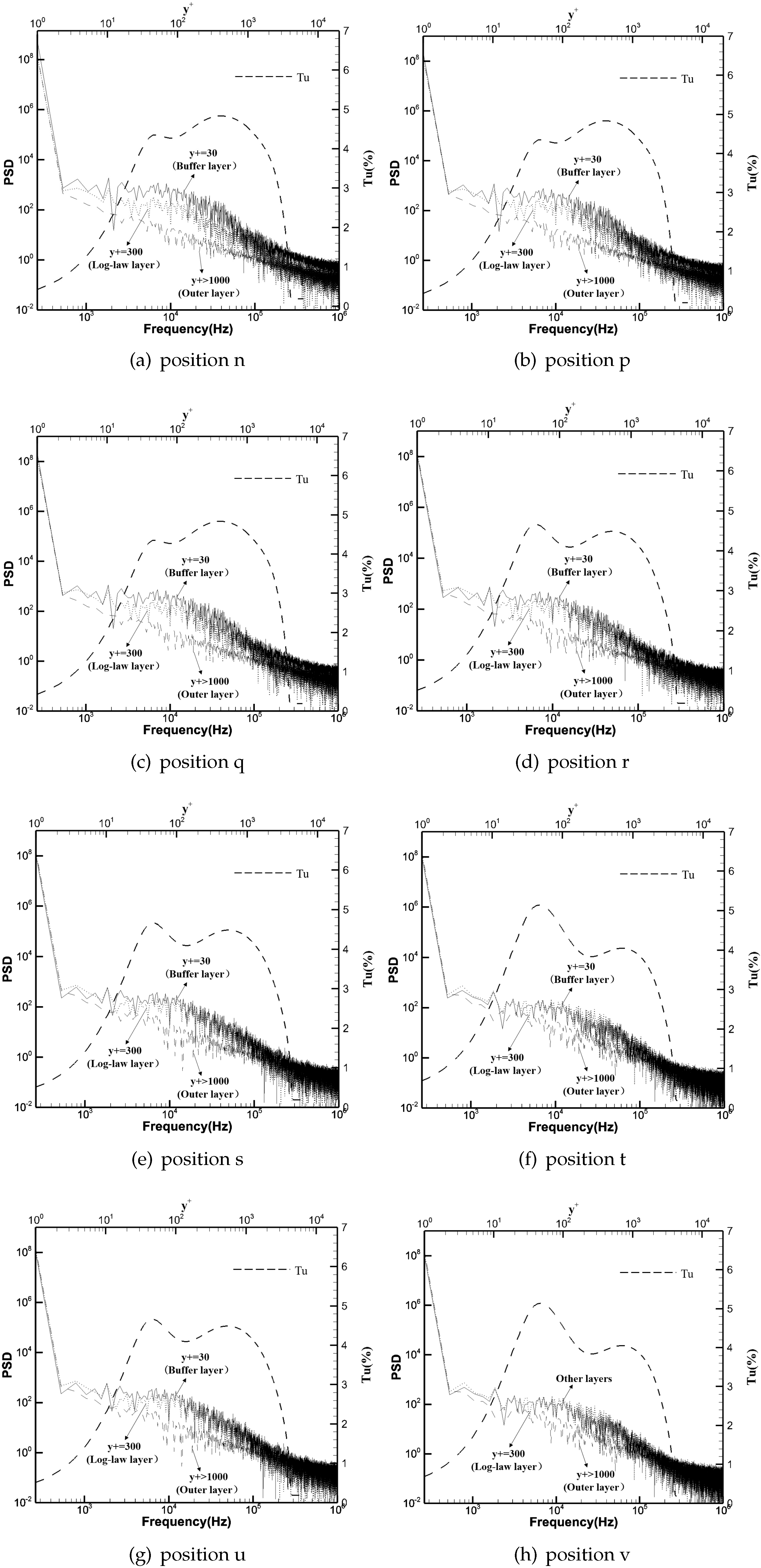
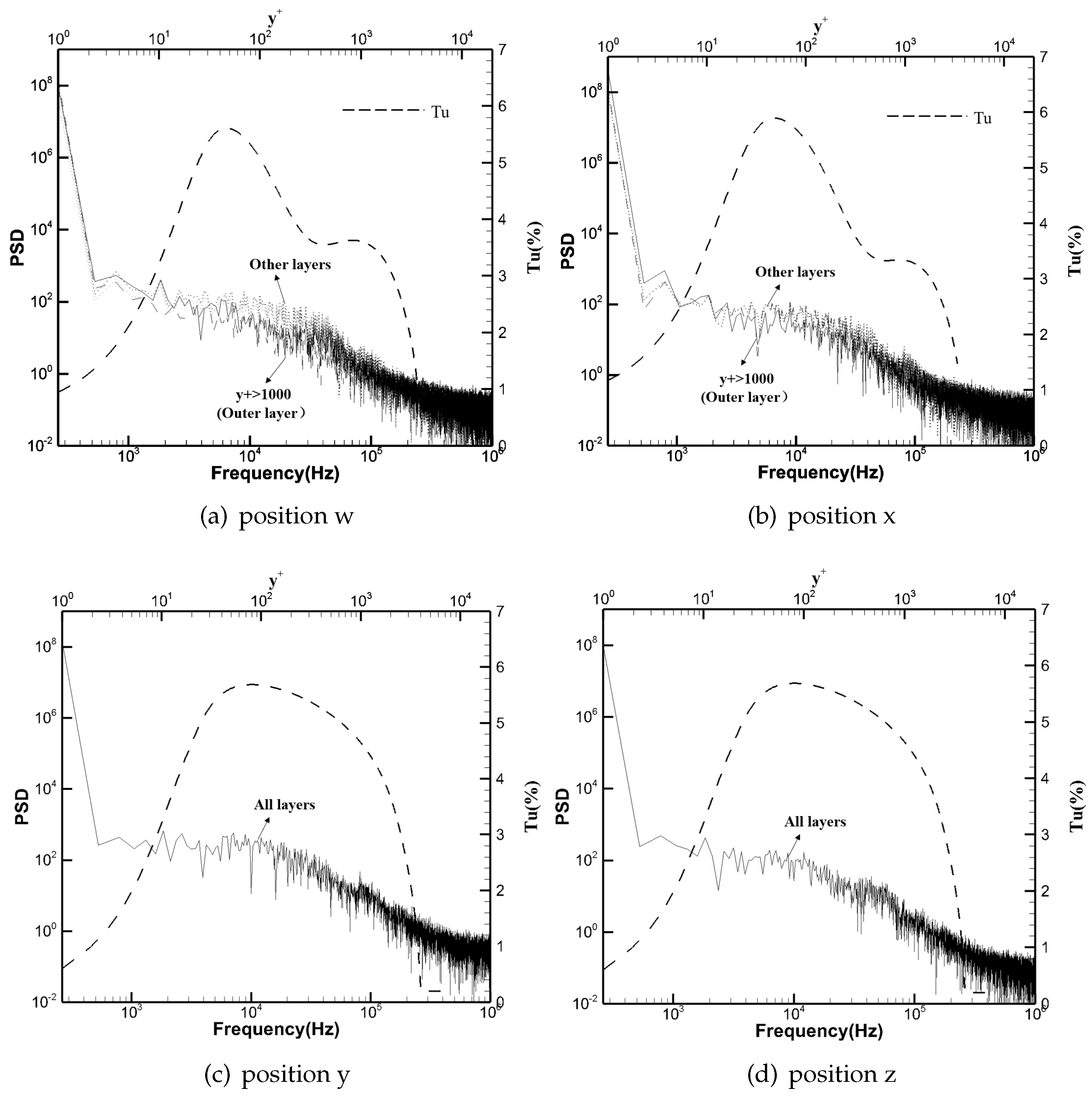
The distribution of $PSD$ at positions “n~v” (sufficiently far downstream from the expansion corner) is displayed in Figure 11 and, at position “w~z”, is displayed in Figure 12. For positions n~z, the $PSD$ in the mid-frequency band gradually decreases with the increasing distance from the wall surface, and in the direction away from the expansion corner, the difference of PSD in the mid-frequency band gradually decreases. For positions y and z, where all the four layer points are inside the D-zone, the curves of $PSD$ at $y^{+}=0$ (wall surface), $y^{+}=30$ (buffer layer), $y^{+}=300$ (log-law layer) and $y^{+}>1000$ (outer layer) almost overlap along the vertical direction of the wall surface within the boundary layer; that is, the frequency properties of fluctuating pressure do not change much in “D-zone”.

5. Summary of Fluctuating Properties and Feedback Mechanism

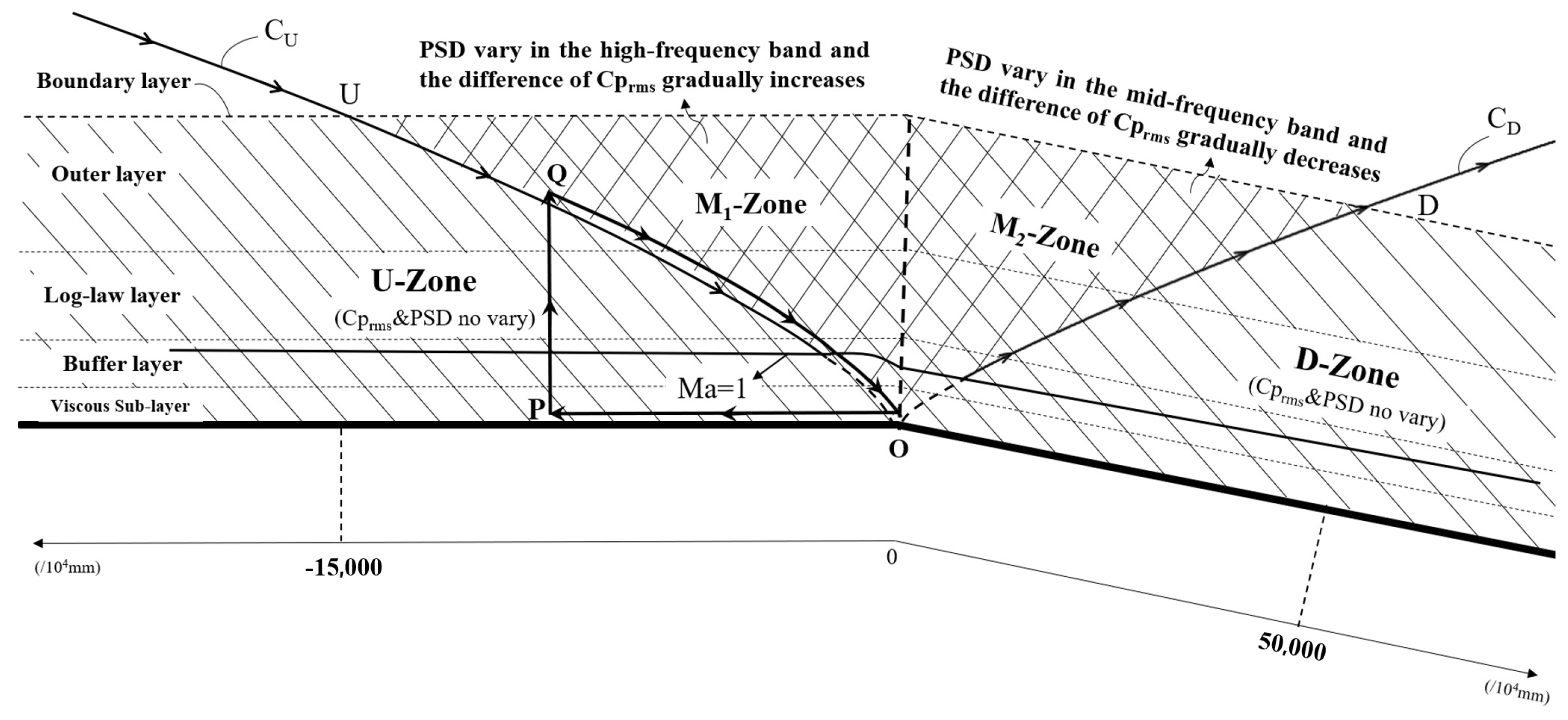
Based on the observation presented in Section 4, we use Figure 13 to summarize the distribution of the fluctuating properties in the vicinity of the expansion corner. There are three zones, U-zone, M-zone and D-zone, as defined in Section 3, using the characteristic lines $C_U$ and $C_D$.

In the U-zone and D-zone, the two key parameters of fluctuating pressure—$C{p}_{rms}$ and $PSD$—are almost constant along the vertical direction of the wall surface within the boundary layer.

The M-zone can be divided into two subzones: M${}_1$ zone is upstream of the expansion corner, and M${}_2$ zone is downstream. The $C{p}_{rms}$ changes significantly along the vertical direction of the wall surface within boundary layer. In the M${}_1$ zone, when approaching the expansion corner, the difference of the $C{p}_{rms}$ gradually increases along the vertical direction of the wall surface, and the PSD varies in the high-frequency band. In the M${}_2$ zone, the difference of $C{p}_{rms}$ in each layer gradually decreases to zero when the distance from the expansion corner becomes large, and the variation of the PSD occurs in the mid-frequency band downstream of the corner. Moreover, in the upstream of the expansion corner, the difference of $PSD$ in the high-frequency band gradually increases when approaching expansion corner and the difference of $PSD$ in mid-frequency band gradually decreases to disappear along the flow direction.

It is desirable to understand why the fluctuation properties have different spatial distributions in the M-zone compared to the U-zone and D-zone. Here, we tentatively provide an explanation. For this purpose, we design a triangle (with one curved side) in Figure 13. Point O of this triangle is near the expansion corner. Point P is upstream so that the side OP lies inside the subsonic region within the boundary layer. The point Q is above and near the characteristic line $C_U$, such that PQ is perpendicular to the wall and the curved side QO is close and parallel to the characteristic line $C_U$.

The expansion corner is supposed to yield a perturbation of the pressure fluctuation, and this perturbation can propagate upstream along $QP$ to the point P since $OP$ is in the subsonic region within the boundary layer (information can propagate upstream in subsonic flow). This perturbation can then propagate to point Q along $PQ$. Since $QO$ is along the propagation direction of the characteristic line $C_U$, the above-mentioned perturbation (originally from the expansion corner) can propagate back to O. This defines a feedback loop, which may explain why the pressure fluctuation properties change inside the M${}_1$-zone compared to that inside the U-zone. The feedback mechanism can be similarly defined to explain the change of fluctuation properties in the M${}_2$-zone compared to that inside the D-zone.

It is also interesting to see the correlation of instantaneous pressure at two different points once these points cross the characteristic line $C_U$ or $C_D$.

The correlation coefficient $r_{AB}$ of the instantaneous pressure at two different points A and B is

$$r_{AB}=\frac{cov(p_A\left(t\right),p_B\left(t\right))}{\sqrt{Var\left[p_A\left(t\right)\right]·Var\left[p_B\left(t\right)\right]}}$$

(3)

where $p_A\left(t\right)$ is the instantaneous pressure at point A; $p_B\left(t\right)$ is the instantaneous pressure at point B; $cov(p_A\left(t\right),p_B\left(t\right))$ is the covariance of $p_A\left(t\right)$ and $p_B\left(t\right)$; $Var\left[p_A\left(t\right)\right]$ is the variance of $p_A\left(t\right)$; and $Var\left[p_B\left(t\right)\right]$ is the variance of $p_B\left(t\right)$.

The points A and B will be both inside zones U, M or D or in different zones among $U,M$ and D. The correlation coefficients computed by Equation (3) are displayed in Figure 14, where three curves are displayed. For the wall surface and buffer layer curve, point A is in the wall layer and point B is in the buffer layer, for the buffer layer and log-law layer curve, point A is in the buffer layer, and point B is in the log-law layer. For the log-law layer and outer layer curve, point A is in the log-law layer, and point B is in the outer layer. The abscissa corresponds to different positions, and the ordinate corresponds to the correlation coefficient.

We observe that, inside the U-zone and D-zone, the correlation coefficient between any two layers is near 1.

If point A is inside the U-zone and point B is inside the M-zone, the correlation coefficient is less than 1. Consider, for instance, position c. At this position, the wall surface is in the “U-zone”, and the buffer layer is in the “M-zone”, so the correlation coefficient between wall surface and buffer layer is 0.96.

If both points are inside the M-zone, the correlation coefficient is much lower than 1. Consider, for instance, position c, the log-law layer and outer layer are in the “M-zone”, so the correlation coefficient between buffer layer and log-law layer is 0.71, and the correlation coefficient between log-law layer and outer layer is 0.62.

If point A is inside the D-zone and point B is inside the M-zone, the correlation coefficient is less than 1. Consider, for instance, position n. At this position, the wall surface is in the “D-zone”, and the buffer layer is in the “M-zone”, so the correlation coefficient between wall surface and buffer layer is 0.94. Moreover, both the log-law layer and outer layer are in the “M-zone”, so the correlation coefficient between buffer layer and log-law layer is 0.45, and the correlation coefficient between log-law layer and outer layer is 0.24.

6. Conclusions

In this work, the fluctuating pressure in the vicinity of the expansion corner in supersonic flow is studied using numerical results from DES simulation. We use characteristics (as if the flow is inviscid and isentropic) to determine the direction of wave propagation and identify three different zones — U-zone, M-zone and D-zone. These zones are bound by the characteristic lines of the first and second families and start from the expansion corner (in an approximative way).

In the U-zone, which is upstream of the upstream characteristic line connecting the expansion corner, both $C{p}_{rms}$ and PSD are almost constant along the vertical direction within the boundary layer, and the correlation coefficient between two vertical points within this zone is close to 1. In the D-zone, which is downstream of the downstream characteristic line connecting the expansion corner, both $C{p}_{rms}$ and PSD are almost constant along the vertical direction within the boundary layer, and the correlation coefficient between two vertical points within this zone is close to 1.

In the “M-zone”, however, the values of $C{p}_{rms}$ differ across the vertical direction of the boundary layer, and the difference gradually increases along the flow direction in regions upstream of the expansion corner. Downstream of the expansion corner, the difference of $C{p}_{rms}$ gradually decreases and almost shrinks to zero finally. Moreover, the variation of PSD occurs in the high-frequency band upstream of the corner and mid-frequency band downstream of the corner. The correlation of $C{p}_{rms}$ between two points with at least one point inside the M-zone is less than 1.

A feedback mechanism is tentatively used to explain the difference of spatial distribution of fluctuation properties inside the M-zone: the change of fluctuation properties by the expansion corner can propagate upstream from the subsonic region inside the boundary layer and then propagate vertically to the M-zone, where this perturbation can be brought back to the expansion corner.