Fluid–Structure Interaction Simulation of a Coriolis Mass Flowmeter Using a Lattice Boltzmann Method
Abstract
1. Introduction
2. Methodology
2.1. Fluid Domain
2.1.1. Navier–Stokes Equations
2.1.2. Lattice Boltzmann Method
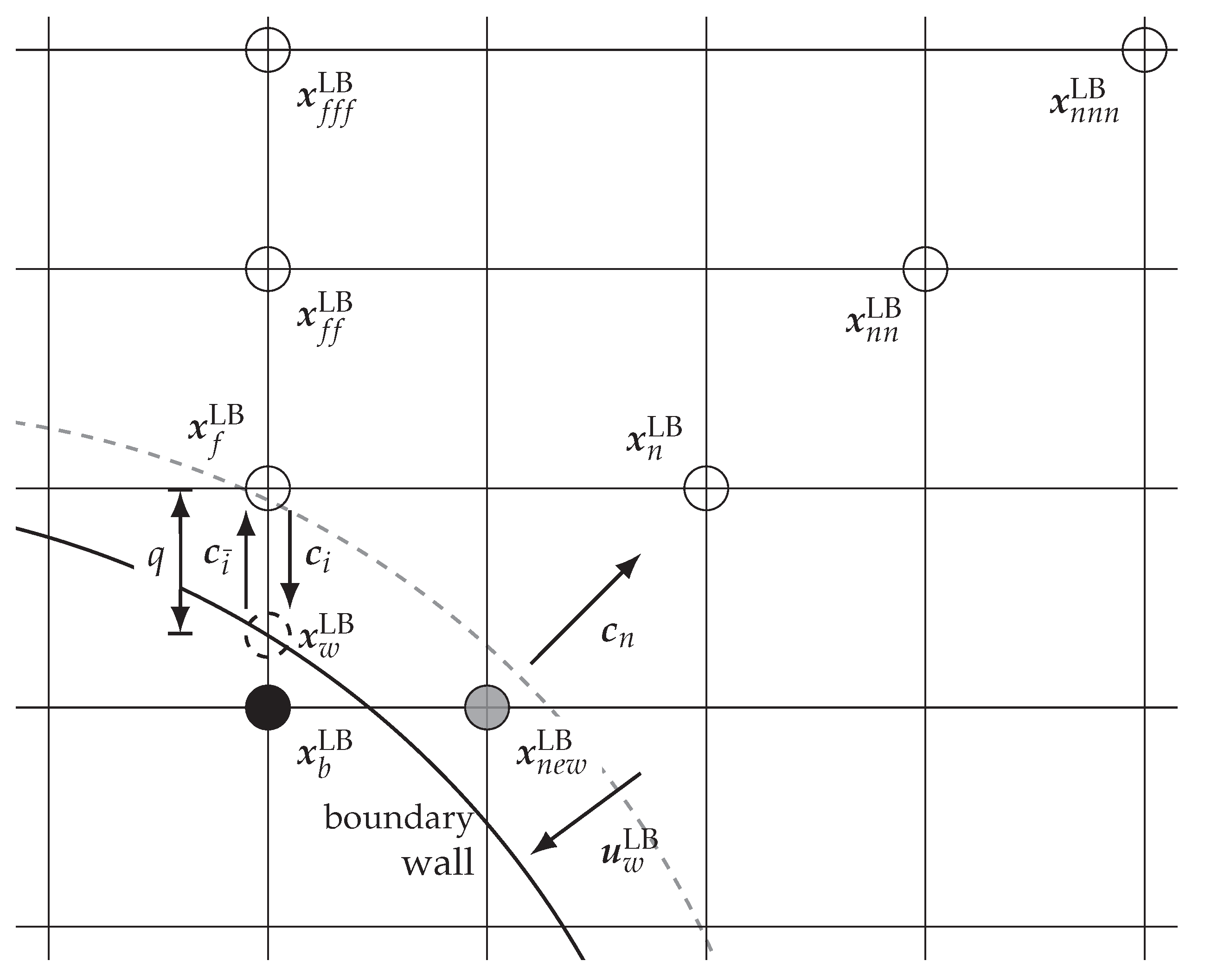
2.1.3. Moving Boundary Methods
2.2. Structural Domain
2.2.1. Navier–Cauchy Equation
2.2.2. Direct Methods
2.3. Fluid-Structure Interaction
2.3.1. Coupling Conditions
Kinematic Condition
Dynamic Condition
Geometric Condition
2.3.2. Segregated Approaches
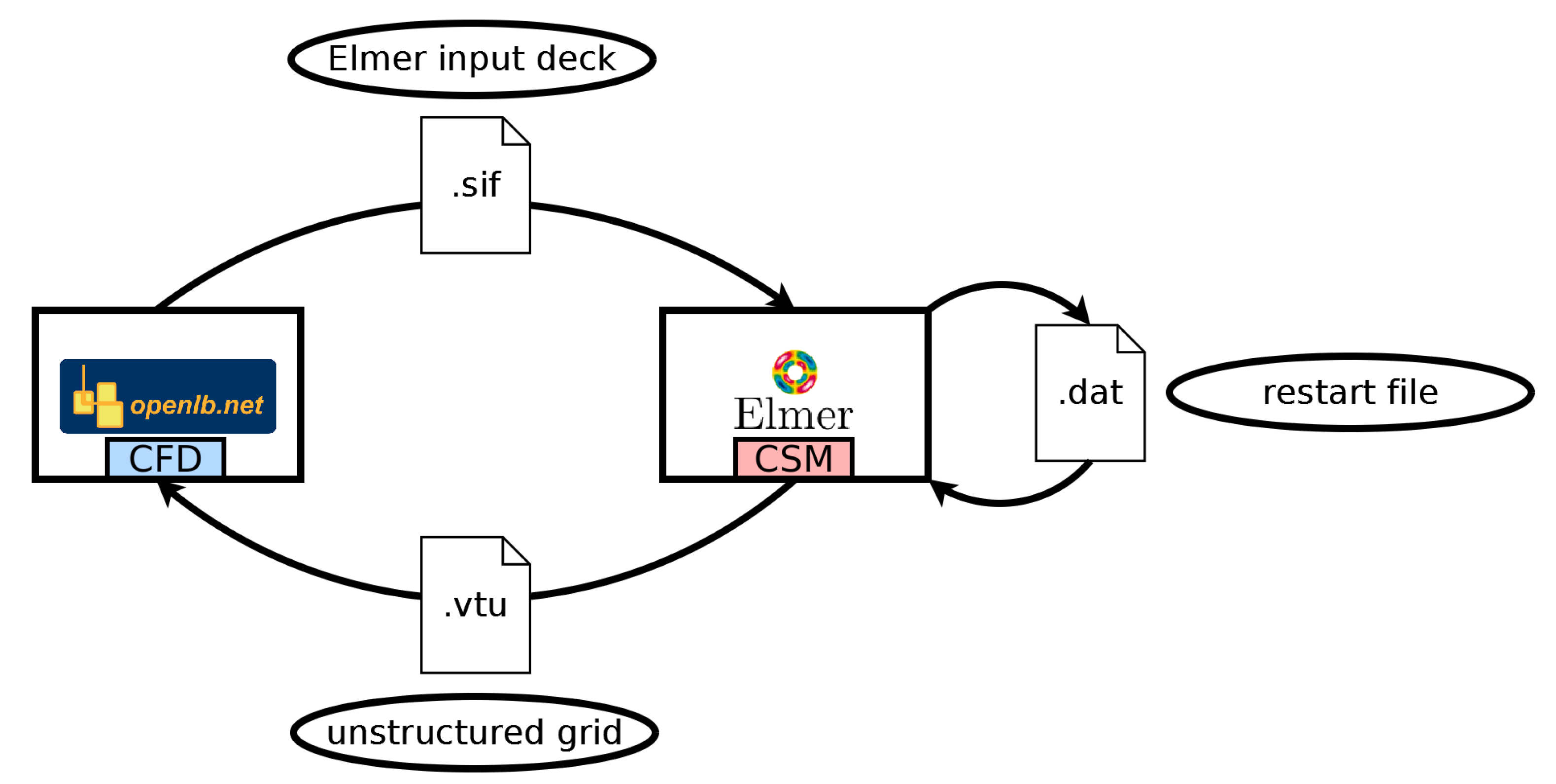
2.3.3. Implementation
- The OpenLB instance calculates the hydrodynamic forces acting on the boundary for each solid node according to Equation (17).
- The hydrodynamic forces are communicated and collected from each worker to the master process.
- The master process maps the collected boundary forces to the finite element grid by integrating the force on each finite element mesh point.
- The mapped boundary forces are written into an Elmer input deck file (.sif).
- Elmer is restarted by the master process using the input deck file (.sif) and a related restart file (.dat).
- The Elmer instance is closed after the displacement velocity and the deformed mesh is written to disk as an unstructured mesh file (.vtu) and a new Elmer restart file (.dat) is created.
- The master process reads the mesh file (.vtu) and uses the built-in OpenLB voxelizer, which decides whether a point is outside or inside the fluid domain and allows the later distance calculation.
- The master process maps the displacement velocity of the FEM grid to the LBM link intersection points by a linear interpolation procedure and distributes the information to each worker process.
- The OpenLB instance reconstructs the particle distribution functions for the fresh nodes by using the extrapolation refill algorithm (see Equation (16)).
- The collide and stream algorithm is executed (see Equation (5)).
- After the streaming step is executed, the unknown particle distribution function is calculated by the curved boundary approach using the mapped displacement velocity (see Equation (15)).
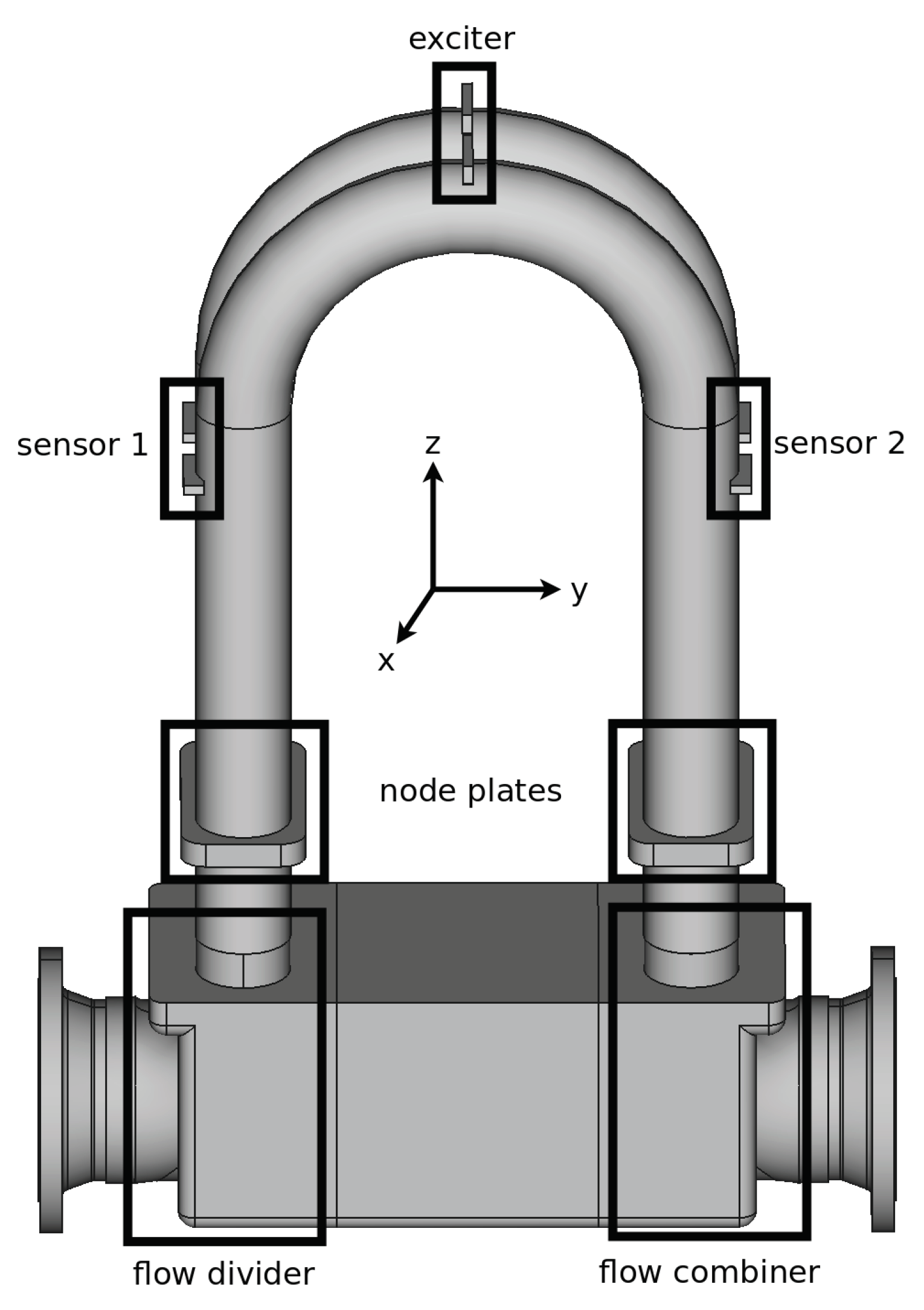
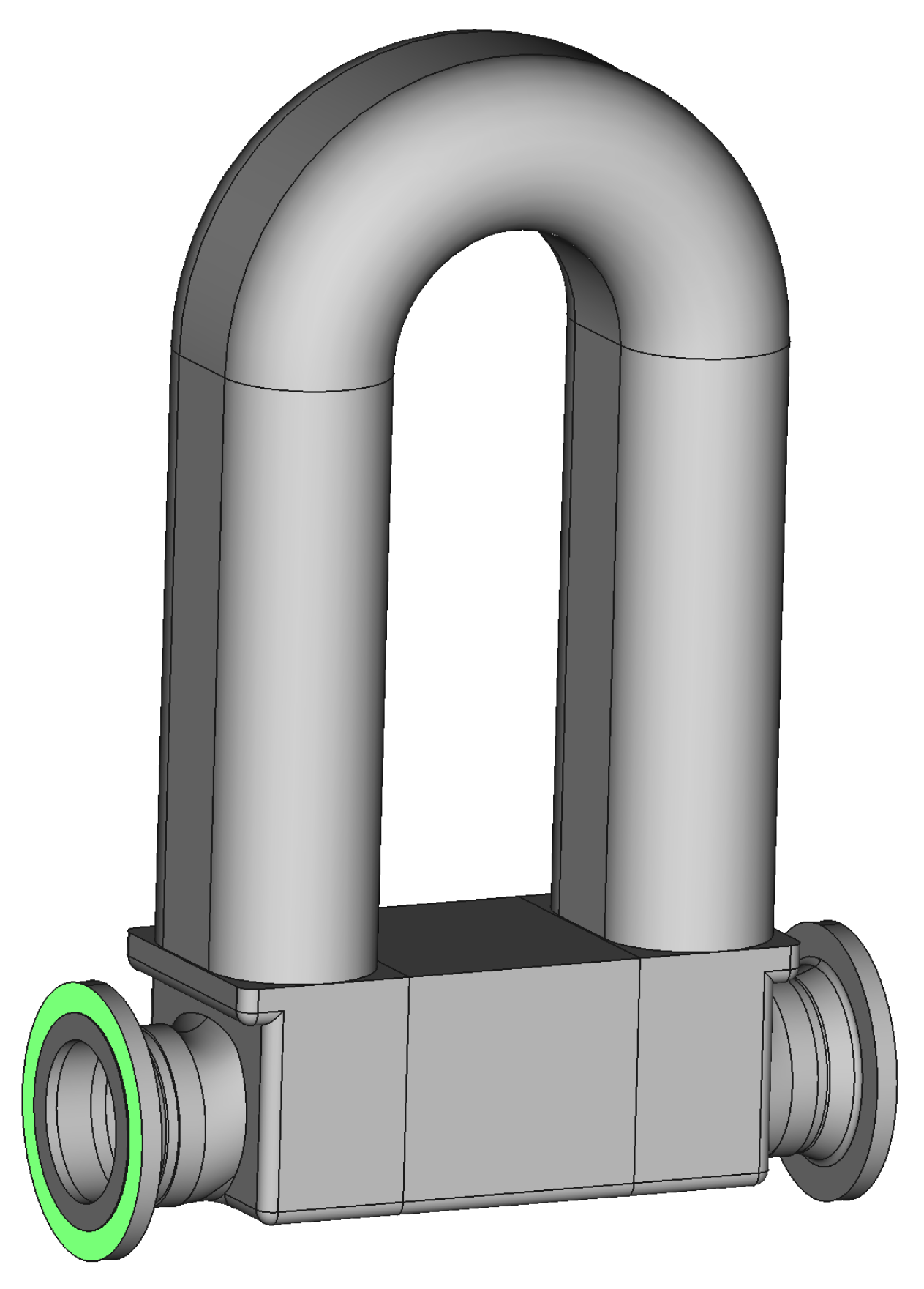
3. Setup of the Coriolis Mass Flowmeter Test Case
3.1. Boundary Conditions and Initial Conditions
3.1.1. Structural Domain
3.1.2. Fluid Domain
3.1.3. Coupling Conditions
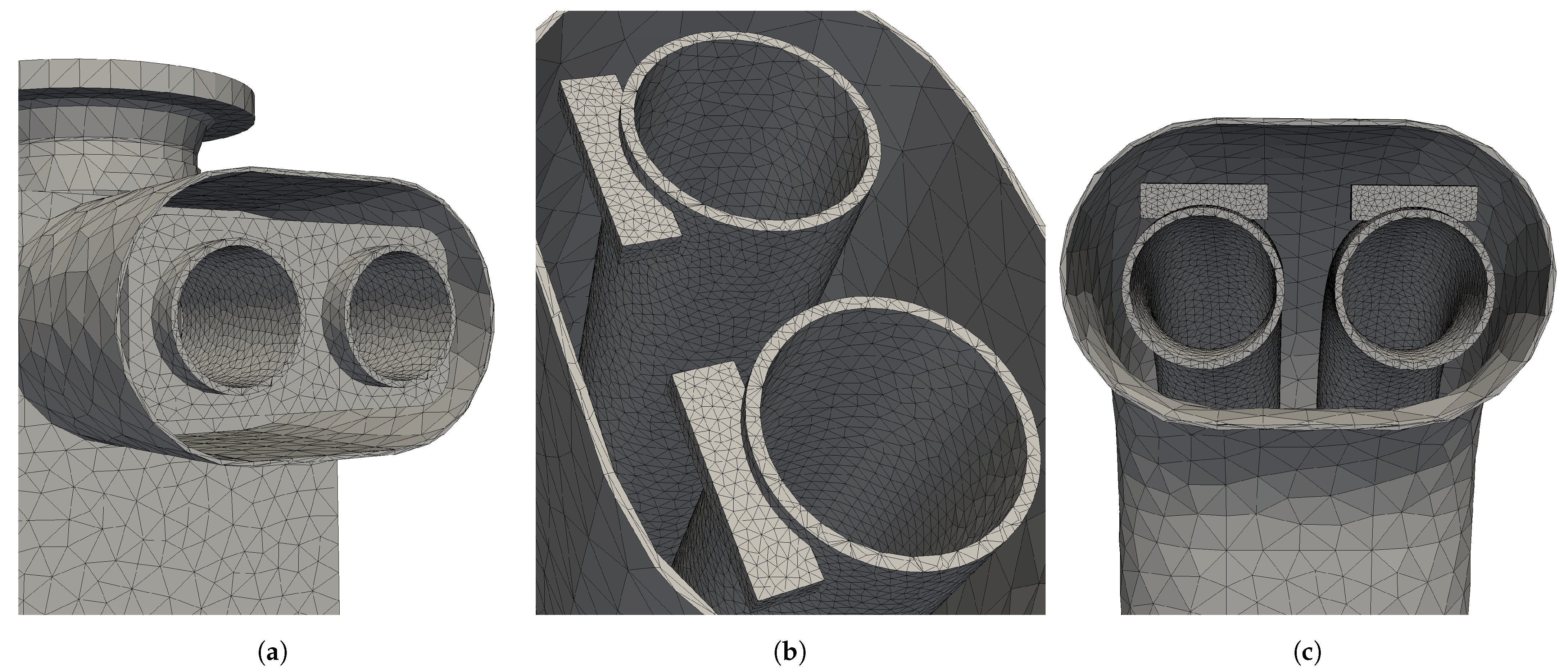
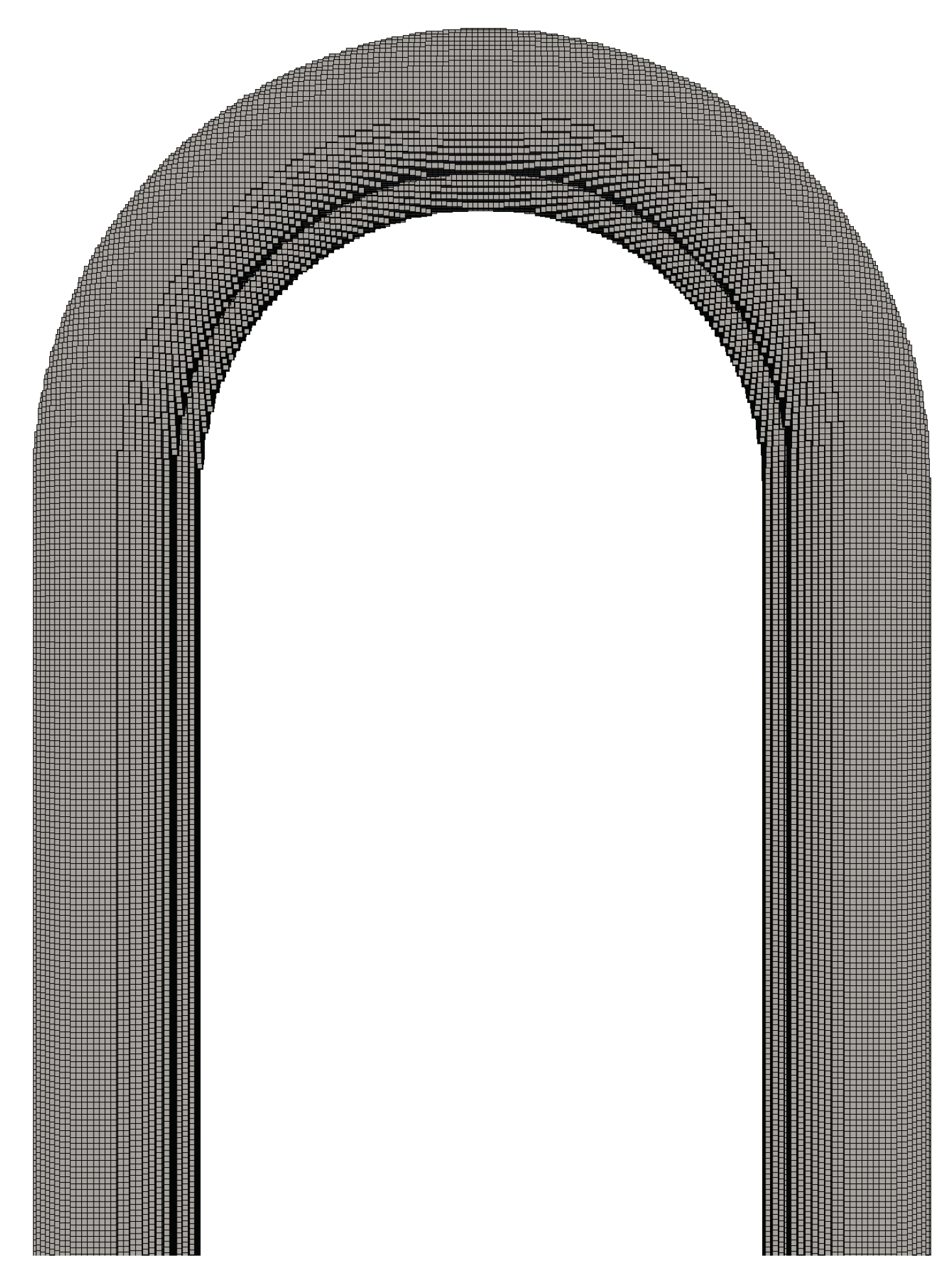
3.2. Mesh Generation
3.2.1. Structural Domain
3.2.2. Fluid Domain
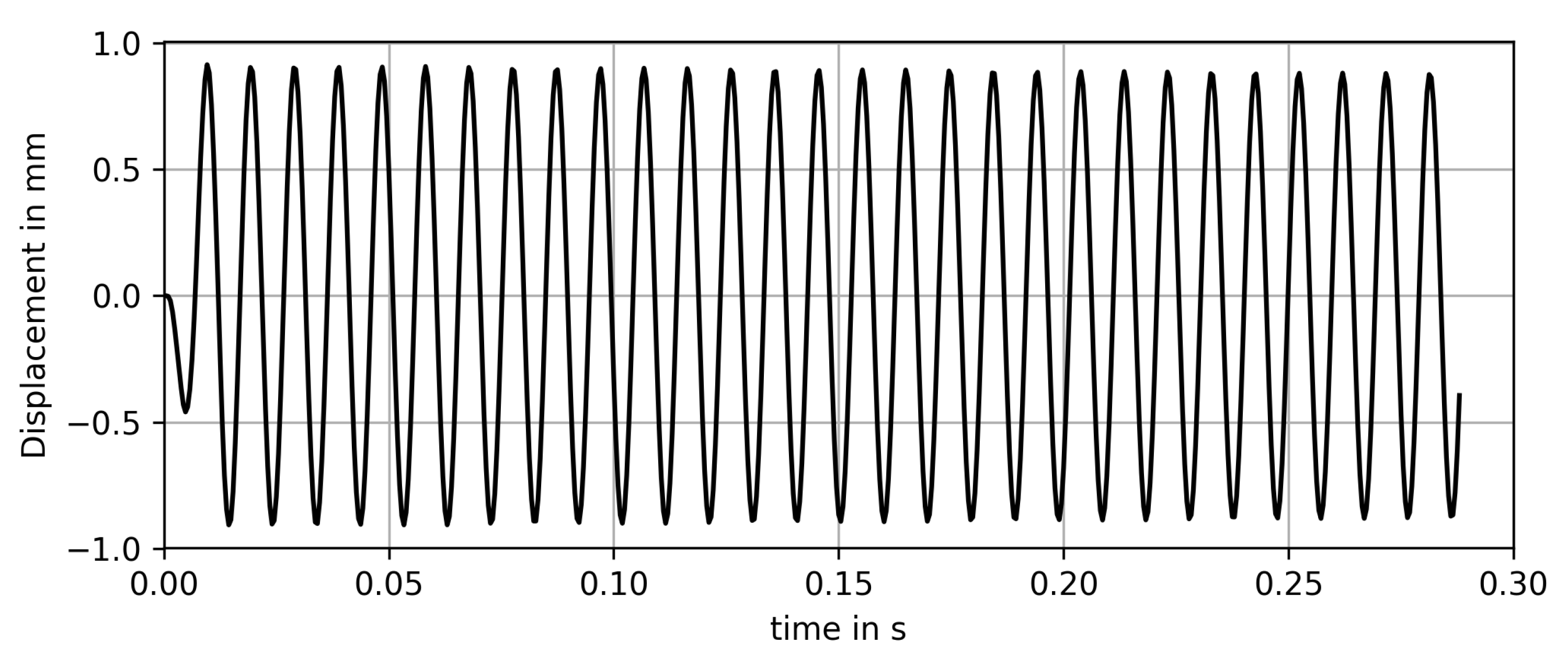
4. Results of the Coriolis Mass Flowmeter Test Case
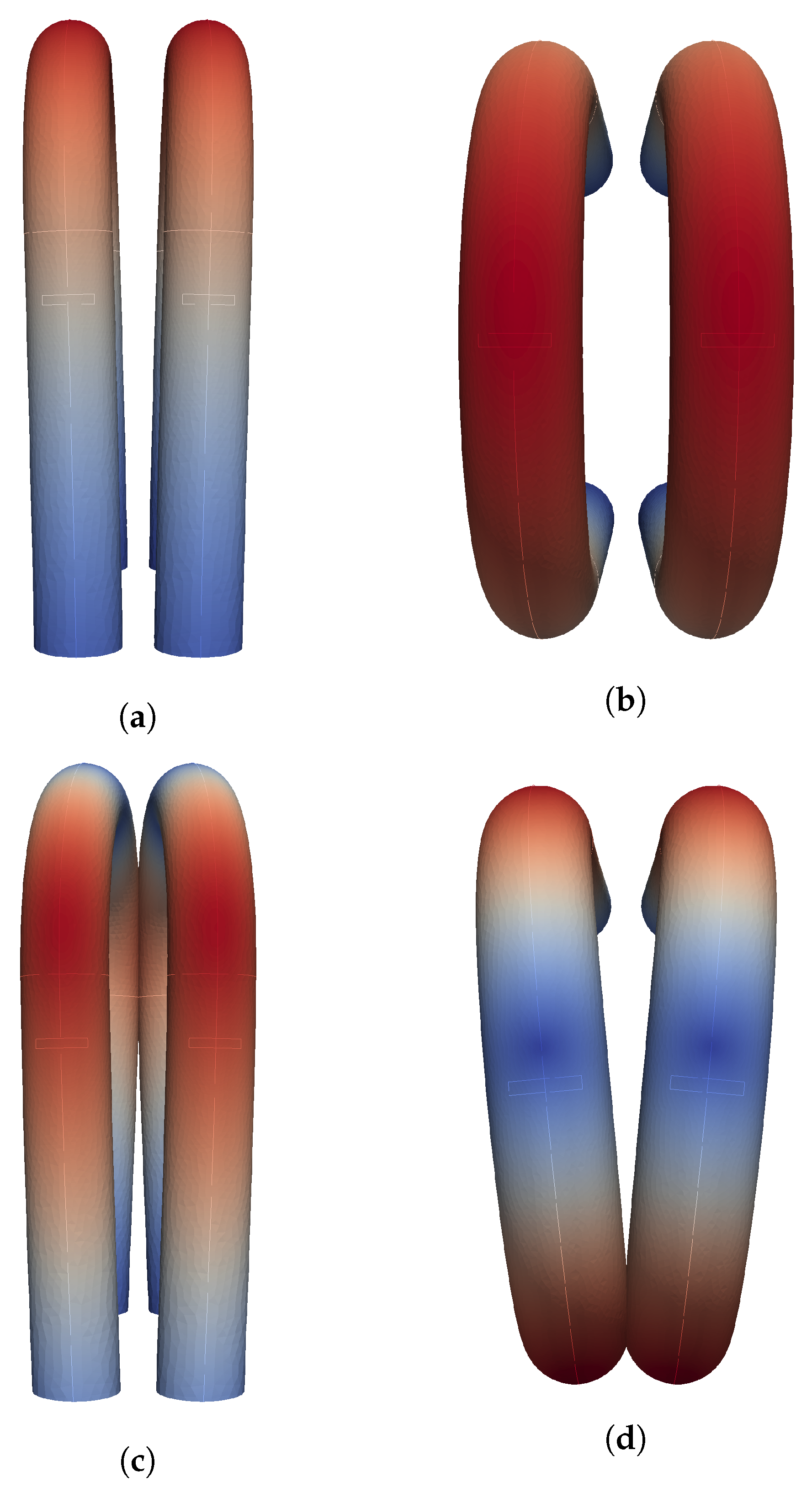
4.1. Modal Analysis
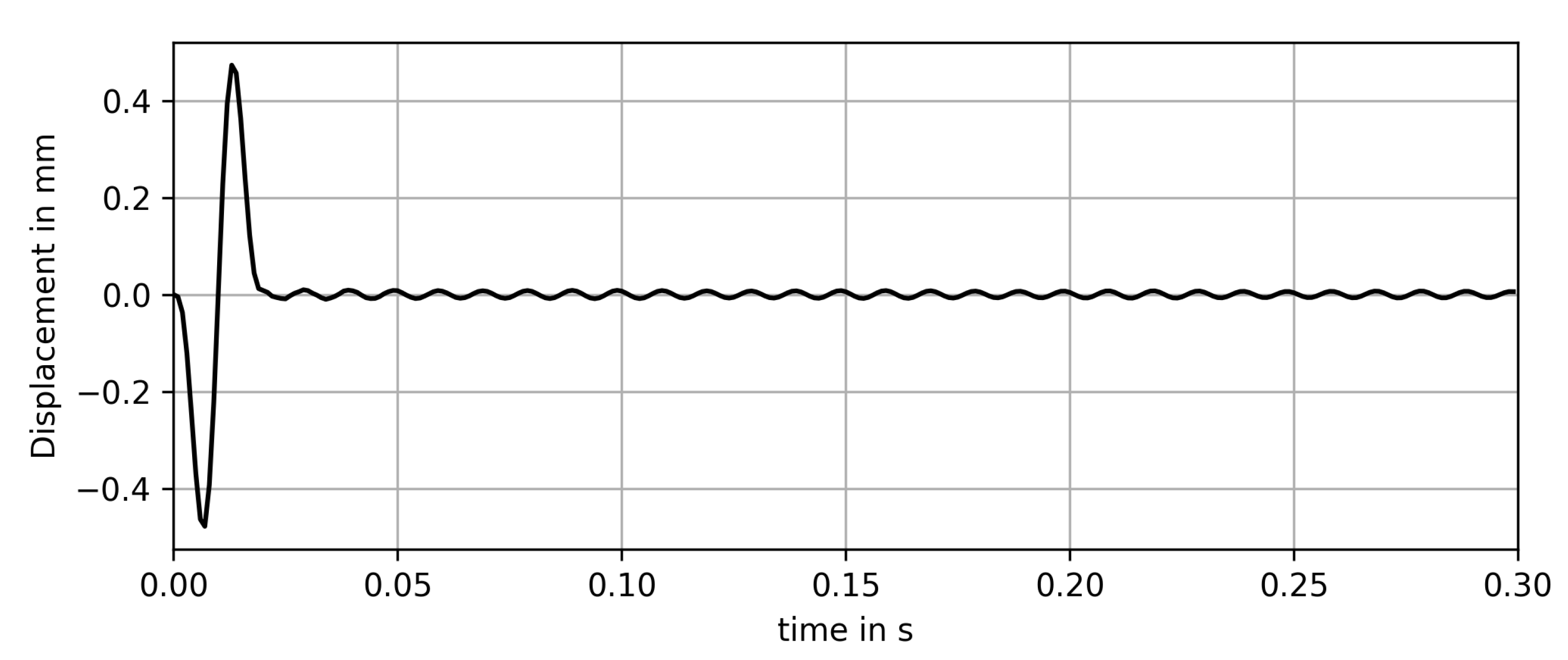
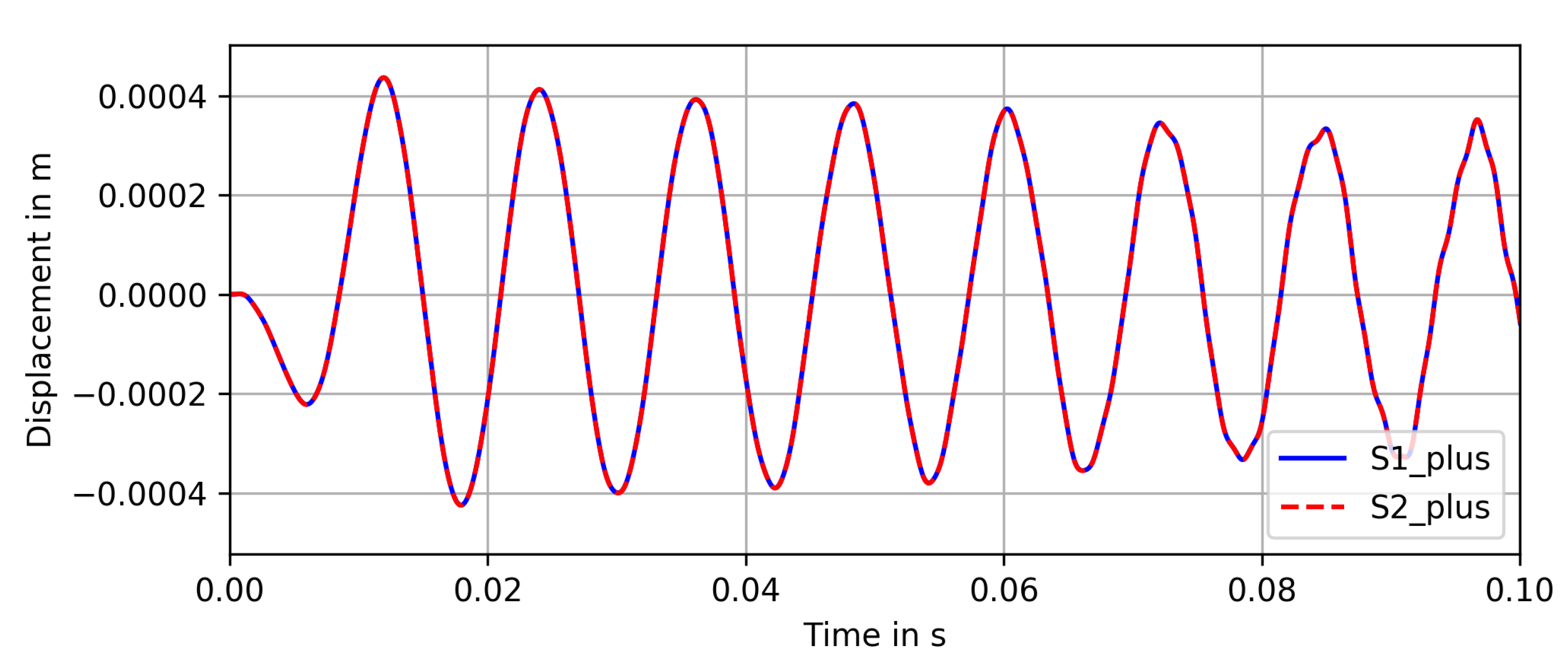
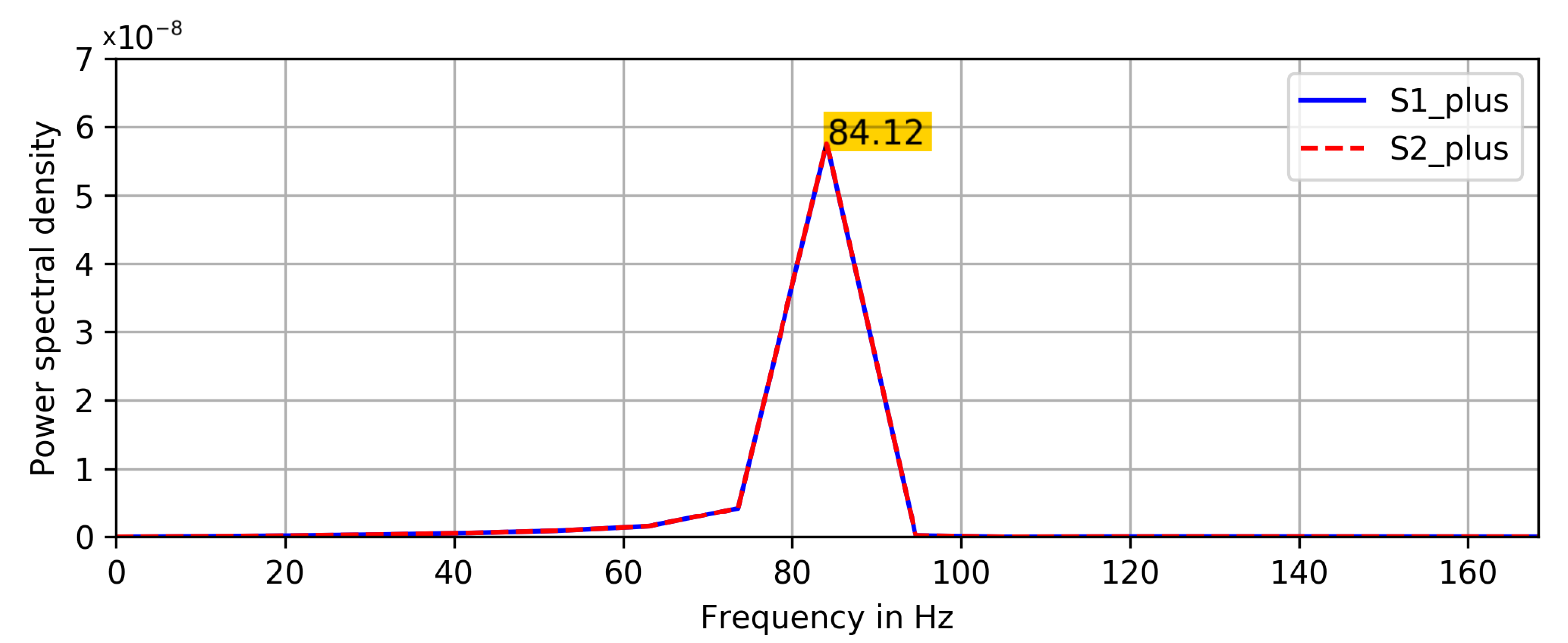
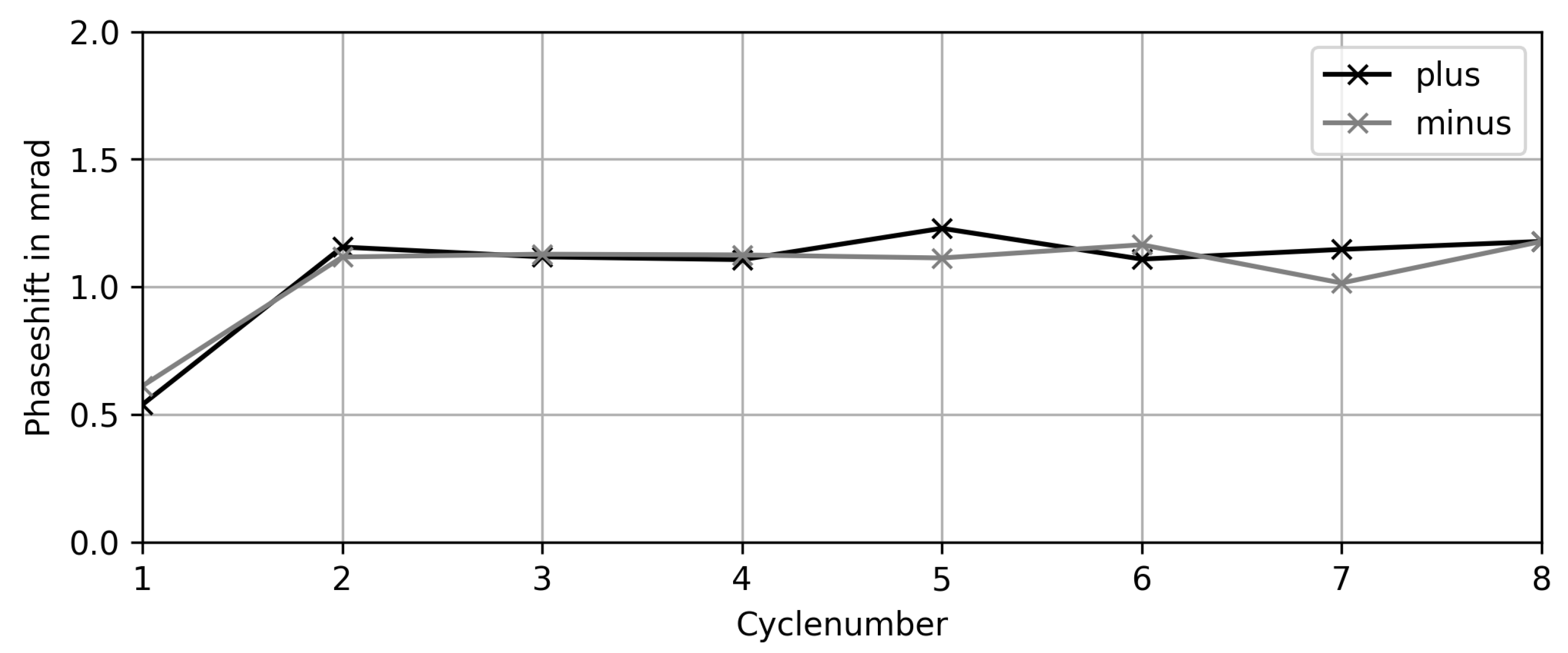
4.2. Phase Shift Calculation
5. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Wang, T.; Baker, R. Coriolis flowmeters: A review of developments over the past 20 years, and an assessment of the state of the art and likely future directions. Flow Meas. Instrum. 2014, 40, 99–123. [Google Scholar] [CrossRef]
- Belhadj, A.; Cheesewright, R.; Clark, C. The simulation of Coriolis meter response to pulsating flow using a general purpose fe code. J. Fluids Struct. 2000, 14, 613–634. [Google Scholar] [CrossRef]
- Cheesewright, R.; Clark, C. The effect of flow pulsations on Coriolis mass flow meters. J. Fluids Struct. 1998, 12, 1025–1039. [Google Scholar] [CrossRef]
- Hemp, J. The weight vector theory of Coriolis mass flowmeters. Flow Meas. Instrum. 1994, 5, 247–253. [Google Scholar] [CrossRef]
- Kazahaya, M. A mathematical model and error analysis of Coriolis mass flowmeters. IEEE Trans. Instrum. Meas. 2010, 60, 1163–1174. [Google Scholar] [CrossRef]
- Kutin, J.; Bajsić, I. An analytical estimation of the Coriolis meter’s characteristics based on modal superposition. Flow Meas. Instrum. 2002, 12, 345–351. [Google Scholar] [CrossRef]
- Wang, L.J.; Hu, L.; Zhu, Z.C.; Ye, P.; Fu, X. Analytical calculation of sensitivity for Coriolis mass flowmeter. Measurement 2011, 44, 1117–1127. [Google Scholar] [CrossRef]
- Bobovnik, G.; Mole, N.; Kutin, J.; Štok, B.; Bajsić, I. Coupled finite-volume/finite-element modelling of the straight-tube Coriolis flowmeter. J. Fluids Struct. 2005, 20, 785–800. [Google Scholar] [CrossRef]
- Mole, N.; Bobovnik, G.; Kutin, J.; Štok, B.; Bajsić, I. An improved three-dimensional coupled fluid–structure model for Coriolis flowmeters. J. Fluids Struct. 2008, 24, 559–575. [Google Scholar] [CrossRef]
- Bobovnik, G.; Kutin, J.; Mole, N.; Štok, B.; Bajsić, I. Numerical analysis of installation effects in Coriolis flowmeters: A case study of a short straight tube full-bore design. Flow Meas. Instrum. 2013, 34, 142–150. [Google Scholar] [CrossRef]
- Kumar, V. FSI Simulations of Flow Measurement Devices Using ANSYS-CFX; Endress + Hauser Flowtec AG: Reinach, Switzerland, 2009. [Google Scholar]
- Kumar, V.; Anklin, M. Numerical simulations of Coriolis flow meters for low Reynolds number flows. J. Metrol. Soc. India 2011, 26, 225–235. [Google Scholar] [CrossRef]
- Rongmo, L.; Jian, W. Fluid-Structure Coupling Analysis and Simulation of Viscosity Effect on Coriolis Mass Flowmeter. In Proceedings of the Conferenece Proceeding of APCOM & ISCM, Singapore, 11–14 December 2013. [Google Scholar]
- Heuveline, V.; Krause, M.J.; Latt, J. Towards a hybrid parallelization of lattice Boltzmann methods. Comput. Math. Appl. 2009, 58, 1071–1080. [Google Scholar] [CrossRef]
- Heuveline, V.; Krause, M.J. Openlb: Towards an efficient parallel open source library for lattice Boltzmann fluid flow simulations. In Proceedings of the International Workshop on State-of-the-Art in Scientific and Parallel Computing—PARA, Reykjavik, Iceland, 6–9 June 2010; Volume 9. [Google Scholar]
- Henn, T.; Heuveline, V.; Krause, M.J.; Ritterbusch, S. Aortic coarctation simulation based on the lattice Boltzmann method: Benchmark results. In Statistical Atlases and Computational Models of the Heart. Imaging and Modelling Challenges; Camara, O., Mansi, T., Pop, M., Rhode, K., Sermesant, M., Young, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 34–43. ISBN 978-3-642-36961-2. [Google Scholar]
- Augusto, L.D.X.; Ross-Jones, J.; Lopes, G.C.; Tronville, P.; Gonçalves, J.A.S.; Rädle, M.; Krause, M.J. Microfiber filter performance prediction using a lattice Boltzmann method. Commun. Comput. Phys. 2018, 23, 910–931. [Google Scholar] [CrossRef]
- Haussmann, M.; Barreto, A.C.; Kouyi, G.L.; Rivière, N.; Nirschl, H.; Krause, M.J. Large-eddy simulation coupled with wall models for turbulent channel flows at high reynolds numbers with a lattice Boltzmann method—Application to Coriolis mass flowmeter. Comput. Math. Appl. 2019, 78, 3285–3302. [Google Scholar] [CrossRef]
- Haussmann, M.; Simonis, S.; Nirschl, H.; Krause, M.J. Direct numerical simulation of decaying homogeneous isotropic turbulence—Numerical experiments on stability, consistency and accuracy of distinct lattice Boltzmann methods. Int. J. Mod. Phys. C (IJMPC) 2019, 30, 1–29. [Google Scholar] [CrossRef]
- Scholz, D.; Kollmannsberger, S.; Düster, A.; Rank, E. Thin solids for fluid-structure interaction. In Fluid-Structure Interaction; Springer: Berlin/Heidelberg, Germany, 2006; pp. 294–335. [Google Scholar]
- Geller, S.; Tölke, J.; Krafczyk, M. Lattice-Boltzmann method on quadtree-type grids for fluid-structure interaction. In Fluid-Structure Interaction; Springer: Berlin/Heidelberg, Germany, 2006; pp. 270–293. [Google Scholar]
- Turek, S.; Hron, J. Proposal for numerical benchmarking of fluid-structure interaction between an elastic object and laminar incompressible flow. In Fluid-Structure Interaction; Springer: Berlin/Heidelberg, Germany, 2006; pp. 371–385. [Google Scholar]
- Kollmannsberger, S.; Geller, S.; Düster, A.; Tölke, J.; Sorger, C.; Krafczyk, M.; Rank, E. Fixed-grid fluid–structure interaction in two dimensions based on a partitioned lattice Boltzmann and p-FEM approach. Int. J. Numer. Methods Eng. 2009, 79, 817–845. [Google Scholar] [CrossRef]
- Valero-Lara, P. Analysis and Applications of Lattice Boltzmann Simulations; IGI Global: Hershey, PA, USA, 2018. [Google Scholar]
- Geller, S.; Kollmannsberger, S.; Bettah, M.E.; Krafczyk, M.; Scholz, D.; Düster, A.; Rank, E. An explicit model for three-dimensional fluid-structure interaction using LBM and p-FEM. In Fluid Structure Interaction II; Springer: Berlin/Heidelberg, Germany, 2011; pp. 285–325. [Google Scholar]
- Krause, M.J.; Avis, S.; Dapalo, D.; Hafen, N.; Haußmann, M.; Gaedtke, M.; Klemens, F.; Kummerländer, A.; Maier, M.-L.; Mink, A.; et al. OpenLB Release 1.3: Open Source Lattice Boltzmann Code; Zenodo: Geneve, Switzerland, 2019. [Google Scholar]
- Krause, M.J.; Kummerländer, A.; Avis, S.J.; Kusumaatmaja, H.; Dapelo, D.; Klemens, F.; Gaedtke, M.; Hafen, N.; Mink, A.; Trunk, R.; et al. OpenLB—open source lattice Boltzmann code. Comput. Math. Appl. 2021, 81, 258–288. [Google Scholar] [CrossRef]
- Elmer FEM Open Source Multiphysical Simulation Software. Available online: https://www.csc.fi/web/elmer (accessed on 17 April 2021).
- Kang, S.K.; Hassan, Y.A. The effect of lattice models within the lattice Boltzmann method in the simulation of wall-bounded turbulent flows. J. Comput. Phys. 2013, 232, 100–117. [Google Scholar] [CrossRef]
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 1954, 94, 511–525. [Google Scholar] [CrossRef]
- He, X.; Luo, L. Theory of the lattice Boltzmann method: From the Boltzmann equation to the lattice Boltzmann equation. Phys. Rev. E 1997, 56, 6811–6817. [Google Scholar] [CrossRef]
- Shan, X.; Yuan, X.; Chen, H. Kinetic theory representation of hydrodynamics: A way beyond the Navier–Stokes equation. J. Fluid Mech. 2006, 550, 413–441. [Google Scholar] [CrossRef]
- Holdych, D.J. Lattice Boltzmann Methods for Diffuse and Mobile Interfaces. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Champaign, IL, USA, 2003. [Google Scholar]
- Noble, D.R.; Torczynski, J.R. A lattice-Boltzmann method for partially saturated computational cells. Int. J. Mod. Phys. C 1998, 9, 1189–1201. [Google Scholar] [CrossRef]
- Coclite, A.; Ranaldo, S.; de Tullio, M.D.; Decuzzi, P.; Pascazio, G. Kinematic and dynamic forcing strategies for predicting the transport of inertial capsules via a combined lattice Boltzmann—Immersed Boundary method. Comput. Fluids 2020, 180, 41–53. [Google Scholar] [CrossRef]
- Feng, Z.; Michaelides, E.E. The immersed boundary-lattice Boltzmann method for solving fluid–particles interaction problems. J. Comput. Phys. 2004, 195, 602–628. [Google Scholar] [CrossRef]
- Kang, S.K.; Hassan, Y.A. A comparative study of direct-forcing immersed boundary-lattice Boltzmann methods for stationary complex boundaries. Int. J. Numer. Methods Fluids 2011, 66, 1132–1158. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhu, L.; Zhang, C. Numerical study of stability and accuracy of the immersed boundary method coupled to the lattice Boltzmann BGK model. Commun. Comput. Phys. 2014, 16, 136–168. [Google Scholar] [CrossRef]
- Filippova, O.; Hänel, D. Grid refinement for lattice-BGK models. J. Comput. Phys. 1998, 147, 219–228. [Google Scholar] [CrossRef]
- Yu, D.; Mei, R.; Shyy, W. A unified boundary treatment in lattice Boltzmann method. In Proceedings of the 41st Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 2003; p. 953. [Google Scholar]
- Lallemand, P.; Luo, L.-S. Lattice Boltzmann method for moving boundaries. J. Comput. Phys. 2003, 184, 406–421. [Google Scholar] [CrossRef]
- Haussmann, M.; Hafen, N.; Raichle, F.; Trunk, R.; Nirschl, H.; Krause, M.J. Galilean invariance study on different lattice Boltzmann fluid–solid interface approaches for vortex-induced vibrations. Comput. Math. Appl. 2020, 80, 671–691. [Google Scholar] [CrossRef]
- Bouzidi, M.; Firdaouss, M.; Lallemand, P. Momentum transfer of a Boltzmann-lattice fluid with boundaries. Phys. Fluids 2001, 13, 3452–3459. [Google Scholar] [CrossRef]
- Kao, P.; Yang, R. An investigation into curved and moving boundary treatments in the lattice Boltzmann method. J. Comput. Phys. 2008, 227, 5671–5690. [Google Scholar] [CrossRef]
- Wen, B.; Zhang, C.; Tu, Y.; Wang, C.; Fang, H. Galilean invariant fluid–solid interfacial dynamics in lattice Boltzmann simulations. J. Comput. Phys. 2014, 266, 161–170. [Google Scholar] [CrossRef]
- Tao, S.; Hu, J.; Guo, Z. An investigation on momentum exchange methods and refilling algorithms for lattice Boltzmann simulation of particulate flows. Comput. Fluids 2016, 133, 1–14. [Google Scholar] [CrossRef]
- Larson, M.G.; Bengzon, F. The Finite Element Method: Theory, Implementation, and Applications; Springer: Berlin/Heidelberg, Germany, 2013; Volume 10. [Google Scholar]
- Richter, T. Fluid-Structure Interactions: Models, Analysis and Finite Elements; Springer: Berlin/Heidelberg, Germany, 2017; Volume 118. [Google Scholar]
- Geuzaine, C.; Remacle, J.-F. Gmsh: A 3-D finite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Heil, M. An efficient solver for the fully coupled solution of large-displacement fluid–structure interaction problems. Comput. Methods Appl. Mech. Eng. 2004, 193, 1–23. [Google Scholar] [CrossRef]


| Structural Properties | Fluid Properties | ||
|---|---|---|---|
| E | |||
| Region | in m |
|---|---|
| Outer housing | 0.035 |
| Body | 0.030 |
| Sensors and exciter | 0.005 |
| Measuring pipes | 0.010 |
| Node plates | 0.005 |
| Mass Flow in | in m | in s | |
|---|---|---|---|
| 20,000 | |||
| 40,000 |
| Mode | in | f in | Physical Meaning |
|---|---|---|---|
| 1 | 86.02 | ||
| 2 | 104.28 | excitation mode | |
| 3 | 123.42 | ||
| 4 | 155.14 | ||
| 5 | 167.65 | ||
| 6 | 193.85 | ||
| 7 | 238.87 | ||
| 8 | 277.26 | Coriolis twist mode | |
| 9 | 402.60 | ||
| 10 | 451.44 |
| Simulation | Measurement | Error in % | |
|---|---|---|---|
| 104.28 | 101.00 | 3.24 | |
| 83.94 | 81.41 | 3.11 | |
| 277.26 | 249.00 | 11.35 | |
| 222.92 | 205.00 | 8.74 |
| Mass Flow in | in | in | Error in % | Coupling Steps |
|---|---|---|---|---|
| 20,000 | - | 0.62 | Instable | 51 |
| 20,000 | - | 0.62 | Instable | 101 |
| 20,000 | 0.59 | 0.62 | 4.7 | 202 |
| 40,000 | 1.18 | 1.23 | 4.1 | 202 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haussmann, M.; Reinshaus, P.; Simonis, S.; Nirschl, H.; Krause, M.J. Fluid–Structure Interaction Simulation of a Coriolis Mass Flowmeter Using a Lattice Boltzmann Method. Fluids 2021, 6, 167. https://doi.org/10.3390/fluids6040167
Haussmann M, Reinshaus P, Simonis S, Nirschl H, Krause MJ. Fluid–Structure Interaction Simulation of a Coriolis Mass Flowmeter Using a Lattice Boltzmann Method. Fluids. 2021; 6(4):167. https://doi.org/10.3390/fluids6040167
Chicago/Turabian StyleHaussmann, Marc, Peter Reinshaus, Stephan Simonis, Hermann Nirschl, and Mathias J. Krause. 2021. "Fluid–Structure Interaction Simulation of a Coriolis Mass Flowmeter Using a Lattice Boltzmann Method" Fluids 6, no. 4: 167. https://doi.org/10.3390/fluids6040167
APA StyleHaussmann, M., Reinshaus, P., Simonis, S., Nirschl, H., & Krause, M. J. (2021). Fluid–Structure Interaction Simulation of a Coriolis Mass Flowmeter Using a Lattice Boltzmann Method. Fluids, 6(4), 167. https://doi.org/10.3390/fluids6040167






