Aerodynamic Dispersion of Respiratory Droplets and Aerosols by Turbulent Airflow
Abstract
1. Introduction
2. Governing Equations
2.1. Aerodynamics
2.2. Respiratory Droplets and Aerosols Propagation
3. Computational Model
| Variable | Value | References |
|---|---|---|
| Freestream velocity magnitude of airflow | 2 and 4 m/s | [29,30] |
| Environment temperature | 26 °C | [31] |
| Freestream turbulence intensity | 2% | [32] |
| Nasal and oral area | 1.5 and 2.5 cm2 | [10] |
| Body temperature | 31 °C | [31] |
| Sneeze total time 1 s | 1 s | [10,33] |
| Airflow during sneeze | 250 L/min | [10,33] |
| Volume fraction of droplets during sneeze | 1 × 10−5 | [20] |
| Diameter distribution of droplets during sneeze | 100–900 μm | [11] |
| Diameter distribution of aerosols | 0.5–2.25 μm | [34] |
| Breathing frequency | 15.5 times/min | [33,35] |
| Airflow temperature during breathing | 34 °C | [33,35] |
| Pulmonary ventilation rate during breathing | 10 L/min | [33,35] |
| Volume fraction of aerosols during breathing | 2.13 × 10−14 | [34] |
| Diameter distribution of aerosols during breathing | 0.5–2.25 μm | [33] |
4. Simulations
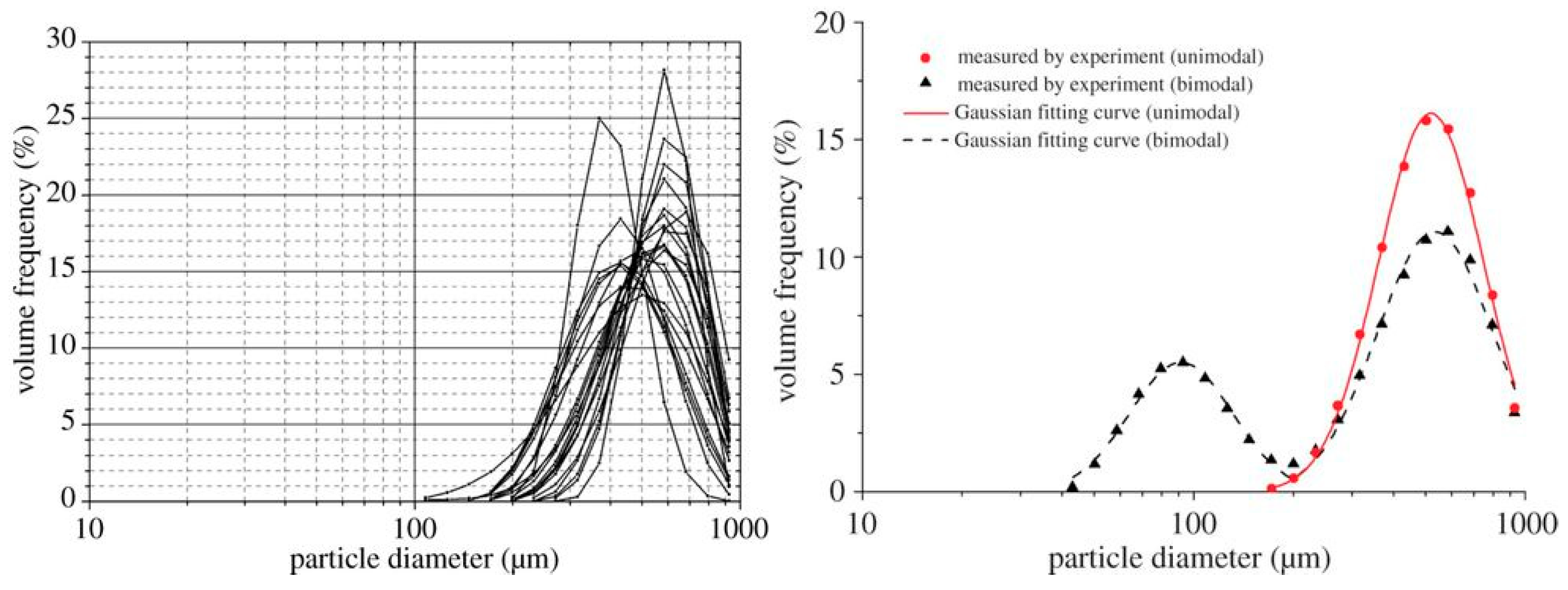
4.1. Comparison with Existing Experimental Data
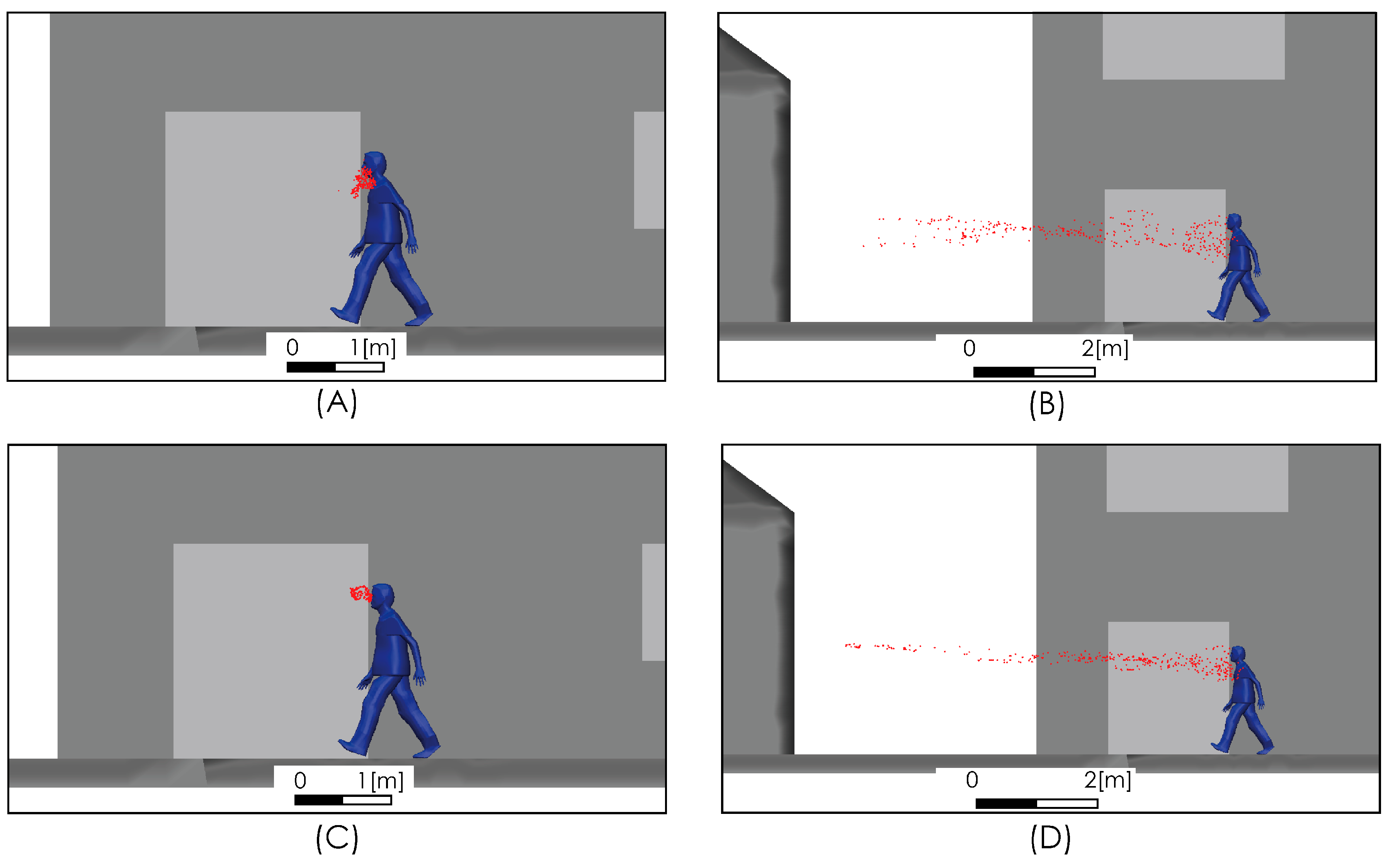
4.2. Results
5. Discussion
6. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Heymann, D. What We Do (and Don’t) Know about the Coronavirus. February 2020. Available online: https://www.ted.com/talks/david_heymann_what_we_do_and_don_t_know_about_the_coronavirus (accessed on 1 November 2020).
- World Health Organization (WHO). Advice for the Public on COVID-19. Available online: https://www.who.int/emergencies/diseases/novel-coronavirus-2019/advice-for-public (accessed on 1 November 2020).
- Wells, W.F. On air-borne infection. Study II. Droplets and droplet nuclei. Am. J. Hyg. 1934, 20, 611–618. [Google Scholar]
- Setti, L.; Passarini, F.; De Gennaro, G.; Barbieri, P.; Perrone, M.G.; Borelli, M.; Palmisani, J.; Di Gilio, A.; Piscitelli, P.; Miani, A. Airborne Transmission Route of COVID-19: Why 2 Meters/6 Feet of Inter-Personal Distance Could Not Be Enough. Int. J. Environ. Res. Public Health 2020, 17, 2932. [Google Scholar] [CrossRef]
- UN-Habitat. World Cities Report 2016: Urbanization and Development–Emerging Futures; UN-Habitat: Nairobi, Kenya, 2016. [Google Scholar]
- Lewis, D. Mounting evidence suggests coronavirus is airborne—But health advice has not caught up. Nature 2020, 583, 510–513. [Google Scholar] [CrossRef] [PubMed]
- Lewis, D. Is the coronavirus airborne? Experts can’t agree. Nat. Cell Biol. 2020, 580, 175. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. Modes of Transmission of Virus Causing COVID-19: Implications for IPC Precaution Recommendations: Scientific Brief, 29 March 2020. World Health Organization. Licencia: CC BY-NC-SA 3.0 IGO. Available online: https://apps.who.int/iris/handle/10665/331616 (accessed on 21 November 2020).
- Gao, N.; Niu, J. Transient CFD simulation of the respiration process and inter-person exposure assessment. Build. Environ. 2006, 41, 1214–1222. [Google Scholar] [CrossRef] [PubMed]
- Han, Z.Y.; Weng, W.G.; Huang, Q.Y. Characterizations of particle size distribution of the droplets exhaled by sneeze. J. R. Soc. Interface 2013, 10, 20130560. [Google Scholar] [CrossRef]
- Ong, S.W.X.; Tan, Y.K.; Chia, P.Y.; Lee, T.H.; Ng, O.T.; Wong, M.S.Y.; Marimuthu, K. Air, surface environmental, and personal protective equipment contamination by severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) from a symptomatic patient. JAMA 2020, 323, 1610–1612. [Google Scholar] [CrossRef]
- Prather, K.A.; Marr, L.C.; Schooley, R.T.; McDiarmid, M.A.; Wilson, M.E.; Milton, D.K. Airborne transmission of SARS-CoV-2. Science 2020, 370, 303. [Google Scholar]
- Morawska, L.; Cao, J. Airborne transmission of SARS-CoV-2: The world should face the reality. Environ. Int. 2020, 139, 105730. [Google Scholar] [CrossRef]
- Mandavilli, A. 239 Experts with One Big Claim: The Coronavirus Is Airborne; The New York Times: New York, NY, USA, 2020; p. 7. [Google Scholar]
- World Health Organization. Transmission of SARS-CoV-2: Implications for Infection Prevention Precautions: Scientific Brief, 09 July 2020 (No. WHO/2019-nCoV/Sci_Brief/Transmission_modes/2020.3); World Health Organization: Geneva, Switzerland, 2020. [Google Scholar]
- Zhang, H.; Li, D.; Xie, L.; Xiao, Y. Documentary Research of Human Respiratory Droplet Characteristics. Procedia Eng. 2015, 121, 1365–1374. [Google Scholar] [CrossRef]
- Zhu, S.; Kato, S.; Yang, J.-H. Study on transport characteristics of saliva droplets produced by coughing in a calm indoor environment. Build. Environ. 2006, 41, 1691–1702. [Google Scholar] [CrossRef]
- Xie, X.; Li, Y.; Chwang, A.T.Y.; Ho, P.L.; Seto, W.H. How far droplets can move in indoor environments? revisiting the Wells evaporation? falling curve. Indoor Air 2007, 17, 211–225. [Google Scholar] [CrossRef]
- Bourouiba, L.; Dehandschoewercker, E.; Bush, J.W.M. Violent expiratory events: On coughing and sneezing. J. Fluid Mech. 2014, 745, 537–563. [Google Scholar] [CrossRef]
- Das, S.K.; Alam, J.-E.; Plumari, S.; Greco, V. Transmission of airborne virus through sneezed and coughed droplets. Phys. Fluids 2020, 32, 097102. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.W.; Nicolle, A.D.; Klettner, C.A.; Pantelic, J.; Wang, L.; Bin Suhaimi, A.; Tan, A.Y.L.; Ong, G.W.X.; Su, R.; Sekhar, C.; et al. Airflow Dynamics of Human Jets: Sneezing and Breathing—Potential Sources of Infectious Aerosols. PLoS ONE 2013, 8, e59970. [Google Scholar] [CrossRef] [PubMed]
- Bourouiba, L. Turbulent Gas Clouds and Respiratory Pathogen Emissions Potential Implications for Reducing Transmission of COVID-19. JAMA 2020, 323, 1837–1838. [Google Scholar]
- Pendar, M.-R.; Páscoa, J.C. Numerical modeling of the distribution of virus carrying saliva droplets during sneeze and cough. Phys. Fluids 2020, 32, 083305. [Google Scholar] [CrossRef]
- Dbouk, T.; Drikakis, D. On coughing and airborne droplet transmission to humans. Phys. Fluids 2020, 32, 053310. [Google Scholar] [CrossRef] [PubMed]
- Fortuniak, K.; Kłysik, K.; Wibig, J. Urban–rural contrasts of meteorological parameters in Łódź. Theor. Appl. Climatol. 2006, 84, 91–101. [Google Scholar] [CrossRef]
- Asgary, A.; Najafabadi, M.M.; Karsseboom, R.; Wu, J. A Drive-through Simulation Tool for Mass Vaccination during COVID-19 Pandemic. Health 2020, 8, 469. [Google Scholar] [CrossRef]
- Ounis, H.; Ahmadi, G.; McLaughlin, J.B. Brownian diffusion of submicrometer particles in the viscous sublayer. J. Colloid Interface Sci. 1991, 143, 266–277. [Google Scholar] [CrossRef]
- Higgins, C.; Parlange, M.; Meneveau, C. Energy dissipation in large-eddy simulation: Dependence on flow structure and effects of eigenvector alignments. Atmos. Turbul. Mesoscale Meteorol. 2004, 51–70. [Google Scholar] [CrossRef]
- Grassi, S.; Veronesi, F.; Schenkel, R.; Peier, C.; Neukom, J.; Volkwein, S.; Raubal, M.; Hurni, L. Mapping of the global wind energy potential using opensource GIS data. In Proceedings of the 2nd International Conference on Energy and Environment (ICEE 2015): Bringing Together Engineering and Economics, Guimarães, Portugal, 18–19 June 2015; pp. 647–653. [Google Scholar]
- Badeau, A.; Afshari, A.; Goldsmith, T.; Frazer, D. Preliminary prediction of flow and particulate concentration produced from normal human cough dispersion. In Proceedings of the Second Joint 24th Annual Conference and the Annual Fall Meeting of the Biomedical Engineering Society, Engineering in Medicine and Biology, Houston, TX, USA, 23–26 October 2002; Volume 1, pp. 246–247. [Google Scholar]
- Piomelli, U. Wall-layer models for large-eddy simulations. Prog. Aerosp. Sci. 2008, 44, 437–446. [Google Scholar] [CrossRef]
- Ai, Z.T.; Melikov, A.K. Airborne spread of expiratory droplet nuclei between the occupants of indoor environments: A review. Indoor Air 2018, 28, 500–524. [Google Scholar] [CrossRef]
- Papineni, R.S.; Rosenthal, F.S. The Size Distribution of Droplets in the Exhaled Breath of Healthy Human Subjects. J. Aerosol Med. 1997, 10, 105–116. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.-J.; Baik, J.-J. Effects of inflow turbulence intensity on flow and pollutant dispersion in an urban street canyon. J. Wind Eng. Ind. Aerodyn. 2003, 91, 309–329. [Google Scholar] [CrossRef]
- Sun, C.; Zhai, Z. The efficacy of social distance and ventilation effectiveness in preventing COVID-19 transmission. Sustain. Cities Soc. 2020, 62, 102390. [Google Scholar] [CrossRef] [PubMed]
- Shafaghi, A.H.; Talabazar, F.R.; Koşar, A.; Ghorbani, M. On the Effect of the Respiratory Droplet Generation Condition on COVID-19 Transmission. Fluids 2020, 5, 113. [Google Scholar] [CrossRef]
- Smagorinsky, J. General Circulation Experiments with the Primitive Equations. I. The Basic Experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Shah, A.; Challener, D.; Tande, A.J.; Mahmood, M.; O’Horo, J.C.; Berbari, E.; Crane, S.J. Drive-Through Testing: A Unique, Efficient Method of Collecting Large Volume of Specimens During the SARS-CoV-2 (COVID-19) Pandemic. In Mayo Clinic Proceedings; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Gupta, A.; Evans, G.W.; Heragu, S.S. Simulation and optimization modeling for drive-through mass vaccination—A generalized approach. Simul. Model. Pract. Theory 2013, 37, 99–106. [Google Scholar] [CrossRef]
- Sandoval, V.; Sarmiento, J.P. A neglected issue: Informal settlements, urban development, and disaster risk reduction in Latin America and the Caribbean. Disaster Prev. Manag. Int. J. 2020, 29, 731–745. [Google Scholar] [CrossRef]
- Nielsen, P.V.; Olmedo, I.; Ruiz de Adana, M. Airborne cross-infection risk between two people standing in surroundings with a vertical temperature gradient. HVAC&R Res. 2012, 18, 552–561. [Google Scholar]
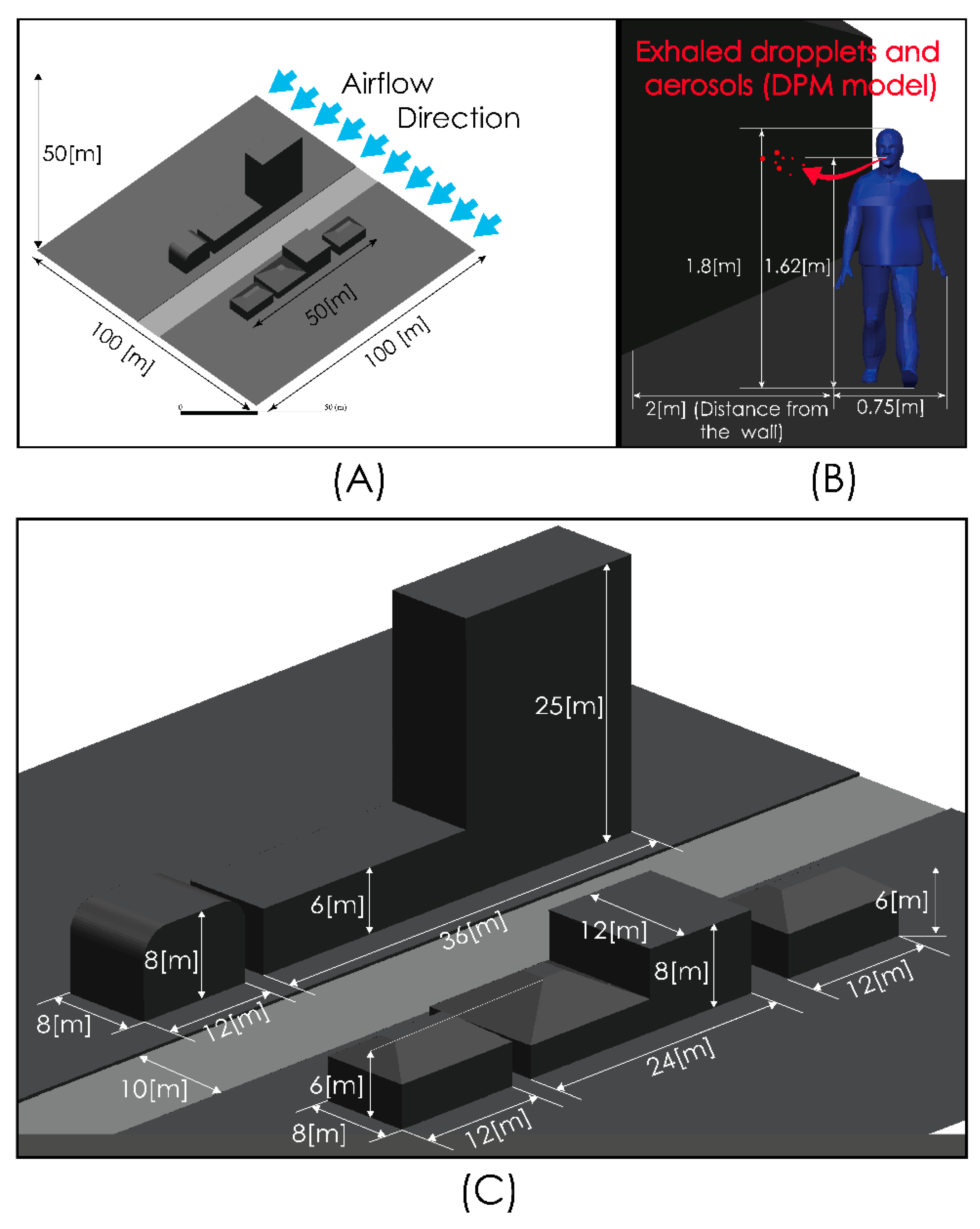


| Action | Particle Tracked | Airflow Velocity Magnitude |
|---|---|---|
| Sneezing | Respiratory droplet | 2, 4 m/s |
| Breathing | Droplet nuclei (aerosol) | 2, 4 m/s |
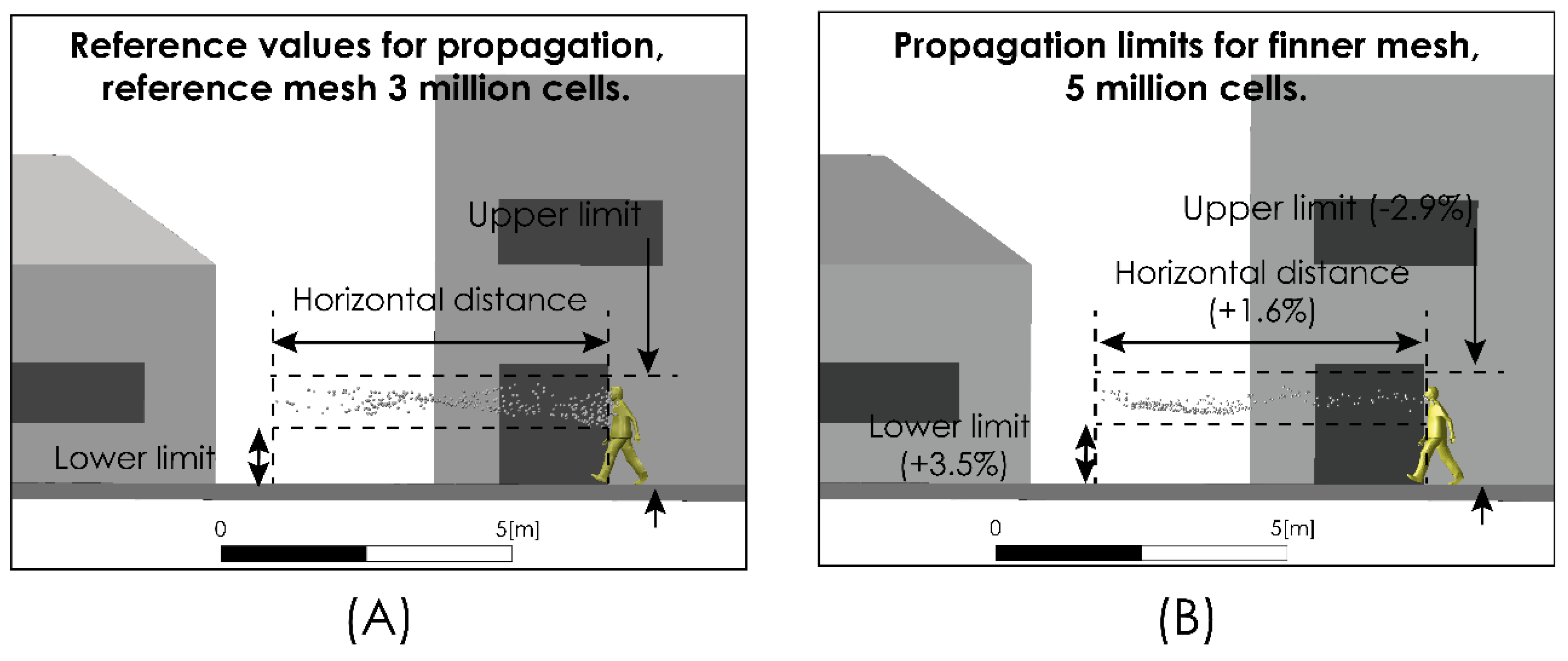
| Variable | 3 Million Cells Grid | 5 Million Cells Grid | Difference% |
|---|---|---|---|
| Maximum horizontal range | 6.14 m | 6.24 m | 1.6% |
| Range of vertical dispersion (from ground) | Min: 0.694 m | Min: 0.718 | 3.5% |
| Max: 1.837 m | Max: 1.783 | −2.9% | |
| Range of lateral dispersion (from person center line) | Right: +0.397 m | Right: +0.43 | 8.3% |
| Left: +0.396 m | Left: +0.372 | −6.1% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cornejo, P.; Guerrero, N.; Sandoval, V. Aerodynamic Dispersion of Respiratory Droplets and Aerosols by Turbulent Airflow. Fluids 2021, 6, 119. https://doi.org/10.3390/fluids6030119
Cornejo P, Guerrero N, Sandoval V. Aerodynamic Dispersion of Respiratory Droplets and Aerosols by Turbulent Airflow. Fluids. 2021; 6(3):119. https://doi.org/10.3390/fluids6030119
Chicago/Turabian StyleCornejo, Pablo, Nicolás Guerrero, and Vicente Sandoval. 2021. "Aerodynamic Dispersion of Respiratory Droplets and Aerosols by Turbulent Airflow" Fluids 6, no. 3: 119. https://doi.org/10.3390/fluids6030119
APA StyleCornejo, P., Guerrero, N., & Sandoval, V. (2021). Aerodynamic Dispersion of Respiratory Droplets and Aerosols by Turbulent Airflow. Fluids, 6(3), 119. https://doi.org/10.3390/fluids6030119








