On the Origin of the Magnetic Concentration Gradient Force and Its Interaction Mechanisms with Mass Transfer in Paramagnetic Electrolytes
Abstract
1. Introduction
2. Materials and Methods: The Concept of Minimum Reluctance Principle
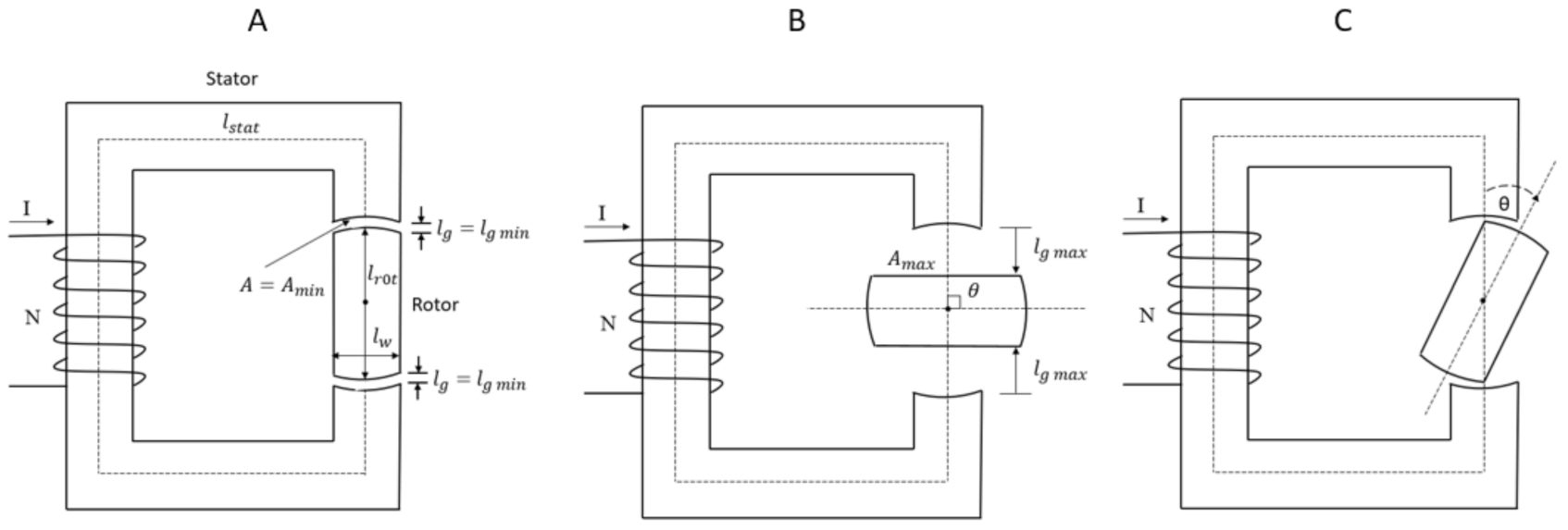
2.1. Magnetic Field Theory Applied to a Simplified Magnetic Circuit
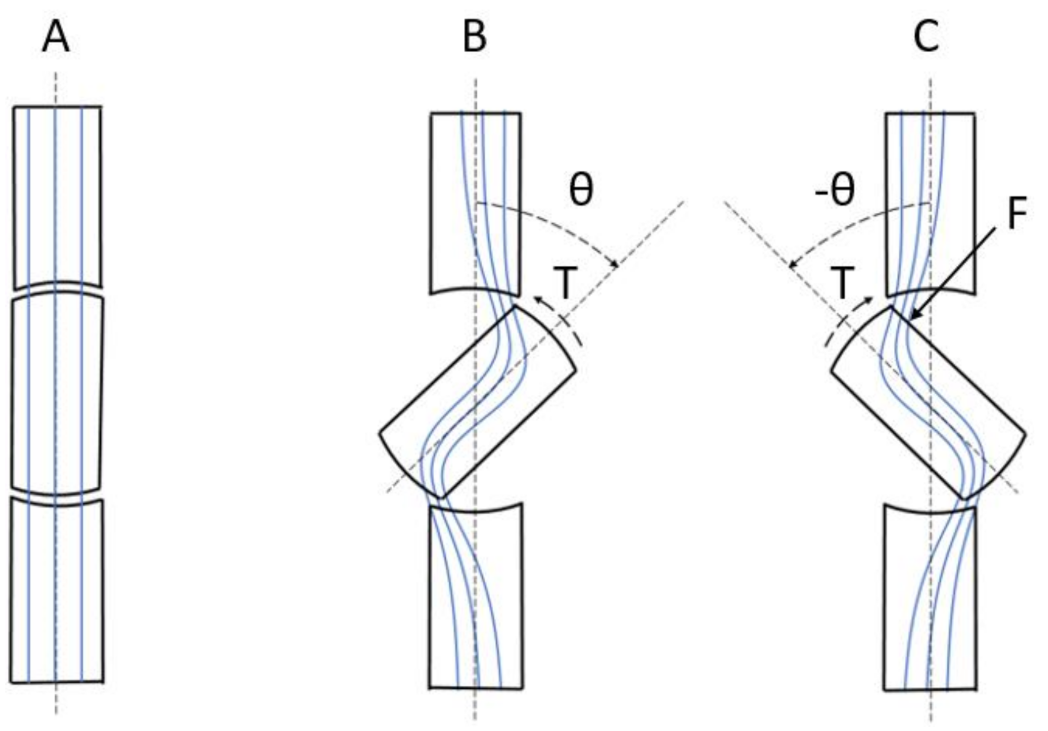
2.2. The Minimum Reluctance Principle
- The attraction mechanism, where a ferromagnetic, or paramagnetic, moving part is attracted into the magnetic field;
- The hindrance mechanism, where the moving part is hindered from leaving the magnetic field.
3. Results and Discussion
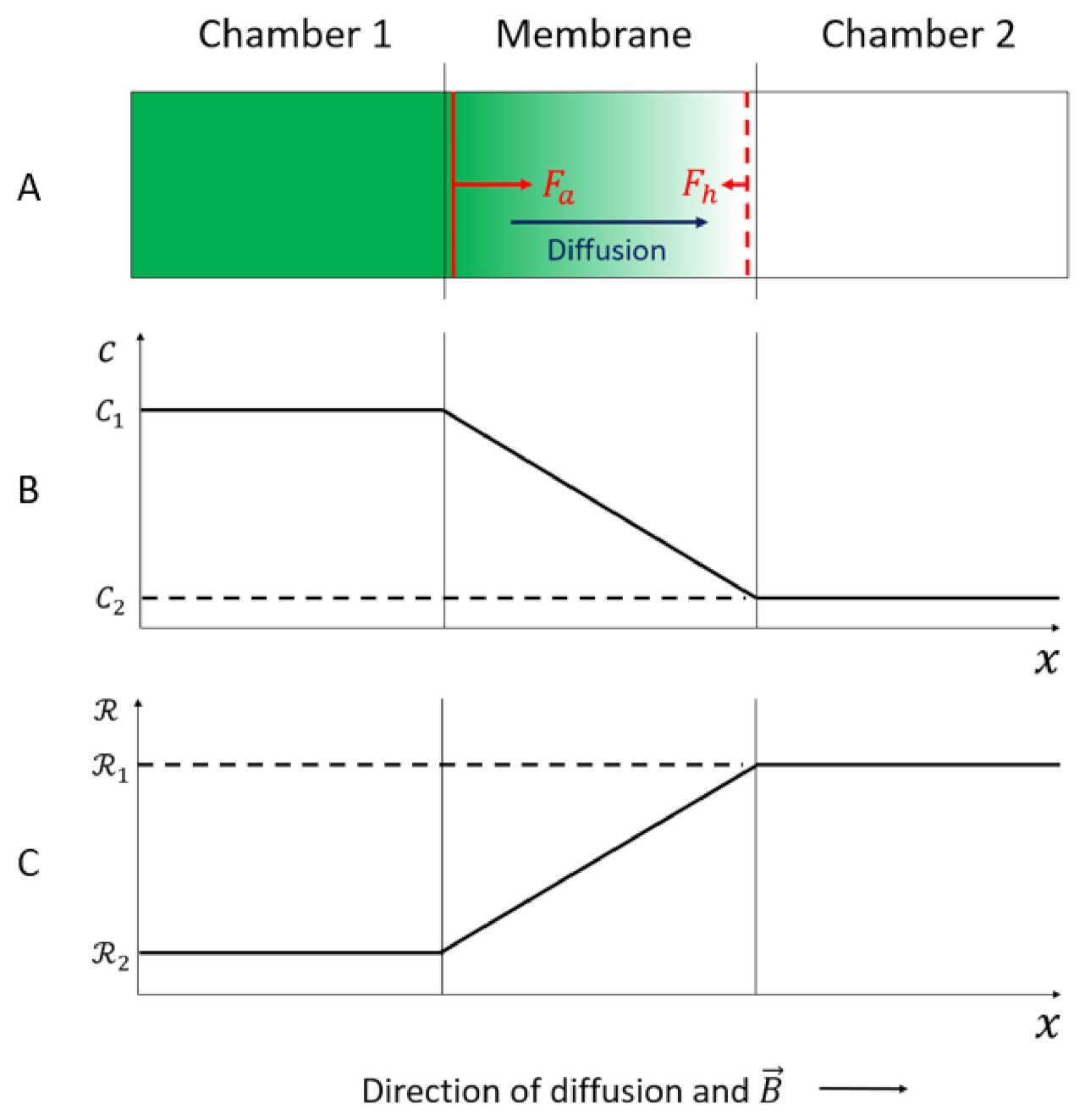
3.1. Diffusion of a Paramagnetic Electrolyte Through a Thin Membrane
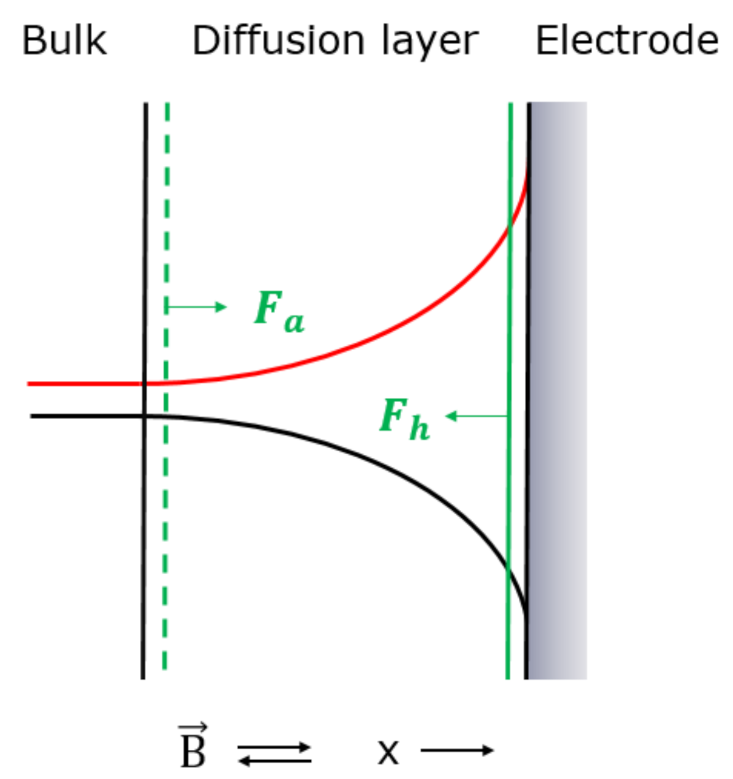
3.2. Deposition of Paramagnetic Ions on an Electrode Surface
3.3. Mass Transfer of Paramagnetic Ions from an Electrode Surface
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| A | Area (m2) |
| B | Magnetic flux density (T) |
| c | Electrolyte concentration (mol/m3) |
| F | Force (N) |
| I | Electric current (A) |
| K | Constant (dimensionless) |
| l | Length (m) |
| N | Number of turns (dimensionless) |
| r | Position vector (m) |
| Reluctance (H−1) | |
| Re | Reynolds number (dimensionless) |
| Sc | Schmidt number (dimensionless) |
| Sh | Sherwood number (dimensionless) |
| T | Torque (Nm) |
| x | Position (m) |
| θ | Angle (°) |
| μ | Magnetic permeability (H/m) |
| Φ | Magnetic flux (Wb) |
| χ | Magnetic susceptibility (dimensionless) |
| 0 | Reference value |
| 1 | Chamber 1 |
| 2 | Chamber 2 |
| a | Attraction |
| eff | Effective |
| g | Gap |
| h | Hindrance |
| max | Maximum |
| min | Minimum |
| mol | Molar |
| r | Relative |
| rot | Rotor |
| stat | Stator |
| total | Total |
| w | Width |
References
- Fahidy, T.Z. Magnetoelectrolysis. J. Appl. Electrochem. 1983, 13, 553–563. [Google Scholar] [CrossRef]
- Tacken, R.R.; Janssen, L.J.J. Applications of magnetoelectrolysis. J. Appl. Electrochem. 1995, 25, 1–5. [Google Scholar] [CrossRef]
- Fahidy, T.Z. The effect of magnetic fields on electrochemical processes. Electrodepos. Surf. Finish. 2005, 32, 333–354. [Google Scholar] [CrossRef]
- Hinds, G.; Coey, J.; Lyons, M. Influence of magnetic forces on electrochemical mass transport. Electrochem. Commun. 2001, 3, 215–218. [Google Scholar] [CrossRef]
- Alemany, A.; Chopart, J.P. An Outline of Magnetoelectrochemistry. In Magnetohydrodynamics—Historical Evolution and Trends; Molokov, S., Moreau, R., Moffatt, H.K., Eds.; Springer: Dordrecht, The Netherlands, 2007; pp. 391–407. [Google Scholar]
- Monzon, L.M.A.; Coey, J.M.D. Magnetic fields in electrochemistry: The Lorentz force. A mini-review. Electrochem. Commun. 2014, 42, 38–41. [Google Scholar] [CrossRef]
- Song, K.; Wu, S.; Tagawa, T.; Shi, W.; Zhao, S. Thermomagnetic convection of paramagnetic gas in an enclosure under no gravity condition. Fluids 2019, 4, 49. [Google Scholar] [CrossRef]
- Tagawa, T. Numerical analysis of magnetohydrodynamic flows. Fluids 2020, 5, 23. [Google Scholar] [CrossRef]
- Levich, G. Physicochemical Hydrodynamics; Prentice Hall: Englewood Cliffs, NJ, USA, 1962; pp. 60–72, 286–293. [Google Scholar]
- Newman, J.; Thomas-Alyea, K.E. Electrochemical Systems, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2004; pp. 172–177, 340–358, 400–403. [Google Scholar]
- Shevchuk, I.V. Modelling of Convective Heat and Mass Transfer in Rotating Flows; Springer Science and Business Media LLC: Cham, Switzerland, 2016; pp. 145–170. [Google Scholar]
- Braithwaite, D.; Beaugnon, E.; Tournier, R. Magnetically controlled convection in a paramagnetic fluid. Nature 1991, 354, 134–136. [Google Scholar] [CrossRef]
- Ragsdale, S.R.; Grant, K.M.; White, H.S. Electrochemically generated magnetic forces. Enhanced transport of a paramagnetic redox species in large, nonuniform magnetic fields. J. Am. Chem. Soc. 1998, 120, 13461–13468. [Google Scholar] [CrossRef]
- Sugiyama, A.; Hashiride, M.; Morimoto, R.; Nagai, Y.; Aogaki, R. Application of vertical micro-disk MHD electrode to the analysis of heterogeneous magneto-convection. Electrochim. Acta 2004, 49, 5115–5124. [Google Scholar] [CrossRef]
- Mutschke, G.; Tschulik, K.; Weier, T.; Uhlemann, M.; Bund, A.; Fröhlich, J. On the action of magnetic gradient forces in micro-structured copper deposition. Electrochim. Acta 2010, 55, 9060–9066. [Google Scholar] [CrossRef]
- Yang, X.; Tschulik, K.; Uhlemann, M.; Odenbach, S.; Eckert, K. Magnetic separation of paramagnetic ions from initially homogeneous solutions. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Pleskacz, Ł; Fornalik-Wajs, E. Identification of the structures for low reynolds number flow in the strong magnetic field. Fluids 2019, 4, 36. [Google Scholar] [CrossRef]
- O’Brian, R.N.; Santhanam, K.S.V. Electrochemical hydrodynamics in a magnetic field with laser interferome-try. Electrochim. Acta 1987, 32, 1679–1691. [Google Scholar]
- Waskaas, M. Short-term effects of magnetic fields on diffusion in stirred and unstirred paramagnetic solutions. J. Phys. Chem. 1993, 97, 6470–6476. [Google Scholar] [CrossRef]
- Waskaas, M. Magnetic field effect on electrode reactions. I. Effects on the open-circuit potential of electrodes in solutions of different magnetic properties. Acta Chem. Scand. 1996, 50, 516–520. [Google Scholar] [CrossRef][Green Version]
- Mogi, K.; Sakihama, T.; Hirota, N.; Kitazawa, K. Magnetic field effect on the transport process of paramagnetic or diamagnetic substances in the aqueous solution. J. Appl. Phys. 1999, 85, 5714–5716. [Google Scholar] [CrossRef]
- Waskaas, M.; Kharkats, Y.I. Magnetoconvection phenomena: A mechanism for influence of magnetic fields on electrochemical processes. J. Phys. Chem. B 1999, 103, 4876–4883. [Google Scholar] [CrossRef]
- Leventis, N.; Gao, X. ND−Fe−B permanent magnet electrodes. Theoretical evaluation and experimental demonstration of the paramagnetic body forces. J. Am. Chem. Soc. 2002, 124, 1079–1088. [Google Scholar] [CrossRef]
- Perov, N.S.; Sheverdyaeva, P.M.; Inoue, M. Effect of magnetic field on the electrode potential of metals. J. Appl. Phys. 2002, 91, 8557. [Google Scholar] [CrossRef]
- Ručinskien, A.; Bikulčius, G.; Gudavičiūt, L.; Juzeliūnas, E. Magnetic field effect on stainless steel corrosion in FeCl3 solution. Electrochem. Commun. 2002, 4, 86–91. [Google Scholar] [CrossRef]
- Krause, A.; Uhlemann, M.; Gebert, A.; Schultz, L. The effect of magnetic fields on the electrodeposition of cobalt. Electrochim. Acta 2004, 49, 4127–4134. [Google Scholar] [CrossRef]
- Rabah, K.; Chopart, J.-P.; Schloerb, H.; Saulnier, S.; Aaboubi, O.; Uhlemann, M.; Elmi, D.; Amblard, J. Analysis of the magnetic force effect on paramagnetic species. J. Electroanal. Chem. 2004, 571, 85–91. [Google Scholar] [CrossRef]
- Uhlemann, M.; Schlörb, H.; Msellak, K.; Chopart, J.-P. Electrochemical deposition of CU under superimposition of high magnetic fields. J. Electrochem. Soc. 2004, 151, C598–C603. [Google Scholar] [CrossRef]
- Bund, A.; Kuehnlein, H.H. Role of magnetic forces in electrochemical reactions at microstructures. J. Phys. Chem. B 2005, 109, 19845–19850. [Google Scholar] [CrossRef]
- Dass, A.; Counsil, J.A.; Gao, X.; Leventis, N. Magnetic field effects on the open circuit potential of ferromagnetic electrodes in corroding solutions. J. Phys. Chem. B 2005, 109, 11065–11073. [Google Scholar] [CrossRef]
- Leventis, N.; Dass, A. Demonstration of the elusive concentration-gradient paramagnetic force. J. Am. Chem. Soc. 2005, 127, 4988–4989. [Google Scholar] [CrossRef] [PubMed]
- Uhlemann, M.; Krause, A.; Chopart, J.P.; Gebert, A. Electrochemical deposition of CO under the influence of high magnetic fields. J. Electrochem. Soc. 2005, 152, C817–C826. [Google Scholar] [CrossRef]
- Coey, J.M.D.; Rhen, F.M.F.; Dunne, P.; McMurry, S. The magnetic concentration gradient force—Is it real? J. Solid State Electrochem. 2007, 11, 711–717. [Google Scholar] [CrossRef]
- Krause, A.; Koza, J.; Ispas, A.; Uhlemann, M.; Gebert, A.; Bund, A. Magnetic field induced micro-convective phenomena inside the diffusion layer during the electrodeposition of Co, Ni and Cu. Electrochim. Acta 2007, 52, 6338–6345. [Google Scholar] [CrossRef]
- Lioubashevski, O.; Katz, E.; Willner, I. Effects of magnetic field directed orthogonally to surfaces on electrochemical processes. J. Phys. Chem. C 2007, 111, 6024–6032. [Google Scholar] [CrossRef]
- Weier, T.; Eckert, K.; Mühlenhoff, S.; Cierpka, C.; Bund, A.; Uhlemann, M. Confinement of paramagnetic ions under magnetic field influence: Lorentz versus concentration gradient force based explanations. Electrochem. Commun. 2007, 9, 2479–2483. [Google Scholar] [CrossRef]
- Aaboubi, O.; Douglade, J. Application of magnetic field to control mass transport process during silver cementation on copper. J. Electroanal. Chem. 2013, 693, 42–50. [Google Scholar] [CrossRef]
- Yu, Y.; Song, Z.; Ge, H.; Wei, G.; Jiang, L. Effects of magnetic fields on the electrodeposition process of Cobalt. Int. J. Electrochem. Sci. 2015, 10, 4812–4819. [Google Scholar]
- Svendsen, J.A.; Waskaas, M. Mathematical modelling of mass transfer of paramagnetic ions through an inert membrane by the transient magnetic concentration gradient force. Phys. Fluids 2020, 32, 013606. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Z.; Zhou, Z.; Yang, G.; Cai, X. Impact of magnetic field on corrosion performance of Al–Mg alloy with different electrode potential phases. Intermetallics 2021, 129, 107037. [Google Scholar] [CrossRef]
- Wolfson, R. Essential University Physics, 2nd ed.; Pearson: Essex, UK, 2014; Volume 2, pp. 133–148, 216–219. [Google Scholar]
- El-Hawary, M.E. Principles of Electric Machines with Power Electronic Applications, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2002; pp. 23–77. [Google Scholar]
- Boylestad, R.L. Introductory Circuit Analysis, 13th ed.; Pearson: Boston, MA, USA, 2016; pp. 543–561. [Google Scholar]
- Fitzgerald, A.E.; Kingsley, C., Jr.; Umans, S.D. Electric Machinery, 6th ed.; MCGraw-Hill: New York, NY, USA, 2003; pp. 1–9, 214–221. [Google Scholar]
- Electric Machines, Torque. Available online: https://people.ucalgary.ca/~aknigh/electrical_machines/fundamentals/f_ac_torque.html (accessed on 22 February 2021).
- Mablekos, V.E. Electric Machine Theory for Power Engineers, 1st ed.; Harper and Row: New York, NY, USA, 1980; pp. 384–394. [Google Scholar]
- Gan, C.; Wu, J.; Sun, Q.; Kong, W.; Li, H.; Hu, Y. A review on machine topologies and control techniques for low-noise switched reluctance motors in electric vehicle applications. IEEE Access 2018, 6, 31430–31443. [Google Scholar] [CrossRef]
- Hu, W.; Zhang, X.; Yin, H.; Geng, H.; Zhang, Y.; Shi, L. Analysis of magnetic field and electromagnetic performance of a new hybrid excitation synchronous motor with dual-V type magnets. Energies 2020, 13, 1501. [Google Scholar] [CrossRef]
- Wendt, H.; Kreysa, G. Electrochemical Engineering, 1st ed.; Springer-Verlag: Berlin, Germany, 1999; pp. 97–98. [Google Scholar]
- Tobias, C.W.; Eisenberg, M.; Wilke, C.R. Diffusion and convection in electrolysis—A theoretical review. J. Electrochem. Soc. 1952, 99, 359C–365C. [Google Scholar] [CrossRef]
- Ragsdale, S.R.; White, H.S. Imaging microscopic magnetohydrodynamic flows. Anal. Chem. 1999, 71, 1923–1927. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Waskaas, M. On the Origin of the Magnetic Concentration Gradient Force and Its Interaction Mechanisms with Mass Transfer in Paramagnetic Electrolytes. Fluids 2021, 6, 114. https://doi.org/10.3390/fluids6030114
Waskaas M. On the Origin of the Magnetic Concentration Gradient Force and Its Interaction Mechanisms with Mass Transfer in Paramagnetic Electrolytes. Fluids. 2021; 6(3):114. https://doi.org/10.3390/fluids6030114
Chicago/Turabian StyleWaskaas, Magne. 2021. "On the Origin of the Magnetic Concentration Gradient Force and Its Interaction Mechanisms with Mass Transfer in Paramagnetic Electrolytes" Fluids 6, no. 3: 114. https://doi.org/10.3390/fluids6030114
APA StyleWaskaas, M. (2021). On the Origin of the Magnetic Concentration Gradient Force and Its Interaction Mechanisms with Mass Transfer in Paramagnetic Electrolytes. Fluids, 6(3), 114. https://doi.org/10.3390/fluids6030114





