Biomagnetic Fluid Flow and Heat Transfer Study of Blood with Gold Nanoparticles over a Stretching Sheet in the Presence of Magnetic Dipole
Abstract
1. Introduction
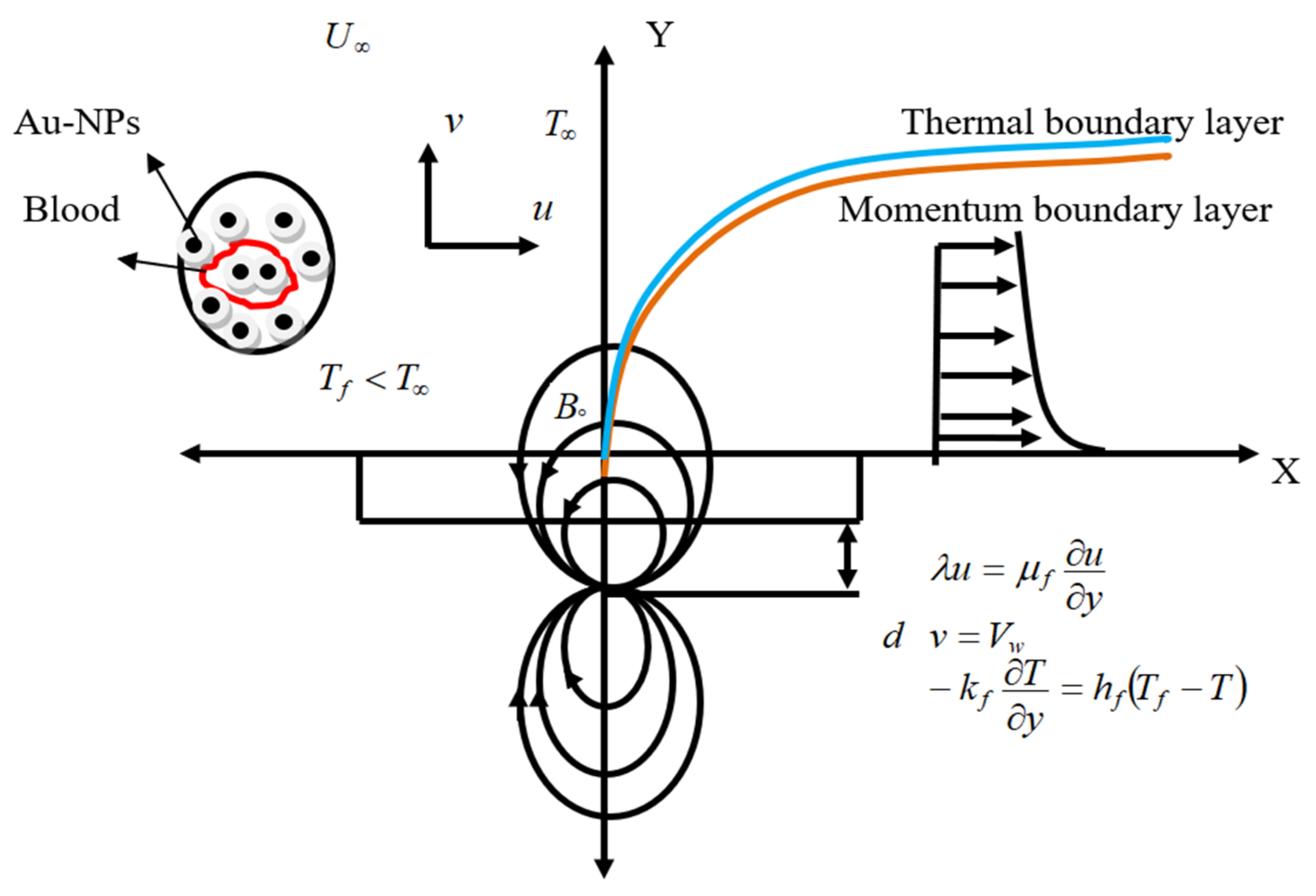
2. Problem Formulation
3. Solution Procedure
4. Numerical Method for Solution
5. Comparison with Previous Work and Values of Thermophysical Properties
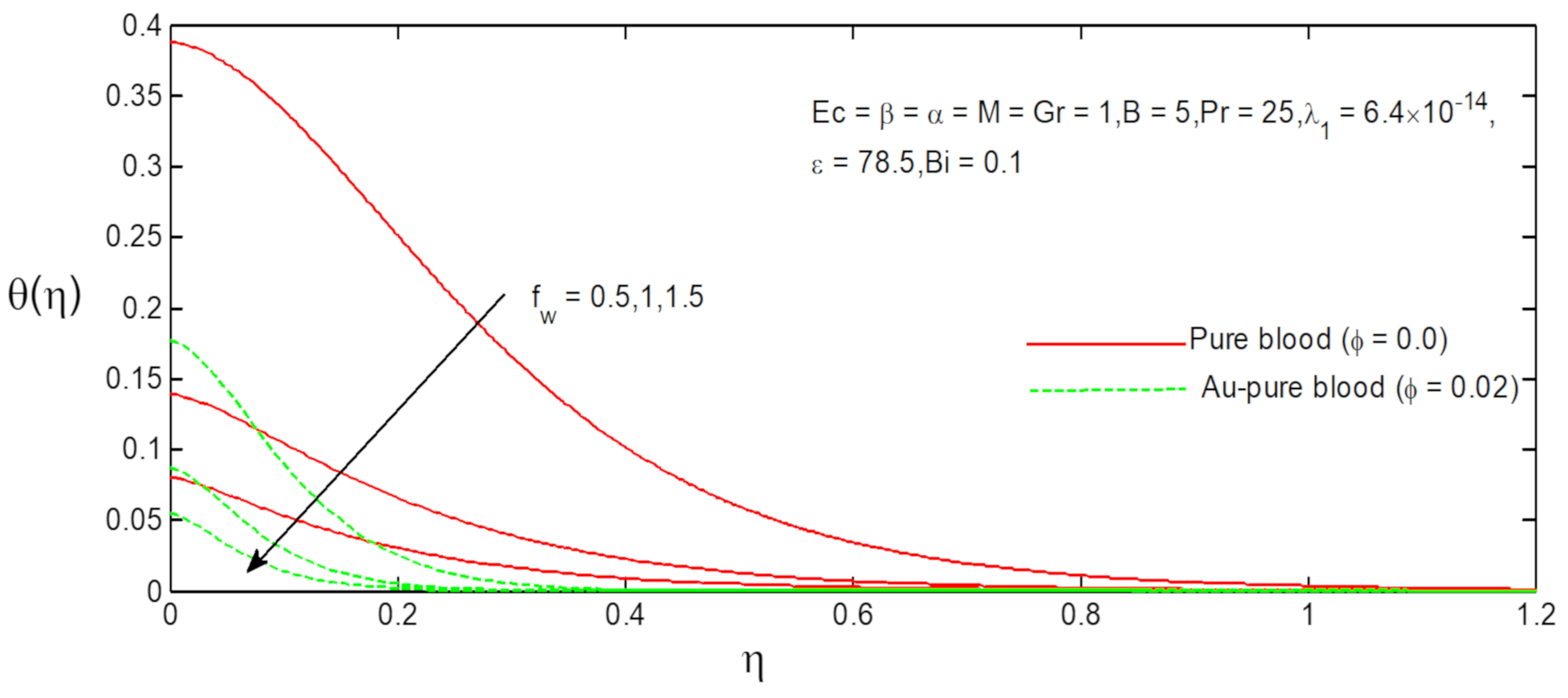
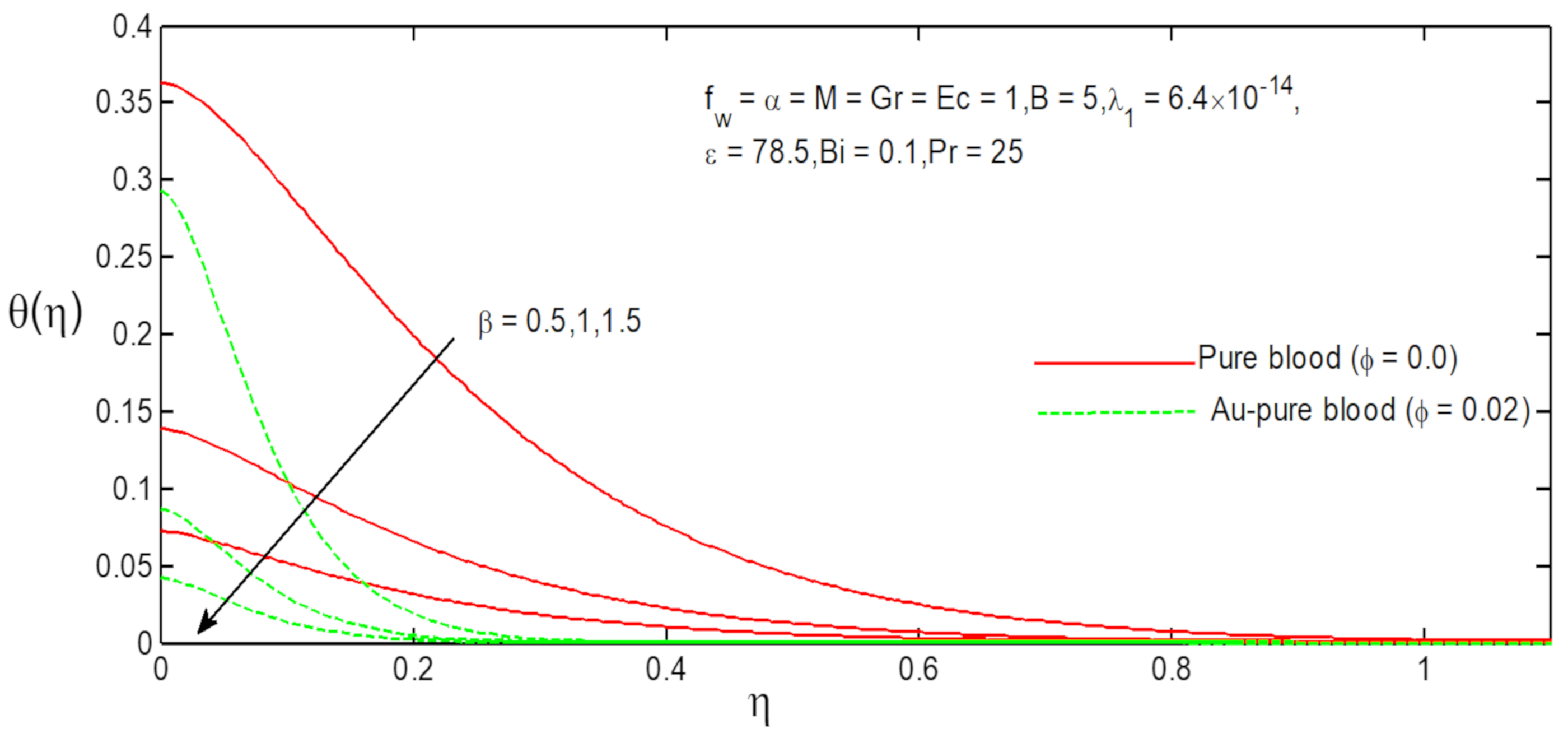
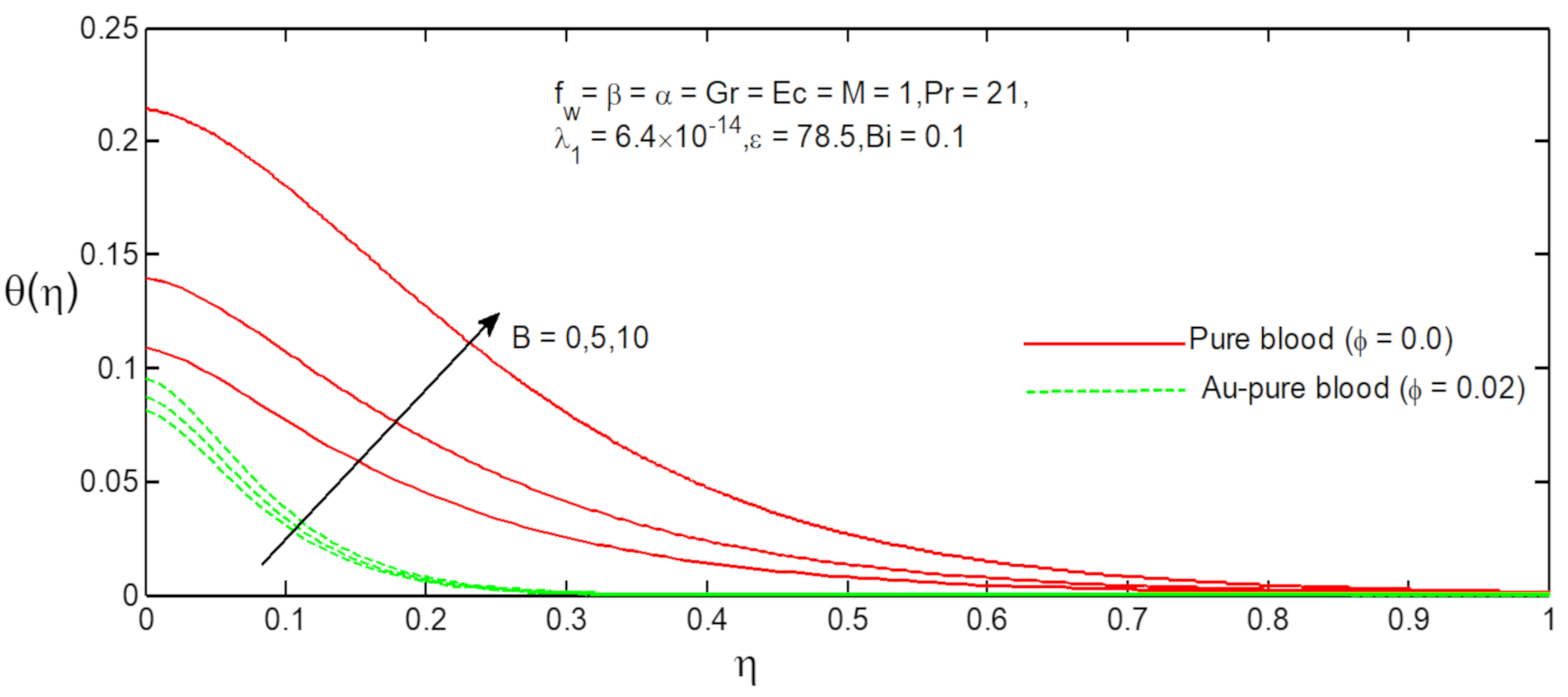
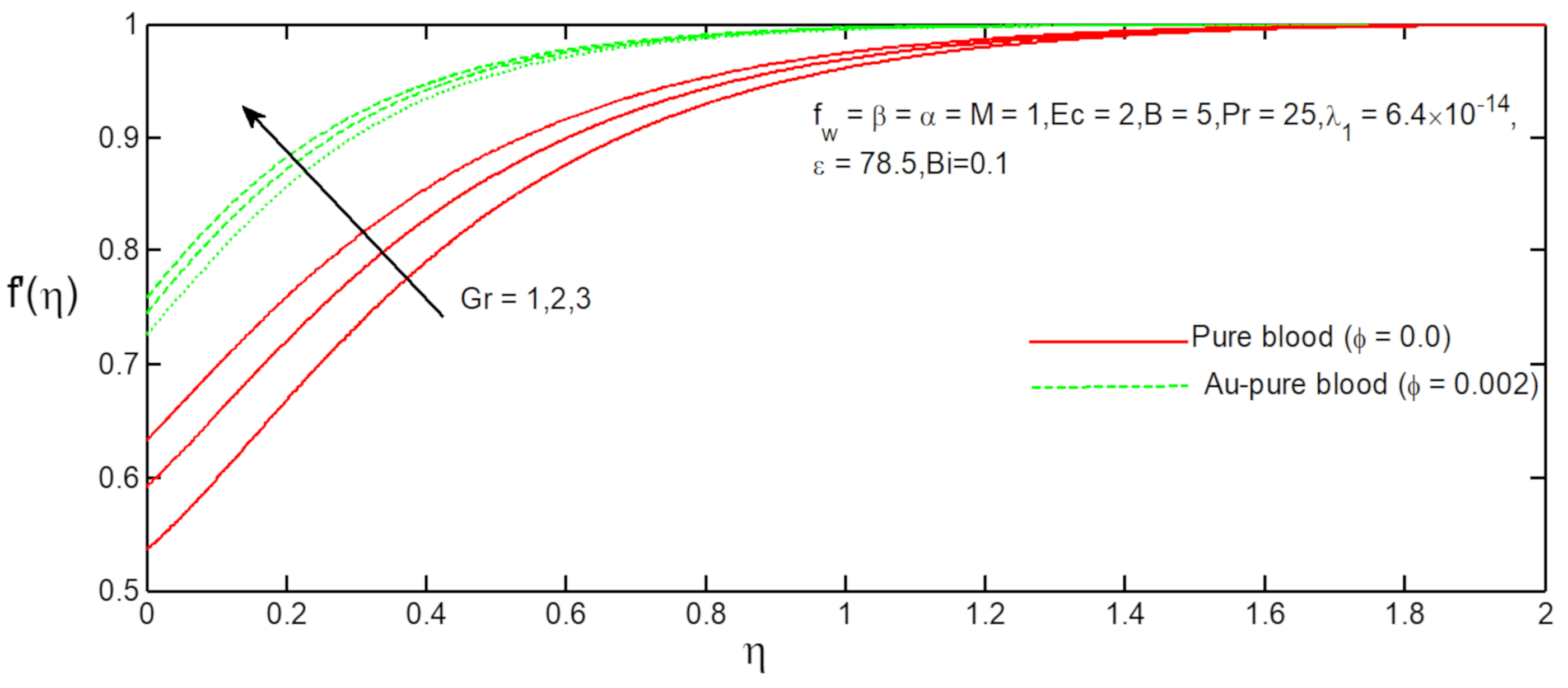
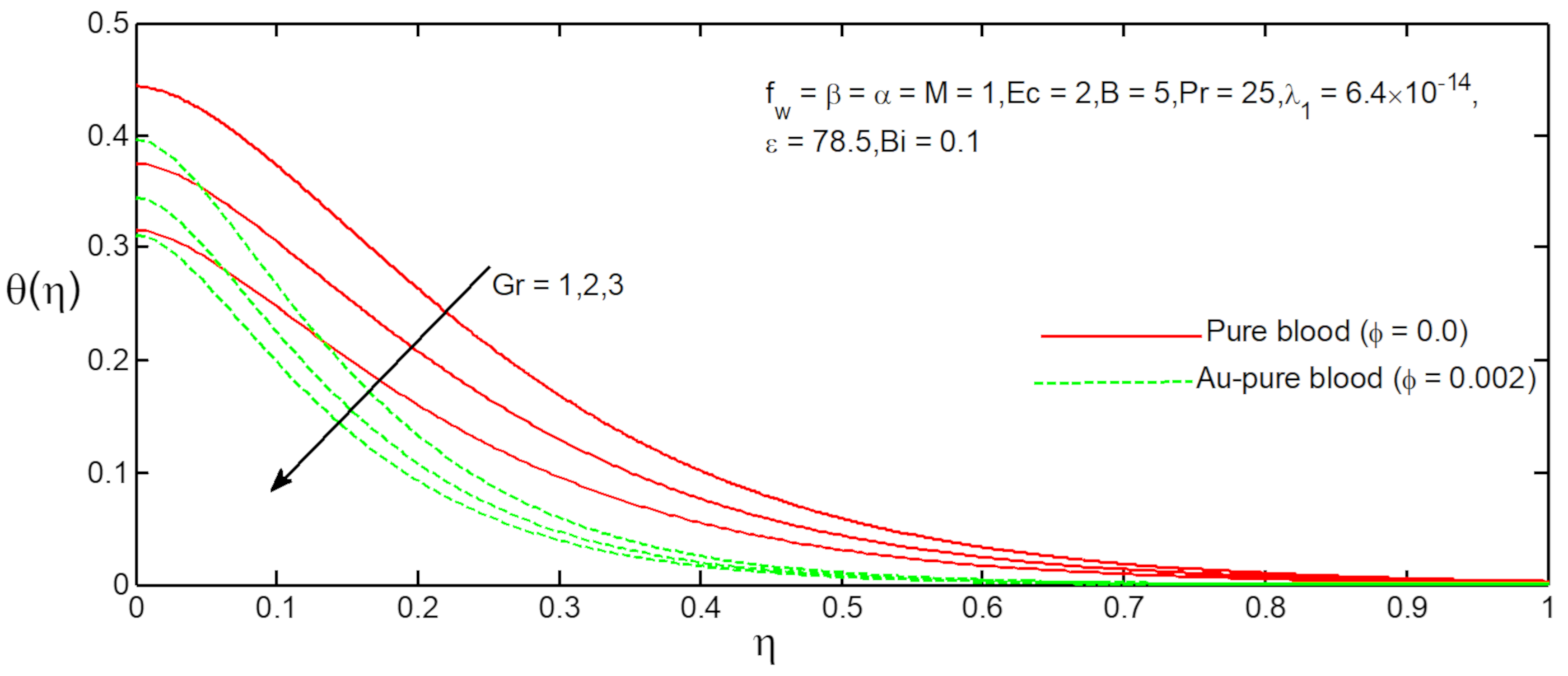
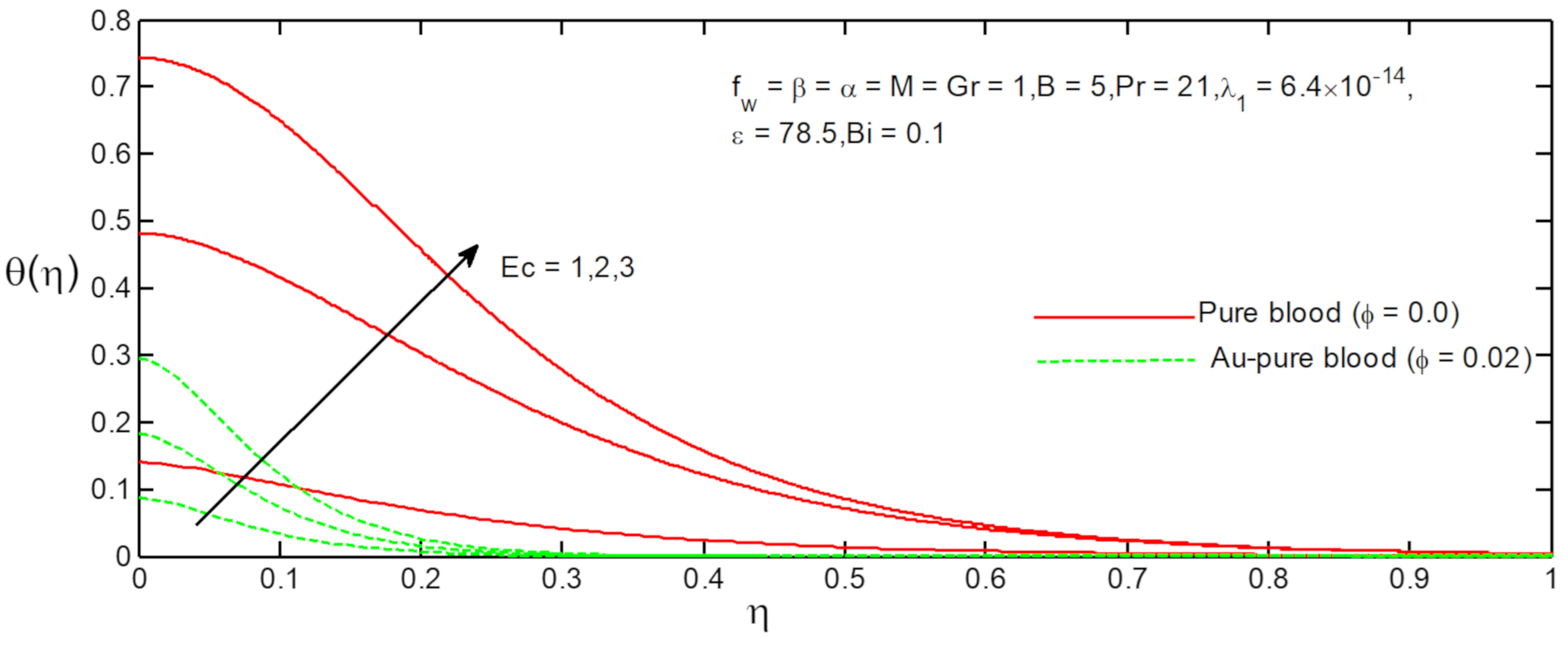
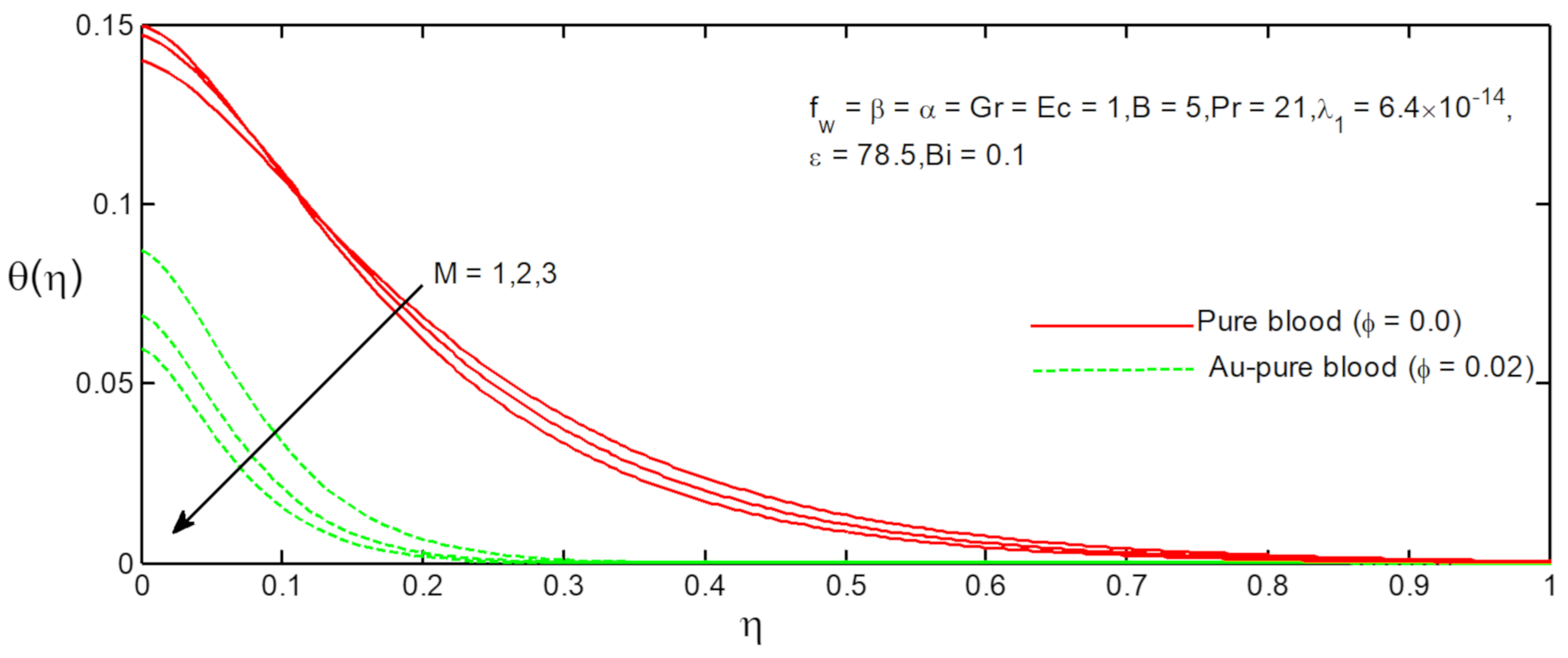
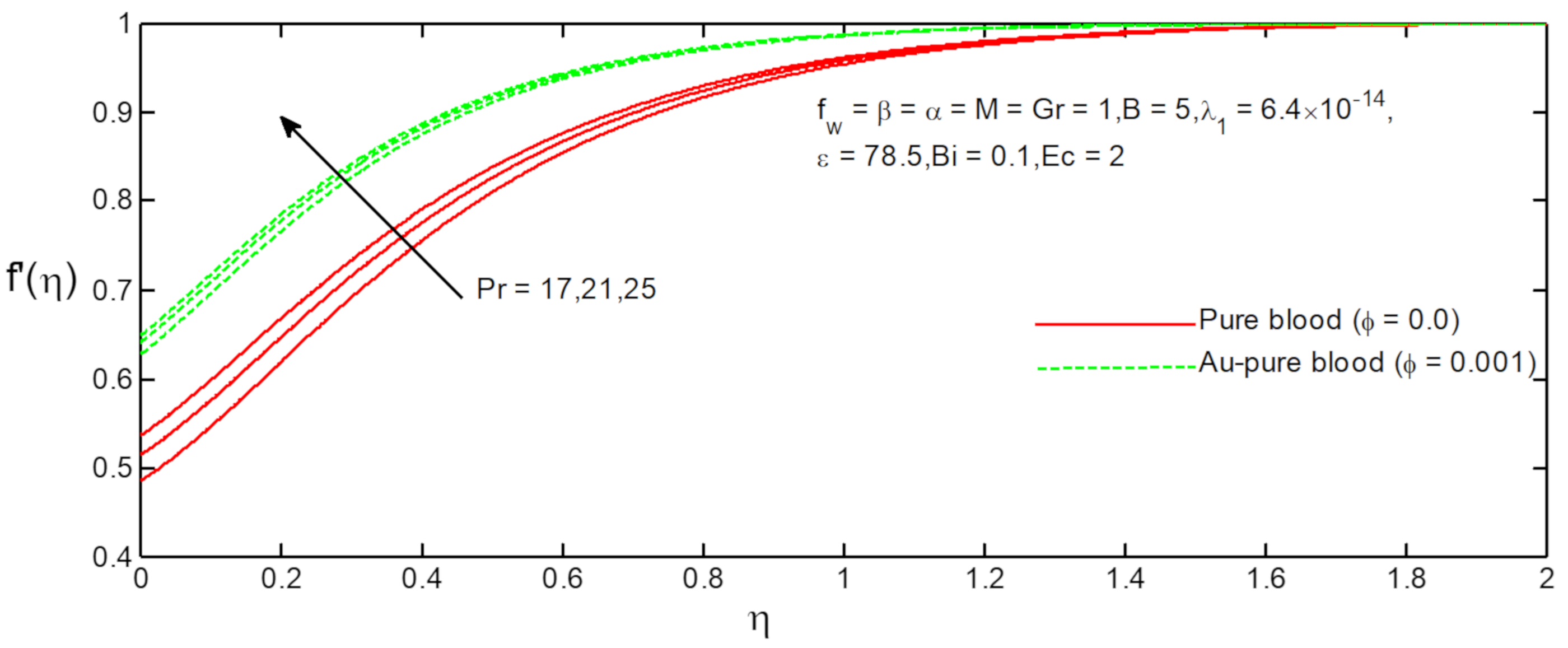
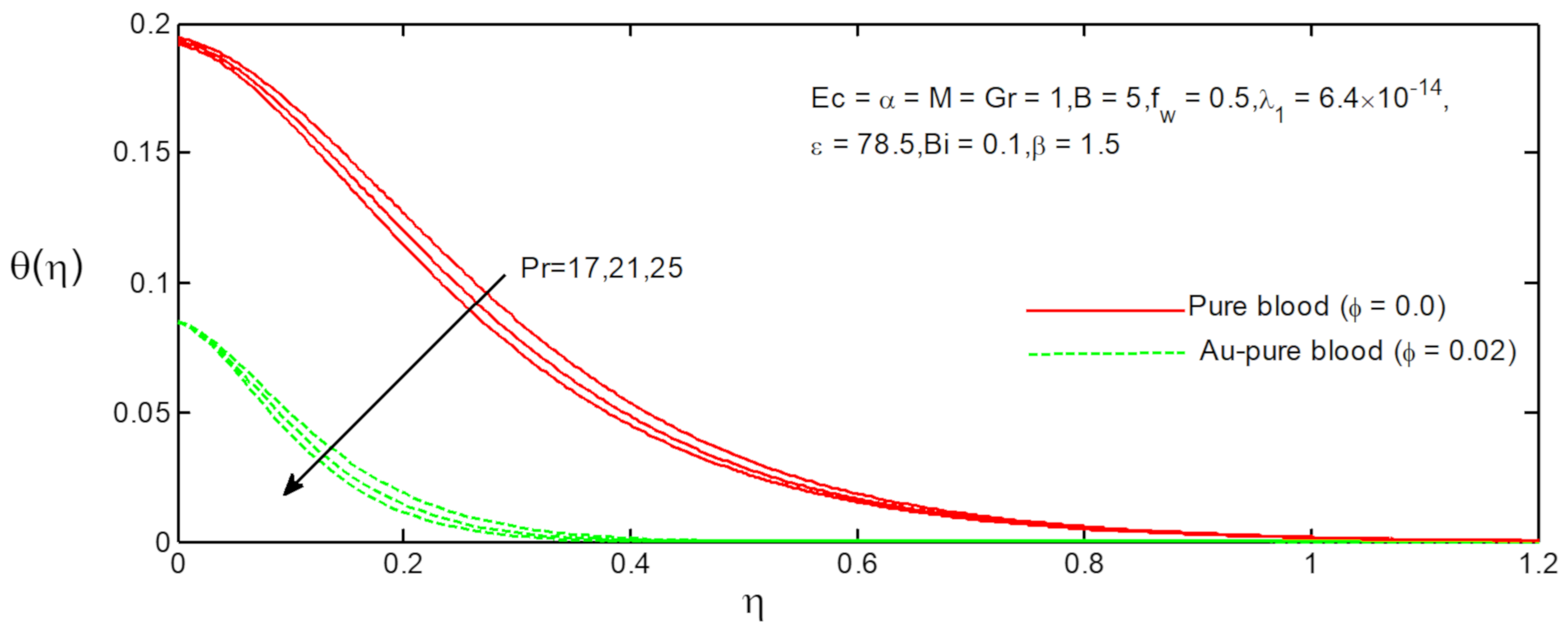
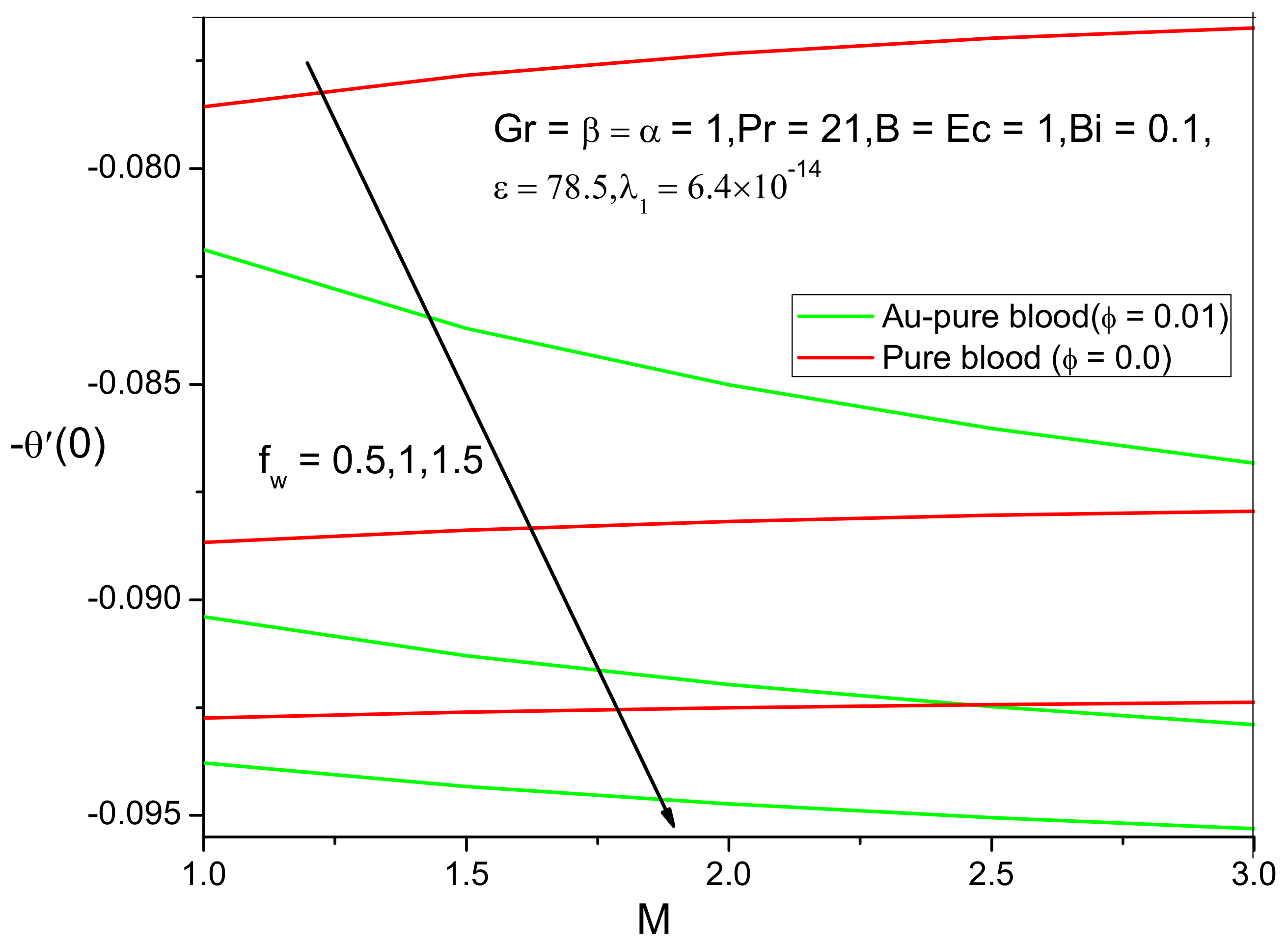
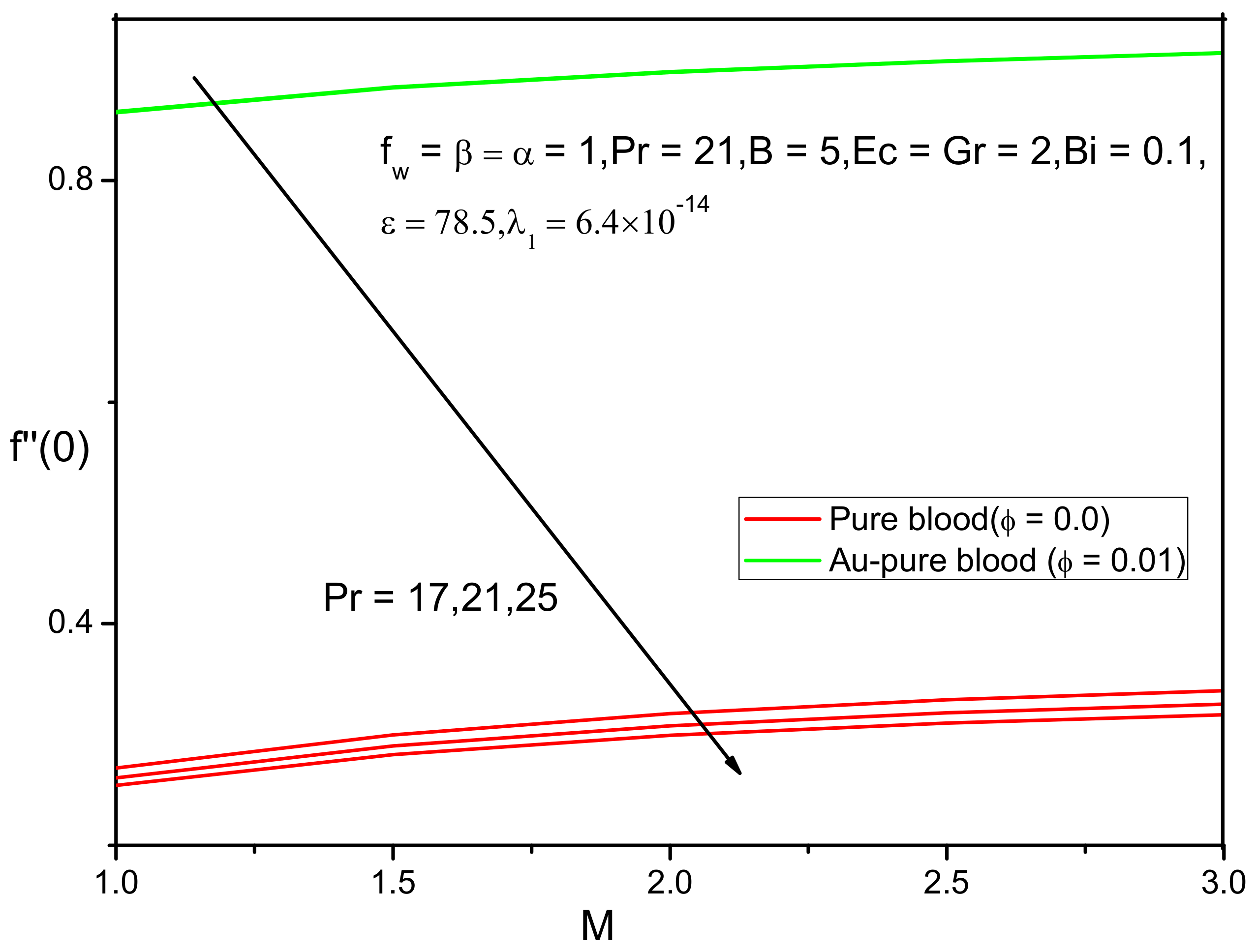
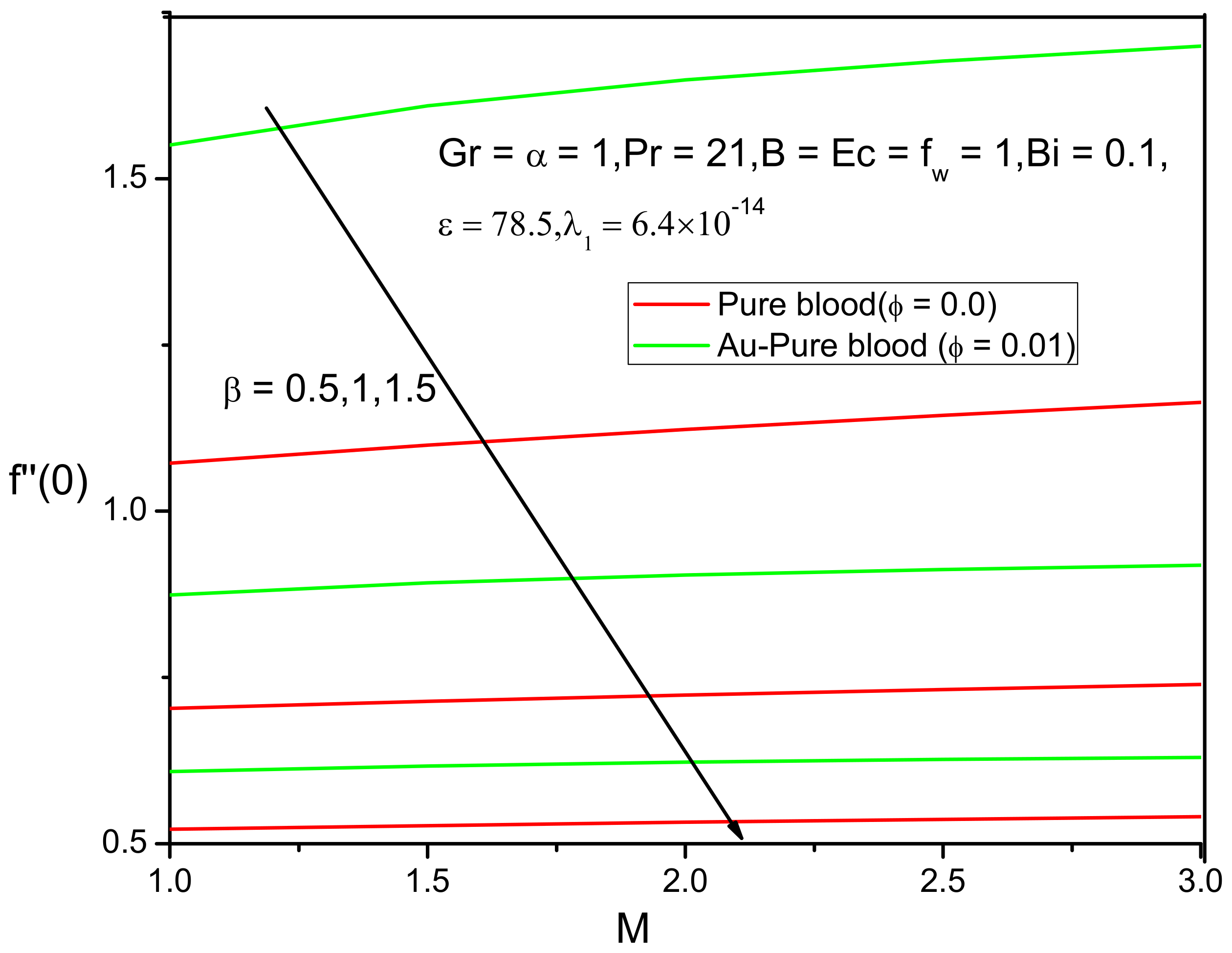
6. Results and Discussion
7. Conclusions
- The velocity profiles of Au-pure blood and pure blood nanofluid increase with increasing values of suction parameter, slip parameter, Grashof number, magnetic field parameter and Prandtl number;
- The temperature profiles of Au-pure blood and pure blood nanofluid increase with increasing values of Ferromagnetic field parameter;
- The velocity profiles of pure blood nanofluid increase with increasing values of Biot number and Eckert number, whereas those of Au-pure blood decrease in these cases;
- The skin friction coefficient of Au-pure blood and pure blood nanofluid decreases with increased values of Prandtl number and slip parameter;
- The heat transfer rate of Au-pure blood and pure blood nanofluid is augmented with increasing values of Eckert number and ferromagnetic parameter;
- The heat transfer rate of Au-pure blood and pure blood nanofluid decreases with increasing values of Grashof number and suction parameter.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Misra, J.C.; Sinha, A.; Shit, G.C. Flow of a biomagnetic viscoelastic fluid: Application to estimate of blood flow in arteries during electromagnetic hyperthermia, a therapeutic procedure for cancer treatment. App. Math. Mech. Engl. 2010, 31, 1405–1420. [Google Scholar] [CrossRef]
- Nelson, P.W.; Gilchrist, M.A.; Coombs, D.; Hyman, J.M.; Perelson, A.S. An age-structured model of HIV infection that allow for variations in the production rate of viral particles and the death rate of productively infected cells. Math. Biosci. Eng. 2004, 1, 267–288. [Google Scholar] [CrossRef]
- Wang, J.; Dong, X. Analysis of an HIV infection model incorporating latency age and infection age. Math. Biosci. Eng. 2018, 15, 569–594. [Google Scholar] [CrossRef]
- Choi, S.U.S. Enhancing thermal conductivity of fluids with nanoparticles. In Proceedings of the ASME InternationalMechanical Engineering Congress and Exposition, San Francisco, CA, USA, 12–18 November 1995; pp. 99–105. [Google Scholar]
- Michael, Faraday’s Gold Colloids, The Royal Institution: Science Lives Here. Available online: www.rigb.org (accessed on 4 December 2015).
- Akbari, N.; Ganji, D.D.; Gholinia, M.; Gholinia, S. Computer simulation of blood flow with nanoparticles in a magnetic field as a third grade non-Newtonian through porous vessels by flex PDE software. Innov. Ener. Res. 2017, 6, 1–7. [Google Scholar]
- Huang, X.; El-Sayed, M.A. Gold nanoparticles and implementations in cancer diagnosis and photo thermal therapy. J. Adv. Res. 2010, 1, 13–28. [Google Scholar] [CrossRef]
- Olubode, K.K.; Issac, L.C.; Mahanthesh, B.; Salman, S. Heat transfer in the flow of Blood-gold carreaunanofluid induced by partial slip and buoyancy. Heat Transf. Asia Res. 2018, 47, 806–823. [Google Scholar] [CrossRef]
- Srinivas, S.; Vijayalakshmi, A.; Reddy, A.S. Flow and heat transfer of gold-blood nanofluid in a porous channel with moving/stationary walls. J. Mech. 2017, 33, 395–404. [Google Scholar] [CrossRef]
- Elgazery, N.S. Flow of non-Newtonian magneto fluid with gold and alumina nanoparticles through a non Darcian porous medium. J. Egypt. Math. Soc. 2019, 27. [Google Scholar] [CrossRef]
- Eid, M.R. Effects of nanoparticles shapes on non-Newtonian Bio-nanofluid flow ina suction/Blowing process with convective condition: Sisko model. J. Non Equilib. Thermodyn. 2019, 45. [Google Scholar] [CrossRef]
- Ferdows, M.; Khan, M.S.; Bég, O.A.; Azad, M.A.K.; Alam, M.M. Numerical study of transient magnetohydrodynamic radiative free convection nanofluid flow from a stretching permeable surface. J. Process. Mech. Eng. 2014, 228, 181–196. [Google Scholar] [CrossRef]
- Jamal abadi, M.Y.A.; DaqiqShirazi, M.; Nasiri, H.; Safaei, M.R.; Nguyen, T.K. Modeling and analysis of biomagnetic blood Car reau fluid flow through a stenosis artery with magnetic heat transfer: A transient study. PLoS ONE 2018, 13, e0192138. [Google Scholar]
- Ferdows, M.; Murtaza, M.G.; Tzirtzilakis, E.E.; Alzahrani, F. Numerical study of blood flow and heat transfer through stretching cylinder in the presence of a magnetic dipole. Z. Angew. Math. Mech. 2020, 100, e201900278. [Google Scholar] [CrossRef]
- Umair, K.; Anum, S.; Aurang, Z.; El-Sayed, M.S.; Dumitru, B. MHD radiative blood flow embracing gold particles via a slippery sheet through an erratic heat source/sink. Mathematics 2020, 8, 1597. [Google Scholar] [CrossRef]
- Mutuku-Njane, W.N.; Makinde, O.D. Combined effect of buoyancy force and Navier slip on MHD flow of a Nanofluid over a convectively heated vertical porous plate. Sci. World J. 2013. [Google Scholar] [CrossRef]
- Tzirtzilakis, E.E. A simple numerical methodology for BFD problems using stream function vortices formulation. Commun. Numer. Methods Eng. 2000, 2, 1–6. [Google Scholar]
- Anderson, H.I.; Valens, O.A. Flow of a heated Ferro fluid over a stretching sheet in the presence of a magnetic dipole. Acta Mech. 1998, 28, 39–47. [Google Scholar] [CrossRef]
- Daniel, Y.S. Steady MHD boundary-layer slip flow and heat transfer of Nanofluid over a convectively heated of a non-linear permeable sheet. J. Adv. Mech. Eng. 2016, 3, 1–14. [Google Scholar] [CrossRef]
- Tzirtzilakis, E.E. A mathematical model for blood flow in magnetic field. Phys. Fluids 2005, 17, 077103. [Google Scholar] [CrossRef]
- Gabriely, S.; Lau, R.W.; Gabriel, C. The dielectric properties of biological tissues: III. Parametric models for the dielectric spectrum of tissues. Phys. Med. Biol. 1996, 41, 2271–2293. [Google Scholar] [CrossRef]
- Hinghofer-Szalkay, H. Volume and density changes of biological fluids with temperature. J. Appl. Physiol. 1985, 59, 1686–1689. [Google Scholar] [CrossRef]
- Tzirtzilakis, E.E. Biomagnetic fluid flow in an aneurysm using ferrohydrodynamics principles. Phys. Fluids 2015, 27, 061902. [Google Scholar] [CrossRef]
- Reddy, S.R.R.; Reddy, P.B.A. Biomathematical analysis for the stagnation point flow over a nonlinear stretching surface with the second order velocity slip and Titanium alloy nanoparticle. Front. Heat Mass Transf. 2018, 10. [Google Scholar] [CrossRef]
- Alam, M.J.; Murtaza, M.G. Two Dimensional Biomagnetic fluid flow and heat transfer over a nonlinear stretching sheet with temperature dependent viscosity. Sch. J. Phys. Math. Stat. 2020, 7, 131–142. [Google Scholar] [CrossRef]
- Murtaza, M.G.; Ferdows, M.; Misra, J.C.; Tzirtzilakis, E.E. Three-dimensional biomagnetic Maxwell fluid flow over a stretching surface in presence of heat source/sink. Int. J. Biomath. 2019, 12, 1950036-20. [Google Scholar] [CrossRef]












| Thermo Physical Properties | Blood | Gold |
|---|---|---|
| 129 | ||
| 1050 | 19,300 | |
| 0.8 | ||
| 0.5 | 318 | |
| Daniel [19] | Present Result | |||
|---|---|---|---|---|
| 1 | 0.2 | 0.610262 | 0.610112 | 0.0246 |
| 1 | 0.5 | 0.595277 | 0.595863 | 0.0984 |
| 1 | 1.5 | 0.574537 | 0.574898 | 0.0629 |
| 5 | 0.2 | 0.607175 | 0.607160 | 0.0024 |
| 5 | 0.5 | 1.586744 | 1.607160 | 1.2869 |
| 5 | 1.5 | 1.557413 | 1.557214 | 0.0128 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alam, J.; Murtaza, G.; Tzirtzilakis, E.; Ferdows, M. Biomagnetic Fluid Flow and Heat Transfer Study of Blood with Gold Nanoparticles over a Stretching Sheet in the Presence of Magnetic Dipole. Fluids 2021, 6, 113. https://doi.org/10.3390/fluids6030113
Alam J, Murtaza G, Tzirtzilakis E, Ferdows M. Biomagnetic Fluid Flow and Heat Transfer Study of Blood with Gold Nanoparticles over a Stretching Sheet in the Presence of Magnetic Dipole. Fluids. 2021; 6(3):113. https://doi.org/10.3390/fluids6030113
Chicago/Turabian StyleAlam, Jahangir, Ghulam Murtaza, Efstratios Tzirtzilakis, and Mohammad Ferdows. 2021. "Biomagnetic Fluid Flow and Heat Transfer Study of Blood with Gold Nanoparticles over a Stretching Sheet in the Presence of Magnetic Dipole" Fluids 6, no. 3: 113. https://doi.org/10.3390/fluids6030113
APA StyleAlam, J., Murtaza, G., Tzirtzilakis, E., & Ferdows, M. (2021). Biomagnetic Fluid Flow and Heat Transfer Study of Blood with Gold Nanoparticles over a Stretching Sheet in the Presence of Magnetic Dipole. Fluids, 6(3), 113. https://doi.org/10.3390/fluids6030113








