Fluid-Structure Interaction of Flexible Whisker-Type Beams and Its Implications for Flow Sensing by Pair-Wise Correlation
Abstract
1. Introduction
2. Materials and Methods
2.1. Sea Lion Model with Whiskers
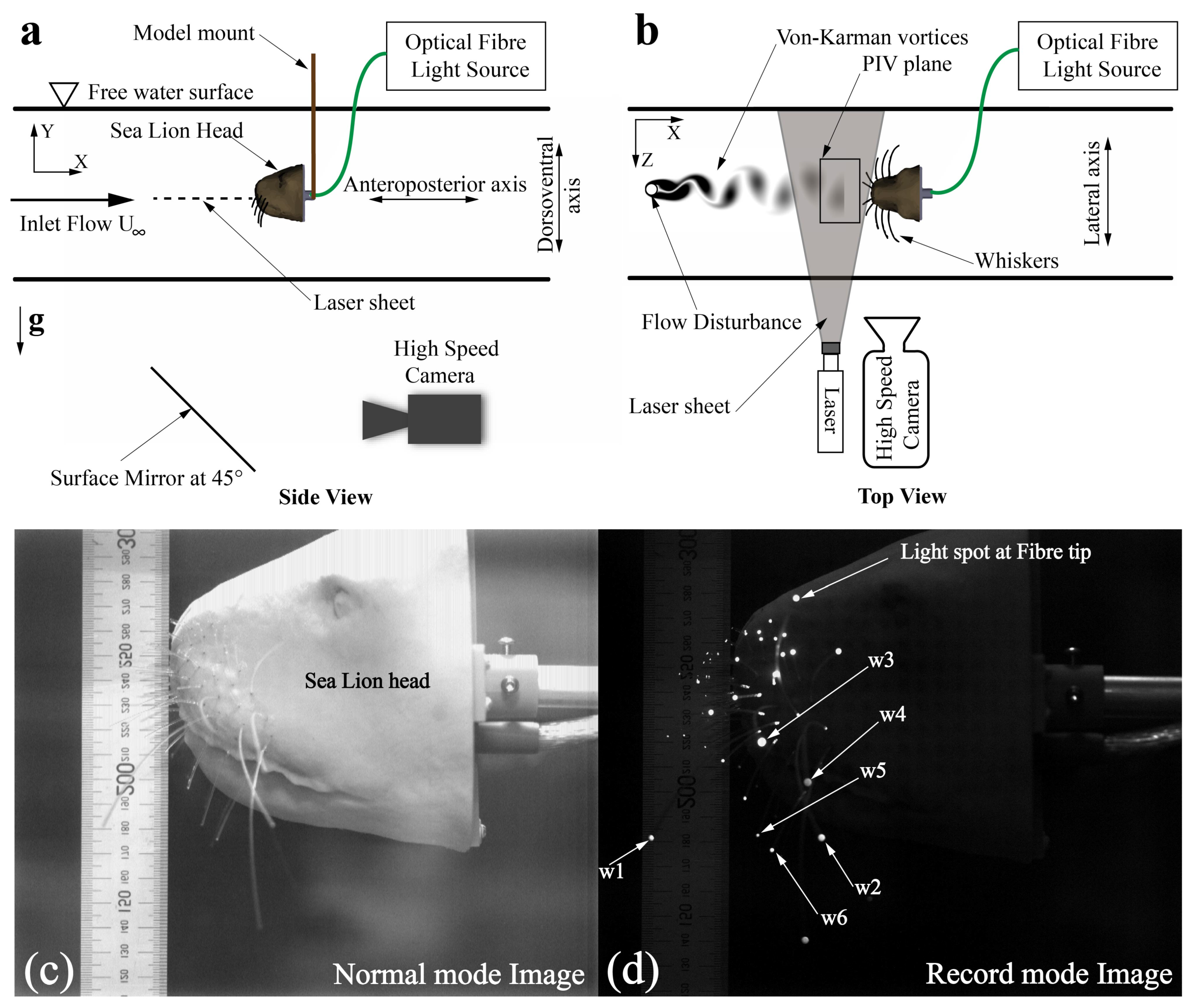
2.2. Experimental Setup for Motion Tracking
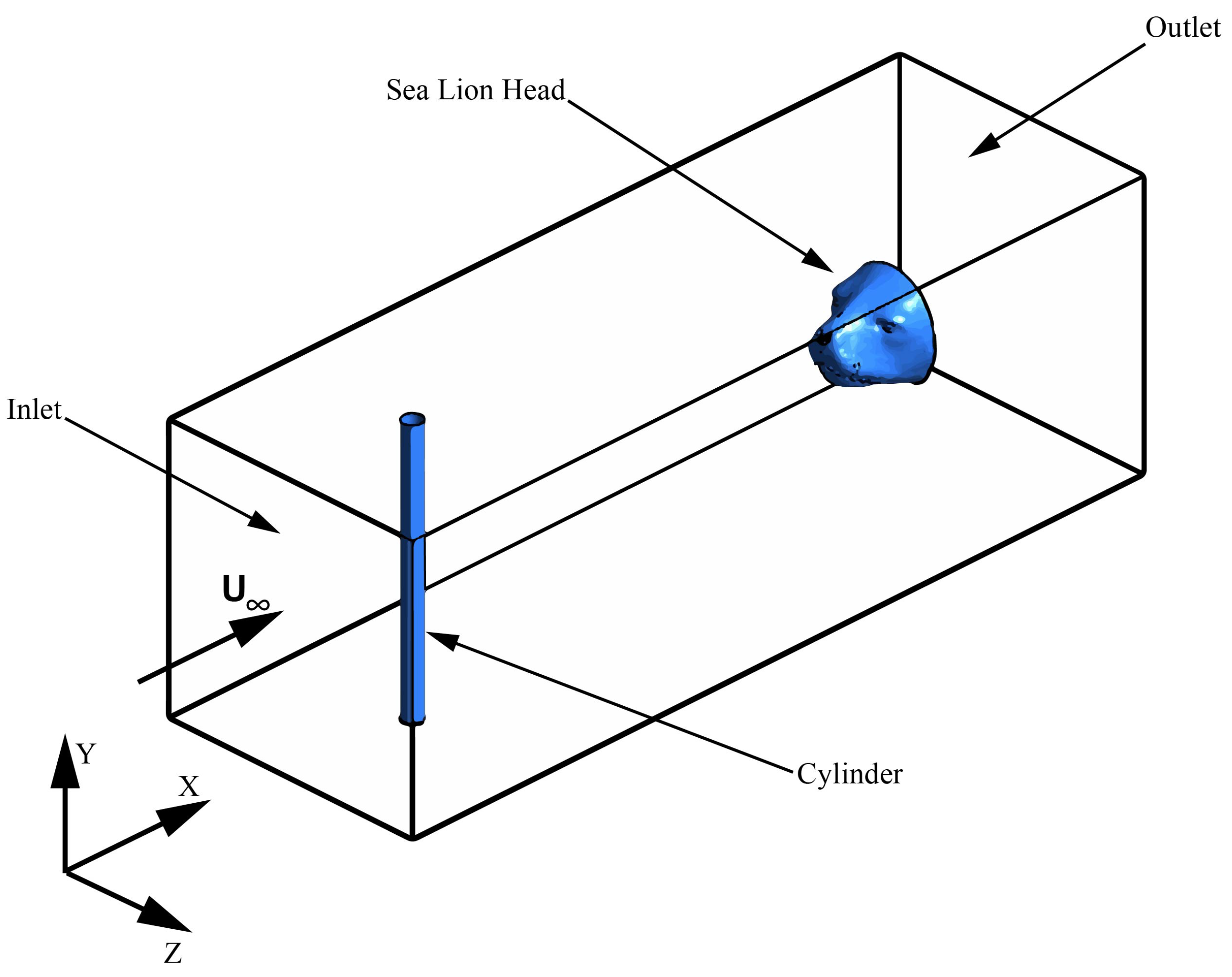
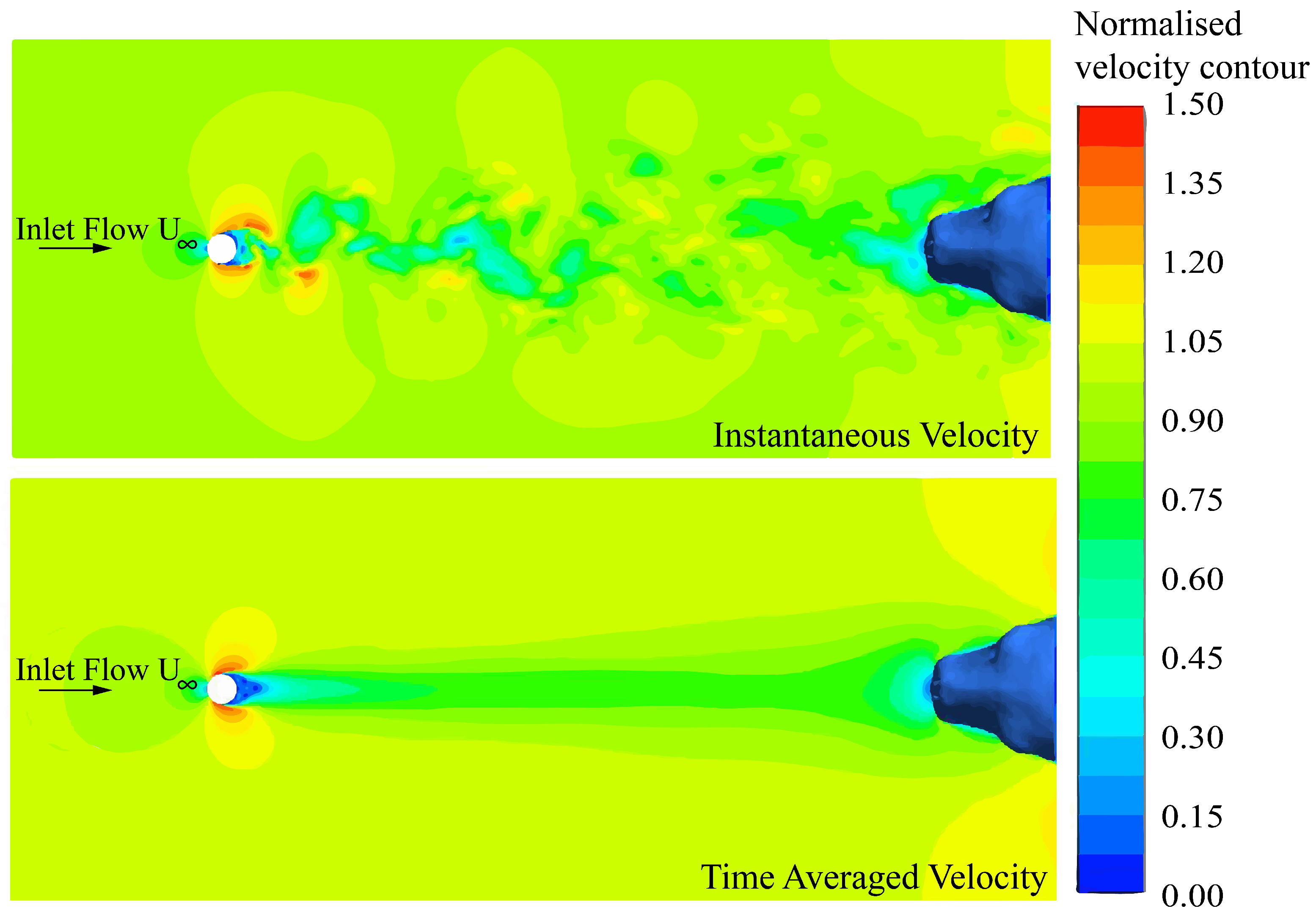
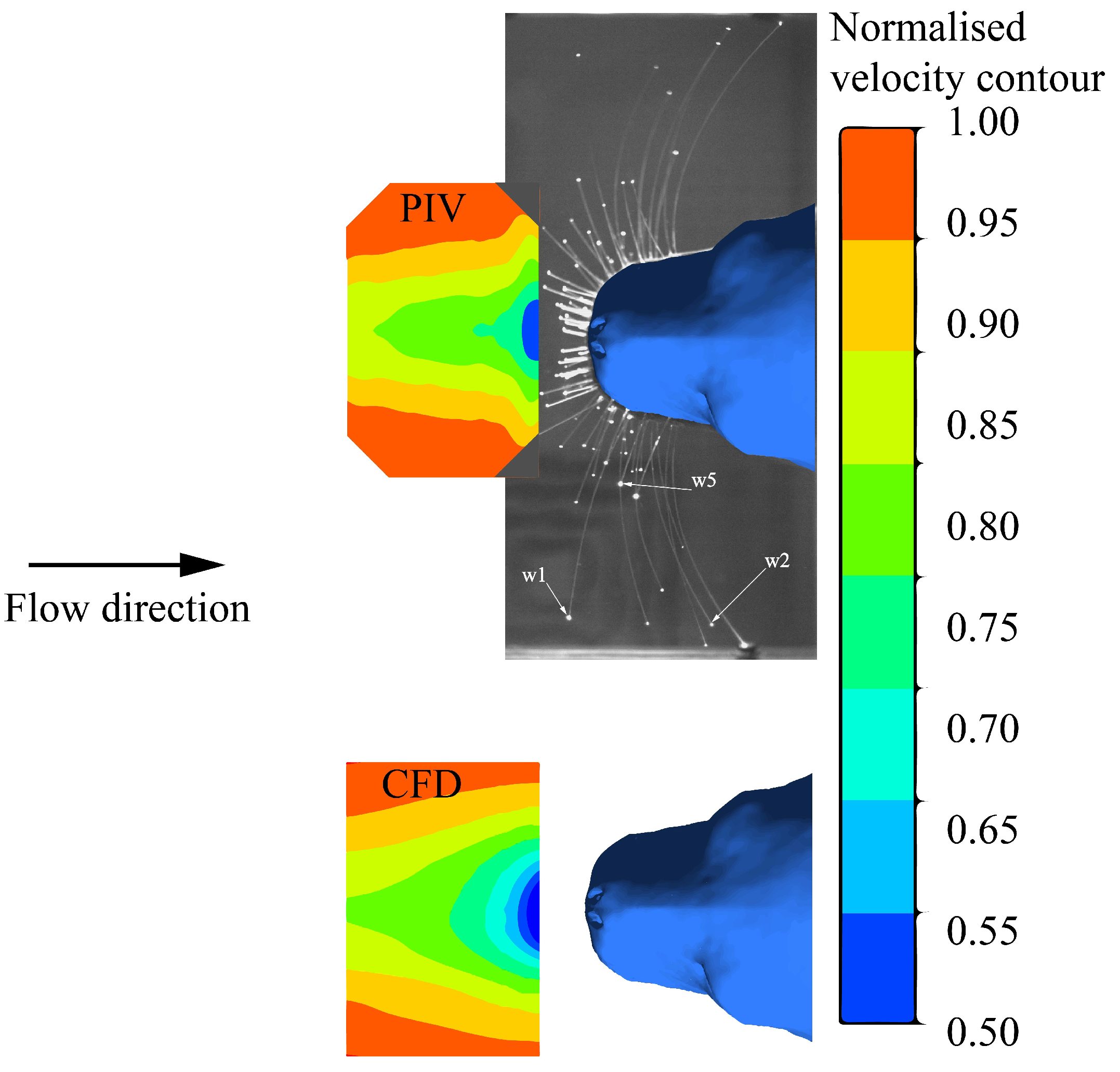
2.3. Flow Studies Using PIV and CFD
3. Results
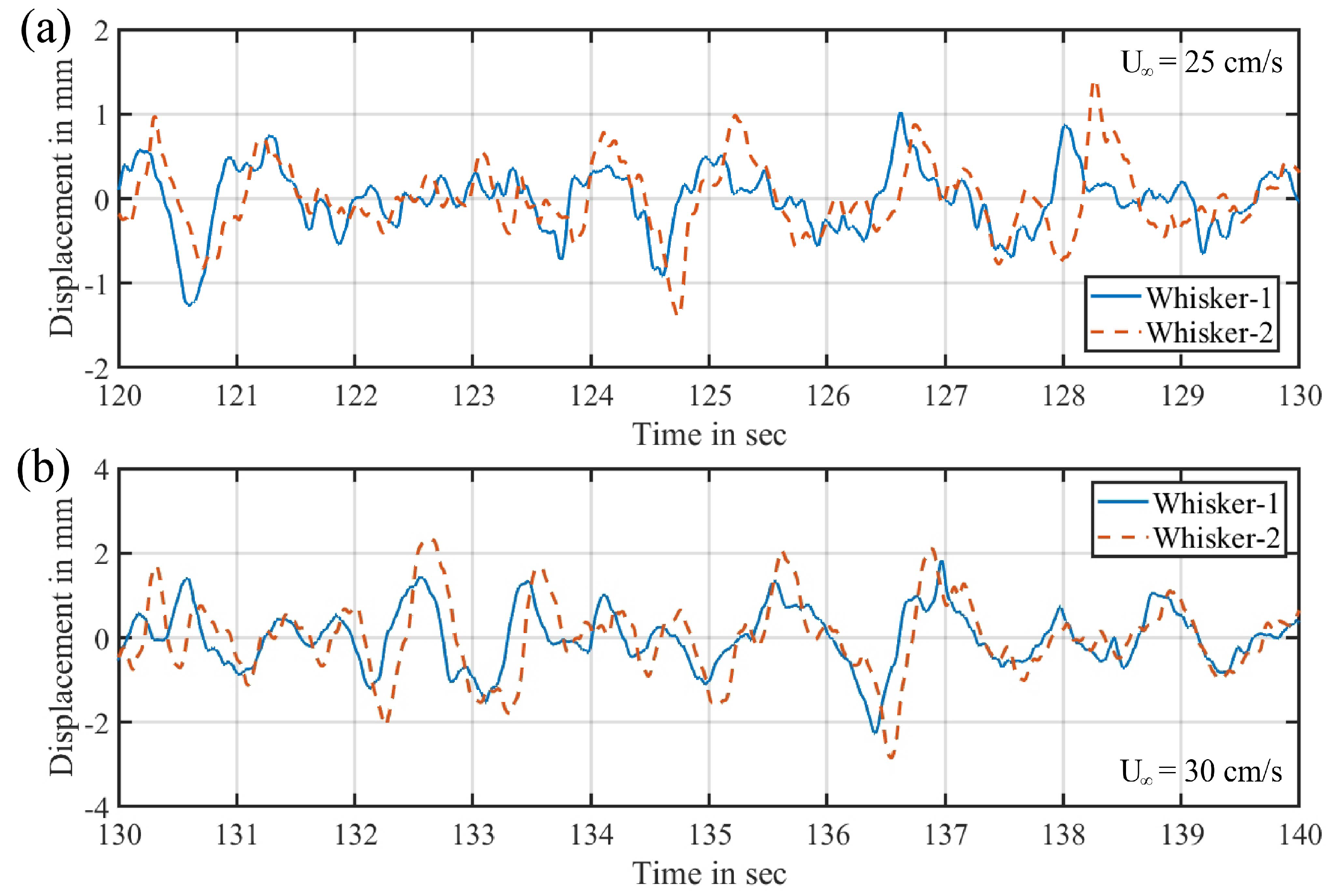
3.1. Typical Whisker Response
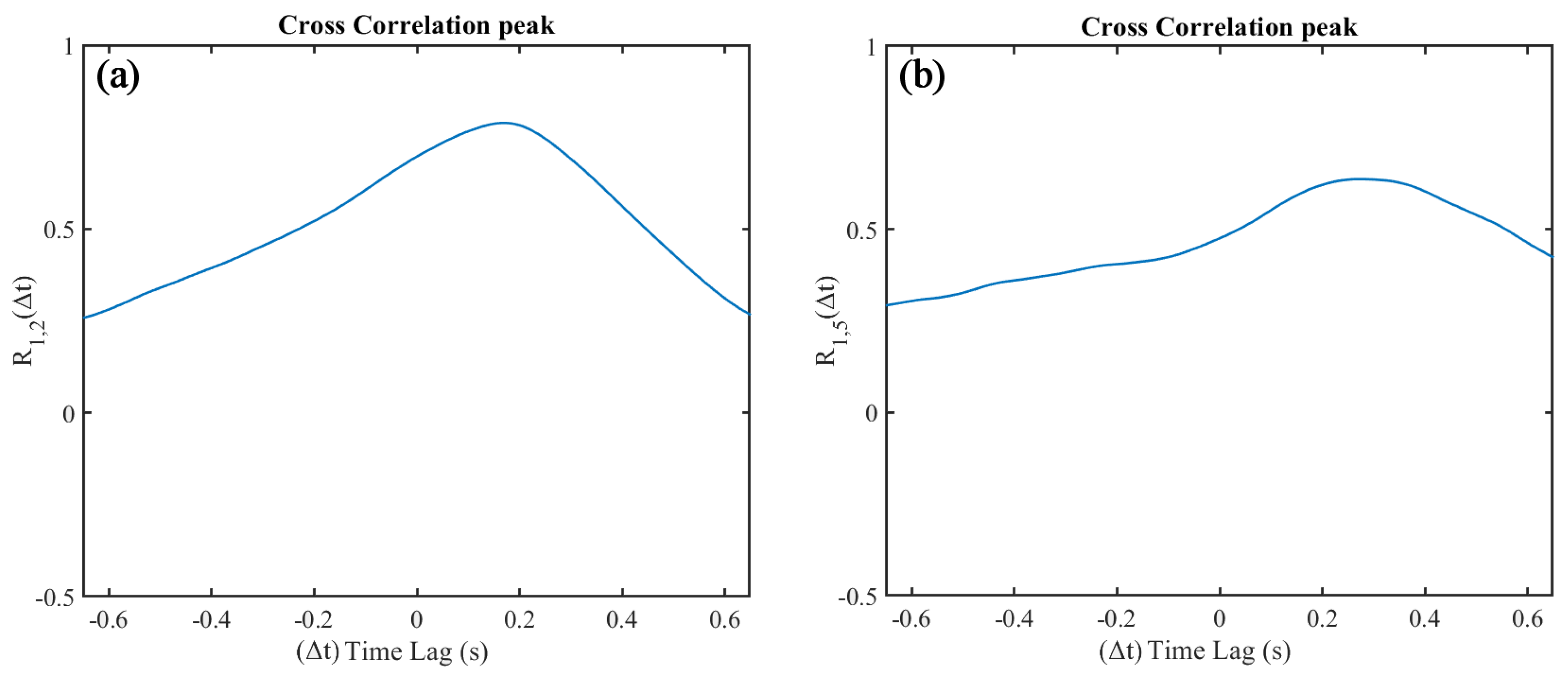
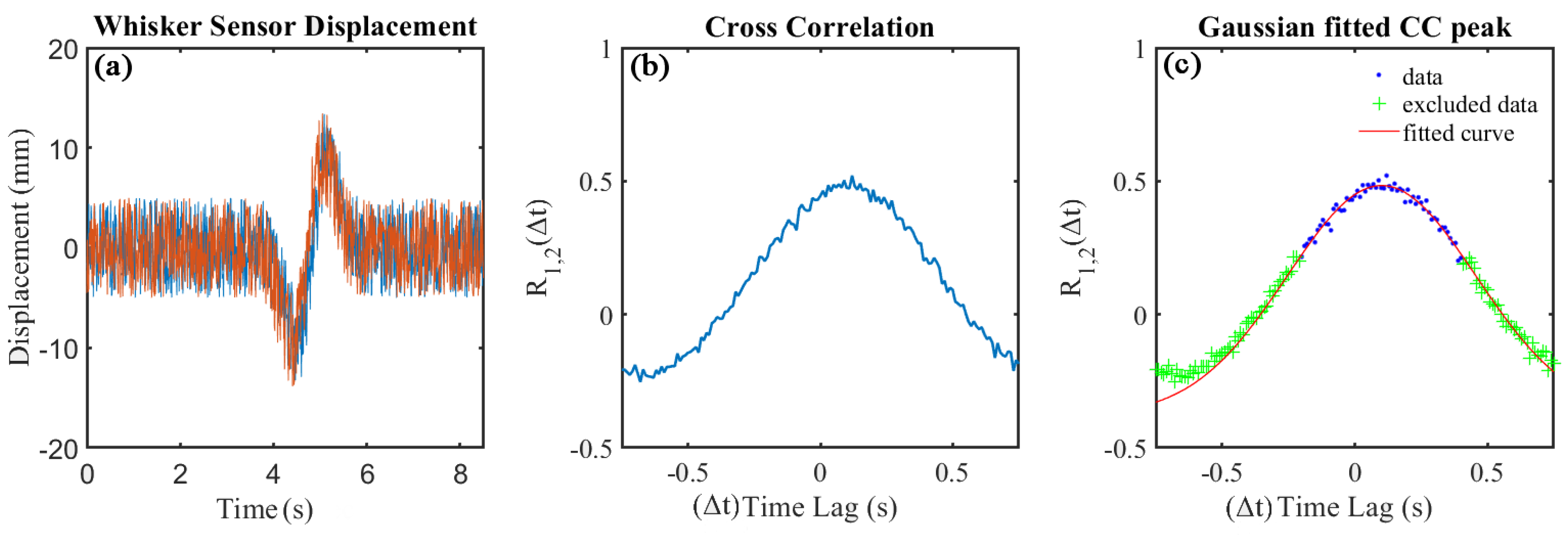
3.2. Pair-Wise Correlation of Whisker Motion
3.3. Simulation of Noise Effects
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CC | Cross Correlation |
| CFD | Computational Fluid Mechanics |
| DPIV | Digital Particle Image Velocimetry |
| FSI | Fluid Structure Interaction |
| IW | Interrogation Window |
| LES | Large Eddy Simulation |
| SNR | signal to Noise Ratio |
| PIV | Particle Image velocimetry |
| Recyl | Re-number based on cylinder diameter |
| Red | Re-number based on whisker diameter |
| RMS | Root Mean Square |
References
- Bearman, P. Vortex shedding from oscillating bluff bodies. Ann. Rev. Fluid Mech. 1984, 16, 195–222. [Google Scholar] [CrossRef]
- Barth, F.; Humphrey, J.; Secomb, T. Sensors and Sensing in Biology and Engineering, 1st ed.; Springer: New York, NY, USA, 2003. [Google Scholar]
- Brücker, C.; Rist, U. Complex Flow Detection by Fast Processing of Sensory Hair Arrays; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Chagnaud, B.; Brücker, C.; Hofmann, M.; Bleckmann, H. Measuring Flow Velocity and Flow Direction by Spatial and Temporal Analysis of Flow Fluctuations. J. Neurosci. 2008, 28, 4479–4487. [Google Scholar] [CrossRef] [PubMed]
- Axtmann, G.; Hegner, F.; Brücker, C.; Rist, U. Investigation and prediction of the bending of single and tandem pillars in a laminar cross flow. J. Fluids Struct. 2016, 66, 110–126. [Google Scholar] [CrossRef]
- Dehnhardt, G.; Mauck, B.; Bleckmann, H. Seal whiskers detect water movements. Nature 1998, 394, 235–236. [Google Scholar] [CrossRef]
- Muthuramalingam, M.; Brücker, C. Seal and Sea lion Whiskers Detect Slips of Vortices Similar as Rats Sense Textures. Sci. Rep. 2019, 9, 12808. [Google Scholar] [CrossRef] [PubMed]
- Wieskotten, S.; Dehnhardt, G.; Mauck, B.; Miersch, L.; Hanke, W. Hydrodynamic determination of the moving direction of an artificial fin by a harbour seal (Phoca vitulina). J. Exp. Biol. 2010, 293, 2194–2200. [Google Scholar] [CrossRef] [PubMed]
- Estebanez, L.; El Boustani, S.; Destexhe, A. Correlated input reveals coexisting coding schemes in a sensory cortex. Nat. Neurosci. 2012, 15, 1691–1699. [Google Scholar] [CrossRef] [PubMed]
- Elshalakani, M.; Muthuramalingam, M.; Brücker, C. A deep-learning model for underwater position sensing of a wake’s source using artificial seal whiskers. Sensors 2020, 20, 3522. [Google Scholar] [CrossRef] [PubMed]
- Miersch, L.; Hanke, W.; Wieskotten, S.; Hanke, F.; Oeffner, J.; Leder, A.; Brede, M.; Witte, M.; Dehnhardt, G. Flow sensing by pinniped whiskers. Philos. Trans. R. Soc. B Biol. Sci. 2011, 366, 3077–3084. [Google Scholar] [CrossRef] [PubMed]
- ANSYS. Ansys Fluent Tutorial Guide; ANSYS: Houston, TX, USA, 2019. [Google Scholar]
- Müller, U.; Van Den Heuvel, B.; Stamhuis, E.; Videler, J. Fish foot prints: Morphology and Energetics of the wake behind a continuously swimming mullet (Chelon Labrosus Risso). J. Exp. Biol. 1997, 200, 2893–2906. [Google Scholar]
- Videler, J.; Muller, U.; Stamhuis, E. Aquatic vertebrate locomotion: Wakes from body waves. J. Exp. Biol. 1999, 202, 3423–3430. [Google Scholar] [PubMed]
- Kogan, I.; Pacholak, S.; Licht, M.; Schneider, J.W.; Brücker, C.; Brandt, S. The invisible fish: Hydrodynamic constraints for predator-prey interaction in fossil fish Saurichthys compared to recent actinopterygians. Biol. Open 2015, 4, 1715–1726. [Google Scholar] [CrossRef] [PubMed]
- Blevins, R. Flow-Induced Vibration, 2nd ed.; Van Nostrand Reinhold Company: New York, NY, USA, 1990. [Google Scholar]
- Raffel, M.; Willert, C.; Scarano, F.; Kähler, C.; Wereley, S.; Kompenhans, J. Particle Image Velocimetry: A Practical Guide, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Brücker, C.; Spatz, J.; Schroder, W. Feasability study of wall shear stress imaging using microstructured surfaces with flexible micropillars. Exp. Fluids 2005, 39, 464–474. [Google Scholar]
- Brücker, C.; Bauer, D.; Chaves, H. Dynamic response of micro-pillar sensors measuring fluctuating wall-shear-stress. Exp. Fluids 2007, 42, 737–749. [Google Scholar]
- Krüger, Y.; Hanke, W.; Miersch, L. Detection and direction discrimination of single vortex rings by harbour seals (Phoca vitulina). J. Exp. Biol. 2018, 221. [Google Scholar] [CrossRef] [PubMed]
| Freestream Velocity (cm/s) | Local Velocity (cm/s) | CC Velocity (cm/s) |
|---|---|---|
| 20 | 20.8 | 21.2 |
| 25 | 26.0 | 26.1 |
| 30 | 31.2 | 30.9 |
| Freestream Velocity (cm/s) | Local Velocity (cm/s) | CC Velocity (cm/s) |
|---|---|---|
| 20 | 18.2 | 18.0 |
| 25 | 22.8 | 22.6 |
| 30 | 27.3 | 26.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Glick, R.; Muthuramalingam, M.; Brücker, C. Fluid-Structure Interaction of Flexible Whisker-Type Beams and Its Implications for Flow Sensing by Pair-Wise Correlation. Fluids 2021, 6, 102. https://doi.org/10.3390/fluids6030102
Glick R, Muthuramalingam M, Brücker C. Fluid-Structure Interaction of Flexible Whisker-Type Beams and Its Implications for Flow Sensing by Pair-Wise Correlation. Fluids. 2021; 6(3):102. https://doi.org/10.3390/fluids6030102
Chicago/Turabian StyleGlick, Raphael, Muthukumar Muthuramalingam, and Christoph Brücker. 2021. "Fluid-Structure Interaction of Flexible Whisker-Type Beams and Its Implications for Flow Sensing by Pair-Wise Correlation" Fluids 6, no. 3: 102. https://doi.org/10.3390/fluids6030102
APA StyleGlick, R., Muthuramalingam, M., & Brücker, C. (2021). Fluid-Structure Interaction of Flexible Whisker-Type Beams and Its Implications for Flow Sensing by Pair-Wise Correlation. Fluids, 6(3), 102. https://doi.org/10.3390/fluids6030102






