Abstract
The onset of oscillatory bifurcations in a porous horizontal layer L, uniformly rotating about a vertical axis, with vertically stratified porosity, heated from below and salted from above and below, is investigated. Denoting by , the Prandtl numbers of the salt salting L from below and above respectively, it is shown that: (i) in L the oscillatory bifurcations can occur only if one of the structural conditions
or or is verified; (ii) exists a bound for the Rayleigh number of such that guarantees the absence of cold convection; (iii) via a new approach based on the instability power of each coefficient of the spectrum equation, criteria of existence, location and frequency of oscillatory (Hopf) bifurcations are furnished for any porosity stratification law. These criteria, as far as we know are, for the case at stake, the first criteria of Hopf bifurcations appearing in literature. We are confident that, via experimental results, will be validated.
1. Introduction
The onset of thermal convection in porous layers with vertically stratified permeability and/or viscosity, for its importance in geophysical phenomena and in the construction of artificial porous materials, has attracted—in the past as nowadays—the attention of scientists [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. The increase in viscosity with depth in the earth’s mantle has been studied in [1,2]; the changes in permeability due to mineral diagenesis in fractured crust has been analyzed in [3]; in references [4,5] the porosity changes due to the subterranean movement and the increase in permeability and porosity near solid wall, are considered; the influence of porosity stratification on the onset of thermal convection in the construction of artificial porous materials is studied in [2].
In the present paper a porous horizontal layer with depth-dependent permeability and viscosity—heated from below, rotating uniformly about a vertical axis and salted from above and from below—is considered. The scope is to analyze the effects of such stratifications on the onset of Hopf bifurcations. The paper is organized as follows. In Section 2 and Section 3 same basic preliminaries concerning the model equations (Section 2) and the linear stability of the thermal solution (Section 3) are given. Section 4 is devoted to the spectrum equation of the problem at stake, while in the subsequent Section 5 the instability basic property of the coefficients of the spectrum equation is recalled. In Section 6 it is shown the existence of hidden symmetries and structural conditions on the salts necessary for the existence of oscillatory bifurcations are found.The condition for avoiding the onset of instability for each value of the thermal Rayleigh number (cold convection) is found in Section 7. The criteria for the onset of oscillatory bifurcations are obtained in the subsequent Section 8. Section 9 is devoted to the exponentially increasing porosity. The paper ends with some final remarks (Section 10).
2. Preliminaries
Let two different chemical components (“salts”) , be dissolved in the fluid porous layer L and let the equation of state be
where are the density, temperature and salts concentrations with reference values and thermal and solute expansion coefficients. We denote by an orthogonal frame of reference with fundamental unit vectors ( pointing vertically upwards). Let and . The isochoric motions in L—rotating uniformly around the z axis with velocity – are governed, in the Boussinesq approximation [6], by
with the list of symbols given by
defined in [6]. Passing to the boundary conditions, since in (2) there are not derivatives in the velocity, one needs only to prescribe the normal component of : we require that this component is null. As concerns the temperature and the salts, we assume that their values are fixed. Therefore to (2) we append precisely the boundary conditions
with positive constants and . The boundary value problem (2) and (3) admits the conduction solution given by
where is a constant. Setting
and introducing the scalings
since in the case at stake the layer is heated from below and salted from below by and from above by , it follows hat and the equations governing the dimensionless perturbations , omitting the stars, and setting , are
under the boundary conditions
In (6) and (7) R and are the thermal and salt Rayleigh numbers respectively while are the salt Prandtl numbers and is the Taylor-Darcy number. We set and assume, as usually done, that:
- (i)
- the perturbations are periodic in the x and y directions, respectively of periods ;
- (ii)
- is the periodicity cell;
- (iii)
- belong to and are such that all their first derivatives and second spatial derivatives can be expanded in Fourier series uniformly convergent in Ω
and denote by the set of the functions such that
- (1)
- is periodic in the x and y directions of period respectively and ;
- (2)
- Φ together with all the first derivatives and second spatial derivatives can be expanded in a Fourier series absolutely uniformly convergent in .
3. Preliminaries to Linear Instability
Since (7) is linear, the linear stability of is governed by
under the boundary conditions
Let a.e. and set
In view of
the third component of the curl of (9) gives
Furthermore, in view of
where , one has that the third component of the double curl of (9) is
and (13) implies
Since the set is a complete orthogonal basis of , one has
and the periodicity in the directions implies
The following property holds.
Property 1.
Setting
one has
where
Proof.
One easily obtains that
which implies
i.e.,
Then in view of
one has that (23) gives (21). □
Remark 1.
We remark that the previous proof of property 1 follows, step by step, the which one given in [2], but some missprints concerning and (appearing in [2]) have been eliminated.
4. Spectrum Equation
Let , i.e., let L be salted from below by and from above by . Then (9) implies
where is given by (20). It follows that
where
and
The spectrum equation is given by
where
One easily obtains that
Remark 2.
In the sequel we will set
and, since it is sufficient for the instability, we consider only . Then it follows that the spectrum equation is
with
5. Power Property of the Spectrum Equation Coefficients
In the present section the existence and location property of the Hopf bifurcations in dynamical system, via the spectrum equation instability coefficients power, is recalled.
Let be a real matrix. As it is well known, the set of its eigenvalues is called the spectrum of and the algebraic equation
with Kronecker coefficients, is the spectrum equation, since the eigenvalues are its roots.
Further
with characteristic values of given by
In terms of the entries , is obtained by adding the determinants of the principal diagonal minors of order r of [7].
The spectrum and are said to be
- unstable if at least one eigenvalue has positive real part,
- bifurcating if and only if contains—at least—a zero or pure imaginary eigenvalue.
The following properties hold.
- Each conditionis necessary for the stability of and each conditionis sufficient for the instability (coefficient instability power).
- Ifthen the instability is implied by the existence of a zero eigenvalue and one has steady instability.
- If exists a positive number such that the pure imaginary number belongs to :and one has oscillatory or Hopf bifurcation.
- If the entries depend on a positive parameter , denoting by the lowest value of at which and by the lowest value of at which for at least a real , one has
A direct proof of (1) is given in the appendix of [7]; (2) and (3) are obvious; (4) depends on the fact that at the growing of , (44) implies the occurrence of instability respectively via: a zero eigenvalue, a pure imaginary eigenvalue or via the presence of both such eigenvalues [7]. In [7] Rionero has put in evidence that the coefficients of the spectrum equation have the property of driving not only the onset of instability via the condition
In fact he has shown that, via (45), the following property guaranteeing the existence of Hopf bifurcations holds.
Property 2.
Let be stable at and let be the lowest positive value of at which a coefficient of the spectrum equation is zero. Then
implies that exists a
at which an oscillatory bifurcation occurs.
Proof.
Since the instability occurs only via a steady state or via a rotatory bifurcation eventually coupled to a steady state – at the growing of from the stability state at to the instability state at – (46) implies the existence of an at which an oscillatory bifurcation occurs. □
6. Salts Structural Conditions, Necessary for the Onset of Oscillatory Bifurcations
Property 3.
In a porous horizontal layer with stratified porosity, rotating uniformly about a vertical axis, heated from below and salted from below by , and from above by , the oscillatory bifurcations can occur only if the salts satisfy one of the structural conditions
7. Cold Convection Influence
Let us choose, as requested by the physics of the phenomenon at stake, the thermal Rayleigh number R as bifurcation parameter.
Then in order to apply property 2, one has to require linear stability at . On the other hand, the existence of the salt salting L from above, implies the existence of the cold convection which implies instability at . We called cold convection the onset of instability for any value of R, included [8]. In view of (35) one has that the instability is implied by each one of the following conditions
Therefore one has
Property 4.
The cold convection is avoided and one has a pure thermal convection only if
Setting
in view of
one has
and it follows that
Therefore setting
in view of
it follows that
i.e.,
and hence setting
one has that the cold convection is avoided by requiring (63).
8. Oscillatory Bifurcations via the Spectrum Equation Coefficients Power Approach
Let (48) and (63) hold in view of (33)–(36) the spectrum equation is
with
and given by (35). Setting
one has that
The “instability coefficient power” of can be defined by setting
and the following property holds
Property 5.
Let be the spectrum equation coefficient with the biggest and let the thermal conduction be linearly asymptotically stable at . Then, at the growing of R and , from , the instability occurs at and one has a steady bifurcation if , while an oscillatory bifurcation occurs at an if .
Proof.
Let us begin by recalling that the (Routh-Hurwitz) stability conditions in the case at stake are
and that
At , in view of (29) reduces to
with and bigger than zero. The eigenvalues are
i.e., is asymptotically linearly stable and one has
- (1)
- Let . Then at one hasTherefore, in view of the continuity of , exists a in whichwhich is the lowest root of (84) in and a simple oscillatory bifurcation (SOB) occurs at having the frequency such thatwith
- (2)
- if , then at the spectrum equation reduces toand at one has a steady+oscillatory bifurcation of frequency with
- (3)
- if , the spectrum equation at reduces toThereforeand a SOB occurs at an .
- (4)
- if , a SOB occurs at a with frequency given by (86) with lowest root of .
□
In view of (1)–(4) and (75), criteria guaranteeing the existence of oscillatory bifurcations are easily obtained. We confine ourselves to the following.
Property 6.
Let and let one of (48) holds. Then
guarantees the existence of a at which an oscillatory bifurcation occurs.
Proof.
In fact (85) implies
and hence (97) implies . □
Property 7.
Let and let one of (48) holds. Then
guarantees the existence of a at which an oscillatory bifurcation occurs.
Property 8.
Proof.
In fact: (95), (95). □
Property 9.
Proof.
In fact: (96), (96). □
We end by remarking that:
- (1)
- (2)
- the values of have to be taken into account;
- (3)
- in the case the following criterion holds.
Property 10.
Let
then an oscillatory bifurcation occurs at a .
Proof.
In fact one has and . □
9. Applications
The knowledge of the function given by (71), is necessary for the applications of Hopf bifurcation criteria. One has to remark that—accounting for (68) and (68) and the presence of in (71), does not simplify .
We here, for the sake of simplicity and concreteness, confine ourselves to the case
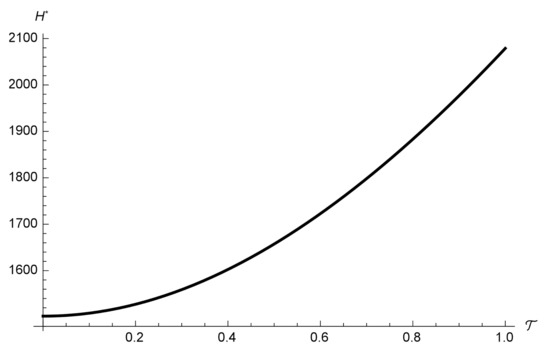
Figure 1.
.
- (1)
- the contruction of in the cases of stratification laws of type , with , is obtained following, step by step, the previous procedure. In particular, one can consider the law const. proposed in [1] for the increase of viscosity in the earth’s mantle;
- (2)
- in [2], upper and lower bounds of are furnished for any stratification law.
10. Final Remarks
- The results obtained can be applied for any stratification law of porosity f and the oscillatory bifurcations depend on f via given in (71).
- Property 5 guarantees the existence of oscillatory bifurcations (giving also an estimate of their locations).
- The condition for at least a is simpler than the looking for the roots of .
Compliance with ethical standards.
Funding
This research received no external funding.
Acknowledgments
This paper has been performed under the auspices of the GNFM of INdAM.
Conflicts of Interest
The corresponding author states that there is no conflict of interest.
References
- Torrance, K.E.; Turcotte, D.L. Thermal convection with large viscosity variations. J. Fluid Mech. 1971, 47, 113–125. [Google Scholar] [CrossRef]
- Rionero, S. Convection in Ternary Porous Layers with Depth Dependent Permeability and Viscosity. Contemp. Math. 2016, 289–304. [Google Scholar] [CrossRef]
- Fontaine, F.J.; Rabinowicz, M.; Boulegue, J. Permeability changes due to mineral diagenesis in fractured crust. Earth Planet. Sci. Lett. 2011, 184, 407–425. [Google Scholar] [CrossRef]
- Hamdan, M.H.; Kamel, M.T. Flow through variable permeability porous layer. Adv. Theor. Appl. Mech. 2011, 4, 135–145. [Google Scholar]
- Hamdan, M.H.; Kamel, M.T.; Sivvam, H.I. A permeability function for Brinkmann’s equation. In Proceedings of the 11th WSEAS International Conference on Mathematical Methods, Computational Techniques and Intelligent Systems, Timisoara, Romania, 21–23 October 2010. [Google Scholar]
- Nield, D.A.; Bejan, A. Convection in Porous Media, V ed.; Springer International Publishing AG: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Rionero, S. Hopf bifurcations in dynamical systems. Ric. Mat. 2019. [Google Scholar] [CrossRef]
- Rionero, S. Cold convection in porous layer salted from above. Meccanica 2014, 49, 2061–2068. [Google Scholar] [CrossRef]
- Kassoy, D.R.; Zebib, A. Variable viscosity effects on the onset of convection in porous media. Phys. Fluids. 1975, 18, 1649–1651. [Google Scholar] [CrossRef]
- McKibbin, R. Heat transfer in a Vertically-layered porous medium heated from below. Transp. Porous Med. 1986, 1, 361–370. [Google Scholar] [CrossRef]
- Rosenberg, N.J.; Spera, F.J. Role of anisotropic and/or layered permeability in hydrothermal system. Geophys. Res. Lett. 1990, 17, 235–238. [Google Scholar] [CrossRef]
- Rees, D.A.S.; Pop, I. Vertical free convection in a porous medium with variable permeability effects. Int. J. Heat. Mass. Transfer. 2000, 43, 2565–2571. [Google Scholar] [CrossRef]
- Nield, D.A.; Kuznetsov, A.V. The effect of a transistion layer between a fluid and a porous medium: Shear flow in a channel. Transp. Porous Med. 2009, 72, 477–487. [Google Scholar] [CrossRef]
- Alloui, Z.; Bennacer, R.; Vasseur, P. Variable Permeability effect on convection in binary mixtures saturating a porous layer. Heat. Mass. Transfer. 2009, 45, 1117–1127. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).