Dynamics of Shock Structure and Frontal Drag Force in a Supersonic Flow Past a Blunt Cone under the Action of Plasma Formation †
Abstract
:1. Introduction
2. Experimental Study
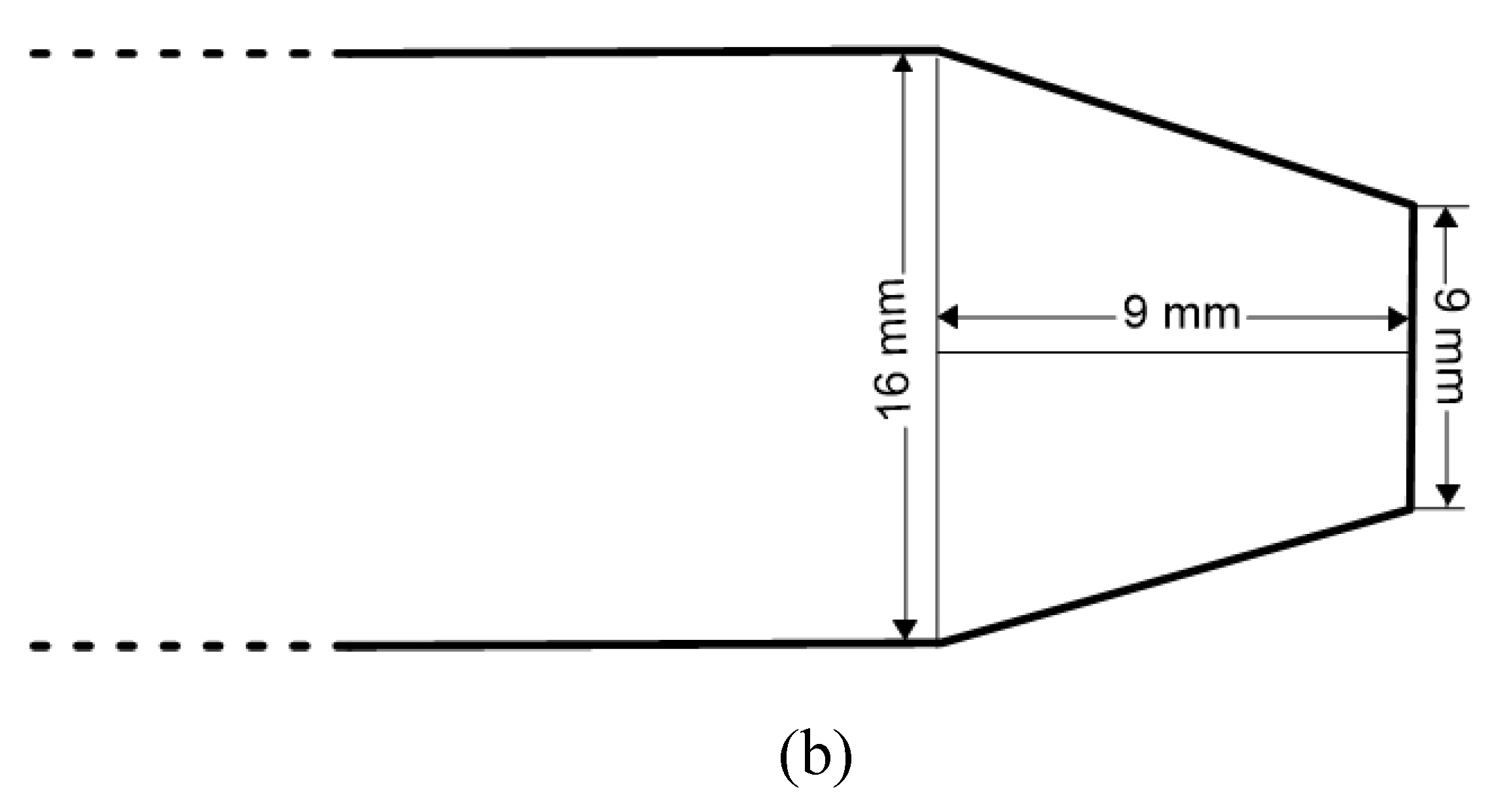
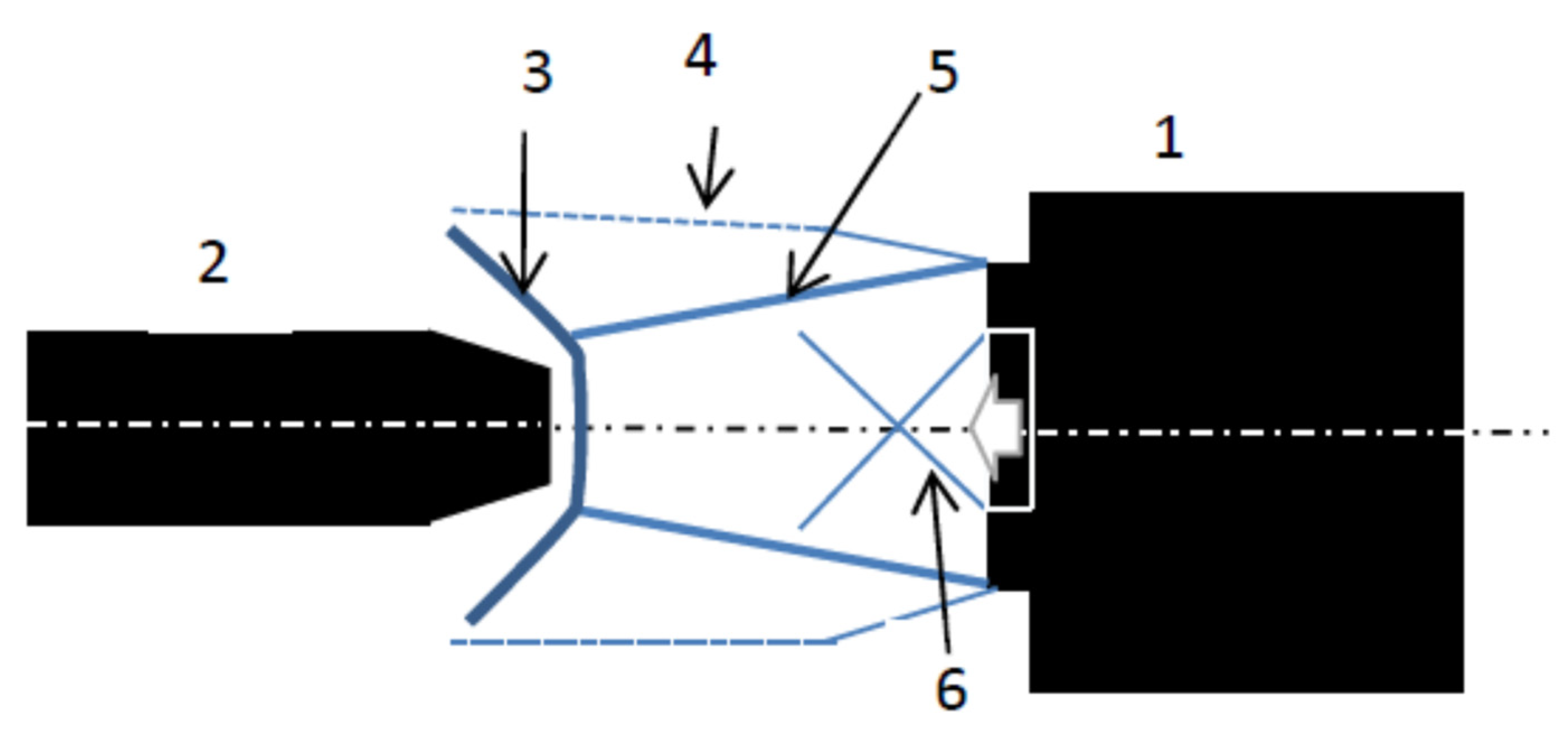
2.1. Experimental Setup
2.2. Experimental Results
3. Numerical Simulations
3.1. Methodology, Statement of the Problem, and Grid Convergence
3.2. Results of the Simulations
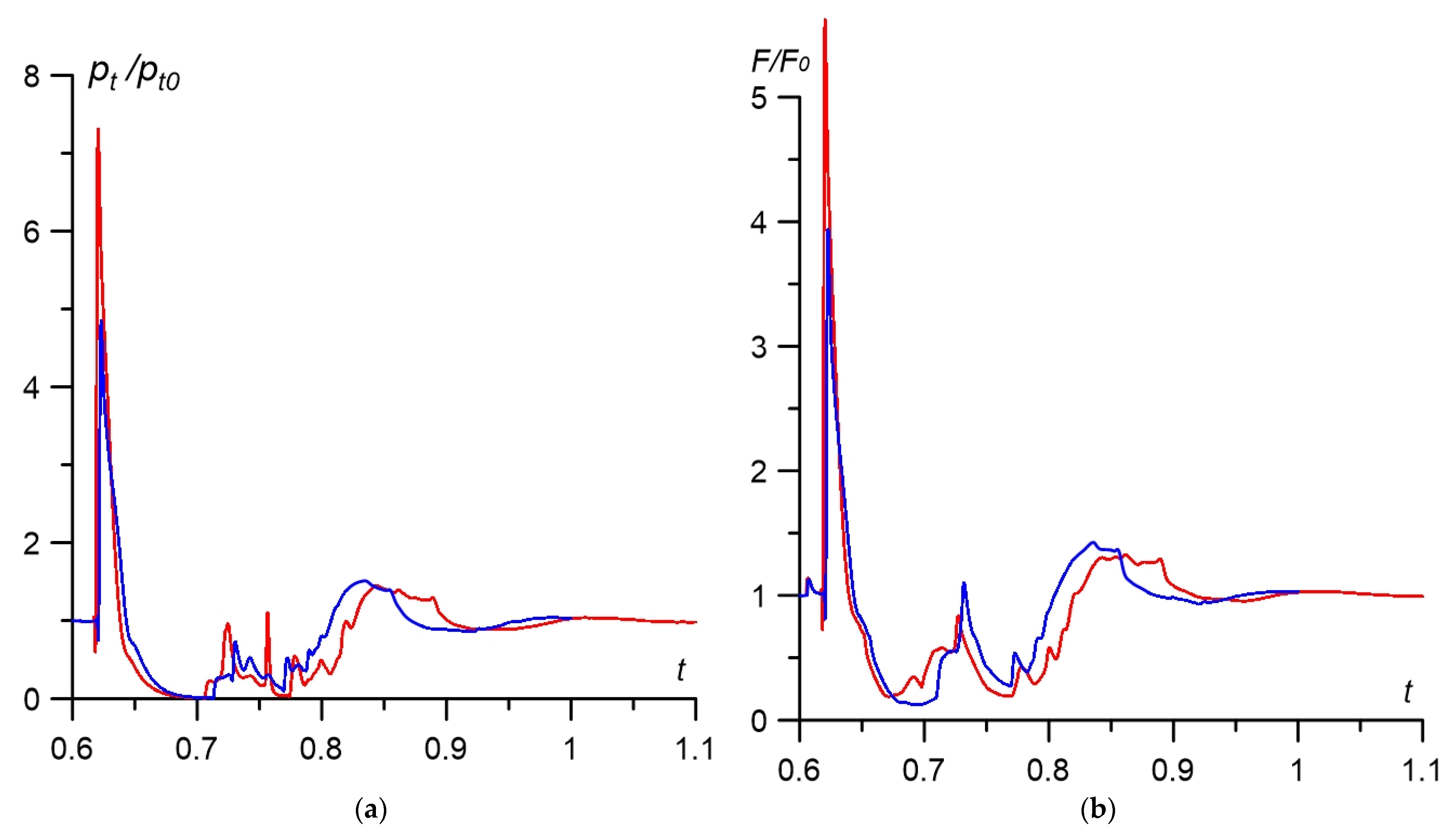
4. Discussion
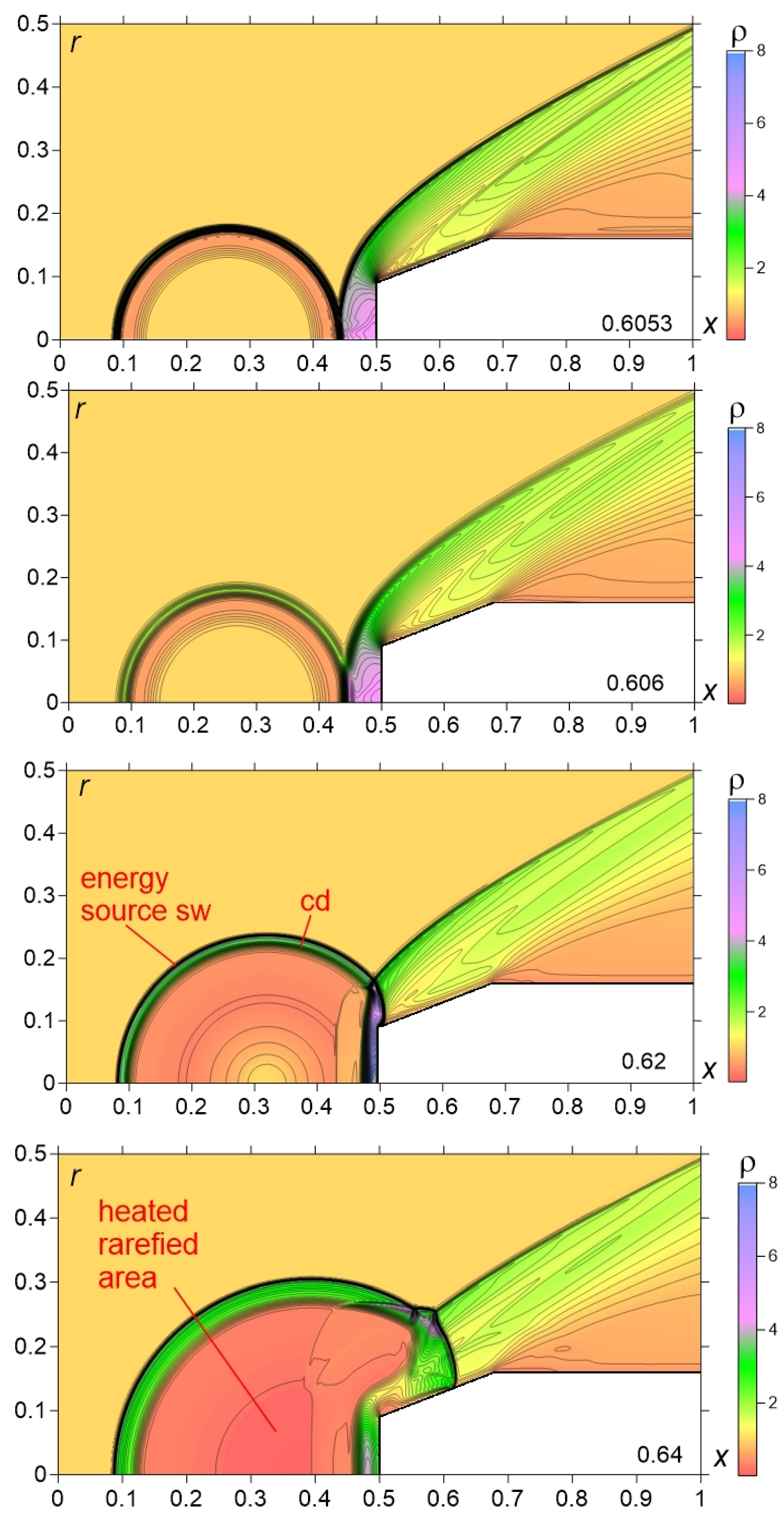
- Steady flow with the close values of numerical and experimental standoff of the bow shock wave and the close numerical and experimental shapes of the bow shock waves were obtained (Figure 6).
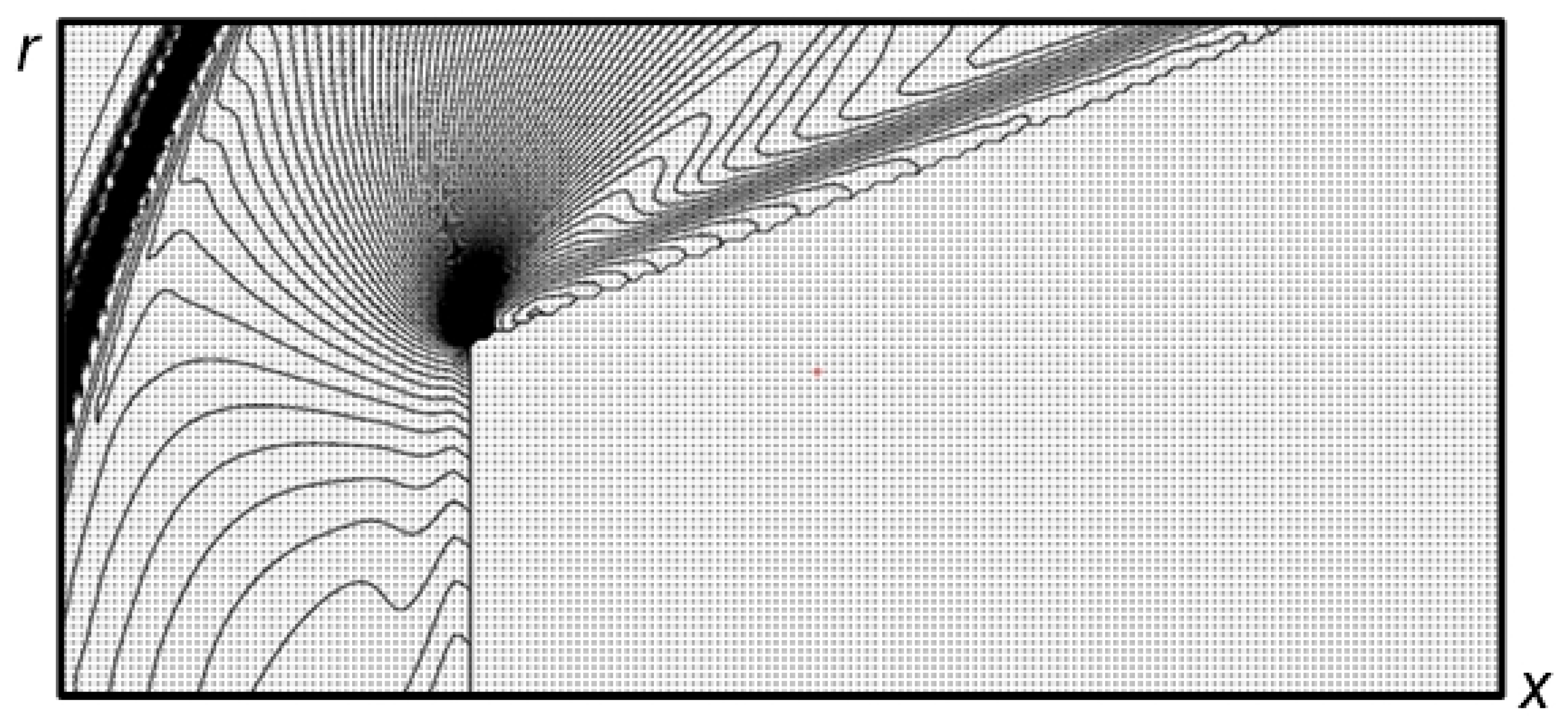
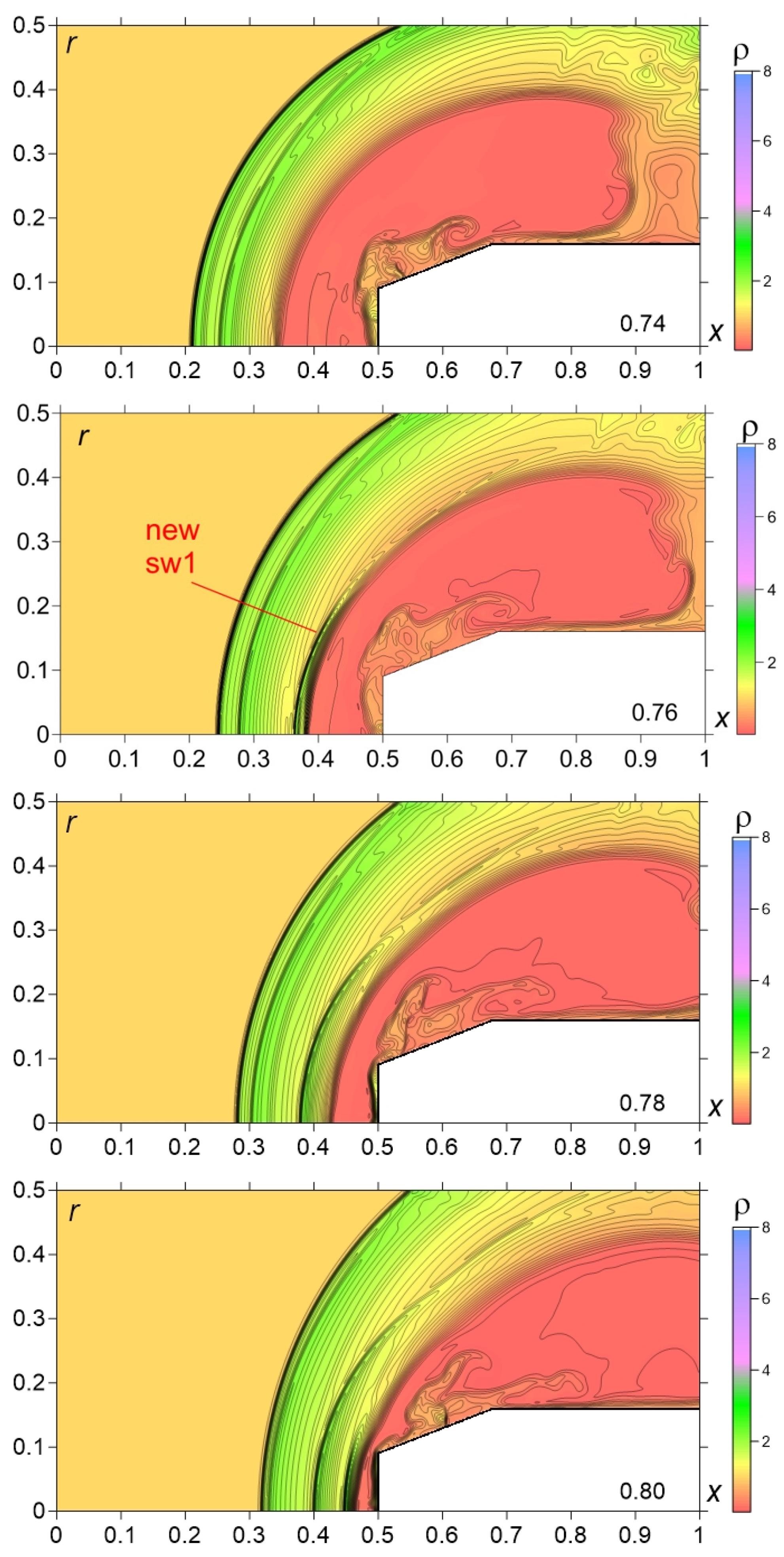
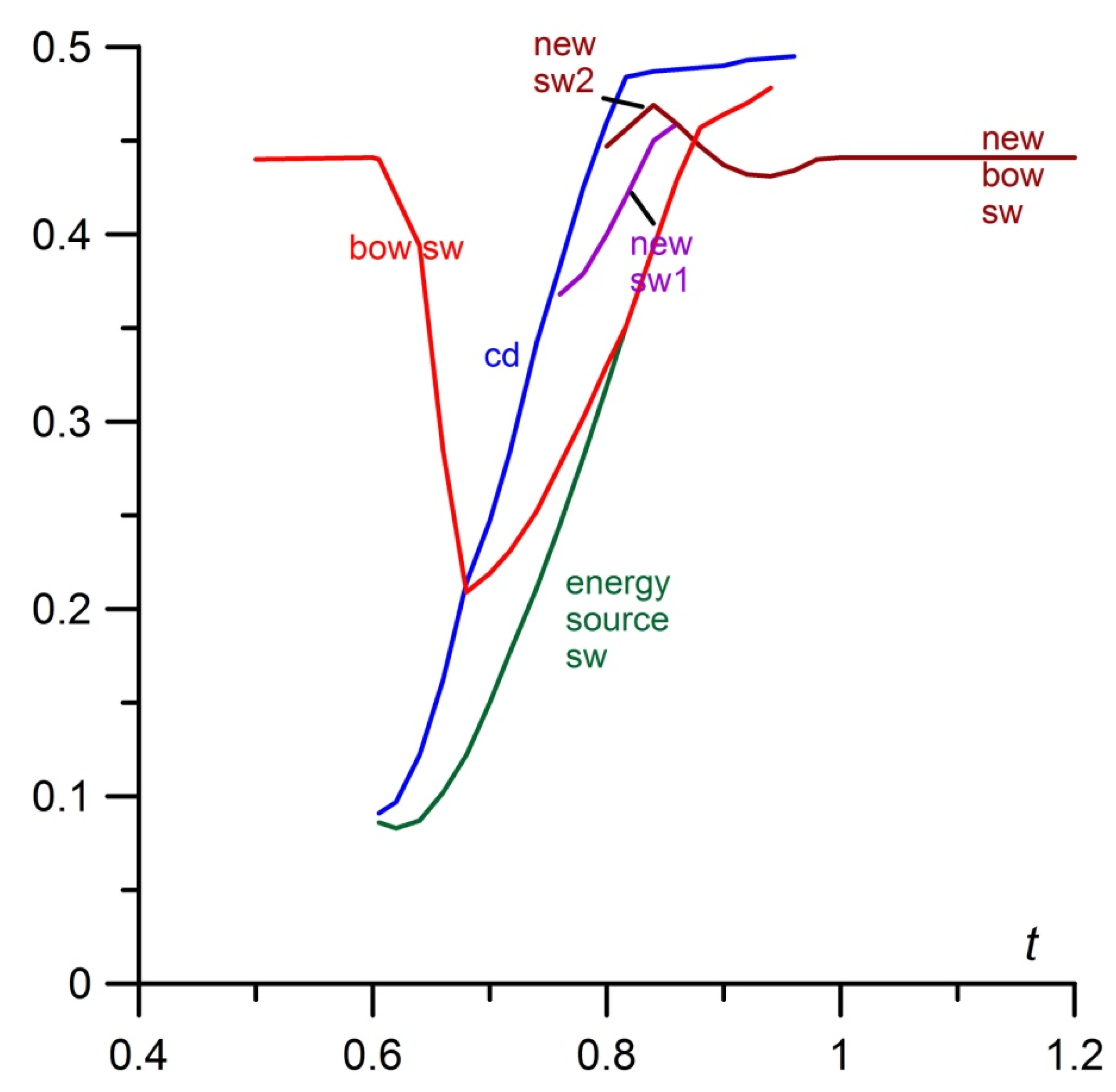
- The generation of three shocks (two shock waves and a contact discontinuity—a boundary of the heated area) in the region between the left part of the source shock wave and the body at the initial and middle stages of the interaction has been obtained numerically and recorded at the schlieren pictures (Figure 3c vs. flow image in Figure 7 for t = 0.7174) (Figure 12a).
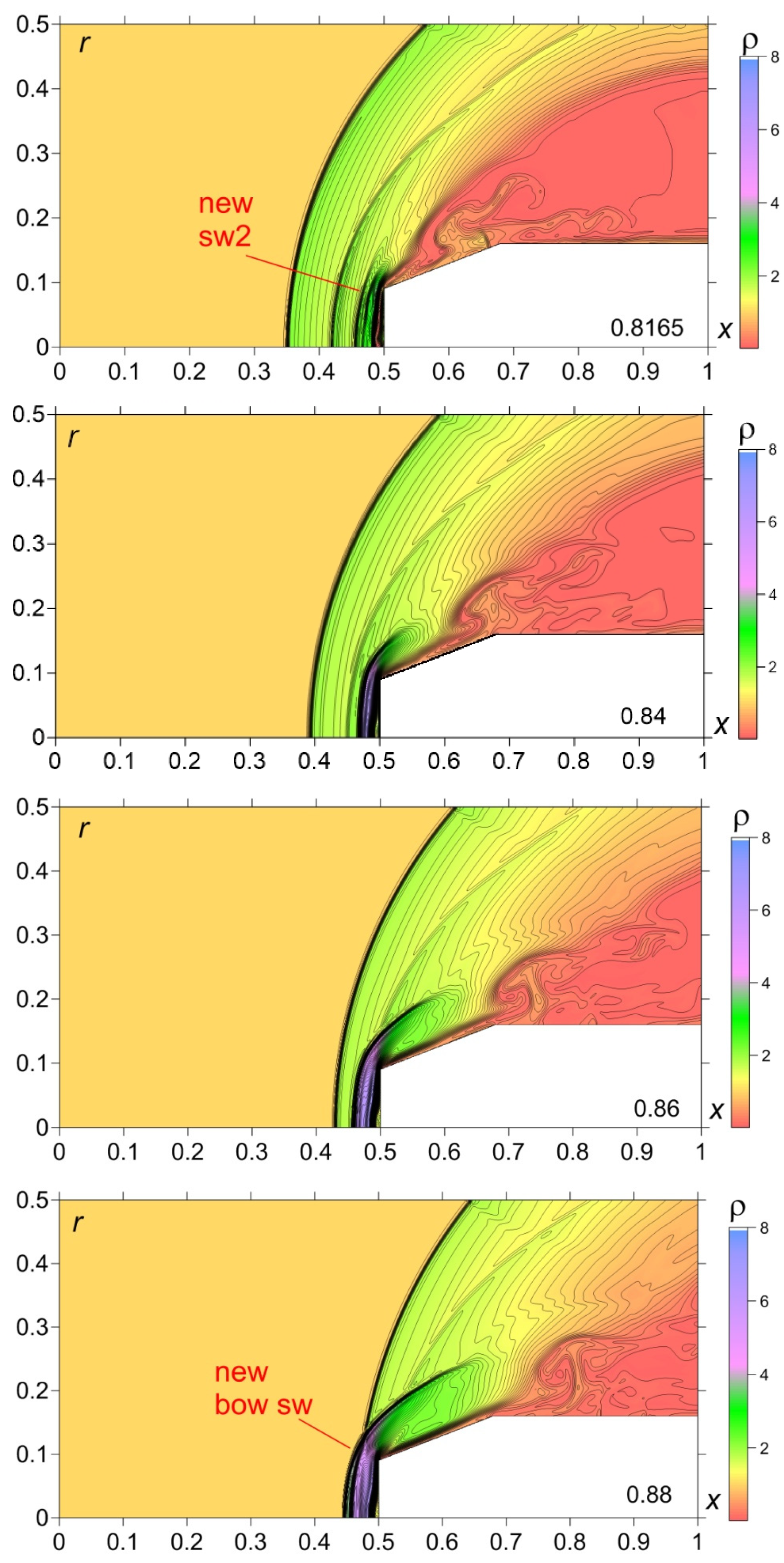
- The formation of a new bow shock from this shock wave which is accompanied by the pulsation of this new bow shock (during the steady flow establishing at the final stage of the interaction). This result can be observed in the experimental flow images (Figure 3e–g) and in the numerical flow patterns in Figure 8 and Figure 9 for t = 0.86–1.2 (Figure 12c, t = 0.88).
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| M | freestream Mach number |
| γ | ratio of specific heats |
| p∞, ρ∞, u∞, v∞ | freestream pressure, density and velocity components |
| R | diameter of a cylinder part of a body |
| ti | time moment of an energy source arising |
| pi | pressure in an energy source |
| ri | radius of an energy source |
| x0 | distance between the center of an energy source and a frontal surface of a body |
| η | part of the discharge energy spent to the expansion of a gas |
| pG, rG | pressure and r-coordinate at the body’s boundary |
| SW | shock wave |
| CD | contact discontinuity |
References
- Knight, D.D. Energy Deposition for High-Speed Flow Control; Cambridge University Press: Cambridge, UK, 2019; 450p. [Google Scholar] [CrossRef]
- Knight, D. Survey of aerodynamic drag reduction at high speed by energy deposition. J. Propuls. Power. 2008, 24, 1153–1167. [Google Scholar] [CrossRef]
- Russell, A.; Zare-Behtash, H.; Kontis, K. Joule heating flow control methods for high-speed flows. J. Electrost. 2016, 80, 34–68. [Google Scholar] [CrossRef] [Green Version]
- Leonov, S.B. Review of plasma-based methods for high-speed flow control. In Proceedings of the Sixth International Conference on Fluid Mechanics AIP Conference Proceedings, Guangzhou, China, 30 June–3 July 2011; Volume 1376, pp. 498–502. [Google Scholar] [CrossRef]
- Starikovskiy, A.Y.; Aleksandrov, N.L. Gasdynamic flow control by ultrafast local heating in a strongly nonequilibrium pulsed plasma. Plasma Phys. Rep. 2021, 47, 148–209. [Google Scholar] [CrossRef]
- Ahmed, M.Y.; Qin, N. Forebody shock control devices for drag and aero-heating reduction: A comprehensive survey with a practical perspective. Prog. Aerosp. Sci. 2020, 112, 100585. [Google Scholar] [CrossRef]
- Shneider, M.N.; Macheret, S.O.; Zaidi, S.H.; Girgis, I.G.; Miles, R.B. Virtual Shapes in Supersonic Flow Control with Energy Addition. J. Propuls. Power 2008, 24, 900–915. [Google Scholar] [CrossRef]
- Georgievsky, P.Y.; Levin, V.A. Supersonic flow over bodies in the presence of external energy input. Pis’ma Zhurnal Tekh. Fiziki. 1988, 14, 684–687. (In Russian) [Google Scholar]
- Artem’ev, V.I.; Bergel’son, V.I.; Nemchinov, I.V.; Orlova, T.I.; Smirnov, V.A.; Hazins, V.M. Changing the regime of supersonic streamlining obstacles via raising the thin channel of low density. Izv. Akad. Nauk SSSR Meh. Židk. Gaza. 1989, 5, 146–151. (In Russian) [Google Scholar]
- Nemchinov, I.V.; Artem’ev, V.I.; Bergel’son, V.I.; Hazins, V.M.; Orlova, T.I.; Rybakov, V.A. Rearrangement of the bow shock shape using a “hot spike”. Shock. Waves 1994, 4, 35–40. [Google Scholar] [CrossRef]
- Riggins, D.; Nelson, H.; Johnson, E. Blunt-body wave drag reduction using focused energy deposition. AIAA J. 1999, 37, 460–467. [Google Scholar] [CrossRef]
- Miles, R.B. Flow Control by Energy Addition into High-Speed Air. In Proceedings of the 38th AIAA Aerospace Sciences Meeting and Exhibit, AIAA, Denver, CO, USA, 19 June–22 June 2000; pp. 1–14, Paper AIAA-2000-2324. [Google Scholar]
- Kolesnichenko, Y.F.; Brovkin, V.G.; Azarova, O.A.; Grudnitsky, V.G.; Lashkov, V.A.; Mashek, I.C. Microwave energy release regimes for drag reduction in supersonic flows. In Proceedings of the 40th AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 14 January–17 January 2002; pp. 1–12, Paper AIAA-2002-0353. [Google Scholar]
- Knight, D.D.; Kolesnichenko, Y.F.; Brovkin, V.G.; Khmara, D.; Lashkov, A.V.; Mashek, I.C. Interaction of microwave-generated plasma with a hemisphere cylinder at Mach 2.1. AIAA J. 2009, 47, 2996–3010. [Google Scholar] [CrossRef]
- Knight, D.D.; Kolesnichenko, Y.F.; Brovkin, V.G.; Khmara, D.; Lashkov, A.V.; Mashek, I.C. Interaction of microwave-generated plasma with hemisphere-cone-cylinder. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4 January 2010–7 January 2010; pp. 1–16, Paper AIAA-2010-1005. [Google Scholar]
- Azarova, O.A.; Knight, D.D. Numerical prediction of dynamics of microwave filament interaction with supersonic combined cylinder bodies. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015; pp. 1–12, Paper AIAA-2015-0581. [Google Scholar]
- Myrabo, L.N.; Raizer, Y.P. Laser-induced air spike for advanced transatmospheric vehicles. In Proceedings of the 25th Plasmadynamics and Lasers Conference, Colorado Springs, CO, USA, 20 June–23 June 1994. Paper AIAA-1994-2451. [Google Scholar]
- Tretyakov, P.K.; Fomin, V.M.; Yakovlev, V.I. New principles of control of aerophysical processes—research development. In Proceedings of the International Conference on the Methods Aerophysical Research, Novosibirsk, Russia, 29 June–3 July 1996; The Institute of Theoretical and Applied Mechanics: Novosibirsk, Russia, 1996; pp. 210–220. [Google Scholar]
- Adelgren, R.G.; Yan, H.; Elliott, G.S.; Knight, D.D.; Beutner, T.J.; Zheltovodov, A.A. Control of Edney IV interaction by pulsed laser energy deposition. AIAA J. 2005, 43, 256–269. [Google Scholar] [CrossRef]
- Zheltovodov, A.A.; Pimonov, E.A.; Knight, D.D. Energy deposition influence on supersonic flow over axisymmetric bodies. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8 January–11 January 2007; pp. 1–31, Paper AIAA-2007-1230. [Google Scholar]
- Mortazavi, M.; Knight, D.D.; Azarova, O.A.; Shi, J.; Yan, H. Numerical simulation of energy deposition in a supersonic flow past a hemisphere. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MD, USA, 13–17 January 2014; pp. 1–18, Paper AIAA-2014-0944. [Google Scholar]
- Azarova, O.A.; Knight, D.D. Interaction of microwave and laser discharge resulting “heat spots” with supersonic combined cylinder bodies. Aerosp. Sci. Technol. 2017, 43, 343–349. [Google Scholar] [CrossRef]
- Kim, S.; Lee, H.J. Influence of laser energy deposition conditions on the drag of a sphere in supersonic flow. Energies 2019, 16, 3914. [Google Scholar] [CrossRef] [Green Version]
- Alberti, A.; Munafo, A.; Pantano, C.; Panesi, M. Supersonic and hypersonic non-equilibrium flow control using laser energy deposition. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019; pp. 1–27, Paper AIAA 2019-2867. [Google Scholar]
- Lapushkina, T.A.; Erofeev, A.V. Supersonic flow control via plasma, electric and magnetic impacts. Aerosp. Sci. Technol. 2017, 69, 313–320. [Google Scholar] [CrossRef]
- Znamenskaya, I.A.; Naumov, D.S.; Sysoev, N.N.; Chernikov, V.A. Analysis of dynamic processes occurring during generation of plasmoid formations in a supersonic flow. Tech. Phys. 2019, 64, 802–806. [Google Scholar] [CrossRef]
- Azarova, O.A.; Gvozdeva, L.G. Control of triple-shock configurations in high speed flows over a cylindrically blunted plate in gases at different Mach numbers. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2018. [Google Scholar] [CrossRef]
- Azarova, O.A.; Gvozdeva, L.G. Control of triple-shock configurations and vortex structures forming in high speed flows of gaseous media past AD body under the action of external energy sources. Aerospace 2017, 4, 9. [Google Scholar] [CrossRef] [Green Version]
- Azarova, O.A. Complex conservative difference schemes for computing supersonic flows past simple aerodynamic forms. Comput. Math. Math. Phys. 2015, 55, 2025–2049. [Google Scholar] [CrossRef]



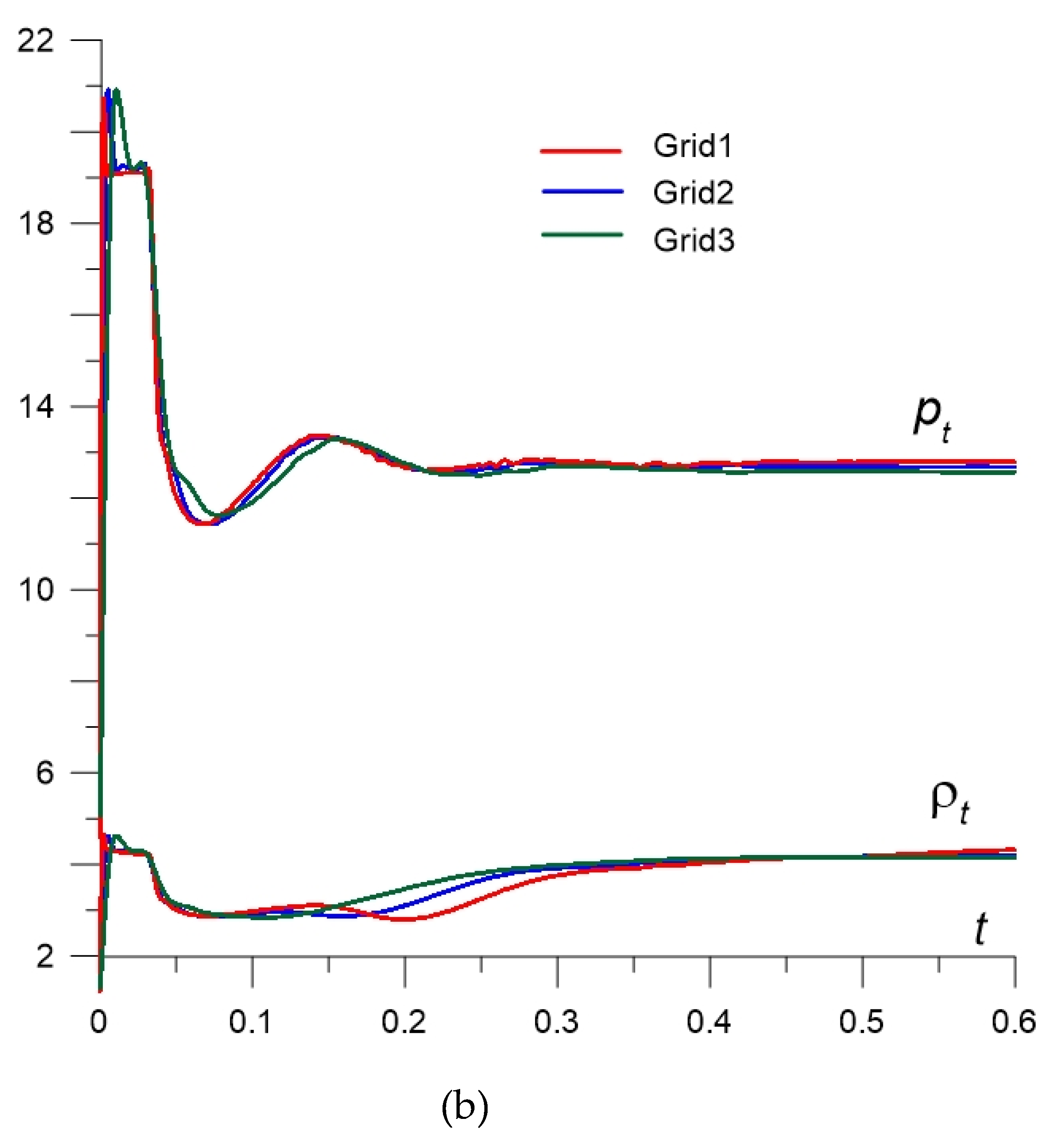

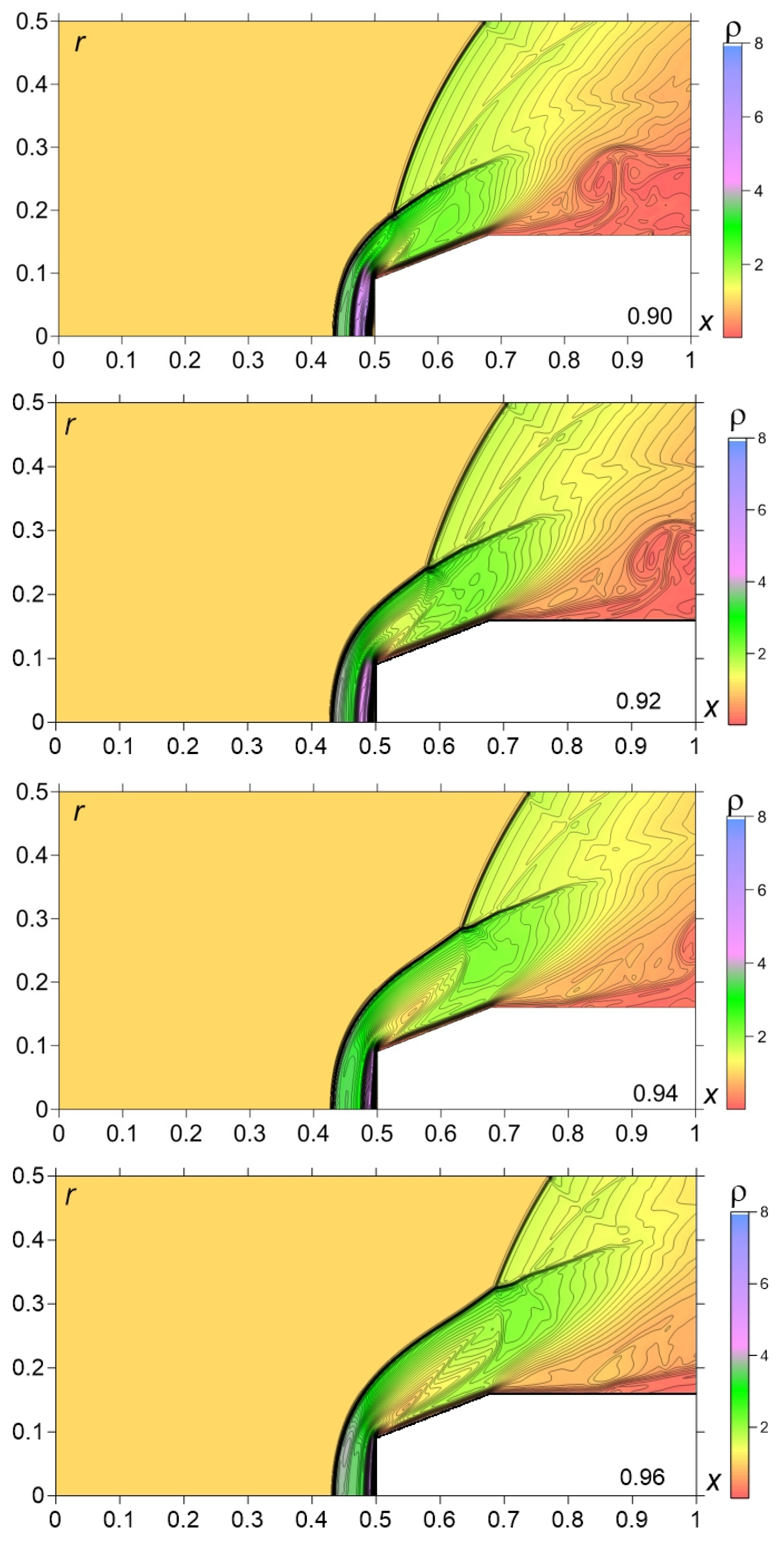
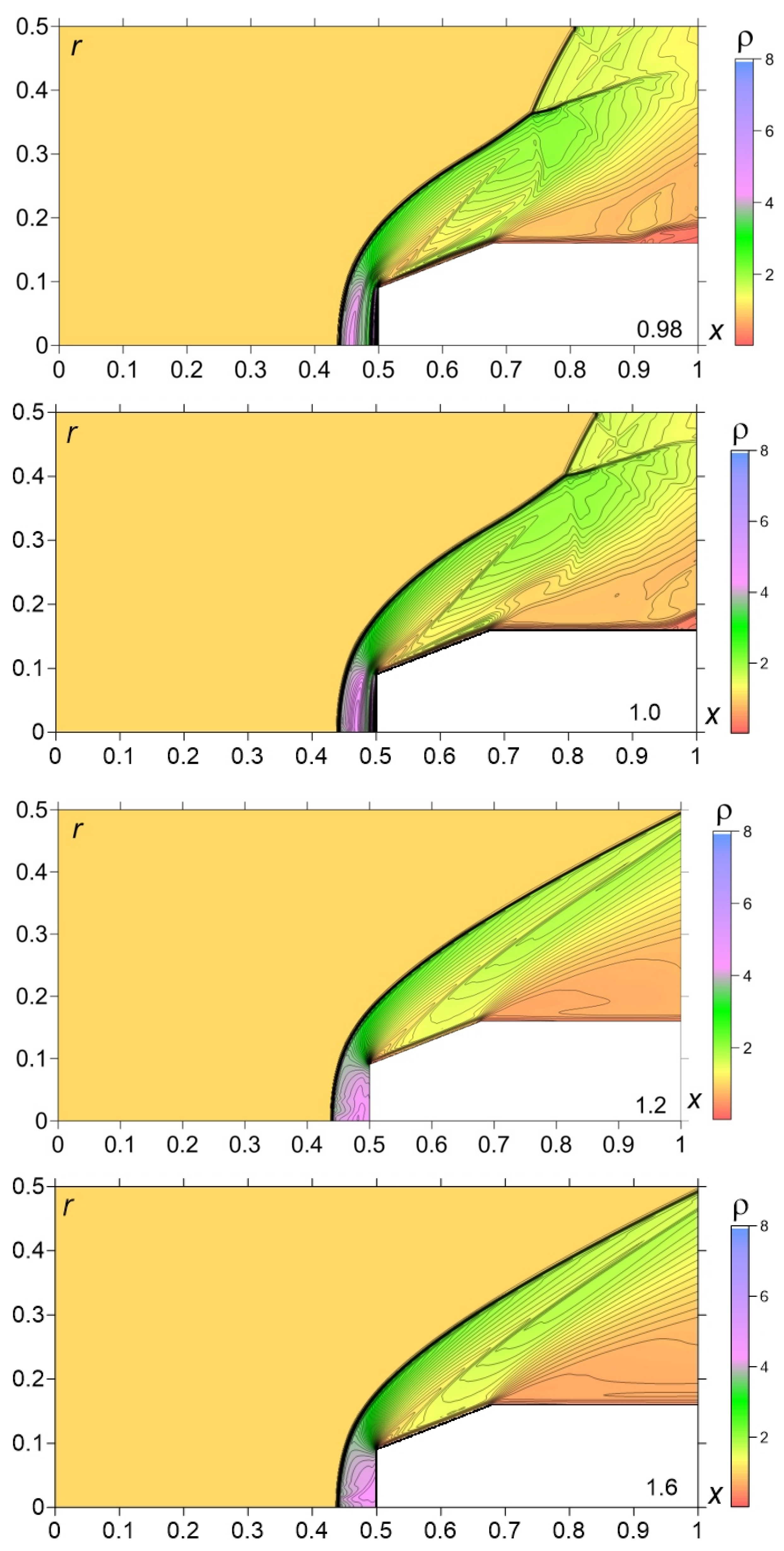

| Grid | Steps hx = hy | Sizes | Relative Error, pt | Relative Error, ρt |
|---|---|---|---|---|
| Grid1 | 0.0005 | 2000 × 1000 | 0.469% | 1.873% |
| Grid2 | 0.001 | 1000 × 500 | 1.336% | 4.477% |
| Grid3 | 0.002 | 500 × 250 | 2.182% | 5.536% |
| Parameter | Dimensional Value | Dimensionless Value | Normalizing Coefficient |
|---|---|---|---|
| Mach number of the incoming flow М∞ | 3.1 | ||
| Ratio of specific heats γ | 1.4 | ||
| Initial gas pressure p∞ | 2 atm | 1.0 | pn = 2 atm = 2 × 1.01325 × 105 Pa |
| Initial gas density ρ∞ | 4.71 kg/m3 | 1.0 | ρn = 4.71 kg/m3 |
| Initial gas temperature T∞ | 150 K | 1.0 | Tn =150 K |
| Pressure in the energy supply zone pi | 66.42 atm | 33.2124 | pn = 2 atm = 2 × 1.01325 × 105 Pa |
| Radius of the energy supply zone ri | 8 × 10−3 m | 0.16 | ln= 5 × 10−2 m |
| Energy spent on the expansion of the gas | 35 J | 1.3817 | En= ln3pn |
| Length | 1 | ln= 5 × 10−2 m | |
| Velocity | 1 | un = (pn/ρn)0.5 = 207.4258 m/s | |
| Time | 1 | tn= ln/un = 2.4105 × 10−4 s = 241 µs | |
| The time of switching on the energy source | 144.8 µs | 0.601 | tn= 241 µs |
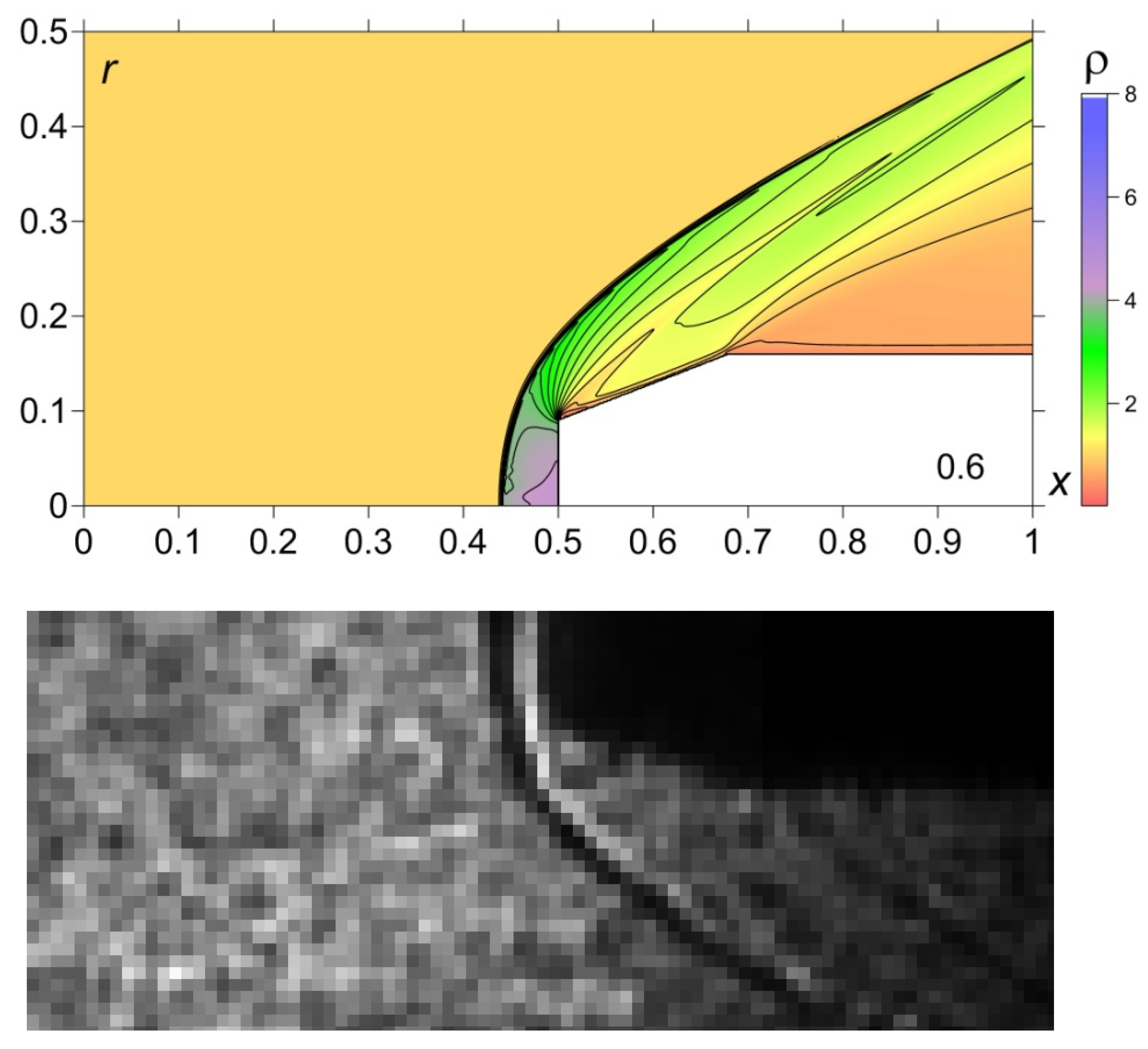
| Interaction start time | 145.9 µs | 0.6053 | tn= 241 µs |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Znamenskaya, I.; Chernikov, V.; Azarova, O. Dynamics of Shock Structure and Frontal Drag Force in a Supersonic Flow Past a Blunt Cone under the Action of Plasma Formation. Fluids 2021, 6, 399. https://doi.org/10.3390/fluids6110399
Znamenskaya I, Chernikov V, Azarova O. Dynamics of Shock Structure and Frontal Drag Force in a Supersonic Flow Past a Blunt Cone under the Action of Plasma Formation. Fluids. 2021; 6(11):399. https://doi.org/10.3390/fluids6110399
Chicago/Turabian StyleZnamenskaya, Irina, Vladimir Chernikov, and Olga Azarova. 2021. "Dynamics of Shock Structure and Frontal Drag Force in a Supersonic Flow Past a Blunt Cone under the Action of Plasma Formation" Fluids 6, no. 11: 399. https://doi.org/10.3390/fluids6110399
APA StyleZnamenskaya, I., Chernikov, V., & Azarova, O. (2021). Dynamics of Shock Structure and Frontal Drag Force in a Supersonic Flow Past a Blunt Cone under the Action of Plasma Formation. Fluids, 6(11), 399. https://doi.org/10.3390/fluids6110399







