Testing Basic Gradient Turbulent Transport Models for Swirl Burners Using PIV and PLIF
Abstract
:1. Introduction
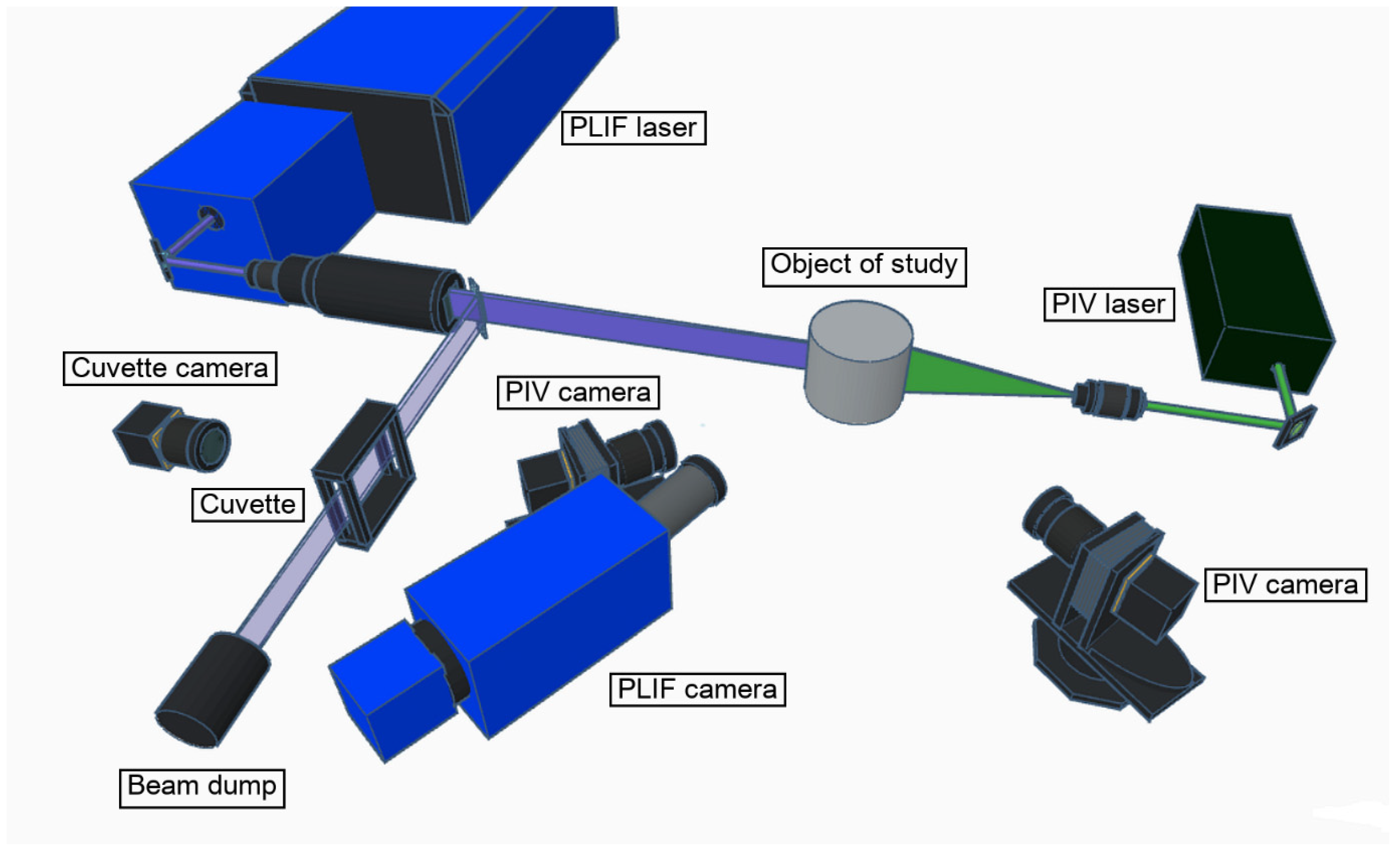
2. Experimental Setup
2.1. Test Facilities
2.2. PIV/PLIF Equipment
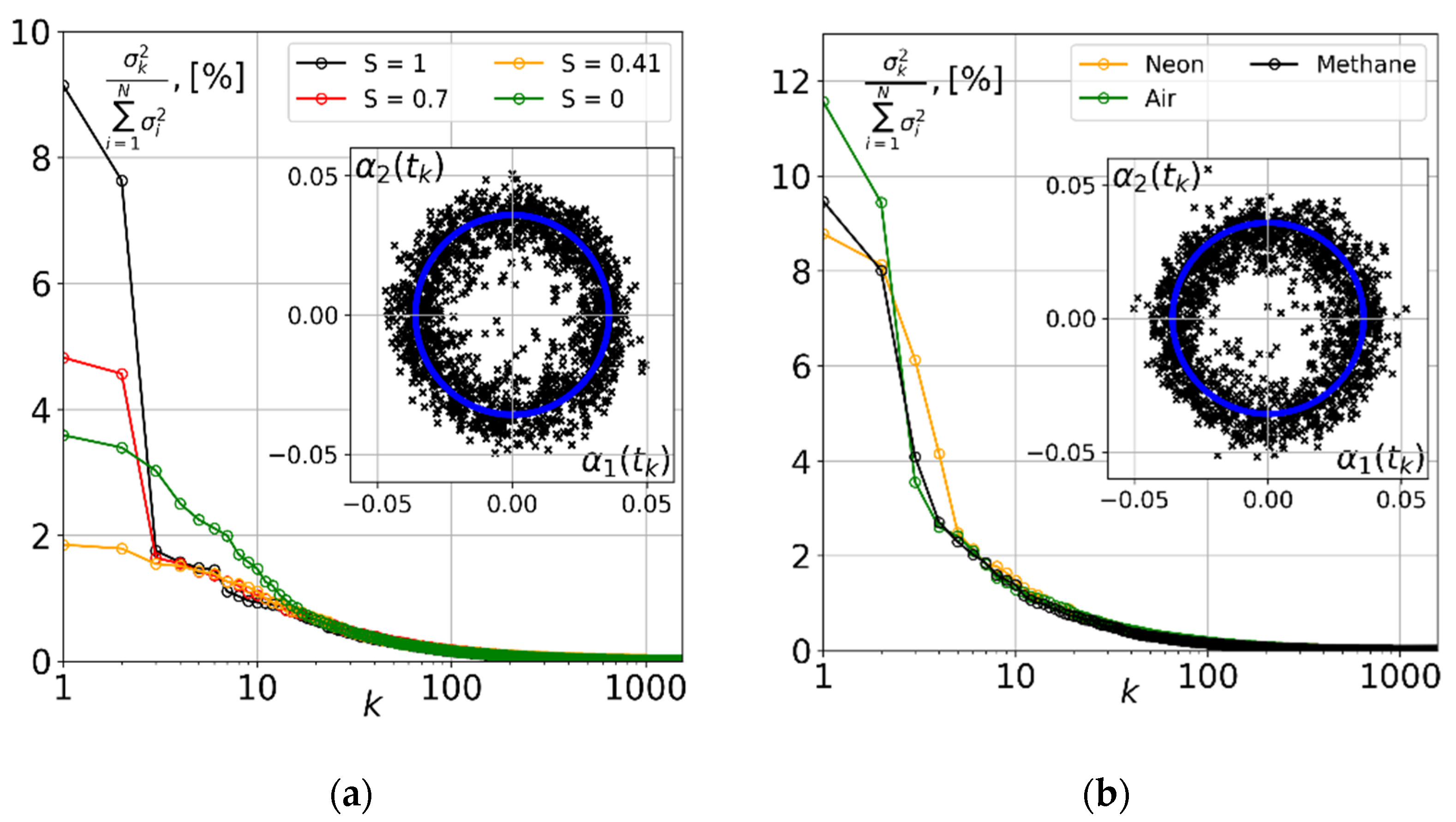
2.3. Data Processing
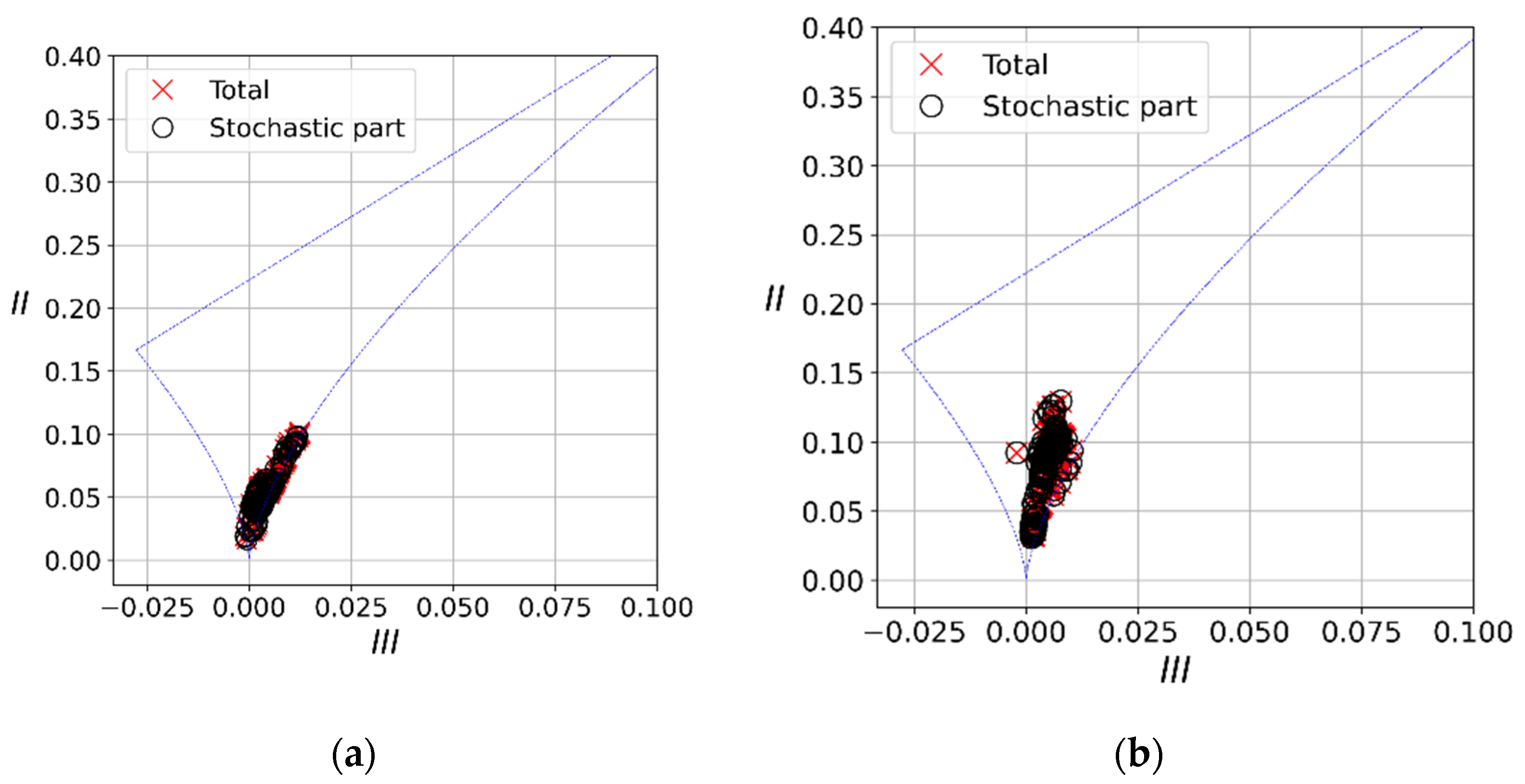
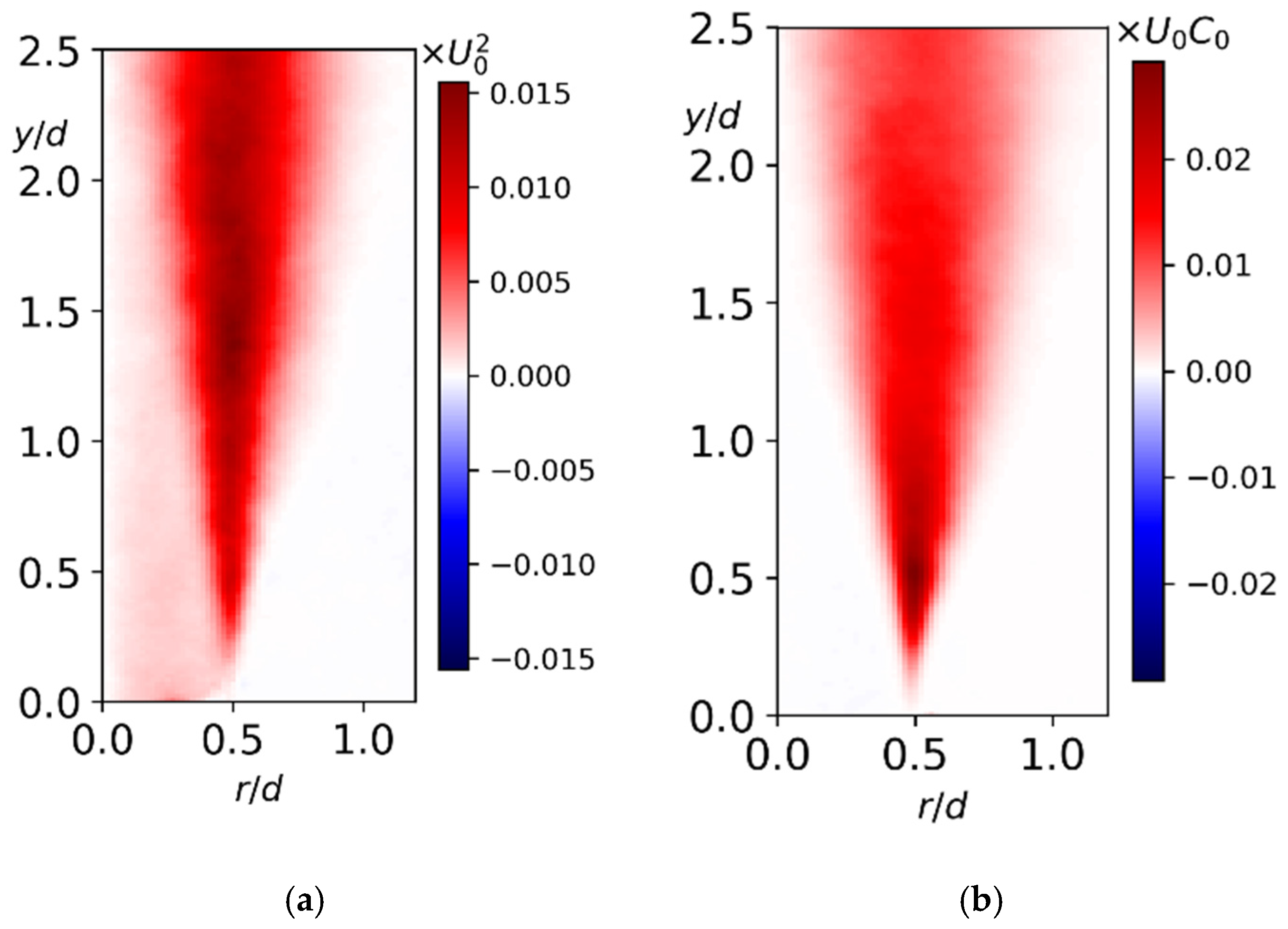
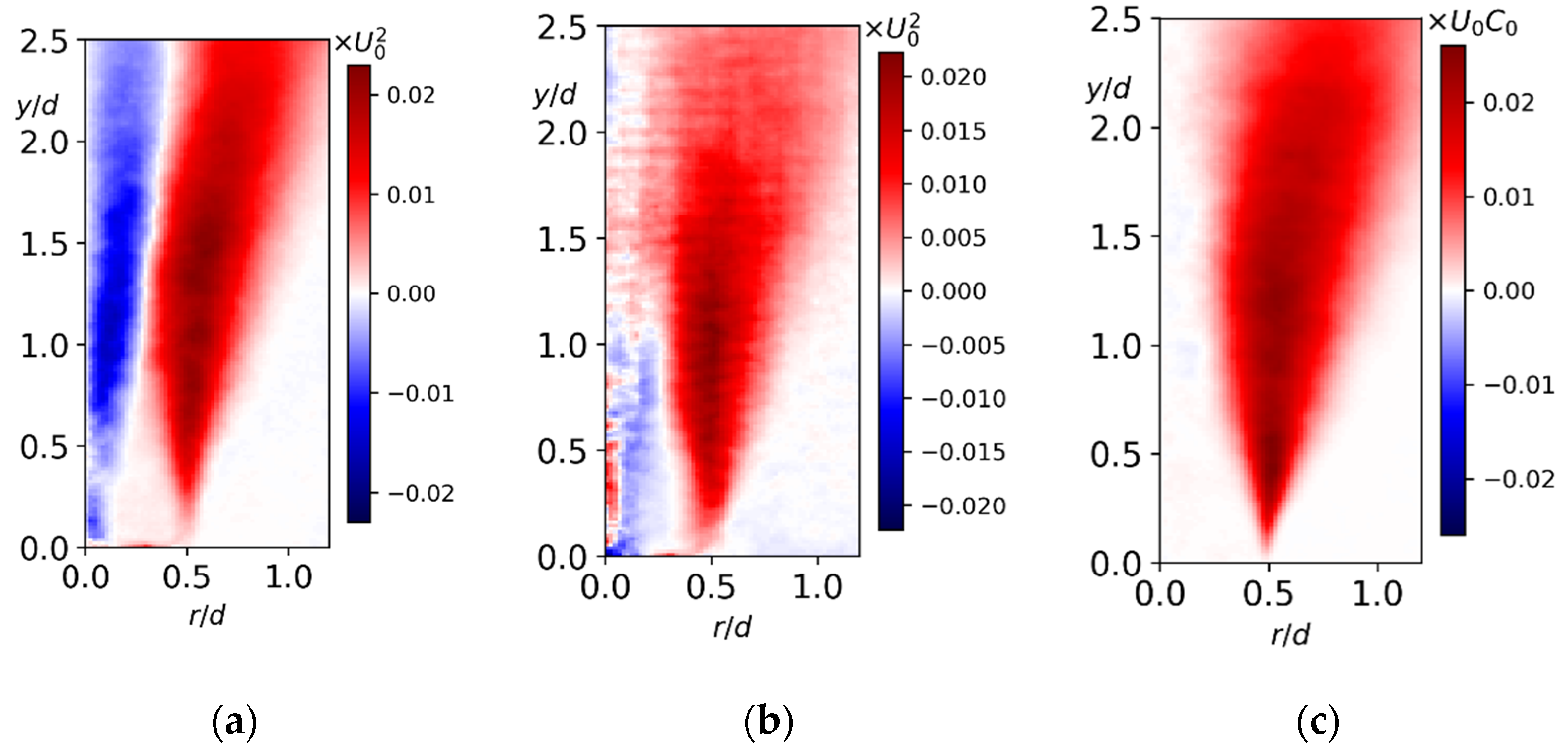
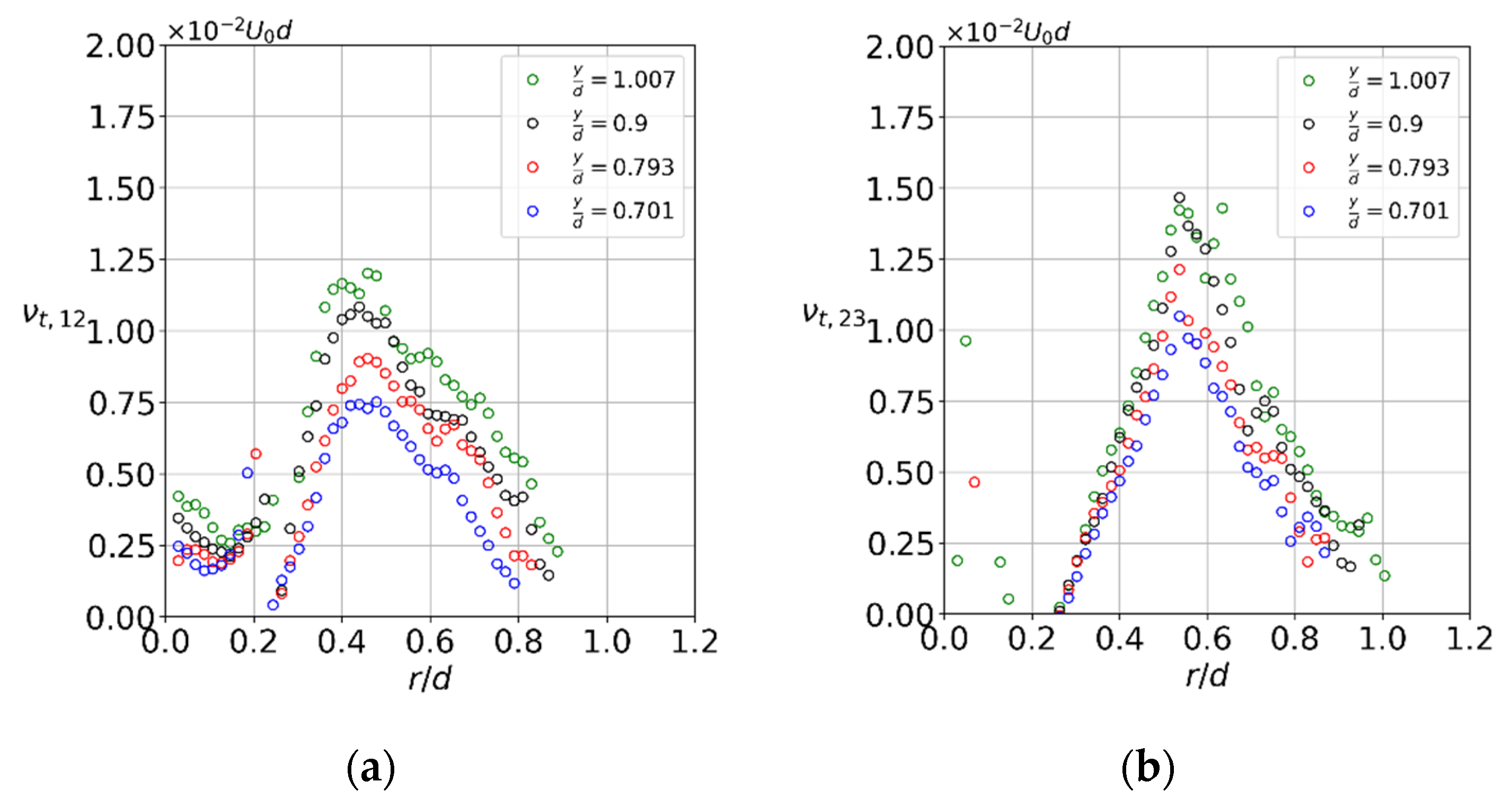
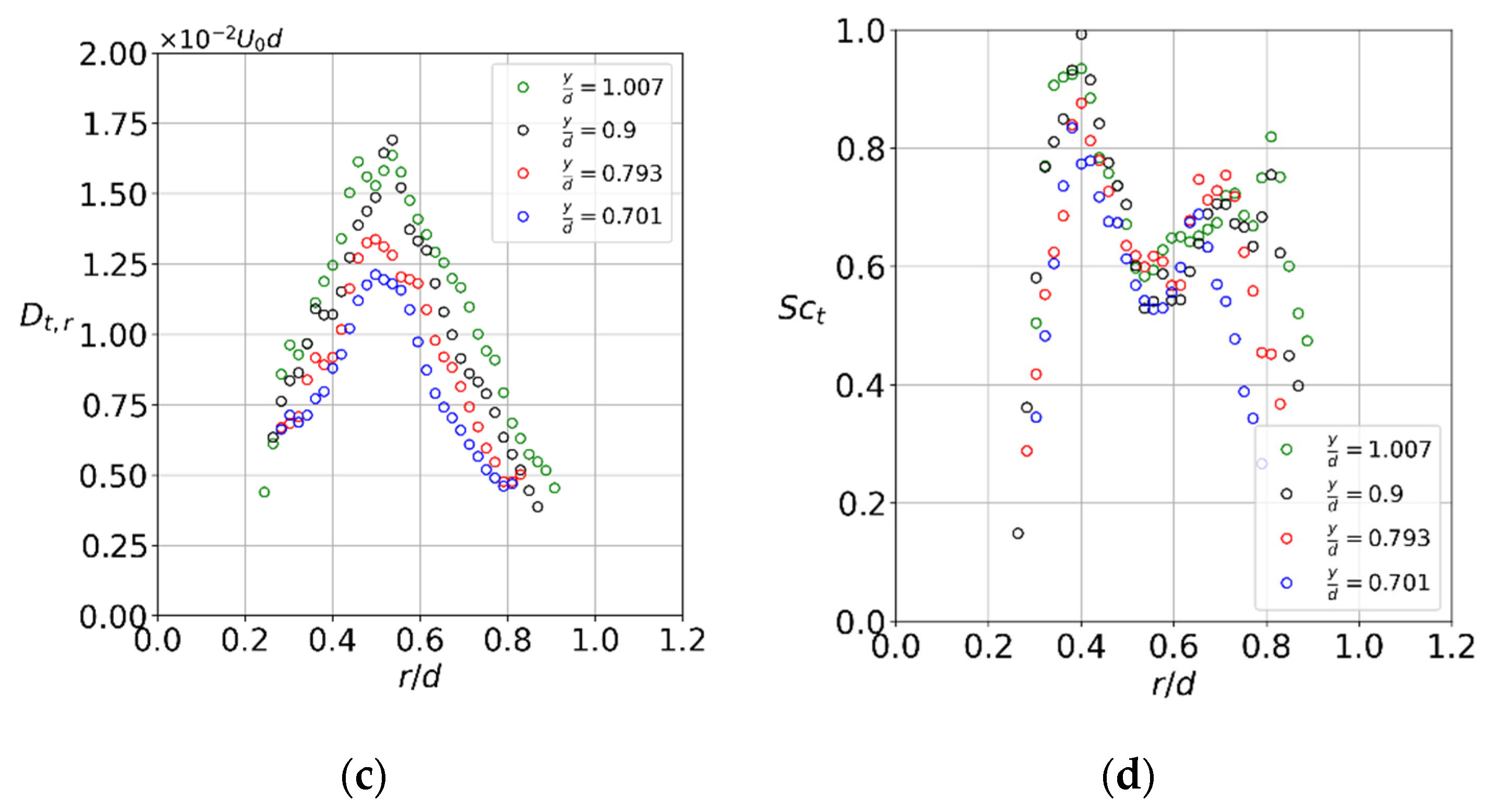
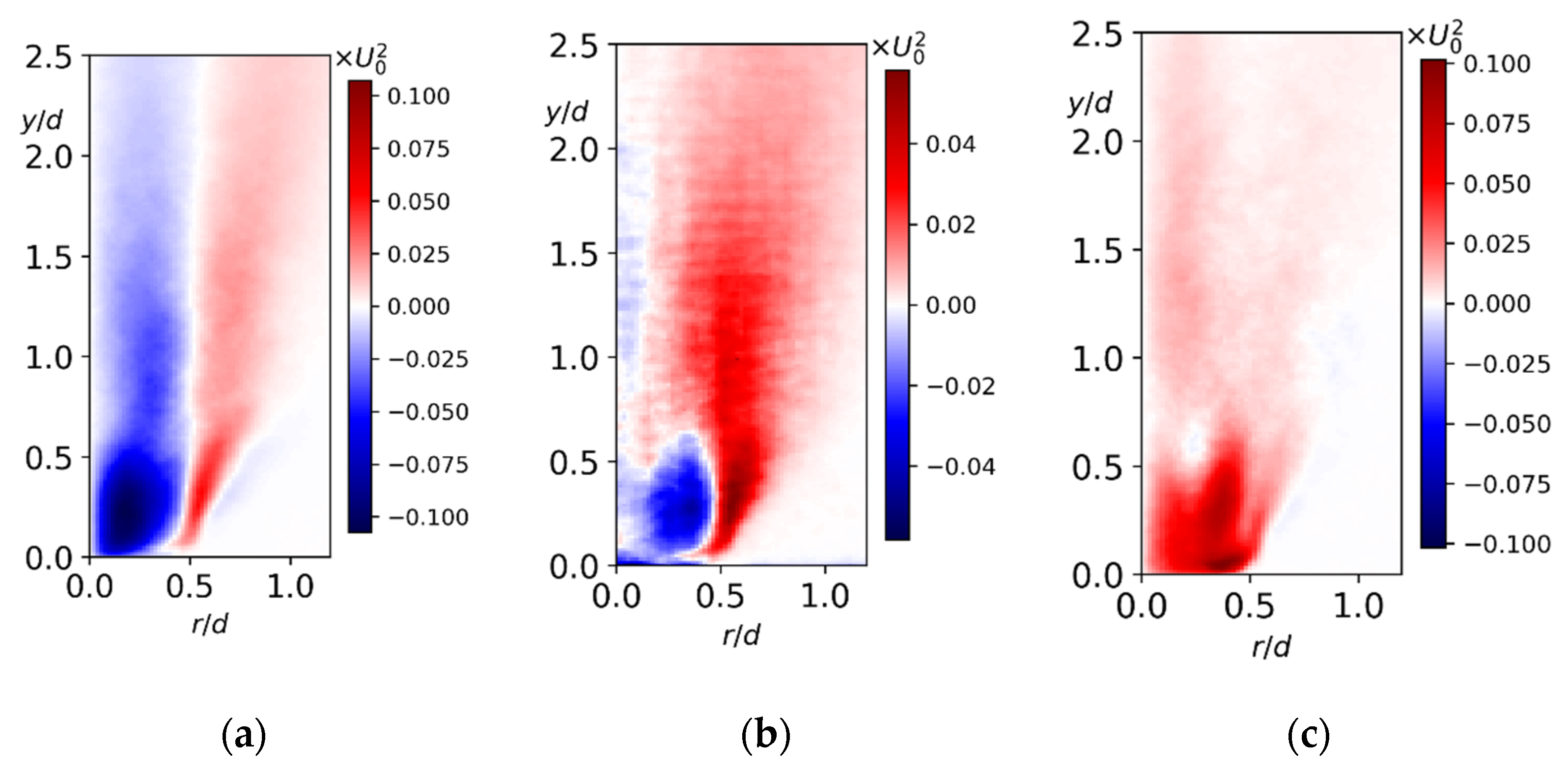
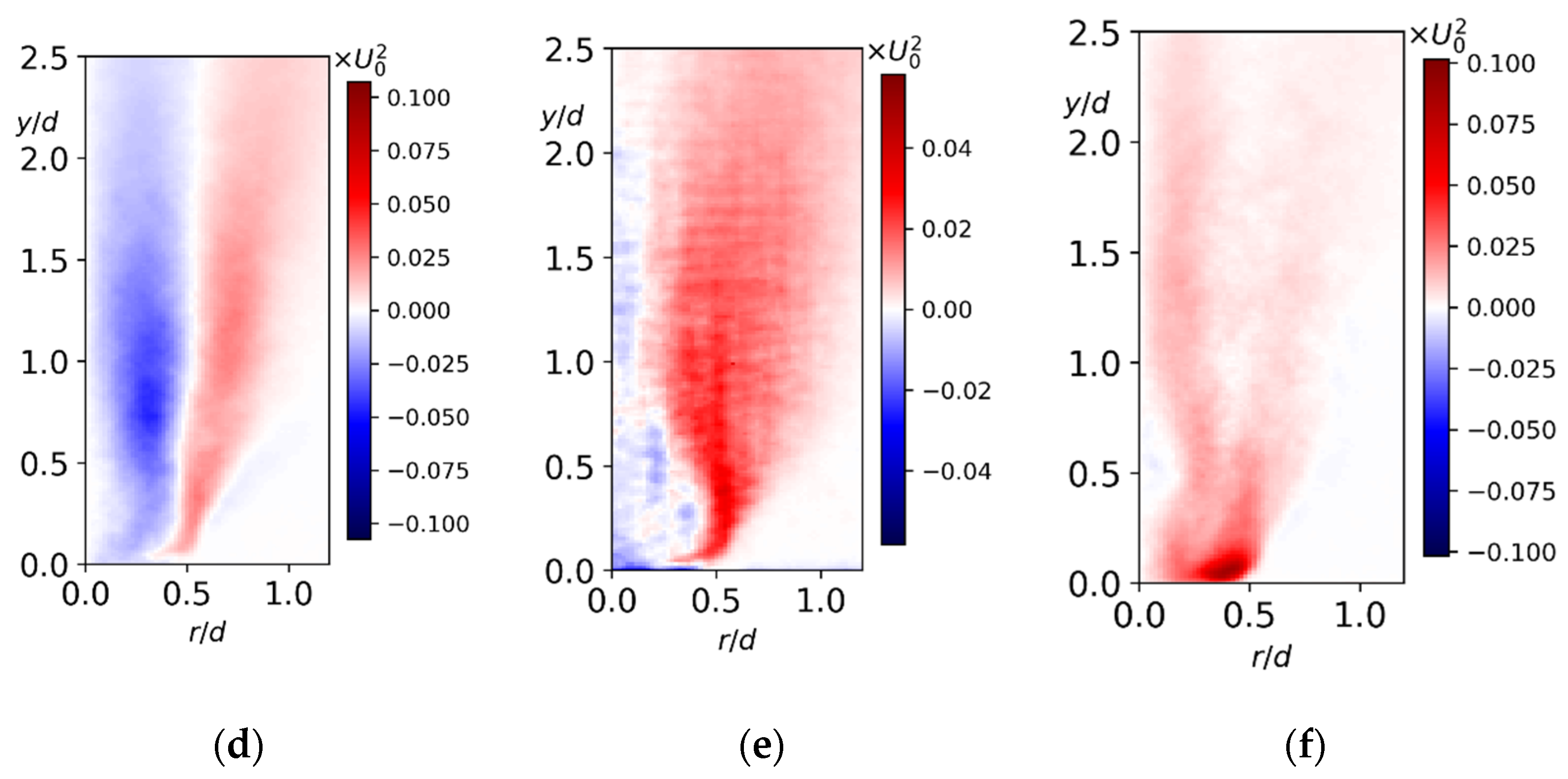
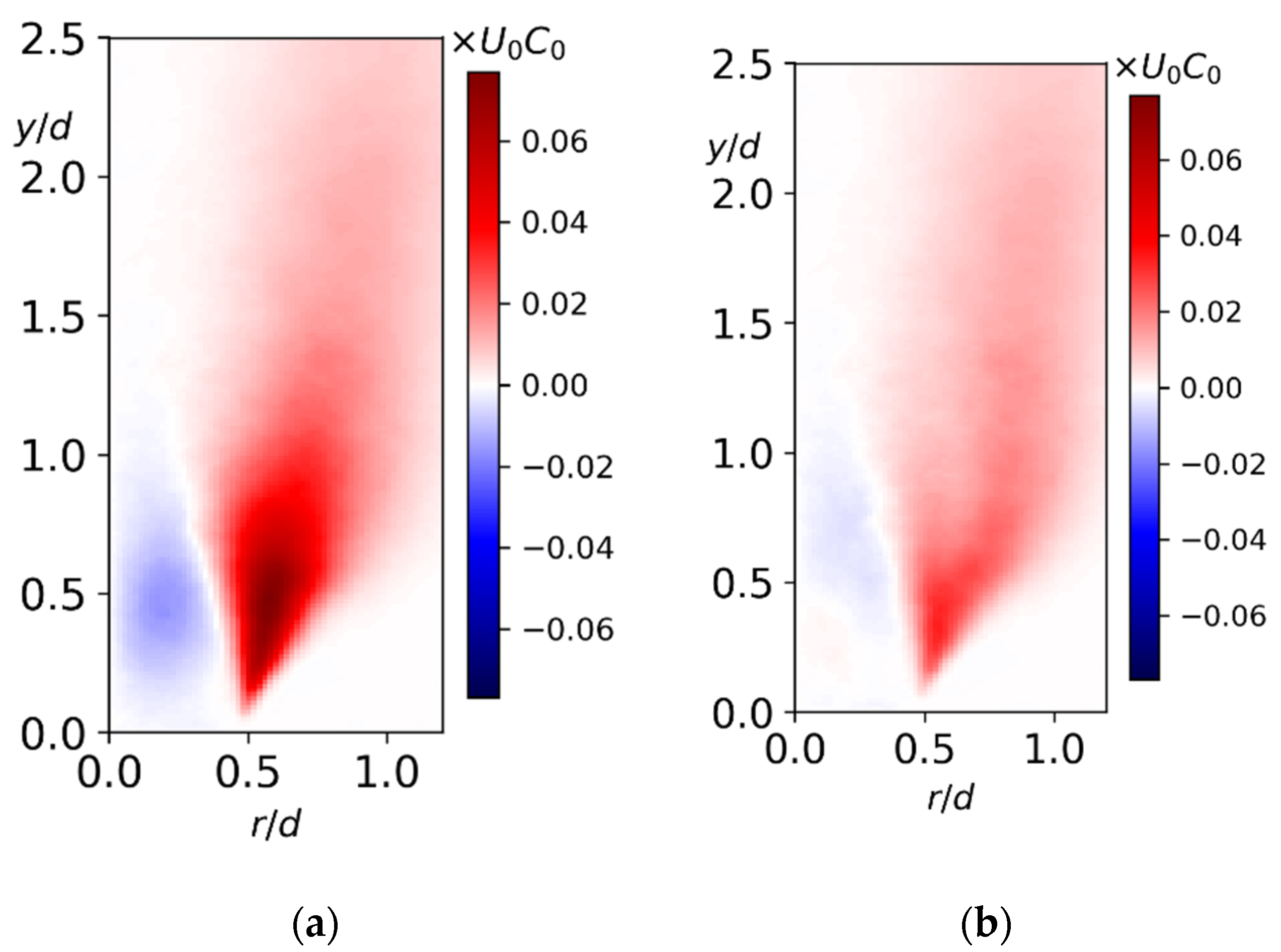
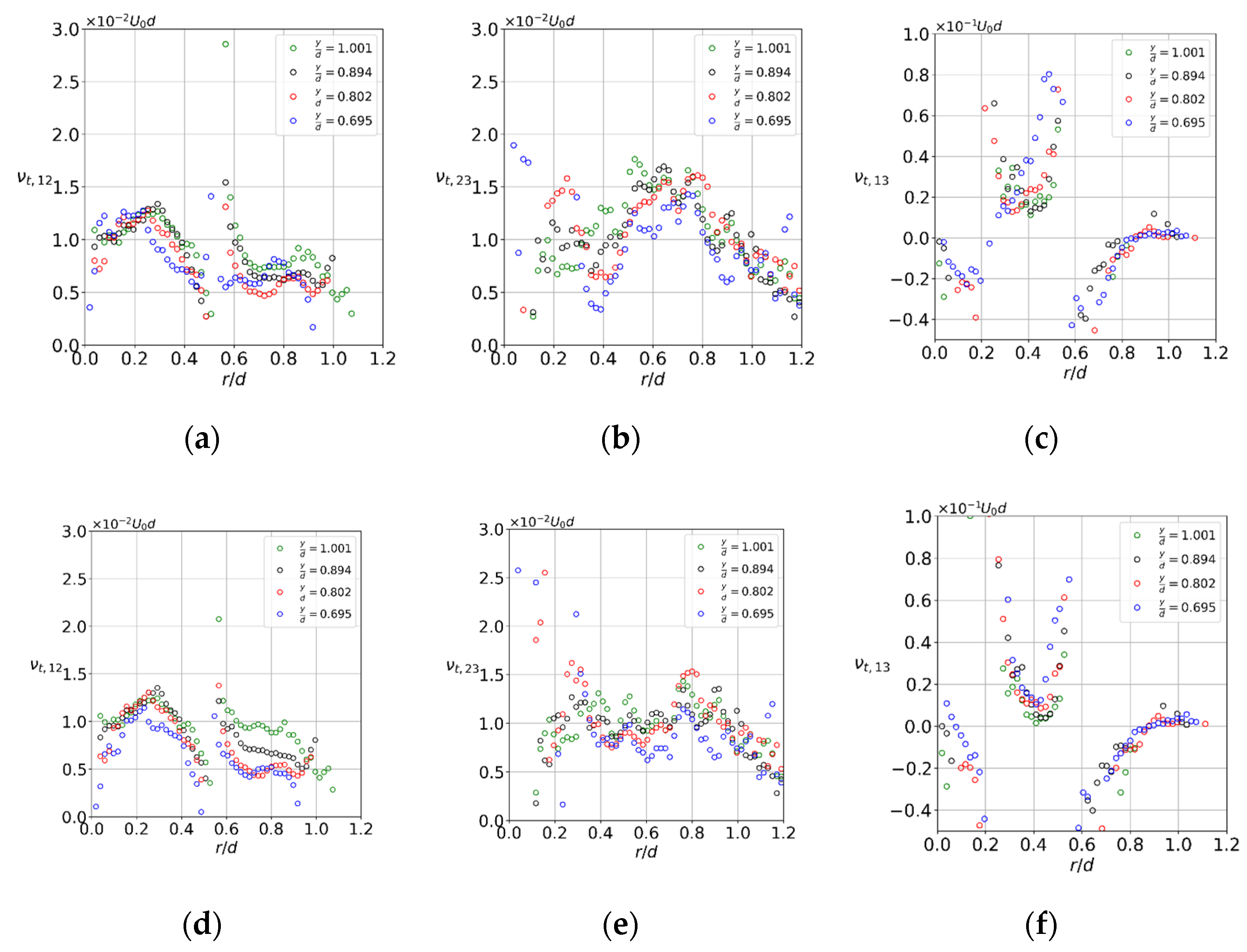
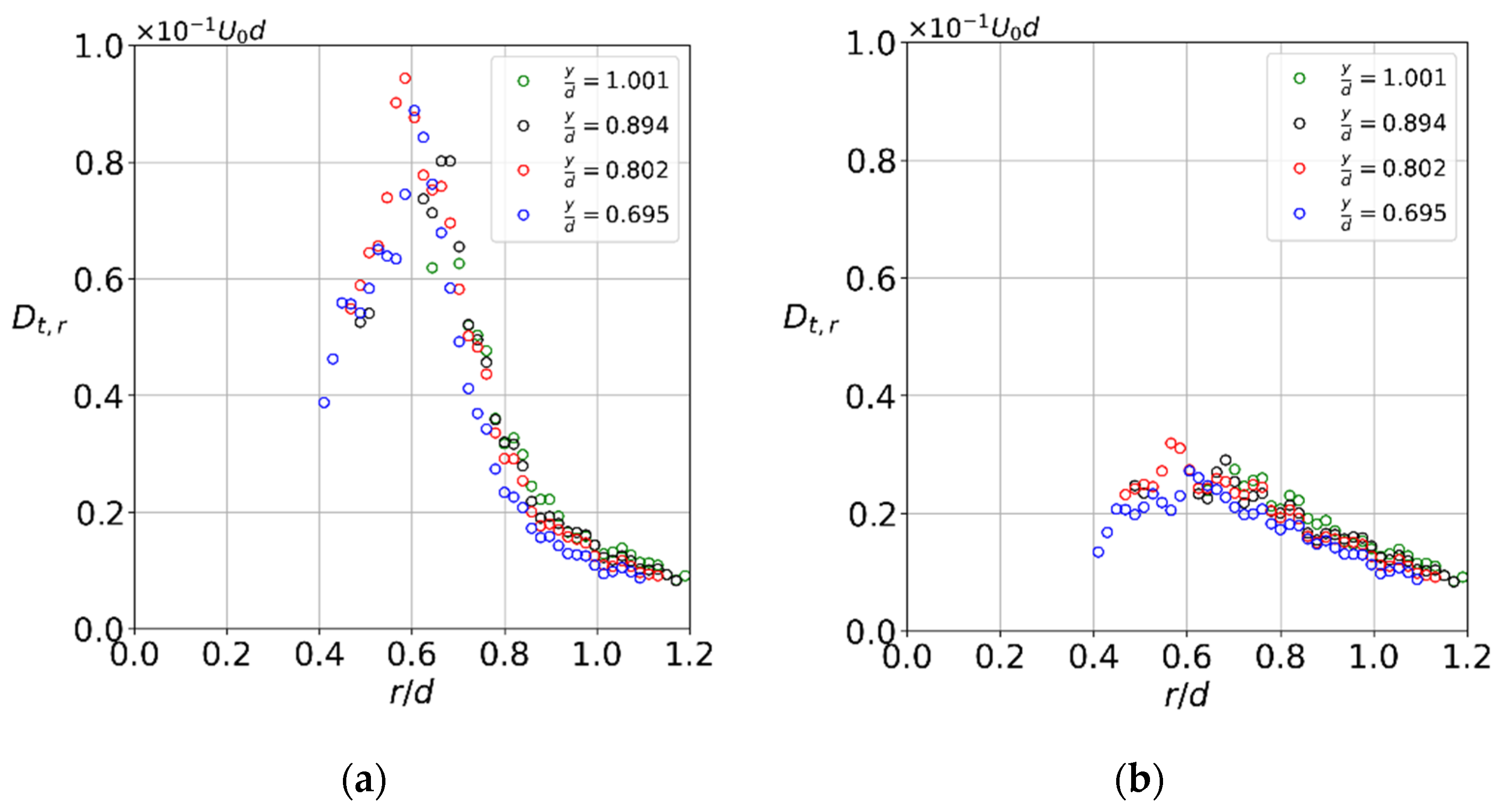
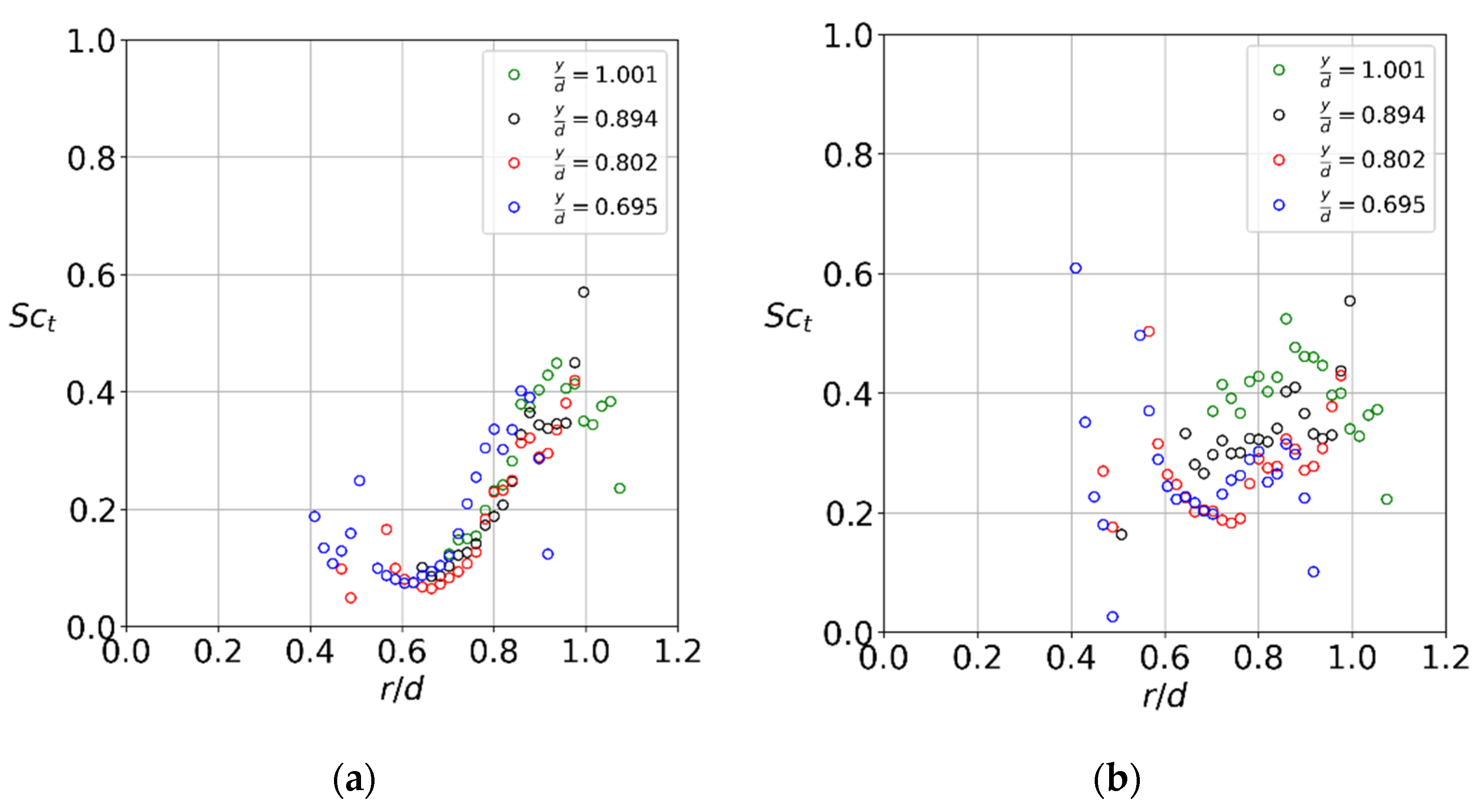
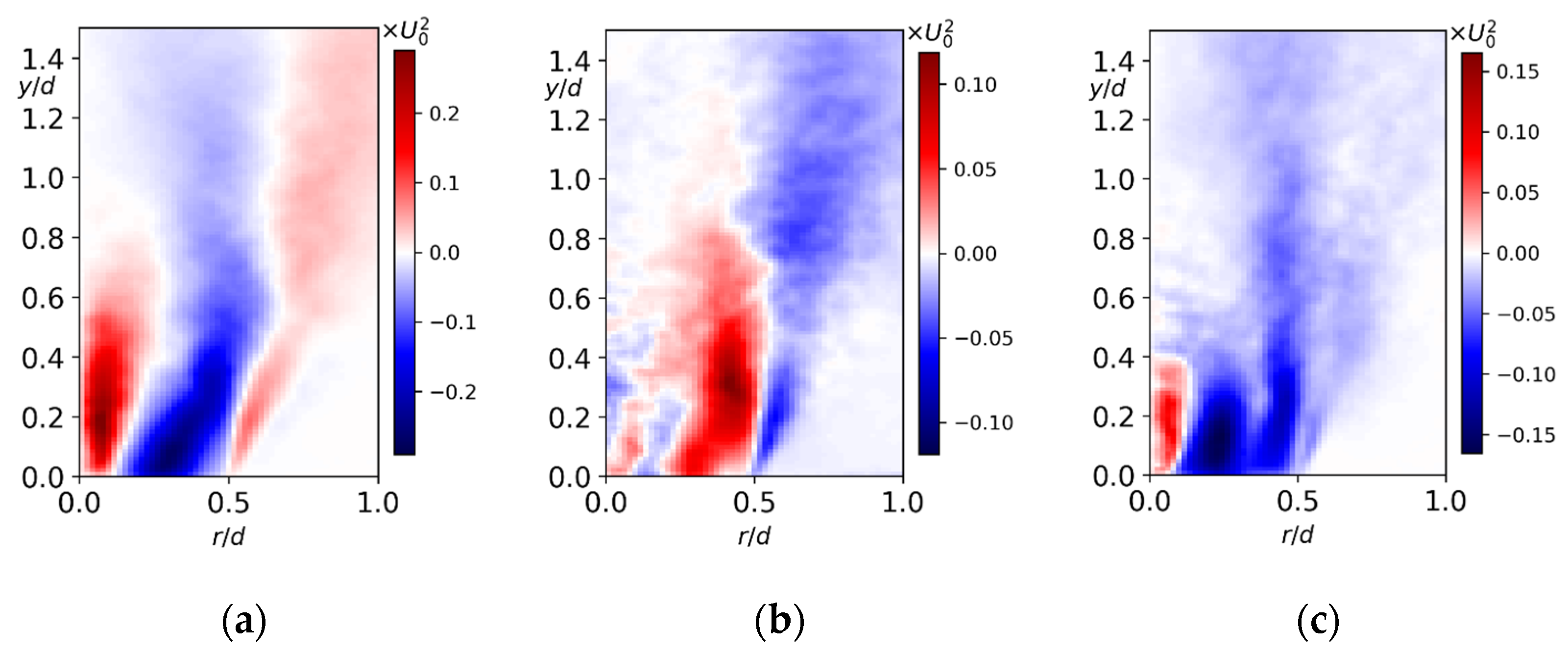
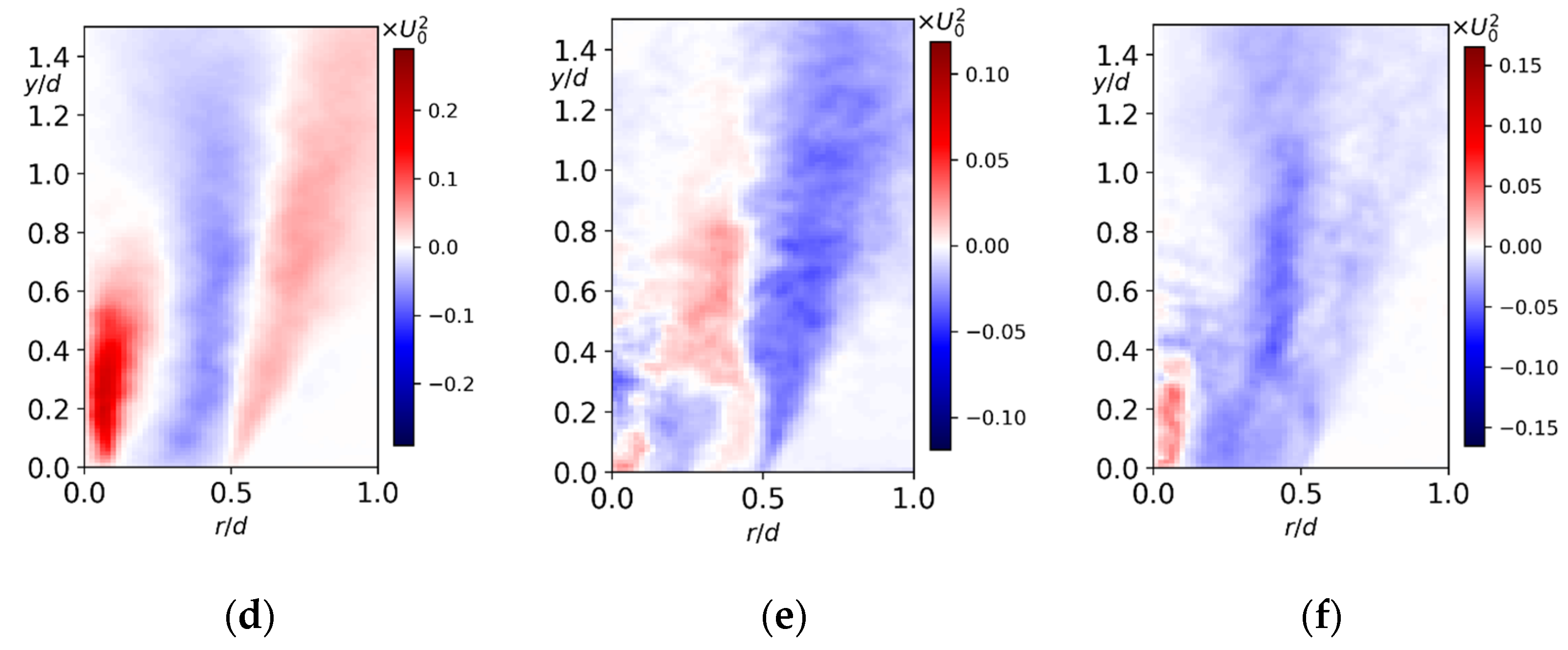
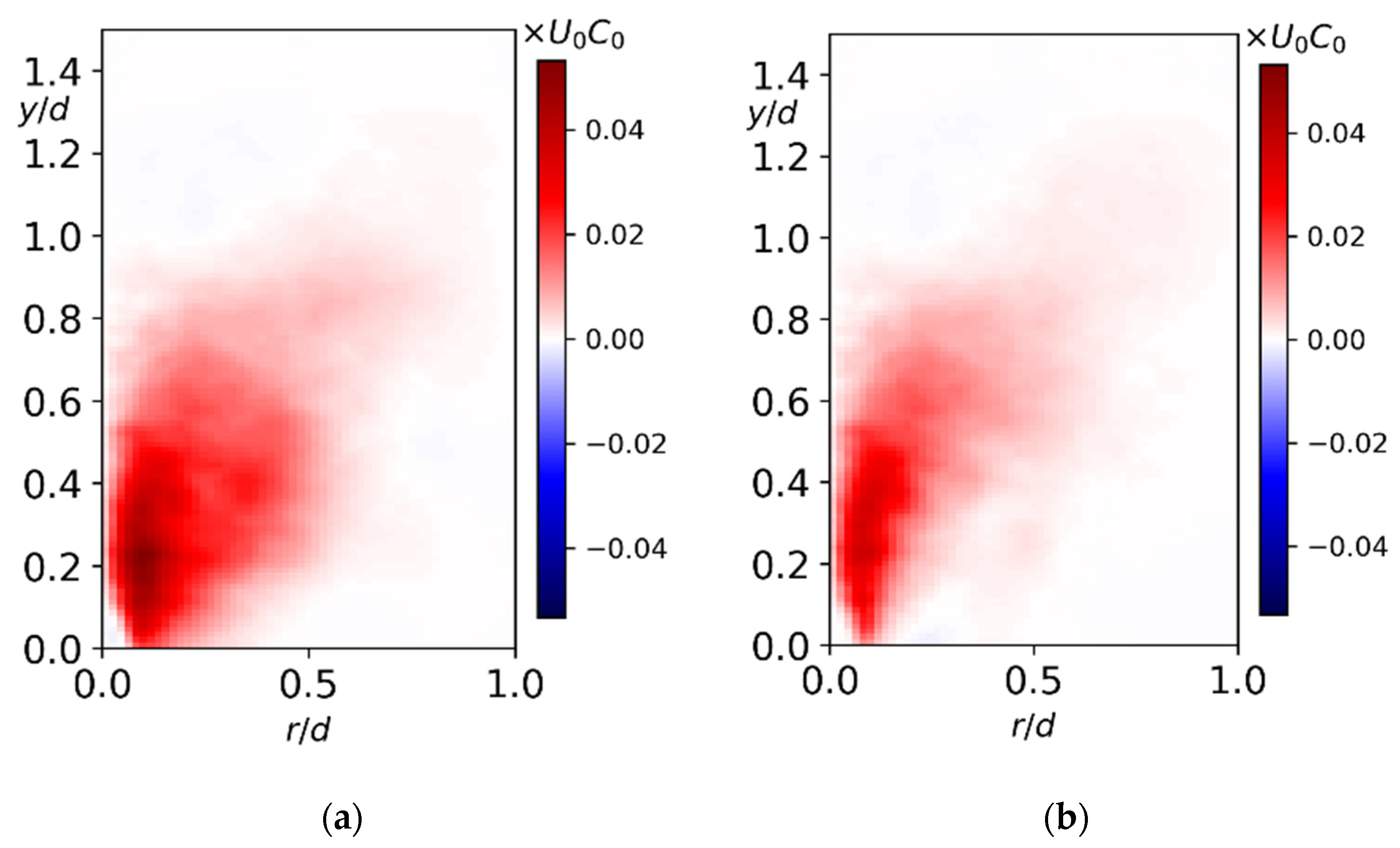
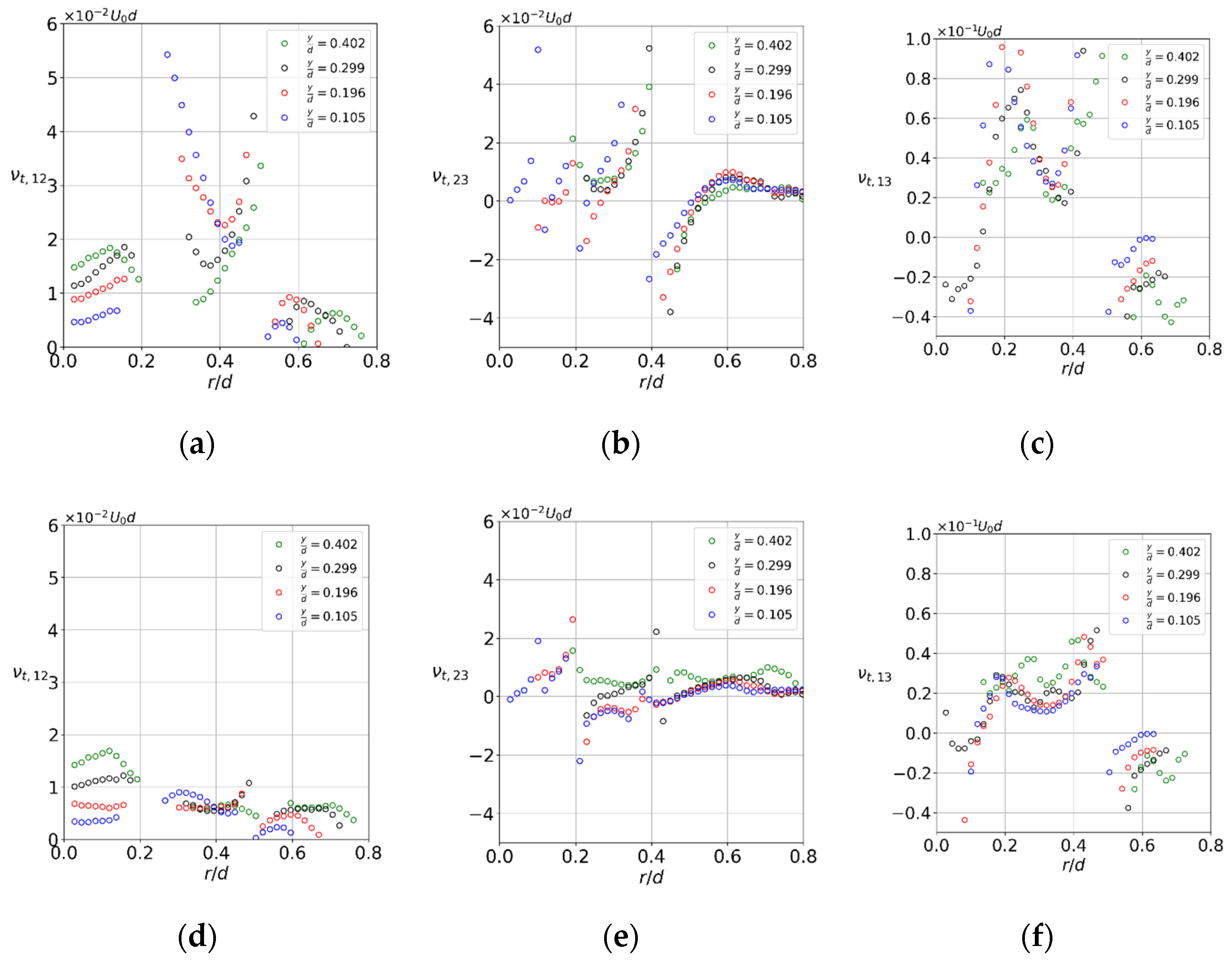
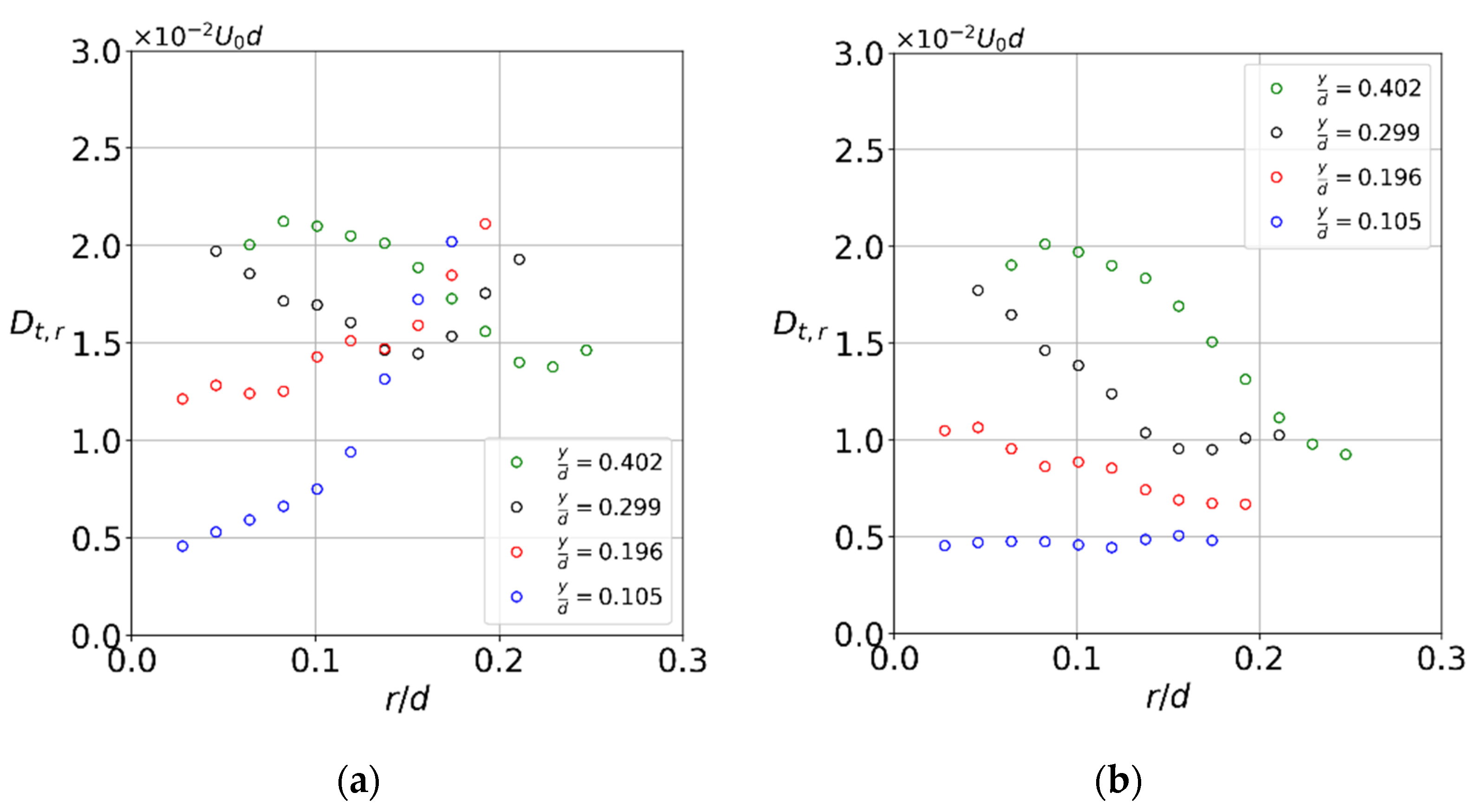
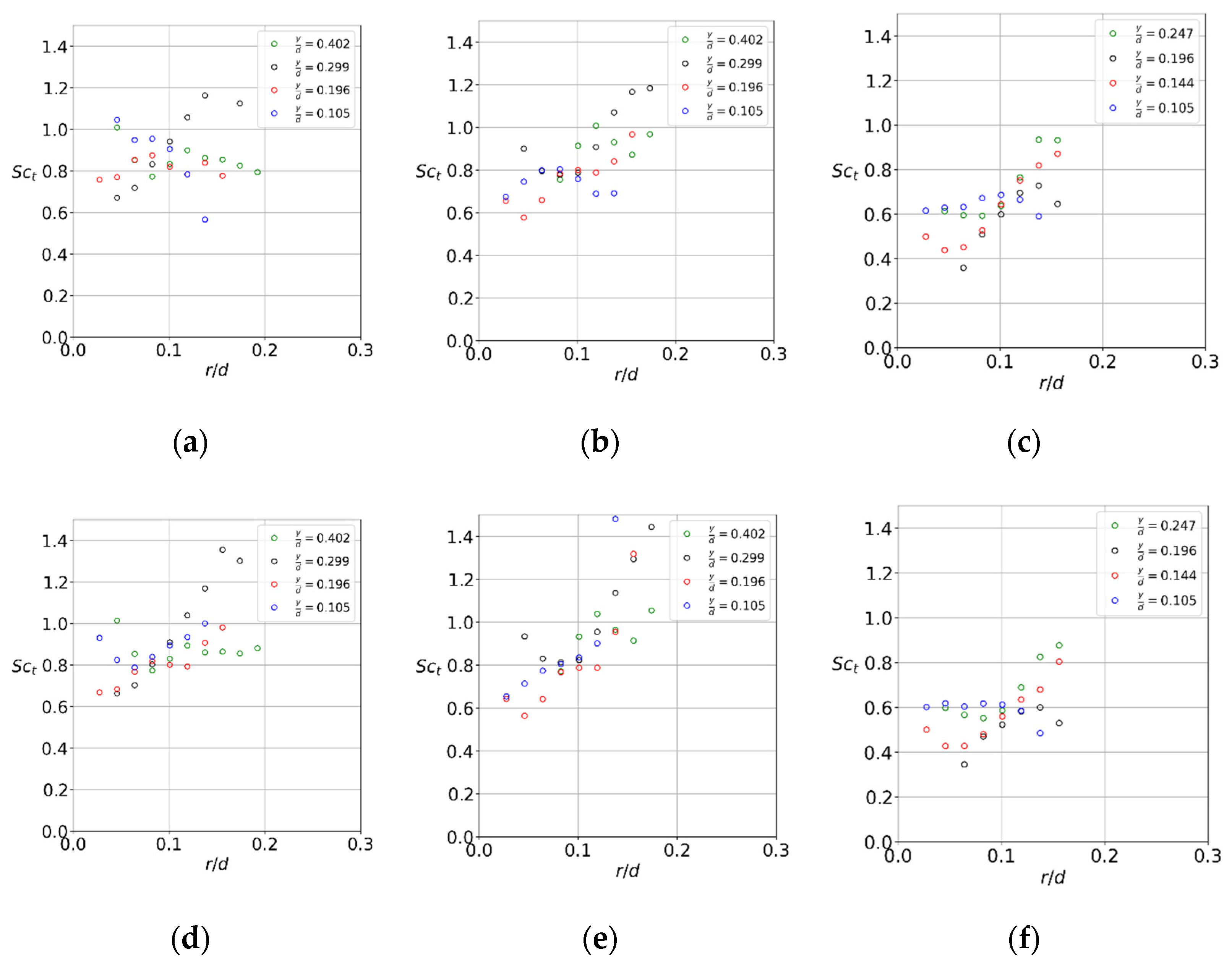
3. Results
3.1. Flow Structure and Coherent Fluctuations
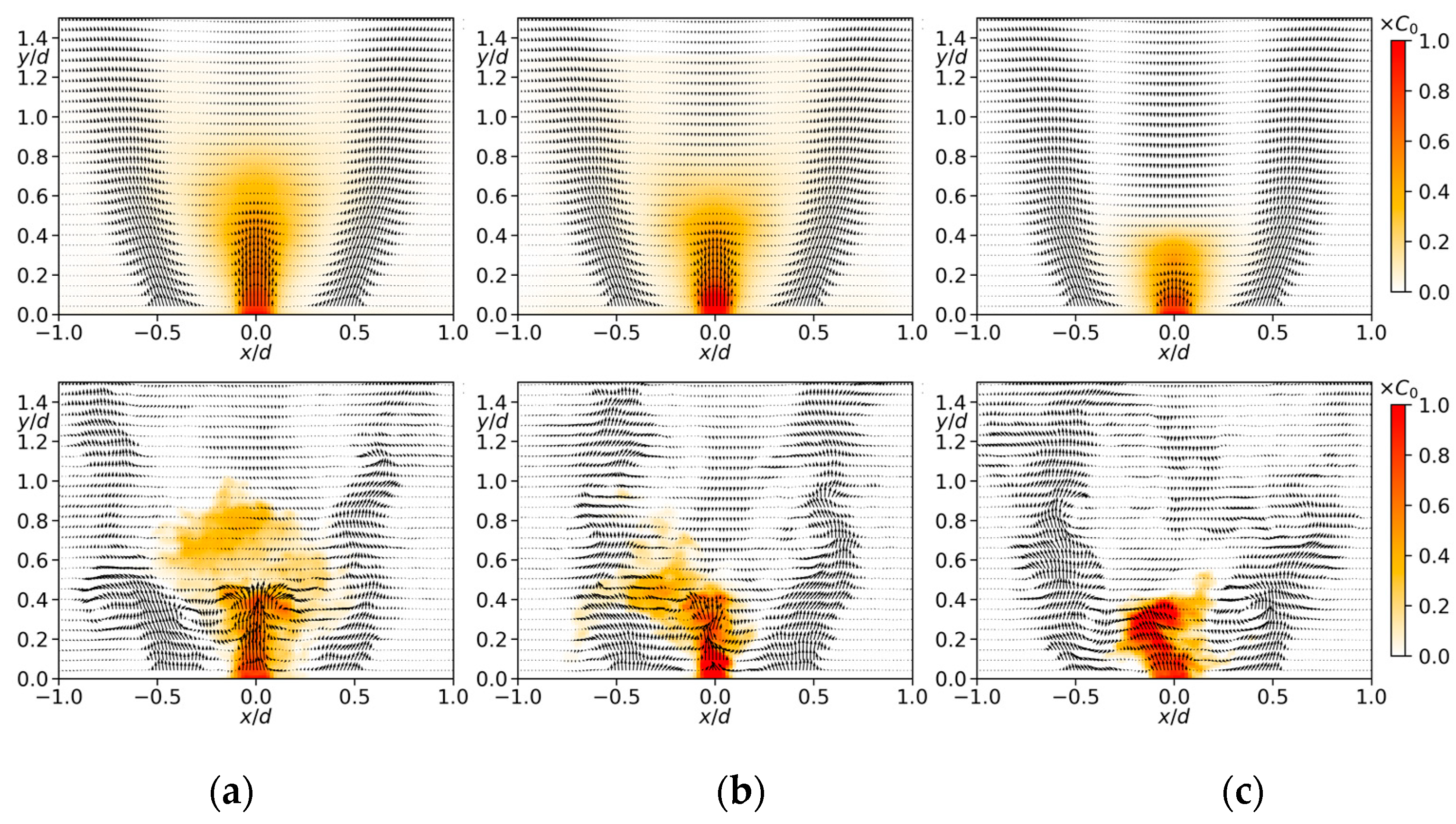
3.2. Nonswirling Jet
3.3. Low-Swirl Jet
3.4. High-Swirl Jet
3.5. Gas Turbine Swirler
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lucca-Negro, O.; O’Doherty, T. Vortex breakdown: A review. Prog. Energy Combust. Sci. 2001, 27, 431–522. [Google Scholar] [CrossRef]
- Syred, N. A review of oscillation mechanisms and the role of the precessing vortex core (PVC) in swirl combustion systems. Prog. Energy Combust. Sci. 2006, 32, 93–161. [Google Scholar] [CrossRef]
- Dunn-Rankin, D. Lean Combustion: Technology and Control; Academic Press: Cambridge, UK, 2008. [Google Scholar]
- Lieuwen, T.; Torres, H.; Johnson, C.; Zinn, B.T. A mechanism of combustion instability in lean premixed gas turbine combustors. J. Eng. Gas Turb. Power 2001, 123, 182–189. [Google Scholar] [CrossRef]
- Meier, W.; Weigand, P.; Duan, X.R.; Giezendanner-Thoben, R. Detailed characterization of the dynamics of thermoacoustic pulsations in a lean premixed swirl flame. Combust. Flame 2007, 150, 2–26. [Google Scholar] [CrossRef]
- Huang, Y.; Yang, V. Dynamics and stability of lean-premixed swirl-stabilized combustion. Prog. Energy Combust. Sci. 2009, 35, 293–364. [Google Scholar] [CrossRef]
- Estefanos, W.; Bhayaraju, U.; Hamza, M.; Jeng, S.M. Evaluation of Two Measurement Techniques to Quantify Fuel-Air Mixing of a Gas Turbine Pre-mixer at Atmospheric Conditions. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2015; Volume 56680, p. V04AT04A060. [Google Scholar] [CrossRef]
- Schulz, C.; Sick, V. Tracer-LIF diagnostics: Quantitative measurement of fuel concentration, temperature and fuel/air ratio in practical combustion systems. Prog. Energy Combust. Sci. 2005, 31, 75–121. [Google Scholar] [CrossRef]
- Stohr, M.; Sadanandan, R.; Meier, W. Experimental study of unsteady fame structures of an oscillating swirl fame in a gas turbine model combustor. Proc. Combust. Inst. 2009, 32, 2925–2932. [Google Scholar] [CrossRef]
- Renaud, A.; Yokomori, T.; Tachibana, S. Study of a thermo-acoustic instability triggering in a low-swirl burner using simultaneous time-resolved acetone and OH-PLIF. Proc. Combust. Inst. 2019, 37, 2627–2633. [Google Scholar] [CrossRef]
- Felden, A.; Riber, E.; Cuenot, B. Impact of direct integration of Analytically Reduced Chemistry in LES of a sooting swirled non-premixed combustor. Combust. Flame 2018, 191, 270–286. [Google Scholar] [CrossRef]
- Agostinelli, P.W.; Laera, D.; Boxx, I.; Gicquel, L.; Poinsot, T. Impact of wall heat transfer in Large Eddy Simulation of flame dynamics in a swirled combustion chamber. Combust. Flame 2021, 234, 111728. [Google Scholar] [CrossRef]
- Hartmann, H.; Derksen, J.J.; Van den Akker, H.E.A. Mixing times in a turbulent stirred tank by means of LES. AIChE J. 2006, 52, 3696–3706. [Google Scholar] [CrossRef]
- Gualtieri, C.; Angeloudis, A.; Bombardelli, F.; Jha, S.; Stoesser, T. On the values for the turbulent Schmidt number in environmental flows. Fluids 2017, 2, 17. [Google Scholar] [CrossRef] [Green Version]
- Daly, B.J.; Harlow, F.H. Transport equations in turbulence. Phys. Fluids 1970, 13, 2634–2649. [Google Scholar] [CrossRef]
- Jakirlić, S.; Hanjalić, K.; Tropea, C. Modeling rotating and swirling turbulent flows: A perpetual challenge. AIAA J. 2002, 40, 1984–1996. [Google Scholar] [CrossRef]
- Hanjalić, K.; Launder, B.E. A Reynolds stress model of turbulence and its application to thin shear flows. J. Fluid Mech. 1972, 52, 609–638. [Google Scholar] [CrossRef]
- Paglianti, A.; Montante, G. Simultaneous measurements of liquid velocity and tracer concentration in a continuous flow stirred tank. Chem. Eng. Sci. 2020, 216, 115495. [Google Scholar] [CrossRef]
- Hitimana, E.; Fox, R.O.; Hill, J.C.; Olsen, M.G. Experimental characterization of turbulent mixing performance using simultaneous stereoscopic particle image velocimetry and planar laser-induced fluorescence. Exp. Fluids 2019, 60, 28. [Google Scholar] [CrossRef]
- Lobasov, A.S.; Alekseenko, S.V.; Markovich, D.M.; Dulin, V.M. Mass and momentum transport in the near field of swirling turbulent jets. Effect of swirl rate. Int. J. Heat Fluid Flow 2020, 83, 108539. [Google Scholar] [CrossRef]
- Janus, B.; Dreizler, A.; Janicka, J. Experimental study on stabilization of lifted swirl flames in a model GT combustor. Flow Turbul. Combust. 2005, 75, 293–315. [Google Scholar] [CrossRef]
- Sharaborin, D.K.; Savitskii, A.G.; Bakharev, G.Y.; Lobasov, A.S.; Chikishev, L.M.; Dulin, V.M. PIV/PLIF investigation of unsteady turbulent flow and mixing behind a model gas turbine combustor. Exp. Fluids 2021, 62, 96. [Google Scholar] [CrossRef]
- Scarano, F. Iterative image deformation methods in PIV. Meas. Sci. Technol. 2001, 13, R1–R19. [Google Scholar] [CrossRef]
- Soloff, S.M.; Adrian, R.J.; Liu, Z.C. Distortion compensation for generalized stereoscopic particle image velocimetry. Meas. Sci. Technol. 1997, 8, 1441–1454. [Google Scholar] [CrossRef]
- Sirovich, L. Turbulence and the dynamics of coherent structures. I. Coherent structures. Q. Appl. Math. 1987, 45, 561–571. [Google Scholar] [CrossRef] [Green Version]
- Kerschen, G.; Golinval, J.C.; Vakakis, A.F.; Bergman, L.A. The method of proper orthogonal decomposition for dynamical characterization and order reduction of mechanical systems: An overview. Nonlinear Dyn. 2005, 41, 147–169. [Google Scholar] [CrossRef]
- Van Oudheusden, B.W.; Scarano, F.; Van Hinsberg, N.P.; Watt, D.W. Phase-resolved characterization of vortex shedding in the near wake of a square-section cylinder at incidence. Exp. Fluids 2005, 39, 86–98. [Google Scholar] [CrossRef]
- Alekseenko, S.V.; Dulin, V.M.; Kozorezov, Y.S.; Markovich, D.M. Effect of high-amplitude forcing on turbulent combustion intensity and vortex core precession in a strongly swirling lifted propane/air flame. Combust. Sci. Technol. 2012, 184, 1862–1890. [Google Scholar] [CrossRef]
- Hussain, A.K.M.F.; Reynolds, W.C. The mechanics of an organized wave in turbulent shear flow. J. Fluid Mech. 1970, 41, 241–258. [Google Scholar] [CrossRef]
- Duwig, C.; Fuchs, L. Large eddy simulation of vortex breakdown/flame interaction. Phys. Fluids 2007, 19, 075103. [Google Scholar] [CrossRef]
- Markovich, D.M.; Dulin, V.M.; Abdurakipov, S.S.; Kozinkin, L.A.; Tokarev, M.P.; Hanjalić, K. Helical modes in low-and high-swirl jets measured by tomographic PIV. J. Turbul. 2016, 17, 678–698. [Google Scholar] [CrossRef]
- Kitoh, O. Experimental study of turbulent swirling flow in a straight pipe. J. Fluid Mech. 1991, 225, 445–479. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Savitskii, A.; Lobasov, A.; Sharaborin, D.; Dulin, V. Testing Basic Gradient Turbulent Transport Models for Swirl Burners Using PIV and PLIF. Fluids 2021, 6, 383. https://doi.org/10.3390/fluids6110383
Savitskii A, Lobasov A, Sharaborin D, Dulin V. Testing Basic Gradient Turbulent Transport Models for Swirl Burners Using PIV and PLIF. Fluids. 2021; 6(11):383. https://doi.org/10.3390/fluids6110383
Chicago/Turabian StyleSavitskii, Alexey, Aleksei Lobasov, Dmitriy Sharaborin, and Vladimir Dulin. 2021. "Testing Basic Gradient Turbulent Transport Models for Swirl Burners Using PIV and PLIF" Fluids 6, no. 11: 383. https://doi.org/10.3390/fluids6110383
APA StyleSavitskii, A., Lobasov, A., Sharaborin, D., & Dulin, V. (2021). Testing Basic Gradient Turbulent Transport Models for Swirl Burners Using PIV and PLIF. Fluids, 6(11), 383. https://doi.org/10.3390/fluids6110383






