Abstract
Electroless plating in micro-channels is a rising technology in industry. In many electroless plating systems, hydrogen gas is generated during the process. A numerical simulation method is proposed and analyzed. At a micrometer scale, the motion of the gaseous phase must be addressed so that the plating works smoothly. Since the bubbles are generated randomly and everywhere, a volume-averaged, two-phase, two-velocity, one pressure-flow model is applied. This fluid system is coupled with a set of convection–diffusion equations for the chemicals subject to flux boundary conditions for electron balance. The moving boundary due to plating is considered. The Galerkin-characteristic finite element method is used for temporal and spatial discretizations; the well-posedness of the numerical scheme is proved. Numerical studies in two dimensions are performed to validate the model against earlier one-dimensional models and a dedicated experiment that has been set up to visualize the distribution of bubbles.
1. Introduction
Electroless plating is an industrial chemical process aimed at forming a thin film or layer on a base substrate by reducing complex metal cations in a liquid solution [1,2,3]. This technique has been widely applied in various industries. For instance, surface decoration, hard-wearing coating, manufacture of hard-disc drive, printed circuit boards, etc. [3,4]. It is well known that many electroless plating processes produce parasite hydrogen bubbles, such as electroless nickel and electroless copper systems [5,6,7]. There are several works on the simulation of electroless processes that study the convection or migration of chemical species under a single-phase flow (e.g., [8,9]). As far as we know, there is no computational work on bubble generation in an electroless process. In large-scale electroless plating processes, the gas generation will not be a serious issue, in general, however, for micro-scale plating, hydrogen bubbles may prevent electrolytes from going into the region needed to be plated. The existence of relatively large bubbles has been an important issue in the study of micro-fluids [10,11,12]. As experiments are difficult, there is a need for a reliable numerical simulation tool.
From a theoretical physics point of view, electroless processes are complex; the entire physical system participates to the plating. Therefore, for the simulation, we chose a system that includes a gas–liquid two-phase flow, chemical species transport, surface reaction, and moving boundary due to deposition.
1.1. The Modeling
Because bubbles and sprays are frequent in engineering design with fluids, numerous papers on the modeling and simulation of gas–liquid two-phase flows have been published such as [13,14,15,16,17]. Working models to compute gas–fluid flows can be sorted into two classes: (i) phase field or level set models where the gas–liquid interface is traced [18,19,20,21]; (ii) averaged models [22,23,24]. Several reasons support our choice for an averaged model: (i) There are many bubbles and their generation seems random, we only know that there is a higher chance of gas generation occurring in regions of higher concentration of dissolved gas; (ii) even if the bubble generation can be well predicted, vast amounts of bubbles are generated in short moments and the computational cost for capturing each bubble is prohibitive; (iii) interfacial terms (e.g., terms caused by a phase change) can be easily estimated with an averaged model (see Appendix A).
Experimentally, the bubbles are seen to get stuck at unexpected regions of the micro-channel. This indicates that the velocities of the two phases are quite different. To allow a disparity of motion between the liquid phase and gaseous phase, a two-velocity model is preferred. Two-velocity one pressure models have been used earlier either with the Navier–Stokes equations for both phases [25] or with the Navier–Stokes equations for the liquid phase and a potential flow equation for the gaseous phase [26]; yet, while mathematical analyses for one-velocity models of multiphase flows are numerous, few are those which deal with two-velocity models [27,28,29]. Moreover, we are not aware of a mathematical analysis of the two-velocity one-pressure model, namely the existence of solutions in a variational setting, stability and convergence of the numerical schemes. In the present study, both velocities (liquid and gaseous phase) are governed by the Navier–Stokes equations for incompressible fluids with single common pressure, interpreted as the Lagrange multiplier (see [30,31] for the incompressibility equation of the mixture). In addition, the mass conservation for the fluids is coupled with the chemical species transport. By using the saddle point theorem known as the LBB condition for the Navier–Stokes equations we are able to derive well-posedness and stability results to this more complex two-velocity one-pressure system.
A system of linear convection–diffusion equations, with source terms due to phase changes, is used to define the concentration profiles of the chemical species. We use the mixed potential theory (see for instance [32]) to model the reaction boundary condition describing the electroless process; it is a Robin boundary condition subject to electron balance constraints. We further consider the boundary motion induced by the chemical species deposition on the reaction surface. The net result is a set of coupled equations for a system that includes gas–liquid fluid motion, chemical species transport, and moving boundary to simulate the plating process. Note that, in absence of bubbles, the proposed model reduces to the usual single-phase model (i.e. neglecting the existence of gas) which is compatible with previous studies such as [33]. Note also that the potential flow assumption for the gas in [26] is, to some extent, a special case of the current model.
1.2. Discretization, Stability, and Convergence
For numerical simulations, the Galerkin-characteristic method [34] is applied for temporal discretization. The finite element method, of degree two for the velocities and one for pressure and concentrations, is used for spatial discretization. The well-posedness of the numerical scheme for the coupled system is proved, i.e. existence of solution, stability, and uniqueness of solution for the linear systems at each time step.
The computer code is written for two-dimensional problems using FreeFEM++ [35], a high level partial differential equations (PDE) solver like COMSOL [36]. Using invariance in one spatial direction, we can reproduce the one-dimensional numerical simulation of [8]. Then we compare the numerical results with a real-world experiment done by one of the authors for this purpose.
1.3. Experiment and Comparison
An electrolyte with copper ions and formaldehyde flows in micro-channel between two parallel glass sheets (Figure 1). One piece of the sheet is partially glued on a copper plate whose longer side coincides with an edge of the inlet. Electroless copper plating was conducted in a water tank controlled at 50 °C with in situ recording via stereomicroscope (charged coupled device 311 digital camera CCD).
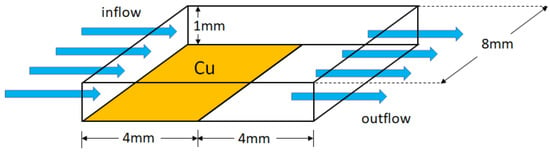
Figure 1.
The geometry setting for both experiment and numerical simulation. Here, the yellow region indicates the copper plate glued on the sheet glass.
Results show that the bubbles are not only appearing on the copper plate, but also near the top glass sheet. In the video, one can see that there were several bubbles going to the top from the center or the bottom side of the channel. The bubble size distribution was not measured and it ought to be done in the future and combined with numerical simulations as in [37]. The measurement of the bubble densities in the experiment is possible by means of acoustic, optical, and laser diffraction approaches [38]. However, these techniques are hard (or expensive) to be adapted on a microfluidic scale.
The computer simulations qualitatively arrive at the same conclusion. The experiment indicates that the clustering of bubbles happens on both the top side and the bottom side of the channel. Second, the numerical simulation predicts that most bubbles are generated at an early stage and near the inlet. The experiment shows that the bubble generation is more exuberant near the inlet. This observation coincides with that of Figure 2 and Figure 3a. The region near the inlet at is of the highest concentration of dissolving hydrogen gas. In addition, large bubbles were observed at the back end of the copper plates, which is also the case numerically as seen in Figure 3b.
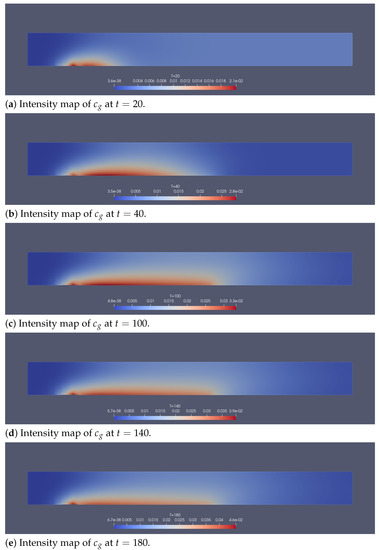
Figure 2.
For Section 5.2: Intensity maps of the concentration of dissolved gas. Notice that the gas seems to prefer to go up rather than to the right.
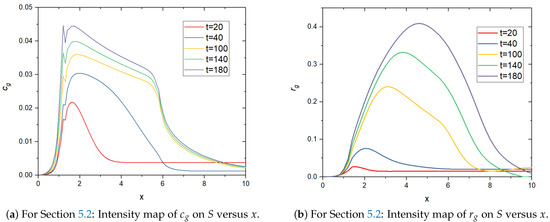
Figure 3.
Plots of and versus x on the reaction surface S. The gas bubble density in the plating reaction zone can be observed.
The comparison is qualitative but sufficient to assert that the simulation software is a more powerful tool to prototype future industrial designs. Potentially, it seems more reliable than experiments and it gives detailed information on the free boundary and on the speeds and concentrations of the chemical, which is highly important for the design of commercial systems. Thus, we are confident in the future of the numerical method. The mathematical properties of robustness, stability, and convergence, verified here numerically, are a certification of the computer software for future use.
2. Modeling Equations for Liquid-Gas Flow
Let be the time-dependent physical domain which is a thin channel between a top and a bottom plate. The boundary of consists of the inlet , the outlet , the solid wall , and the reacting surface (see Figure 4).
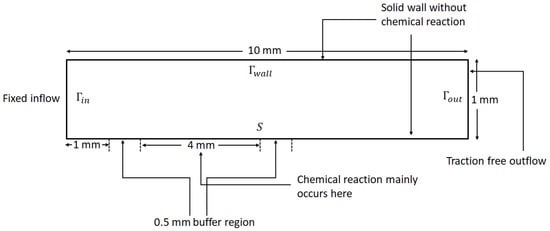
Figure 4.
The computational domain for the test problem in Section 5.2 is initially a rectangle of size 10 mm × 1 mm. We assume a fixed inflow velocity and given chemical concentrations from the left on , a solid wall on the top side with a no-slip condition for the velocity, and a traction-free outflow on . On the bottom side, is a free boundary and its motion is given by (23). However as the reaction site is active mostly for (1.5 mm, 5.5 mm), we may block the chemical reactions for mm to avoid a corner singularity at the entrance and also for mm because experiments show that almost no plating occurs there. In the regions (1.0 mm, 1.5 mm) ∪ (5.5 mm, 6.0 mm) the numerical simulations may not be accurate due to the singularity caused by the discontinuity in the boundary conditions (see Figure 3 for details).
2.1. Volume Averaging
We review the derivation proposed by Ni and Beckermann [39].
Let be an small open set to be observed in and the set occupied by phase k and bounded by the interface . Assume that and . Let be a outer normal to and the normal velocity of .
Let be a function of a slow variable x and a fast variable y due to the phase change. The volume average of in phase k is where is the indicator function of the domain of phase k and , assumed constant. The intrinsic volume average is defined as
The volume fraction has the properties and Some useful averaging formulas are listed below [40,41]:
In principle, one should also introduce fast and slow time variables but it is assumed that spatially averaged functions are no longer varying fast in time.
2.2. Mass Conservation
We consider a gas and a liquid phase. Let be the density of gas, the density of liquid. We have the mass conservation for both phases (l for liquid and g for gas):
where is the mass gained owing to the precipitation of dissolved gas, is the mass loss when liquid evaporates into gas; , are the volume averaged fluid flow of gas and liquid, respectively. Since the mass gained in gas balances the mass lost in liquid, we have
For chemical species, we assume that the ions are transported only by the liquid electrolyte. Let be the volume averaged concentration of metallic ions destined to be deposited on the reacting surface, the volume averaged concentration of dissolved gas, and , the volume averaged concentration of other chemical species participating to the chemical reactions. The equations for the concentrations are
where , are interfacial terms due to the phase change. By (3), we can rewrite the above equation as
where are the diffusion coefficients. In particular, since the gas is consumed by the phase change, by assuming that the gas precipitation is linearly dependent on the dissolving gas concentration [42,43], we have
In the above, is the interface velocity of and K is a constant independent of , ; is the saturated concentration of the gas, is the reciprocal of the molar mass of the gas,
Moreover, , can be estimated by (see Appendix A)
For incompressible fluids, a volume conservation is derived from (3):
By (4), the above reduces to
Recall that the physical domain is occupied either by gas or liquid, therefore at all times.
2.3. Equations of Motion
Let , be the viscosities of gas and liquid. The volume averaged Navier–Stokes equations are used for momentum balance (see [39]):
where are pressure, drag and external force terms. Following [24,39]
where is a drag coefficient, and the external force are in fact the interfacial terms and is twice the symmetric gradient of ; and can be estimated by (see Appendix A)
2.4. Boundary Conditions
We consider a fluid flow from an input boundary to an output boundary with a solid wall at the bottom, :
The boundary conditions for , are
where is a fixed positive small constant.
The boundary conditions for the concentrations of chemicals are, with given:
Referring to Figure 5, if is the reaction surface, we denote the region occupied by the liquid and the region occupied by gas. Choosing an arbitrary subset , the surface reaction takes place only on . Assuming that the concentration profile is uniform near the small region W, we have: . Therefore by dividing both sides by :
for a positive number indicating the chemical equivalence for gaseous molecular generation; F is the Faraday constant, and z is the atomic number of the material. is the current density satisfying the Butler–Volmer equation
where R is the gas constant, are the chemical potentials of species j, is the temperature, ,, are constants, and is given by writing electrical neutrality:
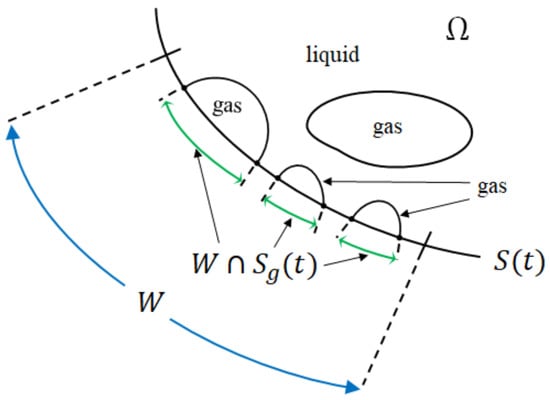
Figure 5.
The reaction surface.
On , the fluid velocity induced by the deposition is
where is a constant.
Finally, moves according to
2.5. Single-Phase Flow
If there is no gaseous phase in the system and no dissolved gas in liquid, i.e., , then and and mass conservation reduces to . The convection–diffusion of chemicals become,
and the fluid system reduce to the Navier–Stokes equations:
3. Numerical Method
3.1. Notations
If , we denote by and by . We denote by the norm on , the norm, and , , . Remembering that is a vector, let us denote .
We assume the densities constant and denote the mass fractions and the kinematic viscosities. The system is
In addition as , we may use the redundant Equation (11):
3.2. Semi-Discrete Schemes
Let T be the final time and a time step. We denote by , , the numerical solution of any physical quantity at time . Convection terms are approximated in time by the method of characteristics. Let . Then
Consider the following scheme
For electroless plating the domain is , so it is updated by
3.3. Positivity
Positivity of holds only if is small enough. When positivity is required absolutely, an modification of (30) forces the positivity of :
Indeed assume that is strictly positive, or more precisely that for all x; then we have
3.4. Stability
- Let us show first that (30) generates a bounded sequence . For clarity we assume homogeneous data at the boundaries. With simplified notationsA multiplication by and an integration on leads toBy the Cauchy Schwarz inequality and the positivity of ,The inverse of the determinant of the Jacobian of the transformation is ; therefore, for any smooth function f, in particular with ,where C is a generic constant function of , the norm of the Hessian of u.
- Stability of the scheme for C is shown by the same argument.
- Stability of the scheme for and is a consequence of a similar argument combined with the Ladhyzenskaya–Babuska–Brezzi saddle point theory (LBB) [46].We denote by the inner product. For tensor-valued functions such that , , . With self explanatory notations, the equations for the velocities (32) and (33) are written in variational form as:Find and p satisfying the Dirichlet conditions and such that, and ,where, for , ,and where . Here is the subspace of of functions which are zero on the Dirichlet boundaries.Note that the above is a semi-linearization of (32) and (33). However in Algorithm 1 below, the nonlinear problem is solved by an iterative fixed point which uses (41) and (42).The LBB theorem says that the solution of (41) exists and is unique because, for every there is a (non-unique) withprovided that Let us show stability in the special case because one can always subtract from so as to work with and .Thus, setting , and leads toBy the same argument used above, it implies that is bounded. Indeed, assuming ,for some generic constant C depending on and . Finally, we obtainwhereThis estimate would be optimal if the constant C did not depend on the Hessian of the velocities. This is a drawback of the characteristic method and of the unsophisticated treatment of the nonlinearity. At the expense of long mathematical arguments it could be fixed as in [34], the scheme would be stable.
- Note that we have swept under the rug the fact that at level m the domain of definition of the functions is and at level it is . The problem can be solved but at the cost of difficult notations and iterations between and ; for details see [47].
4. Finite Element Implementation
For simplicity, the physical domain is assumed to be a two-dimensional polygonal domain.
4.1. Mesh
Let be an affine, shape regular (in the sense of Ciarlet [48]) family of mesh conforming to . The conforming Lagrange finite element space of degree p on is
where is the space of polynomials of degree p of .
Let be the nodal Lagrange basis of . If the vertices are denoted by , then . Let be the support of and let . If E is a union of triangles, define . Finally, the local minimum mesh size of is and the global minimum mesh size is .
We assume that the connectivity of the mesh never changes with time.
4.2. Spatial Discretization
We use the Hood–Taylor element: the velocities are in and the pressure is in . For the volume fractions and the concentrations we use also .
Recall that the nodes of are the vertices and the middle of the edges. Denote by the nodal Lagrange basis of . As before , and .
On the boundaries where Dirichlet conditions are set, the functions are known. We denote and , the corresponding spaces where basis functions attached to a Dirichlet node are removed.
4.2.1. Mass Fractions
Given and , find satisfying the Dirichlet boundary conditions and such that
where for , . Then we let .
Remark 2.
A modification similar to (39) will insure the positivity of .
4.2.2. Concentration Profiles
4.2.3. Two-Phase Flow
Given , , , and , find , and such that
for all , and .
4.3. Fixed Point Iterative Solution of (50) and (51)
4.4. Consistence and Stability
Variational formulations discretized by finite element methods inherit the stability and consistency of the continuous equations. The LBB theorem applies also to the Hood–Taylor element for velocity pressure problems. Therefore, as in the continuous case, the norms of are less than times the norms of . If we could show that is bounded, then it would imply that the scheme converges when .
4.5. Solvability of the Linear System in Matrix Form
Let , , for some constant , .
To study the solvability of (50)–(51), we consider a simpler case with on , and take the linearized approximation on the drag force terms. The problem reads: Find and satisfying
where, for , ,
On the basis of and , we can write
More precisely is for and .
Problem (53) can be formally expressed as a system of linear equations:
where is a matrix, and are vectors. Note that has the form
with, for
Proposition 1.
The linear system (56) is uniquely solvable.
Proof.
According to the LBB theorem [46] the saddle point problem (52) is well posed when for , there exists such that
Therefore has full rank and is non singular. □
4.6. Iterative Process
At each time step, (47), is solved first, then (48) and (49) is solved iteratively by using a semi-linearization of the nonlinear boundary terms. Then (50) and (51) is solved iteratively by a semi-linearization of the nonlinear terms; each block involves the solution of a well posed symmetric linear system. Finally is updated by (23). Algorithm 2 summarizes the procedure.
Note that the computational domain is .
5. Numerical Simulation
5.1. One-Dimensional Electroless Nickel Plating Problem
Here we reproduce, with a two-dimensional computation, the one-dimensional study by Kim and Sohn [8]. In their work, the electroless nickel plating process on a rotating disk with constant angular velocity is considered. In this situation, the velocity field near the surface of the rotating disk can be approximated by a uniformly distributed flow towards the plating surface. In addition, the thickness of the diffusion layer is assumed uniform on the surface. Consequently, for the modeling, the domain becomes one-dimensional. Given that the gas generation is not considered and only the steady state is computed in [8], a single-phase recovery , is applied. Finally, four partial reactions in the electroless nickel plating process are considered:
| Algorithm 2: Algorithm for solving the full system of equations. |
 |
All chemical species are labeled as follows: is the concentration of the anodic hypophosphite (), the concentration of the cathodic hypophosphite, the concentration of the nickel ion (), and the concentration of the hydrogen ion (). Now the two-dimensional analog can be formulated: Let , where is the thickness of the diffusion layer for nickel and is a small positive number. The thickness of the diffusion layer for species j is given in [32]:
The governing equation for the concentration profile is given by
subject to the boundary conditions
with the electron balance constraint
The velocity field can be expressed as in [32]:
where is an experimental constant, is the ratio between the hypophosphite anodic part and the cathodic part on the reacting surface. The equilibrium potential for species j can be approximated by the Nernst equation, with :
By simulating system (64), (65), and (66), with the physical constants given in Table 1 and Table 2, until a steady state is reached, the numerical tests show that the present model agrees well with the previous 1D studies of Kim and Sohn [8]: see Figure 6 and Figure 7.

Table 1.
Physical parameters used in [8], valid for and the concentration of M.

Table 2.
Conditions assumed in [8] for performing our simulations.
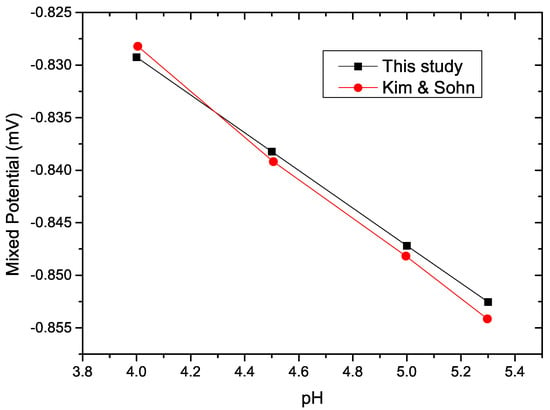
Figure 6.
In red, the mixed potential computed by the one dimensional system (65) versus pH . In black, the same but computed with the full two dimensional system.
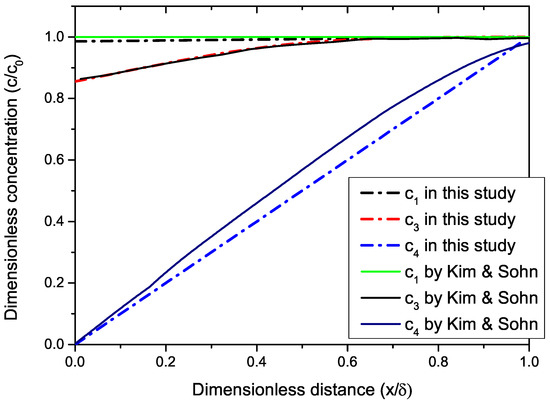
Figure 7.
Concentration profiles of three chemical species versus x computed by the one-dimensional system (65) and compared with the results of the full two-dimensional system.
5.2. Two Species in a Gas–Liquid Two-Phase Flow
Let the initial domain be a rectange of size (in meters). We consider complexed (by tartrate, denoted by L) copper ions, formaldehyde, and hydrogen dissolved in water, which are denoted by the subscriptions , respectively, for the chemical species transport equations.
The chemical reaction can be expressed as the following two partial reactions:
Given the above equations, we also use the subscriptions s and k to represent the quantities corresponding to (70) and (71), respectively.
The values of the physical constants are listed in Table 3.

Table 3.
Parameters used in Section 5.2.
For convenience, the following scalings are applied:
The initial conditions are set to: constant phase ratio and Poiseuille flow:
with . Additionally, let satisfies
plus the first equation in (76) subject to (21). The inflow values are
The boundary conditions on are
where and
Boundary conditions on and are as in Section 2.4. See also Figure 4.
Remark 3.
We note that is much larger than the experimental values; the numerical simulations produce (and ) of magnitude in the order . On the other hand, the deposition rate in a typical experiment is of order 1 μm per hours [52], which is not larger than . Yet the numerical test is conducted to validate the numerical method when the evolution of the domain is larger than real-life values.
5.2.1. Convergence
First, we conduct the convergence test for different time step with a fixed mesh. To obtain a “reference solution”, the system (47)–(51) is solved with a uniform mesh and a small time step and . The convergence with respect to is studied without changing the mesh; results are given in Table 4 and the rate of convergence for each variable is presented in Figure 8. Numerical tests for solving two-phase flow problem and volume fraction problem present a linear decay of error with respect to the time step. However, the convergence for solving the concentration profiles does not reach the expectation due to extremely low diffusion coefficients and large current densities.

Table 4.
error with respect to the reference solution provided with time step , uniform mesh, and for numerical simulation in Section 5.2 at .
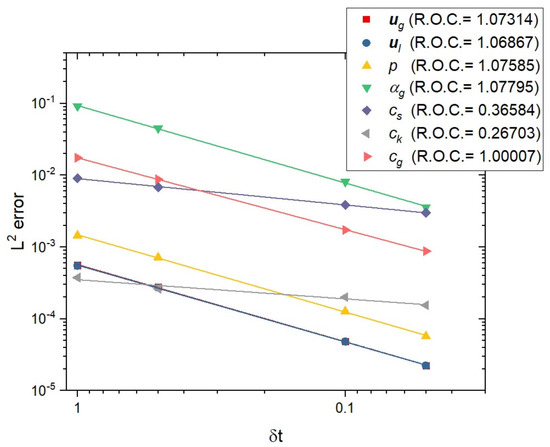
Figure 8.
Convergence with respect to for the case described in Section 5.2; log–log plot of the error for each unknown (note that the curves for and overlap). R.O.C. means “Rate Of Convergence”. The reference solution is a computation with a very small time step.
Second, we conduct the convergence tests for different time steps and mesh pairs; the time step is always proportional to the mesh size. The reference solution is obtained with uniform mesh and at . Figure 9 and Table 5 present a linear decay of error with respect to the time step for each variable.
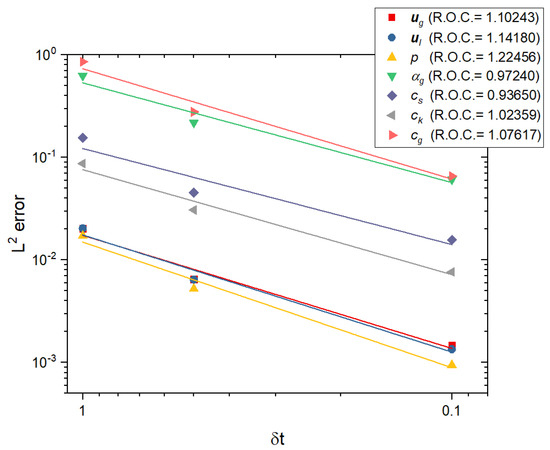
Figure 9.
Convergence with respect to and mesh size for the case described in Section 5.2 (see Table 5 for the time step and mesh size pair): log–log plot of the error for each unknown (note that the curves for and overlap).

Table 5.
error with respect to the reference solution provided with time step , uniform mesh, and for numerical simulation in Section 5.2 at .
Third, a convergence test similar to the second test above is performed with different time steps and mesh pairs, but the errors are computed at . The reference solution is obtained with uniform mesh and . Figure 10 and Table 6 show a nearly linear decay of error with respect to the time step for each variable. In this test, and vary significantly as the grid is refined. The intensity maps of are given in Figure 11. The intensity maps of all variables present no significant differences with the reference solutions when .
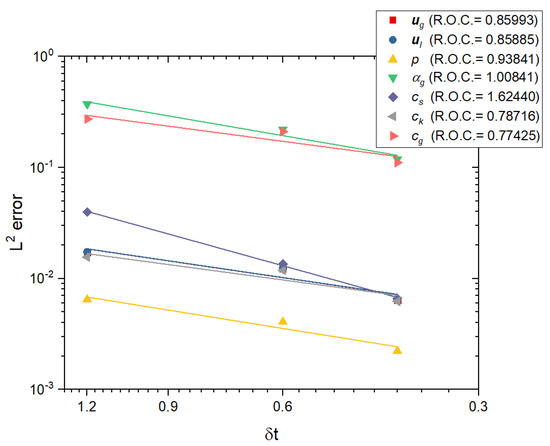
Figure 10.
Convergence with respect to and mesh size for the case described in Section 5.2 (see Table 5 for the time step and mesh size pair): log–log plot of the error for each unknown (note that the curves for and overlap and the curve of is closed to them).

Table 6.
error with respect to the reference solution provided with time step , uniform mesh, and for numerical simulation in Section 5.2 at .

Figure 11.
For Section 5.2: The intensity maps of for different time step and mesh size pairs.
5.2.2. Robustness for Large Time Steps
With a large time step and uniform mesh, the product of the maximal liquid fluid speed with the time step is around times of the mesh size, which is optimal for the Galerkin-characteristic method. Solutions are displayed in Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16.
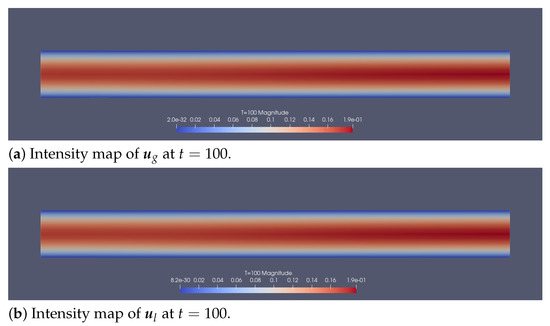
Figure 12.
For Section 5.2: The velocity magnitudes of and .

Figure 13.
For Section 5.2: Intensity maps of the volume fraction of the gas phase computed with and a uniform mesh.
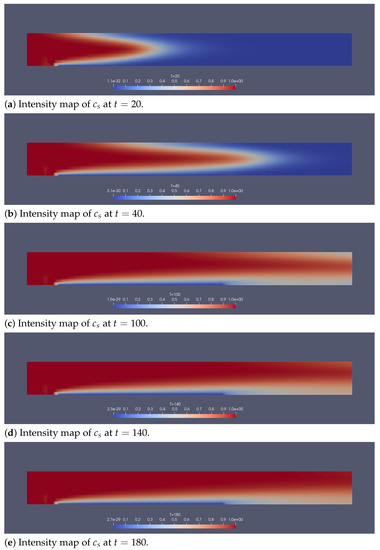
Figure 14.
For Section 5.2: Intensity maps of the concentration electrolyte ions computed with and a uniform mesh. The blue zone in the plating region on the lower plate shows that the electrolyte is absorbed by the plating process.
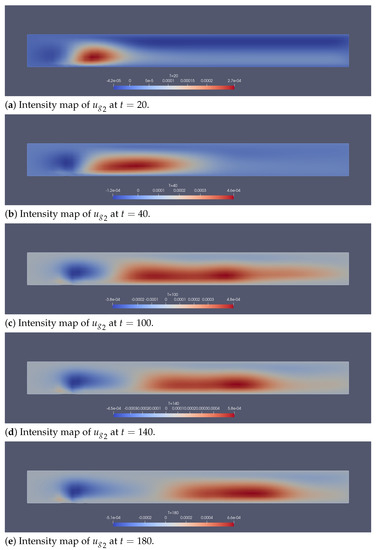
Figure 15.
For Section 5.2: The vector fields and are very closed to Poiseuille flow. In this case, phase change and moving boundary contribute to the second component of (and ) together. The numerical test is conducted with and uniform mesh. The intensity maps indicate the bubble rising in the red region. Indeed, there exists high gas volume fraction region near the top side (see Figure 13).
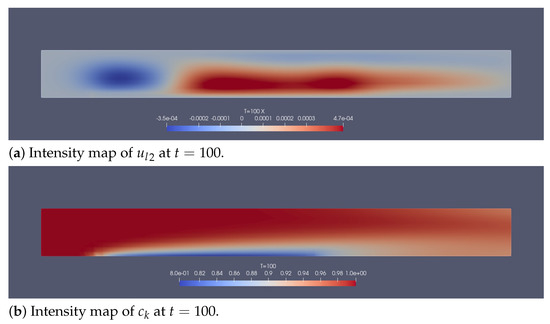
Figure 16.
For Section 5.2: Intensity maps of and at .
5.2.3. CPU Time
With and uniform mesh, it took 5832 s to reach the final time with an Intel Core i7-8750H @ 2.20 GHz. During the computation, it took of the total CPU to solve the volume fraction problem, to solve the chemical species transport problem, and to solve the two-velocities/pressure flow problem.
The computer program is written using the FreeFEM++ toolkit [35].
5.2.4. Results
In Figure 12a,b the velocity vector fields and are seen to be almost parabolic in y (Poiseuille flow), but the phase change and moving boundary induce a non-zero asymmetric vertical component (see Figure 15); both play important roles for the bubble distribution. Bubble density can be inferred by analyzing and (see Figure 3). The color maps of Figure 13 display a high gas volume fraction area near the top and bottom plates. Figure 14 shows how the steady state is established and how the electrolyte disappears in the plating region due to the plating. Figure 2 displays a high volume fraction of the gaseous phase near the reacting surface. The deposition-induced movement of S is presented in Figure 17. Figure 3b shows that the region of highest bubble density is moving away from the inlet as the electroless plating proceeds.
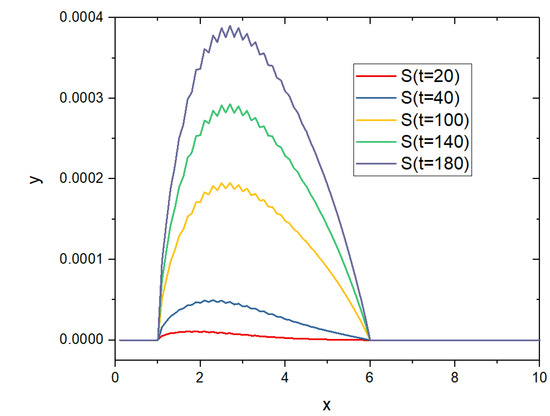
Figure 17.
The thickness of the deposition is given by the motion of , plotted here at 5 instants of time, with respect to the x-axis (in mm). Notice that the motion is very small; the oscillations are blown-out of proportion by the scaling used in the graphic.
6. Comparison with Experimental Results
To validate the numerical method on a real-life problem, an experiment for reproducing the numerical study in Section 5.2 is conducted. Here, we shall show that the experimental result can be qualitatively fitted by the numerical simulation.
The experimental setting is described as the following: A micro-channel is enclosed by two sheet glasses of size 8 mm × 8 mm and another two of size 8 mm × 1 mm, which form a rectangular channel. The electrolyte goes in the channel from the left and exit on the right. One piece of the square sheet glasses is partially glued on a copper plate of size 8 mm × 4 mm, where the longer side of the copper plate coincides with an edge of the inlet (see Figure 1 for geometry setting). The inflow is set to be of average velocity 0.115 mm/s. At inlet, the copper ion concentration is mol/m3 and the formaldehyde concentration is mol/m3. Here, the inlet concentrations and are the reference concentrations for copper ion and formaldehyde, respectively. We further define the reference concentration of the hydrogen gas to be mol/m3. Other physical parameters are given in Table 3. Some parameters, for example, reference current densities , and , may not be exactly same as what are given in Table 3. Nevertheless, they are acceptably closed to reality, or at least in the same order.
6.1. Experimental
To fabricate the test vehicle, a 4 inch glass wafer was first sputtered with 30 nm chromium and 200 nm copper which served as an adhesion layer and seed layer, respectively. The wafer was then diced into each 8 mm × 8 mm glass dies. To ensure a significant comparison between the regions being plated or not, each test die was half immersed in SPS () solution and hydrochloric acid to remove the copper and chromium layer. The glass die turned out half transparent and half coated with copper where the electroless copper plating took place. Thereafter, a fully transparent glass, which was identical to the size of the test die, was face-to-face aligned and bonded via using a flip-chip die-bonder in order to obtain a clear observation view. Two tungsten wires which were 8 mm in length and 2 mm in diameter were glued by UV gel and placed on the periphery of the test die for the purpose of restricting the flow direction and defining the height between the dies (see Figure 18).
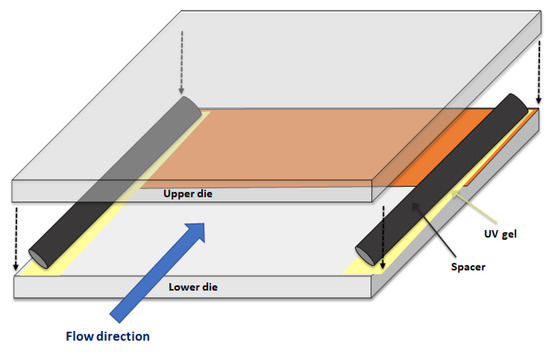
Figure 18.
Test vehicle formation.
The test vehicle was then subjected to a micro-fluidic system composed of a PDMS mode containing a micro-fluidic channel and a bottom glass. Clips were used to seal the micro-fluidic system and prevent the leakage of electrolyte. A peristatic pump was used to control the flow and connect the micro-fluidic system with a silicone tube. Prior to the electroless plating, the test vehicle was immersed in sulfuric acid to remove copper oxide. Finally, the electroless copper plating was conducted in a water tank controlled at 50 °C with in situ recording via stereomicroscope (charged coupled device digital camera CCD). The electrolyte PHE-1 Uyemura possessing the given reference concentrations of (complexed) copper ion and of formaldehyde was used for the experiment. The complete equipment setup is described in Figure 19.
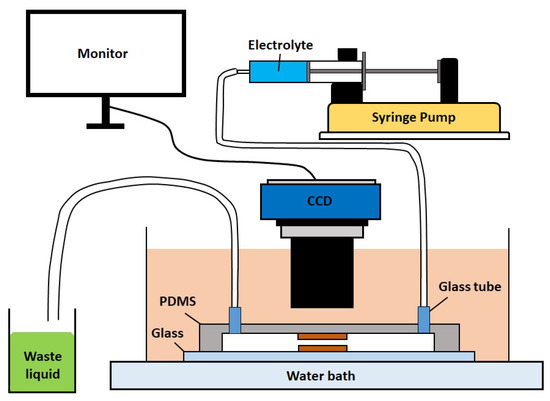
Figure 19.
Electroless copper plating via using microfluidic system.
6.2. Results
Experimental results (see Figure 20) show that the bubbles are not only appearing on the copper plate, but also appearing on the top. In the video, one can see that there were several bubbles going to the top from the center or the bottom side of the channel. The region above the glass becomes darker with time. The simulation results (see Figure 13) qualitatively arrive at the same conclusion. The experiment indicates that the clustering of bubbles happens on both the top side and the bottom side of the channel. Second, the numerical simulation predicts that most bubbles are generated at an early stage and near the inlet. The experiment shows that the bubble generation is more exuberant near the inlet in comparison with other regions at . This observation coincides with that of Figure 2 and Figure 3a. The region near the inlet at is of the highest concentration of dissolving hydrogen gas. In addition, large bubbles were observed at the back end of the copper plates (i.e., region near (x,y) = (6,0) corresponding to Figure 4), which is also the case in Figure 3b.

Figure 20.
The pictures are taken from the top side and the region near the center between two 8 mm × 1 mm sheet glasses. The brown region is covered by the copper plate, where the surface reaction occurs.
6.3. Discussion
For an electroless plating process accompanying gas generation, the bubble distribution with respect to time, in the micro-channel, is the most important index for evaluating the quality of deposition. To measure it quantitatively, a high-quality optical system installed in the micro-channel is indispensable. For example, several types of fiber optical probes have been used to measure the particle (or bubble) size and distribution in a channel flow (or micro-channel flow) [53,54,55,56]. However, such an optical system is difficult to install in our case because there is no appropriate place to set up the light source and the detector in the micro-channel. The signal interference caused by the copper plate or glued gel on two sides is almost inevitable.
7. Conclusions
The numerical simulation of electroless plating is difficult for two reasons: multi-phase modeling and nonlinearities. We have proposed a phase averaged liquid–gas two-fluid-velocity/one-pressure system combined with phase densities and chemical concentration equations. The nonlinearities being similar to those of the Navier–Stokes equations, we have used a semi-Eulerian time discretization leading to a generalized Stokes operator for the two-velocity/one-pressure system; the inf-sup saddle point theorem has lead to a proof of stability and well-posedness of the discretized system by the Hood–Taylor finite element method. The two-phase flow model is compatible with single phase models when the volume fraction of gas and the concentration of the gas in the liquid phase are set to zero. The model is also compatible with the one-dimensional model proposed in [8]. The numerical results confirm the robustness of the method. To validate the model, a real-life experiment has been performed. The numerical results agree qualitatively with the experiment for the repartition of bubbles near the plating boundary. We believe that in the future the computer code will be used to design industrial and experimental systems. However, as to the measurement of the deposition rate, It takes at least one hour to obtain an observable thickness of plating. In this case, bubbles have accumulated everywhere in the micro-channel and there is ground for an extension of the present code with a level set or phase field model which tracks the main liquid to gas interface. To establish a mathematical model suitable for a larger time simulation is left as future work.
Author Contributions
Conceptualization, P.-Y.W., O.P.; methodology, P.-Y.W., O.P.; software, P.-Y.W.; validation, P.-Y.W., O.P., P.-S.S., C.R.K.; formal analysis, P.-Y.W., O.P.; investigation, P.-Y.W., P.-S.S.; resources, O.P., C.R.K.; data curation, P.-Y.W., P.-S.S.; Writing—original draft preparation, P.-Y.W.; Writing—review and editing, O.P.; visualization, P.-Y.W., P.-S.S.; funding acquisition, C.R.K. All authors have read and agreed to the published version of the manuscript.
Funding
The experimental section of this research was financially supported by the Ministry of Science and Technology, Taiwan, under grant No. MOST 110-2622-E-002-016-CC1, the Ministry of Education, Taiwan. The authors are also grateful for the technical help provided by Taiwan Uyemura Co., Ltd.
Data Availability Statement
Not applicable.
Acknowledgments
We appreciate Han-Tang Hung provided several suggestions in terms of the experimental design. We are also grateful to Tony Wen-Hann Sheu for having initiated this work.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Estimation of the Interfacial Terms
Let be a local volume to be observed which is occupied by gas and liquid. In a liquid–gas two-phase system, we have and further on the interface. If the size of each single bubble in the electrolyte is small enough, then we can assume that the bubbles are spherical. Assuming that there is a typical radius for all bubbles such that is the average of among all bubbles in the system, the growth rate of bubbles governed by the local mass loss prescribed by Equation (3) can be computed by the relation
where is the amount of bubbles in a local volume . Therefore, we have the following formulae on and , respectively
The quantity is useful when the fluid velocity is large enough so that each bubble will not stay at the observed physical domain, because every bubble has not been far from the state that is just after nucleation.
Given a small cube of size and a typical radius , the ratio of its surface area and volume is , where can be estimated by
Therefore, if d is small enough so that the physical quantities in defined in Section 2.3 can be assumed uniform, then we have the approximation
Similarly,
References
- Brenner, A.; Riddell, G.E. Nickel plating on steel by chemical reduction. J. Res. Nat. Bureau. Stand. 1946, 37, 31–34. [Google Scholar] [CrossRef]
- Paunovic, N. Electrochemical aspects of electroless deposition of metal. Plating 1968, 51, 11–61. [Google Scholar]
- Mallory, G.O.; Hajdu, J.B. Electroless Plating: Fundamentals and Applications; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Shacham-Diamand, Y.; Osaka, T.; Okinaka, Y.; Sugiyama, A.; Dubin, V. 30 years of electroless plating for semiconductor and polymer micro-systems. Microelectron. Eng. 2015, 132, 35–45. [Google Scholar] [CrossRef] [Green Version]
- Gottesfeld, S.; Beery, J.; Paffett, M.; Hollander, M.; Maggiore, C. On the anodic oxidation of formaldehyde during the electroless copper plating process. J. Electrochem. Soc. 1986, 133, 1344. [Google Scholar] [CrossRef]
- Krishnan, K.H.; John, S.; Srinivasan, K.N.; Praveen, J.; Ganesan, M.; Kavimani, P.M. An overall aspect of electroless Ni-P depositions—A review article. Metall. Mater. Trans. A 2006, 37, 1917–1926. [Google Scholar] [CrossRef]
- Shukla, S.; Seal, S.; Akesson, J.; Oder, R.; Carter, R.; Rahman, Z. Study of mechanism of electroless copper coating of fly-ash cenosphere particles. Appl. Surf. Sci. 2001, 181, 35–50. [Google Scholar] [CrossRef]
- Kim, Y.S.; Sohn, H.J. Mathematical modeling of electroless nickel deposition at steady state using rotating disk electrode. J. Electrochem. Soc. 1996, 143, 505–509. [Google Scholar] [CrossRef]
- Ramasubramanian, M.; Popov, B.N.; White, R.E.; Chen, K.A. Mathematical model for electroless copper deposition on planar substrates. J. Electrochem. Soc. 1999, 146, 111–116. [Google Scholar] [CrossRef]
- Lochovsky, C.; Yasotharan, S.; Günther, A. Bubbles no more: In-plane trapping and removal of bubbles in microfluidic devices. Lab Chip 2012, 12, 595–601. [Google Scholar] [CrossRef]
- Hibara, A.; Iwayama, S.; Matsuoka, S.; Ueno, M.; Kikutani, Y.; Tokeshi, M.; Kitamori, T. Surface modification method of microchannels for gas- liquid two-phase flow in microchips. Anal. Chem. 2005, 77, 943–947. [Google Scholar] [CrossRef]
- Yang, Z.; Matsumoto, S.; Maeda, R. A prototype of ultrasonic micro-degassing device for portable dialysis system. Sensor. Actuat. A Phys. 2002, 95, 274–280. [Google Scholar] [CrossRef]
- Triplett, K.A.; Ghiaasiaan, S.M.; Abdel-Khalik, S.I.; Sadowski, D.L. Gas–liquid two-phase flow in microchannels part I: Two-phase flow patterns. Int. J. Multiphas. Flow 1999, 25, 377–394. [Google Scholar] [CrossRef]
- Triplett, K.A.; Ghiaasiaan, S.M.; Abdel-Khalik, S.I.; LeMouel, A.; McCord, B.N. Gas–liquid two-phase flow in microchannels part II: Void fraction and pressure drop. Int. J. Multiphas. Flow 1999, 25, 395–410. [Google Scholar] [CrossRef]
- Akbar, M.K.; Plummer, D.A.; Ghiaasiaan, S.M. On gas-liquid two-phase flow regimes in microchannels. Int. Mech. Eng. Congress Expo. 2003, 7, 527–534. [Google Scholar] [CrossRef]
- Delnoij, E.; Lammers, F.A.; Kuipers, J.A.M.; van Swaaij, W.P.M. Dynamic simulation of dispersed gas-liquid two-phase flow using a discrete bubble model. Chem. Eng. Sci. 1997, 52, 1429–1458. [Google Scholar] [CrossRef] [Green Version]
- Fukano, T.; Kariyasaki, A. Characteristics of gas-liquid two-phase flow in a capillary tube. Nucl. Eng. Des. 1993, 141, 59–68. [Google Scholar] [CrossRef]
- Abels, H.; Garcke, H.; Grün, G. Thermodynamically consistent, frame indifferent diffuse interface models for incompressible two-phase flows with different densities. Math. Mod. Meth. Appl. Sci. 2012, 22, 1150013. [Google Scholar] [CrossRef]
- Shen, J.; Yang, X. Decoupled, energy stable schemes for phase-field models of two-phase incompressible flows. SIAM J. Numer. Anal. 2015, 53, 279–296. [Google Scholar] [CrossRef]
- Sussman, M.; Smereka, P.; Osher, S. A Level Set Approach for Computing Solutions to Incompressible Two-Phase Flow. Ph.D. Thesis, Department of Mathematics, University of California, Los Angeles, CA, USA, 1994. [Google Scholar]
- Olsson, E.; Kreiss, G. A conservative level set method for two phase flow. J. Comput. Phys. 2005, 210, 225–246. [Google Scholar] [CrossRef]
- Ishii, M.; Hibiki, T. Thermo-Fluid Dynamics of Two-Phase Flow; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Zuber, N.; Findlay, J. Average volumetric concentration in two-phase flow systems. J. Heat. Transf. 1965, 87, 453–462. [Google Scholar] [CrossRef]
- Drew, D.A. Mathematical modeling of two-phase flow. Annu. Rev. Fluid. Mech. 1983, 15, 261–291. [Google Scholar] [CrossRef]
- Huang, Q.; Yang, C.; Yu, G.; Mao, Z.S. CFD simulation of hydrodynamics and mass transfer in an internal airlift loop reactor using a steady two-fluid model. Chem. Eng. Sci. 2010, 65, 5527–5536. [Google Scholar] [CrossRef]
- Mahmood, K.A.; Wilkinson, S.J.; Zimmerman, W.B. Airlift bioreactor for biological applications with microbubble mediated transport processes. Chem. Eng. Sci. 2015, 137, 243–253. [Google Scholar]
- Keyfitz, B.L.; Sanders, R.; Sever, M. Lack of hyperbolicity in the two-fluid model for two-phase incompressible flow. Discrete Cont. Dyn. B 2003, 3, 541. [Google Scholar] [CrossRef]
- Buist, J.; Sanderse, B.; Dubinkina, S.; Henkes, R.; Oosterlee, C. Energy-conserving formulation of the two-fluid model for incompressible two-phase flow in channels and pipes. arXiv 2021, arXiv:2104.07728. [Google Scholar]
- Gallouët, T.; Hérard, J.M.; Seguin, N. Numerical modeling of two-phase flows using the two-fluid two-pressure approach. Math. Mod. Meth. Appl. Sci. 2004, 14, 663–700. [Google Scholar] [CrossRef] [Green Version]
- Sanderse, B.; Veldman, A. Constraint-consistent Runge–Kutta methods for one-dimensional incompressible multiphase flow. J. Comput. Phys. 2019, 384, 170–199. [Google Scholar] [CrossRef] [Green Version]
- Sanderse, B.; Buist, J.; Henkes, R. A novel pressure-free two-fluid model for one-dimensional incompressible multiphase flow. J. Comput. Phys. 2021, 426, 109919. [Google Scholar] [CrossRef]
- Levich, V.G.; Technica, S. Physicochemical Hydrodynamics; Prentice-Hall Englewood Cliffs: Hoboken, NY, USA, 1962. [Google Scholar]
- Girault, V.; Pironneau, O.; Wu, P.Y. Analysis of an Electroless Plating Problem. Unpublished Work. 2019. Available online: https://hal.archives-ouvertes.fr/hal-02361746/ (accessed on 19 June 2021).
- Pironneau, O. On the transport-diffusion algorithm and its applications to the Navier-Stokes equations. Numer. Math. 1982, 38, 309–332. [Google Scholar] [CrossRef]
- Hecht, F. New developments in FreeFem++ (www.freefem.org). J. Numer. Math. 2012, 20, 251–265. [Google Scholar]
- COMSOL Multiphysics. v. 5.6. COMSOL AB, Stockholm, Sweden. Available online: www.comsol.com (accessed on 14 October 2021).
- Bandulasena, H.C.; Zimmerman, W.B.; Rees, J.M. Rheometry of non-Newtonian polymer solution using microchannel pressure driven flow. Appl. Rheol. 2010, 20. [Google Scholar] [CrossRef]
- Desai, P.D.; Ng, W.C.; Hines, M.J.; Riaz, Y.; Tesar, V.; Zimmerman, W.B. Comparison of bubble size distributions inferred from acoustic, optical visualisation, and laser diffraction. Colloids Interfaces 2019, 3, 65. [Google Scholar] [CrossRef] [Green Version]
- Ni, J.; Beckermann, C. A volume-averaged two-phase model for transport phenomena during solidification. Metall. Trans. B 1991, 22, 349–361. [Google Scholar] [CrossRef]
- Whitaker, S. Diffusion and dispersion in porous media. AIChE J. 1967, 13, 420–427. [Google Scholar] [CrossRef]
- Slattery, J.C. Flow of viscoelastic fluids through porous media. AIChE J. 1967, 13, 1066–1071. [Google Scholar] [CrossRef]
- Nielsen, A.E. Kinetics of Precipitation; Pergamon Press: New York, NY, USA, 1964. [Google Scholar]
- Wachi, S.; Jones, A.G. Mass transfer with chemical reaction and precipitation. Chem. Eng. Sci. 1991, 46, 1027–1033. [Google Scholar] [CrossRef]
- Bresch, D.; Desjardins, B.; Ghidaglia, J.M.; Grenier, E.; Hilliairet, M. Multifluid models including compressible fluids. Handb. Math. Anal. Mech. Viscous Fluids 2018, 52, 2927–2978. [Google Scholar]
- Bresch, D.; Renardy, M. Well-posedness of two-layer shallow-water flow between two horizontal rigid plates. Nonlinearity 2011, 24, 1081–1088. [Google Scholar] [CrossRef]
- Girault, V.; Raviart, P.A. Finite Element Methods for Navier-Stokes Equations; Springer: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Hecht, F.; Pironneau, O. An energy stable monolithic Eulerian fluid-structure finite element method. Int. J. Numer. Meth. Fl. 2017, 85, 430–446. [Google Scholar] [CrossRef]
- Ciarlet, P.G. The Finite Element Method for Elliptic Problems; SIAM: Philadelphia, PA, USA, 2002. [Google Scholar]
- Andricacos, P.C.; Arana, C.; Tabib, J.; Dukovic, J.; Romankiw, L.T. Electrodeposition of nickel-iron alloys. J. Electrochem. Soc. 1989, 136, 1336–1340. [Google Scholar] [CrossRef]
- Hessami, S.; Tobias, C.W. A mathematical model for anomalous codeposition of nickel-iron on a rotating disk electrode. J. Electrochem. Soc. 1989, 136, 3611–3616. [Google Scholar] [CrossRef]
- Criss, C.M.; Cobbie, J.W. The thermodynamic properties of high temperature aqueous solutions. J. Am. Chem. Soc. 1964, 86, 5385–5390. [Google Scholar] [CrossRef]
- Yang, S.; Hung, H.T.; Wu, P.Y.; Wang, Y.W.; Nishikawa, H.; Kao, C.R. Materials merging mechanism of microfluidic electroless interconnection process. J. Electrochem. Soc. 2018, 165, D273–D281. [Google Scholar] [CrossRef]
- Cartellier, A. Simultaneous void fraction measurement, bubble velocity, and size estimate using a single optical probe in gas–liquid two-phase flows. Rev. Sci. Instrum. 1992, 63, 5442–5453. [Google Scholar] [CrossRef]
- Blue, R.; Uttamchandani, D. Recent advances in optical fiber devices for microfluidics integration. J. Biophotonics 2016, 9, 13–25. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ide, H.; Kimura, R.; Kawaji, M. Optical measurement of void fraction and bubble size distributions in a microchannel. Heat Transfer Eng. 2007, 28, 713–719. [Google Scholar] [CrossRef]
- Vejražka, J.; Večeř, M.; Orvalho, S.; Sechet, P.; Ruzicka, M.C.; Cartellier, A. Measurement accuracy of a mono-fiber optical probe in a bubbly flow. Intl. J. Multiphas. Flow 2010, 36, 533–548. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).