A Coupled OpenFOAM-WRF Study on Atmosphere-Wake-Ocean Interaction
Abstract
1. Introduction
2. Computational Approach
2.1. Atmospheric Model
2.2. Ocean Model
2.2.1. Governing Equations
2.2.2. Turbulence Modeling
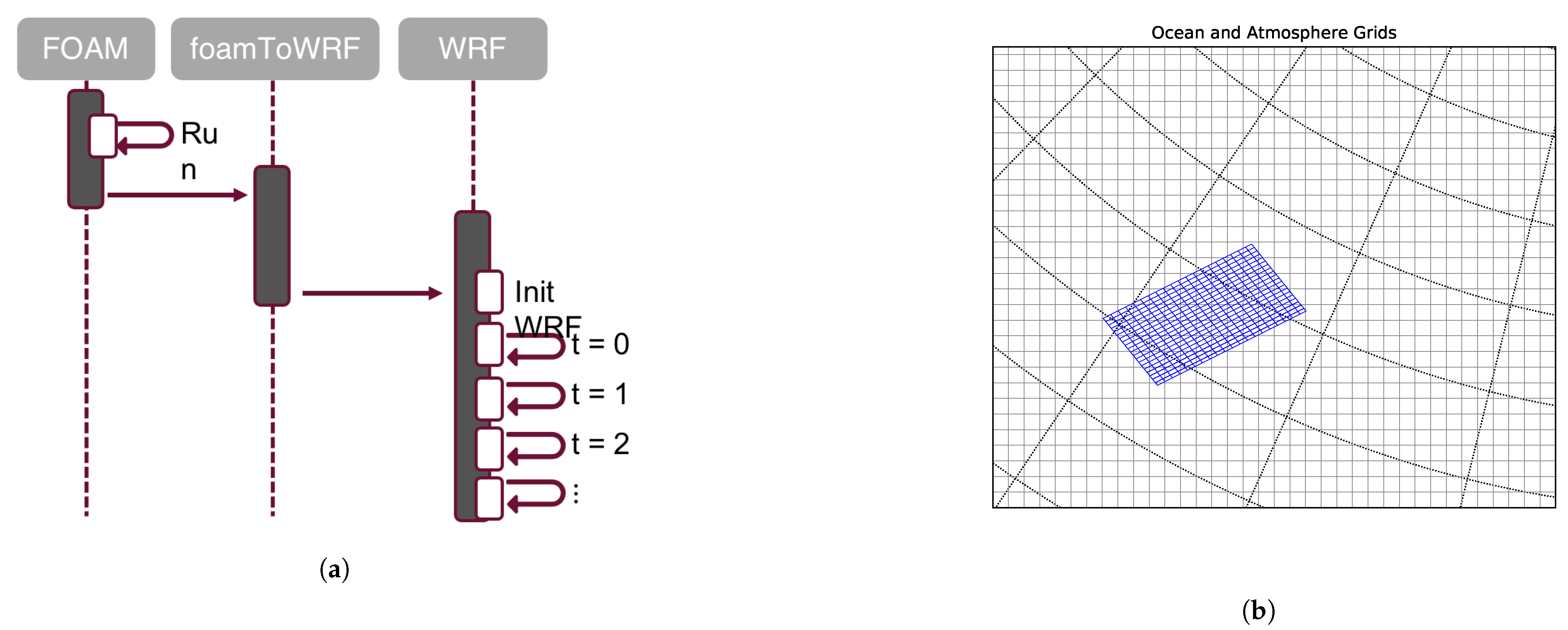
2.3. One-Way Coupling Approach
- initialize the ocean and atmospheric models with a consistent ambient environment;
- run the ocean model and extract relevant surface fields ();
- map surface fields from the ocean domain onto the atmospheric domain;
- overwrite initial atmospheric environment with mapped ocean fields; and,
- run the atmospheric simulation as normal.
2.3.1. Mapping Data Fields
3. Results and Discussion
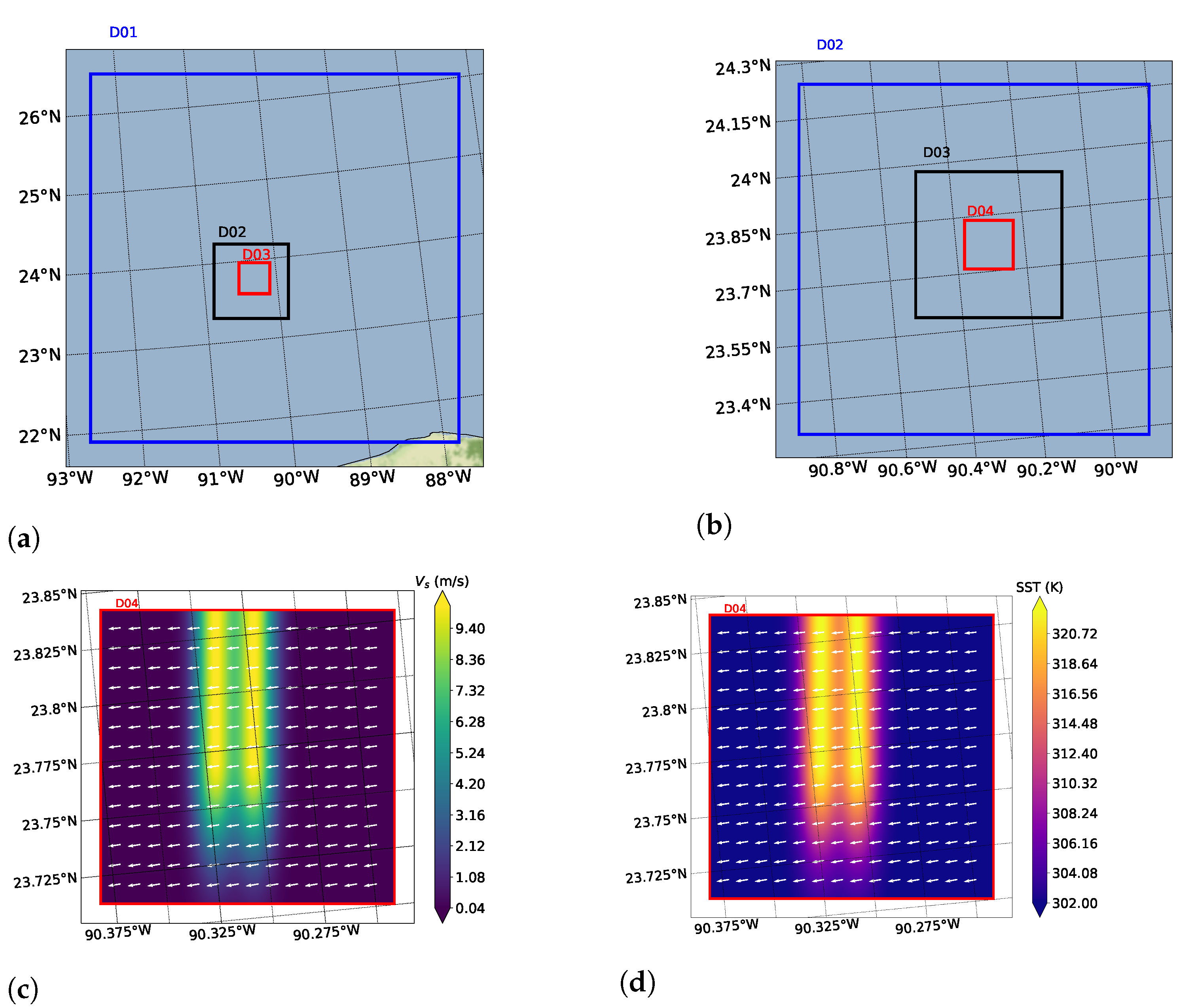
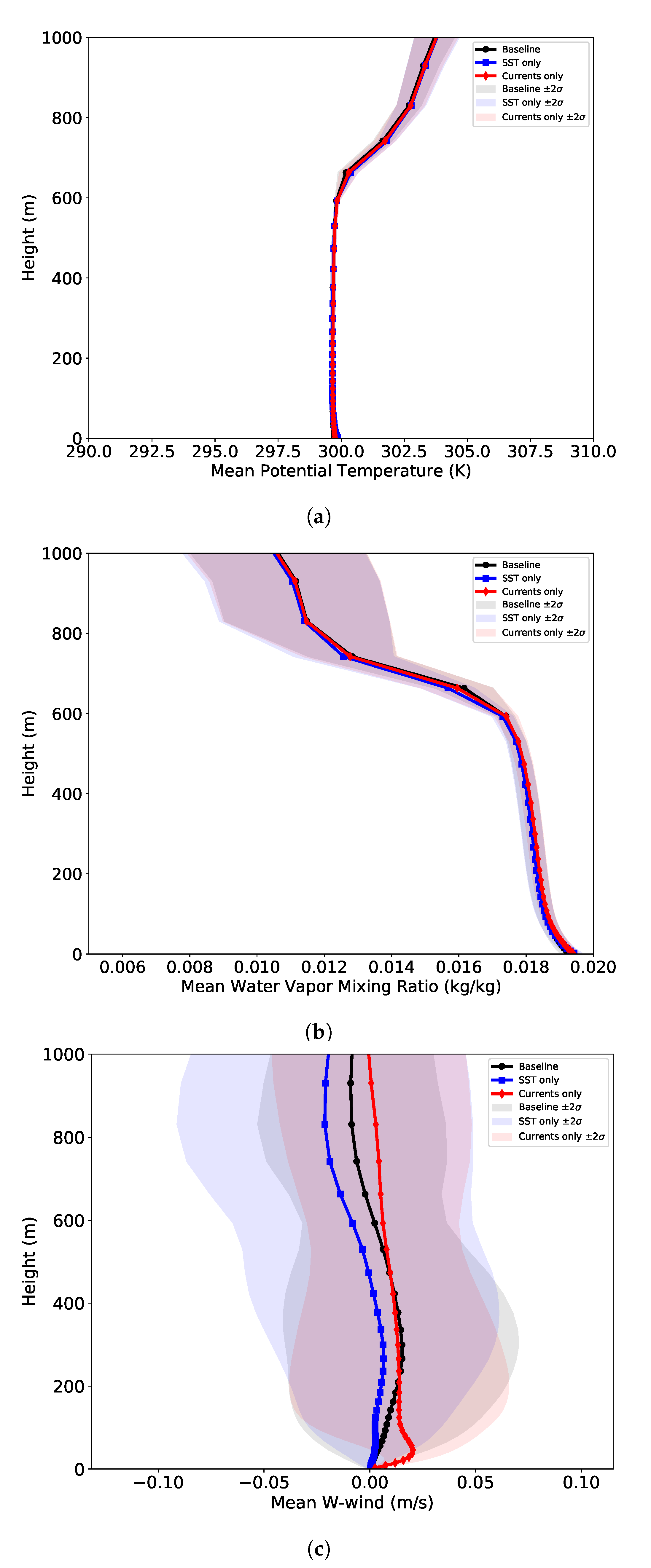
3.1. Application to Surface Jets
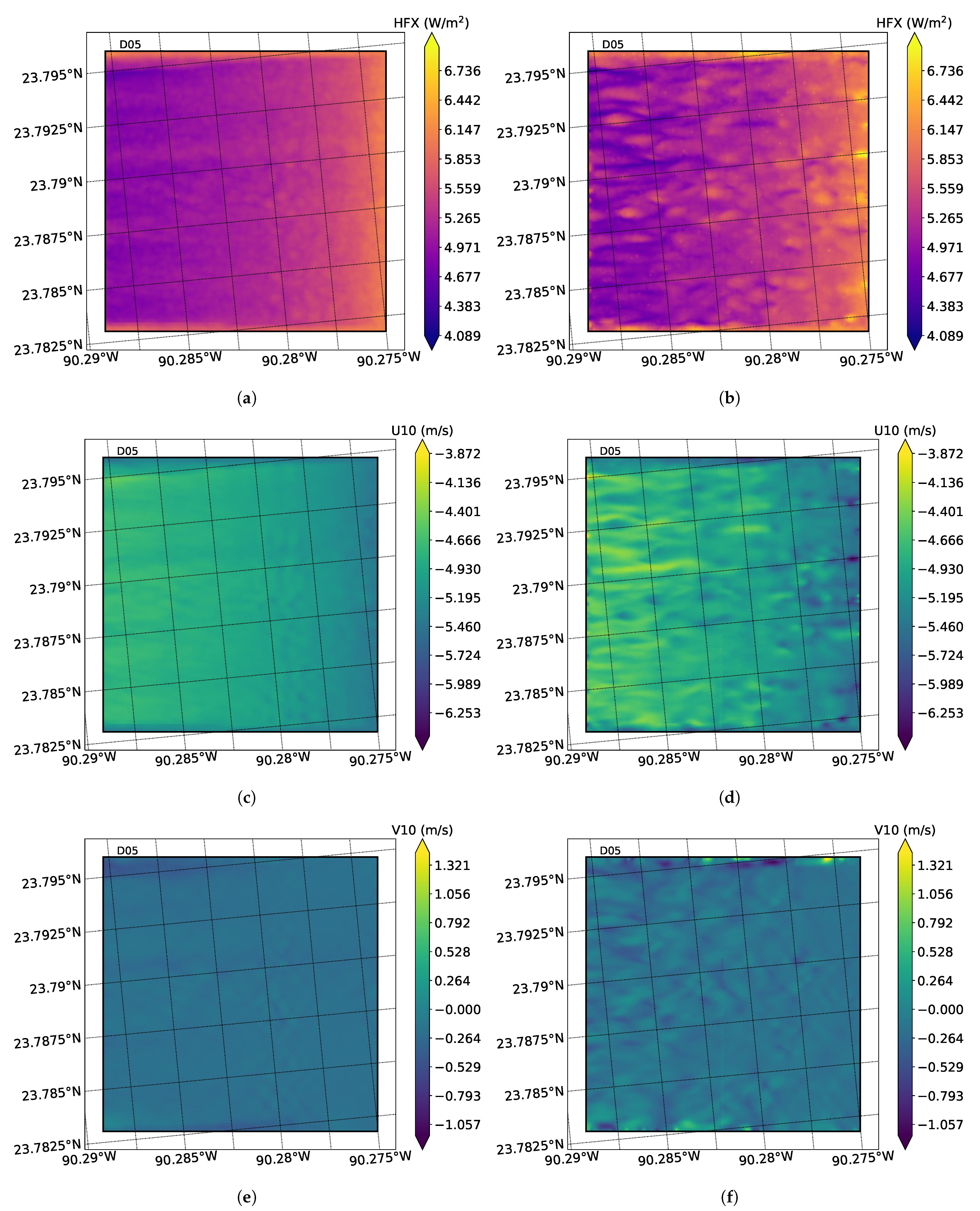
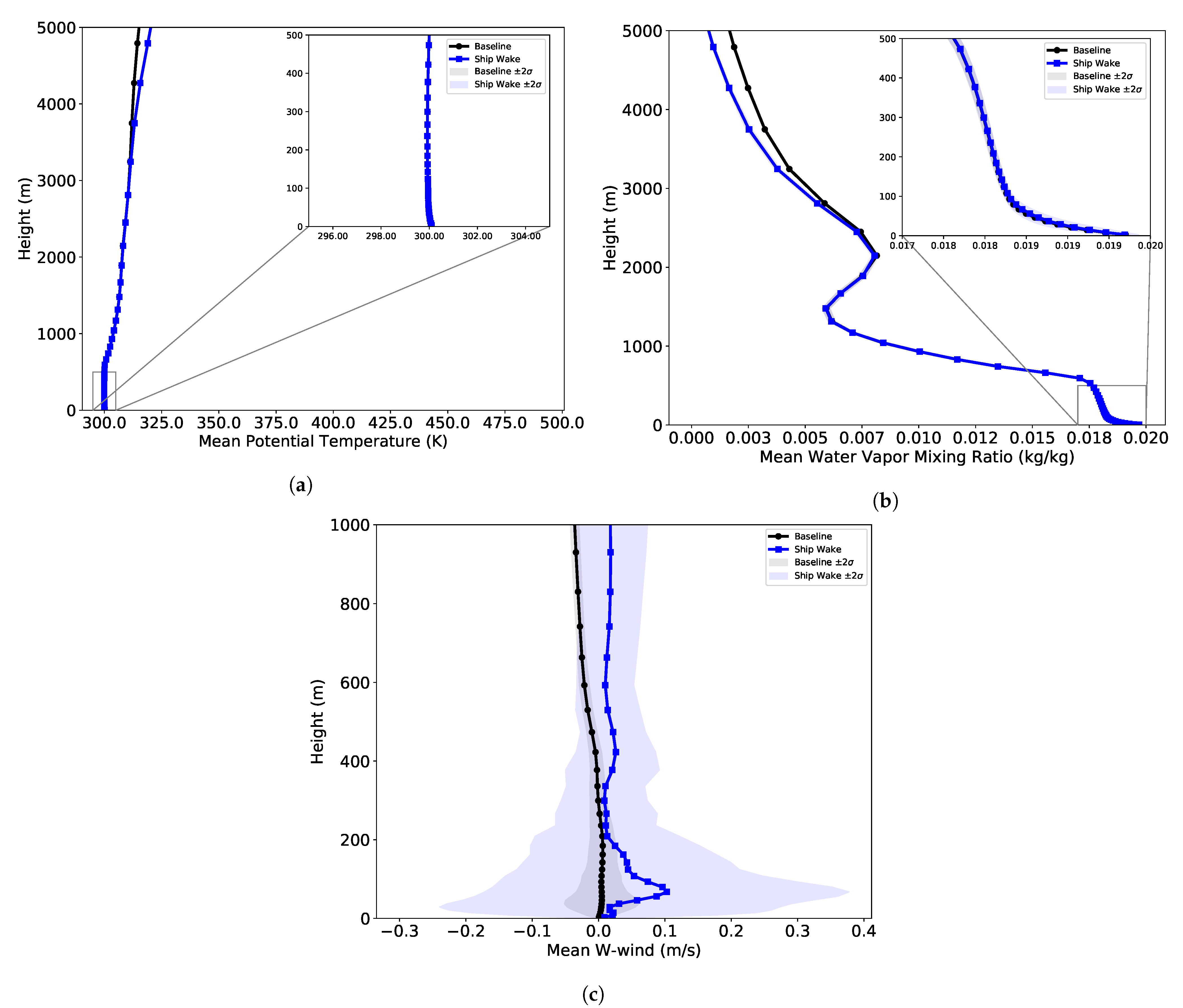
3.2. Application to Surface Ship Wake
4. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| WRF | Weather Research and Forecasting model |
| FVM | Finite Volume Method |
| RANS | Reynolds Averaged Navier Stokes |
| URANS | Unsteady RANS |
| 2D + t | Two dimensions plus time |
| OpenFOAM | Open Field Operation And Manipulation |
| ROMS | Regional Ocean Modeling System |
References
- Komjathy, A.; Yang, Y.M.; Meng, X.; Verkhoglyadova, O.; Mannucci, A.J.; Langley, R.B. Review and perspectives: Understanding natural-hazards-generated ionospheric perturbations using GPS measurements and coupled modeling: NATURAL-HAZARDS-CAUSED TEC PERTURBATIONS. Radio Sci. 2016, 51, 951–961. [Google Scholar] [CrossRef]
- Savastano, G.; Komjathy, A.; Verkhoglyadova, O.; Mazzoni, A.; Crespi, M.; Wei, Y.; Mannucci, A.J. Real-Time Detection of Tsunami Ionospheric Disturbances with a Stand-Alone GNSS Receiver: A Preliminary Feasibility Demonstration. Sci. Rep. 2017, 7, 46607. [Google Scholar] [CrossRef] [PubMed]
- Yuan, T.; Wang, C.; Song, H.; Platnick, S.; Meyer, K.; Oreopoulos, L. Automatically Finding Ship Tracks to Enable Large-Scale Analysis of Aerosol-Cloud Interactions. Geophys. Res. Lett. 2019, 46, 7726–7733. [Google Scholar] [CrossRef]
- Cooper, D.; Eichinger, W.; Barr, S.; Cottingame, W.; Hynes, V.; Keller, C.; Lebbda, C.; Poling, D.A. High-Resolution properties of the Equatorial Pacific marine atmospheric boundary layer from lidar and radiosonde observations. J. Atmos. Sci. 1996, 53, 2054–2074. [Google Scholar] [CrossRef][Green Version]
- Hagelberg, C.; Cooper, D.; Winter, C.; Eichinger, W. Scale properities of microscale convection in the marine surface layer. J. Geophys. Res. 1998, 103, 16897–16907. [Google Scholar] [CrossRef]
- Boutanios, Z.; Miller, C.; Hangan, H. Computational Analysis of the Manitoba September 5 1996 Storm: Mesoscale WRF-ARW Simulations Coupled with Microscale OpenFOAM CFD Simulations. In Proceedings of the Fifth International Symposium on Computational Wind Engineering, Chapel Hill, NC, USA, 23–27 May 2010; p. 8. [Google Scholar]
- Wyszogrodzki, A.A.; Miao, S.; Chen, F. Evaluation of the coupling between mesoscale-WRF and LES-EULAG models for simulating fine-scale urban dispersion. Atmos. Res. 2012, 118, 324–345. [Google Scholar] [CrossRef]
- Miao, Y.; Liu, S.; Chen, B.; Zhang, B.; Wang, S.; Li, S. Simulating urban flow and dispersion in Beijing by coupling a CFD model with the WRF model. Adv. Atmos. Sci. 2013, 30, 1663–1678. [Google Scholar] [CrossRef]
- Leblebici, E.; Tuncer, I.H. Coupled Unsteady Openfoam and WRF Solutions for an Accurate Estimation of Wind Energy Potential. In Proceedings of the VII European Congress on Computational Methods in Applied Sciences and Engineering, Crete Island, Greece, 5–10 June 2016; p. 8. [Google Scholar]
- Leblebici, E.; Tuncer, D.I.H. Development of OpenFOAM—WRF Coupling Methodolgy for Wind Power Production Estimations. In Proceedings of the 4th Symposium on OpenFOAM in Wind Energy, Delft, The Netherlands, 2–4 May 2016; p. 3. [Google Scholar]
- Haupt, S.E.; Berg, L.; Anderson, A.; Brown, B.; Churchfield, M.; Draxl, C.; Ennis, B.; Feng, Y.; Kosovic, B.; Kotamarthi, R.; et al. First Year Report of the A2e Mesoscale to Microscale Coupling Project; Technical Report; Pacific Northwest National Laboratory: Richland, WA, USA, 2015. [Google Scholar] [CrossRef]
- Haupt, S.E.; Kotamarthi, R.; Feng, Y.; Mirocha, J.D.; Koo, E.; Linn, R.; Kosovic, B.; Brown, B.; Anderson, A.; Churchfield, M.J.; et al. Second Year Report of the Atmosphere to Electrons Mesoscale to Microscale Coupling Project: Nonstationary Modeling Techniques and Assessment; Technical Report PNNL-26267, 1573811; Pacific Northwest National Laboratory: Richland, WA, USA, 2017. [Google Scholar] [CrossRef]
- Temel, O.; Bricteux, L.; van Beeck, J. Coupled WRF-OpenFOAM study of wind flow over complex terrain. J. Wind Eng. Ind. Aerodyn. 2018, 174, 152–169. [Google Scholar] [CrossRef]
- Mughal, M.O.; Lynch, M.; Yu, F.; Sutton, J. Forecasting and verification of winds in an East African complex terrain using coupled mesoscale—And micro-scale models. J. Wind Eng. Ind. Aerodyn. 2018, 176, 13–20. [Google Scholar] [CrossRef]
- Warner, J.C.; Armstrong, B.; He, R.; Zambon, J.B. Development of a Coupled Ocean–Atmosphere–Wave–Sediment Transport (COAWST) Modeling System. Ocean Model. 2010, 35, 230–244. [Google Scholar] [CrossRef]
- Samson, G.; Masson, S.; Lengaigne, M.; Keerthi, M.G.; Vialard, J.; Pous, S.; Madec, G.; Jourdain, N.C.; Jullien, S.; Menkes, C.; et al. The NOW regional coupled model: Application to the tropical Indian Ocean climate and tropical cyclone activity. J. Adv. Model. Earth Syst. 2014, 6, 700–722. [Google Scholar] [CrossRef]
- Varlas, G.; Katsafados, P.; Papadopoulos, A.; Korres, G. Implementation of a two-way coupled atmosphere-ocean wave modeling system for assessing air-sea interaction over the Mediterranean Sea. Atmos. Res. 2018, 208, 201–217. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Liu, Z.; Berner, J.; Wang, W.; Powers, J.G.; Duda, M.G.; Barker, D.M.; et al. A Description of the Advanced Research WRF Model Version 4; NCAR Technical Notes NCAR/TN-556+STR; National Center for Atmospheric Research: Boulder, CO, USA, 2019; p. 162. [Google Scholar]
- Jiménez, P.A.; Dudhia, J.; González-Rouco, J.F.; Navarro, J.; Montávez, J.P.; García-Bustamante, E. A Revised Scheme for the WRF Surface Layer Formulation. Mon. Weather Rev. 2012, 140, 898–918. [Google Scholar] [CrossRef]
- Hong, S.Y.; Noh, Y.; Dudhia, J. A New Vertical Diffusion Package with an Explicit Treatment of Entrainment Processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Thompson, G.; Field, P.R.; Rasmussen, R.M.; Hall, W.D. Explicit Forecasts of Winter Precipitation Using an Improved Bulk Microphysics Scheme. Part II: Implementation of a New Snow Parameterization. Mon. Weather Rev. 2008, 136, 5095–5115. [Google Scholar] [CrossRef]
- Niu, G.Y.; Yang, Z.L.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Kumar, A.; Manning, K.; Niyogi, D.; Rosero, E.; et al. The community Noah land surface model with multiparameterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- IOC; SCOR; IAPSO. The International Thermodynamic Equation of Seawater—2010: Calculation and Use of Thermodynamic Properties; Intergovernmental Oceanographic Commission, Manuals and Guides No. 56; UNESCO: Paris, France, 2010. [Google Scholar]
- Beljaars, A.C.M. The parametrization of surface fluxes in large-scale models under free convection. Q. J. R. Meteorol. Soc. 1995, 121, 255–270. [Google Scholar] [CrossRef]
- Mahrt, L.; Sun, J. The Subgrid Velocity Scale in the Bulk Aerodynamic Relationship for Spatially Averaged Scalar Fluxes. Mon. Weather Rev. 1995, 123, 3032–3041. [Google Scholar] [CrossRef]
- Werner, K. Nesting in WRF. In Proceedings of the Basic WRF Tutorial, Boulder, CO, USA, 27–31 January 2020. [Google Scholar]
- Miner, E.W.; Ramberg, S.E.; Swean, T.J. A Method for Approximating the Initial Data Plane for Surface Ship Wake Simulations; Technical Report NRL Memorandum Report 6376; Naval Research Laboratory: Washington, DC, USA, 1988. [Google Scholar]
- Somero, J.R.; Basovich, A.; Paterson, E.G. Structure and Persistence of Ship Wakes and the Role of Langmuir-Type Circulations. arXiv 2018, arXiv:1807.00441. [Google Scholar] [CrossRef]
- LYNCH, P.; HUANG, X.Y. Diabatic initialization using recursive filters. Tellus A 1994, 46, 583–597. [Google Scholar] [CrossRef][Green Version]




| Atmospheric Model | Configuration |
|---|---|
| Software | WRF Version 4.2.1 |
| Integration Domain | Gulf of Mexico |
| Grid | Arakawa semi-staggered C-grid |
| Initial and boundary conditions | NCEP GDAS/FNL Reanalysis, 0.25 × 0.25 |
| 6-hour update of boundary conditions | |
| SST | NCEP GDAS/FNL Reanalysis |
| Surface Layer | Revised MM5 Monin-Obukhov scheme [19] |
| Planetary Boundary Layer | YSU [20] |
| Microphysics | Thompson scheme [21] |
| Cumulus | None |
| Land surface | Noah [22] |
| Radiation | RRTMG scheme used for longwave and shortwave radiation [23] |
| Parameter | Value for SST | Value for U | Value for V |
|---|---|---|---|
| 20 K | 0 m/s | 10 m/s | |
| 8500 m | - | 8500 | |
| 6500 m | - | 6500 | |
| 1× 10 m2 | - | 1 × 10 m2 |
| Simulation Type | PBL Treatment | (m) | Height of 1st Grid Point (m) | Grid Points | (s) |
|---|---|---|---|---|---|
| D01 mesoscale | YSU PBL | 4500 | 5 | 120 × 120 × 81 | 27.0 |
| D02 mesoscale | YSU PBL | 900 | 5 | 121 × 121 × 81 | 5.4 |
| D03 mesoscale | YSU PBL | 300 | 5 | 151 × 151 × 81 | 1.8 |
| D04 microscale | LES | 100 | 5 | 151 × 151 × 81 | 0.6 |
| Parameter | Value |
|---|---|
| Forward speed (m/s) | 13 |
| Draft (m) | 6.16 |
| Beam (m) | 18.9 |
| Heading (deg) | 5.52 |
| Simulation Type | PBL Treatment | (m) | Height of 1st Grid Point (m) | Grid Points | (s) |
|---|---|---|---|---|---|
| D01 mesoscale | YSU PBL | 2500 | 5 | 120 × 120 × 81 | 13.0 |
| D02 mesoscale | YSU PBL | 450 | 5 | 121 × 121 × 81 | 2.6 |
| D03 mesoscale | YSU PBL | 90 | 5 | 151 × 151 × 81 | 0.52 |
| D04 microscale | LES | 30 | 5 | 151 × 151 × 81 | 0.17 |
| D05 microscale | LES | 10 | 5 | 151 × 151 × 81 | 0.06 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gilbert, J.; Pitt, J. A Coupled OpenFOAM-WRF Study on Atmosphere-Wake-Ocean Interaction. Fluids 2021, 6, 12. https://doi.org/10.3390/fluids6010012
Gilbert J, Pitt J. A Coupled OpenFOAM-WRF Study on Atmosphere-Wake-Ocean Interaction. Fluids. 2021; 6(1):12. https://doi.org/10.3390/fluids6010012
Chicago/Turabian StyleGilbert, John, and Jonathan Pitt. 2021. "A Coupled OpenFOAM-WRF Study on Atmosphere-Wake-Ocean Interaction" Fluids 6, no. 1: 12. https://doi.org/10.3390/fluids6010012
APA StyleGilbert, J., & Pitt, J. (2021). A Coupled OpenFOAM-WRF Study on Atmosphere-Wake-Ocean Interaction. Fluids, 6(1), 12. https://doi.org/10.3390/fluids6010012





