Experimental and Mathematical Tools to Predict Droplet Size and Velocity Distribution for a Two-Fluid Nozzle
Abstract
1. Introduction
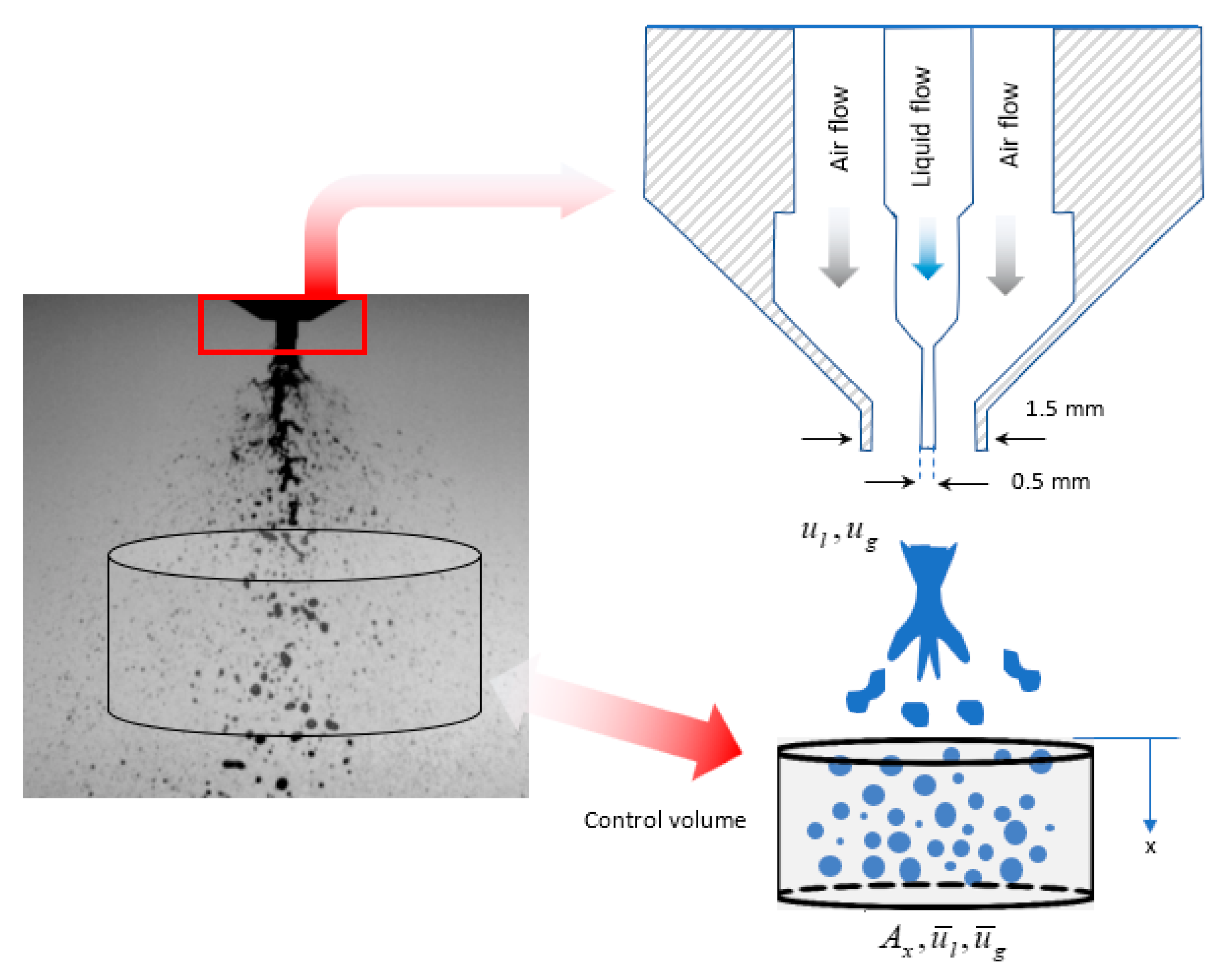
2. Experimental Methods
3. Mathematical Formulation
4. Results and Discussion
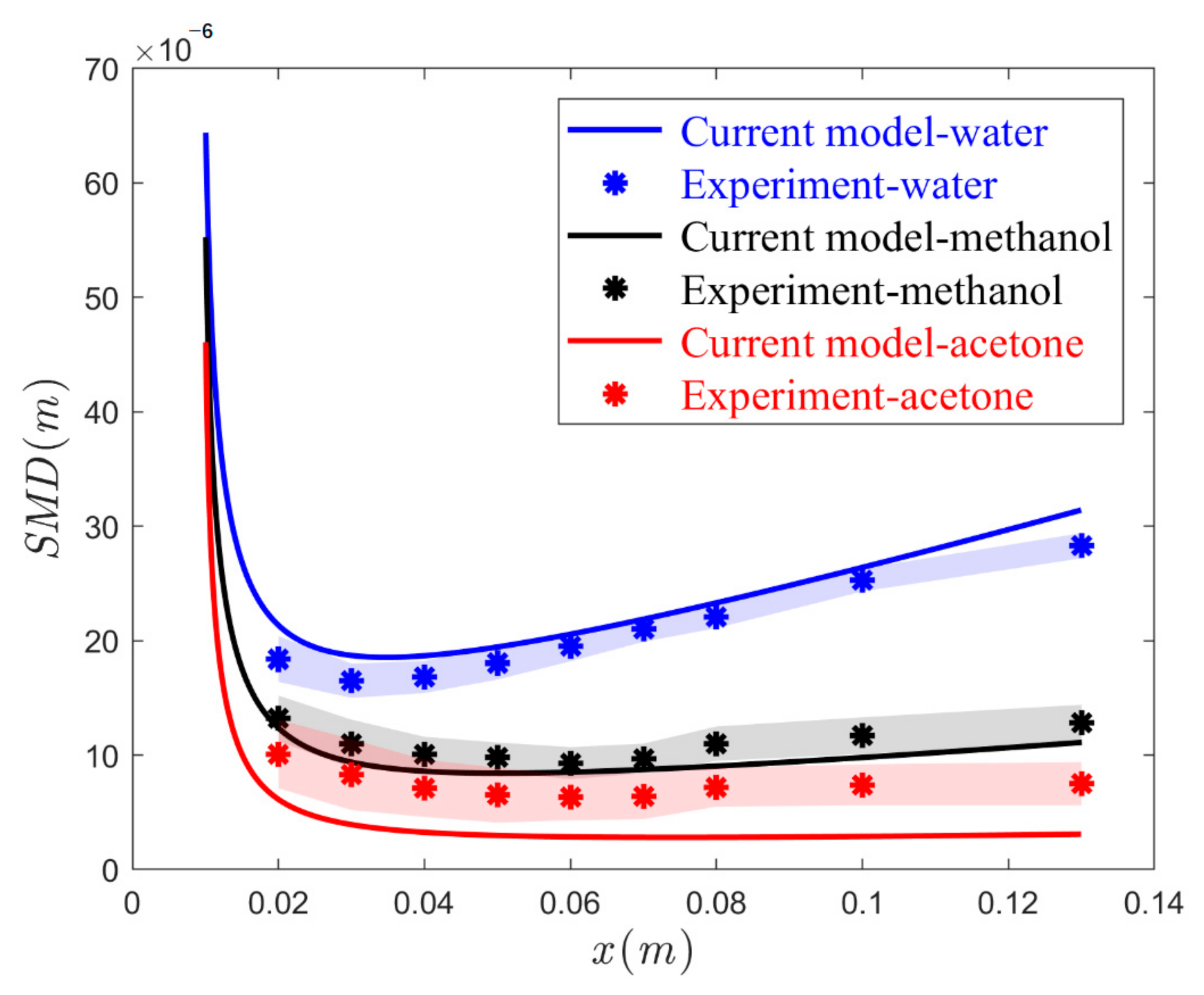
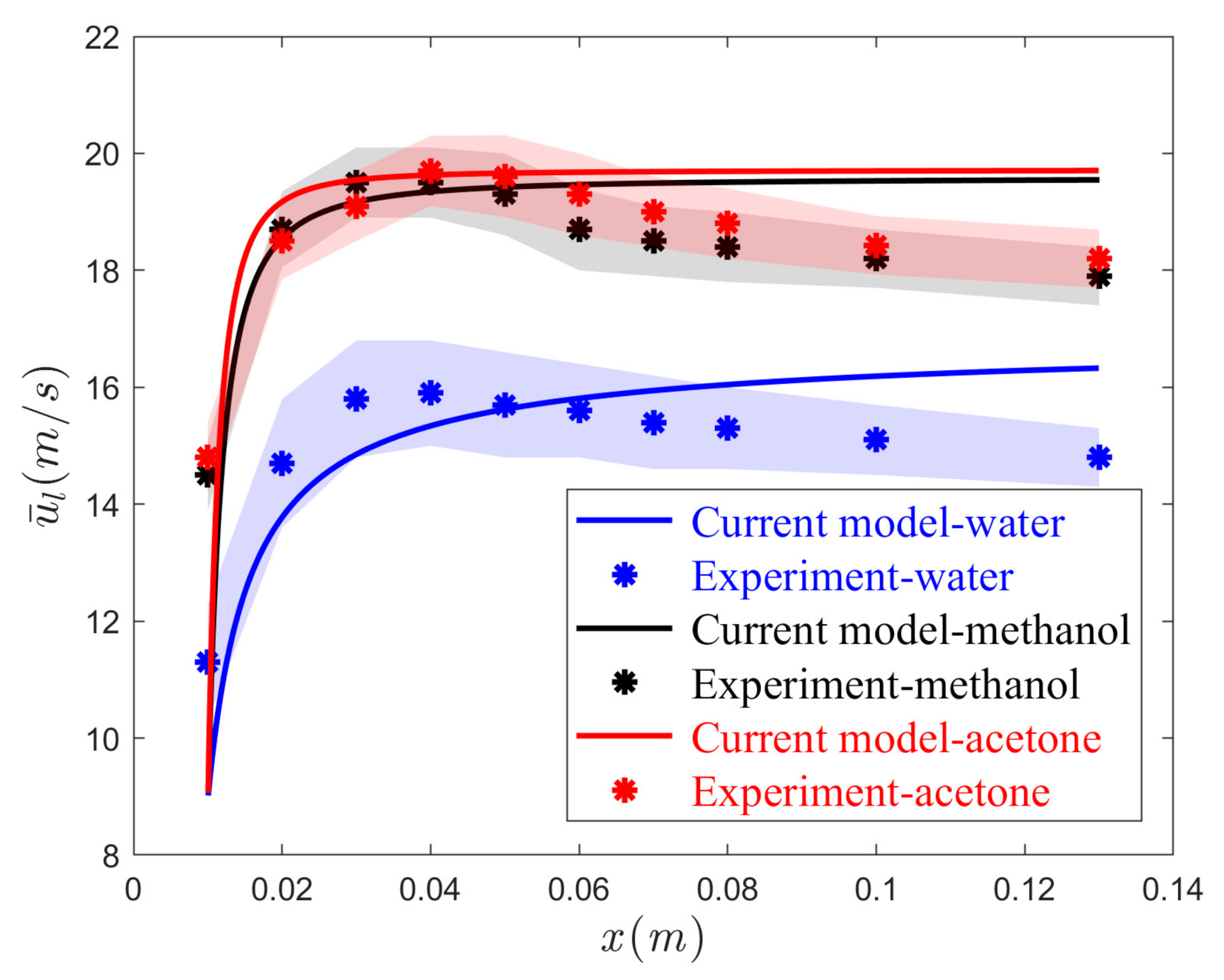
4.1. Data Comparison
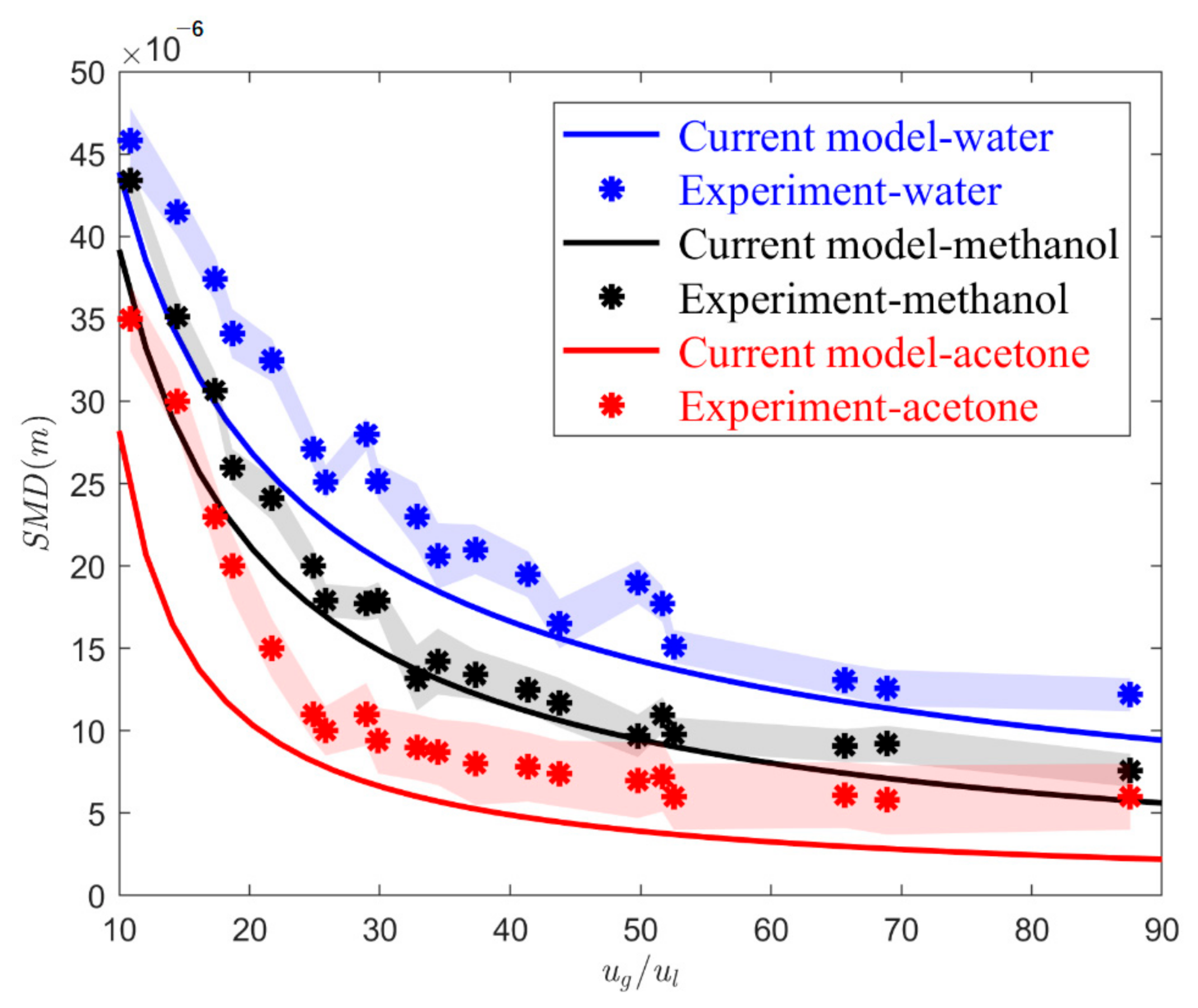
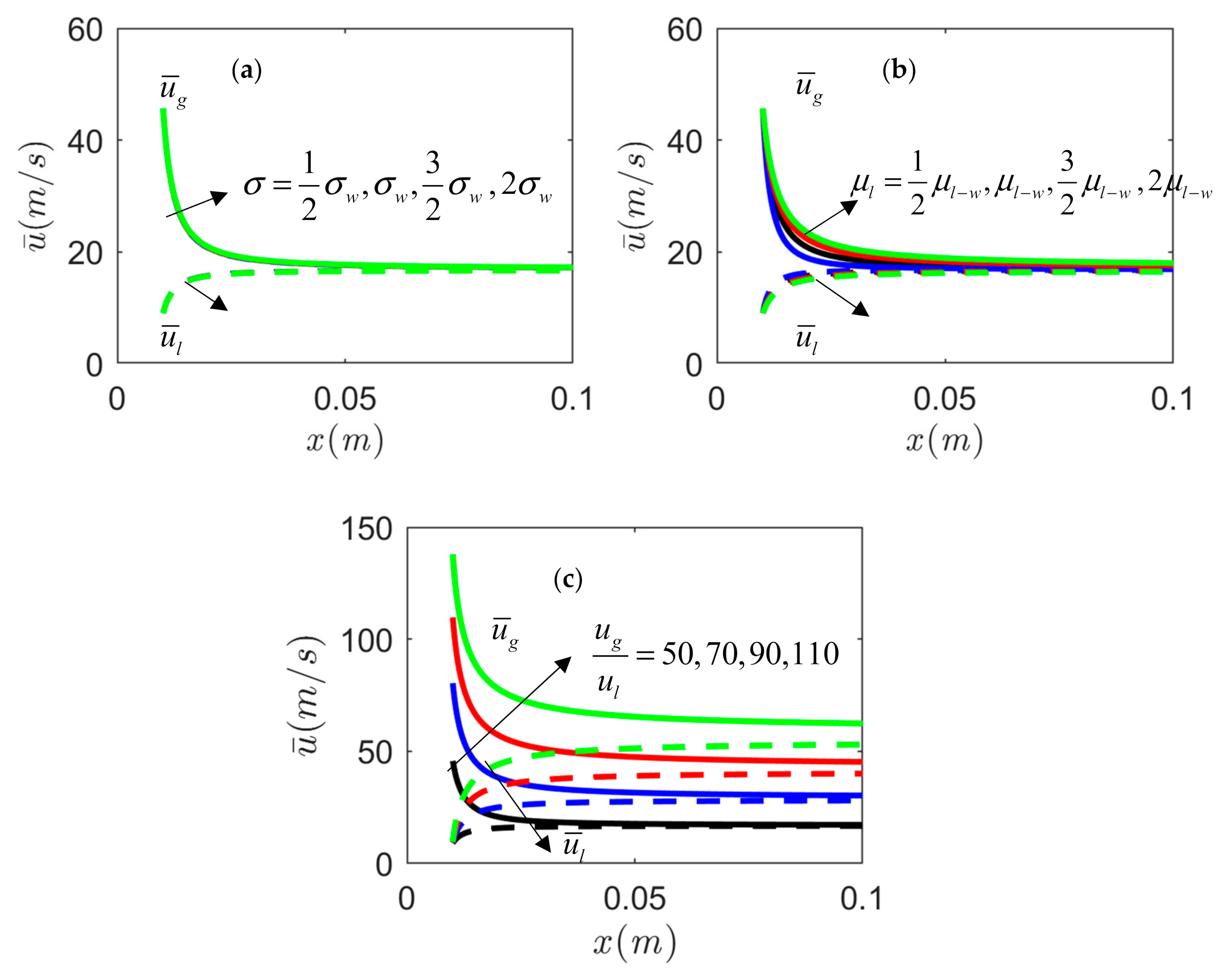
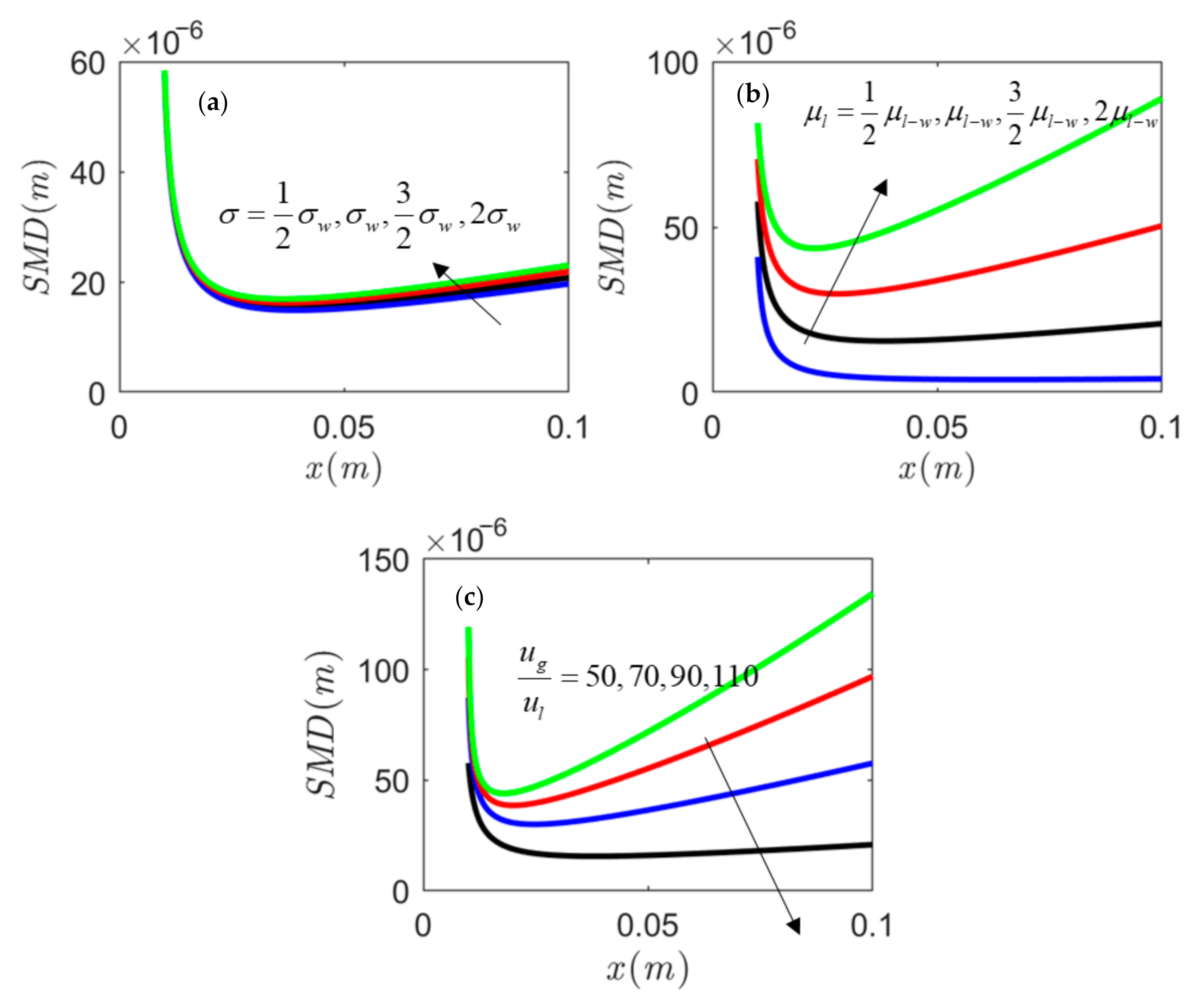
4.2. Effects of Feed Physiochemical and Relative Velocity
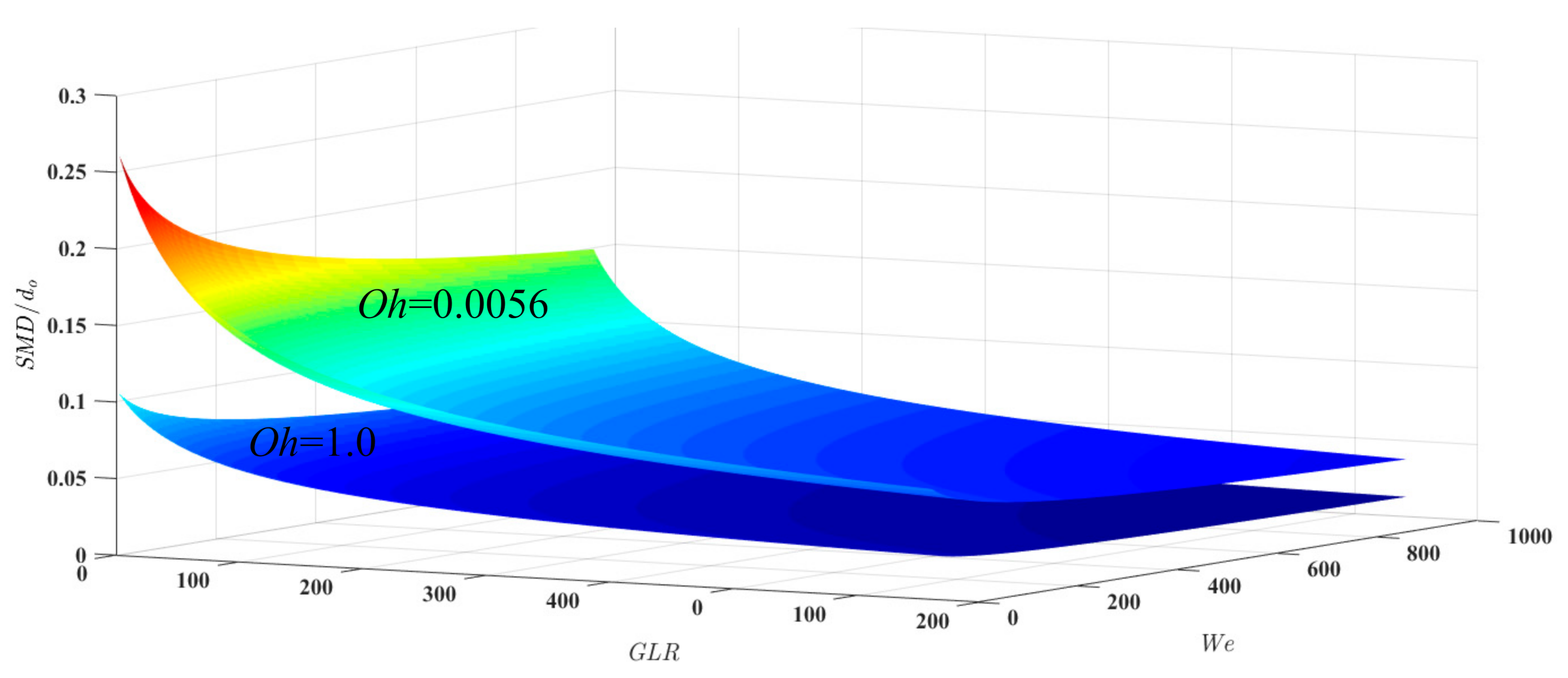
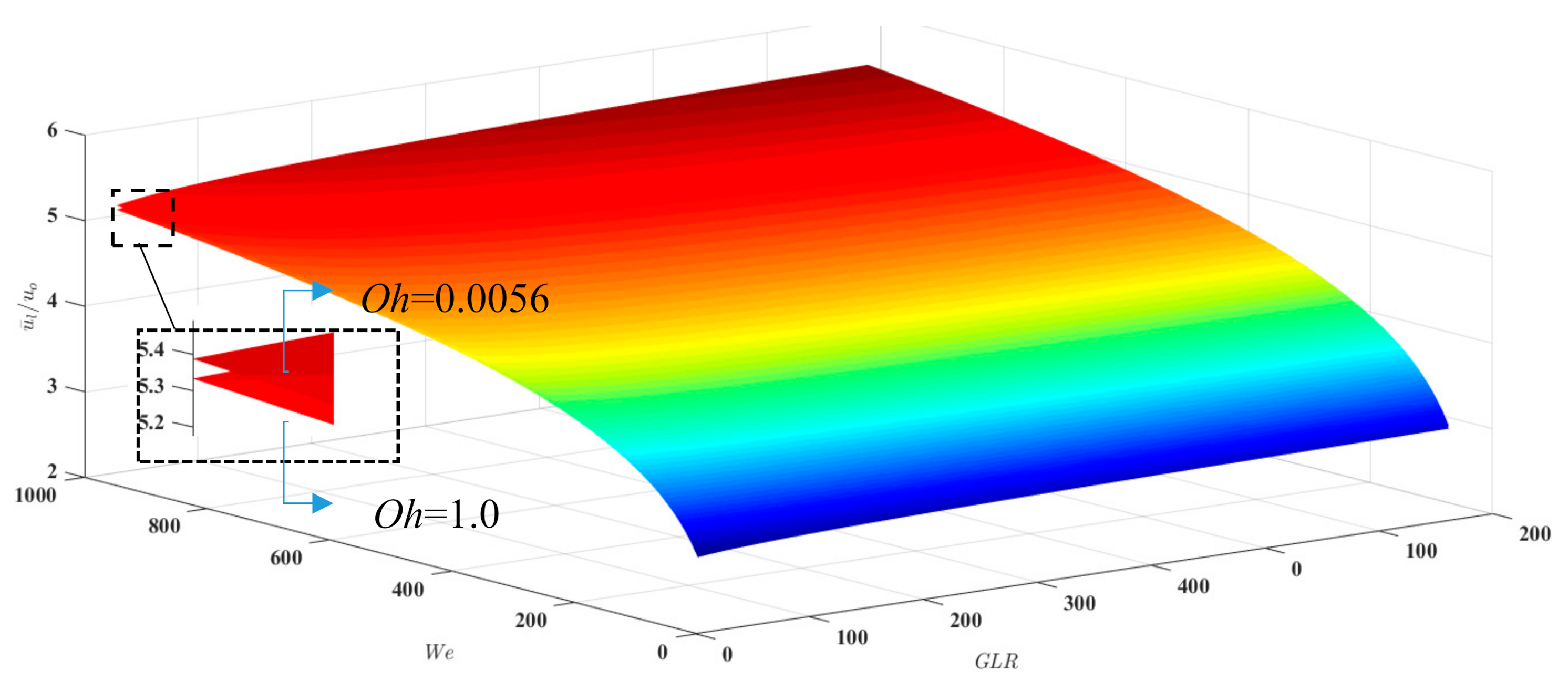
4.3. Use of Atomization Scaling Parameters
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclatures
| Normal | |
| A | Surface area (m2) |
| CD | Drag coefficient |
| D | Droplet diameter (m) |
| d | Differential |
| dg | Gas orifice diameter (m) |
| do | Liquid orifice diameter (m) |
| GLR | Ratio of Gas to liquid mass flow rates |
| K | proportionality constant for the viscous dissipation term |
| ṁ | Mass flow rate (kg/s) |
| n | Drop number density |
| Oh | Ohnesorge number |
| P | Pressure |
| p(D) | Normalized drop size distribution function |
| Re | Reynolds number |
| SMD | Sauter mean diameter (m) |
| u | Velocity (m/s) |
| ū | Mean velocity in control volume (m/s) |
| We | Weber number |
| X | Axial coordination (m) |
| V | volume of the spray bounded by A and spray length (m3) |
| Greek Symbols | |
| ρ | Density (kg/m3) |
| μ | Latent heat of vaporization (J/kg) |
| Δ | Difference in states |
| σ | Surface tension (N/m) |
| Subscripts | |
| g | Gas phase |
| i | Index for droplet size bins |
| l | Liquid phase |
| o | Orifice |
| w | water |
| x | Atomization axis |
References
- Shrigondekar, H.; Chowdhury, A.; Prabhu, S. Characterization of solid-cone simplex mist nozzles. Fire Saf. J. 2020, 111, 102936. [Google Scholar] [CrossRef]
- Tang, M.; Chen, S.-C.; Pui, D.Y. An improved atomizer with high output of nanoparticles. J. Aerosol Sci. 2018, 124, 10–16. [Google Scholar] [CrossRef]
- Sapra, M.; Mayya, Y.; Venkataraman, C. Air-jet atomization for preparation of lipid nanoparticles: Dependence of size on solute concentration. J. Aerosol Sci. 2016, 100, 1–13. [Google Scholar] [CrossRef]
- Poozesh, S.; Bilgili, E. Scale-up of pharmaceutical spray drying using scale-up rules: A review. Int. J. Pharm. 2019, 562, 271–292. [Google Scholar] [CrossRef] [PubMed]
- Sander, A.; Penović, T. Droplet Size Distribution Obtained by Atomization with Two-Fluid Nozzles in a Spray Dryer. Chem. Eng. Technol. 2014, 37, 2073–2084. [Google Scholar] [CrossRef]
- Andrade, R.D.; Skurtys, O.; Osorio, F.A. Atomizing spray systems for application of edible coatings. Compr. Rev. Food Sci. Food Saf. 2012, 11, 323–337. [Google Scholar] [CrossRef]
- Poozesh, S.; Setiawan, N.; Arce, F.; Sundararajan, P.; Della Rocca, J.; Rumondor, A.; Wei, D.; Wenslow, R.; Xi, H.; Zhang, S. Understanding the process-product-performance interplay of spray dried drug-polymer systems through complete structural and chemical characterization of single spray dried particles. Powder Technol. 2017, 320, 685–695. [Google Scholar] [CrossRef]
- Oh, Y.S.; Choi, D.Y.; Son, J.Y.; Kim, B.Y.; Kang, H.W.; Chang, C.B.; Moon, J.-T.; Sung, H.J. Breakup behavior of a molten metal jet. Int. J. Heat Fluid Flow 2014, 50, 27–37. [Google Scholar] [CrossRef]
- Babinsky, E.; Sojka, P. Modeling drop size distributions. Prog. Energy Combust. Sci. 2002, 28, 303–329. [Google Scholar] [CrossRef]
- Beaucage, G.; Kammler, H.K.; Pratsinis, S.E. Particle size distributions from small-angle scattering using global scattering functions. J. Appl. Crystallogr. 2004, 37, 523–535. [Google Scholar] [CrossRef]
- Yan, K.; Ning, Z.; Lü, M.; Sun, C. Study on droplet size and velocity distributions of a pressure swirl atomizer based on the Maximum Entropy Formalism. Entropy 2015, 17, 580–593. [Google Scholar] [CrossRef]
- Dasgupta, D.; Nath, S.; Bhanja, D. Dual-mode nonlinear instability analysis of a confined planar liquid sheet sandwiched between two gas streams of unequal velocities and prediction of droplet size and velocity distribution using maximum entropy formulation. Phys. Fluids 2018, 30, 044104. [Google Scholar] [CrossRef]
- Kolodnytska, R.; Skurativskyi, S.; Moskvin, P. Maximum entropy method for biodiesel spray droplet distribution. In Proceedings of the ILASS Europe. 28th European Conference on Liquid Atomization and Spray Systems, Valencia, Spain, 6–8 September 2017; pp. 464–471. [Google Scholar]
- Pei, Y.; Hawkes, E.R.; Kook, S.; Goldin, G.M.; Lu, T. Modelling n-dodecane spray and combustion with the transported probability density function method. Combust. Flame 2015, 162, 2006–2019. [Google Scholar] [CrossRef]
- Hu, Y.; Gutheil, E. Numerical simulations of turbulent poly-disperse acetone spray flows using a transported joint probability density function method. At. Sprays 2016, 26, 275–299. [Google Scholar] [CrossRef]
- González-Tello, P.; Camacho, F.; Vicaria, J.; González, P. A modified Nukiyama–Tanasawa distribution function and a Rosin–Rammler model for the particle-size-distribution analysis. Powder Technol. 2008, 186, 278–281. [Google Scholar] [CrossRef]
- Nukiyama, S.; Tanazawa, Y. An experiment on the atomization of liquid by means of an air stream. Trans. JSME 1942, 4, 8. [Google Scholar]
- Pacheco, C.; Pina, J.; Saleh, K. Atomization of molten materials for particle coating: Prediction of mean droplet size for two-fluid nozzles. At. Sprays 2016, 26, 1031–1050. [Google Scholar] [CrossRef]
- Castel, V.; Rubiolo, A.C.; Carrara, C.R. Droplet size distribution, rheological behavior and stability of corn oil emulsions stabilized by a novel hydrocolloid (Brea gum) compared with gum arabic. Food Hydrocoll. 2017, 63, 170–177. [Google Scholar] [CrossRef]
- Tomar, G.; Fuster, D.; Zaleski, S.; Popinet, S. Multiscale simulations of primary atomization. Comput. Fluids 2010, 39, 1864–1874. [Google Scholar] [CrossRef]
- Tryggvason, G.; Scardovelli, R.; Zaleski, S. Direct Numerical Simulations of Gas—Liquid Multiphase Flows; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Vincent, S.; Osmar, L.; Estivalezes, J.-L.; Zaleski, S.; Auguste, F.; Aniszewski, W.; Ling, Y.; Menard, T.; Pedrono, A.; Magnaudet, J. A phase inversion benchmark for multiscale multiphase flows. arXiv 2019, arXiv:1906.02655. [Google Scholar]
- Ling, Y.; Fuster, D.; Tryggvason, G.; Zaleski, S. A two-phase mixing layer between parallel gas and liquid streams: Multiphase turbulence statistics and influence of interfacial instability. J. Fluid Mech. 2019, 859, 268–307. [Google Scholar] [CrossRef]
- Jain, S.S.; Tyagi, N.; Prakash, R.S.; Ravikrishna, R.; Tomar, G. Secondary breakup of drops at moderate Weber numbers: Effect of Density ratio and Reynolds number. Int. J. Multiph. Flow 2019, 117, 25–41. [Google Scholar] [CrossRef]
- Lee, T.-W.; An, K. Quadratic formula for determining the drop size in pressure-atomized sprays with and without swirl. Phys. Fluids 2016, 28, 063302. [Google Scholar] [CrossRef]
- Lee, T.-W.; Park, J. Determination of the Drop Size During Air-Blast Atomization. J. Fluids Eng. 2019, 141, 121301. [Google Scholar] [CrossRef]
- Lee, T.-W.; Ryu, J.-H. Analyses of spray break-up mechanisms using the integral form of the conservation equations. Combust. Theory Model. 2014, 18, 89–100. [Google Scholar] [CrossRef]
- Hede, P.D.; Bach, P.; Jensen, A.D. Two-fluid spray atomisation and pneumatic nozzles for fluid bed coating/agglomeration purposes: A review. Chem. Eng. Sci. 2008, 63, 3821–3842. [Google Scholar] [CrossRef]
- Poozesh, S.; Grib, S.W.; Renfro, M.W.; Marsac, P.J. Near-field dynamics of high-speed spray dryer coannular two fluid nozzle: Effects of operational conditions and formulations. Powder Technol. 2018, 333, 439–448. [Google Scholar] [CrossRef]
- Sänger, A.; Jakobs, T.; Djordjevic, N.; Kolb, T. Effect of primary instability of a high viscous liquid jet on the spray quality generated by a twin-fluid atomizer. In Proceedings of the European Conference for Liquid Atomization and Spray System (ILASS), Bremen, Germany, 8–10 September 2014; pp. 8–10. [Google Scholar]
- Pougatch, K.; Salcudean, M.; Chan, E.; Knapper, B. A two-fluid model of gas-assisted atomization including flow through the nozzle, phase inversion, and spray dispersion. Int. J. Multiph. Flow 2009, 35, 661–675. [Google Scholar] [CrossRef]
- Leroux, B.; Delabroy, O.; Lacas, F. Experimental study of coaxial atomizers scaling. Part I: Dense core zone. At. Sprays 2007, 17, 381–407. [Google Scholar] [CrossRef]
- Aliseda, A.; Hopfinger, E.J.; Lasheras, J.C.; Kremer, D.; Berchielli, A.; Connolly, E. Atomization of viscous and non-Newtonian liquids by a coaxial, high-speed gas jet. Experiments and droplet size modeling. Int. J. Multiph. Flow 2008, 34, 161–175. [Google Scholar] [CrossRef]
- Poozesh, S.; Setiawan, N.; Akafuah, N.K.; Saito, K.; Marsac, P.J. Assessment of predictive models for characterizing the atomization process in a spray dryer’s bi-fluid nozzle. Chem. Eng. Sci. 2018, 180, 42–51. [Google Scholar] [CrossRef]
- Dennison, T.J.; Smith, J.; Hofmann, M.P.; Bland, C.E.; Badhan, R.K.; Al-Khattawi, A.; Mohammed, A.R. Design of experiments to study the impact of process parameters on droplet size and development of non-invasive imaging techniques in tablet coating. PLoS ONE 2016, 11, e0157267. [Google Scholar] [CrossRef] [PubMed]
- Xiao, F.; Dianat, M.; McGuirk, J.J. LES of turbulent liquid jet primary breakup in turbulent coaxial air flow. Int. J. Multiph. Flow 2014, 60, 103–118. [Google Scholar] [CrossRef]
- Charalampous, G.; Hardalupas, Y.; Taylor, A. Structure of the continuous liquid jet core during coaxial air-blast atomisation. Int. J. Spray Combust. Dyn. 2009, 1, 389–415. [Google Scholar] [CrossRef]
- Kaiser, R.; Li, C.; Yang, S.; Lee, D. A numerical simulation study of the path-resolved breakup behaviors of molten metal in high-pressure gas atomization: With emphasis on the role of shock waves in the gas/molten metal interaction. Adv. Powder Technol. 2018, 29, 623–630. [Google Scholar] [CrossRef]
- Kihm, K.D.; Chigier, N. Effect of shock waves on liquid atomization of a two-dimensional airblast atomizer. At. Sprays 1991, 1, 113–136. [Google Scholar] [CrossRef]
- Urbán, A.; Zaremba, M.; Malý, M.; Józsa, V.; Jedelský, J. Droplet dynamics and size characterization of high-velocity airblast atomization. Int. J. Multiph. Flow 2017, 95, 1–11. [Google Scholar] [CrossRef]
- Lasheras, J.; Villermaux, E.; Hopfinger, E. Break-up and atomization of a round water jet by a high-speed annular air jet. J. Fluid Mech. 1998, 357, 351–379. [Google Scholar] [CrossRef]
- Chigier, N.; Farago, Z. Morphological classification of disintegration of round liquid jets in a coaxial air stream. At. Sprays 1992, 2, 137–153. [Google Scholar] [CrossRef]
- Poozesh, S.; Akafuah, N.; Saito, K. New criteria for filament breakup in droplet-on-demand inkjet printing using volume of fluid (VOF) method. Korean J. Chem. Eng. 2016, 33, 775–781. [Google Scholar] [CrossRef]
- Saito, K.; Williams, F. Scale Modeling in the Age of High-Speed Computation. In Progress in Scale Modeling, Volume II; Springer: Berlin/Heidelberg, Germany, 2015; pp. 1–18. [Google Scholar]
- Lefebvre, A.H. Airblast atomization. Prog. Energy Combust. Sci. 1980, 6, 233–261. [Google Scholar] [CrossRef]
- Oroian, M. Measurement, prediction and correlation of density, viscosity, surface tension and ultrasonic velocity of different honey types at different temperatures. J. Food Eng. 2013, 119, 167–172. [Google Scholar] [CrossRef]
- Kolaitis, D.; Founti, M. A comparative study of numerical models for Eulerian–Lagrangian simulations of turbulent evaporating sprays. Int. J. Heat Fluid Flow 2006, 27, 424–435. [Google Scholar] [CrossRef]
- Poozesh, S.; Lu, K.; Marsac, P.J. On the particle formation in spray drying process for bio-pharmaceutical applications: Interrogating a new model via computational fluid dynamics. Int. J. Heat Mass Transf. 2018, 122, 863–876. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poozesh, S.; Akafuah, N.K.; Campbell, H.R.; Bashiri, F.; Saito, K. Experimental and Mathematical Tools to Predict Droplet Size and Velocity Distribution for a Two-Fluid Nozzle. Fluids 2020, 5, 231. https://doi.org/10.3390/fluids5040231
Poozesh S, Akafuah NK, Campbell HR, Bashiri F, Saito K. Experimental and Mathematical Tools to Predict Droplet Size and Velocity Distribution for a Two-Fluid Nozzle. Fluids. 2020; 5(4):231. https://doi.org/10.3390/fluids5040231
Chicago/Turabian StylePoozesh, Sadegh, Nelson K. Akafuah, Heather R. Campbell, Faezeh Bashiri, and Kozo Saito. 2020. "Experimental and Mathematical Tools to Predict Droplet Size and Velocity Distribution for a Two-Fluid Nozzle" Fluids 5, no. 4: 231. https://doi.org/10.3390/fluids5040231
APA StylePoozesh, S., Akafuah, N. K., Campbell, H. R., Bashiri, F., & Saito, K. (2020). Experimental and Mathematical Tools to Predict Droplet Size and Velocity Distribution for a Two-Fluid Nozzle. Fluids, 5(4), 231. https://doi.org/10.3390/fluids5040231






