Vertical Round Buoyant Jets and Fountains in a Linearly, Density-Stratified Fluid
Abstract
1. Introduction
2. Dimensional Analysis—Review of Earlier Experiments
- (i)
- A jet-like discharge (B ≈ 0, ρο ≤ ρa) will rise up to an elevation Z = Z(M,N) that is only a function of the initial specific momentum flux M and the buoyancy frequency N, thus leading to a dimensionless elevation,which must be constant.
- (ii)
- A plume (M ≈ 0, ρο ≤ ρa), will rise up to a dimensionless elevation,which must also be constant.
- (iii)
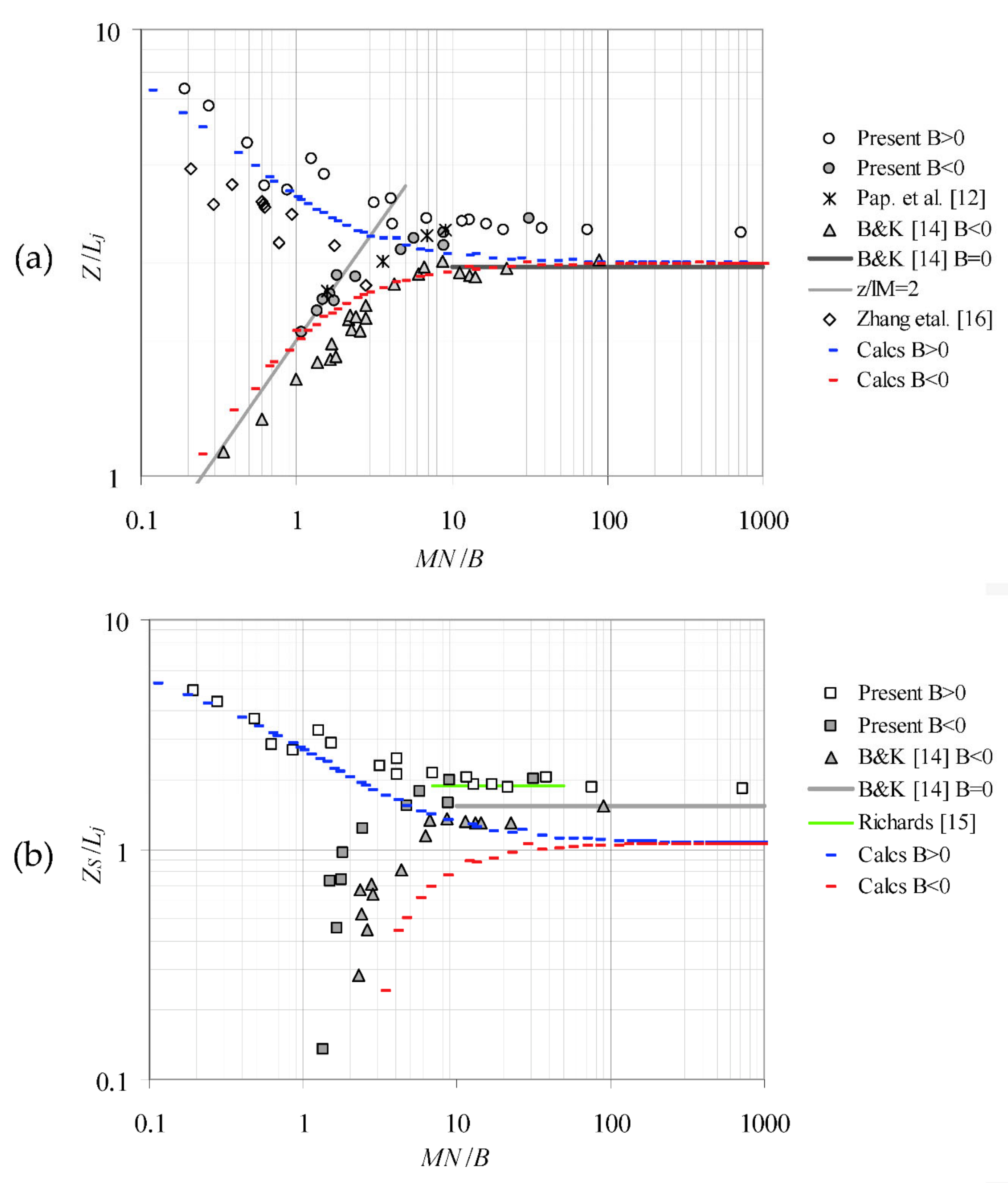
- A buoyant jet with initial kinematic momentum and buoyancy fluxes M and B, respectively, of similar strength that discharges into an ambient fluid with linear density stratification of buoyancy frequency N will rise to an elevation Z that is a function of M, B, and N. Then, the normalized rise height will attain a functional form,where MN/B is a characteristic dimensionless parameter. In asymptotically jet-like flows (M >> B), MN/B >> 1 and Equation (4) is valid, while, in plumes, MN/B < 1 and Equation (5) is valid. If MN/B >> 1, dividing both sides of Equation (4) by Lp obtainsmeaning that the dimensionless jet rise Z/Lp is proportional to (MN/B) 1/4. Similarly, in plumes (MN/B < 1),
- (iv)
- A fountain is the flow when the initial momentum flux is large but the buoyancy flux B is negative (opposite to the direction of motion). In a uniform, calm ambient, the normalized terminal height of rise of a turbulent fountain is constant [21],if the length scale lM = M3/4/|B|1/2 [2,4] is large, or alternatively when the initial jet Richardson number Rio = Q|B1/2|/M5/4 <<1 [21]. For fountains (large lM) in a linearly density-stratified ambient, the asymptotic normalized terminal height of rise Z is a function of M and N only and, therefore, Z/Lj takes a limiting value as shown from Equation (4). Thus, for large values of the parameter MN/|B|, Z/Lj = constant, regardless of the sign of B. Rearranging the terms in Equation (4) gives
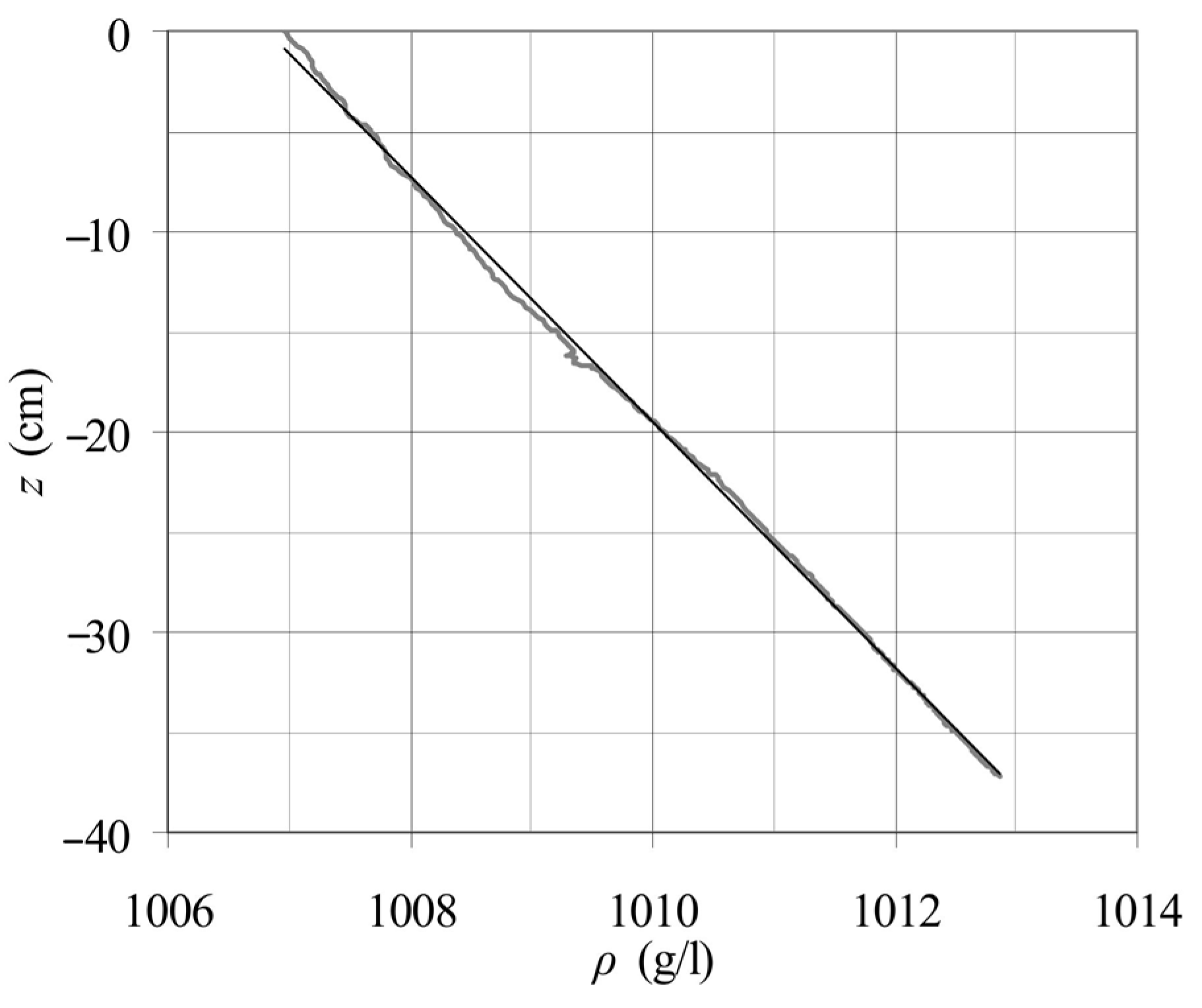
3. Experiments—The Integral Model
4. Results
4.1. Positively Buoyant Jet Experiments
4.2. Negatively Buoyant Jet (Fountain) Experiments
4.3. Numerical Results: THR and SH, Average Dilution
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. The Entrainment of Round Vertical Turbulent Buoyant Jets Re-Revisited
Appendix A.1. Introduction
Appendix A.2. Derivation of Entrainment Coefficient in Round Buoyant Jets
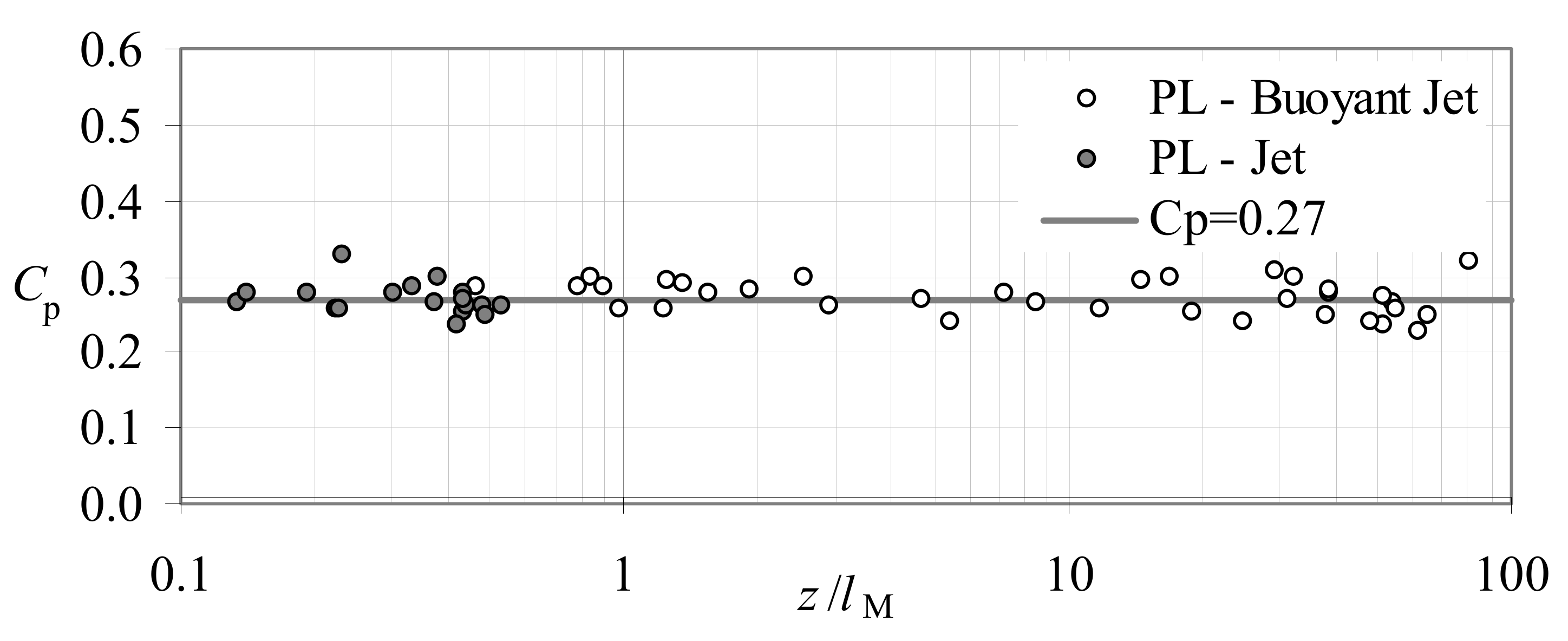
Appendix A.3. Verification of Entrainment Coefficient in Round Buoyant Jets
- (i)
- Momentum flux: When (jet-like flow), Equation (A6) leads to m = M, while, when (plume-like flow), it leads to
- (ii)
- Volume flux: Similarly, when , from Equation (A8), one may obtainwhile, when , from Equation (A8) one may obtain
- (iii)
- Richardson number: In jets (z/lM→0), from Equation (A10), , while, in plumes, (z/lM→∞)
- (iv)
- Entrainment coefficient: In momentum jets (lM→∞), , while, in plumes (z/lM→∞),
| Jet | Plume | Jet | Plume | Jet | Plume | Plume | |
|---|---|---|---|---|---|---|---|
| 0.270 | 1 | 0.345 | 0.270 | 0.159 | 0.076 | 0.127 | 0.600 |
| 0.254 | 1 | 0.331 | 0.254 | 0.146 | 0.072 | 0.119 | 0.582 |
| Fischer et al. [4] | 0.250 | 0.150 | 0.076 | 0.118 | 0.557 | ||
| Papanicolaou and List [30] | 0.290 | 0.250 | 0.140 | 0.077 | 0.124 | 0.630 | |
| Wang and Law [38] | 0.074 | 0.124 | 0.584 |
Appendix A.4. Conclusions
References
- Morton, B.R.; Taylor, G.I.; Turner, J.S. Turbulent gravitational convection from maintained instantaneous sources. Proc. R. Soc. Lond. 1956, A234, 1–23. [Google Scholar]
- Turner, J.S. Jets and plumes with negative or reversing buoyancy. J. Fluid Mech. 1966, 26, 779–792. [Google Scholar] [CrossRef]
- Abraham, G. Jets with negative buoyancy in homogeneous fluid. J. Hydraul.Res. 1967, 5, 235–248. [Google Scholar] [CrossRef]
- Fischer, B.H.; List, J.E.; Koh, R.C.Y.; Imberger, J.; Brooks, N.H. Mixing in Inland and Coastal Waters; Academic Press, Inc.: New York, NY, USA, 1979. [Google Scholar]
- Fan, L.-N. Turbulent Buoyant Jets into Stratified or Flowing Ambient Fluids; Technical Report, KH-R-15; WM Keck Laboratory of WM Keck Laboratory of Hydraulics & Water Resources, California Institute of Technology: Pasadena, CA, USA, 1967. [Google Scholar]
- Fox, D.G. Forced plumes in a stratified fluid. J. Geophys. Res. 1970, 75, 6818–6835. [Google Scholar] [CrossRef]
- Chen, C.J.; Rodi, W. Vertical Turbulent Buoyant Jets—A Review of Experimental Data; Pergamon Press: Oxford, UK, 1980. [Google Scholar]
- Crawford, T.V.; Leonard, A.S. Observations of buoyant plumes in calm stably stratified air. J. Appl. Meteorol. 1962, 1, 251–256. [Google Scholar] [CrossRef]
- Briggs, G.A. Plume Rise; TID 25075; Clearinghouse of Federal Scientific and Technical Information: Springfield, VA, USA, 1969. [Google Scholar]
- Wong, D.R.; Wright, S.J. Submerged turbulent jets in stagnant linearly stratified fluids. J. Hydraul. Res. 1988, 26, 199–223. [Google Scholar] [CrossRef]
- Abraham, G.; Eysink, W.D. Jets issuing into fluid with density gradient. J. Hydraul. Res. 1969, 7, 145–175. [Google Scholar] [CrossRef]
- Papanicolaou, P.N.; Synolakis, C.E.; Hodge, D. The Maximum Height of Rise of Elliptical and Round Buoyant Jets in A Linear Density—Stratified Fluid; School of Engineering, University of Southern California: Los Angeles, CA, USA, 1990. [Google Scholar]
- Konstantinidou, K.; Papanicolaou, P.N. Vertical round and orthogonal buoyant jets in a linear density-stratified fluid. In Proceedings of the 30th IAHR Congress, Thessaloniki, Greece, 24–29 August 2003; Theme C. Volume 1, pp. 293–300. [Google Scholar]
- Bloomfield, L.J.; Kerr, R.C. Turbulent fountains in a stratified fluid. J. Fluid Mech. 1998, 358, 335–356. [Google Scholar] [CrossRef]
- Richards, T.S.; Aubourg, Q.; Sutherland, B.R. Radial intrusions from turbulent plumes in uniform stratification. Phys. Fluids 2014, 26, 036602. [Google Scholar] [CrossRef]
- Zhang, W.; He, Z.; Jiang, H. Scaling for turbulent viscosity of buoyant plumes in stratified fluids: PIV measurement with implications for submarine hydrothermal plume. Deep Sea Res. Part I 2017, 129, 89–98. [Google Scholar] [CrossRef]
- Carazzo, G.; Kaminski, E.; Tait, S. On the rise of turbulent plumes: Quantitative effects of variable entrainment for submarine hydrothermal vents, terrestrial and extra terrestrial explosive volcanism. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Kaminski, E.; Tait, S.; Carazzo, G. Turbulent entrainment in jets with arbitrary buoyancy. J. Fluid Mech. 2005, 526, 361–376. [Google Scholar] [CrossRef]
- Papanicolaou, P.N.; Papakonstantis, I.G.; Christodoulou, G.C. On the entrainment coefficient in negatively buoyant jets. J. Fluid Mech. 2008, 614, 447–470. [Google Scholar] [CrossRef]
- Wood, I.R.; Bell, R.G.; Wilkinson, D.R. Ocean Disposal of Wastewater; World Scientific: Singapore, 1993. [Google Scholar]
- Papanicolaou, P.N.; Kokkalis, T.J. Vertical buoyancy preserving and non-preserving fountains, in a homogeneous calm ambient. Int. J. Heat Mass Transfer 2008, 51, 4109–4120. [Google Scholar] [CrossRef]
- Michas, S.N.; Papanicolaou, P.N. Horizontal round heated jets into calm uniform ambient. Desalination 2009, 248, 803–815. [Google Scholar] [CrossRef]
- Oster, G.; Yamamoto, M. Density gradient techniques. Chem. Rev. 1963, 63, 257–268. [Google Scholar] [CrossRef]
- Papanicolaou, P.N. A piston driven jet for the study of the zone of flow establishment. Exp. Fluids 1994, 17, 287–289. [Google Scholar] [CrossRef]
- Mi, J.; Nobes, D.S.; Nathan, G.J. Influence of jet exit conditions on the passive scalar field of an axisymmetric free jet. J. Fluid Mech. 2001, 432, 91–125. [Google Scholar] [CrossRef]
- Head, M.J. The Use of Miniature 4-Electrode Conductivity Probes for High Resolution Measurements of Turbulent Density or Temperature Variations in Salt Stratified Water Flows. Ph.D. Thesis, University of California San Diego, San Diego, CA, USA, 1983. [Google Scholar]
- Kwon, S.J.; Seo, I.W. Reynolds number effects on the behavior of a non-buoyant round jet. Exp. Fluids 2005, 38, 801–812. [Google Scholar] [CrossRef]
- Stamoulis, G. Vertical Round Positively and Negatively Buoyant Jets in a Linearly Density-Stratified Ambient. Diploma Thesis, University of Thessaly, Department of Civil Engineering, Volos, Greece, 2010. (In Greek). [Google Scholar]
- List, E.J.; Imberger, J. Turbulent entrainment in buoyant jets and plumes. ASCE J. Hyraul. Div. 1973, 99, 1461–1474. [Google Scholar]
- Papanicolaou, P.N.; List, E.J. Investigations of round vertical turbulent buoyant jets. J. Fluid Mech. 1988, 195, 341–391. [Google Scholar] [CrossRef]
- Papakonstantis, E.G.; Christodoulou, G.C.; Papanicolaou, P.N. Inclined negatively buoyant jets 1: Geometrical characteristics. J. Hydraul. Res. 2011, 49, 3–12. [Google Scholar] [CrossRef]
- Bloomfield, L.J.; Kerr, R.C. A theoretical model of a turbulent fountain. J. Fluid Mech. 2000, 424, 197–216. [Google Scholar] [CrossRef]
- Jirka, G.H. Integral model for turbulent buoyant jets in unbounded stratified flows. Part I: Single round jet. Env. Fluid Mech. 2004, 4, 1–56. [Google Scholar] [CrossRef]
- Carazzo, G.; Kaminski, E.; Tate, S. The route to self similarity in turbulent jets and plumes. J. Fluid Mech. 2006, 547, 137–148. [Google Scholar] [CrossRef]
- Priestley, C.H.B.; Ball, F.K. Continuous convection from an isolated sourse of heat. Q.J.R. Met. Soc. 1955, 81, 144–157. [Google Scholar] [CrossRef]
- Papanicolaou, P.N. Analytical solution in vertical buoyant jets. In Proceedings of the 11th HSTAM International Congress on Mechanics, Athens, Greece, 27–30 May 2016. [Google Scholar]
- Papanicolaou, P.N. Mass and Momentum Transport in a Turbulent Buoyant Vertical Axisymmetric Jet. Ph.D. Thesis, W.M. Keck Laboratory of Hydraulics and Water Resources, California Institute of Technology, Pasadena, CA, USA, 1984. Report No. KH-R-46. [Google Scholar]
- Wang, H.; Law, A.W.-K. Second-order integral model for a round turbulent buoyant jet. J. Fluid Mech. 2002, 459, 397–428. [Google Scholar] [CrossRef]

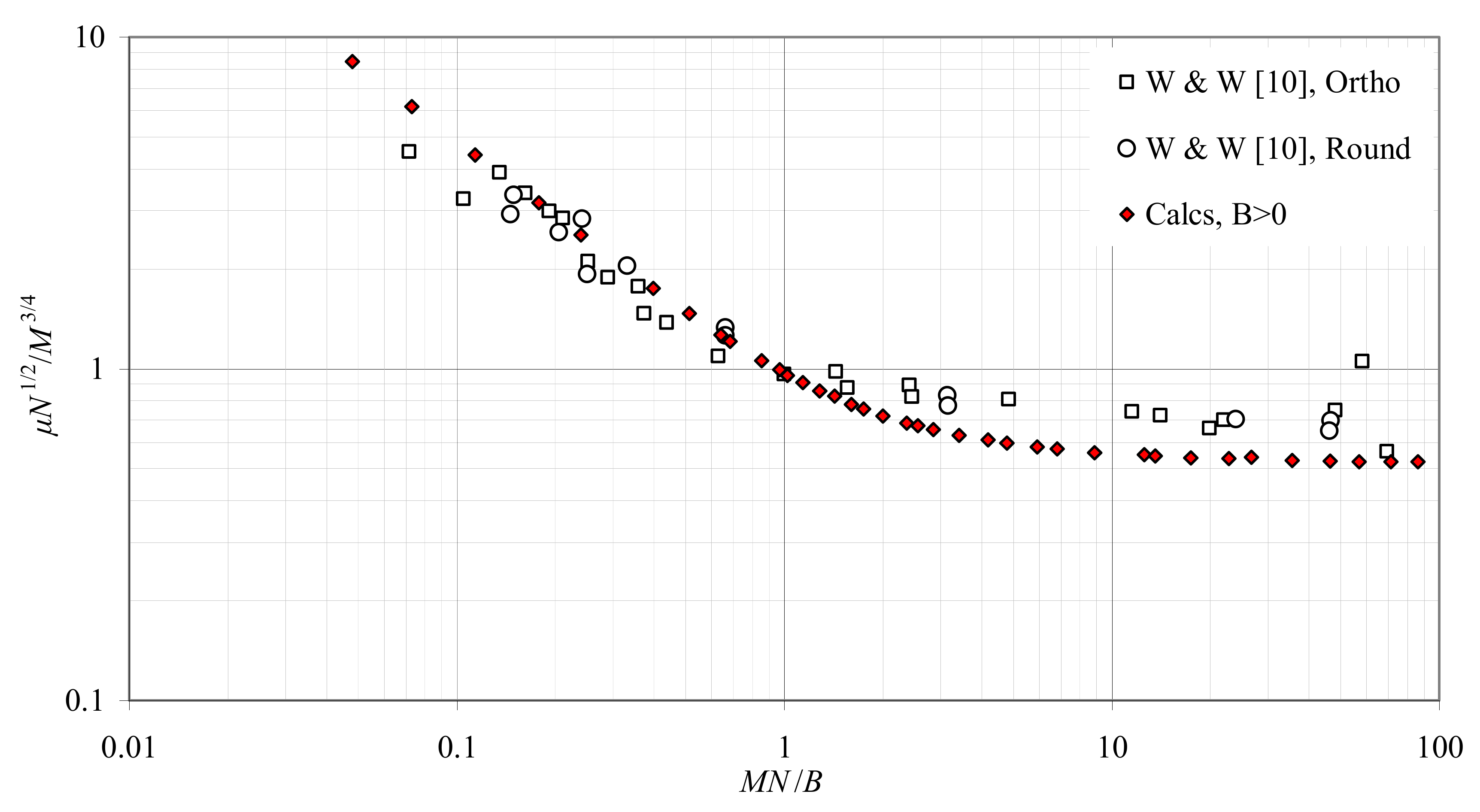
| MN/B >> 1 | ||||
| Jets and fountains | ||||
| MN/B < 1 | ||||
| Plumes | ||||
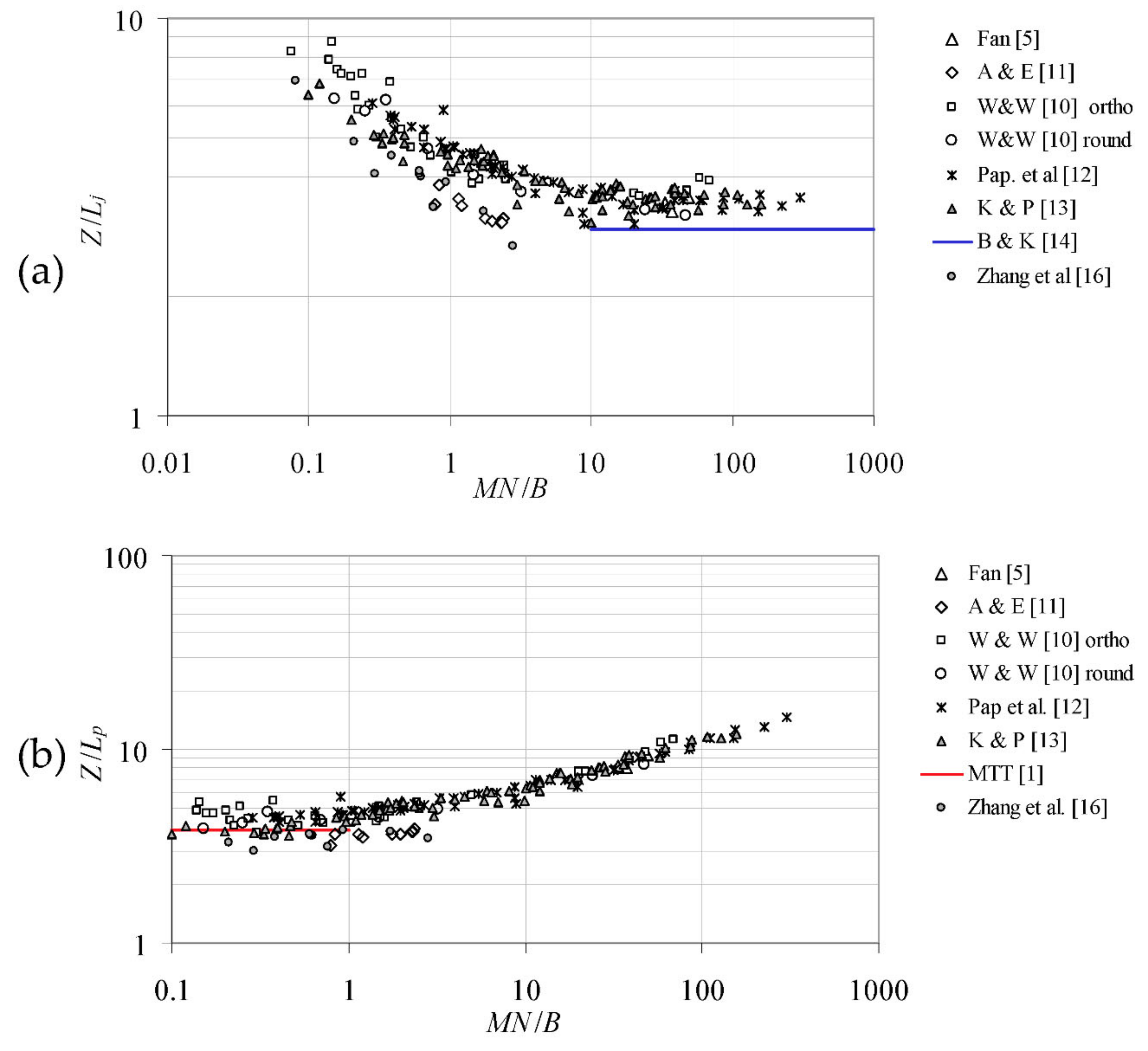
| Author | Z/Lj | ZS/Lj | Z/Lp | ZS/Lp | dj | dp | Comments |
|---|---|---|---|---|---|---|---|
| Morton, Taylor, and Turner [1] 1 | 3.81 ± 0.25 | Plume | |||||
| Fan [5] | 3.41 ± 0.13 | MN/B > 10 | |||||
| Abraham and Eysink [11] | 3.63 ± 0.20 | MN/B = 0.80–2.40 | |||||
| Wong and Wright [10] for rectangular tank | 3.72 ± 0.17 | 4.50 ± 0.46 | 0.77 ± 0.14 | 0.78 ± 0.11 | MN/B > 10 MN/B < 1 | ||
| Wong and Wright [10] for circular tank | 3.23 ± 0.09 | 4.28 ± 0.37 | 0.68 ± 0.03 | 0.84 ± 0.12 | MN/B > 10 MN/B < 1 | ||
| Wong and Wright [10] for all data | 3.60 ± 0.27 | 4.46 ± 0.44 | 0.74 ± 0.12 | 0.81 ± 0.11 | MN/B > 10 MN/B < 1 | ||
| Papanicolaou et al. [12] | 3.46 ± 0.16 | 4.60 ± 0.39 | MN/B > 10 MN/B < 1 | ||||
| Bloomfield and Kerr [14] 1,2 | 3 ± 0.23 (3.15) * | 1.53 ± 0.10 (1.52) * | B = 0 | ||||
| Bloomfield and Kerr [14] 1,3 | 2.88 ± 0.10 | 1.35 ± 0.11 | B < 0 | ||||
| Konstantinidou and Papanicolaou [13] | 3.55 ± 0.16 | 2.38 ± 0.39 | 3.97 ± 0.29 | 2.99 ± 0.29 | MN/B > 10 MN/B < 1 | ||
| Richards et al. [15] | 1.50 (1.89) * | 2.7 (2.78) * | MN/B = 0.4 ÷ 46 | ||||
| Zhang et al. [16] | 3.47 ± 0.26 | MN/B < 2.80 | |||||
| Fischer et al. [4] | 3.80 | 3.80 | Proposed values | ||||
| Chen and Rodi [7] | 3.80 | 5.00 | Proposed values |
| Run | D | Q | ρa | ρο | N2 | Re | Ro | Z | ZS |
|---|---|---|---|---|---|---|---|---|---|
| (cm) | (cm3/s) | (gr/cm3) | (gr/cm3) | (s−2) | (cm) | (cm) | |||
| Positively buoyant jets | |||||||||
| Exp-1 | 1.00 | 51.26 | 1.0073 | 1.0092 | 0.1303 | 7120 | 0.020 | 47.3 | 24.2 |
| Exp-3 | 1.00 | 30.25 | 1.0066 | 1.0066 | 0.1350 | 4304 | 0.003 | 33.9 | 17.7 |
| Exp-4 | 1.00 | 21.25 | 1.0069 | 1.0100 | 0.1302 | 3023 | 0.061 | 33.3 | 18.8 |
| Exp-5 | 0.50 | 15.24 | 1.0057 | 1.0062 | 0.1541 | 4338 | 0.005 | 33.3 | 17.4 |
| Exp-10 | 1.50 | 25.75 | 1.0083 | 1.0140 | 0.1074 | 2055 | 0.185 | 33.7 | 20.7 |
| Exp-14 | 0.75 | 27.25 | 1.0070 | 1.0091 | 0.1584 | 4240 | 0.019 | 37.8 | 20.8 |
| Exp-15 | 0.50 | 28.75 | 1.0075 | 1.0100 | 0.1276 | 7238 | 0.007 | 47.8 | 25.1 |
| Exp-16 | 0.50 | 28.75 | 1.0073 | 1.0087 | 0.1269 | 6711 | 0.005 | 48.2 | 27.7 |
| Exp-20 | 1.50 | 21.25 | 1.0045 | 1.0142 | 0.1454 | 2063 | 0.294 | 36.0 | 23.9 |
| Exp-21 | 1.50 | 19.75 | 1.0031 | 1.0150 | 0.0809 | 1918 | 0.350 | 48.6 | 31.4 |
| Exp-22 | 1.50 | 19.75 | 1.0028 | 1.0188 | 0.0705 | 1873 | 0.405 | 55.1 | 36.6 |
| Exp-23 | 1.00 | 24.25 | 1.0032 | 1.0101 | 0.0745 | 3450 | 0.079 | 51.5 | 33.0 |
| Exp-24 | 1.00 | 24.25 | 1.0070 | 1.0100 | 0.1505 | 3450 | 0.052 | 35.1 | 20.7 |
| Exp-25 | 1.50 | 28.75 | 1.0076 | 1.0119 | 0.1520 | 2727 | 0.145 | 35.2 | 21.5 |
| Exp-26 | 1.00 | 33.25 | 1.0059 | 1.0095 | 0.1176 | 4731 | 0.042 | 38.2 | 22.2 |
| Exp-27 | 1.00 | 25.75 | 1.0065 | 1.0084 | 0.1473 | 3406 | 0.039 | 32.8 | 18.7 |
| Exp-28 | 1.50 | 27.25 | 1.0063 | 1.0151 | 0.1196 | 2403 | 0.218 | 34.4 | 22.0 |
| Exp-29 | 1.00 | 36.25 | 1.0049 | 1.0060 | 0.1545 | 4679 | 0.021 | 37.3 | 19.4 |
| Fountains | |||||||||
| Exp-2 | 1.00 | 36.25 | 1.0066 | 1.0060 | 0.1492 | 5036 | 0.015 | 38.9 | 20.7 |
| Exp-6 | 0.50 | 21.25 | 1.0071 | 1.0032 | 0.0978 | 6046 | 0.012 | 43.3 | 24.8 |
| Exp-7 | 0.50 | 30.25 | 1.0065 | 0.9969 | 0.1226 | 8710 | 0.013 | 47.6 | 24.8 |
| Exp-8 | 0.75 | 30.25 | 1.0081 | 0.9969 | 0.0584 | 5807 | 0.040 | 34.0 | 10.0 |
| Exp-9 | 1.00 | 36.25 | 1.0089 | 0.9986 | 0.1604 | 4340 | 0.065 | 28.4 | 9.8 |
| Exp-11 | 1.00 | 36.25 | 1.0074 | 1.0054 | 0.1377 | 4340 | 0.028 | 34.3 | 16.7 |
| Exp-12 | 0.75 | 28.15 | 1.0095 | 0.9986 | 0.1634 | 4493 | 0.042 | 28.5 | 12.5 |
| Exp-13 | 0.50 | 27.25 | 1.0098 | 0.9988 | 0.1352 | 6361 | 0.016 | 41.4 | 20.0 |
| Exp-17 | 1.00 | 27.25 | 1.0105 | 0.9988 | 0.1297 | 3180 | 0.092 | 19.4 | 0.3 |
| Exp-18 | 1.00 | 26.65 | 1.0098 | 1.0015 | 0.1565 | 3526 | 0.079 | 22.3 | 4.0 |
| Exp-19 | 1.00 | 21.25 | 1.0058 | 0.9975 | 0.1662 | 2881 | 0.099 | 17.9 | 1.0 |
| Exp-30 | 1.00 | 30.25 | 1.0049 | 0.9978 | 0.1041 | 4002 | 0.065 | 25.3 | 7.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papanicolaou, P.N.; Stamoulis, G.C. Vertical Round Buoyant Jets and Fountains in a Linearly, Density-Stratified Fluid. Fluids 2020, 5, 232. https://doi.org/10.3390/fluids5040232
Papanicolaou PN, Stamoulis GC. Vertical Round Buoyant Jets and Fountains in a Linearly, Density-Stratified Fluid. Fluids. 2020; 5(4):232. https://doi.org/10.3390/fluids5040232
Chicago/Turabian StylePapanicolaou, Panos N., and George C. Stamoulis. 2020. "Vertical Round Buoyant Jets and Fountains in a Linearly, Density-Stratified Fluid" Fluids 5, no. 4: 232. https://doi.org/10.3390/fluids5040232
APA StylePapanicolaou, P. N., & Stamoulis, G. C. (2020). Vertical Round Buoyant Jets and Fountains in a Linearly, Density-Stratified Fluid. Fluids, 5(4), 232. https://doi.org/10.3390/fluids5040232




