Abstract
During boiling at a solid surface, it is often the case that a liquid layer of a few microns of thickness (’microlayer’) is formed beneath a bubble growing on the heated surface. Microlayers have been observed forming beneath bubbles in various transparent fluids, such as water and refrigerants, subsequently depleting due to evaporation, thus contributing significantly to bubble growth and possibly generating the majority of vapor in a bubble. On the other hand, boiling of opaque fluids, such as liquid metals, is not amenable to optical observations, and microlayers have not yet been observed in liquid metals. Among that class of fluids is sodium, suitable as a coolant for nuclear reactors and as the working fluid in phase-change solar power receivers. In order to support these applications, it is necessary to understand the boiling behavior of sodium and identify the parameters that might influence microlayer formation during boiling of this important fluid. This paper presents simulations of the hydrodynamics of sodium vapor bubble growth at a surface. An interface capturing flow solver has been implemented in the OpenFOAM code and used to predict the behavior of a sodium vapor bubble near a solid surface in typical boiling conditions. The methodology has been validated using recently reported direct experimental observations of microlayer formation in water and then applied to sodium boiling cases. Simulations indicate that microlayers are formed in sodium in a similar fashion to water. Comparison of simulation results with an extant algebraic model of microlayer formation showed good agreement, which increases confidence in the current predictions of microlayer formation. Typical values of microlayer thickness thus computed indicate that the microlayer is likely to play an important role during bubble growth in sodium.
1. Introduction
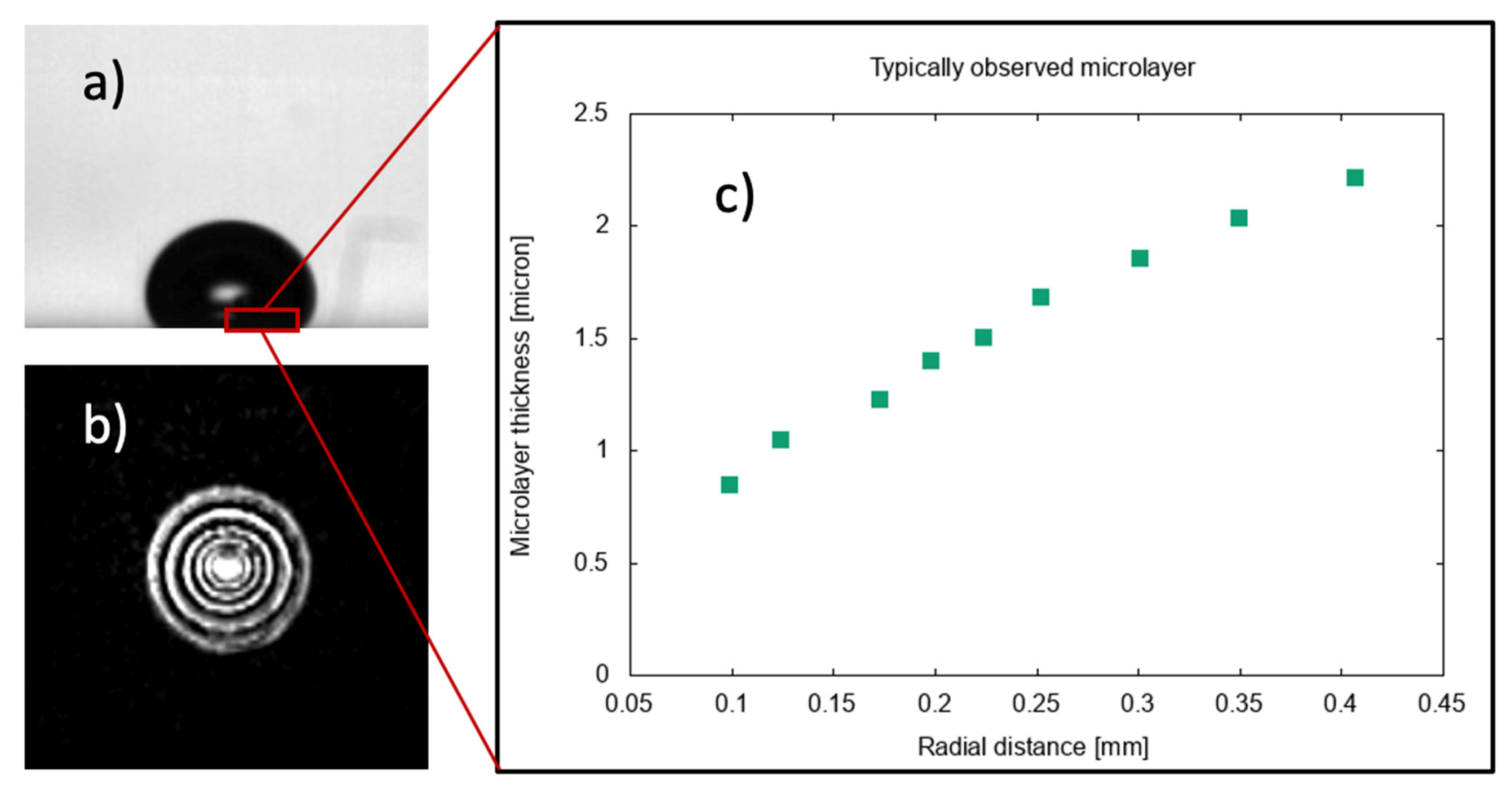
As a vapor bubble grows on a heated surface, a very thin layer of liquid is typically observed to form [1] beneath the bubble. This ‘microlayer’, initially of a few microns in thickness, gradually disappears due to evaporation [2], thus contributing to the generation of vapor in a growing bubble. The typical shape of a steam bubble and of the liquid film formed at its base during the early stages of growth at a solid surface is shown in Figure 1, where typical interferometric measurements [3], used to detect the presence of a microlayer beneath the bubble, are reproduced.
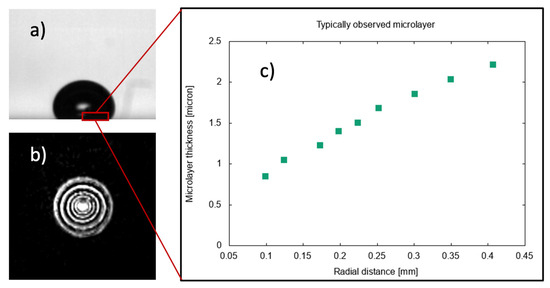
Figure 1.
Observations of the microlayer in boiling at a surface. (a) Typical bubble shape during the early stages of growth. (b) Interferometric measurements of phase distribution on the solid surface used to detect the presence of a liquid film. (c) Measured microlayer thickness as a function of radial distance from the center of the bubble base. Data [1] for pool boiling of water in atmospheric conditions at 10 K of wall superheat.
There is no consensus on what the physical processes are that limit the rate of depletion [2,4,5,6,7,8] and, thus, the microlayer’s contribution to a bubble’s growth rate (i.e., how rapidly a bubble expands); nevertheless, it is commonly accepted that evaporation of liquid trapped in the microlayer contributes significantly [9] to bubble formation, perhaps up to 50–70% of the bubble volume [10]. As boiling heat transfer rates depend strongly on latent heat transfer associated with bubble formation [11], it is crucial to be able to estimate the likely contribution of microlayer evaporation to generating the vapor in a bubble and the amount of liquid, i.e., the layer thickness, that is initially trapped in a microlayer when it forms during the initial stages of bubble growth. While there are now sufficient experimental data [1,2,7] and simulation results [5,6,12,13] confirming typical values of initial thicknesses and depletion rates of microlayers in the boiling of water and refrigerants, knowledge of microlayers in the boiling of liquid metals, such as sodium, is non-existent. Sodium is widely used in industrial applications as a coolant, likely to undergo boiling, in fast spectrum nuclear reactors [14] and in phase-change solar power receivers [15]. In the microlayer, hydrodynamics and heat transfer determine, to a large extent, boiling heat transfer rates; an understanding of the relative magnitudes of heat transfer rates in the case of a sodium coolant is desirable for design purposes. It is, therefore, important to understand the boiling behavior of sodium and ascertain if bubble growth at a surface during sodium boiling is characterized by the formation of a microlayer on the heated surface. In this paper, numerical simulation is used to study the hydrodynamics of sodium vapor bubble growth at a surface and to determine what are the parameters that influence microlayer formation in nucleate boiling of sodium. Compared to other fluids, such as boiling water, for which there are experimental observations of microlayer formation, differences in microlayer behavior are expected due to markedly different fluid properties, as detailed herein.
The current paper is structured as follows. Section 2 presents an overview of the current understanding of microlayer behavior, derived from experimental observations of bubble growth during nucleate boiling of water and refrigerants. Section 3 presents an overview of the interface-capturing simulation methodology used to simulate the hydrodynamics of bubble growth at a surface and its validation, using direct measurements of microlayer thicknesses in boiling water. As noted, there are no reported micro-scale observations of bubble or microlayer formation in sodium, and validation with water boiling data increases our confidence in applying the current methodology to model the as yet unknown microlayer behavior in sodium boiling. Application of interface-capturing simulations to bubble growth in sodium boiling is presented in Section 4, where differences in bubble behavior and microlayer thickness for different values of simulation input parameters are explored. Comparisons between the current simulation results and predictions of an extant analytical model of microlayer formation [12] are presented in Section 5, showing good agreement between predictions of the analytical model and of the current simulation methodology. Conclusions follow in Section 6.
2. Our Current Understanding of the Microlayer
In the early stages of bubble formation at a wall, the bubble’s curved surface experiences significant fluid reaction forces due to the initially quick expansion of the bubble [16] (of order 1 m/s for low-pressure boiling of water at a few degrees of superheat). Such reaction forces are cause of the approximately hemispherical bubble shape that is characteristically observed in the early stages of bubble growth. During hemispherical bubble expansion, the contact line at the bubble base typically remains ‘pinned’ and a liquid microlayer is observed to be left behind on the surface as the bubble expands.
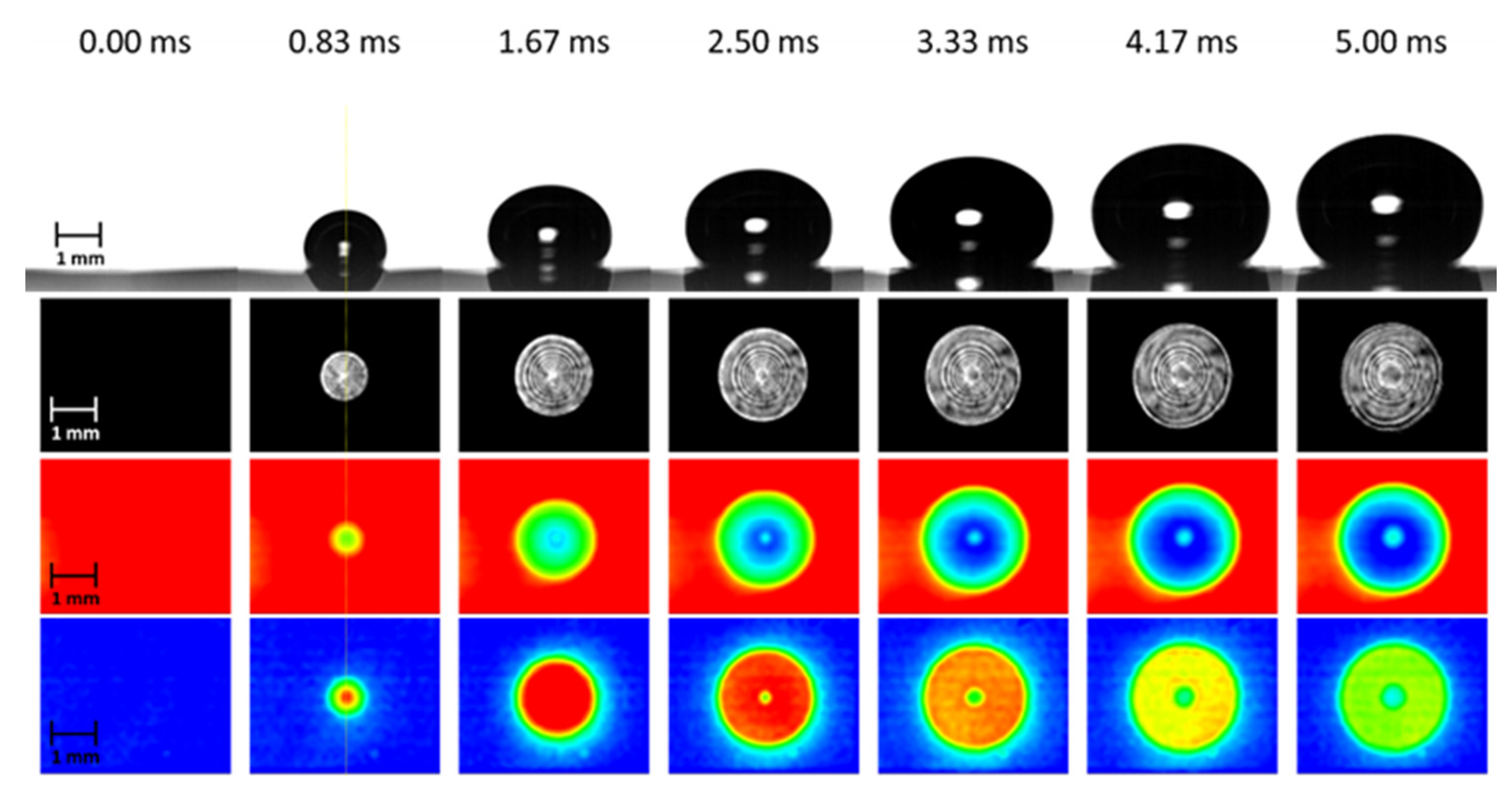
Our current understanding of microlayer behavior has been inferred mainly from experimental observations of single-bubble growth during nucleate pool boiling on a horizontal solid surface. In what is perhaps the most comprehensive set of measurements of bubble formation, Jung et al. [1] were able to detect the presence of the liquid phase in contact with a solid surface beneath steam bubbles growing in water at atmospheric pressure. For a comprehensive optical study of microlayer characteristics associated with a single boiling bubble in a pool of liquid, Jung et al. [1] used a unique combination of heater and substrate materials—an indium-tin-oxide thin-film heater (transparent to visible light but opaque to infrared light) coated on a CaF2 substrate (transparent to both visible and infrared light). Using a He-Ne laser as a light source for an integrated optical technique of total internal reflection and thin film interferometry, they were able to simultaneously observe the liquid–vapor phase distribution beneath a growing steam bubble and the fringe pattern of the wedge-shaped microlayer existing on the liquid phase, as well as typical bubble growth images captured from the side, as shown in Figure 2. Complementary sequential measurements of the temperature distribution at the solid–fluid interface beneath the bubble indicated substantial cooling of the surface due to evaporation of the microlayer, as indicated by the temperature and wall heat flux distribution measurements reproduced, in Figure 2, from Jung et al’s work [3].
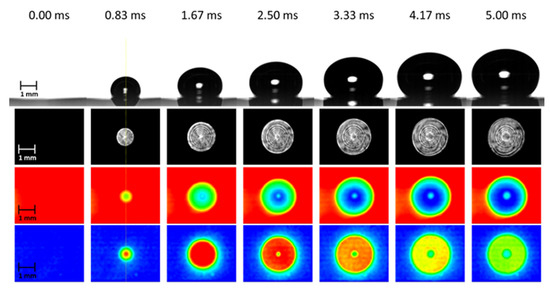
Figure 2.
Complementary observations of the early stages of bubble growth at a solid surface [3]. From top to bottom: bubble side view, phase distribution on the heated surface, temperature distribution at the solid surface, and surface normal heat flux distribution derived from the temperature distribution.
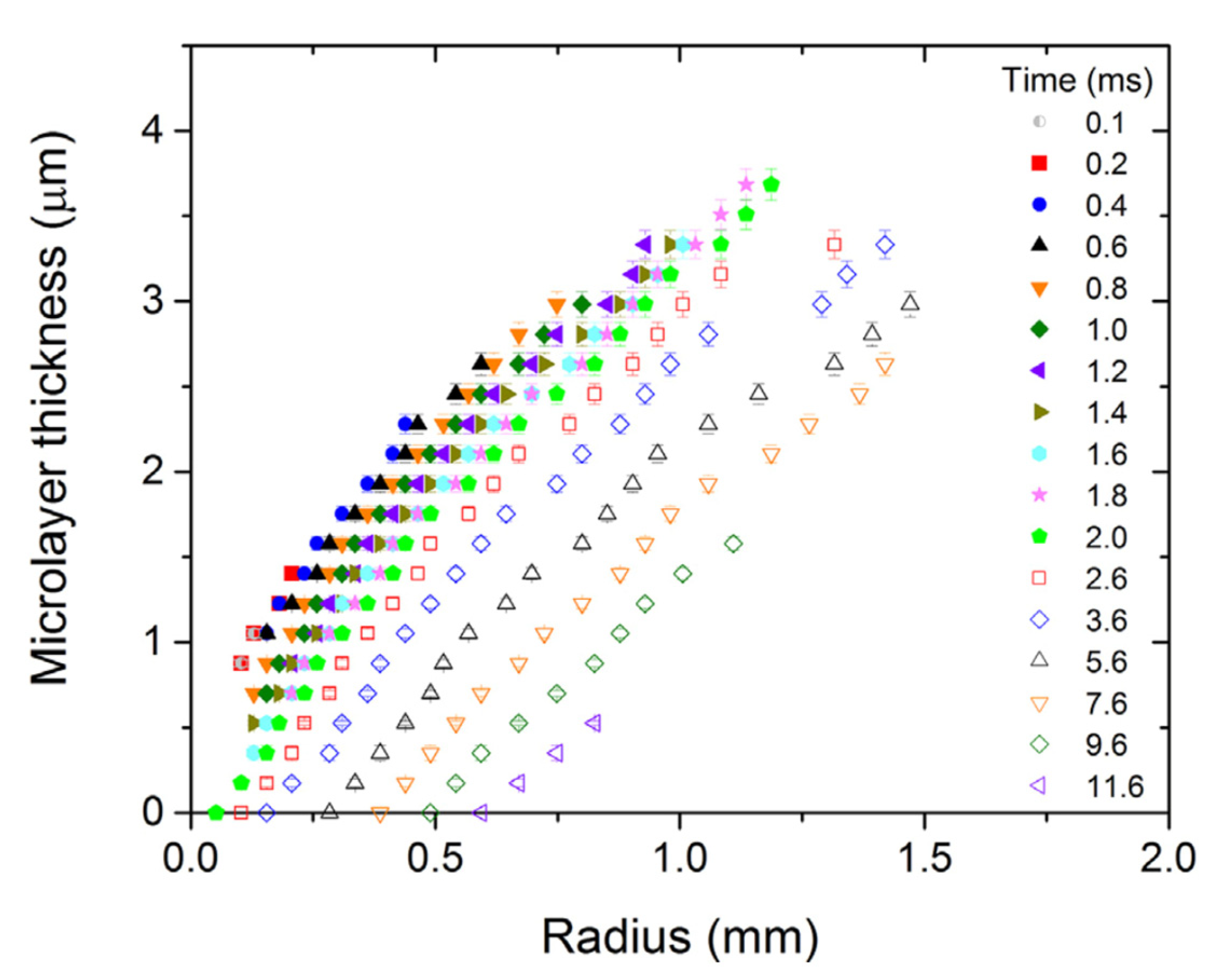
Figure 3 shows a sequence of measurements of the radial distribution of film thickness beneath a bubble, indicating the progressive retreat of the film due to evaporation. The initial thickness of the microlayer is representative of the amount of liquid that may subsequently contribute to the generation of vapor in a bubble. It is, thus, important to be able to reliably predict the hydrodynamics of microlayer formation and likely values of the layer thickness [12] as it is formed on the solid surface. For water boiling at atmospheric pressure, interface-capturing simulation has been demonstrated to be a powerful tool to model the hydrodynamics of bubble growth [13] and determine the likely initial thickness of the microlayer as formed on the surface. The methodology applied here to model such a process during sodium bubble growth is outlined in the following section.
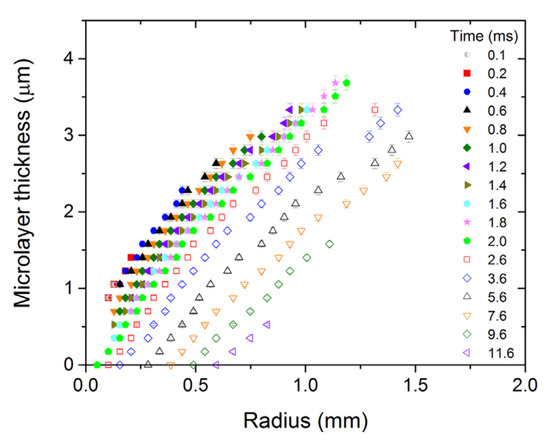
Figure 3.
Sequential measurements of the radial distribution of microlayer thickness, adapted from Ref [1].
3. Simulation MethodologyS
3.1. Interface-Capturing Model
For all simulations presented in this work, the volume of fluid (VOF) method [17] was used for tracking the location of the liquid–vapor interface, and the PISO method [18,19] was used to solve for the velocity and pressure fields. The current simulation methodology has been implemented via modification of the interFoam solver embedded in the open-source library OpenFOAM version 2.4 [20]. Bubble expansion is driven by mass transfer, which is computed from theory and imposed locally at the vapor-liquid interface.
The current set of simulations aims to explore the hydrodynamic behavior of a bubble as it grows while attached to a solid surface in order to study microlayer formation at the base of the bubble. In boiling conditions, bubble growth is driven by mass transfer from the liquid to the vapor. Analytical expressions for bubble growth rates and for the rate of mass transfer computed from theory [21] are applicable to arbitrary fluids, including transparent fluids, such as water, and opaque fluids, such as sodium. The expressions detailed herein have been used in order to ‘grow’ a bubble with the present interface-capturing model rather than model the actual evaporation process. Thus, mass transfer is not computed as part of the model (as, for example, in some other interface-capturing approaches [6]), rather it is imposed a priori at the bubble surface. As the imposed mass transfer is computed from analytical solutions available for bubble growth, the current methodology does not employ an energy transport equation or a mechanistic mass transfer model. The current simulations are, in that respect, ‘hydrodynamics only’ [5,12,13], in that only fluid flow is modelled by the current approach.
The mass transfer source term was modelled following the well-established method of Hardt et al. [22]. The equations solved by the modified interFoam solver are:
In the VOF model, any fluid property, say, the density , varies with the volume fraction of liquid as , where the subscripts l and v indicate the liquid and vapor phases, respectively. In the above equations, is the fluid velocity, is the deviatoric stress tensor (computed for laminar flow of a Newtonian fluid with constant viscosity), p is the pressure, and f is the body force, including gravity and surface tension forces. The latter, including wall adhesion in the near-wall cells, is computed with the well-established continuum surface force method of [23].
The volumetric rate of mass transfer was computed from the theoretical rate of mass transfer as
and redistributed around the interfacial region using the method of [22] in order to compute the source term used in the continuity equation (2) and in the interface advection equation (3). Here, is the rate of mass transfer computed locally at the interface and is the rate of mass transfer redistributed using the method of [22]. Details of the method have been described elsewhere [24,25] and will not be reproduced here.
In all simulations presented in this work, two velocity-correction steps were used in the PISO procedure. Time steps were adjusted dynamically during the simulation based on the predicted flow behavior. Theoretically, time step values may be dictated by both the capillary constraint [26], , and by the Courant–Friedrichs–Lewy (CFL) condition, , where is the surface tension coefficient, is the cell size and is the velocity magnitude, and and are coefficients normally smaller than unity to ensure stability. The VOF solver used for the current simulations, described in Refs [27,28], updates the time step dynamically based on the CFL condition and taking as the maximum velocity magnitude in the region where the interface is contained, corresponding to . A value of was used for all simulations in this work, corresponding to typical values of the time step of order .
3.2. Simulation Setup
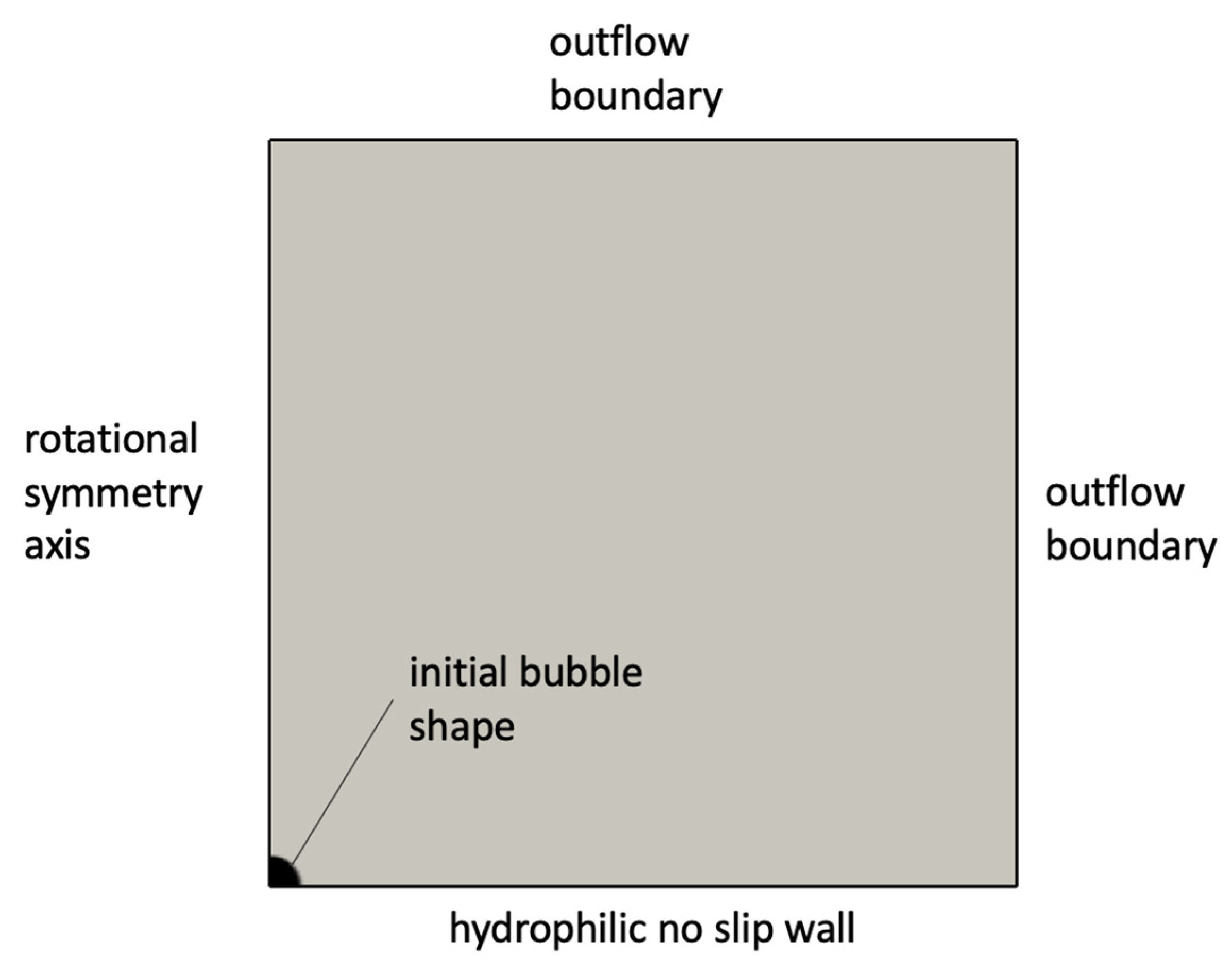
The simulation setup consisted of a rotationally symmetric domain with a no-slip wall boundary at the bottom and open boundaries elsewhere, as indicated in Figure 4. Domain dimensions were 900 × 900 microns in the radial and vertical directions. In order to resolve the likely micrometric thickness of the microlayer, the grid was refined close to the wall boundary. A contact angle of zero degrees was imposed at the wall in order to cause pinning of the triple contact line and formation of the microlayer. For simplicity, the bubble was initialized with an initially hemispherical shape, corresponding to a hemisphere with its base (vapor) completely in contact with the wall; the bubble shape was then free to adjust itself depending on the predicted flow behavior and on the value of the contact angle imposed at the wall. As indicated in Figure 5, the imposed volumetric mass transfer rate was set to zero in a region near the wall where the microlayer was likely to form. The height of the region was set equal to 5 microns for all simulations presented in this work; the microlayer behavior was observed to be independent from the different values that were tested of the height of the region with zero imposed rate of mass transfer.
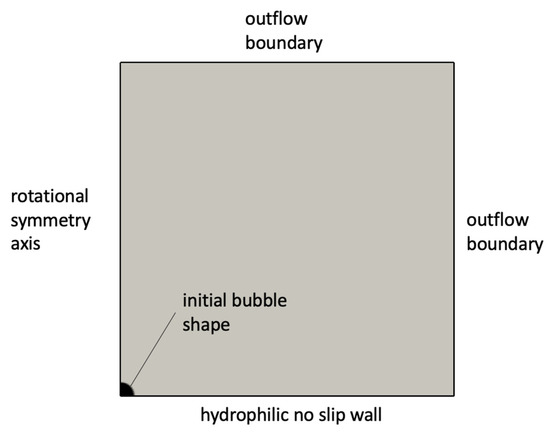
Figure 4.
Setup of microlayer formation simulations.
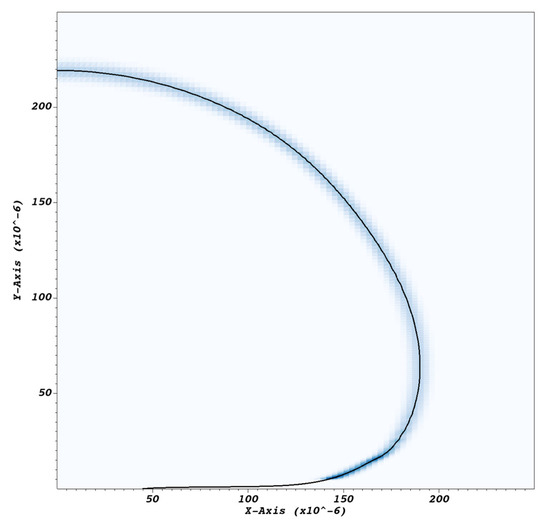
Figure 5.
Visualization of indicative distribution of the volumetric rate of mass transfer imposed at the bubble curved surface in order to mimic bubble growth due to evaporation. The black line represents the vapor–liquid interface; the shaded region indicates where mass transfer is imposed.
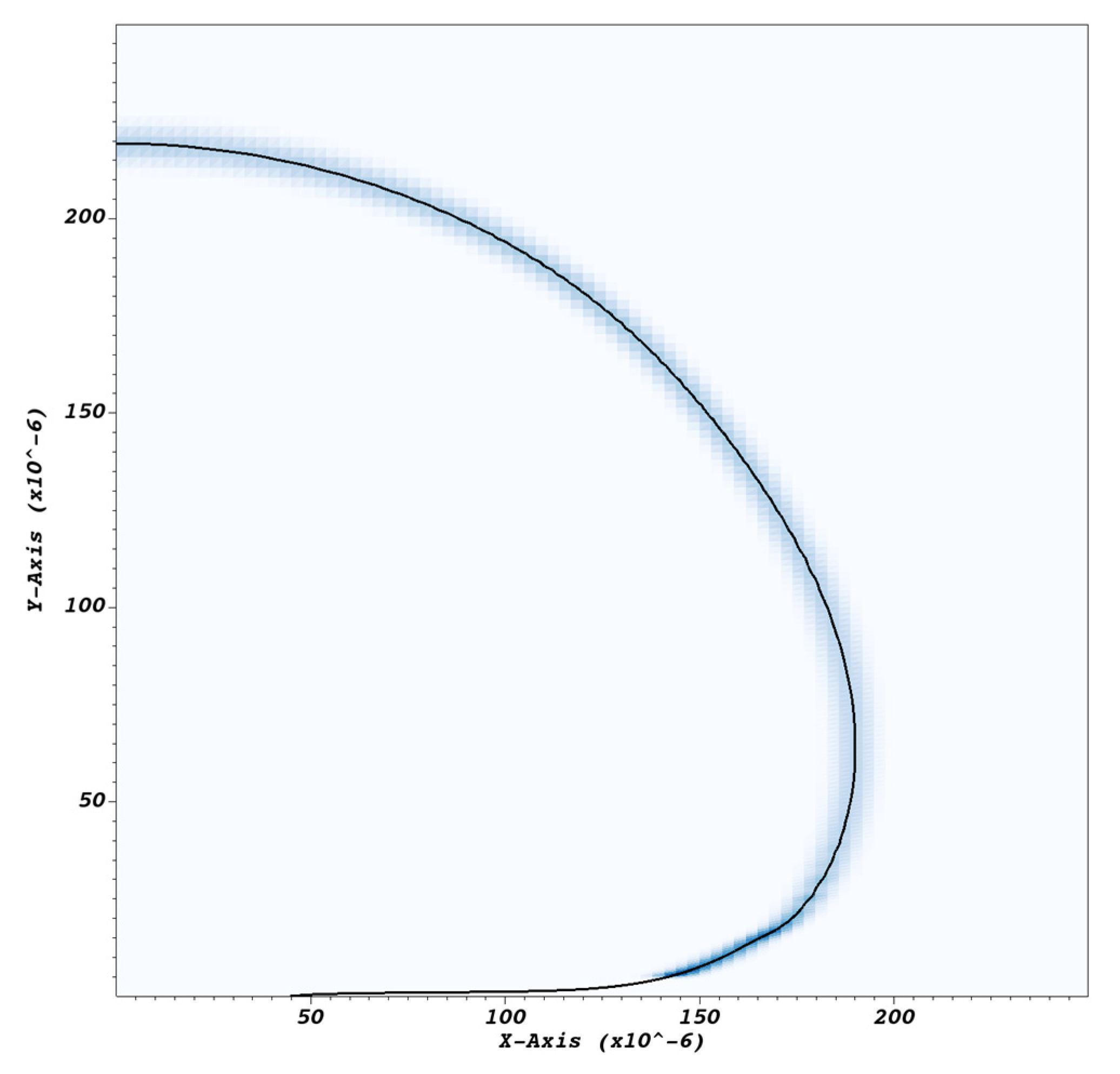
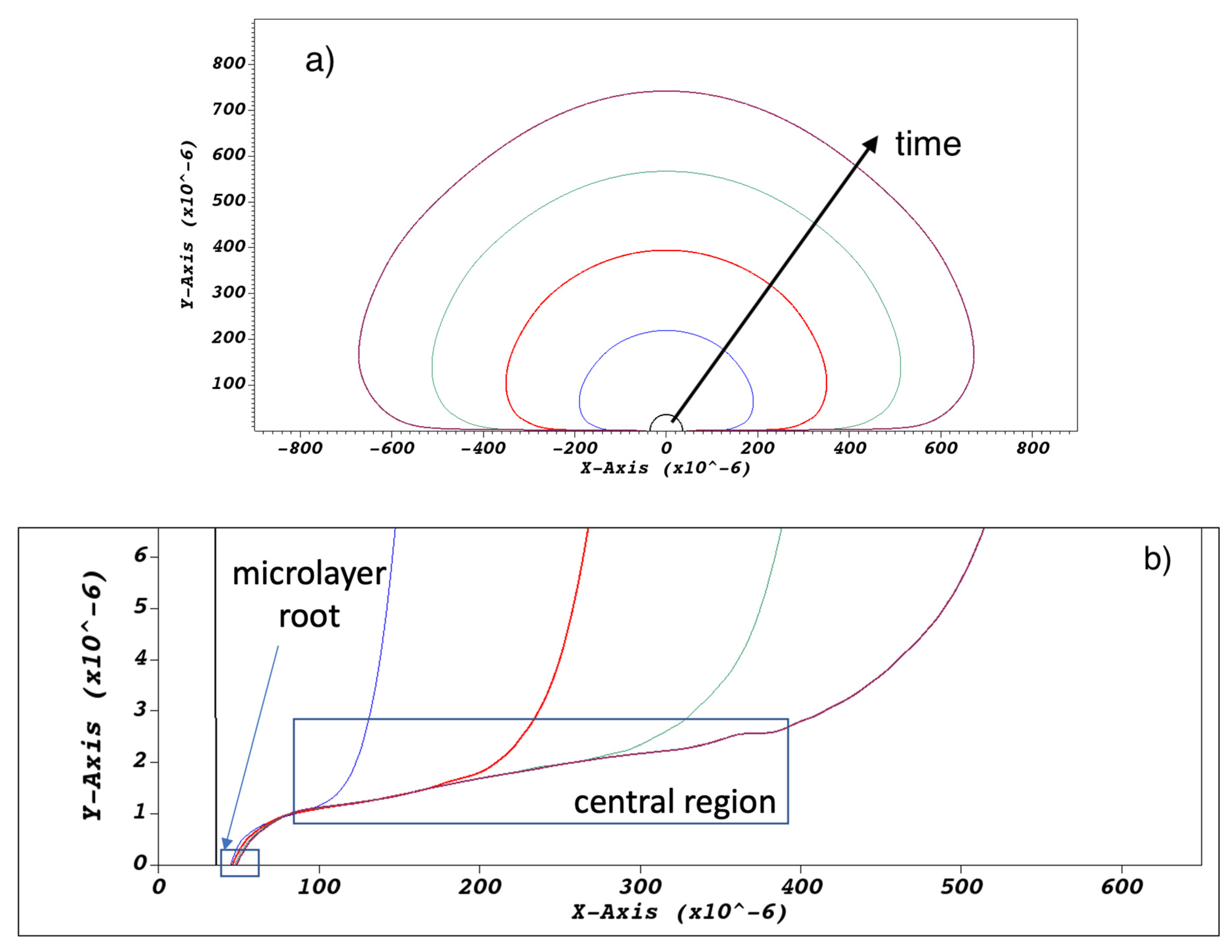
Typical bubble and microlayer shapes obtained with the current simulation methodology are shown in Figure 6a. Pinning of the triple contact line and microlayer formation at the bubble ‘root’, shown in Figure 6b, was enforced using a zero contact angle condition at the wall; as the focus of the current paper is on the behavior of the microlayer ‘central region’, also indicated in Figure 6b, an exploration of predictions of the current model for different values of the imposed contact angle is deferred to a future study. The bubble ‘root’ can be broadly defined as the microlayer region where the layer’s shape is affected by wall-adhesion forces localized at the triple contact line. Conversely, the ‘central region’ can be defined as the region where the shape of the microlayer is unaffected by the behavior of the triple contact line. At the outer edge of the central region, the slope of the microlayer changes as the vapor–liquid interface transitions to a hemispherical shape typical of the bubble curved surface at a distance from the wall. The spatial bounds of these regions vary depending on conditions and time into the simulation, and the distinction is meaningful only from a qualitative point of view.
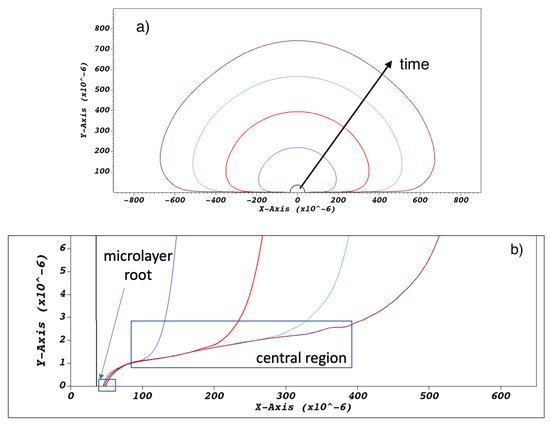
Figure 6.
(a) Typical modelled bubble shapes at a sequence of times, namely at t = 0 and at 0.05, 0.1, 0.15, and 0.2 ms into bubble growth. Magnification (b) of the near-wall region shows the microlayer being left behind on the no-slip wall boundary.
3.3. Model Validation Using Water Boiling Data
There are no micro-scale measurements of single bubble growth or microlayer formation in sodium reported so far, a lack that is, indeed, the main driver for the current investigation. Prior to applying the current model to bubble growth in sodium, predictions of the model were checked using data for water boiling. The test case chosen for validation is that of Ref [1], where data for microlayer formation during pool boiling of water at atmospheric pressure are presented. In the Ref [1] experiments, the fluid superheat (excess temperature above the saturation value) at bubble inception was approximately 10 K, a value that is representative of typical pool boiling laboratory conditions. Hydrodynamic simulation of microlayer formation requires knowledge of the growth rate of a bubble, which can be computed if the fluid superheat is known. According to the theory [21], two regimes of bubble growth can be identified as follows. In the ealy stages, the growth of a bubble is limited by the inertia of the surrounding liquid; hence, the bubble radius can be computed as a function of time as
where the growth rate A depends on fluid properties and temperature and is computed as
where is the latent heat of vaporization, is the saturation temperature at the prevailing system pressure, and is the fluid superheat. For water in typical atmoshperic pressure conditions, such an initial ‘inertial’ growth regime is short lived; in conditions of interest, the theory [29] indicates that it lasts approximately 22 . Later on, the bubble growth rate is limited by the diffusion of heat from superheated liquid to the bubble surface.
In the Ref [1] experiments, the superheat at bubble inception was approximately 10 K and, except for the above-noted short-lived inertial transient, bubble growth was observed at a rate typical of the heat diffusion controlled regime [21], for which the bubble radius increases with the square root of time:
where the growth factor depends [16] on fluid properties and superheat and is the liquid thermal diffusivity, with k being the thermal conductivity and c the specific heat capacity. The corresponding mass transfer rate at the bubble curved surface, used as an input for the hydrodynamic simulation, is computed using the heat diffusion-controlled bubble growth model as
The properties of water used for evaluation of the mass transfer rate are listed in Table 1. At a superheat of 10 K, the value of the growth constant is 30.5 [16]. The simulation was started with an intial bubble radius of 80 microns, which is the likely value of the bubble radius shortly after the early inertial growth transient.

Table 1.
Properties of saturated water at 373.15K and 1 bar.
For comparison between modelled and measured microlayer thicknesses, it is necessary to ensure that experimental data are suitable for comparison with a hydrodynamics-only simulation that does not account for depletion of the liquid film due to evaporation and is, therefore, applicable only to the early stages of bubble growth, during which no significant evaporation of the microlayer occurs. Therefore, only data on early bubble growth, collected at a time interval of 0.2 ms from bubble inception, during which the film depletion rate is zero, have been retained from Ref [1] for comparison with the current model.
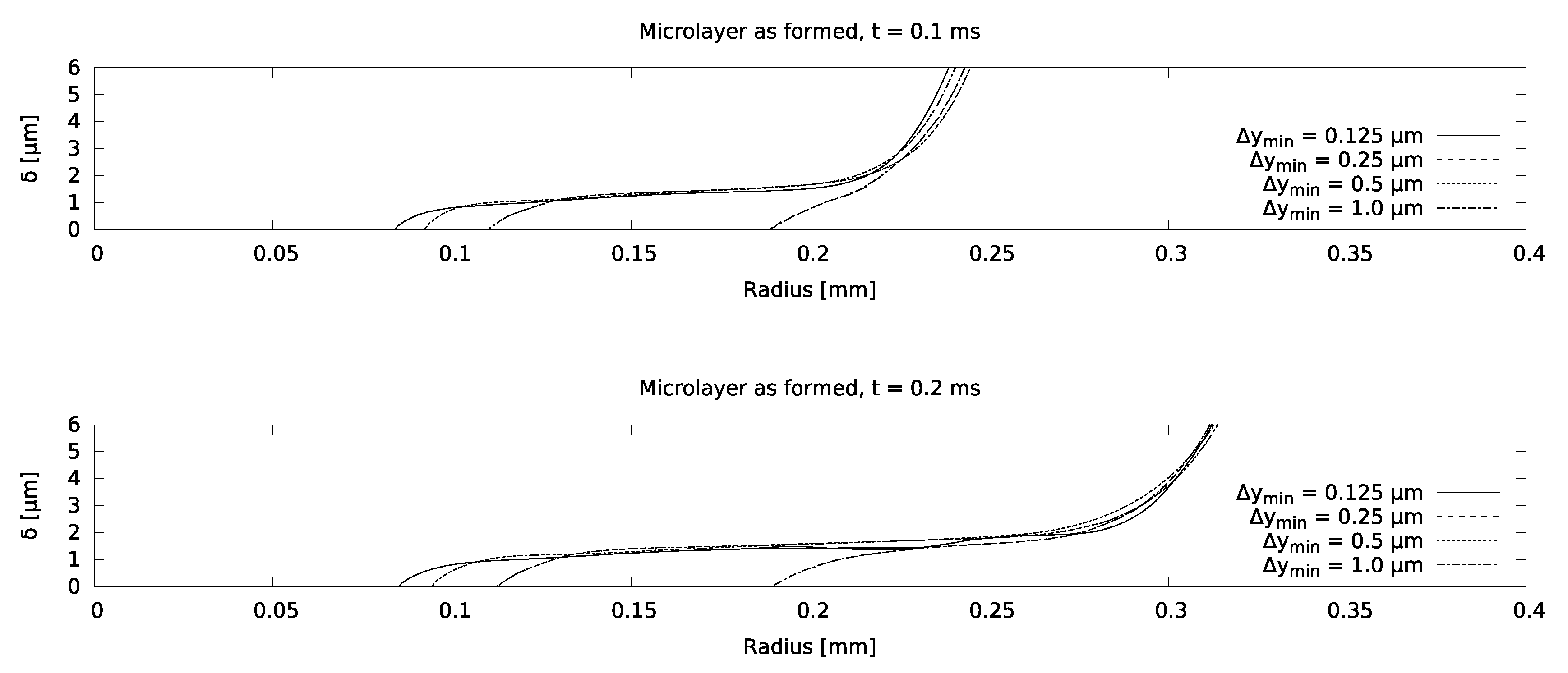
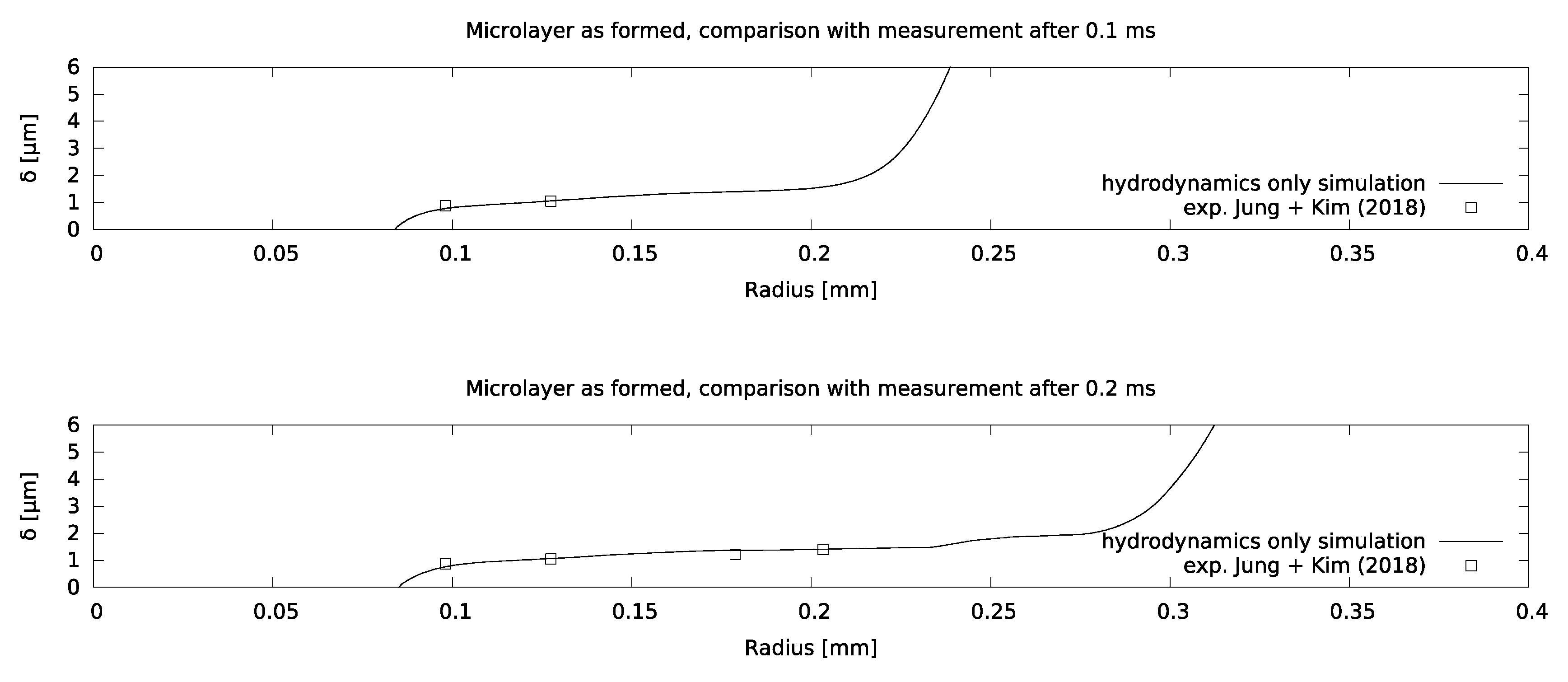
Mesh sensitivity of the model was checked using increasingly refined grids, corresponding to a near-wall cell thickness of 0.125 microns for the finest grid, as indicated in Figure 7. It was found that the microlayer thickness in the central region is essentially grid-independent for a near-wall cell thickness of 0.25 microns. Excellent agreement between the simulation and the measurement was obtained, as indicated in Figure 8, which increases confidence in setting the contact angle equal to zero at the no-slip boundary.
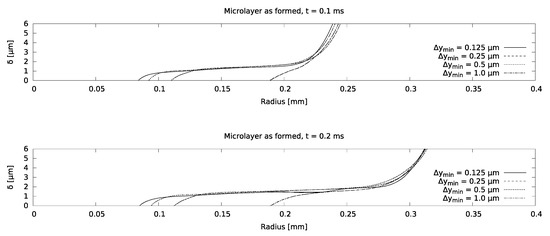
Figure 7.
Mesh sensitivity study for the water boiling case.
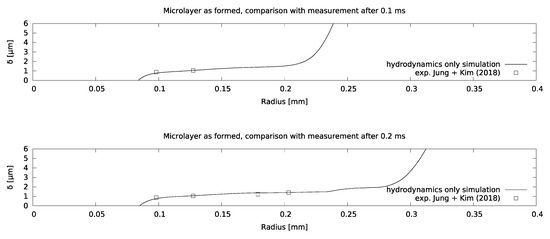
Figure 8.
Comparison between modelled and measured microlayer thicknesses for the water boiling case.
4. Modelling Microlayer Formation in Boiling of Sodium
For the current set of simulations, sodium bubble growth was modelled at the same superheat of 10 K (fairly typical of actual nucleate boiling conditions) that was considered for the water boiling test case. The fluid properties of saturated sodium at 1200 K, corresponding to a near-atmospheric vapor pressure of 1.48 bar, have been considered; these are shown in Table 2 and are typical of actual liquid metal reactor operating conditions [14]. The hydrodynamic behavior of small-scale two-phase phenomena, here under investigation, can be characterized using suitable non-dimensional parameters that express the relative importance of viscous and surface tension forces, which are likely to influence microlayer behavior. One such parameter is the Ohnesorge number, defined based on liquid viscosity , surface tension coefficient , and liquid density as , being a characteristic bubble size, here taken equal to 1 mm. In conditions of interest, Ohnesorge numbers of the fluids here considered are of the same order of magnitude, for water and for sodium, which confirms that experimental validation for water boiling can be used to support extension of the current set of simulations to sodium boiling cases. As for the water boiling case, a value of the contact angle equal to zero has been imposed on the no-slip boundary in order to enforce pinning of the contact line and formation of the microlayer.

Table 2.
Properties of saturated sodium at 1200K in near-atmospheric conditions typical of reactor operation.
4.1. Likely Bubble Growth Regime in Sodium; Differences with the Case of Water Boiling
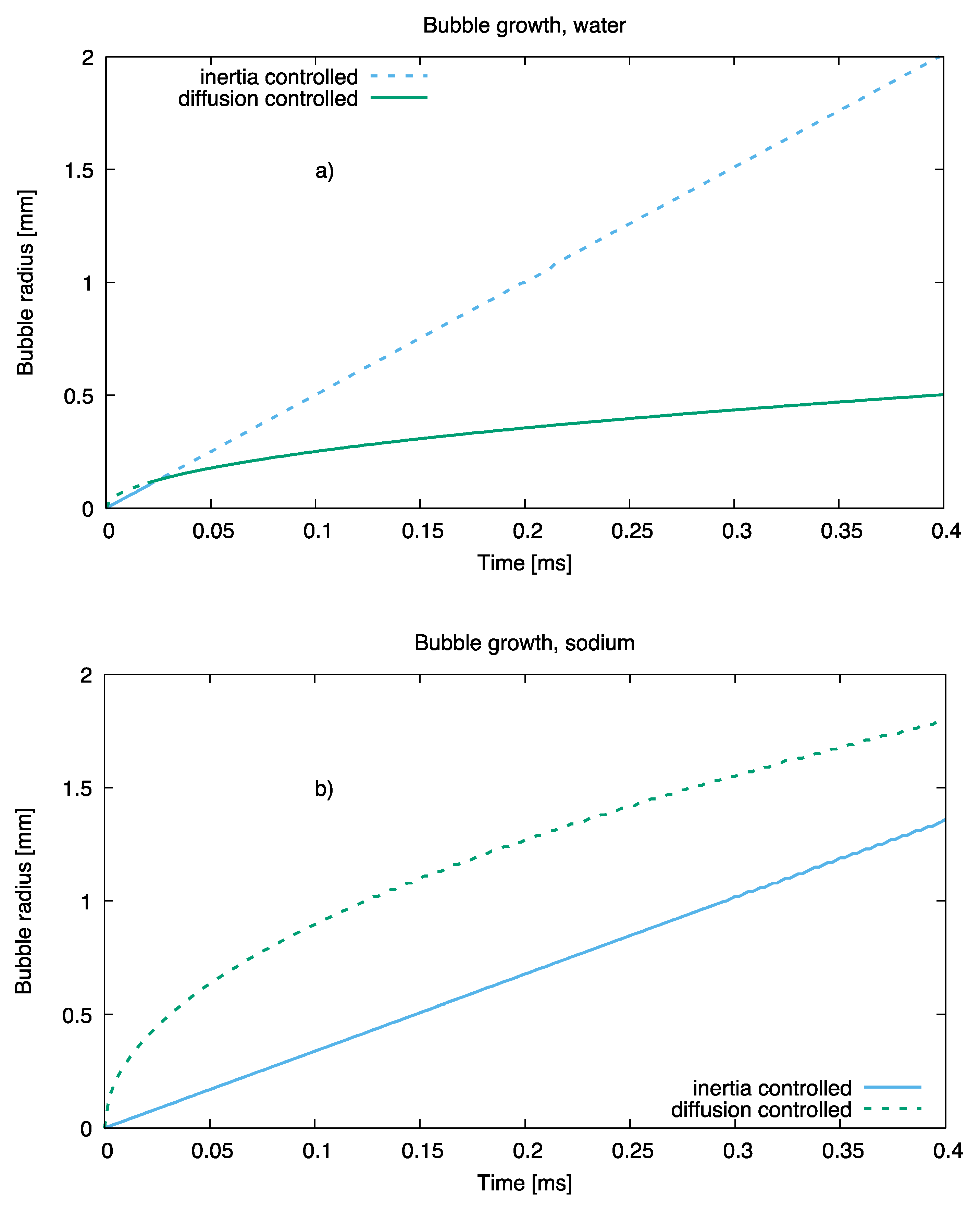
Analysis of bubble growth rates with the theory of Ref [29] indicates that the growth of a sodium bubble at ordinary superheats of order 10 K is limited by the inertia of the surrounding body of liquid and not by the rate of heat diffusion towards the bubble surface, as is the case of water, as noted. The different growth regimes for the two fluids are shown, at equal superheat (that is, 10 K), in Figure 9.
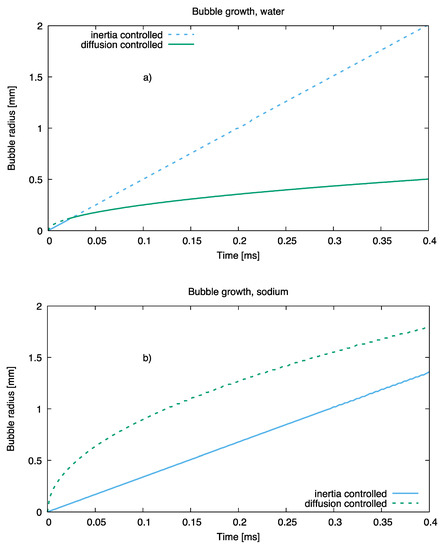
Figure 9.
Bubble growth in water (a) and sodium (b) at equal superheat.
For all simulations that follow, the rate of mass transfer at the bubble curved surface has been computed, using the inertial growth law, as
with the growth rate A defined in Equation (6).
4.2. Parametric Trends of Simulation Results
The current set of simulations aims to explore variations in microlayer behavior as model input parameters, namely bubble growth rate, surface tension coefficient, and liquid viscosity, are varied. Prior to the parametric study, a base case was analyzed in order to determine the mesh sensitivity of the model. For the base case, in conditions corresponding to 10 K of liquid superheat, the reference fluid properties are indicated in Table 3.

Table 3.
Parameters relevant to microlayer formation: base case parameters.
Results of the mesh sensitivity study are shown in Figure 10, based on which a mesh with near-wall cells of 0.5-micron thickness was chosen for all the simulations that follow. An overview of the set of simulations considered in the parametric study, indicating the sections in which they are discussed, is shown in Table 4; ‘base’ input parameters have been defined in Table 3. Different parameters, namely bubble growth rate and fluid properties, were varied one at a time in order to study their separate effects on microlayer behavior. Varying the growth rate (which, as noted, depends linearly on fluid superheat) corresponds to varying fluid superheat. Variations of fluid properties (here, viscosity and surface tension coefficient) correspond to changes in operating conditions, e.g., system temperature.

Figure 10.
Microlayer thickness modelled with increasingly refined computational meshes.

Table 4.
Parametric study on microlayer formation.
4.2.1. Effect of Bubble Growth Rate
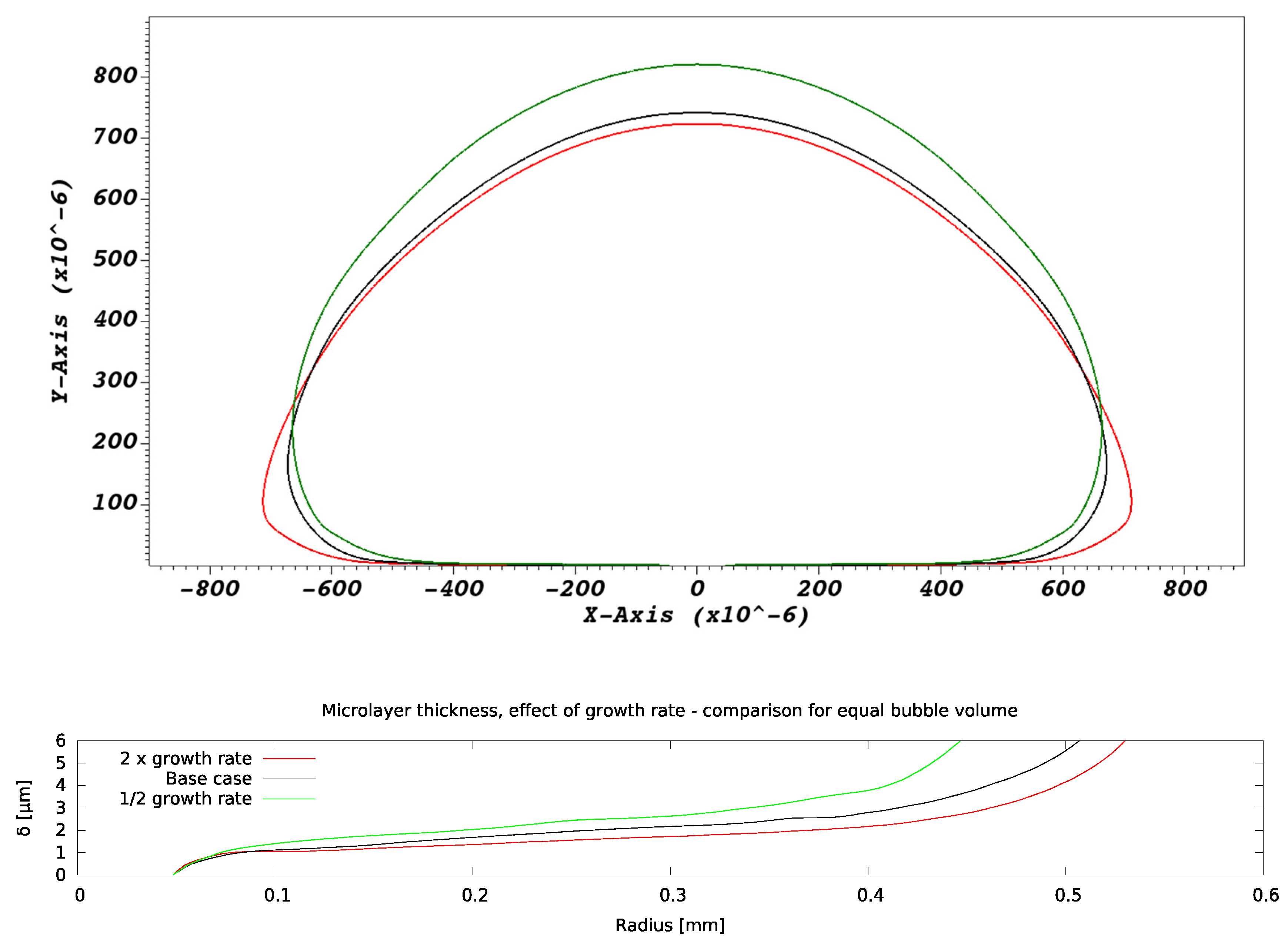
As the bubble growth rate A is increased, changes are observed in both bubble shape and microlayer thickness. Figure 11 shows a comparison of bubble and microlayer geometries at equal bubble volume. The bubble appears increasingly ‘flattened’ against the wall as the growth rate increases, a consequence of the increasingly large magnitude of the fluid reaction forces [16] due to the higher growth rates. The microlayer appears thinner as the bubble growth rate is increased, a trend that is consistent with hydrodynamic simulations of microlayer formation in water [12,13].
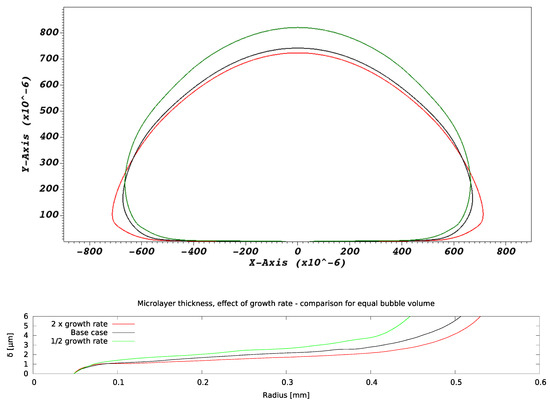
Figure 11.
Effect of bubble growth rate on microlayer formation. Bubble and microlayer shapes are compared at constant bubble volume.
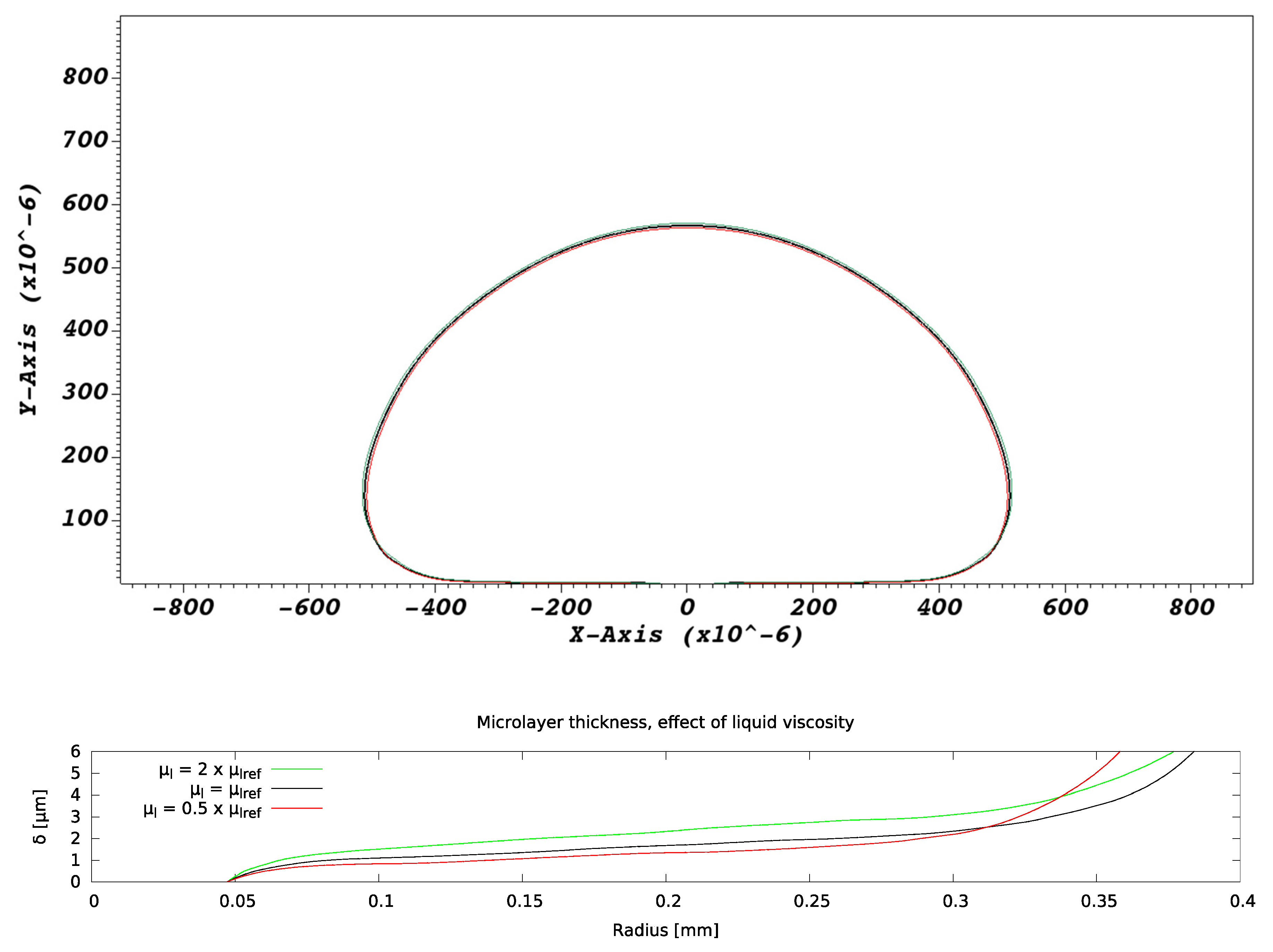
4.2.2. Effect of Liquid Viscosity
There is no effect on bubble growth due to variations in liquid viscosity, as expected from all extant hydrodynamic models of bubble formation [16]. As indicated in Figure 12, the microlayer thickness, however, increases with increasing liquid viscosity, which is expected from our basic understanding of microlayer formation. The basic theory of [29] indicates that the thickness of the layer is approximately proportional to the thickness of the hydrodynamic boundary layer created in the near-wall liquid by the velocity field, pointing in the radially outward direction and tangential to the wall, generated by bubble expansion [29]. The thickness of this boundary layer is proportional to the square root of the liquid viscosity and is, therefore, expected to increase as the viscosity increases.
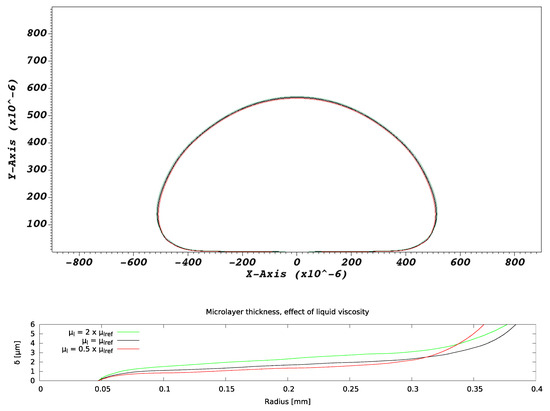
Figure 12.
Effect of liquid viscosity on microlayer formation. Bubble and microlayer shapes are compared at the same instant of time into bubble growth.
4.2.3. Effect of Surface Tension Coefficient
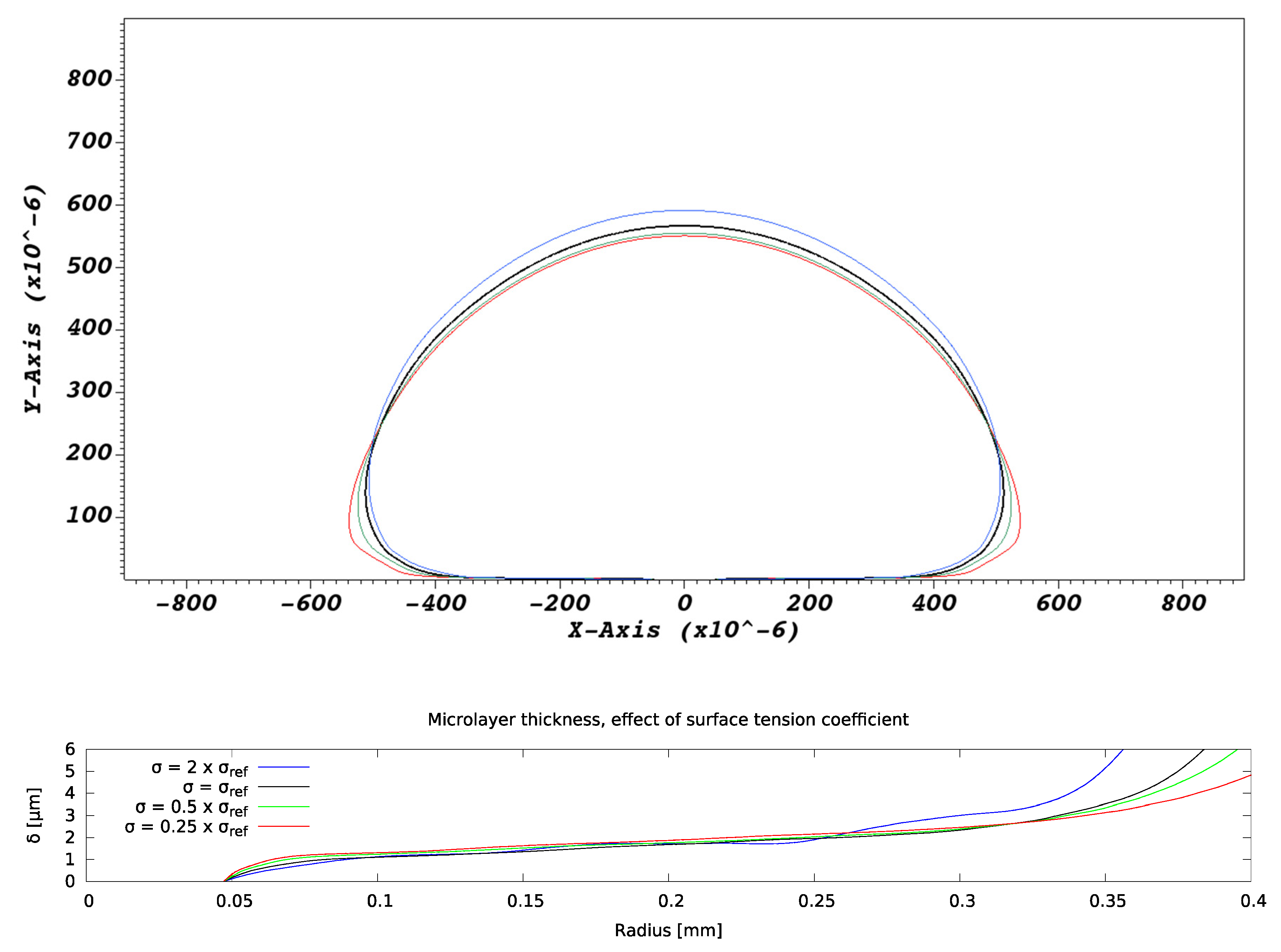
Variations in values of the surface tension coefficient were found to affect bubble shapes but not microlayer profiles in the ‘central’ region (defined in Figure 6), as indicated in Figure 13. A slight propensity of bubble shapes to retain sphericity as the surface tension coefficient increases was observed, but the effect is of little importance, at least in conditions of interest, as regards microlayer shape in the central region. On the other hand, it does alter the shape of a microlayer in the inner region, near the layer ‘root’ and in the outer region; furthermore, bubble geometry is affected around the bubble base. These trends are consistent with modelled microlayer behavior in water [12,13].
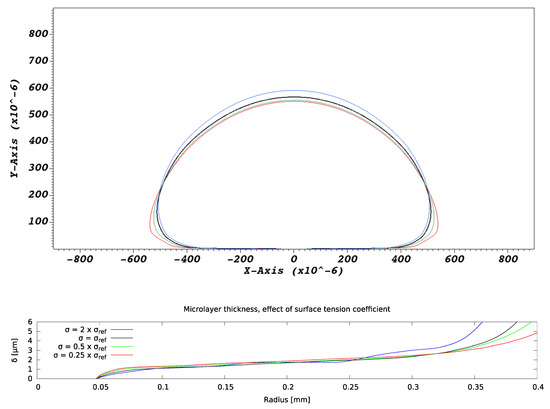
Figure 13.
Effect of surface tension coefficient on microlayer formation.
5. Comparison of Simulation Results with an Extant Analytical Model of Microlayer Formation
A number of theoretical models have been developed for predicting the thickness of a microlayer as it is formed on a heated substrate during bubble growth. These models are applicable to hypothetical conditions where the microlayer thickness does not decrease in time due to evaporation and, therefore, are strictly applicable only to the very early stages of bubble growth, during which, as noted, the effect of evaporation is negligible. The physical basis of any such model assumes rotational symmetry of bubble geometry and is predicated on the assumption that, moving outwards and away from the center of the bubble base along the radial direction r, the thickness of the newly formed microlayer increases or, equivalently, the newly formed microlayer is thicker at locations reached at later times by the leading edge of the expanding bubble base. It was thus shown that the microlayer thickness increases at the leading edge of the bubble base. A fluid-dependent parameter, which includes dependence on liquid viscosity [29], is typically used to express the relationship. If the law governing bubble radius R(t) is known, then it is possible to compute the radial variation of the thickness of the microlayer as formed on the surface. For example, to this end, the model in [1] assumes , typical of the heat diffusion controlled bubble growth regime. More relevant to the conditions of interest here is the model in [12], which is applicable to predicting the thickness of a microlayer as it is formed during the early inertial (R~t) regime of bubble growth. Under the assumptions that i) the effect of evaporation is negligible and ii) bubble growth takes place in the inertia-controlled regime, that model predicts a square-root-dependence of microlayer thickness as a function of the radial distance r from the layer ‘root’ (as defined in Figure 6):
where is the liquid density, is the liquid viscosity, and the bubble growth rate A is defined in Equation (6). The model, which is applicable to modelling the shape of the central region of the microlayer, i.e., at a distance from the triple contact line, has been tuned in [12] via comparison against interface-capturing simulations of microlayer formation.
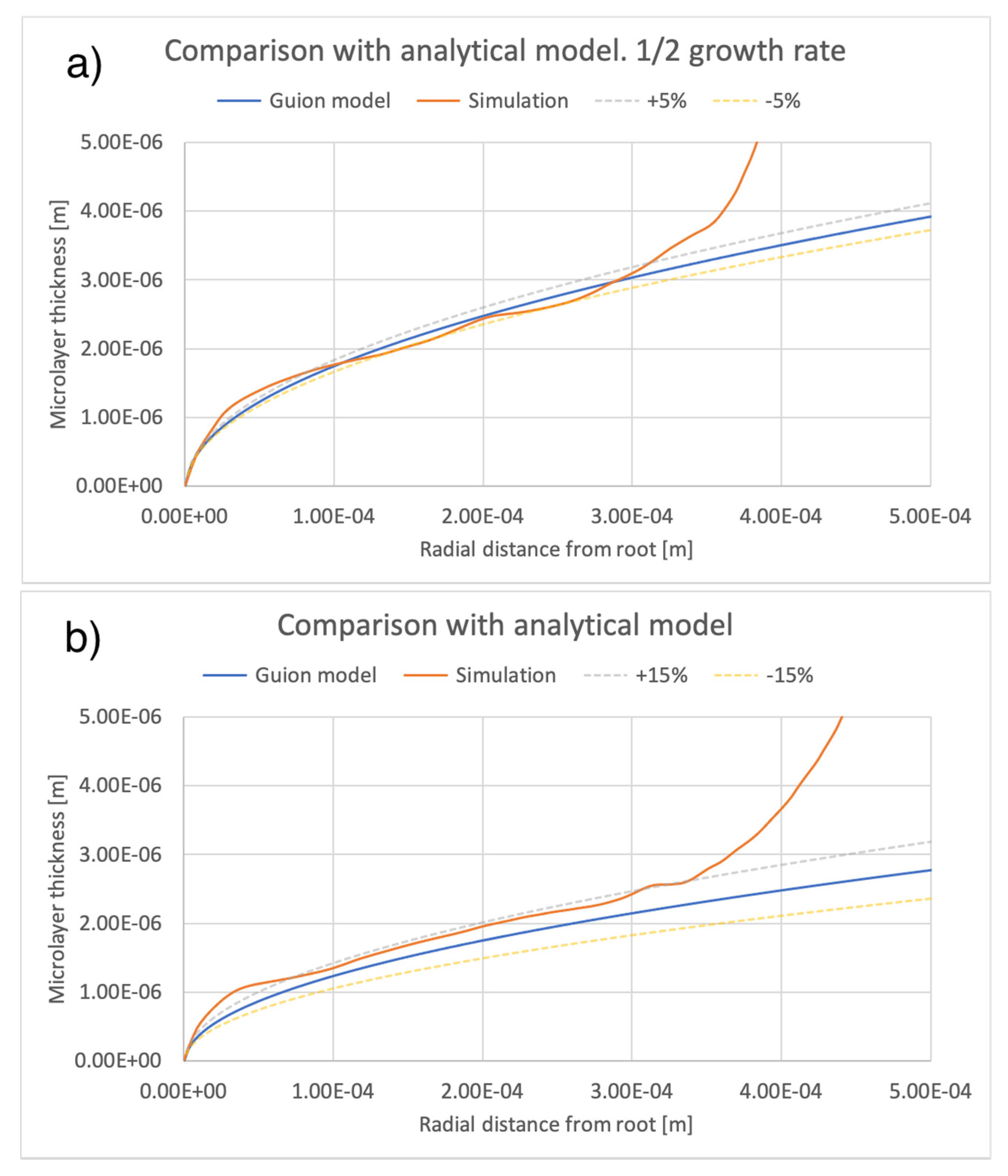
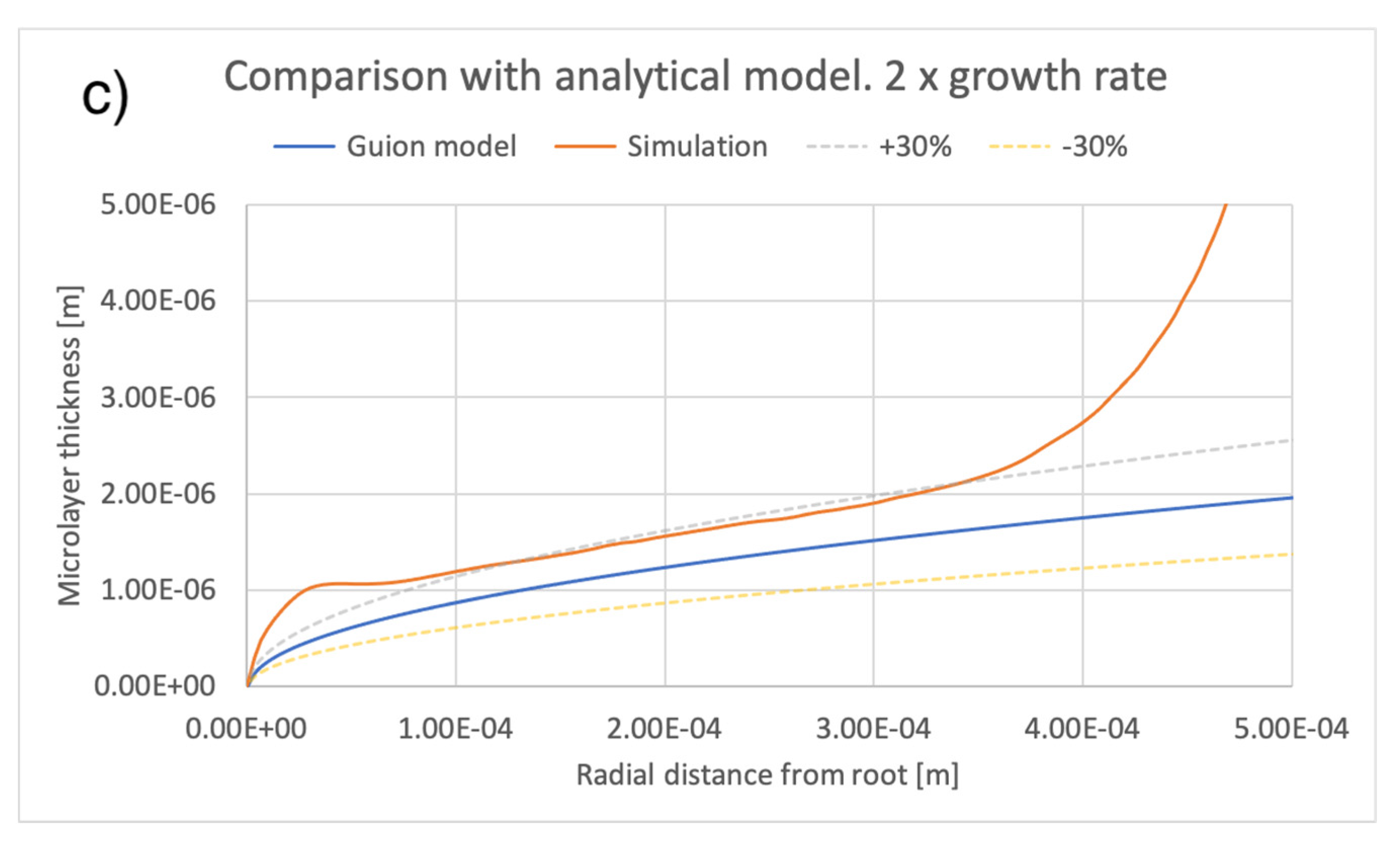
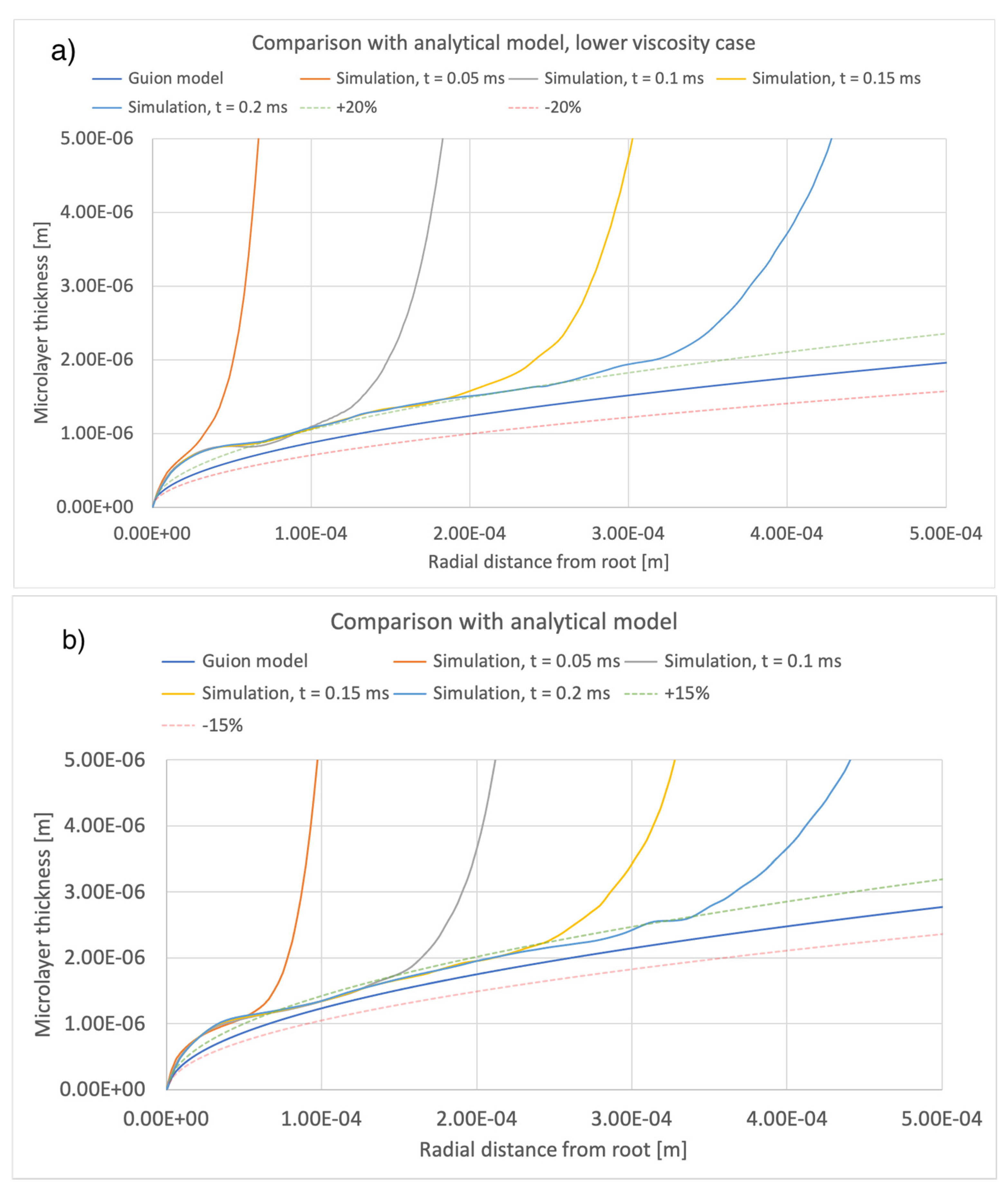
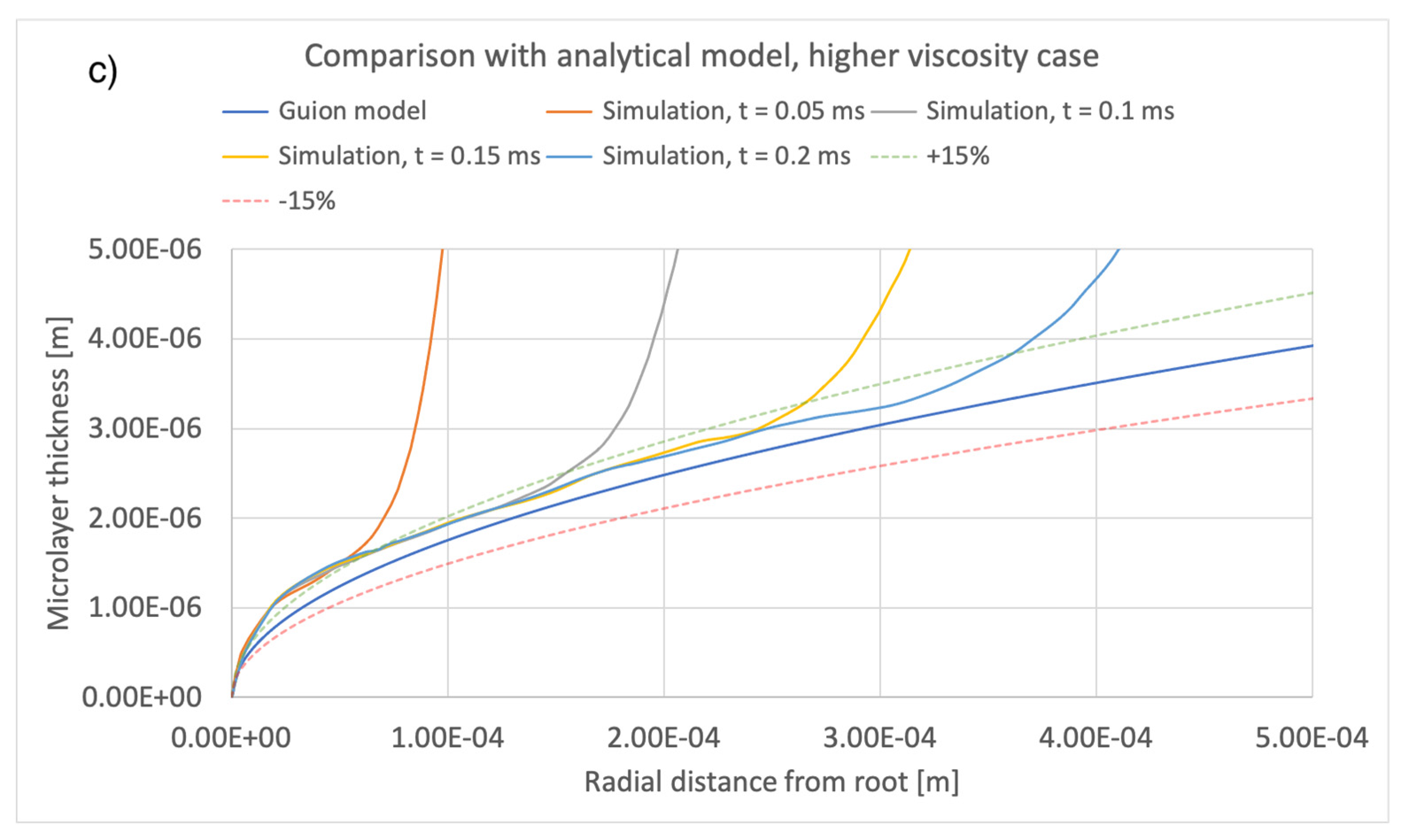
A comparison between the current simulations and predictions of the model of [12] is shown in Figure 14 and Figure 15, comparing the effects of different values of bubble growth rates as well as the values of liquid viscosity indicated in Table 4. On the whole, there is good qualitative agreement between the theoretical model and the current simulations in terms of the shape of the microlayer in the central region, while the discrepancy between values of the microlayer thickness generated with the current simulation methodology and the theoretical values is below 30% of the theoretical prediction for all values of the input parameters considered in the current work. Uncertainty bands of different widths in Figure 14 and Figure 15 are provided in order to indicate the varying magnitude of the discrepancy between the theoretical and simulation results. Variations outside the uncertainty bands are observed near the bubble root, i.e., in the region near the solid–liquid–vapor contact line where the model of [12] is not applicable.
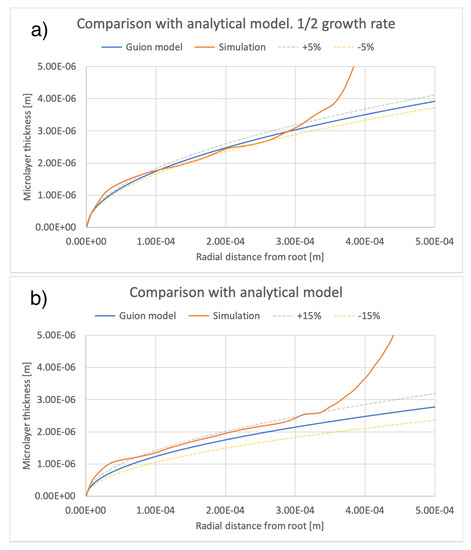
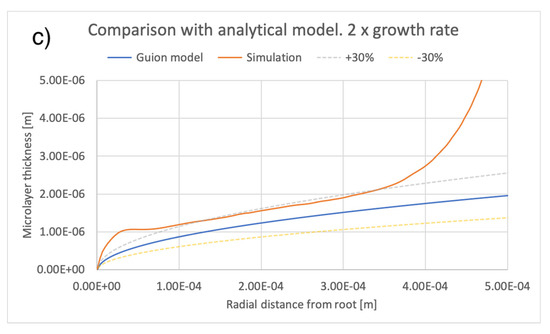
Figure 14.
Comparison of current simulation results with the model of [12]; effect of bubble growth rate. Radial distributions of microlayer thickness corresponding to the same bubble volume, presented in Figure 11, are compared with predictions of the model of [12]. Panels (a–c) show microlayer profiles for different values of the bubble growth rate.
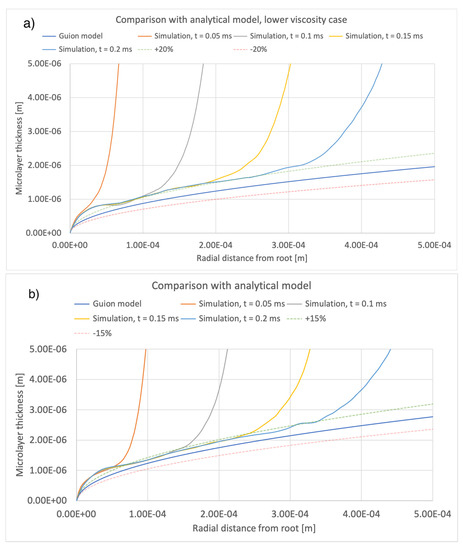
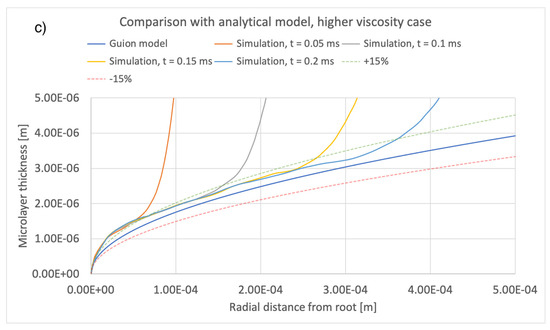
Figure 15.
Comparison of current simulation results with the model of [12]; effect of liquid viscosity. Radial distributions of microlayer thickness at a sequence of times into bubble growth are compared with predictions of the model of [12]. Panels (a–c) show microlayer profiles for different values of the liquid viscosity.
6. Conclusions
In this paper, the interface-capturing CFD simulation method was used to model the hydrodynamics of sodium bubble growth at a solid surface. The simulations clearly demonstrated the formation of a liquid microlayer beneath a vapor bubble in boiling of sodium. The current model was validated via comparison with microlayer observations in boiling water; the comparison increases confidence in the current simulations in the absence of any direct micro-scale observations of bubble growth or microlayer formation in sodium.
In the current set of simulations, a parametric study assessing the dependence of model predictions on fluid properties and bubble growth rates indicated that microlayer thickness increases with increasing liquid viscosity and decreases with increasing bubble growth rate. The shape of vapor bubbles is influenced, to some extent, by variations in the surface tension coefficient; however, the thickness of a microlayer is independent of that parameter. These findings are consistent with our current understanding of microlayer behavior in boiling water and are confirmed by comparison with an extant algebraic model of microlayer formation [12].
The current findings on microlayer formation lay down the foundation for a future study on microlayer depletion [5] due to evaporation, which, for the case of sodium, has not been attempted yet. Analysis of the process of sodium microlayer depletion due to evaporation is deferred to future work.
Author Contributions
Conceptualization, G.G., H.K., R.I.I. and M.J.B.; methodology, G.G.; formal analysis, G.G, H.K. and R.I.I.; investigation, G.G.; writing—original draft preparation, G.G., H.K.; writing—review and editing, R.I.I. and M.J.B.; funding acquisition, G.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the United Kingdom Engineering and Physical Sciences Research Council (EPSRC), grant number EP/T027061/1.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jung, S.; Kim, H. Hydrodynamic formation of a microlayer underneath a boiling bubble. Int. J. Heat Mass Transf. 2018, 120, 1229–1240. [Google Scholar] [CrossRef]
- Giustini, G.; Jung, S.; Kim, H.; Ardron, K.H.; Walker, S.P. Microlayer evaporation during steam bubble growth. Int. J. Therm. Sci. 2019, 137, 45–54. [Google Scholar] [CrossRef]
- Jung, S.; Kim, H. An experimental method to simultaneously measure the dynamics and heat transfer associated with a single bubble during nucleate boiling on a horizontal surface. Int. J. Heat Mass Transf. 2014, 73, 365–375. [Google Scholar] [CrossRef]
- Giustini, G.; Jung, S.; Kim, H.; Walker, S.P. Evaporative thermal resistance and its influence on microscopic bubble growth. Int. J. Heat Mass Transf. 2016, 101, 733–741. [Google Scholar] [CrossRef]
- Hänsch, S.; Walker, S. Microlayer formation and depletion beneath growing steam bubbles. Int. J. Multiph. Flow 2019, 111, 241–263. [Google Scholar] [CrossRef]
- Urbano, A.; Tanguy, S.; Huber, G.; Colin, C. Direct numerical simulation of nucleate boiling in micro-layer regime. Int. J. Heat Mass Transf. 2018, 123, 1128–1137. [Google Scholar] [CrossRef]
- Utaka, Y.; Kashiwabara, Y.; Ozaki, M. Microlayer structure in nucleate boiling of water and ethanol at atmospheric pressure. Int. J. Heat Mass Transf. 2013, 57, 222–230. [Google Scholar] [CrossRef]
- Yabuki, T.; Nakabeppu, O. Microscale wall heat transfer and bubble growth in single bubble subcooled boiling of water. Int. J. Heat Mass Transf. 2016, 100, 851–860. [Google Scholar] [CrossRef]
- Kim, J. Review of nucleate pool boiling bubble heat transfer mechanisms. Int. J. Multiph. Flow 2009, 35, 1067–1076. [Google Scholar] [CrossRef]
- Gerardi, C.; Buongiorno, J.; Hu, L.-W.; McKrell, T. Study of bubble growth in water pool boiling through synchronized, infrared thermometry and high-speed video. Int. J. Heat Mass Transf. 2010, 53, 4185–4192. [Google Scholar] [CrossRef]
- Sugrue, R.; Buongiorno, J. A modified force-balance model for prediction of bubble departure diameter in subcooled flow boiling. Nucl. Eng. Des. 2016, 305, 717–722. [Google Scholar] [CrossRef]
- Guion, A.; Afkhami, S.; Zaleski, S.; Buongiorno, J. Simulations of microlayer formation in nucleate boiling. Int. J. Heat Mass Transf. 2018, 127, 1271–1284. [Google Scholar] [CrossRef]
- Hänsch, S.; Walker, S. The hydrodynamics of microlayer formation beneath vapour bubbles. Int. J. Heat Mass Transf. 2016, 102, 1282–1292. [Google Scholar] [CrossRef]
- Kottowski, H.M.; Savatteri, C. Fundamentals of liquid metal boiling thermohydraulics. Nucl. Eng. Des. 1984, 82, 281–304. [Google Scholar] [CrossRef]
- Coventry, J.; Andraka, C.; Pye, J.; Blanco, M.; Fisher, J. A review of sodium receiver technologies for central receiver solar power plants. Sol. Energy 2015, 122, 749–762. [Google Scholar] [CrossRef]
- Ardron, K.H.; Giustini, G.; Walker, S.P. Prediction of dynamic contact angles and bubble departure diameters in pool boiling using equilibrium thermodynamics. Int. J. Heat Mass Transf. 2017, 114, 1274–1294. [Google Scholar] [CrossRef]
- Tryggvason, G.; Scardovelli, R.; Zaleski, S. Direct Numerical Simulations of Gas–Liquid Multiphase Flows; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar] [CrossRef]
- Issa, R.I. Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Issa, R.I.; Gosman, A.D.; Watkins, A.P. The computation of compressible and incompressible recirculating flows by a non-iterative implicit scheme. J. Comput. Phys. 1986, 62, 66–82. [Google Scholar] [CrossRef]
- Greenshields, C. OpenFOAM User Guide; The OpenFOAM Foundation Ltd.: London, UK, 2017. [Google Scholar]
- Mikic, B.B.; Rohsenow, W.M.; Griffith, P. On bubble growth rates. Int. J. Heat Mass Transf. 1970, 13, 657–666. [Google Scholar] [CrossRef]
- Hardt, S.; Wondra, F. Evaporation model for interfacial flows based on a continuum-field representation of the source terms. J. Comput. Phys. 2008, 227, 5871–5895. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Ferrari, A.; Magnini, M.; Thome, J.R. Numerical analysis of slug flow boiling in square microchannels. Int. J. Heat Mass Transf. 2018, 123, 928–944. [Google Scholar] [CrossRef]
- Magnini, M.; Pulvirenti, B.; Thome, J.R. Numerical investigation of hydrodynamics and heat transfer of elongated bubbles during flow boiling in a microchannel. Int. J. Heat Mass Transf. 2013, 59, 451–471. [Google Scholar] [CrossRef]
- Denner, F.; van Wachem, B.G.M. Numerical time-step restrictions as a result of capillary waves. J. Comput. Phys. 2015, 285, 24–40. [Google Scholar] [CrossRef]
- Damiàn, S.M. An Extended Mixture Model for the Simultaneous Treatment of Short and Long Scale Interfaces. Ph.D. Thesis, Universidad Nacional del Litoral, Santa Fe, Argentina, 2013. [Google Scholar]
- Nabil, M.; Rattner, A.S. interThermalPhaseChangeFoam—A framework for two-phase flow simulations with thermally driven phase change. SoftwareX 2016, 5, 216–226. [Google Scholar] [CrossRef]
- Cooper, M.G.; Lloyd, A.J.P. The microlayer in nucleate pool boiling. Int. J. Heat Mass Transf. 1969, 12, 895–913. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).