Parametric Study of Turbulent Couette Flow over Wavy Surfaces Using RANS Simulation: Effects of Aspect-Ratio, Wave-Slope and Reynolds Number

Abstract

A turbulent Couette flow over a wavy surface is subject to a detailed parametric study in which three parameters—Aspect Ratio, Wave Slope and Reynolds number—are independently varied over an order of magnitude to investigate their influence on the flow. Std k−ε turbulence model with enhanced wall functions is used to simulate all cases in the study and the results are validated against experimental data as well as analytical theories pertaining to flow over wavy surfaces. Gross flow properties such as mean velocity profiles, mass flow rate, shear stress and pressure on the walls, as well as turbulent flow characteristics such as inner-wall coordinates, log-law fit, eddy viscosity profiles and turbulence kinetic energy across the domain, are presented and their corroboration with existing literature is discussed. The effect of the three parameters on the flow variables is investigated. It is observed that while all response flow variables scale monotonically with a progressive change in the parameters, there are certain flow characteristics that can be ascribed exclusively to one of the three parameters. The study also discusses the influence of the top plate, a much-needed discussion that seems to be absent in most literature pertaining to Couette flow in wavy channels.

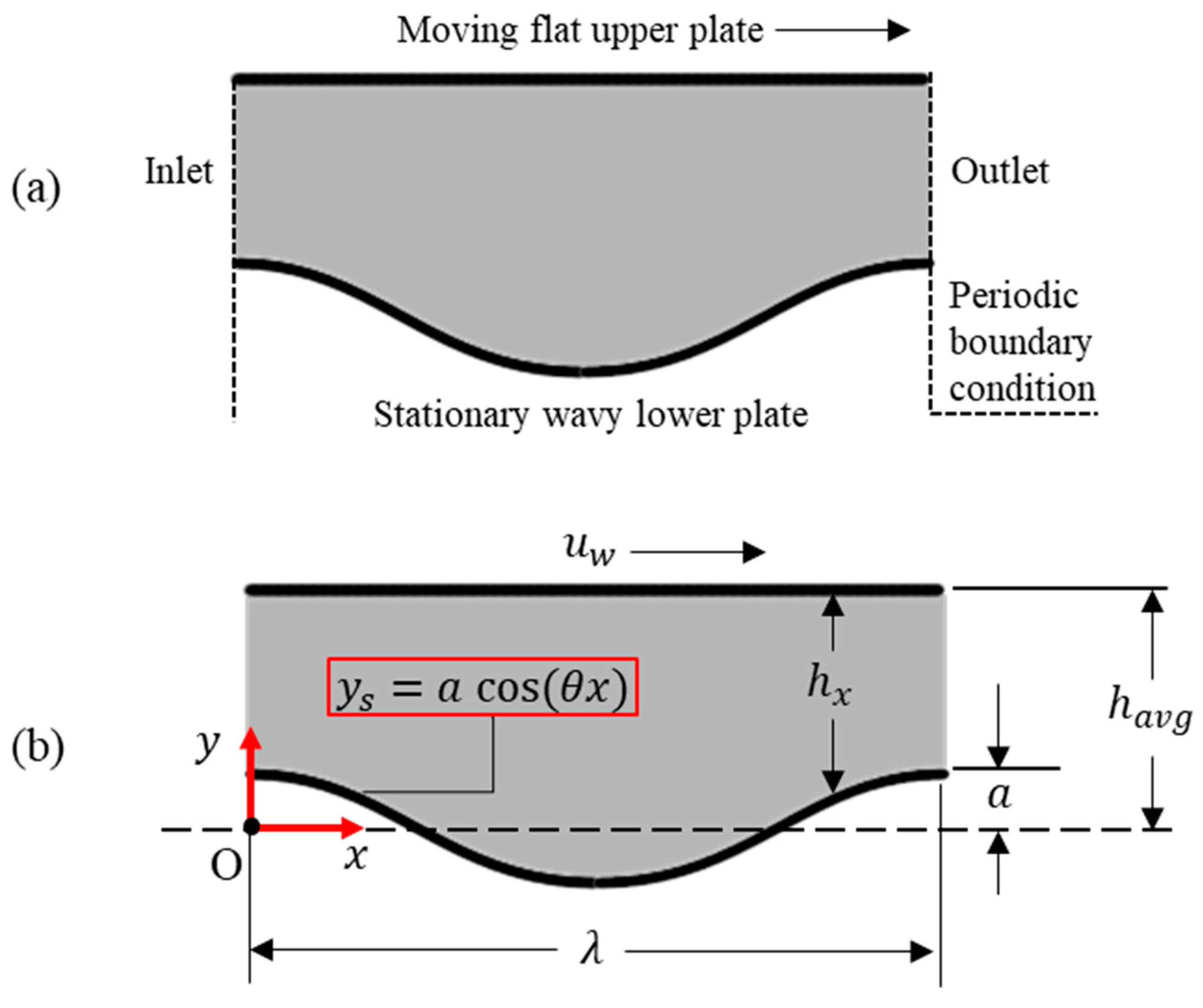
1. Introduction

Turbulent flows over wavy surfaces are ubiquitous in nature. A study of such flows found its application in understanding complex phenomena like the surface interaction of two immiscible fluids: Interaction of air over sea waves, sand dunes, ripples in desert and on the ocean floor. Additionally, they may be observed in heat exchangers with wavy channels and fins, vehicles using wing-in-ground effect (WIG) for transportation, rail guns and systems employing lubrication. The Hyperloop, for instance, is a new paradigm of transport in its conception which employs a mobile pod housed in a tube with a clearance between the two. The fluid flow in the clearance between the stationary tube with small undulations and the mobile pod can be a subject of rigorous study of high-speed turbulent flows through a wavy channel. In such a case, the study becomes pertinent as the need to control the lift, drag, pod stability, as well as its air conditioning and ventilation becomes important for efficient transport. Introduction of a wavy wall in a Couette flow complicates its study as it introduces flow dependence on various new geometrical features, like the wavelength and amplitude of the wavy solid surface, mean height of the channel and aspect-ratio of the flow domain. It also introduces new flow features like separation and oscillating pressure on the bounding surfaces apart from dynamic phenomena like unsteady lift and drag forces.

This flow has been subject to many investigations in the past, but the focus has been divided among the various attributes mentioned above, resulting in a weak consensus among different studies, as may be apparent in the account given here. Notably among analytical studies on the topic is the work of Benjamin [1], where a linear theory was developed to calculate the shear stress and the normal pressure on the stationary wavy boundary. Benjamin validated the theory for laminar and pseudo-laminar flows with very small wave slopes. Davis [2] presented an analytical investigation of the shear flow over wavy boundary with small amplitude in the infinite Reynolds number limit. He concluded that when the Reynolds number approaches infinity, the amplitude of the solid wave that negligible viscous stresses approaches zero. In 1985, Disimile and Wang [3] analyzed a Couette flow between two corrugated plates using an analytic approach. They assumed small amplitude ‘$b$’ of the solid waves with respect to channel width ‘$a$’, such that the ratio $\frac{b}{a}\ll 1$ and low Reynolds number. The authors published the analytical relations, for the first time, to determine the unsteady lift and drag induced by the corrugations. While, developing a rigorous and accurate theory, both these works [1,3] do not assume validity for turbulent flows with high Reynolds numbers or flows with larger wave amplitudes.

There is ample focus in the literature on a niche regime of non-separated turbulent flow over small stationary solid waves, such that the flow variables can be modeled in a linear response to the wave contour. There are many accounts of a linear theory developed over stages, some of them incorporating the advantages of using a boundary layer coordinate system over a cartesian system, and the advantages of modeling the Reynolds stresses over a quasi-laminar assumption. Thorsness et al. [4] conducted experimental investigations to lend much needed validation to the many linear theories proposed before them, and also developed a new theory that combines the mixing length model proposed by Loyd et al. (per [4]) and an energy method developed by Mellor and Herring [5]. They published measurements of pressure and shear stress on the stationary solid wave along with their respective phase angles, and compared them to their theory. Abrams (per [6]) later proposed a modification to the linear theory suggested by Thorsness et al. [4], applicable to only a certain range of flows, in the form of relaxation of an equilibrium condition used to describe Reynolds stresses induced by the wall. He also concluded that the $k-\epsilon$ model naturally induces that relaxation as the pressure gradient influences the shear stress variation and consequently affects the turbulence production.

Frederick and Hanratty [7] with measurements from a laser-Doppler velocimeter obtained the streamwise velocity of flow over wavy surface with very small amplitude ($a/\lambda$ = 0.015625 and 0.025) and appropriate bulk Reynolds numbers ($Re$ = 6400 and 38,800 respectively) making sure that there was no existence of separated flow. They compared their measurements with computations that employed linear eddy viscosity models. They found that the shear stress along the wavy wall was successfully predicted, while the wave-induced velocity variations were under-predicted. They suggested that the differences in experimental observations and computations were due to the inadequacy of the eddy-viscosity model in accounting for nonlinear effects, while predicting the wave-induced Reynolds stresses. When the Reynolds stress was ignored for most of the flow-field, such that the flow could be assumed as quasi-laminar, the wave-induced velocity showed a maximum amplitude to be closer to their experimental observations. They concluded that the wave-induced variations of intensity in the streamwise turbulent velocity fluctuations were only prominent for the region of $y^{+}$ < 30, but they are not strong enough to affect the rest of the velocity field. Zilker et al. [8] presented measurements of shear-stress variation, pressure variation and velocity profiles along the solid wave and corroborated their results with Thorsness et al. [4] and Morrisroe (per [8]). While, they presented their results for two distinct wave slopes ($2a/\lambda )$ of 0.0312 and 0.05, the Reynolds numbers in their study ranged approximately from 6000 to 32,000. They observed that the response variables increasingly departed from being sinusoidal with increase in the wave height and velocity of the flow, and concluded that a nonlinear response is observed for non-dimensional wave height, $a^{+}\ge$27.

Cherukat et al. [9] conducted a Direct Numerical Simulation (DNS) investigation of turbulent flow over solid waves with $a/\lambda$ = 0.05 and a bulk Reynolds number of 3640. In comparison to Frederick and Hanratty’s [7] test cases, Cherukat et al. [9] employed twice the amplitude-to-wavelength ratio and a Reynolds number lower by an order of magnitude, making their flow regime approximate a quasi-laminar flow. While Frederick and Hanratty [7] observed a flow with no separation, Cherukat et al. observed pressure gradients large enough to cause flow separation and compared their computational results favorably with Hudson’s work in 1993 [10]. While Cherukat et al. documented separation of flow at $a/\lambda$ = 0.05, Yoon et al. [11], in their DNS study at the same Reynolds number as Cherukat et al. [9] observed small recirculation at the trough of the solid wave for $a/\lambda$ = 0.02 and a distinct reversal of flow at $a/\lambda$ = 0.03. Turbulent flow over wavy surfaces is extensively studied in the context of air flow over water waves [12,13,14,15,16,17]. Notable among them is the DNS investigation in a three-dimensional (3D) domain presented by Sullivan et al. [12]. They presented mean flow characteristics and turbulent statistics for a range of flows with increasing wave age, $c/u_{*}$, which is the ratio of the speed of the wave with respect to the friction velocity experienced by the wind. It was concluded that its combination with the wave slope plays a crucial role in determining the mean flow, pressure and shear stress on the wave, apart from vertical momentum fluxes and velocity variances. While, Sullivan et al. [12] focused their study on water waves that are modeled not to evolve due to wind, Yang and Shen [15] took the investigation further, as they accounted for wind-induced wave drift with three different wave ages, and concluded that its effect on turbulence was important only in the slow wave age case. They also identified two different types of coherent vortical structures for the intermediate wave age case and presented analysis of their locations and sizes. They documented their finding over a Reynolds number (as defined in Section 2.2 of the current study) varying from $Re$ = 9491 to 11,008.

In the recent works of Esquivelzeta-Rabell et al. [18], the investigators summarized the limits of the linear response of flow variables by performing a set of DNS simulations on combinations of wave slopes and Reynolds numbers over a particular range. They compared their results of shear stress and pressure on the bottom wave with the predictions of linear theory, as well as the limits of the combinations of wave slope and Reynolds number, where recirculation was observed with the analytical predictions of Malevich [19]. Esquivelzeta-Rabell et al. take their study a step further in [20], where they define one more parameter, which takes into account the ratio of wavelength to the average height of the domain. Like their previous investigation [18], the object of their study [20] was to study the onset of recirculation subject to the three parameters, although they do not report the pressure and shear stress characteristics on the bottom wall. Although both their works provide a substantial insight into the limits of observable recirculation in flow over wavy surfaces, due to the difficulties of DNS studies associated with large-Reynolds number turbulent flows, they present their analysis for laminar flows only, and make no comment on the turbulent characteristics of flow over wavy surfaces. Large Eddy Simulations (LES) have been employed for the study of turbulent flow over wavy surfaces [21,22,23]. Henn and Sykes [21] in their formative work presented shear stress variation, mean velocity profiles along with turbulent characteristics like turbulence intensity, velocity variance perturbations, mean flow field statistics and higher order statistics. They studied a turbulent flow over a wave with the wave slope (defined as $2a/\lambda )$ varied in the range from 0 to 0.2 and their Reynolds numbers based on bulk velocity and half of mean channel height, $R{e}_b$ varying between 10,000 and 20,000. Apart from discussing the deliverables of LES in studying the turbulent flow over a wavy surface, by comparing their results with experimental and DNS data in the literature, they suggested that drag on the wavy wall increases quadratically with small wave slopes, while its rate of decreased slightly for larger wave slopes. Although turbulent Couette flow over wavy surfaces is extensively investigated, there is limited research that employs turbulence closure models to investigate the topic [24,25].

It may be apparent, from the account provided above, that the motivation for consensus among different studies is weak. This is, in part, because the range of flow regimes studied among different investigations is not contiguous, and in part, because the analytical studies, which did encompass a large range of flow regimes, did not account for the deficiencies of their models when applied to such a range where the assumptions for similarity between different flows cease to be valid. Additionally, none of them consider the effect of top plate and the aspect ratio of the flow domain on the flow. To address these gaps, this study focuses on turbulent Couette flow over a stationary solid wave with small amplitude over a range of parameters, using a RANS turbulence model. As a precursor to this study, Sherikar and Disimile [26] substantiated the use of $Std k-\epsilon$ model with Enhanced Wall functions for simulating turbulent Couette flow. Hence, within the context of the deliverables of the $Std k-\epsilon$ model, this study aims to analyze the dependence of turbulent Couette flow on three parameters namely Aspect Ratio ($AR$), Wave Slope ($WS$) and Reynolds number ($Re$). The range of these parameters is bound by the upper and lower limits of the amplitude-to-wavelength ratio of the solid wave for a given Reynolds number, such that it does not cause a flow separation and simultaneously induces pressure and shear stresses in a manner that their response is linear with respect to the solid wave.

2. Computational Setup

2.1. Geometry and Boundary Conditions

The computational fluid domain is defined for $x \in \left[0, \lambda \right]$, bound by a stationary wavy wall on the bottom and a movable plane wall on the top. The stationary solid-wave is defined by $y_s=a \cos \left(\theta x\right)$, where $a$ is the solid-wave amplitude and $\theta$ is the wave-number defined by $\theta =\frac{2\pi }{\lambda }$, and $\lambda$ is the wavelength of the solid wave. The mean height of the channel is $h_{avg}= \frac{1}{\lambda }{\int }_0^{\lambda }{h}_{x}dx$, where $h_x$ is the height of the top plate measured from the bottom plate at any arbitrary streamwise location, $x$. The inlet and outlet of the domain are subject to periodic boundary condition with zero pressure gradient between them. The top plate moves with a velocity, $u_w$. Figure 1 shows the geometry of the computational domain and boundary conditions applied to it along with the geometric notation used in the study.

2.2. Design of Computations

Parametric analysis of wavy plate Couette flow is carried out subject to the parameters Aspect-Ratio ($AR$) = $\frac{\lambda }{h_{avg}}$, Wave-Slope ($WS$) = $\frac{2\pi a}{\lambda }$ and Reynolds number ($Re$) = $\frac{u_w\lambda }{\upsilon }$. Each parameter is varied over 5 levels. Any combination of the three parameters set to their individual level forms a part of an experimental space considered for this study. Any computation performed in this experimental space is denoted by a general point $\mathit{C}\left(AR, WS, Re\right)$, where the coordinates denoted by parameters $AR$, $WS$ and $Re$ assume any of the 5 levels defined in

Table 1. Description of parameter levels designed for this study.

Factors	Levels
	I	II	III	IV	V
$AR$	1	2	4	8	10
$WS$	0.01	0.02	0.04	0.08	0.1
$Re$	104	2 × 104	4 × 104	8 × 104	105

. For example, let $\mathit{C}\left(\mathrm{II}, \mathrm{IV}, \mathrm{III}\right)$ denote a computation carried out with the following parameter set; $AR$ = 2, $WS$ = 0.08 and $Re$ = $4\ast {10}^4$.

Each parameter is individually and independently varied over 5 levels. A total of 13 simulations are performed as a part this analysis—A base case: $\mathit{C}$(I, I, I); variation of aspect ratio, $AR$: $\mathit{C}$(II, I, I) … $\mathit{C}$(V, I, I); variation of wave slope, $WS$: $\mathit{C}$(I, II, I) … $\mathit{C}$(I, V, I) and variation of Reynolds number, $Re$: $\mathit{C}$(I, I, II) … $\mathit{C}$(I, I, V).

Notation

To organize and present the results of this study and for ease of its interpretation, the following naming convention and color codes are adopted. Unless specified—the data along the height of the channel is presented for $\frac{x}{\lambda }=0$; the base case, $\mathit{C}$(I, I, I) is always denoted in black; data for variation in each parameter is represented by a specific color—$AR$-variation: red; $WS$-variation: green; $Re$-variation: blue. The levels of each parameter considered in increasing order are color-coded by a corresponding increase in intensity of the color that is ascribed to the parameter. For example, in Figure 9a the normalized velocity profiles at $\frac{x}{\lambda }=0$ for increasing levels in $AR$, ($\mathit{C}$(II, I, I) … $\mathit{C}$(V, I, I)) is denoted by progressively darker shades of red.

2.3. Governing Equations and Turbulence Model

The $Std k-\epsilon$ turbulence model is characterized by two independent equations to mitigate the Reynolds stress closure problem—one for the turbulent kinetic energy, $k$ and the other for the rate of dissipation of turbulent kinetic energy, $\epsilon$. While, no new information is required to attain Reynolds stress closure, the model itself makes some assumptions which may be grossly violated in some flows. It assumes isotropic turbulence, and by consequence, is known to simulate free shear flows like jet plumes, wakes, mixing layers, as well as high Reynolds number flows, while making it unsuitable for high shear and non-equilibrium flows. The transport equations of kinetic energy and its dissipation rate are given by Equations (1), and (2), respectively:

$$\frac{\partial \left(\rho k\right)}{\partial t}+\frac{\partial \left(\rho k{u}_i\right)}{\partial x_i}=\frac{\partial \left(\frac{\left(\mu +\frac{{\mu }_t}{{\sigma }_k}\right)\partial k}{\partial x_j}\right)}{\partial x_j}+G_k-\rho \epsilon$$

(1)

$$\frac{\partial \left(\rho \epsilon \right)}{\partial t}+\frac{\partial \left(\rho \epsilon u_i\right)}{\partial x_i}=\frac{\partial \left(\frac{\left(\mu +\frac{{\mu }_t}{{\sigma }_{\epsilon }}\right)\partial \epsilon }{\partial x_j}\right)}{\partial x_j}+\frac{C_{1\epsilon }\epsilon G_k}{k}-\frac{C_{2\epsilon }\rho {\epsilon }^2}{k}$$

(2)

$${\mu }_t=\frac{\rho C_{\mu }{k}^2}{\epsilon }$$

(3)

The subscripts $i, j$ refer to coordinates while ${\mu }_t$ is the turbulent eddy viscosity. $G_k$ represents the production of kinetic energy due to mean velocity gradients. $C_{\mu }, C_{1\epsilon }$ and $C_{2\epsilon }$ are constants generally assigned values of 0.09, 1.44 and 1.92 respectively, based on experiments on turbulent shear flows of air and water. ${\sigma }_k$ and ${\sigma }_{\epsilon }$ are turbulent Prandtl numbers for turbulent kinetic energy and dissipation rate and are assigned the values 1, and 1.3, respectively. The values of constants, mentioned above, are empirical in nature, and are found to work fairly for many flows [27].

To simulate the near wall flow regimes, where the flow is significantly different from the mean flow, $Std k-\epsilon$ model is applied to the flow domain in conjunction with an enhanced wall treatment, given its shortcomings in simulating high shear and wall bounded flows. In effect, the wall treatment includes semi-empirical formulae that bridge the solution variables from a high shear wall bounded regime to the mean flow. In particular, the Enhanced Wall Treatment achieves blending of the linear (laminar) and the logarithmic (turbulent) regimes of a turbulent boundary layer by the Equation (4) [28]. The super script ‘+’ denotes that the variable is taken in its non-dimensional form. Constants $c$ and $d$ are given the value of 0.01 and 5 respectively:

$$u^{+}=e^{\mathsf{\Gamma }}{u}_{lam}^{+}+e^{\frac{1}{\mathsf{\Gamma }}}{u}_{turb}^{+}$$

(4)

$$\mathsf{\Gamma }= -\frac{c{\left(y^{+}\right)}^4}{1+d{y}^{+}}$$

(5)

All the equations are solved using ANSYS Fluent solver.

3. Grid and Grid Sensitivity Tests

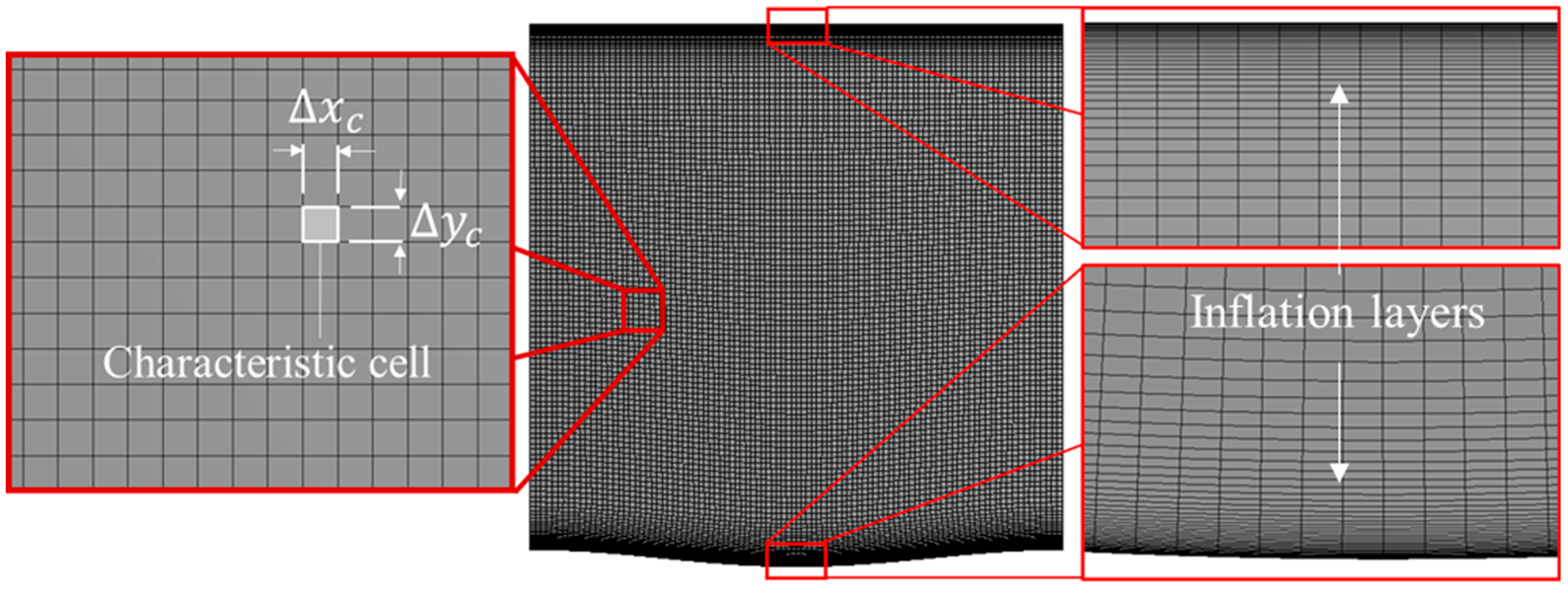
A rectangular cartesian grid is transformed to conform with the curvature of solid wave on the bottom. Layer height near the walls increases in geometric progression with a growth rate, $r_{in}$, set at either 1.1 or 1.2. For all 13 cases the first layer is designed to be at a $y^{+}$ = 0.25 to ensure that more than one grid point lies inside the viscous sublayer. For this study specifically, a ‘characteristic grid’ is defined as a rectangular cartesian grid applied to the computational domain in the absence of inflation layers applied near the wall. As an illustrative example, Figure 2 shows the grid used for the simulations $\mathit{C}$(I, V, I) and identifies the characteristic grid cell and the inflations layers present. The dimensions of the characteristic grid determine the number of grid points available in the domain. All simulations require that the dimensions of the characteristic grid cell are defined, so that the grid is not overly fine and the computational cost is not needlessly increased, neither be overly coarse such that the computed variables do not vary smoothly over the domain. The ratio of the length of the characteristic cell to its width, referred to as the cell-aspect-ratio, $A{R}_{cell}= \frac{\mathsf{\Delta }{x}_c}{\mathsf{\Delta }{y}_c}$, is an important parameter that effects the convergence of simulations. The $A{R}_{cell}$ ideally needs to be as close as possible to 1, implying that the length and width of the characteristic grid cell be equal to facilitate equivalent rates of information flow across the grid, per iteration of solution. Generally, depending on the size of the computational grid, $A{R}_{cell}$ between 0.01 to 100 is acceptable. Since the flow domain is not very large, $A{R}_{cell}$ is chosen as 1/0.9. The choice of 1/0.9 is deliberate so that the gradients of flow variables across the height of the channel, which are numerically much greater than streamwise gradients, are calculated with relatively tighter precision. Grids used for the 13 cases are characterized by the following gridding parameters: First layer height: $\mathsf{\Delta }{y}_1$, growth rate of inflation layers: $r_{in}$, characteristic grid cell dimensions: $\mathsf{\Delta }{x}_c$ and $\mathsf{\Delta }{y}_c$ and cell-aspect-ratio: $A{R}_{Cell}$.

Table 2. Details of gridding parameters.

	Simulation	$\frac{\mathsf{\Delta }{\mathit{y}}_1}{\mathsf{\Delta }{\mathit{y}}_{1, \mathit{C}\left(\mathit{I}, \mathit{I}, \mathit{I}\right)}}$	${\mathit{r}}_{\mathit{i}\mathit{n}}$	$\frac{\mathsf{\Delta }{\mathit{y}}_{\mathit{c}}}{\mathsf{\Delta }{\mathit{y}}_{1,\mathit{C}\left(\mathit{I},\mathit{I},\mathit{I}\right)}}$	$\frac{\mathsf{\Delta }{\mathit{x}}_{\mathit{c}}}{\mathsf{\Delta }{\mathit{y}}_{1, \mathit{C}\left(\mathit{I},\mathit{I},\mathit{I}\right)}}$	Nodes	Sensitivity Test Group
Base Case	$\mathit{C}$(I, I, I)	1	1.1	6	6.67	13,433	A
$AR$-variation	$\mathit{C}$(II, I, I)	1	1.1	6	6.67	7878	B
	$\mathit{C}$(III, I, I)	1	1.1	3	3.33	13,266	C
	$\mathit{C}$(IV, I, I)	1	1.1	3	3.33	7638	D
	$\mathit{C}$(V, I, I)	1	1.1	3	3.33	6633	E
$WS$-variation	$\mathit{C}$(I, II, I)	1	1.1	6	6.67	13,433	A
	$\mathit{C}$(I, III, I)	1	1.1	6	6.67	13,433	A
	$\mathit{C}$(I, IV, I)	1	1.1	6	6.67	13,332	A
	$\mathit{C}$(I, V, I)	1	1.1	6	6.67	13,332	A
$Re$-variation	$\mathit{C}$(I, I, II)	0.5	1.1	6	6.67	14,746	A
	$\mathit{C}$(I, I, III)	0.3	1.2	5	5.55	18,876	F
	$\mathit{C}$(I, I, IV)	0.16	1.2	5	5.55	19,602	F
	$\mathit{C}$(I, I, V)	0.1	1.2	5	5.55	20,328	F

lists the values for the gridding parameters for all 13 simulations. $A{R}_{cell}$ is maintained at 1/0.9 for all simulations for consistency. All dimensions are normalized by $\mathsf{\Delta }{y}_1$ for $\mathit{C}$(I, I, I) which is set at 30 $\mathsf{\mu }$m.

With increase in $Re$, higher velocity gradients are pushed closer to the wall. To capture these gradients, $\mathsf{\Delta }{y}_1$ is designed to be proportionally thinner with increase in $Re$. The base case is simulated with the first layer height of 30 microns and is gradually decreased down to 3 microns for the case with $Re$ = 100,000. For all other simulations however, $\mathsf{\Delta }{y}_1$ is maintained constant at 30 microns as the flow Reynolds number does not change. $r_{in}$ defines the rate of transition from the smallest grid height of the first grid layer near the wall, $\mathsf{\Delta }{y}_1$, to the characteristic grid cell height, $\mathsf{\Delta }y$. $r_{in}$ is maintained at 1.1 for all cases except $\mathit{C}$(I, I, III), $\mathit{C}$(I, I, IV) and $\mathit{C}$(I, I, V), where it is increased to 1.2. Since the first layer height corresponding to those three cases is very small, and with $r_{in}$ = 1.1, it takes many inflation layers to attain the characteristic grid height which translates to a very slow transition computationally.

To mitigate the computational cost of performing grid sensitivity tests on 13 simulations, a method is devised to anchor the outcome of the sensitivity study of one grid on the characteristics it shares commonly among different grids. Towards that effort, grids of the 13 cases are classified into six groups. All simulation cases in that group are modeled with similar combination of gridding parameters as used by the single grid of that group for which the grid sensitivity study is performed.

The simulation cases in $WS$ variation use geometry that is slightly different from the base case, in that the curvature of the bottom solid wave increases. Since the grid is cartesian-transformed to conform to the curvature, and, since the bounds on the $WS$ are such that linear response of variables can be expected, the change in curvature in solid wave cannot be classified as large enough to require a new grid for every case. Subject to concerns aforementioned, all cases of $WS$ variation—$\mathit{C}$(I, II, I) … $\mathit{C}$(I, V, I) along with the base case and $\mathit{C}$(I, I, II) are grouped under group A. Note that all the gridding parameters of group A are exactly alike except for $\mathit{C}$(I, I, II) where the increase in $Re$ requires that the first layer thickness is reduced to 15 microns. Note that 15 microns corresponds to $y^{+}$ = 0.25, which ensures that there are adequate number of grid points embedded in the viscous flow regime, and it ceases to be an influencing parameter in the grid sensitivity test. The other cases of $Re$-variation are grouped under group F as they require a finer characteristic grid along with thinner first layer. The simulations in groups A and F derive their gridding characteristics from $\mathit{C}$(I, I, I) and $\mathit{C}$(I, I, V) respectively. The case with the highest $Re$ is chosen to drive the gridding characteristics of group F as the grid of $\mathit{C}$(I, I, V) requires the smallest characteristic cell dimensions, which is also sufficient for the other two simulations. Groups B–E each contain 1 case corresponding to $AR$ variation. As the geometry changes drastically from one case to another with change in $AR$, it is required that every case of $AR$ variation is subjected to its own grid sensitivity test.

For the grid sensitivity study, three successive levels of grids, I, II and III, are conceived for every simulation set. Every successive grid level is designed by reducing the characteristic grid dimensions, $\mathsf{\Delta }{x}_c$ and $\mathsf{\Delta }{y}_c$, from the previous grid level in such a way that $A{R}_{cell}$ is maintained constant at 1/0.9 and $y^{+}$ is set at 0.25.

Table 3. Details of grid sensitivity study.

Sensitivity Test Group	Sensitivity Test Conducted on	Grid Level	${\mathit{r}}_{\mathit{i}\mathit{n}}$	$\frac{\mathsf{\Delta }{\mathit{y}}_1}{\mathsf{\Delta }{\mathit{y}}_{1, \mathit{C}\left(\mathit{I}, \mathit{I}, \mathit{I}\right)}}$	$\frac{\mathsf{\Delta }{\mathit{x}}_{\mathit{c}}}{\mathsf{\Delta }{\mathit{y}}_{1,\mathit{C}\left(\mathit{I},\mathit{I},\mathit{I}\right)}}$	$\frac{\mathsf{\Delta }{\mathit{y}}_{\mathit{c}}}{\mathsf{\Delta }{\mathit{y}}_{1, \mathit{C}\left(\mathit{I},\mathit{I},\mathit{I}\right)}}$	Nodes
A	$\mathit{C}$(I, I, I)	I	1.1	1	13.33	12	4641
		II	1.1	1	8.33	7.5	9315
		III	1.1	1	6.67	6	13,433
B	$\mathit{C}$(II, I, I)	I	1.1	1	13.3	12	3162
		II	1.1	1	8.33	7.5	5751
		III	1.1	1	6.67	6	7878
C	$\mathit{C}$(III, I, I)	I	1.1	1	6.67	6	5050
		II	1.1	1	4.17	3.75	9499
		III	1.1	1	3.33	3	13,266
D	$\mathit{C}$(IV, I, I)	I	1.1	1	6.67	6	4343
		II	1.1	1	4.17	3.75	5796
		III	1.1	1	3.33	3	7638
E	$\mathit{C}$(V, I, I)	I	1.1	1	6.67	6	4141
		II	1.1	1	4.17	3.75	5474
		III	1.1	1	3.33	3	6633
F	$\mathit{C}$(I, I, V)	I	1.2	0.1	11.11	10	6588
		II	1.2	0.1	6.94	6.23	13,871
		III	1.2	0.1	5	5.55	20,328

lists the details of the three grid levels of every simulation set. All dimensions are normalized by $\mathsf{\Delta }{y}_1$ for $\mathit{C}$(I, I, I) which is set at 30 $\mathsf{\mu }$m.

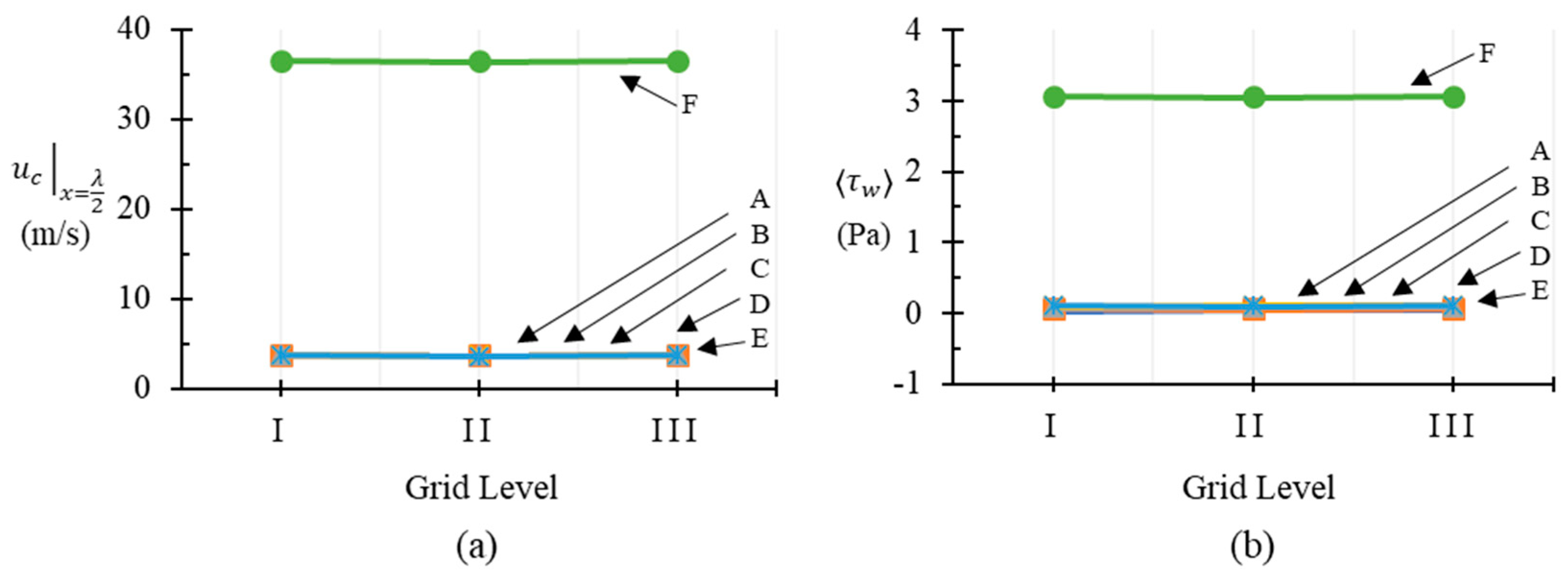
Figure 3 shows the results of the grid sensitivity study. Centerline velocity at $x=\frac{\lambda }{2}$ and wavelength average of wall shear stress are chosen to compare results of the three grid levels of every simulation set. For every set, the evaluated parameters remain practically constant over the three grid levels. The values of the parameters considered at grid levels II and III differ from grid level I by an average of 0.11% and a maximum by 0.38%. The data clearly suggests that the computations are grid-insensitive over the range of grid levels I to III. Hence, grid level III from every simulation set is chosen for analysis in this study.

4. Validation

For the solid wave defined as $y_s=a \cos \left(\theta x\right)$, flow modeled by a linear theory assumes a linear response of flow variables. Hence, the resolved flow variables will be a waveform with a single harmonic phase-shifted with respect to the solid wave. The time averaged shear stress and pressure on the solid boundary predicted by linear theory can then be denoted as follows (formulations inspired from Abrams and Hanratty [6]),

$${\tau }_w= \langle {\tau }_w\rangle +\left|\widehat{{\tau }_w}\right|\cos \left(\theta x+{\varphi }_{{\tau }_w}\right)$$

(6)

$$p_w= \langle p_w\rangle +\left|\widehat{p_w}\right|\cos \left(\theta x+{\varphi }_{p_w}\right)$$

(7)

$\langle {\tau }_w\rangle$ is the wavelength-average of ${\tau }_w$, $\left|\widehat{{\tau }_w}\right|$ is the amplitude of shear stress variation and ${\varphi }_{{\tau }_w}$ is the angle by which the shear stress leads the solid-wave. $\left|\widehat{{\tau }_w^{+}}\right|$, $a^{+}$ and ${\theta }^{+}$ are dimensionless quantities obtained by normalizing the shear-amplitude, solid-wave amplitude and the phase angle with either the kinematic viscosity ($\nu$) and friction velocity ($u_{*}$) or both. Benjamin’s [1] analytical predictions of shear stress and pressure on the solid wave were based on a quasi-laminar assumption. This meant that the wave induced variation of Reynolds stresses was assumed to be zero. Contrarily, linear theory applied to boundary layer coordinates model the Reynolds shear stress in different ways. Some widely adopted theories use modified versions of van Driest’s mixing length model. The essence of van Driest’s model lies in a constant $A_D$, which is indicative of the thickness of the viscous region in the turbulent boundary layer. $A_D$ is dependent on the formulation of the local effective pressure gradient subject to more control parameters. While, many investigators have suggested a number of formulations of $A_D$ for channel flows, Abrams and Hanratty [6], based on their studies and available literature on relaxation theory, proposed modifications to Loyd et al.’s formulations and found that it accurately traced experimental data for 0.0006 < ${\theta }^{+}$ < 0.01. Moreover, they compared their experimental data with the behavior of $k-\epsilon$ model and concluded the model did not adequately describe their measurements. Still, the current study uses the $Std k-\epsilon$ model in conjunction with Enhanced Wall Treatment to assess its credibility in simulating turbulent Couette flow over a solid wave.

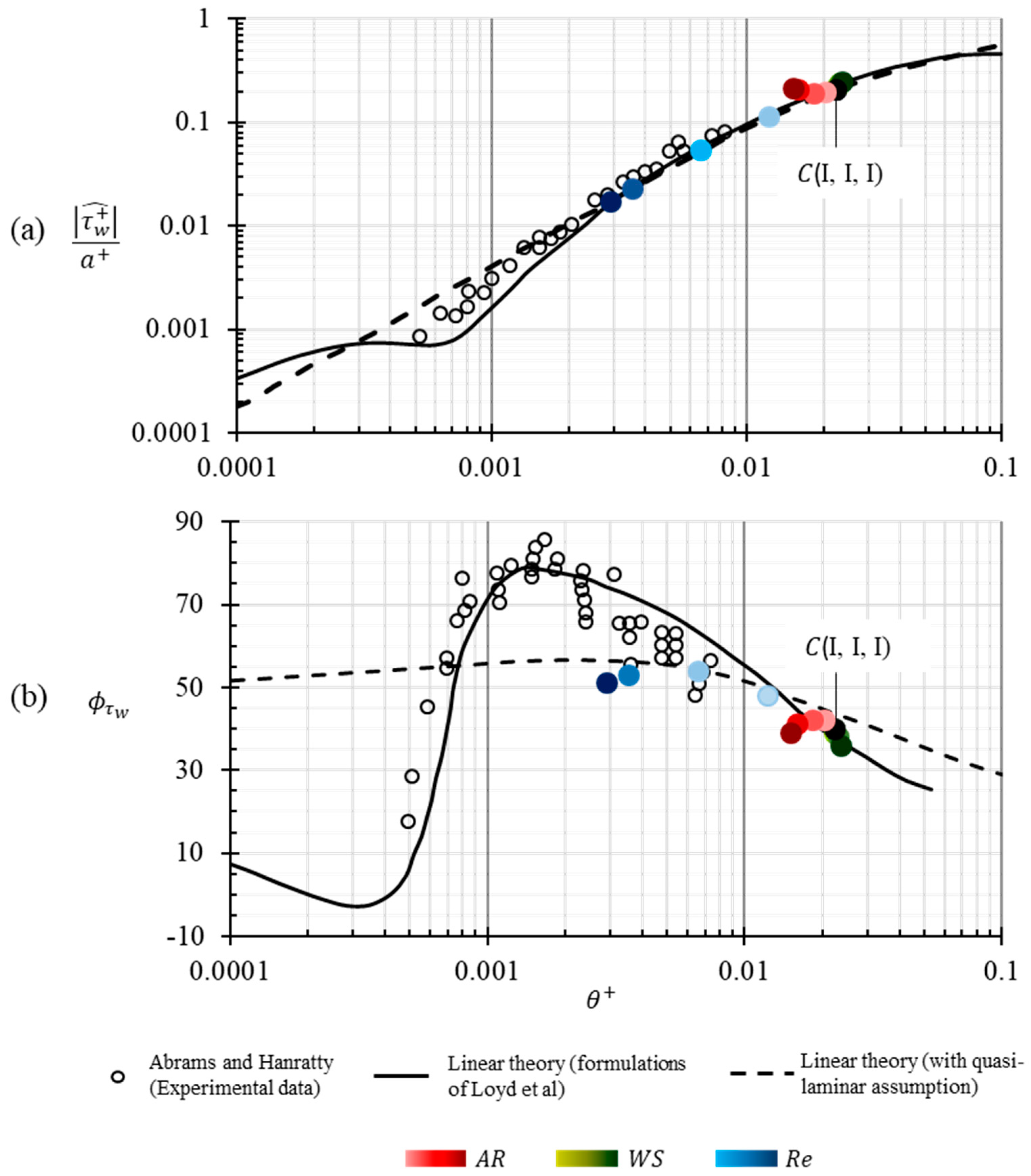
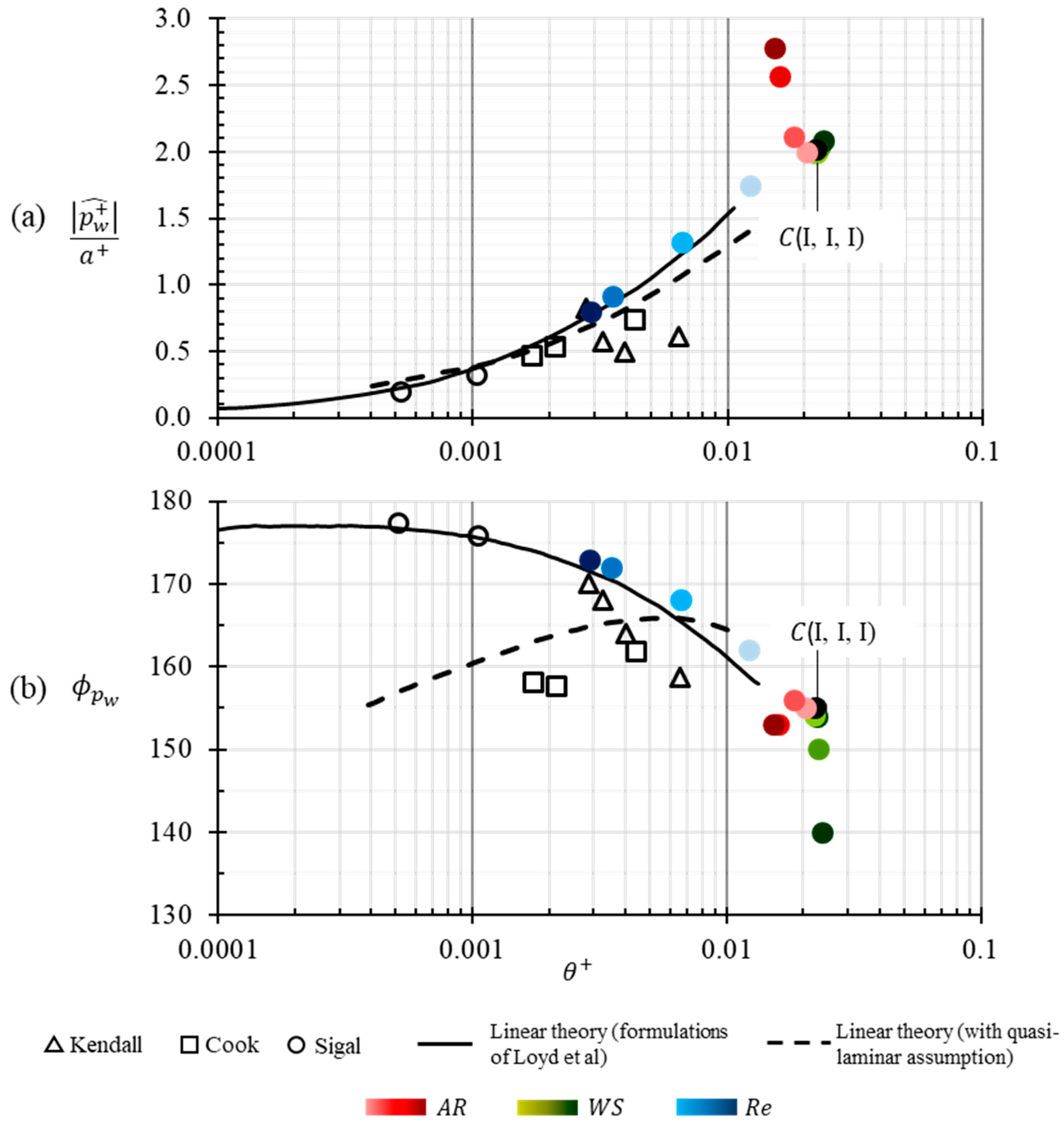
Figure 4 presents experimental data and performance of linear theory, along with the linear theory applied with a quasi-laminar assumption, in prediction of surface shear stress and its phase angle for different flow regimes. For ${\theta }^{+}$ > 0.007, where the laminar flow regime is expected to dominate, we see that the linear theory, as well as the theory applied with a quasi-laminar assumption predict the same surface shear. According to the linear theory, this behavior may be interpreted as the result of thickening of the viscous sublayer thus reducing the effect of wave induced turbulent shear and making the flow regime suitable for a quasi-laminar assumption. For increasingly turbulent flow regimes ${\theta }^{+}$ < 0.007, the quasi-laminar predictions deviate from linear theory suggesting an increased effect of wave-induced Reynolds shear. Most noticeable among the two charts is the precipitous drop of phase angle for 0.0005 < ${\theta }^{+}$ < 0.02 indicated by experimental investigations of Abrams and Hanratty. The linear theory accurately predicts this drop while the quasi-laminar predictions of phase shift primarily remain insensitive for ${\theta }^{+}$ < 0.006.

Figure 5 presents the prediction of linear theory—with and without the quasi-laminar assumption—and experimental data for surface pressure and its phase for different flow regimes. Linear theory, also applied with the quasi-laminar assumption, as well as experimental data concur and suggest that as turbulent character increases (${\theta }^{+}$ decreases), the normalized pressure-amplitude becomes insensitive to ${\theta }^{+}$. For ${\theta }^{+}$ > 0.003, while the normalized shear-amplitude predicted by linear theory and quasi-laminar assumption start to agree with each other, the normalized pressure-amplitude starts to diverge. There is also a noticeable disagreement of experimental data with predictions of the theory in that flow regime. There is no agreement on the prediction of phase angle of pressure between the linear theory and the theory applied with quasi-laminar assumption, except near the vicinity of ${\theta }^{+}$ = 0.006. Although, the experimental data is in general agreement of trend with the linear theory with no quasi-laminar assumption.

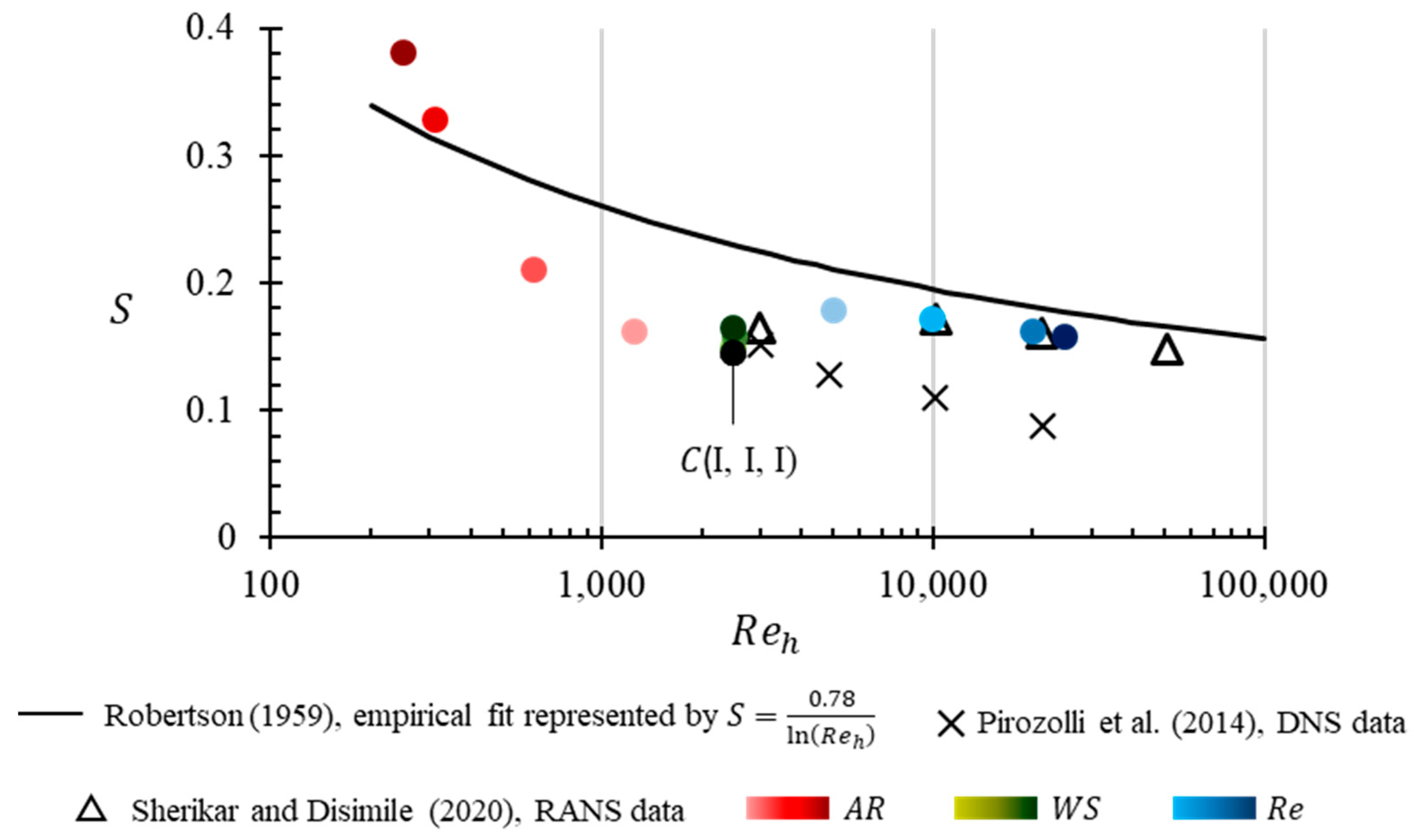
The base (or validation) case for the current study, $\mathit{C}$(I, I, I) was simulated resulting in a ${\theta }^{+}$ = 0.02233 which lies in range where there is good general agreement of the linear theory and the quasi-laminar predictions for surface shear stress and phase angle. Although, this data lies outside the range of available experimental data, the non-dimensional shear stress is in excellent agreement with both, the linear theory and the quasi-laminar prediction. To reinforce the validating stance of $\mathit{C}$(I, I, I), data from other simulations of the parametric analysis (independent variations of $Re$, $WS$ and $AR$) was also compared. Only the variation of $Re$ produced a considerable change in ${\theta }^{+}$ to display a trend suggesting that out of the three parameters considered, only the Reynolds number is effectual in influencing the overall shear stress experienced by the solid wave. The shear stress data from simulations varying in Reynolds number range from 0.0029 < ${\theta }^{+}$ < 0.02233 agrees with the linear theory and quasi-laminar predictions, and overlaps with the available experimental data. The phase data of the current study deviates largely from experiments in terms of the trend and in the values of phase shift. This observation is consistent with the observations of Abrams and Hanratty [6] with regards to $Std k-\epsilon$ model. However, it closely follows the predictions of linear theory applied with the quasi-laminar assumption. The normalized pressure-amplitude and the phase angle of pressure for $\mathit{C}$(I, I, I) seem to be in agreement with the prediction of linear theory if they were extrapolated. The simulations corresponding to $Re$-variation are in excellent agreement with linear theory’s predictions of normalized pressure-amplitude and its phase angle, as well as with the experimental data available in that flow regime.

5. Results and Discussion

Couette flow over a flat plate is very different from a Couette flow over a wavy plate, both in terms of gross flow properties and the potential turbulent structure. To elaborate this point, base case $\mathit{C}$(I, I, I) is compared against an equivalent Flat Plate Couette (FPC) flow. By an equivalent FPC it is to be noted that the geometry of the FPC case is rectangular with its length equal to the wavelength of the solid wave in $\mathit{C}$(I, I, I), its height equal to the mean height, $h_{avg}$ in $\mathit{C}$(I, I, I), as well as its height-based Reynolds number numerically equal to the wavelength-based Reynolds number used for $\mathit{C}$(I, I, I). To start with, the mean velocity profiles in a Couette flow over a wavy plate change periodically along the flow direction while those in an FPC flow are congruent to each other. 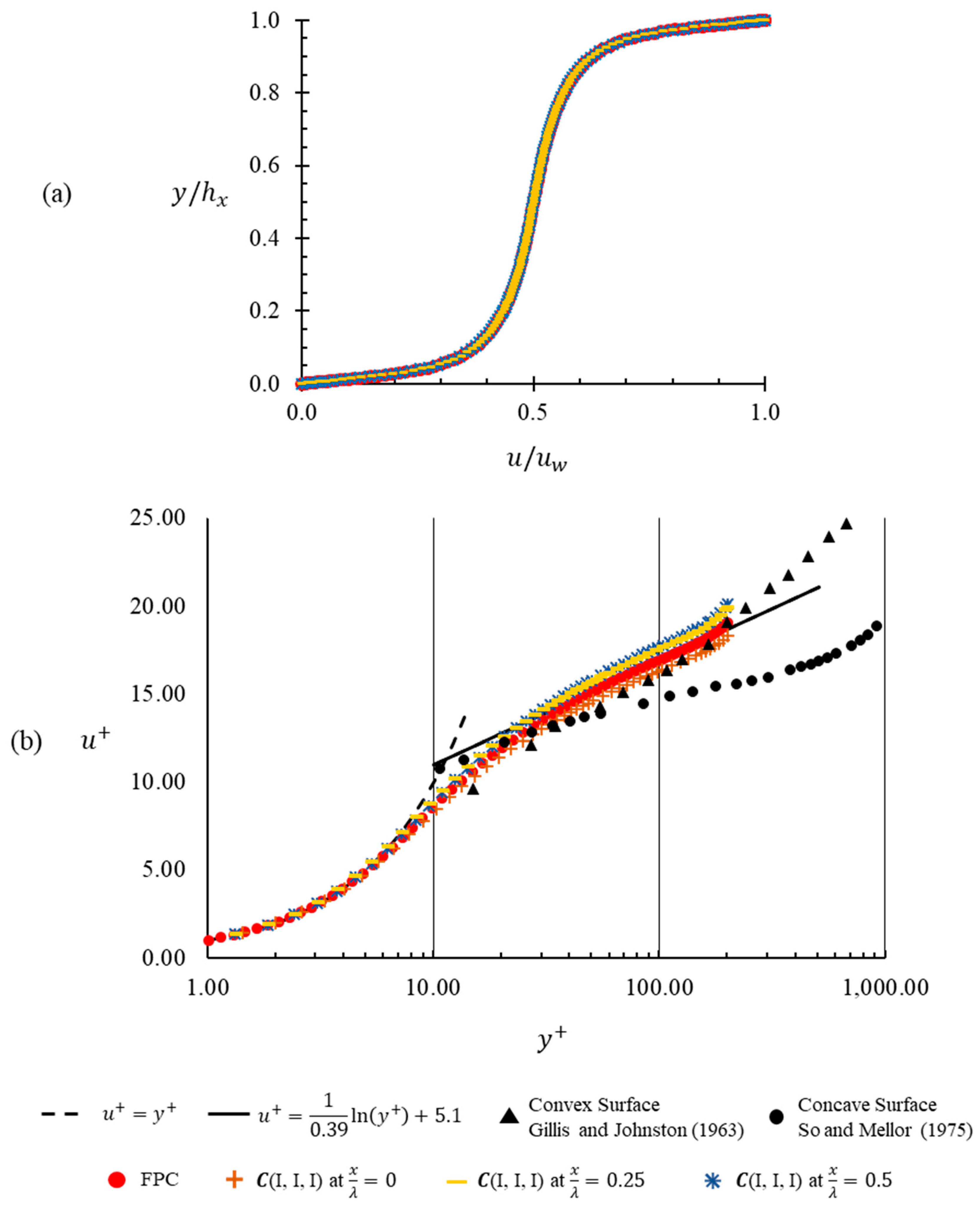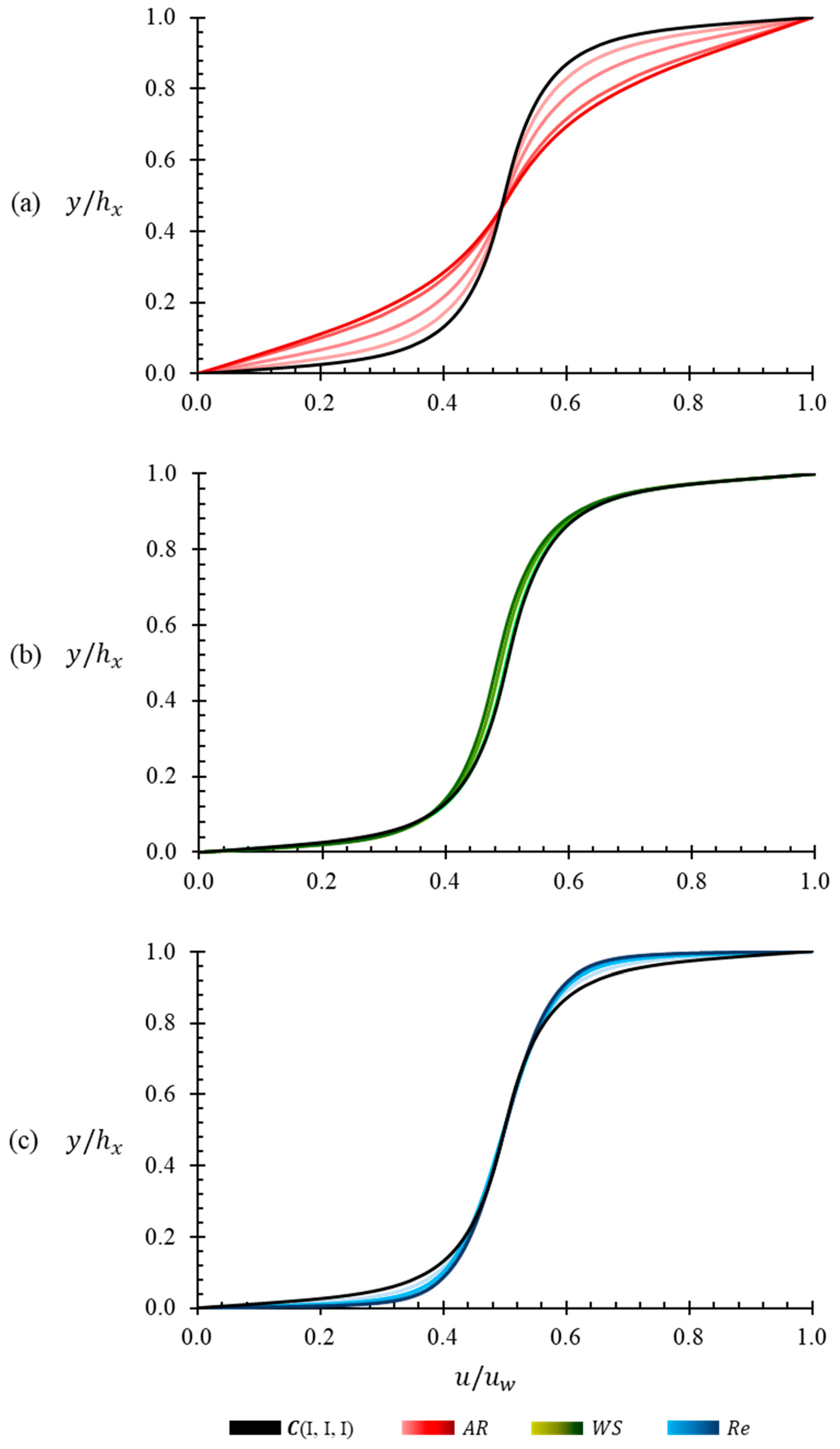At no point along the solid wave does the velocity profile across the channel in $\mathit{C}$(I, I, I) completely concur with the velocity profile of FPC flow. The distinction in the mean velocity profiles at different streamwise locations of the base case and FPC flow is not apparent in Figure 6a. It may be because a wave-slope of 0.01 is not large enough to affect a conceivable deviation in gross flow properties. It will, however, be clarified in further sections that the gross flow properties are sensitive to changes in the wave geometry, and are drastically different from those in an FPC flow. Unlike the mean velocity profile, the inner wall coordinates of the normalized velocity show remarkable and consistent deviations, not just with respect to FPC flow, but also with respect to other streamwise locations of $\mathit{C}$(I, I, I). In $\mathit{C}$(I, I, I). However, the viscous sublayer remains unaffected throughout the wavelength, while the inertial sub layer seems to flex and relax about the log law fit of the flat plat Couette flow as curvature of the solid wave is traversed. The streamwise locations are chosen at the peak ($\frac{x}{\lambda }=0$), at the trough ($\frac{x}{\lambda }=0.5$) and half-way between the two ($\frac{x}{\lambda }=0.25$) on the sinusoidal solid wave where its curvature progressively changes from convex to concave. Consequently, the plots of the inertial sublayer at those streamwise locations display a trend corresponding to the change in wall curvature. The non-dimensional velocity at the peak is slightly lower than the log law fit unlike the trough where it is slightly higher than the log law fit. This trend is consistent with the literature available for turbulent boundary layers in curved streamlines. Data from Bandyopadhyay’s review [29] is included in Figure 6b to demonstrate a qualitative consensus on characteristic deviations in turbulent boundary layer over curved surfaces.

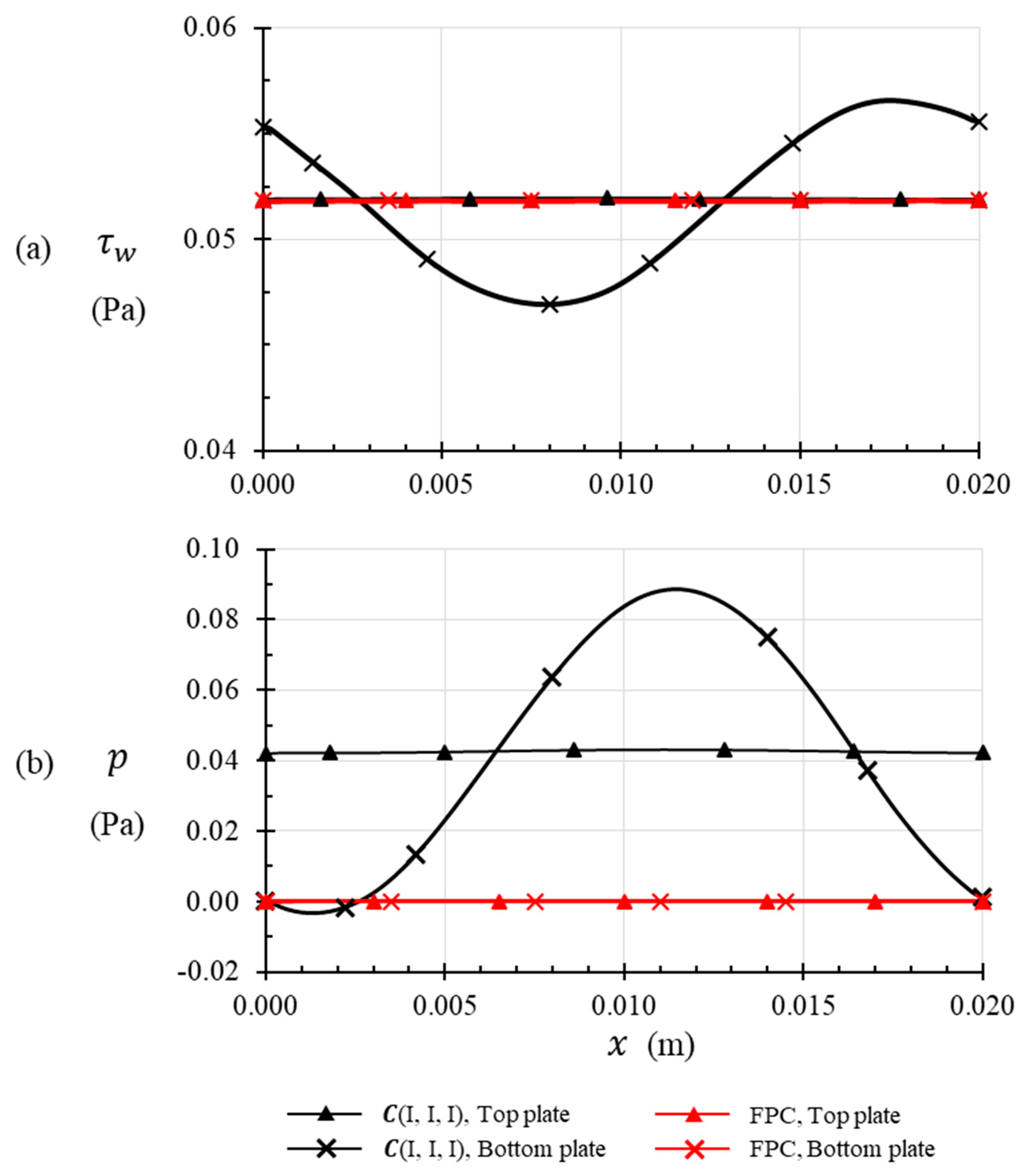
The static pressure on the bounding walls of an FPC flow is constant, and equal to any reference pressure the flow domain may be subject to. In the case of FPC flow the reference pressure was set to 0 Pa as it is indicated by the red lines in Figure 7b. In the base case, the curvilinear streamlines induce a sinusoidal variation in static pressure along the bottom wall. Shear stress is also observed to vary sinusoidally on the wall. It is to be noted that Figure 7 plots only the magnitude of shear stress and pressure. The direction of shear stress tensor at any point on a wall is tangent to the slope at that point and needs to be interpreted as being in the direction of local flow experienced at that point. Integral momentum equations applied to the control volume assert that the total force along x and y directions independently must amount to zero. In FPC flow, as can be discerned from Figure 7, the only forces on control volume are in the streamwise and in the opposite direction, due to shear stress on the flat walls. Since the shear stresses on both walls are equal and in the opposite direction, the integral momentum equations are conserved.

In the base case, the force on the bottom plate is two-dimensional as it is the result of the combination of sinusoidal shear stress and sinusoidal pressure both of which have varying components along the x and y directions. The force on the top plate is due to a constant shear stress and pressure that act only in one direction. Figure 7 demonstrates that the forces on the top and bottom walls, due to shear stress are equal and opposite to each other, and the total force on the domain, due to the shear stress is zero. Pressure forces on the top and bottom walls also cancel each other in the similar fashion.

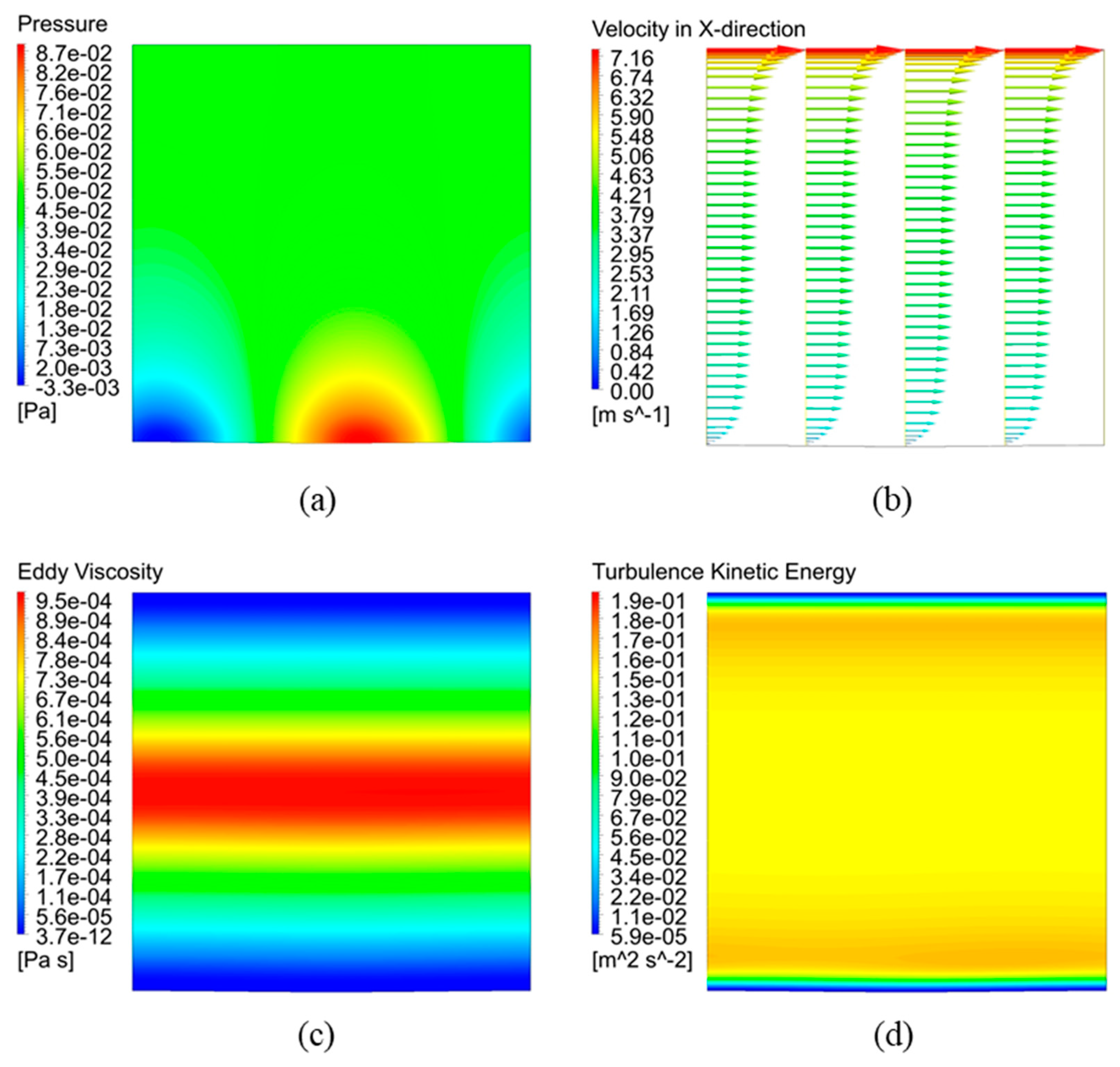
Figure 8a presents the contours of pressure in the flow domain for $\mathit{C}$(I, I, I). A high-pressure region forms near the trough and is shifted slightly towards the windward side of the solid wave. The same shift in peak of pressure is experienced by the wall, as seen in Figure 7b and was quantified in Figure 5b. It is noted that the contours of pressure for $\mathit{C}$(I, I, I,) are characteristic for all simulations in the study, but with changes in intensity and phase-shift with respect to the solid wave. Contours of eddy viscosity and turbulent kinetic energy (TKE) for the base case are plotted in Figure 8c,d. Additionally, velocity vectors are plotted in Figure 8b. Eddy viscosity decreases near the walls but reaches its maximum at the central region of the flow. TKE peaks close to the wall and depletes towards the core region. The variation for the three quantities in Figure 8b–d is negligible with respect to the streamwise direction, as seen in the contours and vector plots. Hence, wherever applicable, comparisons are presented along a line through a longitudinal cross-section of the domain to facilitate comparison of these quantities and to track their dependence on the three parameters.

It is also important to note that the only independent parameter in a steady-state, infinite FPC flow, is the Reynolds number because it accounts for every flow defining attribute of an FPC, namely: Relative velocity of bounding plates as the source of shear, distance between the plates as a complete geometry definition and fluid properties like density and viscosity, as the parameters that set the tone of inertia and resistance in response to the applied shear. However, in the case of a wavy plate Couette flow, there are three independent parameters, $Re$, $WS$ and $AR$, that completely define a wavy plate Couette flow. Also, different cases of a flat plate Couette flow can be considered more similar to each other than different cases of wavy plate Couette flow, which is to say that, in a given range of parameters, changes in geometry and flow conditions in an FPC flow affect changes in flow variables that may be predicted by a linear extrapolation of pre-analyzed cases. However, changes in wavy plate Couette flow will result in flow characteristics that may need a higher order approximation, rather than a simple linear extrapolation of previous case data. Therein, lies the importance of this study.

5.1. Velocity Profiles

Figure 9a shows the effect of increasing $AR$ on normalized mean velocity profiles at $\frac{x}{\lambda }$ = 0. The slope of mean velocity at the centerline gradually decreases with increase in $AR$, and is reminiscent to the effect of change in Reynolds number in an FPC as recorded by Sherikar and Disimile [26]. The change in aspect ratio of an infinite FPC flow culminates to an effective change in Reynolds number. In the same way, the change in $AR$ of a wavy plate Couette flow may also be interpreted as inducing a change in terms of Reynolds number based on mean height, $R{e}_h$. Notice that $R{e}_h$ is defined based on the half of the average height of the channel, and average centerline velocity, which is assumed to be equal to the half of plate velocity $u_w$. The literature [26,30] provides ample evidence of decrease in the centerline slope, measured by a quantity $S=\frac{h_x}{2u_{c_x}}\left(\frac{du}{dy}\right)$, with increase in Reynolds number of FPC flow. The centerline slopes for mean velocity profiles are plotted with respect to $R{e}_h$ in Figure 10. The data is plotted only for $\frac{x}{\lambda }=0.5$, as the variation of centerline slope along the streamwise direction for every case in this study is negligible. The following statistics are presented to quantify the variation: the deviation in centerline slope for different streamwise locations in a particular case on an average is 1.67% while its maximum was found for $\mathit{C}$(V, I, I) at 2.75%. For all cases of $Re$-variation, the deviation in centerline slope along different streamwise locations on an average is 0.81%, while $\mathit{C}$(I, I, V) exhibited the maximum deviation at 1.05%. The trend exhibited by the centerline slopes in Figure 10 is in general agreement with literature. Also, the increase in centerline slope, in combination with the decrease in the curvature of velocity profile, seen in Figure 9, is indicative of the flow profile tending towards a straight laminar profile, and is in consensus with the reduction in $R{e}_h$. In contrast, from Figure 4 and Figure 5 it can be established that increasing $AR$ results in a decrease in ${\theta }^{+}$ which can be interpreted as increase in turbulent character of the flow. This discrepancy boils down to the observation that the shear stress, and by extension, the friction velocity increases as $AR$ is increased, even though the velocity gradient at the walls decreases.

Change in the wave slope of the solid wave results in change of its curvature. Figure 9b shows that there is no appreciable change in normalized velocity profiles with respect to $WS$ over an increase of an order of magnitude, implying that the centerline velocity slope, $S$ remains fairly constant at the value demonstrated by the base case $\mathit{C}$(I, I, I). Although the amplitude of the solid wave changes, the average height of the channel, $h_{avg}$ remains constant and so does $R{e}_h$. The constancy of $R{e}_h$ explains the apparent unchanging centerline slope of mean velocity profile for cases with increasing $WS$ in Figure 9b. However, in Figure 10 the centerline slope is seen to monotonically increase very slightly with increase in $WS$, with the difference of slopes between $\mathit{C}$(I, I, I) and the $\mathit{C}$(I, V, I) being 13.5%.

Figure 9c suggests the gradient of mean velocity increases at the walls with higher $Re$ while the gradient at center is approximately identical although Figure 10 indicates a slightly decreasing trend. $R{e}_h$ also increases by virtue of the increase in velocity of the top plate. The centerline slopes plotted in Figure 10 match very closely with data from Sherikar and Disimile [26]. The centerline slope increases by 23.27% going from $R{e}_h$ = 2500 for $\mathit{C}$(I, I, I) to $R{e}_h$ = 5000 for $\mathit{C}$(I, I, II) and then continues to follow a slow decreasing trend exhibited by literature.

To summarize the observations made above, for the range of parameters considered, it can be asserted that the normalized mean velocity profiles depend only on the Reynolds number, based on channel’s half-height, $R{e}_h$, despite the wavy nature of the bottom wall. Absolute velocity profiles for different streamwise locations are not identical because of differences in curvature and channel height, but when they are normalized by the local height of the channel at that streamwise location, the profile is identical to those at any other streamwise location.

5.2. Pressure and Shear Stress

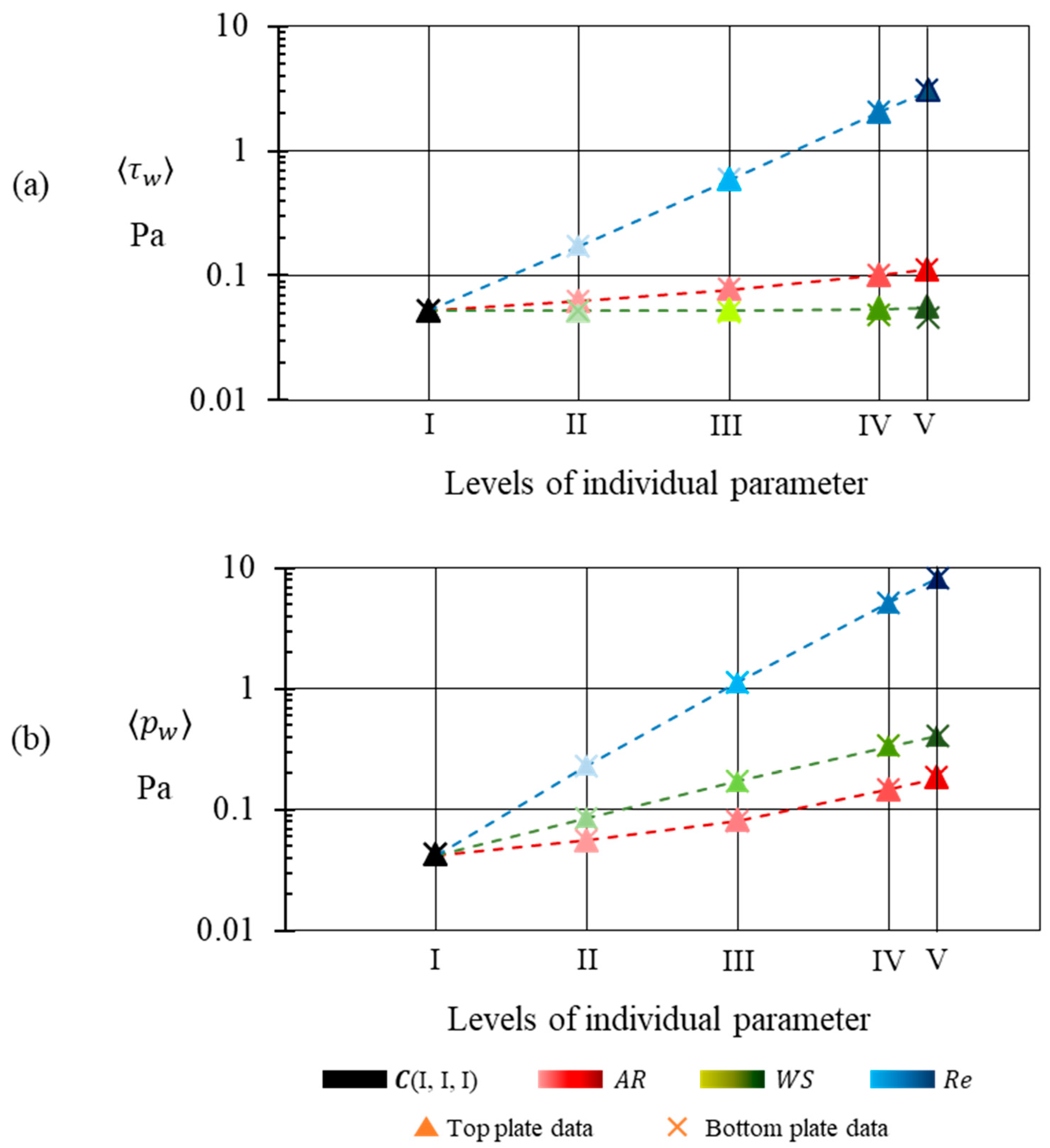
Figure 11 presents the wavelength average of shear stress and pressure on the top and bottom plates for all 13 cases simulated in this study. For every case, the average wavelength of the shear stress for the top and bottom plate is equal. The same hold true for wavelength average of pressure. Since the data plotted for the top and bottom plates are equal for every case simulated in this study, Figure 11 immediately confirms that the integral momentum equations are conserved.

The levels of the three parameters are designed to increase exponentially till the fourth level. The fifth level is chosen to accommodate an order of magnitude increase from the base level. The variation in $Re$ has the most prominent impact on both the wavelength averaged shear stress, as well as pressure as they increase by almost three orders of magnitude over just one order of magnitude increase in $Re$. Wavelength-average of shear stress on the top and bottom plate is unaffected by changes in $WS$. Figure 11 shows that the variation of average pressure and shear stress is far less sensitive to change in $AR$ as compared to change in $Re$.

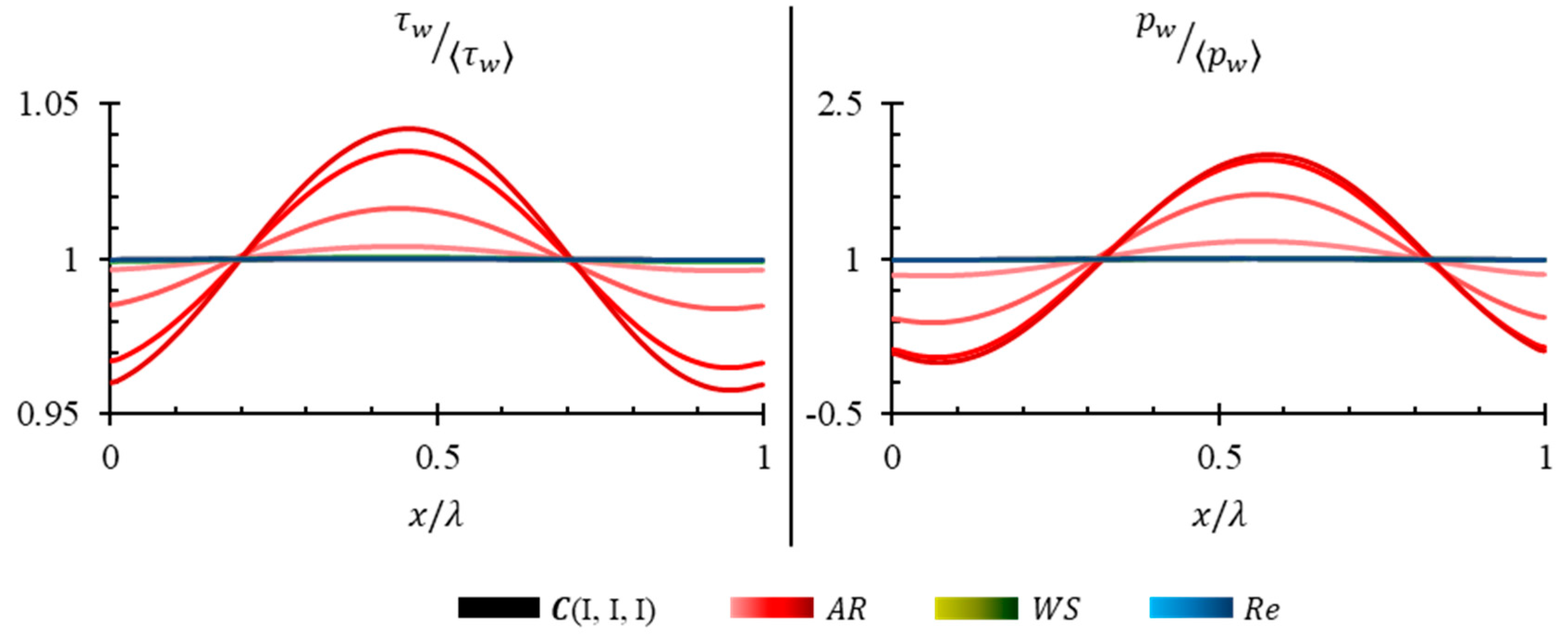
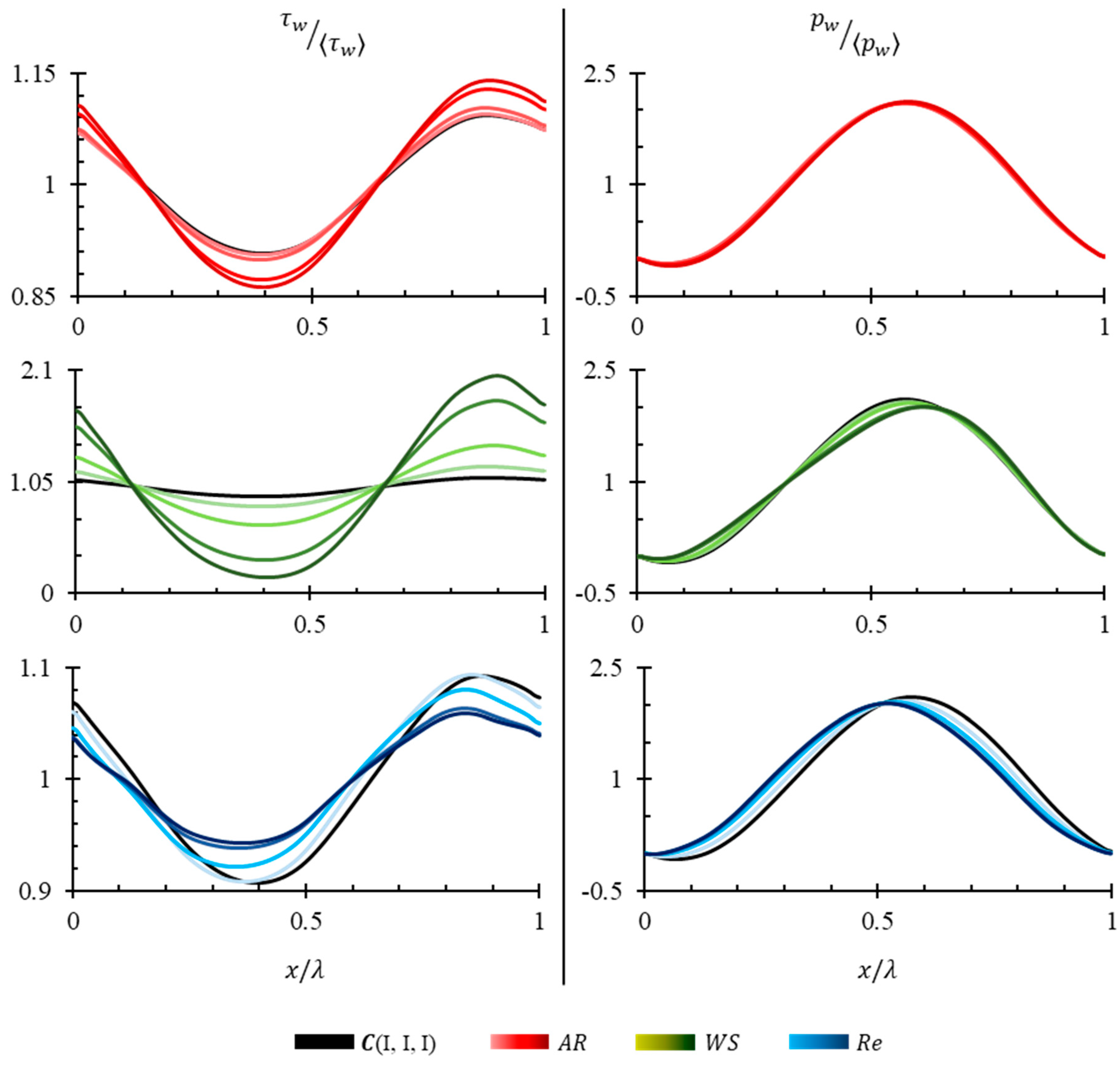
Pressure and shear stress along the top plates normalized by their respective wavelength averages are represented in Figure 12. The same quantity for the bottom plate is shown in Figure 13. The shear stress and pressure are sinusoidal in nature but phase shifted with respect to the solid wave. Peculiarly, only the normalized pressure-amplitude on the bottom plate in Figure 13 does not scale with change in any parameter. It implies that the absolute value of pressure on the bottom plates scales with the same rate as shown by Figure 11b. The normalized shear stress on the bottom plate however varies uniquely with variation in levels of each parameter. It implies that the shear stress on the bottom plate scales in the same rate as the wavelength-average of shear stress in addition with an overlaying scaling factor indicated by Figure 11a.

The phase-shift of pressure and shear stress does not change with $AR$ and remains constant at approximately $40°$ and $155°$ respectively (refer Figure 4 and Figure 5). Figure 12 shows that the top plate experiences higher amplitudes of pressure and shear stress uniquely only with increase in $AR$. In a dynamic scenario, the sinusoidal response of pressure and shear stress translates to vibration and fatigue in the top plate. For example, given the case $\mathit{C}$(V, I, I) we know $Re$ = 10⁴. Assuming an arbitrary system wall moving over a small undulation of $\lambda$ = 0.02 m, it can be evaluated that the system wall experiences a significant first order excitation of 365 Hz. It is important to note that the resultant force, due to a sinusoidal pressure or shear stress on a plate, be it flat or wavy, is only in one direction, and its magnitude is equal to its corresponding force’s wavelength average. Figure 11, Figure 12 and Figure 13 viewed in conjunction give a complete description of variation of shear stress and pressure response. While $\langle {\tau }_w\rangle$ scales linearly with increasing $AR$, Figure 12 and Figure 13 indicate the normalized shear-amplitude on the top and bottom plates scales monotonically. The same behavior is exhibited by pressure, but only on the top plate. On the bottom plate, the normalized pressure-amplitude does not scale with $AR$.

Normalized shear-amplitude for variation of $WS$ scales the most with change in $WS$, although $\langle {\tau }_w\rangle$ does not change with change in $WS$. The peak and the trough of normalized pressure-amplitude response on the bottom plate do not shift in the same way, suggesting that the response may be deviating from being sinusoidal in character. This deviation from a linear response of pressure is also visible in Figure 5 where the phase shift for $WS$ = 0.08 and $WS$ = 0.1 deviates immensely from the trend suggested by the linear theory, as well as the trend suggested by other simulations of this study. For $WS$ = 0.08 and 0.1, while the peaks of a sinusoid were adjusted to judge the shift in phase, a satisfactory curve fit with a sinusoid was never achieved.

Uniquely, the normalized shear-amplitude on the bottom plate reduces for increase in $Re$. Figure 13 shows a slight waviness being introduced to shear stress response for higher values of $Re$ implying the emergence of a higher order harmonic. Although, as indicated earlier, the normalized velocity profiles for all streamwise locations are congruent and indicate no evidence of separation, which is also corroborated by the fact that the shear stress is observed to never change its sign on the bottom wall. This observation is true for all cases in the current study and corroborates the fact that there was no reversal of flow observed for any case.

5.3. Velocity Coordinates Near the Wall

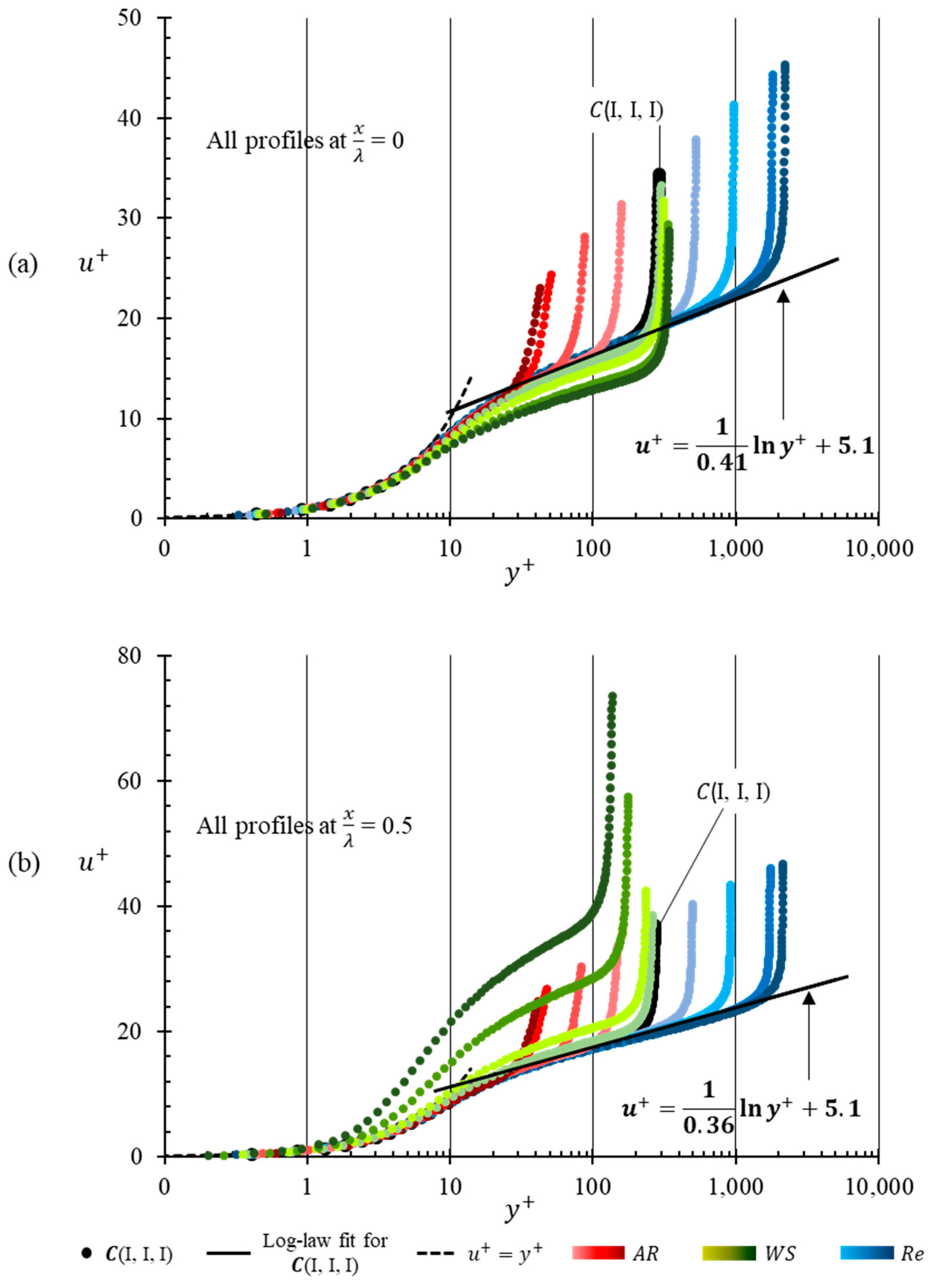
$AR$ determines the distance between the top and the bottom plates. The inner wall coordinates clearly show the effect of variation of $AR$ in Figure 14. As $AR$ increases, the top wall moves closer to the wavy wall, and hence, exerts a greater influence on the wavy wall shear layers. First impressions suggest that a free wake region is almost non-existent for all cases, including the base case. With increase in $AR$, the non-dimensional velocity diverges from the log-law fit at distinct values of $y^{+}$, and finally becomes insensitive to the lower wall indicating a strong influence of the top wall. For the base case the divergence from log-law is approximately at $y^{+}\approx 200$. A $y^{+}$ of 150 corresponds to half channel height, $h_x$, at $\frac{x}{\lambda }$ = 0 and $\frac{x}{\lambda }$= 0.5. The observation that the non-dimensional velocity deviates from log-law approximately at half channel height is consistent for all cases of $AR$. The most important consequence of this observation is that the inertial region gets cut shorter as $AR$ increases. The only conceivable difference between Figure 14a,b is that the log-law fits with $\kappa$ = 0.41 and 0.365 respectively, due to change in curvature, and by consequence, the change in local pressure. It is interesting to note that for the highest aspect-ratio case, $\mathit{C}$(V, I, I), the inertial region is effectively non-existent. For this case, a $y^{+}\approx$ 23 corresponds to half channel height at the peak of the solid wave. It implies that approximately 80–85% of the flow domain is under the influence of the viscous sublayer, and the remaining part experiences transition.

Figure 14 also shows the effect of curvature on the inner wall coordinates of velocity. The curvature of the solid wave distorts the velocity near the wall. The velocity coordinates plotted at the peak and trough of the solid wave differ in characteristics in that the non-dimensional velocity decreases notably for a given $y^{+}$ at the peak, while it increases remarkably at the trough. This result was obtained despite the normalizing factor, the local $u_{*}$ decreasing as we go from peak to the trough of the solid wave as indicated by Figure 13. Viscosity dominated region at the peak of the solid wave is of the same thickness for all cases of $WS$ variation as the deviation starts in the buffer layer. At the trough of the solid wave, the deviation in the velocity profiles starts in the middle of the viscosity dominated region at $y^{+}\approx$ 2. For $y^{+}$ > 2, $u^{+}$ = $\alpha y^{+}$ where $\alpha$ can be assumed to be a scaling factor such that it is a function of $WS$ along with other unknown parameters.

Though higher $Re$ results in higher velocity gradients near the wall, increasing the contribution to wall shear stress and $u_{*}$, the inner-wall coordinates for the velocity for all cases of $Re$-variation follow the log-law fit ascribed for the base case. In all these cases viscosity dominates the region above the bottom wall until $y^{+}\approx$ 8, which, for the base case, $\mathit{C}$(I, I, I), corresponds to a height of 0.55 mm. For the cases constituting $Re$-variation $y^{+}$ = 8 corresponds to progressively shorter heights, tentatively following a geometric progression. It implies that the viscosity dominated region progressively becomes thinner, from being about 2.7% of the channel height for $\mathit{C}$(I, I, I) to reducing to about 0.36% for $\mathit{C}$(I, I, V). The inertial region however varies in a bit more complex way. Nondimensional velocity coordinates become insensitive to the bottom wavy wall at a $y^{+}$ which increases with increase in $Re$. Although, the variation of the actual height at which they deviate from the log-law fit does not increase monotonically. It can be evaluated from

Table 4. Boundary layer details near for $Re$ variation.

Simulation	Viscous Region Ends at		Inertial Region Starts at		Inertial Region Ends at		Width of Inertial Region
	${\mathit{y}}^{+}$	$\left|\mathit{y}-{\mathit{y}}_{\mathit{s}}\right| \left(\mathbf{mm}\right)$	${\mathit{y}}^{+}$	$\left|\mathit{y}-{\mathit{y}}_{\mathit{s}}\right| \left(\mathbf{mm}\right)$	${\mathit{y}}^{+}$	$\left|\mathit{y}-{\mathit{y}}_{\mathit{s}}\right| \left(\mathbf{mm}\right)$	$\% \mathbf{of} {\mathit{h}}_{\mathit{a}\mathit{v}\mathit{g}}$
$\mathit{C}$(I, I, I)	8	0.550	30	2.094	200	13.76	58.3
$\mathit{C}$(I, I, II)	8	0.303	30	1.169	300	11.53	51.8
$\mathit{C}$(I, I, III)	8	0.165	30	0.651	500	10.28	48.1
$\mathit{C}$(I, I, IV)	8	0.089	30	0.364	1000	11.08	53.6
$\mathit{C}$(I, I, V)	8	0.073	30	0.304	1500	13.62	66.6

that the width of the inertial layer decreases as much as 14.5% between $\mathit{C}$(I, I, I) and $\mathit{C}$(I, I, III) and then increases by 17.3% at $\mathit{C}$(I, I, V).

5.4. Eddy Viscosity Across Channel

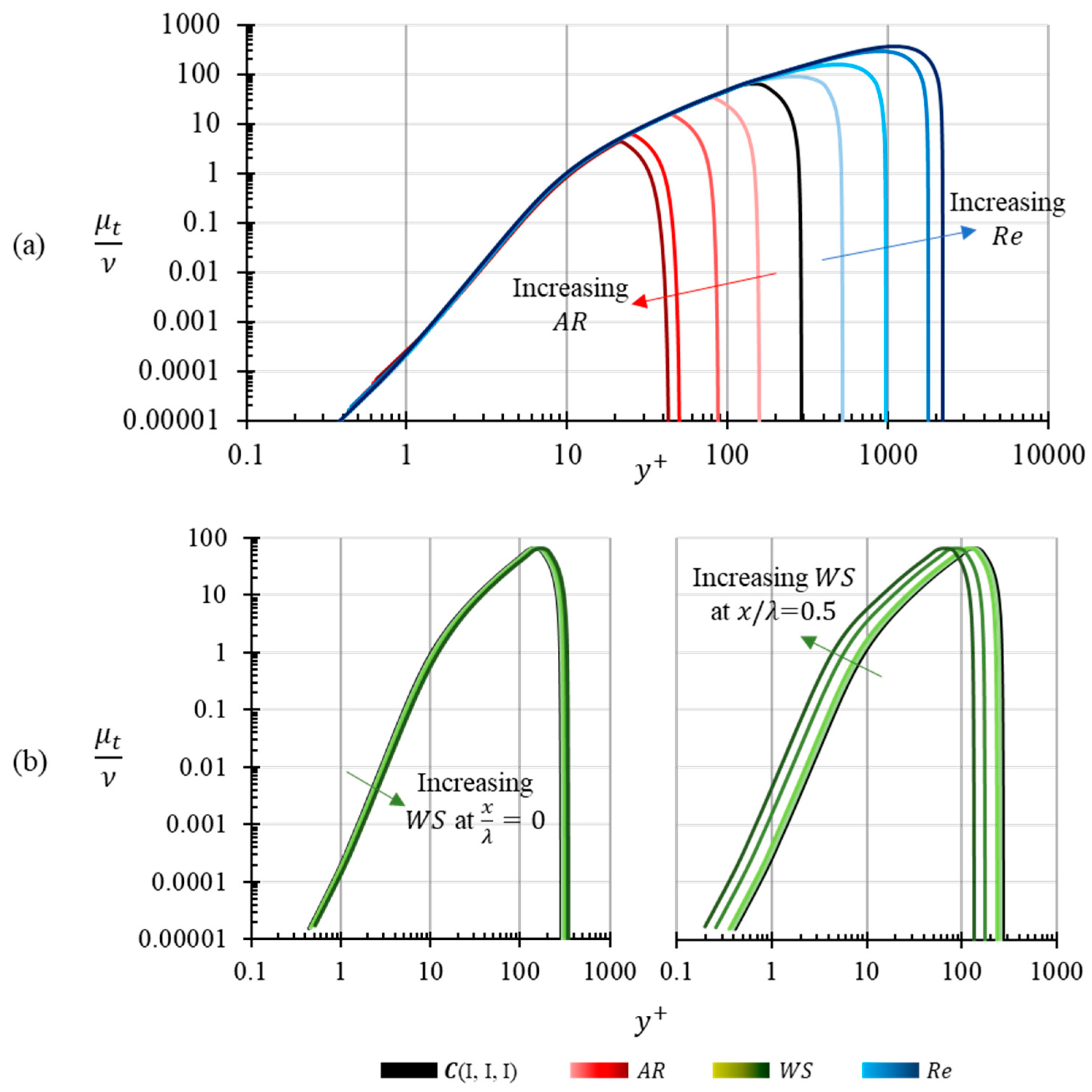
Figure 15 presents the eddy viscosity profiles across the channel for all 13 simulations. Eddy viscosity for any case tends to zero at the walls. The variation of eddy viscosity in the viscous region for $y^{+}$ < 10 seems universal as it is identical with no discernable deviation for simulations performed as a part of $AR$ and $Re$ variation. It is important to note that the eddy viscosity profiles, at any two distinct streamwise locations, are slightly offset from each other, due to a difference in curvature, but their trends, with respect to variation in $AR$ and $Re$, are consistent and identical at all streamwise locations. However, for $WS$-variation, the eddy viscosity characteristics vary with respect to the streamwise locations. The difference in trends is shown by Figure 15b, where it is evident that the eddy viscosity characteristics at the peak and trough are remarkably different from each other.

The influence of $WS$ on eddy viscosity may be of particular interest here. For a $y^{+}$ < 10, we see that trend of eddy viscosity does not change with respect to any parameter except $WS$. This effect seems to be more pronounced at the trough of the solid wave, rather than at its peak. It can be evaluated from Figure 15b that for any given $y^{+}$ < 10, there is an order of magnitude change in eddy viscosity going from $\mathit{C}$(I, I, I) to $\mathit{C}$(I, V, I). This result may be qualitatively interpreted to suggest that there is an increase of Reynolds stresses at the trough with increase in wave-slope. This observation corroborates many analytical theories modeled on various assumptions of wave-induced Reynolds stresses [1,4,6,32]. In relation to this observation, it will be seen in the next section that the turbulence kinetic energy increases by 5 times in the range of $y^{+}$ < 10.

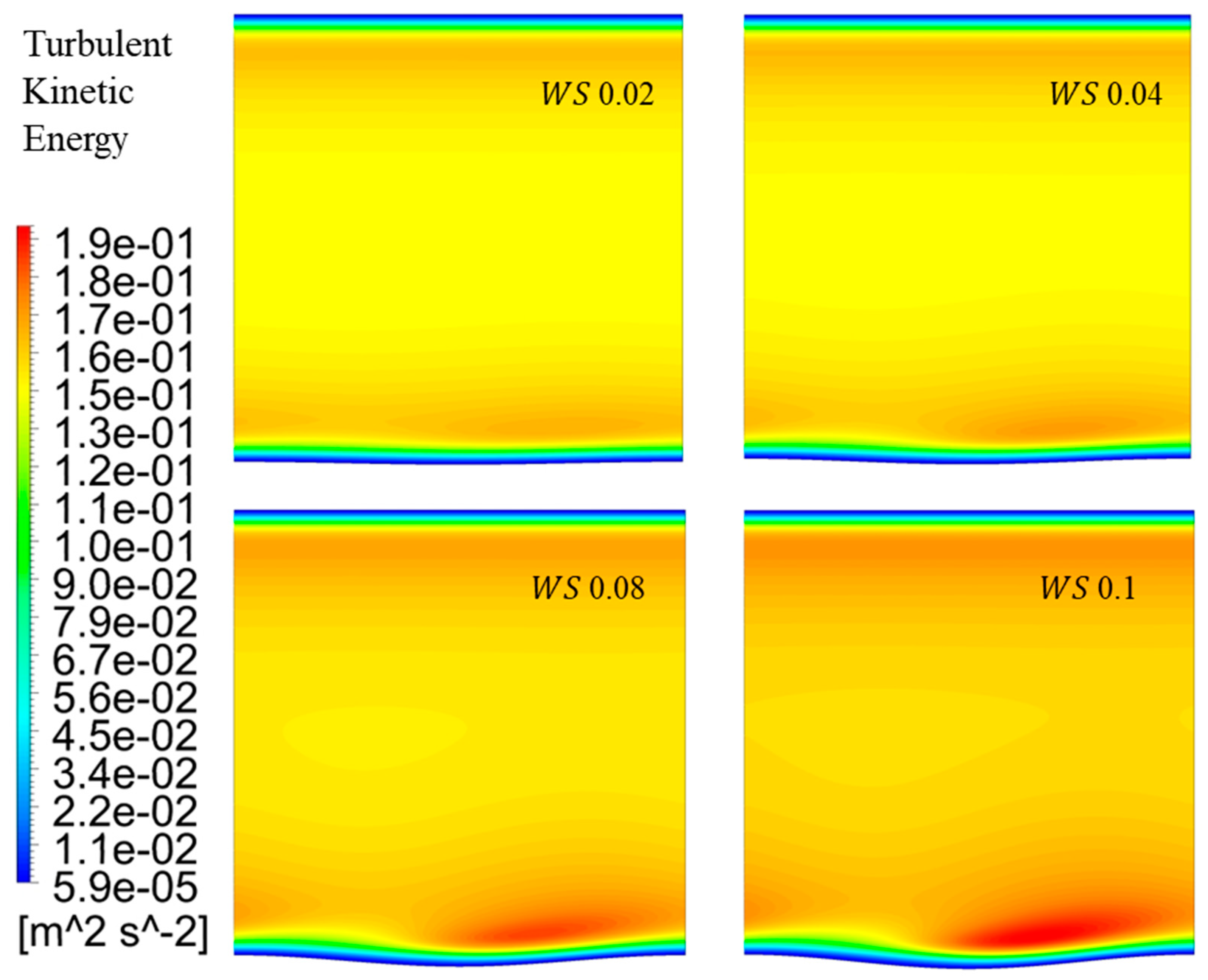
5.5. Turbulence Kinetic Energy Near the Bottom Wall

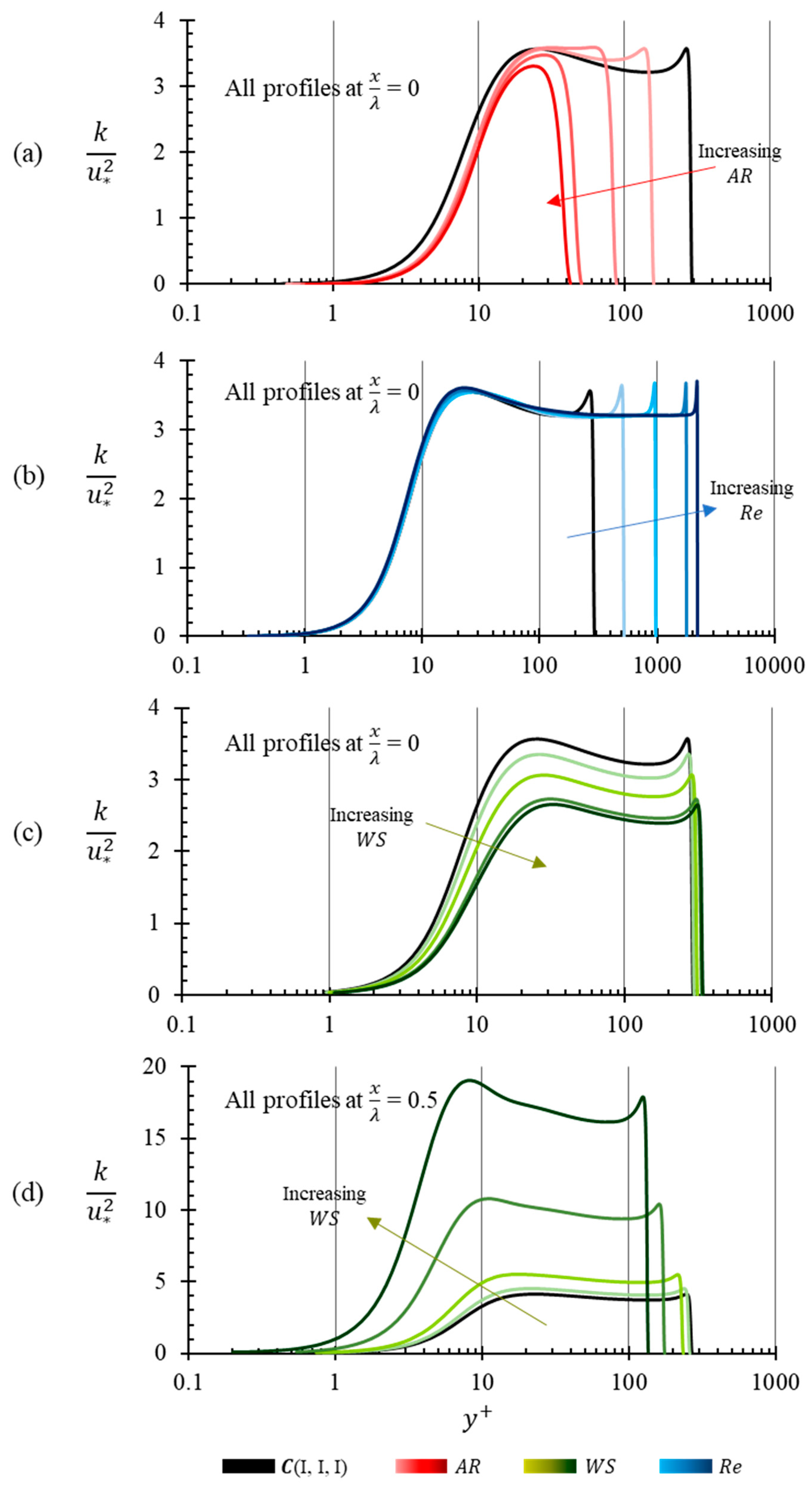
Figure 16a shows the normalized turbulent kinetic energy (TKE) variation across the channel for $AR$ variation. The location of the peak of TKE shifts insignificantly with respect to the walls but as the height of the channel reduces, the locations of the peaks corresponding to the two walls shift closer towards each other. For $\mathit{C}$(IV, I, I) and $\mathit{C}$(V, I, I) there is only one peak of TKE at $y^{+}\approx$ 20, which is approximately in the middle of the channel and corresponds to the buffer region of the turbulent boundary layer. For $\mathit{C}$(III, I, I) the location of the maximum TKE extends over a wide region from $y^{+}\approx$ 20 to 70, covering almost 68.6% of the flow domain. As pointed out earlier, the discrepancy of increase in friction velocity with reduction in $R{e}_h$ has another interesting implication in that the absolute value of TKE increases as the ‘laminar character’ of the mean velocity profiles increases with increase in $AR$.

TKE peaks at the same $y^{+}$ for all cases of $Re$-variation. As discussed earlier, variation of $AR$ and $Re$ may be viewed in a context of variation in $R{e}_h$. In that context, reducing $AR$ by a factor is equivalent to increasing $Re$ by the same factor and eventually, both operations should result in the same $R{e}_h$. Although the two cases are equivalent non-dimensionally, they are not remotely similar when turbulence and its effects are considered. The case in point here is that the turbulent characteristics, achieved by increasing the velocity of the top plate, are different for the same $R{e}_h$ achieved by increasing the channel height. The focus of this argument is to highlight the difference in rates of change of friction velocity due to the difference in the two ways the same $R{e}_h$ is achieved. The slopes based on $Re$-variation and $AR$-variation represented in Figure 11a are remarkably different. The difference in the two slopes implies that, for the same $R{e}_h$, $u_{*}$ at the walls would greatly depend on the velocity of the top wall rather than the height of the channel. In a much broader context, the argument emphasizes the difference in energy per unit of mass that is input into the fluid domain, due to the speed of the top plate. It can be hypothesized that this extra energy results in an increased TKE of the flow. The difference in TKE can be interpreted from Figure 16a,b, as it can be evaluated that the absolute TKE for cases with increasing $Re$ greatly differ from each other, about 340% on average, while they differ only about 124% for the $AR$-variation. This observation may support the hypothesis made above as a logical conjecture rather than as a rigorous proof.

Figure 16c,d suggest that TKE near the bottom wall at its peak is lower than the TKE at its trough. Also, it is interesting to note that TKE further decreases at the peak, while it increases at the trough for an increase in $WS$. Since the total kinetic energy input by the virtue of the top plate velocity is the same, it can be asserted that $WS$ plays a unique role in redistribution of this energy into turbulent kinetic energy, although the mechanism by which this energy distribution takes place is not clear. The role of $WS$ in this redistribution is evident as for $\mathit{C}$(I, V, I), a wave-slope of 0.1 results in accumulation of TKE about 5 times more than it would for the base case with wave-slope of 0.01. Simultaneously, a drop in TKE observed at the trough with increase in $WS$ corroborates the fact that $WS$ is instrumental in the redistribution of TKE. Since the characteristics of TKE at two different streamwise location is fundamentally different, TKE contours are presented in Figure 17, in addition to Figure 8d, to give a comprehensive picture of the TKE distribution with respect to $WS$-variation. There is a clear and a marked increase in TKE in the windward direction of the solid wave along with an average increase in the whole domain. This observation can be leveraged in many applications, especially the ones involving heat transfer and lubrication.

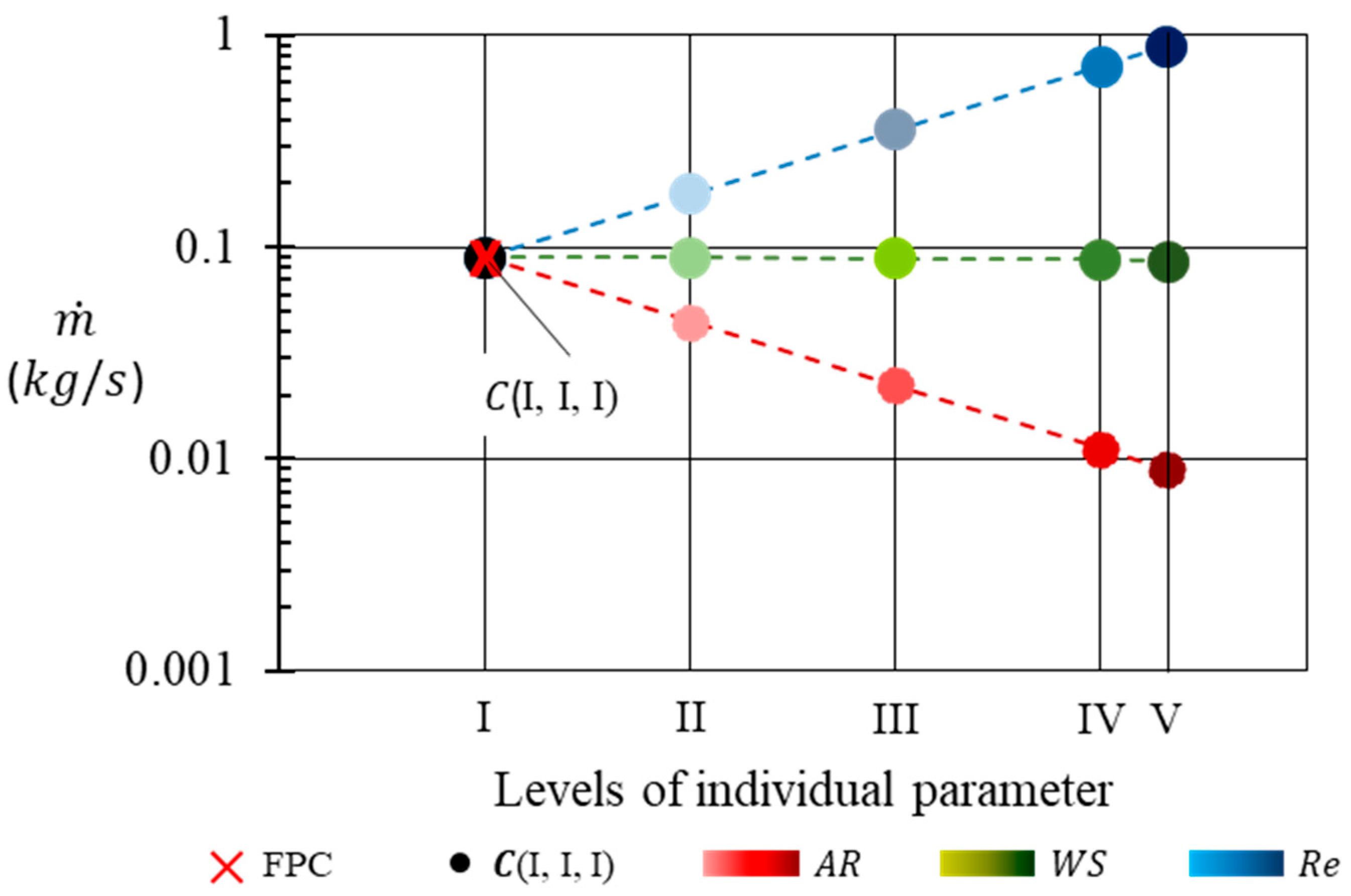
5.6. Mass Flow Rate

The mass flow rate for any case of incompressible Couette flow is directly dependent on its velocity field. Figure 18 shows that the variation of mass flow rate with respect to $Re$ and $AR$, respectively is linear. The mass flow rate increases with increase in $Re$, due to increase in the velocity of the top plate, while it decreases with increase in $AR$ as the cross-sectional area of the fluid domain reduces. Interestingly, the mass flow rate is insensitive to $WS$. It may be hypothesized that the constancy of $h_{avg}$ may be the reason why the mass flow rate is constant for different cases of $WS$, and by extension, it could be the reason for the FPC case and $\mathit{C}$(I, I, I) to have the same mass flow rate. While the constancy of $h_{avg}$ may explain the unchanging mass flow rate, the effect of the curvature of the solid wave remains unexplained and raises questions about the way velocity profiles may be set up at different streamwise locations. If the constancy of $h_{avg}$ is to be asserted as the reason for constant mass flow rate, it would follow that the flow characteristics at every streamwise location are affected by flow characteristics at every other location to average out the effect of solid wave.

Wang C. Y., [33] in his analytical work evaluated that the mass flow rate reduces due to the waviness of the bottom plate in a Couette flow subject to a creeping flow. The flow conditions evaluated in that study were different in that the $Re$ was approaching zero, which would imply a strictly laminar and a highly viscous flow condition. The quantity ‘$a/h_{avg}$’ was assumed to be much smaller than unity, as is also true for the current study. Unlike the flow condition [33], the Reynolds number in the current study is much higher and inertial effects become significant. Although this does not explain the reason for the insensitivity of the mass flow rate with respect to $WS$.

6. Conclusions

A total of 13 simulations were studied by changing three flow-defining parameters, $AR$, $WS$ and $Re$, over five levels. A grid sensitivity study was conducted to ensure that the data used to present the analysis is computationally reliable. For validation, normalized wall shear and pressure on the wavy bottom plate, along with the corresponding phase angles, were compared and found in general agreement with the predictions from analytical theories, as well as experimental data available on the subject. The initial comparisons of a wavy plate Couette flow with its equivalent flat plate Couette flow revealed remarkable differences in terms of mean velocity profiles, inner wall coordinates of velocity, surface pressure and shear stress.

Gross flow characteristics like mass flow rate, mean velocity profiles, wall shear and pressure, as well as turbulent flow characteristics, such as inner wall coordinates, turbulent kinetic energy and eddy viscosity across the channel were analyzed to evaluate the effect of the three parameters. Apart from the scaling of mean flow and turbulent characteristics, the effect of $AR$ highlights the influence of the top plate on wavy Couette flow, especially in very thin flow regimes. With increase in $AR$, the inertial region between the plates is gradually attenuated, resulting in interactions at the buffer layer and the viscous sublayers of the two plates. For the case with the maximum $AR$, it was observed that the inertial layer is almost non-existent as the influence of the top wall is felt in the buffer layer of the bottom wall. It is also clarified that change in $AR$ may be equivalent to change in $R{e}_h$ in terms of gross flow properties like mean velocity profiles. Although, the equivalence is not true for turbulent characteristics as their evolution is heavily dependent on the energy input in the fluid domain and on mechanisms of redistribution of that energy.

The effect of $WS$ has been studied in a range where the amplitude of the solid wave is small enough to stimulate only a linear response with the solid wave. The change in $WS$ has a unique effect on the pressure and shear stress on the wall. It was observed that only with the change in $WS$ can the average pressure be increased or decreased, while the average shear stress remains unaffected. In the case of change of $AR$ and $Re,$ but the average shear stress and pressure on the wall scale quasi-linearly. It is also important to note that the averages of shear stress and pressure increase more sensitively with respect to $Re$ than they do with respect to $AR$.

The inertial region for the peak and the trough deviate from the log law because of the change in curvature. With respect to the log law fit for the flat plate Couette flow, the coordinates of the inertial layer at the peak lie below, while those coordinates for the trough lie above it. Since the curvature of the solid wave can only be changed by a change in $WS$, it was observed that with the increase in $WS$, the deviation from the log law fit increased as the non-dimensional velocity continuously decreased at the peak and increased at the trough. These observations are compliant with literature available on general turbulent boundary layer flow over curved surfaces. For the change in $AR$ and $Re$, the deviation from the log-law fit remains constant.

The effect of $AR$ on the turbulent kinetic energy (TKE) is unique in its higher ranges. While every other case demonstrated two different peaks of TKE, each corresponding to the top and bottom wall, the cases with high $AR$ demonstrated peak TKE over a considerable width of the central region. The highest $AR$ case demonstrated just one peak. Increasing $Re$ is the only way to input more energy into the whole fluid domain. It is observed that the increased energy input leads to a proportional increase in TKE. It is unclear how energy is redistributed as TKE. It was observed that increasing $WS$ can lead to increased accumulation of TKE near the trough on the windward side of the bottom plate, as much as five times the TKE observed for the base case and a consequential decrease at the peaks. This observation suggests that the redistribution of the available energy into turbulent kinetic energy is dependent on the curvature of the bottom plate.