Theoretical Analysis of a Vertical Cylindrical Floater in Front of an Orthogonal Breakwater
Abstract
1. Introduction
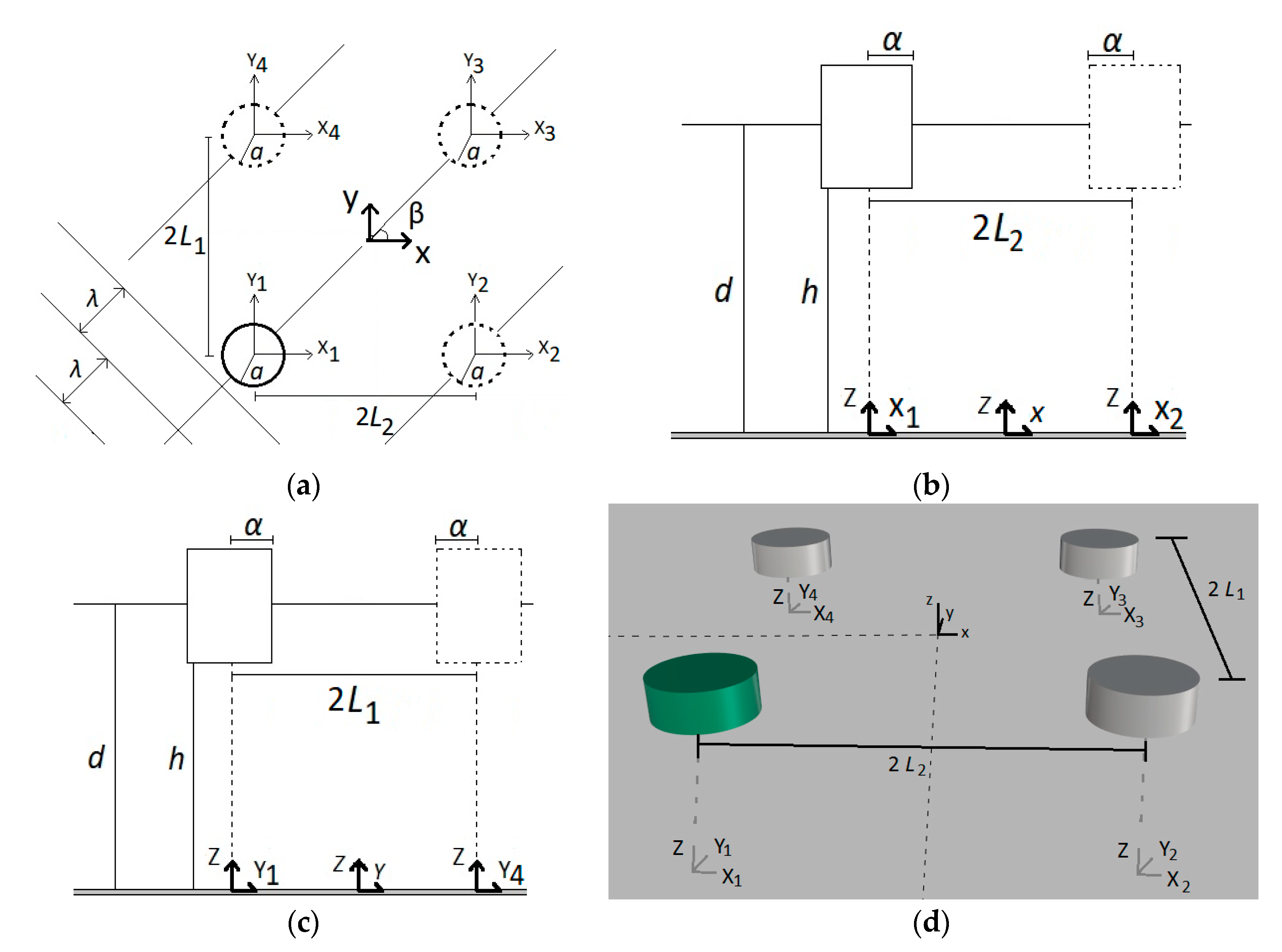
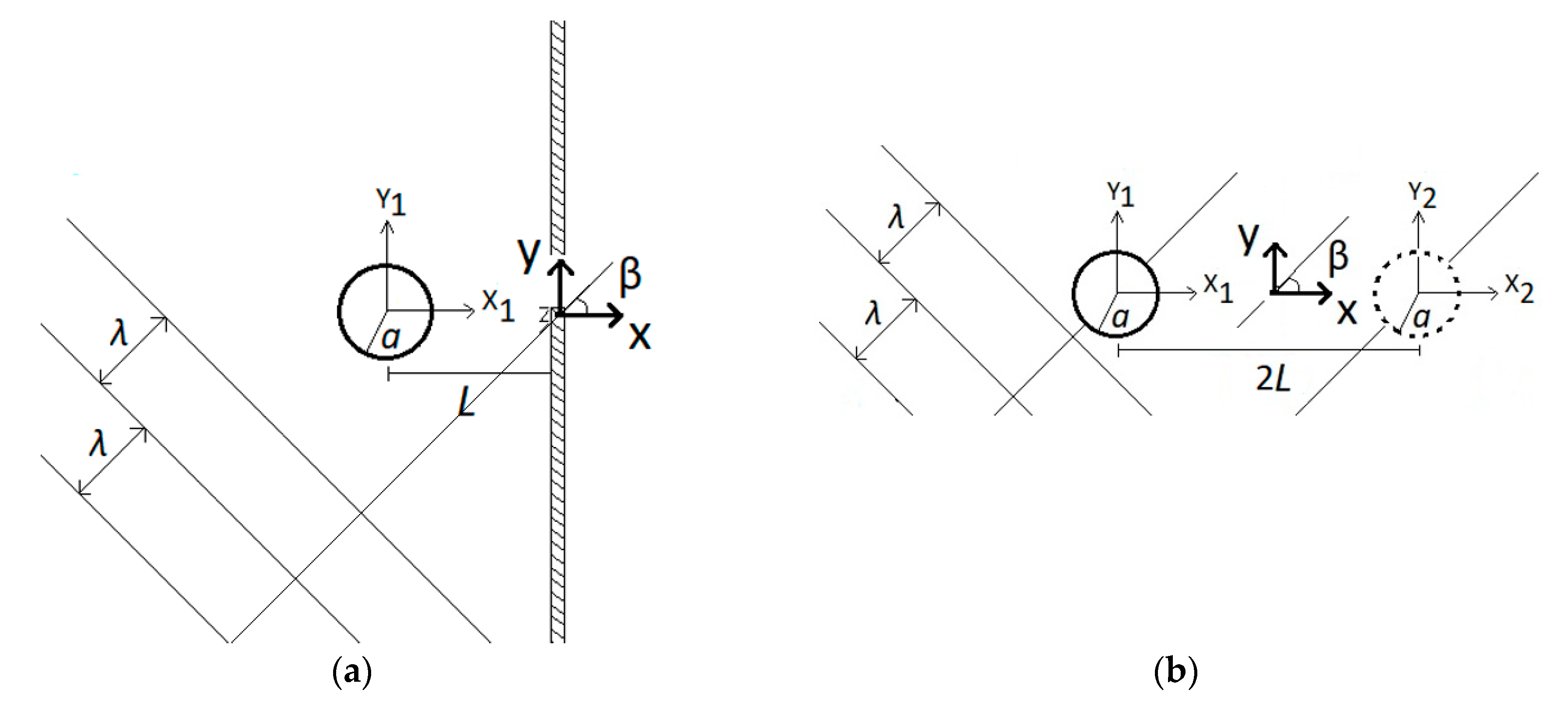
2. Breakwater Simulation
3. Theoretical Modeling
4. Hydrodynamic Forces
5. Numerical Results
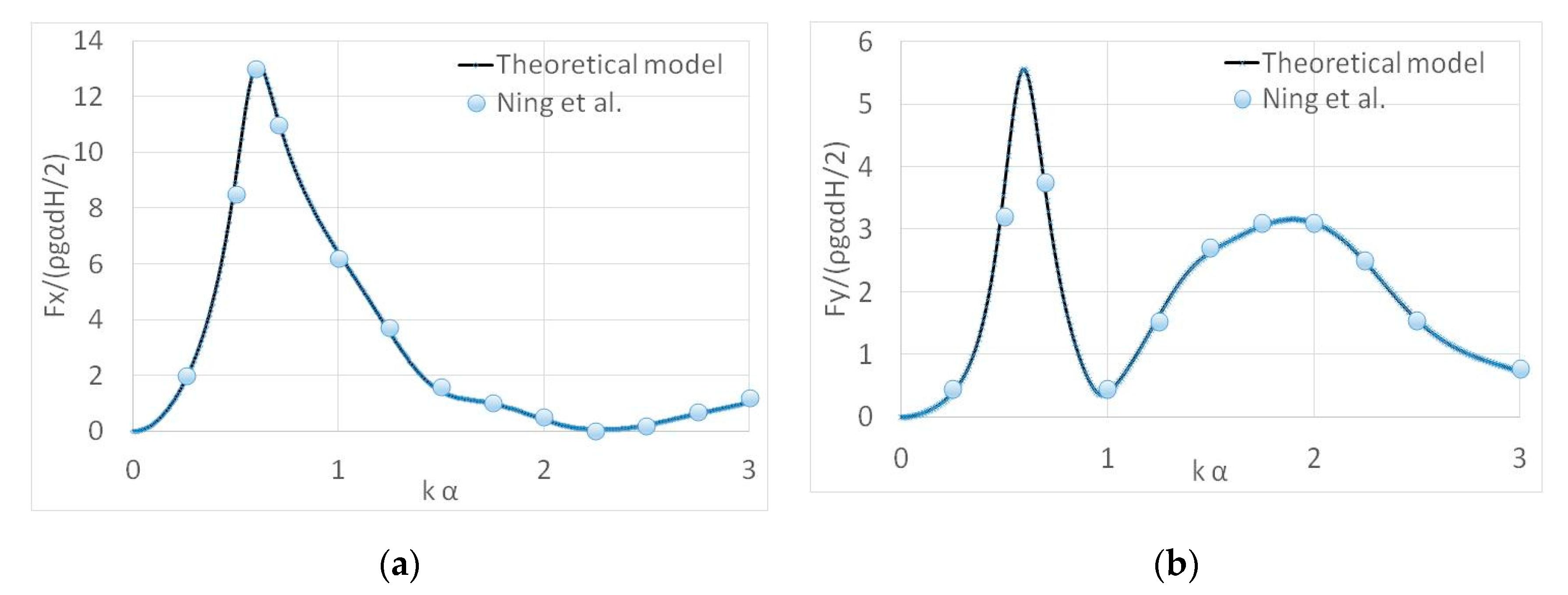
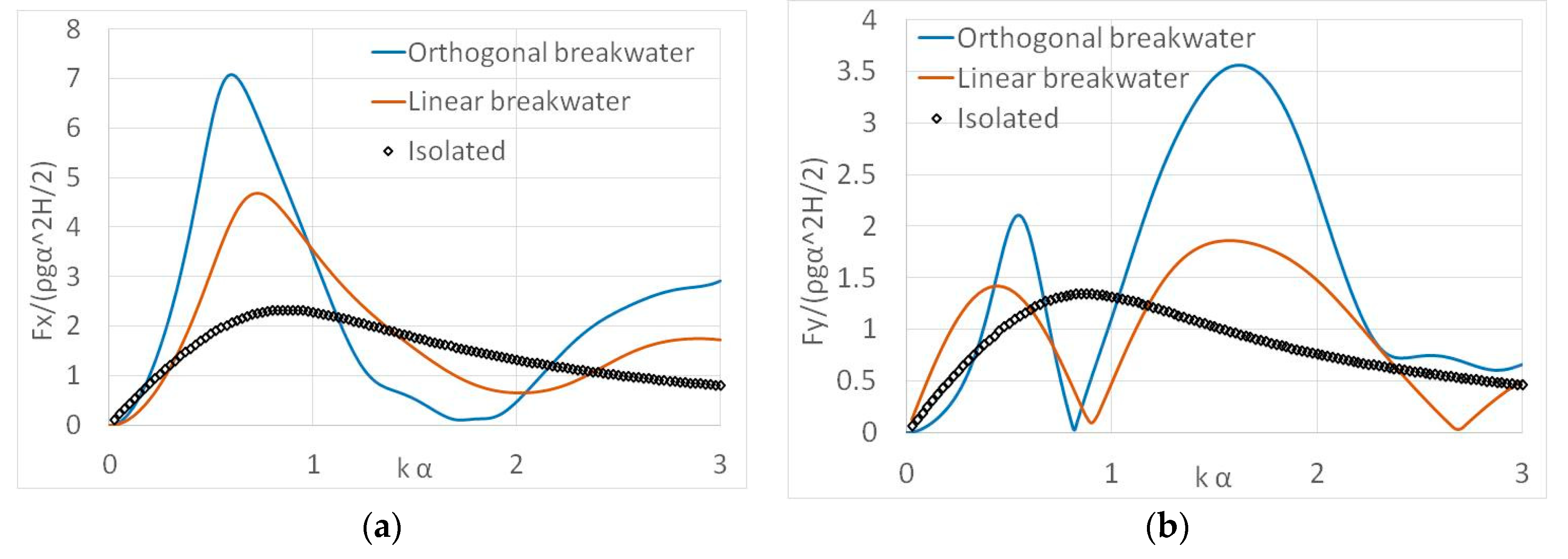
5.1. Validation of Results
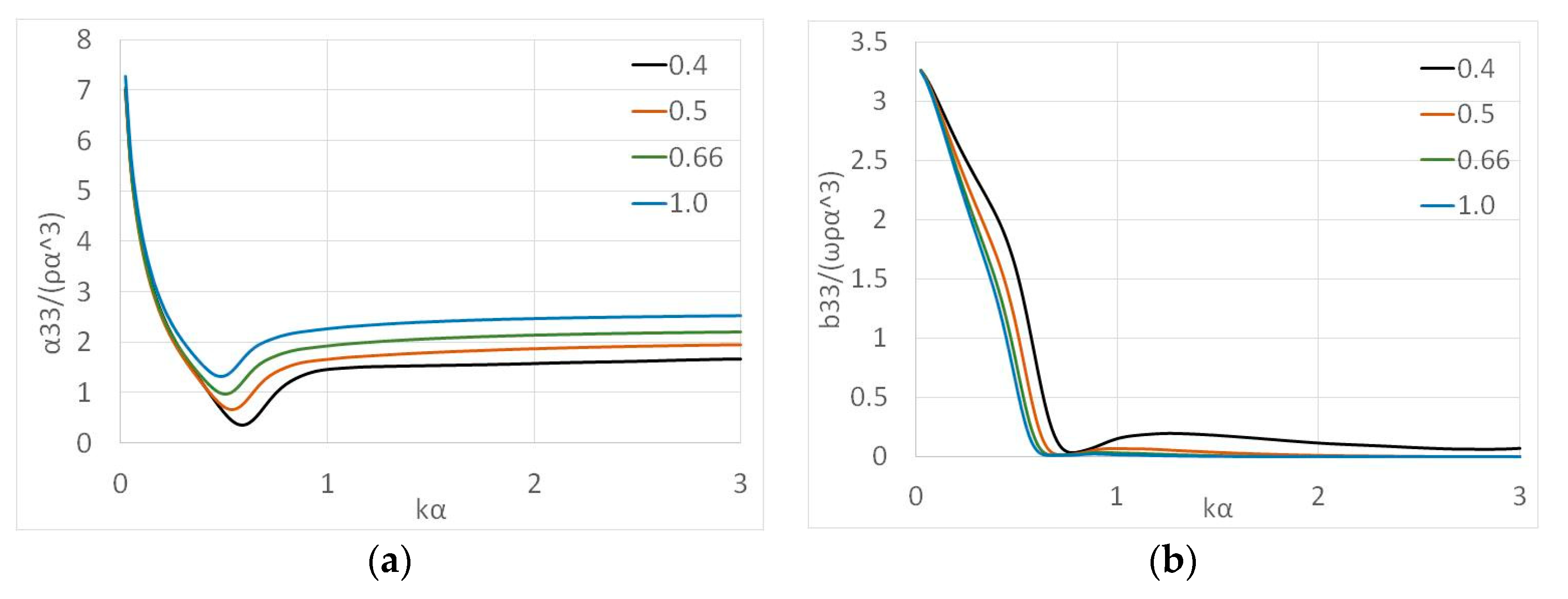
5.2. Test Cases
5.2.1. Effect of the Distance between the Walls and the Floater
5.2.2. Effect of the Wave Heading Angle
5.2.3. Effect of the Floater’s Draught
5.2.4. Effect of the Breakwater Type
5.2.5. Effect of the Length of the Walls
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
References
- Vona, I.; Gray, M.W.; Nardin, W. The impact of submerged breakwaters on sediment distribution along marsh boundaries. Water 2020, 12, 1016. [Google Scholar] [CrossRef]
- Wave Energy Market by Technology (OSW, OBC, & Overtopping Converters), Location (Onshore, Nearshore, Offshore), Application (Desalination, Power Generation, and Environmental Protection), and Region—Global Forecast to 2025; Research and Markets ID: 5011806. Available online: https://www.researchandmarkets.com/ (accessed on 13 August 2020).
- MacGillivray, A.; Jeffrey, H.; Hanmer, C.; Magagna, D.; Raventos, A.; Badcock-Broe, A. Ocean Energy Technology: Gaps and Barriers. Si Ocean, 2013. Available online: www.si-ocean.eu (accessed on 1 May 2020).
- Mavrakos, S.A.; Katsaounis, G.M.; Nielsen, K.; Lemonis, G. Numerical performance investigation of an array of heaving wave power converters in front of a vertical breakwater. In Proceedings of the 14th International Offshore and Polar Engineering Conference (ISOPE 2004), Toulon, France, 23–28 May 2004. [Google Scholar]
- Mavrakos, S.A.; Katsaounis, G.M.; Kladas, A.; Kimoulakis, N. Numerical and experimental investigation of performance of heaving WECs coupled with DC generators. In Proceedings of the 9th European Wave and Tidal Energy Conference, Southampton, UK, 5–9 September 2011. [Google Scholar]
- Teng, B.; Ning, D.Z. Wave diffraction from a uniform cylinder in front of a vertical wall. Ocean Eng. 2003, 21, 48–52. [Google Scholar]
- Teng, B.; Ning, D.Z.; Zhang, X.T. Wave radiation by a uniform cylinder in front of a vertical wall. Ocean Eng. 2004, 31, 201–224. [Google Scholar] [CrossRef]
- Zheng, S.; Zhang, Y. Wave diffraction from a truncated cylinder in front of a vertical wall. Ocean Eng. 2015, 104, 329–343. [Google Scholar] [CrossRef]
- Zheng, S.; Zhang, Y. Wave radiation from a truncated cylinder in front of a vertical wall. Ocean Eng. 2016, 111, 602–614. [Google Scholar] [CrossRef]
- Schay, J.; Bhattacharjee, J.; Soares, C. Numerical modelling of a heaving point absorber in front of a vertical wall. In Proceedings of the 32nd International Conference on Ocean, Offshore and Artic Engineering (OMAE 2013), Nantes, France, 9–14 June 2013. [Google Scholar] [CrossRef]
- Loukogeorgaki, E.; Boufidi, I.; Chatjigeorgiou, I. Performance of an array of oblate spheroidal heaving wave energy converters in front of a wall. Water 2020, 12, 188. [Google Scholar] [CrossRef]
- Zhao, X.L.; Ning, D.Z.; Liang, D.F. Experimental investigation on hydrodynamic performance of a breakwater-integrated WEC system. Ocean Eng. 2019, 171, 25–32. [Google Scholar] [CrossRef]
- Rosa-Santos, P.; Taveira-Pinto, F.; Clemente, D.; Cabral, T.; Fiorentin, F.; Belga, F.; Morais, T. Experimental Study of a Hybrid Wave Energy Converter Integrated in a Harbor Breakwater. J. Mar. Sci. Eng. 2019, 7, 18. [Google Scholar] [CrossRef]
- Cabral, T.; Clemente, D.; Rosa-Santos, P.; Taveira-Pinto, F.; Morais, T.; Belga, F.; Cestaro, H. Performance Assessment of a Hybrid Wave Energy Converter Integrated into a Harbor Breakwater. Energies 2020, 13, 236. [Google Scholar] [CrossRef]
- Cascajo, R.; Garcia, E.; Quiles, E.; Correcher, A.; Morat, F. Integration of marine wave energy converters into seaports: A case study in the port of Valencia. Energies 2019, 12, 787. [Google Scholar] [CrossRef]
- Zhao, X.L.; Ning, D.Z.; Zou, Q.P.; Qiao, D.S.; Cai, S.Q. Hybrid floating breakwater-WEC system: A review. Ocean Eng. 2019, 186, 106126. [Google Scholar] [CrossRef]
- Zhao, X.L.; Ning, D.Z.; Zhang, C.W.; Liu, Y.Y.; Kang, H.G. Analytical study on an oscillating buoy wave energy converter integrated into a fixed box-type breakwater. Math. Probl. Eng. 2017, 2017, 1–9. [Google Scholar] [CrossRef]
- Zhao, X.L.; Ning, D.Z.; Zhang, C.W.; Kang, H.G. Hydrodynamic investigation of an oscillating buoy wave energy converter integrated into a pile-restrained floating breakwater. Energies 2017, 10, 712. [Google Scholar] [CrossRef]
- Zhao, X.; Ning, D. Experimental investigation of breakwater type wec composed of both stationary and floating pontoons. Energy 2018, 155, 226–233. [Google Scholar] [CrossRef]
- Ning, D.; Zhao, X.; Zhao, M.; Hann, M.; Kang, H. Analytical investigation of hydrodynamic performance of a dual pontoon WEC-type breakwater. Appl. Ocean Res. 2017, 65, 102–111. [Google Scholar] [CrossRef]
- Ning, D.; Zhao, X.; Goteman, M.; Kang, H. Hydrodynamic performance of a pile restrained wec-type floating breakwater: An experimental study. Renew. Energy 2016, 95, 531–541. [Google Scholar] [CrossRef]
- Madhi, F.; Yeung, R.W.; Sinclair, M.E. The “Berkeley Wedge”: An asymmetrical energy-capturing floating breakwater of high performance. Mar. Syst. Ocean Technol. 2014, 9, 5–16. [Google Scholar] [CrossRef]
- Zingale, G. Modular Floating Breakwater of the Transformation of Wave Energy. U.S. Patent No. 6,443,653, 3 September 2002. [Google Scholar]
- Martinelli, L.; Ruol, P.; Favaretto, C. Hybrid structure combining a wave energy converter and a floating breakwater. In Proceedings of the International Offshore and Polar Engineering Conference, Rhodes, Greece, 26 June–1 July 2016; pp. 622–628. [Google Scholar]
- Favaretto, C.; Martinelli, L.; Ruol, P.; Cortellazzo, G. Investigation on possible layouts of a catamaran floating breakwater behind a wave energy converter. In Proceedings of the International Ocean and Polar Engineering Conference, San Francisco, CA, USA, 25–30 June 2017. [Google Scholar]
- Chen, B.; Ning, D.; Liu, C.; Greated, C.; Kang, H. Wave energy extraction by horizontal floating cylinders perpendicular to wave propagation. Ocean Eng. 2016, 121, 112–122. [Google Scholar] [CrossRef]
- Michailides, C.; Angelides, D. Wave energy production by a flexible floating breakwater. In Proceedings of the International Offshore and Polar Engineering Conference, Maui, HI, USA, 19–24 June 2011; pp. 614–621. [Google Scholar]
- Sundar, V.; Subbarao, B.V.V. Hydrodynamic performance characteristics of quadrant front face pile supported breakwater. J. Waterw. PortCoast. Ocean Eng. 2003, 129, 22–33. [Google Scholar] [CrossRef]
- Suh, K.D.; Jung, H.Y.; Pyun, C.K. Wave reflection and transmission by curtain wall-pile breakwaters using circular piles. J. Waterw. PortCoast. Ocean Eng. 2007, 34, 2100–2106. [Google Scholar] [CrossRef]
- Hu, P. Dynamic responses analysis of permeable breakwater subjected to random waves. Adv. Mater. Res. 2015, 1061, 809–812. [Google Scholar]
- Elkotby, M.; Rageh, O.; Sarhan, T.; Ezzeldin, M. Wave transformation behind permeable breakwater. Int. J. Sci. Eng. Res. 2019, 10, 83–90. [Google Scholar] [CrossRef]
- Yoo, J.; Kim, S.-Y.; Kim, J.-M.; Cho, Y.-S. Experimental Investigation of the Hydraulic Performance of Caisson-Pile Breakwaters. J. Coast. Res. 2010, 263, 444–450. [Google Scholar] [CrossRef]
- Pourteimouri, P.; Hejazi, K. Development of An Integrated Numerical Model for Simulating Wave Interaction with Permeable Submerged Breakwaters Using Extended Navier–Stokes Equations. J. Mar. Sci. Eng. 2020, 8, 87. [Google Scholar] [CrossRef]
- Mellink, B.A. Numerical and Experimental Research of Wave Interaction with a Porous Breakwater. Master’s Thesis, Faculty of Civil Engineering and Geosciences TU Delft, Delft, The Netherlands, 2012. [Google Scholar]
- Wave Star Energy. Available online: www.wavestarenergy.dk (accessed on 13 August 2020).
- Steenstrup, P.R. Wave Star Energy—New wave energy converter, which is now under going sea trial in Denmark. In Proceedings of the International Conference Ocean Energy, Bremerhaven, Germany, 23–24 October 2006. [Google Scholar]
- Jiang, X.L.; Zou, Q.P.; Zhang, N. Wave load on submerged quarter-circular and semicircular breakwaters under irregular waves. Coast. Eng. 2017, 121, 265–277. [Google Scholar] [CrossRef]
- Gomes, A.; Pinho, J.; Valante, T.; Antuanes do Carmo, J.; Hegde, A.V. Performance assessment of a semi-circular breakwater through CFD modelling. J. Mar. Sci. Eng. 2020, 8, 226. [Google Scholar] [CrossRef]
- Rao, S.; Shirlal, K.G.; Varghese, R.V.; Govindaraja, K.R. Physical model studies on wave transmission of a submerged inclined plate breakwater. Ocean Eng. 2009, 36, 1199–1207. [Google Scholar] [CrossRef]
- Shirlal, K.G. Wave transmission of submerged inclined serrated plate breakwater. Int. J. Chem. Environ. Biol. Sci. 2013, 1, 657–660. [Google Scholar]
- Retief, G.; Muller, F.; Prestedge, G. Detailed design of a wave energy conversion plant. In Proceedings of the 19th Conference on Coastal Engineering, Houston, TX, USA, 19 November 1984. [Google Scholar]
- Kelly, T.; Dooley, T.; Campbell, J.; Ringwood, J.V. Comparison of the experimental and numerical results of modelling a 32-oscillating water column, V-shaped floating wave energy converter. Energies 2013, 6, 4045–4077. [Google Scholar] [CrossRef]
- Ackerman, P.H. Air Turbine Design Study for a Wave Energy Conversion System. Master’s Thesis, Department of Mechanical and Mechatronic Engineering, University of Stellenbosch, Stellenbosch, South Africa, 2009. [Google Scholar]
- Ning, D.; Teng, B.; Song, X. Analytical study on wave diffraction from a vertical circular cylinder in front of orthogonal vertical walls. Mar. Sci. Bull. 2005, 7, 1. [Google Scholar]
- Ning, D.; Teng, B. Study on the oscillation of a uniform cylinder in front of two vertical walls intersecting normally. Chin. Eng. Sci. 2003, 5, 84–91. [Google Scholar]
- Spring, B.W.; Monkmeyer, P.L. Interaction of plane waves with a row of cylinders. In Proceedings of the 3rd Specialty Conference of Civil Engng in Oceans, ASCE, Newark, DE, USA, 9–12 June 1975; pp. 979–998. [Google Scholar]
- Yeung, R.W.; Sphaier, S.H. Wave-interference effects on a truncated cylinder in a channel. J. Eng. Math. 1989, 23, 95–117. [Google Scholar] [CrossRef]
- Mavrakos, S.A. The scattered wave field by vertical cylinders in a narrow tank. In Proceedings of the 4th National Symposium on Theoretical and Applied Mechanics, Xanthi, Greece, 26–29 June 1995; Volume 2, pp. 819–829. [Google Scholar]
- Mavrakos, S.A.; Koumoutsakos, P. Hydrodynamic interaction among vertical axisymmetric bodies restrained in waves. Appl. Ocean Res. 1987, 9, 128–140. [Google Scholar] [CrossRef]
- Mavrakos, S.A. Hydrodynamic coefficients for groups of interacting vertical axisymmetric bodies. Ocean Eng. 1991, 18, 485–515. [Google Scholar] [CrossRef]
- Newman, J.N. The exciting forces on fixed bodies in waves. J. Ship Res. 1962, 6, 10–17. [Google Scholar]
- Faltinsen, O.M. Sea Loads on Ships and Offshore Structures; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Bardis, L.; Mavrakos, S.A. User’s Manual for the Computer Code HAQ; Laboratory for Floating Bodies and Mooring Systems, National Technical University of Athens: Athens, Greece, 1988. [Google Scholar]
- Kokkinowrachos, K.; Mavrakos, S.A.; Asorakos, S. Behavior of vertical bodies or revolution in waves. Ocean Eng. 1986, 13, 505–538. [Google Scholar] [CrossRef]










© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konispoliatis, D.N.; Mavrakos, S.A. Theoretical Analysis of a Vertical Cylindrical Floater in Front of an Orthogonal Breakwater. Fluids 2020, 5, 135. https://doi.org/10.3390/fluids5030135
Konispoliatis DN, Mavrakos SA. Theoretical Analysis of a Vertical Cylindrical Floater in Front of an Orthogonal Breakwater. Fluids. 2020; 5(3):135. https://doi.org/10.3390/fluids5030135
Chicago/Turabian StyleKonispoliatis, Dimitrios N., and Spyridon A. Mavrakos. 2020. "Theoretical Analysis of a Vertical Cylindrical Floater in Front of an Orthogonal Breakwater" Fluids 5, no. 3: 135. https://doi.org/10.3390/fluids5030135
APA StyleKonispoliatis, D. N., & Mavrakos, S. A. (2020). Theoretical Analysis of a Vertical Cylindrical Floater in Front of an Orthogonal Breakwater. Fluids, 5(3), 135. https://doi.org/10.3390/fluids5030135






