Revisiting Mean Flow and Mixing Properties of Negatively Round Buoyant Jets Using the Escaping Mass Approach (EMA)
Abstract
:1. Introduction
2. Materials and Methods
3. Variation of Basic Parameters
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Abraham, G. Jet diffusion in stagnant ambient fluid 1963 (Vol. Tech. Rep. 29). Delft. Available online: https://resolver.tudelft.nl/uuid:6ad300a4-94d9-44f7-9b1a-787d010d2844 (accessed on 1 July 2020).
- Fischer, B.H.; List, J.E.; Koh, R.C.; Imberger, J.; Brooks, N.H. Mixing in Inland and Coastal Waters; Academic Press, Inc.: New York, NY, USA, 1979. [Google Scholar] [CrossRef]
- Hanna, S.R.; Briggs, G.A.; Hosker, R.P. Handbook on Atmospheric Diffusion; U.S. Department of Energy: Washington, DC, USA, 1982. [CrossRef] [Green Version]
- Pasquill, F.; Smith, F.B. Atmospheric Diffusion, 3rd ed.; John Wiley and Sons: Chichester, UK, 1983. [Google Scholar] [CrossRef]
- Papanicolaou, P.N.; List, J.E. Investigations of round vertical turbulent buoyant jets. J. Fluid Mech. 1988, 195, 341–391. [Google Scholar] [CrossRef]
- Wang, H.; Law, A.W.-K. Second-order integral model for a round turbulent buoyant jet. J. Fluid Mech. 2002, 459, 397–428. [Google Scholar] [CrossRef]
- Jirka, G.H. Integral model for turbulent buoyant jets in unbounded stratified flows. Part I: Single Round Jet. Environ. Fluid Mech. 2004, 4, 1–56. [Google Scholar] [CrossRef]
- Lee, J.H.-W.; Chu, V. Turbulent Jets and Plumes. A Lagrangian Approach; Springer US: New York, NY, USA, 2003. [Google Scholar] [CrossRef]
- Yannopoulos, P.C. An improved integral model for plane and round turbulent buoyant jets. J. Fluid Mech. 2006, 547, 267–296. [Google Scholar] [CrossRef]
- Britter, R.E. Atmospheric dispersion of dense gases. Annu. Rev. Fluid Mech. 1989, 21, 317–344. [Google Scholar] [CrossRef]
- Ohba, R.; Kouchi, A.; Vieillard, V.; Nedelka, D. Validation of heavy and light gas dispersion models for the safetyanalysis of LNG tank. J. Loss Prev. Process. Ind. 2004, 17, 325–337. [Google Scholar] [CrossRef]
- Bellasio, R.; Bianconi, R. Online simulation system for industrial accidents. Environ. Model. Softw. 2005, 20, 329–342. [Google Scholar] [CrossRef] [Green Version]
- Liu, D.; Wei, J. Modelling and simulation of continuous dense gas leakage for emergency response application. J. Loss Prev. Process. Ind. 2017, 48, 14–20. [Google Scholar] [CrossRef]
- Sklavounos, S.; Rigas, F. Validation of turbulence models in heavy gas dispersion over obstacles. J. Hazard. Mater. 2004, 108, 9–20. [Google Scholar] [CrossRef]
- Gavelli, F.; Bullister, E.; Kytomaa, H. Application of CFD (Fluent) to LNG spills into geometrically complex environments. J. Hazard. Mater. 2008, 159, 158–168. [Google Scholar] [CrossRef]
- Tominaga, Y.; Stathopoulos, T. CFD simulations of near-field pollutant dispersion with different plume buoyancies. Build. Environ. 2018, 131, 128–139. [Google Scholar] [CrossRef]
- Mezher, T.; Fath, H.; Abbas, Z.; Khaled, A. Techno-economic assessment and environmental impacts of desalination technologies. Desalination 2011, 266, 263–273. [Google Scholar] [CrossRef]
- Petersen, K.L.; Paytan, A.; Rahav, E.; Levy, O.; Silverman, J.; Barzel, O.; Bar-Zeev, E. Impact of brine and antiscalants on reef-building corals in the Gulf of Aqaba—Potential effects from desalination plants. Water Res. 2018, 144, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Petersen, K.L.; Frank, H.; Paytan, A.; Bar-Zeev, E. Impacts of seawater desalination on coastal environment. In Sustainable Desalination Handbook. Plant Selection, Design and Implementation; Gude, V.G., Ed.; Butterworth—Heinemann: Oxford, UK, 2018; pp. 437–464. [Google Scholar] [CrossRef]
- Lattemann, S.; Höpner, T. Environmental impact and impact assessment. Desalination 2008, 220, 1–15. [Google Scholar] [CrossRef]
- Drami, D.; Yacobi, Y.Z.; Stambler, N.; Kress, N. Seawater quality and microbial communities at a desalination plant marine outfall. A field study at the Israeli Mediterranean coast. Water Res. 2011, 45, 5449–5462. [Google Scholar] [CrossRef]
- Lin, Y.-C.; Chang-Chien, G.-P.; Chiang, P.-C.; Chen, W.-H.; Lin, Y.-C. Potential impacts of discharges from seawater reverse osmosis on Taiwan marine environment. Desalination 2013, 322, 84–93. [Google Scholar] [CrossRef]
- Frank, H.; Rahav, E.; Bar-Zeev, E. Short-term effects of SWRO desalination brine on benthic heterotrophic microbial communities. Desalination 2017, 417, 52–59. [Google Scholar] [CrossRef]
- Cambridge, M.L.; Zavala-Perez, A.; Cawthray, G.R.; Mondon, J.; Kendrick, G.A. Effects of high salinity from desalination brine on growth, photosynthesis, water relations and osmolyte concentrations of seagrass Posidonia australis. Mar. Pollut. Bull. 2017, 115, 252–260. [Google Scholar] [CrossRef]
- Cambridge, M.L.; Zavala-Perez, A.; Cawthray, G.R.; Statton, J.; Mondon, J.; Gary, K.A. Effects of desalination brine and seawater with the same elevated salinity on growth, physiology and seedling development of the seagrass Posidonia australis. Mar. Pollut. Bull. 2019, 140, 462–471. [Google Scholar] [CrossRef]
- Roberts, D.A.; Johnston, E.L.; Knott, N.A. Impacts of desalination plant discharges on the marine environment. A critical review of published studies. Water Res. 2010, 44, 5117–5128. [Google Scholar] [CrossRef]
- Missimer, T.M.; Maliva, R.G. Environmental issues in seawater reverse osmosis desalination: Intakes and outfalls. Desalination 2018, 434, 198–215. [Google Scholar] [CrossRef]
- Frank, H.; Fussmann, K.E.; Rahav, E.; Zeev, E.B. Chronic effects of brine discharge form large-scale seawater reverse osmosis. Water Res. 2019, 151, 478–487. [Google Scholar] [CrossRef] [PubMed]
- Jones, E.; Qadir, M.; van Vliet, M.T.H.; Smakhtin, V.; Kang, S.-M. The state of desalination and brine production. A global outlook. Sci. Total Environ. 2019, 657, 1343–1356. [Google Scholar] [CrossRef] [PubMed]
- Voutchkov, N. Overview of seawater concentrate disposal alternatives. Desalination 2011, 273, 205–219. [Google Scholar] [CrossRef]
- Shrivastava, I.; Adams, E.E. Pre-dilution of desalination reject brine: Impact on outfall dilution in. J. Hydro-Environ. Res. 2019, 24, 28–35. [Google Scholar] [CrossRef]
- Turner, J. Jets and plumes with negative or reversing buoyancy. J. Fluid Mech. 1966, 26, 779–792. [Google Scholar] [CrossRef]
- Abraham, G. Jets with Negative Buoyancy in Homogeneous Fluid. J. Hydraul. Res. 1967, 5, 235–248. [Google Scholar] [CrossRef]
- Bloomfield, L.J.; Kerr, R.C. A theoretical model of a turbulent fountain. J. Fluid Mech. 2000, 424, 197–216. [Google Scholar] [CrossRef]
- Kaminski, E.; Tait, S.; Carazzo, G. Turbulent entrainment in jets with arbitrary buoyancy. J. Fluid Mech. 2005, 526, 361–376. [Google Scholar] [CrossRef] [Green Version]
- Baddour, R.E.; Zhang, H. Density Effect on Round Turbulent Hypersaline Fountain. J. Hydraul. Eng. 2009, 135, 57–59. [Google Scholar] [CrossRef]
- Ahmad, N.; Baddour, R.E. A review of sources, effects, disposal methods, and regulations of brine into marine environments. Ocean Coast. Manag. 2014, 87, 1–7. [Google Scholar] [CrossRef]
- Zeitoun, M.A.; Mcllhenny, W.F.; Reid, R.O.; Wong, C.-M.; Savage, W.F.; Rinne, W.W.; Gransee, C.L. Conceptual Designs of Outfall Systems for Desalting Plants; Report No. 550; United States Department of the Interior: Washington, DC, USA, 1970.
- Pincince, A.B.; List, E.J. Disposal of brine into an estuary. J. Water Pollut. Control Fed. 1973, 45, 2335–2344. [Google Scholar]
- Roberts, P.J.; Toms, G. Inclined dense jets in flowing current. J. Hydraul. Eng. 1987, 113, 323–341. [Google Scholar] [CrossRef]
- Roberts, P.J.; Ferrier, A.; Daviero, G. Mixing in Inclined Dense Jets. J. Hydraul. Eng. 1997, 123, 693–699. [Google Scholar] [CrossRef]
- Lane-Serff, G.F.; Linden, P.F.; Hillel, M. Forced, angled plumes. J. Hazard. Mater. 1993, 33, 75–99. [Google Scholar] [CrossRef]
- Lindberg, W.R. Experiments on negatively buoyant jets, with and without cross-flow. In Recent Research Advances in the Fluid Mechanics of Turbulent Jets and Plumes; NATO Science Series; Davies, P.A., Valente Neves, M.J., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2012; pp. 131–145. [Google Scholar]
- Bloomfield, L.J.; Kerr, R.C. Inclined turbulent fountains. J. Fluid Mech. 2002, 451, 283–294. [Google Scholar] [CrossRef]
- Cipollina, A.; Brucato, A.; Grisafi, F.; Nicosia, S. Bench-Scale Investigation of Inclined Dense Jets. J. Hydraul. Eng. 2005, 131, 1017–1022. [Google Scholar] [CrossRef]
- Ferrari, S.; Querzoli, G. Sea discharge of brine from desalination plants a laboratory model of negatively buoyant jets. In Proceedings of the MWWD 2004-3rd International Conference on Marine Waste Water Discharges and Marine, Catania, Italy, 27 September–2 October 2004. [Google Scholar]
- Ferrari, S.; Querzoli, G. Mixing and re-entrainment in a negatively buoyant jet. J. Hydraul. Res. 2010, 48, 632–640. [Google Scholar] [CrossRef]
- Nemlioglu, S.; Roberts, P.J. Experiments on Dense Jets Using Three-Dimensional Laser-Induced Fluorescence (3DLIF). In Proceedings of the 4th International Conference on Marine Wastewater Disposal and Marine Environment (MWWD), Antalya, Turkey, 6–10 November 2006. [Google Scholar]
- Kikkert, G.A.; Davidson, M.J.; Nokes, R.I. Inclined Negatively Buoyant Discharges. J. Hydraul. Eng. 2007, 133, 545–554. [Google Scholar] [CrossRef]
- Shao, D.; Law, A.W.-K. Mixing and boundary interactions of 30° and 45° inclined dense jets. Environ. Fluid Mech. 2010, 10, 521–533. [Google Scholar] [CrossRef]
- Lai, C.C.-K.; Lee, J.H.-W. Mixing of inclined dense jets in stationary ambient. J. Hydro-Environ. Res. 2012, 6, 9–28. [Google Scholar] [CrossRef]
- Jiang, B.; Law, A.W.-K.; Lee, J.H.-W. Mixing of 30° and 45° Inclined Dense Jets in Shallow Coastal Waters. J. Hydraul. Eng. 2014, 140, 241. [Google Scholar] [CrossRef]
- Papakonstantis, I.G.; Christodoulou, G.C.; Papanicolaou, P.N. Inclined negatively buoyant jets 1: Geometrical characteristics. J. Hydraul. Res. 2011, 49, 3–12. [Google Scholar] [CrossRef]
- Papakonstantis, I.G.; Christodoulou, G.C.; Papanicolaou, P.N. Inclined negatively buoyant jets 2: Concentration measurements. J. Hydraul. Res. 2011, 49, 13–22. [Google Scholar] [CrossRef]
- Nikiforakis, I.K.; Stamou, A.I.; Christodoulou, G.C. A modified integral model for negatively buoyant jets in a stationary ambient. Environ. Fluid Mech. 2015, 15, 939–957. [Google Scholar] [CrossRef]
- Papakonstantis, I.G.; Tsatsara, E.I. Trajectory characteristics of inclined turbulent dense jets. Environ. Process. 2018, 5, 539–554. [Google Scholar] [CrossRef]
- Papakonstantis, I.G.; Tsatsara, E.I. Mixing characteristics of inclined turbulent dense jets. Environ. Process. 2019, 6, 525–541. [Google Scholar] [CrossRef]
- Oliver, C.J.; Davidson, M.J.; Nokes, R.I. Predicting the near-field mixing of desalination discharges in a stationary environment. Desalination 2013, 309, 148–155. [Google Scholar] [CrossRef]
- Oliver, C.J.; Davidson, M.J.; Nokes, R.I. Removing the boundary influence on negatively buoyant jets. Environ. Fluid Mech. 2013, 13, 625–648. [Google Scholar] [CrossRef]
- Abessi, O.; Roberts, P.J. Effect of nozzle orientation on dense jets in stagnant environments. J. Hydraul. Eng. 2015, 141. [Google Scholar] [CrossRef]
- Crowe, A.T.; Davidson, M.J.; Nokes, R.I. Modified reduced buoyancy flux model for desalination discharges. Desalination 2016, 378, 53–59. [Google Scholar] [CrossRef]
- Crowe, A.T.; Davidson, M.J.; Nokes, R.I. Velocity measurements in inclined negatively buoyant jets. Environ. Fluid Mech. 2016, 16, 503–520. [Google Scholar] [CrossRef]
- Wood, I.R.; Bell, R.G.; Wilkinson, D.L. Ocean Disposal of Wastewater; Advanced series on ocean engineering; World Scientific: Singapore, 1993; Volume 8. [Google Scholar] [CrossRef]
- Morton, B.R.; Taylor, G.I.; Turner, J.S. Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. A 1956, 234, 1196. [Google Scholar] [CrossRef]
- Papanicolaou, P.N.; Papakonstantis, I.G.; Christodoulou, G.C. On the entrainment coefficient in negatively buoyant jets. J. Fluid Mech. 2008, 614, 447–470. [Google Scholar] [CrossRef]
- Lee, J.H.; Cheung, V. Generalized Lagrangian Model for Buoyant Jets in Current. J. Environ. Eng. 1990, 116, 1085–1106. [Google Scholar] [CrossRef]
- Jirka, G.H. Improved Discharge Configurations for Brine Effluents from Desalination Plants. J. Hydraul. Eng. 2008, 134, 116–120. [Google Scholar] [CrossRef] [Green Version]
- Oliver, C.J. Near Field Mixing of Negatively Buoyant Jets. Ph.D. Thesis, Department of Civil and Natural Resources Engineering, University of Canterbury, Christchurch, New Zealand, 2012. [Google Scholar]
- Crowe, A.T. Inclined Negatively Buoyant Jets and Boundary Interaction. Ph.D. Thesis, Department of Civil and Natural Resources Engineering, University of Canterbury, Christchurch, New Zealand, 2013. [Google Scholar]
- Besalduch, L.A.; Badas, M.G.; Ferrari, S.; Querzoli, G. Experimental studies for the characterization of the mixing processes in negative buoyant jets. EPJ Web Conf. 2013, 45. [Google Scholar] [CrossRef] [Green Version]
- Besalduch, L.A.; Badas, M.G.; Ferrari, S.; Querzoli, G. On the near field behavior of inclined negatively buoyant jets. EPJ Web Conf. 2014, 67, 2007. [Google Scholar] [CrossRef] [Green Version]
- Jiang, M.; Law, A.W.-K.; Lai, A.C. Turbulence characteristics of 45° inclined dense jets. Environ. Fluid Mech. 2019, 19, 27–54. [Google Scholar] [CrossRef]
- Ramakanth, A. Quantifying Boundary Interaction of Negatively Buoyant Jets. Ph.D. Thesis, Department of Civil and Natural Resources Engineering, University of Canterbury, Christchurch, New Zealand, 2016. [Google Scholar]
- Yannopoulos, P.C.; Bloutsos, A.A. Escaping mass approach for inclined plane and round buoyant jets. J. Fluid Mech. 2012, 695, 81–111. [Google Scholar] [CrossRef]
- Vafeiadou, P.; Papakonstantis, I.; Christodoulou, G. Numerical simulation of inclined negatively buoyant jets. In Proceedings of the 9th International Conference on Environmental Science and Technology, Rhodes, Greece, 1–3 September 2005. [Google Scholar]
- Oliver, C.J.; Davidson, M.J.; Nokes, R.I. k-ε Predictions of the initial mixing of desalination discharges. Environ. Fluid Mech. 2008, 8, 617–625. [Google Scholar] [CrossRef]
- Gildeh, H.K.; Mohammadian, A.; Nistor, I.; Qiblawey, H. Numerical Modeling of Turbulent Buoyant Wall Jets in Stationary Ambient Water. J. Hydraul. Eng. 2014, 140. [Google Scholar] [CrossRef] [Green Version]
- Gildeh, H.K.; Mohammadian, A.; Nistor, I.; Qiblawey, H. Numerical modeling of 30° and 45° inclined dense turbulent jets in stationary ambient. Environ. Fluid Mech. 2015, 15, 537–562. [Google Scholar] [CrossRef]
- Gildeh, H.K.; Mohammadian, A.; Nistor, I.; Qiblawey, H.; Yan, X. CFD modeling and analysis of the behavior of 30° and 45° inclined dense jets—New numerical insights. J. Appl. Water Eng. Res. 2016, 4, 112–127. [Google Scholar] [CrossRef]
- Ardalan, H.; Vafaei, F. CFD and Experimental Study of 45° Inclined Thermal-Saline Reversible Buoyant Jets in Stationary Ambient. Environ. Process. 2019, 6, 219–239. [Google Scholar] [CrossRef]
- Zhang, S.; Jiang, B.; Law, A.W.-K.; Zhao, B. Large eddy simulations of 45° inclined dense jets. Environ. Fluid Mech. 2016, 16, 101–121. [Google Scholar] [CrossRef]
- Zhang, S.; Law, A.W.-K.; Jiang, M. Large eddy simulations of 45° and 60° inclined dense jets with bottom. J. Hydro-Environ. Res. 2017, 15, 54–66. [Google Scholar] [CrossRef]
- Cintolesi, C.; Petronio, A.; Armenio, V. Turbulent structures of buoyant jet in cross-flow studied through large-eddy simulation. Environ. Fluid Mech. 2019, 19, 401–433. [Google Scholar] [CrossRef] [Green Version]
- Bloutsos, A.A.; Yannopoulos, P.C. Curvilinear Coordinate System for Mathematical Analysis of Inclined Buoyant Jets Using the Integral Method. Math. Probl. Eng. 2018, 2018. [Google Scholar] [CrossRef]
- Yannopoulos, P.C. Advanced integral model for groups of interacting round turbulent buoyant jets. Environ. Fluid Mech. 2010, 10, 415–450. [Google Scholar] [CrossRef]
- Kreyszig, E. Advanced Engineering Mathematics, 10th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011. [Google Scholar]
- Bosanquet, C.H.; Horn, G.; Thring, M.W.; Taylor, G.I. The effect of density differences on the path of jets. Proc. R. Soc. A 1961, 263, 340–352. [Google Scholar] [CrossRef]
- Bashitialshaaer, R.; Larson, M.; Persson, K.M. An Experimental Investigation on Inclined Negatively Buoyant Jets. Water 2012, 2012, 720–738. [Google Scholar] [CrossRef]
- Nikiforakis, I.K.; Christodoulou, G.C.; Stamou, A.I. Bottom concentration field due to impingement of inclined dense jet on a slope. In Proceedings of the 7th International Symposium of Environmental Hydraulics, Singapore, 7–8 January 2014. [Google Scholar]
- Baines, W.; Turner, J.; Campbell, I. Turbulent fountains in an open chamber. J. Fluid Mech. 1990, 212, 557–592. [Google Scholar] [CrossRef]
- Jiang, M.; Law, A.W.-K.; Song, J. Mixing characteristics of inclined dense jets with different nozzle geometries. J. Hydro-Environ. Res. 2019, 27, 116–128. [Google Scholar] [CrossRef]
- Marti, C.L.; Antenucci, J.P.; Luketina, D.; Okely, P.; Imberger, J. Near-Field Dilution Characteristics of a Negatively Buoyant Hypersaline Jet Generated by a Desalination Plant. J. Hydraul. Eng. 2011, 137, 57–65. [Google Scholar] [CrossRef] [Green Version]
- Papakonstantis, I.; Kampourelli, M.; Christodoulou, G. Height of rise of inclined and vertical negatively buoyant. In Proceedings of the 32nd IAHR Congress, Venice, Italy, 1–6 July 2007. [Google Scholar]
- Ramaprian, R.B.; Chandrasekhara, M. Study of Vertical Plane Turbulent Jets and Plumes; Tech. Rep. IIHR No. 257; Iowa Institute of Hydraulic Research, University of Iowa: Iowa City, IA, USA, 1983. [Google Scholar]
- Christodoulou, G.C.; Papakonstantis, I.G. Simplified estimates of trajectory of inclined negatively buoyant jets. In Environmental Hydraulics, Proceedings of the 6th International Symposium on Environmental Hydraulics, Athens, Greece, 23–25 June 2005; Christodoulou, G.C., Stamou, A.I., Eds.; Taylor and Francis Group: London, UK, 2010. [Google Scholar]

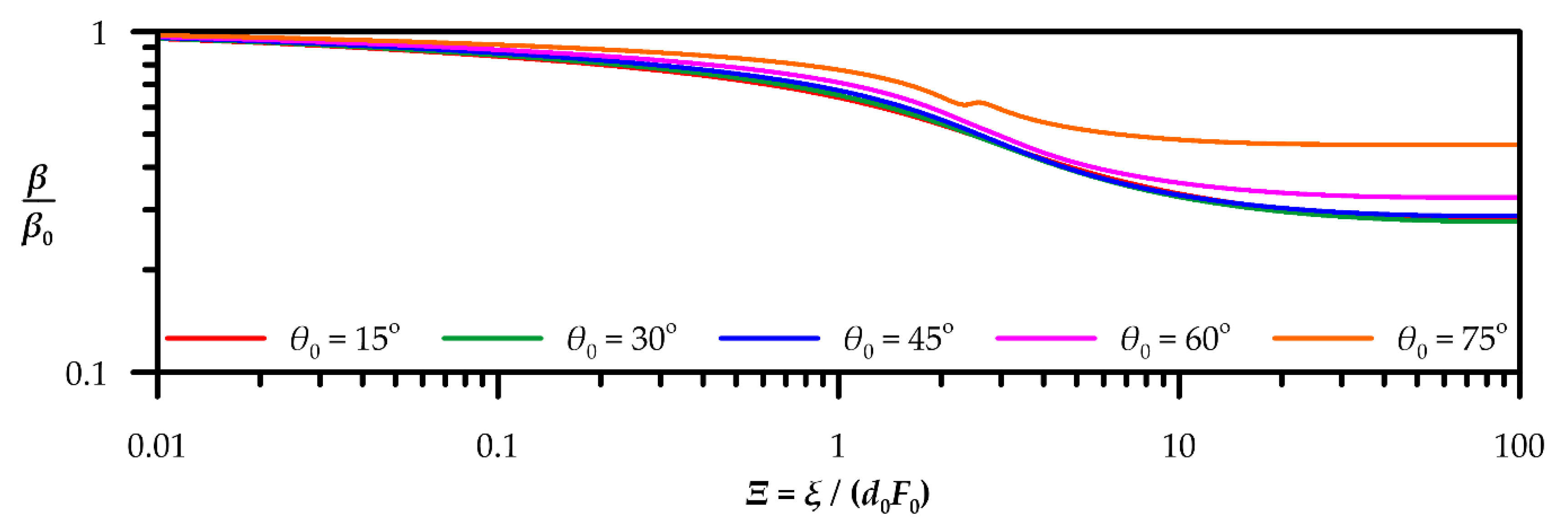
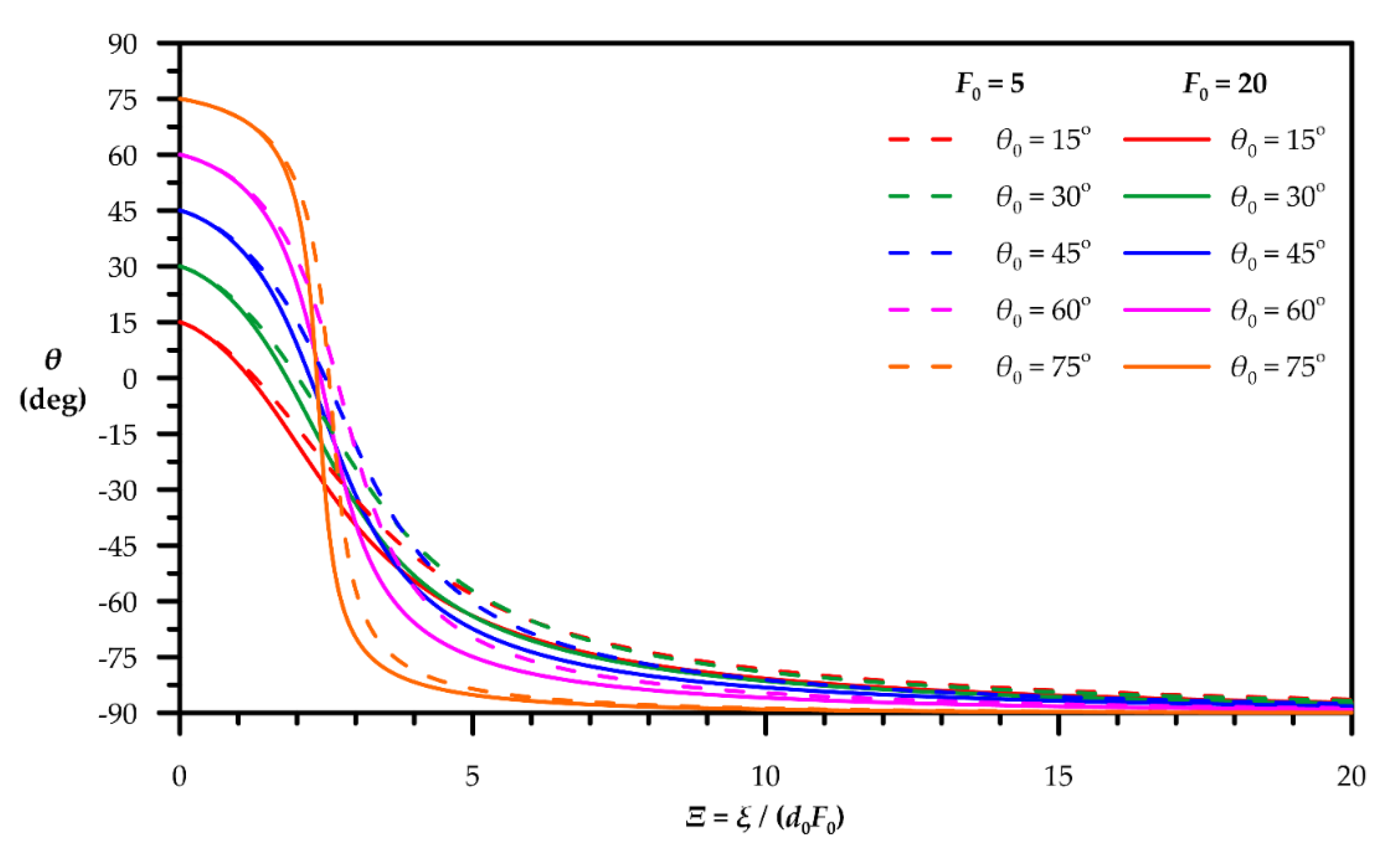
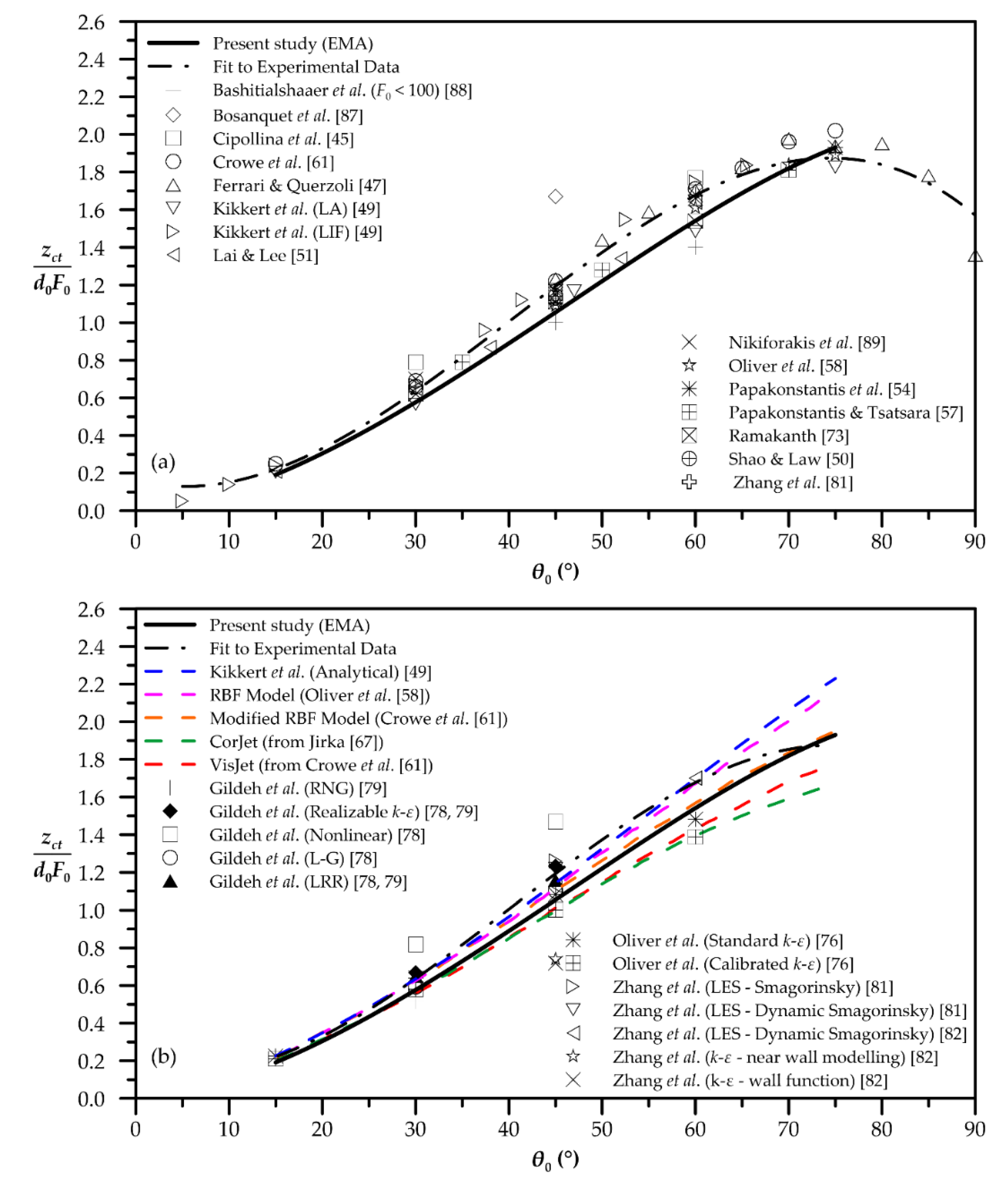
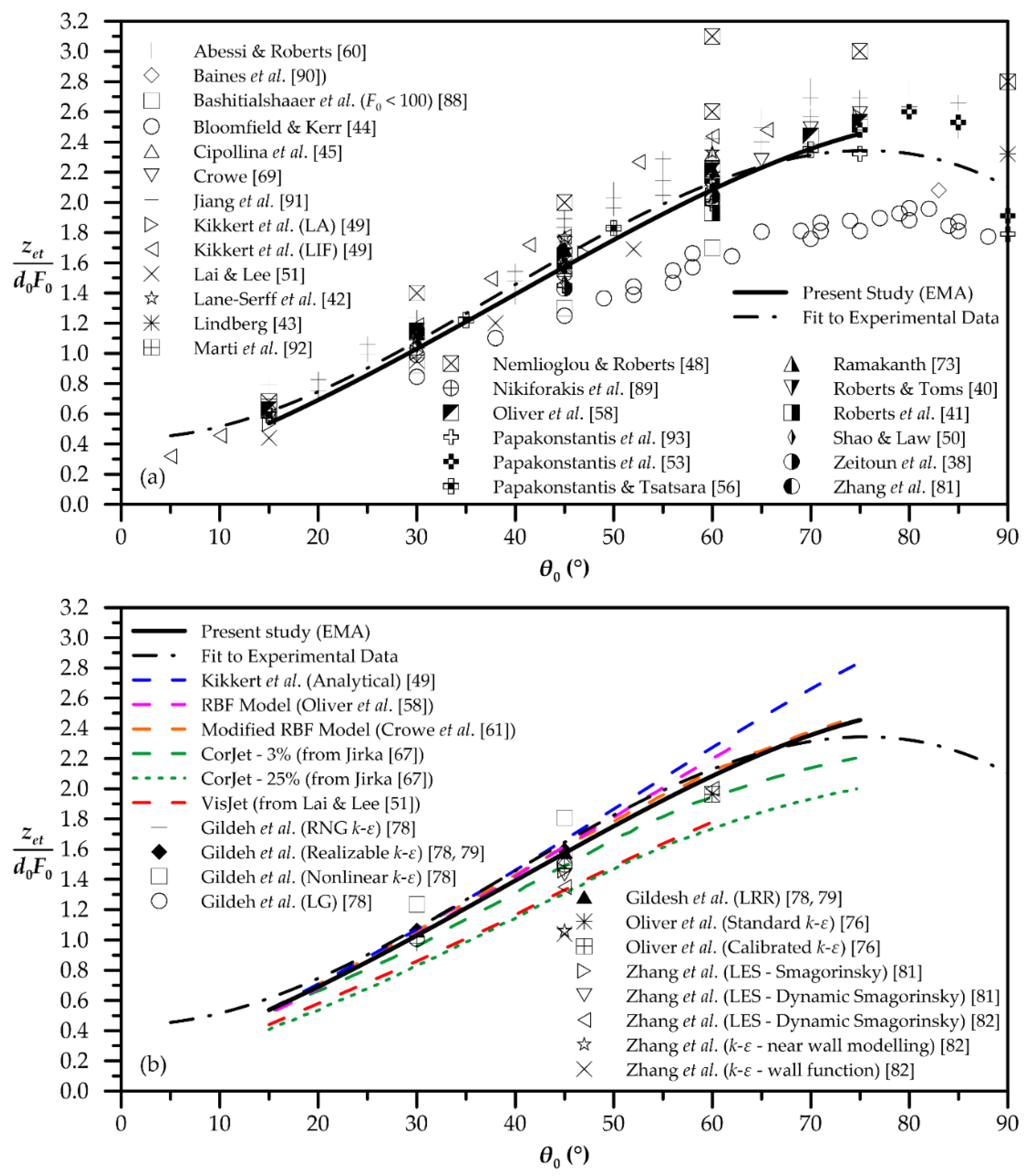
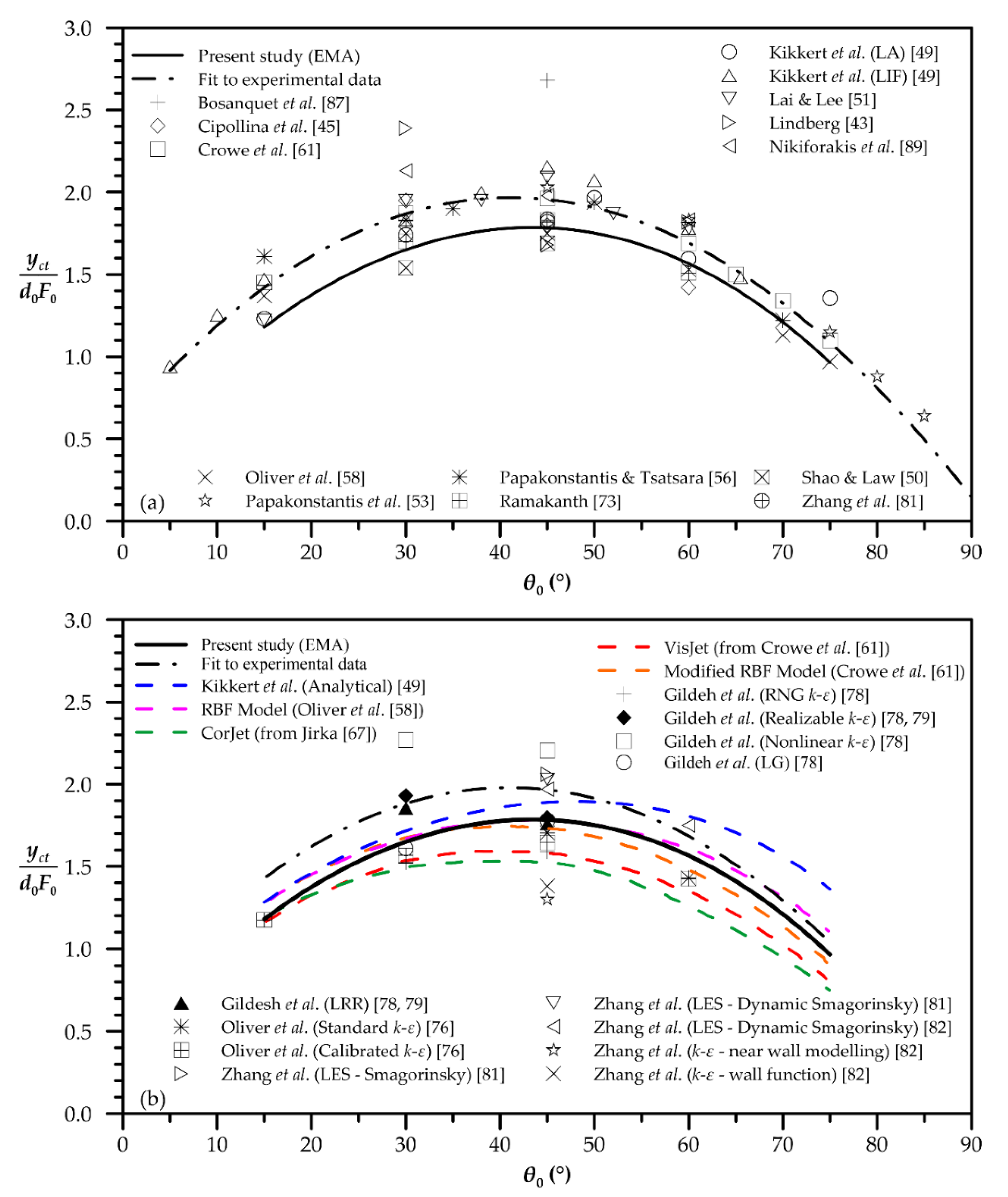
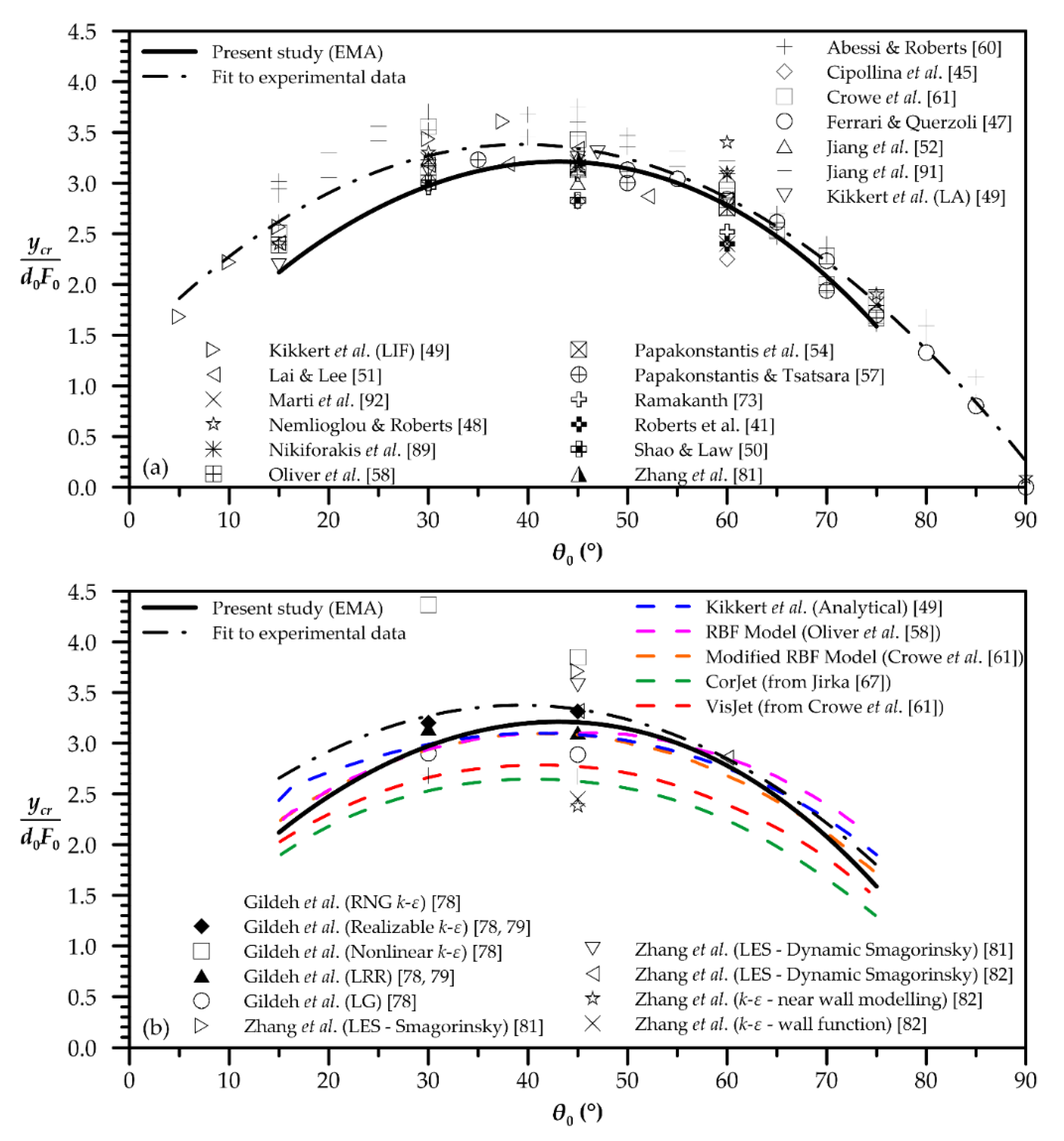
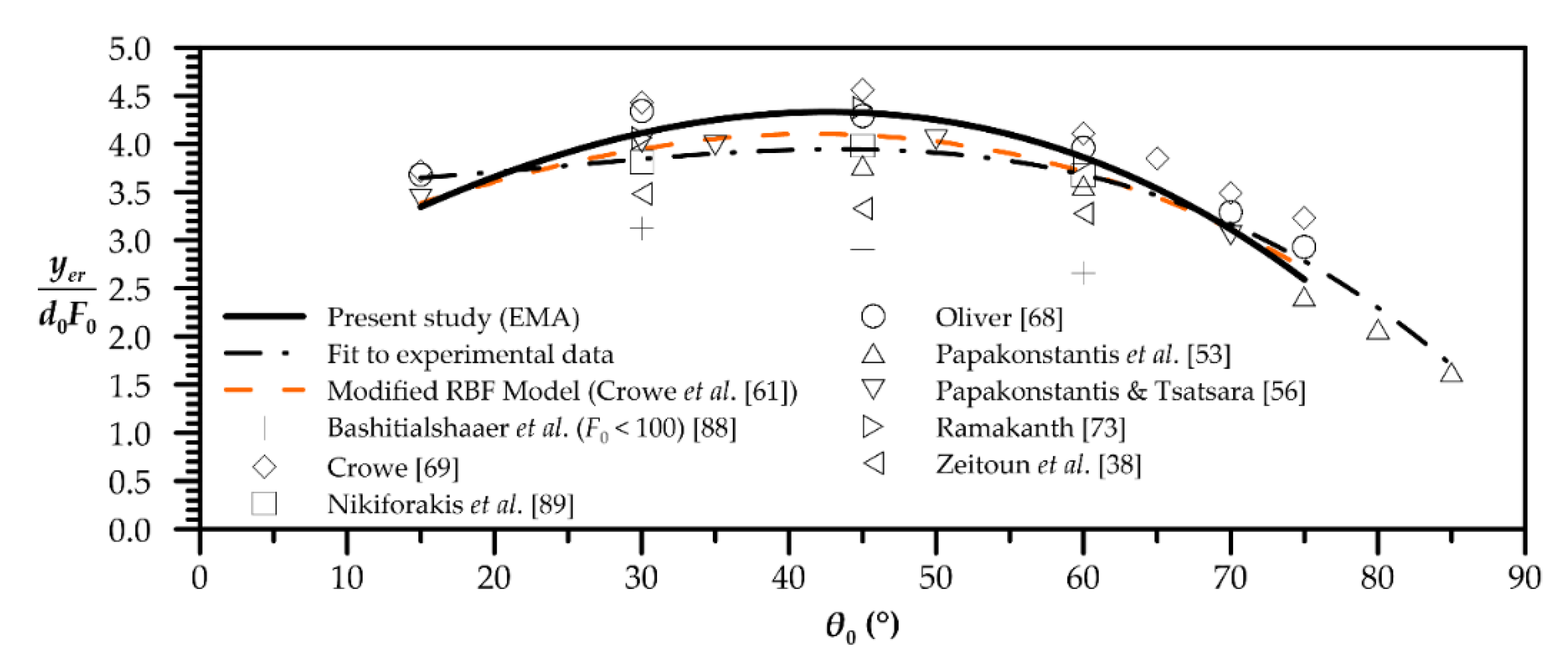
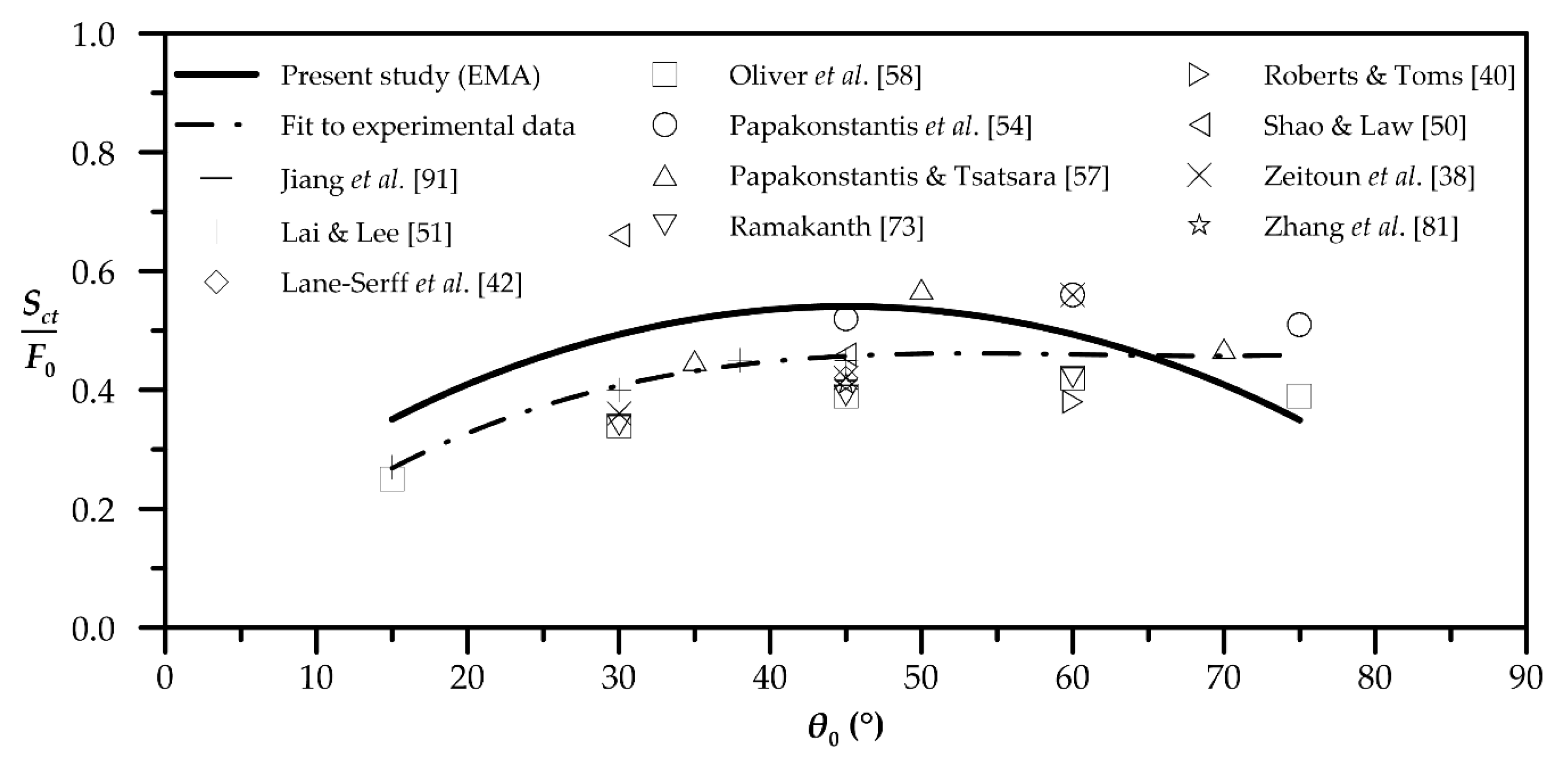
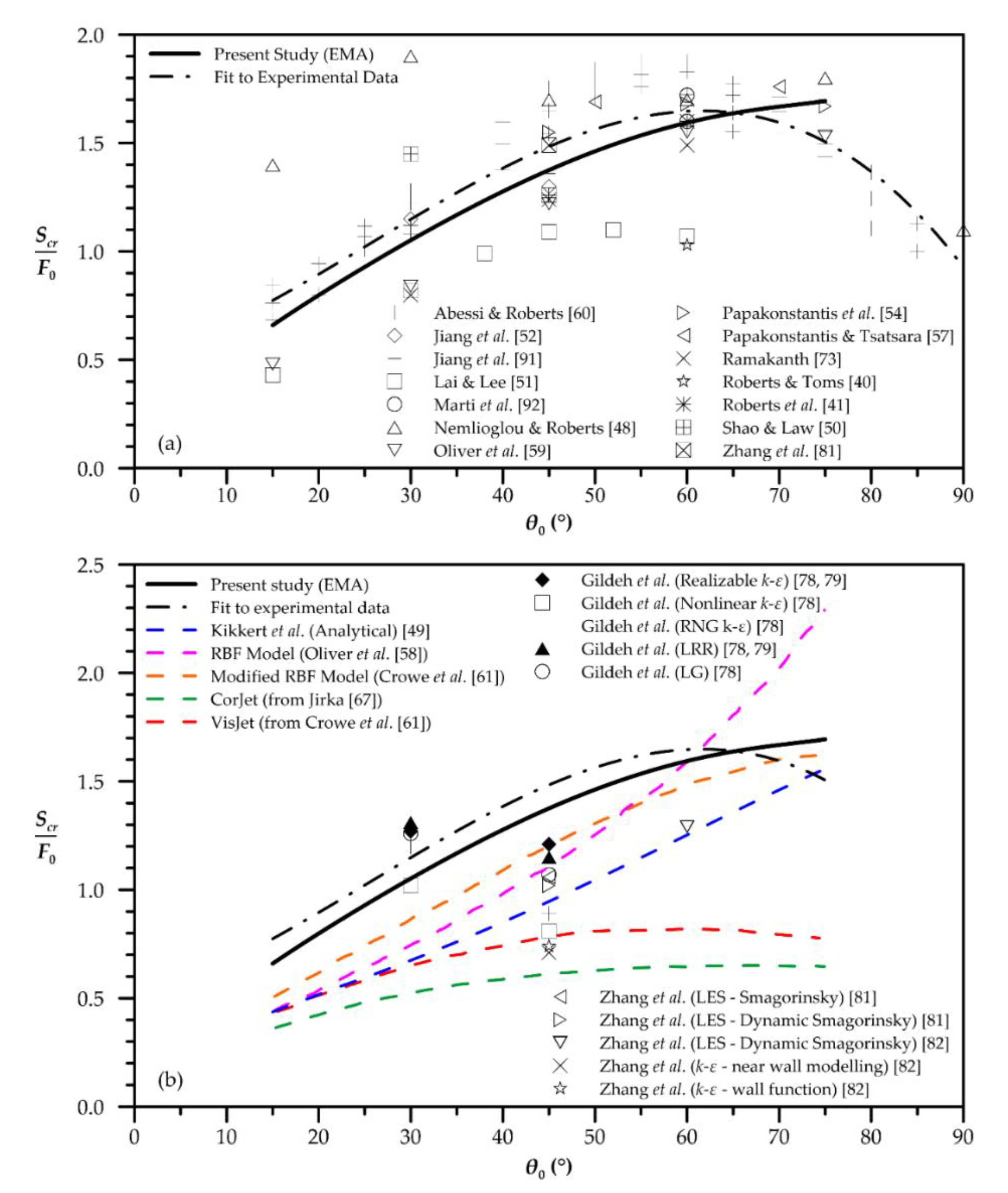
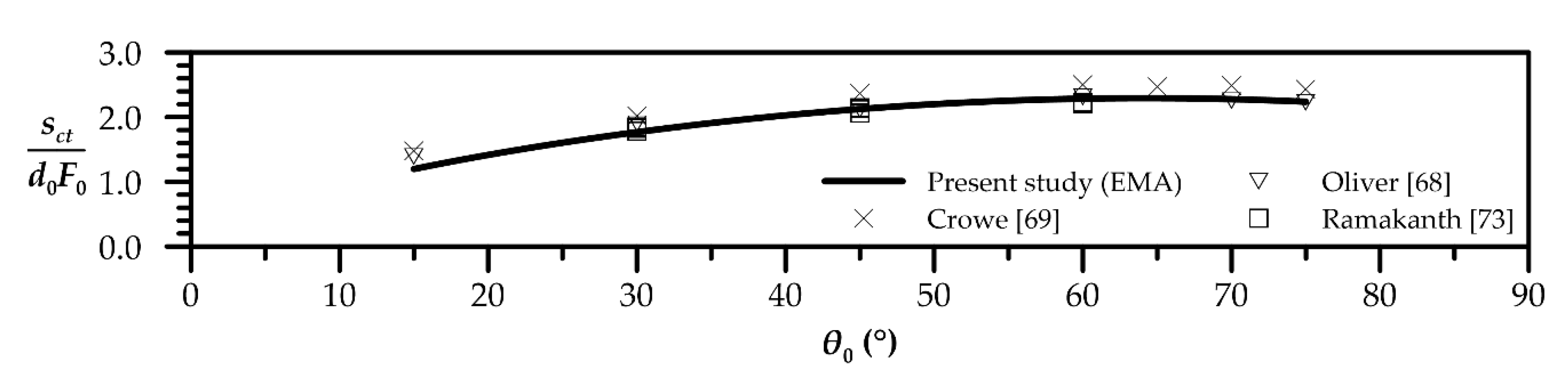
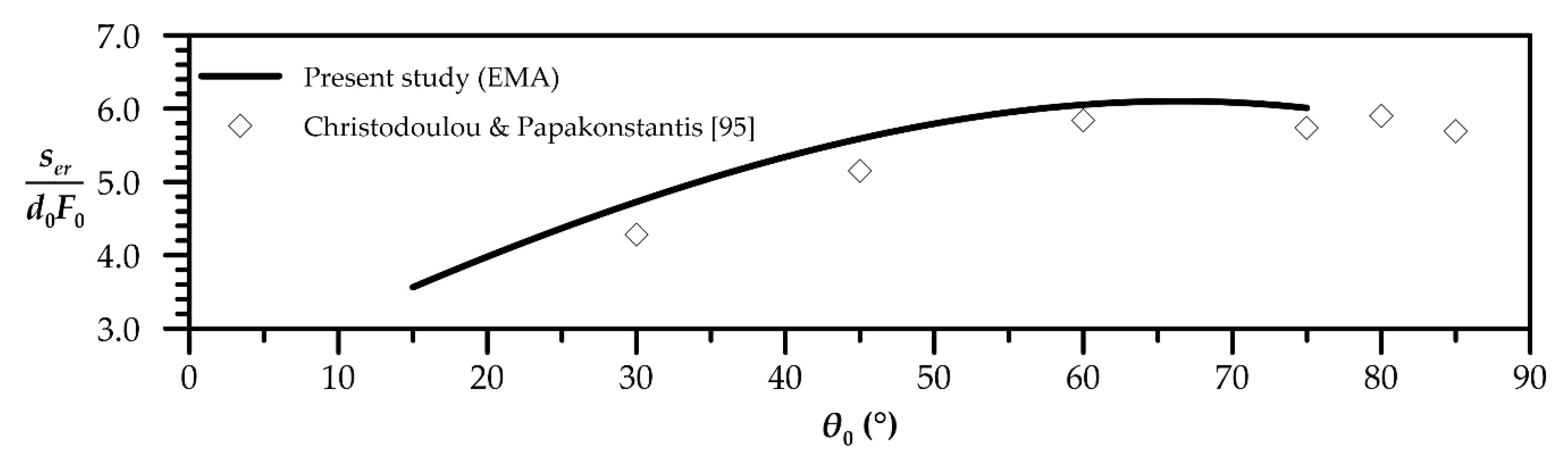
| Quantity | Figure | Polynomial Fit |
|---|---|---|
| Centerline terminal height | 2 | |
| External edge terminal height | 3 | |
| Horizontal distance to terminal height | 4 | |
| Horizontal distance to centerline return point | 5 | |
| Horizontal distance to external edge’s return point | 6 | |
| Minimum dilution at terminal height | 7 | |
| Minimum dilution at return point | 8 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bloutsos, A.A.; Yannopoulos, P.C. Revisiting Mean Flow and Mixing Properties of Negatively Round Buoyant Jets Using the Escaping Mass Approach (EMA). Fluids 2020, 5, 131. https://doi.org/10.3390/fluids5030131
Bloutsos AA, Yannopoulos PC. Revisiting Mean Flow and Mixing Properties of Negatively Round Buoyant Jets Using the Escaping Mass Approach (EMA). Fluids. 2020; 5(3):131. https://doi.org/10.3390/fluids5030131
Chicago/Turabian StyleBloutsos, Aristeidis A., and Panayotis C. Yannopoulos. 2020. "Revisiting Mean Flow and Mixing Properties of Negatively Round Buoyant Jets Using the Escaping Mass Approach (EMA)" Fluids 5, no. 3: 131. https://doi.org/10.3390/fluids5030131
APA StyleBloutsos, A. A., & Yannopoulos, P. C. (2020). Revisiting Mean Flow and Mixing Properties of Negatively Round Buoyant Jets Using the Escaping Mass Approach (EMA). Fluids, 5(3), 131. https://doi.org/10.3390/fluids5030131





