Data-Driven Pulsatile Blood Flow Physics with Dynamic Mode Decomposition
Abstract
1. Introduction
2. Methods
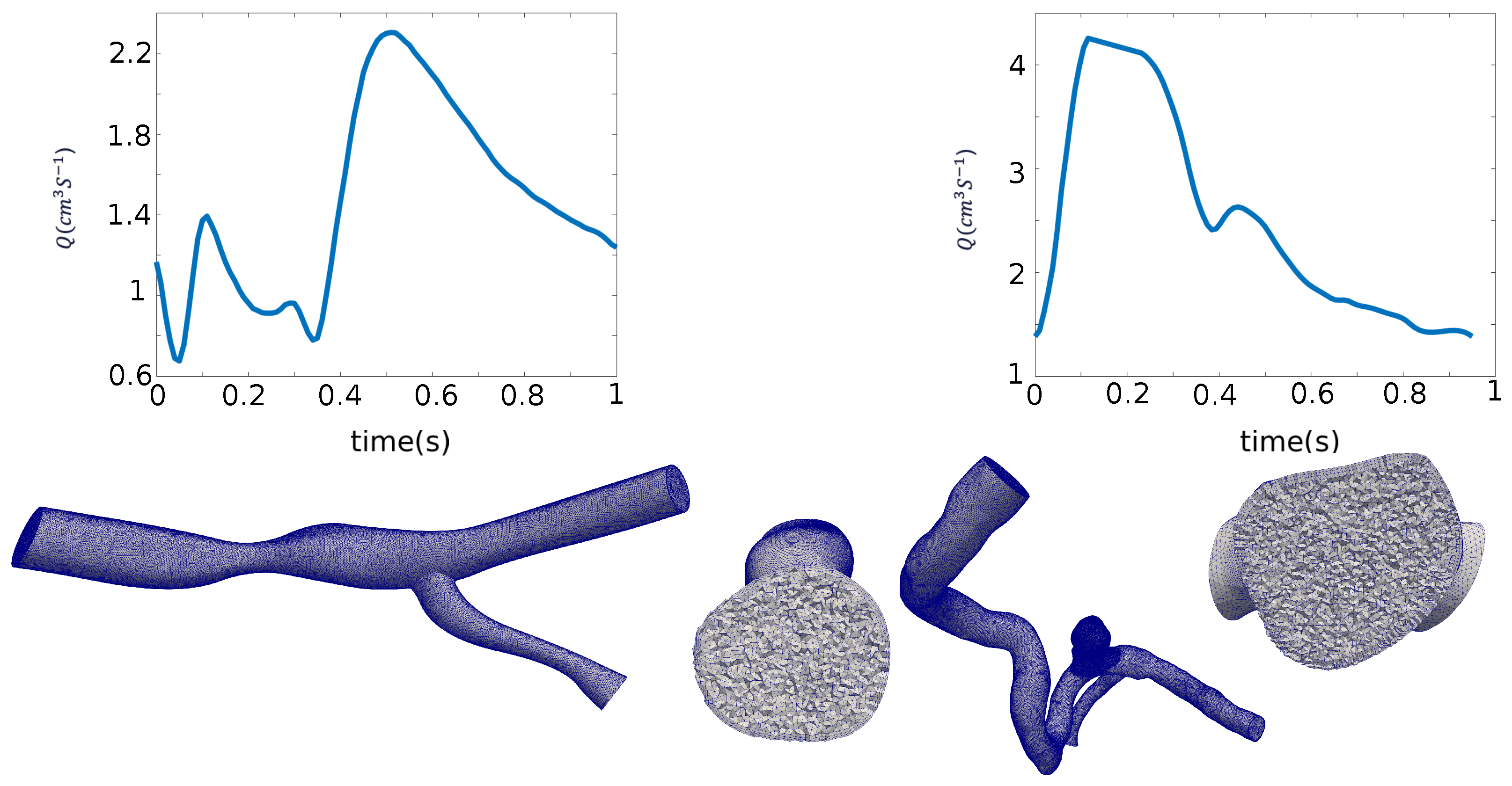
2.1. Computational Fluid Dynamics (CFD)
2.1.1. Cerebral Aneurysm
2.1.2. Coronary Artery Stenosis
2.2. Dynamic Mode Decomposition with Control (DMDc)
- Given data, construct snapshot matrices , , and . Then construct the augmented matrix based on and .
- Compute the SVD of the augmented matrix to get with truncation value q. Subsequently, based on the SVD results and the truncation value q, divide the complex conjugate transpose of into two distinct components .
- Compute the SVD of and obtain the truncated SVD decomposition with truncation value r ().
- Compute a reduced-order approximation of the linear operators and using:
- Compute the spectral decomposition of as to find its eigenvectors () and eigenvalues ().
- Extract the dynamic modes of the operator
2.3. Dynamic Mode Decomposition in Cardiovascular Flows
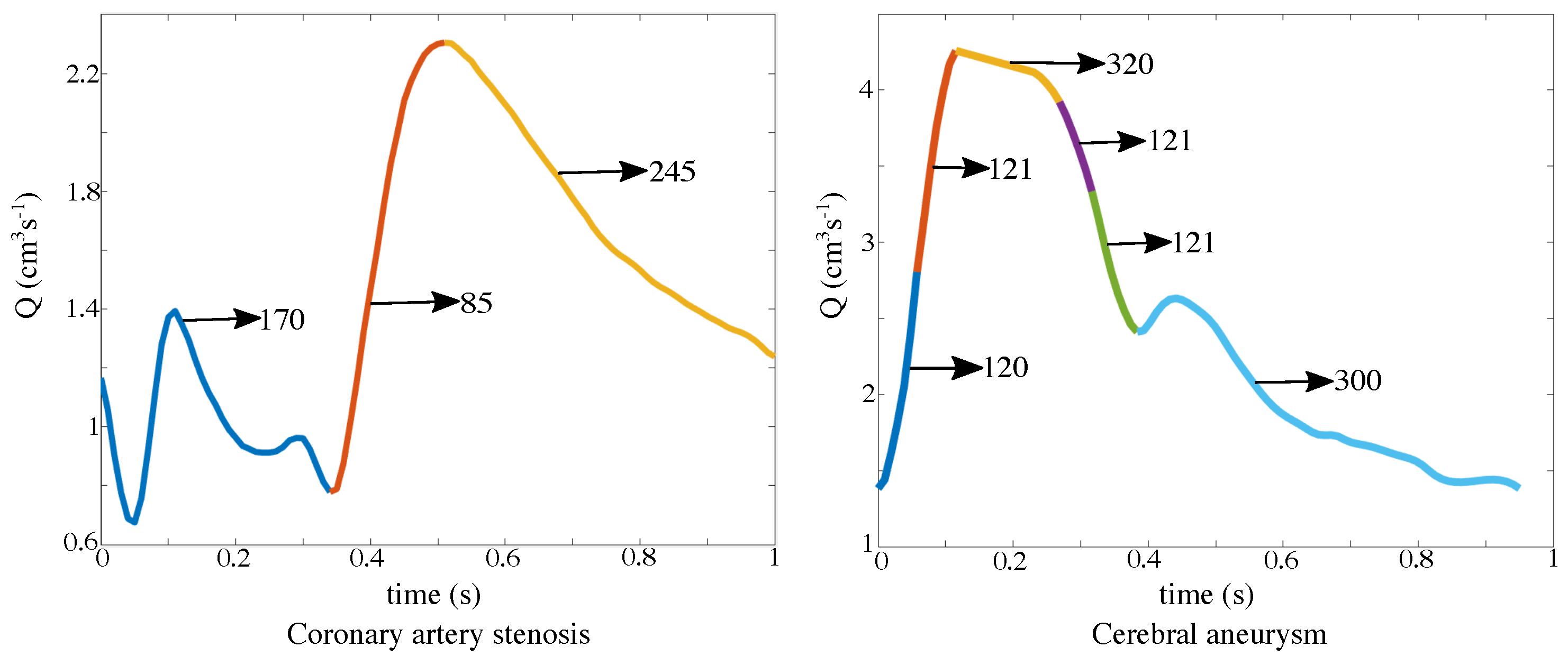
- Multistage dynamic mode decomposition with control (mDMDc)To model the effect of pulsatile flow ejected by the heart, the input matrix could be constructed as where is the mean velocity at the inlet and is computed from Q, the volumetric flow rate at the inlet boundary. Therefore, the mean velocity at the inlet is assumed to be the input controller. To account for different flow topologies in different parts of the cardiac cycle, we use multiple time windows and apply DMDc to each window separately. The different stages of the cardiac cycle are shown in Figure 2 where each stage is colored differently. The coronary artery stenosis flow rate is divided into three parts (low flow rate, acceleration, and deceleration). Since the blood flow in the aneurysm model is more complex and chaotic, we used six stages to capture distinct flow topologies.
- Augmented mDMDcTo model coherent structures (from velocity) and near-wall coherent structures (from WSS) separately, we consider an augmented matrix of velocity and WSS to construct the state space matrix as:Subsequently, the augmented multistage dynamic mode decomposition with control (mDMDc) leads to the following equation:
2.4. Performance Evaluation
3. Results
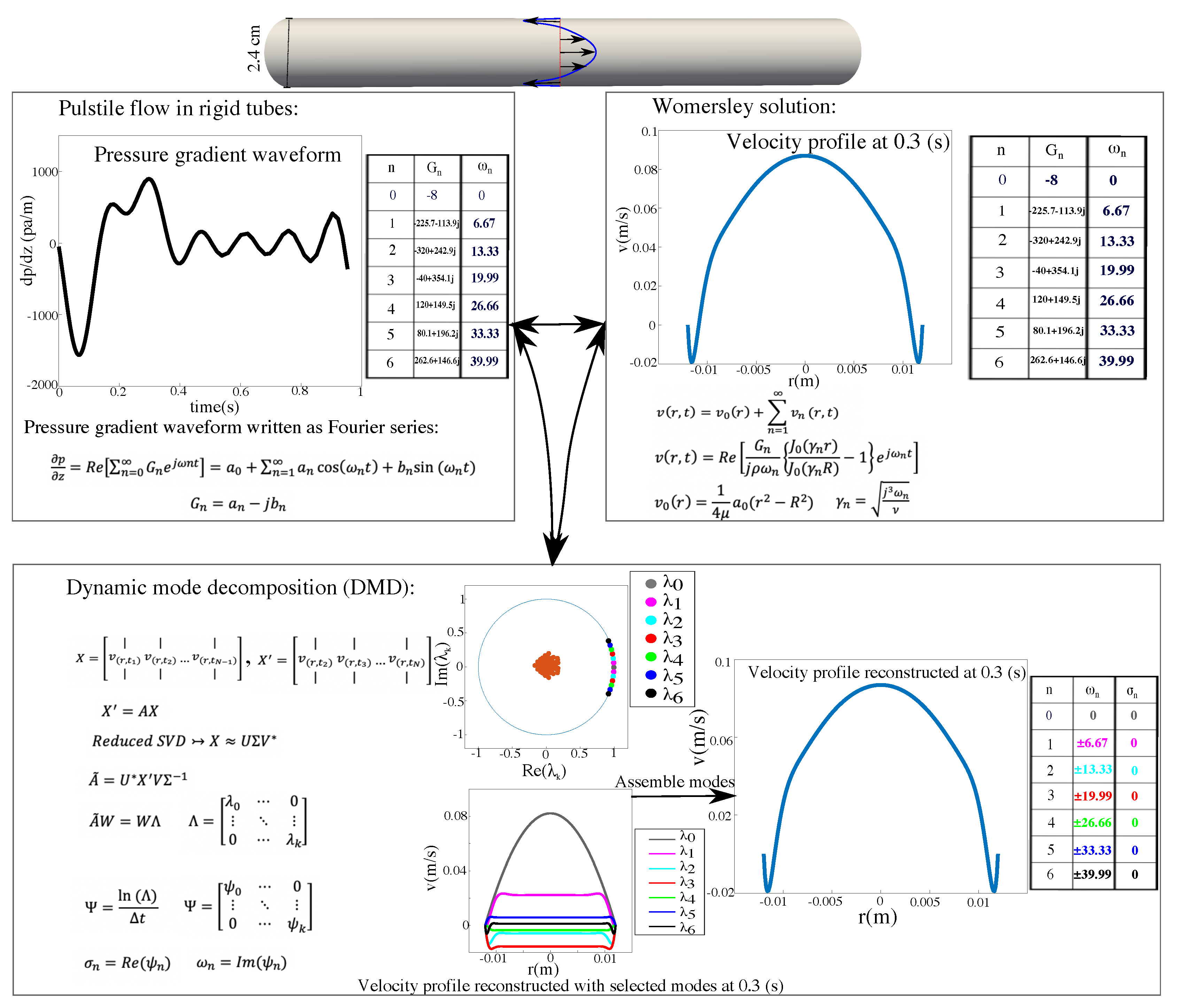
3.1. DMD and Womersley’s Analytical Solution
3.2. Data Reconstruction Accuracy
3.3. Flow Physics Using mDMDc
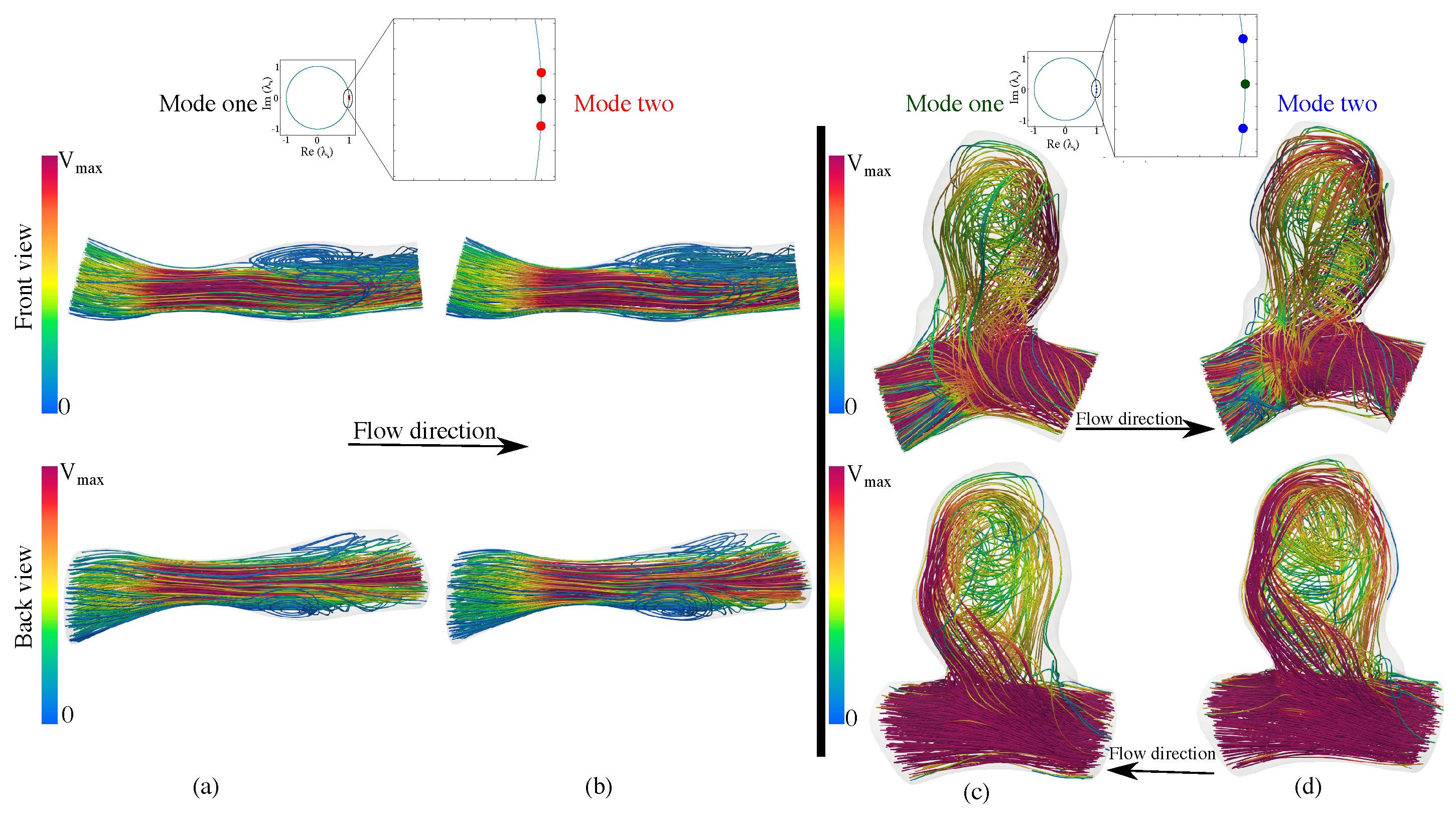
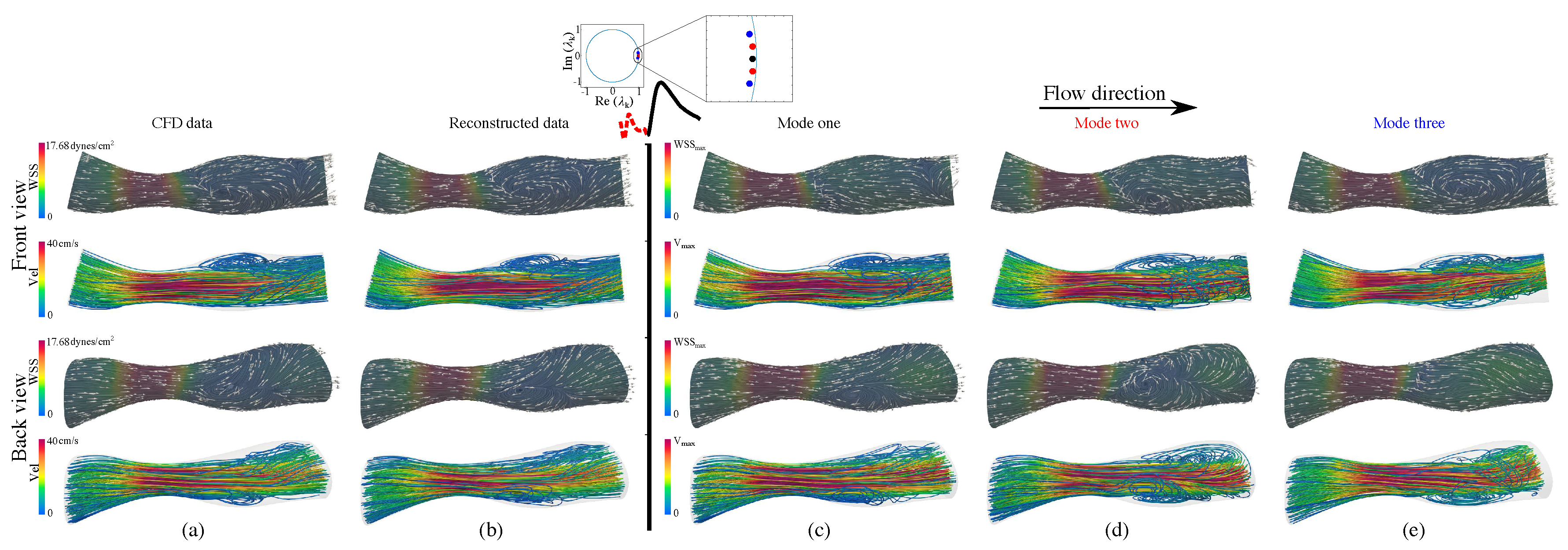
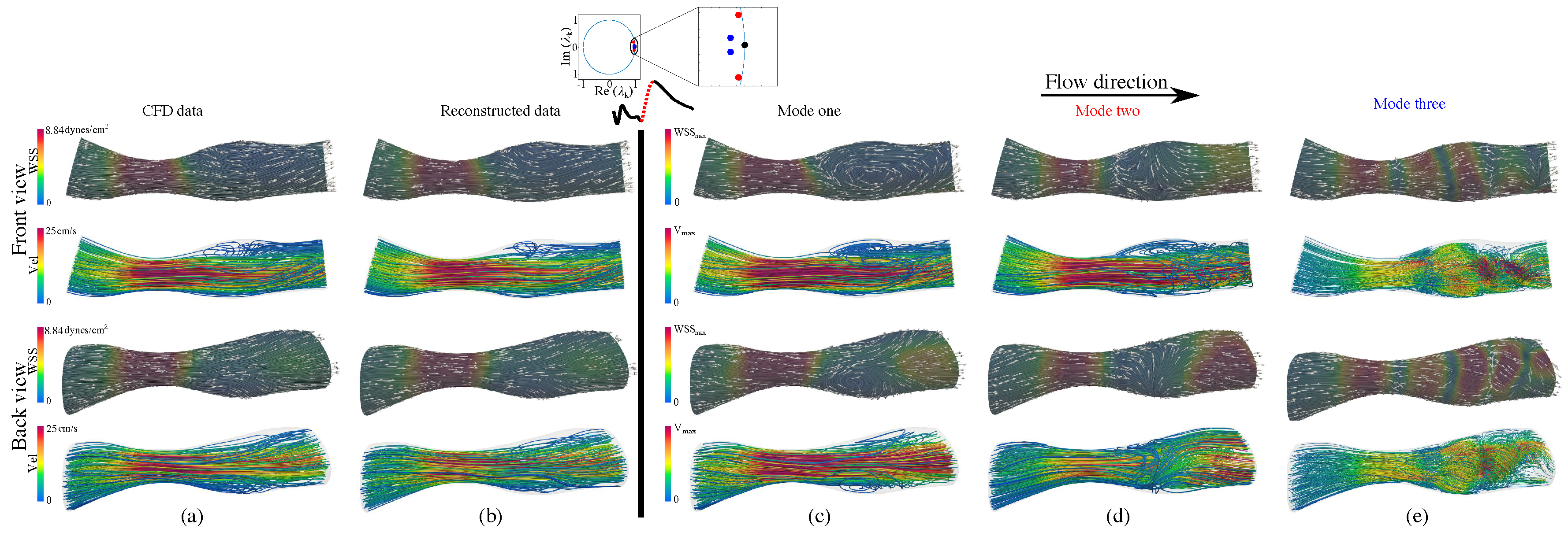
3.3.1. Flow Physics Using mDMDc Modes in Coronary Artery Stenosis
3.3.2. Flow Physics Using mDMDc Modes in Cerebral Aneurysm
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Taylor, C.A.; Figueroa, C.A. Patient-specific modeling of cardiovascular mechanics. Ann. Rev. Biomed. Eng. 2009, 11, 109–134. [Google Scholar] [CrossRef] [PubMed]
- Morris, P.D.; Narracott, A.; von Tengg-Kobligk, H.; Soto, D.A.S.; Hsiao, S.; Lungu, A.; Evans, P.; Bressloff, N.W.; Lawford, P.V.; Hose, D.R.; et al. Computational fluid dynamics modelling in cardiovascular medicine. Heart 2016, 102, 18–28. [Google Scholar] [CrossRef] [PubMed]
- Taylor, C.A.; Fonte, T.A.; Min, J.K. Computational fluid dynamics applied to cardiac computed tomography for noninvasive quantification of fractional flow reserve: Scientific basis. J. Am. Coll. Cardiol. 2013, 61, 2233–2241. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.O.; Valen-Sendstad, K.; Steinman, D.A. Narrowing the expertise gap for predicting intracranial aneurysm hemodynamics: Impact of solver numerics versus mesh and time-step resolution. Am. J. Neuroradiol. 2015, 36, 1310–1316. [Google Scholar] [CrossRef] [PubMed]
- Arzani, A. Accounting for residence-time in blood rheology models: Do we really need non-Newtonian blood flow modeling in large arteries? J. R. Soc. Interface 2018, 15, 20180486. [Google Scholar] [CrossRef] [PubMed]
- Taira, K.; Brunton, S.L.; Dawson, S.T.M.; Rowley, C.W.; Colonius, T.; McKeon, B.J.; Schmidt, O.T.; Gordeyev, S.; Theofilis, V.; Ukeiley, L.S. Modal analysis of fluid flows: An overview. AIAA J. 2017, 102, 4013–4041. [Google Scholar] [CrossRef]
- Brunton, S.L.; Noack, B.R.; Koumoutsakos, P. Machine learning for fluid mechanics. Ann. Rev. Fluid Mech. 2020, 52, 477–508. [Google Scholar] [CrossRef]
- Bamieh, B.; Giarre, L. Identification of linear parameter varying models. Int. J. Robust Nonlinear Control 2002, 12, 841–853. [Google Scholar] [CrossRef]
- Paoletti, S.; Juloski, A.; Ferrari-Trecate, G.; Vidal, R. Identification of hybrid systems: A tutorial. Eur. J. Control 2007, 13, 242–260. [Google Scholar] [CrossRef]
- Kutz, J.N.; Brunton, S.L.; Brunton, B.W.; Proctor, J.L. Dynamic Mode Decomposition: Data-Driven Modeling of Complex Systems; SIAM: Philadelphia, PA, USA, 2016. [Google Scholar]
- Mirramezani, M.; Diamond, S.L.; Litt, H.I.; Shadden, S.C. Reduced order models for transstenotic pressure drop in the coronary arteries. J. Biomech. Eng. 2019, 141, 031005. [Google Scholar] [CrossRef]
- Sankaran, S.; Lesage, D.; Tombropoulos, R.; Xiao, N.; Kim, H.J.; Spain, D.; Schaap, M.; Taylor, C.A. Physics driven reduced order model for real time blood flow simulations. arXiv 2019, arXiv:1911.01543. [Google Scholar]
- Berkooz, G.; Holmes, P.; Lumley, J.L. The proper orthogonal decomposition in the analysis of turbulent flows. Ann. Rev. Fluid Mech. 1993, 25, 539–575. [Google Scholar] [CrossRef]
- Holmes, P.; Lumley, J.L.; Berkooz, G.; Rowley, C.W. Turbulence, Coherent Structures, Dynamical Systems and Symmetry; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Glenn, A.L.; Bulusu, K.V.; Shu, F.; Plesniak, M.W. Secondary flow structures under stent-induced perturbations for cardiovascular flow in a curved artery model. Int. J. Heat Fluid Flow 2012, 35, 76–83. [Google Scholar] [CrossRef]
- Chang, G.H.; Schirmer, C.M.; Modarres-Sadeghi, Y. A reduced-order model for wall shear stress in abdominal aortic aneurysms by proper orthogonal decomposition. J. Biomech. 2017, 54, 33–43. [Google Scholar] [CrossRef]
- Grinberg, L.; Yakhot, A.; Karniadakis, G. Analyzing transient turbulence in a stenosed carotid artery by proper orthogonal decomposition. Ann. Biomed. Eng. 2009, 37, 2200–2217. [Google Scholar] [CrossRef] [PubMed]
- Kefayati, S.; Poepping, T.L. Transitional flow analysis in the carotid artery bifurcation by proper orthogonal decomposition and particle image velocimetry. Med. Eng. Phys. 2013, 35, 898–909. [Google Scholar] [CrossRef]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Schmid, P.J. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef]
- Noack, B.R. From snapshots to modal expansions–bridging low residuals and pure frequencies. J. Fluid Mech. 2016, 802, 1–4. [Google Scholar] [CrossRef]
- Rowley, C.W.; Mezić, I.; Bagheri, S.; Schlatter, P.; Henningson, D.S. Spectral analysis of nonlinear flows. J. Fluid Mech. 2009, 641, 115–127. [Google Scholar] [CrossRef]
- Mezić, I. Spectral properties of dynamical systems, model reduction and decompositions. Nonlinear Dyn. 2005, 41, 309–325. [Google Scholar] [CrossRef]
- Perko, L. Differential Equations and Dynamical Systems; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Wynn, A.; Pearson, D.; Ganapathisubramani, B.; Goulart, P. Optimal mode decomposition for unsteady flows. J. Fluid Mech. 2013, 733, 473–503. [Google Scholar] [CrossRef]
- Jovanović, M.; Schmid, P.; Nichols, J. Sparsity-promoting dynamic mode decomposition. Phys. Fluids 2014, 26, 024103. [Google Scholar] [CrossRef]
- Proctor, J.; Brunton, S.; Kutz, J. Dynamic mode decomposition with control. SIAM J. Appl. Dyn. Syst. 2016, 15, 142–161. [Google Scholar] [CrossRef]
- Kutz, J.N.; Fu, X.; Brunton, S. Multiresolution dynamic mode decomposition. SIAM J. Appl. Dyn. Syst. 2016, 15, 713–735. [Google Scholar] [CrossRef]
- Dawson, S.T.M.; Hemati, M.S.; Williams, M.O.; Rowley, C. Characterizing and correcting for the effect of sensor noise in the dynamic mode decomposition. Exp. Fluids 2016, 57, 42. [Google Scholar] [CrossRef]
- Annoni, J.; Seiler, P. A method to construct reduced-order parameter-varying models. Int. J. Robust Nonlinear Control 2017, 27, 582–597. [Google Scholar] [CrossRef]
- Kou, J.; Zhang, W. Dynamic mode decomposition with exogenous input for data-driven modeling of unsteady flows. Phys. Fluids 2019, 31, 057106. [Google Scholar]
- Lu, H.; Tartakovsky, D.M. Lagrangian Dynamic Mode Decomposition for Construction of Reduced-Order Models of Advection-Dominated Phenomena. J. Comput. Phys. 2020, 407, 109229. [Google Scholar] [CrossRef]
- Schmid, P.J.; Li, L.; Juniper, M.P.; Pust, O. Applications of the dynamic mode decomposition. Theor. Comput. Fluid Dyn. 2011, 25, 249–259. [Google Scholar] [CrossRef]
- Seena, A.; Sung, H.J. Dynamic mode decomposition of turbulent cavity flows for self-sustained oscillations. Int. J. Heat Fluid Flow 2011, 32, 1098–1110. [Google Scholar] [CrossRef]
- Dawson, S.T.M.; Schiavone, N.; Rowley, C.; Williams, D. A data-driven modeling framework for predicting forces and pressures on a rapidly pitching airfoil. In Proceedings of the 45th AIAA Fluid Dynamics Conference, Dallas, TX, USA, 22–26 June 2015; p. 2767. [Google Scholar]
- Le Clainche, S.; Han, Z.H.; Ferrer, E. An alternative method to study cross-flow instabilities based on high order dynamic mode decomposition. Phys. Fluids 2019, 31, 094101. [Google Scholar] [CrossRef]
- Alessandri, A.; Bagnerini, P.; Gaggero, M.; Lengani, D.; Simoni, D. Dynamic mode decomposition for the inspection of three-regime separated transitional boundary layers using a least squares method. Phys. Fluids 2019, 31, 044103. [Google Scholar] [CrossRef]
- Pain, R.; Weiss, P.E.; Deck, S.; Robinet, J.C. Large scale dynamics of a high Reynolds number axisymmetric separating/reattaching flow. Phys. Fluids 2019, 31, 125119. [Google Scholar] [CrossRef]
- Delorme, Y.; Kerlo, A.; Anupindi, K.; Rodefeld, M.; Frankel, S. Dynamic mode decomposition of Fontan hemodynamics in an idealized total cavopulmonary connection. Fluid Dyn. Res. 2014, 46, 041425. [Google Scholar] [CrossRef] [PubMed]
- Di Labbio, G.; Kadem, L. Reduced-order modeling of left ventricular flow subject to aortic valve regurgitation. Phys. Fluids 2019, 31, 031901. [Google Scholar] [CrossRef]
- Arzani, A.; Shadden, S.C. Characterization of the transport topology in patient-specific abdominal aortic aneurysm models. Phys. Fluids 2012, 24, 081901. [Google Scholar] [CrossRef] [PubMed]
- Womersley, J.R. Method for the calculation of velocity, rate of flow and viscous drag in arteries when the pressure gradient is known. J. Physiol. 1955, 127, 553–563. [Google Scholar] [CrossRef]
- Mortensen, M.; Valen-Sendstad, K. Oasis: A high-level/high-performance open source Navier–Stokes solver. Comp. Phys. Commun. 2015, 188, 177–188. [Google Scholar] [CrossRef]
- Valen-Sendstad, K.; Steinman, D.A. Mind the gap: Impact of computational fluid dynamics solution strategy on prediction of intracranial aneurysm hemodynamics and rupture status indicators. Am. J. Neuroradiol. 2014, 35, 536–543. [Google Scholar] [CrossRef]
- Updegrove, A.; Wilson, N.; Merkow, J.; Lan, H.; Marsden, A.; Shadden, S. SimVascular: An open source pipeline for cardiovascular simulation. Ann. Biomed. Eng. 2017, 45, 525–541. [Google Scholar] [CrossRef]
- Hoi, Y.; Wasserman, B.; Xie, Y.; Najjar, S.; Ferruci, L.; Lakatta, E.; Gerstenblith, G.; Steinman, D. Characterization of volumetric flow rate waveforms at the carotid bifurcations of older adults. Physiol. Meas. 2010, 31, 291. [Google Scholar] [CrossRef] [PubMed]
- Valen-Sendstad, K.; Piccinelli, M.; KrishnankuttyRema, R.; Steinman, D. Estimation of inlet flow rates for image-based aneurysm CFD models: Where and how to begin? Ann. Biomed. Eng. 2015, 43, 1422–1431. [Google Scholar] [CrossRef] [PubMed]
- Arzani, A. Coronary artery plaque growth: A two-way coupled shear stress–driven model. Int. J. Numer. Methods Biomed. Eng. 2020, 36, e3293. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Vignon-Clementel, I.; Coogan, J.; Figueroa, C.A.; Jansen, K.; Taylor, C.A. Patient-specific modeling of blood flow and pressure in human coronary arteries. Ann. Biomed. Eng. 2010, 38, 3195–3209. [Google Scholar] [CrossRef]
- Tu, J.H.; Rowley, C.W.; Luchtenburg, D.M.; Brunton, S.L.; Kutz, J.N. On dynamic mode decomposition: Theory and applications. J. Comput. Dyn. 2014, 1, 391–421. [Google Scholar] [CrossRef]
- Xiao, N.; Alastruey, J.; Figueroa, C.A. A systematic comparison between 1-D and 3-D hemodynamics in compliant arterial models. Int. J. Numer. Methods Biomed. Eng. 2014, 30, 204–231. [Google Scholar] [CrossRef]
- Arzani, A.; Shadden, S.C. Wall shear stress fixed points in cardiovascular fluid mechanics. J. Biomech. 2018, 73, 145–152. [Google Scholar] [CrossRef]
- Chen, K.K.; Tu, J.H.; Rowley, C.W. Variants of dynamic mode decomposition: Boundary condition, Koopman, and Fourier analyses. J. Nonlinear Sci. 2012, 22, 887–915. [Google Scholar] [CrossRef]
- Shadden, S.C.; Lekien, F.; Marsden, J.E. Definition and properties of Lagrangian coherent structures from finite-time Lyapunov exponents in two-dimensional aperiodic flows. Phys. D Nonlinear Phenom. 2005, 212, 271–304. [Google Scholar] [CrossRef]
- Haller, G. Lagrangian coherent structures. Ann. Rev. Fluid Mech. 2015, 47, 137–162. [Google Scholar] [CrossRef]
- Arzani, A.; Gambaruto, A.M.; Chen, G.; Shadden, S.C. Lagrangian wall shear stress structures and near-wall transport in high-Schmidt-number aneurysmal flows. J. Fluid Mech. 2016, 790, 158–172. [Google Scholar] [CrossRef]
- Valen-Sendstad, K.; Mardal, K.A.; Steinman, D.A. High-resolution CFD detects high-frequency velocity fluctuations in bifurcation, but not sidewall, aneurysms. J. Biomech. 2013, 46, 402–407. [Google Scholar] [CrossRef] [PubMed]
- Sieber, M.; Paschereit, C.O.; Oberleithner, K. Spectral proper orthogonal decomposition. J. Fluid Mech. 2016, 792, 798–828. [Google Scholar] [CrossRef]
- Ghate, A.S.; Towne, A.; Lele, S.K. Broadband reconstruction of inhomogeneous turbulence using spectral proper orthogonal decomposition and Gabor modes. J. Fluid Mech. 2020, 888, 1–13. [Google Scholar] [CrossRef]
- Scherl, I.; Strom, B.; Shang, J.K.; Williams, O.; Polagye, B.L.; Brunton, S.L. Robust Principal Component Analysis for Modal Decomposition of Corrupt Fluid Flows. arXiv 2019, arXiv:1905.07062. [Google Scholar] [CrossRef]
- Williams, M.; Kevrekidis, I.; Rowley, C. A data–driven approximation of the Koopman operator: Extending dynamic mode decomposition. J. Nonlinear Sci. 2015, 25, 1307–1346. [Google Scholar] [CrossRef]


| Accuracy | 90% | 95% | 98% | 99% | 99.5% | (cm/s) | |
|---|---|---|---|---|---|---|---|
| Stage Number | |||||||
| 1st stage | 8 | 13 | 14 | 23 | 30 | 4.5 | |
| 2nd stage | 4 | 4 | 5 | 7 | 10 | 7.6 | |
| 3rd stage | 2 | 2 | 3 | 3 | 8 | 7.8 | |
| Accuracy | 90% | 95% | 98% | 99% | 99.5% | (dynes/cm2) | |
|---|---|---|---|---|---|---|---|
| Stage Number | |||||||
| 1st stage | 10 | 13 | 23 | 32 | 41 | 1.5 | |
| 2nd stage | 4 | 5 | 6 | 8 | 18 | 3.0 | |
| 3rd stage | 2 | 2 | 3 | 4 | 10 | 3.1 | |
| Accuracy | 90% | 95% | 98% | 99% | 99.5% | (cm/s) | |
|---|---|---|---|---|---|---|---|
| Stage Number | |||||||
| 1st stage | 3 | 3 | 4 | 5 | 12 | 7.1 | |
| 2nd stage | 2 | 2 | 3 | 5 | 6 | 17.8 | |
| 3rd stage | 5 | 5 | 7 | 13 | 22 | 22.1 | |
| 4th stage | 3 | 3 | 4 | 9 | 20 | 19.2 | |
| 5th stage | 3 | 6 | 6 | 10 | 18 | 14.1 | |
| 6th stage | 5 | 5 | 13 | 31 | 48 | 8.4 | |
| Accuracy | 90% | 95% | 98% | 99% | 99.5% | (dynes/cm2) | |
|---|---|---|---|---|---|---|---|
| Stage Number | |||||||
| 1st stage | 3 | 3 | 4 | 5 | 19 | 23.6 | |
| 2nd stage | 2 | 2 | 3 | 5 | 6 | 78.5 | |
| 3rd stage | 5 | 10 | 10 | 13 | 25 | 105.6 | |
| 4th stage | 7 | 7 | 7 | 9 | 20 | 86.9 | |
| 5th stage | 3 | 3 | 4 | 9 | 17 | 56.6 | |
| 6th stage | 5 | 13 | 13 | 31 | 53 | 3.6 | |
| Accuracy | 90% | 95% | 98% | 99% | 99.5% | (cm/s) |
|---|---|---|---|---|---|---|
| Coronary artery stenosis | 27 | 41 | 53 | 77 | 88 | 6.7 |
| Cerebral aneurysm | 96 | 110 | 155 | 165 | 173 | 12.1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Habibi, M.; Dawson, S.T.M.; Arzani, A. Data-Driven Pulsatile Blood Flow Physics with Dynamic Mode Decomposition. Fluids 2020, 5, 111. https://doi.org/10.3390/fluids5030111
Habibi M, Dawson STM, Arzani A. Data-Driven Pulsatile Blood Flow Physics with Dynamic Mode Decomposition. Fluids. 2020; 5(3):111. https://doi.org/10.3390/fluids5030111
Chicago/Turabian StyleHabibi, Milad, Scott T. M. Dawson, and Amirhossein Arzani. 2020. "Data-Driven Pulsatile Blood Flow Physics with Dynamic Mode Decomposition" Fluids 5, no. 3: 111. https://doi.org/10.3390/fluids5030111
APA StyleHabibi, M., Dawson, S. T. M., & Arzani, A. (2020). Data-Driven Pulsatile Blood Flow Physics with Dynamic Mode Decomposition. Fluids, 5(3), 111. https://doi.org/10.3390/fluids5030111





