Three-Dimensional Convective Planforms for Inclined Darcy-Bénard Convection
Abstract
1. Introduction
2. Governing Equations and Stability Analysis
3. Results and Discussion
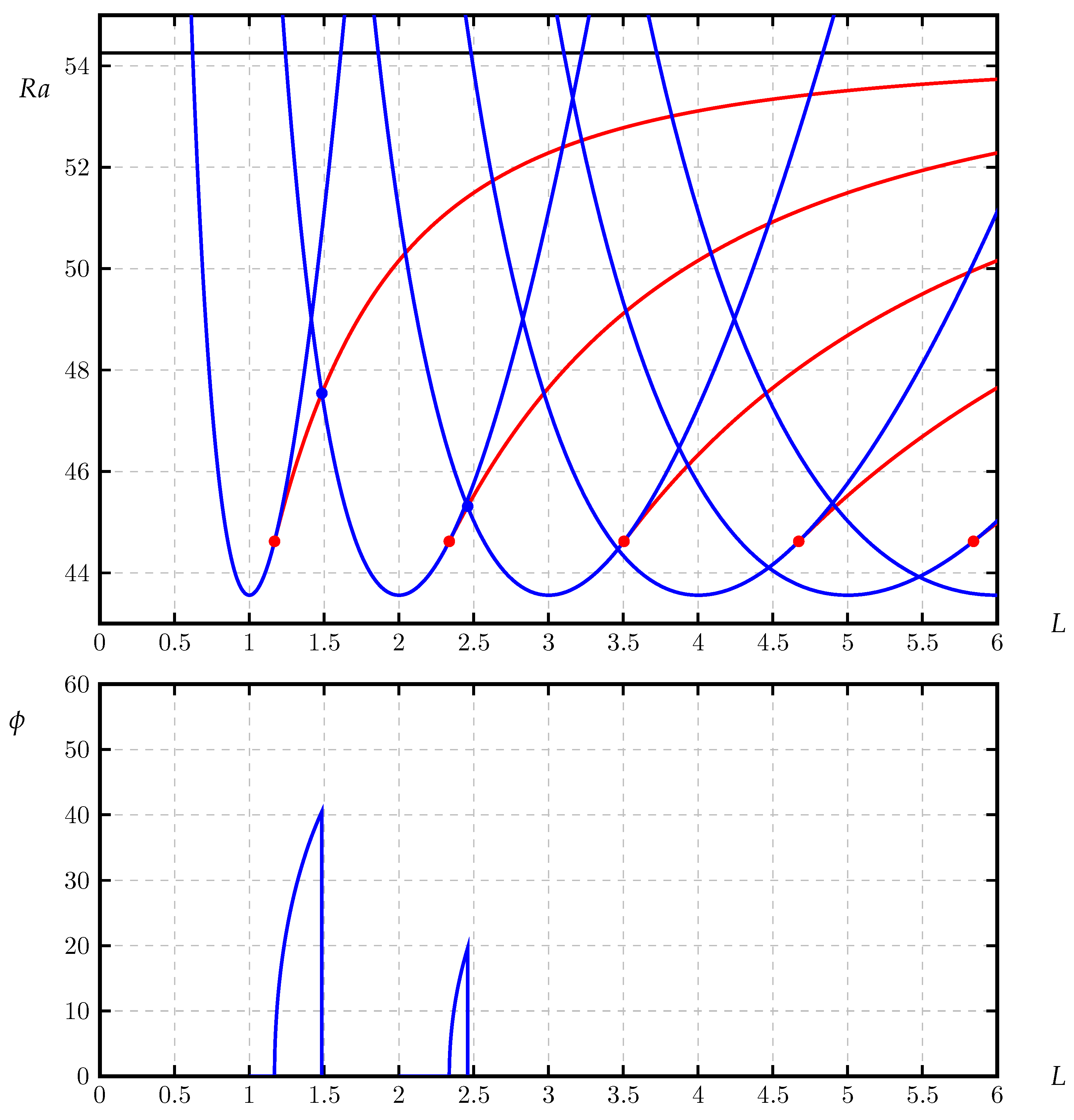
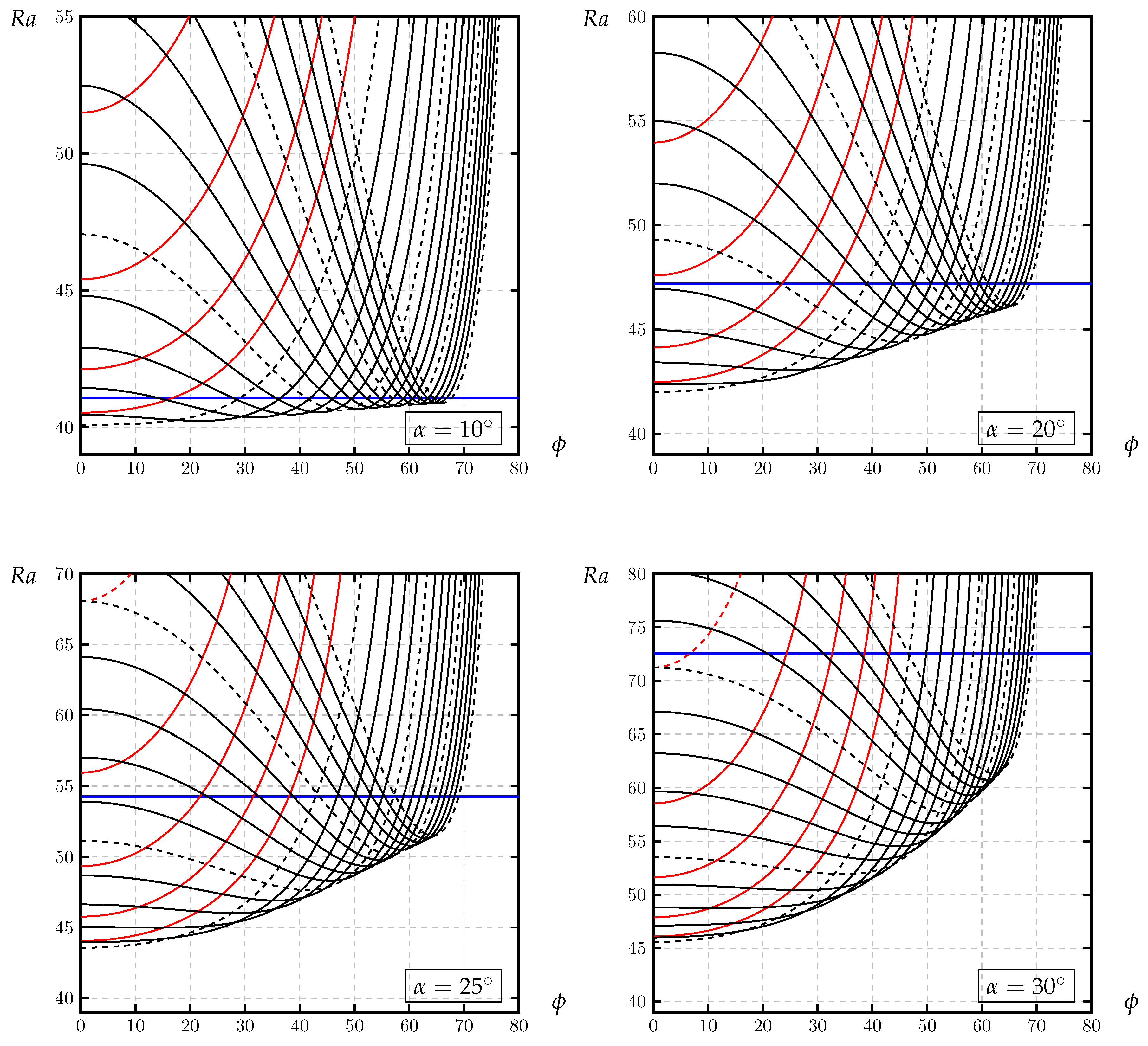
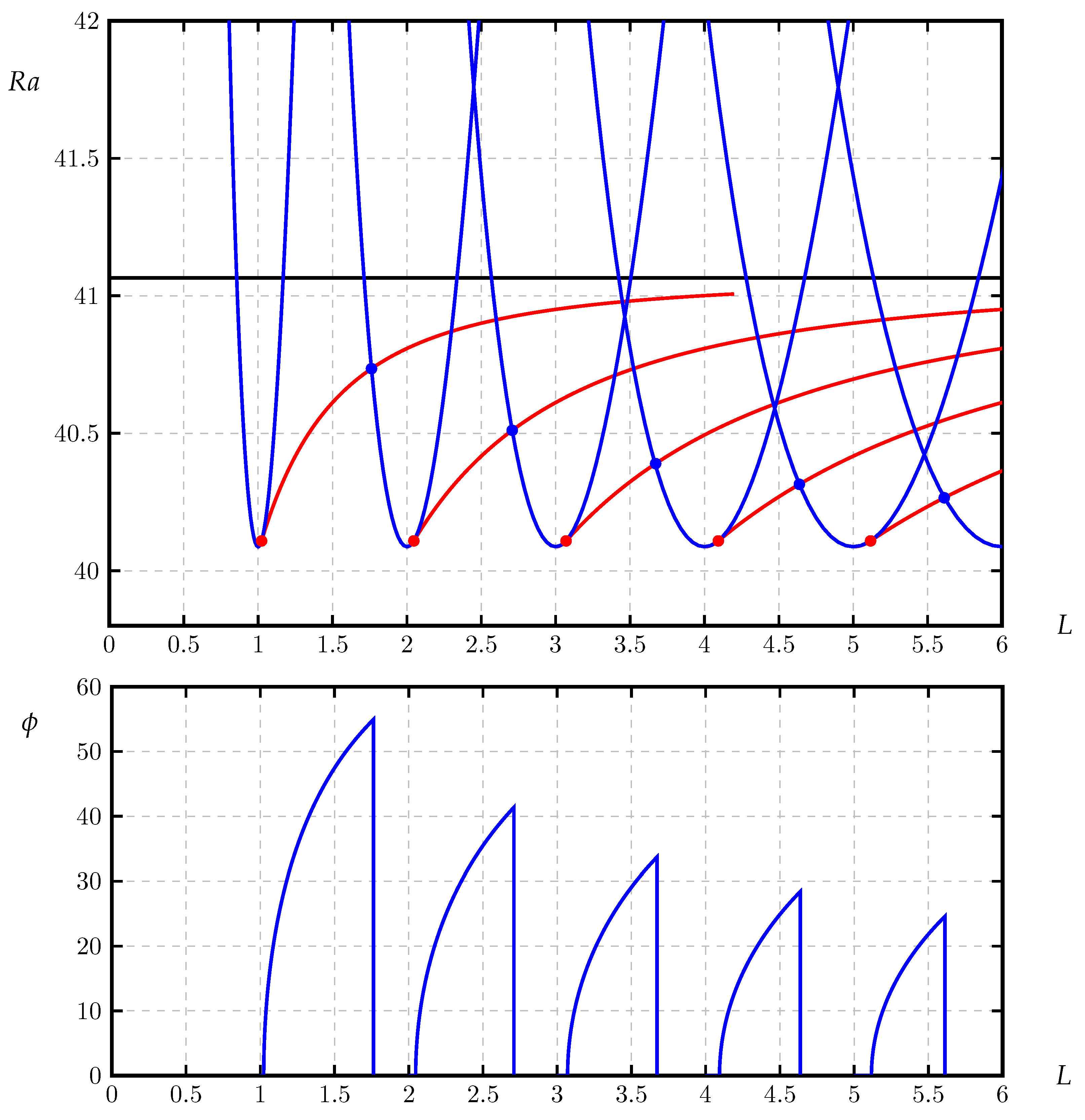
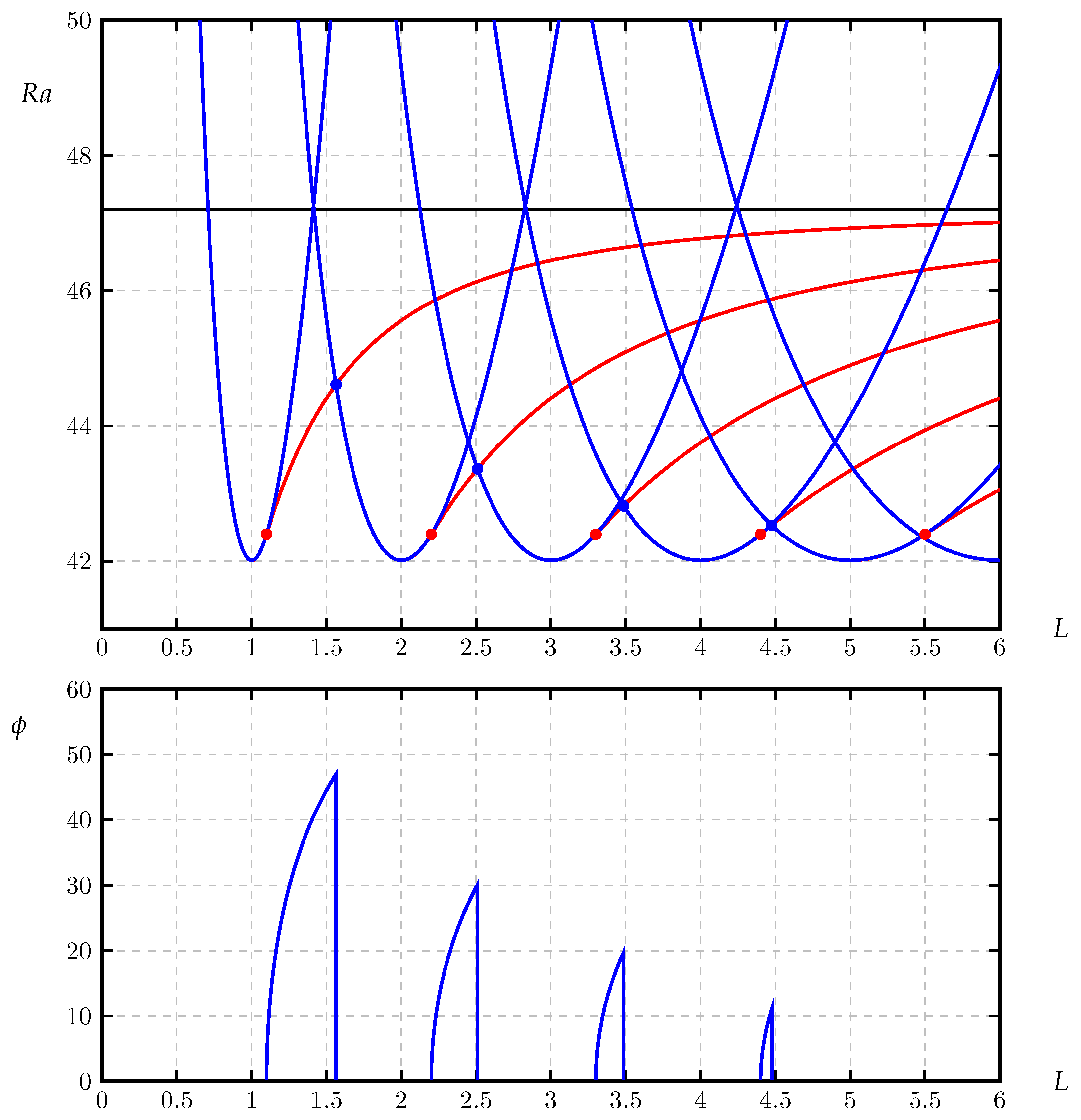
3.1. Sample Neutral Curves
3.2. The Modal Map
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Latin letters | |
| imaginary constant | |
| particular integral coefficients for | |
| complementary function coefficient | |
| particular integral coefficients for | |
| d | height of the channel |
| reduced pressure and temperature | |
| g | gravity |
| k | wave number |
| K | permeability |
| L | channel aspect ratio |
| differential operators in Equation (A41) | |
| m | wave number |
| n | number of rolls |
| N | number of intervals |
| p | pressure |
| Darcy-Rayleigh number | |
| right hand sides in Equation (A41) | |
| t | time |
| u | Darcy velocity along the layer |
| v | Darcy velocity across the layer |
| w | spanwise Darcy velocity |
| x | coordinate along the layer |
| y | coordinate across the layer |
| z | spanwise coordinate |
| Greek letters | |
| inclination angle | |
| coefficient of cubical expansion | |
| temperature difference | |
| temperature | |
| thermal diffusivity | |
| exponential growth rate | |
| dynamic viscosity | |
| reference density | |
| orientation of oblique roll | |
| Other symbols | |
| terms in series expansion | |
| i | imaginary component |
| r | real component |
| differentiation with respect to y |
Appendix A
References
- Nield, D.A.; Bejan, A. Convection in Porous Media, 5th ed.; Springer: New York, NY, USA, 2017. [Google Scholar]
- Bories, S.A.; Combarnous, M.A. Natural convection in a sloping porous layer. J. Fluid Mech. 1973, 57, 63–79. [Google Scholar] [CrossRef]
- Weber, J.E. Thermal convection in a tilted porous layer. Int. J. Heat Mass Transf. 1975, 18, 474–475. [Google Scholar] [CrossRef]
- Gill, A.E. A proof that convection in a porous vertical slab is stable. J. Fluid Mech. 1939, 35, 545–547. [Google Scholar] [CrossRef]
- Lewis, S.; Bassom, A.P.; Rees, D.A.S. The stability of vertical thermal boundary layer flow in a porous medium. Eur. J. Mech. B Fluids 1995, 14, 395–408. [Google Scholar]
- Straughan, B. A nonlinear analysis of convection in a porous vertical slab. Geophys. Astrophys. Fluid Dyn. 1988, 42, 269–275. [Google Scholar] [CrossRef]
- Rees, D.A.S.; Bassom, A.P. Onset of Darcy-Bénard convection in an inclined porous layer heated from below. Acta Mech. 2000, 144, 103–118. [Google Scholar] [CrossRef]
- Postelnicu, A.; Rees, D.A.S. The onset of convection in an anisotropic porous layer inclined at a small angle from the horizontal. Int. Commun. Heat Mass Transf. 2001, 28, 641–650. [Google Scholar] [CrossRef]
- Rees, D.A.S.; Postelnicu, A. The onset of convection in an inclined anisotropic porous layer. Int. J. Heat Mass Transf. 2001, 44, 4127–4138. [Google Scholar] [CrossRef]
- Rees, D.A.S.; Postelnicu, A.; Storesletten, L. The onset of Darcy-Forchheimer convection in inclined porous layers heated from below. Transp. Porous Media 2006, 64, 15–23. [Google Scholar] [CrossRef]
- Rees, D.A.S.; Storesletten, L.; Postelnicu, A. The onset of convection in an inclined anisotropic porous layer with oblique principle axes. Transp. Porous Media 2006, 62, 139–156. [Google Scholar] [CrossRef]
- Barletta, A.; Rees, D.A.S. Local thermal non-equilibrium analysis of the thermoconvective instability in an inclined porous layer. Int. J. Heat Mass Transf. 2015, 83, 327–336. [Google Scholar] [CrossRef]
- Barletta, A.; Storesletten, L. Thermoconvective instabilities in an inclined porous channel heated from below. Int. J. Heat Mass Transf. 2011, 54, 2724–2733. [Google Scholar] [CrossRef]
- Rees, D.A.S.; Barletta, A. Linear instability of the isoflux Darcy-Bénard problem in an inclined porous layer. Transp. Porous Media 2011, 87, 665–678. [Google Scholar] [CrossRef]
- Barletta, A.; Rees, D.A.S. Linear instability of the Darcy-Hadley flow in an inclined porous layer. Phys. Fluids 2012, 24, 074104. [Google Scholar] [CrossRef]
- Barletta, A.; Celli, M. The Horton-Rogers-Lapwood problem for an inclined porous layer with permeable boundaries. Proc. Royal Soc. A 2018, 474, 20180021. [Google Scholar] [CrossRef] [PubMed]
- Celli, M.; Barletta, A. Onset of buoyancy driven convection in an inclined porous layer with an isobaric boundary. Int. J. Heat Mass Transf. 2019, 132, 782–788. [Google Scholar] [CrossRef]
- Rees, D.A.S.; Bassom, A.P. The inclined Wooding problem. Transp. Porous Media 2018, 125, 465–482. [Google Scholar] [CrossRef]
- Wen, B.; Chini, G.P. On Moderate-Rayleigh-number convection in an inclined porous layer. Fluids 2019, 4, 101. [Google Scholar] [CrossRef]
- Riley, D.S.; Winters, K.H. A numerical bifurcation study of natural convection in a tilted two-dimensional porous cavity. J. Fluid Mech. 1990, 215, 309–329. [Google Scholar] [CrossRef]
- Beck, J.L. Convection in a box of porous material saturated with fluid. Phys. Fluids 1972, 15, 1377–1383. [Google Scholar] [CrossRef]
- Guerrero-Martínez, F.J.; Karimi, N.; Ramos, E. Numerical modelling of multiple steady-state convective modes in a tilted porous medium heated from below. Int. Commun. Heat Mass Transf. 2018, 92, 64–72. [Google Scholar] [CrossRef]


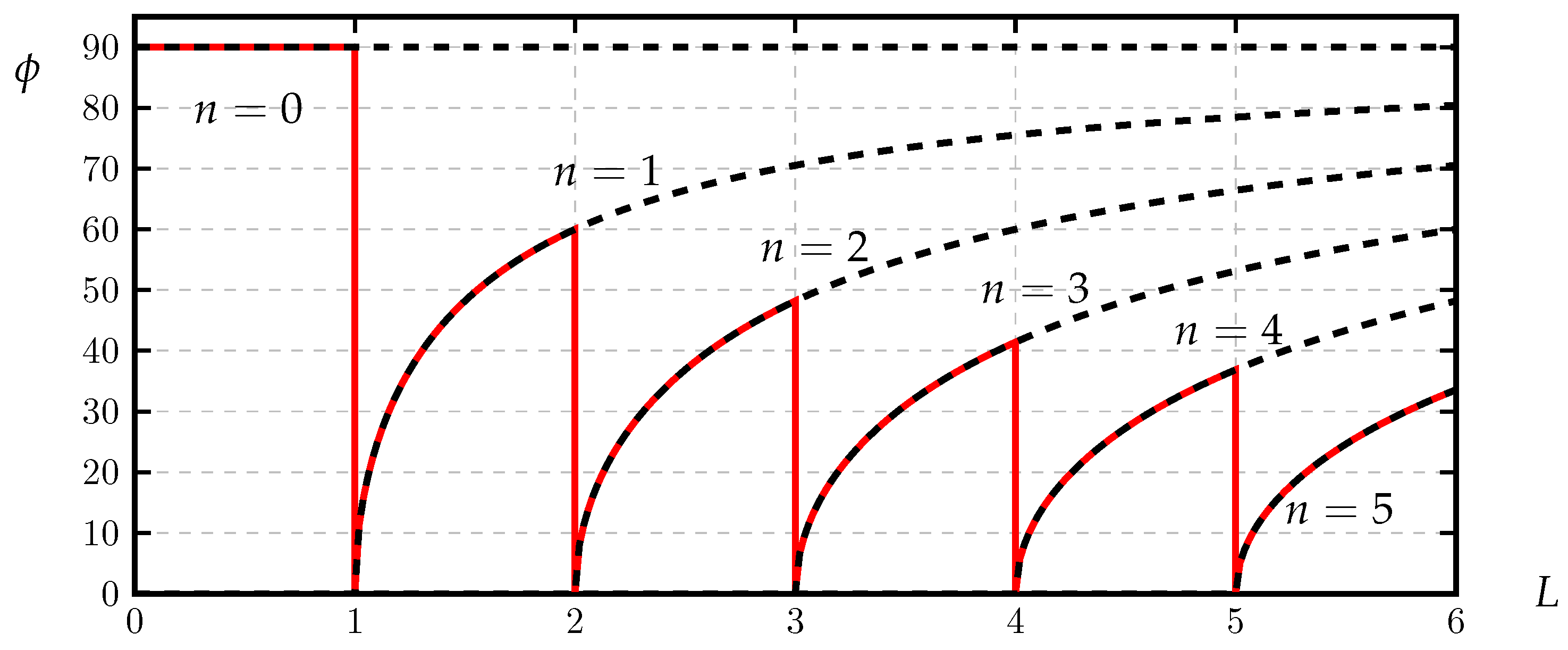
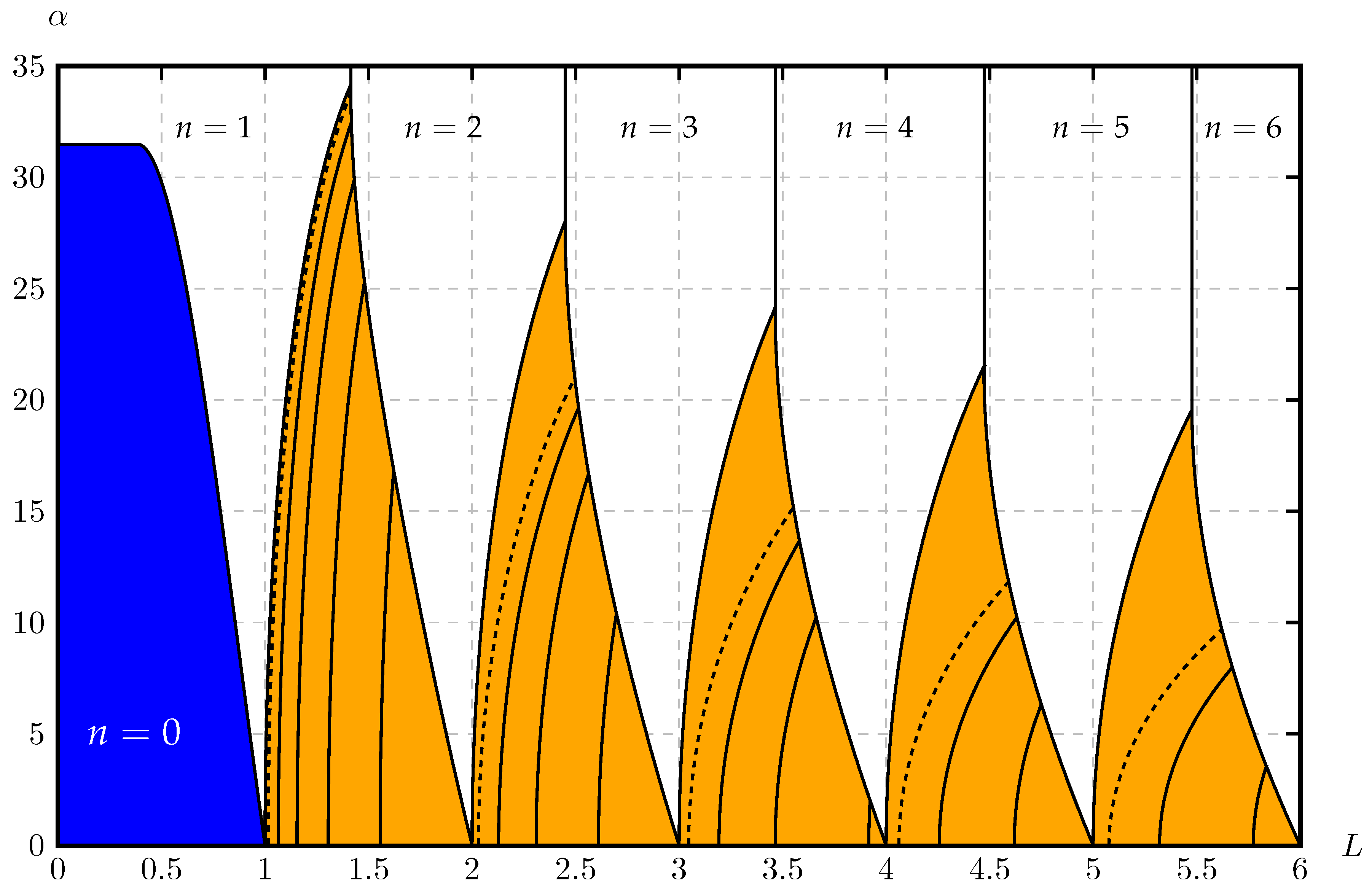
| N | Error | Error | ||
| 25 | 0.000 163 16 | 45.024 341 41 | 0.000 201 46 | |
| 50 | 0.000 010 24 | 45.024 152 58 | 0.000 012 63 | |
| 100 | 0.000 000 65 | 45.024 140 74 | 0.000 000 79 | |
| 200 | 0.000 000 04 | 45.024 140 00 | 0.000 000 05 | |
| 400 | 0.000 000 00 | 45.024 139 95 | 0.000 000 00 | |
| 800 | 0.000 000 00 | 45.024 139 95 | 0.000 000 00 | |
| n | (Degrees) | |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 10 | ||
| 20 | ||
| 50 | ||
| 100 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rees, D.A.S.; Barletta, A. Three-Dimensional Convective Planforms for Inclined Darcy-Bénard Convection. Fluids 2020, 5, 83. https://doi.org/10.3390/fluids5020083
Rees DAS, Barletta A. Three-Dimensional Convective Planforms for Inclined Darcy-Bénard Convection. Fluids. 2020; 5(2):83. https://doi.org/10.3390/fluids5020083
Chicago/Turabian StyleRees, D. Andrew S., and Antonio Barletta. 2020. "Three-Dimensional Convective Planforms for Inclined Darcy-Bénard Convection" Fluids 5, no. 2: 83. https://doi.org/10.3390/fluids5020083
APA StyleRees, D. A. S., & Barletta, A. (2020). Three-Dimensional Convective Planforms for Inclined Darcy-Bénard Convection. Fluids, 5(2), 83. https://doi.org/10.3390/fluids5020083